1. Introduction
1.1. Standard CDM Model
The standard
CDM cosmological model has enjoyed remarkable success over the past two decades, providing a consistent framework that explains a vast array of observations, from the temperature anisotropies of the cosmic microwave background (CMB) to the large-scale distribution of galaxies [
1,
2]. Based on a spatially flat universe dominated by cold dark matter (CDM) and a cosmological constant
[
3,
4,
5,
6], the
CDM model is specified by six parameters, which have been constrained with sub-percent precision by the Planck satellite mission [
1]. On the other hand, the cosmological constant itself presents one of the most profound theoretical challenges in physics today, known by its components as the cosmological constant problem (CCP) and the density coincidence problem (DCP), respectively [
7,
8]:
- (1)
CCP: Quantum field theory predicts a vacuum energy density vastly greater than the observed value by more than 120 orders of magnitude [
9,
10].
- (2)
DCP: The effective density corresponding to
and the density of matter are comparable at the present epoch, requiring highly contrived initial conditions to reach this universal state [
11,
12].
These fundamental puzzles motivate a search for cosmological mechanisms that can drive the late-time acceleration of the universe without relying on extreme fine-tuning assumptions.
1.2. Major Cosmological Tensions
As observational precision has improved over the years, some statistically significant cracks have appeared in the
CDM foundation. In particular, two major discrepancies have persisted and intensified, suggesting the presence of systematic errors in diverse observational datasets and the need for more physics unaccounted for in
CDM—or, alternatively, the necessity to modify gravity at large scales by including exotic new physics and more dark, undetected fields in cosmological theories [
13,
14,
15].
The first and most prominent discrepancy is the “Hubble tension,” concerning the value of the current expansion rate
. Estimates of
inferred from early-universe physics (CMB) assuming
CDM consistently yield lower values of
km s
−1 Mpc
−1 [
1]. In stark contrast, local late-universe measurements using the cosmic distance ladder (CDL) consistently favor a higher value of
km s
−1 Mpc
−1 [
15,
16,
17]. The statistical significance of this discrepancy has reached the
level, rendering it impossible to dismiss as a mere statistical fluctuation [
16].
The second major discrepancy is the “
tension,” which involves the clumpiness of baryonic matter observed in the late universe. The parameter
quantifies the amplitude of density fluctuations. Predictions based on Planck CMB data project a relatively high degree of clustering (
) [
1]. Conversely, direct measurements of late-time large-scale structure (LSS) from weak gravitational lensing and galaxy clustering surveys, such as the Kilo-Degree Survey (KiDS) [
18] and the Dark Energy Survey (DES) [
19], consistently measure a lower amplitude (
–0.78). The growth history of the LSS provides a powerful test of the background evolution [
20]. While the statistical significance of this tension (∼2–3
) is lower than that of
, its persistence across independent low-redshift probes suggests a genuine physical anomaly: our universe is smoother than what
CDM predicts.
1.3. A Remarkable Coincidence and a New Path Forward
In this work, we highlight first a striking coincidence that has largely gone unnoticed: the relative difference of the two major tensions is virtually identical:
- (a)
The relative discrepancy in
[
1,
15,
16] is
- (b)
The relative discrepancy in
[
1,
15,
18] is
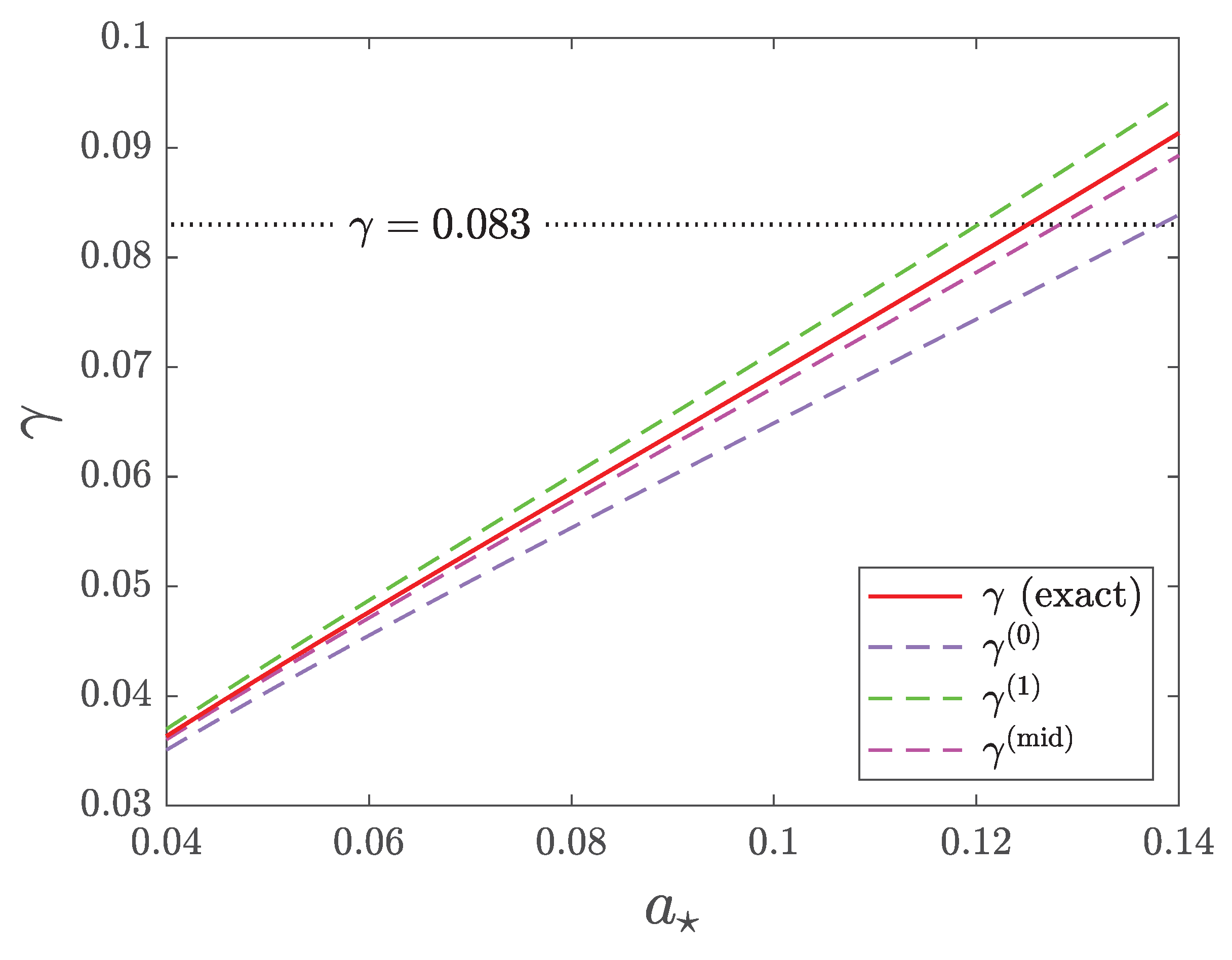
We argue that this concordance in relative discrepancies is not coincidental. Rather, it points toward a single underlying physical mechanism responsible for both cosmological tensions. The missing physics ought to be capable of simultaneously (i) suppressing the predicted LSS growth rates by about 8.3%, and (ii) resolving the 8.3% overestimate of that currently appears in the local CDL measurements.
While numerous extensions to
CDM have been proposed—ranging from early dark energy [
21] to modified gravity theories [
22] and models involving coupled dark sectors [
23]—these solutions typically introduce complex exotic fields with multiple free parameters, a generally undesirable trade-off. Furthermore, such fields often struggle to resolve both tensions simultaneously; mechanisms that alleviate the
tension frequently exacerbate the
tension [
24,
25]. For these reasons, we choose to improve
CDM without invoking new exotic physics.
To this end, we revisit the standard model, searching for minimal adjustments that could simultaneously account for both of the above
tensions, and we consider linear density perturbations within this framework [
10,
26]. Standard treatments typically assume a perfect cosmic fluid of collisionless dust, in which perturbations grow by gravitational instability [
27], while gravitational attraction is counteracted to a degree by the Hubble flow. The fluid peculiar velocities affecting the linear density perturbations have traditionally been neglected in the linearized Euler equation (as a nonlinear effect [
28,
29]), even in the low-redshift universe when the cosmic deceleration has significantly diminished. But peculiar velocities are also the source of noise and uncertainty that complicate the determination of recession velocities in the local CDL measurements [
30]. Thus, if tidal interactions from exterior nonlinear structures introduce radial velocities into the linear regime at late times [
28], the resulting drag forces could systematically distort our interpretations of both key local rates, the background expansion rate
and the LSS growth rate
.
Based on the above reasoning, we test a modification of the linear perturbation equation in the sub-horizon limit of the conformal Newtonian gauge by introducing a first-order drag force proportional to the amplitude of the peculiar velocity itself. This drag acts as an additional friction that suppresses somewhat the growth of structure. In this paper, we demonstrate that a drag amplitude
of
at low redshifts, along with the Hubble friction
, is sufficient to suppress the LSS growth rate and resolve the
tension. Furthermore, we argue that the same mechanism may account for the apparent excess in the locally measured
values, thereby offering a unified “
CDM” resolution of the two major tensions in modern
CDM cosmology and other identified discrepancies [
15].
1.4. Outline
The remainder of the paper is organized as follows:
In
Section 2, we introduce an additional drag term to the Euler equation and perform the linear perturbation analysis in the conformal Newtonian gauge within the FLRW background.
In
Section 3, we determine typical values of
in our modified
CDM framework and we examine whether the
tension can be resolved by accounting for the added time-dependent friction (
% of
) induced by drag forces due to an exterior tidal field (statistically isotropized, but with a nonzero mean value).
In
Section 4, we examine how this kinematic enhancement of the Hubble expansion modifies the background dynamics of the standard
CDM model to linear order in
.
In
Section 5, we develop a simplified 1-D radial line-of-sight model and estimate the
net tidal acceleration acting on a target galaxy, as well as the implied magnitude of
.
In
Appendix A, we show that the modifications introduced to the kinematics and the dynamics of the Hubble flow are consistent with one another.
2. Linear Perturbations with a Time-Dependent Drag Force
We formulate the linear scalar perturbation equations for a FLRW universe with dust, a cosmological constant, and a time-dependent drag force due to a peculiar velocity field. The analysis is performed in comoving spatial coordinates and cosmic time t. The background dynamics follows the standard spatially flat CDM model, while the perturbations obey modified Euler dynamics due to the additional friction term.
2.1. Initial Assumptions and Kinematic Framework
We consider a spatially flat FLRW spacetime with line element
where
is the scale factor and
c is the speed of light in vacuum. The background expansion rate is given by the Hubble function
The matter sector is assumed to be a pressureless perfect fluid (dust) with background density
satisfying the continuity equation
The background evolution of
, and
is governed by the usual Friedmann equations (FEs) with a cosmological constant
and a gravitational constant
G, viz.
Combining the FEs and using the identity
, we obtain the Raychaudhuri–Landau equation for
[
31], viz.
This equation relates the cosmic acceleration with the Hubble expansion rate H and the cosmological constant .
2.2. Linearized Perturbation Equations
2.2.1. Preliminaries
In the FLRW background, we introduce small perturbations to linear order. The density field is decomposed as
where
is the density contrast in comoving coordinates
.
The gravitational potential
, which encodes the perturbation of the metric sourced by these density fluctuations, represents the scalar metric perturbation in the conformal Newtonian gauge. In the Newtonian (sub-horizon) limit, where time derivatives of the metric potentials are negligible and spatial gradients dominate, the linearized fluid equations reduce to their familiar comoving Newtonian forms. In this regime,
satisfies the standard Poisson equation relating the gravitational potential to the comoving density perturbations [
10,
26].
The proper velocity of the fluid relative to an observer at the origin
is defined as
. We decompose
into the Hubble flow and the peculiar velocity
as
where
is the Hubble rate and
. The peculiar velocity measures departures from the pure Hubble flow and is related to the comoving coordinates
by
The perturbed Euler equation is modified by the introduction of a time-dependent drag force per unit mass
. When expressed in terms of the peculiar velocity, this physical deceleration is assumed to take the form
where
is an arbitrary non-negative function of cosmic time with the dimension of frequency. This ensures that the friction enters the linear growth equation as an additive damping term.
2.2.2. First-Order Equations
To first order in the quantities
, and
, the continuity, Euler, and Poisson equations for a fluid of dust subject to the time-dependent drag deceleration (
10), respectively, are
This system of equations is closed and can be reduced to a single differential equation for the linear growth of density perturbations
: We define the comoving divergence of peculiar velocities
which represents the rate at which the fluid is fluctuating in comoving space. The continuity equation (
11) then becomes
Next, taking the comoving divergence of the Euler equation (12), we obtain the equation
and substituting
from the Poisson equation (13) and
from equation (
15), we obtain the final form
Equation (
17) is an ordinary differential equation (ODE) that governs the cosmic evolution of a linear density Fourier mode
with comoving wavenumber
k. Because the perfect fluid is assumed to be dust, the evolution of
becomes independent of
k on sub-horizon scales. In this sense, this equation generalizes the standard
CDM growth equation by including the friction coefficient
. This term enhances the conventional Hubble friction and results in greater suppression of the growth of linear density perturbations relative to the growth in the standard
CDM model with
.
2.3. Scaling the Friction Coefficient
In the subsequent analysis, we scale
to the expansion-induced Hubble friction with coefficient
. We adopt the convenient form
where
is a dimensionless constant parameterizing the strength of the drag forces relative to the usual Hubble damping term. This choice ensures that the added friction is naturally scaled to the universal expansion, thereby simplifying further investigations. It is however expected that
.
Substituting Equation (
18) into Equation (
17), we find that the evolution of the density contrast
satisfies the linear differential equation
Naturally, for
, we recover the standard
CDM linear growth equation [
10,
26].
The scaling constant
in Equation (
19) naturally provides a framework for addressing the observed
tension, and it may also potentially alleviate the
tension. In the following section, we determine the range of
values that reconcile the predicted linear growth with current observational constraints on
–0.78) [
15].
3. Clustering Amplitudes and Growth Rates in CDM with a Drag Force
3.1. Preliminaries
The linear growth factor (
D) of structure is commonly defined in terms of the matter density contrast
[
10,
26], viz.
where
is usually taken to be the scale factor at recombination (redshift
). For this reason, we introduce the scale factor as the independent variable in the ODE (
19) for the matter density contrast, as shown in
Section 3.2 and
Section 3.3 below. For the calculations, we also adopt
corresponding to
.
The RMS fluctuation amplitude
, linearly extrapolated to the present epoch and corresponding to the Planck-2018
CDM normalization [
1], is defined in terms of
[
10,
26]. In our modified
CDM model, we correspondingly write
, which we determine from the scaling relation
where
[
1].
The observational clustering parameter
[
1,
32] is then determined by the relation
where
is the matter density fraction at present time. Our modified model is essentially
CDM with enhanced friction, so we adopt the Planck-2018 value of
, for which Equation (
23) reduces to
precise to 6 significant digits.
In general, the matter density fraction varies with the scale factor and is defined as [
10,
26]
where
is the background matter density,
at present (
), and
is the critical density in FLRW cosmology. We note that
refers to the total (CDM plus baryonic) matter component; on the linear scales of interest, the growth of structure
is dominated by dark matter with baryons acting as passive tracers of the overall gravitational potential wells.
It is convenient to introduce the dimensionless Hubble function
, in terms of which the fraction
may be written as
which satisfies
. The dimensionless Hubble function
is given by the well-known relation
where
is the vacuum energy fraction at present [
1,
10,
26]. These quantities naturally appear in the gravitational source term of the linear growth equation derived below.
3.2. The ODE of the Matter Density Contrast
We change the independent variable in Equation (
19) from cosmic time
t to scale factor
a [
33] by using the identities
Using primes to denote the derivatives with respect to
a and replacing
from Equation (
20), we find that the linear growth equation is transformed to
In this ODE, a factor of effectively enhances the coefficient of Hubble friction () and the gravitational source term depends on the mean universal density of matter at each instance.
For computational efficiency, it is convenient to also express the coefficient of friction in Equation (
30) in terms of
. The procedure simplifies the ODE considerably, viz.
where
can be computed from the compact expression
which is derived by combining Equations (
27) and (
28). Here, the fiducial ratio
, precise to 7 significant digits [
1].
3.3. Analytic Approximation for the Matter-Dominated Epoch
To gain analytic insight into the effect of the enhanced friction parameter
, we consider an approximate solution of the growth Equation (
31) in the matter-dominated regime. At early times (
), Equation (
32) implies that
, so that Equation (
31) reduces to a Cauchy-Euler ODE [
34,
35], viz.
that admits power-law solutions of the form
, where
p is a constant to be determined.
Substituting the power-law form into Equation (
33), we find a quadratic equation for
p, viz.
The power
of the growing mode, expanded to linear order in
, is
. Since
(Equation (
20)), the growing solution of the matter-dominated ODE (
33) is
In standard CDM where , then and the growing mode is simply .
Extrapolating this solution to the present epoch (
), we apply the results to Equation (
22) for
; using Equation (
21), we find to linear order that
and that
The steep slope of in reflects the cumulative effect of a slightly enhanced Hubble friction (by ) over the long timescale from recombination () to today. In a realistic CDM background, this cumulative suppression of growth is expected to be mitigated because the drag forces are expected to become significant only at late times, when the causal nonlinear structures have been formed in the universe and has significantly decreased with time.
Finally, a qualitative comparison with observations may be carried out using Equation (
23) for
, with the important caveats that the analytic approximations above assume
and
. Within this framework, small values of the enhanced friction parameter of
–
reduce the
CDM-predicted clustering amplitude and alleviate the
tension because the drag forces have been active at all times since recombination. In
Section 3.4, we refine this rough estimate by numerically integrating the full growth Equation (
31) for a range of
-values and a range of initial conditions in a realistic
CDM background. In these computations, the critical redshift
at which drag forces first appear becomes a free parameter.
3.4. Numerical Solutions of the Growth Equation
To obtain precise estimates of the impact of the enhanced Hubble friction parameter
on the growth of linear density perturbations for redshifts
, we integrate numerically the growth Equation (
31). The integration of the growing solution begins in the early matter-dominated regime (standard
CDM with
and
) at a scale factor corresponding to recombination, viz.
, where
The
integration is carried out from
to an intermediate value of
(a free parameter corresponding to
), where the
term, the other free parameter, is activated smoothly and persists up to the present epoch (
). The numerical algorithm uses the adaptive-step Runge-Kutta solver
ode45, which has been widely employed in computational physics [
36,
37]. This solver automatically adjusts the step size to maintain accuracy, making it suitable for integrating the rapidly varying growth function over many orders of magnitude in scale factor
a.
The resulting growth factors at
are then used to compute the corresponding linear clustering amplitude
via
where
is obtained from Equation (
24) for
and
[
1], thereby allowing for a direct comparison with observational results.
The numerical solutions are controlled by the two free parameters and (or ) and are grouped into two sets (A and B) according to the chosen typical values of the parameter .
3.4.1. Parameter of the Hubble Friction
In the first set of solutions listed in
Table 1, we choose
and we determine the critical values of
and
that result in reduced growth at the present time relative to the standard
CDM solution. The reduced growth results in the listed values of
, where one-half of the values determined by observations lie [
15] (a total of
published measurements of
, excluding 4 outliers, with mean
and standard deviation
). The complete solution with
and
that results in
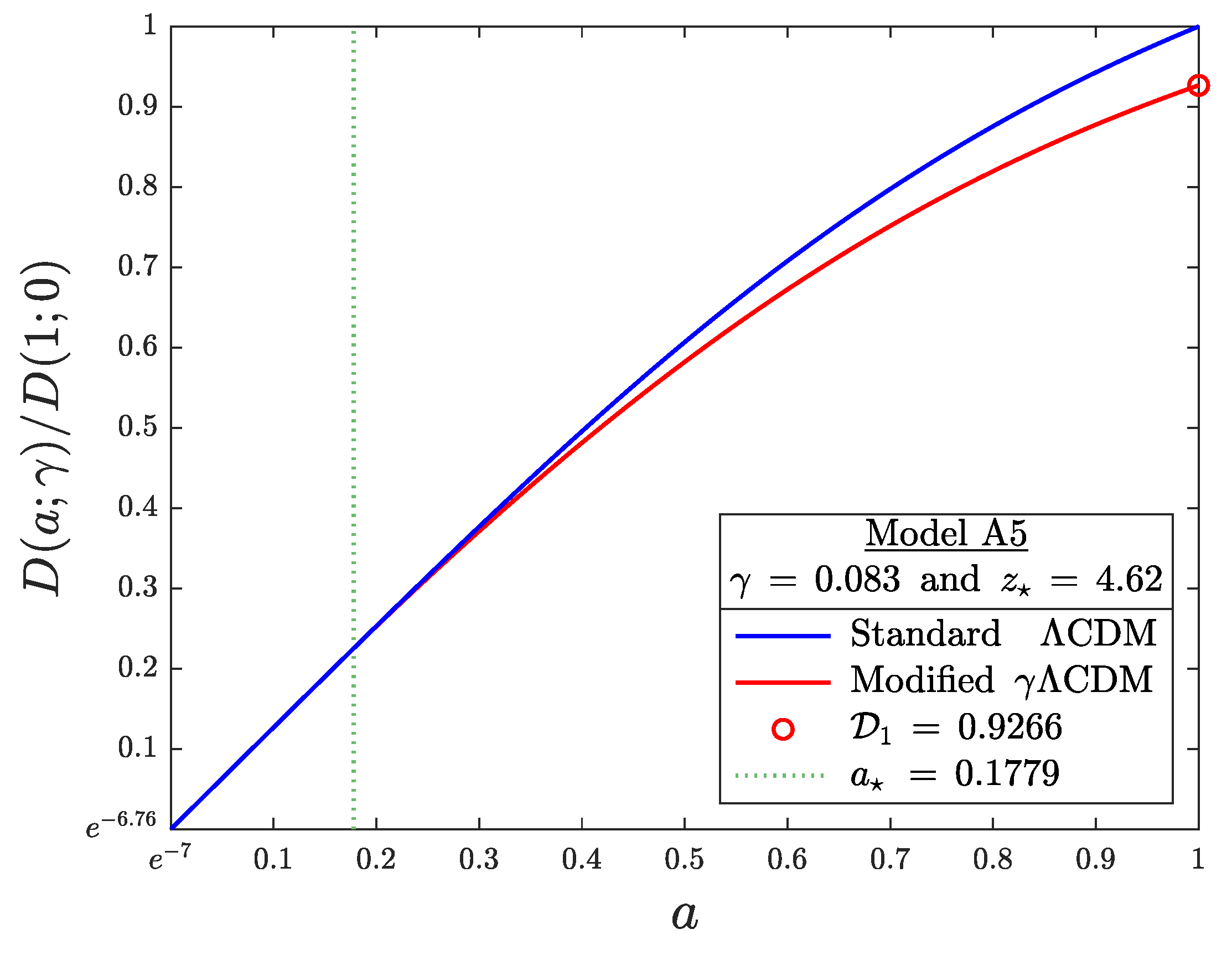
(Model A5 in
Table 1) is illustrated in
Figure 1.
3.4.2. Parameter of the Hubble Friction
In the second set of solutions listed in
Table 2, we choose
and we analyze critical values of
(perhaps a palatable upper limit [
28]) that result in reduced growth at the present time. This smaller value of
characterizes the smaller
tension between standard
CDM [
1] and a subset of the SnIa-TRGB measurements that have resulted in
km s
−1 Mpc
−1 [
15,
17]. Evidently, drag forces of such a lower magnitude (only
of the Hubble friction
) are capable of resolving the
tension only if
truly lies at the high end (∼0.79) of the observational range, and even then,
has to be
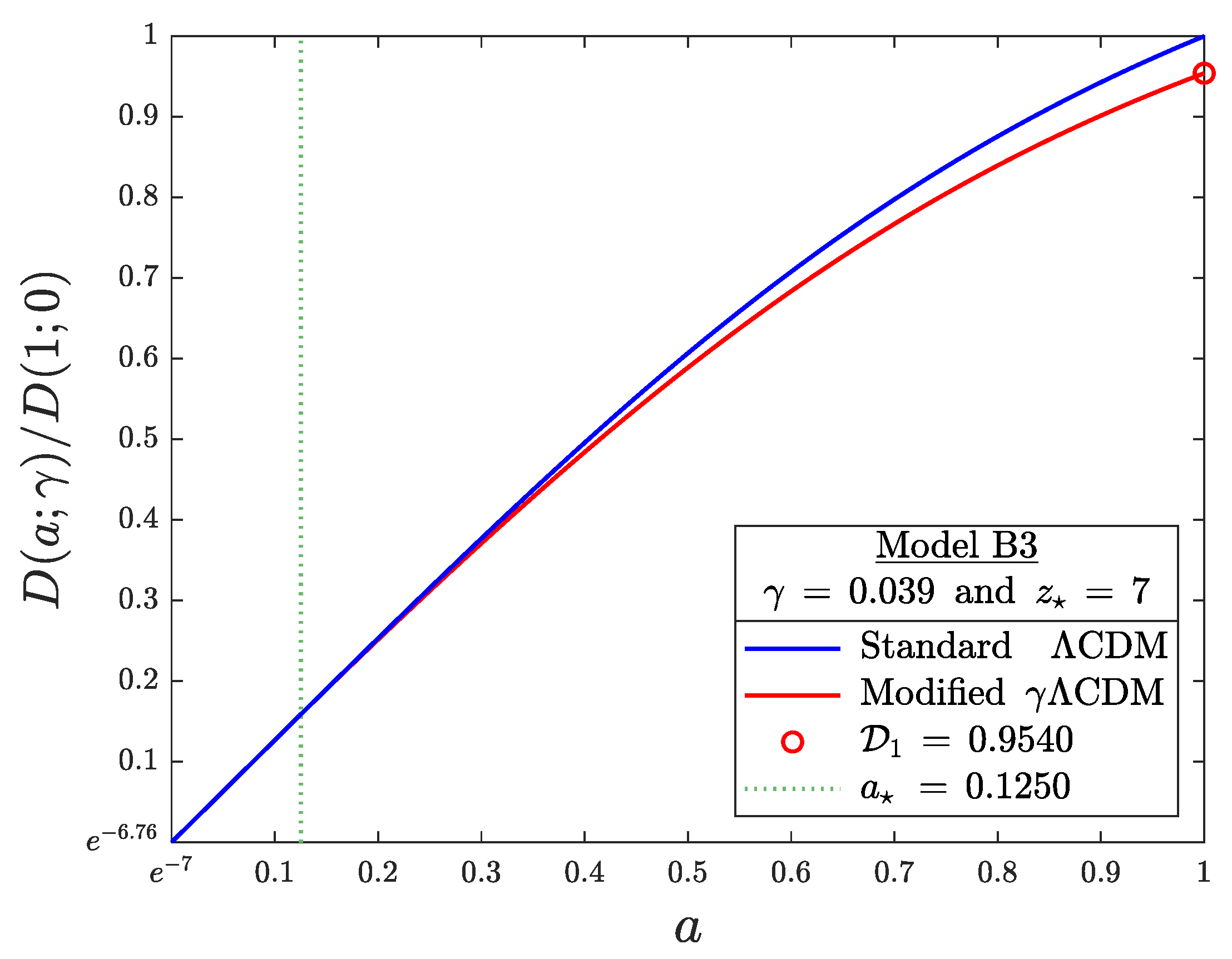
, a relatively high threshold. The complete solution with
and
that results in
(Model B3 in
Table 2) is illustrated in
Figure 2.
3.5. Growth Rate from the Nonlinear First-Order Growth ODE
Another characterization of the linear growth of structure is provided by the dimensionless growth rate
where the initial value problem (IVP) for
is described by Equations (
31), (
32), and (
38) [
26,
28].
Recast in terms of
, the IVP is described by a nonlinear first-order ODE of Riccati type, viz.
along with the initial condition
where
.
Table 3 summarizes the present-day growth rates
obtained for
CDM and the
CDM Models A1–A7 of
Table 1. In general terms, the growth rates of the
models are reduced by
, in contrast to the
ratios that are reduced by 5–10%.
The two diagnostics in
Table 3,
copied from
Table 1 and the new ratio
, quantify different aspects of the same growth history:
Ratio measures an integrated amplitude effect: once is activated at , the enhanced friction suppresses growth over the entire interval , and the accumulated suppression increases substantially when the activation redshift is set farther into the past.
By contrast, ratio
probes only a local logarithmic slope at the present epoch. Because this slope is determined mainly by the late-time background evolution (near
) and the local friction term, varying
leaves the late-time slope
largely unaffected. Consequently, the spread in
is much smaller than that in
across the
models in
Table 3.
3.5.1. Application: Models of Growth Rate
Table 4 summarizes two power-law representations of the numerically integrated linear growth rate
over the interval
for the models shown in
Table 1 and
Table 3. The standard
CDM model [
20] is also listed for comparison.
For each choice of
, we solve the IVP (
41)-(
42) numerically across the interval
and evaluate
on a dense sampling in (
) space. Then, we perform two least-squares fits of the resulting curve in terms of the matter fraction
: (a) a two-parameter
fit of the standard form
, and (b) a one-parameter
fit of the form
, in which the amplitude is fixed to the value
predicted by the analytic model of
Section 3.3 and only the exponent
ℓ is optimized.
Table 4 displays the best-fit parameters for each ansatz, along with a goodness-of-fit metric based on the RMS residuals over the interval
. A comparison between
and
isolates the deviation from a pure
power law that is absorbed by the floating normalization
versus the pure power law in which the amplitude is constrained to be fixed (
for
).
In Models A1–A7, the best-fit exponents are systematically higher than those determined for the
CDM model and listed in row 1 of
Table 4 with
and fitted parameters
This is the expected model behavior in
CDM: for fixed
, a higher power makes
smaller at late times (when
), reflecting the modest additional suppression of growth relative to standard
CDM. In this sense, the growth rates listed in
Table 4 are consistent with the suppressed clustering amplitudes reported in
Section 3.4.1 above.
4. Modified Background Dynamics in CDM
The drag force per unit mass introduced to the perturbed Euler Equation (12) in
Section 2 has the effect of enhancing slightly the Hubble flow by a factor of (
), where
. Accounting for this enhancement in the kinematics of the flow, Equation (
8) takes the form
and the modified Hubble rate then affects the dynamics of the background Hubble expansion to
in the
CDM model. The effect can be implemented in the dynamical Equations (
3), (
4), and (
6) of
Section 2.1 by substituting
and expanding terms to linear order in
.
Below we analyze various diagnostics of the CDM expansion, all related to the evolution of the Hubble rate , which is discussed first.
4.1. Hubble-Rate Evolution
In the
regime of
CDM, Equation (
6) with
reads
or, in compact form,
where
In the matter-dominated regime, where , we see that , and the factor always makes more negative relative to its CDM value. In fact, at any fixed H, the decrease of is slightly faster in CDM, and the location of the late-time attractor fixed point also changes slightly, as compared to the de Sitter value of (see below).
4.2. Hubble-Rate Fixed Point
Setting
in the above equations for
, we derive the location of the fixed point of the late-time attractor to
, viz.
or, equivalently,
The value of
does not signal an inconsistency; rather, it reflects the fact that the standard closure relation
is modified in
CDM when the standard definitions of the
CDM parameters are retained (see
Section 4.3): Equation (
47) shows that
since
, and Equation (
48) follows directly from the standard definition of the parameter
(Equation (
46)). The end result is that the fixed point of the late-time attractor moves higher by
(see also
Section 4.4).
At the expanding FLRW background level, the stability of the fixed point is not changed by
to linear order. Considering Equation (
44) in the form
, viz.
as a function of
H, we find that
Therefore, small perturbations about decay exponentially in time as .
4.3. Vacuum and Matter Scaling
To interpret the
modifications to the background dynamics, we recast the FEs in a form that makes the effective changes in the vacuum and matter couplings explicit. In the
regime of
CDM, the first Friedmann Equation (
4) reads
Thus, the contributions of the dark and matter fields to
are lowered by the same factor, and this is where our interpretation of an exterior tidal field comes in: a radially outward tidal force effectively counteracts the source of gravity (
) and also holds back the acceleration of the background. In effect, because of the
scaling of
and
, the dark energy is pushing forward a little less, and gravity is pulling inward a little less (for more details, see
Section 4.8 below).
We quantify the contribution of the outward field in the following manner: After some straightforward manipulations, we recast Equation (
49) to the convenient
form
where
and
is defined in Equation (
46). Naturally, at the asymptotic limit
, Equation (
50) reduces to Equation (
48) of the fixed point of the late-time attractor.
4.4. Cosmic Acceleration
In this part, we consider the onset of the accelerated expansion in
CDM. We begin with the kinematic identity
, which cannot be rescaled by hand, just as the kinematic definition of
H (Equation (
2)) cannot be rescaled. To build this identity in the
regime, we rearrange the various terms in Equation (
45), which becomes
Then, the condition
is satisfied at all times for which
We proceed to determine the onset of acceleration in redshift space: For convenience, we calculate the derivative
using Equation (
45) and the definition of redshift
, we find a logistic-type Riccati ODE, viz.
In what follows, we do not display the closed-form solution
of this first-order ODE, as it is cumbersome and adds little to our physical intuition. Instead, we integrate the ODE for various initial conditions
set at recombination (
) to construct the phase portraits shown in
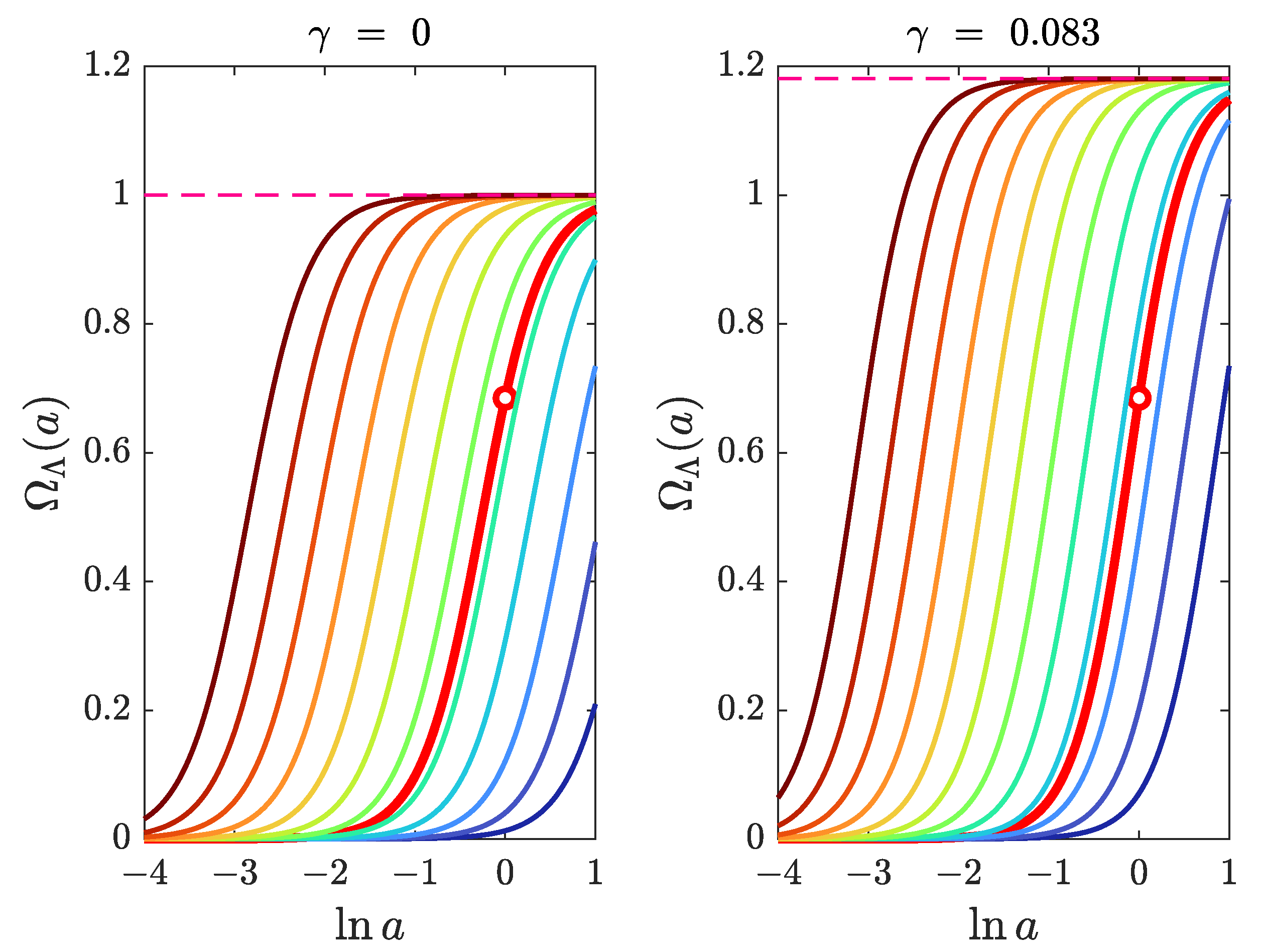
Figure 3 for
(
CDM) and
(
CDM). In each portrait, the particular solution that matches the present-day condition
[
1] is singled out by a thick red curve, and the fixed point
is indicated by a horizontal dashed line.
Next, we formulate the evolution of
as a Cauchy problem implied by the definition (
46) together with the
modified Hubble dynamics, and we integrate Equation (
54) subject to the present-day condition
The resulting solutions are strictly monotonic: for any choice of
, parameter
rises from negligible values at high redshifts to
at present, and tends to the attractor (
48) at much later times. In this way,
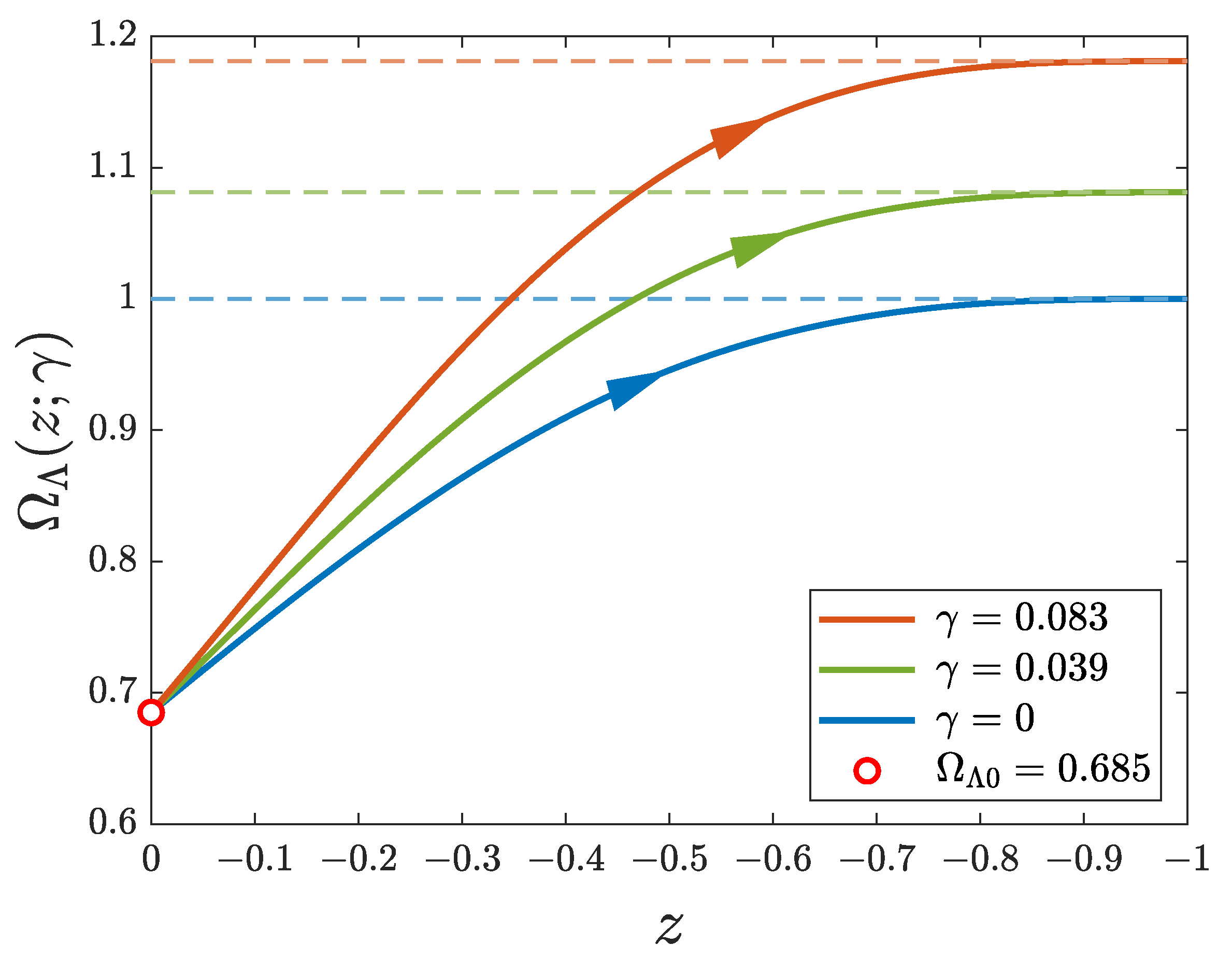
generates a one-parameter family of past and future histories,
, including the standard
CDM evolution with
.
Figure 4 illustrates the future trajectories of three family members with
.
4.4.1. Application: The Transition Redshift
In the solutions of the Cauchy problem (
54)-(
55), the inequality
is satisfied for redshifts
. To continue our assessment, we choose
and we solve the Cauchy problem to determine
. Using the Planck-2018 condition that
[
1], we find that
a threshold to be compared to the
CDM value of
.
The dramatic decrease of
in
CDM is a nonlinear
effect that can be traced to the Riccati ODE (
54), although the
modification also pushes
lower by raising the threshold value of
. The
-modified nonlinear Riccati term displaces the late-time attractor (Equation (
48)) to a higher value, and the higher fixed point selects a different family of trajectories, as compared to the
CDM fixed point of
. Together, these two effects manage to reduce
relative to
by more than 50%.
4.5. Matter–Vacuum Equality Threshold
We now turn to the “matter–vacuum equality” (MVE) threshold underlying the DCP in standard
CDM (
Section 1.1). This “recent” threshold,
, is also modified in
CDM relative to the standard
CDM value of
.
For
, the same tidal field that modifies the background dynamics also modifies the effective dilution of matter. In fact, this dual action is the key reason that makes
CDM a successful model, and it will be discussed in more detail in
Section 4.8 and
Section 5. In the matter sector of
CDM, the solution
of the (
)-modified continuity Equation (
3) is
so that the threshold of matter–vacuum equality
(where
) is reached at a different redshift
than in the
CDM.
Equating
to the constant vacuum density
, replacing the densities by their
parameters, and solving for
, we find that
Using Planck-2018 values [
1] and
, we obtain
a value that is lower than
by 8.6%.
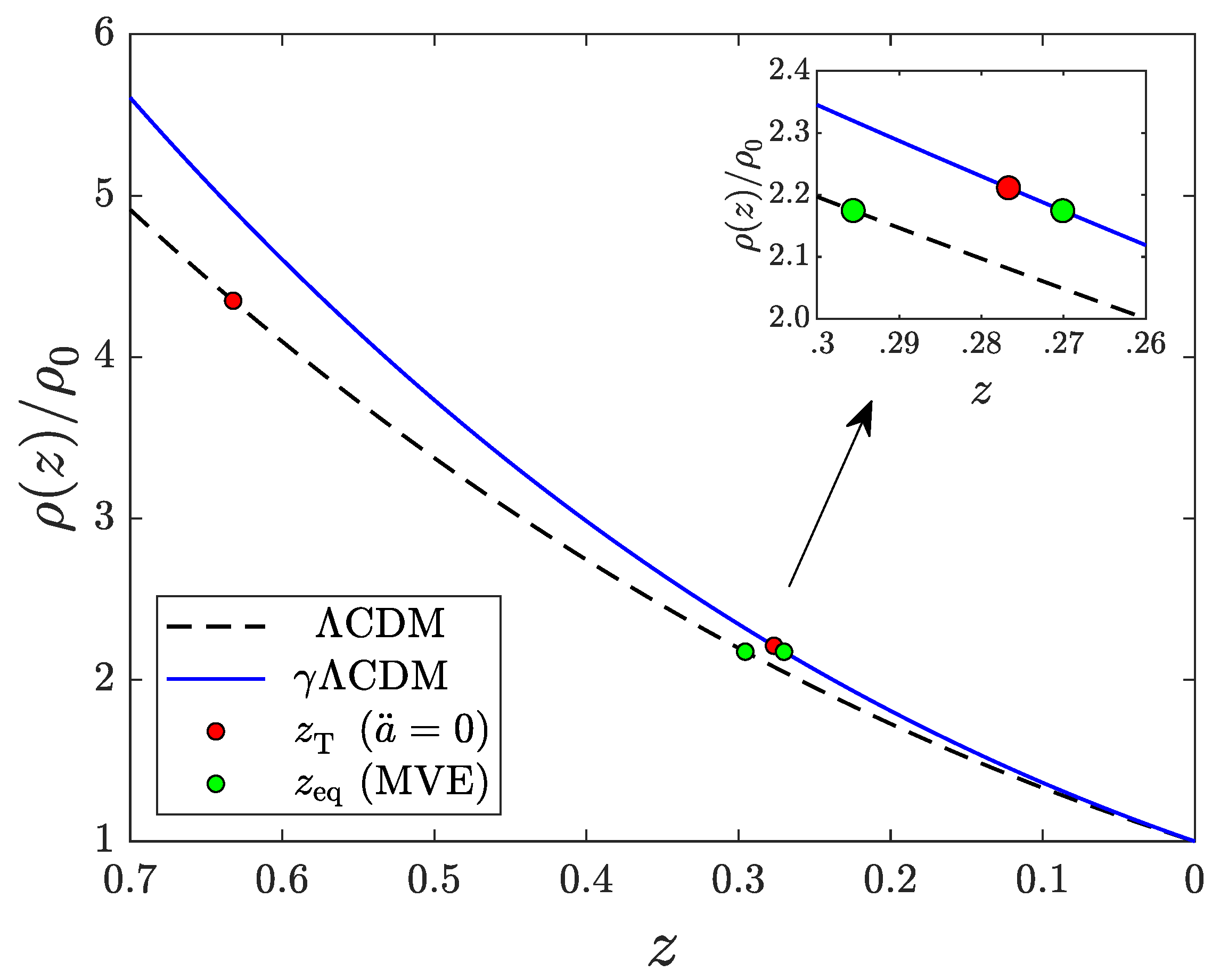
4.5.1. Application: No Density Coincidence Problem in CDM
At this point, we can compare the
redshift thresholds of Equations (
56) and (
59). We find that
that is, the acceleration threshold was crossed only 65 Myr before the MVE threshold was reached. Furthermore, each of these redshift thresholds differs from the mean
by only
, where
corresponds to a lookback time of 3.28 Gyr in the standard
CDM universe of age 13.8 Gyr [
1].
Based on these numerical results, we can argue that the DCP is effectively absent in
CDM: the
onset of the accelerated epoch nearly coincides with the MVE threshold, with corresponding densities (relative to the present-day density
) of
and
respectively, showing a relative difference of merely
.
Figure 5 summarizes the matter density profiles and the corresponding thresholds for both
CDM models (
, 0.083) in the recent epoch with
.
4.6. Deceleration Parameter
The deceleration parameter is defined kinematically by
Using Equation (
45), the
deceleration parameter reads
The
term increases
q in the matter-dominated epoch, and the deceleration
is stronger at fixed
H. Thus, the transition point
occurs at a lower redshift
or, equivalently, at a higher value of
, as seen in Equation (
52).
Equation (
64) highlights some interesting properties of the deceleration parameter in
CDM: We adopt the
CDM form of
, viz.
and we use it to eliminate
from Equation (
64), which then takes the compact
form
Besides its simplicity, Equation (
66) is also physically important for the following reasons:
- ➢
Since
in
CDM and
, the
term increases
q, and since
, the difference
makes
more negative at fixed
H and enhances deceleration (or holds back acceleration in the corresponding regime), as noted above in the discussion of Equation (
64).
- ➢
The difference is modulated by CDM baseline kinematics through the factor . In particular, (matter domination) and ( domination). Thus, the same constant produces an larger correction in the acceleration era than in the deceleration era, with the magnitude of remaining bounded across all intermediate epochs.
- ➢
-
The acceleration transition point
occurs when
, and it is shifted in
CDM to
This is a kinematic statement that the modification delays the onset of acceleration until redshift relative to the higher CDM threshold of .
- ➢
The
CDM model does not permit an arbitrary
z-dependent departure of the deceleration history
. To
, the deviation
is proportional to the constant parameter
(Equation (
67)). Hence, varying
only rescales a definite, model-prescribed departure of
(relative to
CDM), rather than introducing a free correction function of
z. Consequently, observational reconstructions of
—from distance indicators or via the transition redshift
—can constrain the parameter
directly.
4.6.1. Application: Present-Day Deceleration Parameter
Applying Equation (
64) with
to the present time (
[
1]), we find that
Compared to the corresponding
CDM value of
[
38], the magnitude of
is reduced by about
. This implies that the present-day acceleration
is nearly
smaller in
CDM.
4.7. Effective Equation of State
In the standard FLRW framework (cf. [
38]), the deceleration diagnostic may be written as
where the total EOS index
is determined by the total pressure
and density
. This relation remains valid in our treatment because in the Friedmann Equation (
49) both contributions to
are modified by the same constant factor
. Then, the matter pressure
P appears to be nonzero, but it does not come from the dust; the solution (
57) of the (1 +
)-modified continuity equation shows that, effectively,
an EOS that corresponds to an effective index
So, in CDM, we have two contributions to , the effective index and the index of the cosmological dark fluid with negative pressure .
On the other hand, the modified Friedmann Equation (
49) alters the standard sum rule
to the
CDM rule
as is also seen in Equation (
50). Then, the total index
is determined from the weighted average
or, equivalently, from the
equation
Substituting Equation (
75) into (
70) reproduces Equation (
64), which indicates that the
modifications of the FEs can be described within the relativistic FLRW framework by an effective pressure term,
, assigned to the matter sector along with the modified sum rule (
73).
4.7.1. Application: Present-Day Effective EOS Index
To make a connection with the standard two-component general relativistic phenomenology (presureless matter plus a single dark fluid), we introduce an effective dark-energy index
defined as the constant EOS index which reproduces the same deceleration
in a universe of dust. According to this definition, the effective index reads [
38]
Using
[
1] and Equation (
69), we obtain
corresponding to a shift of
relative to the
CDM value of
. Here,
is introduced as a purely phenomenological mapping to the usual “dust plus dark-energy” fit and should not be confused with the EOS indices
and
evaluated above.
4.8. Global Energy Conservation
The
modifications discussed in
Section 4.3 can be thought as arising from an isotropic tidal field described by a stress–energy tensor
in the Einstein field equations, viz.
where superscripts also label the matter sector and the vacuum sector. Each component is taken to be a perfect fluid comoving with the background four-velocity
. The matter and vacuum sectors obey the usual
CDM properties, viz.
for dust and
for vacuum, respectively.
In this framework, the vacuum–matter coupling Equation (
49) takes the form
where the critical FLRW density
is given by Equation (
26). This equation implies that the
effective tidal density is
Thus, at the background level, the tidal sector provides a screening contribution that produces the particular
rescaling of both the matter and vacuum sectors in Equations (
49) and (
80).
The continuity equation is derived from the contracted Bianchi identity of the Einstein tensor, viz.
, which enforces conservation of the total stress–energy tensor in Equation (
78). In the flat FLRW background, the vacuum terms do not appear in the continuity equation and global energy conservation is expressed by a pair of coupled equations, viz.
where the
CDM rate
encodes the energy transfer between dust and the effective tidal reservoir (whereas
and
remain strictly constant in time).
Equation (
82) is the (
)-modified FLRW continuity equation for dust (as compared to the
CDM Equation (
3)). Equation (83) helps determine the effective tidal pressure
as follows: differentiating Equation (
81) with respect to cosmic time and setting
, we find that
and, to
, that
. Then, Equation (83), solved for
, is reduced to the form
Equations (
81)–(
85) demonstrate that the
CDM background evolution, as described by Equations (
49) and (
80), admits a fully conservative interpretation in which energy–momentum is redistributed between the dust sector and the isotropic tidal sector, while the global relativistic conservation law
is exactly preserved to linear order in the parameter
. In particular, when the above relations are recast into the conventional two-component form (dust plus a single dark fluid), they reproduce to
the effective EOS index
of
Section 4.7.1.
Equations (
81) and (
85) show that the tidal sector is characterized by a negative energy density
and a positive pressure
, with both quantities evolving in time. The signs are opposite to those of the density and pressure of the vacuum sector (Equation (
79)). More generally, any time-dependent dark component (or exotic field) with the same sign structure—entering the Einstein field Equations (
78) in the same manner as the stress–energy tensor
—could provide an alternative source/origin of the modified kinematics and dynamics produced by
CDM. The essential requirement is that such a dark component or field
must simultaneously rescale the effective contributions of both the matter and vacuum sectors to the expansion history to
as follows:
In this fundamental set of
CDM equations, notice, in particular, the dual action of the reduction factor
on to both
and
(cf. Equation (
49)), as well as the remarkable appearance of the “dust pressure” term given by Equation (
71)—which, of course, does not come from the dust, but it is traced to the (1 +
)-modified matter continuity Equation (
82).
We do note however that the specific
modification of Equations (
78) or other sources of
modifications supporting Equations (
86) effectively rule out exotic dark fields that require effective EOS indices
or total EOS indices
(see
Section 4.7).
4.8.1. Application: Tidal-Sector EOS Index
In
CDM, the tidal sector itself admits a well-defined, albeit time-dependent, EOS index, viz.
where
is given by Equation (
32). At the present epoch,
[
1] and
In the
-dominated de Sitter future
, then
and
. In this asymptotic limit, the tidal density and pressure saturate to
and
, respectively, where they continue to modify to
the Hubble flow
(Equations (
49) and (
80)) and partially counteract the background acceleration
. But note that the sign structure of the tidal field is markedly opposite to that of the constant
field. This generally means that any introduced exterior field replacing the tidal field
must also have negative energy density and positive pressure.
4.9. – Comparison
For comparison purposes,
Table 5 lists several widely known parameter values of standard
CDM and the corresponding values obtained in this work from the benchmark
CDM model with
.
The most remarkable difference appears in row 6 which shows the transition redshift
of the inflection point
. The benchmark
CDM value of
has shifted down to the level of the MVE redshift (row 8). The nonlinearity responsible for this large shift was discussed in
Section 4.4.1. Besides the dramatic decrease of the
threshold, (a) the LSS parameter
has clearly decreased to the serviceable range required by observations, resolving thus the
tension (row 3); and (b) the effective
-EOS index
is now
in
CDM, rather than
in standard
CDM (row 11).
5. The Dual Action of the Tidal Field in γΛCDM
We noted in
Section 4 that the dual action of the radial tidal field (Equation (
49)) distinguishes
CDM from other models that modify gravity/drag or the background dark energy, but not both at the same time [
13,
14,
15]. This dual action can also be seen in
Table 5 by comparing the results listed in rows 3–4 and 11–12, respectively.
Here, we analyze a simplified model of tidal forces that can systematically bias CDL inferences of toward higher values relative to the CDM–CMB outcome. The main idea is that along an observer’s line of sight (LOS) leading to a low-redshift target at , there are always more nearby nonlinear perturbers at distances than on the side of the observer at . This is independent of the observer’s location lying at the origin .
5.1. Preliminaries
We assume a spherical isotropic distribution or perturbers that can be reduced to an effective 1-D radial model along the observer’s LOS. But we want to preserve the shell geometry of the 3-D distribution, so we adopt a “coherence” cone with a fixed solid angle
anchored at
and extending out to the Hubble radius
. However, the integrations will not extend that far, they will be limited by the assumption that nonlinear perturbers are formed at late times and their mean tidal field becomes active only for scale factors
(
Section 3.4).
The target galaxy is assumed to have a physical radius
, so there are no perturbers in the interval
at a given epoch
. In comoving coordinates
, the mean density of the perturbers is assumed to be
where
m is a typical perturber mass and
is the comoving mean number density. Then, the section of a shell of width
at distance
x within the coherence cone contains mass
, and the comoving density per unit length then is
excluding the interval
, where
and
. Then, the radial profile (
90) has the domain
where
and the cutoff scale
is determined from the requirement that
and the epoch of the observation
(
Section 3.4). Specifically,
and it specifies the conformal distance that a signal propagating at the speed of light
c can traverse between
and
in a flat FLRW background.
5.2. Tidal Acceleration Components
First we derive the differential tidal acceleration along the observer’s LOS produced by a perturbing mass element
located at comoving radius
x on to the target at
. The relevant Newtonian separation between the two galaxies is their physical separation
where
is the comoving separation. In the far-field regime (where
), the magnitude of the Newtonian tidal acceleration
generated by an exterior mass
then is
where
when it points away from the observer.
Using Equation (
90), subtracting the interior from the exterior contribution, and integrating, we find that the net tidal acceleration of the target is
where
is given by Equation (
92).
Using new variables
for the exterior integral and
for the interior integral, we transform Equation (
95) to the form
Performing the integrations in the regime of interest
, we find that
where
and
The zeroth-order term is clearly the most significant term in
. Evaluating then the zeroth-order tidal acceleration for the present time, we set
and
, and we determine that
where
is given by Equation (
89) and
is the normalized solid angle of the coherence cone that we adopted for the 1-D radial model.
It is worth pointing out that
is also obtained (much easier) by replacing the interior upper limit
by
in Equation (
96). But then, the interior integration is extended past
and on to the opposite ray of the observer’s LOS. In the 1-D radial model analyzed here, such a two-ray extension may be acceptable because some nonlinear perturbers “behind” the observer are within the same activation-limited causal range and contribute to the long-range tidal environment of the target galaxy.
5.3. Characteristic Estimates
We return to the comoving form of the zeroth-order tidal acceleration of Equation (
97), viz.
and we approximate
by
, where
is the present-day participation fraction of the perturber population, and
The approximation is justified in practice as we are working in the
domain, when the perturber galaxies are already well-formed [
39,
40,
41] and exert tidal forces throughout the domain of
. Then, Equation (
100) becomes
and reduces at the present epoch to
The parenthesis highlights the geometric factors that are sources of uncertainty in evaluations of the net tidal acceleration.
The recession speed due to the acceleration (
102) accumulated up to the present is
In the matter-dominated epoch of
CDM, the Hubble parameter is written as
, where the dimensionless function
is given by Equation (
28). Then, Equation (
104) takes the form
where the tidal activation integral
is given by
We can form now the dimensionless ratio
at
that, according to our heuristic drag model of
Section 2, is a measure of the coefficient of friction
. An added benefit is that the uncertain geometric factors and the distance to the target galaxy cancel out when Equation (
103) is divided by Equation (
105). Then, we find that
Thus, in this approximation, the zeroth-order 1-D radial model shows that is determined primarily by the tidal activation epoch within the standard CDM expanding background.
For
, the integral
does not admit a closed-form expression in terms of elementary functions, so in our estimates, we revert to numerical evaluations and a first-order approximation in the small parameter
. Expanding the integrand of
and the right-hand side of Equation (
107) to first order, we find that
Some representative results in which the resulting exact values of
are listed in
Table 6 for the corresponding
and
values, and for
and
[
1]. The zeroth-order approximation,
shows deviations from the exact numerical
values by about 4–8%, and the first-order approximation (
108) shows deviations of about 2–4%. The exact and approximate results are plotted in
Figure 6.
For the tidal activation scales of
in
Table 6, the exact
values are bracketed by the approximate analytic values, with
underpredicting and
overpredicting the exact results (
Figure 6). For this reason, analytic values of higher accuracy can be obtained by the midpoint estimator
without having to calculate the next higher-order approximation. This amounts to simply halving the coefficient
of the correction term in Equation (
108) and results in deviations of
–2%. The
estimates are also listed in
Table 6 and plotted in
Figure 6.
5.4. Comparisons Between Tables
We single out the results of the 1-D radial model with
and 0.039 (
Table 6), and we compare them with the
models listed in
Table 1 and
Table 2. There is a general consensus in the following sense:
The
models indicate that the
tension can only be resolved if the tidal activation redshift is enormous (typically
–12 for
–0.78). Unless
turns out to be
(see
Table 2), this
amplitude is inadequate for
CDM.
The
models consistently demonstrate that an exterior drag force resolves the tensions in
and
, provided that the tidal activation redshift is
(see also the 1-D radial Model C4 with
in
Table 6). Given the approximate nature of the 1-D radial model and the exact models listed in
Table 1, this threshold may have to be revised lower, notably to
–6.5 (see Models A3–A6 in
Table 1). At any rate, the adopted estimate of
is clearly the best choice for the benchmark
CDM model.
The agreement between the
Models A2 and C4 (
Table 1 and
Table 6, respectively) raises an important issue: in this work, ad-hoc modifications (
terms) were introduced in both the kinematic description of the Hubble flow and the dynamical equations that determine the growth of linear density perturbations. Then, it is not entirely clear why these two, seemingly independent, arbitrary modifications produced very similar outcomes. We undertake this issue in
Appendix A, where we show that the two independent modifications of the kinematics and the dynamics are consistent with one another.
6. Summary and Conclusions
6.1. Summary
This cosmological study can be summarized as follows:
- (a)
In
Section 1, we reviewed the two foundational
CDM problems (CCP and DCP) and the two major observational tensions (
and
), emphasizing the empirical
difference in observations that motivates a unified late-time explanation within the new
CDM model.
- (b)
In
Section 2, we introduced a late-time drag term in the Euler equation and derived the corresponding linear perturbation equations in the conformal Newtonian gauge (sub-horizon limit) on a flat FLRW
CDM background.
- (c)
In
Section 3, we solved the modified growth equation and showed that the added friction can suppress late-time structure growth and lower the predicted clustering amplitude into the observed low-redshift range, thereby addressing the
tension.
- (d)
In
Section 4, we analyzed the associated
background modifications implied by the same kinematical prescription, including its impact on standard late-time and present-day expansion diagnostics.
- (e)
In
Section 5, we developed a simplified 1-D radial LOS model for the late-time tidal environment of nonlinear structures and used it to estimate both the accumulated LOS recession contribution and the implied drag amplitude
, where
is the scale factor of the tidal activation epoch.
6.2. Conclusions
- ➀
Tension.—After activation, the drag force adds more friction to the linear growth equation of perturbations, suppressing late-time growth and lowering the predicted clustering amplitude [
42,
43,
44]. The solutions presented in
Section 3 demonstrate that the parameter range consistent with the kinematic
interpretation simultaneously yields the required reduction of parameter
in a
CDM background with a benchmark value of
.
- ➁
Hubble Tension.—The
CDM model provides a late-time mechanism that biases local CDL determinations of the Hubble flow through an additional LOS contribution sourced by a statistically isotropized tidal environment with nonzero mean value (
Section 5) [
44,
45,
46]. In this picture, the inferred expansion rate is shifted relative to the
CDM background in a manner controlled by the same parameter
that enters the modified kinematics (cf. Equation (
43)).
- ➂
Density Coincidence Problem.—In
CDM, parameter
modifies both the recent acceleration threshold and the matter–vacuum equality threshold [
26,
38]. For the benchmark case analyzed in
Section 4.5, these thresholds occur at nearly the same redshift (cf. Equations (
56) and (
59)), so the “recent” coincidence underlying the DCP in standard
CDM is effectively absent in
CDM (
Section 4.5.1).
- ➃
Cosmological Constant Problem.—The present framework does not address the magnitude of the vacuum energy predicted by quantum field theory (cf. [
47,
48]). As in the standard
CDM, the
field is treated phenomenologically as an input to the background dynamics (
Section 4). We do however find a scaled-down value
in
CDM, with the same scaling also modifying the dust-matter density field (cf. Equations (
49) and (
86)).
Author Contributions
Conceptualization, D.C. and D.K.; methodology, D.C. and S.L.; formal analysis, D.C.; investigation, D.C., D.K. and S.L.; resources, D.K. and S.L.; writing—original draft preparation, D.C.; writing—review and editing, D.K. and S.L.; project administration, D.K.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
DMC and SGTL acknowledge support from NSF-AAG grant No. AST-2109004.
Data Availability Statement
No new data were created or analyzed in this study. The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
NASA, NSF, and LoCSST support over the years is gratefully acknowledged by the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CCP |
Cosmological Constant Problem |
| CDL |
Cosmic Distance Ladder |
| CDM |
Cold Dark Matter |
| CMB |
Cosmic Microwave Background |
| DCP |
Density Coincidence Problem |
| DES |
Dark Energy Survey |
| EOS |
Equation Of State |
| FEs |
Friedmann Equations |
| FLRW |
Friedman–Lemaître–Robertson–Walker |
| IVP |
Initial Value Problem |
| KiDS |
Kilo-Degree Survey |
| LOS |
Line Of Sight |
| LSS |
Large-Scale Structure |
| MVE |
Matter–Vacuum Equality |
| ODE |
Ordinary Differential Equation |
| RMS |
Root Mean Square |
| SnIa |
Supernovae of type Ia |
| TRGB |
Tip of Red Giant Branch |
| 1-D |
One-Dimensional |
| 3-D |
Three-Dimensional |
Appendix A. Reconciling Hubble-Flow Kinematics and Dynamics in γΛCDM
Appendix A.1. Modified Hubble-Flow Kinematics
In a purely kinematic model, the recession velocity of a target moving in an expanding FLRW background assumes the modified form
where the drag parameter
.
Differentiating with respect to cosmic time and using dot notation for the operator
, we find to order
that
Subtracting the conventional
terms
, we find to order
that the tidal part of the acceleration is
Appendix A.2. Modified Hubble-Flow Dynamics
The recession velocity of a target in
CDM was assumed to take the modified form
where the drag parameter
is a constant and the peculiar velocity
.
The peculiar velocity field
is described by the linearized Euler equation modified to include a drag acceleration term of
, viz.
where the del operator is taken in comoving coordinates
x, as in
Section 2.2.2 of the main text.
Differentiating Equation (
A4) with respect to cosmic time, we find that
or, after some algebraic manipulations preserving only
terms, that
Using next Equation (
A5) to replace the term
and subtracting finally the conventional
terms
, we find to order
that the tidal part of the acceleration is
The term
represents the drag exerted on the peculiar velocity field
. Since
, this term is of mixed higher order, viz.
, and can subsequently be ignored. So, the tidal acceleration added to the Hubble expansion formally becomes
Appendix A.3. Linear First-Order ODE for the Drag Parameter ϵ(t)
Comparing Equations (
A3) and (
A9), we find a linear first-order ODE for the time-dependent drag parameter
to
, viz.
The fraction can be further simplified by introducing the deceleration parameter
defined by Equation (
63) and a new independent variable
Then, Equation (
A10) takes the homogeneous form
The trivial solution of this ODE is
, which implies that
Thus, the kinematic drag parameter
turns out to be independent of time and equal to constant
. This is the desired mathematical result that we set out to derive in the first place (see
Section 5.4), but it may not be the most interesting result in the realm of universal expansion. We discuss the general solution of Equation (
A10) below.
Appendix A.4. General Solution of the Drag Parameter ϵ(t)
Remarkably, the nontrivial solution of the ODE (
A12) implies a time-dependent general solution
of the ODE (
A10), viz.
where
is the integration constant and
is a dimensionless constant.
We investigate the general case in which
. The time-dependent part of
, viz.
although set to zero in
CDM, is physically very interesting for two reasons:
- (1)
In the matter-dominated CDM, the product increases with cosmic time as , so decays in time and at late times. For example, considering the set of redshifts , then is diluted by factors of between those epochs and the present, respectively. This dilution becomes much faster in the -dominated future.
- (2)
The time-dependent term
can be written most transparently in conformal rather than cosmic time. In what follows, we recast Equation (
A15) in conformal time
, thereby making its conformal properties explicit.
Appendix A.5. The Conformal Nature of Δϵ(t)
Conformal time
[
26] is defined (up to an additive constant that we set to zero) by
so that
In this convention, cosmic time is mapped monotonically to , where is the finite late-time limit in an eternally expanding matter+ universe.
Using the definition of the Hubble parameter
, as well as prime notation for the operator
, we recast Equation (
A15) to its conformal form, viz.
Thus, the product
is an invariant of the homogeneous ODE (
A12) (that is, the ODE admits a first integral fixed by initial conditions). Furthermore, Equation (
A18) shows that
is naturally expressed in conformal time, since it is directly tied to the conformal-time expansion
(with the conformal Hubble parameter defined by
), rather than to the cosmic-time rate
.
Then, in the matter-dominated and
-dominated epochs, we find that
and
respectively. Thus, during matter domination,
decreases as a mild power law in conformal time, whereas in the
-dominated regime, it is driven rapidly to zero as
, reflecting the asymptotic de Sitter scaling of the conformal expansion
. (Here,
as
, but the physical Hubble rate
tends to a finite constant, as
too.)
On the other hand, our present time lies in the transition regime of
, where the above limiting behaviors are not representative. For
, it is easier to work with cosmic time
and Equation (
A15), which takes the form
which provides an initial condition that fixes the integration constant
of the solution of ODE (
A12). Thus, in
CDM, we have effectively chosen to set
, in which case
is constant at all times.
References
- Planck Collaboration; Aghanim, N.; Akrami, Y.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results. VI. Cosmological parameters. Astron. Astrophys. 2020, 641, A6. [Google Scholar]
- Alam, S.; Aubert, M.; Avila, S.; Balland, C.; Bautista, J.E.; Bershady, M.A.; Bizyaev, D.; Blanton, M.R.; Bolton, A.S.; Bovy, J.; (eBOSS Collaboration); et al. Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: Cosmological implications from two decades of spectroscopic surveys at the Apache Point Observatory. Phys. Rev. D 2021, 103, 083533. [Google Scholar] [CrossRef]
- Einstein, A. Cosmological considerations in the general theory of relativity. Sitzungsber. Preuss. Akad. Wiss. Phys. Math. Kl. 1917, 142. [Google Scholar]
- Riess, A.G.; Filippenko, A.V.; Challis, P.; Clocchiatti, A.; Diercks, A.; Garnavich, P.M.; Gilliland, R.L.; Hogan, C.J.; Jha, S.; Kirshner, R.P.; et al. Observational Evidence from Supernovae for an Accelerating Universe and a Cosmological Constant. Astron. J. 1998, 116, 1009. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Ω and Λ from 42 High-Redshift Supernovae. Astrophys. J. 1999, 517, 565. [Google Scholar] [CrossRef]
- Shajib, A.J.; Frieman, J.A. Scalar-field dark energy models: Current and forecast constraints. Phys. Rev. D 2025, 112, 063508. [Google Scholar] [CrossRef]
- Carroll, S.M. The Cosmological Constant. Living Rev. Relativity 2001, 3, 1. [Google Scholar] [CrossRef] [PubMed]
- Martin, J. Everything you always wanted to know about the cosmological constant problem (but were afraid to ask). Comptes Rendus Physique 2012, 13, 566. [Google Scholar] [CrossRef]
- Weinberg, S. The Cosmological Constant Problem. Rev. Mod. Phys. 1989, 61, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E. Principles of Physical Cosmology; Princeton University Press: Princeton, NJ, USA, 1993. [Google Scholar]
- Ostriker, J.; Steinhardt, P. The observational case for a low-density Universe with a non-zero cosmological constant. Nature 1995, 377, 600. [Google Scholar] [CrossRef]
- Steinhardt, P.J. Cosmological implications of the end of inflation. Phys. Rev. D 1998, 58, 103512. [Google Scholar]
- Verde, L.; Treu, T.; Riess, A.G. Tensions between the early and late Universe. Nature Astronomy 2019, 3, 891. [Google Scholar] [CrossRef]
- Di Valentino, E.; Mena, O.; Pan, S.; Visinelli, L.; Yang, W.; Melchiorri, A.; Mota, D.F.; Riess, A.G.; Silk, J. In the realm of the Hubble tension—a review of solutions. Class. Quantum Grav. 2021, 38, 153001. [Google Scholar] [CrossRef]
- Perivolaropoulos, L.; Skara, F. Challenges for ΛCDM: An update. New Astron. Rev. 2022, 95, 101659. [Google Scholar] [CrossRef]
- Riess, A.G.; Yuan, W.; Macri, L.M.; Scolnic, D.; Brout, D.; Casertano, S.; Jones, D.O.; Murakami, Y.; Anand, G.S.; Breuval, L.; et al. A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team. Astrophys. J. Lett. 2022, 934, L7. [Google Scholar] [CrossRef]
- Freedman, W.L. Measurements of the Hubble Constant: Tensions in Perspective. Astrophys. J. 2021, 919, 16. [Google Scholar] [CrossRef]
- Asgari, M.; Lin, C.A.; Joachimi, B.; Giblin, B.; Heymans, C.; Hildebrandt, H.; Kannawadi, A.; Kuijken, K.; Wright, A.H.; Bilicki, M.; (KiDS Collaboration); et al. KiDS-1000 cosmology: Cosmic shear constraints and comparison between two point statistics. Astron. Astrophys. 2021, 645, A104. [Google Scholar] [CrossRef]
- Abbott, T.M.C.; Aguena, M.; Alarcon, A.; Allam, S.; Alves, O.; Amon, A.; Andrade-Oliveira, F.; Annis, J.; Avila, S.; Bacon, D.; (DES Collaboration); et al. Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing. Phys. Rev. D 2022, 105, 023520. [Google Scholar] [CrossRef]
- Linder, E.V. Cosmic Growth History and Expansion History. Phys. Rev. D 2005, 72, 043529. [Google Scholar] [CrossRef]
- Poulin, V.; Smith, T.L.; Karwal, T.; Kamionkowski, M. Early Dark Energy can Resolve the Hubble Tension. Phys. Rev. Lett. 2019, 122, 221301. [Google Scholar] [CrossRef]
- Heisenberg, L. A systematic approach to generalisations of General Relativity and their cosmological implications. Phys. Rep. 2019, 796, 1. [Google Scholar] [CrossRef]
- Wang, B.; Abdalla, E.; Atrio-Barandela, F.; Pavón, D. Dark matter and dark energy interactions: theoretical challenges, cosmological implications and observational signatures. Rep. Prog. Phys. 2016, 79, 096901. [Google Scholar] [CrossRef] [PubMed]
- Hill, J.C.; McDonough, E.; Toomey, M.W.; Alexander, S. Early dark energy does not restore cosmological concordance. Phys. Rev. D 2020, 102, 043507. [Google Scholar] [CrossRef]
- Turner, M.S. Everyone wants something better than ΛCDM. arXiv 2025, 2510.05483. Available online: https://arxiv.org/abs/2510.05483 (accessed on 1 January 2026). [CrossRef]
- Dodelson, S. Modern Cosmology; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Jeans, J.H.I. The Stability of a Spherical Nebula. Phil. Trans. Roy. Soc. London A 1902, 199, 1. [Google Scholar] [CrossRef]
- Peebles, P.J.E. The Large-Scale Structure of the Universe; Princeton University Press: Princeton, NJ, USA, 1980; pp. 48, 128, 391. [Google Scholar]
- Ellis, G.F.R. The evolution of inhomogeneities in expanding Newtonian cosmologies. Mon. Not. R. Astron. Soc. 1990, 243, 509. [Google Scholar]
- Jones, D.O.; Scolnic, D.M.; Foley, R.J.; Rest, A.; Kessler, R.; Challis, P.M.; Chambers, K.C.; Coulter, D.A.; Dettman, K.G.; Foley, M.M.; et al. The Foundation Supernova Survey: Measuring Cosmological Parameters with Supernovae from a Single Telescope. Astrophys. J. 2019, 881, 19. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The large scale structure of space-time; Cambridge University Press: Cambridge, UK, 1973; p. 84. [Google Scholar]
- Hildebrandt, H.; Viola, M.; Heymans, C.; Joudaki, S.; Kuijken, K.; Blake, C.; Erben, T.; Joachimi, B.; Klaes, D.; Miller, L. KiDS-450: cosmological parameter constraints from tomographic weak gravitational lensing. Mon. Not. R. Astron. Soc. 2017, 465, 1454. [Google Scholar] [CrossRef]
- Nesseris, S.; Sapone, D. Accuracy of the growth index in the presence of dark energy perturbations. Phys. Rev. D 2015, 92, 023013. [Google Scholar] [CrossRef]
- Hartman, P. Ordinary Differential Equations; Wiley: New York, NY, USA, 1964. [Google Scholar]
- Christodoulou, D.M.; Katatbeh, Q.D. A powerful diagnostic tool of analytic solutions of ordinary second-order linear homogeneous differential equations. Advances in Difference Equations 2017, 2018, 208. [Google Scholar] [CrossRef]
- Shampine, L.F.; Reichelt, M.W. The MATLAB ODE Suite. SIAM Journal on Scientific Computing 1997, 18, 1. [Google Scholar] [CrossRef]
- MathWorks. MATLAB Documentation, ode45 - Runge-Kutta (4,5) method for solving ODEs. Available online: https://www.mathworks.com/help/matlab/ref/ode45.html (accessed on 27 December 2025).
- Ryden, B. Introduction to Cosmology, Second Edition Section 6.1 and 5.4.2; Cambridge University Press: New York, NY, USA, 2017. [Google Scholar]
- Shibuya, T.; Ouchi, M.; Harikane, Y. Morphologies of ∼190,000 Galaxies at z=0–10 Revealed with HST Data. I. Size Evolution. Astrophys. J. Suppl. Series 2015, 219, 15. [Google Scholar] [CrossRef]
- Oesch, P.A.; Bouwens, R.J.; Illingworth, G.D.; Labbé, I.; Stefanon, M. The Dearth of z∼10 Galaxies in All HST Legacy Fields—The Rapid Evolution of the Galaxy Population in the First 500 Myr. Astrophys. J. 2018, 855, 105. [Google Scholar] [CrossRef]
- Bradley, L.D.; Coe, D.; Brammer, G.; Furtak, L.J.; Larson, R.L.; Kokorev, V.; Andrade-Santos, F.; Bhatawdekar, R.; Bradač, M.; Broadhurst, T. High-redshift Galaxy Candidates at z=9–10 as Revealed by JWST Observations of WHL0137-08. Astrophys. J. 2023, 955, 13. [Google Scholar] [CrossRef]
- Nguyen, N.-M.; Huterer, D.; Wen, Y. Evidence for Suppression of Structure Growth in the Concordance Cosmological Model. Phys. Rev. Lett. 2023, 131, 111001. [Google Scholar] [CrossRef] [PubMed]
- Lin, M.-X.; Jain, B.; Raveri, M.; Baxter, E.J.; Chang, C.; Gatti, M.; Lee, S.; Muir, J. Late time modification of structure growth and the S8 tension. Phys. Rev. D 2024, 109, 063523. [Google Scholar] [CrossRef]
- Poulin, V.; Bernal, J.L.; Kovetz, E.D.; Kamionkowski, M. Sigma-8 tension is a drag. Phys. Rev. D 2023, 107, 123538. [Google Scholar] [CrossRef]
- Weinberg, D.H.; Mortonson, M.J.; Eisenstein, D.J.; Hirata, C.; Riess, A.G.; Rozo, E. Observational Probes of Cosmic Acceleration. Phys. Rep. 2013, 530, 87. [Google Scholar] [CrossRef]
- Di Valentino, E.; Melchiorri, A.; Silvestri, A. Cosmology Intertwined: A Roadmap for the Hubble Tension. Nat. Astron. 2021, 5, 851. [Google Scholar]
- Ryskin, G. Vanishing vacuum energy. Astroparticle Phys. 2020, 115, 102387. [Google Scholar] [CrossRef]
- Ryskin, G. The emergence of cosmic repulsion. Astroparticle Phys. 2015, 62, 258. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).