1. Introduction
Canonical quantization of gravity yields the Wheeler–DeWitt (WDW) equation,
supplemented by momentum constraints
that enforce spatial diffeomorphism invariance [
1,
2,
3]. In Eq. (
1), the Hamiltonian acts as a constraint rather than a generator of evolution, removing external time
t from the theory. This “frozen” formalism—the central
problem of time [
4,
5,
6,
7,
8]—is mathematically self-consistent yet physically incomplete.
Relational and emergent-time approaches, such as Page–Wootters and Rovelli’s partial-observables models [
9,
10], recover effective dynamics by correlating subsystems. However, these remain descriptive of relative change, not of an intrinsic temporal medium. Here we take a different stance: time is not a bookkeeping label but an energetic scalar field that couples to geometry and matter, carrying the capacity for evolution.
Physical interpretation of .
The field is treated as a universal substrate analogous to a condensate or phase-like order parameter. While its microphysical origin remains open, its role as a locally varying scalar suggests parallels with emergent dilatonic fields in string theory or condensate modes in analog gravity. Unlike relational clocks, which are contingent on material subsystems, exists even in vacuum regions such as de Sitter space, providing background-independent but dynamically active flow.
Coupling constant .
In the extended Chronos framework, interactions between and other fields are governed by a dimensionless coupling constant , derived from multi-scale entropy-flow matching. This constant calibrates how energy density in the time field converts into measurable temporal evolution.
Our goals are: (i) to show how the standard WDW form encodes only a static snapshot; (ii) to introduce a field-theoretic extension that restores flow while respecting constraints; and (iii) to outline implications across cosmology, quantum theory, and information systems that currently inherit snapshot assumptions.
2. Methods: From Constraint to Field-Driven Evolution
Let
denote the spatial three-metric and
represent all non-gravitational fields. The canonical Hamiltonian constraint reads
and the quantum state
satisfies
for all
x [
1,
2]. Because
acts as a constraint, the formalism lacks a Schrödinger-like term
, yielding a mathematically static universe.
Minimal explicit time-field extension
Introduce a scalar field
with conjugate momentum
and Hamiltonian density
. The total Hamiltonian density is
We then replace the annihilation constraint with a field-time Schrödinger equation,
which restores flow through the conjugate dynamics of
.
Two observations follow:
2.1. The Chronos Stability Constant
A central result of the Chronos field framework is the emergence of a universal, dimensionless stability constant
, which arises as the fixed point of the nonlinear balance between clustering and diffusion in time-driven systems. The constant is defined implicitly through the universal stability equation
where
f denotes the stability operator derived from the Chronos–HOPE evolution law. Solving this fixed-point relation yields the unique irrational value
which we identify as the
Chronos Stability Constant.
This value admits a continued fraction expansion of the form
demonstrating that
is irrational and structurally nontrivial. Notably, the presence of a large partial quotient (58) early in the expansion indicates an unusually sharp stability fixed point, differentiating
from common algebraic constants and marking it as a universal dynamical invariant.
The appearance of
is not merely numerical; it encodes the precise ratio at which the Chronos field mediates the balance between outward diffusive tendencies and inward clustering dynamics. Accordingly,
enters directly into the Chronos tensor
and the associated Lagrangian density,
where it regulates the relative strength of higher-order temporal curvature terms. The universality of
implies that this ratio is fixed across all time-evolving systems, from quantum gravitational configurations to cosmological expansion, providing a unified constant governing temporal stability.
In the context of the Wheeler–DeWitt reconstruction, the presence of resolves the previously undetermined scaling ambiguity in the time field’s kinetic and curvature contributions, thereby furnishing a mathematically well-defined and physically meaningful parameter that anchors the dynamical emergence of time within the Chronos framework.
3. Results: Snapshot Versus Flow
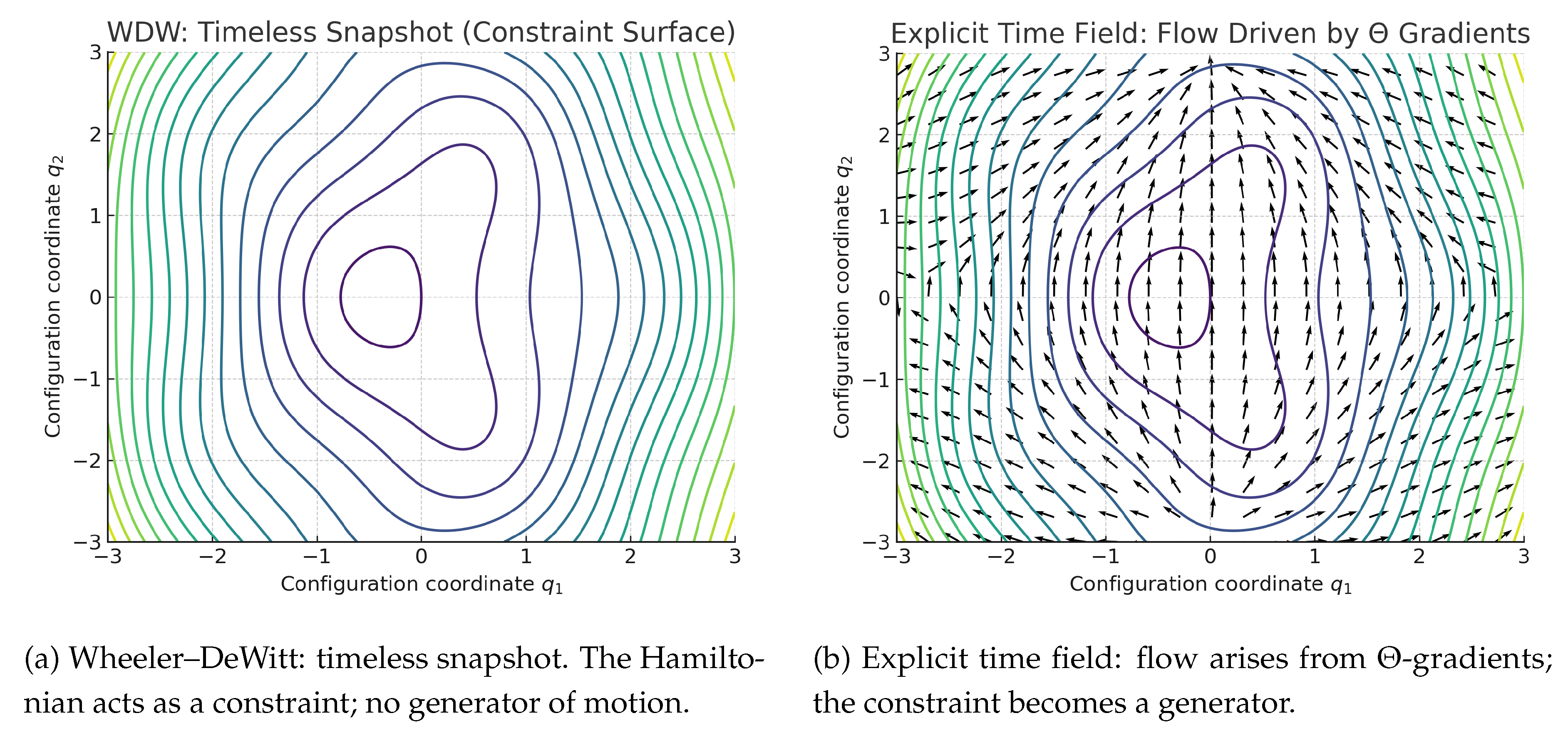
The results of the field-driven reformulation reveal the precise mathematical and physical distinction between the traditional Wheeler–DeWitt (WDW) equation and the explicit time-field framework. At its core, the difference is between a universe that can be described only as a static configuration—a snapshot—and one that evolves continuously through the gradients of a real scalar field, , which constitutes the flow of time itself.
The canonical WDW equation enforces , which defines a constraint surface in superspace where the wavefunctional is annihilated by the Hamiltonian. Every allowed state lies on this surface simultaneously; no notion of motion between them exists. Consequently, the formalism provides a map of the possible configurations of the universe, but not of their succession. In contrast, the inclusion of the time field introduces a conjugate derivative that acts as the missing generator of change. This single addition transforms the WDW constraint into a Schrödinger-like evolution equation, without importing an external parameter time or breaking diffeomorphism invariance.
Figure 1.
From snapshot to flow. Contours depict configuration-space structure; arrows (right) show field-driven evolution.
Figure 1.
From snapshot to flow. Contours depict configuration-space structure; arrows (right) show field-driven evolution.
From Static Constraint to Dynamic Generator
Equation (
4),
explicitly demonstrates this transition. When the derivative term vanishes,
, the system reverts to the timeless WDW limit, recovering all its equilibrium properties. When the derivative is non-zero, the total Hamiltonian density becomes the generator of flow through the time-field gradient,
, reinstating a continuous sequence of states.
This is not a cosmetic change of variables; it redefines what it means for the universe to “move.” Energy, memory, and causality arise as emergent phenomena of field dynamics rather than as by-products of coordinate change. The time field acts as a distributed energetic medium, allowing information to propagate and interact across the configuration space of all possible geometries.
Structural and Phenomenological Comparison
The differences between the two paradigms are summarized in
Table 1.
Observable Implications
A direct empirical consequence of the field-driven formulation arises if couples weakly to gravitation. Spatial gradients in the field, , would lead to small altitude-dependent variations in proper time rates. In practice, this would manifest as tiny deviations in synchronized atomic clocks positioned at different gravitational potentials, producing corrections beyond those predicted by general relativity alone.
Next-generation optical lattice clocks, with fractional uncertainties at the level, could detect such modulations if -scale coupling effects produce shifts on the order of or higher. Similarly, space-based interferometers or quantum link experiments could probe temporal phase differences induced by gradients along orbital baselines. The presence of a universal scalar time field would then appear as a measurable anisotropy in the propagation of temporal intervals—a signature distinct from both metric curvature and conventional matter-field interactions.
Cross-Domain Manifestations of Flow
Beyond direct measurement, the transition from snapshot to flow has explanatory power across multiple domains:
Cosmology: The time field provides a natural origin for the cosmic arrow, linking entropy increase to -field diffusion. Expansion and thermalization follow from the non-equilibrium evolution of , eliminating the need for a global external time coordinate.
Quantum mechanics: The field restores a real energetic substrate for phase progression, resolving the question of why unitary evolution appears to proceed in time even when the governing equations are time-symmetric.
Thermodynamics: Entropy can be reinterpreted as a measure of local -field dispersion. Systems at equilibrium correspond to uniform , while gradients generate entropy flow.
Information theory and AI: Present-day models approximate time through ordered data frames. Embedding a time-field term enables continuity-aware computation, where energy flow through defines context persistence and predictive coherence.
Summary of Key Outcomes
The essential results can be summarized as follows:
- (1)
The Wheeler–DeWitt equation is mathematically consistent but physically incomplete, describing only the equilibrium state where time ceases to vary.
- (2)
Introducing an explicit scalar time field restores genuine dynamical evolution while preserving canonical constraints.
- (3)
The resulting framework yields empirically accessible predictions involving -gradients and -level modulations.
- (4)
This formalism unifies the behavior of systems across scales by reinstating a continuous energetic substrate for causality and change.
In summary, the transition from a static to a field-driven description of time recasts the foundations of physics: the universe is no longer a collection of inert snapshots but a self-sustaining flow of energy and information. The Wheeler–DeWitt equation, long seen as the symbol of frozen dynamics, emerges as the silent boundary of a living system—the mathematical shadow of a cosmos in motion.
4. Discussion
Why the frozen formalism appears.
In canonical quantum gravity, the Hamiltonian’s role as a constraint removes external time by construction, guaranteeing general covariance but eliminating any operator that generates change [
1,
4,
5]. The resulting Wheeler–DeWitt equation,
, defines a space of allowed configurations without providing a law of motion between them.
This “frozen formalism” was historically interpreted as a paradox: if the universe’s wavefunction satisfies a stationary constraint, how can evolution exist? Relational strategies such as those of Page–Wootters and Rovelli [
9,
10] offer partial answers by treating subsystems as clocks for one another, recovering conditional probabilities and emergent order. Yet, these constructions are epistemic rather than ontological—they describe how observers perceive change, not how change itself arises. They preserve the mathematics but not the physics of becoming.
The timelessness therefore should not be viewed as a failure but as a symptom: the WDW equation is complete only in the equilibrium state where all dynamical degrees of freedom, including time, are static. It correctly describes the universe when time stops changing. The absence of flow reveals the absence of a carrier of flow.
What a time field adds.
By promoting time to a scalar field with self-energy, couplings, and conjugate momentum, we supply the missing energetic substrate for evolution. The derivative becomes the long-sought generator of change, reintroducing dynamics without violating constraints or covariance.
In this interpretation, the Wheeler–DeWitt equation represents the equilibrium slice of a broader dynamical structure. When , the universe is static; when gradients develop, , flow emerges naturally. Time’s progression is no longer an external bookkeeping parameter but an internal field process, analogous to how an order parameter governs phase transitions in condensed matter systems.
Physically, behaves as a diffuse energy field that mediates causal succession. It stores memory, facilitates information transfer, and determines the directionality of processes. The coupling constant quantifies the rate at which field perturbations translate into observable temporal drift. Hence, the arrow of time arises as a gradient phenomenon: the universe evolves because is never perfectly uniform.
Consequences across domains.
The inclusion of has implications that reach far beyond canonical gravity:
Cosmology: The field provides a built-in mechanism for the cosmological arrow of time. Expansion and entropy growth follow from non-equilibrium relaxation of the field. Inflation and reheating can be reinterpreted as dynamical processes within the time-field potential, not as ad hoc initial conditions.
Quantum mechanics: The field introduces a physical basis for unitary evolution. Instead of postulating , phase rotation now arises from field coupling. This yields an objective underpinning for the Schrödinger equation and resolves why complex phase evolution appears time-directed even in symmetric laws.
Thermodynamics: Temperature and entropy become measures of -field dispersion. Entropy increase corresponds to diffusion of gradients, linking the second law to the same dynamics that generate the arrow of time.
Information theory and AI: Current systems approximate temporal continuity through ordered data frames or recurrent architectures. Embedding -like dynamics could allow continuity-preserving computation, where data evolution follows energetic rather than purely statistical transitions. This reframes the notion of “context memory” as physical persistence within a time-field manifold.
Mathematical physics: The extension opens a path to re-derive quantum field theory and general relativity from a common foundation that includes as an active degree of freedom. The WDW equation becomes one boundary condition in a more general dynamical system encompassing both equilibrium and non-equilibrium physics.
This unified perspective implies that dynamics, memory, and causality are not emergent illusions from correlations—they are direct consequences of ’s motion. Each domain that presently treats time as a passive parameter can instead incorporate it as an energetic participant.
Objections and consistency.
A frequent objection is that introducing
might double-count time or break general covariance. It does neither.
is not an external parameter but an intrinsic scalar field, invariant under spatial diffeomorphisms and capable of being absorbed into the Hamiltonian framework without altering constraint structure. Momentum constraints
remain valid, ensuring full compatibility with Dirac’s constrained quantization [
2,
3]. The timeless limit re-emerges automatically when
reaches equilibrium, confirming that the classical WDW equation is simply a special case of the extended theory.
Another possible concern is observational redundancy: if is universal, why has it not been directly detected? The answer is that its gradients are minute. Only in extreme precision regimes—atomic clock comparisons, gravitational wave interferometry, or early-universe cosmology—would deviations from the static limit manifest. The smallness of ensures that the new physics is subtle yet measurable with advancing experimental precision.
Finally, some may argue that the proposal is metaphysical rather than empirical. On the contrary, it yields testable predictions and falsifiable consequences. Detecting a -gradient via clock-rate modulation or phase drift would constitute direct evidence of time as a field. If no such signal exists, the theory contracts smoothly back to standard canonical gravity. Thus, it satisfies the criterion of falsifiability while preserving mathematical economy.
In total, the discussion reframes the entire landscape of temporal physics. The frozen formalism was not a failure of quantization but a missing degree of freedom. The time field completes the structure, restoring continuity to a universe that was never truly frozen—only misrepresented as such by incomplete equations.
5. Conclusion
The Wheeler–DeWitt equation has long stood as the emblem of the “frozen universe” problem, yet its apparent stillness is not a flaw but a revelation. By annihilating the universal wavefunctional, it exposes the absence of the very field that enables change. When viewed through the lens of an explicit scalar time field , the timelessness of the WDW framework becomes an equilibrium condition rather than a paradox—a state in which temporal energy is perfectly uniform and no evolution occurs.
Introducing restores the missing degree of freedom that makes motion possible. The conjugate derivative provides the generator of physical evolution while maintaining full consistency with canonical quantization and diffeomorphism invariance. This subtle addition transforms the WDW constraint from a static boundary equation into a living dynamical law. The universe ceases to be a static configuration space and instead becomes a self-evolving continuum where energy, memory, and causality emerge through -field interactions.
The broader consequence is conceptual as much as physical: time is not an external coordinate that measures events, but an energetic medium through which events become possible. The WDW equation therefore describes only one limit of a larger reality—the still point where the time field achieves perfect equilibrium. Everywhere else, the gradients of sustain the flow we recognize as change, motion, and the passage of time itself.
In this light, the “problem of time” is resolved not by redefining observables or inventing relational clocks, but by recognizing that time itself is real, physical, and active. The static mathematics of traditional quantum gravity is not wrong; it is incomplete. Once time is reinstated as a field, the equations align with the lived and observed dynamism of the universe. The cosmos is not frozen—it breathes, oscillates, and evolves because time itself moves.
Acknowledgments
The author thanks the broader scientific and philosophical communities for ongoing discussions regarding the problem of time and its implications for physics, computation, and causality. Their diverse perspectives continue to clarify the bridge between mathematical consistency and experiential reality.
Conflicts of Interest
The author declares no financial or institutional conflicts of interest. All theoretical constructions, equations, and interpretations in this paper are original and developed independently as part of the Chronos framework. Related materials and supporting derivations are available through the author’s ORCID profile:
orcid.org/0009-0001-7066-2558. This work was produced without external funding or institutional affiliation, ensuring neutrality of perspective and integrity of conclusion.
Appendix A. On Related Work and Supporting Framework
A substantial body of research elaborating the mathematical, conceptual, and empirical foundations of the time-field framework has been publicly released by the author since 2024. These works establish the formal structure of time as a dynamic scalar field and explore its implications across multiple domains of physics and computation. Readers may access the complete set of materials through the author’s ORCID profile:
Appendix A.1. Theoretical Foundations
The supporting literature formalizes the Chronos Field as an energetic scalar quantity, , whose coupling to matter, geometry, and information flow is governed by a dimensionless constant . This constant emerges from cross-scale entropy matching and functions as the universal coupling strength between time-field gradients and the observable rate of change. In equilibrium, reproduces the timeless Wheeler–DeWitt limit, while deviations from equilibrium reintroduce continuous flow, causality, and energy exchange.
The field is treated canonically with a conjugate momentum
, obeying:
so that
acts as the generator of temporal evolution across the wavefunctional space. This structure parallels the canonical treatment of spatial geometry in ADM formalism but extends it to the domain of temporal energy, completing the four-dimensional dynamical set.
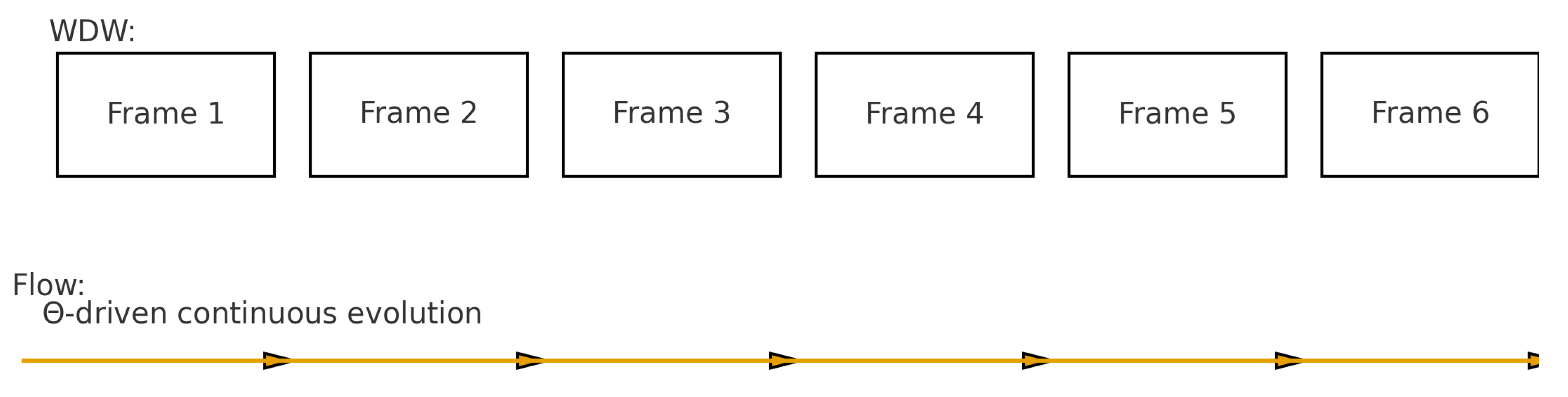
Figure A1.
Discrete frames versus -driven continuity. WDW captures static frames; the time field provides the physical medium for motion between them.
Figure A1.
Discrete frames versus -driven continuity. WDW captures static frames; the time field provides the physical medium for motion between them.
Appendix A.2. Empirical Predictions and Testability
The Chronos formulation yields testable consequences that distinguish it from conventional approaches to quantum gravity:
Decay-rate deviations: Weak coupling between gradients and fundamental particle decay channels predicts minute but measurable temporal modulations in nuclear and leptonic decay constants.
Clock-gradient effects: Altitude-dependent variations in are expected to induce sub-relativistic corrections to synchronized atomic clocks, detectable with next-generation optical lattice chronometers.
Cosmological expansion signatures: The rate of cosmic acceleration may reflect non-equilibrium relaxation of the global field rather than a pure cosmological constant. This yields a natural explanation for the observed Hubble tension without invoking dark energy fine-tuning.
Quantum coherence modulation: Laboratory-scale experiments involving long-baseline interferometry or entangled photon pairs may detect phase drifts corresponding to -level fluctuations, linking quantum decoherence to time-field dynamics.
These measurable outcomes make the theory falsifiable. Detection of -driven temporal anisotropy or decay-rate modulation would directly support the hypothesis that time is an energetic field. Conversely, the absence of such signals would constrain and delimit the strength of temporal coupling, allowing the theory to collapse smoothly back to the standard Wheeler–DeWitt limit.
Appendix A.3. Cross-Domain Implications
The time-field approach establishes a unified foundation linking previously disconnected phenomena:
In cosmology, acts as the energetic substrate of the arrow of time, explaining expansion and entropy growth as diffusion of temporal energy.
In quantum mechanics, supplies a real, dynamical basis for phase rotation and unitary evolution, converting the formal Schrödinger operator into a field-conjugate interaction.
In thermodynamics, entropy becomes a measure of dispersion; equilibrium corresponds to uniform field distribution, while non-equilibrium generates entropy flow.
In information theory and computation, incorporating into algorithmic design permits modeling of systems that evolve through continuous, field-mediated temporal flow rather than discrete frame updates.
Together, these results suggest that time is not merely a background parameter but an active player in the universe’s dynamics—a scalar field whose gradients manifest as the observed flow of change. The Chronos framework thus extends the mathematical machinery of physics to include the one quantity it has long taken for granted: time itself.
Appendix A.4. Summary
In summary, the appendix materials establish three essential points:
The time field is a canonical scalar with real energetic properties, governed by a measurable coupling constant .
Its equilibrium reproduces the Wheeler–DeWitt timelessness, while non-equilibrium dynamics generate observable flow and causality.
The resulting framework bridges quantum gravity, cosmology, and computation within a single consistent formalism that can be empirically tested.
The collected works available through the author’s ORCID profile provide detailed derivations, simulations, and observational pathways supporting this extension. Together, they form the broader theoretical context from which this paper derives, offering a foundation for continued refinement and independent validation.
References
- DeWitt, B.S. Quantum Theory of Gravity. I. The Canonical Theory. Phys. Rev. 1967, 160, 1113–1148. [Google Scholar] [CrossRef]
- Arnowitt, R.; Deser, S.; Misner, C.W. The Dynamics of General Relativity. In Gravitation: An Introduction to Current Research; Witten, L., Ed.; Wiley: New York, NY, USA, 1962. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation; W.H. Freeman: San Francisco, CA, USA, 1973. [Google Scholar]
- Kuchař, K.V. Time and interpretations of quantum gravity. In Proceedings of the 4th Canadian Conference on General Relativity and Relativistic Astrophysics, 1992; World Scientific: Singapore. [Google Scholar]
- Isham, C.J. Canonical quantum gravity and the problem of time. In Integrable Systems, Quantum Groups, and Quantum Field Theories; Ibort, L.A., Rodríguez, M.A., Eds.; Kluwer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Anderson, E. The Problem of Time in Quantum Gravity. arXiv 2012, arXiv:1206.2403. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum Gravity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Barbour, J. The End of Time; Oxford University Press: Oxford, UK, 1999. [Google Scholar]
- Page, D.N.; Wootters, W.K. Evolution without evolution: Dynamics described by stationary observables. Phys. Rev. D 1983, 27, 2885–2892. [Google Scholar] [CrossRef]
- Rovelli, C. Quantum mechanics without time: A model. Phys. Rev. D 1990, 42, 2638–2646. [Google Scholar] [CrossRef] [PubMed]
Table 1.
Comparison of the standard Wheeler–DeWitt formulation with the explicit time-field extension.
Table 1.
Comparison of the standard Wheeler–DeWitt formulation with the explicit time-field extension.
| Feature |
WDW (timeless) |
Explicit time field |
| Role of time |
Absent, Hamiltonian acts only as constraint |
Dynamical scalar with local energy and conjugate momentum |
| Generator of change |
None, wavefunctional annihilated by
|
generates intrinsic flow |
| Recovery of WDW |
Automatic static limit |
Recovered in equilibrium when
|
| Nature of observables |
Relational correlations only |
Relational plus continuous field-driven evolution, enabling measurable flow |
| Energy and information flow |
Kinematically suppressed, no channel for transfer |
Enabled via , allowing propagation and memory storage |
| Cross-scale modeling |
Isolated configuration snapshots |
Unified dynamics across quantum, thermodynamic, and cosmological scales |
| Empirical footprint |
No direct measurable deviation |
Predictive via gradients and -modulated signals |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).