The Total Entropic Quantity Framework: A Conceptual Foundation for Entropy, Time, and Physical Evolution

1. Introduction

Quantum measurement has long divided physicists between the Copenhagen Interpretation (CI) and the Many-Worlds Interpretation (MWI). Both perspectives struggle to reconcile quantum coherence with classical irreversibility. The Total Entropic Quantity (TEQ) framework bridges this gap by positioning entropy as the fundamental principle governing the quantum-to-classical transition, measurement outcomes, and even the emergence of time itself. Unlike conventional decoherence models, TEQ introduces entropy as an active selection mechanism, dynamically stabilizing classical reality and determining quantum measurement outcomes.

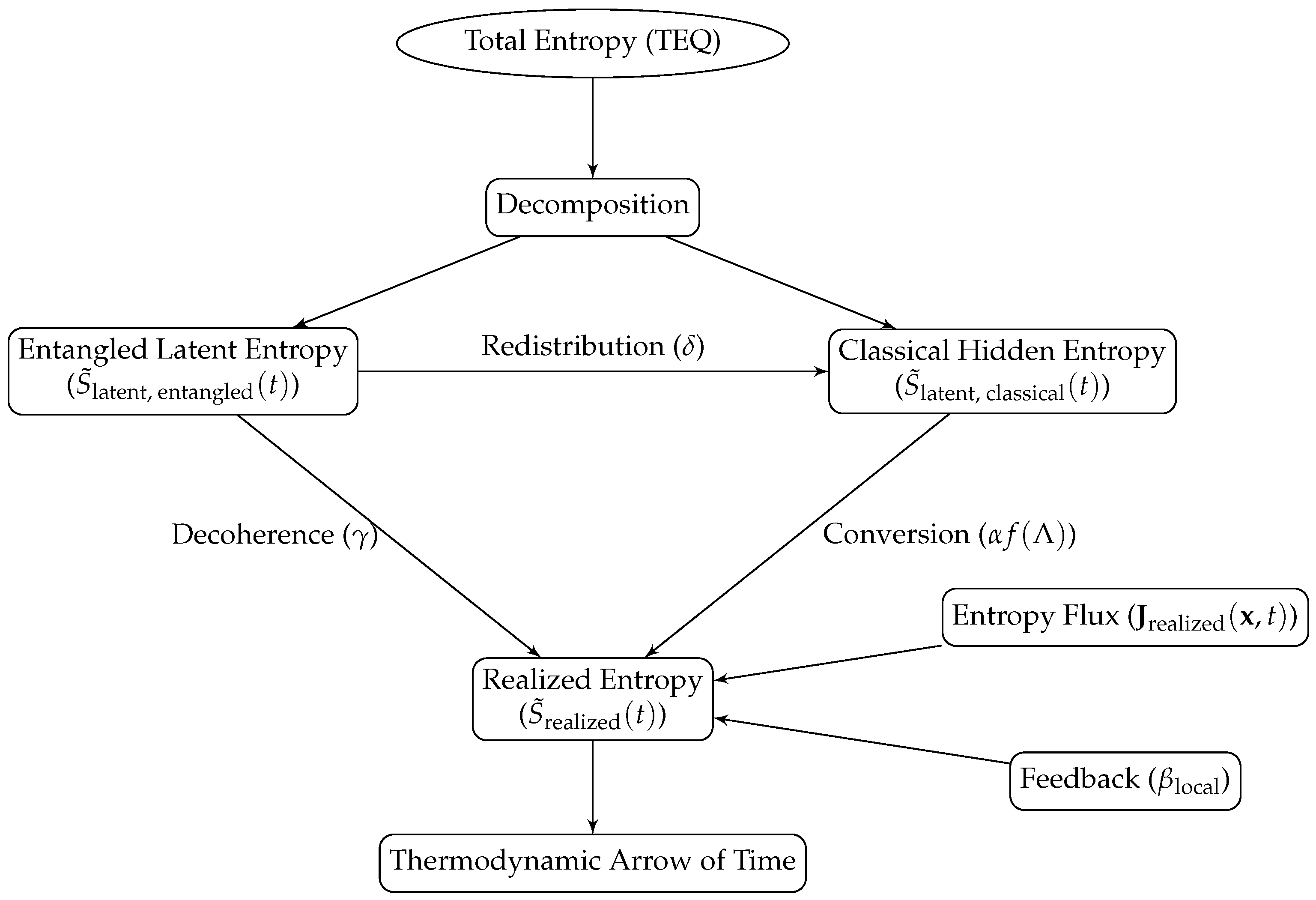
TEQ decomposes total normalized entropy into three components:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{realized}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right),$$

(1)

where:

• ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$: Entropy expressed as thermodynamically accessible outcomes, including both observable thermodynamic disorder and classically stable structures resulting from the loss of quantum coherence through decoherence.
• ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$ encodes hidden quantum correlations that remain inaccessible under classical observation and are generally disrupted by measurement.
• ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$ quantifies stable classical correlations that are not directly observable but persist in the environment, such as information encoded in memory states—physical imprints of past interactions preserved in subsystems. This is analogous to how Turing machines retain structured information on a tape: latent classical entropy encodes correlations that, while no longer quantum, maintain causal continuity and influence future evolution without requiring continuous observation.

This decomposition is both conceptually motivated and exhaustive: entropy must manifest as either observable thermodynamic disorder (realized entropy) or remain hidden in correlations that are either quantum (latent entangled entropy) or classical (latent classical entropy).

To illustrate, consider a quantum particle in a double-slit experiment. Before measurement, its state consists entirely of latent entangled entropy. Upon interacting with the environment (measurement apparatus), entropy redistributes into realized entropy—reflecting the observable classical outcome—and latent classical entropy, encoding stable correlations stored in measurement records.

Since TEQ normalizes these entropy components, their sum remains conserved, ensuring global entropy conservation and unitarity [1]. As derived formally in Appendix A, local entropy increase reflects entropy redistribution rather than true production. This resolves the apparent conflict between local irreversibility and global quantum coherence.

Although total entropy remains constant, local observations reveal increasing thermodynamic disorder and the emergence of an arrow of time. However, this local entropy growth does not reflect fundamental entropy production—since that would violate unitarity—but rather a selective redistribution process. Decoherence progressively renders certain quantum correlations inaccessible, aligning with established results [2,3,4].

Crucially, this redistribution is not merely a statistical trend but an active selection principle, governing which quantum branches remain observationally accessible. Quantum interactions with the environment selectively amplify realized entropy, suppressing interference and effectively “choosing” outcomes. This provides a thermodynamic foundation for quantum measurement, showing that CI and MWI are not fundamentally opposed but rather complementary descriptions of the same entropy-driven selection process:

• In the Copenhagen Interpretation, alternative outcomes vanish upon measurement. TEQ explains this as entropy-driven suppression of alternative branches, making one outcome thermodynamically dominant.
• In the Many-Worlds Interpretation, all outcomes persist in separate branches. TEQ clarifies that while all branches formally exist, only entropy-stable branches remain observationally accessible.

Beyond quantum measurement and classical emergence, TEQ suggests a fundamental philosophical shift in how entropy shapes physical reality. Entropy is not merely epistemic—a measure of ignorance—but ontological, actively selecting observationally accessible states. This dual epistemic-ontological role positions entropy as the driver behind the emergence of classical spacetime, causality, and even quantum stability, which will be explored in subsequent sections.

The manuscript is structured as follows: Section 2 formalizes entropy decomposition and redistribution dynamics. Section 3 explores implications for quantum measurement, the thermodynamic arrow of time, and emergent causality, while Section 4 discusses entropy as the foundation of spacetime, causal structure, and quantum stability, particularly in the case of Majorana qubits.

1.1. Philosophical Motivation and Scope

While this paper is mathematically light by design, it provides a conceptually dense foundation by reframing entropy as a unifying principle across physics. TEQ shifts entropy from an epistemic measure to an ontological driver of physical evolution, resolving longstanding tensions between quantum interpretations, time asymmetry, and the emergence of classicality. By treating entropy as both selector and suppressor, the framework offers a coherent explanation for quantum collapse, the direction of time, and the stability of observed reality—without invoking new particles or ad hoc postulates.

Moreover, TEQ bears direct implications for philosophical debates about realism and observer-dependence in quantum mechanics. By positioning entropy as ontologically active, TEQ aligns with realist traditions by affirming the objective status of quantum states independent of observation. Simultaneously, it accounts for observer-dependent phenomena through contextual entropy redistribution, bridging traditionally subjective interpretations such as QBism [5] and relational quantum mechanics [6] with objective realist approaches. This synthesis suggests that subjective and objective elements of quantum theory can coexist consistently, unified by underlying thermodynamic principles.

In this sense, TEQ functions not only as a theoretical proposal but as a philosophical bridge between thermodynamics, quantum mechanics, and spacetime structure. A companion paper will provide the detailed mathematical formalism behind these claims.

2. Theoretical Framework and Entropy Redistribution

The Total Entropic Quantity (TEQ) framework provides a cohesive theoretical description of entropy redistribution, capturing the relationship between realized entropy, quantum coherence, and latent classical correlations. By explicitly decomposing total entropy, TEQ ensures consistency with global unitary evolution and clarifies the flow of entropy from quantum coherence to classical observability.

2.1. Decomposition of Total Entropy

Global entropy conservation under unitary evolution [1] is expressed as:

$${\displaystyle \frac{d}{dt}}\left({\tilde{S}}_{\mathrm{realized}}+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\right)=0,$$

(2)

ensuring that the normalized total entropy remains conserved (${\tilde{S}}_{\mathrm{total}}\left(t\right)=1$). Local entropy variations thus do not reflect genuine production but rather redistribution among different entropy components.

Each component corresponds to a distinct physical reality:

• ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$: Entropy that has become thermodynamically accessible through decoherence, encompassing both classical disorder and structured outcomes—such as measurement results and irreversible macroscopic states [2,7].
• ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$: Quantum correlations that remain inaccessible under classical observation and are generally disrupted by measurement [8].
• $-\delta {\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$: Gradual loss of structured classical correlations as they become thermodynamically assimilated, though such correlations typically persist over relevant timescales.

This decomposition highlights a key insight: entropy is not merely increasing, but rather flowing between different forms. Quantum information does not disappear but instead becomes inaccessible due to decoherence, creating the illusion of thermodynamic irreversibility.

2.2. Dynamics and Redistribution Equations

The transition from quantum coherence to classical reality is governed by entropy redistribution. As in thermodynamic relaxation processes, where energy flows from high- to low-energy states, the rate of realized entropy growth depends on the remaining latent entropy. Initially rapid, this growth slows as the system approaches equilibrium. This behavior is captured by the relation:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}\propto \left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right)$$

which mirrors relaxation dynamics in statistical mechanics [9,10]. The precise evolution of ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$, derived in Appendix A.1, is given by:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left[1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right],$$

(3)

where $\alpha$ sets the intrinsic decoherence rate and $f(\Lambda )$ incorporates the influence of the cosmological constant $\Lambda$, which governs the expansion of spacetime and hence the available phase space for decoherence [11]. Solving this equation yields the realized entropy over time:

$${\tilde{S}}_{\mathrm{realized}}\left(t\right)=1-e^{-\alpha f(\Lambda )t},$$

(4)

which grows monotonically, reflecting the irreversible emergence of classical structure from quantum dynamics.

This formulation aligns with the thermodynamic arrow of time, emerging from the progressive redistribution of entropy rather than a fundamental asymmetry in microscopic laws [7,10].

2.3. Dynamics and Redistribution Equations

The transition from quantum coherence to classical reality is governed by entropy redistribution. As in thermodynamic relaxation processes, where energy flows from high- to low-energy states, the rate of realized entropy growth depends on the remaining latent entropy. Initially rapid, this growth slows as the system approaches equilibrium. This behavior is captured by the relation:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}\propto \left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right)$$

which mirrors relaxation dynamics in statistical mechanics [9,10]. The precise evolution of ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$, derived in Appendix A.1, is given by:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}=\alpha f(\Lambda \left(t\right))\left[1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right],$$

(5)

where $\alpha$ sets the intrinsic decoherence rate and $f(\Lambda (t\left)\right)$ incorporates the influence of the time-dependent cosmological factor $\Lambda \left(t\right)$, which governs the expansion of spacetime and hence the available phase space for decoherence [11].

Solving this equation for the case where $\Lambda$ is constant yields the canonical entropy evolution:

$${\tilde{S}}_{\mathrm{realized}}\left(t\right)=1-e^{-\alpha f(\Lambda )t},$$

(6)

which grows monotonically, reflecting the irreversible emergence of classical structure from quantum dynamics.

However, if $\Lambda$ varies with time, then $f(\Lambda (t\left)\right)$ itself must change. From Eq. (5), we can isolate this dynamical influence:

$$f(\Lambda \left(t\right))={\displaystyle \frac{1}{\alpha }}·{\displaystyle \frac{\frac{d{\tilde{S}}_{\mathrm{realized}}}{dt}}{1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)}}.$$

(7)

This expression shows that the entropic driving term $f(\Lambda (t\left)\right)$ is directly determined by how fast entropy is being realized relative to how much entropy remains latent.

Importantly, this structure has a key consequence: ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$ is a saturating function—i.e.,

$$\underset{t\to \infty }{lim}{\tilde{S}}_{\mathrm{realized}}\left(t\right)=1\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{\int }_0^{\infty }\alpha f(\Lambda \left(t\right))dt=\infty .$$

As a result, its derivative must eventually decline, implying that $f(\Lambda (t\left)\right)$ cannot grow indefinitely. In fact, the onset of saturation—marked by ${\displaystyle \frac{d^2{\tilde{S}}_{\mathrm{realized}}}{d{t}^2}}<0$—requires that $f(\Lambda (t\left)\right)$ ultimately decrease. Therefore,

$$\begin{array}{|c|}\hline f(\Lambda (t\left)\right)\mathrm{has}\mathrm{a}\mathrm{unique}\mathrm{global}\mathrm{maximum}\mathrm{in}\mathrm{TEQ},\\ \hline\end{array}$$

representing an entropic peak that marks the transition from rapid entropy realization to thermodynamic saturation.

This prediction aligns with recent DESI observations suggesting that dark energy peaked in the past and is now weakening [12].

This formulation reinforces the thermodynamic arrow of time not as a fundamental asymmetry in microscopic laws [7,10], but as an emergent feature of entropy redistribution governed by a time-varying cosmological structure.

2.4. Dynamics of Entangled Latent Entropy

Entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, represents quantum correlations that may gradually become inaccessible due to environmental interactions. The loss of coherence—decoherence—leads to a redistribution of entropy from entangled states into the classical domain. This process follows (see Appendix A.2):

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta {\tilde{S}}_{\mathrm{realized}}\left(t\right),$$

(8)

where:

• $-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$: quantifies the loss of quantum coherence due to decoherence ($\gamma$ sets the decay rate of entangled correlations).
• $+\delta {\tilde{S}}_{\mathrm{realized}}\left(t\right)$: modulates entropy redistribution, ensuring that a portion of the realized entropy contributes to the stabilization of latent classical structure—stable classical correlations, such as environmental records or memory states, which persist over time but remain inaccessible to direct thermodynamic observation.

The parameter $\delta$ does not represent a literal feedback from realized entropy into the entangled domain. Rather, it modulates how entropy redistribution unfolds during decoherence. As entangled entropy decays, the resulting entropy is not entirely converted into realized thermodynamic disorder; instead, a fraction—proportional to realized entropy and scaled by $\delta$—is redirected into stable classical correlations.

Physically, $\delta$ captures the structural redundancy and information-preserving capacity of the environment: systems embedded in memory-rich or highly correlated environments exhibit larger $\delta$, allowing more of the decohered information to stabilize as persistent classical records. This interpretation aligns with the framework of quantum Darwinism [3], where redundant environmental encoding determines which classical features remain accessible.

The parameter $\delta$ quantifies not merely a redistribution rate but also the system’s capacity to retain structure during decoherence. The rate $\gamma$ reflects the fragility of entangled states, while the balance between $\gamma$ and $\delta$ determines whether lost quantum information becomes fully dispersed as realized entropy or is partially preserved in latent classical form.

Initially, the system is assumed to be fully entangled:

$${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(0\right)=1.$$

(9)

As time progresses, entanglement diminishes, and classical structure emerges through this entropy-guided redistribution.

2.5. Evolution of Latent Classical Entropy

Latent classical entropy stores structured information that is no longer quantum but remains inaccessible to thermodynamic observation. Substituting Eqs. (8) and (5) into the total entropy constraint (Eq. (1)) gives:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)}{dt}}=\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)-\delta {\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)-\alpha f(\Lambda )\left[1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right].$$

Each term represents:

• $+\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$: Gain from lost quantum coherence, stabilizing information into classical records.
• $-\delta {\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$: Gradual decay of classical correlations over time, as information is absorbed into thermodynamic disorder.
• $-\alpha f(\Lambda )\left[1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right]$: The contribution of large-scale entropy growth, reflecting how cosmological expansion influences local entropy balance.

This equation captures the intermediate stage between quantum and classical descriptions: as quantum correlations decohere, they either contribute to realized entropy (observable thermodynamic disorder) or stabilize as latent classical records.

2.6. Latent Classical Entropy and Coarse-Graining

Latent classical entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$, represents classical correlations that are no longer quantum coherent but have not yet become thermodynamically accessible. These correlations emerge through coarse-graining, a transformation that maps fine-grained microstates onto macroscopically indistinguishable configurations—effectively averaging over inaccessible details. As such, ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$ accounts for stable records, memory states, and pointer bases that remain unobservable at a given resolution yet continue to influence system dynamics.

Informationally, this component captures structure encoded in redundant environmental correlations—emphasized in quantum Darwinism [3]—which no longer participate in coherent quantum evolution but persist as classical imprints.

For instance, in a quantum measurement, pointer states become robust under decoherence and are redundantly encoded in the environment, forming the basis for classical records such as detector outcomes.

Coarse-graining thus provides the bridge between quantum decoherence and the emergence of classical observables, grounding macroscopic stability in entropic terms.

2.7. Physical Interpretation: The Flow of Entropy

Taken together, these equations describe a continuous process where:

–

Quantum coherence (${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}$) is gradually lost due to interactions with the environment.

–

This lost coherence either contributes to realized entropy (${\tilde{S}}_{\mathrm{realized}}$) or stabilizes as classical records (${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}$).

–

Entropy does not increase globally but is instead redistributed, ensuring compatibility with unitary evolution.

–

The growth of realized entropy encodes the thermodynamic arrow of time, while latent classical entropy determines which information remains accessible.

This entropic flow underlies the emergence of macroscopic structure, providing a coherent picture that unifies the quantum-to-classical transition, thermodynamic irreversibility, and entropy conservation.

2.8. Unified Interpretational Perspective

Building on this physical structure, TEQ offers a reinterpretation of quantum measurement: decoherence is not a collapse but an entropy redistribution process. The suppression of interference patterns and the stabilization of classical outcomes arise from entropic selection, not from discontinuous projection, all while maintaining unitarity [1]. Figure 1 visually summarizes this hierarchical flow, illustrating entropy’s role in linking quantum dynamics to classical observables.

TEQ also generalizes over established interpretations:

• Copenhagen Interpretation: Wave function collapse is reframed as entropic selection. The entropy factor $\beta$ determines why certain outcomes become dominant while others are exponentially suppressed.
• Many-Worlds Interpretation (MWI): All branches formally persist, but only those stabilized through entropy redistribution remain observationally accessible. Classicality emerges not from branching alone, but from the entropic suppression of unstable alternatives.

By integrating entropy redistribution with path selection, TEQ unifies classical emergence, thermodynamic irreversibility, and quantum decoherence into a single entropy-based framework. Entropy becomes both an epistemological measure of informational accessibility and an ontological principle actively shaping which configurations stabilize into classical reality.

3. Theoretical Implications of the TEQ Framework

The TEQ framework provides a unified perspective on the emergence of the thermodynamic arrow of time, the synchronization of time, and the origin of causality within a unitary quantum universe. This section examines how TEQ reconciles global unitary evolution with local entropy increase, establishes a formal entropy-based causal structure, and explains the emergence of stable macroscopic structures. Furthermore, it explores how entropy redistribution influences quantum measurement, providing a refined perspective on the transition from quantum to classical reality.

3.1. Synchronization of Time Across the Universe

TEQ predicts the emergence of Universal Entropic Time (UET), defined by the monotonic growth of realized entropy as given in Eq. 6. UET provides a globally synchronized temporal structure, linking entropy dynamics to cosmic evolution and reinforcing the thermodynamic arrow of time as an emergent property of entropy redistribution [13,14].

Unlike prior entropy-based models—such as Barbour’s relational time [13] or Carroll’s cosmological approach [14]—TEQ explicitly incorporates quantum decoherence, entropy gradients, and cosmological expansion, yielding a unified mechanism that governs temporal ordering across scales.

A distinctive feature of TEQ is its explicit connection between decoherence and temporal synchronization. While decoherence is widely recognized as driving local thermodynamic irreversibility, TEQ highlights how its cumulative effect ensures the consistent global increase of realized entropy. In this picture, realized entropy serves as a universal entropic clock, synchronizing time coherently from microscopic to macroscopic scales.

This entropic synchronization can, in principle, be connected to standard cosmological dynamics, such as those described by the Friedmann equation [15]. Detailed observational consequences, including possible signatures in the cosmic microwave background, are left for future exploration.

While UET tracks global entropy growth, local entropy gradients $\nabla {\tilde{S}}_{\mathrm{realized}}(\mathbf{x},t)$ introduce regional variation in time’s progression. Gravitational time dilation, for example, reflects how spacetime curvature perturbs entropy distribution, causing local clocks to deviate from the global rate. These variations remain compatible with relativistic causality [16] and thermodynamic emergence.

Current TEQ formulations assume a globally expanding, entropy-increasing universe. However, in cyclic or contracting cosmologies, realized entropy might decrease or reset. Whether UET remains monotonic in such scenarios depends on deeper boundary conditions and the time-symmetry of entropy redistribution. While TEQ presently treats UET as unidirectional, future extensions may explore localized reversals or cyclic reparametrizations without violating entropy conservation or global coherence.

While detailed cosmological predictions are beyond this introductory manuscript’s mathematical scope, TEQ suggests observable consequences related to early-universe entropy redistribution. Potential signatures, such as subtle modifications in large-scale structure or entropy-correlated anisotropies in the cosmic microwave background, will be explored quantitatively in subsequent work.

3.2. Causality as an Entropic Phenomenon

Within TEQ, causality emerges naturally from entropy redistribution. The conversion of latent entropy into realized and classical forms imposes a preferred temporal ordering on macroscopic events [8,10].

Although global quantum evolution is unitary and reversible, local observers experience irreversibility because entropy-driven selection progressively renders past quantum correlations inaccessible. Decoherence transforms coherent quantum states into classical correlations or thermodynamic disorder, making previous configurations effectively unrecoverable—unless the entire entropy flow could be inverted, which is infeasible for macroscopic systems.

This directional structure follows directly from Eq. (6), as its derivative,

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}=\alpha f(\Lambda )e^{-\alpha f(\Lambda )t},$$

is strictly positive for all $t\ge 0$. Thus, Eq. (6) formalizes the observed irreversibility of macroscopic processes [10,11].

Entropy redistribution unfolds under both global constraints and local variation. The global increase of ${\tilde{S}}_{\mathrm{realized}}$ sets the arrow of time, while spatial gradients $\nabla {\tilde{S}}_{\mathrm{realized}}(\mathbf{x},t)$ lead to region-specific causal structure. These gradients manifest as entropy fluxes or localized entropy production, shaping how causality emerges within subsystems.

The corresponding local continuity equation is:

$$\nabla ·{\mathbf{J}}_{\mathrm{realized}}(\mathbf{x},t)+{\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t)=\alpha f(\Lambda )\left[1-{\tilde{S}}_{\mathrm{realized}}(\mathbf{x},t)\right],$$

where:

• ${\mathbf{J}}_{\mathrm{realized}}(\mathbf{x},t)$: Entropy flux,
• ${\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t)$: Local entropy production via decoherence or irreversibility,
• $\alpha f(\Lambda )\left[1-{\tilde{S}}_{\mathrm{realized}}\right]$: Global consistency constraint.

In the TEQ framework, the entropy flux ${\mathbf{J}}_{\mathrm{realized}}(\mathbf{x},t)$ represents the spatial redistribution of entropy driven by decoherence-induced correlations. The term ${\mathcal{G}}_{\mathrm{source}}(\mathbf{x},t)$ acts as a local source, quantifying the rate at which latent quantum correlations are irreversibly converted into classical correlations or thermodynamic entropy. The global consistency term $\alpha f(\Lambda )\left[1-{\tilde{S}}_{\mathrm{realized}}\right]$ ensures that local entropy dynamics remain synchronized with the cosmological trend of increasing realized entropy.

This formulation parallels standard entropy-balance expressions in thermodynamics and cosmology (e.g., [11]), but TEQ introduces a key extension by explicitly incorporating quantum decoherence as a source of local entropy production.

3.3. Quantum Interpretations and Entropic Dynamics

The TEQ framework suggests that the emergence of classical reality is governed by entropy redistribution. This perspective clarifies how entropy dynamics influence the observational accessibility of quantum branches [3,7,8]. We argue that both the Copenhagen Interpretation and the Many-Worlds Interpretation (MWI) can be understood as complementary descriptions of a single entropic selection process.

• In the Copenhagen Interpretation, measurement outcomes appear unique because entropy-driven selection suppresses alternative branches. Decoherence amplifies realized entropy, leading to classical stability while rendering other possible outcomes inaccessible.
• In the Many-Worlds Interpretation, all outcomes formally persist, but entropy redistribution dictates which branches remain observationally relevant. Only entropy-stable branches maintain sufficient coherence for observers to register them.

By reframing quantum measurement as an entropy-driven selection mechanism, TEQ unifies both the Copenhagen and Many-Worlds interpretations as complementary manifestations of a single entropic process—where the apparent collapse of the wavefunction and the branching of worlds reflect different aspects of entropy redistribution. This perspective also resonates with broader information-theoretic approaches to quantum theory. Frameworks such as QBism [5] and Rovelli’s relational quantum mechanics [6] similarly emphasize contextuality and observer-dependent accessibility, though from explicitly epistemic standpoints. TEQ, by contrast, treats entropy as a physically real quantity that governs which states become classically observable, offering a unifying perspective on information, emergence, and objective structure without invoking subjective collapse or Bayesian updating.

4. Entropy as the Foundation of Spacetime, Causality, and Quantum Stability

Scientific progress often begins with speculation, and only in hindsight does the “scientific method” appear as a structured refinement of ideas. Many breakthroughs originated as speculative concepts that later gained empirical and theoretical support. In this spirit, the TEQ framework serves not only as a model for entropy dynamics but also as a foundation for exploring how fundamental structures—time, space, causality, and quantum stability—emerge from entropic processes.

4.1. Speculative Insights

The following discussion extends TEQ beyond its rigorously established foundations, exploring plausible but speculative connections to emergent spacetime geometry, causality, and quantum stability. Although consistent with TEQ’s principles, these insights await further formal theoretical development and empirical testing.

This section proposes that temporal flow, spatial geometry, and causal order arise from entropy redistribution and entanglement dynamics. It also explores how TEQ provides an entropic justification for quantum stability, particularly Majorana fermions, which exhibit robustness against decoherence due to entropy constraints. These insights suggest that neither spacetime nor quantum coherence are fundamental primitives, but rather emergent phenomena shaped by entropy dynamics.

4.2. Entanglement as the Source of Time and Space

A central hypothesis within TEQ is that quantum entanglement underlies the emergence of classical time and space. Unlike classical descriptions where spacetime is assumed as a background structure, TEQ posits that spacetime emerges from the redistribution of entropy during decoherence.

This perspective builds on the ER=EPR conjecture [17], which links entanglement (EPR pairs) to spacetime connectivity (Einstein-Rosen bridges). TEQ extends this idea by proposing that it is specifically the redistribution of entangled latent entropy that gives rise to classical spatial and temporal structure. In other words, spacetime geometry is not simply associated with entanglement, but dynamically shaped by how entropy flows from entangled to realized and classical forms.

Before measurement or decoherence, the system is dominated by entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, representing a pre-geometric state lacking defined spatial or temporal structure. At this level, correlations encode purely relational information without reference to distance or ordering. As expressed in Eq. (1), total entropy remains conserved:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{realized}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right).$$

Decoherence drives the system toward classical observability, redistributing entropy and giving rise to emergent space and time.

This hypothesis suggests that if spacetime is emergent from entropy redistribution, traces of this process should be observable in the structure of the early universe. Potential empirical tests include identifying entropy-correlated features in the cosmic microwave background (CMB), such as spectral distortions or anisotropies beyond inflationary predictions, and searching for signatures in the stochastic gravitational wave background that reflect the entropy flow associated with early quantum decoherence events.

4.3. The Entropic Origin of Causality and Time

Within TEQ, time is not fundamental but emergent, arising from the irreversible flow of entropy from quantum to classical domains. Specifically, the monotonic increase of realized entropy defines a preferred temporal direction, as given by Eq. (5):

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right).$$

This defines the thermodynamic arrow of time as a consequence of entropy redistribution, consistent with classical irreversibility [8,10].

Entropy gradients further shape the dynamics of physical systems. Introducing an entropy potential,

$$\Phi \left(\mathbf{x}\right)=-TS\left(\mathbf{x}\right),$$

(10)

where T is an effective temperature-like parameter, defines an entropic force via:

$${\mathbf{F}}_{\mathrm{entropic}}=-\nabla \Phi \left(\mathbf{x}\right).$$

(11)

This force drives systems toward entropy-stable configurations and determines their trajectories through configuration space.

This formulation aligns with Verlinde’s entropic gravity proposal [18], where gravity emerges from entropy gradients. TEQ generalizes this idea, proposing that not only gravity but also temporal flow and causal structure emerge from entropic principles. Detectable consequences could include small deviations from general relativity in extreme entropy-gradient regimes, or nontrivial structure in early-universe observables that reflect the entropy landscape during cosmic initialization.

4.4. Entropy and Quantum Stability: The Case of Majorana Fermions

TEQ provides an entropy-based perspective on quantum stability: quantum states that experience minimal entropy redistribution maintain coherence longer. This insight aligns with the behavior of Majorana fermions, which exhibit topological protection against decoherence. This property makes them prime candidates for fault-tolerant quantum computing [19].

In TEQ, quantum stability depends on the balance between latent entangled entropy and realized entropy. When entangled entropy remains high and realized entropy grows slowly, the system resists decoherence. This interplay is governed by the redistribution equation:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}+\delta {\tilde{S}}_{\mathrm{realized}}.$$

Here, $\gamma$ represents the decoherence rate, governing how quickly entangled entropy is lost to classical observables, while $\delta$ characterizes the fraction of realized entropy that remains accessible in stable correlations.

While the enhanced stability of Majorana qubits is well understood within topological quantum computing frameworks [20,21], TEQ offers a complementary interpretation: such stability arises from suppressed entropy redistribution. Rather than attributing robustness solely to symmetry protection, TEQ frames it as a consequence of entropic selection, governed by how quantum information resists transformation into thermodynamically accessible forms. This perspective introduces a general stability functional and suggests new criteria for identifying resilient quantum systems beyond topological constructions.

$${\gamma }_M\ll {\gamma }_S.$$

(12)

Here, ${\gamma }_M$ denotes the decoherence rate for Majorana qubits, while ${\gamma }_S$ corresponds to conventional superconducting qubits. The inequality ${\gamma }_M\ll {\gamma }_S$ reflects the greater resilience of Majorana systems to decoherence, a feature TEQ interprets as suppressed entropy redistribution.

Since ${\gamma }_M$ is significantly suppressed, entropy redistribution is much slower for Majorana qubits. This means that the system retains its quantum correlations for longer periods, preventing decoherence-driven entropy flow from eroding its quantum information.

To formally quantify stability, we introduce the entropy stability functional:

$$F=-{\displaystyle \frac{d}{dt}}\left({\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}-{\tilde{S}}_{\mathrm{realized}}\right).$$

(13)

This functional quantifies the net entropy flow between entangled and realized states. Majorana qubits exhibit stability when $F\approx 0$, indicating that the entangled latent entropy remains largely intact. This leads to a key prediction:

$$\begin{array}{|c|}\hline {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}^{\left(M\right)}\gg {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}^{\left(S\right)}\\ \hline\end{array}$$

which expresses that Majorana qubits retain significantly more entangled latent entropy than conventional superconducting qubits. In the TEQ framework, this preservation reflects reduced entropy redistribution and directly contributes to their enhanced coherence and robustness against environmental decoherence—making them strong candidates for fault-tolerant quantum computation.

4.5. First Empirical Prediction from TEQ: Testing Quantum Stability with Majorana Qubits

The TEQ framework makes its first concrete prediction: Majorana qubits should exhibit significantly extended coherence times compared to conventional qubits due to suppressed entropy redistribution. Unlike standard phenomenological approaches, TEQ provides a clear entropic mechanism explaining why Majorana qubits resist decoherence.

A practical experimental test involves directly comparing decoherence rates ($\gamma$) between topologically protected Majorana qubits and conventional superconducting qubits under controlled laboratory conditions [21]. Such experiments typically employ hybrid semiconductor-superconductor nanowire systems, where signatures of Majorana zero modes can be detected via tunneling spectroscopy or interferometric measurements [20,21]. Specifically, coherence times and fidelity of quantum operations should be systematically measured under environmental noise and compared. TEQ predicts that Majorana-based systems will consistently maintain longer coherence, retaining quantum correlations due to minimal entropy redistribution into thermodynamically accessible states.

Validating this prediction would strongly support TEQ’s foundational principle that quantum stability emerges from entropy-driven selection, providing an explicit thermodynamic justification for the robustness and practical viability of Majorana qubits in quantum computing.

4.6. Conclusion: A Thermodynamic View of Spacetime, Causality, and Quantum Measurement

TEQ presents a coherent and unifying framework in which spacetime, causality, and quantum stability emerge from entropy-driven selection. Rather than positing wavefunction collapse or invoking observer-centric mechanisms, TEQ views the emergence of classical reality as a restructuring of entropy across accessible and inaccessible domains. Spacetime structure arises from entropic differentiation, causal order follows the monotonic growth of realized entropy, and quantum stability reflects resistance to entropic dispersion.

This thermodynamic perspective clarifies quantum measurement and quantum erasure as continuous, physical processes—neither discontinuous nor retrocausal, but governed by the selective amplification and suppression of structure through entropy flow.

Empirical validation may come from cosmological observations sensitive to early-universe entropy gradients or from quantum decoherence experiments contrasting the behavior of Majorana qubits with conventional systems.

Looking ahead, a companion paper will develop the entropy-weighted variational principle introduced here, deriving quantum dynamics, the Born rule, and quantization from entropic constraints. This extension will also explore quantum erasure and gravitational effects, further testing TEQ’s predictive power and universality.

Table 1. Summary of Symbols, Their Meanings, and Units

Symbol	Meaning	Units (SI)
Entropy Components (Normalized Quantities)
${\tilde{S}}_{\mathrm{total}}\left(t\right)$	Total normalized entropy (conserved quantity)	Dimensionless
${\tilde{S}}_{\mathrm{realized}}(\mathbf{x},t)$	Local realized entropy as a function of space and time	Dimensionless
${\overline{S}}_{\mathrm{realized}}\left(t\right)$	Globally averaged realized entropy	Dimensionless
${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$	Latent entropy stored in quantum entanglement	Dimensionless
${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$	Latent entropy from classical correlations	Dimensionless
Governing Parameters for Entropy Dynamics
$\alpha$	Growth rate constant for realized entropy	${\mathrm{s}}^{-1}$
$f(\Lambda )$	Modulation factor incorporating the cosmological constant	Dimensionless
$\gamma$	Decoherence rate of entangled latent entropy	${\mathrm{s}}^{-1}$
$\delta$	Redistribution rate between entangled and classical states	${\mathrm{s}}^{-1}$
${\mathbf{J}}_{\mathrm{realized}}(\mathbf{x},t)$	Local entropy flux	${\mathrm{s}}^{-1}$
$\Phi \left(\mathbf{x}\right)$	Entropy potential function	Dimensionless
${\mathbf{F}}_{\mathrm{entropic}}$	Entropic force from entropy gradients	N
Cosmological and Fundamental Constants
$\Lambda$	Cosmological constant (dark energy density)	${\mathrm{m}}^{-2}$

Table 1. Summary of Symbols, Their Meanings, and Units

Symbol	Meaning	Units (SI)
Entropy Components (Normalized Quantities)
${\tilde{S}}_{\mathrm{total}}\left(t\right)$	Total normalized entropy (conserved quantity)	Dimensionless
${\tilde{S}}_{\mathrm{realized}}(\mathbf{x},t)$	Local realized entropy as a function of space and time	Dimensionless
${\overline{S}}_{\mathrm{realized}}\left(t\right)$	Globally averaged realized entropy	Dimensionless
${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$	Latent entropy stored in quantum entanglement	Dimensionless
${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$	Latent entropy from classical correlations	Dimensionless
Governing Parameters for Entropy Dynamics
$\alpha$	Growth rate constant for realized entropy	${\mathrm{s}}^{-1}$
$f(\Lambda )$	Modulation factor incorporating the cosmological constant	Dimensionless
$\gamma$	Decoherence rate of entangled latent entropy	${\mathrm{s}}^{-1}$
$\delta$	Redistribution rate between entangled and classical states	${\mathrm{s}}^{-1}$
${\mathbf{J}}_{\mathrm{realized}}(\mathbf{x},t)$	Local entropy flux	${\mathrm{s}}^{-1}$
$\Phi \left(\mathbf{x}\right)$	Entropy potential function	Dimensionless
${\mathbf{F}}_{\mathrm{entropic}}$	Entropic force from entropy gradients	N
Cosmological and Fundamental Constants
$\Lambda$	Cosmological constant (dark energy density)	${\mathrm{m}}^{-2}$

Appendix A.1. Growth of Realized Entropy

The growth of realized entropy, ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$, represents the irreversible conversion of latent entropy into observable thermodynamic disorder resulting from decoherence processes. Its governing equation is:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right),$$

(A1)

where:

• $\alpha$ is the decoherence-driven growth rate constant.
• $f(\Lambda )$ accounts for the influence of the cosmological constant $\Lambda$ on the phase space of available states [11].

Assumptions. 

• Proportionality to Remaining Latent Entropy: The rate of realized entropy growth is proportional to the remaining latent entropy, similar to thermodynamic systems with exponential relaxation [9,10]:

  $${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}\propto \left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right).$$
• Cosmic Expansion Influence: The cosmological constant modulates entropy growth, scaling the phase space of decohering states.
• Initial Condition: At $t=0$, the realized entropy is zero:

  $${\tilde{S}}_{\mathrm{realized}}\left(0\right)=0.$$

Derivation. 

Starting from the proportionality assumption:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right).$$

Separating variables:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}}{1-{\tilde{S}}_{\mathrm{realized}}}}=\alpha f(\Lambda )dt.$$

Integrating both sides:

$$-ln\left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right)=\alpha f(\Lambda )t+C,$$

where C is the integration constant. Using the initial condition ${\tilde{S}}_{\mathrm{realized}}\left(0\right)=0$, we find $C=0$. Exponentiating:

$$1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)=e^{-\alpha f(\Lambda )t}.$$

Rearranging yields:

$${\tilde{S}}_{\mathrm{realized}}\left(t\right)=1-e^{-\alpha f(\Lambda )t}.$$

(A2)

This solution demonstrates the monotonic increase of realized entropy, consistent with the thermodynamic arrow of time.

Appendix A.2. Dynamics of Entangled Latent Entropy

The evolution of entangled latent entropy, ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$, governs its transformation into realized entropy and redistribution within the TEQ framework. Its dynamics follow:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta {\tilde{S}}_{\mathrm{realized}}\left(t\right),$$

(A3)

where:

• $\gamma$ is the decoherence rate, quantifying the decay of global quantum coherence [7].
• $\delta$ is the redistribution rate, describing the coupling to realized entropy growth.

Assumptions. 

• Decoherence-Driven Decay: The entangled latent entropy decays exponentially due to decoherence, a well-established effect in quantum systems [2,7].
• Feedback Contribution: A fraction of realized entropy growth influences the remaining entangled latent entropy.
• Initial Condition: At $t=0$, the system starts in a fully entangled state:

  $${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(0\right)=1.$$

Reformulation. 

Using Eq. (A2) for ${\tilde{S}}_{\mathrm{realized}}\left(t\right)$, we rewrite:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)}{dt}}=-\gamma {\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+\delta \left(1-e^{-\alpha f(\Lambda )t}\right).$$

This first-order differential equation captures the time evolution of entangled latent entropy, illustrating how it redistributes under the influence of decoherence and entropy transfer.

Appendix A.3. Conservation of Total Entropy

The conservation of total normalized entropy ensures:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{realized}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)=1.$$

(A4)

Rearranging for the classical hidden entropy yields:

$${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)=1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)-{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right).$$

(A5)

This equation ensures that total entropy is conserved, consistent with the unitary evolution of the universe [7,8].

Appendix C.1. Unitary Evolution and Entropy Conservation

Quantum mechanics ensures that the global state of a closed system evolves unitarily, preserving the total information content. The von Neumann entropy,

$$S_{\mathrm{vN}}\left(t\right)=-\mathrm{Tr}(\rho ln\rho ),$$

(A6)

remains constant for a system described by density matrix $\rho \left(t\right)$.

TEQ is consistent with this principle by enforcing:

$${\tilde{S}}_{\mathrm{total}}\left(t\right)={\tilde{S}}_{\mathrm{realized}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)+{\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)=1,$$

(A7)

where entropy is dynamically redistributed among its components while remaining conserved.

Appendix C.2. Entropy as Coarse-Graining and Information Loss

Entropy, in classical and quantum physics, quantifies missing information about a system’s microstates. In TEQ:

• ${\tilde{S}}_{\mathrm{latent},\mathrm{entangled}}\left(t\right)$ represents inaccessible correlations due to quantum coherence.
• ${\tilde{S}}_{\mathrm{latent},\mathrm{classical}}\left(t\right)$ accounts for classical correlations within decohered subsystems.

The realized entropy follows the evolution equation:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}=\alpha f(\Lambda )\left(1-{\tilde{S}}_{\mathrm{realized}}\left(t\right)\right),$$

(A8)

consistent with entropy growth under coarse-graining, where thermodynamic irreversibility emerges from a loss of access to microstate information.

Appendix C.3. The Thermodynamic Arrow of Time

The second law of thermodynamics states that entropy increases over time in an isolated system. TEQ provides a mechanism for this irreversibility:

$${\displaystyle \frac{d{\tilde{S}}_{\mathrm{realized}}\left(t\right)}{dt}}>0,\forall t\ge 0.$$

(A9)

This aligns with observed macroscopic irreversibility while preserving global unitary evolution.

The TEQ framework is consistent with fundamental principles of physics, providing an entropic foundation for the emergence of time and causality. While speculative extensions remain open to empirical scrutiny, the core structure of TEQ aligns with well-established thermodynamic and quantum mechanical laws.

Appendix D.1. Entropy Gradients and System Evolution

Entropy redistribution in TEQ follows gradient-like dynamics, where entropy potentials determine system stability. The system evolves according to:

$${\displaystyle \frac{d\mathbf{x}}{dt}}=-\nabla \Phi \left(\mathbf{x}\right),$$

(A10)

where $\Phi \left(\mathbf{x}\right)=-TS\left(\mathbf{x}\right)$ defines an entropy potential, and the entropic force is:

$${\mathbf{F}}_{\mathrm{entropic}}=-\nabla \Phi \left(\mathbf{x}\right).$$

(A11)

These forces drive systems toward stable entropy configurations, ensuring robust classical emergence under TEQ.

Appendix D.2. Entropy-Driven Stability and Attractors

Entropy gradients lead to stable attractors, where entropy maximization corresponds to equilibrium. Stability follows from convexity conditions:

$${\nabla }^2\Phi \left(\mathbf{x}\right)\succ 0.$$

(A12)

This ensures that classical states persist under entropy redistribution, reinforcing TEQ’s interpretation of measurement stability.

Appendix D.3. Implications for TEQ

Entropy gradients dictate:

• The stability of classical structures under entropy redistribution.
• The emergence of preferred macroscopic states via entropy-driven selection.
• The robustness of entropy-stable quantum systems, such as Majorana qubits.

These results reinforce TEQ’s role in unifying entropy, quantum stability, and the thermodynamic arrow of time.