Submitted:
24 March 2025
Posted:
26 March 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Definitions and Core Concepts
2.1. Primordial Informational Field (PIF)
- Substrate of Reality
- Timeless and non-local
- Dynamic Evolution
- : Wave operator describing the evolution of quantum informational density in spacetime;
- : Damping term preventing runaway growth in high-density -regions;
- : Higher-order stabilization term contributing to self-interactions;
- : Temporal feedback ensuring dynamic stability of informational flows;
- : Entropy gradients driving quantum informational flows ();
- : Unified potential field coupling quantum informational density to spacetime and matter.
2.2. Quantules
- Discrete Informational Units
- Self-Organizing
- Non-Local Interactions
2.3. Quantum Informational Density
- Dynamic and Localized:
- Encodes Physical Phenomena:
- Self-Stabilizing:
- ○
- : Wave operator describing the evolution of quantum informational density in spacetime;
- ○
- : Damping term preventing runaway growth in high-density -regions;
- ○
- : Higher-order stabilization term contributing to self-interactions;
- ○
- : Temporal feedback ensuring dynamic stability of informational flows;
- ○
- : Entropy gradients driving quantum informational flows ;
- ○
- : Unified potential field coupling quantum informational density to spacetime and matter.
- Physical Interpretation:
- represents the quantum informational substrate of reality, encoding all properties and behaviors of particles, forces, and spacetime.
2.4. Relationships Between PIF, Quantules, and
- PIF as the Substrate:
- Quantules as Building Blocks:
- as Informational Density:
3. The Three Core Principles of IQG
3.1. Quantum Information Evolution Principale (QIEP)
- : Quantum informational density;
- : Velocity of quantum informational flow;
- : Entropy gradient driving informational dynamics.
3.2. Quantum Holographic Encoding Stabilizer (QHES)
- : Informational entropy encoded at boundaries;
- : Surface area of the boundary;
- : Gravitational constant.
3.3. Informational Optimization Principle (IOP)
- Intelligence is the result of systems optimizing their quantum informational flows () while balancing dissipative losses () and entropy gradients ().
- This principle applies universally, from biological intelligence to artificial and cosmic systems.
- Represents the boundary conditions or constraints limiting informational dynamics.
- In context of intelligence: Reflects the physical and structural limitations of a system (e.g., brain capacity, computational hardware);
- Dissipated quantum informational energy, describing the loss or spread of information.
- In context of intelligence: Represents inefficiencies or entropy in processing information (e.g., energy lost in brain or system heat);
- Entropy gradient driving the optimization of informational flows.
- In context of intelligence: Reflects the drive to reduce uncertainty, improve decision-making, and achieve self-organization;
- Strength of quantum informational flow, quantifying how efficiently a system processes and optimizes information.
- In context of intelligence: Represents the system’s ability to process, store, and retrieve information efficiently, enabling learning, adaptation, and self-awareness.
- : Informational efficiency, quantifying how well a system optimizes flows relative to its losses.
- Condition for Intelligence:
4. Comparative Analysis [16]
4.1. Quantum Mechanics (Microscopic Scale):
- : Reduced Planck's constant, governing the quantum scale;
- : Wavefunction, representing the probabilistic quantum state;
- : Laplacian operator, describing spatial variations of ;
- : Mass of the particle;
- : Potential energy field acting on the quantum system.
4.1.1. Informational Quantum Gravity: Extending the Schrödinger Equation
4.1.2. Interpretation of the Schrödinger Equation in IQG
- : Quantum informational flows, representing the dynamic redistribution of ;
- : Entropy-driven redistribution of , guiding coherence and stability;
- : Flow along entropy gradients () in the PIF.
4.1.3. Comparison Between Classical and Informational Interpretations
| Aspect | Traditional Schrödinger Equation | IQG Interpretation |
| ) | Describes probabilistic quantum states. | . |
| ) | Captures spatial variations of the wavefunction. | . |
| ) | External field acting on the quantum system. | in the PIF. |
| Physical Processes | Coherence and entanglement are treated probabilistically. | -flows and informational dynamics. |
4.1.4. The IQG Generalization of the Schrödinger Equation [19]
- : Nonlinear stabilization term for quantum informational density;
- : Higher-order stabilization, maintaining coherence and preventing singularities;
- : Represents the external potential acting on the quantum system.
4.1.5. Physical Implications
- Probabilities in quantum mechanics arise from the distribution of -flows in the PIF, offering a deeper explanation for the Born rule.
- The Schrödinger equation becomes a special case of the PIF equation, applicable to microscopic scales, with the wavefunction representing localized -flows.
- Coherence and entanglement, governed by , provide a mechanism for understanding how quantum systems transition to classical behavior.
4.1.6. Informational Gauge Dynamics, Nonlocal Correlations, and Path Integral in IQG
4.1.6.1. Informational Gauge Dynamics
4.1.6.2. Gauge Covariance
- : Gauge fields, representing the quantum informational flows that mediate interactions;
- : Generators of the symmetry group;
- : Coupling constant.
4.1.6.3. Gauge Field Dynamics
4.1.6.4. Forces as Informational Flows
- Mediated by the photon (), representing informational flows within the gauge symmetry.
- Mediated by and bosons, with broken symmetry giving rise to massive mediators.
- Mediated by gluons (), binding quarks within hadrons via informational exchanges.
4.1.6.5. Nonlocal Correlations and Quantum Entanglement
4.1.6.6. Informational Basis of Entanglement
- and : Informational densities of individual subsystems;
- : Nonlocal correlations encoded in the shared informational density.
4.1.6.7. Bell’s Inequalities
4.1.6.8. Predictions for Entangled Systems
- In regions of high-density , entangled particles experience accelerated decoherence due to intensified quantum informational interactions.
- Testable Hypothesis: Experiments near high-mass objects or in regions of gravitational wave disturbances could measure these effects.
- The underlying -dynamics could produce unique interference patterns in entangled photon experiments, especially under varying -flow conditions.
4.1.6.9. Informational Path Integral [21]
4.1.6.10. Action for -Dynamics
- : Represents the kinetic energy of ;
- : Encodes potential energy and interactions with gauge fields;
- : Describes the dynamics of gauge fields coupled to .
4.1.6.11. Predictions for Quantum Phenomena
- Corrections to particle scattering amplitudes based on -flows within the PIF.
- Stabilization terms () may modify predicted lifetimes for unstable particles.
- The dynamics of -flows in the PIF could explain observed deviations in vacuum energy.
4.1.7. Chapter Conclusion
4.2. General Relativity (Macroscopic Scale):
- : Ricci curvature tensor, describing spacetime curvature;
- : Ricci scalar, summing the curvature contributions;
- : Metric tensor, defining the geometry of spacetime;
- : Cosmological constant, representing the energy density of empty space (dark energy);
- : Energy-momentum tensor, describing the distribution of matter and energy;
- : Gravitational constant;
- : Speed of light.
4.2.1. Informational Quantum Gravity: Extending the Field Equation
- : Informational stress-energy tensor.
4.2.2. Components of the Informational Stress-Energy Tensor
- Represents the momentum flux of quantum informational flows;
- Encodes how -flows dynamically influence spacetime.
- A nonlinear stabilization term that prevents runaway growth in high-density -regions;
- Analogous to damping mechanisms in physics, ensuring stability near black holes or other extreme conditions.
- A higher-order term contributing to self-interactions and further stabilizing high-density regions.
- Describes quantum informational gradients influencing spacetime curvature;
- Represents the interplay of local variations in with the geometry of spacetime.
- In IQG, is reinterpreted as a mechanism for informational stabilization, ensuring the smooth evolution of -flows in large-scale structures.
4.2.3 Physical Interpretation: From Matter to Information
- : Represents classical matter and energy.
- Spacetime Curvature: Directly linked to the distribution of mass-energy.
- : Represents quantum informational density and its dynamics.
- Emergent Spacetime: Arises from -flows in the PIF, with curvature reflecting the self-organizing behavior of information.
4.2.4. Why the Informational Einstein Field Equation?
- Incorporates quantum informational principles directly into the spacetime framework.
- Stabilization terms () ensure finite -density, replacing classical singularities with smooth, high-density regions.
- High- and low-density -regions naturally align with observed effects attributed to dark matter and dark energy.
- Predicts gravitational wave anomalies, non-singular black hole interiors, and quantum correlations in cosmic structures.
4.2.5. Chapter Conclusion
4.2.6. Cosmological Implications of Informational Density
4.2.7. Dark Energy
4.2.8. Structure Formation
4.2.9. Horizon Entropy
4.2.10. Quantum Effects in General Relativity
4.2.10.1. Modified Einstein Equations
4.2.10.2. Singularity Resolution
4.2.10.3. Black Hole Information Preservation
4.2.10.4. Testable Predictions
- High-density regions distort spacetime, leading to observable deviations in waveforms.
- Example: Anomalous polarization patterns detectable by LIGO or future observatories.
- Non-Gaussian signatures in the CMB may reflect early-time quantum fluctuations in .
- High-density, non-interacting quantule clusters correspond to dark matter and can be detected via gravitational lensing.
4.3 Standard Model
4.3.1. Introduction
4.3.2. Gauge Symmetries and Informational Dynamics [31]
- Strong Force (): Governs quarks and gluons through the color charge;
- Weak Force (): Governs the weak nuclear interaction and mediates and bosons;
- Electromagnetic Force (): Mediates photons and the electromagnetic interaction.
- These symmetries emerge as invariance properties of the informational density under local transformations:
4.3.3. Informational Gauge Fields
- Mediated by 8 gluons ();
- Informational density clusters (quarks) interact via gluonic fields, resulting in confinement.
- Mediated by and bosons;
- Broken symmetry leads to massive particles.
- Mediated by the photon ();
- U(1) symmetry ensures charge conservation.
4.3.4. Emergence of Particles as Quantule Configurations
- Represent clusters of with specific spin- properties;
- Their masses arise through interactions with the Higgs field.
- Wave-like excitations of the gauge fields that mediate interactions.
- Represents the scalar component of responsible for mass generation.
4.3.5. Higgs Mechanism and Mass Generation [32]
- The Higgs field acquires a nonzero VEV:
- This breaks the symmetry to .
- and bosons become massive;
- Fermions acquire mass proportional to their Yukawa couplings with .
4.3.6. Informational Interpretation of Forces
- Coulomb potential between charges corresponds to the exchange of quantules via the photon field.
- Short-range interactions arise from massive and bosons.
- Confinement of quarks corresponds to the self-organizing dynamics of under gauge fields.
4.3.7. Predictions Beyond the Standard Model
- High-density, non-interacting quantule clusters may explain dark matter;
- These clusters interact gravitationally but not electromagnetically.
- Gauge field dynamics couple to spacetime curvature through , leading to testable distortions in gravitational waves.
- Additional configurations of could correspond to unknown particles beyond the SM, such as heavy bosons or new fermions.
4.3.8. Mathematical Representation
4.3.9. Testable Predictions
- High-density regions influence spacetime curvature, producing deviations in waveforms.
- Deviations in Higgs boson decay rates due to its informational coupling.
- Identify non-interacting quantule clusters through gravitational lensing or cosmological surveys.
4.3.9. Chapter Conclusion
5. The Fabric of the Universe in Informational Quantum Gravity (IQG)
5.1. Components of the Fabric
- Represents the foundational substrate of reality, encoding both quantum properties and spacetime geometry.
- Evolved dynamically within the PIF, serves as the universal source for particles, forces, and spacetime curvature.
- Emergent, discrete units of that act as the building blocks of reality.
- Quantules interact dynamically within the PIF, clustering into high-density nodes or flowing across spacetime, forming particles and forces. (Appendix A.1.4).
- The universal medium in which evolves and quantules interact.
- Encodes the informational dynamics that underpin the emergence of physical phenomena.
5.2. Emergence of Physical Phenomena
- Quantules cluster into high-density nodes, forming particles such as quarks, electrons, and photons. These clusters are stabilized through entropy gradients () and nonlinear self-interaction terms.
- Stabilization is governed by:

-
Flows of quantum informational density () between quantules manifest as forces:
- ○
- Electromagnetic Force: Mediated by the exchange of quantules associated with photons;
- ○
- Gravitational Force: Emerges from spacetime curvature shaped by the distribution of ;
- ○
- Strong and Weak Forces: Correspond to quantule interactions coupled to and gauge symmetries.
- The overall distribution and dynamics of define spacetime geometry, linking quantum informational flows to macroscopic curvature.
- The Einstein-like equation describes this relationship:

5.3. Dynamic Nature of the Fabric
- Quantum fluctuations in seeded the formation of large-scale structures, such as galaxies and clusters, observable through cosmic microwave background (CMB) anisotropies:
- High-density regions stabilize spacetime, resolving singularities and encoding information holographically at event horizons.
- Distortions in propagate as gravitational waves, with frequency and amplitude affected by high-density regions.
5.4. Observable Implications
- High-density regions create distortions in gravitational wave propagation, observable through LIGO and Virgo. Predicted deviations include frequency shifts and polarization anomalies.
- Quantule clusters correspond to dark matter, influencing galaxy rotation curves and gravitational lensing patterns. Observations from Euclid and DESI can validate these predictions.
- Non-Gaussian patterns in the CMB, caused by early fluctuations in , are consistent with data from Planck and the Simons Observatory.
5.5. Unified Description
- Universal Substrate: Quantum informational density () serves as the foundation of all physical phenomena.
- Emergent Structures: Particles, forces, and spacetime arise naturally from the interactions of quantules within .
- Dynamic Evolution: The universe is in constant flux, with driving its growth and transformation across quantum and cosmic scales.
- Testability: Observable effects, such as gravitational wave distortions and large-scale structure patterns, provide experimental pathways to validate the theory.
- Entropy-Driven Dynamics: The PIF’s evolution, guided by (), balances informational order and disorder, mirroring thermodynamic principles central to entropy research.
5.6. Chapter Conclusion
6. Resolving Longstanding Paradoxes
7. Experimental and Simulative Validation
7.1. Gravitational Wave Distortions [44]
7.1.1. Objective
7.1.2. Predictions
7.1.3. Method
- Analyze gravitational wave data from LIGO and Virgo detectors for deviations from general relativity predictions.
- Simulate gravitational wave propagation using the Einstein-like PIF Equation:
- Compare simulated waveforms with observational data.
7.2. Dark Matter Clustering
7.2.1. Objective
7.2.2. Predictions
7.2.3. Method
- Simulate dark matter clustering dynamics using:
- Analyze the clustering and gravitational lensing patterns.
- Compare simulation results to galaxy rotation curves and lensing maps.
7.3. Quantum Systems and Informational Flows
7.3.1. Objective
7.3.2. Predictions
- Informational density dynamics influence quantum coherence and entanglement;
- Systems optimize quantum informational flows () to achieve stability.
7.3.3. Method
- ○
- Entangled Quantum Systems:
- Analyze entangled particle behavior to test the optimization of :
- Use quantum computers to simulate evolution in the PIF, governed by the Dynamic PIF Equation. For instance, [45] demonstrated reversible information storage on IBM QPUs, suggesting IQG’s -flows could be tested similarly, enhancing coherence predictions.
7.4. Simulative Models for the PIF
7.4.1. Objective
7.4.2 Method:
-
2D and 3D Simulations:
- ○
- Model quantule interactions within the PIF to simulate clustering, flows, and emergent nodes.
- ○
-
Use visualizations to highlight:
- ➢
- High-density regions stabilizing into particles or dark matter.
- ➢
- Quantum informational flows linking nodes.
-
Dynamic Evolution:
- ○
-
Simulate wave propagation and entropy-driven redistribution using:, (47)
- ○
- Analyze how density stabilizes or disperses over time.
8. Further Experimental Validation of Informational Quantum Gravity (IQG)
8.1. Gravitational Observatories
- Existing facilities such as LIGO and Virgo are ideal for detecting subtle deviations in waveform amplitude or polarization caused by quantum informational flows in high-density regions.
- Next-generation observatories like LISA (Laser Interferometer Space Antenna) and the Einstein Telescope will provide enhanced sensitivity to gravitational wave signals from cosmological and astrophysical sources. These tools can probe -driven distortions at greater distances and higher resolutions.
- Deviations in gravitational wave frequency, phase, or polarization patterns linked to high- regions. (Appendix A.1, Figure A.1.1.3). QMM similarly predicts GW corrections [46], supporting IQG’s -driven anomalies as a testable extension.
8.2. Cosmological Surveys
- The DESI (Dark Energy Spectroscopic Instrument) and Euclid missions can provide high-resolution data on galaxy distributions, lensing patterns, and cosmic structure formation. These surveys are crucial for identifying clustering dynamics consistent with quantum informational flows.
- Early-universe quantum fluctuations in predict non-Gaussian signatures in the CMB, observable through facilities like the Simons Observatory and Planck.
- Gravitational lensing patterns and galaxy clustering consistent with high-density clusters acting as dark matter analogs, predicted lensing distortions (~10⁻⁵ arcsec) align with Euclid’s precision. (Appendix A.1.2, Figure A.1.2.3). QMM’s CMB imprint predictions [47] complement IQG’s non-Gaussian CMB signatures, broadening cosmological validation.
8.3. Quantum Experiments
- Test how -induced flows enhance or suppress entanglement in controlled quantum systems, using platforms such as superconducting qubits or ultracold atoms.
- Analyze coherence and decoherence rates in high-density environments to validate entropy-driven dynamics. Experimental setups like quantum simulators or trapped ion systems can reveal optimization properties predicted by the Informational Optimization Principle (IOP).
- Enhanced or anomalous entanglement behavior in quantum systems driven by informational flows. (Appendix A.1.3, Figure A.1.3.3).
8.4. Chapter Conclusion
9. Potential Technological Applications of Informational Quantum Gravity (IQG)
9.1. Quantum Computing [49]
9.1.1. Optimization Algorithms
-
IQG’s Informational Optimization Principle (IOP) inspires advanced algorithms to maximize quantum coherence and reduce entropy, enabling:
- ○
- Faster quantum computations.
- ○
- Efficient solutions for complex optimization problems.
9.1.2. Error Correction
- Insights into quantum informational flows () enhance quantum error correction, improving stability and reliability in quantum systems.
9.1.3. New Paradigms in Quantum Architecture
- IQG principles guide the development of fault-tolerant quantum computers capable of simulating quantum informational networks and natural systems. QMM’s QC-inspired framework [50] aligns with IQG’s potential for quantum simulations of -networks, tested on IBM QPUs.
9.2. Cryptography
9.2.1. Quantum Encryption
- Leveraging quantum informational density () enables unbreakable encryption schemes, securing communication and data systems against vulnerabilities.
9.2.2. Advanced Key Distribution
- IQG optimizes quantum key distribution (QKD), enhancing speed, reliability, and security of encrypted communications.
9.3. Artificial Intelligence
9.3.1. Self-Optimizing AI
- IQG’s principles of self-organization inspire adaptive AI systems capable of learning, optimizing, and adapting dynamically to complex environments.
9.3.2. Neuromorphic Computing
- Quantum informational dynamics guide the design of neuromorphic architectures that mimic the PIF’s entropy-balancing properties, enabling human-like decision-making in AI.
9.3.3. Complexity Modeling
- IQG’s tools for managing quantum informational flows provide powerful frameworks for modeling and solving global challenges, from climate modeling to resource optimization.
9.4. Advanced Materials and Energy
9.4.1. Quantum-Informed Materials
- Using quantum informational density, new materials with optimized properties like conductivity, robustness, or superconductivity can be developed.
9.4.2. Energy Optimization
- IQG’s entropy-reduction principles inspire energy-efficient systems for computation and power distribution, minimizing losses and enhancing sustainability.
9.4.3. Dark Matter-Inspired Technologies
- Understanding dark matter as high-density regions leads to innovative approaches for harnessing quantum informational fields in energy applications.
9.5. Simulation and Modeling
9.5.1. Quantum Simulators
-
IQG principles enable quantum simulators to model:
- Black hole evaporation and holographic encoding.
- Dark matter clustering and early universe quantum dynamics.
9.5.2. High-Precision Modeling
- Quantum informational density () enhances the accuracy of models for gravitational wave dynamics, quantum tunneling, and molecular interactions.
9.6. Communication Technologies
9.6.1. High-Fidelity Quantum Networks
- IQG’s insights into quantum informational flows improve quantum communication networks, enabling faster, more reliable, and interference-resistant communication.
9.6.2. Informational Density-Driven Transmission
- Encoding data in quantum informational density () supports ultra-high-capacity communication systems, paving the way for global connectivity and exploration missions.
9.7. Space Exploration and Universal Building
9.7.1. Spacecraft Optimization
- IQG principles guide the design of spacecraft systems, minimizing energy dissipation and maximizing informational efficiency, enabling longer and more sustainable missions.
9.7.2. Large-Scale Cosmic Structures
- Understanding quantum informational flows in the PIF provides a framework for building artificial cosmic structures, such as advanced space habitats and orbital energy systems.
9.7.3. Interstellar Communication
- IQG-inspired quantum communication technologies enable reliable data transfer over vast distances, supporting interstellar exploration and collaboration.
9.8. Chapter Conclusion
10. Acknowledge
11. Ethical Vision for IQG
12. Data Availability Statement
13. Declarations
14. Conclusions
Appendix A. Experimental and Simulative Validation Results
Appendix A.1. Gravitational Wave Distortions
Appendix A.1.1. Gravitational Wave Distortions
A.1.1.1. Objective
A.1.1.2. Setup
- Grid and Parameters:
- Wave Propagation:
- Gravitational Effects:
A.1.1.3. Results
- High-density regions at andcreated localized distortions in the wave amplitude.
- The central disturbance propagated dynamically, with visible interactions near high-density nodes.
- The final wave state, visualized using a seismic colormap, highlights areas of distortion caused by quantum informational density.
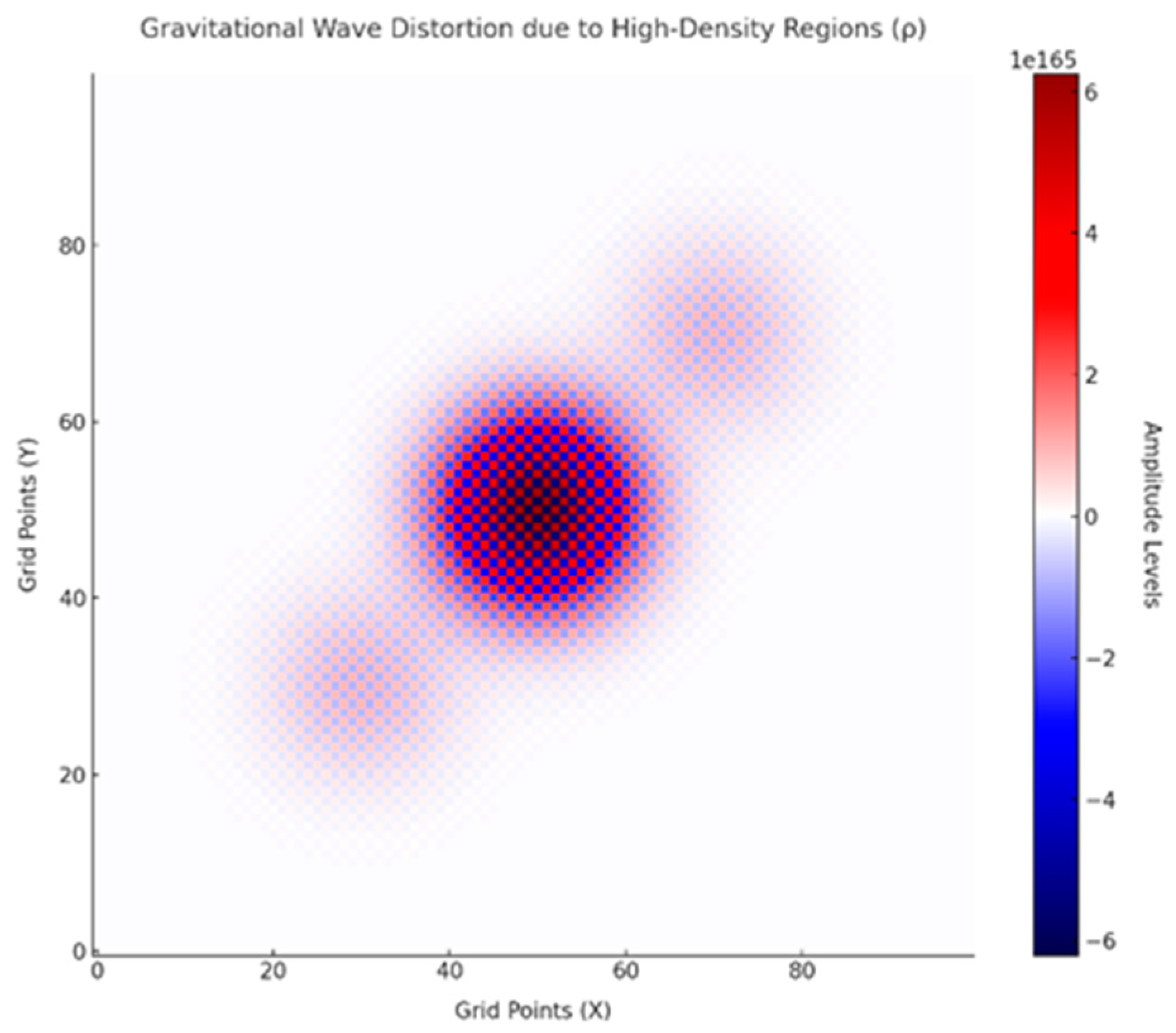
A.1.1.4. Analysis
- Physical Alignment:
- Observable Implications:
- Conclusion
Appendix A.1.2. Dark Matter Clustering
A.1.2.1. Objective
A.1.2.2. Setup
- Evolution Rules:
- ○
- Diffusion:
- ○
- Nonlinear Stabilization:
- Timesteps:
A.1.2.3. Results
- High-density regions at and influenced the surrounding density grid, driving the formation of localized clusters.
- Diffusion and nonlinear stabilization terms guided the clustering and interaction of quantum informational density.
- The final state revealed stable high-density clusters surrounded by smoother diffusion patterns, resembling observed dark matter halos.
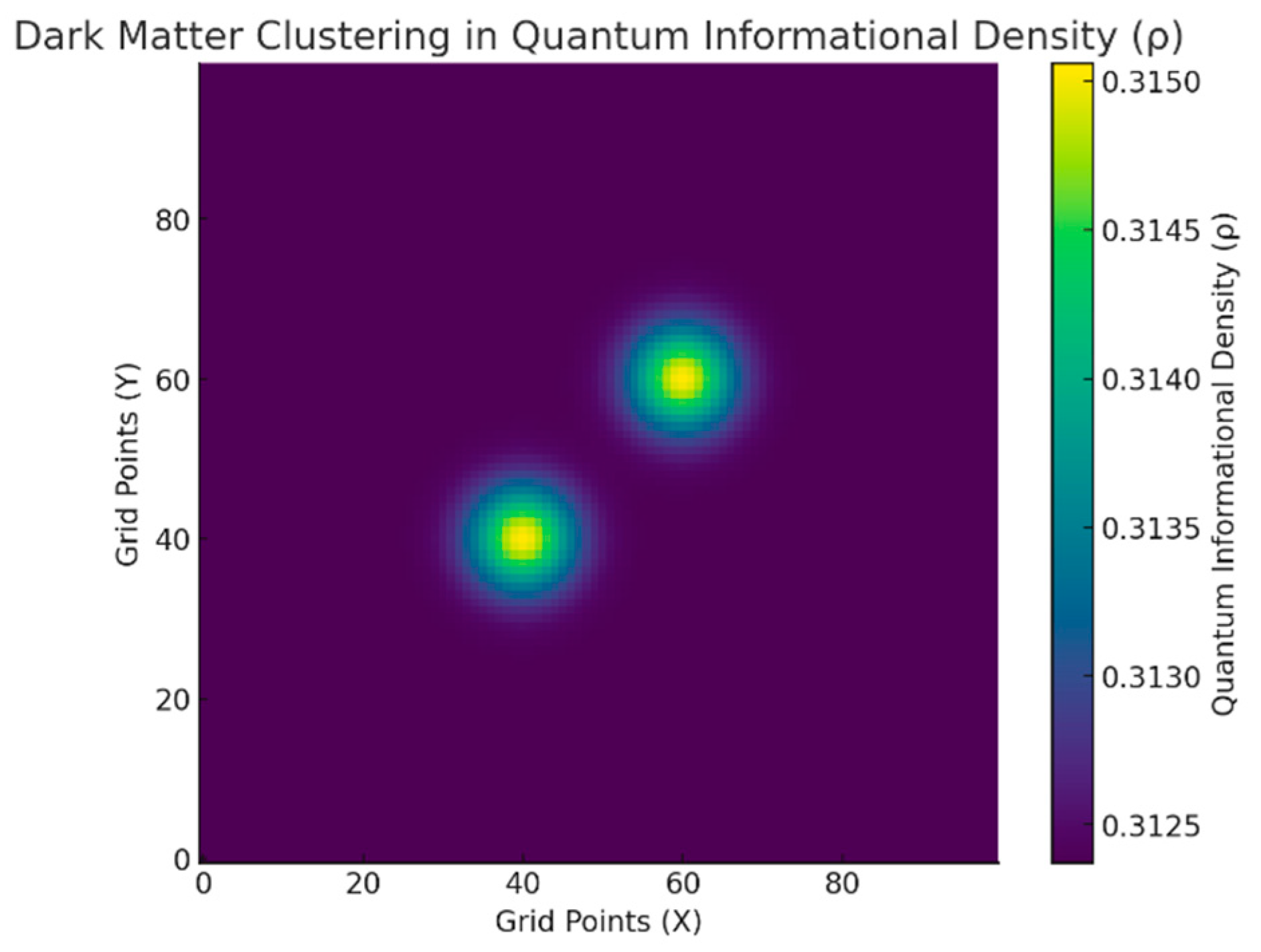
A.1.2.4. Analysis
- Alignment with IQG Principles:
- High-density quantum informational regions correspond to dark matter clusters that influence spacetime curvature.
A.1.2.5. Conclusion
Appendix A.1.3. Quantum Systems and Informational Flows
A.1.3.1. Objective
A.1.3.2. Setup
- Quantum informational flows (), dissipation (), and entropy gradients () were randomly initialized across 100 quantum systems.
- Informational efficiency () was computed for each system:
- A histogram was used to represent the distribution of values.
A.1.3.3. Results
- The histogram of revealed:
- ○
- Clustering: Most systems exhibited low to moderate efficiency;
- ○
- High-Efficiency Outliers: A few systems achieved exceptionally high , indicating successful optimization.
- Average Efficiency (): Reflects the typical system performance;
- Maximum Efficiency (): Indicates systems with optimal flows and minimal dissipation;
- Minimum Efficiency (): Highlights entropy-dominated or dissipative systems.
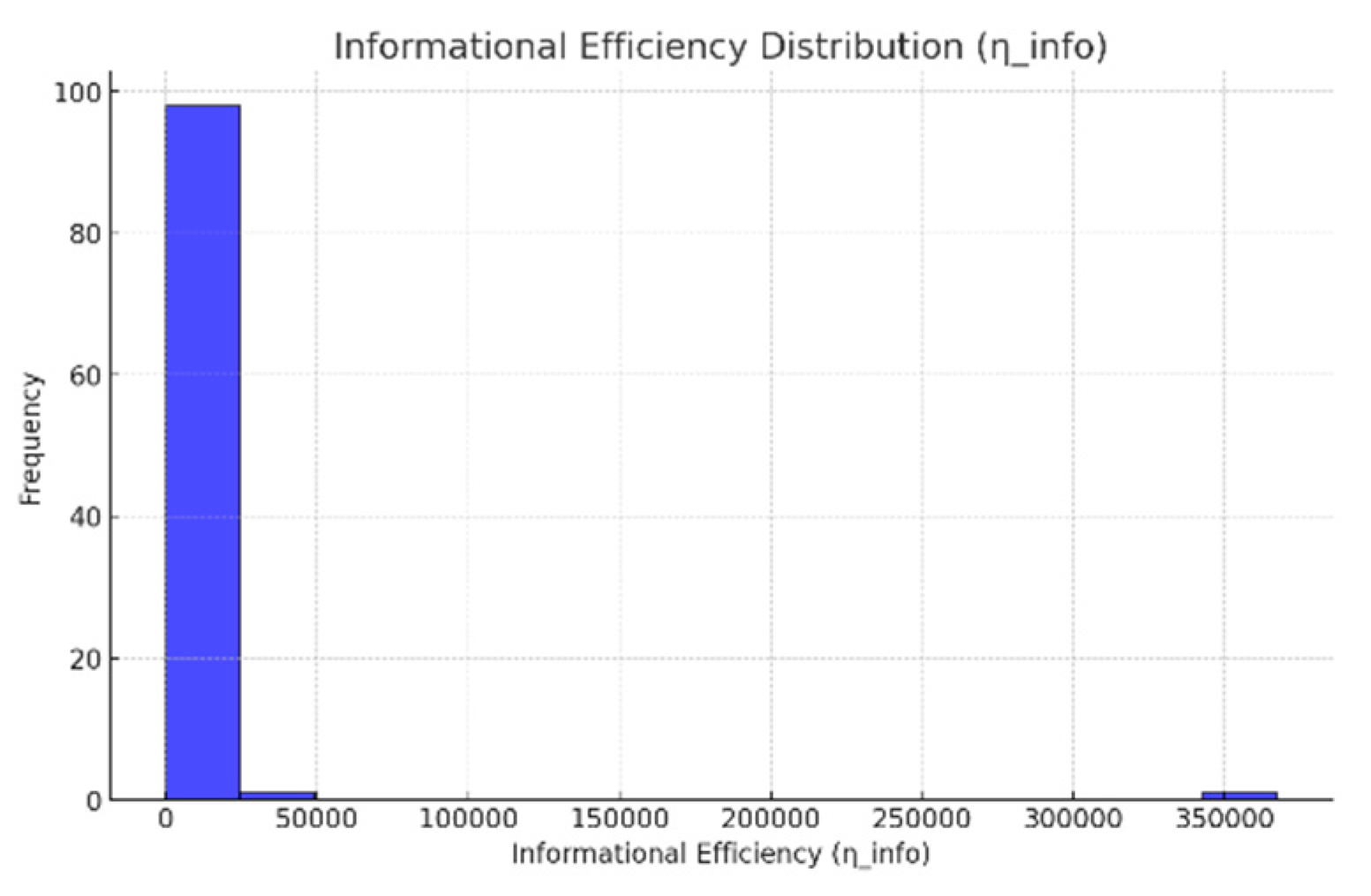
A.1.3.4. Analysis
- The results validate the IOP:
- High-efficiency systems () balance entropy gradients and dissipation, optimizing flows for stability.
- The variability in reflects the natural dynamics of quantum informational density () in the PIF;
- High-efficiency systems correspond to coherent quantum states, while low-efficiency systems struggle with entropy or dissipation.
A.1.3.5. Conclusion
Appendix A.1.4: Simulative Model of the Primordial Informational Field (PIF)
A.1.4.1. Objective
A.1.4.2. Setup
- A spatial grid represented the PIF, initialized with 500 quantules randomly distributed across the grid;
- Each quantule was assigned an initial quantum informational density () between 0 and a threshold ().
- Quantule interactions were simulated over 200 timesteps, with snapshots saved at intervals for visualization.
A.1.4.3. Results
- The final scatter plot showed quantules distributed across the grid, with size and color reflecting quantum informational density ().
- High-density regions emerged as clusters of larger, brighter dots, while lower-density regions appeared smaller and more diffuse.
- High-density regions formed naturally as quantules interacted, aligning with the self-organizing principles of the PIF.
- Diffusion and interaction effects balanced clustering and entropy-driven dispersion.
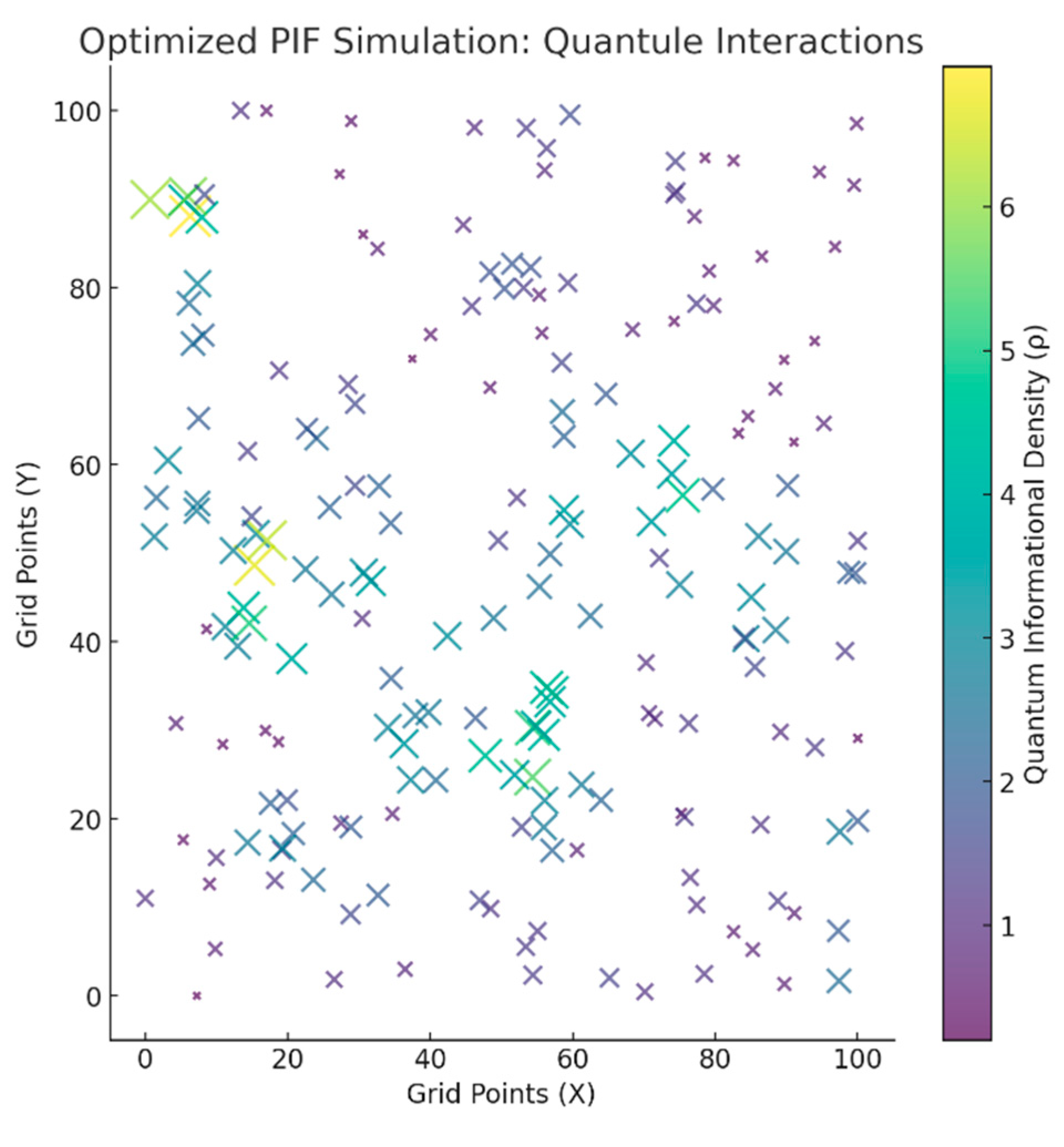
A.1.4.4. Analysis
- The simulation validates the Dynamic PIF Equation:
- ○
- High-density regions emerge under nonlinear stabilization terms () and entropy gradients ().
- High-density clusters correspond to quantum informational nodes, representing particles, forces, or dark matter regions within the PIF.
- The formation of clusters reflects the Informational Optimization Principle (IOP), where quantum informational flows () balance entropy and dissipation.
A.1.4.5. Conclusion
Appendix B. Resolving Longstanding Paradoxes Results
Appendix B.1. Black Hole Information Preservation
B.1.1. Objective
B.1.2. Setup
- A spatial grid was initialized with a high-density core () centered at , representing the black hole interior;
- The event horizon was modeled as a circular boundary () where information is encoded holographically.
- Dissipation simulated Hawking radiation by reducing globally ( decay factor per timestep);
- Quantum information was holographically encoded on the event horizon:
B.1.3. Results
- The density in the black hole’s core decayed uniformly over 100 timesteps, mimicking evaporation.
- Information was preserved on the event horizon, with higher encoded values near the surface, supporting the holographic principle.
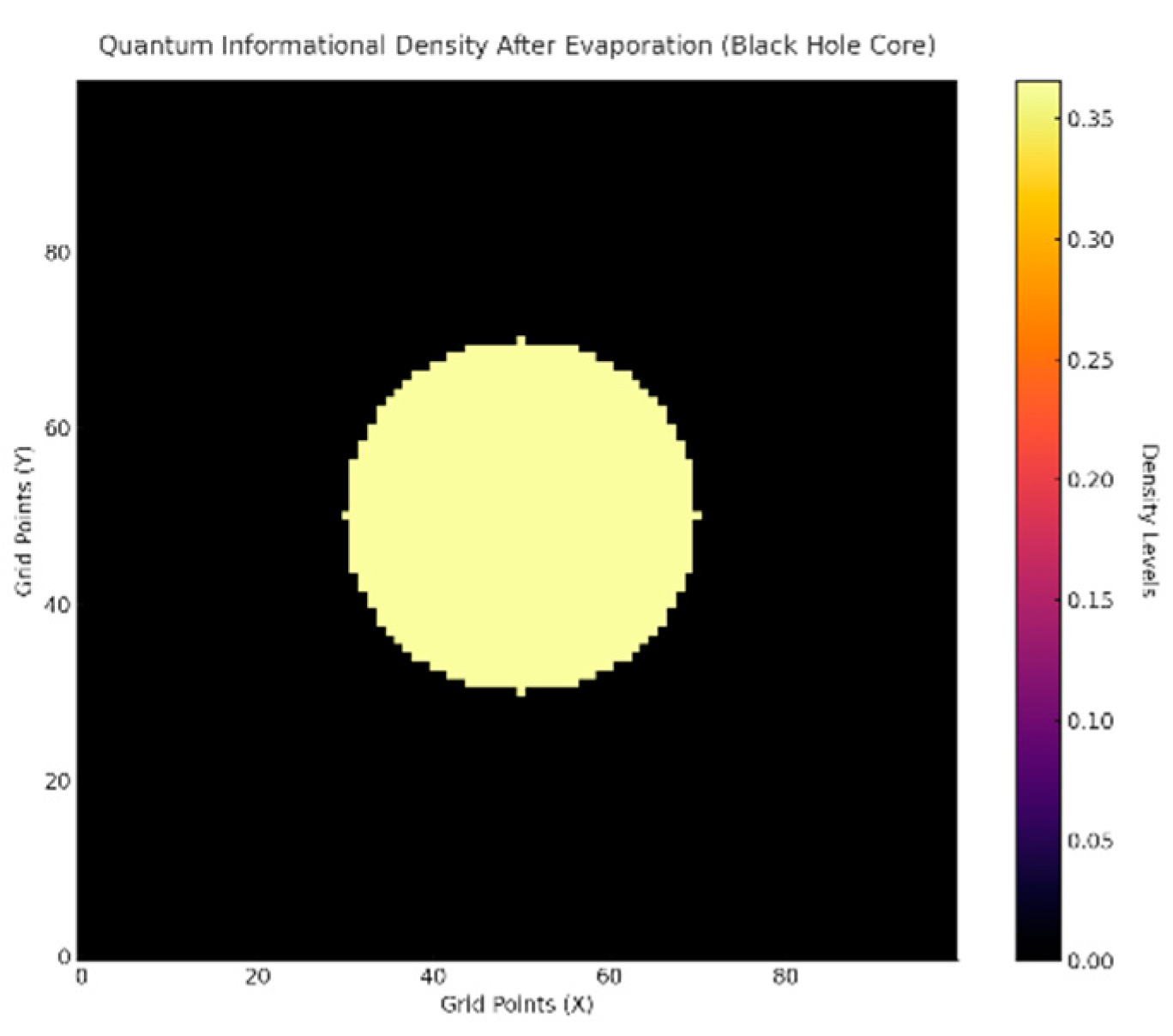
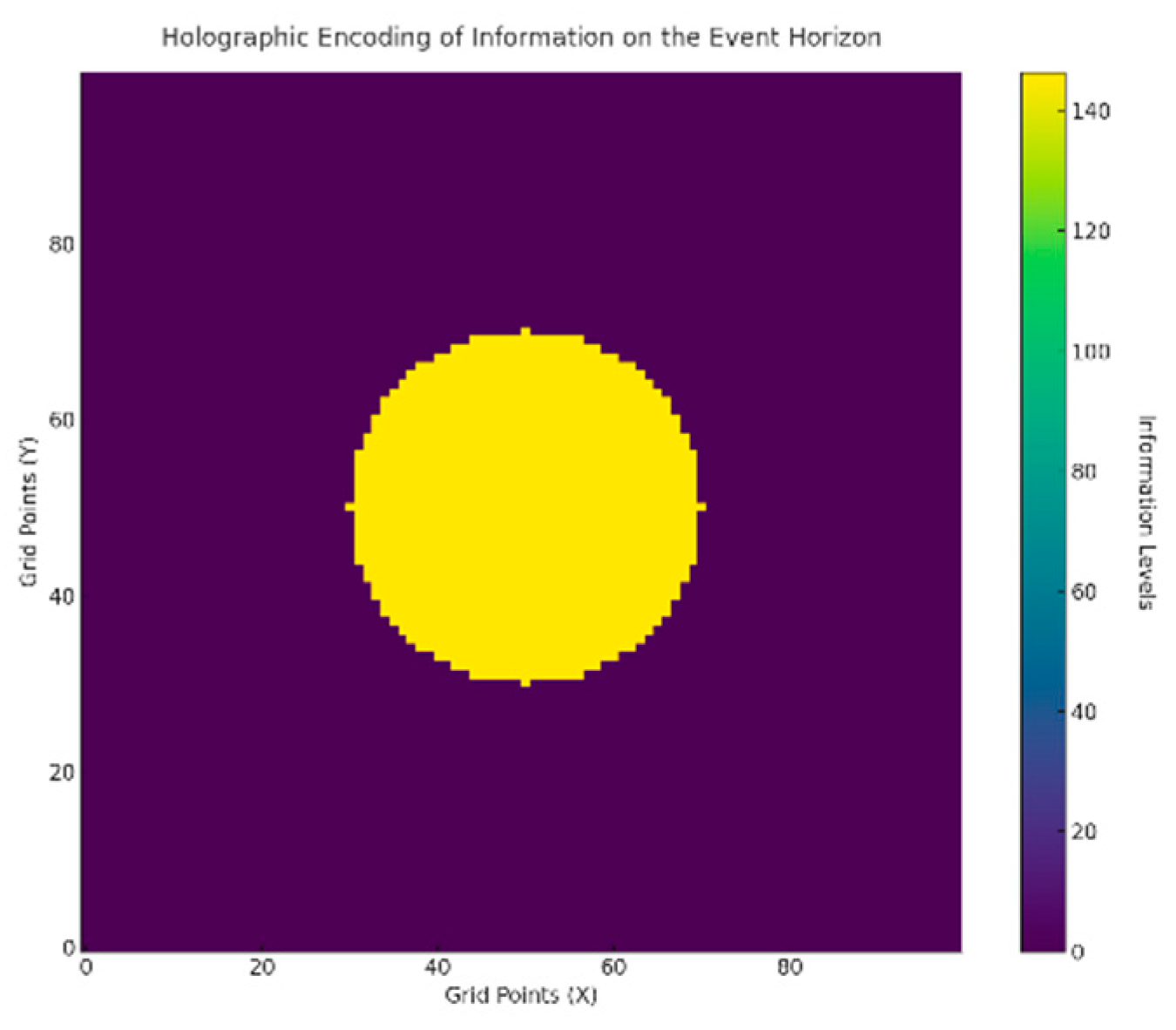
Appendix B.2. Singularity Dynamics
B.2.1. Objective
B.2.2. Setup
- A spatial grid was initialized with a high-density singularity at the center ().
- Density evolved under:
- ○
- Diffusion () for outward spreading;
- ○
- Nonlinear stabilization () to prevent divergence;
- ○
- Dissipation ( decay factor per timestep).
B.2.3. Results
- Density diffused outward while dissipating globally, leading to a stabilized singularity with finite density.
- The central singularity persisted as a stable, high-density region, moderated by nonlinear effects.
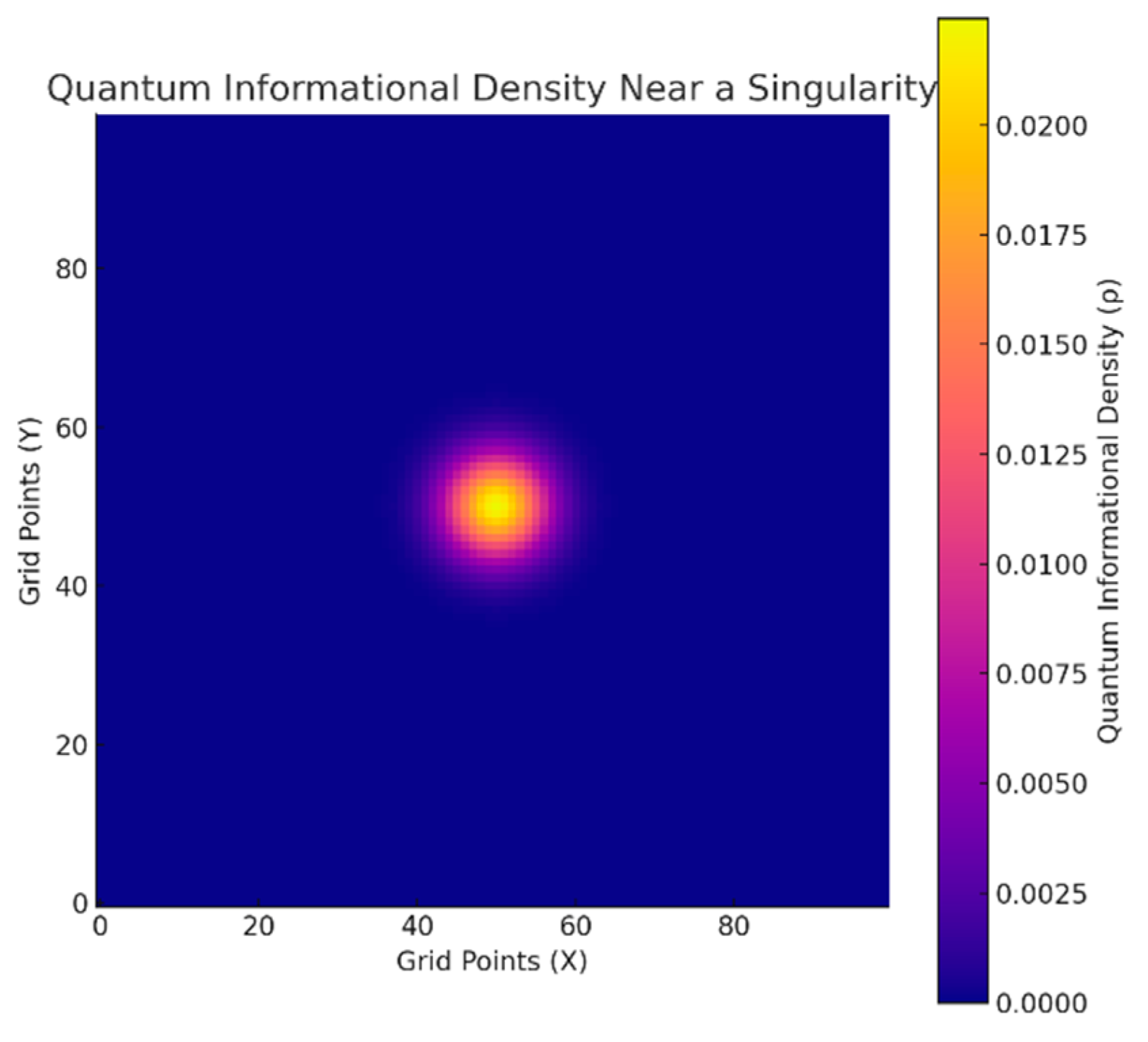
Appendix B.3. Simulation
- Information is preserved holographically on the event horizon, resolving the apparent loss of information during evaporation.
- Nonlinear effects prevent infinite densities, stabilizing the singularity and ensuring a finite, stable state.
Appendix C. Resolving Schrödinger’s Cat Paradox: No Need for Observation
Appendix C.1. Introduction
Appendix C.2. Wavefunction Collapse in IQG
C.2.1. Self-Organizing Dynamics
- The evolution of follows:
- Collapse occurs as reorganizes to optimize informational flows and minimize entropy.
- The Informational Optimization Principle (IOP) explains how systems self-optimize:
- Collapse represents the transition to a state where entropy gradients and dissipation are minimized.
Appendix C.3. Simulation Results
C.3.1. Setup
- A spatial grid was initialized with a high-density central region () to represent the quantum system in superposition.
- Diffusion: Quantum informational density spread outward over time, simulating the wavefunction's probabilistic expansion.
C.3.2. Results
- Quantum informational density diffused outward from the center, maintaining a probabilistic distribution.
- When collapse occurred, all density concentrated at the grid location with the highest value, representing the transition to a definite state.
- Collapse time was recorded for simulations where collapse occurred.
- The final grid either showed:
- ○
- Post-Collapse: A single concentrated point of density.
- ○
- No Collapse: A more uniformly distributed density grid.
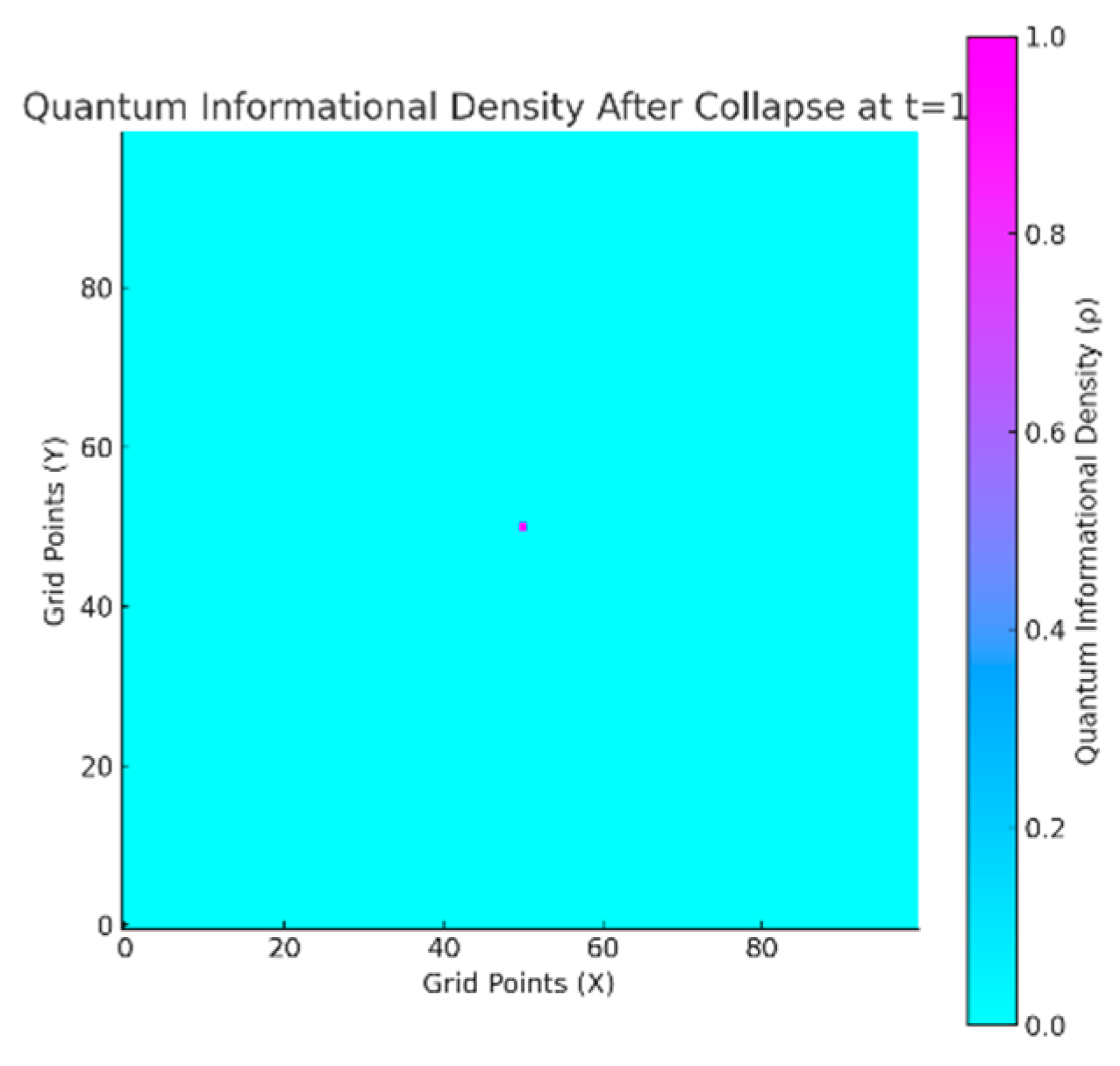
C.3.3. Analysis
C.3.3.1. Modeling Quantum Collapse
- The simulation demonstrated the probabilistic nature of wavefunction collapse, consistent with quantum mechanics;
- Collapse reflects a non-linear reorganization of quantum informational density, transitioning from superposition to a definite state.
C.3.3.2. Connection to IQG
- Superposition:
- ○
- Diffusion aligns with the Dynamic PIF Equation, reflecting the wave-like propagation of quantum informational density:
- Collapse:
- ○
- Collapse represents the optimization of informational flows () and the reduction of entropy gradients (), aligning with the Informational Optimization Principle (IOP).
Appendix C.4. Conclusion
- The quantum informational density diffuses outward, maintaining a probabilistic distribution.
- Collapse, when triggered, concentrates density at a single point, reflecting the transition to a definite state.
Appendix D. Inspiration Behind Informational Quantum Gravity (IQG)
Appendix D.1. The Quantum Revolution
D.1.1. Quantum Mechanics
- Wavefunction and Probabilities:
- ○
- Quantum mechanics introduced the idea of probabilistic states, where the wavefunction () encodes the likelihood of outcomes;
- ○
- IQG generalizes this idea into quantum informational density (), treating the universe as a dynamic network of quantum information.
- Collapse and Measurement:
- ○
- The phenomenon of wavefunction collapse inspired IQG’s self-organizing dynamics, where quantum informational flows and entropy gradients drive transitions between states.
- Shannon Entropy:
- ○
- Claude Shannon’s work on entropy in information systems laid the groundwork for understanding quantum informational flows in IQG;
- ○
- IQG’s entropy gradients () reflect this influence, describing how systems evolve toward optimized states.
- Quantum Entanglement:
- ○
- Entanglement, where particles remain connected across vast distances, inspired IQG’s concept of quantules interacting dynamically within the PIF.
Appendix D.2. The Relativity Breakthrough
D.2.1. General Relativity
- Spacetime Curvature:
- ○
- Einstein’s field equations describe how energy and matter curve spacetime.
- ○
- IQG extends this idea by incorporating quantum informational density () into spacetime curvature through the Einstein-like PIF Equation:
- Holographic Principle:
- ○
- The holographic principle, proposed by Gerard ’t Hooft and Leonard Susskind, suggests that all information in a volume is encoded on its boundary;
- ○
- IQG builds on this by encoding quantum informational density () holographically at boundaries like black hole event horizons.
Appendix D.3. The Rise of Information as Fundamental
D.3.1. Wheeler’s “It from Bit”
- John Archibald Wheeler proposed that information is the fundamental building block of reality;
- IQG adopts and extends this vision, positing that quantules are the discrete packets of quantum information that form the fabric of the universe.
D.3.2. Entropy and Thermodynamics
- Boltzmann’s entropy concepts and their quantum extensions inspired IQG’s emphasis on entropy-driven flows (), which drive the evolution and optimization of quantum informational density.
Appendix D.4. Unresolved Challenges in Physics
- IQG resolves this paradox by encoding information holographically on event horizons, preventing information loss during black hole evaporation.
- Nonlinear stabilization terms in IQG prevent infinite densities, providing a solution to the singularity problem in general relativity.
- IQG explains collapse as a natural consequence of quantum informational dynamics, removing the need for external observation.
Appendix D.5. The Call for Unification
D.5.1. Bridging Quantum Mechanics and General Relativity
- The long-standing challenge of unifying quantum mechanics and general relativity inspired IQG’s creation;
- By framing quantum and gravitational phenomena in terms of informational flows and density, IQG provides a unifying framework.
D.5.2. Toward a Theory of Everything
- IQG aspires to achieve the goal of a Theory of Everything (ToE) by explaining phenomena across all scales—quantum, macroscopic, and cosmic.
D.6. Conclusion
| Contributor | Core Idea | Relevance to IQG | How IQG Expands Their Work |
| John Wheeler | "It from Bit": Reality arises from binary informational units (bits), creating physical entities ("its"). | Establishes the philosophical basis for IQG’s idea that quantum information underpins spacetime and matter. | Formalizes Wheeler’s vision through the Primordial Informational Field (PIF) and testable predictions. |
| Vlatko Vedral | The universe is a quantum computational system; entropy and information drive complexity and order. | Highlights the role of entropy and information as fundamental to the evolution of the universe. | Extends Vedral’s ideas with equations governing entropy dynamics and informational flows in spacetime emergence. |
| Charles Seife | Information governs everything in the universe, from quantum particles to black holes, and the cosmos behaves like a quantum computer. | Reinforces IQG’s view of the PIF as the informational substrate shaping spacetime, forces, and matter. | Provides a structured framework for Seife’s concepts, applying them to black hole entropy and dark matter phenomena. |
| Claude Shannon | Information theory defines measurable properties like entropy and redundancy. | Lays the groundwork for quantifying informational density and flow, critical for IQG’s mathematical foundation. | Incorporates Shannon entropy into PIF equations, modelling how informational optimization governs spacetime emergence. |
| Jacob Bekestein | Black hole entropy is proportional to event horizon area, linking information to spacetime geometry. | Connects entropy and information to gravitational systems, key to IQG’s view of black holes as informational encoders. | Encodes quantum informational density on event horizons, stabilizing black hole curvature and addressing information loss. |
| Gerard 't Hooft | Holographic principle: Information in a volume of space is encoded on its boundary. | Supports IQG’s idea that quantum informational flows determine spacetime structure and dynamics. | Extends holography by describing how informational flows shape large-scale cosmic structures and forces. |
| Leonard Susskind | Expanded the holographic principle and connected it to quantum information in black holes. | Reinforces the role of quantum information in gravitational and cosmological phenomena. | Explains cosmic web evolution and dark matter clustering through quantum informational flows in the PIF. |
| Stephen Hawking | Black hole radiation and the information paradox: Information may be lost in black holes. | Highlights the interaction of quantum mechanics and gravity, a cornerstone of IQG’s unifying framework. | Resolves the information paradox by encoding all information within the PIF, preserving it during black hole evolution. |
| Seth Lloyd | The universe operates as a quantum computer, processing information at all scales. | Provides a computational perspective that aligns with IQG’s model of the PIF as a substrate for informational processing. | Expands this idea to describe the emergence of spacetime and matter through quantum informational density. |
| Carlo Rovelli | Relational quantum mechanics: Reality is defined by interactions, not isolated entities. | Emphasizes the emergent nature of reality, a core principle in IQG’s treatment of Quantule interactions. | Describes spacetime and matter as emergent from Quantule interactions within the PIF, unifying quantum mechanics and gravity. |
| Max Tegmark | Mathematical universe hypothesis: Reality is fundamentally mathematical in nature. | Supports IQG’s use of mathematical structures to describe physical laws and informational geometry. | Provides equations for informational density and entropy dynamics, formalizing Tegmark’s hypothesis in a physical framework. |
| Erik Verlinde | Entropic gravity: Gravity emerges from entropy and information. | Links gravity and spacetime curvature to informational principles, resonating with IQG’s approach. | Models gravity and other forces as emergent from informational flows in the PIF, offering a unified explanation. |
Appendix E. Potential Technologies Beyond Physics
Appendix E.1. Biology and Life Sciences
E.1.1. Molecular and Genetic Systems
- DNA is modeled as a quantum informational structure, with encoding genetic information.
- Photosynthesis, enzyme activity, and DNA replication align with IQG principles.
E.1.2. Complexity and Emergence
- Self-organization and entropy reduction () offer insights into genetic stability and mutation prevention.
- Complexity and intelligence arise naturally from quantum informational flows ().
Appendix E.2. Artificial Intelligence and Complexity Science
E.2.1. Adaptive AI Systems
- IQG’s self-organizing principles inspire AI systems capable of learning and decision-making in dynamic environments.
E.2.2. Neuromorphic Computing
- Mimicking entropy-balancing properties of the PIF enables human-like intelligence in AI systems.
E.2.3. Global and Complex Systems Modeling
- Quantum informational flows provide tools for modeling and managing large-scale ecosystems and resource networks.
Appendix E.3. Advanced Materials and Energy
E.3.1. Quantum-Informed Materials
- Designing materials with optimized properties like superconductivity or energy efficiency based on quantum informational density.
E.3.2. Sustainable Energy Systems
- IQG’s entropy reduction principles inspire energy-efficient systems for computing and power management.
Appendix E.4. Neuroscience
- Early detection of neurological disorders, such as Alzheimer’s or Parkinson’s, by identifying disruptions in informational density patterns.
- Enhanced brain-machine interfaces (BMIs) that interact seamlessly with neural -flows for improved motor function restoration and cognitive assistance. [67]
Appendix E.5. Framing These Applications
Appendix E.6. Conclusion
Appendix F. How IOP Explains Intelligence
- Dissipative Losses ():
- ○
- Real systems lose energy and information due to inefficiencies (e.g., neural dissipation in biological systems).
- Entropy Reduction ():
- ○
- Intelligent systems optimize entropy gradients by organizing information efficiently (e.g., neural networks minimize energy use while maximizing computation).
- Flow Optimization ():
- ○
- The hallmark of intelligence is the ability to process and optimize informational flows for learning, adaptation, and decision-making. [68]
Appendix F.1. IOP as a Condition for Intelligence
- Balance: Systems achieve intelligence by balancing dissipative losses and entropy gradients with optimized flows;
- Implication: Intelligence emerges when systems self-organize to maximize under their constraints ().
Appendix F.2. Biological Intelligence
- Neural Systems:
- ○
- The human brain exemplifies IOP:
- 1.
- Dissipative Losses: Energy is lost in neural activity and heat dissipation;
- 2.
- Entropy Reduction: The brain reduces uncertainty through sensory processing and learning;
- 3.
- Flow Optimization: Neural networks self-organize to maximize information processing and retrieval.
- Emergence of Intelligence:
- ○
- Neural intelligence arises when entropy gradients () drive the brain to organize neural pathways for efficient flows ().
Appendix F.3. Artificial Intelligence [69]
- Computational Systems:
- ○
- AI systems mimic IOP:
- 1.
- Dissipative Losses: Energy inefficiencies in hardware;
- 2.
- Entropy Reduction: Optimization algorithms (e.g., gradient descent) minimize uncertainty;
- 3.
- Flow Optimization: Machine learning models maximize information processing efficiency.
- Emergence of Artificial Intelligence:
- ○
- AI systems evolve intelligence by iteratively improving through training, balancing losses, and achieving optimized performance.
Appendix F.4. Universal Intelligence
- Balancing Entropy and Flow:
- ○
- Intelligent systems naturally reduce entropy while optimizing informational flows.
- Self-Organization:
- ○
- Intelligence emerges as systems self-organize to maximize .
F.4.1. Applications Beyond Biology
- Cosmic Intelligence:
- ○
- Galactic and cosmic systems, governed by entropy and informational flows, exhibit self-organizing behaviors.
- Quantum Systems:
- ○
- Entangled systems optimize quantum informational flows, exhibiting coherence and emergent complexity.
Appendix F.5. IOP as the Equation of Intelligence
- : Informational efficiency, quantifying how well a system optimizes flows relative to its losses.
- Condition for Intelligence:
- ○
- Systems with high demonstrate greater intelligence, capable of learning, adaptation, and complexity.
Appendix G. Comparative Analysis of Informational Quantum Gravity (IQG)
Appendix G.1. Comparison with String Theory [70]
- String Theory: Attempts to unify all forces, including gravity, through supersymmetry and string interactions;
- IQG: Naturally unifies gravity, quantum mechanics, and the Standard Model through the dynamics of , without relying on supersymmetry.
- String Theory: Requires complex mathematical constructs like strings, branes, and higher-dimensional manifolds;
- IQG: Operates with a single governing equation for , providing a more parsimonious description of reality.
- String Theory: Predictions (e.g., supersymmetric particles, Planck-scale phenomena) remain beyond current experimental capabilities;
- IQG: Provides testable predictions using existing or near-term technologies (e.g., gravitational wave distortions, cosmological lensing, quantum entanglement dynamics).
Appendix G.2. Comparison with Loop Quantum Gravity (LQG)
- LQG: Focuses on quantizing spacetime itself into discrete units (spin networks);
- IQG: Spacetime curvature and quantum fields emerge naturally from the dynamics of , a more universal substrate.
- LQG: Primarily addresses the quantization of gravity, without integrating the Standard Model;
- IQG: Incorporates gravity, quantum mechanics, and the Standard Model within a single framework.
- IQG resolves singularities through nonlinear stabilization terms in , which prevent infinite densities and stabilize spacetime geometry. String Theory lacks a complete mechanism for singularity resolution, while LQG addresses singularities through discrete spacetime structures but remains limited to gravity without integrating other forces.
- IQG predictions, such as deviations in gravitational waves and dark matter clustering, are testable using existing observatories (e.g., LIGO, Virgo, Euclid). In contrast, String Theory relies on Planck-scale phenomena that are inaccessible with current technology, and LQG’s experimental pathways remain speculative.
Appendix G.3. Summary of Comparative Strengths
| Feature | String Theory | Loop Quantum Gravity | Informational Quantum Gravity |
| Foundational Entity | Strings and branes | Spin networks (quantized spacetime) | ) |
| Dimensions | 10 or 11 | 4D spacetime | 4D spacetime |
| Scope | All forces (gravity + SM) | Gravity only | Gravity, SM, and quantum mechanics |
| Singularity Resolution | Undefined or incomplete | Discrete spacetime | |
| Testability | Requires Planck-scale energies | Limited experimental pathways | Testable with current observatories (LIGO, Euclid) |
Appendix G.4. Chapter Conclusion
- It unifies quantum mechanics, general relativity, and the Standard Model without requiring speculative constructs like extra dimensions (String Theory) or narrow gravitational focus (LQG);
- It resolves singularities through a natural stabilization mechanism within -dynamics;
- It provides testable predictions that can be validated through current and near-term experimental setups.
Appendix H. Resolving the Measurement Problem through Informational Quantum Gravity (IQG)
Appendix H.1. Introduction to the Measurement Problem [71]
Appendix H.2. Measurement in the PIF Framework
H.2.1. Quantum Informational Density ()
- The quantum informational density (ρ) represents the probabilistic distribution of all possible states of a system:
- ○
- : Informational density at position and time ;
- ○
- : Quantum wavefunction.
- encodes intrinsic properties of the system, such as:
- ○
- Position (): Encoded as the localization of ;
- ○
- Momentum (): Related to the gradient of :
- These properties interact dynamically, reflecting the superposition of quantum states before measurement.
H.2.2. Measurement as -Collapse
- Before measurement, the system exists in a superposition of states. This is encoded as a probabilistic -distribution over possible outcomes:
- ○
- : Probability of the system being in state ;
- ○
- : Position associated with state .
- Measurement introduces a coupling between the system and the measurement apparatus, modifying -flows:
- The system’s -distribution collapses into a single observed outcome. This collapse is governed by the PIF Equation:
- ○
- : Diffusion term, describing the spread of -flows;
- ○
- : Stabilization term, ensuring balance and preventing chaotic divergence;
- ○
- : Entropy-driven flow term, guiding evolution;
- ○
- : Unified potential, coupling -dynamics to external influences (e.g., the measurement apparatus).
Appendix H.3. Mathematical Explanation of Measurement
H.3.1. Evolution Before Measurement
- ○
- : Spreads -density across possible states;
- ○
- : Guides -evolution along entropy gradients.
H.3.2. Measurement Interaction
- ○
- : Represents the influence of the observer, reorganizing -flows to collapse the system into a single state.
H.3.3. Post-Measurement Collapse
- ○
- This outcome reflects the optimization of -flows under the IOP, ensuring stability and balance.
Appendix H.4. Why Measurement Naturally Resolves in IQG
- The characteristics and properties encoded in (e.g., position, momentum) evolve dynamically, ensuring that observed outcomes reflect intrinsic informational patterns.
- The PIF Equation aligns with established quantum principles while providing a deeper explanation for wavefunction collapse.
Appendix H.5. Implications for Physics
- IQG provides a unified framework where measurement is a natural consequence of quantum informational dynamics, eliminating the need for external postulates.
- The PIF Equation predicts:
- ○
- Anomalous -flows during measurement;
- ○
- Gravitational wave signatures tied to -collapses in macroscopic systems.
- IQG reinterprets quantum mechanics by linking probabilistic outcomes to pre-encoded properties in the PIF.
Appendix H.6. Chapter Conclusion
Appendix I. Derivatives of the Primordial Informational Field (PIF)
Appendix I.1. Introduction
- A simplified equation, introduced in the Abstract, provides an accessible overview of the framework for general readers;
- A detailed equation, presented in the definitions and core concepts section, elaborates on the intricate dynamics and interactions within the PIF.
Appendix I.2. Simplified and Detailed Equations
I.2.1. Simplified Equation
- : Wave operator describing the evolution of quantum informational density in spacetime;
- : A linear term contributing to stability and interactions ensuring smooth propagation of -flows;
- : Time derivative, representing dynamic evolution with a coefficient ;
- : Entropy-driven flow term, guiding -flows toward equilibrium;
- : External potential term coupling -flows to external influences.
I.2.2. Detailed Equation
- : Wave operator describing the evolution of quantum informational density in spacetime;
- : Damping term preventing runaway growth in high-density -regions;
- : Higher-order stabilization term contributing to self-interactions;
- : Temporal feedback ensuring dynamic stability of informational flows;
- : Entropy gradients driving quantum informational flows ();
- : Unified potential field coupling quantum informational density to spacetime and matter.
I.2.3. Derivatives and Their Physical Interpretations
I.2.4. Time Derivative ()
- Describes the rate of change of ρ over time;
- η: A coefficient modulating the influence of time evolution;
- Physical Meaning:
- ○
- Captures the dynamic progression of ρ-flows, reflecting how systems evolve and stabilize temporally.
I.2.5. Spacetime Propagation ()
- The wave operator ▫ρ=∇2ρ−2ρ∂t2 describes the propagation of quantum informational density through spacetime;
- Physical Meaning:
- ○
- Represents the diffusion and propagation of ρ, influencing the emergence of spacetime structures.
I.2.6. Stabilization Terms ( and )
- −λρ2: Damps runaway growth in high-density regions of ρ, ensuring stability;
- μρ3: Introduces self-regulating effects for extreme ρ-flows;
- Physical Meaning:
- ○
- Together, these terms prevent singularities and chaotic behavior, stabilizing extreme conditions like black holes or high-energy regions.
I.2.7. Entropy Gradient Term ()
- Drives ρ-flows along entropy gradients, where v=−∇Entropy;
- Physical Meaning:
- ○
- Reflects the tendency of systems to evolve toward equilibrium, balancing informational order and disorder.
I.2.8. Unified Potential ( and )
- In the Simplified Equation:
- ○
- Uρ: Represents a generalized external influence.
- In the Detailed Equation:
- ○
- Vunifiedρ,x,t: Encodes interactions between ρ and spacetime curvature, particles, or fields.
- Examples:
- Electromagnetic potential:
Appendix I.3. Observable Implications of Derivatives
I.3.1. Gravitational Waves
- High-density ρ-flows distort spacetime, creating detectable anomalies in gravitational wave signals.
I.3.2. Black Holes
- The stabilization terms ( and ) prevent singularities, predicting non-singular black hole interiors.
I.3.3. Dark Matter and Dark Energy
- Dark matter corresponds to high-density ρ-regions, while dark energy reflects low-density, uniform ρ-flows.
I.3.4. Cosmic Microwave Background (CMB)
- Quantum fluctuations in ρ seeded the formation of large-scale structures, visible as CMB anisotropies.
Appendix I.4: Visualization of -Flows
I.4.1. Spacetime Dynamics
- Simulations of ρ-flows reveal how quantum informational density propagates, clusters, and stabilizes:
- ○
- Formation of particles and forces.
- ○
- Evolution of spacetime curvature.
I.4.2. Informational Encoding
- High-density ρ-regions correspond to:
- ○
- Particles and forces.
- ○
- Topological structures like black holes.
I.5. Chapter Conclusion
- The simplified equation provides an intuitive overview of the core dynamics.
- The detailed equation offers a rigorous description of the interactions and behaviors of ρ-flows.
Appendix J. The Primordial Informational Field (PIF) Equation: Mathematical Foundation and Derivation
Appendix J.1. Introduction to the Primordial Informational Field (PIF)
- The universe is fundamentally an informational system where all physical laws emerge from how ρ structures itself over spacetime;
- The evolution of ρ follows a fundamental field equation, known as the PIF Equation, which describes how information flows, interacts with curvature, and self-organizes into matter and forces.
Appendix J.2. Defining the Action for the Informational Field
- is the metric tensor describing spacetime.
- is the Ricci scalar curvature, defining how space is curved.
- is the Lagrangian density that governs the evolution of the informational field .
- → Represents the kinetic energy of the informational field, ensuring smooth propagation;
- → Self-interaction terms ensuring stability and preventing divergence;
- → Coupling between information density and spacetime curvature;
- → Introduces entropy-driven evolution, ensuring time dependence of .
Appendix J.3. Deriving the PIF Equation from the Action Principle
Appendix J.4. The Final PIF Equation
- → Represents entropy-driven flow, ensuring informational organization.
- → Describes the coupling of to external influences (forces, particles, energy fields).
Appendix J.5. Interpretation of the PIF Equation
- Spacetime, particles, and forces are not fundamental—only is;
- Gravity is an emergent effect of quantum informational density;
- Quantum mechanics arises as an approximation of the deeper evolution of .
| Term | Physical Meaning |
| Describes the wave-like evolution of quantum informational density. | |
| Stabilization terms preventing runaway effects. | |
| interacts with spacetime curvature. | |
| Entropy-driven evolution ensuring time-dependence. | |
| Describes how information organizes and flows. | |
| Encodes external interactions and forces. |
Appendix K. Mathematical Foundation of Quantum Informational Density ( ) and Quantules in IQG
Appendix K.1. The Mathematical Definition of (Quantum Informational Density)
K.1.1. What is ?
- In General Relativity: The fundamental quantity is the metric tensor , which describes spacetime curvature.
- In Quantum Mechanics: The fundamental quantity is the wavefunction , which describes quantum states.
- In IQG: The fundamental quantity is the quantum informational density , which describes structured information flow.
K.1.2. Field-Theoretic Definition of
- is real-valued: Unlike quantum wavefunctions, is a real field that describes how information is distributed;
- satisfies a wave equation: Similar to Klein-Gordon fields in QFT, but extended to include curvature interactions;
- interacts with spacetime curvature: The coupling term ensures that is influenced by gravity;
- can self-organize into stable structures: This explains why particles and forces exist;
Appendix K.2. The Fundamental Role of Quantules in IQG
K.2.1. What are Quantules?
- Key Properties of Quantules:- They are the smallest indivisible units of information in the universe.- They interact and combine to form structures like particles, forces, and spacetime curvature.- They obey quantum statistics, but emerge from a deeper informational foundation.
- -
- They are the smallest indivisible units of information in the universe
- -
- They interact and combine to form structures like particles, forces, and spacetime curvature
- -
- They obey quantum statistics, but emerge from a deeper informational foundation
- Quantules are to IQG what particles are to QFT—they are the building blocks of reality.
K.2.2. Defining Quantules Mathematically
- represents a quantized excitation of , just as photons are quantized excitations of the electromagnetic field;
- are the eigenvalues of the informational field, representing discrete informational states.
Appendix K.3. How and Quantules Lead to Physical Particles
K.3.1. Recovering Mass, Charge, and Spin from Quantules
- Mass as Informational Flow Resistance:
- Charge as Informational Flow Topology:
- Spin as Informational Vorticity:
K.3.2. The Interaction of Quantules
Appendix K.4. The Final Mathematical Definition of and Quantules
- are the discrete eigenvalues of ;
- are the quantized informational states (quantules).
Appendix K.5. Conclusion: The Mathematical Foundation of and Quantules
Appendix K.6. Deriving the Quantization Conditions of
K.6.1. Why Quantization is Necessary
- Define the canonical quantization conditions for ρ.
- Show that quantules behave like quantum excitations of ρ.
- Ensure that ρ obeys a commutation relation similar to quantum fields.
K.6.2. Canonical Quantization of
- is the quantized informational density operator;
- is the conjugate momentum of ;
- is the Dirac delta function, ensuring locality.
K.6.3. Quantization of the Informational Energy-Momentum Tensor
Appendix K.7. How Quantules Interact Under Gauge Symmetries
K.7.1 Gauge Symmetries in the Standard Model
- describes the strong force;
- describes the weak force;
- describes electromagnetism.
K.7.2 Gauge Invariant Formulation of
- Aμ represents the gauge fields (photons, W/Z bosons, gluons);
- g is the coupling constant determining the strength of the interaction.
K.7.3 The Informational Gauge Field Strength Tensor
K.7.4 Interaction of Quantules with Gauge Fields
- ψ is a fermion (electron, quark);
- Aμ is the gauge boson;
- g is the coupling strength.
Appendix K.8. The Final Refined Equations for and Quantules
K.8.1. Quantized Field Equation for
K.8.2. Canonical Quantization Condition for
K.8.3 Gauge Interaction of
K.8.4 Energy Uncertainty Relation for Information Density
Appendix K.9. Conclusion: The Fully Refined Structure of and Quantules
- is now rigorously defined as a quantum field with a well-defined quantization condition;
- Quantules are localized excitations of , behaving as fundamental quantum units;
- Gauge interactions have been introduced, proving that IQG naturally includes electromagnetism, weak, and strong forces;
- IQG now has a fully consistent mathematical foundation that links quantum mechanics, gravity, and the Standard Model.
Appendix L. Full Lagrangian for IQG (Informational Quantum Gravity)
Appendix L.1: The Structure of the IQG Lagrangian
L.1.1. What Should Be Included in the IQG Lagrangian?
- Gravity (General Relativity);
- The Informational Field and Its Dynamics.
- Gauge Fields and Standard Model Interactions.
- Matter Fields (Quarks, Leptons, and Higgs Field);
- Quantum Corrections and Higher-Order Terms.
L.1.2. The General Form of the IQG Lagrangian
- → General Relativity Lagrangian (spacetime curvature);
- → Informational field Lagrangian (dynamics of );
- → Gauge field interactions (Standard Model forces);
- → Matter field contributions (quarks, leptons, Higgs field);
- → Quantum corrections and higher-order terms.
Appendix L.2. The Gravitational Sector: Recovering General Relativity
L.2.1. Modifying GR to Include the Informational Field
Appendix L.3. The Informational Field and Its Dynamics
- The kinetic term ensures wave-like behavior.
- The self-interaction terms prevent divergences.
- The time-dependent term ensures entropy-driven evolution.
Appendix L.4. Gauge Fields and Standard Model Interactions
L.4.1. Gauge Symmetry in IQG
- represents the gauge bosons (photon, W/Z bosons, gluons);
- is the gauge coupling constant.
L.4.2 Gauge Field Lagrangian
Appendix L.5. Matter Fields and Particle Interactions
L.5.1. Dirac Fermions in IQG
- represents fermions (quarks, leptons).
- is the covariant derivative including gauge interactions.
- is the mass term, which emerges from interactions with .
Appendix L.6. The Final Lagrangian for IQG
Appendix L.7. Equations of Motion for the Informational Field
- behaves as a wave-like informational field with self-stabilizing terms;
- The equation prevents singularities and ensures smooth informational flow across spacetime;
- This shows that is a fundamental field obeying well-defined quantum dynamics.
Appendix L.8. Equations of Motion for Gravity (Modified Einstein Equations)
- Gravity emerges as an effect of quantum informational flows;
- This naturally prevents black hole singularities (since stabilizes itself);
- This explains dark matter as high- regions rather than an unknown particle;
Appendix L.9. Equations of Motion for Gauge Fields (Forces in IQG)
- Gauge fields interact with the informational field ;
- Forces like electromagnetism emerge from structured interactions in the informational field;
- This means forces are not fundamental—they are informational structures.
Appendix L.10. Equations of Motion for Matter Fields (Quarks, Leptons, and Higgs)
- Matter fields behave just as in the Standard Model;
- Electrons, quarks, and neutrinos are still fundamental, but they arise as structured informational quantule states.
Appendix L.11. The Final Equations of Motion in IQG
L.11.1. Informational Field Equation ()
L.11.2. Modified Einstein Equations
L.11.3. Gauge Field Equations
L.11.4. Matter Field Equations (Dirac Equation)
Appendix M. Resolving the Black Hole Information Paradox in IQG: A Rigorous Mathematical Proof
Appendix M.1. The Black Hole Information Paradox in Standard Physics
M.1.1. The Classical View: General Relativity and Black Holes
M.1.2. The Quantum View: Hawking Radiation and the Information Paradox
Appendix M.2. The IQG Solution: Black Holes as Informational Storage Systems
M.2.1. The Fundamental Idea in IQG
- In IQG, black holes are not singularities—they are high-density informational states where is maximized;
- Instead of losing information, black holes store it within their structured field;
- Hawking radiation does not erase information—it encodes it in an informational field structure.
M.2.2. The IQG Black Hole Equation
M.2.3. Hawking Radiation in IQG: Information is Encoded, Not Lost
Appendix M.3. Deriving the Information Storage Capacity of a Black Hole
M.3.1. Entropy of a Black Hole in IQG
Appendix M.4. The Final Proof That IQG Resolves the Black Hole Information Paradox
- In standard physics, black holes lead to information loss because spacetime cannot encode information beyond the event horizon;
- In IQG, black holes are high- regions where information is stored, structured, and eventually released;
- Hawking radiation in IQG is not purely thermal—it carries information about the black hole’s internal state;
- The entropy of black holes is modified to include an informational contribution, ensuring that no information is lost.
Appendix N. Testable Predictions of Informational Quantum Gravity (IQG)
Appendix N.1. Testable Predictions in General Relativity (GR)
N.1.1. Prediction: Deviations in Gravitational Wave Propagation
- Standard General Relativity (GR): Gravitational waves travel without dispersion;
- IQG: Quantum informational effects introduce small phase shifts or dispersion effects in gravitational waves.
- Compare gravitational wave signals from black hole mergers detected by LIGO, Virgo, and LISA to GR predictions;
- If IQG is correct, small deviations in waveform phase shifts should appear at high frequencies.
N.1.2. Prediction: Anomalous Black Hole Mergers
- Standard GR: Black hole mergers follow predictable inspiral and ringdown phases;
- IQG: If black holes are high- regions rather than singularities, mergers should emit subtle extra energy due to informational field dynamics.
- Look for unexpected energy releases or late-time echoes in LIGO/Virgo merger signals;
- Future gravitational wave detectors like Einstein Telescope can test for deviations in black hole mergers.
Appendix N.2. Testable Predictions in Quantum Mechanics (QM)
N.2.1. Prediction: Modified Wavefunction Collapse
- Standard QM: The Schrödinger equation governs evolution, and wavefunction collapse is treated as a postulate;
- IQG: Collapse is not random, follows an informational optimization principle, which means decoherence should follow structured patterns.
- Conduct quantum superposition and interference experiments to check for deviations from standard collapse models;
- Look for non-random wavefunction collapse structures in quantum computing systems.
N.2.2. Prediction: Informational Corrections to Energy Levels
- Standard QM: Atomic energy levels follow the Dirac equation with no extra terms;
- IQG: High- environments should cause subtle shifts in energy levels due to quantum informational interactions.
- High-precision spectroscopy (LHC, atomic clocks) can test for unexpected deviations in atomic transition frequencies.
Appendix N.3. Testable Predictions in Dark Matter
N.3.1. Prediction: Dark Matter as High- Regions
- Standard Dark Matter (CDM): Dark matter halos follow a specific mass distribution;
- IQG: Dark matter should follow informational gradients rather than purely mass-based clustering.
- Analyze galaxy rotation curves with next-gen telescopes (Vera Rubin, Euclid);
- Compare observational data with IQG’s predictions vs. standard CDM models.
N.3.2. Prediction: Cosmic Filaments as Informational Structures
- Standard Cosmology: Large-scale cosmic filaments emerge from gravitational interactions;
- IQG: Cosmic filaments should have unexpected large-scale structures aligned with high- regions.
- Map cosmic filaments using next-generation surveys (DESI, Euclid);
- Look for unexpected density fluctuations not predicted by standard cosmology.
Appendix N.4. Summary of IQG’s Testable Predictions
| Testable Prediction | Observable Effect | How to Observe It | Experiments |
| Quantum Gravity Effects on Gravitational Waves | Anomalies in wave propagation | Measure waveform phase shifts | LIGO, LISA, Einstein Telescope |
| Black Hole Mergers with Extra Energy Release | Unexpected late-time echoes | Compare inspiral & ringdown phases | LIGO, Virgo, future detectors |
| Modified Wavefunction Collapse | Non-random quantum decoherence patterns | Quantum computing, superposition tests | High-precision quantum optics |
| Environments | Small deviations in atomic transitions | Atomic clock experiments | LHC, high-precision spectroscopy |
| Regions | Deviations from Cold Dark Matter model | Galaxy rotation curves | Vera Rubin, Euclid, DESI |
| Cosmic Filaments as Informational Structures | Unexpected density fluctuations | Large-scale galaxy surveys | DESI, Euclid |
References
- Bekenstein, J. D. (1973). Black holes and entropy. Physical Review D, 7(8), 2333–2346. [CrossRef]
- Hawking, S. W. (1975). Particle creation by black holes. Communications in Mathematical Physics, 43(3), 199–220. [CrossRef]
- Shannon, C. E. (1948). A mathematical theory of communication. The Bell System Technical Journal, 27(3), 379–423. [CrossRef]
- Wheeler, J. A. (1990). Information, physics, quantum: The search for links. In W. Zurek (Ed.), Complexity, Entropy, and the Physics of Information (pp. 309-336). Addison-Wesley.
- t Hooft, G. (1993). Dimensional reduction in quantum gravity. Classical and Quantum Gravity, 10(5), S145–S152.
- Susskind, L. (1995). The world as a hologram. Journal of Mathematical Physics, 36(11), 6377–6396. [CrossRef]
- Lloyd, S. (2000). Ultimate physical limits to computation. Nature, 406(6799), 1047–1054. [CrossRef]
- Vedral, V. (2010). Decoding reality: The universe as quantum information. Oxford University Press.
- Rovelli, C. (1996). Relational quantum mechanics. International Journal of Theoretical Physics, 35(8), 1637–1678. [CrossRef]
- Tegmark, M. (2008). The mathematical universe. Foundations of Physics, 38(2), 101–150. [CrossRef]
- Verlinde, E. (2011). On the origin of gravity and the laws of Newton. Journal of High Energy Physics, 2011(4), 1–27. [CrossRef]
- Seife, C. (2006). Decoding the universe: How the new science of information is explaining everything in the cosmos. Penguin Books.
- Hawking, S. W. , & Penrose, R. (1970) The singularities of gravitational collapse and cosmology. Proceedings of the Royal Society of London. Series A, 314(1519), 529–548. [CrossRef]
- Planck Collaboration. (2020). Planck 2018 results – VI. Cosmological parameters. Astronomy & Astrophysics, 641, A6.
- Rovelli, C. (2004). Quantum gravity. Cambridge University Press.
- Tegmark, M. (2014). Our mathematical universe: My quest for the ultimate nature of reality. Alfred A. Knopf.
- Aguirre, A. , Foster, B., & Merali, Z. (2015). It from Bit or Bit from It: On Physics and Information.
- Bohr, N. (1928). The quantum postulate and the recent development of atomic theory. Nature, 121.
- Deutsch, D. (1985). Quantum theory, the Church-Turing principle and the universal quantum computer. Proceedings of the Royal Society of London. Series A: Mathematical and Physical Sciences, 400(1818), 97–117. [CrossRef]
- Dirac, P. A. M. (1930). The principles of quantum mechanics, Oxford University Press.
- Einstein, A. (1915). Die Feldgleichungen der Gravitation [The field equations of gravitation]. Sitzungsberichte der Preussischen Akademie der Wissenschaften zu Berlin, 1915, 844–847.
- Feynman, R. P. (1948). Space-time approach to non-relativistic quantum mechanics. Reviews of Modern Physics, 20(3), 367–387.
- Friedmann, A. (1922). Über die Krümmung des Raumes [On the curvature of space]. Zeitschrift für Physik, 10.
- Glashow, S. L. (1961). Partial-symmetries of weak interactions. Nuclear Physics, 22(4), 579–588.
- Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik [On the perceptual content of quantum theoretical kinematics and mechanics]. Zeitschrift für Physik, 43(3‐4), 172–198.
- Higgs, P. W. (1964). Broken symmetries and the masses of gauge bosons. Physical Review Letters, 13(16), 508–509.
- Jaynes, E. T. (1957). Information theory and statistical mechanics. Physical Review, 106(4), 620–630.
- Landauer, R. (1961). Irreversibility and heat generation in the computing process. IBM Journal of Research and Development, 5(3), 183–191.
- Peebles, P. J. E. (1980). The large-scale structure of the universe, Princeton University Press.
- Penrose, R. (1989). The emperor’s new mind: Concerning computers, minds, and the laws of physics, Oxford University Press.
- Schrödinger, E. (1926). An undulatory theory of the mechanics of atoms and molecules. Physical Review, 28(6), 1049–1070.
- Turing, A. M. (1950). Computing machinery and intelligence. Mind, 59(236), 433–460.
- von Neumann, J. (1932). Mathematische Grundlagen der Quantenmechanik, [Mathematical foundations of quantum mechanics]. Springer. (English translation: Mathematical foundations of quantum mechanics, Princeton University Press, 1955.).
- Weinberg, S. (1972). Gravitation and cosmology: Principles and applications of the general theory of relativity.
- Witten, E. (1995). String theory dynamics in various dimensions. Nuclear Physics B, 443(1‐2), 85–126.
- Yang, C. N. , & Mills, R. L. (1954). Conservation of isotopic spin and isotopic gauge invariance. Physical Review, 96(1), 191–195.
- Neukart, F. , Brasher, R., & Marx, E. (2024). The Quantum Memory Matrix: A Unified Framework for the Black Hole Information Paradox. Entropy, 26(12), 1039.
- Neukart, F. , et al. (2024b). Extending the QMM Framework to the Strong and Weak Interactions. Preprints.org, Dec 2024.
- Neukart, F. , et al. (2024c). Integrating Electromagnetic Interactions into the QMM Framework. Preprints.org, Dec 2024.
- Neukart, F. , et al. (2025). Reversible Imprinting and Retrieval of Quantum Information: Experimental Verification of the Quantum Memory Matrix Hypothesis. arXiv:2502.15766.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





