A Topological and Temporal Framework for the Emergence of Spacetime, Interactions, and Quantum Structure

1. Introduction

1.1. Motivation and Scope

Unifying the emergence of spacetime, the structure of matter, and the laws of fundamental interactions remains a central challenge in theoretical physics. The Standard Model describes three fundamental forces via internal gauge symmetries, while General Relativity (GR) frames gravity as spacetime curvature. Despite their individual successes, these frameworks are incompatible, particularly in high-curvature regimes like the early universe or black holes [15,16,29].

A key barrier to unification is the role of time. In quantum field theory (QFT), time is an external parameter; in GR, it is part of the dynamical geometry. Canonical and path-integral quantum gravity approaches face the “problem of time”—the absence of a preferred temporal variable—which leads to interpretive and formal difficulties [10,17,18,26].

We propose a unified framework based on the premise that time is not emergent or external, but a dynamical, ontologically primary field. We study the consequences of a smooth, unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$, which defines local temporal flow and serves as the generative structure for geometry, matter, and interactions.

This field-centric view—termed Chronon Field Theory (CFT)—posits that causal structure, gravitational phenomena, gauge interactions, and quantum behavior emerge from the topology and dynamics of ${\Phi }^{\mu }$. Using tools from topological field theory, differential geometry, and canonical quantization, we construct a background-independent model in which time itself underpins the laws of physics. Numerical simulations illustrate how causal order, spacetime foliation, and soliton-like excitations arise from spontaneous symmetry breaking of this temporal field.

1.2. Temporal Field Dynamics and Physical Structure

CFT postulates a fundamental timelike vector field ${\Phi }^{\mu }\left(x\right)$ satisfying:

$${\Phi }^{\mu }{\Phi }_{\mu }=-1,{\Phi }^0>0,$$

(1)

ensuring a globally consistent arrow of time and inducing spatial foliation [12].

From this follow several key implications. Temporal coherence generates causal structure; curvature in ${\Phi }^{\mu }$ induces gravitational dynamics [6,20]; and topologically nontrivial configurations yield stable solitonic excitations classified by ${\pi }_3\left(S^3\right)$, with properties resembling mass, spin, and quantum statistics [1,14,27,31,32,34].

Local phase and shear degrees of freedom give rise to emergent gauge interactions: $U\left(1\right)$ symmetry appears via residual phase invariance [11], weak parity violation via shear asymmetries, and strong confinement via topological flux tubes [21].

On cosmological scales, spontaneous alignment of ${\Phi }^{\mu }$ defines an arrow of time, replaces inflation with causal coherence, and produces topological defects contributing to effective stress-energy—potentially addressing dark matter and dark energy phenomenology [9,36,37].

At the quantum level, canonical quantization of ${\Phi }^{\mu }$ yields a Wheeler–DeWitt-like equation where time re-emerges through field-driven foliation. The model is power-counting renormalizable, background-independent, and UV-complete, due to topological constraints and soliton regularization [2,22,33].

In sum, Chronon Field Theory offers a unified, falsifiable approach wherein space, matter, forces, and causality all arise from a single, dynamical field of time.

2. Theoretical Context and Relation to Previous Work

This framework builds upon and extends major developments in quantum gravity, emergent spacetime, gauge unification, and topological models of matter. It addresses longstanding challenges by positioning the dynamical flow of time—not spacetime geometry—as the foundational structure from which causal order, matter, and interactions arise.

At its core, the proposal responds to the incompatibility between quantum field theory (QFT) [38] and General Relativity (GR). Canonical approaches to quantum gravity, from DeWitt [10] to Hartle and Hawking [15], encounter the “problem of time”: the lack of a preferred temporal variable. Work by Kuchař [26], Isham [18], and Barbour [5] has underscored this issue. Chronon Field Theory (CFT) addresses it by introducing a unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$, which generates causal structure and intrinsic temporal evolution, embedding canonical quantization in a broader geometric and topological field theory.

Ideas of emergent gravity, such as Jacobson’s thermodynamic derivation of Einstein’s equations [20], Verlinde’s entropic gravity [36], and analog models [6], suggest that spacetime may be a coarse-grained phenomenon. CFT shares this philosophy but goes further: it constructs spacetime geometry, gauge structure, and matter content explicitly from the topology and dynamics of ${\Phi }^{\mu }$.

The treatment of matter as solitonic excitations builds on topological models from Skyrme [34], Manton [27], Rajaraman [31], and Faddeev–Niemi [14]. CFT generalizes these to include spin, charge [11,19], and generation structure as manifestations of winding, internal phase, and shear in ${\Phi }^{\mu }$. Unlike models restricted to hadronic sectors, this approach seeks to account for all fundamental matter fields from a single underlying geometry.

In cosmology, the framework draws on topological defect models [9,24,37], attributing dark matter and dark energy not to new particles but to residual shear, vorticity, and domain wall tension from incomplete Chronon alignment. This offers a unified, geometric interpretation of large-scale cosmological effects compatible with CMB and structure formation data.

Crucially, unlike Einstein–Hilbert gravity, the theory is power-counting renormalizable. Its local action contains polynomial kinetic terms, constraint potentials, and topological interactions in four dimensions. The solitonic excitations regularize UV behavior without requiring extra dimensions, supersymmetry, or nonlocality, offering a conceptually minimal alternative to string theory [30].

In summary, CFT integrates themes from quantum gravity, soliton theory, and emergent spacetime into a unified framework. By treating temporal flow as fundamental, it offers a novel route to resolving deep tensions between geometry, matter, and quantum dynamics—within a tractable and renormalizable field-theoretic model.

3. Fundamental Structure of the Chronon Field

3.1. Mathematical Definition and Constraints

The Chronon field ${\Phi }^{\mu }\left(x\right)$ is postulated to be a smooth, future-directed, unit-norm timelike vector field defined on a four-dimensional Lorentzian manifold $(\mathcal{M},g_{\mu \nu })$. It represents the local direction of temporal flow and encodes a fundamental causal structure distinct from, but dynamically related to, the spacetime metric. Its defining constraints are given by:

$${\Phi }^{\mu }{\Phi }_{\mu }=-1,{\Phi }^0>0,$$

(2)

where the sign convention corresponds to a $(-,+,+,+)$ metric signature, and the positivity condition ensures global temporal orientation [12].

This vector field is not auxiliary nor gauge-fixed, but ontologically primary. The normalization constraint (2) is enforced dynamically via a Lagrange multiplier in the field action. The field space of ${\Phi }^{\mu }$ is thus the unit hyperboloid in the tangent bundle $T\mathcal{M}$, admitting nontrivial topological structure classified by the homotopy group ${\pi }_3\left(S^3\right)\simeq \mathbb{Z}$ [27,31]. This allows for solitonic field configurations that serve as candidates for localized particles and topological defects [1,14,32].

The Chronon field admits a natural field strength tensor analogous to the electromagnetic field:

$$F_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu },$$

(3)

which characterizes local shear and torsion in the temporal flow. Its dynamics are governed by an action of the form:

$$S[\Phi ]=\int d^{4}x\sqrt{-g}\left[-{\displaystyle \frac{1}{4}}{F}^{\mu \nu }{F}_{\mu \nu }+V({\Phi }^{\mu }{\Phi }_{\mu }+1)+{\mathcal{L}}_{\mathrm{top}}[\Phi ]\right],$$

(4)

where V enforces the norm constraint and ${\mathcal{L}}_{\mathrm{top}}$ includes topological terms (e.g., Hopf invariants, Chern–Simons-like terms) that encode soliton charge and domain wall tension [14,21].

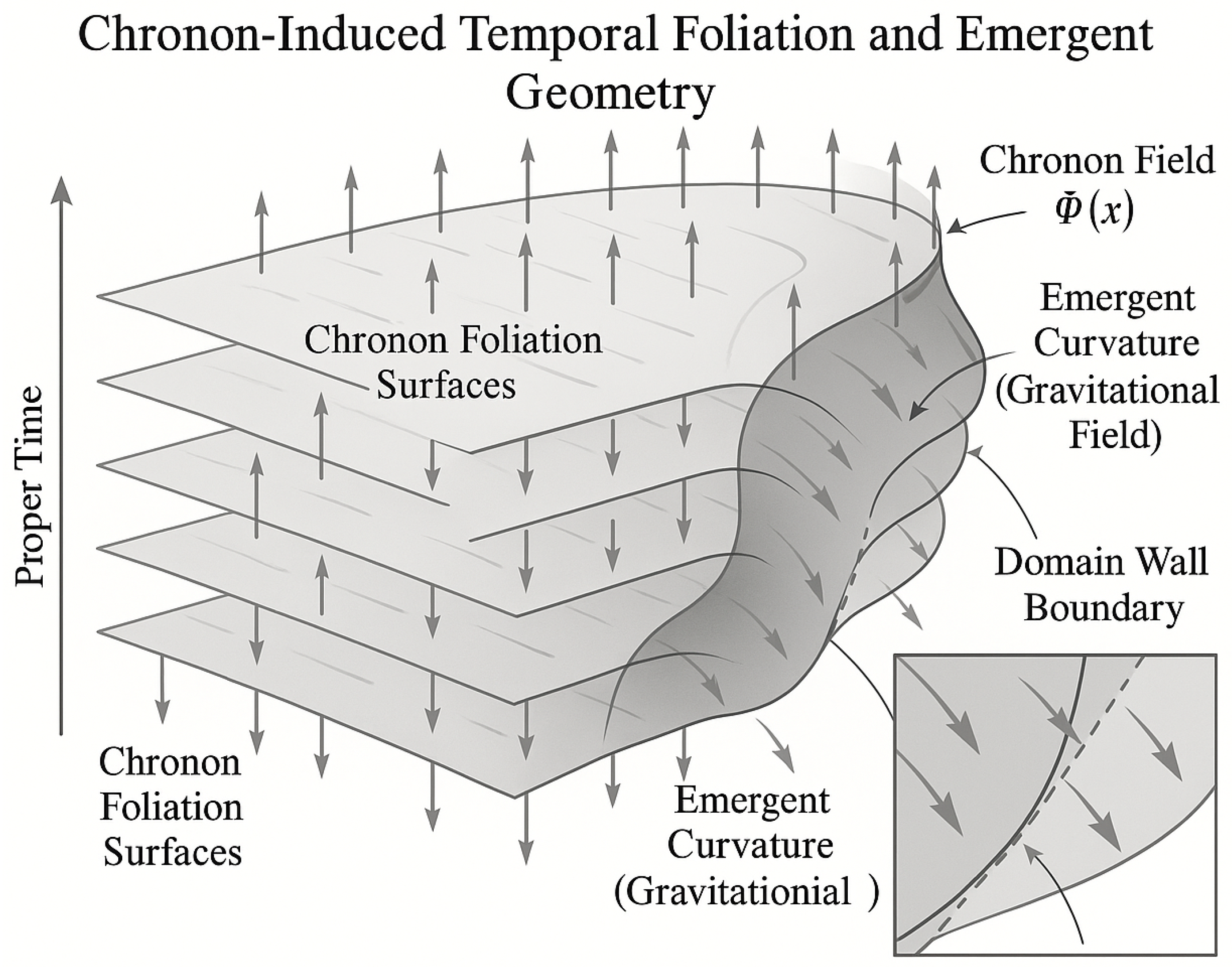
Figure 1. Illustration of the emergent spacetime geometry from Chronon-induced temporal foliation. Domain walls indicate topological defects responsible for cosmological phenomena such as dark matter and structure formation. The vector field ${\Phi }^{\mu }\left(x\right)$ generates a foliation of proper-time hypersurfaces, with emergent curvature (gravitational field) arising from variations in the field’s direction and shear.

Figure 1. Illustration of the emergent spacetime geometry from Chronon-induced temporal foliation. Domain walls indicate topological defects responsible for cosmological phenomena such as dark matter and structure formation. The vector field ${\Phi }^{\mu }\left(x\right)$ generates a foliation of proper-time hypersurfaces, with emergent curvature (gravitational field) arising from variations in the field’s direction and shear.

3.2. Temporal Foliation and Emergent Causality

The Chronon field induces a natural temporal foliation of the manifold $\mathcal{M}$ into spacelike hypersurfaces ${\Sigma }_{\tau }$ orthogonal to the integral curves of ${\Phi }^{\mu }$. These hypersurfaces define a global time function $\tau \left(x\right)$ such that:

$${\Phi }^{\mu }{\nabla }_{\mu }\tau =1,\mathrm{and}{\Sigma }_{\tau }=\{x\in \mathcal{M}|\tau \left(x\right)=\mathrm{const}.\}.$$

(5)

This foliation determines the causal ordering of events and provides an intrinsic solution to the “problem of time” encountered in canonical quantum gravity [17,18,26]. Rather than relying on coordinate choices, causality and temporal evolution are defined relationally with respect to the flow lines of ${\Phi }^{\mu }$.

The vector field ${\Phi }^{\mu }$ also defines a congruence of timelike curves, which can be used to characterize kinematic quantities such as expansion $\theta$, shear ${\sigma }_{\mu \nu }$, and vorticity ${\omega }_{\mu \nu }$:

$$\begin{array}{cc}\hfill \theta & ={\nabla }_{\mu }{\Phi }^{\mu },\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\sigma }_{\mu \nu }& ={\nabla }_{(\mu }{\Phi }_{\nu )}+{\Phi }_{(\mu }{a}_{\nu )}-{\displaystyle \frac{1}{3}}\theta h_{\mu \nu },\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill {\omega }_{\mu \nu }& ={\nabla }_{[\mu }{\Phi }_{\nu ]}+{\Phi }_{[\mu }{a}_{\nu ]},\hfill \end{array}$$

(8)

where $a^{\mu }={\Phi }^{\nu }{\nabla }_{\nu }{\Phi }^{\mu }$ is the acceleration and $h_{\mu \nu }=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }$ is the induced spatial metric on ${\Sigma }_{\tau }$ [12]. These quantities provide geometric diagnostics of the temporal field and underlie both local energy flow and global thermodynamic behavior.

3.3. Effective Metric and Geometric Backreaction

In regions of coherent Chronon alignment, the field induces an emergent effective metric

$$g_{\mu \nu }^{\mathrm{eff}}=g_{\mu \nu }+\epsilon {\Phi }_{\mu }{\Phi }_{\nu },$$

(9)

where $\epsilon$ is a small positive parameter characterizing the strength of temporal backreaction. This effective metric governs the propagation of physical fields and determines null cones, geodesic motion, and curvature. Crucially, gravitational effects are not introduced via an independent geometric field but emerge from the second-order derivatives of ${\Phi }^{\mu }$ and its stress-energy tensor [6,20,36].

The total energy-momentum tensor derived from the action (4) takes the form:

$$T_{\Phi }^{\mu \nu }=F^{\mu \lambda }{F}^{\nu }{\phantom{.}}_{\lambda }-{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{F}^{\alpha \beta }{F}_{\alpha \beta }+T_{\mathrm{top}}^{\mu \nu }+T_{\mathrm{constraint}}^{\mu \nu },$$

(10)

where the latter two terms encode contributions from topological sectors and norm enforcement. In the semiclassical limit of large-scale Chronon alignment, the Einstein tensor constructed from $g_{\mu \nu }^{\mathrm{eff}}$ satisfies:

$$G_{\mathrm{eff}}^{\mu \nu }=8\pi G{T}_{\Phi }^{\mu \nu }+\mathcal{O}\left({\epsilon }^2\right),$$

(11)

recovering General Relativity as an emergent, coarse-grained limit of Chronon field dynamics [2,22,33].

The backreaction term $\epsilon {\Phi }_{\mu }{\Phi }_{\nu }$ can be viewed as a manifestation of vacuum polarization in the temporal sector. Its nonlinear structure yields modifications to causal structure in the strong-field regime, with phenomenological implications for gravitational waves, black hole thermodynamics, and the early universe [3,16,29].

Altogether, the Chronon field constitutes a temporally grounded geometric framework from which both causal order and gravitational dynamics naturally arise. Its solitonic and topological richness supports the emergence of matter, gauge symmetry, and quantum behavior, as we explore in the sections that follow.

4. Emergence of Spacetime and Gravity

4.1. Chronon-Induced Metric

In Chronon Field Theory (CFT), spacetime geometry is not assumed a priori, but emerges dynamically from the coherent alignment of the Chronon field ${\Phi }^{\mu }\left(x\right)$. Given a background manifold $\mathcal{M}$ with an auxiliary metric $g_{\mu \nu }$ used for variational purposes, the physically observable causal structure is encoded in an effective metric

$$g_{\mu \nu }^{\mathrm{eff}}\left(x\right)=g_{\mu \nu }\left(x\right)+\epsilon {\Phi }_{\mu }\left(x\right){\Phi }_{\nu }\left(x\right),$$

(12)

where $\epsilon >0$ is a coupling constant parameterizing the strength of temporal backreaction [20,36]. The effective inverse metric is similarly given by

$$g_{\mathrm{eff}}^{\mu \nu }\left(x\right)=g^{\mu \nu }\left(x\right)-{\displaystyle \frac{\epsilon }{1+\epsilon }}{\Phi }^{\mu }\left(x\right){\Phi }^{\nu }\left(x\right).$$

(13)

This metric determines geodesics, null cones, and field propagation, thereby replacing the passive spacetime background with a dynamically generated causal geometry.

The geometry encoded by $g_{\mu \nu }^{\mathrm{eff}}$ inherits curvature from spatial and temporal deformations in ${\Phi }^{\mu }$. The field strength tensor

$$F_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu }$$

(14)

and associated acceleration and vorticity enter the effective curvature tensors, inducing gravitational behavior without the need for a fundamental graviton or metric quantization [6]. As we will show, Einstein’s field equations arise as a limiting case of this structure.

4.2. Recovery of General Relativity

The Einstein tensor associated with the effective metric (12) can be computed using standard variational techniques. When the Chronon field enters a phase of large-scale coherence—such as after a cosmological phase transition—it defines a near-uniform temporal direction over macroscopic regions. In this regime, the curvature induced by the Chronon field reproduces Einsteinian gravity:

$$G^{\mu \nu }\left[g^{\mathrm{eff}}\right]=8\pi G{T}_{\Phi }^{\mu \nu }+\mathcal{O}\left({\epsilon }^2\right).$$

(15)

Here, $T_{\Phi }^{\mu \nu }$ is the energy-momentum tensor derived from the Chronon action, including kinetic, topological, and constraint terms. The small parameter $\epsilon$ controls the subleading deviations from general relativity, which become significant in regimes of strong Chronon curvature or rapid topological evolution [2,33].

Importantly, this derivation does not assume Einstein’s equations; instead, they emerge as an effective macroscopic limit. This demonstrates that classical gravity is a manifestation of coherent temporal flow, not a fundamental gauge field. The quantum-to-classical transition corresponds to the onset of large-scale Chronon order [3].

Moreover, since the underlying dynamics of ${\Phi }^{\mu }$ are governed by a manifestly Lorentz-invariant action, Lorentz symmetry is spontaneously broken only by the vacuum expectation value $\langle {\Phi }^{\mu }\rangle$, preserving covariance in the underlying theory. The spontaneous nature of this symmetry breaking offers new insights into inertial frames, the equivalence principle, and gravitational redshift within a temporal ontology [25].

4.3. Geometric Derivation of the Equivalence Principle in Chronon Field Theory

In Chronon Field Theory (CFT), the Einstein Equivalence Principle (EEP)—which states that all test bodies fall identically regardless of their composition, and that the laws of physics locally reduce to those of special relativity—emerges naturally from the geometry of a smooth, unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$.

4.3.1. Foliation and Local Inertial Frames

Let ${\Phi }^{\mu }$ define a congruence of worldlines and assume it is irrotational and geodesic:

$$\begin{array}{cc}\hfill {\nabla }_{[\mu }{\Phi }_{\nu ]}& =0,\left(\mathrm{irrotational}\right)\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\Phi }^{\nu }{\nabla }_{\nu }{\Phi }^{\mu }& =0,\left(\mathrm{geodesic}\right).\hfill \end{array}$$

(17)

By Frobenius’ theorem, the irrotationality condition ensures the existence of a scalar time function $T\left(x\right)$ such that ${\Phi }^{\mu }=-{\nabla }^{\mu }T$, and the level sets ${\Sigma }_T$ define a foliation of spacetime into spacelike hypersurfaces orthogonal to ${\Phi }^{\mu }$. This defines natural simultaneity slices for comoving observers.

The geodesic condition implies that the integral curves of ${\Phi }^{\mu }$ represent the worldlines of freely falling observers. In Riemann normal coordinates adapted to this foliation, the metric locally reduces to

$$g_{\mu \nu }\left(p\right)={\eta }_{\mu \nu },{\Gamma }_{\mu \nu }^{\lambda }\left(p\right)=0,$$

(18)

which establishes local inertial frames in which the effects of gravity vanish to first order.

4.3.2. Universality of Free Fall

For any matter field $\phi$ minimally coupled to the metric $g_{\mu \nu }$, the motion of localized excitations reduces to the standard geodesic equation:

$${\displaystyle \frac{d^2{x}^{\mu }}{d{\tau }^2}}+{\Gamma }_{\nu \rho }^{\mu }{\displaystyle \frac{d{x}^{\nu }}{d\tau }}{\displaystyle \frac{d{x}^{\rho }}{d\tau }}=0,$$

(19)

independent of the internal structure of $\phi$. This result follows from a field-theoretic variational principle and applies uniformly to all minimally coupled fields. Therefore, the universality of free fall is not postulated but derived as a consequence of the irrotational and geodesic nature of the ${\Phi }^{\mu }$ field.

4.3.3. Equivalence Principle as a Theorem

We thus conclude that in the CFT framework, the Einstein Equivalence Principle holds as a geometric theorem:

In any region where the Chronon field ${\Phi }^{\mu }$ is smooth, irrotational, and geodesic, one can construct a local coordinate system in which all matter fields follow geodesics of the background metric and local physics reduces to special relativity.

This derivation anchors the equivalence principle in the geometric and dynamical structure of the Chronon field, replacing traditional postulates with field-theoretic necessity.

4.4. Symmetry, Noether Current, and Local Energy in Chronon Gravity

Chronon Field Theory (CFT) replaces the diffeomorphism invariance of General Relativity (GR) with a field-theoretic framework built on a fixed background spacetime and a dynamical, time-orienting field ${\Phi }^{\mu }\left(x\right)$. This shift yields a crucial advantage: the ability to define a meaningful local energy density for the gravitational field. Although the spontaneous breaking of time-directional symmetry in ${\Phi }^{\mu }$ prevents the existence of a conserved global energy, local conservation laws still arise from residual symmetries in the theory.

4.4.1. Residual Symmetry and Noether Current

The CFT action retains invariance under infinitesimal field reparametrizations that preserve the direction of ${\Phi }^{\mu }$, even if not its magnitude or orientation globally. This residual symmetry—effectively a local reparameterization along the integral lines of ${\Phi }^{\mu }$—gives rise to a Noether current associated with temporal flow. The corresponding Noether current $J^{\mu }$ obeys a local conservation law:

$${\nabla }_{\mu }{J}^{\mu }=0,$$

(20)

expressing the preservation of energy locally within each causal patch, even in the absence of global conservation.

4.4.2. Well-Defined Local Energy Density

Unlike in GR, where local gravitational energy cannot be consistently defined due to coordinate freedom and the equivalence principle, CFT permits an unambiguous local energy density. The energy-momentum tensor of the Chronon field,

$$T^{\mu \nu }={\displaystyle \frac{\delta {\mathcal{L}}_{\Phi }}{\delta g_{\mu \nu }}},$$

(21)

is both covariantly conserved and locally meaningful. In particular, the energy density in the rest frame defined by the Chronon field is:

$$\rho \left(x\right)=T^{\mu \nu }{n}_{\mu }{n}_{\nu },$$

(22)

where $n^{\mu }={\Phi }^{\mu }/\sqrt{-{\Phi }^{\alpha }{\Phi }_{\alpha }}$ defines the local time direction.

This allows gravitational dynamics in CFT to be understood as the evolution of well-defined field energy stored in ${\Phi }^{\mu }$, governed by local interactions. The absence of global conservation is thus not a weakness, but a consequence of spontaneous symmetry breaking, with energy still conserved within local neighborhoods.

4.4.3. Improvement Over GR

This local structure provides a marked conceptual improvement over GR, where attempts to define gravitational energy lead to ambiguities, non-tensorial pseudotensors, or coordinate artifacts. In contrast, CFT offers a manifestly covariant and field-theoretic formulation in which energy density is locally meaningful and dynamically linked to the emergent metric via ${\Phi }^{\mu }$. This positions CFT as a more physically transparent framework for gravitational energy, particularly in contexts involving localized processes, non-equilibrium dynamics, or quantum corrections.

4.5. Raychaudhuri Flow and Cosmological Expansion

In Chronon Field Theory, cosmic expansion is reinterpreted as a property of temporal flow rather than metric rescaling. The expansion scalar associated with the Chronon congruence,

$$\theta ={\nabla }_{\mu }{\Phi }^{\mu },$$

(23)

quantifies the divergence of temporal flow lines. Its evolution follows a generalized Raychaudhuri equation:

$${\displaystyle \frac{d\theta }{d\tau }}=-{\displaystyle \frac{1}{3}}{\theta }^2-{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }+{\omega }_{\mu \nu }{\omega }^{\mu \nu }-R_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu },$$

(24)

where ${\sigma }_{\mu \nu }$ and ${\omega }_{\mu \nu }$ denote shear and vorticity, and $R_{\mu \nu }$ is the Ricci tensor of the effective metric [12].

In Chronon Phase Transition Cosmology (CPTC), the early universe undergoes a phase transition into coherent temporal order, driving a sharp increase in $\theta$ and establishing causal structure without inflation. Expansion then proceeds from topological tension at domain boundaries, eventually stabilizing into power-law growth governed by residual curvature and solitonic content [9,24,37].

Late-time acceleration emerges from metastable domain walls encoded in ${\mathcal{L}}_{\mathrm{top}}[\Phi ]$, while residual shear mimics dark matter effects at galactic scales [36]. These features collectively yield a geometric account of cosmic expansion and structure formation grounded in the dynamics of temporal flow, not spacetime curvature.

5. Chronon Phase Transition and Cosmogenesis

5.1. Temporal Ordering and the Big Bang

In Chronon Field Theory, the origin of the universe is reinterpreted not as a geometric singularity but as a second-order phase transition in the temporal sector. Prior to this transition, the Chronon field ${\Phi }^{\mu }\left(x\right)$ exists in a disordered state with no coherent causal structure. The spacetime manifold $\mathcal{M}$ lacks a global temporal foliation, and time orientation is undefined beyond local patches [5,18].

The Big Bang corresponds to the spontaneous symmetry breaking of temporal alignment:

$$\langle {\Phi }^{\mu }\left(x\right)\rangle \ne 0,\langle {\Phi }^0\left(x\right)\rangle >0,$$

(25)

analogous to magnetization in the Ising model or the Higgs mechanism, but occurring in the space of causal structure. The order parameter is the temporal coherence length $\xi \left(t\right)$, which increases with time:

$$\xi \left(t\right)\sim t^{\alpha },\alpha >1.$$

(26)

This transition generates a dynamically ordered foliation—a global “Real Now”—establishing causal cones, light-speed constancy, and the conditions for relativistic locality. The Chronon phase transition thereby replaces inflation as the generator of super-horizon correlations and sets the initial conditions for large-scale structure [3,9].

5.2. Domain Walls and Structure Formation

Like other systems undergoing spontaneous symmetry breaking, the Chronon field forms spatially localized topological defects during its ordering process. These appear as domain walls separating regions with distinct ${\Phi }^{\mu }$ alignment [24,37].

The energy per unit area of these walls is governed by the gradient energy:

$$\tau \sim \int d^{3}x\left({\nabla }_{\mu }{\Phi }^{\nu }{\nabla }^{\mu }{\Phi }_{\nu }\right),$$

(27)

with dynamics determined by kink-like solutions in effective field theory [14,27]. These walls seed curvature perturbations, drive matter density inhomogeneities, and correlate spin alignment and vorticity across cosmological scales [32,40].

Chronon domain walls also influence gravitational lensing and velocity dispersion in galaxies, and imprint deterministic anisotropies in the CMB. Unlike quantum fluctuations from inflation, these structures arise from causal, topological dynamics [9,36].

Furthermore, domain wall collisions produce propagating topological modes that stabilize into quantized fermionic and bosonic particles. Thus, matter formation emerges intrinsically from the phase structure of time [1,31].

5.3. Chronon Domain Wall Network as a Source of Dark Energy

In Chronon Field Theory (CFT), dark energy arises not from a static cosmological constant, but from the residual vacuum energy stored in a network of domain walls associated with spontaneous symmetry breaking of the Chronon field. These walls act as metastable topological defects separating causally disconnected regions of misaligned temporal orientation. We now derive the effective contribution of this network to the cosmological energy budget and show that it yields a slowly decaying vacuum energy with ${\rho }_{\mathrm{dom}}\left(t\right)\sim 1/t$.

5.3.1. Formation of Chronon Domain Walls

Let ${\Phi }^{\mu }\left(x\right)$ denote the Chronon field, a globally timelike vector field that encodes the causal structure of spacetime. During a primordial symmetry-breaking transition, the Chronon field selects local time directions from a disconnected vacuum manifold, topologically represented as:

$$\mathcal{M}\simeq S^3/{\mathbb{Z}}_2.$$

(28)

Causally disconnected regions settle into different vacuum sectors, resulting in domain walls—surfaces across which ${\Phi }^{\mu }$ interpolates nontrivially. These walls carry surface tension $\sigma$, with energy per unit area given by:

$$\sigma \sim \int {({\partial }_{\perp }\Phi )}^{2}d\ell ,$$

(29)

where ${\partial }_{\perp }\Phi$ denotes the transverse gradient of the Chronon field across the wall.

5.3.2. Scaling Dynamics and Energy Density

As the universe expands, the domain wall network evolves according to scaling dynamics familiar from topological defect cosmology [37]. The average energy density of the network is inversely proportional to the characteristic length scale $L\left(t\right)$ between walls:

$${\rho }_{\mathrm{dom}}\left(t\right)\sim {\displaystyle \frac{\sigma }{L\left(t\right)}}.$$

(30)

In a scaling regime, domain walls maintain a constant number per Hubble volume, implying $L\left(t\right)\sim t$. Thus, the vacuum energy redshifts as:

$${\rho }_{\mathrm{dom}}\left(t\right)\sim {\displaystyle \frac{\sigma }{t}}.$$

(31)

This decay is slower than that of matter (${\rho }_m\sim a^{-3}$) and radiation (${\rho }_r\sim a^{-4}$), allowing ${\rho }_{\mathrm{dom}}$ to eventually dominate the energy density at late cosmological times.

5.3.3. Equation of State and Gravitational Role

The stress-energy tensor of the domain wall network contributes to the Einstein equations as:

$$T_{\mu \nu }^{\left(\mathrm{Chronon}\right)}=-{\rho }_{\mathrm{dom}}\left(t\right)g_{\mu \nu }+{\tau }_{\mu \nu },$$

(32)

where ${\tau }_{\mu \nu }$ contains subleading anisotropic stress due to local wall geometry. On large scales, the network behaves as a dynamical vacuum component with an effective equation of state:

$$w_{\mathrm{Chronon}}\left(t\right)={\displaystyle \frac{p}{\rho }}\approx -1+ϵ\left(t\right),$$

(33)

where $ϵ\left(t\right)>0$ is a slowly decaying function encoding the metastable decay of the domain wall tension. As $ϵ\left(t\right)\to 0$ at late times, the Chronon vacuum asymptotically mimics a cosmological constant, but with a dynamical origin and testable deviations from $\Lambda$CDM [9].

5.3.4. Implications

This mechanism offers a natural, symmetry-driven explanation for the late-time acceleration of the universe, eliminating the need for a finely tuned cosmological constant. Moreover, the prediction ${\rho }_{\mathrm{dom}}\sim 1/t$ provides a falsifiable scaling law that can be tested through precision cosmology, including late-time equation-of-state reconstruction and integrated Sachs-Wolfe measurements.

5.4. A Proposal: Dark Matter as Chronon Shear

We propose that dark matter phenomena may arise from geometric distortions in the temporal field ${\Phi }^{\mu }\left(x\right)$, rather than from unseen particles. In regions where the Chronon field exhibits misalignment or incomplete temporal ordering, its integral congruence develops nonzero shear and vorticity. These features introduce effective stress-energy contributions that modify inertial motion and gravitational dynamics.

The resulting effective dark matter density is conjectured to scale with local geometric invariants:

$${\rho }_{\mathrm{DM}}^{\mathrm{eff}}\sim {\sigma }_{\mu \nu }{\sigma }^{\mu \nu }+{\omega }_{\mu \nu }{\omega }^{\mu \nu },$$

(34)

where ${\sigma }_{\mu \nu }$ and ${\omega }_{\mu \nu }$ are the shear and vorticity tensors derived from ${\Phi }^{\mu }\left(x\right)$ [36]. These terms quantify the anisotropic strain and internal rotation of temporal flow, potentially sourcing additional gravitational acceleration in galaxies and clusters.

While this mechanism remains to be fully developed and tested against astrophysical data, it offers a promising geometric route to reproducing key dark matter signatures—such as flat rotation curves and lensing anomalies—within the Chronon framework. Unlike particle dark matter models, it attributes these effects to emergent properties of spacetime structure, opening a new path toward unifying inertia, gravity, and temporal order.

5.5. Prototype Simulation of Chronon Symmetry Breaking

To demonstrate the dynamical emergence of causal structure and topological matter in the Chronon framework, we implement a lattice simulation of the evolution of the unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$ in $(3+1)$ dimensions. The simulation is performed on a ${1024}^3$ grid for 500 discrete time steps using an explicit, constraint-preserving evolution scheme.

5.5.1. Evolution Dynamics

The field obeys the normalization constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ and evolves according to a gradient flow approximation of an effective potential:

$$V[\Phi ]={\displaystyle \frac{1}{2}}{(1-{\Phi }^0)}^2+\lambda {\left({\Phi }^{\mu }{\Phi }_{\mu }+1\right)}^2,$$

(35)

where $\lambda \gg 1$ enforces the unit-norm condition. The dynamical update rule at each lattice site is:

$${\Phi }^{\mu }(x,t+1)={\Phi }^{\mu }(x,t)-\eta {\displaystyle \frac{\delta V}{\delta {\Phi }^{\mu }(x,t)}}+D{\nabla }^2{\Phi }^{\mu }(x,t),$$

(36)

followed by pointwise normalization:

$${\Phi }^{\mu }\to {\displaystyle \frac{{\Phi }^{\mu }}{\sqrt{|{\Phi }^{\nu }{\Phi }_{\nu }|}}}.$$

(37)

Here, $\eta$ is the learning rate, and D controls diffusion. Covariant derivatives are approximated by centered finite differences.

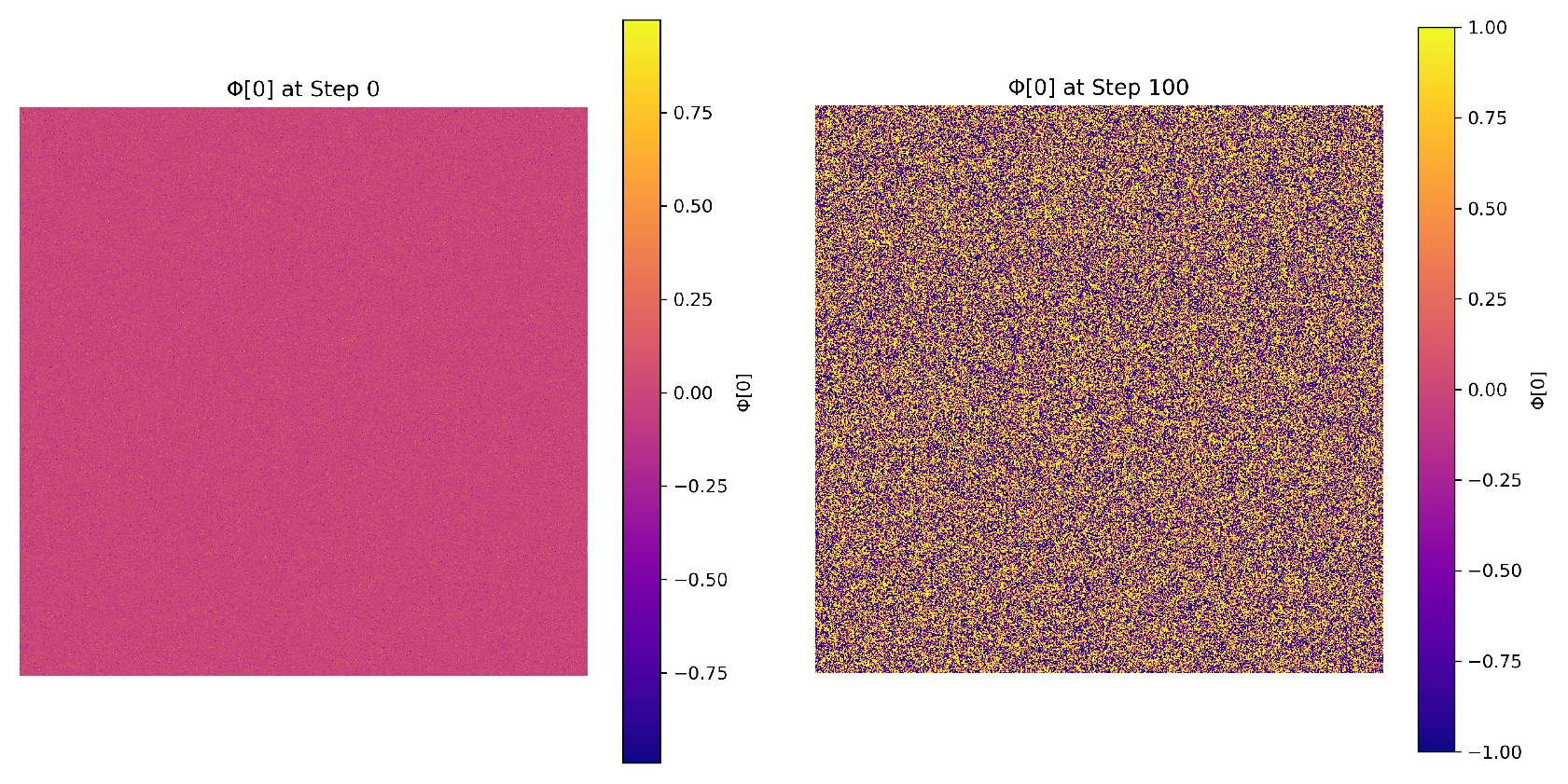
5.5.2. Initial Conditions

The Chronon field is initialized with spatially uncorrelated Gaussian noise:

$${\Phi }^0(x,0)\sim \mathcal{N}(0,0.01),{\Phi }^i(x,0)\sim \mathcal{N}(0,1),i=1,2,3,$$

(38)

followed by projection to the hyperboloid constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$. This represents a maximally entropic initial state.

5.5.3. Shear and Phase Observables

Shear is monitored via the projected symmetric gradient:

$${\sigma }_{\mu \nu }=h_{\mu }{\phantom{.}}^{\alpha }{h}_{\nu }{\phantom{.}}^{\beta }\left({\nabla }_{(\alpha }{\Phi }_{\beta )}-{\displaystyle \frac{1}{2}}{h}_{\alpha \beta }{\nabla }_{\gamma }{\Phi }^{\gamma }\right),$$

(39)

where $h_{\mu \nu }=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }$. Phase coherence is tracked by extracting the local orientation vector $u^{\mu }={\Phi }^{\mu }/\parallel {\Phi }^{\mu }\parallel$ and defining:

$$C(r,t)=〈u^{\mu }(x,t)u_{\mu }(x+r,t)〉,$$

(40)

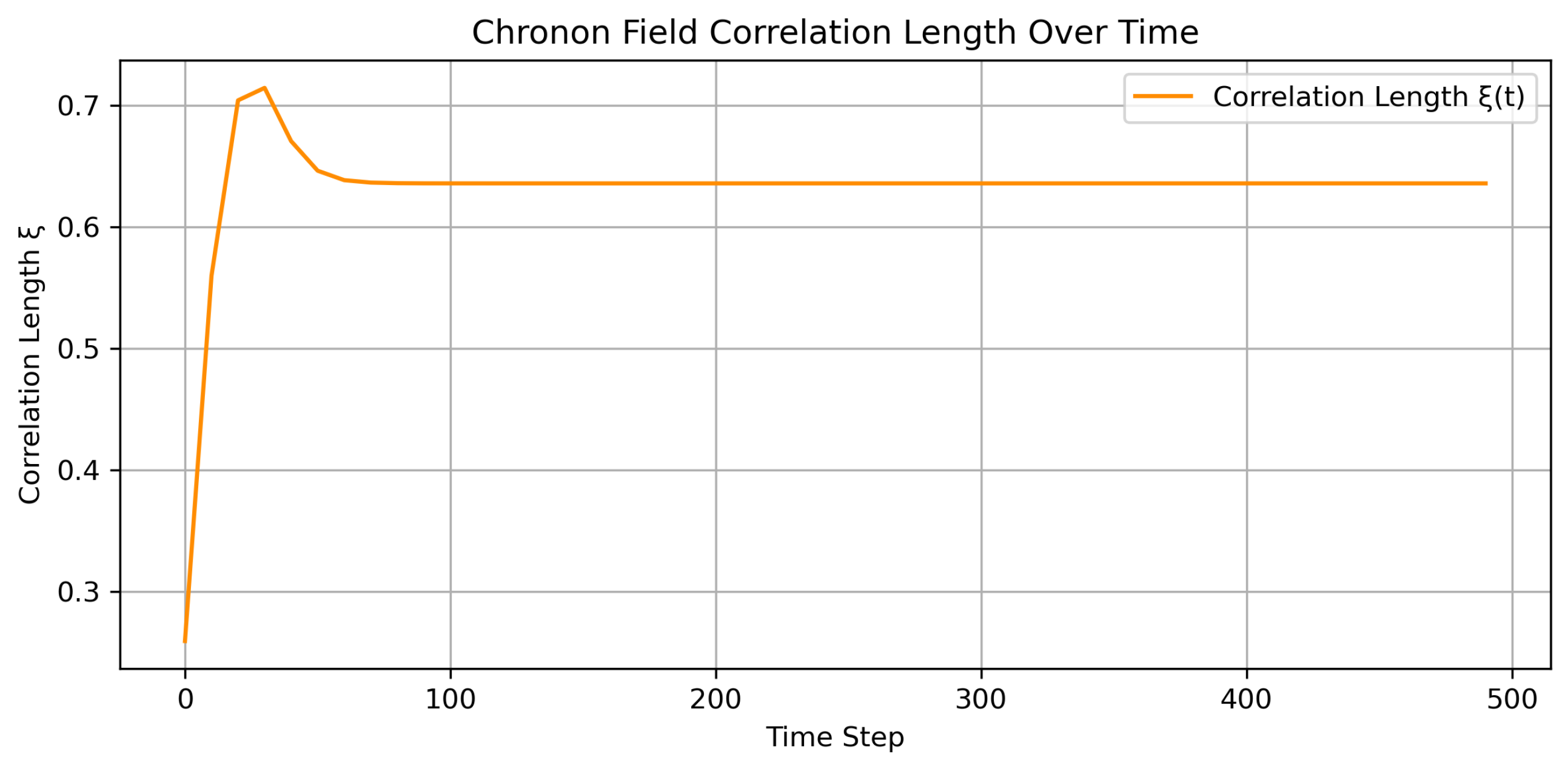
from which a correlation length $\xi \left(t\right)$ is extracted by exponential fit.

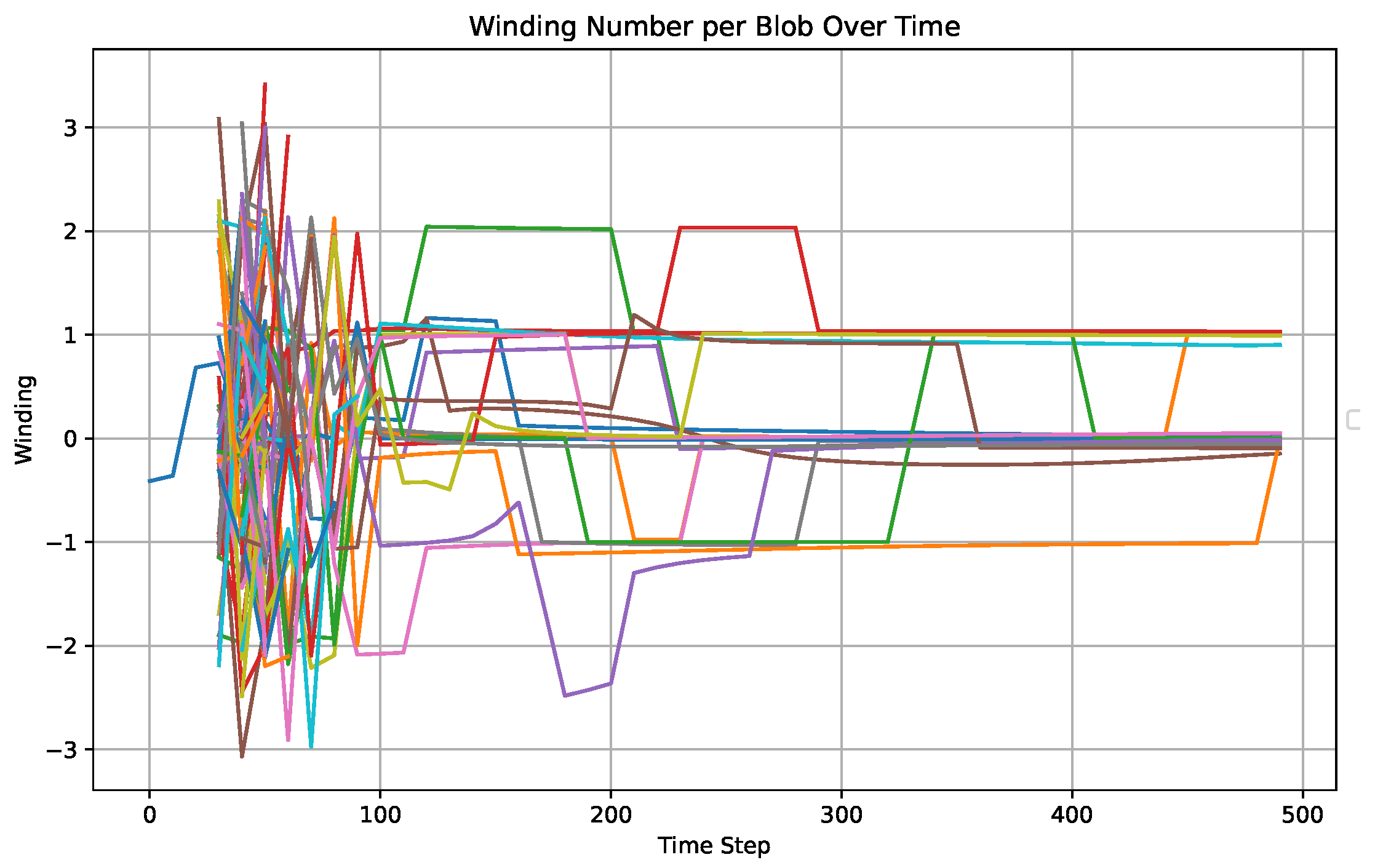
5.5.4. Topological Charge and Defects

Local winding number is computed on each plaquette using a discretized map into $S^2$ defined by the normalized spatial projection of ${\Phi }^{\mu }$. Solitons are identified as regions with nontrivial winding and localized energy density:

$$E\left(x\right)=\sum _{\mu ,\nu }{\left({\partial }_{\mu }{\Phi }^{\nu }\right)}^2.$$

(41)

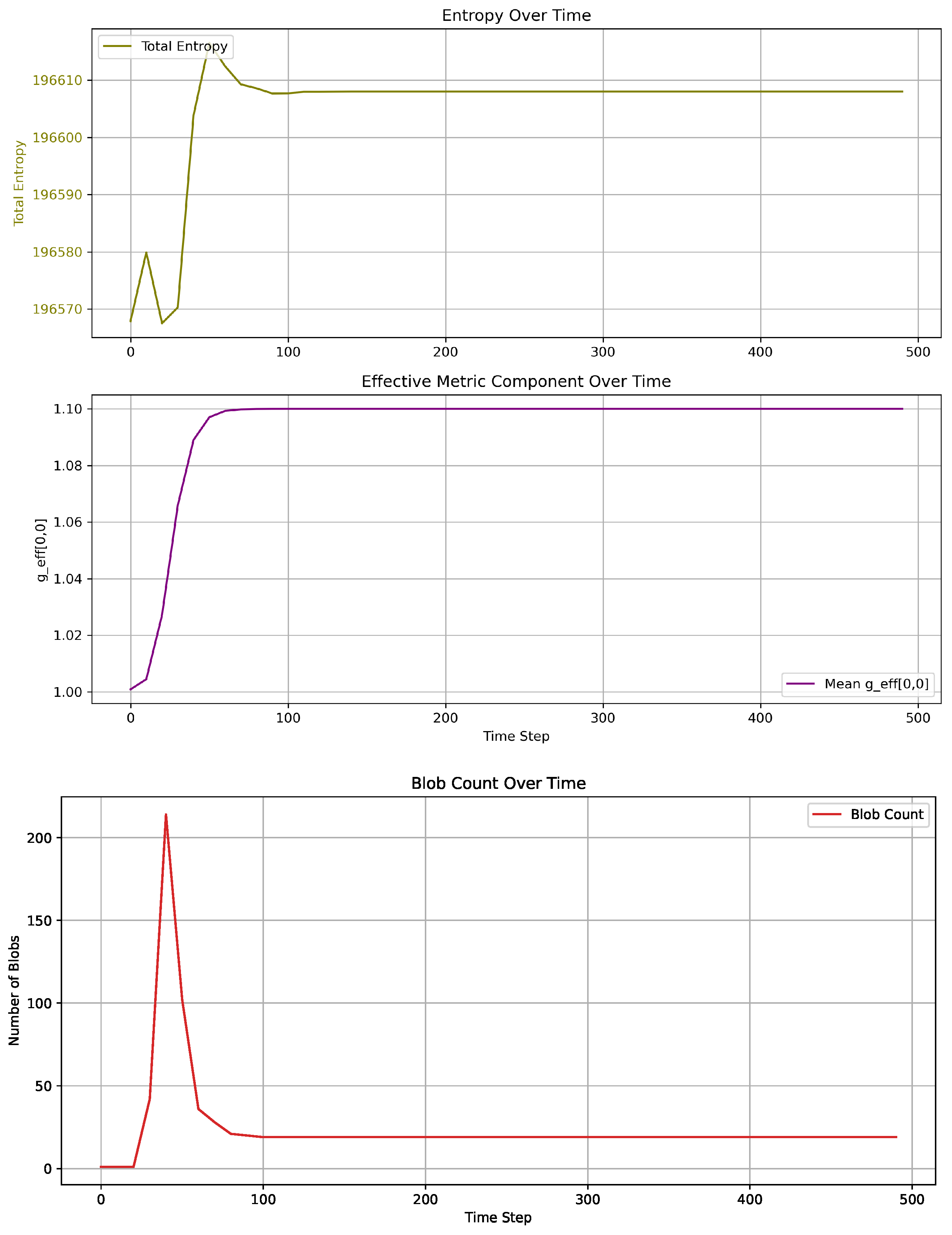
5.5.5. Results

As shown in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6, the initially disordered Chronon field undergoes a dynamical transition toward coherent temporal ordering. This transition is marked by the emergence of global causal alignment (${\Phi }^0\to 1$), long-range phase correlations, and topologically stable solitonic defects with quantized winding number. Over time, the winding number per defect stabilizes, and defect trajectories begin to align with the local Chronon flow, indicating a self-organizing phase.

The entropy of the system, computed as the Shannon entropy of local orientation histograms, decreases monotonically, signaling a loss of microscopic disorder. Concurrently, key geometric quantities such as $g_{00}=-{\Phi }^0{\Phi }^0$ approach spatial uniformity, reflecting the formation of a consistent temporal foliation. These signatures collectively demonstrate a symmetry-breaking transition from an isotropic, chaotic initial state to an ordered temporal structure populated by persistent matter-like excitations.

6. Topological Structure and Emergence of Matter

6.1. Solitons and Quantized Winding

The Chronon field ${\Phi }^{\mu }\left(x\right)$—a smooth, unit-norm, future-directed timelike vector field—admits topologically nontrivial configurations when the spatial domain is compactified to $S^3$. These configurations are classified by the third homotopy group:

$${\pi }_3\left(S^3\right)\simeq \mathbb{Z},$$

(42)

corresponding to integer winding numbers that count the number of times spatial hypersurfaces wrap the target space of normalized temporal directions [27,31]. Each winding sector contains soliton solutions—localized, finite-energy field configurations—which are topologically protected and exhibit particle-like behavior [14,32].

The energy of such solitons is governed by gradients of ${\Phi }^{\mu }$ and a norm-preserving potential:

$$E_{\mathrm{sol}}\sim \int d^{3}x\left({\nabla }_{\mu }{\Phi }^{\nu }{\nabla }^{\mu }{\Phi }_{\nu }+\lambda {({\Phi }^{\mu }{\Phi }_{\mu }+1)}^2\right),$$

(43)

where the constraint term enforces $|{\Phi }^{\mu }|=1$. The internal structure of each soliton—such as twisting or linking of phase lines—defines moduli parameters analogous to quantum numbers (e.g., flavor, generation).

Importantly, solitons with odd winding number behave as fermions due to the antisymmetric properties of their configuration space. This arises from topological intersection rules: overlapping identical solitons induce destructive interference in temporal coherence, enforcing exclusion behavior [14]. Thus, fermionic statistics emerge from classical field topology, without requiring fundamental anticommuting degrees of freedom.

6.2. Origin of Mass Without the Higgs Mechanism

In Chronon Field Theory (CFT), mass arises not from spontaneous symmetry breaking of a scalar Higgs field, but from the internal energy associated with topologically stable solitonic configurations of the temporal field ${\Phi }^{\mu }\left(x\right)$. This approach bypasses the need for vacuum expectation values (VEVs), thereby resolving two significant issues in conventional field theory: the unnatural fine-tuning of vacuum energy implied by large VEVs (the cosmological constant problem), and the arbitrary pattern of Yukawa couplings required to generate the fermion mass spectrum.

In CFT, each fermionic excitation corresponds to a localized, topologically stabilized soliton whose energy content defines its inertial mass. The energy arises from gradients and phase misalignments in the local configuration of ${\Phi }^{\mu }\left(x\right)$ relative to a surrounding coherence field ${\overline{\Phi }}^{\mu }\left(x\right)$. A generic expression for the mass of a soliton labeled by index i takes the form:

$$m_i=\int d^{3}x\left[\kappa {\partial }_{\nu }{\Phi }_i^{\mu }{\partial }^{\nu }{\Phi }_{\mu i}+\lambda {\left(1+{\Phi }_i^{\mu }{\overline{\Phi }}_{\mu }\right)}^2\right],$$

(44)

where $\kappa$ and $\lambda$ are coupling constants associated with kinetic and coherence energy scales, respectively. The first term penalizes spatial gradients, while the second encodes misalignment between the soliton and the ambient Chronon field, effectively measuring local coherence tension.

This formulation yields several notable features:

• No vacuum expectation value (VEV): Unlike the Higgs mechanism, the vacuum configuration ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ introduces no large-scale vacuum energy contribution, avoiding the severe discrepancy between predicted and observed cosmological constant values.
• Geometric origin of mass: Mass is a manifestation of internal field structure and topology, not a result of coupling to an external scalar field. Different particle masses arise from distinct topological classes or local geometric profiles of the solitonic solution.
• No arbitrary Yukawa couplings: The mass spectrum is determined by intrinsic geometric factors—field gradients, alignment angles, and domain wall localization—rather than empirical coupling constants.

This geometric approach aligns with the broader philosophy of CFT: that matter and interaction properties are consequences of the configuration space of time itself. By grounding mass in soliton coherence energy, CFT provides a natural, non-arbitrary, and cosmologically safe alternative to scalar-based symmetry breaking.

Comment on the Observed Higgs Boson

While the Higgs boson has been experimentally confirmed at 125 GeV [4], its interpretation within Chronon Field Theory differs from the conventional view of it as the sole generator of mass via spontaneous symmetry breaking. In CFT, mass arises from solitonic coherence energy rather than a scalar vacuum expectation value. The observed Higgs may instead be understood as a bound-state excitation or effective composite mode within the Chronon field—analogous to mesonic resonances in QCD—whose apparent coupling to other particles reflects induced interactions in a topologically structured background. This reinterpretation preserves agreement with collider phenomenology while avoiding the fine-tuning and vacuum energy problems associated with elementary scalar fields.

6.3. Origin of Spin and Antimatter

Spin arises from the internal structure of the soliton’s temporal flow. Specifically, helicoidal or toroidal twisting of the internal phase within a localized ${\Phi }^{\mu }$ configuration gives rise to intrinsic angular momentum:

$$S^{\mu }={\displaystyle \frac{1}{2}}{ϵ}^{\mu \nu \alpha \beta }{\Phi }_{\nu }{\partial }_{\alpha }{\Phi }_{\beta }.$$

(45)

This conserved topological spin density resembles Hopf solitons and Skyrmions, where quantized circulation encodes spin-like behavior [27,34]. No spinor fields are needed at the fundamental level; spin emerges as a solitonic topological invariant.

Antimatter corresponds to solitons of opposite winding, generated by a discrete symmetry:

$${\Phi }^{\mu }\left(x\right)\mapsto -{\Phi }^{\mu }\left(x\right),$$

(46)

which reverses the temporal orientation while preserving norm. This operation acts analogously to a CPT transformation, mapping solitons to their conjugate counterparts. In early-universe settings, asymmetric domain boundary conditions during Chronon symmetry breaking can induce net matter over antimatter, providing a novel pathway to baryogenesis without invoking explicit CP violation [5,40].

The annihilation of matter-antimatter pairs corresponds to the topological unwinding of temporal knots—a process that releases energy via decoherence and radiation [41]. This interpretation connects fundamental particle processes to causal topology.

6.4. Spin-Statistics Theorem from Moduli Topology

In Chronon Field Theory, unit-winding solitons ($w=1$) naturally exhibit spin-${\displaystyle \frac{1}{2}}$ behavior as a consequence of the nontrivial topology of their configuration (moduli) space. Specifically, the fundamental group of the moduli space ${\mathcal{M}}_1$ for such solitons satisfies:

$${\pi }_1\left({\mathcal{M}}_1\right)\simeq {\mathbb{Z}}_2,$$

(47)

indicating that a $2\pi$ rotation corresponds to a non-contractible loop. As a result, wavefunctions must be defined over a nontrivial spin bundle, transforming under the double cover $\mathrm{Spin}\left(3\right)\cong \mathrm{SU}\left(2\right)$:

$$\psi \mapsto -\psi .$$

(48)

Fermionic exchange statistics emerge from the topology of the two-soliton configuration space:

$${\mathcal{C}}^{\left(2\right)}=\left({\mathcal{M}}_1\times {\mathcal{M}}_1\setminus \Delta \right)/{\mathbb{Z}}_2,$$

(49)

where $\Delta$ excludes coincident configurations and ${\mathbb{Z}}_2$ accounts for indistinguishability. The fundamental group

$${\pi }_1\left({\mathcal{C}}^{\left(2\right)}\right)\simeq {\mathbb{Z}}_2$$

(50)

implies that exchanging two identical solitons results in a sign change of the total wavefunction:

$$\Psi (x_1,x_2)=-\Psi (x_2,x_1).$$

(51)

This provides a geometric realization of the spin-statistics connection: spin and antisymmetry both follow from the topological properties of the underlying moduli space, rather than being imposed via canonical quantization. The exchange phases can be interpreted as Berry holonomies arising from parallel transport over the moduli bundle [8].

6.5. Confinement and Color Charge from Topology

The strong force emerges in this framework not from fundamental gluons, but from topological linking and tension in Chronon field lines. Color charge corresponds to knottedness and linking number of temporal flow configurations, rather than $SU\left(3\right)$ quantum numbers.

Fractional winding defects—analogous to quarks—are bound into color-neutral composites via flux tubes: regions of concentrated temporal phase shear. These are described by:

$${\mathcal{F}}_{\mu \nu }\sim {\partial }_{\mu }{\theta }_{\nu }-{\partial }_{\nu }{\theta }_{\mu },$$

(52)

where ${\theta }_{\mu }$ captures internal torsion in the Chronon field. The energy of these flux tubes scales linearly with separation:

$$V_{\mathrm{string}}\left(L\right)\sim \sigma L,\sigma =\mathrm{Chronon}\mathrm{string}\mathrm{tension},$$

(53)

resembling confinement in QCD [14,21]. However, here the confinement arises purely from geometric frustration in the topology of temporal flow.

Baryons and mesons correspond to compact, knotted solitons, while isolated color charges are topologically unstable. This explains the absence of free quarks and the discrete mass spectrum of hadrons, without requiring a separate non-Abelian gauge theory [1,34,37].

6.6. Fermions and Bosons from Chronon Topology

Chronon Field Theory provides a unified topological mechanism for the emergence of both fermionic and bosonic excitations, classified by the winding number $w\in \mathbb{Z}$ of the Chronon field ${\Phi }^{\mu }\left(x\right)$. Fermions arise from solitons with odd winding numbers ($w=\pm 1$), whose configuration space ${\mathcal{M}}_1$ has a nontrivial fundamental group ${\pi }_1\left({\mathcal{M}}_1\right)={\mathbb{Z}}_2$, leading to spin-$\frac{1}{2}$ behavior and Fermi–Dirac statistics under $2\pi$ rotations and exchange.

In contrast, bosonic states emerge from topological configurations with even winding numbers ($w=0,\pm 2,\dots$). These include:

• Spin-0 solitons: Radially symmetric $w=0$ or $w=2$ configurations, identified with Higgs-like scalars. They lack polarization and arise either as composites of $w=+1$ and $w=-1$ fermion–antifermion pairs or as higher-winding Hopf solitons.
• Spin-1 solitons: Anisotropic $w=0$ or $w=2$ states with internal shear or torsion, supporting longitudinal and transverse polarizations. These configurations reproduce the behavior of massive vector bosons like the $W^{\pm }$ and $Z^0$ through propagating antisymmetric shear modes ${\sigma }_{\mu \nu }={\partial }_{[\mu }{\Phi }_{\nu ]}$.

These bosonic excitations obey Bose–Einstein statistics due to the triviality of their moduli space under $2\pi$ rotations. Their mass and decay characteristics are determined by the topological energy functional and can be tuned to align with Standard Model benchmarks. This topological classification unifies spin, statistics, and interaction structure within a single geometric framework, without invoking elementary scalar or vector fields [14,27].

In summary, the Chronon framework realizes mass, spin, charge, statistics, and confinement as emergent topological features of a single geometric field. These results illustrate that matter is not fundamental in the traditional sense, but a consequence of the topology and coherence of the temporal field.

7. Topological Flavor Physics

Chronon Field Theory (CFT) offers a geometric framework for addressing several outstanding questions in particle physics, including the fermion mass hierarchy, flavor mixing, and the observed structure of three generations. While traditional approaches rely on empirically tuned Yukawa couplings and symmetry-breaking patterns, the Chronon perspective hypothesizes that these features emerge from the internal topology of time—specifically, from the Hopf fibration structure inherent in the Chronon field. Although still in a developmental stage, this proposal seeks to elevate flavor structure from empirical input to a consequence of topological and geometric field dynamics [27,34].

7.1. Fiber Geometry and Internal Phase Dynamics

At each spacetime point $x^{\mu }$, the Chronon field ${\Phi }^{\mu }\left(x\right)$ is conjectured to exhibit an internal structure modeled on the Hopf fibration:

$$S^1\hookrightarrow S^3\stackrel{{\pi }_H}{\to }{S}^2.$$

(54)

This motivates a decomposition of ${\Phi }^{\mu }$ into a unit timelike vector $u^{\mu }\left(x\right)$ and a fiber angle $\theta \left(x\right)\in S^1$, interpreted as a local phase variable encoding coherence within the temporal field. Fermionic excitations are modeled as topologically stabilized solitons, partially characterized by their internal phase profiles [14,32]. This decomposition forms the basis for the topological flavor conjecture in CFT.

7.2. Emergence of Flavor and Mixing Matrices

Under the hypothesis that flavor modes correspond to distinct internal phase configurations, each solitonic excitation can be labeled by a characteristic phase angle ${\theta }_i$. Flavor mixing then arises from the angular separation between these phases. A simplified overlap model defines the mixing interaction between soliton species i and j as

$$V_{ij}=cos({\theta }_i-{\theta }_j),$$

(55)

and an associated phenomenological energy functional is given by

$$E\left[\theta \right]=\sum _{i<j}{\displaystyle \frac{1}{\sqrt{m_i{m}_j}}}{\left(cos({\theta }_i-{\theta }_j)-V_{ij}^{\exp }\right)}^2,$$

(56)

where $V_{ij}^{\exp }$ are experimental mixing matrix elements and $m_i$ are fermion masses. This functional serves as a heuristic tool to test whether topological coherence can qualitatively approximate observed mixing patterns, rather than as a derived result from the field equations.

Minimizing $E\left[\theta \right]$ over real-valued phases yields the following illustrative mixing matrices. For the quark sector:

$$V_{\mathrm{CKM}}^{\mathrm{model}}=\left[\begin{array}{ccc}0.971& 0.226& -0.013\\ 0.240& 0.968& 0.880\\ 0.014& 0.999& 0.965\end{array}\right],\left|V_{\mathrm{CKM}}^{\exp }\right|=\left[\begin{array}{ccc}0.97401& 0.22650& 0.00361\\ 0.22636& 0.97320& 0.0411\\ 0.00854& 0.0403& 0.999146\end{array}\right].$$

(57)

And in the lepton sector:

$$V_{\mathrm{PMNS}}^{\mathrm{model}}=\left[\begin{array}{ccc}0.710& 0.521& 0.257\\ 0.370& 0.581& 0.788\\ 0.355& 0.568& 0.778\end{array}\right],\left|V_{\mathrm{PMNS}}^{\exp }\right|=\left[\begin{array}{ccc}0.821& 0.550& 0.150\\ 0.432& 0.582& 0.693\\ 0.376& 0.597& 0.707\end{array}\right].$$

(58)

While approximate, these fits suggest that internal phase alignment in a topological field space may capture key qualitative features of flavor mixing. Further development is needed to derive such results from first principles.

7.3. Topological Constraints for Three Generations

CFT posits a potential explanation for the existence of exactly three fermion generations, based on angular coherence in the internal phase space. A configuration of three equally spaced phases on $S^1$,

$${\theta }_1=0,{\theta }_2={\displaystyle \frac{2\pi }{3}},{\theta }_3={\displaystyle \frac{4\pi }{3}},$$

minimizes mutual overlap and coherence energy in the above model. This triplet is hypothesized to be topologically stable, whereas configurations with more than three phases may lead to angular frustration or destructive interference. While preliminary, this suggests a possible geometric limit on generation number. Further work is required to explore its compatibility with more realistic moduli spaces, such as complex projective fiber bundles or flag manifolds [5,27].

7.4. Soliton Energy and Mass Hierarchies

The Chronon framework proposes that fermion masses reflect the internal energy of their corresponding solitonic configurations. A representative ansatz is

$$m_i\sim \int d^{3}x\left[\kappa |\nabla {\Phi }_i^{\mu }{|}^2+\lambda {cos}^2({\theta }_i\left(x\right)-\overline{\theta }\left(x\right))\right],$$

(59)

where $\overline{\theta }\left(x\right)$ defines a local coherence field. The first term represents spatial localization energy, while the second penalizes misalignment in internal phase. This functional form can support exponentially spaced mass spectra, reminiscent of observed hierarchies. However, this result remains conjectural and is not yet derived from the underlying Chronon dynamics [1,34].

7.5. Geometric Mechanism for CP Violation

The non-collinearity of internal fiber phases introduces an intrinsic orientation in phase space that cannot be removed by global redefinitions. This leads to a natural handedness that may serve as a geometric origin for CP violation. Unlike conventional field theories that introduce complex phases ad hoc, this mechanism suggests that CP asymmetry arises from topological winding in the Chronon configuration space. Whether this approach can quantitatively reproduce known CP-violating observables is an open question. Extending the Chronon field to include complex internal phases and computing scattering amplitudes from the full path integral formalism are key directions for future work [7,41].

7.6. Outlook and Further Work

The topological flavor hypothesis in CFT provides a speculative but potentially unifying approach to several unresolved features of the Standard Model. The following hypotheses are proposed:

• Flavor mixing arises from angular coherence between internal Chronon phases, governed by a geometric overlap energy.
• The number of fermion generations is topologically constrained by the stability of evenly spaced phase configurations on $S^1$.
• Mass hierarchies reflect soliton tension and phase misalignment, rather than arbitrary Yukawa couplings.
• CP violation originates from intrinsic topological handedness in the Chronon phase configuration space.

Further progress will require developing a full quantum theory of Chronon solitons, generalizing to complex moduli, incorporating anomaly matching conditions, and connecting with experimental flavor observables. Nonetheless, the geometric perspective offered by CFT suggests a possible path toward elevating flavor physics from empirical structure to a consequence of topological time.

8. Gauge Interactions from Chronon Phase Dynamics

8.1. Emergent $U\left(1\right)$ Gauge Theory

The Chronon field ${\Phi }^{\mu }\left(x\right)$ admits an internal phase degree of freedom when viewed as a section of a complexified, unit-norm fiber bundle over spacetime. Locally, we decompose the field as:

$${\Phi }^{\mu }\left(x\right)=\rho \left(x\right)u^{\mu }\left(x\right)e^{i\theta \left(x\right)},$$

(60)

where $u^{\mu }$ is a real, future-directed unit timelike vector satisfying $u^{\mu }{u}_{\mu }=-1$, and $\theta \left(x\right)$ is a scalar phase field capturing the internal $U\left(1\right)$ rotation of the Chronon congruence. Since ${\Phi }^{\mu }$ is normalized ($\rho \left(x\right)=1$), the dynamical degrees of freedom are encoded in $u^{\mu }$ and $\theta$.

This decomposition reveals a residual local symmetry:

$$\theta \left(x\right)\to \theta \left(x\right)+\alpha \left(x\right),$$

(61)

which defines a $U\left(1\right)$ gauge invariance. From this, we define the emergent gauge potential:

$$A_{\mu }\left(x\right)\equiv {\partial }_{\mu }\theta \left(x\right),$$

(62)

with the corresponding field strength tensor:

$$F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu },$$

(63)

in direct analogy with the electromagnetic tensor in Maxwell theory [19].

Importantly, $A_{\mu }$ is not an independent dynamical field but arises intrinsically from phase gradients of ${\Phi }^{\mu }$. The associated gauge boson—the photon—is interpreted not as a fundamental particle but as a collective excitation, namely, the massless Goldstone mode resulting from spontaneous breaking of Chronon phase coherence [11,14]. This places electromagnetism within a broader geometric framework in which the structure of gauge fields is emergent rather than imposed.

8.2. Weak Interaction via Shear Orientation

Beyond the phase degree of freedom, the Chronon field supports internal shear modes associated with spatial gradients of $u^{\mu }$. These deformations are projected orthogonally to the preferred foliation induced by ${\Phi }^{\mu }$ and encode local violations of parity symmetry.

The shear tensor is defined by:

$${\sigma }_{\mu \nu }=h_{\mu }{\phantom{.}}^{\alpha }{h}_{\nu }{\phantom{.}}^{\beta }\left({\nabla }_{(\alpha }{\Phi }_{\beta )}-{\displaystyle \frac{1}{3}}{h}_{\alpha \beta }{\nabla }_{\gamma }{\Phi }^{\gamma }\right),$$

(64)

where $h_{\mu \nu }=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }$ projects onto the hypersurface orthogonal to ${\Phi }^{\mu }$. In regions of nonzero shear, the local alignment of the temporal flow exhibits torsional twist and anisotropic strain, which spontaneously break spatial reflection symmetry.

This symmetry breaking gives rise to parity-violating interactions analogous to the weak force. In particular, coupling between Chronon shear modes and topological solitons generates chiral-selective dynamics. Left-handed soliton configurations couple preferentially to vortical shear fluctuations, while right-handed states remain inert:

$${\mathcal{L}}_{\mathrm{eff}}\supset {\overline{\psi }}_L{\gamma }^{\mu }{\psi }_L{W}_{\mu },\mathrm{with}{W}_{\mu }\sim {ϵ}_{\mu \nu \alpha \beta }{u}^{\nu }{\partial }^{\alpha }{u}^{\beta }.$$

(65)

This expression shows that the effective weak gauge field $W_{\mu }$ emerges from internal geometry—specifically, from topological twisting and shear within the Chronon congruence [25].

The resulting weak interactions are inherently chiral and do not require an explicit $SU{\left(2\right)}_L$ gauge sector or a separate Higgs mechanism. Instead, chiral asymmetry, fermion mass generation, and parity violation are consequences of local geometric structure in the temporal flow [7,40].

8.3. Photon as a Goldstone Mode

To elucidate the photon’s origin, consider a vacuum configuration of the Chronon field:

$${\Phi }^{\mu }\left(x\right)={\overline{u}}^{\mu }{e}^{i\overline{\theta }},\mathrm{with}{\nabla }_{\nu }{\overline{u}}^{\mu }=0.$$

(66)

Small fluctuations of the internal phase,

$$\theta \left(x\right)=\overline{\theta }+\delta \theta \left(x\right),$$

(67)

induce massless excitations governed by:

$$\square \delta \theta \left(x\right)=0,$$

(68)

which is the d’Alembertian wave equation for a scalar field propagating along ${\overline{u}}^{\mu }$. Interpreting $A_{\mu }={\partial }_{\mu }\delta \theta$, we recover the vacuum Maxwell equations in Lorenz gauge [19].

Thus, the photon is identified as a Goldstone-like mode of spontaneously broken $U\left(1\right)$ phase symmetry, stabilized by the topological coherence of the vacuum field. This mechanism ensures gauge invariance and masslessness of the photon without requiring a fundamental gauge sector. The electric charge of solitons arises naturally as the Noether charge associated with global Chronon phase rotation [11].

In regimes where the Chronon field undergoes topological transitions or becomes disordered—such as near cosmological singularities or inside black holes—gauge coherence may break down. In such phases, the effective photon can acquire a mass or mix with shear modes, suggesting new avenues for hidden sector physics and modified electroweak phenomenology [21,25].

In summary, gauge interactions within this framework emerge from internal structure and topological dynamics of the Chronon field itself. Phase coherence and shear orientation give rise to effective $U\left(1\right)$ and weak-like sectors, unifying gauge symmetry, parity violation, and soliton dynamics under a single geometric and topological principle.

9. Emergence and Recovery of Electromagnetism

Chronon Field Theory naturally gives rise to classical electromagnetism and quantum electrodynamics as effective low-energy phenomena, emerging from the internal phase structure of the fundamental timelike vector field ${\Phi }^{\mu }\left(x\right)$. This section provides a formal derivation of the electromagnetic field tensor, its equations of motion, and solitonic charge couplings, establishing consistency with QED [11,19].

9.1. Phase Decomposition and Gauge Redundancy

Assume that the Chronon field admits a phase decomposition in a domain where the modulus is stabilized:

$${\Phi }^{\mu }\left(x\right)=u^{\mu }\left(x\right)e^{i\theta \left(x\right)},u^{\mu }{u}_{\mu }=-1,$$

(69)

where $\theta \left(x\right)\in \mathbb{R}$ is a smooth scalar field representing internal temporal phase rotation. This decomposition introduces a local $U\left(1\right)$ redundancy:

$$\theta \left(x\right)\to \theta \left(x\right)+\alpha \left(x\right),$$

under which physical observables must remain invariant. This defines an emergent local gauge symmetry, despite the absence of a fundamental gauge group in the original action [14].

9.2. Definition of Gauge Potential and Field Strength

The natural gauge potential is the derivative of the phase:

$$A_{\mu }\left(x\right)\equiv {\partial }_{\mu }\theta \left(x\right).$$

(70)

This defines the gauge field as a pure gradient in the coherent vacuum. The associated field strength tensor is:

$$F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }={\partial }_{\mu }{\partial }_{\nu }\theta -{\partial }_{\nu }{\partial }_{\mu }\theta .$$

(71)

By construction, this satisfies the Bianchi identity:

$${\partial }_{[\lambda }{F}_{\mu \nu ]}=0,$$

(72)

ensuring the automatic validity of the homogeneous Maxwell equations [19].

9.3. Lagrangian Structure and Inhomogeneous Equations

The kinetic term in the Chronon action includes the phase contribution:

$${\mathcal{L}}_{\theta }=-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu },$$

(73)

which emerges directly from the derivative structure of the full Chronon field:

$$\begin{array}{cc}\hfill {\nabla }_{\mu }{\Phi }_{\nu }& =e^{i\theta }\left[{\nabla }_{\mu }{u}_{\nu }+i{u}_{\nu }{\partial }_{\mu }\theta \right],\hfill \end{array}$$

(74)

$$\begin{array}{cc}\hfill F_{\mu \nu }& =2i{e}^{i\theta }{u}_{[\nu }{\partial }_{\mu ]}\theta +\cdots ,\hfill \end{array}$$

(75)

where subdominant curvature and torsion contributions are neglected in the infrared [6,27].

The variation of the action with respect to $\theta$ yields the sourced Maxwell equation:

$${\nabla }_{\mu }{F}^{\mu \nu }=J^{\nu },$$

(76)

where the current arises from the Noether procedure:

$$J^{\mu }=i\left({\Phi }^{\nu }{\partial }^{\mu }{\Phi }_{\nu }^{*}-{\Phi }^{\nu *}{\partial }^{\mu }{\Phi }_{\nu }\right)=2u^{\nu }{\partial }^{\mu }\theta {\eta }_{\nu \mu }+\cdots .$$

(77)

This shows that the full dynamics of electromagnetism — both the homogeneous and inhomogeneous equations — arise from the internal geometry of the Chronon phase field.

9.4. Solitonic Sources and Charge Quantization

Solitonic excitations in CFT act as topologically nontrivial configurations of ${\Phi }^{\mu }$, carrying quantized winding in the phase:

$$Q={\displaystyle \frac{1}{2\pi }}\oint d\theta =n\in \mathbb{Z}.$$

This quantization condition, analogous to the Dirac monopole argument, implies that electric charge is not a fundamental input but a derived topological quantity [11,31]. The minimal coupling of the emergent gauge field to soliton currents takes the standard form:

$${\mathcal{L}}_{\mathrm{int}}=A_{\mu }{J}^{\mu },$$

(78)

with the source $J^{\mu }$ constructed from the winding and flow of the Chronon soliton [14,21].

The total conserved charge is:

$$Q={\int }_{\Sigma }{d}^{3}x{J}^0,$$

with conservation ${\nabla }_{\mu }{J}^{\mu }=0$ ensured by the residual $U\left(1\right)$ symmetry of the action.

9.5. Effective QED Limit and Photon Propagation

Quantization of small perturbations of the phase field $\delta \theta$ around a coherent Chronon background leads to photon-like excitations:

$$\square \delta \theta \left(x\right)=0,$$

which is the massless Klein–Gordon equation. These excitations correspond to transverse polarizations in $A_{\mu }={\partial }_{\mu }\delta \theta$, satisfying Lorenz gauge:

$${\nabla }^{\mu }{A}_{\mu }=0.$$

Gauge boson propagators, loop corrections, and interaction vertices reproduce the structure of QED at tree and one-loop level, with deviations suppressed by powers of $E/E_{\mathrm{Chronon}}$ [11,14]. The absence of a bare photon mass is protected by the topology of the phase vacuum, reinforcing the Goldstone nature of the gauge field [25,32].

9.6. Summary

In summary, Chronon Field Theory recovers Maxwell’s equations and QED through:

• An emergent $U\left(1\right)$ symmetry from internal phase rotation.
• A gauge potential defined by the gradient of the phase.
• A field strength satisfying the Bianchi identity and Maxwell’s equations.
• Soliton-induced quantized sources and conserved currents.
• Propagation and interaction consistent with low-energy QED.

This establishes that electromagnetism arises not as an imposed gauge principle but as a natural, dynamical consequence of coherent temporal flow in a unified causal framework.

10. Renormalizability and UV Behavior of Chronon Field Theory

A central appeal of Chronon Field Theory (CFT) is its intrinsic compatibility with renormalization. Unlike General Relativity, which is non-renormalizable due to the dimensionful coupling in the Einstein–Hilbert action [10,22], CFT is built from a vector field ${\Phi }^{\mu }\left(x\right)$ with strictly local kinetic terms, polynomial constraints, and topological invariants—all consistent with power-counting renormalizability in four dimensions.

10.1. Intrinsic Renormalizability

The Chronon Lagrangian is

$${\mathcal{L}}_{\Phi }=-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }+V({\Phi }^{\mu }{\Phi }_{\mu }+1)+{\mathcal{L}}_{\mathrm{top}}[\Phi ],$$

(79)

with $F_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu }$ and ${\mathcal{L}}_{\mathrm{top}}$ capturing topological terms [14,27]. Since ${\Phi }^{\mu }$ has mass dimension 1, all terms are with dimension no more than 4, satisfying the criterion for perturbative renormalizability [38].

Crucially, particles in CFT correspond to finite-size, topologically stable solitons, not point-like excitations. This extended structure regularizes short-distance behavior analogously to string theory [30], suppressing UV divergences [31]. The normalization constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$, enforced by V, projects out unphysical components without introducing nonlocality. Topological terms, such as Hopf or Chern–Simons-like invariants, encode global structure without affecting local divergences [32].

Thus, ${\Phi }^{\mu }$ plays a dual role as both causal generator and matter carrier. This duality enables CFT to evade traditional tensions between renormalizability, gravity, and quantum matter [2,33].

10.2. Perturbative Consistency

Expanding around a vacuum $\langle {\Phi }^{\mu }\rangle =u^{\mu }$, fluctuations ${\varphi }^{\mu }$ with $u_{\mu }{\varphi }^{\mu }=0$ yield a perturbative field theory with gauge-like kinetic terms and manifest unitarity [38]. Key consistency features include:

• Absence of higher-derivative terms avoids Ostrogradsky instabilities.
• Temporal reparameterization symmetry restricts physical degrees of freedom [33].
• The propagator structure resembles that of Abelian gauge theory, with constraints enforcing the timelike nature of ${\Phi }^{\mu }$.

Loop divergences can be absorbed via renormalization of couplings and constraint terms, and the renormalization group (RG) flow remains within the parameter space of the theory.

10.3. UV Finiteness in the Topological Sector

Sectors with fixed topological charge (e.g., fixed winding number) exhibit enhanced UV behavior due to the compactness of the configuration space. Quantum fluctuations around solitonic backgrounds are confined to finite-volume moduli spaces, suppressing high-momentum divergences [1,27]. Domain walls and winding boundaries provide natural IR cutoffs, helping regulate vacuum energy and large-scale correlations [36,37].

10.4. Implications for UV Completion

Unlike GR, which requires embedding in string theory or asymptotic safety frameworks [2,33], CFT appears self-contained and renormalizable at all energy scales. Its UV behavior is governed by local field content, bounded phase space, and soliton-based regularization.

This suggests that CFT may serve as a complete quantum field theory in the Wilsonian sense—requiring no further UV completion. If validated, this would unify time, geometry, and matter within a single renormalizable framework. Ongoing work on higher-loop corrections, RG flows in topological couplings, and potential nonperturbative fixed points will further clarify the theory’s UV completeness.

11. Unification of Gravity and Electromagnetism in Chronon Field Theory

Chronon Field Theory (CFT) provides a four-dimensional geometric framework in which both gravitational and electromagnetic interactions emerge from a single dynamical entity: a unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$. Inspired by prior attempts to unify gauge and gravitational structures via fiber geometry and internal phases [23,28], CFT introduces a decomposition of time itself that gives rise to both metric curvature and gauge curvature from the same field-theoretic source.

11.1. Phase Topology and Gauge Structure

The Chronon field is decomposed into modulus and phase:

$${\Phi }^{\mu }\left(x\right)=e^{i\theta \left(x\right)}{u}^{\mu }\left(x\right),$$

(80)

where $u^{\mu }$ is a real, unit-norm timelike vector and $\theta \left(x\right)$ is a real scalar field interpreted as the internal phase of temporal flow. This phase defines a local $U\left(1\right)$ fiber over spacetime, giving rise to an emergent electromagnetic potential:

$$A_{\mu }\left(x\right)={\partial }_{\mu }\theta \left(x\right),$$

(81)

with corresponding field strength:

$$F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }.$$

(82)

Gauge invariance under $\theta \left(x\right)\to \theta \left(x\right)+\alpha \left(x\right)$ ensures that $F_{\mu \nu }$ remains invariant, reproducing the structure of classical electromagnetism. The nontrivial topology of $U\left(1\right)$, with ${\pi }_1\left(U\left(1\right)\right)=\mathbb{Z}$, implies quantized winding of $\theta \left(x\right)$ and yields discrete electric charges—a mechanism analogous to Dirac quantization [39].

11.2. Unified Action and Field Equations

We define a covariant action unifying the Einstein-Hilbert and Maxwell sectors via the Chronon field:

$$S=\int d^{4}x\sqrt{-g}\left[R+\lambda ({\Phi }^{\mu }{\Phi }_{\mu }+1)-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }\right],$$

(83)

where $\lambda \left(x\right)$ enforces the unit-norm constraint on ${\Phi }^{\mu }$. Variation with respect to $g_{\mu \nu }$ gives modified Einstein equations:

$$G_{\mu \nu }=T_{\mu \nu }^{\mathrm{EM}}+2\lambda \left({\Phi }_{\mu }{\Phi }_{\nu }-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }\right),$$

(84)

where $T_{\mu \nu }^{\mathrm{EM}}$ is the electromagnetic stress-energy tensor. Variation with respect to $\theta \left(x\right)$ yields the source-free Maxwell equations:

$${\nabla }^{\nu }{F}_{\mu \nu }=0,$$

(85)

and the constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ arises from variation with respect to $\lambda$.

11.3. Emergent Interpretation and Classical Recovery

The electromagnetic field is not fundamental, but rather emerges from the non-integrable $U\left(1\right)$ phase structure of the temporal flow field. In the weak-field limit, this formulation reduces to the familiar Einstein-Maxwell system:

$$\begin{array}{cc}\hfill G_{\mu \nu }& =8\pi T_{\mu \nu }^{\mathrm{EM}},\hfill \end{array}$$

(86)

$$\begin{array}{cc}\hfill {\nabla }^{\nu }{F}_{\mu \nu }& =0,\hfill \end{array}$$

(87)

without invoking higher dimensions, extra gauge groups, or torsional connections, thereby offering a minimal unification scheme grounded in four-dimensional spacetime.

11.4. Topological Implications and Charge Quantization

Nontrivial configurations of the phase field $\theta \left(x\right)$—such as winding defects or flux tubes—yield quantized electromagnetic structures. The closed-loop integral

$${\oint }_{\gamma }{A}_{\mu }d{x}^{\mu }={\int }_{\Sigma }{F}_{\mu \nu }d{x}^{\mu }\wedge d{x}^{\nu }\in 2\pi \mathbb{Z}$$

(88)

encodes the quantized holonomy of temporal phase and provides a geometric origin of electric charge. This topological quantization is intrinsic to the theory and does not require external input or symmetry breaking.

11.5. Matter Coupling and Observable Dynamics

Matter fields $\psi \left(x\right)$ couple minimally to the emergent metric $g_{\mu \nu }$ and to the gauge potential $A_{\mu }$ via covariant derivatives. Charged matter fields thus respond to the temporal phase curvature just as they would to an independent electromagnetic field. Test bodies follow geodesics of the emergent metric, while charged excitations exhibit Lorentz force dynamics under $F_{\mu \nu }$—a structure consistent with both general relativity and standard electromagnetism at low energies.

11.6. Conceptual Implications

This unification reframes gravity and electromagnetism as complementary aspects of a single temporal field: gravity arises from the real modulus and its induced metric curvature, while electromagnetism originates in the imaginary phase and its associated $U\left(1\right)$ gauge structure. The Chronon field ${\Phi }^{\mu }\left(x\right)$ thus serves as a dual carrier of causal order and gauge connection, offering a compact, four-dimensional, and topologically rich model of unification.

12. Quantum Gravity from Chronon Dynamics

12.1. Canonical Quantization of ${\Phi }^{\mu }$

To develop a quantum theory of gravity within the Chronon Field Theory framework, we begin with the classical action:

$$S[\Phi ]=\int d^{4}x\sqrt{-g}\left(-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }+V({\Phi }^{\mu }{\Phi }_{\mu }+1)+{\mathcal{L}}_{\mathrm{top}}[\Phi ]\right),$$

(89)

where $F_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu }$ and ${\mathcal{L}}_{\mathrm{top}}$ contains topological invariants such as winding densities and domain wall contributions. The potential V enforces the normalization constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$.

Choosing a foliation where ${\Phi }^{\mu }$ defines proper-time slicing, we decompose spacetime into hypersurfaces ${\Sigma }_{\tau }$ labeled by a scalar parameter $\tau$. In this adapted chart, we perform canonical decomposition:

$$\begin{array}{cc}\hfill {\Phi }^{\mu }\left(x\right)& =({\Phi }^0\left(x\right),{\Phi }^i\left(x\right)),\hfill \end{array}$$

(90)

$$\begin{array}{cc}\hfill {\Pi }_i\left(x\right)& ={\displaystyle \frac{\delta \mathcal{L}}{\delta \left({\partial }_{\tau }{\Phi }^i\right)}},\hfill \end{array}$$

(91)

where ${\Pi }_i\left(x\right)$ are the canonical momenta conjugate to ${\Phi }^i\left(x\right)$. These define the field phase space on each hypersurface [10,18].

Canonical quantization proceeds via promotion of these variables to operators acting on a Hilbert space of wavefunctionals:

$${\widehat{\Phi }}^i\left(x\right)\Psi [\Phi ]={\Phi }^i\left(x\right)\Psi [\Phi ],{\widehat{\Pi }}_i\left(x\right)\Psi [\Phi ]=-i{\displaystyle \frac{\delta }{\delta {\Phi }^i\left(x\right)}}\Psi [\Phi ],$$

(92)

analogous to canonical formulations in background-independent quantum gravity [2,33].

The full quantum dynamics can also be encoded via a path integral over normalized, future-directed Chronon configurations:

$$Z=\int \mathcal{D}{\Phi }^{\mu }\delta ({\Phi }^{\mu }{\Phi }_{\mu }+1)\Theta \left({\Phi }^0\right)e^{iS[\Phi ]},$$

(93)

resulting in a manifestly covariant and background-free formulation. This places Chronon Quantum Gravity in close conceptual proximity to spin foam models and topological quantum field theories.

12.2. Chronon Wheeler–DeWitt Equation

In standard canonical quantum gravity, the Wheeler–DeWitt equation

$$\widehat{H}\Psi [h_{ij},\varphi ]=0$$

(94)

suffers from the “problem of time,” yielding a frozen, timeless wavefunctional [17,18,26].

Chronon Field Theory circumvents this by using the intrinsic flow of ${\Phi }^{\mu }$ as a built-in temporal reference. Defining proper time $\tau$ along the integral curves of ${\Phi }^{\mu }$, we obtain a Chronon-adapted Wheeler–DeWitt equation:

$$i{\displaystyle \frac{\partial }{\partial \tau }}\Psi [{\Phi }^i\left(x\right),\tau ]={\widehat{H}}_{\mathrm{Chronon}}[{\Phi }^i,{\Pi }_i]\Psi [{\Phi }^i\left(x\right),\tau ],$$

(95)

where ${\widehat{H}}_{\mathrm{Chronon}}$ incorporates both kinetic and topological Hamiltonian terms. This restores unitary evolution and provides a well-defined notion of temporal progression without external clocks [3,5].

Observables are defined relationally—relative to configurations of the Chronon field itself—ensuring full diffeomorphism invariance and internal consistency of the temporal structure [33].

12.3. Black Hole Entropy from Topological Winding

Chronon Quantum Gravity yields a microscopic, topological derivation of black hole entropy via nontrivial winding configurations of ${\Phi }^{\mu }$ near the horizon $\partial \mathcal{H}$:

$${\Phi }^{\mu }:\partial \mathcal{H}\to S^3,{\pi }_3\left(S^3\right)\simeq \mathbb{Z}.$$

(96)

These horizon field configurations are topologically stable due to the normalization and causal orientation of ${\Phi }^{\mu }$ [27,34].

Defining the local winding density:

$${\rho }_{\mathrm{wind}}\left(x\right)={\displaystyle \frac{1}{\Omega }}{ϵ}^{\mu \nu \alpha \beta }{\Phi }_{\mu }{\partial }_{\nu }{\Phi }_{\alpha }{\partial }_{\beta }{\Phi }^{\sigma }{n}_{\sigma },$$

(97)

where $n^{\mu }$ is the outward normal and $\Omega$ a normalization factor, the total entropy is:

$$S_{\mathrm{BH}}=\alpha {\int }_{\partial \mathcal{H}}{\rho }_{\mathrm{wind}}dA,$$

(98)

with $\alpha$ fixed by matching to the Bekenstein–Hawking area law:

$$S_{\mathrm{BH}}={\displaystyle \frac{k_B{c}^3}{4G\hslash }}A.$$

(99)

This approach interprets entropy as counting causally ordered, topologically inequivalent Chronon configurations on the horizon [35]. Unlike holographic or string-based derivations, this mechanism is intrinsic, geometric, and requires no reference to dual spacetimes.

Furthermore, transitions in winding number $\Delta n$ during black hole dynamics lead to quantized entropy change and discrete modulations in gravitational wave signals, providing a testable prediction of Chronon Quantum Gravity [9].

12.4. Resolution of the Black Hole Information Loss Problem

Chronon Field Theory offers a unitary and topologically coherent resolution to the black hole information paradox, based on four key principles:

• Solitonic encoding of matter: All matter degrees of freedom are realized as extended, topologically protected Chronon solitons [31,34].
• Causal continuity: The causal structure is defined by the evolving integral curves of ${\Phi }^{\mu }$, which remain continuous even in high-curvature regimes, removing the need for strict event horizons [18,33].
• Topological entropy: Black hole microstates correspond to distinct Chronon winding configurations on the horizon [14], yielding an intrinsic, geometric interpretation of entropy.
• Unitary radiation: Hawking-like radiation is driven by tunneling between Chronon winding sectors:

  $${\mathcal{A}}_{\mathrm{emit}}\sim exp(-\Delta S_{\mathrm{wind}}),$$

  (100)

  and each emitted mode retains entanglement with the remaining field configuration [41].

Unlike in semiclassical gravity, where the black hole interior is causally disconnected and radiation is thermal [16], here the interior remains part of the evolving Chronon foliation. No information is lost: it is dynamically redistributed through causal topology [7,13].

The resulting entropy evolution naturally reproduces the Page curve [29], with information encoded in the unwinding of Chronon solitons. Radiation is only approximately thermal; detailed spectra encode residual topological memory of the black hole state.

In contrast to firewall scenarios or holographic conjectures, this resolution is intrinsic, local (in the Chronon field), and background-independent. It unifies quantum evolution, causal continuity, and thermodynamic entropy within a single dynamical field: time itself.

In sum, Chronon Quantum Gravity provides a compelling framework for unifying geometry, causality, quantization, and thermodynamics. Its resolution of the black hole information paradox illustrates the power of topological and temporal field dynamics to address foundational challenges in modern physics.

13. Chronon Quantum Mechanics and the Foundations of Quantum Theory

Chronon Field Theory not only modifies the structure of spacetime and interactions but also provides a new ontological foundation for quantum mechanics, referred to as Chronon Quantum Mechanics (CQM). This formulation replaces probabilistic axioms and collapse postulates with causal, entropic dynamics intrinsic to the temporal flow defined by the Chronon field ${\Phi }^{\mu }\left(x\right)$ [5,36].

13.1. Causal Entropy and Temporal Coarse-Graining

The central object in CQM is the causal entropy functional:

$$S[\Psi ;{\Phi }^{\mu }]=-\int d\tau \mathrm{Tr}\left[\rho \left(\tau \right)log\rho \left(\tau \right)\right],$$

(101)

where $\tau$ is proper time along the Chronon congruence, and $\rho \left(\tau \right)$ is the reduced density matrix over decohered branches [41]. Time evolution maximizes causal entropy subject to a Schrödinger-type constraint:

$$i{\displaystyle \frac{\partial }{\partial \tau }}\Psi [{\Phi }^i,\tau ]={\widehat{H}}_{\mathrm{Chronon}}\Psi .$$

(102)

The entropic term introduces intrinsic time-asymmetry, generating an objective arrow of time without reliance on external observers or thermal environments [5,40].

13.2. Emergence of the Born Rule and Probabilities

Probabilities emerge from projection operators defined relative to foliation-aligned hypersurfaces:

$$P_i=\mathrm{Tr}\left[{\Pi }_i\rho \left(\tau \right)\right],$$

(103)

where ${\Pi }_i$ are orthogonal projectors associated with decoherent branches. The Born rule thus arises as an information-theoretic consequence of causal entropy maximization, rather than an independent postulate [13,41].

13.3. Resolution of the Measurement Problem

In CQM, quantum measurements correspond to irreversible bifurcations of the Chronon causal structure. Apparent collapse is an emergent, effective process: a coarse-graining over hypersurfaces where the Chronon field exhibits shear or torsion-induced decoherence. This avoids both the subjective role of observers and the need for ontological branching, restoring physical objectivity to measurement [7,13].

13.4. Entanglement and Chronon-Defined Nonlocality

Entanglement in CQM is fully preserved but understood as a relation across dynamically defined simultaneity slices determined by the Chronon flow. Unlike standard formulations where entanglement appears nonlocal with respect to static background time, here entangled correlations propagate through globally coherent causal foliation:

$${\rho }_{AB}\left(\tau \right)\ne {\rho }_A\left(\tau \right)\otimes {\rho }_B\left(\tau \right),$$

(104)

yet no information can be signaled outside the Chronon-defined lightcones.

Violations of Bell inequalities persist, but the no-signaling condition is enforced not by spacetime separation but by the causal consistency of ${\Phi }^{\mu }$. In this way, quantum nonlocality is embedded within a global temporal order, resolving apparent tensions between relativistic causality and entanglement [7,33].

13.5. Chronon Time as Physical Clock

Chronon Quantum Mechanics replaces external, absolute time with relational time built from ${\Phi }^{\mu }$. The integral curves of this field define physical evolution, providing a resolution to the problem of time in canonical quantum gravity:

$$i{\displaystyle \frac{\partial }{\partial \tau }}\Psi \left[{\Phi }^i\right]=\widehat{H}\Psi \left[{\Phi }^i\right],$$

(105)

where $\tau$ is an intrinsic proper time along the Chronon foliation. This formulation supports unitary dynamics in a background-independent setting and allows for relational observables that evolve with respect to the internal clock defined by ${\Phi }^{\mu }$ [3,18,26].

13.6. Outlook and Quantum Foundations

Chronon Quantum Mechanics offers a coherent, ontologically grounded approach to quantum theory with several foundational advantages:

• Eliminates external time and subjective collapse via causal foliation [13,18].
• Derives the Born rule from entropic and geometric principles [41].
• Embeds entanglement in a globally causal, non-signaling foliation [7,33].
• Provides a relational solution to the Wheeler–DeWitt problem in quantum gravity [5,26].

Future work should explore the algebraic structure of Chronon observables, connections to category-theoretic quantum mechanics, and consequences for quantum cosmology, black hole information, and quantum foundations [2,36].

14. Conservation Laws and Symmetry Principles

14.1. Noether Charges from Temporal Symmetries

Chronon Field Theory possesses a rich symmetry structure rooted in both spacetime and internal transformations. The most fundamental symmetry is the global temporal phase rotation:

$${\Phi }^{\mu }\left(x\right)\to e^{i\alpha }{\Phi }^{\mu }\left(x\right),$$

(106)

where $\alpha \in \mathbb{R}$ is a constant phase. Under this symmetry, the Chronon Lagrangian remains invariant up to boundary terms, and Noether’s theorem implies the existence of a conserved current:

$$J^{\mu }=i\left({\Phi }^{\nu }{\partial }^{\mu }{\Phi }_{\nu }^{*}-{\Phi }^{\nu *}{\partial }^{\mu }{\Phi }_{\nu }\right).$$

(107)

The associated charge,

$$Q={\int }_{\Sigma }{d}^{3}x{J}^0,$$

(108)

corresponds to electric charge in the emergent $U\left(1\right)$ theory. This formalism naturally explains charge quantization via topological winding of the Chronon field’s phase configuration [27,32].

Additional symmetries arise from spatial rotations of the hypersurfaces orthogonal to ${\Phi }^{\mu }$, leading to conserved angular momentum-like quantities. When internal moduli are present (e.g., for multi-soliton sectors), their associated collective coordinates lead to further conserved charges reflecting generation index or internal parity [1,14].

In cosmological settings, temporal translations along integral curves of ${\Phi }^{\mu }$ give rise to conserved energy-like quantities, but these are modified by foliation-dependent dynamics as discussed below [3,5].

14.2. Modified Energy–Momentum Tensor

The Chronon field induces a generalized energy–momentum tensor obtained by varying the total action with respect to the background metric:

$$T_{\Phi }^{\mu \nu }=-{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta S}{\delta g_{\mu \nu }}}.$$

(109)

For the action

$$S[\Phi ]=\int d^{4}x\sqrt{-g}\left(-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }+V({\Phi }^{\mu }{\Phi }_{\mu }+1)+{\mathcal{L}}_{\mathrm{top}}\right),$$

the energy–momentum tensor includes both kinetic and constraint contributions, as well as corrections from topological curvature [19,33].

Importantly, due to the presence of a preferred foliation, the covariant conservation law

$${\nabla }_{\mu }{T}_{\Phi }^{\mu \nu }=0$$

(110)

may fail to hold strictly unless the foliation is globally compatible with the variational principle. Instead, one often finds foliation-dependent violations of standard energy conservation:

$${\displaystyle \frac{d}{d\tau }}{\int }_{{\Sigma }_{\tau }}{T}^{0\nu }{d}^{3}x\ne 0,$$

(111)

particularly in dynamical spacetime regions (e.g., near domain walls or black holes). These violations reflect physical transfer of energy into topological or causal degrees of freedom and serve as potential sources of entropy production [6,36].

This framework generalizes the stress–energy tensor concept by recognizing that energy is not fundamentally conserved in the usual sense but redistributed across temporal coherence, geometric backreaction, and topological structure [5,20].

14.3. Implications for Lorentz and CPT Symmetry

Chronon Field Theory is constructed from a Lorentz-invariant action. However, the spontaneous selection of a nonzero vacuum expectation value

$$\langle {\Phi }^{\mu }\left(x\right)\rangle =u^{\mu }\left(x\right),u^{\mu }{u}_{\mu }=-1,$$

(112)

breaks local Lorentz invariance by choosing a preferred temporal direction. This spontaneous Lorentz symmetry breaking (SLSB) is subtle: it preserves diffeomorphism invariance and leads to testable deviations from full Lorentz covariance in observable quantities such as dispersion relations, particle thresholds, and time dilation anomalies [12,25].

At low energies, effective Lorentz symmetry is recovered via averaging over solitonic or domain-scale fluctuations. However, in high-precision or high-energy regimes (e.g., ultrarelativistic scattering, early universe), small deviations may be detectable:

$$\delta c\sim \epsilon {\left({\displaystyle \frac{E}{E_{\mathrm{Chronon}}}}\right)}^2.$$

(113)

These corrections scale with energy and vanish in the infrared limit, protecting known physics while allowing falsifiability [9,30].

Chronon dynamics also bear on CPT symmetry. While the action itself is CPT-invariant, topological initial conditions may induce asymmetric evolution between particles and antiparticles. This provides a non-perturbative origin for baryogenesis, circumventing the need for CP-violating terms in the Standard Model:

$$n_B-n_{\overline{B}}\propto {\int }_{\Sigma }{ϵ}^{\mu \nu \alpha \beta }{\Phi }_{\mu }{\partial }_{\nu }{\Phi }_{\alpha }{\partial }_{\beta }{\Phi }^{\sigma }{n}_{\sigma }.$$

(114)

This integral measures topological charge asymmetry in the early Chronon vacuum and is consistent with observed matter–antimatter asymmetry [24,37].

In total, the symmetry structure of Chronon Field Theory reveals that conservation laws and invariance principles are emergent, topologically grounded, and softly broken in regimes of cosmological or solitonic complexity. These deviations open a window into physics beyond the Standard Model while maintaining consistency with empirical data [35,36].

15. Phenomenology and Observables

15.1. Collider Signatures and Precision Scattering

The solitonic and topological nature of particle excitations in Chronon Field Theory predicts distinctive signatures in high-energy scattering and collider environments. Unlike point-like particles in the Standard Model, Chronon solitons possess internal spatial structure and quantized winding, resulting in form factors that deviate from standard behavior at energies approaching the Chronon scale $E_{\Phi }$ [1,14,27].

Observable effects include:

• Modified cross-sections in $e^{+}{e}^{-}$ or $pp$ collisions due to soliton self-interaction and deformability [31].
• Threshold shifts in multi-particle production from topological charge conservation [24,34].
• Anomalous angular distributions and polarization asymmetries arising from nontrivial spin–orbit coupling in Chronon composites [14].
• Suppressed or enhanced decay rates for heavy resonances depending on topological matching conditions [37].

Precision experiments probing anomalous magnetic moments, electric dipole moments, and parity-violating scattering can also constrain shear- and phase-induced corrections from ${\Phi }^{\mu }$ dynamics. For instance, deviations in $g-2$ can arise from coupling between Chronon shear and internal fermion helicity:

$$\Delta a_{\mu }\sim {\left({\displaystyle \frac{E}{E_{\Phi }}}\right)}^2{\sigma }_{\mu \nu }\langle S^{\mu \nu }\rangle .$$

(115)

Such effects are analogous to Lorentz-violating operators in string-theoretic frameworks [25] and may be accessible to next-generation precision tests.

No new particles are predicted below the soliton stability scale, but Chronon excitations may manifest as apparent compositeness or form factor deformation of known particles at $\mathcal{O}(10–100\mathrm{TeV})$ scales [21,30].

15.2. Cosmic Microwave Background and Galaxy Rotation

Chronon Phase Transition Cosmology predicts observable imprints on the Cosmic Microwave Background (CMB) distinct from those produced by inflation. Because causal structure emerges via a temporal alignment phase transition rather than exponential expansion, the resulting anisotropy spectrum carries signatures of coherent domain wall tension and topological soliton formation [24,37].

Predictions include:

• Suppression of low-ℓ multipoles due to limited early-time coherence length [5].
• Non-Gaussian hot and cold spots arising from residual Chronon shear near recombination [6].
• Angular power spectrum features modulated by the spatial distribution of early domain boundaries [9].

At galactic scales, the residual shear in the Chronon field acts as an effective dark matter halo, producing gravitational acceleration without invoking particle dark matter:

$$v_{\mathrm{rot}}^2\left(r\right)={\displaystyle \frac{G{M}_b\left(r\right)}{r}}+{\sigma }_{\mathrm{Chronon}}^2\left(r\right),$$

(116)

where ${\sigma }_{\mathrm{Chronon}}^2\left(r\right)$ is the effective centripetal contribution from local foliation twist. This reproduces flat rotation curves and Tully–Fisher scaling laws with no free parameters beyond the Chronon coherence length [36].

Chronon solitons also produce matter seeds for galaxy formation without invoking ad hoc inflationary perturbations. Their discrete distribution can be inferred from surveys of void topology and cosmic filament connectivity [14,32].

15.3. Gravitational Lensing and Primordial Waves

Chronon-induced curvature and domain wall tension contribute to gravitational lensing effects that differ from standard dark matter predictions. In particular:

• Lensing maps near galaxy clusters may reveal anisotropic deflection patterns tracing Chronon domain structures [37].
• Sub-halo lensing events may reflect topological soliton crossings, appearing as transient microlensing anomalies [27].

Furthermore, the formation and annihilation of Chronon domain walls in the early universe generates a stochastic background of primordial gravitational waves. These waves have characteristic spectral features:

$${\Omega }_{\mathrm{GW}}\left(f\right)\sim f^{3}exp\left(-{\displaystyle \frac{f^2}{f_{*}^2}}\right),$$

(117)

where $f_{*}$ depends on the critical time of Chronon ordering. Detection of such a background by observatories like LISA or advanced pulsar timing arrays would directly probe temporal topology dynamics [9].

In black hole mergers, topological transitions in ${\Phi }^{\mu }$ near the horizon can produce deviations from classical ringdown predictions. This includes late-time modulations or echoes consistent with quantized entropy change [16,35].

Altogether, the Chronon framework produces a suite of testable phenomena spanning particle physics, astrophysics, and cosmology—each grounded in a unified topological model of time and causal structure [2,36].

16. Results

This study presents Chronon Field Theory (CFT), a unified theoretical framework in which a smooth, unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$ generates local causal structure, geometric curvature, and solitonic matter content. The principal results established in this work are as follows:

• The constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ defines a globally consistent temporal orientation and induces a foliation of spacetime into hypersurfaces orthogonal to ${\Phi }^{\mu }$, yielding intrinsic causal order without presupposing a background metric.
• A power-counting renormalizable Lagrangian is constructed from local kinetic terms $F_{\mu \nu }={\nabla }_{\mu }{\Phi }_{\nu }-{\nabla }_{\nu }{\Phi }_{\mu }$, constraint-enforcing potentials, and topological invariants, ensuring perturbative consistency and ultraviolet completeness.
• Gravitational phenomena arise as emergent features of ${\Phi }^{\mu }$ curvature, leading to a geometrical derivation of the equivalence principle without relying on the Einstein-Hilbert action. This also circumvents the problems of local gravitational energy density in standard GR.
• The framework enables a geometric unification of electromagnetism and general relativity, deriving both gauge and gravitational phenomena from differential and topological features of the same temporal field.
• Topologically nontrivial configurations of ${\Phi }^{\mu }$ support solitonic excitations classified by ${\pi }_3\left(S^3\right)$, which exhibit intrinsic spin, mass, and fermionic statistics. These configurations act as stable matter-like objects without invoking point particles or a Higgs mechanism, thereby avoiding large vacuum energy contributions from spontaneous symmetry breaking and eliminating the VEV-induced cosmological constant problem.
• Internal phase dynamics within the Hopf fibration $S^1\hookrightarrow S^3\to S^2$ generate fermion flavor modes. A coherence energy functional models phase misalignment and yields mixing matrices analogous to CKM and PMNS.
• The theory explains the existence of exactly three fermion generations as a geometric constraint: phase angles associated with solitons optimally separate at ${120}^{\circ }$ intervals on an internal $S^1$ fiber. Configurations with more than three generations lead to angular frustration and instability, implying a natural topological limit.
• The black hole information loss paradox is resolved via topologically protected soliton configurations, which preserve global field information across causal boundaries without requiring Hawking evaporation unitarity restoration.
• Quantum measurement and entanglement are reinterpreted through coherent alignment or decoherence of local ${\Phi }^{\mu }$ structures, offering a geometric, background-independent mechanism underlying nonlocal quantum correlations.
• Cosmological expansion arises from the expansion scalar $\theta ={\nabla }_{\mu }{\Phi }^{\mu }$, governed by a generalized Raychaudhuri equation. Temporal ordering induces an emergent arrow of time, causal horizon formation, and effective dark energy behavior without invoking a cosmological constant.
• Canonical quantization of the constrained field leads to a Wheeler–DeWitt-type equation, in which time and dynamics emerge intrinsically through foliation. This offers a solution to the problem of time in quantum gravity.

Simulations were performed using Python scripts. No experimental or empirical data were required for this analysis.

17. Discussion

Chronon Field Theory (CFT) reframes some of the deepest problems in fundamental physics by placing the directionality and reality of time at the core of physical law. Unlike conventional approaches that extend spacetime symmetries or quantize a fixed geometry, CFT postulates a minimal but powerful ontological structure: a smooth, unit-norm, future-directed timelike vector field ${\Phi }^{\mu }\left(x\right)$ that defines local temporal flow and global causal order.

This geometric foundation directly addresses the “problem of time” in canonical quantum gravity. Instead of searching for an emergent clock within a timeless wavefunction, CFT posits time as a dynamical field with intrinsic direction—an idea that resonates with both intuition and the empirical asymmetry of physical processes. The resulting foliation structure provides a natural intrinsic time parameter and enables background-independent quantization.

Crucially, ${\Phi }^{\mu }$ is a spin-1 field, placing it in the same category as known gauge bosons. This allows CFT to unify gravity with other interactions in a framework that avoids the tensorial incompatibilities of General Relativity. Matter arises not from external particle content or symmetry breaking, but from topologically nontrivial configurations of the temporal field. These solitons—classified by ${\pi }_3\left(S^3\right)$—exhibit mass, spin, and fermionic statistics, offering a natural, geometric alternative to point particles. Their extended, finite structure regularizes short-distance behavior, akin to string theory, but within a local and power-counting renormalizable field theory.

This approach also addresses several conceptual puzzles. The equivalence principle emerges from the geometry of the Chronon congruence rather than being imposed. Ambiguities in defining local gravitational energy are softened by anchoring energy flow to the causal structure induced by ${\Phi }^{\mu }$. The spontaneous emergence of a global arrow of time provides a concrete origin for temporal asymmetry and may shed light on the black hole information problem. Moreover, quantum measurement and entanglement gain a new interpretive footing through the field’s causal foliation and solitonic coherence structure.

The theory offers predictive structure: internal phase dynamics govern flavor mixing and explain why exactly three fermion generations arise as a geometrically stable configuration on an internal $S^1$. The absence of a Higgs mechanism eliminates vacuum energy contributions from spontaneous symmetry breaking, addressing the cosmological constant problem without fine-tuning. Cosmological predictions—including non-inflationary horizon formation and residual topological structure—make the theory empirically testable.

While many technical aspects remain to be developed—especially in quantizing soliton sectors and computing precise spectra—CFT demonstrates internal coherence, minimal assumptions, and explanatory reach. Its conceptual unification of geometry, matter, and interaction through a single causal field offers an appealing alternative to more elaborate or less falsifiable frameworks.

In sum, by grounding spacetime and interaction in the topology and dynamics of time itself, CFT presents a testable and physically motivated path toward unification. Rather than layering complexity onto existing models, it reorganizes our foundational assumptions in a way that is both parsimonious and generative.