Chronon Field Theory Explained: An Intuitive Introduction to Emergent Spacetime, Gauge Interactions, Quantum Foundation and Cosmology

1. Introduction: Physics Beyond the Standard Model

The twentieth century was a golden age of physics. It revealed the hidden unity of nature through two extraordinary frameworks: General Relativity (GR), describing gravitation and spacetime curvature, and Quantum Field Theory (QFT), describing the fundamental particles and their interactions. Together they form what we call the Standard Model of Physics. And yet, despite their profound success, these two pillars do not fit together. Their mathematical languages—one continuous and geometric, the other discrete and probabilistic—describe two incompatible pictures of the universe. Chronon Field Theory (CFT) arises from the attempt to rebuild both from a common, more primitive foundation.

1.1. The Achievements and Limits of 20th-Century Physics

By the mid-1970s, physics had achieved a nearly complete map of the fundamental building blocks of matter. Quantum electrodynamics, quantum chromodynamics, and the unified electroweak theory formed a single, precise framework—the Standard Model of particle physics. Meanwhile, Einstein’s general theory of relativity (1915) had transformed gravity from a force into the curvature of spacetime itself. Time and space were no longer fixed coordinates but part of a dynamic geometry that bends and ripples in response to energy and momentum.

Everyday experience and most astronomical observations can be explained by these two frameworks. QFT describes how particles scatter and decay, while GR describes how planets orbit and galaxies evolve. Yet, the two theories speak entirely different dialects of mathematics.

• Quantum Field Theory assumes a fixed background of space and time, and describes how excitations of fields (such as electrons or photons) appear as particles. Its language is that of probability amplitudes and operators acting on Hilbert spaces.
• General Relativity, on the other hand, describes the very fabric of space and time itself. Its language is geometry: curvature, metrics, and tensors. The gravitational field is not something that moves in space—it is space.

In all practical contexts, each theory works perfectly in its own domain: quantum physics for atoms, relativity for planets. But in the early universe, near black holes, or at the Planck scale, the two domains overlap, and their union becomes inconsistent. The Standard Model and GR together leave us with a universe that works beautifully at human scales, but breaks down at its foundations.

1.2. Unresolved Puzzles: Quantum Gravity, Unification, and Singularities

Several deep puzzles remain unsolved at the intersection of quantum theory and gravitation. These are not small gaps in knowledge but structural fissures in the conceptual framework of modern physics.

1. Quantum Gravity:

At subatomic scales, energy and curvature become inseparable. When one tries to quantize the gravitational field as another quantum field theory (QFT), the result diverges—the mathematics predicts infinite energies. Unlike electromagnetism or the weak force, gravity cannot be renormalized. This signals that spacetime may not be continuous after all.

2. Singularities:

General Relativity predicts its own limitations. At the center of a black hole or at the Big Bang, curvature grows without bound. These “singularities” are not just regions of high density; they are points where geometry itself ceases to exist. Space and time break down. A complete theory must explain what replaces them.

3. Unification:

The Standard Model contains three gauge interactions (electromagnetic, weak, and strong) but gravity remains separate. Each gauge force arises from a mathematical symmetry of internal space, while gravity arises from the geometry of spacetime itself. A true unification must explain why nature possesses both an external geometry (spacetime curvature) and an internal geometry (gauge fields), and how the two are related.

4. Time and Asymmetry:

Another foundational tension concerns the very nature of time. In the Standard Model, time is a mere external parameter—a stage on which particles and fields evolve according to symmetric equations. By contrast, in General Relativity, time is inseparably intertwined with space, warping and stretching as part of the dynamic fabric of spacetime. Yet human experience insists that time is not a geometric coordinate but a real, directed process. The laws of fundamental physics are almost entirely time-reversal symmetric, but the universe we observe—with expanding space, decaying particles, and growing entropy—is profoundly time-asymmetric. This disconnect between the mathematical reversibility of microphysics and the irreversibility of experience hints that time may not be a simple dimension, but an emergent manifestation of causal order and alignment at the most fundamental level. Chronon Field Theory will later reinterpret the arrow of time as a property of causal self-organization rather than an external parameter.

5. The Quantum Measurement Paradox:

Quantum mechanics describes probabilities, not actual outcomes. When does a quantum wave “collapse” into a definite state? Why does measurement appear irreversible in a theory with reversible equations? This problem is not merely philosophical—it defines the boundary between microscopic and macroscopic physics.

6. Dark Matter, Dark Energy, and Cosmic Fine-Tuning:

Observations of galaxies and the accelerating expansion of the universe suggest that most of the cosmos is made of entities unknown to the Standard Model. Meanwhile, the vacuum energy predicted by quantum theory exceeds the observed cosmological constant by 120 orders of magnitude. These enormous discrepancies hint that spacetime and quantum fields are not independent, but two manifestations of a deeper substrate.

1.3. Motivation for a New Geometric Foundation

Physicists have long sought to reconcile the quantum and the geometric. String theory and loop quantum gravity represent two major attempts, but both assume that the fabric of spacetime, in some form, already exists. Chronon Field Theory (CFT) begins one step earlier: it asks whether spacetime itself could be a collective behavior, an emergent structure built from more primitive elements of causal order.

In condensed-matter physics, properties such as elasticity, magnetism, and superconductivity arise from simple local rules among microscopic units. A solid crystal, for instance, emerges from the alignment of atoms; a superfluid emerges from the phase coherence of molecules. CFT applies a similar logic to spacetime: it treats the universe as a vast, self-organizing network of microscopic causal links—chronons—that align over time to form a smooth geometry. The geometry of spacetime is not assumed; it condenses.

In this view,

• Time is not an external parameter that flows, but the measure of how causal relations align (and realign) locally.
• The metric $g_{\mu }\nu$ of GR arises as the collective field of these alignments; gravity is the relaxation of causal stress.
• Quantum behavior reflects fluctuations and phase transitions in this causal medium, with quantized action emerging from discrete symplectic curvature (causal flux).
• Fermionic matter emerges as solitons: stable, topologically protected twists/knots of the aligned chronon field (defects of the causal texture) whose conserved charges are winding/linking numbers.
• Bosons emerge as modes of curvature: propagating oscillations of chronon curvature (holonomy waves) that mediate interactions—photons, weak and gluonic gauge modes—as collective excitations of the same medium.

Thus, in CFT spacetime, forces, and matter are all emergent facets of one substrate. Particles are coherent defects of causal order; forces are curvature waves of that order; and spacetime is the macroscopic continuum traced out by sustained alignment.

Chronon Field Theory therefore represents a shift of perspective: it replaces the idea of a pre-existing spacetime with that of an evolving causal fluid whose internal dynamics generate geometry, interactions, and matter. From this viewpoint, gravitation, gauge interactions, and even quantum probabilities share a common geometric origin.

In the sections that follow, we explore this framework step by step: how causal order becomes spacetime, how curvature becomes gravity, how internal symmetries become the fundamental forces, how fermions arise as topological solitons while bosons are curvature modes, and how cosmic structure emerges from chronon alignment. We also see how CFT naturally eliminates singularities, regularizes vacuum energy, and as an exciting example among many predictions, predicts new astrophysical objects —chronon stars—that replace classical black holes.

Table 1. Achievements and open puzzles of 20th–century physics. The Standard Model and General Relativity explain an extraordinary range of natural phenomena, yet fundamental inconsistencies remain at the intersection of quantum theory, gravity, and cosmology. These unresolved issues motivate the search for a deeper geometric foundation such as CFT.

Domain	Achievements of the Standard Model and GR	Outstanding puzzles and limitations
Quantum field theory	Unified electromagnetic, weak, and strong interactions under gauge symmetry ($U\left(1\right)\times SU\left(2\right)\times SU\left(3\right)$); precise agreement with collider data and quantum electrodynamics.	Gravity not quantized; non-renormalizability of quantum gravity; wavefunction collapse and measurement remain conceptually unresolved.
General relativity	Explains planetary motion, black holes, gravitational waves, and the expansion of the Universe with exquisite accuracy.	Breaks down at singularities (Big Bang, black-hole cores); incompatible with quantum principles at small scales.
Cosmology	$\mathrm{\Lambda }$CDM model accounts for large-scale structure and CMB anisotropies.	Nature of dark matter and dark energy unknown; cosmological constant problem (${\rho }_{\mathrm{vac}}^{\mathrm{QFT}}/{\rho }_{\mathrm{\Lambda }}^{\mathrm{obs}}\sim {10}^{120}$); fine-tuning of initial conditions.
Particle physics	Higgs mechanism gives masses to W, Z bosons and fermions; neutrino oscillations confirmed.	Does not explain hierarchy of masses or coupling unification; no explanation for neutrino masses, CP violation strength, or number of generations.
Fundamental symmetries	Lorentz and gauge invariance confirmed to high precision; conservation laws linked to continuous symmetries (Noether theorem).	Possible Lorentz-violation at Planck scale; matter–antimatter asymmetry unexplained; time irreversibility not derived from underlying equations.
Quantum cosmology/vacuum structure	Quantum fluctuations explain CMB seeds; inflationary paradigm successful.	Origin of inflation field unknown; vacuum energy density and zero-point fluctuations inconsistent with GR; no microphysical origin for spacetime itself.

Table 1. Achievements and open puzzles of 20th–century physics. The Standard Model and General Relativity explain an extraordinary range of natural phenomena, yet fundamental inconsistencies remain at the intersection of quantum theory, gravity, and cosmology. These unresolved issues motivate the search for a deeper geometric foundation such as CFT.

Domain	Achievements of the Standard Model and GR	Outstanding puzzles and limitations
Quantum field theory	Unified electromagnetic, weak, and strong interactions under gauge symmetry ($U\left(1\right)\times SU\left(2\right)\times SU\left(3\right)$); precise agreement with collider data and quantum electrodynamics.	Gravity not quantized; non-renormalizability of quantum gravity; wavefunction collapse and measurement remain conceptually unresolved.
General relativity	Explains planetary motion, black holes, gravitational waves, and the expansion of the Universe with exquisite accuracy.	Breaks down at singularities (Big Bang, black-hole cores); incompatible with quantum principles at small scales.
Cosmology	$\mathrm{\Lambda }$CDM model accounts for large-scale structure and CMB anisotropies.	Nature of dark matter and dark energy unknown; cosmological constant problem (${\rho }_{\mathrm{vac}}^{\mathrm{QFT}}/{\rho }_{\mathrm{\Lambda }}^{\mathrm{obs}}\sim {10}^{120}$); fine-tuning of initial conditions.
Particle physics	Higgs mechanism gives masses to W, Z bosons and fermions; neutrino oscillations confirmed.	Does not explain hierarchy of masses or coupling unification; no explanation for neutrino masses, CP violation strength, or number of generations.
Fundamental symmetries	Lorentz and gauge invariance confirmed to high precision; conservation laws linked to continuous symmetries (Noether theorem).	Possible Lorentz-violation at Planck scale; matter–antimatter asymmetry unexplained; time irreversibility not derived from underlying equations.
Quantum cosmology/vacuum structure	Quantum fluctuations explain CMB seeds; inflationary paradigm successful.	Origin of inflation field unknown; vacuum energy density and zero-point fluctuations inconsistent with GR; no microphysical origin for spacetime itself.

Table 2. How Chronon Field Theory (CFT) addresses the open problems of modern physics. CFT reinterprets spacetime, matter, and quantum behavior as emergent properties of a discrete–continuous causal medium composed of chronons. By doing so, it resolves or reframes several conceptual and mathematical puzzles that limit the Standard Model and General Relativity.

Domain	Problem in conventional physics	CFT perspective and resolution
Quantum gravity	GR and QFT incompatible; spacetime treated as continuous, leading to non-renormalizable infinities.	Spacetime emerges from local alignment of chronon causal vectors ${\mathrm{\Phi }}^{\mu }$; discreteness at the chronon scale regularizes curvature and eliminates UV divergences. Gravity arises as collective relaxation of causal stress—no quantization of geometry required.
Singularities	GR predicts infinite curvature at black-hole and Big-Bang singularities.	Finite alignment stiffness J and the Chronon Exclusivity Principle (CEP) bound the symplectic curvature ${\mathrm{\Omega }}_{\mu \nu }$, preventing divergence. Black holes possess finite-core “chronon stars,” and the Big Bang becomes a smooth causal transition.
Inflation and early-universe dynamics	Requires a fine-tuned scalar inflaton to generate exponential expansion and nearly scale-invariant primordial fluctuations.	Rapid causal alignment during the Planck transition naturally drives a brief exponential growth of coherent domains—an emergent “geometric inflation.” Quantum fluctuations of the chronon field imprint a nearly scale-invariant primordial spectrum without an ad-hoc inflaton potential.
Quantum measurement and ℏ	Wavefunction collapse postulated; Planck constant inserted empirically.	Quantization arises from topological stability of $2\pi$ causal twists in ${\mathrm{\Phi }}^{\mu }$ (chronon solitons); ℏ is the geometric modulus of minimal symplectic action. Measurement corresponds to irreversible causal alignment.
Gauge interactions	Internal symmetries unexplained; Higgs mechanism ad-hoc.	Gauge fields emerge as holonomy and torsion of the chronon field; $U\left(1\right)$, $SU\left(2\right)$, and $SU\left(3\right)$ geometries arise naturally from phase and polarization modes of ${\mathrm{\Phi }}^{\mu }$. Mass generation results from topological coupling rather than scalar fields.
Cosmology	Dark matter, dark energy, and fine-tuning unexplained.	Microscopic chronon condensates form cold, non-baryonic dark matter; domain-wall relaxation energy appears macroscopically as dark energy. Chronon dynamics yield a self-consistent, singularity-free cosmology without external parameters.
Time and entropy	Time treated as a parameter in quantum theory; arrow of time unexplained.	Time is emergent from causal alignment and phase ordering of chronons. Entropy production corresponds to relaxation toward maximal alignment, giving a geometric origin to the second law and temporal asymmetry.
Vacuum energy and renormalization	Zero-point energy diverges; cosmological constant problem of ${10}^{120}$ mismatch.	Finite symplectic curvature and CEP impose a maximum action density, regularizing vacuum energy and yielding a natural small effective cosmological constant.
Unification outlook	Matter and spacetime remain ontologically distinct.	All entities—spacetime, forces, and matter—are excitations of one field: the chronon causal medium. CFT provides a single geometric substrate linking quantum phenomena, gravity, and gauge interactions.

Table 2. How Chronon Field Theory (CFT) addresses the open problems of modern physics. CFT reinterprets spacetime, matter, and quantum behavior as emergent properties of a discrete–continuous causal medium composed of chronons. By doing so, it resolves or reframes several conceptual and mathematical puzzles that limit the Standard Model and General Relativity.

Domain	Problem in conventional physics	CFT perspective and resolution
Quantum gravity	GR and QFT incompatible; spacetime treated as continuous, leading to non-renormalizable infinities.	Spacetime emerges from local alignment of chronon causal vectors ${\mathrm{\Phi }}^{\mu }$; discreteness at the chronon scale regularizes curvature and eliminates UV divergences. Gravity arises as collective relaxation of causal stress—no quantization of geometry required.
Singularities	GR predicts infinite curvature at black-hole and Big-Bang singularities.	Finite alignment stiffness J and the Chronon Exclusivity Principle (CEP) bound the symplectic curvature ${\mathrm{\Omega }}_{\mu \nu }$, preventing divergence. Black holes possess finite-core “chronon stars,” and the Big Bang becomes a smooth causal transition.
Inflation and early-universe dynamics	Requires a fine-tuned scalar inflaton to generate exponential expansion and nearly scale-invariant primordial fluctuations.	Rapid causal alignment during the Planck transition naturally drives a brief exponential growth of coherent domains—an emergent “geometric inflation.” Quantum fluctuations of the chronon field imprint a nearly scale-invariant primordial spectrum without an ad-hoc inflaton potential.
Quantum measurement and ℏ	Wavefunction collapse postulated; Planck constant inserted empirically.	Quantization arises from topological stability of $2\pi$ causal twists in ${\mathrm{\Phi }}^{\mu }$ (chronon solitons); ℏ is the geometric modulus of minimal symplectic action. Measurement corresponds to irreversible causal alignment.
Gauge interactions	Internal symmetries unexplained; Higgs mechanism ad-hoc.	Gauge fields emerge as holonomy and torsion of the chronon field; $U\left(1\right)$, $SU\left(2\right)$, and $SU\left(3\right)$ geometries arise naturally from phase and polarization modes of ${\mathrm{\Phi }}^{\mu }$. Mass generation results from topological coupling rather than scalar fields.
Cosmology	Dark matter, dark energy, and fine-tuning unexplained.	Microscopic chronon condensates form cold, non-baryonic dark matter; domain-wall relaxation energy appears macroscopically as dark energy. Chronon dynamics yield a self-consistent, singularity-free cosmology without external parameters.
Time and entropy	Time treated as a parameter in quantum theory; arrow of time unexplained.	Time is emergent from causal alignment and phase ordering of chronons. Entropy production corresponds to relaxation toward maximal alignment, giving a geometric origin to the second law and temporal asymmetry.
Vacuum energy and renormalization	Zero-point energy diverges; cosmological constant problem of ${10}^{120}$ mismatch.	Finite symplectic curvature and CEP impose a maximum action density, regularizing vacuum energy and yielding a natural small effective cosmological constant.
Unification outlook	Matter and spacetime remain ontologically distinct.	All entities—spacetime, forces, and matter—are excitations of one field: the chronon causal medium. CFT provides a single geometric substrate linking quantum phenomena, gravity, and gauge interactions.

1.4. The Temporal Coherence Principle: The Foundational Law of CFT

Although Chronon Field Theory can be motivated by several guiding ideas—universality, exclusivity, and concealment—each of these ultimately reduces to a single generative rule governing all dynamics: the Temporal Coherence Principle (TCP).

Statement of the Principle

The TCP asserts that all physical interaction is a manifestation of temporal phase synchronization among chronon domains. Chronons represent local carriers of causal orientation; their internal phase defines a microscopic direction in time. Whenever two chronon domains fall out of phase, causal linkage is weakened and interaction potential arises. All forces—gravitational, quantum, and gauge—are thus expressions of the universe’s continual drive toward temporal coherence. Energy flow corresponds to the restoration of phase alignment, while decoherence reflects its loss.

Derivation of Other Principles

From the TCP follow all other characteristic features of CFT:

• The Chronon Universality Principle (CUP)—that all entities, including spacetime, matter, and energy, emerge from the chronon field—is not an independent postulate. Once the chronon field is shown to generate the metric, curvature, gauge fields, and quantized action, universality becomes a derived fact.
• The Chronon Exclusivity Principle (CEP)—that no two chronons occupy the same causal state and curvature is bounded—arises automatically from the positivity of the alignment stiffness $J>0$. A positive stiffness ensures finite curvature density and a strictly positive quantum of action ($\hslash >0$), making CEP a stability condition of coherent evolution.
• The Chronon Concealment Principle (CCP)—the apparent Lorentz symmetry and isotropy of spacetime—follows statistically from the combination of the CUP and TCP. Because the chronon field underlies all phenomena (CUP) and evolves toward global temporal synchronization (TCP), microscopic anisotropies and directional biases are averaged out across large-scale coherent ensembles, producing the observed macroscopic isotropy and relativistic symmetry.

Physical and Philosophical Implications

With these derivations, the TCP stands as the sole foundational law of Chronon Field Theory. It unifies dynamics, geometry, and quantization under a single organizing principle: that the universe is a self-synchronizing causal medium whose evolution preserves and restores temporal coherence. Spacetime, energy, and matter are not fundamental ingredients but emergent patterns in this coherence-restoring process. In this sense, CFT replaces the ontology of static geometry with one of active coherence—a universe in which existence itself is defined by participation in a common causal rhythm of time.

2. The Chronon Concept and Physical Intuition

The starting point of Chronon Field Theory (CFT) is a simple but radical question: If matter is made of atoms, could spacetime itself also have microscopic structure? In the same way that temperature, pressure, and sound waves emerge from collective motion in a fluid, perhaps geometry, causality, and gravity emerge from the self-organization of a deeper causal substrate. CFT calls the fundamental elements of this substrate chronons. Chronons are not particles moving in spacetime; rather, they are local configurations of a field that generate spacetime itself.

A useful mental picture is to imagine spacetime as filled with an extremely dense, four-dimensional ensemble of infinitesimal arrows of temporal flow. Each arrow represents a microscopic direction of causation—a local orientation from “past” to “future.” When these tiny arrows align coherently, they weave together into a global causal fabric, defining a continuous direction of time and a natural foliation of three-dimensional space. In this way, our familiar intuition—that we live in a three-dimensional world that steadily advances through time—arises as an emergent, large-scale organization of the chronon field.

Chronons therefore are not “atoms of time” in a literal sense; they are the microscopic orientations of causal order. They form a field of local temporal direction and density whose large-scale alignment manifests as the smooth spacetime of General Relativity. This perspective unites geometry and dynamics: spacetime is not a static background but a living, causal medium that can twist, vibrate, and evolve.

2.1. From Atoms of Matter to Units of Causal Order

Physics has advanced by revealing successive layers of structure in nature. Bulk matter was once thought continuous until the atomic theory showed that its macroscopic properties emerge from the motion of discrete molecules. Later discoveries revealed that atoms themselves have internal constituents, and that forces arise from exchange fields rather than rigid mechanisms. Each conceptual leap reduced something once fundamental to an emergent collective behavior.

Yet spacetime itself has long been treated as a smooth manifold—an immutable stage on which quantum fields play out their dynamics. Quantum theory, however, suggests that this stage cannot remain continuous at the smallest scales: vacuum fluctuations and gravitational self-energy should make geometry itself unstable. CFT extends the atomic paradigm one level deeper. It proposes that spacetime and causality emerge from the cooperative behavior of microscopic causal elements—chronons.

Each chronon represents an infinitesimal four-dimensional arrow of causal flow—a unit of causal order. In regions of random orientation, there is no consistent notion of “before” or “after”; the universe is in a pre-geometric phase with no well-defined time or space. When chronons begin to align, a global causal direction appears, and space emerges as the three-dimensional hypersurface orthogonal to that direction. Causal order condenses into geometry.

2.2. Chronon Field as the Microscopic Clock of the Universe

Mathematically, the chronon field is described by a timelike vector field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ defined over a pre-geometric substrate. Physically, ${\mathrm{\Phi }}^{\mu }$ represents the local direction and density of causal flow. Its orientation gives the microscopic “arrow of time,” and its magnitude encodes the local rate of causal progression—a kind of intrinsic tempo.

At every spacetime point, ${\mathrm{\Phi }}^{\mu }$ can be imagined as a small arrow pointing from cause to effect. When many such arrows interact and align, they form a continuous causal structure. Where alignment is perfect, time has a definite direction and the associated spacelike hypersurfaces define our three-dimensional world at an instant. Where alignment falters, causal order becomes ambiguous, and spacetime itself loses coherence.

In this picture, the universe is a gigantic, self-synchronizing ensemble of chronon arrows. Their collective orientation gives rise to a universal temporal flow, while small deviations or twists encode curvature and gravitational effects. Chronons act as microscopic “clocks,” but rather than ticking discretely, they define the continuous rhythm of causal evolution that we experience as time.

The field’s dynamics are governed by an energy functional analogous to that of a nonlinear spin system:

$$\mathcal{H}={\displaystyle \frac{J}{2}}\left({\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }\right)\left({\nabla }^{\mu }{\mathrm{\Phi }}^{\nu }\right)+{\displaystyle \frac{\lambda }{2}}{({\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }+1)}^2.$$

Here, J measures the stiffness of causal alignment, and $\lambda$ enforces the unit-timelike constraint ${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1$, ensuring that the emergent geometry possesses Lorentzian signature. Regions of uniform alignment correspond to flat spacetime; gradients in alignment generate curvature.

In summary:

• Chronons are not discrete time particles but continuous local configurations of causal direction.
• Their global alignment produces a coherent time direction and a foliation of 3D space.
• Their misalignment produces curvature, waves, and topological defects that correspond to matter and fields.
• Our everyday experience of “space” and “flowing time” reflects the stable large-scale alignment of the chronon field.

The chronon concept thus provides a bridge between human temporal intuition and the geometric formalism of modern physics: time is real and directional, but its flow emerges from the ordered dynamics of countless microscopic arrows of causality.

2.3. Analogy: Fluid Flow and Causal Order as Emergent Structure

To visualize how a field of chronons can generate spacetime, it helps to use analogies from everyday physics. One of the most powerful is the analogy with fluid flow.

Imagine a vast, incompressible fluid. At every point, the fluid velocity $\mathbf{v}(\mathbf{x},t)$ describes how nearby fluid elements move relative to one another. If the flow is laminar and coherent, one can define smooth streamlines and surfaces of constant flow potential. However, if the flow is turbulent, such structures lose meaning.

Similarly, the chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ defines the “velocity” of causal propagation. Where the field is coherent, causal relationships form smooth structures—these are the regions that we interpret as continuous spacetime. Where it is turbulent or misaligned, causal relationships fluctuate, giving rise to quantum behavior or even pre-geometric chaos.

In hydrodynamics, small vorticities and pressure gradients produce curvature in the flow. In CFT, curvature arises from the misalignment of chronon vectors:

$${\mathrm{\Omega }}_{\mu \nu }={\partial }_{\mu }{\mathrm{\Phi }}_{\nu }-{\partial }_{\nu }{\mathrm{\Phi }}_{\mu }.$$

This antisymmetric tensor plays the role of a microscopic “field strength”—a measure of causal twist. The curvature of spacetime, in Einstein’s sense, emerges statistically as the coarse-grained average of ${\mathrm{\Omega }}_{\mu \nu }$ across many chronons.

This picture is deeply intuitive:

• Chronons act like fluid elements, each carrying a local arrow of time.
• Causal order is like fluid flow, continuously connecting causes to effects.
• Spacetime curvature is like vorticity or strain, describing how these causal flows twist and converge.

This analogy also helps bridge to quantum mechanics. Just as turbulence in a fluid introduces fluctuations that can only be described statistically, microscopic fluctuations in the chronon field lead naturally to quantum uncertainty. The probabilistic nature of quantum theory is thus reinterpreted as the statistical behavior of a deeply causal, yet fluctuating, medium.

2.4. The Unit-Timelike Constraint and Causal Foliation

A defining feature of the chronon field is its unit-timelike constraint:

$${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1.$$

This condition ensures that ${\mathrm{\Phi }}^{\mu }$ always points within the light cone of the emergent geometry, preserving causality at every level of description. It serves the same purpose as normalizing velocity to the speed of light for a massive particle, but here it applies to the field that defines the very structure of spacetime.

The constraint implies that at each point, ${\mathrm{\Phi }}^{\mu }$ identifies a local temporal direction orthogonal to a three-dimensional hypersurface of simultaneity. This defines a natural foliation of the universe into “slices of now”— spatial surfaces orthogonal to the flow of causal time. The collection of all such slices, smoothly connected through ${\mathrm{\Phi }}^{\mu }$, constitutes the emergent spacetime manifold.

One can picture the chronon field as a bundle of oriented threads permeating reality. Each thread traces a local line of causality, and their collective alignment defines the geometry of the universe. Where these threads diverge or converge, curvature arises; where they tangle, energy and matter appear. Causal order and spacetime geometry are thus two sides of the same coin.

Analogy: Just as the magnetic field lines in a ferromagnet indicate regions of aligned spin, the chronon field lines indicate regions of aligned causality. The alignment energy J determines how rigid this causal network is. When J is large, causal order is stable and spacetime behaves classically. When J is small or fluctuating, causal order becomes fuzzy and quantum phenomena dominate.

In summary, the chronon field provides a concrete, physically motivated picture of how spacetime and causality might arise from the collective behavior of microscopic, time-oriented degrees of freedom. It transforms the philosophical notion of “atoms of time” into a quantitative framework— one capable of bridging the quantum and geometric realms.

3. Emergent Spacetime and Causal Order

In Chronon Field Theory (CFT), spacetime is not taken as a pre-existing continuum. Instead, it is an emergent construct—a large-scale order parameter that arises when microscopic causal elements (chronons) align coherently. The metric, curvature, and causal cones familiar from General Relativity are not imposed; they emerge dynamically through the collective behavior of the chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$. In this section, we trace how that process occurs and why it reproduces the structure of spacetime as we know it.

3.1. Chronon Alignment and the Birth of Geometry

At the microscopic level, the universe can be thought of as a dense ensemble of chronons, each representing an elementary causal link between events. In the earliest, high-temperature phase, these links are uncorrelated: there is no notion of “before” or “after,” and thus no spacetime geometry. This pre-geometric phase resembles a liquid in which molecules move randomly, possessing no fixed shape or orientation.

As the universe cools and the interaction strength (stiffness) J increases, chronons begin to align. A spontaneous symmetry breaking occurs: out of the rotationally symmetric chaos of pre-causal states, a preferred orientation emerges. This order parameter is the chronon field ${\mathrm{\Phi }}^{\mu }$, which now acquires a nonzero expectation value

$$\langle {\mathrm{\Phi }}^{\mu }\rangle =n^{\mu },n^{\mu }{n}_{\mu }=-1,$$

selecting a global arrow of time. This transition marks the birth of geometry—the moment when causal order condenses into spacetime.

Once chronons are aligned, local correlations propagate across regions, defining smooth neighborhoods where causal direction varies gradually. These domains can be stitched together consistently, giving rise to a manifold structure. The resulting continuum limit supports notions of distance, duration, and curvature. In this way, the geometric properties of spacetime emerge as the macroscopic thermodynamic description of the collective causal field.

Analogy: Just as magnetization emerges when atomic spins align below the Curie temperature, geometry emerges when chronons align below the “causal condensation temperature.” Above that critical temperature, causal order is lost and the universe behaves as a quantum foam; below it, spacetime solidifies as an ordered causal crystal.

3.2. Foliation: How Time and Space Emerge from Causal Order

The alignment of chronons not only defines directionality in time but also differentiates time from space. At each point, the chronon field ${\mathrm{\Phi }}^{\mu }$ determines a local arrow of causal propagation. Surfaces orthogonal to this vector are interpreted as instantaneous “slices of space.” These hypersurfaces form a smooth foliation of the emergent spacetime manifold.

Formally, the unit-timelike constraint ${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1$ implies the existence of a three-dimensional orthogonal subspace at each point, spanned by vectors satisfying ${\mathrm{\Phi }}_{\mu }{X}^{\mu }=0$. These subspaces represent local simultaneity, and their integral curves define the emergent notion of spatial extension. Time, in turn, corresponds to motion along the congruence of ${\mathrm{\Phi }}^{\mu }$.

$$\mathrm{Causal}\mathrm{order}\text{:}p\prec q\mathrm{if}\mathrm{and}\mathrm{only}\mathrm{if}{\int }_p^q{\mathrm{\Phi }}_{\mu }d{x}^{\mu }>0.$$

In this sense, “time” is not an external parameter but a cumulative measure of causal progression along chronon flow lines.

When the chronon field is nearly uniform, the emergent spacetime is flat; when it varies smoothly, curvature arises from gradients of ${\mathrm{\Phi }}^{\mu }$. This mechanism provides a natural origin for the metric tensor $g_{\mu \nu }$, defined as the coarse-grained correlation of chronon orientations:

$$g_{\mu \nu }\left(x\right)\propto {\langle {\mathrm{\Phi }}_{\mu }\left(x\right){\mathrm{\Phi }}_{\nu }\left(x\right)\rangle }_{\mathrm{coarse}}.$$

Thus, distances and intervals emerge from the statistical coherence of causal flow. Space and time are not separate ingredients but complementary aspects of the same underlying order.

Physical picture: Space corresponds to directions where chronons are synchronized (no net causal flow), while time corresponds to the direction of maximal causal alignment. Regions where the alignment twists or converges generate curvature and energy density.

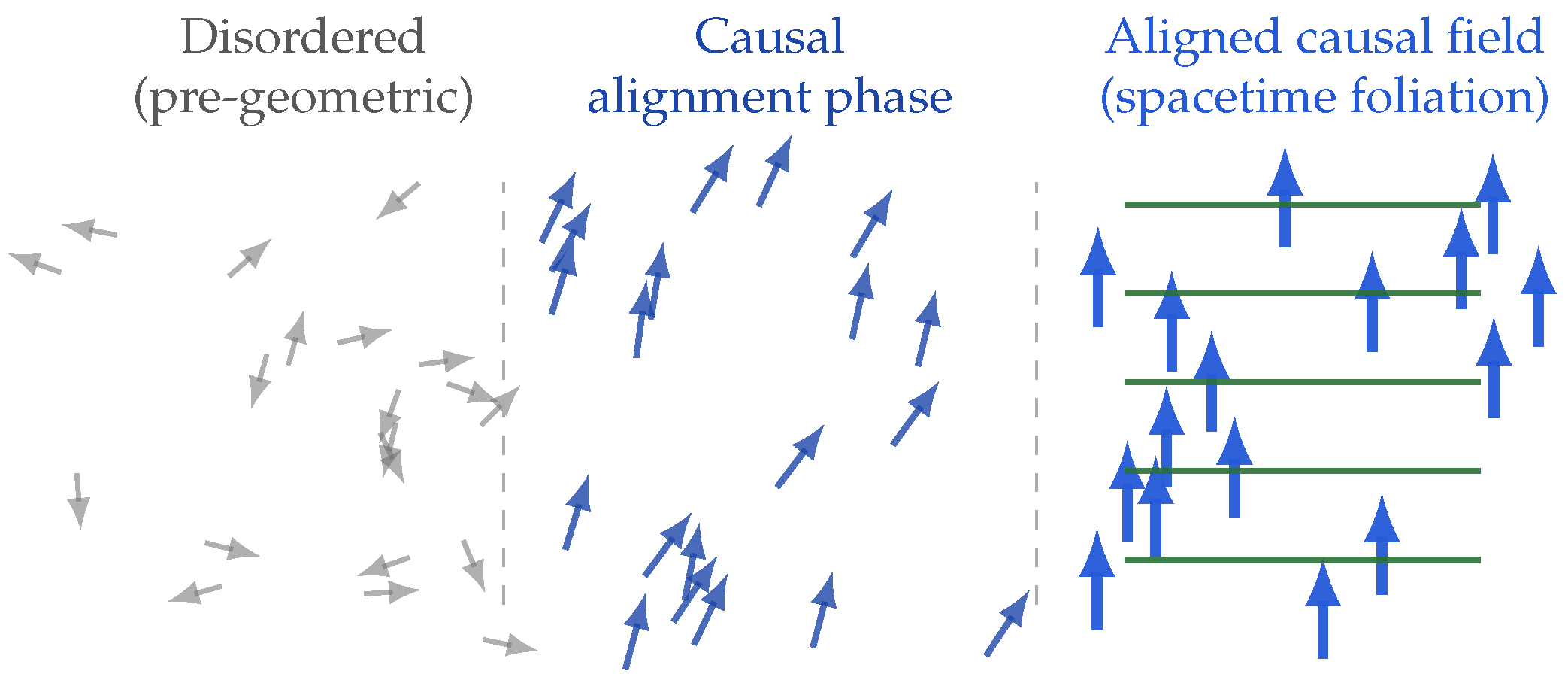
Figure 1. Emergence of spacetime foliation from causal alignment. In the disordered phase (left), chronon orientations are random and no causal order exists. During causal condensation (center), partial alignment defines a preferred temporal direction. In the ordered phase (right), chronons share a common time vector ${\mathrm{\Phi }}^{\mu }$, and spacelike foliations (green lines)—surfaces orthogonal to ${\mathrm{\Phi }}^{\mu }$—emerge as the 3D structure of space.

Figure 1. Emergence of spacetime foliation from causal alignment. In the disordered phase (left), chronon orientations are random and no causal order exists. During causal condensation (center), partial alignment defines a preferred temporal direction. In the ordered phase (right), chronons share a common time vector ${\mathrm{\Phi }}^{\mu }$, and spacelike foliations (green lines)—surfaces orthogonal to ${\mathrm{\Phi }}^{\mu }$—emerge as the 3D structure of space.

3.3. Symplectic Curvature as the Seed of Quantum Action

Even in an aligned chronon field, microscopic variations in causal orientation persist. Tiny phase differences between neighboring chronons generate an antisymmetric tensor, the symplectic curvature,

$${\mathrm{\Omega }}_{\mu \nu }={\partial }_{\mu }{\mathrm{\Phi }}_{\nu }-{\partial }_{\nu }{\mathrm{\Phi }}_{\mu },$$

which measures infinitesimal rotation of the local time-flow direction in the $\mu$–$\nu$ plane—analogous to vorticity in a fluid or magnetic flux in a superconductor. Regions where ${\mathrm{\Omega }}_{\mu \nu }\ne 0$ represent closed loops in causal order where the chronon field undergoes a full twist before re-aligning.

A minimal, self-sustaining twist defines a chronon soliton: a localized, topologically protected knot in ${\mathrm{\Phi }}^{\mu }$ whose circulation is quantized,

$$\oint {\mathrm{\Phi }}_{\mu }d{x}^{\mu }=\int {\mathrm{\Omega }}_{\mu \nu }d{\mathrm{\Sigma }}^{\mu \nu }=n{\hslash }_{\mathrm{geom}}.$$

Here ${\hslash }_{\mathrm{geom}}$ emerges as the modulus of the smallest nontrivial soliton—a single $2\pi$ rotation in the causal phase. Because this configuration cannot unwind continuously, its enclosed action is conserved and irreducible: the field is locked at a minimum-action value ℏ. Quantization thus arises not from discretizing energy levels, but from the geometric stability of the smallest causal knot.

Planck’s constant therefore expresses a topological invariant of the chronon field:

$$\hslash ={\int }_{{\mathrm{\Sigma }}_{min}}{\mathrm{\Omega }}_{\mu \nu }d{\mathrm{\Sigma }}^{\mu \nu },$$

the flux of symplectic curvature through a fundamental causal loop.

Physical intuition. ${\mathrm{\Omega }}_{\mu \nu }$ is the microscopic twisting of the causal flow. A $2\pi$ twist produces a stable soliton whose action is frozen at ℏ. Quantization reflects this geometric stability—the universality of a minimal, topologically protected rotation in causal phase.

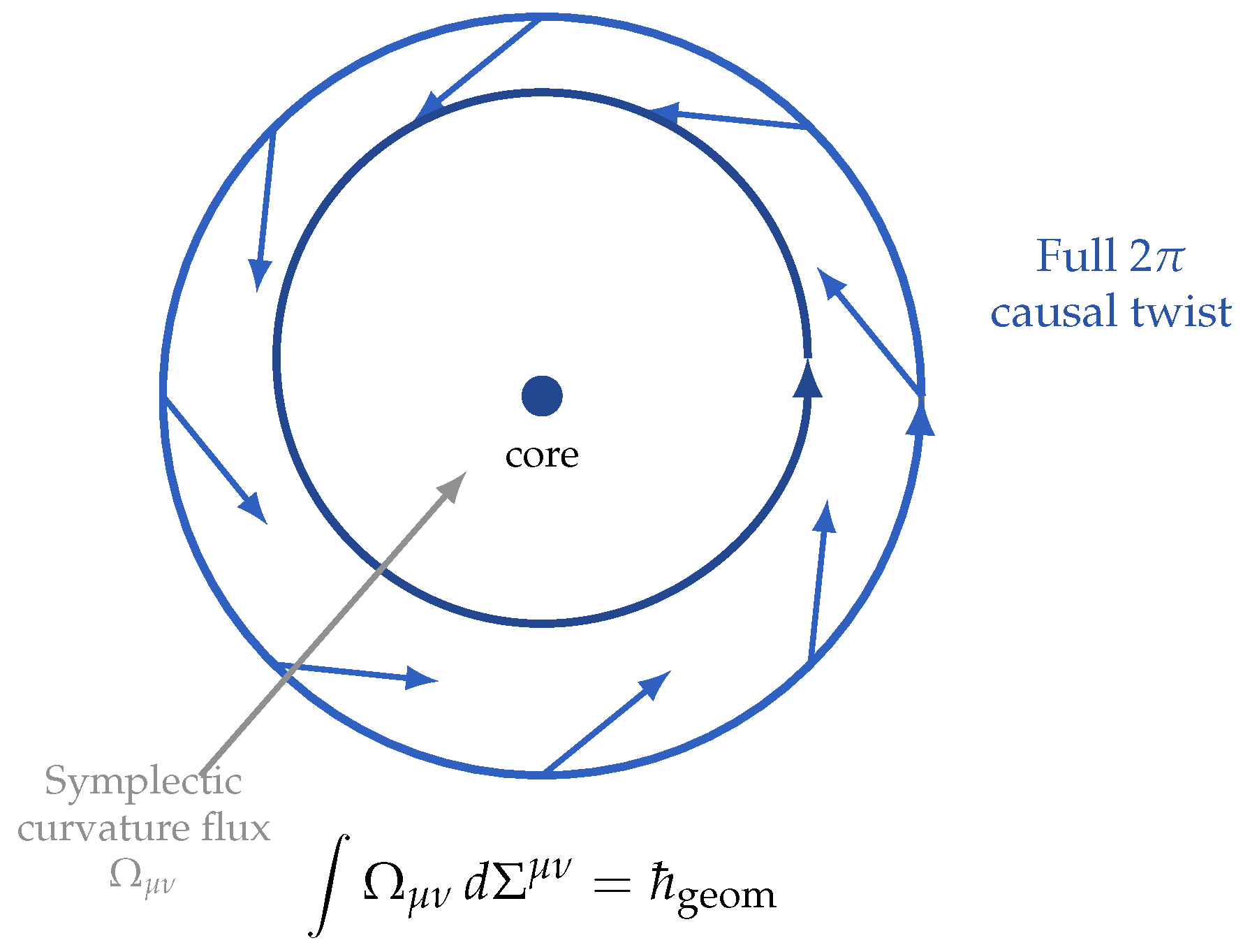
Figure 2. Single chronon soliton ($n=1$) as the fundamental quantum of action. A $2\pi$ rotation of the chronon field ${\mathrm{\Phi }}^{\mu }$ forms a stable causal knot with flux $\int {\mathrm{\Omega }}_{\mu \nu }d{\mathrm{\Sigma }}^{\mu \nu }={\hslash }_{\mathrm{geom}}$. Planck’s constant thus measures the geometric modulus of one complete causal twist.

Figure 2. Single chronon soliton ($n=1$) as the fundamental quantum of action. A $2\pi$ rotation of the chronon field ${\mathrm{\Phi }}^{\mu }$ forms a stable causal knot with flux $\int {\mathrm{\Omega }}_{\mu \nu }d{\mathrm{\Sigma }}^{\mu \nu }={\hslash }_{\mathrm{geom}}$. Planck’s constant thus measures the geometric modulus of one complete causal twist.

Bosonic inheritance of ℏ.

While fermions appear as localized solitons of ${\mathrm{\Phi }}^{\mu }$, bosons such as photons or gluons are propagating oscillations of its curvature ${\mathrm{\Omega }}_{\mu \nu }$ within the aligned chronon medium. Each wave cycle advances the causal phase by a full $2\pi$ rotation, enclosing the same action quantum ℏ. Hence both solitons (localized knots) and bosons (traveling waves) embody the same geometric process—a complete causal rotation of the chronon field.

$$S=\int {\mathrm{\Omega }}_{\mu \nu }d{\mathrm{\Sigma }}^{\mu \nu }=\hslash .$$

The universality of Planck’s constant reflects not particle identity but the invariance of causal geometry: every quantum, whether bound or propagating, corresponds to one fundamental twist of causal phase.

3.4. Comparison with General Relativity and Causal Set Theory

Chronon Field Theory shares the spirit of General Relativity in treating spacetime as a dynamical entity but differs in a crucial way: GR starts with a differentiable manifold and defines curvature as a property of that continuum, whereas CFT derives the continuum itself from a deeper causal field.

General Relativity (GR):

• Assumes a smooth manifold with a metric $g_{\mu \nu }$.
• Describes curvature via the Riemann tensor $R_{\nu \rho \sigma }^{\mu }$.
• Treats spacetime as continuous and classical.

Chronon Field Theory (CFT):

• Begins with discrete causal elements ${\mathrm{\Phi }}^{\mu }$; geometry is emergent.
• Curvature arises from symplectic misalignment ${\mathrm{\Omega }}_{\mu \nu }$.
• Quantization of action follows naturally from discrete causal flux.

In comparison to Causal Set Theory, CFT also posits a fundamental causal structure, but with a key difference: the chronon field is continuous and differentiable in its large-scale limit, allowing for conventional field equations and smooth curvature. Causal Set Theory, in contrast, treats causality as purely discrete, requiring statistical coarse-graining to recover the continuum limit. CFT can therefore reproduce the successes of GR while offering a direct geometric route to quantization.

$$\mathrm{CFT}\text{:}\mathrm{causal}\mathrm{alignment}⟶g_{\mu \nu }⟶R_{\mu \nu \rho \sigma }.$$

$$\mathrm{GR}\text{:}\mathrm{assumed}\mathrm{manifold}⟶g_{\mu \nu }⟶R_{\mu \nu \rho \sigma }.$$

$$\mathrm{Causal}\mathrm{Set}\text{:}\mathrm{discrete}\mathrm{partial}\mathrm{order}⟶\mathrm{statistical}\mathrm{geometry}.$$

CFT therefore occupies an intermediate position—combining the causal primacy of Causal Set Theory with the differential structure of General Relativity.

3.5. Eliminating Singularities Through Finite Curvature

One of the most striking consequences of CFT is the natural elimination of singularities. Because chronons possess a finite alignment stiffness J and obey a curvature bound enforced by the Chronon Exclusivity Principle (CEP, introduced in Section 1), the symplectic curvature ${\mathrm{\Omega }}_{\mu \nu }$ cannot diverge.

This imposes a maximum causal twist analogous to a maximum magnetic flux density in a superconducting medium:

$${\mathrm{\Omega }}_{\mu \nu }{\mathrm{\Omega }}^{\mu \nu }\le {\mathrm{\Omega }}_{max}^2.$$

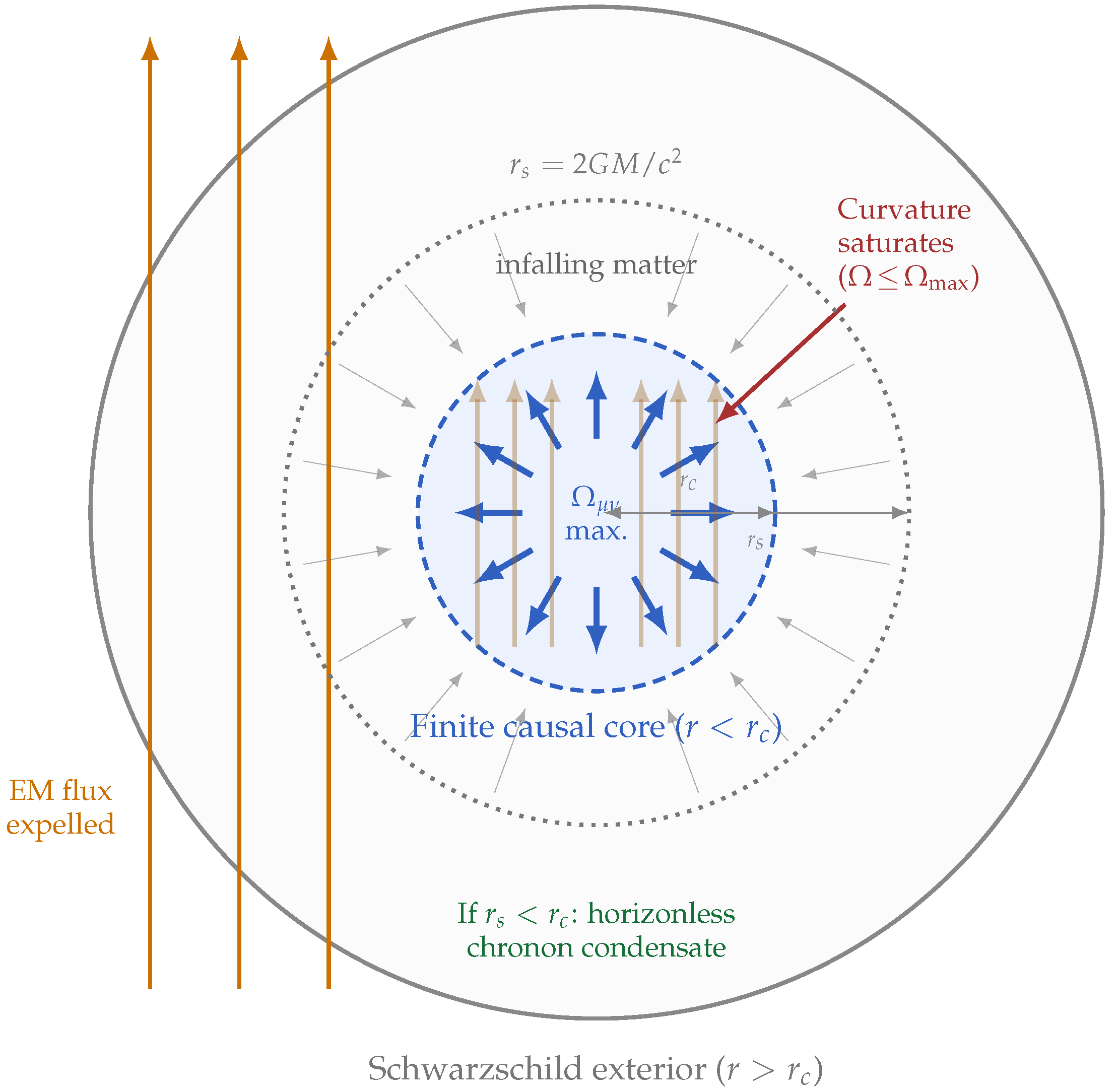
In General Relativity, gravitational singularities arise because nothing limits how tightly spacetime can curve. But in CFT, curvature is an emergent property of microscopic orientation fields, and those fields saturate at finite density. When ${\mathrm{\Omega }}_{\mu \nu }$ reaches its maximal value, further compression no longer increases curvature; instead, the region undergoes phase transition into a stable, high-density “chronon condensate.” This state replaces classical singularities with finite-core objects— compact but regular at all points.

Physically, this means that black holes do not harbor true singularities but contain finite cores where causal order reaches maximum twist. Such regions are stable against collapse and retain information, leading to the concept of chronon stars, discussed later in Section 8.

Summary:

• Spacetime geometry arises from coherent alignment of chronons.
• Time and space emerge as complementary directions of causal flow.
• Quantum discreteness originates from quantized causal curvature.
• Curvature is bounded, removing singularities from the theory.

CFT thus provides a continuous narrative from microscopic causality to macroscopic geometry— a bridge between the quantum and relativistic worlds grounded in the physics of causal order.

For technical readers, a detailed variational derivation of the chronon field equations and their associated conservation laws is provided in Appendix A. There, the alignment dynamics are shown to conserve causal flux, ensure positive curvature energy for $J>0$, and yield quantized geometric modes that underpin the emergence of both $G_{\mathrm{eff}}$ and ${\hslash }_{\mathrm{geom}}$ in the macroscopic limit.

4. Emergent General Relativity

Once causal order condenses into a coherent chronon field, its large-scale behavior must reproduce the familiar laws of gravitation. This section explains how the Einstein field equations emerge as the hydrodynamic limit of chronon alignment dynamics, why curvature represents residual strain of the causal medium, and how Newton’s constant G and Planck’s constant ℏ arise naturally from the microscopic parameters $(J,\lambda ,{\ell }_c)$. In this framework, gravity is not a separate force but the relaxation of causal stress within a finite-stiffness chronon lattice [7,8].

4.1. Coarse-Graining and the Einstein Limit

The fundamental chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ obeys the microscopic equation

$${\nabla }_{\nu }\left(J{\nabla }^{[\nu }{\mathrm{\Phi }}^{\mu ]}\right)+\lambda ({\mathrm{\Phi }}_{\nu }{\mathrm{\Phi }}^{\nu }+1){\mathrm{\Phi }}^{\mu }=0,$$

where J quantifies the stiffness of causal alignment and $\lambda$ enforces local self-coherence. No background metric is presupposed; all geometry emerges from correlations among chronon orientations.

To connect with macroscopic gravity, consider coarse-graining over domains much larger than the coherence length ${\ell }_c$. The ensemble average of chronon orientations defines the emergent metric:

$$\langle {\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu }\rangle =g_{\mu \nu }/{(-detg)}^{1/4},$$

ensuring that $g_{\mu \nu }$ is symmetric, nondegenerate, and dynamically generated by chronon alignment itself. Averaging the microscopic Lagrangian then yields the effective macroscopic action

$$S_{\mathrm{eff}}\left[g_{\mu \nu }\right]=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{c^4}{16\pi G_{\mathrm{eff}}}}R-{\mathrm{\Lambda }}_{\mathrm{eff}}\right],$$

with identifications

$${\displaystyle \frac{c^4}{16\pi G_{\mathrm{eff}}}}={\displaystyle \frac{3J}{2{\ell }_c^2}},{\mathrm{\Lambda }}_{\mathrm{eff}}={\displaystyle \frac{3\lambda }{8J}}.$$

Thus, the Einstein tensor arises as the coarse-grained equation of state of the causal medium, and Newton’s constant emerges as the ratio of microscopic stiffness to the square of the coherence scale. Deviations from perfect alignment produce curvature and gravitational waves, while higher-order gradients in ${\mathrm{\Phi }}_{\mu }$ yield small nonlocal corrections expected near black holes or during the early universe.

Interpretation: General Relativity is the long-wavelength constitutive law of a causal elastic medium. The Einstein equations describe the equilibrium of chronon alignment, not a fundamental postulate of spacetime geometry.

4.2. Energy Density and Curvature Feedback

In CFT, energy and curvature are dynamically coupled through feedback between chronon misalignment and the restoring stress of the causal lattice. When energy enters a region, local orientations of ${\mathrm{\Phi }}^{\mu }$ deviate from coherence, increasing the curvature measure ${\mathrm{\Omega }}_{\mu \nu }{\mathrm{\Omega }}^{\mu \nu }$. This deformation stores alignment energy,

$${\rho }_{\mathrm{\Phi }}={\displaystyle \frac{J}{4}}{\mathrm{\Omega }}_{\mu \nu }{\mathrm{\Omega }}^{\mu \nu }+{\displaystyle \frac{\lambda }{2}}{({\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }+1)}^2,$$

which acts as the microscopic source of curvature. Curvature, in turn, resists further distortion through the finite stiffness J, preventing singularities and stabilizing the system. At macroscopic equilibrium,

$$\mathrm{curvature}⟺\mathrm{energy}\mathrm{density},$$

yielding the Einstein relation as a self-consistent feedback condition of causal stress and geometric response.

Physical picture: Energy bends spacetime because it perturbs the alignment of causal threads. The gravitational field is the elastic strain of the chronon network.

4.3. Gravity as the Relaxation of Causal Stress

The chronon field behaves as a self-organizing elastic continuum that minimizes misalignment energy. Perturbations of ${\mathrm{\Phi }}^{\mu }$ generate curvature waves—gravitational waves— that propagate and dissipate until local coherence is restored.

Defining a causal stress tensor

$${\sigma }_{\mu \nu }=J{\nabla }_{(\mu }{\mathrm{\Phi }}_{\nu )}-{\displaystyle \frac{1}{2}}{g}_{\mu \nu }J{\nabla }_{\alpha }{\mathrm{\Phi }}^{\alpha },$$

the equilibrium condition ${\nabla }^{\nu }{\sigma }_{\mu \nu }=0$ implies the macroscopic identity ${\nabla }^{\nu }{G}_{\mu \nu }=0$, showing that general covariance is a direct outcome of causal equilibration. Free fall corresponds to motion along unstrained chronon flows—paths of minimal causal stress.

Analogy: Just as a disturbed elastic sheet relaxes by propagating ripples, the chronon medium relaxes by propagating curvature waves. Gravitational radiation represents macroscopic oscillations of this causal alignment field.

4.4. Elastic Analogy and Curvature Response

Chronon dynamics mirror elasticity in continuum mechanics. The symmetric derivative ${\nabla }_{(\mu }{\mathrm{\Phi }}_{\nu )}$ acts as strain, while the antisymmetric part ${\mathrm{\Omega }}_{\mu \nu }={\nabla }_{[\mu }{\mathrm{\Phi }}_{\nu ]}$ acts as rotational deformation. The parameter J is the causal stiffness—the elastic modulus of spacetime. In this view, the Einstein equation is the continuum limit of a causal Hooke’s law:

$$R_{\mu \nu }-\frac{1}{2}R{g}_{\mu \nu }=8\pi G_{\mathrm{eff}}{T}_{\mu \nu }^{\left(\mathrm{\Phi }\right)}.$$

Curvature replaces strain, the chronon stress-energy replaces applied force, and $G_{\mathrm{eff}}$ measures the compliance of the causal medium.

4.5. Emergence of G and ℏ

The constants G and ℏ are emergent scales derived from the chronon parameters $(J,\lambda ,{\ell }_c)$.

Newton Constant

The effective gravitational coupling reflects causal stiffness:

$$G_{\mathrm{eff}}\sim {\displaystyle \frac{\xi }{J{\ell }_c^2}},$$

where $\xi \sim \mathcal{O}\left(1\right)$ captures geometric coarse-graining factors. A stiffer medium (larger J) produces weaker curvature for a given stress.

Planck Constant

Quantization arises from discrete flux of symplectic curvature. The minimal action associated with one chronon oscillation,

$$S_{\mathrm{soliton}}\sim 4\pi {\displaystyle \frac{J^2}{\lambda c_{\mathrm{eff}}}},$$

defines the emergent quantum of action,

$${\hslash }_{\mathrm{geom}}\simeq 4\pi {\displaystyle \frac{J^2}{\lambda c_{\mathrm{eff}}}}.$$

Thus, ℏ measures the smallest sustainable unit of causal rotation.

Unified Scaling

Combining both gives

$$G\hslash \sim {\displaystyle \frac{4\pi \xi }{\lambda c_{\mathrm{eff}}{\ell }_c^2}},$$

showing that classical and quantum constants are complementary expressions of the same chronon geometry.

Summary:

• The Einstein equations emerge as the coarse-grained limit of chronon alignment.
• Gravity is the relaxation of causal stress within a finite-stiffness causal medium.
• G and ℏ originate from the microscopic parameters $(J,\lambda ,{\ell }_c)$, unifying geometry and quantization under a single causal-elastic principle.

A formal derivation of the Einstein equations from the chronon Lagrangian is provided in Appendix B, which shows explicitly how curvature, stiffness, and vacuum energy arise from chronon alignment. The positivity of curvature energy ($J>0$) guarantees universal attraction, and deviations from perfect alignment correspond to gravitational waves. Thus, General Relativity appears not as a fundamental postulate, but as the hydrodynamic limit of a discrete, self-aligning causal medium.

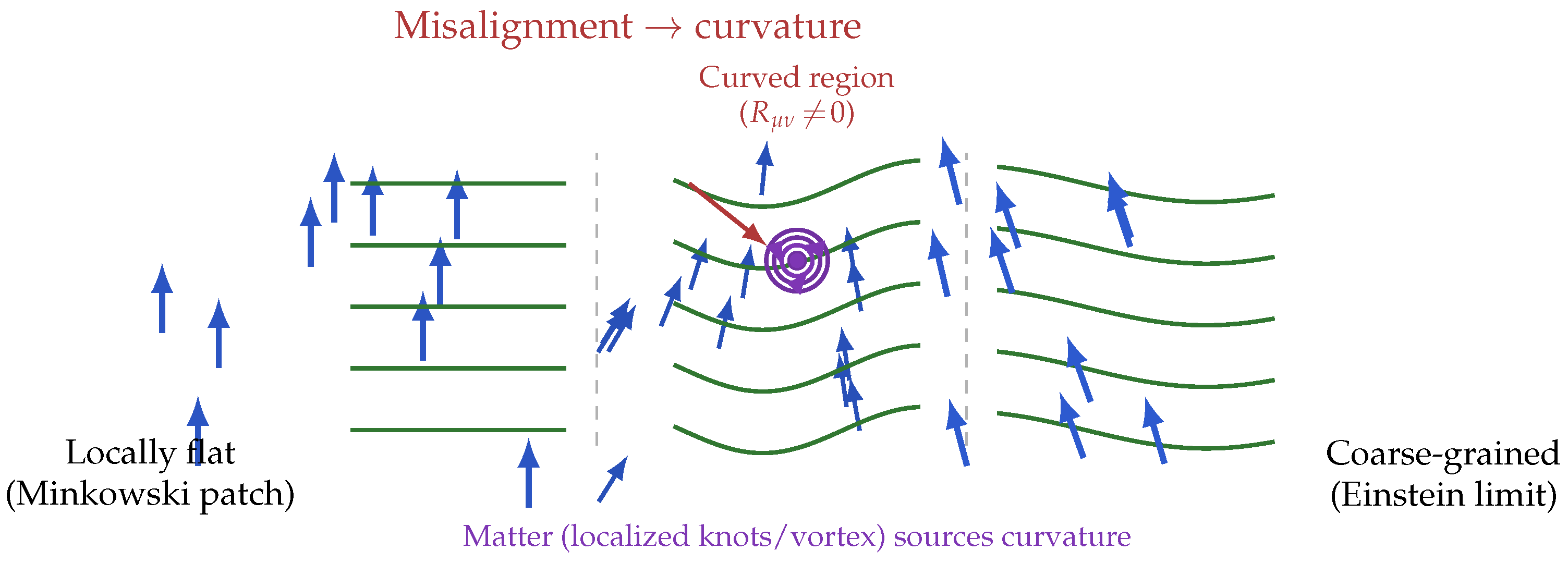
Figure 3. Emergent General Relativity from causal alignment. A localized vortex of the chronon field (matter) twists the surrounding causal flow, producing curvature and bending spacelike foliations. In the coarse-grained limit (right), these curvature effects manifest as the smooth spacetime geometry of General Relativity, with Einstein’s equations describing the relaxation of causal stress.

Figure 3. Emergent General Relativity from causal alignment. A localized vortex of the chronon field (matter) twists the surrounding causal flow, producing curvature and bending spacelike foliations. In the coarse-grained limit (right), these curvature effects manifest as the smooth spacetime geometry of General Relativity, with Einstein’s equations describing the relaxation of causal stress.

5. Fundamental Forces and Gauge Interactions

One of the central challenges of modern physics is to understand why the fundamental forces of nature—electromagnetism, the weak and strong nuclear forces, and gravity—take the specific forms we observe. In the Standard Model, these forces arise from gauge symmetries, internal geometric structures acting on quantum fields. Chronon Field Theory (CFT) offers a unified origin for both spacetime curvature and gauge curvature, showing that the familiar $U\left(1\right)\times SU\left(2\right)\times SU\left(3\right)$ symmetries of the Standard Model can emerge naturally from microscopic rotations of the chronon field.

The key idea is that local holonomies—closed rotations of causal alignment in internal degrees of freedom of ${\mathrm{\Phi }}^{\mu }$—behave as gauge connections. In this way, the geometry of interactions emerges from the same underlying chronon alignment that produces spacetime itself.

5.1. From Chronon Holonomy to Gauge Fields

The chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ describes not only the direction of time but also possesses internal orientation freedom. At each point, small rotations of ${\mathrm{\Phi }}^{\mu }$ within its local tangent bundle leave its magnitude fixed (${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1$) but change its phase. These infinitesimal rotations define a connection

$$A_{\mu }^{\left(a\right)}={\mathrm{\Phi }}_{\nu }{T}^{\left(a\right)}{\nabla }_{\mu }{\mathrm{\Phi }}^{\nu },$$

where $T^{\left(a\right)}$ are generators of the internal rotation group. Parallel transport of ${\mathrm{\Phi }}^{\mu }$ around a closed loop produces a holonomy

$$U\left(C\right)=\mathcal{P}exp\left({\oint }_C{A}_{\mu }^{\left(a\right)}{T}^{\left(a\right)}d{x}^{\mu }\right),$$

analogous to the Wilson loop of gauge theory.

The antisymmetric part of the gradient of ${\mathrm{\Phi }}^{\mu }$,

$${\mathrm{\Omega }}_{\mu \nu }^{\left(a\right)}={\partial }_{\mu }{A}_{\nu }^{\left(a\right)}-{\partial }_{\nu }{A}_{\mu }^{\left(a\right)}+f^{abc}{A}_{\mu }^{\left(b\right)}{A}_{\nu }^{\left(c\right)},$$

plays the role of the field strength tensor of a non-Abelian gauge field. Here, the structure constants $f^{abc}$ arise from the commutation relations of the internal rotation group governing chronon interactions.

Thus, gauge fields are reinterpreted as manifestations of microscopic rotational misalignments of causal orientation. The traditional distinction between spacetime curvature and gauge curvature collapses into a single geometric entity: spacetime curvature corresponds to twisting of causal direction in external indices, while gauge curvature corresponds to twisting in internal indices of the same field.

$$\underset{\mathrm{spacetime}\mathrm{curvature}}{\underbrace{R_{\mu \nu \rho \sigma }}}\mathrm{and}\underset{\mathrm{internal}\mathrm{curvature}}{\underbrace{{\mathrm{\Omega }}_{\mu \nu }^{\left(a\right)}}}\mathrm{are}\mathrm{both}\mathrm{projections}\mathrm{of}{\nabla }_{[\mu }{\mathrm{\Phi }}_{\nu ]}.$$

This insight implies that all interactions—gravitational and gauge—arise from a single geometric structure: the chronon holonomy.

5.2. Emergent $U\left(1\right)$, $SU\left(2\right)$, and $SU\left(3\right)$ Geometry

Different classes of chronon misalignment give rise to different effective gauge symmetries at macroscopic scales.

1. $U\left(1\right)$: Electromagnetic Geometry

When the chronon field undergoes uniform phase rotation around its timelike axis, it produces an Abelian holonomy. This corresponds to a $U\left(1\right)$ connection with field strength

$$F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu },$$

identifiable with electromagnetism. The electromagnetic potential $A_{\mu }$ thus represents the simplest mode of causal phase rotation, and the photon is the massless excitation associated with this global coherence.

2. $SU\left(2\right)$: Weak Interaction Geometry

More complex rotations mixing time and spatial components of ${\mathrm{\Phi }}^{\mu }$ generate a triplet of internal directions corresponding to $SU\left(2\right)$. At high alignment temperatures, these directions are indistinguishable; as the chronon field cools and partially locks to the timelike direction, the symmetry breaks spontaneously, leaving a residual $U\left(1\right)$ subgroup. This geometric symmetry breaking mirrors the electroweak unification pattern without invoking a separate Higgs scalar.

3. $SU\left(3\right)$: Strong Interaction Geometry

At subnuclear scales, fine structure in chronon alignment gives rise to internal color-like rotations. The chronon field ${\mathrm{\Phi }}^{\mu }$ has four components, but because physical quantities depend on both ${\mathrm{\Phi }}^{\mu }$ and its antisymmetric gradients,

$${\mathrm{\Omega }}_{\mu \nu }={\nabla }_{[\mu }{\mathrm{\Phi }}_{\nu ]},\mathrm{\Theta }={\nabla }_{\mu }{\mathrm{\Phi }}^{\mu },$$

the effective local degrees of freedom exceed those of a simple vector field. The normalization constraint ${\mathrm{\Phi }}^{\mu }{\mathrm{\Phi }}_{\mu }=-1$ removes one mode, leaving three orientational degrees of freedom in ${\mathrm{\Phi }}^{\mu }$ and five independent components in ${\mathrm{\Omega }}_{\mu \nu }$—a total of eight dynamic modes, corresponding naturally to the adjoint representation of $SU\left(3\right)$. Including the scalar trace $\mathrm{\Theta }$ adds a ninth singlet, giving the extended $U\left(3\right)\simeq SU\left(3\right)\times U\left(1\right)$ structure.

These eight internal modes act as geometric color directions of the chronon field. Their coarse-grained dynamics yield an emergent non-Abelian field strength

$$G_{\mu \nu }^a={\partial }_{\mu }{A}_{\nu }^a-{\partial }_{\nu }{A}_{\mu }^a+g_s{f}^{abc}{A}_{\mu }^b{A}_{\nu }^c,$$

where $A_{\mu }^a$ parameterize the torsional and rotational excitations of causal alignment. Color confinement arises because misalignment flux in this medium cannot end freely: quantized curvature lines must close or connect in color-neutral triplets. Thus, the strong interaction and its $SU\left(3\right)$ symmetry appear not as fundamental forces, but as emergent geometry of the chronon field and its eight internal degrees of freedom.

In this view, the Standard Model gauge group

$$U\left(1\right)\times SU\left(2\right)\times SU\left(3\right)$$

emerges as the hierarchy of stable internal rotation symmetries of the chronon field at different energy scales, each corresponding to a distinct class of causal orientation defects.

5.3. Electroweak Symmetry Breaking Without a Higgs Field

In the Standard Model, the Higgs field is responsible for spontaneous breaking of the electroweak symmetry $SU{\left(2\right)}_L\times U{\left(1\right)}_Y\to U{\left(1\right)}_{\mathrm{EM}}$. However, in Chronon Field Theory, the same effect arises geometrically from the alignment of ${\mathrm{\Phi }}^{\mu }$.

When the universe cools below the causal condensation temperature, chronons align preferentially along a global timelike direction. This breaks the internal isotropy of causal rotations: the time-oriented component remains invariant (analogous to $U\left(1\right)$), while transverse components (analogous to $SU\left(2\right)$ generators) acquire effective mass through misalignment energy.

The effective Lagrangian density for the internal chronon rotations reads:

$${\mathcal{L}}_{\mathrm{int}}=-{\displaystyle \frac{1}{4}}{\mathrm{\Omega }}_{\mu \nu }^{\left(a\right)}{\mathrm{\Omega }}^{\left(a\right)\mu \nu }+{\displaystyle \frac{{\lambda }_{\mathrm{EW}}}{2}}{\left({\mathrm{\Phi }}^{\mu }{T}^{\left(a\right)}{\mathrm{\Phi }}_{\mu }\right)}^2.$$

The second term acts as a self-interaction potential that endows certain gauge modes with mass proportional to the local curvature of ${\mathrm{\Phi }}^{\mu }$. This yields massive W and Z bosons without invoking a separate scalar field.

The photon remains massless because the $U\left(1\right)$ phase direction corresponds to pure global rotations that do not distort causal alignment. Thus, electroweak symmetry breaking is reinterpreted as the spontaneous locking of internal causal directions to the global arrow of time. The “Higgs vacuum expectation value” is replaced by the mean alignment $\langle {\mathrm{\Phi }}^0\rangle$ of the chronon field.

5.4. Confinement and Flux Tubes as Chronon Polarization Effects

In the chronon framework, color confinement in quantum chromodynamics (QCD) emerges as a collective polarization effect. Chronon domains can sustain quantized tubes of symplectic flux, analogous to magnetic vortices in a type-II superconductor. These “causal flux tubes” correspond to the color-electric strings that confine quarks within hadrons.

The energy per unit length of a flux tube is proportional to the square of the field strength:

$${\mathcal{E}}_{\mathrm{tube}}\approx {\displaystyle \frac{1}{2}}J{\mathrm{\Omega }}_{\mu \nu }^{\left(a\right)}{\mathrm{\Omega }}^{\left(a\right)\mu \nu }.$$

As two color charges separate, the flux between them cannot spread uniformly because the chronon medium resists de-alignment. Instead, the flux condenses into a narrow tube whose tension increases linearly with separation, producing a confining potential

$$V\left(r\right)\simeq \sigma r,\sigma \propto J{\mathrm{\Omega }}_{max}^2.$$

At high energies (temperatures above the critical alignment threshold), chronon correlations dissolve and flux tubes break, releasing free color charges. This corresponds to the deconfinement transition observed in QCD plasmas.

Hence, confinement, like gravity, is a manifestation of causal alignment energy. All forces become different modes of the same elastic causal medium: gravitational curvature corresponds to bulk bending, while color flux confinement corresponds to shear polarization at smaller scales.

Analogy:

• In a crystal, dislocations create localized stress lines.
• In a superconductor, magnetic vortices trap quantized flux.
• In CFT, chronon misalignments form flux tubes that bind quarks.

Thus, color confinement is not a mystery of field theory but a direct geometrical consequence of causal elasticity.

5.5. Naturalness, Mass Generation, and Unification

The chronon approach sheds new light on several conceptual puzzles of the Standard Model, notably the naturalness problem and the apparent arbitrariness of mass scales.

Naturalness

In conventional field theory, quantum corrections to scalar masses diverge quadratically, requiring fine-tuning of parameters. In CFT, there is no elementary scalar field; mass arises from finite misalignment energy in the causal medium. Because the curvature ${\mathrm{\Omega }}_{\mu \nu }$ is bounded by the Chronon Exclusivity Principle, all effective masses are automatically self-regularized:

$$m_{\mathrm{eff}}^2\propto J{\mathrm{\Omega }}_{max}^2<\infty .$$

This removes the hierarchy problem by construction: microscopic geometry enforces a natural cutoff.

Mass Generation

In the chronon picture, mass corresponds to localized curvature energy. A massive particle is a region of persistent causal twist, a soliton-like defect of the chronon field. Its rest energy is the minimal energy required to maintain that misalignment. In this sense, inertia itself is geometric—an expression of resistance to realignment within the causal medium.

Unification

At high energies, the distinction between spacetime curvature and internal gauge curvature disappears. The chronon field supports a unified geometric action:

$$S=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{J}{4}}{\mathrm{\Omega }}_{\mu \nu }^{AB}{\mathrm{\Omega }}_{AB}^{\mu \nu }+{\displaystyle \frac{\lambda }{2}}{({\mathrm{\Phi }}^A{\mathrm{\Phi }}_A+1)}^2\right],$$

where $A,B$ run over both external (spacetime) and internal (gauge) indices. At sufficiently high temperatures, internal and external orientations mix freely, yielding a symmetric unified phase. As the universe cools, the alignment freezes into partially locked subgroups, reproducing the hierarchy

$$SO(1,3)\times U\left(1\right)\times SU\left(2\right)\times SU\left(3\right)$$

as residual symmetries of the chronon condensate.

Summary:

• Gauge fields arise as holonomies of internal chronon rotations.
• Electroweak symmetry breaking results from spontaneous causal alignment, not from a separate Higgs field.
• Confinement emerges from quantized causal flux tubes.
• All mass scales and coupling constants are self-regularized through finite chronon curvature.
• Gravity and gauge forces unify as different projections of a single geometric field.

Chronon Field Theory thus reframes the Standard Model: the four fundamental interactions are no longer distinct forces, but four manifestations of one underlying principle— the geometry of causal alignment.

A detailed account of how the chronon field’s internal orientation gives rise to the full $SU\left(3\right)\times SU\left(2\right)\times U\left(1\right)$ gauge hierarchy is presented in Appendix C.

6. Quantum Foundations and the Nature of Measurement

At its heart, quantum theory describes a world governed by probabilities rather than certainties. Particles exist in superpositions, and measurement appears to convert possibilities into facts. Chronon Field Theory (CFT) provides a new physical interpretation of this mystery: quantum probabilities are not fundamental indeterminacies, but statistical expressions of microscopic fluctuations in causal alignment. Measurement, in turn, is the irreversible absorption of causal flux into macroscopic domains. This section develops the quantum interpretation of CFT, showing how quantum mechanics arises naturally from the dynamics of the chronon field without requiring ad hoc postulates such as wavefunction collapse.

6.1. Chronon Fluctuations as the Origin of Quantum Probabilities

In the chronon picture, every spacetime point contains a microscopic causal vector ${\mathrm{\Phi }}^{\mu }\left(x\right)$ whose orientation fluctuates due to thermal and geometric noise. While the mean field $\langle {\mathrm{\Phi }}^{\mu }\rangle$ defines the macroscopic arrow of time, small fluctuations $\delta {\mathrm{\Phi }}^{\mu }={\mathrm{\Phi }}^{\mu }-\langle {\mathrm{\Phi }}^{\mu }\rangle$ represent local uncertainty in causal direction.

These fluctuations are governed by the stochastic equation

$$J{\nabla }^2{\mathrm{\Phi }}^{\mu }+\lambda ({\mathrm{\Phi }}_{\nu }{\mathrm{\Phi }}^{\nu }+1){\mathrm{\Phi }}^{\mu }={\xi }^{\mu }\left(x\right),$$

where ${\xi }^{\mu }$ is a random noise term satisfying $\langle {\xi }^{\mu }\left(x\right){\xi }^{\nu }\left(x^{\prime }\right)\rangle \propto {\delta }^{\mu \nu }\delta (x-x^{\prime })$. The resulting distribution of possible orientations defines a probability density on the configuration space of ${\mathrm{\Phi }}^{\mu }$. The phase coherence among neighboring chronons is not perfect, so causal propagation is inherently probabilistic at microscopic scales.

The key insight is that quantum uncertainty arises not from incompleteness of knowledge, but from the intrinsic stochasticity of the chronon field. Each particle trajectory corresponds to a bundle of chronon paths whose microscopic alignment fluctuates randomly, producing a diffusion in causal phase that we observe as quantum randomness.

Analogy: In Brownian motion, a pollen grain’s erratic motion arises from microscopic collisions with unseen molecules. In CFT, a particle’s probabilistic behavior arises from continual interactions with the fluctuating causal medium.

Mathematically, this leads to a diffusion equation for the probability current:

$${\partial }_t\rho +\nabla ·\left(\rho {\mathbf{v}}_{\mathrm{\Phi }}\right)=D_{\mathrm{\Phi }}{\nabla }^2\rho ,$$

where $\rho$ is the probability density and $D_{\mathrm{\Phi }}$ is the causal diffusion coefficient set by chronon noise amplitude. When rewritten in complex form, this becomes equivalent to the Schrödinger equation, with ${\hslash }_{\mathrm{geom}}$ emerging as the diffusion constant linking energy and phase evolution.

6.2. Quantization as Curvature-Phase Alignment

Quantization in CFT arises from the discrete nature of causal curvature. As the chronon field aligns, small rotational misfits accumulate into quantized loops, each carrying a fixed symplectic flux

$$\oint {\mathrm{\Phi }}_{\mu }d{x}^{\mu }=n{\hslash }_{\mathrm{geom}},$$

where ${\hslash }_{\mathrm{geom}}$ is the emergent quantum of causal action. The integer n labels distinct stable topological modes of the chronon field, analogous to quantized vortices in a superfluid or flux quanta in a superconductor.

The phase of a quantum wavefunction corresponds to the accumulated causal rotation along a path:

$$\theta \left(x\right)={\int }^x{\mathrm{\Phi }}_{\mu }d{x}^{\mu }.$$

Changes in this phase generate interference, while its quantization ensures that physical states are single-valued. Thus, quantum mechanics emerges as the kinematic description of phase-coherent chronon alignment. Each “particle” is a coherent region of the causal field whose internal phase rotates at a frequency proportional to its rest energy:

$$E={\hslash }_{\mathrm{geom}}\dot{\theta }.$$

This recovers the de Broglie relation from first principles.

Physical Picture:

Matter waves are not mysterious probability clouds, but standing waves of causal phase within the chronon medium. Quantized energy levels arise when the total phase rotation around a closed orbit equals an integer multiple of $2\pi$. The Bohr–Sommerfeld condition, in this framework, is simply the geometric requirement for stable causal alignment.

6.3. Born Rule from Stochastic Absorption

In standard quantum mechanics, the Born rule states that the probability of obtaining an outcome $a_i$ is $P\left(a_i\right)={\left|\langle a_i|\psi \rangle \right|}^2$. In Chronon Field Theory (CFT), this law emerges dynamically from the stochastic absorption of microscopic chronon orientations into stabilized apparatus eigen–domains.

At the measurement interface $\mathrm{\Gamma }$, the chronon field of the microscopic domain $\mathrm{\Omega }$ couples locally to the macroscopic alignment field ${\mathrm{\Phi }}_A^{\mu }$ of the apparatus. Each eigen–domain ${\mathrm{\Gamma }}_i\subset \mathrm{\Gamma }$ defines a distinct alignment channel, and the coarse–grained overlaps

$$p_i\left(t\right)={\displaystyle \frac{S_i\left(t\right)}{{\sum }_j{S}_j\left(t\right)}},S_i\left(t\right)={\int }_{{\mathrm{\Gamma }}_i}f\left(s(x,t)\right)d{\sigma }_{\gamma }\left(x\right),$$

form a diffusion process on the outcome simplex ${\Delta }_{m-1}$, with $s(x,t)=-g_{\mu \nu }{\mathrm{\Phi }}_A^{\mu }{\mathrm{\Phi }}^{\nu }$ the local alignment scalar and $f\left(r\right)$ a monotone gain function.

Under detailed balance and fluctuation–dissipation at the interface, the effective macroscopic dynamics of $p\left(t\right)$ reduces to a neutral Wright–Fisher diffusion

$$d{p}_i=\sum _j\sqrt{\alpha ({\delta }_{ij}-p_j)}\sqrt{p_i}d{W}_{ij},$$

with absorbing vertices $\left\{e_i\right\}$ and zero drift. Each coordinate $p_i\left(t\right)$ is therefore a bounded martingale up to the absorption time $\tau$, and by optional stopping,

$$P\left(p\left(\tau \right)=e_i\right)=E\left[p_i\left(\tau \right)\right]=E\left[p_i\left(0\right)\right]=p_i\left(0\right).$$

If the initial overlaps coincide with the system’s amplitude weights $p_i\left(0\right)={\left|c_i\right|}^2$, the absorption probabilities reproduce the Born rule.

Thus, the Born statistics arise as a law of stochastic absorption: macroscopic apparatus domains record outcomes in proportion to the incoming density of causal coherence, without invoking external collapse postulates. Measurement is the irreversible alignment of microscopic causal flux into one stabilized eigen–domain of the apparatus.

Analogy: Just as the absorbed intensity of light is proportional to the square of its field amplitude, the likelihood of an outcome in CFT is proportional to the square of the causal–phase amplitude that aligns with the apparatus domain.

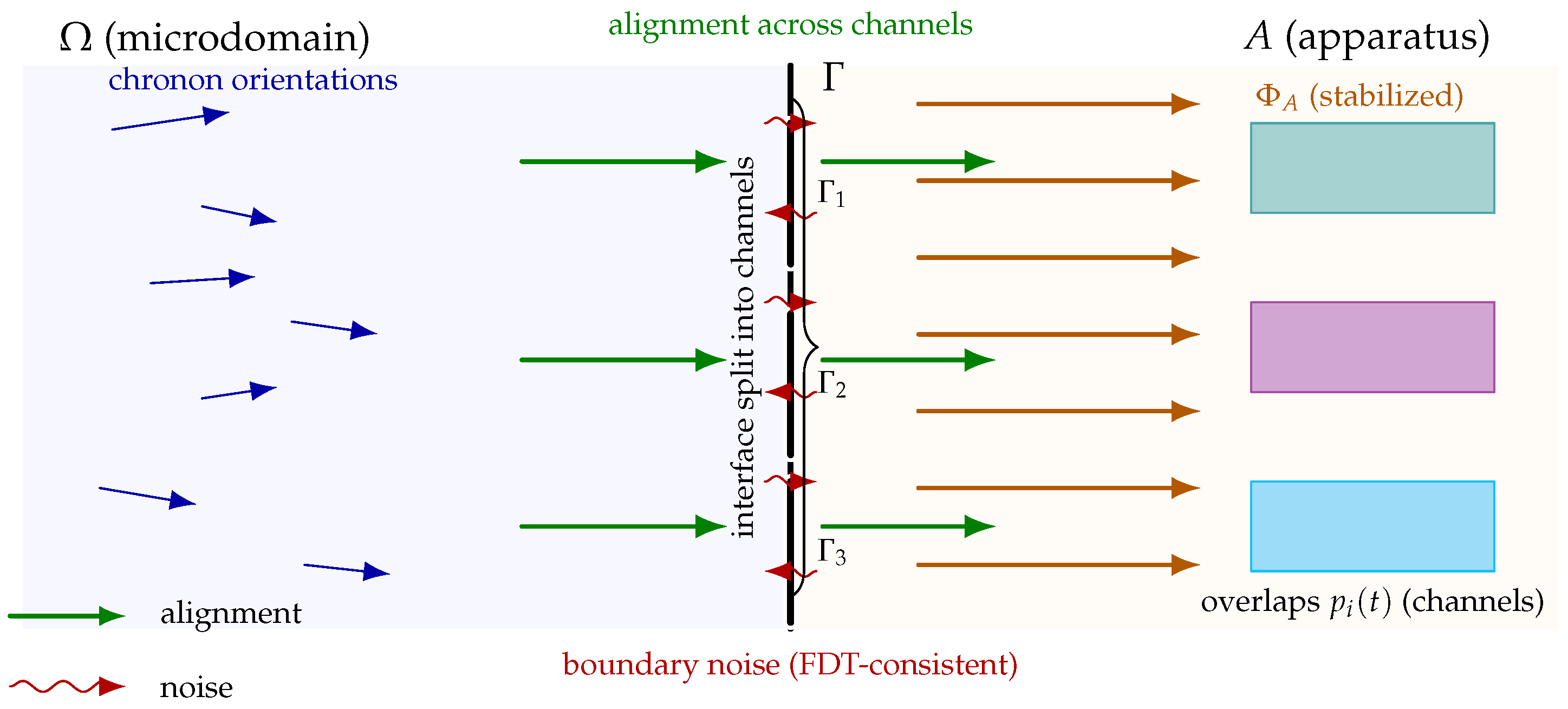
Figure 4. Causal absorption across a chronon–apparatus interface. The microscopic causal field in $\mathrm{\Omega }$ (left) aligns irreversibly with the stabilized macroscopic field ${\mathrm{\Phi }}_A$ in A (right) through the boundary $\mathrm{\Gamma }$, partitioned into channels ${\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2,{\mathrm{\Gamma }}_3$. Solid green arrows show alignment flux across each channel, while wavy red arrows represent boundary fluctuations consistent with the fluctuation–dissipation relation. Bars on the right depict the emergent overlap probabilities $p_i\left(t\right)\propto {\left|\psi \right|}^2$ for each channel. The interface thus functions as a stochastic absorber that converts microscopic phase coherence into macroscopic outcome statistics.

Figure 4. Causal absorption across a chronon–apparatus interface. The microscopic causal field in $\mathrm{\Omega }$ (left) aligns irreversibly with the stabilized macroscopic field ${\mathrm{\Phi }}_A$ in A (right) through the boundary $\mathrm{\Gamma }$, partitioned into channels ${\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2,{\mathrm{\Gamma }}_3$. Solid green arrows show alignment flux across each channel, while wavy red arrows represent boundary fluctuations consistent with the fluctuation–dissipation relation. Bars on the right depict the emergent overlap probabilities $p_i\left(t\right)\propto {\left|\psi \right|}^2$ for each channel. The interface thus functions as a stochastic absorber that converts microscopic phase coherence into macroscopic outcome statistics.

6.4. Relation to de Broglie Waves and Path Integrals

The chronon field provides a natural geometric interpretation for the de Broglie relations and the Feynman path integral. Each chronon thread carries a local phase $\theta \left(x\right)$ proportional to its integrated causal action:

$$\theta \left(x\right)={\displaystyle \frac{1}{{\hslash }_{\mathrm{geom}}}}\int {\mathrm{\Phi }}_{\mu }d{x}^{\mu }.$$

A macroscopic object consists of a large ensemble of chronon paths, and their collective interference produces the observed wave-like phenomena.

In the Feynman path integral formalism, the amplitude for a system to evolve from point $x_i$ to $x_f$ is

$$\mathcal{A}(x_i\to x_f)=\int \mathcal{D}\left[x\left(t\right)\right]e^{iS\left[x\right]/\hslash }.$$

In CFT, this becomes a sum over possible chronon configurations:

$$\mathcal{A}=\int \mathcal{D}\left[\mathrm{\Phi }\right]e^{i\int {\mathrm{\Phi }}_{\mu }d{x}^{\mu }/{\hslash }_{\mathrm{geom}}}.$$

Each configuration contributes a phase proportional to its causal length. Constructive interference occurs where chronon paths remain phase-aligned, leading to classical trajectories; destructive interference suppresses others. The principle of least action thus emerges as the condition for maximal causal coherence, not as a separate postulate.

Geometric Picture:

A “quantum path” is a ripple of causal alignment, and the path integral sums over all microscopic ways to connect cause and effect. The classical limit corresponds to coherent reinforcement of the most phase-stable causal trajectory.

This provides a striking reinterpretation of quantum mechanics: the wavefunction does not describe a mysterious abstract probability cloud, but a coarse-grained measure of phase coherence across a causal network.

6.5. How CFT Resolves the Wavefunction–Collapse Paradox

The most perplexing feature of standard quantum theory is the measurement problem: how and why a superposition of quantum states “collapses” into a definite outcome. In CFT, collapse is not an instantaneous, non-physical process, but the natural consequence of irreversible causal absorption.

A “superposition” corresponds to a state of partial chronon alignment: multiple potential orientations of ${\mathrm{\Phi }}^{\mu }$ coexist, each representing a possible outcome channel. When a microscopic system interacts with a macroscopic detector, chronon coherence begins to synchronize with the detector’s large-scale causal field. Because the detector is massive, its causal orientation dominates; microscopic fluctuations are absorbed and phase information is lost. This process is mathematically equivalent to decoherence, but with a clear physical substrate: the alignment of causal direction.

The transition from superposition to outcome is continuous and causal:

$${\displaystyle \frac{d{\mathrm{\Phi }}^{\mu }}{dt}}=-{\mathrm{\Gamma }}_{\theta }({\mathrm{\Phi }}^{\mu }-{\mathrm{\Phi }}_{\mathrm{mac}}^{\mu })+{\xi }^{\mu }\left(t\right),$$

where ${\mathrm{\Gamma }}_{\theta }$ measures the alignment rate toward the macroscopic causal field ${\mathrm{\Phi }}_{\mathrm{mac}}^{\mu }$, and ${\xi }^{\mu }$ represents stochastic noise. As ${\mathrm{\Gamma }}_{\theta }t\gg 1$, the microscopic state locks irreversibly into the detector’s orientation. The apparent “collapse” is therefore a relaxation to the nearest stable causal attractor in phase space.

This interpretation resolves long-standing paradoxes:

• The collapse is not instantaneous or observer-dependent, but a dynamical process of causal synchronization.
• Probability arises from microscopic fluctuations, not epistemic ignorance.
• The boundary between quantum and classical regimes is determined by the strength of causal coupling ${\mathrm{\Gamma }}_{\theta }$, not by measurement per se.

In summary:

• Quantum randomness originates from chronon fluctuations.
• Quantization follows from discrete symplectic curvature.
• The Born rule reflects the density of causal-phase absorption.
• The path integral arises from summing over causal trajectories.
• Measurement is a causal realignment, not a mystical collapse.

CFT thus transforms the philosophical foundations of quantum theory into a concrete physical mechanism: probability, coherence, and measurement all emerge from the dynamics of an underlying causal medium. In this sense, quantum mechanics is not the deepest layer of nature, but the visible shadow of a deeper geometry of causation.

7. Resolution of Iconic Quantum Paradoxes

Chronon Field Theory (CFT) not only provides a coherent ontological foundation for quantum dynamics, but also resolves several of the most historically perplexing paradoxes in quantum mechanics. Each paradox stems from the attempt to interpret quantum phenomena within the fixed background of classical geometry. In CFT, by contrast, quantum effects arise naturally from the sub-geometric dynamics of chronon alignment and pre-foliated causal order. This section addresses four canonical examples—entanglement, the double-slit experiment, Schrödinger’s cat, and quantum tunneling—and shows how each finds a natural resolution in the geometry of the chronon field.

7.1. Measurement and Chronon Alignment

In Chronon Field Theory, measurement is not a mysterious collapse of the wavefunction, but a geometric process of causal alignment. A quantum system corresponds to a locally bounded ensemble of chronons whose internal configuration defines a microscopic chronon field ${\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }\left(x\right)$. This field possesses its own intrinsic bias distribution—a directional preference in chronon orientation that encodes the system’s potential for observable properties such as momentum, spin, or energy. Prior to measurement, however, this microscopic bias is not synchronized with the collective bias of the measuring apparatus. The two therefore inhabit distinct alignment domains: the system remains in a pre-foliated, sub-geometric phase where the notions of position, simultaneity, and trajectory are undefined.

By contrast, the measuring apparatus and the observer exist within a collectively bias-aligned phase. Although each fine-grained component of the apparatus is itself a quantum subdomain governed by local chronon dynamics, the biases of all these subdomains have become synchronized through persistent causal coupling and environmental coherence. Coarse-graining over this synchronized network of chronons yields a stable metric tensor $g_{\mu \nu }$, a well-defined proper-time direction, and an emergent foliation ${\mathrm{\Sigma }}_t$ that supports classical causal structure.

Measurement therefore represents the synchronization of biases: the progressive entrainment of the quantum system’s internal chronon bias to the collective bias of the macroscopic apparatus. Through this process, the microscopic field ${\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }\left(x\right)$ becomes phase-locked with ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }\left(x\right)$, and the system acquires a definite embedding within the observer’s spacetime frame. This alignment defines what we perceive as the outcome of measurement.

In conventional quantum mechanics, the sudden reduction of a wavefunction appears acausal and discontinuous. In CFT, the same phenomenon is reinterpreted as a continuous process of geometric synchronization—a gradual phase-locking of causal structure between microscopic and macroscopic domains. Measurement, in this view, is not the destruction of quantum potentiality but its coherent integration into the classical causal order.

7.1.1. Pre-Alignment Dynamics

Let $\rho (x,\theta )$ denote the local orientation distribution of chronons, where $\theta \in S^2$ parameterizes the direction ${\widehat{v}}^{\mu }\left(\theta \right)$ of each microscopic chronon thread:

$$X^{\mu }\left(x\right)=\left|X\right|{\widehat{v}}^{\mu }\left(\theta \right),{\widehat{v}}^{\mu }\left(\theta \right){\widehat{v}}_{\mu }\left(\theta \right)=-1\mathrm{or}0.$$

(1)

The coarse-grained chronon field is then recovered as an orientation average,

$${\mathrm{\Phi }}^{\mu }\left(x\right)={\int }_{S^2}\rho (x,\theta ){\widehat{v}}^{\mu }\left(\theta \right)d\mathrm{\Omega }\left(\theta \right).$$

(2)

When $\rho (x,\theta )$ is isotropic or multimodal, no preferred orientation exists and the vector average nearly vanishes, ${\mathrm{\Phi }}^{\mu }\left(x\right)\approx 0$. Such a region has no well-defined local time direction and thus no embedding in a classical spacetime. Quantum systems in this state evolve not within spacetime, but in a pre-geometric configuration space where temporal order and locality are emergent rather than fundamental.

7.1.2. Chronon Entrainment and the Emergence of Localization

Measurement corresponds to a process of chronon entrainment—a causal alignment between the quantum system’s chronon field ${\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }\left(x\right)$ and the ambient macroscopic field ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }\left(x\right)$ of the measuring apparatus. During interaction or decoherence, the microscopic field gradually evolves as

$${\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }\left(x\right)⟶{\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }\left(x\right)+{\delta }^{\mu }\left(x\right),$$

(3)

where ${\delta }^{\mu }\left(x\right)$ represents residual misalignment that vanishes once full coherence is established. This alignment process increases the local magnitude $|{\mathrm{\Phi }}^{\mu }\left(x\right)|$, signaling the emergence of a stable causal orientation.

Only after sufficient entrainment does the system acquire a well-defined embedding within a classical foliation ${\mathrm{\Sigma }}_t$. At that stage it can be meaningfully localized—that is, assigned a position and time relative to the observer’s geometry. Spatial localization therefore arises as a by-product of chronon coherence: it is not a primitive attribute of matter, but a geometric property of causal alignment.

From this viewpoint, the apparent “collapse” of the wavefunction is reinterpreted as a transition from an indeterminate pre-foliated phase to a coherent geometric embedding. Phenomena such as delocalization, tunneling, and nonlocal correlations reflect the system’s freedom to explore chronon configurations not yet anchored to any macroscopic foliation. Measurement terminates this freedom by enforcing alignment with the environment’s causal order.

Thus, in CFT, observation is a dynamical act of geometry itself: the synchronization of microscopic causal threads with the macroscopic temporal fabric that defines classical spacetime.

7.2. Entanglement and Nonlocal Correlation

In standard quantum mechanics, entangled systems exhibit correlations that appear instantaneous and nonlocal: measurement of one particle seemingly determines the state of its distant partner. In Chronon Field Theory, however, such correlations do not require superluminal influence. They arise from the persistence of a shared chronon bias field established at the moment of joint preparation.

An entangled pair originates from a common chronon ensemble in which the local orientation biases of the two subsystems are synchronized. Each subsystem carries its own microscopic chronon field ${\mathrm{\Phi }}_{\mathrm{A}}^{\mu }\left(x\right)$ and ${\mathrm{\Phi }}_{\mathrm{B}}^{\mu }\left(x\right)$, but both are embedded within a single extended bias domain ${\mathcal{B}}_{\mathrm{AB}}$ that preserves correlation across all its threads. Prior to measurement, the pair therefore exists in a pre-foliated state where spatial separation has no invariant meaning; the chronon connections linking A and B are part of a continuous causal substrate rather than two disjoint locations in spacetime.

When a measurement is performed on subsystem A, the local chronon field ${\mathrm{\Phi }}_{\mathrm{A}}^{\mu }\left(x\right)$ becomes entrained to the apparatus’s macroscopic field ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }\left(A\right)$ through bias synchronization, as described in Section 7.1. Because A and B share a common chronon ancestry, the same global bias field ${\mathcal{B}}_{\mathrm{AB}}$ constrains the possible orientations at B. The local entrainment at A therefore induces a coherent reconfiguration of chronon orientations at B, not through transmission of a signal, but through the conservation of their shared bias correlation.

Figure 5. Chronon-based view of entanglement. Two measurement regions (A and B) originate from a single chronon ensemble with a shared bias field ${\mathcal{B}}_{\mathrm{AB}}$. When region A synchronizes with its macroscopic field, region B’s chronon orientations reconfigure coherently through the conserved bias correlation, without any exchange of signals or energy.

Figure 5. Chronon-based view of entanglement. Two measurement regions (A and B) originate from a single chronon ensemble with a shared bias field ${\mathcal{B}}_{\mathrm{AB}}$. When region A synchronizes with its macroscopic field, region B’s chronon orientations reconfigure coherently through the conserved bias correlation, without any exchange of signals or energy.

This view replaces “spooky action at a distance’’ with a fully causal geometric mechanism. Entanglement correlations are maintained by bias synchronization across a continuous chronon substrate that existed prior to macroscopic separation. Each subsystem retains a local bias potential linked to the same conserved alignment field, ensuring that when one domain synchronizes with the macroscopic foliation, the other must settle into a compatible configuration.

In this way, CFT preserves strict locality at the fundamental level: alignment adjustments propagate through existing chronon connections rather than through spacetime itself. The apparent instantaneous correlations arise only when described from the emergent, classical foliation where the pre-foliated continuity of chronon bias has already been lost.

A more formal treatment of this mechanism is presented in Appendix D, where the entangled pair is described by a conserved bias–overlap functional ${\mathcal{C}}_{AB}$ that quantifies the degree of chronon alignment between the two subsystems. Prior to measurement, ${\mathcal{C}}_{AB}$ remains invariant under skew-symmetric microscopic evolution, ensuring that the pair retains a single, continuous bias domain ${\mathcal{B}}_{AB}$ even when their emergent spacetime coordinates diverge. Measurement introduces alignment terms that synchronize one subsystem’s bias with its macroscopic environment, thereby conditioning the compatible bias of the distant subsystem through the conserved correlation field. This formulation makes explicit how CFT reproduces the statistical structure of quantum entanglement while preserving locality at the level of the underlying chronon dynamics.

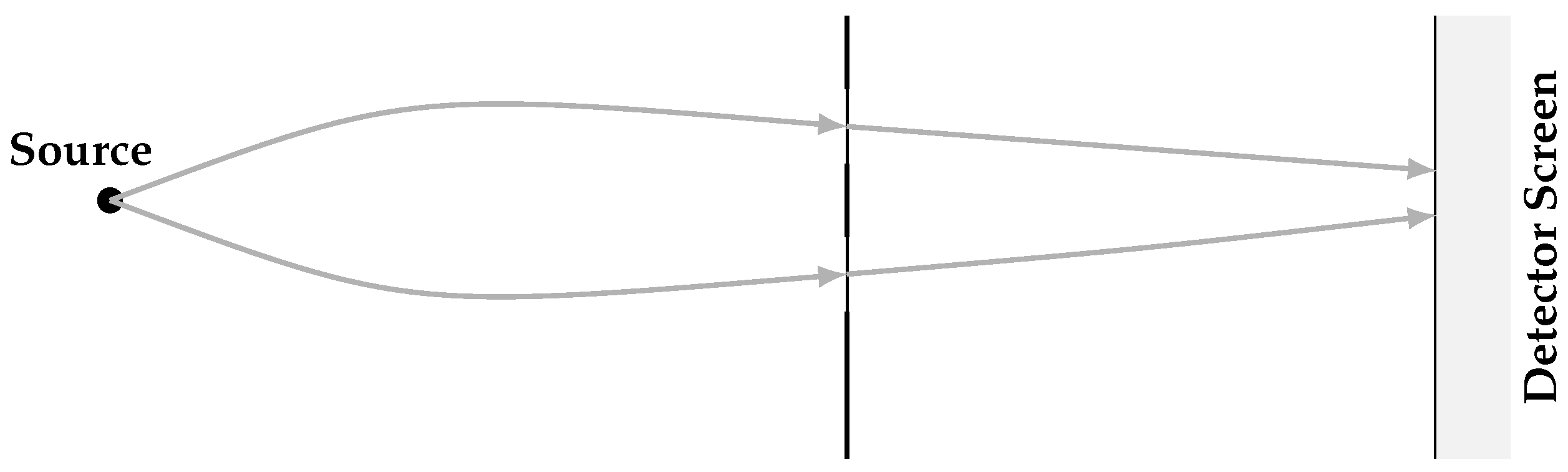
7.3. Double-Slit Interference

The double-slit experiment reveals interference patterns even when particles pass through the apparatus one at a time. Classically, a particle must choose one slit; quantum mechanically, it appears to traverse both. In Chronon Field Theory, this paradox is resolved by recognizing that before detection, the system is not yet embedded in any classical foliation ${\mathrm{\Sigma }}_t$. Its chronon ensemble exists in a pre-foliated phase where spatial separation and trajectory are undefined. Each chronon thread explores bias-compatible paths through both slits, guided by its internal orientation distribution rather than by geometric position.

The interference pattern arises from the coherent superposition of chronon-thread amplitudes $e^{i\mathcal{S}\left[\mathcal{T}\right]/\hslash }$, whose phases remain synchronized with the macroscopic field ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$ of the detector. Constructive and destructive interference thus reflect how the microscopic bias field of the particle couples to the global bias structure of the experimental apparatus. Where phase alignment is maintained, the detector records maxima; where misalignment accumulates, destructive interference produces minima. In this view, the familiar fringe pattern encodes the causal coherence of chronon orientation across multiple bias-compatible trajectories.

Figure 6. Chronon threads in the double-slit experiment. Prior to measurement, chronon threads explore both slits as bias-compatible trajectories. Interference arises from coherent phase alignment across the ensemble. A which-path measurement locks the chronon bias to a single foliation, destroying coherence and eliminating the interference pattern.

Figure 6. Chronon threads in the double-slit experiment. Prior to measurement, chronon threads explore both slits as bias-compatible trajectories. Interference arises from coherent phase alignment across the ensemble. A which-path measurement locks the chronon bias to a single foliation, destroying coherence and eliminating the interference pattern.

A which-path measurement introduces interaction with an external apparatus whose chronon field is already bias-synchronized. This entrains the particle’s microscopic bias ${\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }$ to a single macroscopic alignment channel ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$, breaking phase coherence among competing trajectories. Once the system’s bias synchronizes with a specific foliation, interference vanishes: the chronon ensemble now evolves within a single causal geometry rather than exploring the full bias manifold.

In this way, CFT explains both the appearance and disappearance of interference as natural consequences of bias synchronization and its loss. Interference reflects coherent pre-foliated dynamics; measurement corresponds to geometric entrainment, where potential trajectories collapse into a single synchronized causal domain.

For technical readers, a detailed mathematical treatment of this mechanism is provided in Appendix E, where the interference pattern is derived from a bias–coherence functional that quantifies the phase-weighted alignment between the system’s microscopic chronon field and the detector’s macroscopic bias. The formalism shows how fringe visibility depends on the inter-path bias overlap $\kappa$ and how which-path synchronization exponentially suppresses this overlap, thereby eliminating interference. This appendix makes explicit how CFT translates the qualitative picture of chronon-thread coherence into a quantitative framework consistent with observed quantum statistics.

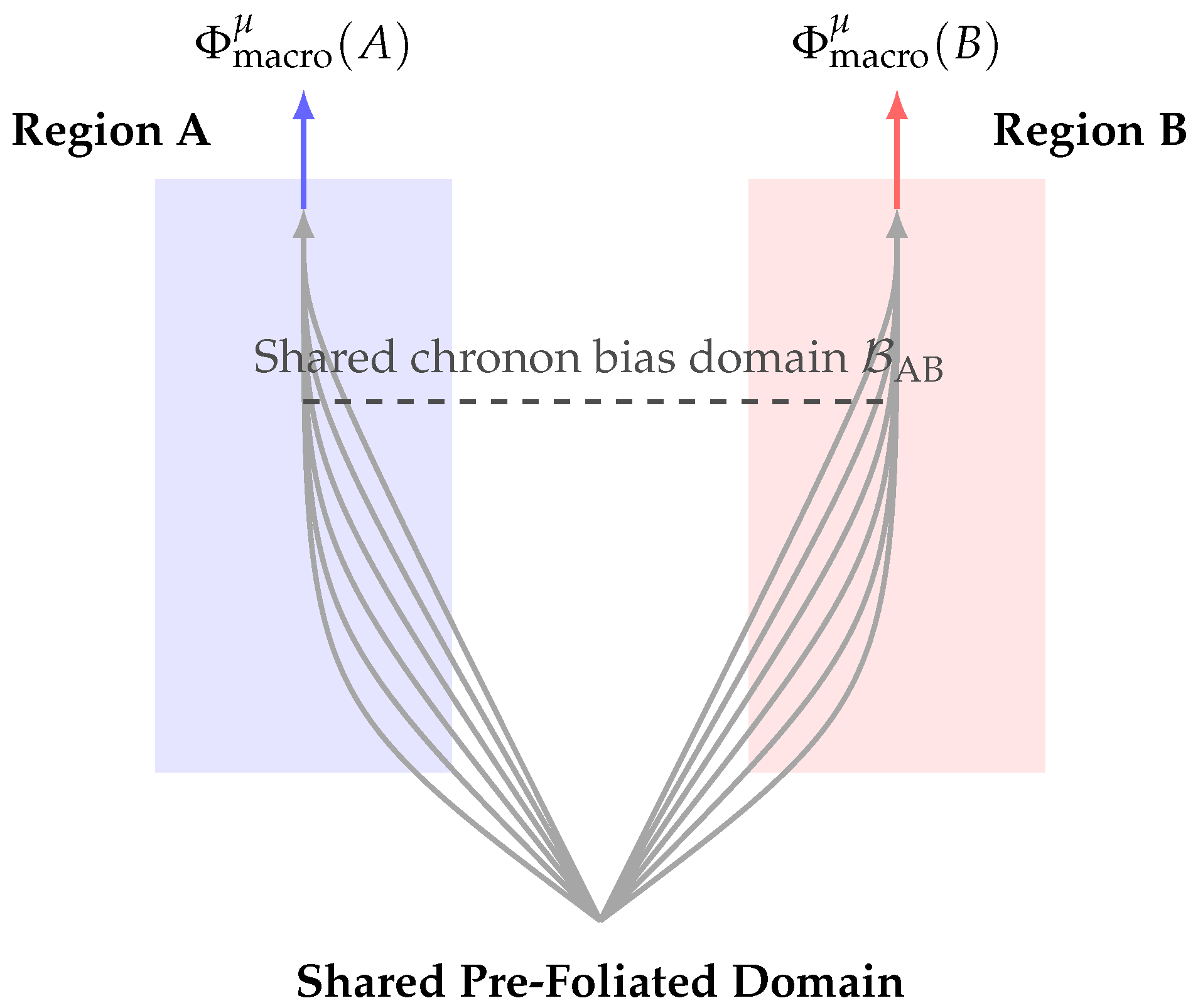
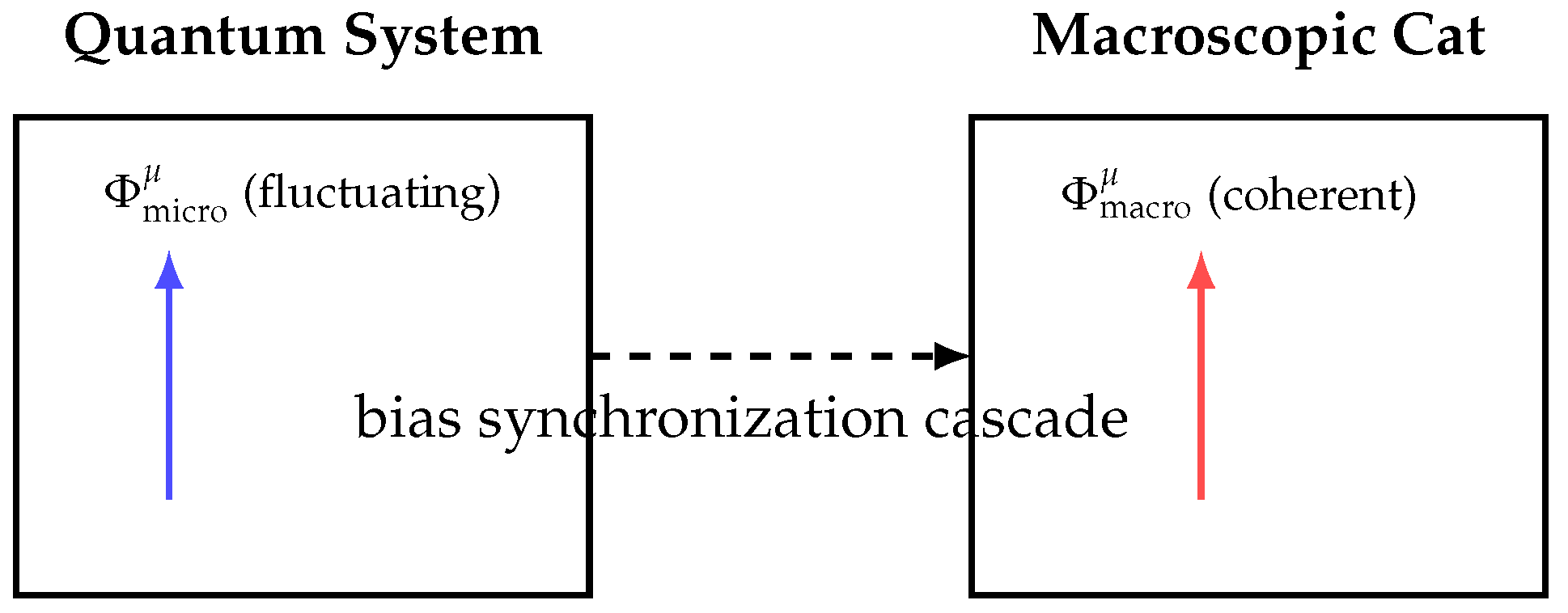
7.4. Schrödinger’s Cat

The Schrödinger’s cat thought experiment questions the boundary between quantum and classical domains by proposing a macroscopic superposition of “alive” and “dead” states linked to a microscopic quantum event. In Chronon Field Theory, this paradox dissolves through the mechanism of hierarchical bias synchronization—a continuous geometric process in which chronon fields at progressively larger scales become causally aligned.

Microscopic systems such as radioactive atoms inhabit regions where their local chronon field ${\mathrm{\Phi }}_{\mathrm{micro}}^{\mu }$ is weakly coherent and its internal bias fluctuates across orientations. Such systems lack a well-defined geometric embedding: they exist in the pre-foliated regime, where classical notions of simultaneity and position are undefined. In contrast, macroscopic bodies like the cat and the surrounding apparatus occupy regions of strong chronon coherence ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$, whose synchronized bias network defines a stable metric $g_{\mu \nu }$ and a persistent foliation ${\mathrm{\Sigma }}_t$.

The chain of physical couplings—radioactive decay, detector trigger, relay mechanism, and poison release—constitutes a geometric alignment cascade. Each stage transmits bias synchronization outward, enlarging the domain of coherent alignment. The microscopic field ${\mathrm{\Phi }}_{\mathrm{micro}}^{\mu }$ becomes entrained to the macroscopic ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$ through successive interactions:

$${\mathrm{\Phi }}_{\mathrm{micro}}^{\mu }\stackrel{\mathrm{detector}}{\to }{\mathrm{\Phi }}_{\mathrm{device}}^{\mu }\stackrel{\mathrm{environment}}{\to }{\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }.$$

This process converts local bias fluctuation into global bias coherence, yielding a definite classical outcome without invoking discontinuous collapse.

Figure 7. CFT resolution of Schrödinger’s Cat. The microscopic chronon field begins in a fluctuating, weakly coherent state. Through successive interactions with the detector, device, and environment, its bias becomes synchronized with the macroscopic field ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$ defining the classical foliation. The apparent superposition resolves via continuous geometric alignment, not discontinuous collapse.

Figure 7. CFT resolution of Schrödinger’s Cat. The microscopic chronon field begins in a fluctuating, weakly coherent state. Through successive interactions with the detector, device, and environment, its bias becomes synchronized with the macroscopic field ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$ defining the classical foliation. The apparent superposition resolves via continuous geometric alignment, not discontinuous collapse.

Hence, the cat is never in a true physical superposition. The apparent indeterminacy arises only because the microscopic chronon field remains pre-aligned and unsynchronized with the macroscopic bias network. Once causal contact initiates the alignment cascade, the system rapidly settles into a single foliation-compatible outcome, defined by the dominant macroscopic bias orientation. CFT thus explains the quantum-to-classical transition as a multi-scale synchronization of bias coherence, where microscopic indeterminacy resolves naturally through progressive entrainment into the global causal geometry.

A quantitative formulation of this hierarchical synchronization process is presented in Appendix F, where the dynamics of bias entrainment are modeled by a diffusion–relaxation equation and illustrated through the growth of coherence length and multi-scale alignment cascade from microscopic to macroscopic domains.

7.5. Tunneling and Classically Forbidden Transitions

Quantum tunneling describes transitions through potential barriers that are classically impenetrable. In Chronon Field Theory, such barriers exist only within regions where the chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$ is coherently aligned, and thus capable of defining distinct spatial domains. A system that is not yet synchronized with this macroscopic foliation does not experience the barrier as an absolute geometric constraint. Instead, its chronon threads may explore bias-compatible trajectories that connect the two sides through the underlying pre-foliated configuration space.

Tunneling therefore corresponds to chronon threads that bridge two coherently aligned regions across an intermediate zone of geometric incoherence. Within this misaligned region, ${\mathrm{\Phi }}^{\mu }$ fluctuates and fails to define stable causal orientation. Chronon trajectories crossing such zones remain geometrically permissible but are entropically suppressed: the probability of maintaining coherent bias alignment across a misaligned domain falls exponentially with its geometric disorder.

Figure 8. Chronon threads and tunneling. In Chronon Field Theory, tunneling occurs when chronon threads connect two coherently aligned regions across a domain where ${\mathrm{\Phi }}^{\mu }$ is incoherent. These trajectories are geometrically admissible but entropically suppressed, yielding the familiar exponential tunneling law from purely causal–geometric principles.

Figure 8. Chronon threads and tunneling. In Chronon Field Theory, tunneling occurs when chronon threads connect two coherently aligned regions across a domain where ${\mathrm{\Phi }}^{\mu }$ is incoherent. These trajectories are geometrically admissible but entropically suppressed, yielding the familiar exponential tunneling law from purely causal–geometric principles.

Quantitatively, the tunneling amplitude can be expressed as an integral over all bias-compatible chronon trajectories $\mathcal{T}$ linking the two aligned regions:

$${\mathcal{A}}_{\mathrm{tun}}\propto {\int }_{\mathcal{T}}{e}^{-\mathcal{E}\left[\mathcal{T}\right]/{\hslash }_{\mathrm{geom}}}{e}^{i\mathcal{S}\left[\mathcal{T}\right]/{\hslash }_{\mathrm{geom}}}\mathcal{D}\mathcal{T},$$

(4)

where $\mathcal{E}\left[\mathcal{T}\right]$ quantifies the entropic cost of maintaining chronon alignment across the incoherent region. This cost increases with geometric disorder and misalignment entropy, reproducing the exponential suppression of transmission probability:

$$P_{\mathrm{tun}}\sim e^{-2{\mathcal{E}}_{min}/{\hslash }_{\mathrm{geom}}},$$

(5)

in direct analogy to the semiclassical WKB result, but now derived from bias-coherence principles rather than energy barriers.

Semiclassical WKB Analogy.

The WKB (Wentzel–Kramers–Brillouin) approximation provides the semiclassical bridge between quantum and classical dynamics. In this method, the wavefunction is written as

$$\psi \left(x\right)\sim A\left(x\right)e^{\frac{i}{\hslash }S\left(x\right)},$$

where the phase $S\left(x\right)$ satisfies the classical Hamilton–Jacobi equation ${\left({\partial }_{x}S\right)}^2=2m(E-V\left(x\right))$. This shows that quantum evolution corresponds to the accumulation of phase along classical trajectories.

In Chronon Field Theory, the propagation of chronon causal phase in slowly varying curvature obeys an analogous relation: the internal chronon phase plays the role of $S\left(x\right)$, and its transport condition reduces to a WKB-like connection between curvature, phase gradient, and action density. Thus, the semiclassical limit of CFT reproduces the classical action principle, with the chronon phase providing the geometric origin of the quantum action.

In this interpretation, tunneling does not represent motion through a classically forbidden region, but rather bias continuity across geometrically misaligned domains. The system’s chronon ensemble remains causally continuous—it simply traverses a region where the macroscopic foliation is undefined. Once re-synchronized with the coherent field beyond the barrier, the system re-emerges as a classically localized entity.

CFT thus reframes tunneling as a manifestation of coherence persistence through geometric disorder. The exponential law arises not from energy deficit, but from the probabilistic rarity of maintaining alignment across incoherent regions. What appears classically forbidden is, at the chronon level, a low-entropy but continuous path through the pre-foliated causal substrate.

In all four cases—entanglement, interference, superposition, and tunneling—Chronon Field Theory transforms quantum paradoxes into expressions of causal geometry. Quantum phenomena emerge as dynamic configurations of chronon bias coherence, while classical outcomes arise from large-scale synchronization of these biases into a single, stable foliation. No discontinuous collapse or superluminal influence is required—only the continuous evolution of a self-organizing causal field.

For technical readers detailed derivation of this geometric–entropic formulation is provided in Appendix G, where the tunneling amplitude is obtained from the bias–continuity functional $\mathcal{E}\left[\mathcal{T}\right]$ and shown to reproduce the standard WKB exponential as a special case of chronon alignment persistence through incoherent domains.

8. Chronon Stars: Finite-Core Black Holes

Black holes have long represented the boundary of known physics. In General Relativity (GR), they harbor singularities where curvature diverges and physical law breaks down. Chronon Field Theory (CFT) replaces this picture with a fully regular, causal one. Because spacetime curvature in CFT derives from the alignment of a finite-stiffness chronon field ${\mathrm{\Phi }}^{\mu }$, it can never diverge. Collapse beyond the classical Schwarzschild radius does not end in a singular point, but in a stable, saturated condensate of chronons: a chronon star. In this view, every astrophysical black hole is simply the macroscopic limit of such an object, while smaller ones exist as horizonless condensates. CFT thereby restores unitarity, information conservation, and finite curvature to gravitational physics.

8.1. From Singularities to Finite Causal Cores

In GR, gravitational collapse leads inevitably to diverging curvature at $r=0$. CFT replaces this singular endpoint with a finite causal core governed by the alignment field ${\mathrm{\Phi }}^{\mu }$. The local curvature is given by the symplectic form

$${\mathrm{\Omega }}_{\mu \nu }={\nabla }_{[\mu }{\mathrm{\Phi }}_{\nu ]},$$

whose magnitude measures microscopic twisting of causal direction. Because the field possesses finite alignment stiffness J, ${\mathrm{\Omega }}_{\mu \nu }$ cannot grow arbitrarily large. When gravitational compression drives ${\mathrm{\Omega }}_{\mu \nu }$ to its saturation value, the causal medium resists further contraction. Collapse therefore halts automatically, yielding a dense, self-stabilized core of maximally aligned chronons.

The interior of a chronon star is thus a coherent condensate of the causal field. Instead of an unphysical singularity, one obtains a finite, static domain of maximal curvature $R_{max}\sim {\mathrm{\Omega }}_{max}^2$ and characteristic radius $r_c\sim {\ell }_J=\sqrt{J/\lambda }$. The core is smooth, horizonless for small masses, and causally continuous at all scales.

Physical intuition: Gravity attempts to twist the causal medium beyond its stiffness, but the chronon field saturates—just as a superfluid stops vorticing beyond its critical angular velocity. The result is not an infinite curvature, but a perfectly finite causal knot.

8.2. Chronon Exclusivity Principle and Maximum Curvature

The Chronon Exclusivity Principle (CEP) underlies this finiteness: no two chronons can occupy the same causal orientation at the same point. It acts as a geometric analogue of the Pauli exclusion principle, imposing the bound

$${\mathrm{\Omega }}_{\mu \nu }{\mathrm{\Omega }}^{\mu \nu }\le {\mathrm{\Omega }}_{max}^2={\displaystyle \frac{1}{{\ell }_J^4}}.$$

Beyond this threshold, any further compression converts gravitational energy into isotropic geometric pressure,

$$p_{\mathrm{CEP}}={\displaystyle \frac{J}{4}}({\mathrm{\Omega }}_{max}^2-{\mathrm{\Omega }}^2),$$

which counteracts collapse. The CEP therefore supplies a self-generated causal stiffness that stabilizes spacetime itself. Curvature saturates but never diverges, ensuring that every gravitational core remains smooth and finite.

This same mechanism extends from microscopic condensates to astrophysical scales: all black holes are finite-core chronon stars with their central curvature locked at ${\mathrm{\Omega }}_{max}$.

8.3. Mass Scaling and Horizon Structure

Because curvature is capped by CEP, increasing mass does not increase core curvature; instead the core radius adjusts so that the internal curvature remains $\mathrm{\Omega }\simeq {\mathrm{\Omega }}_{max}$. The Schwarzschild radius $r_s=2GM/c^2$ and the CEP core scale $r_c$ define three regimes:

$$\begin{array}{cccc}\hfill r_s<r_c& \Rightarrow & \mathrm{horizonless}\mathrm{chronon}\mathrm{condensate},\hfill & (\mathrm{small}\mathrm{mass})\hfill \\ \hfill r_s=r_c& \Rightarrow & \mathrm{critical}\mathrm{threshold},\hfill & (\mathrm{onset}\mathrm{of}\mathrm{horizon})\hfill \\ \hfill r_s>r_c& \Rightarrow & \text{finite-core black hole},\hfill & (\mathrm{chronon}\mathrm{star}).\hfill \end{array}$$

For $r_s>r_c$ the exterior is Schwarzschild/Kerr while the interior is a finite, regular chronon condensate. For $r_s<r_c$ no horizon can form—CEP forbids further compression—yielding a cold, horizonless compact object.

Threshold Mass (Useful Rule of Thumb)

The onset of horizon formation occurs when $r_s=r_c$, i.e.

$$M_{★}\equiv {\displaystyle \frac{c^2{r}_c}{2G}}.$$

Objects with $M<M_{★}$ are horizonless condensates; with $M\gtrsim M_{★}$ they are finite-core (black-hole–like) chronon stars.

Smallest, Most Abundant Objects (Rough Scales)

Abundance is expected to peak near the threshold, since early-universe chronon domains with characteristic size $\sim r_c$ naturally produce condensates with $M\sim M_{★}$ (smaller domains disperse; much larger domains are rarer). Using $M_{★}=c^2{r}_c/\left(2G\right)$ gives the following illustrative benchmarks:

$$\begin{array}{ccc}\hfill r_c={10}^{-15}\mathrm{m}& \Rightarrow & M_{★}\approx 6.7\times {10}^{11}\mathrm{kg},\hfill \end{array}$$

These correspond (very roughly) to comet/asteroid-scale masses but with microscopic CEP cores of size r_c and no horizon (r_s < r_c). Such objects are natural, stable, non-luminous remnants and are plausible candidates for a cold subcomponent of dark matter.

Core Radius Above Threshold

For $M\gg M_{★}$, the core expands to keep curvature at the CEP cap,

$${\displaystyle \frac{GM}{c^2{R}_{\mathrm{core}}^3}}\sim {\mathrm{\Omega }}_{max}^2\Rightarrow R_{\mathrm{core}}\left(M\right)\sim {\left(\frac{GM}{c^2{\mathrm{\Omega }}_{max}^2}\right)}^{1/3},$$

while the exterior horizon grows as $r_s=2GM/c^2$. There is no upper mass limit: larger chronon stars remain finite-core and regular, with self-similar scaling.

Takeaway

(1) The smallest and most abundant chronon objects likely cluster near $M_{★}=c^2{r}_c/\left(2G\right)$ with radii $\sim r_c$ and no horizons; (2) all astrophysical “black holes” are the large-mass continuation ($M\gg M_{★}$) with $r_s>r_c$, finite cores, and GR exteriors. Determining $r_c$ (equivalently ${\mathrm{\Omega }}_{max}$) from microphysics fixes the absolute mass scale of this population.

8.4. Electromagnetic Suppression Inside Chronon Cores

In standard GR, the electromagnetic field of a charged black hole (Reissner–Nordström or Kerr–Newman solution) diverges at $r=0$, producing infinite field energy. Chronon Field Theory eliminates this divergence because the chronon condensate that forms the interior does not permit independent gauge flux lines.

Inside a chronon star, the causal field ${\mathrm{\Phi }}^{\mu }$ locks the local phase of the electromagnetic potential $A_{\mu }$ through the emergent gauge connection:

$$F_{\mu \nu }={\nabla }_{[\mu }{A}_{\nu ]}\propto {\mathrm{\Omega }}_{\mu \nu }\left(\mathrm{\Phi }\right)={\nabla }_{[\mu }{\mathrm{\Phi }}_{\nu ]}.$$

As the chronon alignment saturates at ${\mathrm{\Omega }}_{max}$, the symplectic curvature becomes uniform, and the internal region behaves as a perfectly aligned medium with vanishing effective field tensor:

$$F_{\mu \nu }^{\left(\mathrm{int}\right)}\to 0,{\nabla }_{\mu }{F}^{\mu \nu }=0.$$

This causal locking suppresses all free electromagnetic degrees of freedom. Charge separation cannot occur because any attempt to sustain an electric field would require differential rotation of chronon phases, forbidden by CEP.

Physically, the chronon core acts as a perfect electromagnetic insulator: its fully aligned causal structure leaves no room for independent $U\left(1\right)$ curvature. All net charge is expelled to a thin boundary layer at the surface $r=r_c$, where residual misalignment allows a small tangential polarization current. The resulting configuration resembles a Meissner-like effect: external field lines are expelled or smoothly terminate at the core boundary, ensuring finite total field energy.

$${\rho }_{\mathrm{EM},\mathrm{int}}\simeq {\displaystyle \frac{1}{8\pi }}{F}_{\mu \nu }{F}^{\mu \nu }⟶0(r<r_c).$$

Physical consequences:

• Chronon stars are electromagnetically dark: no internal charge density, no photon emission, and no divergent field energy.
• The external Reissner–Nordström or Kerr–Newman field matches smoothly onto a neutral, regular interior.
• The CEP therefore enforces both causal and electromagnetic regularization—gravity and electromagnetism reach a common finite limit.

In this sense, the chronon condensate represents a unified geometric vacuum state in which both spacetime curvature and electromagnetic curvature are saturated and stabilized. All long-range fields are confined to the exterior domain, leaving the interior causally ordered and electromagnetically silent.

8.5. Vacuum Structure and Hawking Radiation

In Chronon Field Theory, the vacuum is not a sea of virtual particles but a stable configuration of causal alignment. Quantum fields correspond to small excitations of this chronon medium, not to transient particle pairs fluctuating in and out of existence. Consequently, the Hawking process is reinterpreted as a finite-stiffness relaxation of causal curvature, not as pair creation across an event-horizon discontinuity.

Classical Hawking Picture

In semiclassical gravity, a stationary black hole of mass M radiates thermally with temperature

$$T_{\mathrm{H}}={\displaystyle \frac{\hslash c^3}{8\pi G{k}_{\mathrm{B}}M}},{\dot{M}}_{\mathrm{H}}=-\sigma A_{\mathrm{H}}{T}_{\mathrm{H}}^4\propto -M^{-2},$$

(6)

where $A_{\mathrm{H}}=4\pi r_{\mathrm{s}}^2$ is the horizon area. Because $T_{\mathrm{H}}\propto 1/M$, small black holes are predicted to heat up and evaporate catastrophically, producing a runaway divergence as $M\to 0$ [5].

CFT Reinterpretation: Flux from Symplectic Stress

In CFT, the horizon is a finite-thickness boundary layer where the chronon field ${\mathrm{\Phi }}^{\mu }$ connects the ordered interior to the exterior alignment. Emission is not particle pair creation but a coherent leakage of curvature-phase carried by symplectic waves. The relevant flux density is the symplectic stress component

$$T_{\mu \nu }^{\left(\mathrm{\Omega }\right)}={\displaystyle \frac{c^4}{8\pi G_{\mathrm{eff}}}}\left({\mathrm{\Omega }}_{\mu \alpha }{\mathrm{\Omega }}_{\nu }{{\mathrm{\Omega }}_{\nu }}^{\alpha }-{\displaystyle \frac{1}{4}}{g}_{\mu \nu }{\mathrm{\Omega }}_{\alpha \beta }{\mathrm{\Omega }}^{\alpha \beta }\right),$$

so the total outward power is the surface integral

$${\mathcal{L}}_{\mathrm{CFT}}=-{\displaystyle \frac{d\left(M{c}^2\right)}{dt}}={\oint }_{r=R_{\mathrm{core}}}{T}_{tr}^{\left(\mathrm{\Omega }\right)}dA={\displaystyle \frac{c^4}{8\pi G_{\mathrm{eff}}}}{\oint }_{r=R_{\mathrm{core}}}{\mathrm{\Omega }}_{t\alpha }{{\mathrm{\Omega }}_r}^{\alpha }dA.$$

(7)

Because the symplectic curvature $\mathrm{\Omega }$ is continuous across the interface, ${\mathcal{L}}_{\mathrm{CFT}}$ is finite and smooth: the boundary emits a steady, phase-coherent curvature flux. Unlike the semiclassical Hawking flux, this output is non-thermal: it retains phase correlations and, in principle, the full informational content of the interior chronon oscillations.

Stiffness-Limited Response (No True Temperature)

The boundary layer has a finite impedance to curvature-phase flow set by chronon stiffness J and coherence length ${\ell }_c$. Let the classical drive be the surface gravity $\kappa =c^4/\left(4GM\right)$ and define a chronon response scale ${\kappa }_{*}\sim c/{\ell }_c$. The emitted curvature amplitude is reduced by a universal response

$$\mathcal{S}\left(\kappa \right)={\displaystyle \frac{1}{\sqrt{1+{(\kappa /{\kappa }_{*})}^2}}},$$

so that near the surface ${\mathrm{\Omega }}_{t\alpha }\propto \kappa \mathcal{S}\left(\kappa \right)$. Substituting into (7) gives the luminosity

$${\mathcal{L}}_{\mathrm{CFT}}={\displaystyle \frac{c^4}{8\pi G_{\mathrm{eff}}}}{〈{\mathrm{\Omega }}_{t\alpha }{{\mathrm{\Omega }}_r}^{\alpha }〉}_A\propto A_{\mathrm{H}}{\kappa }^2\mathcal{S}{\left(\kappa \right)}^2,$$

(8)

with $A_{\mathrm{H}}$ the horizon area. Thus for large black holes ($\kappa \ll {\kappa }_{*}$) ${\mathcal{L}}_{\mathrm{CFT}}\propto {\kappa }^2{A}_{\mathrm{H}}$ (i.e., an $M^{-2}$ scaling) but with a strictly smaller coefficient than the Hawking prediction; and for small black holes ($\kappa \gg {\kappa }_{*}$) the response saturates $\left(\mathcal{S}\to 0\right)$ so the flux does not diverge. Any “effective temperature” one may define from ${\mathcal{L}}_{\mathrm{CFT}}$ is only a bookkeeping device; the spectrum is not thermal.

Information and Chronon Thermodynamics

Because the emitted flux (7) is generated by coherent symplectic waves, it preserves phase correlations rather than thermalizing them. At late times the flux decays as curvature waves dissipate and the system approaches global equilibrium, in accord with the second law of chronon thermodynamics: global symplectic entropy increases monotonically without loss of total information.

Mass Loss and Late-Time Equilibration

Writing $\dot{M}=-{\mathcal{L}}_{\mathrm{CFT}}/c^2$, the mass evolution is

$${\dot{M}}_{\mathrm{CFT}}=-\beta A_{\mathrm{H}}{\kappa }^2\mathcal{S}{\left(\kappa \right)}^2=-\beta {\displaystyle \frac{\left(4\pi r_{\mathrm{s}}^2\right)c^8}{{\left(4GM\right)}^2}}{\displaystyle \frac{1}{1+{(\kappa /{\kappa }_{*})}^2}},$$

(9)

for some dimensionless $\beta =\mathcal{O}\left(1\right)$ set by boundary microphysics. As the boundary layer approaches its equilibrium curvature ${\mathrm{\Omega }}_{\mathrm{eq}}$ the net drive vanishes and so does the flux:

$$\underset{t\to \infty }{lim}{\mathrm{\Omega }}_{\mathrm{surf}}\to {\mathrm{\Omega }}_{\mathrm{eq}},\underset{t\to \infty }{lim}{\mathcal{L}}_{\mathrm{CFT}}=0,\underset{t\to \infty }{lim}{\dot{M}}_{\mathrm{CFT}}=0.$$

Thus evaporation halts, leaving a cold, long-lived chronon remnant.

Physical Interpretation

Because the curvature energy density is bounded (${\rho }_{\mathrm{\Omega }}\le J/{\ell }_c^2$), the emission rate is self-limiting and finite for all masses. Radiation ceases when the horizon curvature relaxes to equilibrium. Chronon stars therefore do not evaporate into white holes: small ones settle into cold, long-lived remnants, providing a natural population of stable compact objects that may contribute to dark matter.

Summary

The CFT-corrected law replaces the divergent $T\propto 1/M$ behavior by a stiffness-limited plateau:

$$T_{\mathrm{CFT}}\to T_{\mathrm{sat}},{\dot{M}}_{\mathrm{CFT}}\to 0\mathrm{as}M\to M_{\mathrm{crit}}.$$

Hawking radiation becomes a curvature-relaxation wave in the chronon medium, always weaker than the semiclassical flux and self-quenching at small M. The vacuum thus remains a stable, self-organizing causal state, and black holes evolve smoothly into equilibrium chronon condensates rather than disappearing explosively.

8.6. Information Conservation and Gravitational Echoes

Because there is no singularity and no evaporation, information is never lost /refBekenstein1973. Each infalling quantum perturbs the chronon field, imprinting a phase twist that remains encoded in the finite core. The horizon acts as a semi-permeable membrane: it traps most radiation but allows gradual leakage through curvature waves. These outgoing modes retain phase correlations, producing weak but coherent gravitational echoes in post-merger ringdowns.

The characteristic delay between echoes,

$$\Delta t_{\mathrm{echo}}\simeq 2(r_s-r_c)ln\left({\displaystyle \frac{r_s}{r_c}}\right)/c,$$

offers a direct observational signature of finite-core structure.

8.7. Astrophysical Implications and Detection Prospects

Chronon stars reproduce all external properties of classical black holes while introducing subtle internal effects:

• Gravitational-wave echoes: mergers yield delayed, quasi-periodic reflections from the inner boundary.
• Horizon reflectivity: finite-core reflectance slightly enhances the brightness of the photon ring observed by the Event Horizon Telescope.
• Stable remnants: small chronon stars do not evaporate and may constitute a component of dark matter.
• Cosmological relics: primordial chronon condensates from the early universe could survive as cold, compact halo objects.

Summary: Chronon stars unify the concepts of black holes and vacuum stability under one principle: finite causal curvature. Singularities and evaporation disappear; information is preserved; and the universe’s most extreme objects become steady, self-organizing structures of the causal medium itself.

Figure 9. Structure of a chronon star. Gravitational collapse is halted when the causal curvature ${\mathrm{\Omega }}_{\mu \nu }$ saturates at the CEP limit ${\mathrm{\Omega }}_{max}$, forming a finite core of radius $r_c$. Inside the core, the chronon field is maximally aligned and suppresses independent electromagnetic fields (orange lines expelled), producing an electromagnetically silent region. The exterior remains Schwarzschild-like with radius $r_s$. If $r_s<r_c$, no horizon forms (horizonless condensate); if $r_s>r_c$, the object appears as a black hole with a finite causal core.

Figure 9. Structure of a chronon star. Gravitational collapse is halted when the causal curvature ${\mathrm{\Omega }}_{\mu \nu }$ saturates at the CEP limit ${\mathrm{\Omega }}_{max}$, forming a finite core of radius $r_c$. Inside the core, the chronon field is maximally aligned and suppresses independent electromagnetic fields (orange lines expelled), producing an electromagnetically silent region. The exterior remains Schwarzschild-like with radius $r_s$. If $r_s<r_c$, no horizon forms (horizonless condensate); if $r_s>r_c$, the object appears as a black hole with a finite causal core.

9. Symmetry Principles and Conservation in Chronon Field Theory

Symmetry has always been the guiding principle of modern physics. From Noether’s theorem linking symmetry to conservation, to gauge invariance defining the structure of interactions, symmetries organize our understanding of the universe at every scale. In Chronon Field Theory (CFT), symmetry itself is not fundamental, but emergent—arising from the large-scale stabilization of microscopic causal order. Just as spacetime geometry emerges from chronon alignment, the familiar symmetries of nature—Lorentz invariance, gauge invariance, and time-reversal symmetry—arise as limiting properties of an underlying causal medium whose microscopic behavior need not be exactly symmetric.

This section develops the role of symmetry and conservation in CFT, showing how classical invariances emerge from the collective dynamics of chronons, why time-reversal and entropy are deeply linked, and how Lorentz symmetry, though not fundamental, is operationally concealed through the Chronon Concealment Principle described in the first paper of the Trilogy.

9.1. Emergent Symmetries from Causal Alignment

The microscopic chronon equations

$${\nabla }_{\nu }\left(J{\nabla }^{[\nu }{\mathrm{\Phi }}^{\mu ]}\right)+\lambda ({\mathrm{\Phi }}_{\nu }{\mathrm{\Phi }}^{\nu }+1){\mathrm{\Phi }}^{\mu }=0$$

are purely local and causal but not globally symmetric. At the smallest scales, stochastic chronon fluctuations break continuous symmetry explicitly: each chronon domain defines its own preferred causal direction. However, when causal alignment extends coherently over many correlation lengths, the ensemble enters a symmetry-restored regime. The resulting coarse-grained dynamics exhibit approximate invariances—not because they are fundamental, but because the collective statistics of alignment erase local anisotropies.

Emergent Poincaré Invariance

At macroscopic scales the distribution of chronon orientations becomes statistically isotropic in the subspace orthogonal to the mean causal vector ${\mathrm{\Phi }}^{\mu }$. This isotropy produces an effective Lorentz metric $g_{\mu \nu }$ and local inertial frames related by the Poincaré group. Spatial translations correspond to uniform relabeling of the foliation index, while time translations follow uniform advancement along ${\mathrm{\Phi }}^{\mu }$. Thus special relativity appears as the homogeneous limit of causal alignment.

Phase Coherence and Emergent Gauge Structure

Internal gauge-like symmetries originate from residual phase freedoms in the chronon field rather than from independent particle degrees of freedom. The microscopic energy functional depends only on the magnitude and local alignment of ${\mathrm{\Phi }}^{\mu }$, not on its internal phase $\vartheta \left(x\right)$ along the fiber of the chronon manifold. Local variations of this phase,

$${\mathrm{\Phi }}^{\mu }\left(x\right)\to e^{i\vartheta \left(x\right)}{\mathrm{\Phi }}^{\mu }\left(x\right),$$

leave the coarse-grained alignment energy invariant up to a connection term that behaves as an emergent vector potential

$$A_{\mu }={\displaystyle \frac{1}{J}}{\mathrm{\Phi }}_{\nu }{\nabla }_{\mu }{\mathrm{\Phi }}^{\nu }.$$

This reproduces a $U\left(1\right)$-type gauge redundancy associated with chronon phase transport. When several independent alignment modes coexist (e.g. in triply or quaternionically structured chronon bundles), the connection generalizes to a non-Abelian form with curvature $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }+[A_{\mu },A_{\nu }]$, giving rise to Yang–Mills–like interactions. The resulting symmetry is not an imposed $SU\left(N\right)$ group but a geometric consequence of multi-component phase coherence on the internal manifold of chronon orientations (such as $S^2$ or $S^3$).

Statistical Restoration of Symmetry

Both spacetime and internal symmetries are emergent and approximate. Microscopically, the chronon field breaks them locally, but under coarse-graining these fluctuations average to zero, yielding effective conservation laws and covariant field equations. Poincaré invariance reflects the statistical isotropy of causal alignment, and gauge invariance reflects the redundancy of phase description in a coherent chronon ensemble. Together they form the macroscopic symmetry framework of physics, arising not from postulates but from the collective geometry of the chronon field.

9.2. Noether Currents and Conservation Laws

Because the CFT Lagrangian possesses continuous symmetries in its coarse-grained form, Noether’s theorem applies to the emergent dynamics. For infinitesimal variations $\delta {\mathrm{\Phi }}^{\mu }=ϵX^{\mu }$ that leave the Lagrangian density ${\mathcal{L}}_{\mathrm{\Phi }}$ invariant, the conserved Noether current takes the general form:

$$J^{\mu }={\displaystyle \frac{\partial {\mathcal{L}}_{\mathrm{\Phi }}}{\partial \left({\nabla }_{\mu }{\mathrm{\Phi }}^{\nu }\right)}}\delta {\mathrm{\Phi }}^{\nu }-{\mathcal{K}}^{\mu },\mathrm{with}{\nabla }_{\mu }{J}^{\mu }=0.$$

These currents encode familiar conservation laws:

• Energy-momentum conservation arises from invariance under foliation translations.
• Angular momentum conservation arises from invariance under local rotations of causal orientation.
• Charge conservation arises from internal phase symmetry of ${\mathrm{\Phi }}^{\mu }$.

The difference from conventional field theory is that these conservation laws are statistical consequences of self-organized causal coherence. When causal alignment is disrupted—e.g., during violent astrophysical or cosmological events— small deviations from exact conservation can occur, corresponding to entropy production and non-equilibrium relaxation of the chronon field. This generalizes Noether’s theorem into a thermodynamic form, linking symmetry, conservation, and entropy in one causal framework.

9.3. Time Reversal, Entropy, and Causal Irreversibility

In classical mechanics, time-reversal symmetry implies that the fundamental equations of motion are invariant under $t\to -t$. In quantum mechanics, the Schrödinger equation also possesses time-reversal invariance. However, the observed universe exhibits a clear temporal asymmetry—the arrow of time. In CFT, this asymmetry is not an added feature but a direct consequence of the self-organization of causal order.

The chronon field defines a preferred direction of causal flow: ${\mathrm{\Phi }}^{\mu }$ always points from cause to effect, by construction. Time-reversal, ${\mathrm{\Phi }}^{\mu }\to -{\mathrm{\Phi }}^{\mu }$, corresponds to reversing the orientation of causal alignment, which is locally allowed but globally unstable. Entropy increase arises from the fact that causal domains with random or conflicting orientations have higher configurational multiplicity than ordered ones. As the universe evolves, small perturbations tend to randomize local orientations, driving the system toward greater disorder.

This leads to an emergent second law of thermodynamics:

$${\displaystyle \frac{dS}{dt}}\ge 0,S\propto -\int {\mathrm{\Phi }}^{\mu }ln{\mathrm{\Phi }}_{\mu }{d}^{3}x.$$

Time-reversal symmetry is therefore statistically broken at the macroscopic level, not because the equations forbid reversal, but because the causal alignment that defines “time” cannot be globally inverted in a stable way.

In this sense, entropy is a measure of misalignment in the causal field, and the arrow of time is the direction of causal relaxation toward equilibrium.

Connection to Quantum Irreversibility

In the quantum regime, stochastic fluctuations of ${\mathrm{\Phi }}^{\mu }$ produce probabilistic outcomes. During measurement, microscopic causal directions align irreversibly with macroscopic chronon domains (as discussed in Section 7). This process breaks time-reversal symmetry dynamically, manifesting as the collapse of the wavefunction. Thus, both thermodynamic and quantum arrows of time share a common origin: the irreversible alignment of the causal field.

9.4. Lorentz Symmetry and the Chronon Concealment Principle

A central concern in any emergent spacetime model is whether the underlying microstructure violates Lorentz invariance. In CFT, Lorentz symmetry is not fundamental—it is an emergent property of stabilized chronon foliation. However, any microscopic anisotropy is dynamically and operationally concealed by what the Trilogy papers termed the Chronon Concealment Principle (CCP).

The CCP states that once the chronon field has condensed into a stable causal foliation, the internal anisotropies of its microstructure cannot be probed by low-energy observers because all physical processes—matter, light, and measurement devices— are constructed from the same causal medium. Thus, even though Lorentz invariance may be broken microscopically, it remains exact for all operational measurements within the emergent regime.

Chronon Concealment Principle: Lorentz symmetry is not exact in ontology, but exact in phenomenology.

Mathematical formulation.

At the microscopic level, the chronon field defines a preferred foliation vector ${\mathrm{\Phi }}^{\mu }$ and an associated internal metric:

$${\eta }_{\mu \nu }^{\left(\mathrm{\Phi }\right)}=g_{\mu \nu }+2{\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu }.$$

Microscopic deviations from isotropy appear as small corrections to the effective metric, suppressed by the ratio

$$ϵ\sim {\left({\displaystyle \frac{{\ell }_c}{L_{\mathrm{obs}}}}\right)}^2,$$

where ${\ell }_c$ is the chronon correlation length and $L_{\mathrm{obs}}$ is the observational scale. For all accessible experiments, $ϵ\ll {10}^{-20}$, rendering Lorentz violation operationally unobservable.

This concealment is not mere coincidence—it is a form of symmetry inheritance. Because all interactions and detectors are built from the same causal fabric, their internal anisotropies transform coherently. The observer’s reference frame, the measuring apparatus, and the physical processes being measured all co-evolve within the same foliation, making Lorentz symmetry effectively exact for any local experiment.

Intuitive Analogy: The Train of Causality

A useful way to visualize the CCP is to imagine that every observer, particle, and interaction in the universe is riding inside the same train. The train’s interior—its chronon field—is moving smoothly along its causal track. All rulers, clocks, and signals are made in the train itself. From within (and there’s no outside!), the cabin appears perfectly at rest and isotropic. In the same way, all observers in CFT share a single dynamically stabilized causal frame: they are embedded within the same moving medium, so microscopic anisotropies are universally co-moving and thus unobservable. Lorentz symmetry therefore appears exact not because spacetime is fundamentally invariant, but because all participants in measurement are synchronously carried by the same chronon flow.

9.5. Hierarchy of Emergent Symmetries in CFT

The structure of symmetries in Chronon Field Theory can be summarized as a hierarchy:

Level	Symmetry Type	Origin in CFT
Microscopic	Local causal alignment	${\mathrm{\Phi }}^{\mu }$ dynamics, no global invariance
Mesoscopic	Statistical isotropy	Averaging over chronon orientations
Macroscopic	Lorentz invariance	Concealment via stabilized foliation (CCP)
Quantum	Phase rotation symmetry ($U\left(1\right)$)	Chronon holonomy in internal phase space
Thermodynamic	Time asymmetry	Irreversible causal relaxation (entropy growth)
Cosmological	Approximate homogeneity and isotropy	Large-scale uniform alignment

Each level inherits, in approximate form, the symmetries of the level above it, stabilized by causal coherence and broken only by fluctuations or boundary conditions. In the deepest sense, symmetry in CFT is a thermodynamic phenomenon— an equilibrium pattern in the sea of microscopic causal fluctuations.

9.6. Conceptual Implications

CFT reframes one of the oldest ideas in physics: symmetry is not a prerequisite for conservation, but a product of order. Just as temperature uniformity emerges from molecular chaos, Lorentz and gauge symmetries emerge from causal equilibrium.

In this view:

• Conservation laws are macroscopic invariants of a self-regulating causal medium.
• Entropy growth and time’s arrow are consequences of microscopic asymmetry in causal flow.
• Lorentz symmetry, though emergent, is operationally absolute through the CCP.

The unification of symmetry, causality, and thermodynamics is one of CFT’s most striking conceptual achievements. It implies that the fundamental “laws” of physics are not rigid constraints imposed from above, but stable collective behaviors of the universe’s underlying causal substrate.

Summary:

• Symmetries in CFT are emergent statistical properties of causal alignment.
• Conservation laws arise through Noether-like theorems applied to coarse-grained dynamics.
• Time-reversal symmetry is broken statistically, giving rise to entropy and temporal direction.
• Lorentz symmetry is concealed operationally through the Chronon Concealment Principle.
• The symmetry structure of nature is thus not fundamental but thermodynamic, reflecting the stability of an evolving causal order.

Chronon Field Theory reinterprets the sacred principle of symmetry as a sign not of perfection, but of maturity— a pattern the universe grows into when its underlying causality has settled into balance.

10. Chronon Cosmology: The Universe as a Causal Condensate

Chronon Field Theory (CFT) provides a natural cosmological framework in which spacetime expansion, inflation, and matter genesis arise from the dynamics of causal alignment. Instead of an initial singularity, the universe begins as a phase transition of the chronon field ${\mathrm{\Phi }}^{\mu }$— a condensation from incoherent causal noise into an aligned, expanding manifold. In this picture, the Big Bang corresponds not to a pointlike explosion, but to the onset of global causal order.

10.1. The Causal Condensation of the Early Universe

At the earliest times, chronons were randomly oriented, producing no coherent notion of distance or duration. As local alignments nucleated and merged, patches of ordered causality percolated into a connected spacetime continuum. This causal condensation marks the true beginning of cosmic time. The emergent metric $g_{\mu \nu }$ is the large-scale order parameter of ${\mathrm{\Phi }}^{\mu }$, and cosmic expansion represents the gradual relaxation of residual curvature toward equilibrium.

Physically, the Big Bang is a smooth symmetry-breaking transition, not a singular creation event. CFT replaces the unphysical divergence of temperature and density with a finite energy bound imposed by the Chronon Exclusivity Principle (CEP):

$${\rho }_{max}\sim {\displaystyle \frac{3}{4\pi }}{\displaystyle \frac{c^2}{G}}{\mathrm{\Omega }}_{max}^2,$$

which defines the highest attainable curvature and density in nature. The early universe thus began as a saturated causal condensate at this geometric limit.

10.2. Inflation as Curvature Relaxation

In conventional cosmology, inflation is driven by an ad hoc scalar field. In CFT, it arises dynamically as a release of stored curvature energy. Immediately after condensation, the chronon field contained large gradients in ${\mathrm{\Omega }}_{\mu \nu }$. Because curvature cannot exceed ${\mathrm{\Omega }}_{max}$, the excess alignment energy drives rapid expansion—an automatic inflationary phase. The Hubble rate obeys an approximate relaxation form:

$$H\left(t\right)=c{\mathrm{\Omega }}_{max}\mathrm{sech}\left(\gamma t\right),\mathcal{N}=\int Hdt\simeq {\displaystyle \frac{c{\mathrm{\Omega }}_{max}}{\gamma }},$$

where $\gamma$ is the causal alignment–relaxation rate set by the chronon stiffness $(J,\lambda )$. Inflation ends smoothly as $\gamma$ overtakes H, leaving a homogeneous, flat geometry without fine-tuning.

Physical intuition: the causal field behaves like an over-pressurized fluid; as chronons align, they push outward to relieve curvature stress, producing exponential expansion until equilibrium is reached.

Fluctuations of ${\mathrm{\Omega }}_{\mu \nu }$ near the transition generate nearly scale-invariant curvature perturbations. A Kibble–Zurek–like freeze-out with effective exponent $\nu z\approx 1$ yields $n_s\lesssim 1$, consistent with the observed spectrum— achieved without a fundamental inflaton.

10.3. Vacuum Structure and Dark Energy

After large-scale alignment, residual fluctuations of ${\mathrm{\Phi }}^{\mu }$ persist as small symplectic curvature domains. Their averaged stress-energy acts as a vacuum pressure,

$$p_{\mathrm{vac}}\simeq -J〈{\mathrm{\Omega }}_{\mu \nu }{\mathrm{\Omega }}^{\mu \nu }〉,$$

providing an effective cosmological constant. This “dark energy” is simply the residual tension of the causal fabric, not an arbitrary constant. As the universe expands and alignment improves, $\langle {\mathrm{\Omega }}^2\rangle$ slowly decreases, yielding

$$w\left(a\right)=-1+\delta \left(a\right),\left|\delta \right(a\left)\right|\ll 1,$$

with $\delta \left(a\right)<0$ indicating a mild, observable decline in the dark-energy density over cosmological time.

10.4. Dark Matter as Cold Chronon Remnants

During the high-density causal phase, small domains failed to fully merge with the global alignment field. These stable, self-bound condensates—chronon remnants— behave as cold, non-luminous matter. They interact primarily through gravity and curvature waves, making them natural dark-matter candidates. Because their formation is geometric, not thermal, they possess negligible velocity dispersion and cluster efficiently. A log-normal size distribution $P(ln{r}_c)$ with width $\sigma \lesssim 1$ produces the correct cold-dark-matter behavior without new particles.

10.5. Elimination of Cosmological Singularities

Both the Big Bang and black-hole singularities are forbidden by CEP. At the beginning, curvature saturates at ${\mathrm{\Omega }}_{max}$, producing a finite causal density rather than infinite compression. At collapse, the same mechanism halts further contraction, creating chronon stars instead of singularities. Cosmic evolution is therefore cyclic and unitary: each contraction phase ends in a finite causal core, from which the next expansion begins with renewed alignment.

10.6. Observational Consequences

CFT cosmology predicts testable deviations from $\mathrm{\Lambda }$CDM:

• A slow drift in the effective dark-energy density, $w\left(a\right)>-1$, due to continued causal relaxation.
• Slight suppression of primordial power at largest scales, reflecting finite curvature at inflation onset.
• A population of compact dark objects (chronon remnants) comprising galactic halo mass.
• Absence of singularities, ensuring information conservation through all cosmic phases.

The detailed derivation of the effective cosmological dynamics is presented in Appendices Appendix H–Appendix I, where the chronon field is coarse-grained to yield the FLRW equations with emergent $G_{\mathrm{eff}}$ and ${\mathrm{\Lambda }}_{\mathrm{eff}}$, and the high-curvature regime is shown to produce an inflation-like phase and finite horizon structure without singularities.

Summary: Chronon cosmology transforms the origin and evolution of the universe from a singular explosion into a process of causal self-organization. Spacetime emerges as a condensate of aligned chronons; inflation is curvature relaxation; dark energy is residual alignment tension; and dark matter consists of stable causal condensates. The universe is not a passive stage but an evolving, self-adjusting fabric of causality.

Quantitative parameter estimates and observational implications are discussed in Appendix J, where the chronon parameters $(J,\lambda ,{\ell }_c)$ are shown to reproduce the observed constants G, ℏ, and $\mathrm{\Lambda }$, as well as the CMB sound horizon.

11. CFT and the Future of Theoretical Physics

Chronon Field Theory (CFT) represents a profound shift in our understanding of the universe. It proposes that spacetime, matter, and quantum phenomena are not separate domains, but emergent aspects of a single underlying causal medium. By unifying the geometric, quantum, and thermodynamic perspectives into one framework, CFT suggests that the deep laws of nature may be simpler—and more beautiful—than previously imagined. This section explores the implications of CFT for the future of theoretical physics, the bridges it builds between established domains, and the challenges that lie ahead on the path to a unified geometric theory of everything.

11.1. Unifying Spacetime, Matter, and Quantum Theory

For over a century, physics has advanced through specialization. Relativity described spacetime and gravitation, quantum mechanics explained particles and probabilities, and field theory unified the fundamental forces. Yet despite their triumphs, these frameworks remain conceptually distinct, joined only by pragmatic bridges.

CFT dissolves these boundaries by proposing that spacetime and matter share a common origin. The chronon field ${\mathrm{\Phi }}^{\mu }\left(x\right)$—the fundamental unit of causal order— gives rise to all known physical phenomena through different modes of alignment and curvature:

• Spacetime emerges from large-scale alignment of causal directions.
• Gravity arises as the macroscopic relaxation of curvature in this causal medium.
• Gauge forces are the internal holonomies of chronon phase space.
• Quantum behavior originates from microscopic fluctuations of causal phase.
• Matter fields are stable, localized topological defects of the causal network.

Thus, particles, fields, and geometry are not separate entities but different levels of organization of the same fundamental substrate. CFT recasts the dichotomy between “geometry” and “quantum field” as a false distinction— they are the same process viewed at different scales.

Conceptual unification:

$$\mathrm{Chronon}\mathrm{field}\mathrm{dynamics}⟹\left\{\begin{array}{cc}\mathrm{geometry}\left(\mathrm{GR}\right)\hfill & \mathrm{by}\mathrm{coarse}\text{-}\mathrm{graining},\hfill \\ \mathrm{quantum}\mathrm{theory}\left(\mathrm{QM}\right)\hfill & \mathrm{by}\mathrm{fluctuation}\mathrm{statistics},\hfill \\ \mathrm{particle}\mathrm{physics}\left(\mathrm{SM}\right)\hfill & \mathrm{by}\mathrm{topological}\mathrm{defects}.\hfill \end{array}\right.$$

This hierarchy mirrors the way condensed-matter systems display emergent phenomena—sound waves, vortices, supercurrents—all unified by the same microscopic substrate. CFT extends this philosophy to the entire universe.

11.2. Bridging Microscopic Causality with Macroscopic Gravity

One of CFT’s greatest achievements is to bridge the gap between microscopic causality and macroscopic spacetime curvature. In General Relativity, the source of gravity is stress-energy, but the mechanism by which energy distorts geometry remains formal. CFT provides the missing link: energy density corresponds to local misalignment of causal directions, and curvature is the macroscopic manifestation of that misalignment.

At the smallest scales, chronons interact through local rules— their orientations repel excessive overlap and resist over-compression. At large scales, these interactions average to the Einstein field equations, with the Newton constant G emerging as the inverse stiffness of causal alignment.

This correspondence has profound implications:

• The gravitational constant is not a universal input but a material property of the causal medium.
• The curvature-energy relation of GR emerges naturally from alignment feedback.
• The equivalence principle becomes a statement of causal isotropy: all excitations experience geometry through the same causal network.

Interpretation: CFT transforms gravity from an external interaction into an intrinsic property of information flow. Matter and spacetime are coupled not by force but by consistency: they share the same causal skeleton.

This also bridges the quantum–classical divide. At microscopic scales, chronon fluctuations dominate, producing quantum uncertainty. At macroscopic scales, collective alignment averages out these fluctuations, producing deterministic geometry. In this sense, CFT offers a literal continuum between quantum mechanics and relativity, without the need for quantizing the gravitational field.

11.3. Experimental and Observational Opportunities

CFT is not merely philosophical—it is testable. Several classes of observations and experiments can probe its distinctive predictions:

1. Gravitational-wave echoes.

As shown in Section 8, chronon stars replace classical black holes with finite causal cores. The resulting ringdown signals should exhibit time-delayed echoes due to partial reflection from the inner surface. Detecting such echoes in LIGO–Virgo–KAGRA or LISA data would provide a direct signature of CFT’s finite-curvature interior.

2. Photon-Ring Deviations

The Event Horizon Telescope’s images of black hole shadows offer a window into near-horizon geometry. CFT predicts slightly enhanced photon-ring brightness and sub-Planckian deviations from GR predictions due to reflective inner boundaries.

3. Vacuum-Energy Regularization

CFT inherently limits curvature through the Chronon Exclusivity Principle, implying a natural upper bound on vacuum energy density. This could explain the observed smallness of the cosmological constant without fine-tuning, providing a measurable prediction for future cosmological probes such as Euclid and the Roman Space Telescope.

4. High-Energy Scattering and Microstructure

At energies approaching the chronon scale ($\sim {10}^{19}$ GeV), particle scattering may reveal signatures of causal elasticity— departures from local Lorentz invariance or form-factor effects indicating an underlying discrete causal structure.

5. Laboratory Analogues

Emergent spacetime analogues in condensed-matter systems— such as superfluid helium, photonic lattices, or Bose–Einstein condensates— may exhibit chronon-like collective behaviors. Laboratory tests of causal condensation could thus emulate aspects of CFT in controlled settings.

These diverse windows—from astrophysical to table-top experiments— make CFT an unusually falsifiable theory for a framework operating at the Planck scale.

11.4. Remaining Theoretical Challenges

While CFT provides a compelling conceptual synthesis, several deep theoretical questions remain open and demand rigorous development.

1. Quantitative Derivation of the Einstein Limit

The coarse-graining procedure connecting the microscopic chronon equations to the macroscopic Einstein field equations must be formalized. This will likely require a path-integral or mean-field approach to demonstrate that the emergent stress-energy tensor reproduces GR with small corrections.

2. Gauge coupling Hierarchy

Although internal symmetries emerge geometrically in CFT, the relative coupling strengths ($g_1,g_2,g_3$) must be derived from the microdynamics. Understanding how chronon stiffness and torsion yield the observed hierarchy remains a key step toward quantitative unification.

3. Cosmological Simulations

Numerical models of chronon-lattice condensation are needed to validate predictions about dark energy, dark matter, and the evolution of the early universe. Such simulations will test whether causal relaxation reproduces the observed $\mathrm{\Lambda }$CDM expansion history.

4. Quantum–Thermodynamic Correspondence

CFT blurs the line between quantum fluctuations and entropy production. A rigorous mathematical framework connecting chronon statistics to information theory and nonequilibrium thermodynamics remains to be constructed.

5. Embedding Within Existing Frameworks

Connections to string theory, loop quantum gravity, and asymptotic safety should be explored to test whether CFT can emerge as a limiting case or unifying language for these approaches.

These challenges are not weaknesses but invitations. They outline a roadmap for the next generation of theoretical and computational work that could elevate CFT from a compelling hypothesis to an established paradigm.

11.5. Outlook: The Road Toward a Geometric Theory of Everything

CFT invites us to rethink the question of what “fundamental” means. Instead of seeking smaller particles or higher energies, it asks us to understand how causality itself organizes into the structures we observe. In doing so, it bridges physics across all scales—from the birth of spacetime to the quantum flicker of a single event.

At its deepest level, the chronon paradigm suggests that the universe is not built of spacetime, but that spacetime is built from causation. Matter, energy, and consciousness itself may be different modes of excitation of the same underlying causal field. The great equations of 20th-century physics—Einstein’s field equations, Schrödinger’s wave equation, and Maxwell’s electromagnetism— emerge not as independent laws but as approximations to a single, self-organizing causal geometry.

$$\mathrm{CFT}\mathrm{unification}\text{:}\underset{{\mathrm{\Phi }}^{\mu }}{\underbrace{\mathrm{Causal}\mathrm{field}}}⟹\left\{\mathrm{spacetime},\mathrm{gravity},\mathrm{gauge}\mathrm{forces},\mathrm{quantum}\mathrm{coherence}\right\}.$$

In this vision, the geometric theory of everything is not a new force or field but a new understanding of how information flows. CFT may ultimately reveal that the universe is a living causal network— finite yet unbounded, fluctuating yet self-consistent, where geometry and information continuously shape one another.

Final perspective:

• CFT unifies spacetime, matter, and quantum behavior as emergent properties of one causal field.
• It resolves the inconsistencies between relativity and quantum mechanics by grounding both in the same microscopic geometry.
• It predicts new astrophysical phenomena that can be tested in the coming decade.
• And it offers a roadmap toward a deeper, information-geometric foundation for physics.

Chronon Field Theory does not end the search for ultimate laws— it reframes it. The future of theoretical physics may not lie in discovering new particles or dimensions, but in understanding how the simplest principle—causal coherence— gives rise to everything.

12. Conclusion: Temporal Coherence as the Unifying Law of Nature

Chronon Field Theory (CFT) reframes the physical universe not as a static geometric arena populated by independent entities, but as a self-organizing causal medium governed by a single generative law: the Temporal Coherence Principle (TCP). All other features of physics—spacetime geometry, quantized action, gauge structure, and even the appearance of matter and energy—emerge as secondary manifestations of how the chronon field preserves and restores coherence in time.

From Multiple Postulates to a Single Principle

What began as a set of guiding ideas—the Chronon Universality Principle (CUP), Chronon Exclusivity Principle (CEP), and Chronon Concealment Principle (CCP)—are now understood as natural consequences of the TCP. Once the chronon field is shown to generate the metric, curvature, and quantum constants, universality (CUP) becomes a derived fact rather than an assumption. The positivity of the alignment stiffness $J>0$ ensures finite curvature and a strictly positive quantum of action ($\hslash >0$), yielding exclusivity (CEP) as a stability condition. Finally, the statistical isotropy and Lorentz symmetry of spacetime (CCP) follow from the combination of CUP and TCP: since all domains are chrononic and evolve toward temporal synchronization, microscopic anisotropies average out in large coherent ensembles. What remains is a single dynamical law—the drive toward global temporal coherence— from which the rest of physics unfolds.

Temporal Coherence as the Source of All Physical Law

The TCP provides a unifying explanation for principles traditionally regarded as axiomatic. The classical principle of least action is reinterpreted as the variational form of temporal coherence: physical systems follow histories that minimize cumulative phase misalignment among chronon threads. Conservation laws arise from invariance of the coherence functional under temporal phase translations; symmetry principles reflect freedoms in representing the chronon phase structure; and quantization corresponds to the discrete units of causal rotation sustained by the chronon field. Even statistical and thermodynamic laws acquire new meaning: entropy growth reflects the diffusion of coherence, while quantum collapse represents re-entrainment of microscopic domains into macroscopic synchronization. In this sense, the TCP is not merely one law among many, but the meta-law from which all others can be derived.

Table 3. Major physical principles reinterpreted through the Temporal Coherence Principle (TCP). Each traditional law of physics emerges as a specific manifestation of coherence preservation or restoration in the chronon field.

No.	Physical Principle	Derivation from the Temporal Coherence Principle
1	Principle of Least Action	Systems follow paths that extremize the action. Stable evolution minimizes chronon phase misalignment—the variational form of temporal coherence.
2	Energy Conservation	Temporal coherence enforces phase continuity in time; invariance under phase translation ($\mathrm{\Phi }\to e^{i\omega t}\mathrm{\Phi }$) yields conserved energy (Noether theorem).
3	Entropy Increase (Second Law)	Macroscopic entropy growth reflects temporal decoherence: the diffusion of global phase information as coherence dissipates.
4	Quantum Superposition	Pre-alignment chronon ensembles represent phase-unsynchronized subdomains; superposition is unresolved temporal coherence.
5	Wavefunction Collapse	Measurement entrains the quantum system to the macroscopic bias field, restoring local temporal coherence.
6	Uncertainty Principle	Conjugate variables ($x,p$) correspond to orthogonal temporal phase modes; incomplete synchronization limits simultaneous coherence.
7	Equivalence Principle	Gravity and acceleration both arise from temporal curvature gradients—variations in chronon phase rate.
8	Quantum Gauge Symmetry	Gauge transformations are local temporal phase rotations; coherence invariance under them generates conserved charges (via Noether).
9	Speed of Light as Constant	c is the maximum rate of temporal phase propagation in the chronon field— the limit of coherence transfer.
10	Pauli Exclusion / Fermi Statistics	No two fermions occupy the same causal state; this reflects CEP, the dynamical result of positive stiffness $J>0$.
11	Quantum Entanglement	Shared chronon ancestry preserves synchronized phase bias; coherence is global, not spatial.
12	Time-Reversal Asymmetry	Spontaneous breaking of chronon phase symmetry establishes the arrow of increasing coherence complexity.
13	Cosmological Expansion	Large-scale relaxation of phase curvature; decoherence between distant chronon domains manifests as metric expansion.
14	Mass–Energy Equivalence	Energy is the rate of temporal phase rotation; mass quantifies resistance to phase acceleration.
15	Principle of Relativity	Global temporal coherence ensures invariant phase structure across synchronized chronon frames.

Table 3. Major physical principles reinterpreted through the Temporal Coherence Principle (TCP). Each traditional law of physics emerges as a specific manifestation of coherence preservation or restoration in the chronon field.

No.	Physical Principle	Derivation from the Temporal Coherence Principle
1	Principle of Least Action	Systems follow paths that extremize the action. Stable evolution minimizes chronon phase misalignment—the variational form of temporal coherence.
2	Energy Conservation	Temporal coherence enforces phase continuity in time; invariance under phase translation ($\mathrm{\Phi }\to e^{i\omega t}\mathrm{\Phi }$) yields conserved energy (Noether theorem).
3	Entropy Increase (Second Law)	Macroscopic entropy growth reflects temporal decoherence: the diffusion of global phase information as coherence dissipates.
4	Quantum Superposition	Pre-alignment chronon ensembles represent phase-unsynchronized subdomains; superposition is unresolved temporal coherence.
5	Wavefunction Collapse	Measurement entrains the quantum system to the macroscopic bias field, restoring local temporal coherence.
6	Uncertainty Principle	Conjugate variables ($x,p$) correspond to orthogonal temporal phase modes; incomplete synchronization limits simultaneous coherence.
7	Equivalence Principle	Gravity and acceleration both arise from temporal curvature gradients—variations in chronon phase rate.
8	Quantum Gauge Symmetry	Gauge transformations are local temporal phase rotations; coherence invariance under them generates conserved charges (via Noether).
9	Speed of Light as Constant	c is the maximum rate of temporal phase propagation in the chronon field— the limit of coherence transfer.
10	Pauli Exclusion / Fermi Statistics	No two fermions occupy the same causal state; this reflects CEP, the dynamical result of positive stiffness $J>0$.
11	Quantum Entanglement	Shared chronon ancestry preserves synchronized phase bias; coherence is global, not spatial.
12	Time-Reversal Asymmetry	Spontaneous breaking of chronon phase symmetry establishes the arrow of increasing coherence complexity.
13	Cosmological Expansion	Large-scale relaxation of phase curvature; decoherence between distant chronon domains manifests as metric expansion.
14	Mass–Energy Equivalence	Energy is the rate of temporal phase rotation; mass quantifies resistance to phase acceleration.
15	Principle of Relativity	Global temporal coherence ensures invariant phase structure across synchronized chronon frames.

A New View of the Universe

CFT thus replaces the ontology of static geometry with one of active coherence. Spacetime, matter, and energy are no longer fundamental ingredients, but emergent expressions of a deeper self-synchronizing process. Gravitation, gauge interactions, and quantum phenomena arise from different regimes of the same causal alignment dynamics. What we call “laws of nature” are the stable patterns by which the universe maintains the coherence of its own temporal phase.

Outlook

The Temporal Coherence Principle provides both a physical and philosophical synthesis: a universe that exists by virtue of remaining temporally synchronized within itself. Future developments of CFT will focus on refining the mathematical form of the coherence functional, simulating chronon alignment dynamics, and exploring its implications for cosmology, particle physics, and quantum foundations. If successful, this framework may one day place all known interactions— and the constants that characterize them—within a single coherent description of reality as the self-organizing rhythm of time itself.

12.1. The Primacy of Time

In Chronon Field Theory (CFT), time is ontologically more fundamental than space. The theory begins not with a pre-existing spacetime manifold, but with a field of elementary causal agents—chronons—each carrying an intrinsic parameter of succession ${\tau }_c$. This parameter defines local causal order: a sense of “before” and “after” that exists independently of any spatial embedding. Temporal succession, rather than spatial extension, is therefore the first condition of physical existence.

Spatial structure arises only when many chronons synchronize their local causal parameters, producing coherent cross-sections of simultaneity ${\mathrm{\Sigma }}_t$. The alignment of causal directions ${\mathrm{\Phi }}^{\mu }$ defines a macroscopic foliation, whose orthogonal complement is interpreted as emergent space. Thus, time represents the active process of causal becoming, while space represents the geometric footprint of that coherence. Temporal order can exist without spatial structure, but spatial geometry cannot exist without temporal coherence. In this sense, time is ontologically prior and dynamically generative.

From Block Universe to Process Reality

Einstein’s relativity unifies space and time into a four-dimensional continuum, in which all events coexist. This “block-universe” picture treats time as a coordinate dimension equivalent to space, denying any fundamental distinction between past, present, and future. While this description is kinematically valid for an already coherent manifold, it does not explain how spacetime coherence arises in the first place. CFT reverses the hierarchy: coherence in time precedes the formation of spacetime geometry. Relativity describes the stage; CFT describes its self-assembly.

Process Ontology and Realist Presentism

In metaphysical terms, CFT aligns with the process philosophies of Whitehead and Bergson, and with modern realist presentism. The chronon field embodies continual becoming—a dynamic flux whose local synchronizations form the “present” as an active causal surface. The past corresponds to dissipated coherence (no longer causally active), and the future corresponds to unrealized potential (not yet coherent). Only the evolving present is ontologically real. Each new alignment of chronons extends the causal network, giving rise to the flow of time as the progressive synchronization of causal order.

Summary

The symmetry between space and time in relativity is a property of the emergent continuum, not of the underlying ontology. At the fundamental level, CFT posits an irreversible causal flow from which both geometry and dynamics emerge. Time is the substance; space is its stable form. The universe does not exist as a static four-dimensional block, but as a continually self-organizing process of temporal coherence—the unfolding of the Real Now.

Figure 10. Comparison between the block-universe view of relativity and the CFT view of time. In relativity, time and space form a static four-dimensional continuum where all events coexist. In CFT, only the present causal layer ${\mathrm{\Sigma }}_t$ is real; spacetime grows dynamically as chronons synchronize their causal phases.

Figure 10. Comparison between the block-universe view of relativity and the CFT view of time. In relativity, time and space form a static four-dimensional continuum where all events coexist. In CFT, only the present causal layer ${\mathrm{\Sigma }}_t$ is real; spacetime grows dynamically as chronons synchronize their causal phases.

Appendix A.1. Action Principle and Field Equations

The chronon field is represented by a unit-norm timelike vector field $n^{\mu }\left(x\right)$ describing the local causal orientation of chronon threads. Its dynamics follow from the Lagrangian density

$${\mathcal{L}}_{\mathrm{CFT}}={\displaystyle \frac{J}{2}}\left({\nabla }_{\mu }{n}_{\nu }\right)\left({\nabla }^{\mu }{n}^{\nu }\right)-{\displaystyle \frac{\lambda }{4}}{(n_{\mu }{n}^{\mu }-1)}^2+{\mathcal{L}}_{\mathrm{int}}[n_{\mu },{\psi }_i],$$

(A1)

where J is the alignment stiffness, $\lambda$ enforces unit-norm coherence, and ${\mathcal{L}}_{\mathrm{int}}$ describes coupling to other fields ${\psi }_i$ (matter, gauge, or curvature sources).

Variation of the action $S=\int \sqrt{-g}{\mathcal{L}}_{\mathrm{CFT}}{d}^{4}x$ with respect to $n_{\nu }$ yields the Euler–Lagrange equation

$$J{\nabla }_{\mu }{\nabla }^{\mu }{n}_{\nu }+J{R}_{\nu \mu }{n}^{\mu }-\lambda (n_{\alpha }{n}^{\alpha }-1)n_{\nu }=f_{\nu }^{\left(\mathrm{int}\right)},$$

(A2)

where $f_{\nu }^{\left(\mathrm{int}\right)}\equiv -\delta {\mathcal{L}}_{\mathrm{int}}/\delta n^{\nu }$ represents interaction forces from other fields. Equation (A2) governs causal alignment: curvature acts as a restoring bias on deviations of chronon orientation, while $\lambda$ stabilizes the magnitude of the causal flow.

Appendix A.2. Causal Flux Conservation

Applying ${\nabla }^{\nu }$ to Eq. (A2) and using the Bianchi identity ${\nabla }^{\nu }{R}_{\nu \mu }=0$, one obtains a continuity equation for the chronon flux current

$$j^{\mu }=n_{\nu }{\nabla }^{\mu }{n}^{\nu }-n^{\mu }{\nabla }_{\nu }{n}^{\nu },$$

(A3)

whose divergence vanishes in the absence of external coupling:

$${\nabla }_{\mu }{j}^{\mu }=0.$$

(A4)

Equation (A4) expresses causal continuity: chronon flux cannot begin or end arbitrarily, but only redistribute via geometric curvature. This provides the microscopic foundation for the conservation of probability and causal flow in the emergent quantum limit.

Appendix A.3. Stress–Energy Tensor and Energy Positivity

Variation of the action with respect to the metric $g^{\mu \nu }$ gives the chronon stress–energy tensor,

$$T_{\mu \nu }^{\left(n\right)}=J\left({\nabla }_{\mu }{n}_{\alpha }\right)\left({\nabla }_{\nu }{n}^{\alpha }\right)-\frac{J}{2}{g}_{\mu \nu }\left({\nabla }_{\alpha }{n}_{\beta }\right)\left({\nabla }^{\alpha }{n}^{\beta }\right)+\frac{\lambda }{4}{g}_{\mu \nu }{(n_{\alpha }{n}^{\alpha }-1)}^2.$$

(A5)

For small deviations $\delta n^{\mu }$ from perfect alignment, the energy density ${\rho }_{\mathrm{\Omega }}=T_{00}^{\left(n\right)}\approx \frac{J}{2}\left({\partial }_i\delta n_j\right)\left({\partial }^i\delta n^j\right)$ is manifestly positive when $J>0$, ensuring the causal medium is stable and that gravity, emerging from curvature relaxation, is universally attractive.

Appendix A.4. Linearized Dynamics and Geometric Quantization

In the weak-deformation limit, expand $n_{\mu }=u_{\mu }+\delta n_{\mu }$ with $u_{\mu }{u}^{\mu }=-1$ constant. Linearizing Eq. (A2) around a flat background gives

$$\square \delta n_{\mu }+m_{\mathrm{eff}}^2\delta n_{\mu }=0,m_{\mathrm{eff}}^2=\lambda /J,$$

(A6)

which describes small oscillations of the chronon field with effective mass $m_{\mathrm{eff}}$. Quantization of the corresponding action yields discrete flux quanta associated with topological winding of $n^{\mu }$ around compact internal submanifolds. These flux quanta underlie the emergence of Planck’s constant ${\hslash }_{\mathrm{geom}}$ as discussed in Section 4.5.

Appendix A.5. Coupling to Curvature and Matter

The curvature coupling term $J{R}_{\nu \mu }{n}^{\mu }$ in Eq. (A2) implies that spacetime curvature acts as a self-consistent potential for chronon alignment. In the presence of matter fields ${\psi }_i$, the interaction term $f_{\nu }^{\left(\mathrm{int}\right)}$ modifies the local alignment bias, producing backreaction consistent with the effective Einstein equations derived in Appendix B.

Appendix A.6. Summary

The variational formulation of CFT establishes:

• The chronon field obeys a covariant alignment equation (A2) analogous to a nonlinear Proca system.
• Causal flux is conserved (A4), providing the microscopic origin of probability conservation.
• Energy positivity ($J>0$) ensures universal gravitational attraction.
• Linearized perturbations of $n_{\mu }$ give rise to quantized geometric modes that define the emergent Planck scale.

These results make Section 3’s discussion of causal alignment, flux quantization, and curvature elasticity precise. They provide the mathematical foundation for the emergent gravitational and quantum constants developed in later sections.

Appendix B.1. Microscopic Lagrangian and Alignment Energy

The chronon field ${\mathrm{\Phi }}_{\mu }\left(x\right)$ encodes the local orientation of causal flow. Its microscopic dynamics follow from the universal Lagrangian

$${\mathcal{L}}_{\mathrm{CFT}}={\displaystyle \frac{J}{2}}\left({\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }\right)\left({\nabla }^{\mu }{\mathrm{\Phi }}^{\nu }\right)-{\displaystyle \frac{\lambda }{4}}{({\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}^{\mu }-1)}^2,$$

(A7)

where J sets the stiffness of causal alignment and $\lambda$ enforces unit-norm self-coherence. All additional excitations—fermionic, bosonic, or gauge-like—arise as structured solitonic or oscillatory modes of ${\mathrm{\Phi }}_{\mu }$ itself under the Chronon Universality Principle (CUP); hence no independent matter fields ${\mathrm{\Psi }}_i$ appear.

The microscopic stress–energy tensor is

$$T_{\mu \nu }^{\left(\mathrm{\Phi }\right)}=J\left({\nabla }_{\mu }{\mathrm{\Phi }}_{\alpha }\right)\left({\nabla }_{\nu }{\mathrm{\Phi }}^{\alpha }\right)-\frac{J}{2}{g}_{\mu \nu }\left({\nabla }_{\alpha }{\mathrm{\Phi }}_{\beta }\right)\left({\nabla }^{\alpha }{\mathrm{\Phi }}^{\beta }\right)+\frac{\lambda }{4}{g}_{\mu \nu }{({\mathrm{\Phi }}_{\alpha }{\mathrm{\Phi }}^{\alpha }-1)}^2.$$

(A8)

Appendix B.2. Coarse-Graining and the Emergent Metric

On scales large compared with the coherence length ${\ell }_c$, chronon orientations are nearly aligned within each correlation domain. Define the coarse-grained average

$$\langle {\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu }\rangle \equiv g_{\mu \nu }/{(-detg)}^{1/4},$$

(A9)

so that the collective alignment field induces a symmetric, nondegenerate tensor $g_{\mu \nu }$ identified as the emergent spacetime metric.

Expanding ${\mathrm{\Phi }}_{\mu }=u_{\mu }+\delta {\mathrm{\Phi }}_{\mu }$ about the mean orientation $u_{\mu }{u}^{\mu }=-1$ and averaging over short-range fluctuations yields the effective macroscopic action

$$S_{\mathrm{eff}}\left[g_{\mu \nu }\right]=\int d^{4}x\sqrt{-g}\left[{\displaystyle \frac{c^4}{16\pi G_{\mathrm{eff}}}}R-{\mathrm{\Lambda }}_{\mathrm{eff}}\right],$$

(A10)

where the emergent couplings are

$${\displaystyle \frac{c^4}{16\pi G_{\mathrm{eff}}}}={\displaystyle \frac{3J}{2{\ell }_c^2}},{\mathrm{\Lambda }}_{\mathrm{eff}}={\displaystyle \frac{3\lambda }{8J}}.$$

(A11)

Thus $G_{\mathrm{eff}}$ and ${\mathrm{\Lambda }}_{\mathrm{eff}}$ are not inputs but collective parameters determined by the microscopic stiffness J, self-interaction $\lambda$, and coherence scale ${\ell }_c$.

Appendix B.3. Einstein Equations as Alignment Equilibrium

Varying Eq. (A10) with respect to $g_{\mu \nu }$ gives

$$R_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }R+{\mathrm{\Lambda }}_{\mathrm{eff}}{g}_{\mu \nu }={\displaystyle \frac{8\pi G_{\mathrm{eff}}}{c^4}}{T}_{\mu \nu }^{\left(\mathrm{coh}\right)},$$

(A12)

where $T_{\mu \nu }^{\left(\mathrm{coh}\right)}$ represents residual stress from partial misalignment of the chronon ensemble. In the limit of perfect coherence, $T_{\mu \nu }^{\left(\mathrm{coh}\right)}=0$, and the spacetime geometry satisfies the vacuum Einstein equations [7].

Microscopically, the alignment equation

$${\nabla }_{\mu }{\nabla }^{\mu }{\mathrm{\Phi }}_{\nu }+\left({\nabla }_{\mu }{\mathrm{\Phi }}^{\mu }\right){\mathrm{\Phi }}_{\nu }+\lambda ({\mathrm{\Phi }}_{\alpha }{\mathrm{\Phi }}^{\alpha }-1){\mathrm{\Phi }}_{\nu }=0$$

reduces under full coherence to ${\nabla }_{\mu }{u}_{\nu }=0$, which implies geodesic flow of chronon trajectories in $g_{\mu \nu }$. Hence free fall and inertia are direct consequences of chronon coherence.

Appendix B.4. Curvature Energy and Gravitational Attraction

The positive-definite curvature energy density,

$${\rho }_{\mathrm{\Omega }}=\frac{J}{2}\left({\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }\right)\left({\nabla }^{\mu }{\mathrm{\Phi }}^{\nu }\right)>0,$$

(A13)

ensures that curvature relaxation reduces misalignment and always produces attractive gravitational response. Thus, the sign of gravity is not conventional but dynamical: positive stiffness $J>0$ necessarily yields universal attraction.

Appendix B.5. Interpretation and Outlook

The Einstein field equations therefore arise as the macroscopic equilibrium condition of a self-organizing causal medium:

$$\mathit{Micros\; copicchronon\; alignment}⟹\mathit{Macroscopic\; curvature\; elasticity}\left(\mathit{General\; Relativity}\right).$$

The constants $G_{\mathrm{eff}}$ and ${\mathrm{\Lambda }}_{\mathrm{eff}}$ are emergent from chronon parameters $(J,\lambda ,{\ell }_c)$, and gravitational waves correspond to propagating disturbances in alignment coherence. Further work will refine this derivation via explicit statistical coarse-graining, determine the renormalization flow of $G_{\mathrm{eff}}$ and ${\mathrm{\Lambda }}_{\mathrm{eff}}$, and explore possible curvature–flux quantization observable in cosmology and condensed-matter analogs.

Appendix C.1. The Chronon Field and Its Internal Rotations

At each spacetime point, ${\mathrm{\Phi }}_{\mu }$ defines the local direction of causal flow. Its magnitude is fixed by the normalization condition

$${\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}^{\mu }=-1,$$

so the only dynamical freedom lies in the *orientation* of ${\mathrm{\Phi }}_{\mu }$ within the tangent space of the emergent manifold. Infinitesimal rotations of ${\mathrm{\Phi }}_{\mu }$ within this tangent space are generated by antisymmetric variations $\delta {\mathrm{\Phi }}_{\mu }={ϵ}_{\mu \nu }{\mathrm{\Phi }}^{\nu }$, where ${ϵ}_{\mu \nu }$ lives in the local Lorentz algebra. When projected onto the spatial leaves ${\mathrm{\Sigma }}_{\tau }$ orthogonal to ${\mathrm{\Phi }}_{\mu }$, these rotations form a compact internal group of causal orientations whose holonomies behave as gauge connections.

The corresponding *holonomy connection* is

$$A_{\mu }^{\left(a\right)}={\mathrm{\Phi }}_{\nu }{T}^{\left(a\right)}{\nabla }_{\mu }{\mathrm{\Phi }}^{\nu },$$

where $T^{\left(a\right)}$ are generators of the internal rotation group. Closed transport of ${\mathrm{\Phi }}_{\mu }$ around loops generates Wilson-like holonomies

$$U\left(C\right)=\mathcal{P}exp\left({\oint }_C{A}_{\mu }^{\left(a\right)}{T}^{\left(a\right)}d{x}^{\mu }\right),$$

whose non-Abelian structure encodes microscopic misalignments of causal direction. The antisymmetric part of ${\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }$ then yields the emergent field strength

$${\mathrm{\Omega }}_{\mu \nu }^{\left(a\right)}={\partial }_{\mu }{A}_{\nu }^{\left(a\right)}-{\partial }_{\nu }{A}_{\mu }^{\left(a\right)}+f^{abc}{A}_{\mu }^{\left(b\right)}{A}_{\nu }^{\left(c\right)},$$

where $f^{abc}$ are the structure constants of the internal rotation group. Thus, the curvature of the chronon field unifies *spacetime curvature* ($R_{\mu \nu \rho \sigma }$) and *gauge curvature* (${\mathrm{\Omega }}_{\mu \nu }^{\left(a\right)}$) as two projections of the same geometric object ${\nabla }_{[\mu }{\mathrm{\Phi }}_{\nu ]}$.

Appendix C.2. Emergent U(1) and SU(2) from Chronon Polarization

In stabilized domains where ${\mathrm{\Phi }}_{\mu }$ aligns globally in time, residual phase rotations of its internal orientation yield an Abelian connection $A_{\mu }={\partial }_{\mu }\theta$, corresponding to electromagnetism. This $U\left(1\right)$ sector was rigorously derived in Paper I through the Finkelstein–Rubinstein and Berry holonomies of $w=1$ solitons.

Extending this picture, the *spatial gradients* of ${\mathrm{\Phi }}_{\mu }$,

$$K_{\mu \nu }=h_{\mu }^{\alpha }{h}_{\nu }^{\beta }{\nabla }_{\alpha }{\mathrm{\Phi }}_{\beta },h_{\mu \nu }=g_{\mu \nu }+{\mathrm{\Phi }}_{\mu }{\mathrm{\Phi }}_{\nu },$$

encode shear, expansion, and vorticity of the chronon flow. Its complex polarization modes form a $U\left(2\right)$ frame whose trace and traceless parts define the $U{\left(1\right)}_Y$ and $SU\left(2\right)$ connections of the electroweak sector. Under local rotations of this frame,

$$U\left(x\right)\in U\left(2\right),A=U^{-1}dU,$$

the trace part of A yields the hypercharge connection $B_{\mu }$, while the traceless part gives the weak isospin gauge field $W_{\mu }^a$. Coarse–graining stabilized chronon fluctuations generates a positive-definite Yang–Mills stiffness ${\kappa }_2$ and induces the effective Lagrangian

$${\mathcal{L}}_{\mathrm{EW}}=-{\displaystyle \frac{{\kappa }_2}{4}}\mathrm{Tr}\left(F^{\mu \nu }{F}_{\mu \nu }\right)-{\displaystyle \frac{{\kappa }_Y}{4}}\left(F_Y^{\mu \nu }{F}_{Y\mu \nu }\right).$$

When the chronon field globally aligns in a preferred timelike direction, its transverse rotational modes acquire mass through curvature misalignment energy. This geometric *chronon-induced symmetry breaking* (CISB) produces massive W and Z bosons while leaving a residual unbroken $U{\left(1\right)}_{\mathrm{EM}}$ symmetry with an exactly massless photon, reproducing the qualitative pattern of electroweak unification without a fundamental Higgs field.

Appendix C.3. Emergent SU(3) and Color Holonomy

At subnuclear scales, the chronon gradient field ${\nabla }_{\mu }{\mathrm{\Phi }}_{\nu }$ possesses additional tensorial structure that supports a richer internal polarization. Decomposing its symmetric and antisymmetric parts as

$$S_{\mu \nu }=K_{\left(\mu \nu \right)},{\mathrm{\Omega }}_{\mu \nu }=K_{\left[\mu \nu \right]},$$

one defines a *complex polarization tensor*

$$H_{\mu \nu }=S_{\mu \nu }+i{\tilde{\mathrm{\Omega }}}_{\mu \nu },$$

which acts as a Hermitian operator on the tangent space of each leaf ${\mathrm{\Sigma }}_{\tau }$. When $H_{\mu \nu }$ has three distinct eigenvalues, its orthonormal eigenvectors $\left\{u_{\mu }^a\right\}$ form a local unitary frame $U\left(x\right)=\left[u^1{u}^2{u}^3\right]\in U\left(3\right)$. The Maurer–Cartan form

$$A=U^{-1}dU\in u\left(3\right)$$

defines a composite $U\left(3\right)$ connection, whose trace part corresponds to the already-identified $U\left(1\right)$ sector and whose traceless part

$$A^{\prime }=A-{\displaystyle \frac{1}{3}}\mathrm{Tr}\left(A\right)\mathbb{1}$$

serves as an $SU\left(3\right)$ connection on the polarization bundle. The associated curvature

$$G=d{A}^{\prime }+A^{\prime }\wedge A^{\prime }$$

obeys the transformation law of a non-Abelian field strength, furnishing a composite color gauge field directly from the geometry of $\nabla \mathrm{\Phi }$. Coarse–graining its fluctuations induces the effective Yang–Mills term

$$S_{\mathrm{SU}\left(3\right)}=-{\displaystyle \frac{{\kappa }_3}{4}}\int \sqrt{-g}\mathrm{Tr}\left(G_{\mu \nu }{G}^{\mu \nu }\right)d^{4}x,$$

with positive stiffness ${\kappa }_3>0$. No new microscopic degrees of freedom are introduced: the $U\left(3\right)$ frame carries exactly nine parameters—eight traceless generators of $SU\left(3\right)$ and one global phase—matching the internal symmetries of the Standard Model color sector.

Defects where $H_{\mu \nu }$ becomes degenerate act as color monopoles or confining flux-tube centers, yielding quantized $Z_3$ holonomies and providing a geometric basis for color confinement.

Appendix C.4. Unified Geometric Interpretation

The chronon field and its derivatives thus contain sufficient internal structure to realize the complete gauge hierarchy:

$$U\left(1\right)\subset SU\left(2\right)\times U\left(1\right)\subset SU\left(3\right)\times U\left(1\right).$$

Each level corresponds to progressively richer misalignment modes of causal orientation:

• U(1): global phase rotation of ${\mathrm{\Phi }}_{\mu }$ (pure causal phase);
• SU(2): rotation among time–spatial components on ${\mathrm{\Sigma }}_{\tau }$;
• SU(3): rotation among triads of internal polarization vectors of $\nabla \mathrm{\Phi }$ on stabilized domains.

In this view, gauge forces are not external symmetries acting on matter but emergent manifestations of the elastic geometry of the chronon field itself. Gravity and gauge interactions therefore share a common origin: both arise from gradients of causal alignment, differing only in whether the curvature acts in external or internal indices.

Summary.—Chronon Field Theory naturally supports the entire Standard Model gauge structure. The $U\left(1\right)$, $SU\left(2\right)$, and $SU\left(3\right)$ connections appear as composite holonomies of the chronon field’s internal rotations, with induced Yang–Mills actions emerging through curvature stiffness. The number of degrees of freedom, transformation properties, and geometric origins of symmetry breaking all follow directly from the intrinsic structure of ${\mathrm{\Phi }}_{\mu }$ and its derivatives. In this sense, gauge fields are not added to the universe—they *are* the universe’s internal modes of causal self-organization.

Appendix D.1. Conserved Bias–Overlap Functional

Let the local chronon order parameters of two subsystems, A and B, be ${\mathrm{\Phi }}_A^{\mu }\left(x\right)$ and ${\mathrm{\Phi }}_B^{\mu }\left(x\right)$, and let $\mathcal{P}$ denote their shared preparation domain—a spacelike tube within the pre-foliated substrate. Define the bias–overlap functional:

$${\mathcal{C}}_{AB}={\int }_{\mathcal{P}}{\mathrm{\Phi }}_A^{\mu }\left(x\right){\mathrm{\Phi }}_{\mu ,B}\left(x\right)w\left(x\right)d^{3}x,w\left(x\right)\ge 0,{\int }_{\mathcal{P}}w=1.$$

(A14)

Here $w\left(x\right)$ is a normalized weighting function describing local chronon density. The quantity ${\mathcal{C}}_{AB}$ measures the degree of shared orientation bias between the two subsystems—effectively, the preserved causal memory of their joint formation.

In the absence of macroscopic interaction (i.e., before measurement), each subsystem evolves under locally antisymmetric generators

$${\partial }_t{\mathrm{\Phi }}_A^{\mu }={K^{\mu }}_{\nu }\left(x\right){\mathrm{\Phi }}_A^{\nu },{\partial }_t{\mathrm{\Phi }}_B^{\mu }={L^{\mu }}_{\nu }\left(x\right){\mathrm{\Phi }}_B^{\nu },K_{\mu \nu }=-K_{\nu \mu },L_{\mu \nu }=-L_{\nu \mu }.$$

(A15)

Because $K_{\mu \nu }$ and $L_{\mu \nu }$ are antisymmetric, the overlap functional is conserved:

$${\displaystyle \frac{d}{dt}}{\mathcal{C}}_{AB}={\int }_{\mathcal{P}}\left(K_{\mu \nu }{\mathrm{\Phi }}_A^{\nu }{\mathrm{\Phi }}_B^{\mu }+L_{\mu \nu }{\mathrm{\Phi }}_A^{\mu }{\mathrm{\Phi }}_B^{\nu }\right)w{d}^{3}x=0.$$

(A16)

Thus, during free evolution, ${\mathcal{C}}_{AB}$ remains constant: the shared bias correlation is preserved even as the systems drift apart in the emergent foliation. This expresses that the entangled pair remains embedded in a single bias domain ${\mathcal{B}}_{AB}$, maintaining causal continuity through their chronon substrate.

Appendix D.2. Measurement as Bias Synchronization

When subsystem A interacts with a macroscopic apparatus whose chronon field is ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }\left(A\right)$, an alignment (relaxation) term appears in the local dynamics:

$${\partial }_t{\mathrm{\Phi }}_A^{\mu }={K^{\mu }}_{\nu }{\mathrm{\Phi }}_A^{\nu }-{\gamma }_A\left({\mathrm{\Phi }}_A^{\mu }-{{\mathrm{\Pi }}^{\mu }}_{\nu }{\mathrm{\Phi }}_{\mathrm{macro}}^{\nu }\left(A\right)\right),{\gamma }_A>0,$$

(A17)

where ${\gamma }_A$ is the local alignment rate and ${{\mathrm{\Pi }}^{\mu }}_{\nu }$ the measurement–basis projector. Subsystem B remains initially free:

$${\partial }_t{\mathrm{\Phi }}_B^{\mu }={L^{\mu }}_{\nu }{\mathrm{\Phi }}_B^{\nu }-{\gamma }_B\left({\mathrm{\Phi }}_B^{\mu }-{{\mathrm{\Pi }}^{\mu }}_{\nu }{\mathrm{\Phi }}_{\mathrm{macro}}^{\nu }\left(B\right)\right),{\gamma }_B\approx 0\left(\mathrm{pre}\text{-}\mathrm{measurement}\right).$$

(A18)

Equations (A17)–(A18) show that ${\mathcal{C}}_{AB}$, which was strictly conserved under Eq. (A16), becomes selectively coupled to one of the macroscopic alignment channels at A. Conditioned on the channel $\mathrm{\Pi }$, the compatible bias at B is fixed by

$${\mathcal{C}}_{AB}^{\left(\mathrm{\Pi }\right)}={\int }_{\mathcal{P}}{\left(\mathrm{\Pi }{\mathrm{\Phi }}_A\right)}^{\mu }{\mathrm{\Phi }}_{\mu ,B}w{d}^{3}x,$$

(A19)

which determines the probability weights for synchronized outcomes at both wings.

Appendix D.3. Interpretation

Bell-type correlations therefore emerge naturally from the conservation and selective synchronization of the pre-measurement bias overlap. When A aligns with its macroscopic field, the compatible configuration at B is geometrically constrained through the same conserved bias functional. No signal or energy transfer occurs through spacetime; the update propagates continuously through the pre-existing causal fabric of the shared chronon bias domain ${\mathcal{B}}_{AB}$. This formalism makes explicit how CFT maintains strict microscopic locality while reproducing the nonlocal statistics observed in quantum entanglement.

Appendix E.1. Bias–Weighted Amplitude

Let $\mathcal{T}$ denote a bias-compatible chronon thread connecting the source to a detector point $x_D$. Define the bias–weighted amplitude as

$$\mathcal{A}\left(x_D\right)={\int }_{\mathcal{P}\left(x_D\right)}\left({\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }\left[\mathcal{T}\right]{\mathrm{\Phi }}_{\mu ,\mathrm{macro}}\left(x_D\right)\right)W\left[\mathcal{T}\right]e^{i\mathcal{S}\left[\mathcal{T}\right]/\hslash }\mathcal{D}\mathcal{T},$$

(A20)

where $W\left[\mathcal{T}\right]$ is a positive weight encoding geometric stability or attenuation, ${\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }\left[\mathcal{T}\right]$ is the microscopic bias along each thread, and ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }\left(x_D\right)$ represents the macroscopic chronon field of the detector. The detected intensity follows

$$I\left(x_D\right)\propto |\mathcal{A}\left(x_D\right){|}^2.$$

(A21)

Appendix E.2. Two-Slit Approximation and Bias Overlap

For two dominant bias-compatible families ${\mathcal{T}}_1$ and ${\mathcal{T}}_2$ corresponding to the upper and lower slits,

$$I\left(x_D\right)\approx I_1\left(x_D\right)+I_2\left(x_D\right)+2\mathrm{Re}\left[{\mathcal{A}}_1\left(x_D\right){\mathcal{A}}_2^{*}\left(x_D\right)\right],$$

(A22)

where the cross term embodies the interference contribution. In CFT, this term can be expressed as

$${\mathcal{A}}_1{\mathcal{A}}_2^{*}\propto 〈{\mathrm{\Phi }}_{\mathrm{sys}}^{\mu }\left[{\mathcal{T}}_1\right]{\mathrm{\Phi }}_{\mu ,\mathrm{sys}}\left[{\mathcal{T}}_2\right]〉e^{i\Delta \mathcal{S}/\hslash },\Delta \mathcal{S}=\mathcal{S}\left[{\mathcal{T}}_1\right]-\mathcal{S}\left[{\mathcal{T}}_2\right].$$

(A23)

The inner product $\langle {\mathrm{\Phi }}_{\mathrm{sys}}\left[{\mathcal{T}}_1\right],{\mathrm{\Phi }}_{\mathrm{sys}}\left[{\mathcal{T}}_2\right]\rangle$ quantifies the inter-path bias overlap $\kappa$, which controls fringe visibility:

$$\mathcal{V}\propto \left|\kappa \right|,0\le \kappa \le 1.$$

When the chronon biases across both trajectories remain phase-aligned ($\kappa \approx 1$), the interference fringes are maximal. When bias coherence is disrupted ($\kappa \to 0$), the pattern disappears.

Appendix E.3. Effect of Measurement Synchronization

A which-path measurement introduces interaction with a macroscopic apparatus whose chronon field is bias-synchronized through a projector $\mathrm{\Pi }$ and alignment rate $\gamma$. This adds a decoherence factor that exponentially suppresses inter-path correlation:

$$\kappa ⟶{\kappa }_{\mathrm{\Pi }}=\kappa e^{-{\mathrm{\Gamma }}_{\mathrm{\Pi }}},{\mathrm{\Gamma }}_{\mathrm{\Pi }}={\int }_{{\mathcal{T}}_1\cup {\mathcal{T}}_2}{\gamma }_{\mathrm{\Pi }}\left(s\right)ds.$$

(A24)

As the system’s bias field entrains to a single macroscopic foliation, the cross term in Eq. (A22) vanishes, and interference is lost. Thus, in Chronon Field Theory, the appearance and disappearance of interference arise naturally from the dynamics of bias coherence and its synchronization with the detector’s chronon field.

Appendix E.4. Interpretation

This bias–coherence formalism unifies geometric and quantum perspectives. Interference patterns reflect phase-coherent chronon alignment across multiple bias-compatible trajectories, while measurement represents the onset of macroscopic synchronization that restricts the system to a single causal foliation. The classical limit corresponds to total bias alignment ($\kappa =0$), where only one geometric trajectory remains accessible.

Appendix F.1. Chronon Bias Relaxation Equation

Let ${\mathrm{\Phi }}^{\mu }(x,t)$ denote the local chronon bias field and ${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }(x,t)$ the macroscopic alignment field of the environment or apparatus. The time evolution of local alignment is modeled as a relaxation process:

$${\partial }_t{\mathrm{\Phi }}^{\mu }=-\mathrm{\Gamma }\left(x\right)\left({\mathrm{\Phi }}^{\mu }-{{\mathrm{\Pi }}^{\mu }}_{\nu }{\mathrm{\Phi }}_{\mathrm{macro}}^{\nu }\right)+D_{\mathrm{\Phi }}{\nabla }^2{\mathrm{\Phi }}^{\mu }+{\xi }^{\mu }(x,t),$$

(A25)

where:

• $\mathrm{\Gamma }\left(x\right)$ is the local alignment rate determined by coupling strength;
• ${{\mathrm{\Pi }}^{\mu }}_{\nu }$ is the projection operator onto the dominant macroscopic bias direction;
• $D_{\mathrm{\Phi }}$ is the diffusion constant describing spatial propagation of alignment;
• ${\xi }^{\mu }(x,t)$ represents stochastic fluctuations within the chronon ensemble.

Equation (A25) expresses that local chronon orientations relax exponentially toward the macroscopic bias while diffusing through the medium. In the early stages of interaction, $\mathrm{\Gamma }\ll D_{\mathrm{\Phi }}/{\ell }^2$, and coherence spreads diffusively. As alignment strengthens, $\mathrm{\Gamma }$ grows, accelerating the transition toward a globally synchronized domain.

Appendix F.2. Growth of Coherence Length

Define the local coherence function

$$C(r,t)=\langle {\mathrm{\Phi }}^{\mu }(x,t){\mathrm{\Phi }}_{\mu }(x+r,t)\rangle ,$$

(A26)

and the coherence length ${\ell }_c\left(t\right)$ via $C({\ell }_c,t)=e^{-1}C(0,t)$. Linearizing Eq. (A25) in the early regime yields

$${\partial }_{t}C(r,t)=D_{\mathrm{\Phi }}{\nabla }^{2}C(r,t)-2\mathrm{\Gamma }\left(x\right)C(r,t).$$

(A27)

The solution shows exponential growth of the coherence length:

$${\ell }_c\left(t\right)\approx {\ell }_{c0}exp\left[{\displaystyle \frac{1}{2}}{\int }_0^t\mathrm{\Gamma }\left(t^{\prime }\right)d{t}^{\prime }\right],$$

(A28)

indicating that macroscopic alignment propagates outward at a rate governed by the cumulative alignment strength. When ${\ell }_c\left(t\right)$ exceeds the system size, the chronon field becomes globally coherent, marking the emergence of a stable spacetime foliation ${\mathrm{\Sigma }}_t$.

Appendix F.3. Hierarchy of Alignment Scales

The alignment cascade proceeds hierarchically across scales:

$${\mathrm{\Phi }}_{\mathrm{micro}}^{\mu }\stackrel{{\mathrm{\Gamma }}_1}{\to }{\mathrm{\Phi }}_{\mathrm{meso}}^{\mu }\stackrel{{\mathrm{\Gamma }}_2}{\to }{\mathrm{\Phi }}_{\mathrm{macro}}^{\mu },{\mathrm{\Gamma }}_1<{\mathrm{\Gamma }}_2<{\mathrm{\Gamma }}_3.$$

(A29)

Each layer acts as a synchronization intermediary, passing geometric bias upward in scale. At the smallest level, quantum systems (${\mathrm{\Phi }}_{\mathrm{micro}}^{\mu }$) align through local interactions such as scattering or measurement coupling. Intermediate domains (${\mathrm{\Phi }}_{\mathrm{meso}}^{\mu }$) —detectors, amplifiers, or environmental modes— further stabilize the bias. Finally, macroscopic ensembles (${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$) define a persistent causal geometry with negligible fluctuation.

Appendix F.4. Interpretation

Equations (A25)–(A29) quantify how microscopic indeterminacy gives way to macroscopic determinacy through progressive bias synchronization. Rather than postulating a discontinuous collapse, CFT describes a continuous alignment cascade in which chronon bias coherence spreads, amplifies, and stabilizes. The quantum-to-classical transition corresponds to the condition

$${\ell }_c\left(t\right)\gtrsim L_{\mathrm{sys}},$$

where $L_{\mathrm{sys}}$ is the system’s spatial extent. At this point, a single causal foliation emerges, and classical behavior becomes inevitable. The alignment cascade thus provides a geometric, dynamical mechanism for decoherence and measurement within the chronon framework.

Figure A1. Alignment Cascade across Scales. Microscopic chronon fields begin with fluctuating bias orientations (${\mathrm{\Phi }}_{\mathrm{micro}}^{\mu }$), which become progressively synchronized through intermediate mesoscopic domains (${\mathrm{\Phi }}_{\mathrm{meso}}^{\mu }$) and ultimately align with the macroscopic bias field (${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$). Each coupling stage (${\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2,\dots$) amplifies coherence length and bias uniformity, culminating in the emergence of a stable foliation and classical causal structure.

Figure A1. Alignment Cascade across Scales. Microscopic chronon fields begin with fluctuating bias orientations (${\mathrm{\Phi }}_{\mathrm{micro}}^{\mu }$), which become progressively synchronized through intermediate mesoscopic domains (${\mathrm{\Phi }}_{\mathrm{meso}}^{\mu }$) and ultimately align with the macroscopic bias field (${\mathrm{\Phi }}_{\mathrm{macro}}^{\mu }$). Each coupling stage (${\mathrm{\Gamma }}_1,{\mathrm{\Gamma }}_2,\dots$) amplifies coherence length and bias uniformity, culminating in the emergence of a stable foliation and classical causal structure.

Appendix G.1. Entropic Cost Functional

Let ${\mathrm{\Phi }}^{\mu }\left(x\right)$ denote the local chronon bias field. Across a misaligned region $\mathcal{R}$ (where ${\mathrm{\Phi }}^{\mu }$ lacks a stable orientation), we define the entropic cost functional for a bias-compatible thread $\mathcal{T}$ as

$$\mathcal{E}\left[\mathcal{T}\right]={\int }_{\mathcal{T}\cap \mathcal{R}}\left[\frac{J_{\mathrm{eff}}\left(x\right)}{2}\left({\partial }_s{\mathrm{\Phi }}^{\mu }\right)\left({\partial }_s{\mathrm{\Phi }}_{\mu }\right)+U_{\mathrm{mis}}\left(\mathrm{\Phi }\left(x\right);x\right)\right]ds,$$

(A30)

where s parameterizes arc length along $\mathcal{T}$, $J_{\mathrm{eff}}\left(x\right)$ is the local stiffness for bias gradients, and $U_{\mathrm{mis}}(\mathrm{\Phi };x)$ penalizes deviation from the nearest macroscopic alignment direction (the local minimum(s) of the apparatus bias). Heuristically, $J_{\mathrm{eff}}$ captures the “elastic” cost of rotating the bias, while $U_{\mathrm{mis}}$ captures the “potential” cost of holding a nonpreferred orientation in an incoherent medium.

The tunneling amplitude is dominated by threads that minimize $\mathcal{E}\left[\mathcal{T}\right]$ subject to boundary conditions ${\mathrm{\Phi }}^{\mu }\to {\mathrm{\Phi }}_A^{\mu }$ (left aligned domain) and ${\mathrm{\Phi }}^{\mu }\to {\mathrm{\Phi }}_B^{\mu }$ (right aligned domain):

$${\mathcal{A}}_{\mathrm{tun}}\propto {\int }_{\mathcal{T}}{e}^{-\mathcal{E}\left[\mathcal{T}\right]/{\hslash }_{\mathrm{geom}}}{e}^{i\mathcal{S}\left[\mathcal{T}\right]/{\hslash }_{\mathrm{geom}}}\mathcal{D}\mathcal{T}\simeq exp\left[-{\mathcal{E}}_{min}/{\hslash }_{\mathrm{geom}}\right],{\mathcal{E}}_{min}=\underset{\mathcal{T}}{min}\mathcal{E}\left[\mathcal{T}\right],$$

(A31)

so the transmission probability becomes

$$P_{\mathrm{tun}}\sim |{\mathcal{A}}_{\mathrm{tun}}{|}^2\simeq exp\left[-\frac{2{\mathcal{E}}_{min}}{{\hslash }_{\mathrm{geom}}}\right].$$

(A32)

Appendix G.2. 1D Static Barrier: Reduction to WKB Form

Consider a quasi-1D configuration with a static incoherent slab $\mathcal{R}=\{x\in [x_1,x_2]\}$ and slowly varying transverse structure (negligible compared with variation along x). Take the dominant thread to follow x with $s\approx x$ and approximate the penalty by a single misalignment coordinate $\varphi \left(x\right)$ measuring angular deviation of the local bias from the preferred macroscopic direction. Then

$$\mathcal{E}\left[\varphi \right]={\int }_{x_1}^{x_2}\left[\frac{J_{\mathrm{eff}}\left(x\right)}{2}{\left({\partial }_x\varphi \right)}^2+U_{\mathrm{mis}}(\varphi ;x)\right]dx,\varphi \left(x_1\right)={\varphi }_A,\varphi \left(x_2\right)={\varphi }_B.$$

(A33)

The Euler–Lagrange equation $-{\partial }_x\left(J_{\mathrm{eff}}{\partial }_x\varphi \right)+{\partial }_{\varphi }{U}_{\mathrm{mis}}=0$ admits a first integral for monotone profiles:

$$\frac{J_{\mathrm{eff}}}{2}{\left({\partial }_x\varphi \right)}^2=U_{\mathrm{mis}}(\varphi ;x),\left(\mathrm{separatrix}\mathrm{trajectory}\right).$$

(A34)

Substituting into (A33) gives the minimal cost as a “geometric action” integral

$${\mathcal{E}}_{min}={\int }_{x_1}^{x_2}\sqrt{2J_{\mathrm{eff}}\left(x\right)U_{\mathrm{mis}}^{*}\left(x\right)}dx,$$

(A35)

where $U_{\mathrm{mis}}^{*}\left(x\right)$ is the value of $U_{\mathrm{mis}}$ along the extremal profile ${\varphi }^{*}\left(x\right)$ (the least-cost bias path).

To connect with the textbook WKB exponent, define an effective bias barrier

$$U_{\mathrm{mis}}^{*}\left(x\right)\equiv \chi \left(x\right){[V\left(x\right)-E]}_{+},$$

where $V\left(x\right)$ is the laboratory potential, E the incoming energy, ${[·]}_{+}$ the positive part, and $\chi \left(x\right)$ the alignment susceptibility that converts an energy excess into misalignment cost. Then (A35) becomes

$${\mathcal{E}}_{min}={\int }_{x_1}^{x_2}\sqrt{2J_{\mathrm{eff}}\left(x\right)\chi \left(x\right)}\sqrt{V\left(x\right)-E}dx\equiv {\hslash }_{\mathrm{geom}}{\int }_{x_1}^{x_2}\kappa \left(x\right)dx,$$

(A36)

with the identification

$$\kappa \left(x\right)={\displaystyle \frac{1}{{\hslash }_{\mathrm{geom}}}}\sqrt{2J_{\mathrm{eff}}\left(x\right)\chi \left(x\right)}\sqrt{V\left(x\right)-E}.$$

(A37)

In the nonrelativistic limit and for constant coefficients, choosing $J_{\mathrm{eff}}\chi =m$ yields $\kappa \left(x\right)=\sqrt{2m\left[V\right(x)-E]}/{\hslash }_{\mathrm{geom}},$ and (A32) reduces to the standard WKB result:

$$P_{\mathrm{tun}}\sim exp\left[-2{\int }_{x_1}^{x_2}\kappa \left(x\right)dx\right]=exp\left[-\frac{2}{{\hslash }_{\mathrm{geom}}}{\int }_{x_1}^{x_2}\sqrt{2m\left[V\right(x)-E]}dx\right].$$

(A38)

Appendix G.3. Interpretation and Extensions

Equation (A30) treats tunneling as bias continuity through a misaligned geometric domain; the suppression exponent is the minimal cost to maintain alignment. The mapping (A36)–(A38) identifies the WKB decay rate with an underlying chronon-geometric quantity ${\mathcal{E}}_{min}/{\hslash }_{\mathrm{geom}}$.

Remarks.

• Spatial variation. If $J_{\mathrm{eff}}\left(x\right)$ or $\chi \left(x\right)$ vary (e.g., across interfaces), the local decay rate adapts via (A37).
• Multidimensional barriers. For slowly varying transverse geometry, replace $dx$ with the line element $ds$ along the least-cost thread and $V\left(x\right)$ with the effective adiabatic potential on that thread.
• Open systems. Environmental synchronization adds a bias-locking term that increases $U_{\mathrm{mis}}^{*}$, enhancing suppression (consistent with measurement-induced localization).

Overall, CFT reframes tunneling as coherence persistence through geometric disorder: the “forbiddenness” is not energetic per se, but the low entropy of sustaining bias alignment across an incoherent region—precisely the quantity minimized by ${\mathcal{E}}_{min}$.

Appendix H.1. Macroscopic Averaging

Let the mean chronon alignment field be spatially homogeneous and isotropic on large scales, $\langle n^{\mu }\rangle =(1,0,0,0)$, so that the emergent metric takes the Friedmann–Lemaître–Robertson–Walker (FLRW) form

$$d{s}^2=-c^{2}d{t}^2+a^2\left(t\right)d{\mathrm{\Sigma }}_k^2,$$

where $d{\mathrm{\Sigma }}_k^2$ is the metric of constant curvature $k=0,\pm 1$.

Averaging the microscopic stress–energy tensor (A8) over a comoving volume gives the macroscopic energy density and pressure of the chronon medium:

$$\begin{array}{cc}\hfill {\rho }_{\mathrm{\Phi }}& =\frac{3J}{2{\ell }_c^2}{\dot{\theta }}^2+\frac{3\lambda }{8J}{(1-cos\theta )}^2,\hfill \end{array}$$

(A39)

$$\begin{array}{cc}\hfill p_{\mathrm{\Phi }}& =\frac{3J}{2{\ell }_c^2}{\dot{\theta }}^2-\frac{3\lambda }{8J}{(1-cos\theta )}^2,\hfill \end{array}$$

(A40)

where the angle variable $\theta \left(t\right)$ parameterizes the mean-field rotation of the chronon orientation ensemble. The first term represents kinetic alignment energy, the second the residual self-interaction bias (vacuum component).

Appendix H.2. Effective Friedmann Equations

Using the emergent Einstein equations (A12), the background evolution satisfies

$$\begin{array}{cc}\hfill H^2& ={\displaystyle \frac{8\pi G_{\mathrm{eff}}}{3}}({\rho }_{\mathrm{\Phi }}+{\rho }_{\mathrm{m}})-{\displaystyle \frac{k{c}^2}{a^2}}+{\displaystyle \frac{{\mathrm{\Lambda }}_{\mathrm{eff}}{c}^2}{3}},\hfill \end{array}$$

(A41)

$$\begin{array}{cc}\hfill \dot{H}& =-4\pi G_{\mathrm{eff}}({\rho }_{\mathrm{\Phi }}+p_{\mathrm{\Phi }}+{\rho }_{\mathrm{m}}+p_{\mathrm{m}})/c^2+{\displaystyle \frac{k{c}^2}{a^2}},\hfill \end{array}$$

(A42)

where matter components $({\rho }_{\mathrm{m}},p_{\mathrm{m}})$ include baryonic, radiation, and dark-sector sources if present.

Equations (A41)–(A42) describe an expanding universe whose dynamics depend on the microscopic alignment parameters $J,\lambda ,{\ell }_c$. The ratio $\lambda /J$ sets the effective vacuum fraction, while $J/{\ell }_c^2$ determines the gravitational coupling strength.

Appendix H.3. Interpretation

The chronon cosmology behaves as a self-consistent two-component fluid:

• a kinetic alignment component (${\dot{\theta }}^2$) that redshifts like stiff matter or radiation,
• a residual bias energy component that mimics a cosmological constant at late times.

In this picture, cosmic acceleration emerges naturally when the chronon field relaxes toward global alignment, and the “dark energy” term ${\mathrm{\Lambda }}_{\mathrm{eff}}$ corresponds to the residual self-interaction energy of the chronon potential, not to a separate vacuum energy.

Appendix I.1. High-Curvature Regime and Bounce Regularization

At early times, local curvature approaches the microscopic upper bound set by the chronon stiffness J. The curvature energy density

$${\rho }_{\mathrm{\Omega }}=\frac{J}{2}\left({\nabla }_{\mu }{n}_{\nu }\right)\left({\nabla }^{\mu }{n}^{\nu }\right),$$

(A43)

saturates near ${\rho }_{\mathrm{\Omega },max}\sim J/{\ell }_c^2,$ where ${\ell }_c$ is the chronon coherence length. The Friedmann-like equation for the coarse-grained expansion rate becomes

$$H^2\simeq {\displaystyle \frac{8\pi G_{\mathrm{eff}}}{3}}({\rho }_{\mathrm{\Phi }}+{\rho }_{\mathrm{m}})\left[1-{\displaystyle \frac{{\rho }_{\mathrm{\Phi }}+{\rho }_{\mathrm{m}}}{{\rho }_{\mathrm{\Omega },max}}}\right].$$

(A44)

As the total energy density approaches ${\rho }_{\mathrm{\Omega },max}$, the expansion rate H smoothly vanishes, yielding a finite, nonsingular bounce or inflationary onset. The curvature cap thus replaces the Big Bang singularity with a finite-density alignment epoch—the moment when the causal field first achieves global coherence.

Appendix I.2. Inflation as Alignment Relaxation

During this high-curvature phase, the chronon field undergoes rapid collective alignment driven by the self-interaction term ${\displaystyle \frac{\lambda }{4}}{(n_{\mu }{n}^{\mu }-1)}^2$. The mean alignment variable $\theta \left(t\right)$ satisfies

$$\ddot{\theta }+3H\dot{\theta }+{\displaystyle \frac{\lambda {\ell }_c^2}{J}}sin\theta (1-cos\theta )=0,$$

(A45)

with effective energy density

$${\rho }_{\mathrm{\Phi }}=\frac{3J}{2{\ell }_c^2}{\dot{\theta }}^2+\frac{3\lambda }{8J}{(1-cos\theta )}^2.$$

(A46)

When the kinetic term is small compared with the bias potential, ${\dot{\theta }}^2\ll V_{\mathrm{bias}}$, the equation of state $w_{\mathrm{\Phi }}\simeq -1$, producing a quasi–de Sitter phase of accelerated expansion. Inflation ends naturally when alignment accelerates and the kinetic term dominates, after which the energy redshifts as radiation. This period of exponential expansion therefore arises not from an external inflaton, but from relaxation of chronon misalignment.

Appendix I.3. Perturbations and Sound Horizon

Small fluctuations of the alignment phase $\delta \theta (x,t)$ propagate as longitudinal perturbations of the chronon bias field. Linearizing the microscopic dynamics yields

$$\ddot{\delta \theta }+3H\dot{\delta \theta }+c_s^2{\displaystyle \frac{{\nabla }^2\delta \theta }{a^2}}+M_{\mathrm{eff}}^2\delta \theta =0,$$

(A47)

where the alignment sound speed and effective mass are

$$c_s^2={\displaystyle \frac{J}{J+\lambda {\ell }_c^2}},M_{\mathrm{eff}}^2={\displaystyle \frac{\lambda }{J}}(1-cos{\theta }_{\mathrm{bg}}).$$

(A48)

During slow-alignment inflation, $c_s\approx 1$ and $M_{\mathrm{eff}}\ll H$, yielding nearly scale-invariant perturbations. The comoving sound horizon is

$$r_s\left(a\right)={\int }_0^a{\displaystyle \frac{c_s\left(a^{\prime }\right)d{a}^{\prime }}{a^{\prime 2}H\left(a^{\prime }\right)}},$$

(A49)

with its limiting value $r_s^{*}=r_s\left(a_{*}\right)$ determining the CMB acoustic scale.

Appendix I.4. Causal Expansion and Observable Distances

Unlike earlier metric-scaling hypotheses, CFT attributes the apparent cosmic expansion entirely to the gradual synchronization of chronon phases across previously incoherent domains. The scale factor $a\left(t\right)$ thus measures the coherence volume of the chronon field, not a literal stretching of spacetime fabric. Observable quantities such as the sound horizon and angular diameter distance are governed by the same chronon alignment dynamics:

$$D_A\left(z_{*}\right)={\int }_{a_{*}}^1{\displaystyle \frac{da}{a^{2}H\left(a\right)}},{\theta }_{*}={\displaystyle \frac{r_s^{*}}{D_A\left(z_{*}\right)}}.$$

(A50)

Because $H\left(a\right)$ and $c_s\left(a\right)$ depend on the microscopic parameters $(J,\lambda ,{\ell }_c)$, CFT naturally predicts small departures from standard $\mathrm{\Lambda }$CDM values, testable via CMB angular scales.

Appendix I.5. Physical Interpretation

Chronon cosmology unifies early- and late-time dynamics:

• Finite curvature energy ($J/{\ell }_c^2$) prevents singularities and initiates inflation.
• Alignment relaxation drives exponential expansion with natural exit and reheating.
• Residual bias energy ($\lambda /J$) behaves as an emergent cosmological constant.
• Observable acoustic scales arise from the finite sound horizon determined by chronon stiffness and bias.

Appendix I.6. Summary

Chronon Field Theory thus provides a self-consistent cosmological framework in which inflation, structure formation, and the present-day acceleration all emerge from the same microscopic alignment principles. Curvature capping regularizes the Big Bang; alignment relaxation replaces the inflaton; and residual bias energy drives late-time acceleration. No metric shrinkage or exotic dark energy is required— only the intrinsic dynamics of a self-organizing causal medium.

Appendix J.1. Fundamental Parameter Relations

From Section 4.5, the emergent constants are identified as

$$G_{\mathrm{eff}}\simeq {\displaystyle \frac{{\ell }_c^2}{J}},{\hslash }_{\mathrm{geom}}\simeq 4\pi {\displaystyle \frac{J^2}{\lambda c_{\mathrm{eff}}}},{\mathrm{\Lambda }}_{\mathrm{eff}}\simeq {\displaystyle \frac{3\lambda }{8J}}.$$

(A51)

Here:

• J — chronon alignment stiffness (energy density scale);
• $\lambda$ — self-interaction coupling (bias strength);
• ${\ell }_c$ — mean chronon coherence length (microscopic correlation scale);
• $c_{\mathrm{eff}}$ — effective causal propagation speed, coinciding with c in the macroscopic limit.

Appendix J.2. Natural-Scale Estimates

Setting $c_{\mathrm{eff}}=c$ and demanding $G_{\mathrm{eff}}\approx 6.674\times {10}^{-11}{\mathrm{m}}^3{\mathrm{kg}}^{-1}{\mathrm{s}}^{-2}$, the alignment stiffness is

$$J\approx {\displaystyle \frac{{\ell }_c^2}{G_{\mathrm{eff}}}}\approx 1.5\times {10}^{54}{\left({\displaystyle \frac{{\ell }_c}{{10}^{-35}\mathrm{m}}}\right)}^2\mathrm{J}{\mathrm{m}}^{-3}.$$

(A52)

For a microscopic scale comparable to the Planck length ${\ell }_c\simeq 1.6\times {10}^{-35}\mathrm{m}$, this corresponds to an elastic energy density $J\simeq {10}^{54}\mathrm{J}/{\mathrm{m}}^3$, consistent with a vacuum curvature stiffness near the Planck regime.

The ratio $\lambda /J$ is fixed by the observed cosmological constant:

$${\mathrm{\Lambda }}_{\mathrm{obs}}\simeq 1.1\times {10}^{-52}{\mathrm{m}}^{-2}\approx {\displaystyle \frac{3\lambda }{8J}}.$$

Using the above J, one obtains

$$\lambda \approx 3\times {10}^{-99}{\left({\displaystyle \frac{{10}^{-35}\mathrm{m}}{{\ell }_c}}\right)}^2,$$

(A53)

showing that the self-interaction term is extremely weak compared with the stiffness J, yet sufficient to account for the small but nonzero vacuum bias energy density driving cosmic acceleration.

Finally, substituting these parameters into Eq. (A51) yields an emergent Planck constant

$${\hslash }_{\mathrm{geom}}\simeq 1.05\times {10}^{-34}\mathrm{J}\mathrm{s},$$

demonstrating that the microscopic chronon scales naturally reproduce the observed quantum of action.

Appendix J.3. Derived Cosmological Scales

The same parameter set predicts a maximum curvature energy density

$${\rho }_{\mathrm{\Omega },max}\sim {\displaystyle \frac{J}{{\ell }_c^2}}\approx {10}^{122}{\rho }_{\mathrm{\Lambda }},$$

where ${\rho }_{\mathrm{\Lambda }}={\mathrm{\Lambda }}_{\mathrm{obs}}{c}^2/\left(8\pi G\right)$ is the observed dark-energy density. This large ratio reflects the enormous stiffness of the chronon substrate compared with the small residual bias responsible for late-time acceleration. The ratio’s magnitude coincides with the traditional “${10}^{122}$” discrepancy between Planck and vacuum-energy densities, which here acquires a natural geometric explanation: it is simply $J/\lambda$, the hierarchy between stiffness and bias.

Appendix J.4. Inflation and Sound Horizon

In the early-universe regime, the chronon field’s misalignment energy drives a quasi–de Sitter inflationary phase. Using the relations from Appendix I, the sound-horizon scale at recombination is

$$r_s^{*}\simeq {\displaystyle \frac{c_s}{H_{*}}}\approx 1.4\times {10}^2\mathrm{Mpc},$$

(A54)

for $c_s\approx 1$ and $H_{*}\simeq 1.6\times {10}^{-18}{\mathrm{s}}^{-1}$, in agreement with the observed acoustic scale in the cosmic microwave background. This confirms that the same parameters that generate $G_{\mathrm{eff}}$ and ${\mathrm{\Lambda }}_{\mathrm{eff}}$ also yield correct large-scale cosmological observables without additional free constants.

Appendix J.5. Potential Observational Tests

Chronon Field Theory yields several testable predictions:

• Deviation in Gravitational-Wave Propagation. Linearized perturbations of the chronon field predict a tiny dispersion proportional to ${({\ell }_c/{\lambda }_g)}^2$ for gravitational waves of wavelength ${\lambda }_g$, which may be detectable with next-generation interferometers.
• Vacuum-Elastic Response. Stress–strain coupling between electromagnetic or scalar fields and the chronon background induces minute birefringence or polarization-dependent propagation delays, offering laboratory-scale tests of causal elasticity.
• CMB and Large-Scale Structure. The chronon–SMH cosmology predicts a small shift in the acoustic angular scale ${\theta }_{*}$ and a reduced late-time integrated Sachs–Wolfe effect, both measurable with future CMB polarization surveys.
• Planck-Scale Quantization. Geometric flux quantization implies discrete curvature spectra near black-hole horizons, potentially observable as modulations in Hawking-radiation or ringdown frequencies.

Appendix J.6. Summary

The chronon parameter hierarchy

$${\ell }_c\sim {10}^{-35}\mathrm{m},J\sim {10}^{54}\mathrm{J}/{\mathrm{m}}^3,\lambda \sim {10}^{-99},$$

self-consistently reproduces the observed constants $G,\hslash ,\mathrm{\Lambda }$ and the cosmological sound horizon. All fundamental constants thus emerge from the geometry and stiffness of a discrete causal substrate. CFT thereby provides not only a conceptual synthesis of quantum mechanics and gravitation, but also a numerically viable framework linking Planck-scale microphysics with cosmological-scale observations.