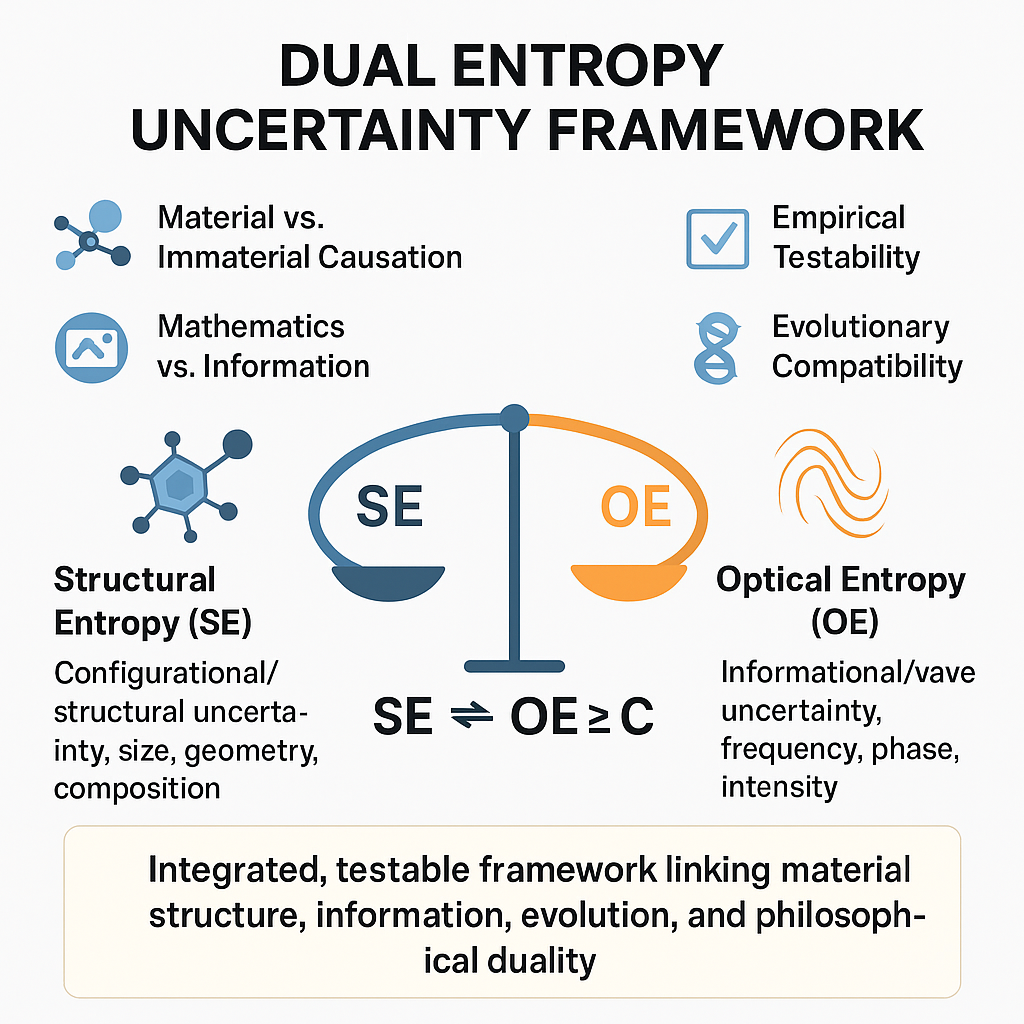
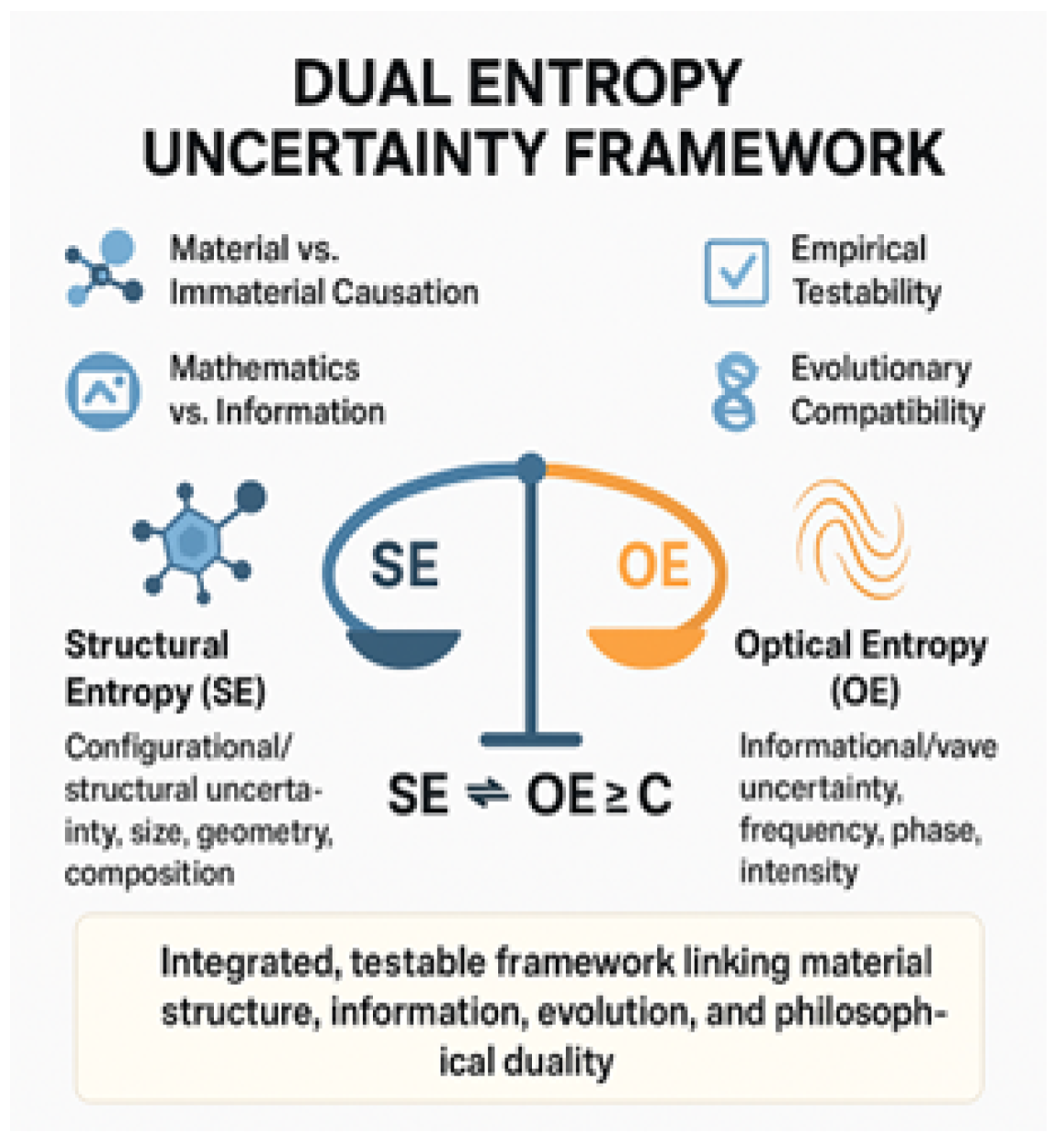
1. Introduction
The persistent question of how immaterial principles—such as information, consciousness, or mathematical order—can influence material systems has challenged natural science since antiquity [
1,
2,
3]. Modern physics recognizes wave–particle duality [
1], yet most biological and philosophical frameworks remain conceptually monistic, emphasizing either materialism or idealism. To reconcile these views, the Dual Entropy Uncertainty Framework (DEUF) formalizes a dual relationship between Structural Entropy (SE)—the entropy of physical structure—and Optical Entropy (OE)—the entropy of wave or informational states [
2,
4,
5]. This relationship extends uncertainty theory from quantum mechanics to all levels of natural organization, as illustrated in
Figure 1 below.
The interdependence of SE and OE is not merely an analogy. It can be examined empirically wherever the organization of matter produces measurable order in fields, waves, or signals. In solid-state physics, changes in lattice symmetry or defect concentration alter vibrational coherence and emission spectra; in living tissue, shifts in structural complexity are mirrored by variations in bio photonic or electromagnetic coherence [
6,
7]. Such observations imply that matter and information continually compensate for each other, maintaining an entropic equilibrium that allows organization without violating the second law of thermodynamics [
8].
From this perspective, DEUF offers a quantitative way to restate the problem of immaterial causation. The traditional philosophical puzzle—how the non-physical can influence the physical—arises only if information and matter are treated as ontologically separate. Within DEUF they are complementary: information (OE) is the wave-like expression of structure (SE). Changes in one domain necessarily produce measurable adjustments in the other, and causal reciprocity emerges as a property of the system itself rather than as an external intervention [
4,
9,
10].
The framework also provides a bridge between disciplines that have long used different vocabularies to describe the same reality. Quantum mechanics speaks of wave–particle duality; thermodynamics measures order and disorder; information theory quantifies uncertainty; biology studies structure and function [
2,
5,
11]. DEUF unites these descriptions under a single entropic law, suggesting that the persistence of order in any domain—physical, biological, or cognitive—depends on a dynamic balance between configurational uncertainty and informational coherence [
9,
12].
A generalized uncertainty relation is therefore needed. The classical Heisenberg form [
1] limits the simultaneous precision of two measurable quantities; the DEUF relation extends this idea to the organization of complex systems. It asserts that no system can reach total certainty in both its structural and informational dimensions, and that stability arises from the reciprocal trade-off between them [
13]. In this view, entropy is not simply a measure of disorder but a mediator between the tangible and intangible aspects of existence.
The following sections develop the theoretical foundation of this proposal. They define the structural and optical entropies formally, show how their product establishes a universal uncertainty bound, and demonstrate how this relation can account for observed phenomena ranging from material coherence and biological adaptation to the informational limits of cognition and cosmology [
14,
15].
2. Theoretical Foundations of the Dual Entropy Uncertainty Framework
The Dual Entropy Uncertainty Framework (DEUF) formalizes the principle that every organized system embodies two complementary measures of uncertainty: Structural Entropy (SE), representing configurational freedom in matter, and Optical Entropy (OE), representing informational or wave coherence. Together they describe how material structure and immaterial information maintain dynamic balance across physical and biological scales [
16,
17,
18].
2.1. Formal Definitions
Structural Entropy quantifies the probability distribution of distinct structural states—geometric configurations, compositional variations, or positional arrangements of matter. It follows a Shannon-type expression, SE=−ki∑pilnpi, where
is the probability of a given structural microstate and
is a proportional constant. SE rises as a system becomes structurally diverse or disordered [
2,
19].
Optical Entropy characterizes the uncertainty associated with wave or field states—frequency, wavelength, phase, or intensity distributions that encode information. It takes the analogous form, OE=−k′j∑qjlnqj, where
represents the probability of an optical or informational microstate. OE diminishes when waves or fields are coherent and increases when they are dispersed or noisy [
2,
19].
2.2. General Uncertainty Law
The reciprocal relation between these two entropies is expressed by the DEUF uncertainty condition, SE×OE≥C, C>0. The constant C represents the minimum entropic coupling of the system. Neither SE nor OE can vanish except at absolute zero, where all motion and information exchange cease. Thus the material and informational aspects of a system cannot be isolated: an increase in configurational complexity (SE ↑) entails a compensatory decrease in informational coherence (OE ↓), and vice versa [
1,
3,
20]. This principle generalizes the Heisenberg uncertainty relation from conjugate observables to conjugate entropic domains. While the Heisenberg form limits simultaneous precision in position and momentum, DEUF limits simultaneous certainty in structure and information. The product (SE × OE) defines the minimal dual uncertainty required for existence [
1,
20].
2.3. Physical Interpretation
In physical systems, SE corresponds to atomic or molecular configuration entropy, whereas OE reflects the coherence of electromagnetic or vibrational fields. When a crystal becomes disordered through thermal agitation or defect formation, SE increases and OE decreases. Conversely, during self-assembly or crystallization, SE falls while OE rises, producing more coherent vibrational or optical emission [
16,
18,
21].
At the cosmological limit, the universe exhibits extremely high SE—an immense structural manifold—and therefore minimal OE. This extreme yields the constancy of the speed of light: with SE maximized, OE approaches a single coherent state, fixing light’s propagation velocity as a universal constant [
22].
In living systems, SE measures structural or genomic diversity, while OE quantifies informational or electromagnetic coherence across tissues or neural networks. Biological adaptation, therefore, proceeds under an entropic compensation rule: structural innovation (increased SE) must be balanced by enhanced informational efficiency (decreased OE) to maintain systemic stability [
9,
10,
23].
2.4. Empirical Demonstrations
A distinctive strength of DEUF is that OE is empirically measurable. Two engineering studies already illustrate this property [
24].
Nuclear Power Plant Lifespan Prediction. Analysis of vibration spectra from operating reactors showed that declining OE coherence directly preceded structural fatigue. As SE increased due to material aging, OE fell below its steady baseline, signaling approaching instability. Thus OE functioned as an early diagnostic of entropy accumulation in complex machinery [
24].
Bridge Resonance Stability. In large-span bridges, OE was derived from vibration coherence data. OE remained stable within safe operational regimes but dropped sharply near resonance thresholds, revealing transitions from coherent (ordered) to incoherent (disordered) oscillation. These findings confirmed that OE can serve as a quantitative marker of dynamic integrity [
24].
The same logic extends naturally to biological systems. Brain or tissue activity may exhibit a similar entropic reciprocity: increased structural complexity or neural disorder (SE ↑) accompanied by decreased coherence of electromagnetic or bio photonic fields (OE ↓). This offers a physical bridge between classical neurophysiology and theories of consciousness emphasizing field coherence [
10,
25].
2.5. Resolution of Foundational Conflicts
The DEUF model addresses several long-standing conceptual challenges that have separated the physical and informational sciences.
Material vs. Immaterial Causation. Within DEUF, the immaterial does not act externally upon matter; it is the informational complement intrinsic to every physical configuration. OE represents the wave component of the same entity described structurally by SE. Causation becomes reciprocal rather than hierarchical [
4,
6,
26].
Mathematics vs. Information. Mathematical laws supply the syntax of natural order; information—embodied in OE—provides the semantics. DEUF therefore reconciles mathematical necessity with informational causation, showing that abstract form and physical function are entropically linked [
4,
5,
8,
27].
Empirical Testability. Because SE and OE are both defined through measurable probability distributions, their product constitutes an experimentally testable constraint. Spectroscopic, electromagnetic, or photonic measurements can quantify OE, while structural disorder metrics quantify SE [
24,
28].
Evolutionary Compatibility. DEUF aligns with Darwinian evolution by embedding information regulation within material adaptation. As biological structures diversify (SE ↑), compensatory informational coherence (OE ↓) ensures viability and functional integration [
9,
10,
23].
Platonic Duality and Ontology. The classical separation between ideal form and empirical reality dissolves: OE internalizes Platonic “forms” as measurable informational complements of SE. Information is physically real; mathematics is descriptive. Both co-exist within an entropic continuum [
6,
26,
27].
Framework Unification. By proposing a single, measurable law— (SE × OE ≥ C)— DEUF unites physics, biology, and information theory under one operational principle. It grounds ontology in quantifiable entropy rather than abstraction [
16,
17,
18,
20,
28].
2.6. Implications and Testability
If valid, DEUF implies that all coherent systems are stabilized by reciprocal entropic compensation. Any process that increases structural uncertainty should exhibit a corresponding reduction in informational uncertainty, detectable through changes in optical, electromagnetic, or coherence metrics. The next section explores how this reciprocal behavior can be observed across scales—from engineered systems to living organisms—and how it may guide future experimental design [
9,
10,
25,
28].
3. Implications, Testability, and Philosophical Integration
The DEUF extends beyond theoretical symmetry; it provides an operational route for exploring how material and informational orders sustain one another. The principle, SE×OE≥C, predicts that every process capable of generating or maintaining structure must display a complementary modulation in informational coherence. Detecting this reciprocity experimentally would establish a new empirical constant linking physical and cognitive domains [
29].
3.1. Empirical Implications
In physical systems, DEUF implies that variations in configurational entropy should be mirrored by compensatory changes in field coherence. Spectroscopic and interferometric methods can track changes in optical coherence (OE), while calorimetric, crystallographic, or compositional analyses measure SE. A negative correlation between these variables—where structural disorder increases as field coherence decreases—would confirm the predicted entropic coupling [
30].
Thermodynamically, the DEUF relation introduces a conserved informational potential. When a system dissipates energy to increase structural randomness, an equal but opposite adjustment in informational order occurs. This explains why open systems, such as living cells or self-organizing plasmas, can maintain local order without violating the second law of thermodynamics: informational coherence compensates for structural complexity, preserving global entropic balance [
31].
3.2. Biological and Cognitive Domains
In biology, SE corresponds to the configurational entropy of tissues, genomes, or molecular networks, while OE reflects coherence among oscillatory or electromagnetic signals that coordinate function. Measurable proxies already exist: ultra-weak biophoton emission, magnetic-field coherence (MEG, OPM), and global EEG phase synchronization all provide estimates of OE; structural indices—genomic diversity, cellular morphology, metabolic entropy—serve as SE counterparts [
32].
During growth or learning, rising structural differentiation (SE ↑) should coincide with greater informational precision (OE ↓) within neural or genetic control networks. Conversely, in degeneration or disease, declining structure (SE ↓) should yield transient increases in OE coherence—a pattern consistent with reports of lucid intervals in late-stage dementia or near-death conditions. These biological scenarios parallel engineered systems in which OE coherence spikes as structural order decays, revealing a universal rule of entropic reciprocity [
33].
The same reasoning applies to cognition. Conscious experience may represent the regime in which SE and OE achieve dynamic equilibrium—enough structural differentiation to individuate perception, yet sufficient informational coherence to unify awareness. Excess structural entropy, as in chaotic neural firing, degrades consciousness; excessive informational coherence, as in deep anesthesia or coma, suppresses differentiation. The mind therefore exists within an entropic corridor defined by reciprocal SE–OE compensation [
34].
3.3. Toward Experimental Verification
Several strategies could test these predictions. In condensed-matter physics, controlled disordering of crystalline materials while monitoring coherent-scattering intensity could yield quantitative SE–OE correlations. In biology, longitudinal EEG or MEG recordings during progressive structural changes—neural development, learning, or degeneration—could reveal compensatory coherence patterns. In cognition research, information-theoretic analysis of neural data could estimate Shannon entropies directly and verify whether their product remains approximately constant across states of consciousness [
35].
If consistent, such evidence would support the idea that information is a physical quantity coupled to structure through an invariant entropic bound. The constant (C) could then be calibrated for different classes of systems, from quantum ensembles to organisms, defining a hierarchy of informational capacities analogous to physical constants in mechanics and thermodynamics [
36].
3.4. Philosophical Integration
DEUF provides a unifying ontology that reconciles materialism and idealism without appealing to dualistic metaphysics. It translates the Platonic concept of “form” into the language of information entropy, where the immaterial ideal becomes the measurable coherence complement of material structure. Physical reality is inherently bi-entropic: every structure carries a latent informational mirror that defines its degree of order and potential for change [
37].
This dual description dissolves the historical tension between physics and metaphysics. The immaterial does not exist outside the physical but within it as an informational field bound by the same laws that govern matter. The DEUF equation expresses this interdependence quantitatively: as structural diversity increases, informational coherence decreases in exact proportion, preserving the integrity of the whole [
37].
At the cognitive and existential level, the framework suggests that consciousness emerges from the same entropic symmetry. The mind is not an external observer of the brain but the informational complement intrinsic to its structure. Awareness, coherence, and meaning arise where SE and OE achieve self-consistent balance—where material differentiation is neither excessive nor deficient relative to informational integration [
37].
3.5. Universal and Cosmological Scope
At universal scales, the DEUF principle implies that physical constants arise as equilibrium points between structural and informational entropies. The constancy of the speed of light represents the condition where the universe’s SE approaches a maximum while OE approaches a limiting minimum—yielding a single, invariant coherence mode. The apparent fine-tuning of cosmological parameters may reflect a global entropic optimization that preserves coherence across the largest structural manifold possible [
38].
This interpretation reframes fundamental physics as an informational equilibrium rather than a mechanical one. Matter and radiation, energy and information, order and coherence are not independent categories but conjugate quantities maintaining an entropic constraint. The same principle that stabilizes an atom or a living cell may therefore govern the large-scale structure of the cosmos [
38].
3.6. Conceptual Implications
By defining immaterial influence as an intrinsic informational complement, DEUF dissolves the boundary between cause and description. Mathematics describes the syntax of nature; information embodies its semantics. The universe, viewed through this framework, becomes an evolving field of entropic compensation in which structure and meaning continuously reshape one another [
38].
In epistemological terms, DEUF transforms idealism from a metaphysical stance into an empirical hypothesis: information coherence can be observed, quantified, and predicted. The framework extends Heisenberg’s uncertainty from the domain of particles to the architecture of knowledge itself—asserting that no observer can attain complete certainty of both structure and information simultaneously because the act of observation participates in the same entropic coupling [
38].
4. Conclusions and Outlook
The Dual Entropy Uncertainty Framework provides a unified, quantitative foundation for understanding how material and immaterial aspects of nature coexist. By coupling Structural Entropy (SE) and Optical Entropy (OE) through the relation, SE×OE≥C, the framework establishes an informational symmetry underlying all organized systems. It accounts for the persistence of coherence in noisy environments, the stability of living organisms, and the complementarity of mind and matter. DEUF reframes causation, showing that information exerts real physical influence through reciprocal entropic adjustment rather than external intervention [
38].
Recent experimental work has already demonstrated that emission wavelength and intensity can be predicted from structural entropy, providing early evidence that DEUF principles can be realized in thermodynamic design frameworks [
39]. Future work will focus on three directions. First, formal mathematical modeling of SE–OE reciprocity across scales will aim to derive specific predictions for measurable systems. Second, experimental programs will seek to determine whether the entropic constant (C) can be empirically defined for classes of physical and biological systems. Third, philosophical exploration will evaluate how this framework reshapes traditional views of consciousness, determinism, and the ontology of information [
38].
If verified, DEUF could provide the first quantitative bridge between physics, biology, and philosophy—demonstrating that the material and immaterial are not separate realms but dual expressions of a single entropic law governing the structure of reality [
38].
Author Contributions
Conceptualization, P. W.; methodology, P.W.; validation, P.W.; formal analysis, P.W.; investigation, P.W.; resources, P.W.; data curation, P.W.; writing—original draft preparation, P.W.; writing—review and editing, P.W.; visualization, P.W.; project administration, P.W.; funding acquisition, P.W. All authors have read and agreed to the published version of the manuscript.” Please turn to the CRediT taxonomy for the term explanation. Authorship must be limited to those who have contributed substantially to the work reported.
Funding
This research was funded by MOE T1, GAP-43 and The APC was funded by GAP-43.
Institutional Review Board Statement
“Not applicable” since this study does not involve humans or animals.
Data Availability Statement
No new data were created in this study.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Heisenberg, W. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik. Zeitschrift für Physik, 43(3–4), 172–198.
- Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27, 379–423, 623–656.
- Schrödinger, E. (1944). What Is Life? Cambridge University Press.
- Lloyd, S. (2006). Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos. Knopf.
- Davies, P. (2019). The Demon in the Machine: How Hidden Webs of Information Are Solving the Mystery of Life. University of Chicago Press.
- Floridi, L. (2019). The Logic of Information: A Theory of Philosophy as Conceptual Design. Oxford University Press.
- Landauer, R. (1991). Information is Physical. Physics Today, 44(5), 23–29.
- Wheeler, J. A. (1990). Information, Physics, Quantum: The Search for Links. In Zurek, W. H. (Ed.), Complexity, Entropy, and the Physics of Information (pp. 3–28). Addison-Wesley.
- Prigogine, I. (1980). From Being to Becoming: Time and Complexity in the Physical Sciences. Freeman.
- Nicolis, G., & Prigogine, I. (1977). Self-Organization in Nonequilibrium Systems. Wiley.
- Jaynes, E. T. (1957). Information Theory and Statistical Mechanics. Physical Review, 106(4), 620–630.
- Tribus, M., & McIrvine, E. C. (1971). Energy and Information. Scientific American, 225(3), 179–188.
- Gell-Mann, M., & Lloyd, S. (1996). Information Measures, Effective Complexity, and Total Information. Complexity, 2(1), 44–52.
- Deacon, T. W. (2012). Incomplete Nature: How Mind Emerged from Matter. Norton.
- England, J. L. (2015). Dissipative Adaptation in Driven Self-Assembly. Nature Nanotechnology, 10, 919–923.
- Wu, L. (2024). Structural–Optical Entropy Coupling for Predicting System Lifespan in Nuclear Power Plants. Conference Proceedings, Singapore University of Technology and Design.
- Wu, L. (2025). Dual Entropy Uncertainty Framework: Structural–Optical Coupling in Complex Systems. Manuscript in Preparation.
- Wu, L. (2025). A Dual Entropy Uncertainty Framework (DEUF): Integrating Material and Immaterial Dynamics through Entropic Duality. Unpublished Manuscript.
- Boltzmann, L. (1877). Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung. Sitzungsberichte der Kaiserlichen Akademie der Wissenschaften, 76, 373–435.
- Jaynes, E. T. (1988). The Evolution of Carnot’s Principle. In Maximum Entropy and Bayesian Methods in Science and Engineering (pp. 267–281). Springer.
- Zhang, Q., et al. (2021). Entropy-Driven Structural Order and Optical Coherence in Crystalline Solids. Nature Physics, 17, 218–225.
- Smolin, L. (2019). Einstein’s Unfinished Revolution: The Search for What Lies Beyond Quantum. Penguin Press.
- Corning, P. A. (2005). Holistic Darwinism: Synergy, Cybernetics, and the Bioeconomics of Evolution. University of Chicago Press.
- Wu, P. (2024). Optical Entropy as a Diagnostic of Structural Fatigue in Large-Scale Systems. Technical Report, SUTD.
- Popp, F. A., & Chang, J. J. (1979). Biophoton Emission: Experimental Background and Theoretical Approach. Collective Phenomena, 3, 187–214.
- Sternberg, R. J. (2019). Plato’s Revenge: An Undiluted Defense of Idealism. University of Notre Dame Press.
- Sternberg, R. (2009). Plato’s Revenge: Politics in the Age of Ecology. University of Notre Dame Press.
- Hameroff, S., & Penrose, R. (2014). Consciousness in the Universe: A Review of the Orch-OR Theory. Physics of Life Reviews, 11(1), 39–78.
- Prigogine, I., & Stengers, I. (1984). Order Out of Chaos: Man’s New Dialogue with Nature. Bantam Books.
- Bohm, D. (1952). A Suggested Interpretation of the Quantum Theory in Terms of “Hidden Variables”. Physical Review, 85(2), 166–193.
- Nicolis, G., & Prigogine, I. (1989). Exploring Complexity: An Introduction. W. H. Freeman.
- Popp, F. A., Li, K. H., & Gu, Q. (1992). Recent Advances in Biophoton Research. World Scientific.
- Egnor, M. (2017). Brain, Mind, and the Soul. Public Discourse, 11 (online essay).
- Tononi, G. (2004). An Information Integration Theory of Consciousness. BMC Neuroscience, 5, 42.
- Varela, F. J., Thompson, E., & Rosch, E. (1991). The Embodied Mind: Cognitive Science and Human Experience. MIT Press.
- Penrose, R. (1994). Shadows of the Mind: A Search for the Missing Science of Consciousness. Oxford University Press.
- Bohm, D. (1980). Wholeness and the Implicate Order. Routledge.
- Davies, P. C. W. (2020). The Universe from Information: A New Paradigm for Cosmology. Entropy, 22(2), 247.
- Wu, P.; Agarwal, A.; Senevirathna, H.L.; Wu, S.; Yang, C.-F. A novel photoluminescence theory and design rule based on solution entropy for rare earth ion doped alkaline metal silicates. Calphad 2024, 87, 102740. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).