Submitted:
21 October 2024
Posted:
22 October 2024
You are already at the latest version
Abstract
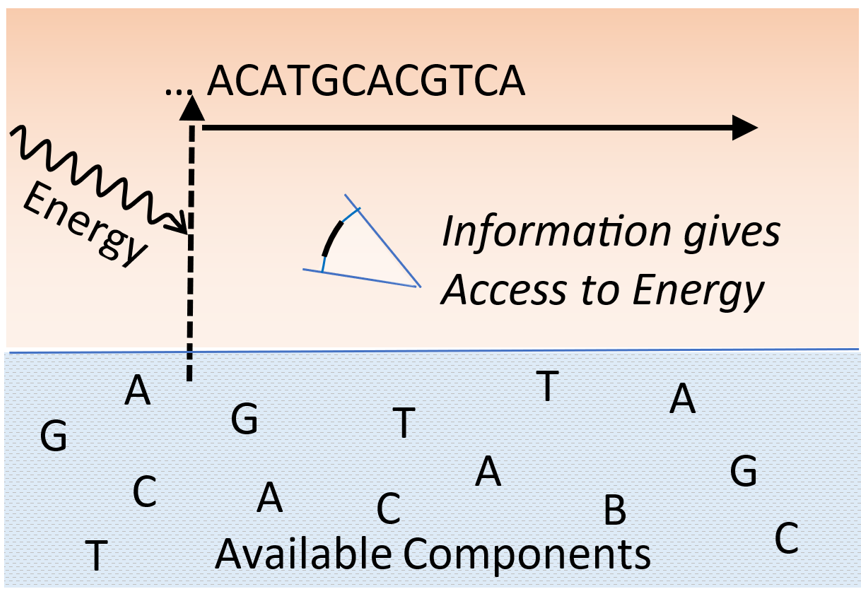
Keywords:
1. Introduction
2. The Two Entropies
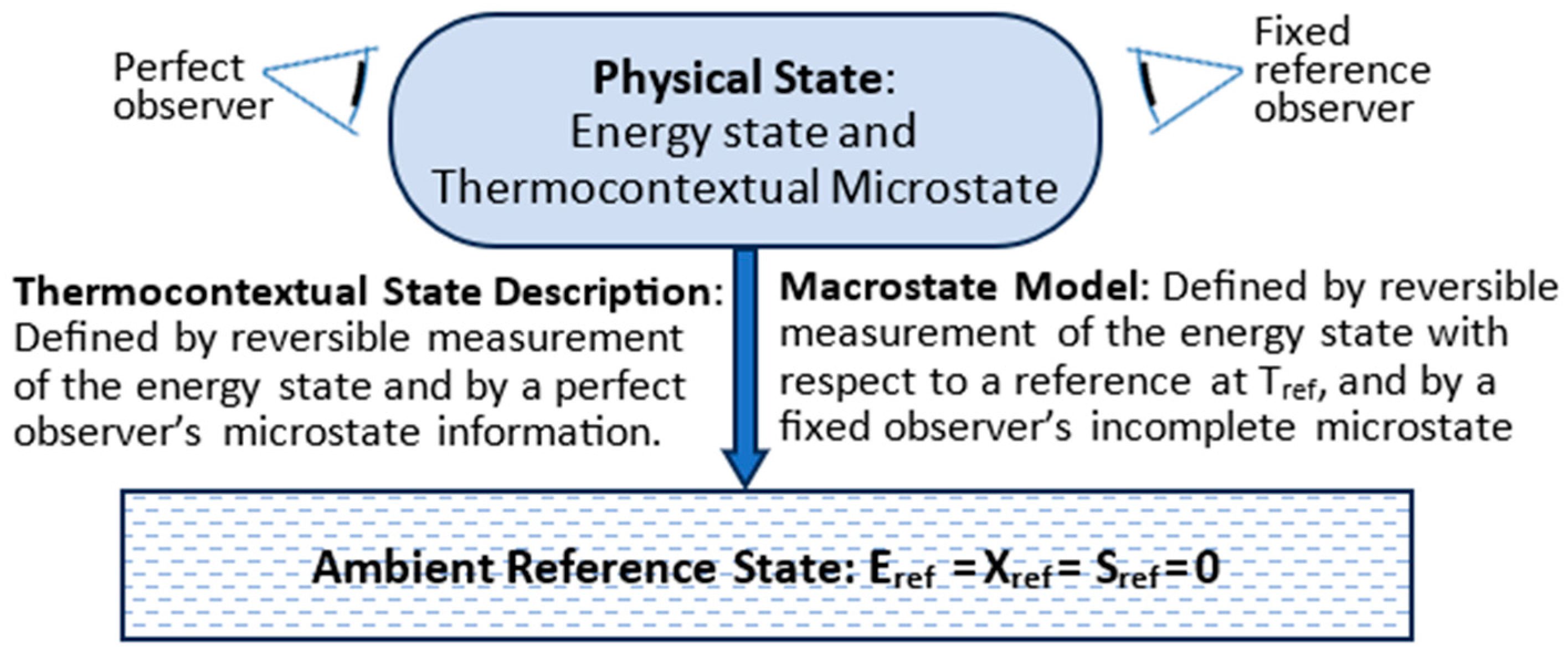
3. The Thermocontextual State
3.1. TCI Postulates of State
3.2. Thermocontextual Properties of State
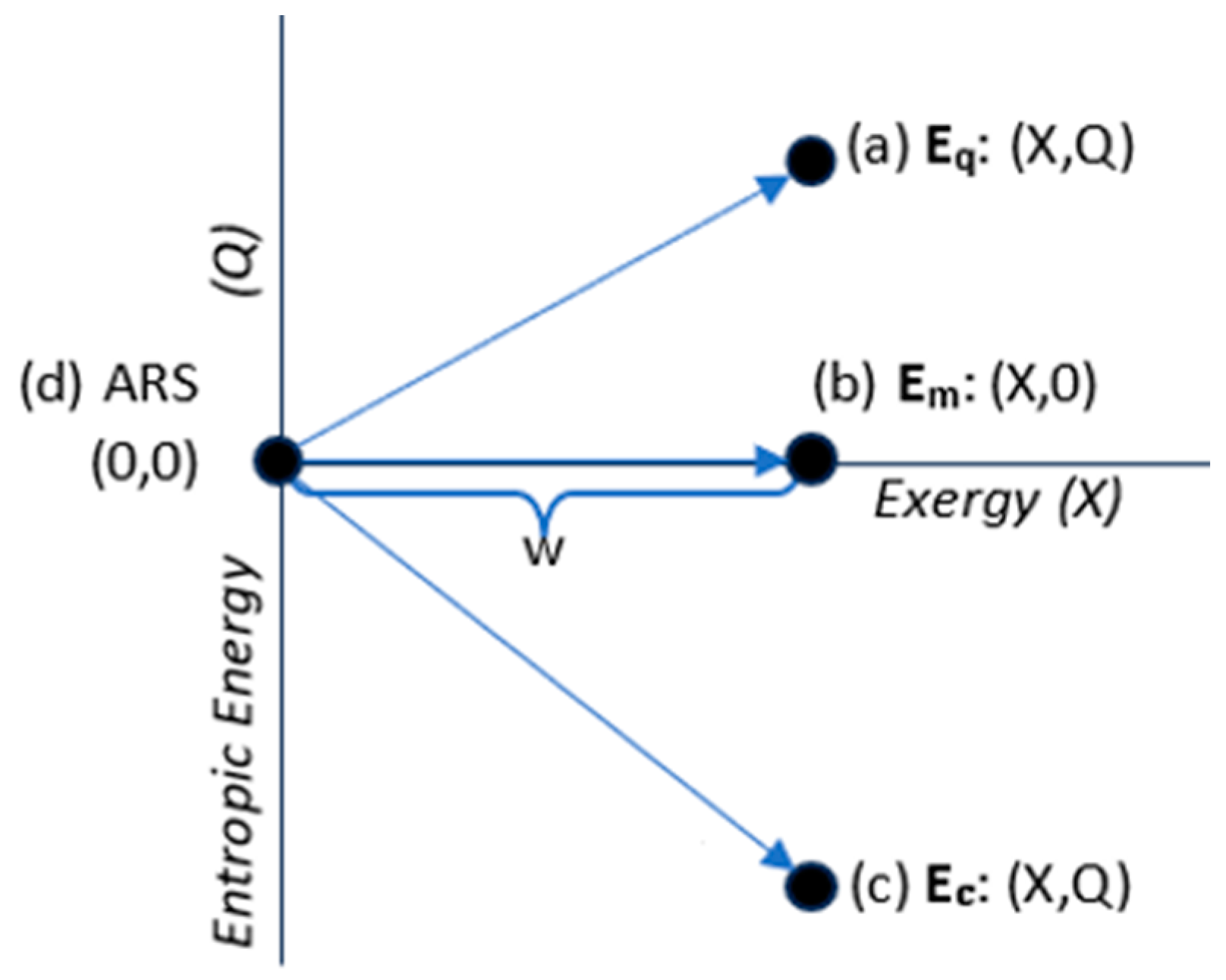
3.3. Energy States
- The system is isolated from exchanges with the surroundings. Isolation means that it is fixed in energy and composition.
- The system is non-dissipative. This means that there is no irreversible dissipation of exergy to ambient heat. It is thermodynamically reversible.
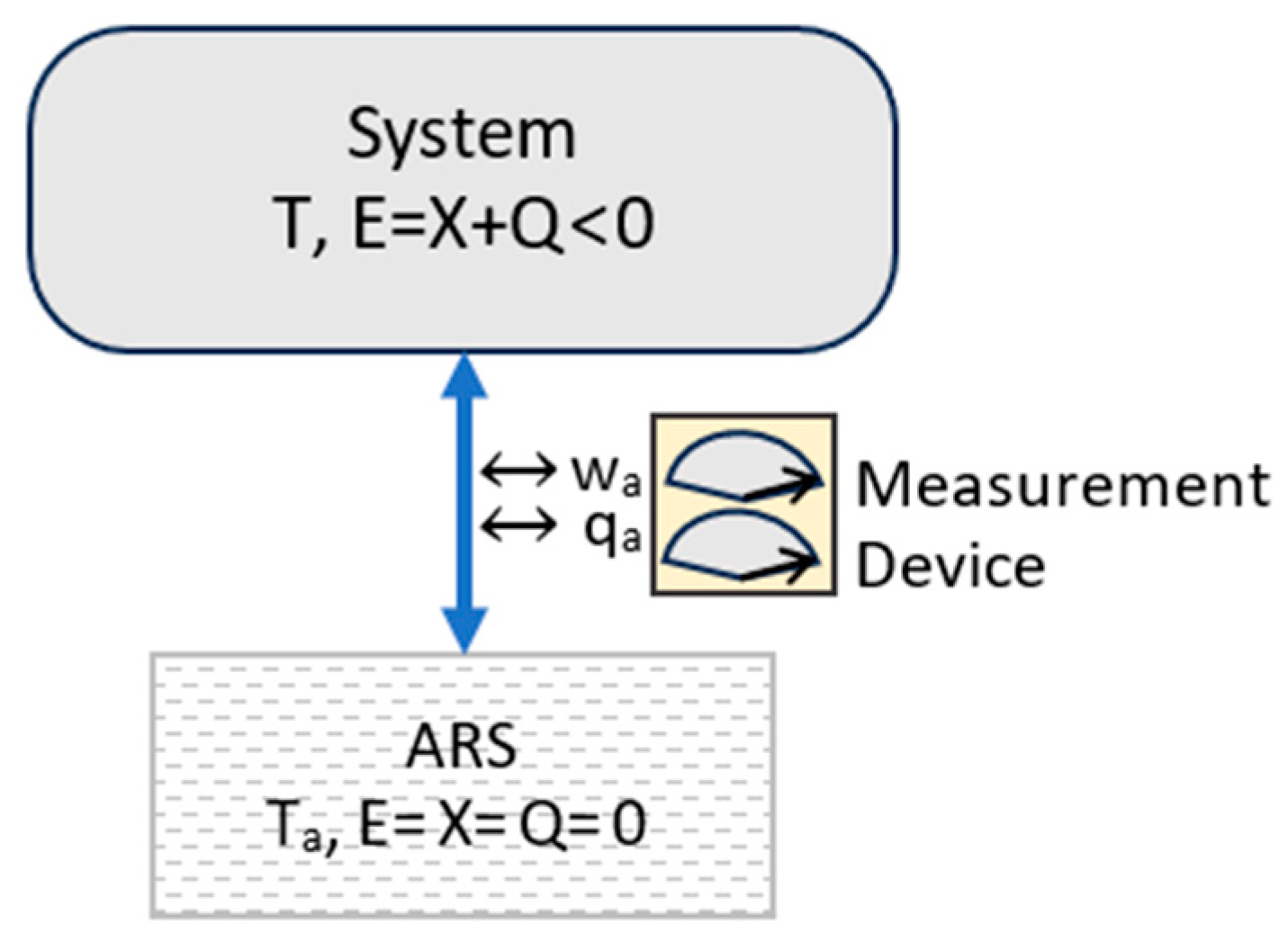
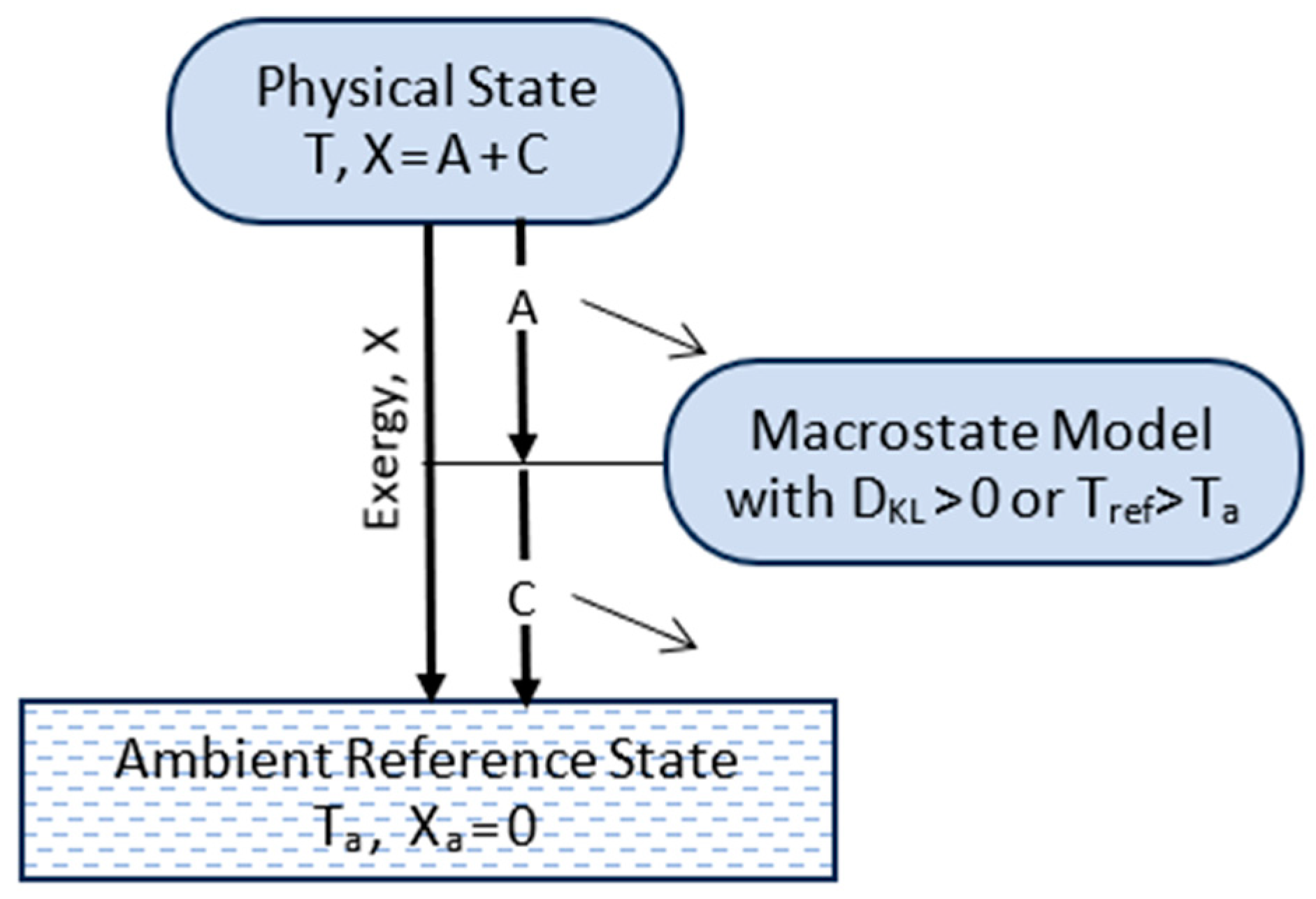
3.4. Microstates, Macrostates, and Information
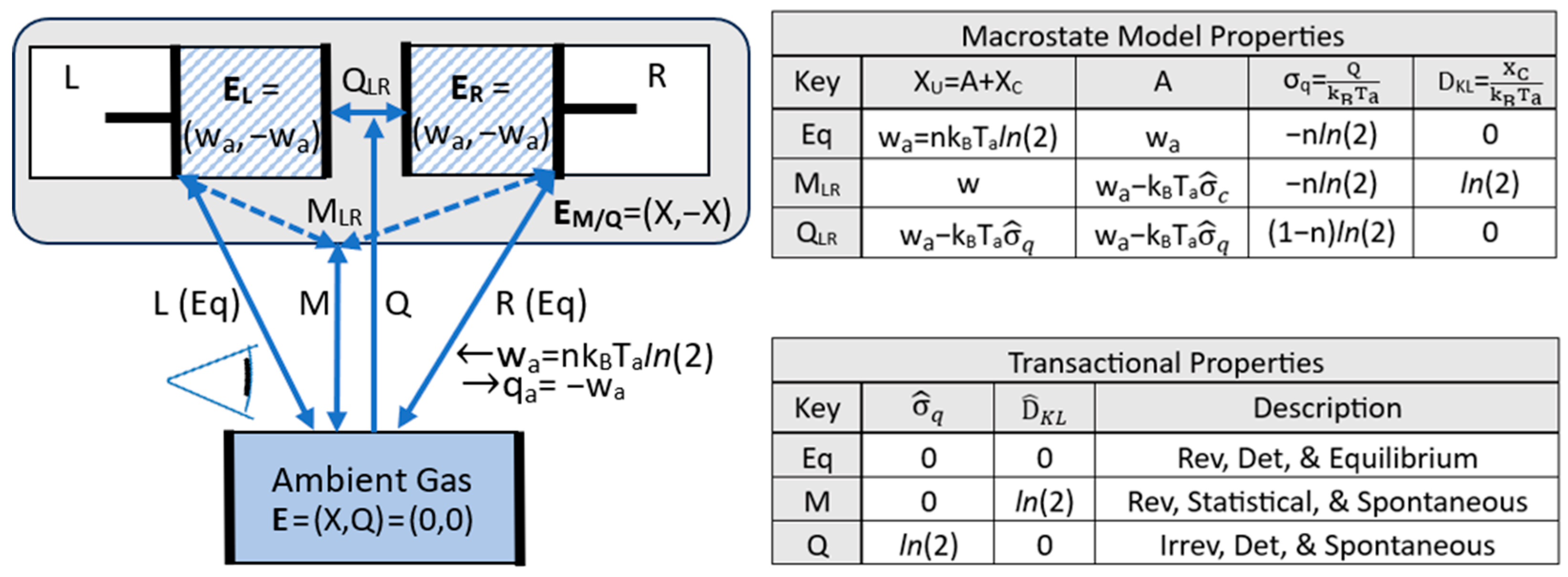
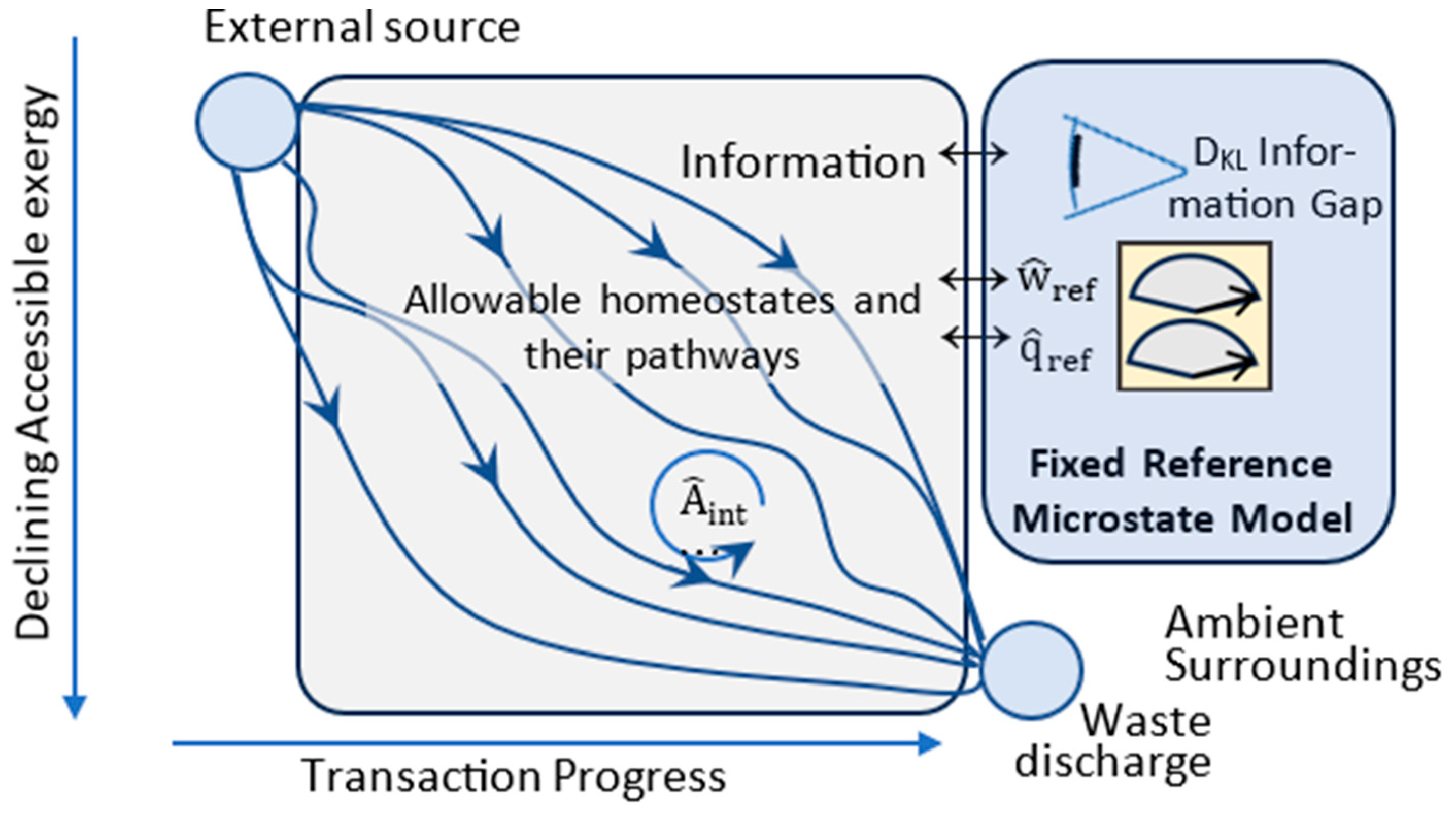
4. Transitions
4.1. Updated Postulates of Transitions
4.2. Transitions, Dissipation, and Dispersion
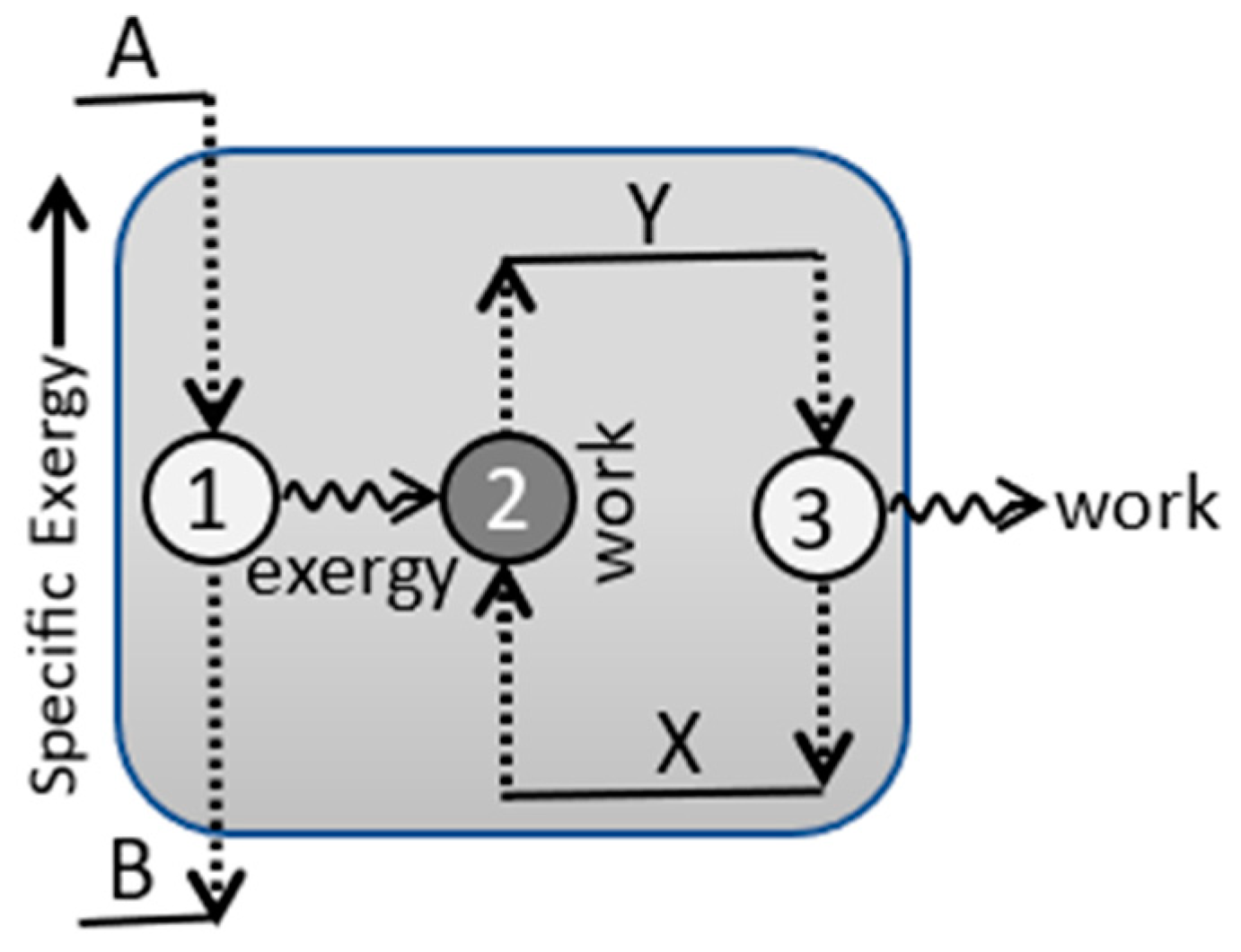
4.3. Efficiency and Refinement
5. Applications
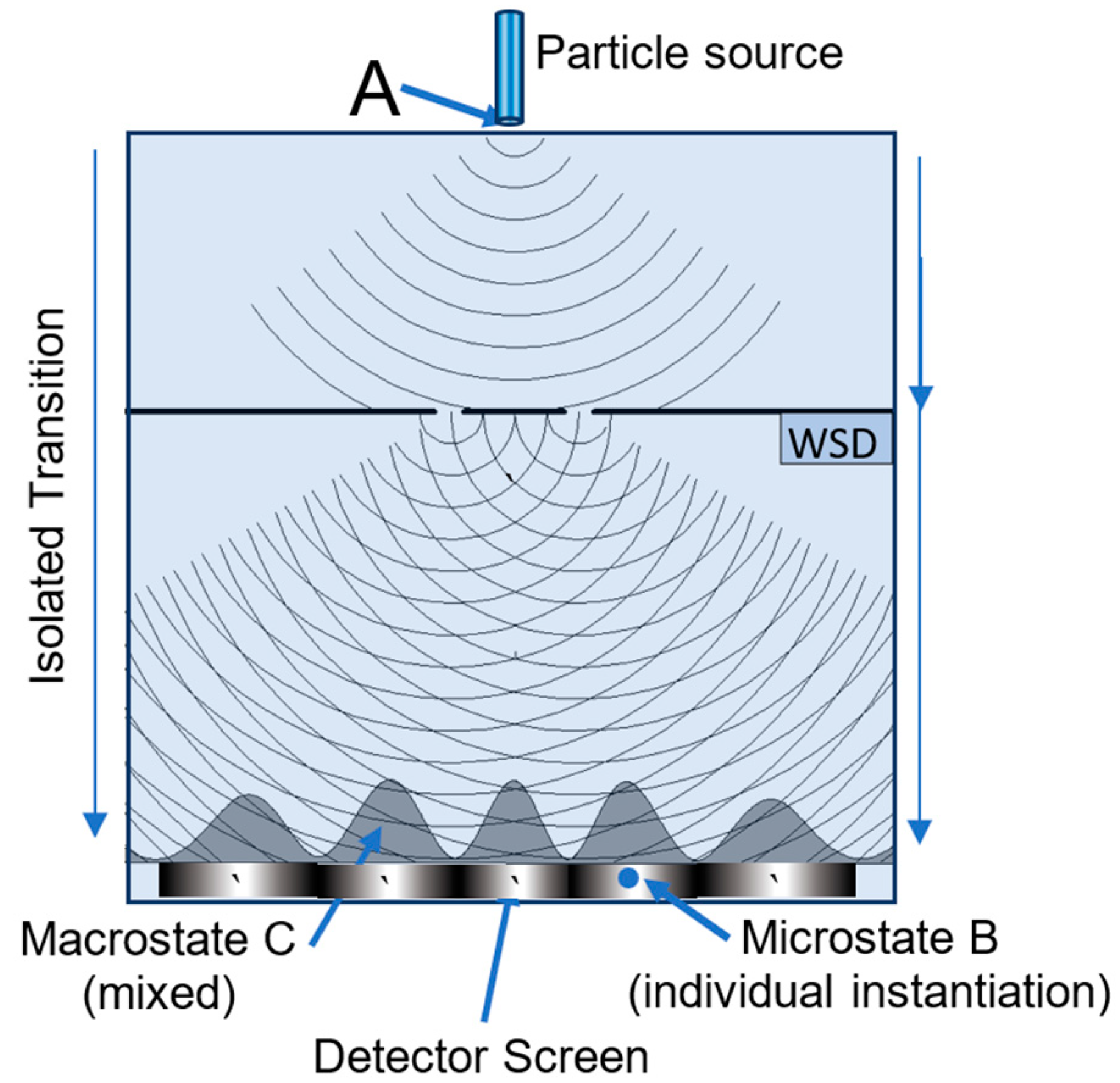
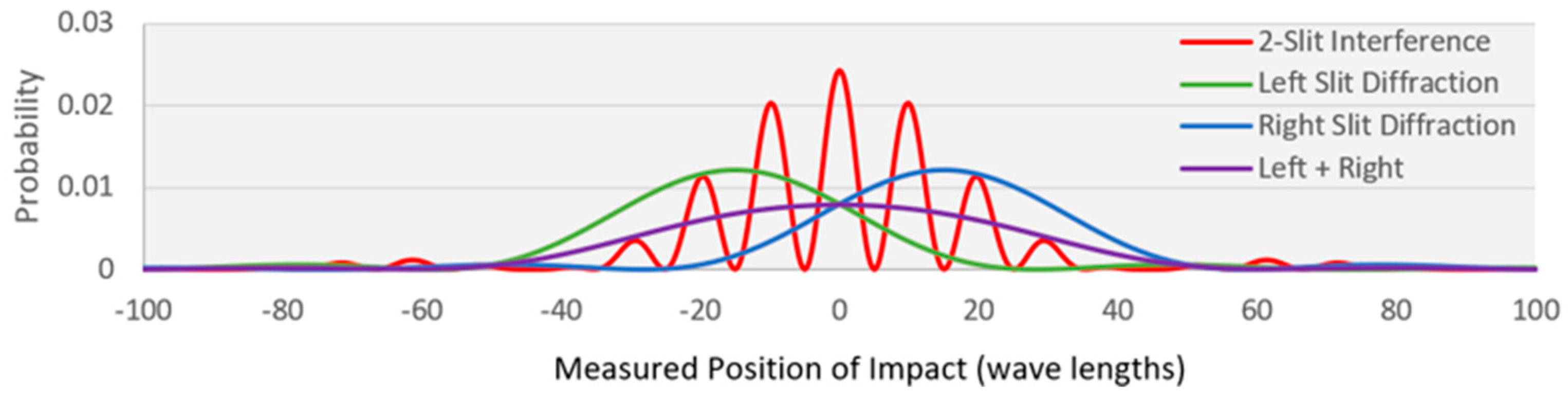
5.1. MaxEnt and the Double Slit Experiment
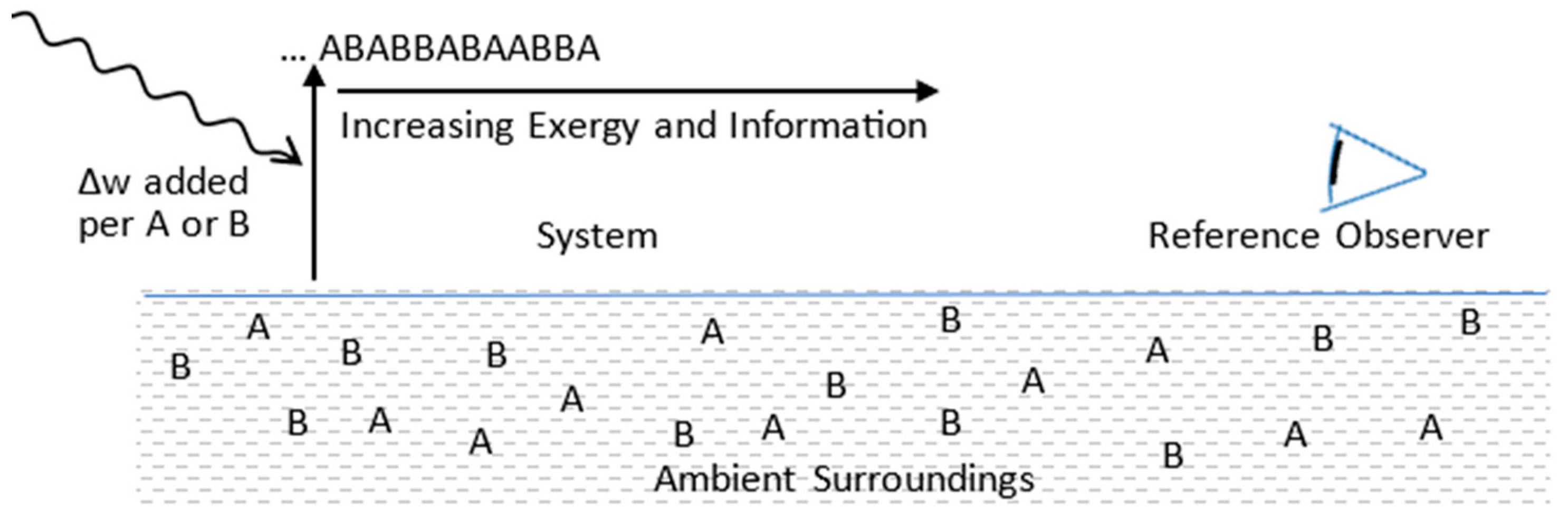
5.2. Configurational Refinement and Replication
6. Summary and Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. State, Macrotate-Model, and Transactional Properties
| Physical State and State Properties: Based on perfect measurement and observation | ||
| Ambient Temperature and pressure | Ta and Pa | The minimum temperature and pressure of the system’s physical surroundings with it could interact. |
| Ambient Surroundings | Idealized equilibrium surroundings at Ta and Pa | |
| Ambient Reference State | ARS | State in thermodynamic equilibrium with ambient surroundings defines zero values for thermocontextual state properties. |
| Thermocontextual microstate |
Complete description of the system’s mechanical configuration of irreducible parts resolvable by a perfect observer. A system’s resolution is limited by thermal randomness at Ta. | |
| Perfect observer | It has perfect resolution at the ambient temperature and complete information on the thermocontextual microstate. Observer and information change with changing system and Ta. | |
| Energy state | Defined by perfect macroscopic (classical) measurement of temperature, energy, and exergy with respect to the ARS | |
| Physical State | Defined by the energy state plus the thermocontextual microstate |
|
| Thermocontextual Macrostate Model | Complete description of a system’s physical state by perfect measurement and observation. | |
| Total Energy | Etot | Total energy relative to reference state at absolute zero (0 K) |
| Volumetric heat capacity | Change in a system’s thermal energy with change in temperature at fixed volume. | |
| Ambient-state energy | Eas= | Ambient reference state’s energy with respect to zero kelvin. |
| System Energy | E=Etot−Eas=X+Q | System Energy with respect to ambient reference state at Ta |
| Thermal energy (heat) | System’s thermal energy with respect to ARS. Equals system’s energy loss as it irreversibly cools to the ambient temperature | |
| Exergy | X ≡ Xm+Xq | System’s reversible work potential on the ambient surroundings |
| Thermal exergy | Xq=q(T-Ta)/T | Reversible work potential by thermal energy on the ARS |
| Mechanical exergy | Xm≡X−Xq=wa | System’s work potential on the ARS after cooling to Ta |
| Entropic energy | Q≡E−X=qa | Randomized thermal energy at Ta with zero work potential. |
| Thermocontextual Entropy |
dS=dq/T = thermodynamic entropy | |
| Thermal entropy | σq=S/kB | Dimensionless thermodynamic entropy |
| Macrostate Model and Transactional Properties: Based on fixed reference observer and temperature | ||
| Fixed Reference Observer | Has complete and fixed information on thermocontextual microstate with respect to its ambient temperature at time zero. | |
| Fixed Reference Temperature | Tref | Set to system’s ambient temperature at time zero. Reference temperature for reversible measurement of energy state. |
| Configurational Entropy | Expresses a reference observer’s expectation values for a system’s microstate configurations. The sum is over the N available microstates, objectively defined by a perfect observer. The Bayesian Pi‘s define the reference observer’s macrostate model for describing the system. A low entropy means high precision for the reference observer’s macrostate model. | |
| DKL Divergence (information gap) | Expresses the statistical separation between a reference observer’s macrostate model, with Bayesian probability distribution P2, and an unknown physical state, described by frequentist probability distribution P1. The physical state’s actual microstate configuration is ‘a’, with probability P1a=1, and the macrostate model’s Bayesian expectation of microstate ‘a’ is P2a. A high P2a and low DKL means high accuracy. | |
| Macrostate Model | [P1,P2,…PN] | Complete description of physical state as it existed at time zero. At later times, statistically described by Bayesian probabilities. |
| Configurational energy | Exergy that is not accessible for work by the reference observer, due to incomplete information (DKL>0) for the microstate and Tref>Ta. | |
| Accessibility | A=X−C | Energy accessible for work measured at Tref and based on reference observer’s information. |
| Reference heat | Heat discharged per transition to Tref. | |
| Reference work | Reversible output of work (and exergy) per transition to Tref | |
| Utilization | Reversible per-transition output of external work (and accessible energy) to the fixed reference plus the internal work of increasing the system’s accessibility. | |
| Other transactional properties | , | Per-transition increases in entropic energy, configurational entropy, and DKL information gap; and decreases in exergy and accessibility |
References
- Vopson, M.; Lepadatu, S. Second law of information dynamics. AIP Advances 2022, 12, 075310. [Google Scholar] [CrossRef]
- Shannon, C. A mathematical theory of communication, in The Bell System Technical Journal 1948, 27, 379–423. [CrossRef]
- Wikipedia Entropy (information theory). Available online: https://en.wikipedia.org/wiki/Entropy_(information_theory) (accessed on 10 August 2024).
- Jaynes, E.T. Information Theory and Statistical Mechanics. The Physical Review 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Wikipedia Boltzmann Distribution. 2024. Available online: https://en.wikipedia.org/wiki/Boltzmann_distribution (accessed on 10 August 2024).
- Crecraft, H. Time and Causality: A Thermocontextual Perspective. Entropy 2021, 23, 1705. [Google Scholar] [CrossRef] [PubMed]
- Dias, T.C.M.; Diniz, M.A.; Pereira, C.A.d.B.; Polpo, A. Overview of the 37th MaxEnt. Entropy 2018, 20, 694. [Google Scholar] [CrossRef]
- D’Ariano, G.M.; Paris, G.A.; Sacchi, M.F. Quantum Tomography arXiv 2008, arXiv:quant-ph/0302028v1.
- Wikipedia Interpretations of quantum mechanics. Available online: https://en.wikipedia.org/wiki/Interpretations_of_quantum_mechanics (accessed on 10 July 2024).
- Takahiro, S. Thermodynamic and logical reversibilities revisited, Jour. Statistical Mechanics: Theory and Experiment, 2014 2014: 03025. [CrossRef]
- Wikipedia Bell Test. Available online: https://en.wikipedia.org/wiki/Bell_test (accessed on 10 August 2024).
- Crecraft, H. Dissipation + Utilization = Self-Organization. Entropy 2023, 25, 229. [Google Scholar] [CrossRef]
- Wikipedia Bayesian Statistics. Available online: https://en.wikipedia.org/wiki/Bayesian_statistics (accessed on 10 August 2024).
- Wikipedia Frequentist Probability. Available online: https://en.wikipedia.org/wiki/Frequentist_probability (accessed on 10 August 2024).
- Wikipedia Kullback–Leibler divergence. Available online: https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence (accessed on 10 August 2024).
- Ribó, J. and Hochberg, D., Stoichiometric network analysis of entropy production in chemical reactions. Phys. Chem. Chem. Phys. 2018, 20. [Google Scholar] [CrossRef]
- Ribó, J. and Hochberg, D., Physical Chemistry Models for Chemical Research in the XXth and XXIst Centuries. ACS Physical Chemistry Au 2024 4, 122–134. [CrossRef]
- Niven, R.K.; Abel, M.; Schlegel, M.; Waldrip, S.H. Maximum Entropy Analysis of Flow Networks: Theoretical Foundation and Applications. Entropy 2019, 21. [Google Scholar] [CrossRef] [PubMed]
- Niven, R.K. , Schlegel, M., Abel, M., Waldrip, S.H., Guimera, R. Entropy Analysis of Flow Networks with Structural Uncertainty (Graph Ensembles). In: Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H. (eds) Bayesian Inference and Maximum Entropy Methods in Science and Engineering. maxent 2017. Springer Proceedings in Mathematics & Statistics, 2018. 239. [CrossRef]
- Albert Einstein, Autobiographical Notes, Open Court Publishing Co ,U.S. 1999; ISBN 10: 0812691792.
- Martyushev, L. Maximum entropy production principle: History and current status. Phys. Uspekhi. 2021, 64, 558. [Google Scholar] [CrossRef]
- Paltridge, G.W. Stumbling into the MEP Racket: An Historical Perspective. In Non-Equilibrium Thermodynamics and the Production of Entropy—Life, Earth, and Beyond; Kleidon, A., Lorenz, R.D., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; 260p, ISBN 3-540-22495-5. [Google Scholar]
- Paltridge, G.W. A Story and a Recommendation about the Principle of Maximum Entropy Production. Entropy 2009, 11, 945–948. [Google Scholar] [CrossRef]
- Wikipedia Baryogenesis. Available online: https://en.wikipedia.org/wiki/Baryogenesis (accessed on 10 August 2024).
- van de Schoot, R. Depaoli, S., King, R. et al. Bayesian statistics and modelling. Nat Rev Methods Primers. 2021. [Google Scholar] [CrossRef]
- Modeling Galaxy formation: Verdoolaege, G. Regression of Fluctuating System Properties: Baryonic Tully–Fisher Scaling in Disk Galaxies. In: Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H. (eds) Bayesian Inference and Maximum Entropy Methods in Science and Engineering. maxent 2017. Springer Proceedings in Mathematics & Statistics, 2018 239. [CrossRef]
- Rapid medical diagnostics: Ranftl, S.; Melito, G.M.; Badeli, V.; Reinbacher-Köstinger, A.; Ellermann, K.; von der Linden, W. Bayesian Uncertainty Quantification with Multi-Fidelity Data and Gaussian Processes for Impedance Cardiography of Aortic Dissection. Entropy 2020, 22. [Google Scholar] [CrossRef]
- Rapid medical diagnostics: Makaremi, M.; Lacaule, C.; Mohammad-Djafari, A. Deep Learning and Artificial Intelligence for the Determination of the Cervical Vertebra Maturation Degree from Lateral Radiography. Entropy 2019, 21. [Google Scholar]
- Thermodynamic computing: Fry, R.L. Physical Intelligence and Thermodynamic Computing. Entropy 2017, 19, 107. [Google Scholar] [CrossRef]
- Thermodynamic computing: Hylton, T. Thermodynamic Computing: An Intellectual and Technological Frontier. Proceedings 2020, 47, 23. [Google Scholar] [CrossRef]
- AI and ML: Enßlin, T. Information Field Theory and Artificial Intelligence. Entropy 2022, 24, 374. [Google Scholar] [CrossRef] [PubMed]
- Machine learning: Mohammad-Djafari, A. Regularization, Bayesian Inference, and Machine Learning Methods for Inverse Problems. Entropy 2021, 23, 1673. [Google Scholar] [CrossRef]
- Ecology: Albert, C.G.; Callies, U.; von Toussaint, U. A Bayesian Approach to the Estimation of Parameters and Their Interdependencies in Environmental Modeling. Entropy 2022, 24, 231. [Google Scholar] [CrossRef] [PubMed]
- MaxEnt applications to macroeconomics: Hubert, P. , Stern, J.M. Probabilistic Equilibrium: A Review on the Application of MAXENT to Macroeconomic Models. In: Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H. (eds) Bayesian Inference and Maximum Entropy Methods in Science and Engineering. maxent 2017. Springer Proceedings in Mathematics & Statistics, 2018. 239. [CrossRef]
- Optimizing imaging: Spector-Zabusky, A. , Spector, D. Schrödinger’s Zebra: Applying Mutual Information Maximization to Graphical Halftoning. In: Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H. (eds) Bayesian Inference and Maximum Entropy Methods in Science and Engineering. maxent 2017. Springer Proceedings in Mathematics & Statistics, 2018. 239. [CrossRef]
- Enhancing MRI: Earle, K.A. , Broderick, T., Kazakov, O Effect of Hindered Diffusion on the Parameter Sensitivity of Magnetic Resonance Spectra. In: Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H. (eds) Bayesian Inference and Maximum Entropy Methods in Science and Engineering. maxent 2017. Springer Proceedings in Mathematics & Statistics, 2018. 239. [CrossRef]
- Image reconstruction: Denisova, N. Bayesian Maximum-A-Posteriori Approach with Global and Local Regularization to Image Reconstruction Problem in Medical Emission Tomography. Entropy 2019, 21, 1108. [Google Scholar] [CrossRef]
- Caticha, N. Entropic Dynamics in Neural Networks, the Renormalization Group and the Hamilton-Jacobi-Bellman Equation. Entropy 2020, 22. [Google Scholar] [CrossRef]
- Optimizing fusion realtors: Nille, D. , von Toussaint, U., Sieglin, B., Faitsch, M. Probabilistic Inference of Surface Heat Flux Densities from Infrared Thermography. In: Polpo, A., Stern, J., Louzada, F., Izbicki, R., Takada, H. (eds) Bayesian Inference and Maximum Entropy Methods in Science and Engineering. maxent 2017. Springer Proceedings in Mathematics & Statistics, 2018. 239. [CrossRef]
- Wikipedia Double-slit experiment. Available online: https://en.wikipedia.org/wiki/Double-slit_experiment (accessed on 10 August 2024).
- Feynman, R. Leighton, R., and Sands, M. The Feynman Lectures on Physics Vol. I: Mainly Mechanics, Radiation, and Heat, Millennium Edition Chapter 37 (Quantum Behavior). California Institute of Technology, 2013. Available online: https://www.feynmanlectures.caltech.edu/I_37.html.
- Crecraft, H. MaxEnt: Selection at the Heart of Quantum Mechanics. Preprints 2022. [CrossRef]
- University Physics III - Optics and Modern Physics (OpenStax) Chapter 3: Interference. Available online: https://phys.libretexts.org/Bookshelves/University_Physics/Book%3A_University_Physics_(OpenStax)/University_Physics_III_-_Optics_and_Modern_Physics_(OpenStax)/03%3A_Interference (accessed on 4 June 2022).
- F Miller, S.L. Production of Amino Acids Under Possible Primitive Earth Conditions. 1953. [Google Scholar]
- Michaelian, K. The Dissipative Photochemical Origin of Life: UVC Abiogenesis of Adenine. Entropy 2021, 23, 217. [Google Scholar] [CrossRef] [PubMed]
- Athel Cornish-Bowden, María Luz Cárdenas, Contrasting theories of life: Historical context, current theories. In search of an ideal theory, Biosystems 2020, 188. [CrossRef]
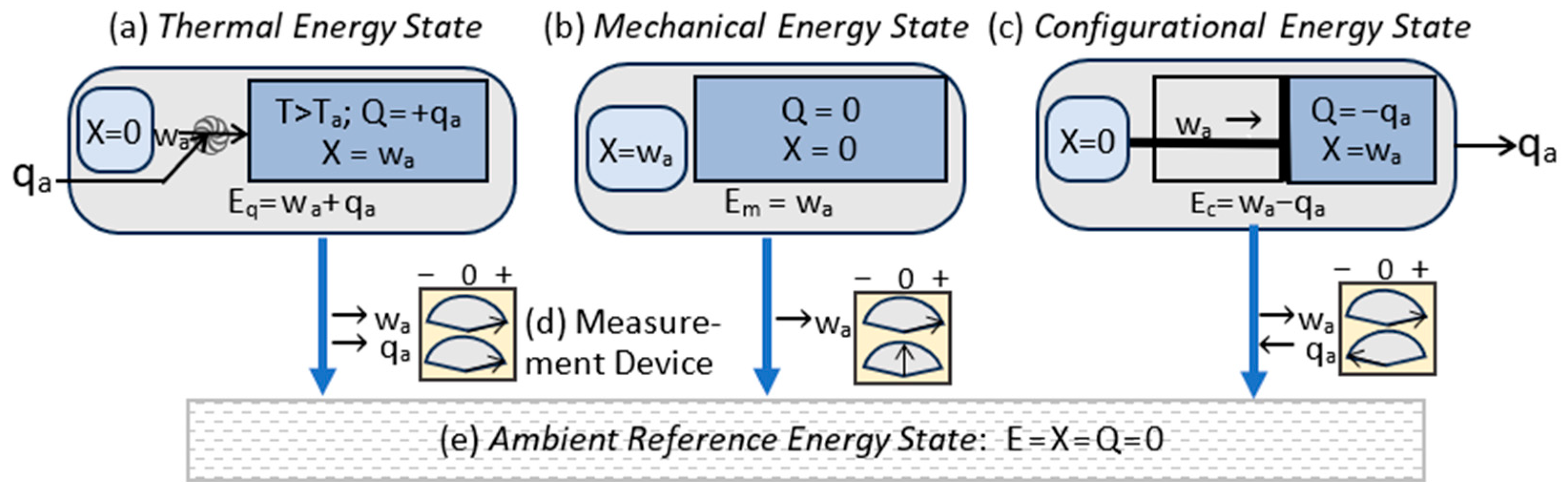
| Energy State Classification | Energy components |
|---|---|
| Thermal state energy (Q>0): | Eq = (X,Q); Eq=X+Q >X |
| Mechanical state energy (Q=0): | Em = (X,0); Em=X |
| Configurational state energy (Q<0): | Ec = (X,Q); Ec=X+Q <X. |
| Detector width | Slit width | Slit positions |
Slit-detector separation | Observer’s Resolution |
|---|---|---|---|---|
| 200 λ | 7 λ | ±15 λ | 300 λ | 0.5 λ |
| Entropy | Transition (normalized probability distribution) | |
|---|---|---|
| 1 | 4.69 | No WSD—source to detector (red profile) |
| 2 | 0.69 | WSD on--source to one of the slits (50% - 50%) |
| 3 | 5.02 | WSD on—slit to detector (green or blue profile) |
| 4 | 5.71 | WSD on—overall: source to detector (purple profile) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





