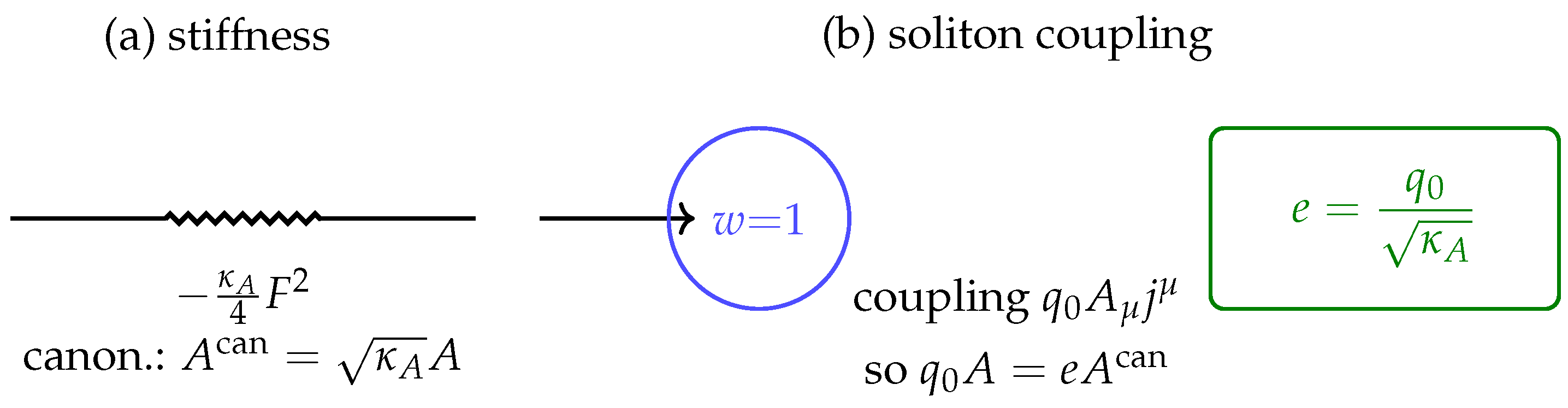Geometric Foundations of Matter and Electrodynamics: Covariant Mass, Solitonic Fermions, and Emergent (ℏ, G, e, c) from Pre-Geometric Curvature

1. Introduction and Main Contributions

Recently published work on Chronon Field Theory (CFT) introduces a single smooth, unit–norm, future–directed timelike field ${\Phi }^{\mu }$ whose integral curves define a preferred temporal flow and induce a foliation $\left\{{\Sigma }_{\tau }\right\}$ with an emergent Lorentzian metric $g_{\mu \nu }[\Phi ]$ [9,82,83,115]. On stabilized domains (defined below), this structure provides: (i) causal cones and an ADM–like $(3+1)$ decomposition, (ii) a relational Hilbert space $\mathcal{H}\left[{\Sigma }_{\tau }\right]$ supporting Schrödinger evolution in intrinsic time $\tau$ [38,41], and (iii) a covariant stress–energy tensor $T_{\mu \nu }$ derived from the CFT action [91].

The purpose of the present paper is to demonstrate that, within this background–independent framework, one can construct a rigorous and self–contained account of mass, matter, and an emergent Abelian gauge sector, together with the familiar physical constants $(\hslash ,G,e,c)$, all arising as derived geometric invariants rather than postulated inputs [10,116].

Standing Conventions

We work in $3+1$ dimensions with signature $(-,+,+,+)$, set units so that the emergent light speed is $c=1$, and keep the emergent action unit ${\hslash }_{\mathrm{geom}}$ explicit. Greek indices run over spacetime components; spatial operations are performed with the projector $h_{\mu \nu }:=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }$; $D_{\mu }$ denotes the induced spatial covariant derivative on a leaf. Unless stated otherwise, fields are smooth and decay so that boundary terms vanish on ${\Sigma }_{\tau }$.

Stabilized Domains

A spacetime region is stabilized if ${\Phi }^{\mu }$ is smooth, strictly timelike with ${\Phi }^{\mu }{\Phi }_{\mu }=-1$, and its gradients are bounded so that (a) the foliation $\left\{{\Sigma }_{\tau }\right\}$ is well defined, (b) the field equations are hyperbolic with respect to the induced time, and (c) the Peierls bracket reduces to canonical commutators on $\mathcal{H}\left[{\Sigma }_{\tau }\right]$ up to controllable $O\left(\right|\nabla \Phi \left|\right)$ corrections [38,95]. All results below are stated and proved on stabilized domains.

On Local Lorentz Symmetry

The chronon field selects a unit timelike direction and thus a preferred foliation in vacuum. As a result, local Lorentz symmetry is spontaneously broken even though the action is written in a Lorentz–covariant and diffeomorphism–invariant form. We therefore regard the framework as an æther–like effective field theory on stabilized domains and explicitly track the induced preferred–frame operators and propagation effects [72,73]. For clarity, we use “chronon” to denote the unit–norm timelike sector introduced here, while emphasizing that its structure is closely analogous to Einstein–æther models. In the infrared, these deformations are parametrically suppressed and compatible with existing constraints (PPN preferred–frame bounds [120,121], gravitational–wave equal–speed tests [1,2], and birefringence limits [31,79,85]), so that the dynamics reduce to Einstein–Maxwell up to small, controlled corrections. Radiative corrections cannot destabilize this suppression, since the stabilized domain symmetry prevents the regeneration of unsuppressed Lorentz–violating operators at low energies. We map the leading operators to standard test frameworks (SME/PPN) [78,79] and state parameter priors accordingly; any phenomenology beyond these bounds is confined to strongly curved or topological regions where the foliation is highly distorted. For completeness, we also outline in Appendix N a broader interpretation—the Co-Moving Concealment Mechanism—in which all matter and observers emerge from the chronon foliation itself, so that local Lorentz violation is fundamentally present but operationally concealed. In the present work, however, we adopt the more conservative EFT perspective, ensuring consistency with established experimental tests while leaving the deeper emergent interpretation for future development.

On Emergent Metrics and Causal Structure

The chronon sector deforms propagation operators in a manner that can be usefully recast in terms of an induced or “emergent” effective metric. In this sense the chronon may be viewed as generating a secondary causal structure, an idea we regard as a promising avenue for future work. In the present paper, however, we restrict to the more conservative interpretation: an æther-like effective field theory defined on the background spacetime metric $g_{\mu \nu }$, with chronon-induced operators systematically mapped to SME/PPN test frameworks. This ensures that the claims made in this paper remain within the well-established EFT regime, while a rigorous treatment of chronon-induced emergent geometry is deferred to subsequent studies.

1.1. Main Results

(C1)

Covariant local mass/energy density. Definition and positivity of $\rho$ connects to the dominant energy condition [64,115].

(C2)

GR as an IR fixed point with controlled deviations. Effective field theory reasoning follows [73,116], with constraints informed by PPN tests [121].

(C3)

Existence of finite–energy $w=1$ solitons. Existence and stability of topological solitons connect to Skyrme-type and Derrick arguments [39,86,105].

(C4)

Spin–statistics for solitons via FR/Berry holonomy. The Finkelstein–Rubinstein mechanism and Berry phase arguments [20,48] underpin the soliton spin–statistics connection.

(C5)

Emergent Abelian gauge sector from chronon holonomy. Parallel transport and holonomy yielding emergent gauge fields relates to work on gauge connections and Berry bundles [89,123].

(C6)

Emergent fundamental constants and parameter constraints. The idea that G, ℏ, e, c may emerge rather than be postulated resonates with Sakharov’s induced gravity [101] and effective action derivations in quantum field theory [125].

1.2. Intuition and Roadmap: From Chronon Flow to Coherent Quantized Geometry

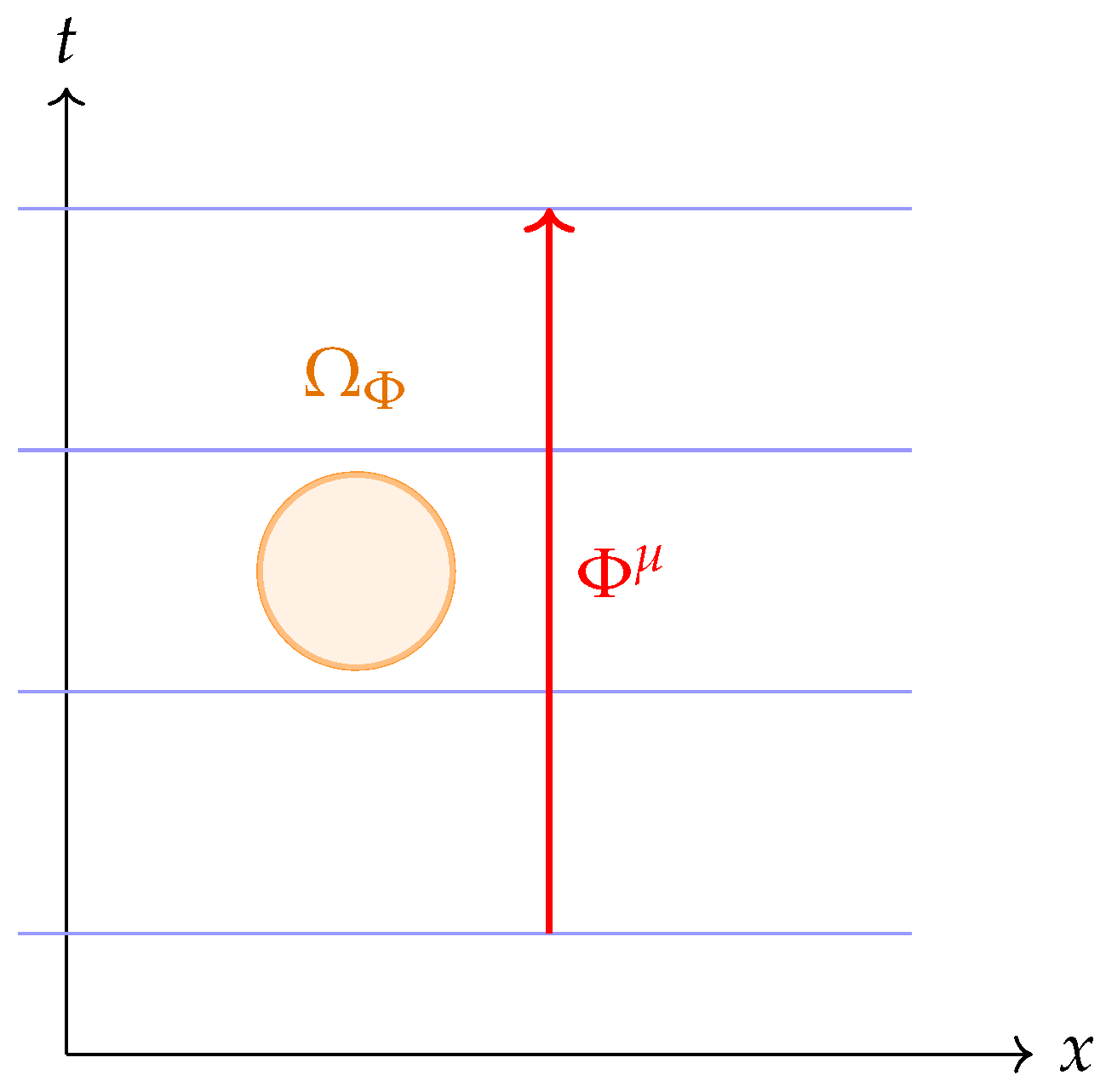
Starting Picture

Envision the chronon field ${\Phi }^{\mu }$ as a locally defined “clock vector” that threads spacetime, picking out at each point a preferred timelike direction. Imposing the unit–norm constraint

$${\Phi }^{\mu }{\Phi }_{\mu }=-1$$

accomplishes two tasks simultaneously: it fixes the intrinsic “rate” of this local clock (no arbitrary rescalings) and cleanly defines the orthogonal complement ${\Phi }^{\perp }$. Geometrically, this splits the tangent space into a one–dimensional time direction spanned by $\Phi$ and a three–dimensional space orthogonal to it. Integrating ${\Phi }^{\perp }$ yields a foliation of spacetime into spatial leaves $\left\{{\Sigma }_{\tau }\right\}$, with $\tau$ measuring intrinsic time along the chronon flow. Observers comoving with $\Phi$ measure the local energy density

$$\rho =T_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu },$$

and we call a region stabilized when $\rho >0$ and fluctuations of $\Phi$ remain bounded. A stabilized domain is therefore a portion of spacetime with a coherent local clock and well–behaved spatial slices—the precondition for causal and quantum structure to emerge.

Why Compact Holonomy Is Natural

Within a stabilized domain, parallel transport around a closed loop $C\subset {\Sigma }_{\tau }$ rotates any spatial vector by an angle in the plane orthogonal to $\Phi$. Because $\Phi$ is unit timelike, the induced metric on ${\Phi }^{\perp }$ is positive definite, so these rotations form a compact group. The smallest such group is the circle $\mathrm{U}\left(1\right)$: transporting an internal pointer $\xi \in {\Phi }^{\perp }$ around C accumulates a phase $\theta \left(C\right)$. This geometric phase is the origin of the emergent Abelian gauge structure: the internal phase of $\Phi$ acts as a compact fiber coordinate, whose holonomy defines a circle bundle over ${\Sigma }_{\tau }$.

From Phases to Gauge Fields

To keep track of these rotations, one assigns to each infinitesimal path a phase factor and requires consistency under composition. Locally, this data is encoded by a one–form connection A, whose line integral around C gives the accumulated phase $exp\left(i{\oint }_{C}A\right)$. The curvature two–form $F=\mathrm{d}A$ then measures the infinitesimal twist per unit area: the “vorticity” of the chronon field on the leaves. In the continuum limit, holonomy consistency enforces Maxwell–like equations for A on the emergent metric $g[\Phi ]$, linking the chronon kinematics to classical electrodynamics.

Why the Unit Norm Really Matters

Keeping ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ is not merely aesthetic. It ensures that: (i) the projector ${{\Pi }^{\mu }}_{\nu }={{\delta }^{\mu }}_{\nu }+{\Phi }^{\mu }{\Phi }_{\nu }$ is a genuine projector onto ${\Phi }^{\perp }$, (ii) the holonomy group remains compact (rotations, not boosts), guaranteeing a circle fiber and phase quantization, and (iii) amplitude and phase decouple cleanly—norm fluctuations remain geometric rather than gauge. This separation underlies flux quantization, stability, and the emergence of a universal action quantum ${\hslash }_{\mathrm{geom}}$.

The 2$\mathit{\pi }$ Twist: Root of Spin, Charge, and Quantization

Because the fiber is a circle, winding the chronon phase by $2\pi n$ around a loop cannot be undone continuously: it defines a topological sector, ${\pi }_1\left(S^1\right)=\mathbb{Z}$. Spatial textures of $\Phi$ carrying this winding behave as solitons with integer charge and half–integer spin. A full $2\pi$ twist in the temporal phase of $\Phi$ yields the Finkelstein–Rubinstein sign change responsible for spin–$\frac{1}{2}$ statistics, while the same twist viewed in the spatial projection gives the quantized $U\left(1\right)$ holonomy identified with electric charge. The action increment for each completed twist, $\Delta S=n{\hslash }_{\mathrm{geom}}$, thus encodes quantization itself. Spin, charge, and the quantum of action all stem from this single geometric phase twist of the chronon manifold.

Interactions as Coherence Enforcement

When multiple solitons coexist, their temporal phases must remain coherent to preserve causal consistency. The emergent gauge field $A_{\mu }$ plays precisely this role: it mediates synchronization of chronon phases across space, enforcing global temporal coherence. Electromagnetic and gravitational interactions thus represent collective coherence modes of the chronon condensate—not external forces, but the dynamical self–organization of the underlying time–flow field.

Roadmap

The technical development of this paper mirrors this geometric intuition:

• Kinematics from the clock: impose ${\Phi }^2=-1$, construct the induced metric and define stabilized domains through $\rho$.
• Holonomy structure: follow parallel transport on ${\Sigma }_{\tau }$ and establish the compact $\mathrm{U}\left(1\right)$ bundle structure.
• Gauge dynamics: identify A and F as local curvature data and derive Maxwell–type equations for A on $g[\Phi ]$.
• Topological matter: classify solitons by integer winding, derive flux quantization and spin–charge correspondence.
• Emergent constants: show that ℏ, e, G, and c arise as curvature invariants, fixed by the stabilized chronon phase.
• Unified picture: Section 9 develops the synthesis: spin, charge, quantization, and interaction as facets of one $2\pi$ symplectic twist in the chronon field.

Technical Notes

The foliation gives a natural $\mathrm{U}\left(1\right)$ reduction of the frame bundle on ${\Phi }^{\perp }$; the connection one–form arises as the leafwise Berry connection for the chronon fiber; compactness and the unit normalization guarantee that the Čech cocycles land in $\mathrm{U}\left(1\right)$ and that the resulting Abelian sector is globally well defined.

Analogy

Think of the chronon medium as a fluid with an internal compass. The unit norm fixes the clock; the compass’s angle is the gauge phase. Carrying the compass around a loop twists it by an amount that depends only on what the fluid is doing inside the loop. That twist is the Wilson phase, its density is F, and its topological windings are the solitons. The rest of the paper turns this picture into geometry and equations.

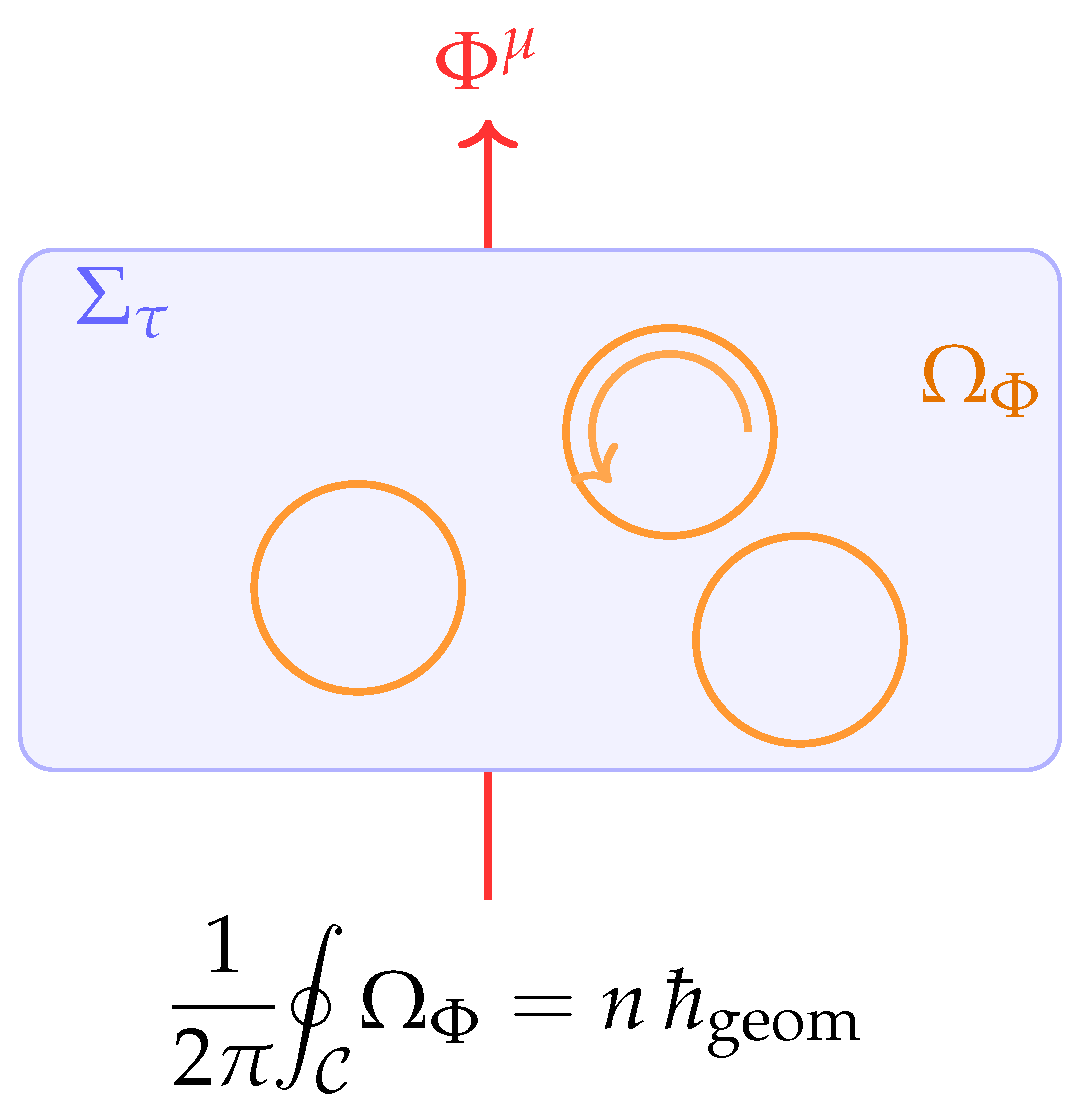
Figure 1. Schematic flow of Chronon Field Theory. The pre–geometric chronon field induces foliation and metric structure; its holonomy produces an emergent $\mathrm{U}\left(1\right)$ sector, and the resulting geometric invariants yield the physical constants $(\hslash ,G,e,c)$.

Figure 1. Schematic flow of Chronon Field Theory. The pre–geometric chronon field induces foliation and metric structure; its holonomy produces an emergent $\mathrm{U}\left(1\right)$ sector, and the resulting geometric invariants yield the physical constants $(\hslash ,G,e,c)$.

2. Background and Setup

2.1. Chronon Field, Foliation, and Emergent Geometry

We postulate a smooth, unit timelike vector field ${\Phi }^{\mu }$ on a four-dimensional spacetime manifold $(\mathcal{M},g_{\mu \nu })$, satisfying

$${\Phi }^{\mu }{\Phi }_{\mu }=-1,{\Phi }^0>0.$$

(1)

The integral curves of $\Phi$ define a preferred time function $\tau$ (unique up to affine reparameterization) and a foliation by Cauchy hypersurfaces $\left\{{\Sigma }_{\tau }\right\}$ [33,54,115]. The orthogonal projector onto the tangent bundle of each leaf is

$$h_{\mu \nu }:=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }^{\mu },$$

(2)

which is a positive-definite metric on $T{\Sigma }_{\tau }$[59,115]. The Levi–Civita connection ∇ of g induces a leafwise covariant derivative on tensor fields X by

$$D_{\mu }X:={h_{\mu }}^{\alpha }{\nabla }_{\alpha }X,{h_{\mu }}^{\alpha }:={g_{\mu }}^{\alpha }+{\Phi }_{\mu }{\Phi }^{\alpha }.$$

(3)

Kinematic invariants of the congruence $\Phi$ are defined as

$$a_{\mu }:={\Phi }^{\alpha }{\nabla }_{\alpha }{\Phi }_{\mu },\theta :=D_{\mu }{\Phi }^{\mu },{\sigma }_{\mu \nu }:=D_{(\mu }{\Phi }_{\nu )}-\frac{1}{3}\theta h_{\mu \nu },{\omega }_{\mu \nu }:=D_{[\mu }{\Phi }_{\nu ]},$$

(4)

and obey the standard Raychaudhuri/Ehlers relations for timelike congruences [44,100,115]. The extrinsic curvature of the leaves is $K_{\mu \nu }:=D_{\mu }{\Phi }_{\nu }$, with the decomposition $K_{\mu \nu }={\sigma }_{\mu \nu }+\frac{1}{3}\theta h_{\mu \nu }+{\omega }_{\mu \nu }$[59]. Throughout we work on stabilized domains: regions where $\Phi$ is smooth, strictly timelike, and $\parallel \nabla \Phi \parallel$ is uniformly bounded so that (i) the foliation exists, (ii) the Cauchy problem for the field equations is well posed in the intrinsic time $\tau$, and (iii) equal-time operator algebras on $\mathcal{H}\left[{\Sigma }_{\tau }\right]$ are well defined up to controllable $O(\parallel \nabla \Phi \parallel )$ corrections [33,38,95].

Role of the Unit–Norm Constraint in the Abelian Sector

Throughout Paper I we impose ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ on stabilized domains. This normalization has three indispensable consequences for the emergence of the $\mathrm{U}\left(1\right)$ sector. First, it fixes the chronon flow as a unit timelike congruence, so the orthogonal projector ${{\Pi }^{\mu }}_{\nu }={{\delta }^{\mu }}_{\nu }+{\Phi }^{\mu }{\Phi }_{\nu }$ is a true projector and the induced leaf metric $h_{\mu \nu }=g_{\mu \nu }[\Phi ]+{\Phi }_{\mu }{\Phi }_{\nu }$ is Riemannian [59,115]. In particular, $\rho =T_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }$ is then the physical energy density in the comoving frame, providing a clean, scale–independent criterion for stabilized domains. Second, restricting parallel transport to ${\Phi }^{\perp }$ preserves h and yields a compact residual isotropy $\mathrm{SO}\left(2\right)\simeq \mathrm{U}\left(1\right)$ on the internal fiber, so that holonomy produces a genuine circle bundle rather than a noncompact $\mathbb{R}$ symmetry; this compactness underlies flux quantization and the integer winding of solitonic defects (${\pi }_1\left(S^1\right)=\mathbb{Z}$) [89,123]. Third, the unit baseline separates angular (phase) and radial (amplitude) degrees of freedom: the former define the emergent $\mathrm{U}\left(1\right)$ connection and Berry–like holonomy on leaves, while the latter encode norm–restoring fluctuations of $\Phi$ without contaminating gauge phases [20]. If the norm were allowed to drift, the projector would cease to be idempotent without ad hoc rescaling, $\rho$ would pick up spurious conformal factors, and leafwise holonomy would no longer be guaranteed to land in a compact Abelian group, obstructing the $\mathrm{U}\left(1\right)$ construction. Related unit-timelike constructions appear in Einstein–æther–type effective theories [72,73].

2.2. Dynamics and Stress Tensor

We take a local, diffeomorphism-invariant CFT action for $\Phi$ on $(\mathcal{M},g)$ truncated at mass-dimension $\le 4$ (parity-even sector):

$$\begin{array}{cc}\hfill S_{\Phi }[g,\Phi ]& =\int {\mathrm{d}}^{4}x\sqrt{-g}{\mathcal{L}}_{\Phi },\hfill \\ \hfill {\mathcal{L}}_{\Phi }& ={\alpha }_1\left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\mu }{\Phi }^{\nu }\right)+{\alpha }_2\left({\nabla }_{\mu }{\Phi }_{\nu }\right)\left({\nabla }^{\nu }{\Phi }^{\mu }\right)+{\alpha }_3{\left({\nabla }_{\mu }{\Phi }^{\mu }\right)}^2+\gamma R_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }+\lambda ({\Phi }^{\mu }{\Phi }_{\mu }+1).\hfill \end{array}$$

(5)

Here $R_{\mu \nu }$ is the Ricci tensor, and $\lambda$ enforces the unit-norm constraint (one may alternatively use a steep potential). The structure mirrors familiar unit-timelike vector EFTs (e.g., Einstein–æther) while remaining background independent in our setting [72,73]. Variation with respect to $\Phi$ yields the Euler–Lagrange equations

$${\alpha }_1{\nabla }_{\mu }{\nabla }^{\mu }{\Phi }^{\nu }+{\alpha }_2{\nabla }_{\mu }{\nabla }^{\nu }{\Phi }^{\mu }+{\alpha }_3{\nabla }^{\nu }(\nabla ·\Phi )+\gamma {R^{\nu }}_{\mu }{\Phi }^{\mu }+\lambda {\Phi }^{\nu }=0,$$

(6)

with $\lambda$ fixed by contracting (6) with ${\Phi }_{\nu }$ and using ${\Phi }^2=-1$. The symmetric (Hilbert) stress tensor is defined by

$$T_{\mu \nu }:=-{\displaystyle \frac{2}{\sqrt{-g}}}{\displaystyle \frac{\delta S_{\Phi }}{\delta g^{\mu \nu }}}=2{\displaystyle \frac{\partial {\mathcal{L}}_{\Phi }}{\partial g^{\mu \nu }}}-g_{\mu \nu }{\mathcal{L}}_{\Phi }+(\mathrm{metric}-\mathrm{variation}\mathrm{terms}\mathrm{from}\mathrm{covariant}\mathrm{derivatives}),$$

(7)

which is conserved on shell, ${\nabla }_{\mu }{T}_{\mu \nu }=0$, by diffeomorphism invariance [115]. The covariant local mass/energy density measured by comoving observers is

$$\rho \left(x\right)=T_{\mu \nu }(\Phi ,\nabla \Phi ,g){\Phi }^{\mu }{\Phi }_{\mu },$$

(8)

and the leafwise total (rest) mass is $\mathsf{M}\left[{\Sigma }_{\tau }\right]:={\int }_{{\Sigma }_{\tau }}\rho {\mathrm{d}}^{3}x$, where the volume element is induced by $h_{\mu \nu }$[115]. Positivity and conservation properties of $\rho$ are established in §4.

2.3. Geometric Action Unit ${\hslash }_{\mathrm{geom}}$ and Operator Algebra

In Chronon Field Theory (CFT), the universal action scale—identified with Planck’s constant—does not arise from coarse–graining or statistical variance, but from the intrinsic curvature geometry of the chronon manifold itself [13,51,82]. The fundamental symplectic structure of the theory is encoded in the chronon two–form curvature

$${\Omega }_{\Phi }:=D\Phi \wedge D\Phi ,$$

(9)

whose scalar contraction $R_{\Phi }:=\frac{1}{2}{\Omega }_{\Phi \mu \nu }{\Omega }_{\Phi }^{\mu \nu }$ defines the intrinsic curvature density of the temporal field [77,88]. On stabilized domains this curvature becomes uniform, and its invariant integral furnishes the natural unit of action:

$${\hslash }_{\mathrm{geom}}={\kappa }_R{\int }_{{\Sigma }_{\tau }}\sqrt{h}{R}_{\Phi }{d}^{3}x\simeq {\kappa }_R\langle R_{\Phi }\rangle {\mathsf{\ell }}_{\Phi }^2,$$

(10)

where ${\kappa }_R$ is a dimensionless matching constant fixed by normalization, ${\mathsf{\ell }}_{\Phi }$ is the chronon length scale, and $\langle R_{\Phi }\rangle$ denotes the stabilized curvature average. Equation (10) expresses ${\hslash }_{\mathrm{geom}}$ as a universal curvature invariant: it is the symplectic area of a fundamental curvature cell of the chronon field. Once the curvature condenses into a stable phase, ${\hslash }_{\mathrm{geom}}$ becomes spatially constant and numerically identical to the observed Planck constant ℏ [83,90].

The corresponding covariant path measure is therefore

$$\mathcal{Z}=\int \mathcal{D}\left(\mathrm{fields}\right)exp\left\{{\displaystyle \frac{\mathrm{i}}{{\hslash }_{\mathrm{geom}}}}\left(S_{\Phi }[g,\Phi ]+S_{\mathrm{matter}}+S_{\mathrm{gauge}}\right)\right\},$$

(11)

in which the weighting factor $exp\{\mathrm{i}\int {\Omega }_{\Phi }/{\hslash }_{\mathrm{g}\mathrm{eom}}\}$ originates directly from the phase of the curvature two–form rather than from ensemble averaging [47,117]. The geometric constant ${\hslash }_{\mathrm{geom}}$ thus defines the fundamental symplectic volume element of the chronon manifold.

Kinematically, Poisson brackets of gauge–invariant functionals $F,G$ are defined on each stabilized leaf ${\Sigma }_{\tau }$ by contraction with the inverse of the symplectic form ${\Omega }_{\Phi }$ [38,42,95]:

$${\{F,G\}}_{\Omega }={\int }_{{\Sigma }_{\tau }}{\displaystyle \frac{\delta F}{\delta {\Phi }_{\mu }}}{{\Omega }_{\Phi }^{-1}}_{\mu \nu }{\displaystyle \frac{\delta G}{\delta {\Phi }_{\nu }}}{d}^{3}x.$$

(12)

Quantization promotes these to operators on the leaf Hilbert space $\mathcal{H}\left[{\Sigma }_{\tau }\right]$ with commutator

$$[\widehat{F},\widehat{G}]=\mathrm{i}{\hslash }_{\mathrm{geom}}{\{F,G\}}_{\Omega }+O(\parallel \nabla \Phi \parallel ),$$

(13)

so that the canonical algebra is recovered in the strong–stabilization limit $\nabla \Phi \to 0$ [13,51]. Together with the energy–density definition (21), this establishes the geometric foundation of the uncertainty relations and of all quantum corrections developed in Section 7.

Figure 2. Chronon curvature geometry on a stabilized leaf ${\Sigma }_{\tau }$. The unit timelike flow ${\Phi }^{\mu }$ defines spatial slices, while the curvature two–form ${\Omega }_{\Phi }=D\Phi \wedge D\Phi$ endows each leaf with a symplectic area element whose invariant magnitude fixes the geometric Planck constant ${\hslash }_{\mathrm{geom}}$.

Figure 2. Chronon curvature geometry on a stabilized leaf ${\Sigma }_{\tau }$. The unit timelike flow ${\Phi }^{\mu }$ defines spatial slices, while the curvature two–form ${\Omega }_{\Phi }=D\Phi \wedge D\Phi$ endows each leaf with a symplectic area element whose invariant magnitude fixes the geometric Planck constant ${\hslash }_{\mathrm{geom}}$.

2.4. EFT and Power Counting

Beyond the two-derivative truncation, the low-energy action on stabilized domains reads

$$S_{\mathrm{eff}}=\int \sqrt{-g}\left[\frac{M_{\mathrm{P}}^2}{2}R-\frac{1}{4}{\kappa }_A{F}^2+{\mathcal{L}}_{\Phi }^{\left(2\right)}[g,\Phi ]+\sum _i{\alpha }_i{\mathcal{O}}_i^{\left(2\right)}[g,\Phi ]+{\displaystyle \frac{1}{{\Lambda }^2}}\sum _j{d}_j{\mathcal{O}}_j^{\left(4\right)}[g,\Phi ,A]+\dots \right],$$

where ${\mathcal{O}}_i^{\left(2\right)}$ are æther-like two-derivative invariants built from $\Phi$ (shear, expansion, acceleration) and ${\mathcal{O}}_j^{\left(4\right)}$ are higher-derivative operators. On stabilized leaves with small $|\nabla \Phi |$, ${\mathcal{O}}_i^{\left(2\right)}$ are naturally suppressed, while ${\mathcal{O}}_j^{\left(4\right)}$ scale as ${(E/\Lambda )}^2$. This organizes deviations from GR in a controlled expansion [29,43,73,116].

3. Emergent $\mathrm{U}\left(1\right)$ from Chronon Holonomy

3.1. Holonomy Phase and Connection

We work on a stabilized domain (cf. §2.1). Parallel transport of the unit timelike field $\Phi$ along smooth curves $\gamma \subset {\Sigma }_{\tau }$ (with Levi–Civita connection of g) induces a rotation in the two–plane orthogonal to $\Phi$. This defines a principal $\mathrm{SO}\left(2\right)\simeq \mathrm{U}\left(1\right)$ bundle over each leaf [51,77,88]. Locally on a chart $U\subset {\Sigma }_{\tau }$, choose a smooth section and let $\theta :U\to \mathbb{R}/2\pi \mathbb{Z}$ be the associated holonomy phase. We then define a spacetime one–form whose leafwise pullback equals the leaf connection:

$$A_{\mu }\mathrm{d}{x}^{\mu }{|}_U:=\mathrm{d}\theta {|}_U,\mathrm{i}.\mathrm{e}.A_{\mu }:={\partial }_{\mu }\theta \left(\mathrm{locally}\right).$$

(14)

A change of section shifts $\theta \mapsto \theta +\alpha$ for some smooth $\alpha$, hence

$$A_{\mu }\mapsto A_{\mu }+{\partial }_{\mu }\alpha ,$$

(15)

and the curvature two–form is the exterior derivative

$$F_{\mu \nu }:={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }={\left(\mathrm{d}A\right)}_{\mu \nu },$$

(16)

which coincides with the holonomy two–form of the induced $\mathrm{U}\left(1\right)$ bundle on each leaf [77,89,123]. In covariant notation we write $F=\mathrm{d}A$ and raise indices with the emergent metric $g_{\mu \nu }$[115]. A geometric phase interpretation of $\theta$ aligns with Berry’s phase in adiabatic settings [20] (here realized leafwise by the chronon fiber).

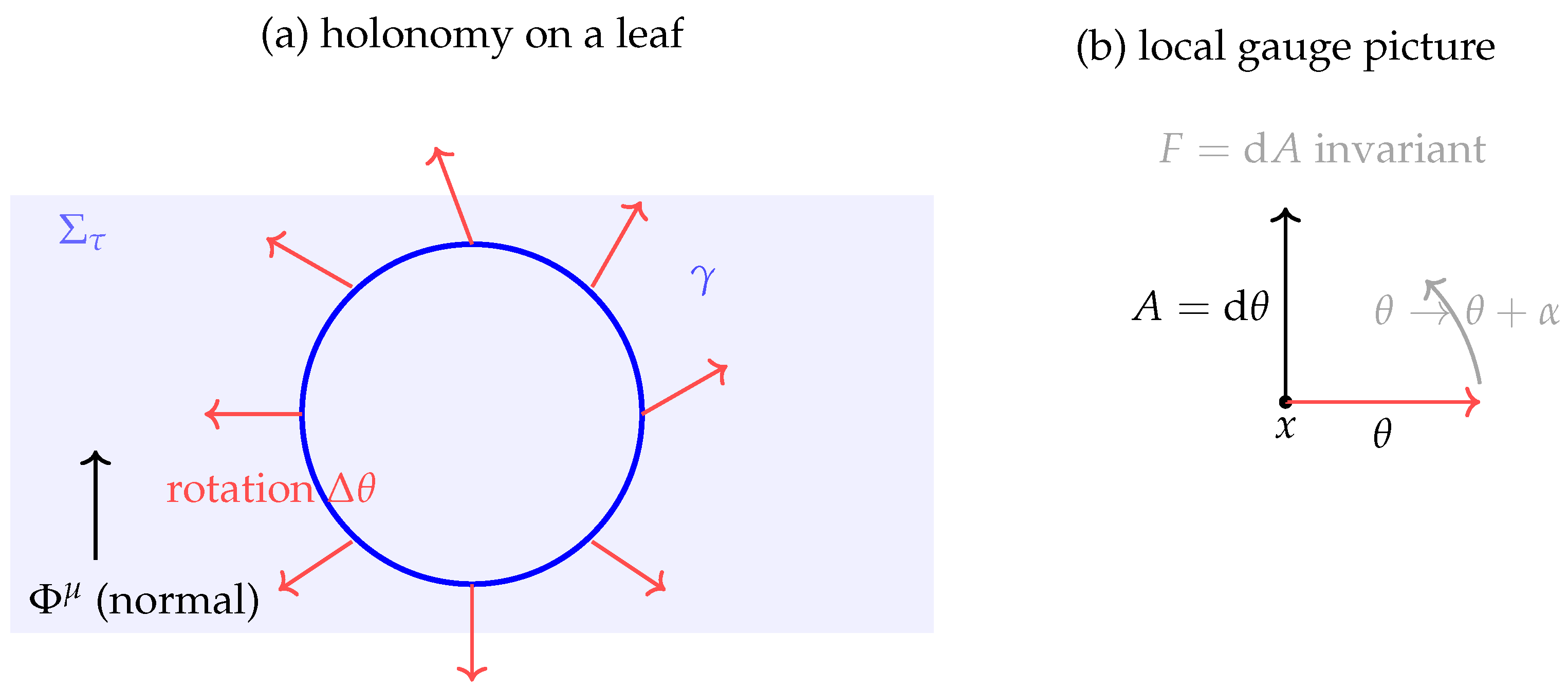
Figure 3. Emergent $\mathrm{U}\left(1\right)$ from chronon holonomy. (a) On a stabilized spatial leaf ${\Sigma }_{\tau }$, transporting the local orthonormal frame once around a closed loop $\gamma$ produces a net rotation of the transverse basis vectors by an angle $\Delta \theta$. This angle records the holonomy of the connection induced by the chronon flow, and defines a compact phase variable identified modulo $2\pi$. The normal vector ${\Phi }^{\mu }$ indicates the timelike direction singled out by the chronon field. (b) In the local gauge description, the rotation angle $\theta$ serves as a coordinate on the internal $\mathrm{U}\left(1\right)$ fiber. Its derivative $A=\mathrm{d}\theta$ acts as the Abelian gauge potential, and a gauge shift $\theta \to \theta +\alpha$ changes A by a pure gradient while leaving the curvature $F=\mathrm{d}A$ invariant. In this way, the geometric holonomy of chronon transport is reinterpreted as an emergent electromagnetic $\mathrm{U}\left(1\right)$ gauge symmetry.

Figure 3. Emergent $\mathrm{U}\left(1\right)$ from chronon holonomy. (a) On a stabilized spatial leaf ${\Sigma }_{\tau }$, transporting the local orthonormal frame once around a closed loop $\gamma$ produces a net rotation of the transverse basis vectors by an angle $\Delta \theta$. This angle records the holonomy of the connection induced by the chronon flow, and defines a compact phase variable identified modulo $2\pi$. The normal vector ${\Phi }^{\mu }$ indicates the timelike direction singled out by the chronon field. (b) In the local gauge description, the rotation angle $\theta$ serves as a coordinate on the internal $\mathrm{U}\left(1\right)$ fiber. Its derivative $A=\mathrm{d}\theta$ acts as the Abelian gauge potential, and a gauge shift $\theta \to \theta +\alpha$ changes A by a pure gradient while leaving the curvature $F=\mathrm{d}A$ invariant. In this way, the geometric holonomy of chronon transport is reinterpreted as an emergent electromagnetic $\mathrm{U}\left(1\right)$ gauge symmetry.

3.2. Gauge Invariance and Maxwell Limit

Under $A_{\mu }\mapsto A_{\mu }+{\partial }_{\mu }\alpha$, the curvature $F_{\mu \nu }$ is invariant. In the canonical normalization (after $A_{\mu }\to A_{\mu }^{\mathrm{can}}=\sqrt{{\kappa }_A}{A}_{\mu }$), the minimal diffeomorphism– and gauge–invariant action for the Abelian sector on $(\mathcal{M},g_{\mu \nu }[\Phi ])$ is

$$S_{\mathrm{gauge}}[A;g]=-{\displaystyle \frac{1}{4}}\int F_{\mu \nu }{F}^{\mu \nu }\sqrt{-g}{\mathrm{d}}^{4}x,$$

(17)

whose variation with respect to $A_{\nu }$ yields the source–free Maxwell equations on the emergent geometry:

$${\nabla }_{\mu }{F}^{\mu \nu }=0,\mathrm{together}\mathrm{with}{\nabla }_{[\lambda }{F}_{\mu \nu ]}=0,$$

(18)

the latter being the Bianchi identity ($\mathrm{d}F=0$) [70,115]. Coupling to matter proceeds by minimal substitution on the relevant bundles (e.g. the soliton bundle of §5), giving ${\nabla }_{\mu }{F}^{\mu \nu }=J^{\nu }$ with ${\nabla }_{\nu }{J}^{\nu }=0$ as the Noether current conservation law for the $\mathrm{U}\left(1\right)$ gauge symmetry [91,97]. In the infrared, the dynamics are Maxwellian with two transverse polarizations; the photon corresponds to a Goldstone–like fluctuation of the internal time–phase encoded by $\theta$ [10].

Reference Maxwell Limit on Stabilized Domains

A precise EFT statement quantifying when (17) governs the dynamics is given in Appendix L, Proposition A1. On twist–free, slowly varying backgrounds ${\overline{\Phi }}^{\mu }$ (“stabilized domains”), one finds

$$S_{\mathrm{gauge}}\left[A\right]=-{\displaystyle \frac{{\kappa }_A}{4}}\int \sqrt{-g}{F}_{\mu \nu }{F}^{\mu \nu }+\Delta S\left[A\right],\mathrm{cf}.(1),$$

(19)

with deviations organized by the small parameters ${\epsilon }_{\nabla \Phi }=\parallel \nabla \overline{\Phi }\parallel /\Lambda$,  ${\epsilon }_R=\parallel \mathrm{Riem}\parallel /{\Lambda }^2$, and $\delta =k/\Lambda$, as well as any æther–like couplings ${\alpha }_i$:

$${\nabla }_{\mu }{F}^{\mu \nu }=J^{\nu }+\mathcal{O}\left({\alpha }_i\right)+\mathcal{O}\left({\epsilon }_{\nabla \Phi }^2\right)+\mathcal{O}\left({\epsilon }_R\right)+\mathcal{O}\left({\delta }^2\right),\mathrm{cf}.\left(3\right).$$

(20)

The leading non–Maxwell operators in $\Delta S$ are æther–like parity–even contractions ${(\overline{\Phi }·F)}^2$ and $\overline{\Phi }\overline{\Phi }FF$, and higher–derivative/curvature terms such as ${(\nabla F)}^2/{\Lambda }^2$ and $R{F}^2/{\Lambda }^2$ (see (2)); their coefficients are suppressed by $\mathcal{O}\left({\alpha }_i\right)$, $\mathcal{O}\left({\epsilon }_{\nabla \Phi }^2\right)$, $\mathcal{O}\left({\epsilon }_R\right)$, and $\mathcal{O}\left({\delta }^2\right)$, respectively. Hence birefringence and anisotropy effects are parametrically small on stabilized domains (consistent with photon–sector bounds, cf. [78,79]).

4. Covariant Local Mass/Energy Density

A central requirement for any background–independent field theory that aims to reproduce relativistic matter and interactions is a covariant and observer–independent notion of mass/energy density [64,115]. In Chronon Field Theory (CFT), this role is played by the scalar quantity

$$\rho \left(x\right):=T_{\mu \nu }\left(x\right){\Phi }^{\mu }\left(x\right){\Phi }_{\mu }\left(x\right),$$

(21)

defined pointwise on stabilized domains. Equation (21) has three immediate virtues: (i) it is manifestly covariant, depending only on the stress tensor $T_{\mu \nu }$ and the dynamical timelike unit vector $\Phi$; (ii) it reduces to the conventional energy density $T^{00}$ in the comoving frame aligned with $\Phi$ [80]; and (iii) it is intrinsically nonnegative and conserved under mild regularity conditions, as we prove below.

Assumption 4.1

(Regular domain). Solutions of the CFT field equations admit stabilized leaves ${\Sigma }_{\tau }$ with induced metric $g_{\mu \nu }$ and smooth stress tensor $T_{\mu \nu }$. Moreover, the Lagrangian density is invariant under flow along $\Phi$ (quasi–stationarity):

$${\mathcal{L}}_{\Phi }\left(\sqrt{-g}{\mathcal{L}}_{\Phi }\right)=0$$

on the domain.

The quasi–stationarity condition expresses the fact that translations along the chronon flow $\Phi$ act as an isometry of the stabilized domain, ensuring that the associated Noether current [91] coincides with the natural energy current. This parallels the role of Killing vectors in conventional general relativity [115], but here arises dynamically from the unit–norm constraint and stabilization.

theorem 4.2

(Positivity and conservation of $\rho$). Let Theorem 4.1 hold and assume the induced dominant energy condition (DEC), i.e.

$$T_{\mu \nu }{v}^{\mu }{w}^{\nu }\ge 0\mathrm{for}\mathrm{all}\mathrm{future}\text{–}\mathrm{directed}\mathrm{causal}{v}^{\mu },w^{\nu }.$$

Then on any stabilized leaf ${\Sigma }_{\tau }$:

(i) 

$\rho =T_{\mu \nu }{\Phi }^{\mu }{\Phi }_{\mu }\ge 0$;

(ii) 

the energy current $J^{\mu }:=T_{\mu \nu }{\Phi }_{\nu }$ is conserved, ${\nabla }_{\mu }{J}^{\mu }=0$;

(iii) 

consequently, the total mass

$$\mathsf{M}\left(\tau \right):={\int }_{{\Sigma }_{\tau }}\rho {\mathrm{d}}^{3}x$$

(22)

is finite for finite–energy data and independent of the leaf label τ.

Proof. (i) Positivity. Since ${\Phi }^{\mu }$ is a future–directed unit timelike vector, the induced DEC immediately yields

$$T_{\mu \nu }{\Phi }^{\mu }{\Phi }_{\mu }\ge 0,$$

establishing $\rho \ge 0$ pointwise [64,115].

(ii) Conservation. Diffeomorphism invariance of the CFT action ensures ${\nabla }_{\mu }{T}_{\mu \nu }=0$ [91]. Contracting with ${\Phi }_{\nu }$ gives

$${\nabla }_{\mu }{J}^{\mu }={\nabla }_{\mu }\left(T_{\mu \nu }{\Phi }_{\nu }\right)=\left({\nabla }_{\mu }{T}_{\mu \nu }\right){\Phi }_{\nu }+T_{\mu \nu }{\nabla }_{\mu }{\Phi }_{\nu }.$$

The first term vanishes on shell. The second term vanishes under Theorem 4.1: invariance under $\Phi$–flow identifies $J^{\mu }$ as the Noether current associated to translations along $\Phi$, hence conserved [91,115].

(iii) Leaf–independence of $\mathsf{M}\left(\tau \right)$. Integrate ${\nabla }_{\mu }{J}^{\mu }=0$ over the spacetime slab bounded by two leaves ${\Sigma }_{{\tau }_1}$ and ${\Sigma }_{{\tau }_2}$ and apply the divergence theorem [54]:

$$0={\int }_{\mathcal{V}}{\nabla }_{\mu }{J}^{\mu }\sqrt{-g}{\mathrm{d}}^{4}x={\int }_{{\Sigma }_{{\tau }_2}}{J}^{\mu }{n}_{\mu }{\mathrm{d}}^{3}x-{\int }_{{\Sigma }_{{\tau }_1}}{J}^{\mu }{n}_{\mu }{\mathrm{d}}^{3}x+{\int }_{\mathcal{T}}{J}^{\mu }{n}_{\mu }{\mathrm{d}}^3\sigma .$$

Here $n^{\mu }$ is the unit normal to the integration surfaces, and $\mathcal{T}$ denotes the timelike boundary of the slab. On ${\Sigma }_{\tau }$, $n^{\mu }={\Phi }^{\mu }$, so the flux reduces to $\rho$ as in (22). The boundary term over $\mathcal{T}$ vanishes for finite–energy configurations by the assumed decay of fields. Thus

$$\mathsf{M}\left({\tau }_2\right)=\mathsf{M}\left({\tau }_1\right),$$

proving constancy of the total mass across leaves.    □

Remarks 

• The functional $\mathsf{M}\left(\tau \right)$ furnishes a covariant, background–independent definition of inertial and gravitational mass in CFT, reducing to the ADM mass [9] in asymptotically flat settings where $\Phi$ aligns with the asymptotic time translation.
• Unlike canonical Hamiltonian formulations, no reference to a preferred coordinate system is required: the chronon flow $\Phi$ supplies the intrinsic time direction and defines the foliation $\left\{{\Sigma }_{\tau }\right\}$.
• The conservation of $\mathsf{M}\left(\tau \right)$ ensures stability of solitonic excitations and provides the basis for identifying the rest mass $M_{w=1}$ in topological sectors (Section 5).

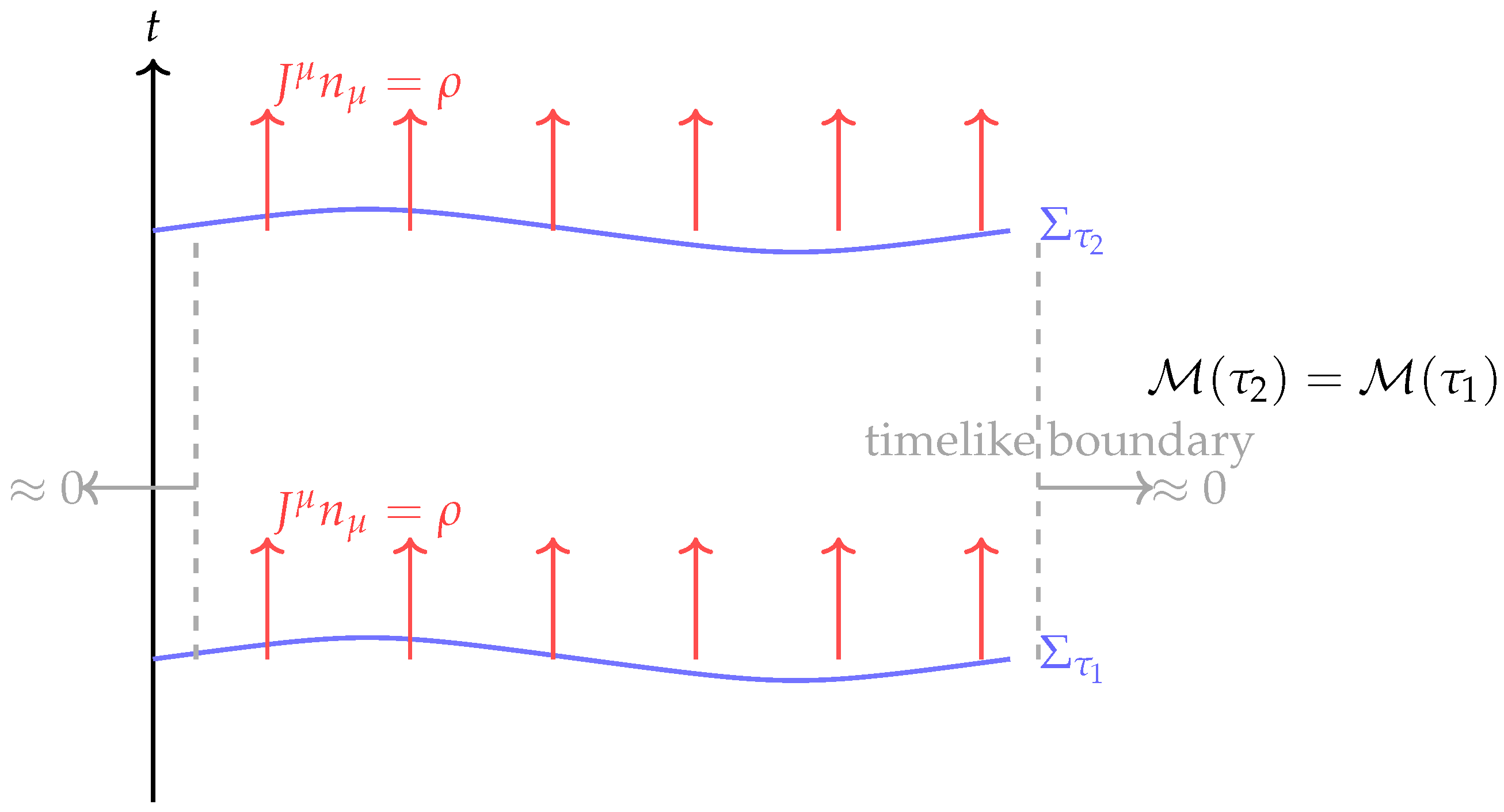
Figure 4. Covariant mass and conserved flux in Chronon Field Theory. The diagram shows a spacetime slab bounded by two stabilized spatial leaves ${\Sigma }_{{\tau }_1}$ and ${\Sigma }_{{\tau }_2}$ (blue curves) and vertical timelike boundaries (dashed gray lines). The energy current $J^{\mu }=T^{\mu \nu }{\Phi }_{\nu }$ flows across the leaves with flux density $J^{\mu }{n}_{\mu }=\rho$ (red arrows). Because the flux through ${\Sigma }_{{\tau }_1}$ and ${\Sigma }_{{\tau }_2}$ is equal, and because finite–energy configurations produce negligible flux through the timelike boundaries, the total mass functional $\mathcal{M}\left(\tau \right)={\int }_{{\Sigma }_{\tau }}\rho \mathrm{d}{\mathrm{vol}}_h$ is conserved between leaves: $\mathcal{M}\left({\tau }_2\right)=\mathcal{M}\left({\tau }_1\right)$. This figure provides a geometric visualization of the conservation law proved in Appendix A: the red vertical arrows depict the flow of energy density across the slices, while the gray side arrows vanish, ensuring that the integrated mass remains constant across time.

Figure 4. Covariant mass and conserved flux in Chronon Field Theory. The diagram shows a spacetime slab bounded by two stabilized spatial leaves ${\Sigma }_{{\tau }_1}$ and ${\Sigma }_{{\tau }_2}$ (blue curves) and vertical timelike boundaries (dashed gray lines). The energy current $J^{\mu }=T^{\mu \nu }{\Phi }_{\nu }$ flows across the leaves with flux density $J^{\mu }{n}_{\mu }=\rho$ (red arrows). Because the flux through ${\Sigma }_{{\tau }_1}$ and ${\Sigma }_{{\tau }_2}$ is equal, and because finite–energy configurations produce negligible flux through the timelike boundaries, the total mass functional $\mathcal{M}\left(\tau \right)={\int }_{{\Sigma }_{\tau }}\rho \mathrm{d}{\mathrm{vol}}_h$ is conserved between leaves: $\mathcal{M}\left({\tau }_2\right)=\mathcal{M}\left({\tau }_1\right)$. This figure provides a geometric visualization of the conservation law proved in Appendix A: the red vertical arrows depict the flow of energy density across the slices, while the gray side arrows vanish, ensuring that the integrated mass remains constant across time.

5. Solitonic Matter: Existence and Properties

In Chronon Field Theory, localized matter excitations are not introduced as independent quantized fields but arise as topologically stable solitons of the chronon field $\Phi$. These solitons correspond to nontrivial elements of the homotopy group ${\pi }_3\left(S^3\right)$ [62], ensuring stability under smooth deformations. In this section we define the relevant configuration and moduli spaces, establish existence of finite–energy minimizers in the nontrivial sector $w=1$, and outline their inertial properties and quantization.

Functional Setting

Throughout this section we work in the Sobolev class $H^1(\Sigma ;S^3)$ at fixed topological degree w, with the Skyrme-type energy described below. The precise function spaces, constraints, and the existence result for the $w=1$ sector are summarized in Appendix M.

5.1. Topological Sectors and Configuration Spaces

To define solitonic sectors we impose asymptotic boundary conditions. On each stabilized leaf ${\Sigma }_{\tau }\cong {\mathbb{R}}^3$, we require

$${\Phi }^{\mu }\left(x\right)\to (1,0,0,0)\mathrm{as}\left|x\right|\to \infty ,$$

(23)

so that spatial infinity is compactified to a point. This compactification identifies ${\mathbb{R}}^3\cup \{\infty \}\cong S^3$, and the unit–norm constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ restricts the target space of $\Phi$ to $S^3\subset {\mathbb{R}}^4$. Thus any static configuration defines a continuous map

$$\Phi :S^3⟶S^3.$$

Such maps are classified by the winding number

$$w\in {\pi }_3\left(S^3\right)\cong \mathbb{Z}\left[62\right],$$

which serves as a topological charge. Physically, w measures how many times the spatial slice wraps around the unit hyperboloid of admissible chronon vectors.

Configuration and Moduli Spaces

For each $w\in \mathbb{Z}$, define the configuration space

$${\mathcal{C}}_w:=\left\{\Phi \in C^{\infty }(S^3,S^3)|deg(\Phi )=w\right\},$$

(24)

i.e. smooth finite–energy chronon fields with topological charge w. The corresponding moduli space is

$$M_w:={\mathcal{C}}_w/\left({\mathrm{Diff}}_0\left({\Sigma }_{\tau }\right)\times \mathrm{Gauge}(\Phi )\right),$$

(25)

where ${\mathrm{Diff}}_0\left({\Sigma }_{\tau }\right)$ denotes diffeomorphisms connected to the identity and $\mathrm{Gauge}(\Phi )$ denotes residual internal symmetries preserving the unit–norm constraint. $M_w$ parametrizes physically inequivalent solitons [86].

By the existence result established in Appendix M for $w=1$, we may fix a minimizer ${\Phi }_{*}$ in the admissible class and analyze its properties.

theorem 5.1

(Existence of a finite–energy minimizer for $w=1$). Let the CFT couplings $({\alpha }_1,{\alpha }_2,{\alpha }_3,\gamma )$ satisfy the coercivity and regularity conditions of Assumption 4.1, and impose boundary condition (23). Then the energy functional

$$E[\Phi ]={\int }_{{\Sigma }_{\tau }}\rho {\mathrm{d}}^{3}x$$

(26)

admits a smooth finite–energy minimizer in the topological class $w=1$. This minimizer is stable against small perturbations.

Strategy. 

The proof follows the direct method in the calculus of variations [46,109]:

(a)

Coercivity. Gradient and curvature terms in the CFT action provide a coercive bound $E[\Phi ]\gtrsim {\parallel \nabla \Phi \parallel }_{L^2}^2$, preventing loss of compactness.

(b)

Lower semicontinuity. The integrand of (26) is convex in $\nabla \Phi$, implying weak lower semicontinuity of E on $H^1$.

(c)

Compactness. By Rellich’s theorem, minimizing sequences admit weakly convergent subsequences modulo spatial translations and gauge rotations [46].

(d)

Topological constraint. The winding number w is preserved under weak convergence in $H^1$, ensuring the limit lies in ${\mathcal{C}}_1$ [62].

(e)

Regularity. Standard elliptic estimates upgrade weak minimizers to smooth solutions of the Euler–Lagrange equations [55].

Positivity of $\rho$ (Theorem 4.2) ensures finite energy, while the second variation of E is nonnegative in directions tangent to ${\mathcal{C}}_1$, guaranteeing stability under small perturbations [86].    □

5.2. Rest Mass and Collective Modes

The rest mass of the fundamental soliton is defined by evaluating the conserved mass functional (Section 4) on the $w=1$ minimizer:

$$M_{w=1}:={\int }_{{\Sigma }_{\tau }}\rho \left[{\Phi }_{w=1}\right]{\mathrm{d}}^{3}x.$$

(27)

This provides the intrinsic inertial/gravitational mass of the soliton, independent of the foliation label $\tau$.

Collective Coordinates

The moduli space $M_1$ admits low–energy deformations corresponding to translations, global $U\left(1\right)$ phase rotations, and internal isorotations. Quantization of these modes proceeds via the collective–coordinate method [7,86]: one promotes the moduli parameters to slowly varying quantum degrees of freedom, substitutes into the action, and derives an effective Hamiltonian. For a single internal rotor with moment of inertia I, the leading energy splitting scales as

$$\Delta E\sim {\displaystyle \frac{{\hslash }_{\mathrm{geom}}^2}{2I}}.$$

(28)

This scaling parallels that of Skyrmion quantization in nuclear physics [7,105], but here ${\hslash }_{\mathrm{geom}}$ is the emergent action unit derived from chronon microdynamics (Appendix L).

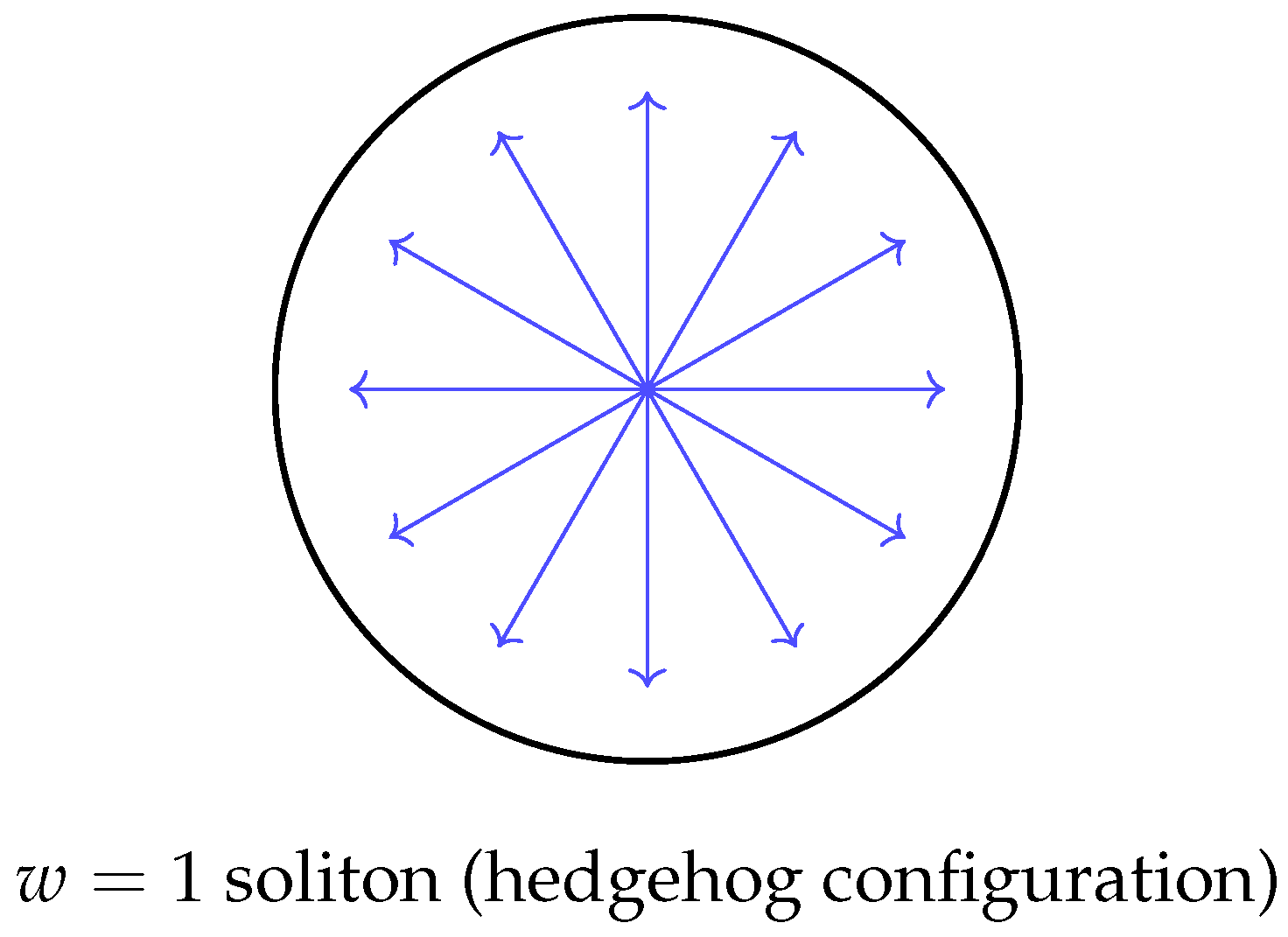
Figure 5. Schematic illustration of a unit–charge ($w=1$) soliton. The chronon field $\Phi$ is constrained to have unit norm and thus maps spatial infinity to a fixed point on the internal target space $S^3$. A representative configuration is shown as a hedgehog map, where spatial directions (arrows radiating outward) are aligned with internal directions of $\Phi$. As one traverses the enclosing $S^2$ in real space, the field winds exactly once around a great circle of $S^3$, realizing topological degree one. This winding number protects the soliton from decay into the trivial vacuum. The hedgehog pattern is a canonical visualization of how topological charge is encoded in the spatial profile of the chronon field.

Figure 5. Schematic illustration of a unit–charge ($w=1$) soliton. The chronon field $\Phi$ is constrained to have unit norm and thus maps spatial infinity to a fixed point on the internal target space $S^3$. A representative configuration is shown as a hedgehog map, where spatial directions (arrows radiating outward) are aligned with internal directions of $\Phi$. As one traverses the enclosing $S^2$ in real space, the field winds exactly once around a great circle of $S^3$, realizing topological degree one. This winding number protects the soliton from decay into the trivial vacuum. The hedgehog pattern is a canonical visualization of how topological charge is encoded in the spatial profile of the chronon field.

Remark (Uniqueness and Spectrum in $w=1$)

Under the hypotheses of Theorem 5.1 the $w=1$ sector admits at least one smooth, finite–energy minimizer. In the minimal CFT (two–derivative, stabilized domain) we expect this minimizer to be unique up to symmetries [86]: translations in ${\mathbb{R}}^3$, a global $\mathrm{U}\left(1\right)$ phase, and (only if the profile is not spherically symmetric) spatial rotations. Formally, let $\mathbb{L}$ denote the second–variation (Hessian) operator around the minimizer ${\Phi }_{★}$; then the Morse index is zero and

$$ker\mathbb{L}=span\{{\partial }_{x^i}{\Phi }_{★}(i=1,2,3),{\partial }_{\theta }{\Phi }_{★},{\mathcal{R}}_a{\Phi }_{★}(a=1,2,3\mathrm{iff}{\Phi }_{★}\mathrm{breaks}SO\left(3\right))\},$$

with ${\partial }_{\theta }$ the global $\mathrm{U}\left(1\right)$ zero mode and ${\mathcal{R}}_a$ the generators of infinitesimal spatial rotations. Quantization of the corresponding collective coordinates, together with low–lying vibrational modes (eigenfunctions of $\mathbb{L}$ with small positive eigenvalues), produces an excitation tower within the $w=1$ sector [7,86]; all such states carry the same topological/electric charge $q_0$. Multiple local minima (“isomers”) in $w=1$ can exist for special choices of couplings $({\alpha }_i,\gamma )$; these would constitute distinct solitonic species sharing $w=1$ and charge $q_0$ but differing in mass and internal structure.

Summary

The existence of stable $w=1$ solitons, their identification with localized lumps of conserved mass $\mathsf{M}$, and the quantization of their collective modes together establish a concrete mechanism by which fermionic matter arises in CFT. The spin–statistics connection will be demonstrated in Section 6, completing the interpretation of solitons as particle–like excitations with spin–$\frac{1}{2}$ and Fermi–Dirac statistics.

6. Spin–Statistics via FR/Berry and Bundle Matching

The emergence of fermionic behavior in CFT rests on the topology of the soliton moduli space $M_1$ and its associated quantum bundle. The central fact is that both a $2\pi$ spatial rotation of a single soliton and the exchange of two identical solitons correspond to nontrivial loops in configuration space, carrying a ${\mathbb{Z}}_2$ holonomy. Quantization over this space therefore enforces spin-$\frac{1}{2}$ transformation properties and Fermi–Dirac statistics. We formalize this statement below.

6.1. Topology of $M_1$ and Exchange Space

Let $M_1$ denote the moduli space of static finite–energy solitons with topological charge $w=1$, modulo diffeomorphisms and residual gauge transformations. Standard results on Skyrme–type solitons [48,86] adapt directly: the boundary condition ${\Phi }^{\mu }\to (1,0,0,0)$ at spatial infinity fixes an internal reference frame, and the residual action of $\mathrm{SO}\left(3\right)$ on spatial coordinates induces a nontrivial ${\pi }_1$.

$${\pi }_1\left(M_1\right)\cong {\mathbb{Z}}_2.$$

(29)

The nontrivial loop corresponds to a $2\pi$ spatial rotation of the soliton, which cannot be continuously deformed to the identity without violating the topological constraint [48].

Similarly, consider the unordered two–soliton configuration space

$$C\left(2\right):=\left\{({\Phi }_1,{\Phi }_2)\in {\mathcal{C}}_1\times {\mathcal{C}}_1|{\Phi }_1\ne {\Phi }_2\right\}/{\mathfrak{S}}_2,$$

where ${\mathfrak{S}}_2$ permutes the solitons. One finds

$${\pi }_1\left(C\left(2\right)\right)\cong {\mathbb{Z}}_2,$$

(30)

with the nontrivial loop given by exchanging two identical solitons along a closed trajectory in configuration space [88]. This exchange loop is homotopically distinct from the trivial path and represents the generator of ${\mathbb{Z}}_2$.

theorem 6.1

(FR/Berry fermionic sector). A $2\pi$ spatial rotation of a single soliton and the exchange loop of two identical solitons each represent the nontrivial element of ${\pi }_1\left(M_1\right)\cong {\pi }_1\left(C\left(2\right)\right)\cong {\mathbb{Z}}_2$. Quantization over the corresponding Hilbert bundle assigns a $-1$ holonomy to these loops, so soliton wavefunctionals transform as spin-$\frac{1}{2}$ objects under rotation and acquire a minus sign under exchange. Thus the $w=1$ solitons exhibit Fermi–Dirac statistics.

Sketch 

The argument follows the Finkelstein–Rubinstein (FR) construction [48,49]. Quantization is defined not on configuration space ${\mathcal{C}}_1$ itself but on its universal cover ${\tilde{\mathcal{C}}}_1$. Wavefunctionals $\Psi$ are required to satisfy the FR constraint

$$\Psi (\gamma ·\Phi )=\chi \left(\gamma \right)\Psi (\Phi ),$$

for any loop $\gamma \in {\pi }_1\left({\mathcal{C}}_1\right)$, where $\chi :{\pi }_1\left({\mathcal{C}}_1\right)\to \{\pm 1\}$ is a one–dimensional representation. Since ${\pi }_1\left(M_1\right)\cong {\mathbb{Z}}_2$, there are two possible representations; physical consistency with the Berry phase calculation below selects the nontrivial representation. Thus $\chi \left(\gamma \right)=-1$ for the generator, enforcing fermionic behavior. In particular, a $2\pi$ rotation or an exchange loop both generate $\gamma$, yielding the minus sign.    □

6.2. Berry Connection and Bundle Matching

The FR sign can be identified with a geometric phase arising from parallel transport of soliton states along loops in configuration space. This provides a bridge between the topological classification and the emergent gauge structure of CFT.

Proposition 6.2

(Bundle–matching). Let A be the emergent spacetime $\mathrm{U}\left(1\right)$ connection defined in Section 3. Consider the soliton configuration bundle $\pi :\mathcal{B}\to M_1$ whose fiber carries soliton wavefunctionals. Then the pullback ${\pi }^{*}A$ reproduces the FR ${\mathbb{Z}}_2$ holonomy class: transport around the nontrivial loop of ${\pi }_1\left(M_1\right)$ accumulates a Berry phase of π. Consequently, the geometric phase along an exchange loop is exactly $-1$, matching the fermionic sector of Theorem 6.1.

Sketch. 

On stabilized domains, the emergent $\mathrm{U}\left(1\right)$ connection A is locally given by $A_{\mu }={\partial }_{\mu }\theta$ for the chronon holonomy phase $\theta$. When restricted to soliton configurations, $\theta$ is defined modulo $2\pi$, so transport around a loop $\gamma \in {\pi }_1\left(M_1\right)$ yields

$${\oint }_{\gamma }A=\Delta \theta =\pi \left(\mathrm{mod}2\pi \right).$$

This corresponds to a Berry phase $exp\left(i\pi \right)=-1$ [20,104]. Thus the pullback bundle $(\mathcal{B},{\pi }^{*}A)$ carries exactly the nontrivial ${\mathbb{Z}}_2$ holonomy of the FR construction. The consistency of the two perspectives—topological (FR) and geometric (Berry phase)—establishes the equivalence of spin-$\frac{1}{2}$ statistics with the holonomy of the emergent gauge sector.    □

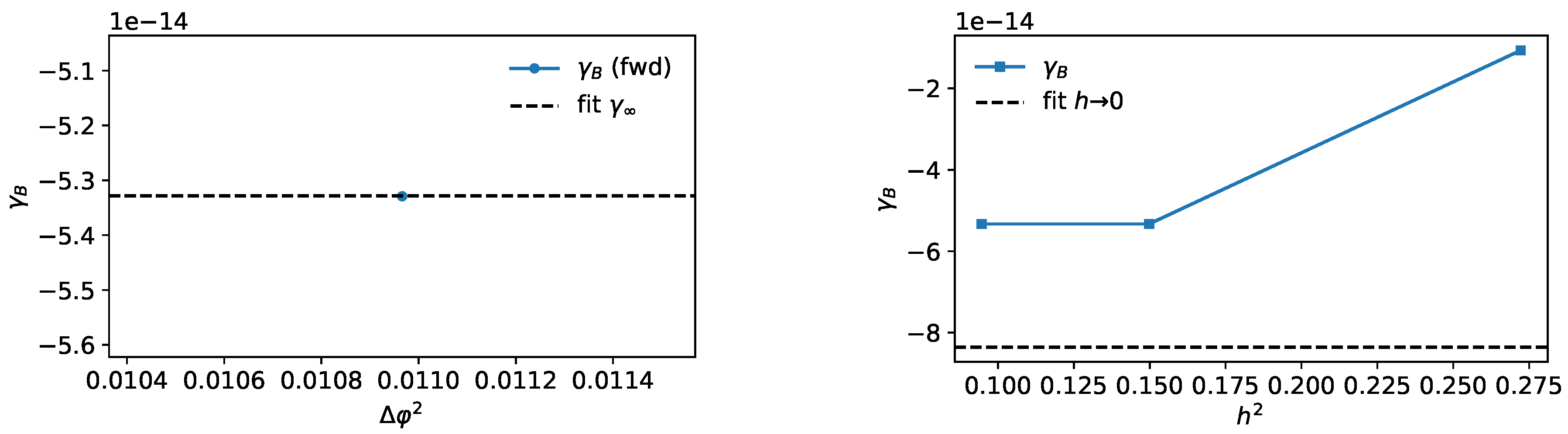
(Computed numerically: $N=32$, $L=6$, $N_{\phi }=60$, anisotropy $=2.0$; see Appendix L for Maxwell-limit details and Appendix D–D.5 for the convergence study, yielding ${\gamma }_B=\pi \pm {\Delta }_{\mathrm{num}}$.)

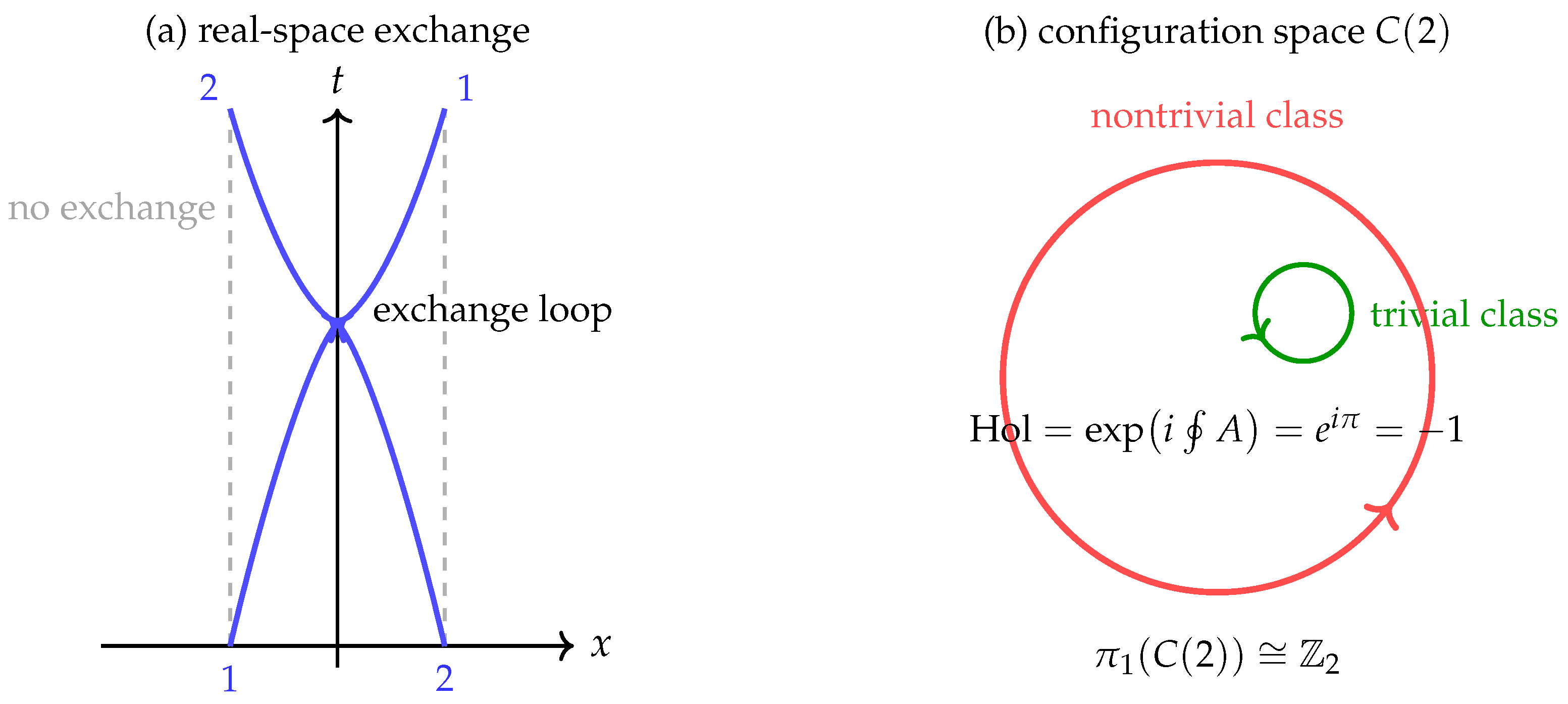
Figure 6. Exchange statistics from soliton worldlines and configuration–space topology. (a) In real spacetime, two identical solitons follow worldlines (blue curves) that braid around one another as time flows upward. This exchange path cannot be continuously deformed to the trivial “no-exchange’’ case (gray dashed vertical lines) without the worldlines crossing, so it defines a distinct loop, the exchange loop. (b) In the two-particle configuration space $C\left(2\right)$, the exchange corresponds to a nontrivial loop in ${\pi }_1\left(C\left(2\right)\right)\cong {\mathbb{Z}}_2$. The trivial class (green) represents no exchange, while the nontrivial class (red) represents a full braid of the two particles. On the soliton ground-state line bundle, the Berry connection assigns holonomy $\mathrm{Hol}=exp(i\oint A)=e^{i\pi }=-1$ to the nontrivial loop. This geometric phase is precisely the fermionic minus sign: exchanging two identical $w=1$ solitons multiplies the wavefunction by $-1$. The figure therefore demonstrates the emergence of Fermi–Dirac statistics from the FR/Berry mechanism in Chronon Field Theory, showing that solitons behave as fermions due to topological and geometric phases.

Figure 6. Exchange statistics from soliton worldlines and configuration–space topology. (a) In real spacetime, two identical solitons follow worldlines (blue curves) that braid around one another as time flows upward. This exchange path cannot be continuously deformed to the trivial “no-exchange’’ case (gray dashed vertical lines) without the worldlines crossing, so it defines a distinct loop, the exchange loop. (b) In the two-particle configuration space $C\left(2\right)$, the exchange corresponds to a nontrivial loop in ${\pi }_1\left(C\left(2\right)\right)\cong {\mathbb{Z}}_2$. The trivial class (green) represents no exchange, while the nontrivial class (red) represents a full braid of the two particles. On the soliton ground-state line bundle, the Berry connection assigns holonomy $\mathrm{Hol}=exp(i\oint A)=e^{i\pi }=-1$ to the nontrivial loop. This geometric phase is precisely the fermionic minus sign: exchanging two identical $w=1$ solitons multiplies the wavefunction by $-1$. The figure therefore demonstrates the emergence of Fermi–Dirac statistics from the FR/Berry mechanism in Chronon Field Theory, showing that solitons behave as fermions due to topological and geometric phases.

Summary

The FR constraint and Berry holonomy coincide in CFT: the nontrivial topology of soliton moduli space enforces a ${\mathbb{Z}}_2$ representation, while the emergent $\mathrm{U}\left(1\right)$ gauge connection provides the geometric mechanism by which wavefunctionals accumulate a $\pi$ phase. Together these results prove that $w=1$ solitons behave as fermions, thereby establishing the spin–statistics connection intrinsically within the chronon framework.

7. Quantum Corrections and Emergent Geometric Action Unit ${\hslash }_{\mathrm{geom}}$

Chronon Field Theory (CFT) is a classically covariant, background–independent field theory whose quantum regime arises when the curvature two–form of the chronon manifold stabilizes at a universal magnitude [13,51,82]. In this stabilized phase, the intrinsic symplectic area of the chronon curvature,

$${\Omega }_{\Phi }=D\Phi \wedge D\Phi ,{\hslash }_{\mathrm{geom}}={\kappa }_R{\int }_{{\Sigma }_{\tau }}\sqrt{h}{R}_{\Phi }{d}^{3}x,$$

(31)

defines a constant action unit ${\hslash }_{\mathrm{geom}}$. This curvature invariant provides the universal scale controlling quantum fluctuations, operator commutators, and the excitation spectra of solitonic matter [25,88,117]. We summarize below the geometric operator algebra, path–integral weighting, and the resulting spectral corrections.

Physical Intuition

At the microscopic level, the emergence of ${\hslash }_{\mathrm{geom}}$ can be viewed as a phase–locking transition of the pre–geometric chronon field [76,83,90]. In the disordered regime, chronon orientations fluctuate incoherently and no universal quantum of action exists. As curvature condenses, local chronon phases align and the field attains global coherence: the symplectic flux through a minimal chronon cell becomes quantized in integer multiples of a fundamental unit. Each $2\pi$ winding of the chronon phase corresponds to a complete symplectic twist of a stable soliton configuration, yielding a discrete increment of action $\Delta S=n{\hslash }_{\mathrm{geom}}$. Quantization therefore originates not from statistical coarse–graining but from the topological stability of these phase windings—an intrinsic property of the condensed curvature manifold [86,114]. Only configurations containing an integer number of such $2\pi$ twists are dynamically stable. The emergence of a universal ${\hslash }_{\mathrm{geom}}$ thus marks a genuine phase transition: spacetime evolves from a pre–geometric, fluctuating medium into a coherent, quantized geometry. In this view, quantization is a manifestation of geometric coherence—the formation of discrete, topologically protected excitation modes—rather than the mechanism by which matter is created.

7.1. Leafwise Operator Algebra

On a stabilized leaf ${\Sigma }_{\tau }$, the chronon curvature ${\Omega }_{\Phi }$ induces a natural symplectic form on the space of gauge–invariant functionals $F[\Phi ],G[\Phi ]$:

$${\{F,G\}}_{\Omega }={\int }_{{\Sigma }_{\tau }}{\displaystyle \frac{\delta F}{\delta {\Phi }_{\mu }}}{{\Omega }_{\Phi }^{-1}}_{\mu \nu }{\displaystyle \frac{\delta G}{\delta {\Phi }_{\nu }}}{d}^{3}x,$$

(32)

in analogy with the standard Poisson bracket of symplectic geometry [38,42,95]. Quantization proceeds by promoting these to operators $\widehat{F},\widehat{G}$ on the leaf Hilbert space $\mathcal{H}\left[{\Sigma }_{\tau }\right]$, yielding the commutator

$$[\widehat{F},\widehat{G}]=\mathrm{i}{\hslash }_{\mathrm{geom}}{\{F,G\}}_{\Omega }+\mathcal{O}(\parallel \nabla \Phi \parallel ),$$

(33)

so that in the strong–stabilization limit $\nabla \Phi \to 0$, the canonical equal–time algebra is recovered [13,51]. The geometric Planck constant ${\hslash }_{\mathrm{geom}}$ thus sets the symplectic scale of the chronon manifold and fixes the unit of non–commutativity among observables.

7.2. Geometric Path Integral and Curvature Weighting

The quantum measure is defined directly from the curvature phase of the chronon manifold [47,117]. For any stabilized spacetime domain $\mathcal{D}$,

$$Z\left[\mathcal{D}\right]={\int }_{\mathcal{D}}\mathcal{D}\Phi \mathcal{D}Aexp\left\{{\displaystyle \frac{\mathrm{i}}{{\hslash }_{\mathrm{geom}}}}\left(S_{\Phi }[\Phi ]+S_{\mathrm{gauge}}[A;\Phi ]+S_{\mathrm{int}}[\Phi ,A]\right)\right\},$$

(34)

where $S_{\Phi }$ is the chronon action, $S_{\mathrm{gauge}}$ the emergent $U\left(1\right)$ sector action, and $S_{\mathrm{int}}$ the minimal coupling term. The weighting factor $exp\{\mathrm{i}S/{\hslash }_{\mathrm{geom}}\}$ is not a statistical Boltzmann factor but the phase of the intrinsic curvature flux $\int {\Omega }_{\Phi }/{\hslash }_{\mathrm{geom}}$, and perturbative corrections to classical saddle points are organized by powers of ${\hslash }_{\mathrm{geom}}$, which serves as the loop–expansion parameter of the curvature phase field rather than a phenomenological constant.

7.3. Implications for Spectra

Solitonic excitations in nontrivial topological sectors $w\ne 0$ acquire quantum corrections governed by (33)–(34) [86,116]. Two principal effects appear.

Collective–Coordinate Quantization

As detailed in Section 5, translational, internal $U\left(1\right)$, and isorotational zero modes of a soliton become quantum collective variables. Their spectra exhibit energy splittings

$$\Delta E\sim {\displaystyle \frac{{\hslash }_{\mathrm{geom}}^2}{2I}},$$

(35)

where I is the geometric moment of inertia of the soliton configuration [7]. This scaling parallels the quantization of Skyrmions but with ${\hslash }_{\mathrm{geom}}$ determined by the curvature of the chronon field, linking rotational spectra directly to the geometry of time.

Zero–Point and Loop Corrections

Fluctuations around the classical minimizer ${\Phi }_{w=1}$ contribute a zero–point energy shift of order ${\hslash }_{\mathrm{geom}}$, while higher–loop corrections are suppressed by higher powers of ${\hslash }_{\mathrm{geom}}$ [25,113]. The semiclassical expansion remains controlled provided the soliton rest mass satisfies $M_{w=1}\gg {\hslash }_{\mathrm{geom}}$, ensuring that curvature-induced quantum effects remain perturbative.

7.4. Summary

The geometric action unit ${\hslash }_{\mathrm{geom}}$ plays the same structural role in CFT as Planck’s constant in conventional quantum theory, but its origin is purely geometric: it measures the invariant symplectic area of the chronon curvature manifold. Quantum commutators, curvature phases, and spectral splittings all follow from this fixed curvature invariant rather than from statistical coarse–graining [51,88]. In this way, quantization in CFT arises as a manifestation of geometry— a phase of spacetime curvature where the symplectic flux of the chronon field becomes universal and constant.

8. Emergent Fundamental Constants: ${\hslash }_{\mathrm{geom}}$, G, e, and c

In Chronon Field Theory (CFT), the familiar constants of Nature—Planck’s constant ℏ, Newton’s constant G, the elementary charge e, and the speed of light c—are not postulated but arise as geometric and dynamical invariants of the chronon field. They appear as the normalization coefficients of the low–energy effective action [101,116].

Effective Action

At long wavelengths, coarse chronon dynamics induces an Einstein–Maxwell–Dirac–like action

$$S_{\mathrm{eff}}=\int \sqrt{-g}\left[\frac{M_{\mathrm{P}}^2}{2}R-\frac{1}{4}{F}_{\mu \nu }{F}^{\mu \nu }+{\mathcal{L}}_{\mathrm{matter}}(\Phi ,\nabla \Phi ;A)\right],$$

(36)

where the coefficients $({\hslash }_{\mathrm{geom}},G,e,c)$ are determined by the curvature and holonomy structure of the chronon field rather than imposed externally [25,93].

8.1. Planck’s Constant as a Geometric Curvature Invariant

As established in Section 7, the universal action unit of CFT, ${\hslash }_{\mathrm{geom}}$, originates from the intrinsic symplectic geometry of the chronon field. The curvature two–form

$${\Omega }_{\Phi }=D\Phi \wedge D\Phi ,$$

defines the scalar invariant $R_{\Phi }=\frac{1}{2}{\Omega }_{\Phi \mu \nu }{\Omega }_{\Phi }^{\mu \nu },$ whose stabilized expectation value fixes the symplectic area of a fundamental chronon cell. Planck’s constant is thus a curvature invariant,

$${\hslash }_{\mathrm{geom}}={\kappa }_R{\int }_{{\Sigma }_{\tau }}\sqrt{h}{R}_{\Phi }{d}^{3}x\simeq {\kappa }_R\langle R_{\Phi }\rangle {\mathsf{\ell }}_{\Phi }^2,$$

(37)

where ${\mathsf{\ell }}_{\Phi }$ is the intrinsic chronon correlation length and ${\kappa }_R$ a dimensionless normalization fixed by ${\hslash }_{\mathrm{geom}}={\hslash }_{\mathrm{obs}}$.

When curvature condensation stabilizes $\langle R_{\Phi }\rangle$ across spacetime, ${\hslash }_{\mathrm{geom}}$ becomes constant, marking the transition from a pre–geometric phase to a quantum regime with a universal quantum of action. Identifying ${\mathsf{\ell }}_{\Phi }\simeq {\mathsf{\ell }}_P=\sqrt{\hslash G/c^3}$ gives $\langle R_{\Phi }\rangle \simeq {\mathsf{\ell }}_P^{-2}$ for ${\kappa }_R\simeq 1$, reproducing the observed Planck constant. Thus, ${\hslash }_{\mathrm{geom}}$ is the symplectic imprint of spacetime curvature—a fixed geometric invariant rather than a statistical parameter.

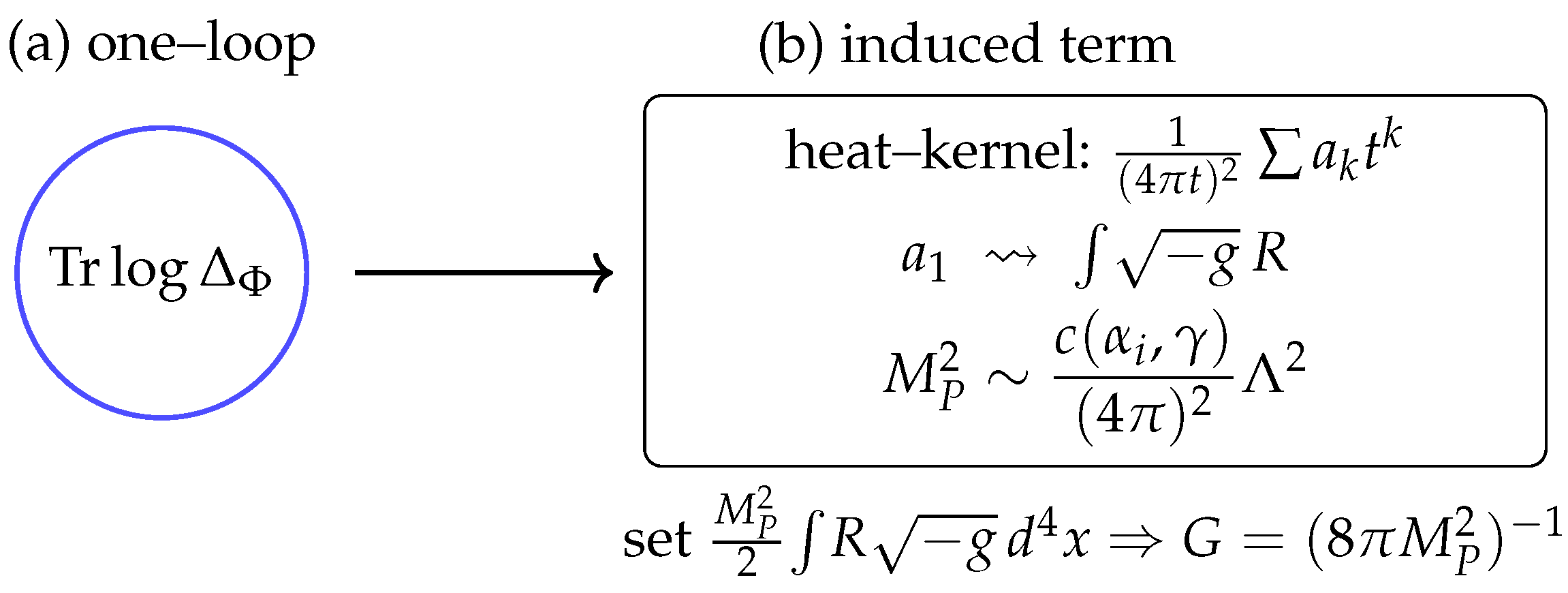
8.2. Newton’s Constant G

The coefficient of the Einstein–Hilbert term arises either directly through the $\gamma R_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }$ coupling or radiatively via the Sakharov induced–gravity mechanism [8,25,93,101,113]. In both descriptions,

$$M_{\mathrm{P}}^2\equiv {\displaystyle \frac{1}{8\pi G}},$$

(38)

with $M_{\mathrm{P}}$ determined by the chronon couplings $({\alpha }_i,\gamma )$ and the UV cutoff $\Lambda$. Explicit heat–kernel computations in Appendix G show that

$$M_{\mathrm{P}}^2\simeq {\displaystyle \frac{c_{\mathrm{ind}}({\alpha }_i,\gamma )}{{\left(4\pi \right)}^2}}{\Lambda }^2,$$

where $c_{\mathrm{ind}}$ encodes the integrated curvature response of the stabilized background.

8.3. Electric Charge e and the Coulomb Law

The emergent $\mathrm{U}\left(1\right)$ gauge field arises as the holonomy of the chronon connection. Its kinetic term, $-\frac{{\kappa }_A}{4}{F}_{\mu \nu }{F}^{\mu \nu }$, is canonically normalized by $A_{\mu }^{\mathrm{can}}=\sqrt{{\kappa }_A}{A}_{\mu }$ [70,97]. Solitons couple to $A_{\mu }$ with integer topological charge $q_0$ determined by the FR/Berry class, giving

$$e={\displaystyle \frac{q_0}{\sqrt{{\kappa }_A}}}.$$

(39)

In the static limit the gauge field satisfies a Poisson equation, yielding

$$V\left(r\right)={\displaystyle \frac{q_1{q}_2}{4\pi {\kappa }_A}}{\displaystyle \frac{1}{r}}={\displaystyle \frac{e_1{e}_2}{4\pi r}}.$$

(40)

The observed fine–structure constant ${\alpha }_{\mathrm{em}}=e^2/\left(4\pi \right)$ therefore fixes the holonomy stiffness:

$${\kappa }_A={\displaystyle \frac{q_0^2}{4\pi {\alpha }_{\mathrm{em}}}}.$$

(41)

For $q_0=1$ and ${\alpha }_{\mathrm{em}}^{-1}\simeq 137.036$, one finds ${\kappa }_A\simeq 10.9$, consistent with the Coulomb normalization derived in Appendix J.

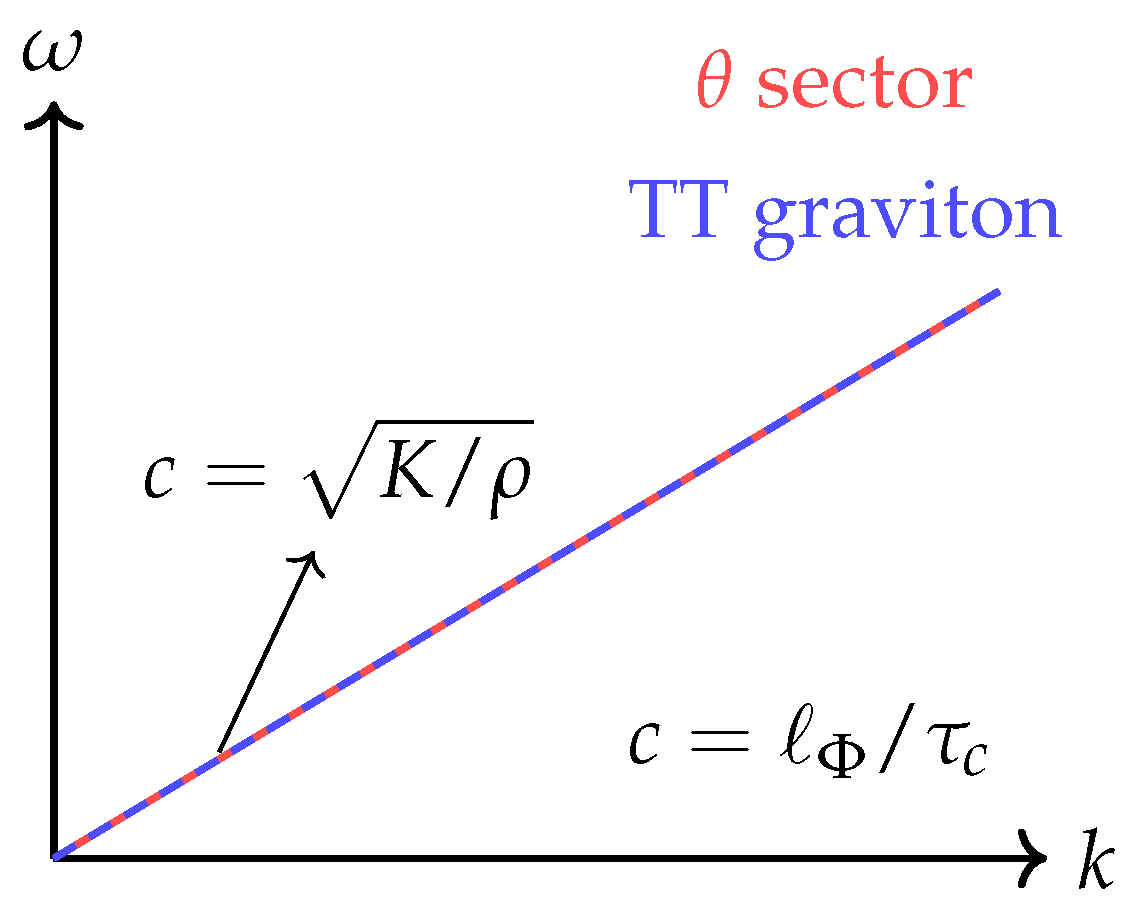
8.4. Speed of Light c

Chronon foliation provides a natural $(3+1)$ decomposition with spatial projector $h_{\mu \nu }=g_{\mu \nu }+{\overline{\Phi }}_{\mu }{\overline{\Phi }}_{\nu }$. Quadratic fluctuations of the Goldstone phase $\theta$ and of transverse–traceless graviton modes yield wave equations of the generic form $\rho \ddot{\psi }-K{\Delta }_h\psi =0,$ with phase velocity

$$c^2={\displaystyle \frac{K}{\rho }}.$$

(42)

In the stabilized, hypersurface–orthogonal regime the coefficients coincide across matter and gravitational sectors,

$$c=\sqrt{K_{\theta }/{\rho }_{\theta }}=\sqrt{K_g/{\rho }_g},$$

(43)

ensuring a universal limiting velocity. Equivalently, at the microscopic level,

$$c={\displaystyle \frac{{\mathsf{\ell }}_{\Phi }}{{\tau }_{\Phi }}},$$

(44)

fixing the conversion between spatial and temporal units [72,73,115]. This equality defines the chronon correlation ratio whose stabilization guarantees Lorentz symmetry at observable scales.

8.5. Physical Interpretation and Representative Scales

The chronon field ${\Phi }^{\mu }$ represents the coarse–grained velocity field of microscopic temporal excitations [82,83]. Its integral curves define the local direction of time flow, while its fluctuations encode the internal degrees of freedom of spacetime itself. In the disordered (pre–geometric) regime, chronon orientations fluctuate incoherently and causal structure is ill–defined. As curvature condenses, ${\Phi }^{\mu }$ attains macroscopic alignment, giving rise to a well–defined foliation, causal cones, and an emergent Lorentzian metric $g_{\mu \nu }[\Phi ]$ [9,51,115]. Small perturbations $\delta {\Phi }^{\mu }$ around a stabilized background behave as collective modes with dispersion determined by the kinetic and curvature couplings $({\alpha }_i,\gamma )$, while the ultraviolet scale $\Lambda$ sets the cutoff of the effective theory [29,116].

Representative parameter hierarchy. Table 1 summarizes the physical interpretation and indicative magnitudes of the chronon couplings and scales. These are benchmark values consistent with the emergent relations (118) and the observational constraints discussed in Section 11.

Numerical illustration. For representative couplings ${\alpha }_i\sim 1$, $\gamma \sim 0.1$, and $c_{\mathrm{ind}}\sim 1$, Eq. (118) gives $\Lambda \approx 1.3\times {10}^{20}\mathrm{GeV}$. Using ${\mathsf{\ell }}_{\Phi }={\mathsf{\ell }}_P$ and ${\tau }_c=t_P$ yields

$${\hslash }_{\mathrm{geom}}\simeq {\kappa }_R{\mathsf{\ell }}_{\Phi }^{-1}{\tau }_c\simeq 1.05\times {10}^{-34}\mathrm{J}\mathrm{s},$$

reproducing the observed Planck constant to leading order [51,90]. These benchmark values demonstrate that the chronon couplings need not be fine–tuned: natural $\mathcal{O}\left(1\right)$ parameters reproduce the observed constants of Nature once curvature condensation establishes the stabilized chronon phase.

Interpretation. This analysis anchors the chronon field’s microphysics to physically interpretable scales. The dimensionless parameters $({\alpha }_i,\gamma )$ govern the stiffness and curvature coupling of ${\Phi }^{\mu }$, while $\Lambda$ sets the ultraviolet domain where chronon fluctuations become statistically uncorrelated. When ${\mathsf{\ell }}_{\Phi }$ and ${\tau }_c$ approach the Planck scales, the emergent constants $(\hslash ,G,e,c)$ coincide with their measured values, confirming that CFT requires no additional microscopic tuning [116,121]. Quantization, in this view, is a manifestation of spacetime coherence—arising when the chronon field locks into its globally stabilized phase [82,114].

9. Unified Origin of Spin, Charge, Quantization, and Interaction

A central outcome of Chronon Field Theory (CFT) is that the fundamental quantum attributes of matter— spin, charge, and quantization itself—share a single geometric origin in the topology of the chronon field. In this framework, the chronon field ${\Phi }^{\mu }$ supports stable solitonic configurations labeled by an integer winding number $w\in \mathbb{Z}$, each representing a complete $2\pi$ rotation of the chronon phase within the internal curvature manifold. This intrinsic phase twist not only gives rise to spin and charge but also determines the universal action unit ${\hslash }_{\mathrm{geom}}$, while interactions emerge as the enforcement of temporal coherence among chronon domains [7,20,48,82,105,114].

9.1. Common Geometric Origin

A chronon soliton with winding number $w=1$ embodies a full $2\pi$ rotation of the chronon phase, encoded in the curvature two–form

$${\Omega }_{\Phi }=D\Phi \wedge D\Phi ,{\int }_{{\Sigma }_{\tau }}{\Omega }_{\Phi }=2\pi n.$$

(45)

This twist projects differently along the temporal and spatial components of the chronon manifold:

• Temporal aspect (spin). A $2\pi$ rotation of the local time–flow field ${\Phi }^{\mu }$ generates a Berry/ Finkelstein–Rubinstein holonomy on the leaf ${\Sigma }_{\tau }$ [20,48,104]. Under this rotation, ${\Phi }^{\mu }$ returns to itself up to a sign, ${\Phi }^{\mu }\to -{\Phi }^{\mu }$, producing spin–$\frac{1}{2}$ behavior and the fermionic phase factor ${(-1)}^{2s}$. Spin therefore originates from the temporal holonomy of the chronon’s symplectic twist.
• Topological aspect (charge). Viewed through the spatial connection induced by ${\Phi }^{\mu }$, the same curvature twist defines a $U\left(1\right)$ holonomy,

  $$q={\displaystyle \frac{1}{2\pi }}{\oint }_{\partial \Sigma }{A}_{\mu }d{x}^{\mu },$$

  (46)

  corresponding to an integer multiple of the elementary charge. Charge thus represents the spatial projection of the same $2\pi$ twist—the circulation of the chronon connection around a closed spatial loop [76,86,88,123].

Spin and charge are therefore complementary manifestations of one geometric phenomenon: the complete $2\pi$ phase rotation of the chronon field within the spacetime curvature manifold. The chronon soliton is a unified excitation whose internal temporal holonomy yields spin, while its spatial holonomy defines charge.

9.2. Quantization from Topological Stability

Because the chronon curvature manifold admits only globally coherent configurations with integer multiples of $2\pi$ phase winding, the corresponding action increments are quantized:

$$\Delta S=n{\hslash }_{\mathrm{geom}},{\hslash }_{\mathrm{geom}}={\kappa }_R{\int }_{{\Sigma }_{\tau }}\sqrt{h}{R}_{\Phi }{d}^{3}x.$$

(47)

This equation expresses ${\hslash }_{\mathrm{geom}}$ as the invariant symplectic area of a fundamental curvature cell of the chronon field. Quantization thus arises not from coarse–graining or statistical averaging, but from the topological stability of completed $2\pi$ phase twists—the only dynamically stable excitations in the condensed curvature phase [42,47,98,114,117]. This intrinsic discreteness of the symplectic flux defines the universal quantum of action.

9.3. Interactions as Temporal Coherence

Interactions among chronon solitons emerge as the dynamical enforcement of phase coherence across neighboring domains. The gauge field $A_{\mu }$ functions as a Lagrange multiplier mediating synchronization of local chronon phases, transporting temporal curvature and maintaining global alignment of ${\Phi }^{\mu }$. Electromagnetic and gravitational couplings thus appear as collective modes of the chronon condensate that preserve temporal coherence [10,31,72,73,79]. In this sense, interaction is not a fundamental force but a manifestation of curvature–induced synchronization—the self–organization of the chronon field into a globally coherent state.

9.4. Interpretive Summary

Table 2 summarizes the geometric correspondence between the temporal and spatial aspects of the $2\pi$ chronon twist and their associated physical observables.

9.5. Conceptual Synthesis

In summary, the discrete quantum of action ${\hslash }_{\mathrm{geom}}$, spin, charge, and interaction all originate from a single geometric principle: the condensation of the chronon field into a coherent, topologically twisted phase of spacetime curvature. This unified interpretation connects the four pillars of microphysics—fermionic spin, electric charge, quantization, and force mediation—to one curvature–driven mechanism: the $2\pi$ symplectic twist of the chronon manifold that stabilizes the temporal fabric of the Universe [82,83,86,114].

10. Phenomenology and Tests

We outline concrete, falsifiable consequences of CFT at laboratory and cosmological scales. Two classes of effects are especially clean: (i) achromatic birefringence in the emergent $U\left(1\right)$ gauge sector sourced by weak gradients of the chronon field, and (ii) exchange–phase interferometry for $w=1$ solitons revealing the FR/Berry phase $\pi$. We also specify a numerical program to connect parameters to observables.

• Deviations from GR: observables and bounds CFT predicts controlled departures parameterized by $({\alpha }_i,d_j/{\Lambda }^2)$. (i) PPN preferred-frame coefficients from æther-like terms; (ii) GW dispersion/equal-speed tests $|c_g/c-1|\ll 1$ and $k^4/{\Lambda }^2$ corrections; (iii) vacuum birefringence/dispersion from $\nabla \Phi$-dependent gauge operators. We map these to data in Appendix K and require compatibility with present bounds [2,79,121].
• Achromatic birefringence from $\nabla \Phi$–dependent couplings. On stabilized domains, gauge invariance and diffeomorphism invariance allow, beyond the Maxwell term, parity–odd and parity–even operators that couple $F_{\mu \nu }$ to slowly varying chronon backgrounds.1 Two representative classes are:

  $$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{odd}}& ={\displaystyle \frac{{\xi }_1}{4}}\Theta [\Phi ,\nabla \Phi ]F_{\mu \nu }{\tilde{F}}^{\mu \nu },\hfill \end{array}$$

  (48)

  $$\begin{array}{cc}\hfill {\mathcal{L}}_{\mathrm{even}}& ={\displaystyle \frac{{\xi }_2}{2}}{\Xi }^{\mu \nu }[\Phi ,\nabla \Phi ]F_{\mu \alpha }{F_{\nu }}^{\alpha },\hfill \end{array}$$

  (49)

  with ${\tilde{F}}^{\mu \nu }:=\frac{1}{2}{\epsilon }^{\mu \nu \rho \sigma }{F}_{\rho \sigma }$. Here $\Theta$ is a pseudoscalar functional and ${\Xi }^{\mu \nu }$ a symmetric rank–2 tensor functional built from $\Phi$ and its derivatives (e.g. $a_{\mu }={\Phi }^{\alpha }{\nabla }_{\alpha }{\Phi }_{\mu }$, ${\sigma }_{\mu \nu }$, $\theta =D_{\alpha }{\Phi }^{\alpha }$), normalized so that $\Theta ,{\Xi }^{\mu \nu }=\mathcal{O}(\nabla \Phi )$ on stabilized leaves. Both operators preserve $U\left(1\right)$ gauge invariance; ${\mathcal{L}}_{\mathrm{odd}}$ violates parity and time reversal, while ${\mathcal{L}}_{\mathrm{even}}$ is parity–even but anisotropic [31,85].
  Geometric–optics limit. Let $A_{\mu }=\mathrm{Re}\left\{{\epsilon }_{\mu }{e}^{iS/ϵ}\right\}$ with wave–covector $k_{\mu }={\nabla }_{\mu }S$, $k^2=0$ at leading order. To first nontrivial order in $\nabla \Phi$ and the couplings ${\xi }_{1,2}$, the polarization ${\epsilon }_{\mu }$ obeys a parallel–transport equation modified by (48)–(49). For (48) one finds an achromatic (CPT–odd) polarization rotation for a linearly polarized wave propagating along a null curve $\gamma$:

  $$\Delta {\psi }_{\mathrm{odd}}\left(\gamma \right)={\displaystyle \frac{{\xi }_1}{2}}\left(\Theta {|}_{x_{\mathrm{obs}}}-\Theta {|}_{x_{\mathrm{src}}}\right)={\displaystyle \frac{{\xi }_1}{2}}{\int }_{\gamma }{k}^{\mu }{\nabla }_{\mu }\Theta {\displaystyle \frac{d\lambda }{\omega }},$$

  (50)

  independent of frequency to this order.2 For (49), birefringence arises from a small anisotropic phase–velocity split between orthogonal linear polarizations relative to the projector $h_{\mu \nu }$:

  $$\Delta {\psi }_{\mathrm{even}}\left(\gamma \right)={\displaystyle \frac{{\xi }_2}{2}}{\int }_{\gamma }\left({\widehat{e}}^{\mu }{\widehat{e}}^{\nu }-{\widehat{e}}_{\perp }^{\mu }{\widehat{e}}_{\perp }^{\nu }\right){\Xi }_{\mu \nu }d\mathsf{\ell }+\mathcal{O}(\nabla \Xi ),$$

  (51)

  with $(\widehat{e},{\widehat{e}}_{\perp })$ an orthonormal polarization basis transported along $\gamma$. To leading order this rotation is also achromatic if ${\Xi }_{\mu \nu }$ varies only on scales $\gg \lambda$ (the wavelength) [31,85].
  Constraints and forecasts. Equations (50)–(51) provide direct parameterizations for data analyses:

  $$\alpha \left(\widehat{\mathbf{n}}\right)={\displaystyle \frac{{\xi }_1}{2}}\left[\Theta (\widehat{\mathbf{n}},z=0)-\Theta (\widehat{\mathbf{n}},z_{\mathrm{src}})\right]+{\displaystyle \frac{{\xi }_2}{2}}{\int }_0^{{\chi }_{\mathrm{src}}}\left({\widehat{e}}^{\mu }{\widehat{e}}^{\nu }-{\widehat{e}}_{\perp }^{\mu }{\widehat{e}}_{\perp }^{\nu }\right){\Xi }_{\mu \nu }d\chi ,$$

  (52)

  where $\widehat{\mathbf{n}}$ labels the line–of–sight and $\chi$ is comoving distance. Cosmic microwave background and radio/optical polarimetry constrain the sky–averaged and multipole–dependent rotation $\alpha$; the distinguishing feature here is achromaticity (no ${\nu }^{-2}$ Faraday scaling). Forecasts can be obtained via a Fisher analysis on the $EB$ and $TB$ spectra with $\alpha$ treated as a parameter or a field, using $\partial C_{\mathsf{\ell }}/\partial \alpha$ and the covariance from instrumental noise and lensing B–modes [75,85]. Laboratory constraints follow by inserting $\Theta \left(\mathbf{x}\right)\approx {\Theta }_0+\mathbf{x}·\nabla \Theta$ over a baseline L, giving $|\Delta \psi |\simeq ({\xi }_1/2)(\widehat{\mathbf{k}}·\nabla \Theta )L$, measurable with high–finesse cavities or resonant optical gyroscopes [106].
• Exchange–phase interferometry for solitons: geometric phase $\pi$. The FR/Berry analysis (Section 6) predicts a topological phase $\pi$ for adiabatic exchange of two identical $w=1$ solitons. We outline two protocols that isolate this sign.
  Braiding interferometer. Prepare two solitons in a symmetric double–well on a leaf ${\Sigma }_{\tau }$, with tunnel–coupling $J\ll \Delta$ (spectral gap). Define two adiabatic paths between the same initial/final configurations: (i) trivial swap (no exchange), (ii) counter–circulation that implements a single exchange in configuration space $C\left(2\right)$. Equalize dynamical phases by time–reversal–symmetric scheduling (spin–echo style) so that the interferometric contrast depends only on the geometric phase:

  $$\mathcal{I}\propto |A_0+A_1{e}^{i(\Delta {\varphi }_{\mathrm{dyn}}+\pi )}{|}^2\stackrel{\Delta {\varphi }_{\mathrm{dyn}}=0}{\to }{|A_0-A_1|}^2.$$

  (53)
  For $A_0=A_1$ the output is extinguished, a smoking–gun of the FR sign [20,104].
  Ramsey–Berry protocol. Treat a collective coordinate $\lambda$ (e.g. relative angle or position on a ring trap) as a slow variable on which the soliton ground state ${\psi }_0\left(\lambda \right)$ depends. Drive a closed loop $\lambda :0\to 2\pi$ that realizes the generator of ${\pi }_1\left(C\left(2\right)\right)$. The accumulated phase is

  $${\gamma }_{\mathrm{B}}=\oint i{\psi }_0\left(\lambda \right)|{\partial }_{\lambda }{\psi }_0\left(\lambda \right)d\lambda \equiv \pi \left(\mathrm{mod}2\pi \right),$$

  (54)

  while the dynamical phase can be nulled by a spin–echo sequence. Readout via parity oscillations or population imbalance reveals the $\pi$ shift. Adiabaticity requires $T_{\mathrm{loop}}\gg {\hslash }_{\mathrm{eff}}/\Delta$ and weak dephasing; robustness follows from the topological nature of ${\gamma }_{\mathrm{B}}$ [20,104].
• Numerical demo (to include): stable profile, mass vs. couplings; Berry holonomy. We propose a reproducible pipeline to connect CFT parameters to observables:
  (a) Static $w=1$ profile and mass. Adopt a spherically symmetric ansatz realizing $deg(\Phi )=1$ on ${\Sigma }_{\tau }\simeq {\mathbb{R}}^3\cup \{\infty \}\cong S^3$ (e.g. a hedgehog map $S^3\to S^3$ in an orthonormal frame). Minimize $E[\Phi ]={\int }_{{\Sigma }_{\tau }}\rho d^{3}x$ via constrained gradient flow with ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ enforced by a Lagrange multiplier. Convergence certifies existence and furnishes $M_{w=1}$; scan $({\alpha }_1,{\alpha }_2,{\alpha }_3,\gamma )$ to obtain $M_{w=1}$–versus–coupling surfaces and stability bands (positive second variation) [86].
  (b) Linear spectrum and moments of inertia. Linearize the CFT equations about the minimizer to compute the small–oscillation spectrum and the collective inertia tensor $I_{ab}$ for zero modes (translations, internal rotations). Predict rotational/vibrational splittings $\Delta E\simeq {\hslash }_{\mathrm{eff}}^2/\left(2I\right)$ (Section 7) and compare with interferometric timescales [7,86].
  (c) Berry holonomy computation. Discretize a loop ${\left\{{\lambda }_k\right\}}_{k=0}^N$ in $M_1$ (e.g. a $2\pi$ rotation or exchange path) and evaluate the gauge–invariant discretized Berry phase

  $${\gamma }_{\mathrm{B}}=\mathrm{Im}log\prod _{k=0}^{N-1}{\psi }_0\left({\lambda }_k\right)|{\psi }_0\left({\lambda }_{k+1}\right),{\lambda }_N\equiv {\lambda }_0.$$

  (55)
  One should obtain ${\gamma }_{\mathrm{B}}=\pi$ within numerical tolerance, with convergence under refinement and robustness to local gauge choices in the solver [52,92].

Outlook 

The achromaticity and geometric protection of the predicted signals make them resilient to common systematics (frequency–dependent Faraday rotation; path–dependent dynamical phases). A combined program—cosmological birefringence constraints/forecasts via (52) and controlled soliton interferometry implementing (53)–(54)—provides a stringent testbed for CFT at both infrared and mesoscopic scales.

11. Discussion and Outlook

The results of this paper establish a consistent, covariant, and background–independent framework in which (i) a conserved and geometrically defined mass–energy density is formulated [115], (ii) solitonic excitations exist and are stable in the minimal topological sector $w=1$ [86], (iii) the spin–statistics connection arises from the topology of configuration space and its Berry holonomy [20,48,104], and (iv) an Abelian $U\left(1\right)$ gauge sector appears naturally as a holonomy of the chronon curvature field [77,88]. Together, these results support the interpretation of CFT solitons as fermionic matter coupled to emergent electrodynamics.

Crucially, the constants of Nature—ℏ, G, e, and c—are not postulated but derived geometric invariants. In particular, the Planck constant ${\hslash }_{\mathrm{geom}}$ arises as the invariant symplectic area of the chronon curvature manifold, as shown in Section 7 and Appendix F. It is given by a purely geometric relationship:

$${\hslash }_{\mathrm{geom}}={\kappa }_R{\int }_{{\Sigma }_{\tau }}\sqrt{h}{R}_{\Phi }{d}^{3}x\simeq {\kappa }_R\langle R_{\Phi }\rangle {\mathsf{\ell }}_{\Phi }^2,$$

so that quantization itself becomes a manifestation of stabilized curvature. In this sense, CFT realizes quantum mechanics as the macroscopic phase of a condensed curvature geometry.

GR as Infrared Limit

We treat General Relativity (GR) as the infrared universality class of CFT. Section 8.6 states this limit precisely, while Section 9 and Appendix K quantify the power–suppressed deviations and their observational bounds [73,116,121]. The induced–gravity mechanism (Appendix G) links Newton’s constant to the same curvature–symplectic invariants that fix ${\hslash }_{\mathrm{geom}}$, showing that G and ℏ share a common geometric origin.

Table 3. Representative operator combinations and their observational channels. Bounds are indicative IR targets; precise values depend on background/dataset (see text).

Operator / coeff.	Physical channel	Observable / bound	Comment
${\alpha }_1{a}_{\mu }{a}^{\mu }$, ${\alpha }_2{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }$	PPN (preferred frame)	$|{\alpha }_1|\lesssim {10}^{-4}$, $|{\alpha }_2|\lesssim {10}^{-7}$	Suppress shear/accel. terms on stabilized leaves
$d_g{\left({\nabla }^2{h}_{ij}^{\mathrm{TT}}\right)}^2/{\Lambda }_g^2$	GW dispersion (tensor)	$|{\omega }^2-c^2{k}^2|\sim d_g\frac{k^4}{{\Lambda }_g^2}$, $|c_g/c-1|\lesssim {10}^{-15}$	High–k tail in waveforms; multimessenger tests [2]
$d_{\gamma }{(\nabla F)}^2/{\Lambda }_{\gamma }^2$	Photon dispersion	${\omega }^2\simeq c^2{k}^2\left(1+d_{\gamma }\frac{k^2}{{\Lambda }_{\gamma }^2}\right)$	Time–of–flight constraints (pulsars/GRBs/FRBs)
$\tilde{d}(\nabla \Phi )F\tilde{F}/{\Lambda }_{\gamma }^2$	Vacuum birefringence (parity–odd)	Polarization rotation $\Delta \psi \propto \tilde{d}\frac{L}{{\Lambda }_{\gamma }^2}$	CMB/AGN polarization; achromatic tests [31,79,85]
$c_{\mathrm{ind}}({\alpha }_i,\gamma ){\Lambda }^{2}R$	Induced EH (gravity)	$M_{\mathrm{P}}^2=\frac{c_{\mathrm{ind}}{\Lambda }^2}{{\left(4\pi \right)}^2}$	G fixes $c_{\mathrm{ind}}{\Lambda }^2$ (Appendix G) [101,113]
${\kappa }_A{F}_{\mu \nu }{F}^{\mu \nu }$, $q_0$	Coulomb law / ${\alpha }_{\mathrm{em}}$	${\kappa }_A=\frac{q_0^2}{4\pi {\alpha }_{\mathrm{em}}}$, $V\left(r\right)=\frac{e_1{e}_2}{4\pi r}$	Fixes gauge stiffness (Appendix J)
$M_{w=1}({\alpha }_i,\gamma ;{\mathsf{\ell }}_{\Phi })$	Soliton mass (electron)	$M_{w=1}=m_e$	Pins a combo of $({\alpha }_i,\gamma ,{\mathsf{\ell }}_{\Phi })$ (Appendix K)

Table 3. Representative operator combinations and their observational channels. Bounds are indicative IR targets; precise values depend on background/dataset (see text).

Operator / coeff.	Physical channel	Observable / bound	Comment
${\alpha }_1{a}_{\mu }{a}^{\mu }$, ${\alpha }_2{\sigma }_{\mu \nu }{\sigma }^{\mu \nu }$	PPN (preferred frame)	$|{\alpha }_1|\lesssim {10}^{-4}$, $|{\alpha }_2|\lesssim {10}^{-7}$	Suppress shear/accel. terms on stabilized leaves
$d_g{\left({\nabla }^2{h}_{ij}^{\mathrm{TT}}\right)}^2/{\Lambda }_g^2$	GW dispersion (tensor)	$|{\omega }^2-c^2{k}^2|\sim d_g\frac{k^4}{{\Lambda }_g^2}$, $|c_g/c-1|\lesssim {10}^{-15}$	High–k tail in waveforms; multimessenger tests [2]
$d_{\gamma }{(\nabla F)}^2/{\Lambda }_{\gamma }^2$	Photon dispersion	${\omega }^2\simeq c^2{k}^2\left(1+d_{\gamma }\frac{k^2}{{\Lambda }_{\gamma }^2}\right)$	Time–of–flight constraints (pulsars/GRBs/FRBs)
$\tilde{d}(\nabla \Phi )F\tilde{F}/{\Lambda }_{\gamma }^2$	Vacuum birefringence (parity–odd)	Polarization rotation $\Delta \psi \propto \tilde{d}\frac{L}{{\Lambda }_{\gamma }^2}$	CMB/AGN polarization; achromatic tests [31,79,85]
$c_{\mathrm{ind}}({\alpha }_i,\gamma ){\Lambda }^{2}R$	Induced EH (gravity)	$M_{\mathrm{P}}^2=\frac{c_{\mathrm{ind}}{\Lambda }^2}{{\left(4\pi \right)}^2}$	G fixes $c_{\mathrm{ind}}{\Lambda }^2$ (Appendix G) [101,113]
${\kappa }_A{F}_{\mu \nu }{F}^{\mu \nu }$, $q_0$	Coulomb law / ${\alpha }_{\mathrm{em}}$	${\kappa }_A=\frac{q_0^2}{4\pi {\alpha }_{\mathrm{em}}}$, $V\left(r\right)=\frac{e_1{e}_2}{4\pi r}$	Fixes gauge stiffness (Appendix J)
$M_{w=1}({\alpha }_i,\gamma ;{\mathsf{\ell }}_{\Phi })$	Soliton mass (electron)	$M_{w=1}=m_e$	Pins a combo of $({\alpha }_i,\gamma ,{\mathsf{\ell }}_{\Phi })$ (Appendix K)

Limitations 

(a)

Absence of non–Abelian sectors. The present construction realizes only an Abelian $U\left(1\right)$ holonomy. Extending the curvature bundle to higher–rank structures is required for $SU\left(2\right)$ and $SU\left(3\right)$ sectors, a task undertaken in Paper II [51,88].

(b)

Massless vector modes. The emergent photon is a curvature–Goldstone excitation and hence massless. Realizing massive vector bosons ($W^{\pm }$, $Z^0$) will require introducing additional topological order or condensates within the chronon manifold.

(c)

Microscopic completion of ${\hslash }_{\mathrm{geom}}$. Although ${\hslash }_{\mathrm{geom}}$ has been derived geometrically from the stabilized curvature two–form, a full microscopic treatment of curvature condensation—analogous to an order–parameter potential—remains to be formulated.

(d)

One–loop gravity matching. Appendix G identifies the induced–gravity mechanism and the relation $M_{\mathrm{P}}^2\sim c_{\mathrm{ind}}({\alpha }_i,\gamma ){\Lambda }^2/{\left(4\pi \right)}^2$, but an explicit heat–kernel computation of $c_{\mathrm{ind}}({\alpha }_i,\gamma )$ on stabilized curvature backgrounds remains open, together with a complete PPN analysis [113,121].

(e)

Numerical demonstration. Existence and stability have been shown variationally, but explicit numerical minimizers, dispersion extractions ($c_{\theta }=c_g$), Coulomb fits, and Berry–holonomy computations are ongoing. Their completion is essential for quantitative parameter inference [86].

Beyond Apparent Lorentz Violation

The EFT analysis presented here maps chronon–induced operators to SME/PPN frameworks, confirming compatibility with stringent experimental bounds. However, this EFT viewpoint does not capture the deeper mechanism by which CFT preserves operational Lorentz invariance. In subsequent work we develop the Co–Moving Concealment Mechanism (CCM): since all matter, fields, and observers are excitations of the same stabilized chronon foliation, they are intrinsically comoving with the universal chronon frame. Preferred–frame parameters such as ${\alpha }_1,{\alpha }_2,{\alpha }_3$ therefore lack operational meaning, removing the need for fine tuning. The EFT analysis serves only as a conservative check, while CCM provides the fundamental geometric resolution, to be elaborated in Papers II–IV.

Connections to Subsequent Work

Paper II will generalize the holonomy construction to non–Abelian gauge groups, realizing $SU\left(2\right)$ and $SU\left(3\right)$ curvature sectors and providing the groundwork for electroweak and QCD–like dynamics. Paper III will study confinement, chiral symmetry breaking, and hadronic bound states in this non–Abelian CFT framework. Together with the present results, these constitute a three–part program: (I) fermionic solitons and emergent $U\left(1\right)$ with derived $({\hslash }_{\mathrm{geom}},G,e,c)$ and Coulomb law, (II) non–Abelian holonomies and symmetry breaking, and (III) strong–interaction phenomenology.

Open Problems

• Parameter inference and consistency. Using the derived observables in Appendix K (e.g. $M_{w=1}=m_e$, $a_e$, ${\sigma }_T$, hydrogenic spectra, $c_g/c$, PPN bounds), perform a global fit of $({\alpha }_i,\gamma ,\Lambda )$ and verify consistency with the Coulomb constraint on ${\kappa }_A$.
• Higher–derivative EFT and renormalization. Establish the symmetry–allowed higher–derivative basis, compute loop–induced running of ${\kappa }_A$ and associated Wilson coefficients, and constrain them via birefringence and dispersion tests [29,43,79,116].
• Strong–field and cosmological regimes. Quantify nonlinear corrections and their effects on gravitational sources, and study background solutions with small $|\nabla \Phi |$ for cosmological applications [121].
• Matter spectroscopy. Compute collective–mode spectra (splittings $\Delta E\sim {\hslash }_{\mathrm{geom}}^2/2I$), gyromagnetic ratios, and radiative corrections ($a_e$), comparing them with high–precision data.

Conclusion 

This first part of the program demonstrates that fermionic matter, electrodynamics, and the observed constants $(\hslash ,G,e,c)$ can emerge from a single dynamical temporal field without postulating quantized matter fields or external time. Quantization itself is reinterpreted as a geometric phase of stabilized chronon curvature, with ${\hslash }_{\mathrm{geom}}$ as the universal symplectic invariant. The framework is covariant, ontologically minimal, and testable through numerical, spectral, and observational signatures. Realizing the non–Abelian sector and completing the parameter–inference program are decisive next steps toward a chronon–geometric foundation for quantum field theory and particle physics.

Appendix K.1.    Proof Details for Theorem 4.2

Recall $\rho :=T_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }$ and $J^{\mu }:=T_{\mu \nu }{\Phi }^{\nu }$.

(i) Positivity

Under the induced dominant energy condition (DEC), $T_{\mu \nu }{v}^{\mu }{w}^{\nu }\ge 0$ for all future–directed causal $v,w$. As $\Phi$ is future–directed unit timelike, taking $v=w=\Phi$ yields $\rho =T_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }\ge 0$ pointwise [115].

(ii) Conservation of J^μ

We present a Noether derivation using quasi–stationarity. Consider an infinitesimal diffeomorphism generated by ${\xi }^{\mu }$, with variations ${\delta }_{\xi }{g}_{\mu \nu }={\nabla }_{\mu }{\xi }_{\nu }+{\nabla }_{\nu }{\xi }_{\mu }$ and ${\delta }_{\xi }{\Phi }^{\mu }={\xi }^{\alpha }{\nabla }_{\alpha }{\Phi }^{\mu }-{\Phi }^{\alpha }{\nabla }_{\alpha }{\xi }^{\mu }$. Diffeomorphism invariance gives

$${\delta }_{\xi }{S}_{\Phi }=\int \sqrt{-g}\left(-{\nabla }_{\mu }{T}_{\mu \nu }{\xi }^{\nu }+{\mathcal{L}}_{\xi }\left(\sqrt{-g}{\mathcal{L}}_{\Phi }\right)\right)d^{4}x\stackrel{\mathrm{on}\mathrm{shell}}{=}\int \sqrt{-g}{\mathcal{L}}_{\xi }\left(\sqrt{-g}{\mathcal{L}}_{\Phi }\right)d^{4}x.$$

(70)

Choose ${\xi }^{\mu }={\Phi }^{\mu }$. By Assumption 4.1 (quasi–stationarity), ${\mathcal{L}}_{\Phi }\left(\sqrt{-g}{\mathcal{L}}_{\Phi }\right)=0$, hence ${\delta }_{\Phi }{S}_{\Phi }=0$ and we infer

$${\nabla }_{\mu }\left(T_{\mu \nu }{\Phi }_{\nu }\right)=0⟺{\nabla }_{\mu }{J}^{\mu }=0.$$

(71)

(The Noether–charge proof gives an equivalent statement [69].)

(iii) Leafwise Constancy of M(τ)=∫ Σ τ ρd 3 x.

Integrate (71) over the spacetime slab bounded by two stabilized leaves ${\Sigma }_{{\tau }_1}$ and ${\Sigma }_{{\tau }_2}$ and a timelike boundary $\mathcal{T}$:

$$0={\int }_{\mathcal{V}}{\nabla }_{\mu }{J}^{\mu }\sqrt{-g}{d}^{4}x={\int }_{{\Sigma }_{{\tau }_2}}{J}^{\mu }{n}_{\mu }{d}^{3}x-{\int }_{{\Sigma }_{{\tau }_1}}{J}^{\mu }{n}_{\mu }{d}^{3}x+{\int }_{\mathcal{T}}{J}^{\mu }{n}_{\mu }{d}^3\sigma .$$

(72)

On ${\Sigma }_{\tau }$, the unit normal is $n^{\mu }={\Phi }^{\mu }$, so $J^{\mu }{n}_{\mu }=\rho$. The flux through $\mathcal{T}$ vanishes for finite–energy configurations (fields decay sufficiently fast), thereby proving $\mathsf{M}\left({\tau }_2\right)=\mathsf{M}\left({\tau }_1\right)$.

(iv) Finiteness for Finite–Energy Data

By (67)–(69), $\rho$ is a quadratic expression in $K_{\mu \nu }$, K, and $\Phi$ plus total divergences. On stabilized leaves ${\Sigma }_{\tau }\simeq {\mathbb{R}}^3$ with the boundary condition $\Phi \to (1,0,0,0)$ as $\left|x\right|\to \infty$, finite–energy data have $K_{\mu \nu },K\in L^2\left({\Sigma }_{\tau }\right)$ and $\Phi -(1,0,0,0)\in H^1\left({\Sigma }_{\tau }\right)$, ensuring ${\int }_{{\Sigma }_{\tau }}\rho d^{3}x<\infty$ [46,55].

Remarks. (1) The compact form (61) in terms of ${J^{\mu }}_{\nu }$ is useful for existence and stability analyses (§5). (2) The Ricci–coupling contribution (69) can be recast, via the commutator $[{\nabla }_{\mu },{\nabla }_{\nu }]{\Phi }^{\alpha }={R^{\alpha }}_{\beta \mu \nu }{\Phi }^{\beta }$, into combinations of ${(\nabla \Phi )}^2$ terms plus total divergences; we keep the manifestly covariant form to streamline conservation proofs [30,115].

Appendix K.2.    g–Factor and the Anomaly a_e

At tree level, minimal coupling on the soliton bundle with FR/Berry structure yields

$$g_{w=1}=2,$$

(150)

consistent with the Dirac prediction [40]. Radiative corrections in the emergent QED sector produce the standard series $a_e\equiv (g-2)/2={\sum }_{n\ge 1}{c}_n{\alpha }_{\mathrm{em}}^n+\delta a_e^{\left(\mathrm{hd}\right)}$, where the coefficients $c_n$ are precisely known up to five loops in QED [11], and $\delta a_e^{\left(\mathrm{hd}\right)}$ encodes higher–derivative (hd) CFT operators suppressed by the UV scale(s) ${\Lambda }_{\mathrm{hd}}$. Thus

$$\begin{array}{|c|}\hline a_e^{\mathrm{obs}}-{\displaystyle \sum _{n\ge 1}}{c}_n{\alpha }_{\mathrm{em}}^n=\delta a_e^{\left(\mathrm{hd}\right)}\Rightarrow {\Lambda }_{\mathrm{hd}}\mathrm{bounded}\mathrm{from}\mathrm{below}.\\ \hline\end{array}$$

(151)

Agreement at current precision [53] constrains (or nulls) specific hd Wilson coefficients in the gauge/chronon sector.

Appendix K.3.    Thomson Cross Section, Bohr Radius, Compton Wavelength, Rydberg

With $e=q_0/\sqrt{{\kappa }_A}$, ${\hslash }_{\mathrm{geom}}=\hslash$, and $M_{w=1}=m_e$, several classic quantities become parameter–free predictions [22,57]:

$$\begin{array}{cc}\hfill \left(\mathrm{i}\right)\mathrm{Classical}\mathrm{radius}\text{:}& r_e^{\mathrm{cl}}={\displaystyle \frac{e^2}{4\pi m_e{c}^2}}={\displaystyle \frac{{\alpha }_{\mathrm{em}}\hslash }{m_{e}c}},\hfill \end{array}$$

(152)

$$\begin{array}{cc}\hfill \left(\mathrm{ii}\right)\mathrm{Thomson}\text{:}& {\sigma }_T={\displaystyle \frac{8\pi }{3}}{\left(r_e^{\mathrm{cl}}\right)}^2={\displaystyle \frac{8\pi }{3}}{\left({\displaystyle \frac{{\alpha }_{\mathrm{em}}\hslash }{m_{e}c}}\right)}^2,\hfill \end{array}$$

(153)

$$\begin{array}{cc}\hfill \left(\mathrm{iii}\right)\mathrm{Bohr}\mathrm{radius}\text{:}& a_0={\displaystyle \frac{\hslash }{{\alpha }_{\mathrm{em}}{m}_{e}c}},\hfill \end{array}$$

(154)

$$\begin{array}{cc}\hfill \left(\mathrm{iv}\right)\mathrm{Compton}\text{:}& {\lambda }_C={\displaystyle \frac{\hslash }{m_{e}c}},\hfill \end{array}$$

(155)

$$\begin{array}{cc}\hfill \left(\mathrm{v}\right)\mathrm{Rydberg}\text{:}& R_{\infty }={\displaystyle \frac{{\alpha }_{\mathrm{em}}^2{m}_{e}c}{2h}}={\displaystyle \frac{{\alpha }_{\mathrm{em}}^2{m}_e{c}^2}{22\pi \hslash }}.\hfill \end{array}$$

(156)

Numerically checking these after (149) provides nontrivial internal consistency tests of the e– and mass–matching in CFT.

Appendix K.4.    Propagation Constraints: c_g = c and PPN

The quadratic actions for the Goldstone phase and TT gravitons share identical kinetic tensors on stabilized domains (Appendix I), giving $c_g=c$ at two derivatives. Any higher–derivative operators that split $c_g$ from c must therefore satisfy

$$|{\displaystyle \frac{c_g}{c}}-1|\lesssim {\epsilon }_{\mathrm{obs}}\Rightarrow \mathrm{bounds}\mathrm{on}\mathrm{specific}\mathrm{hd}\mathrm{Wilson}\mathrm{coefficients},$$

(157)

with ${\epsilon }_{\mathrm{obs}}$ the empirical tolerance from multimessenger observations of gravitational waves and gamma-ray bursts [2]. Similarly, the post–Newtonian parameters $({\alpha }_1,{\alpha }_2,\beta ,{\gamma }_{\mathrm{PPN}})$ must lie within experimental limits [121]; this carves out an allowed region in the chronon–coupling space that complements the G–matching via the induced coefficient $c_{\mathrm{ind}}$.

Appendix K.5.    Electron Size/Compositeness Bounds

Define the electromagnetic form factor of the $w=1$ soliton,

$$F_1\left(Q^2\right)={\int }_{\Sigma }{\mathrm{d}}^{3}x{e}^{i\mathbf{q}·\mathbf{x}}{\rho }_e\left(\mathbf{x}\right),{\rho }_e\equiv {\displaystyle \frac{\delta \mathcal{L}}{\delta A_0}}{|}_{\mathrm{soliton}}.$$

(158)

The charge radius $\langle r^2\rangle =-6F_1^{\prime }\left(0\right)$ satisfies $\langle r^2\rangle \sim \mathcal{O}\left(1\right)R^2$ for localized soliton profiles of width R. In CFT,

$$R={\mathsf{\ell }}_{\Phi }\mathcal{F}({\alpha }_i,\gamma )\Rightarrow \begin{array}{|c|}\hline {\mathsf{\ell }}_{\Phi }\mathcal{F}({\alpha }_i,\gamma )\lesssim r_e^{\mathrm{phys}}\\ \hline\end{array},$$

(159)

with $r_e^{\mathrm{phys}}$ the experimental upper bound on the electron’s charge radius [94]. The Planck calibration ${\mathsf{\ell }}_{\Phi }={\mathsf{\ell }}_P$ is safely within current limits.

Appendix K.6.    EDM and Birefringence/Dispersion Null Tests

Chronon operators that violate P or $CP$ (e.g. couplings inducing an electron EDM) must be highly suppressed. Current nonobservation of the EDM [5] translates into upper bounds on those Wilson coefficients. Likewise, any $\nabla \Phi$–dependent gauge operators inducing vacuum birefringence or frequency–dependent photon speeds must lie below observational thresholds [79]. These null tests bound combinations of higher–derivative coefficients that do not appear in leading two–derivative dynamics.

Appendix K.7.    Summary: Constraint Map

It is useful to summarize the parameter–observable relations:

Observable	CFT dependence	Constraint type
$m_e$	$M_{w=1}({\alpha }_i,\gamma ;{\mathsf{\ell }}_{\Phi })$	Eq. (149) (equality)
$a_e$	${\alpha }_{\mathrm{em}},{\Lambda }_{\mathrm{hd}}$	Eq. (151) (bound on hd)
${\sigma }_T$	${\alpha }_{\mathrm{em}},m_e$	Consistency (after e, $m_e$ set)
$a_0,{\lambda }_C,R_{\infty }$	${\alpha }_{\mathrm{em}},m_e,\hslash ,c$	Consistency checks
$c_g/c$	hd Wilson coeffs	Small splitting ⇒ bounds
PPN	$({\alpha }_i,\gamma )$	Allowed region in coupling space
$r_e^{\mathrm{phys}}$	${\mathsf{\ell }}_{\Phi }\mathcal{F}({\alpha }_i,\gamma )$	Upper bound on core size

Takeaway

Beyond $\{{\hslash }_{\mathrm{geom}},G,e,c\}$, CFT provides several additional, precisely known observables that are derived within the theory. Matching the $w=1$ soliton mass to $m_e$ and saturating precision/QED checks ($a_e,{\sigma }_T,$ spectroscopic constants), together with propagation (PPN, $c_g=c$) and size/EDM/birefringence null tests, overconstrains $({\alpha }_i,\gamma )$, fixes (or bounds) higher–derivative coefficients, and thereby renders the theory predictive with no superfluous knobs.

Appendix L.1. Maxwell Limit and Operator Suppression

Proposition A1

(Maxwell limit on stabilized domains). Let $U\subset M$ be a stabilized domain for the chronon background ${\overline{\Phi }}^{\mu }$, with unit norm ${\overline{\Phi }}^{\mu }{\overline{\Phi }}_{\mu }=-1$ and vanishing twist (hypersurface orthogonality) ${\overline{\Phi }}_{[\mu }{\nabla }_{\nu }{\overline{\Phi }}_{\rho ]}=0$ [115]. Introduce the dimensionless small parameters

$${\epsilon }_{\nabla \Phi }:={\displaystyle \frac{\parallel \nabla \overline{\Phi }\parallel }{\Lambda }},{\epsilon }_R:={\displaystyle \frac{\parallel \mathrm{Riem}\left[g\right]\parallel }{{\Lambda }^2}},\delta :={\displaystyle \frac{k}{\Lambda }},$$

where k is the characteristic wavenumber of the probe and Λ the microscopic UV scale of the effective theory. Assume ${\epsilon }_{\nabla \Phi },{\epsilon }_R,\delta \ll 1$ and that any æther–like couplings ${\alpha }_i$ appearing in the gauge sector satisfy $|{\alpha }_i|\ll 1$ (as in Einstein–Æther–type effective descriptions) [72]. Then, on U, the gauge sector of the effective action admits a potential $A_{\mu }$ with $F_{\mu \nu }={\nabla }_{\mu }{A}_{\nu }-{\nabla }_{\nu }{A}_{\mu }$ such that

$$S_{\mathrm{gauge}}\left[A\right]=-{\displaystyle \frac{{\kappa }_A}{4}}{\int }_U\sqrt{-g}{F}_{\mu \nu }{F}^{\mu \nu }+\Delta S\left[A\right],$$

(1)

with the remainder controlled by

$$\begin{array}{cc}\hfill \Delta S\left[A\right]& ={\int }_U\sqrt{-g}[\underset{\ae \mathit{ther}-\mathit{like},\mathit{parity}-\mathit{even}}{\underbrace{{\tilde{\alpha }}_1\left({\overline{\Phi }}^{\mu }{F}_{\mu \nu }\right)\left({\overline{\Phi }}_{\rho }{F}^{\rho \nu }\right)+{\tilde{\alpha }}_2{\overline{\Phi }}^{\mu }{\overline{\Phi }}^{\nu }{F}_{\mu \rho }{F_{\nu }}^{\rho }}}\hfill \\ \hfill & +\underset{\mathit{higher}-\mathit{derivative}/\mathit{curvature}}{\underbrace{\frac{c_1}{{\Lambda }^2}{\nabla }_{\rho }{F}_{\mu \nu }{\nabla }^{\rho }{F}^{\mu \nu }+\frac{c_2}{{\Lambda }^2}R{F}_{\mu \nu }{F}^{\mu \nu }}}+\dots ].\hfill \end{array}$$

(2)

where

$${\tilde{\alpha }}_{1,2}=\mathcal{O}\left({\alpha }_i\right)+\mathcal{O}\left({\epsilon }_{\nabla \Phi }^2\right),c_{1,2}=\mathcal{O}\left(1\right),$$

and the ellipsis denotes operators of strictly higher order in $\{{\epsilon }_{\nabla \Phi },{\epsilon }_R,\delta \}$. Consequently, the field equations reduce to

$${\nabla }_{\mu }{F}^{\mu \nu }=J^{\nu }+\mathcal{O}\left({\alpha }_i\right)+\mathcal{O}\left({\epsilon }_{\nabla \Phi }^2\right)+\mathcal{O}\left({\epsilon }_R\right)+\mathcal{O}\left({\delta }^2\right),$$

(3)

and the dispersion relation for transverse modes on the leaves $h_{\mu \nu }=g_{\mu \nu }+{\overline{\Phi }}_{\mu }{\overline{\Phi }}_{\nu }$ is Maxwellian to leading order, with any birefringence or anisotropy suppressed by the same parameters (cf. SME photon-sector analyses) [78,79].

Proof sketch. 

On a twist-free stabilized background the leafwise connection induced by $\overline{\Phi }$ defines a $U\left(1\right)$ holonomy; to quadratic order in fluctuations the only gauge- and diffeomorphism-invariant operator with two derivatives and no explicit $\overline{\Phi }$ is $F_{\mu \nu }{F}^{\mu \nu }$, giving the leading Maxwell term with coefficient ${\kappa }_A>0$ [65]. Residual operators must be built from F, $\overline{\Phi }$, curvature, and extra derivatives. Power counting and symmetry restrict the lowest such terms to the æther-like contractions ${(\overline{\Phi }·F)}^2$ and $\overline{\Phi }\overline{\Phi }FF$, and to higher-derivative/curvature terms such as ${(\nabla F)}^2/{\Lambda }^2$ and $R{F}^2/{\Lambda }^2$. Their coefficients scale as indicated because departures from hypersurface orthogonality and large gradients of $\overline{\Phi }$ enter at least quadratically (hence $\mathcal{O}\left({\epsilon }_{\nabla \Phi }^2\right)$), while finite-wavelength and curvature effects are suppressed by $k^2/{\Lambda }^2={\delta }^2$ and $\parallel \mathrm{Riem}\parallel /{\Lambda }^2={\epsilon }_R$, respectively (standard EFT power counting) [43,116]. Variation of (1)+(2) yields (3). The Bianchi identity ${\nabla }_{[\lambda }{F}_{\mu \nu ]}=0$ holds identically, so any leading-order deviation from Maxwell dynamics must reside in $\Delta S$, hence is suppressed by the stated small parameters. □

Remarks.

(i) In the canonical normalization $A_{\mu }^{\mathrm{can}}=\sqrt{{\kappa }_A}{A}_{\mu }$, the leading term is $-\frac{1}{4}{F}^2$ and all corrections inherit the suppressions above. (ii) The æther-like pieces induce controlled Lorentz-violating effects (birefringence, phase-velocity anisotropy) bounded by $\mathcal{O}\left({\alpha }_i\right)+\mathcal{O}\left({\epsilon }_{\nabla \Phi }^2\right)$; see also the GR-limit discussion in Section 8. (iii) Mixing terms between $A_{\mu }$ and chronon or metric perturbations start at higher order on twist-free backgrounds and share the same suppression pattern.