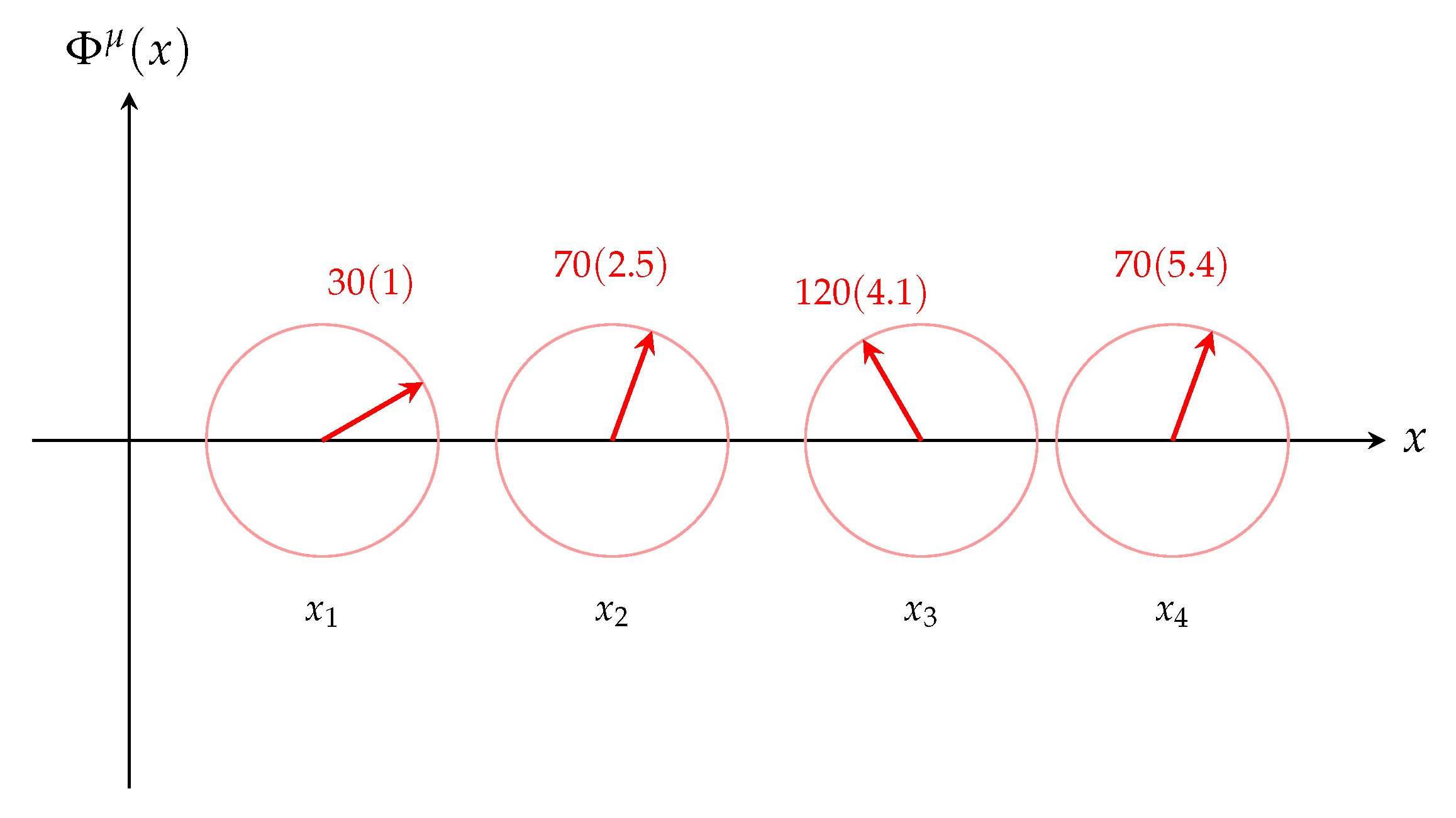Chronon Field Theory in 1+1D: A Solvable Model for Emergent Mass, Charge, and Geometry

1. Introduction

Efforts to unify the core elements of fundamental physics—spacetime geometry, matter fields, and gauge interactions—have long motivated theories that extend beyond the Standard Model. A central challenge in this pursuit is to develop a framework in which these ingredients are not merely interrelated but actually emerge from a shared underlying principle [30,37]. Chronon Field Theory (CFT) offers one such approach: a covariant, dynamical theory in which metric structure, gauge fields, inertial motion, and quantized matter all arise from a single, unit-norm timelike vector field.

The central object in CFT is the Chronon field, denoted ${\Phi }^{\mu }\left(x\right)$, defined on a Lorentzian manifold $(M,g_{\mu \nu })$ with signature $(-,+)$. This field satisfies the constraint $g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1$, thereby assigning a locally preferred, future-directed timelike direction to each spacetime point. Rather than introducing an external time coordinate or foliation, CFT builds temporal and causal structure directly from the dynamics and integral curves of ${\Phi }^{\mu }$. This view connects with broader lines of thought in which time and geometry emerge from deeper informational or relational structures [1,53,56].

In addition to setting a local time direction, the Chronon field supports an internal $U\left(1\right)$ phase due to frame redundancy orthogonal to ${\Phi }^{\mu }$. This phase acts as an emergent gauge degree of freedom. Nontrivial topologies of the phase field give rise to quantized solitonic excitations, interpretable as charged matter. This mirrors mechanisms in Kaluza–Klein theory [28,29], Cartan geometry [51], and holographic tensor networks [39], where internal geometric data yield effective gauge and matter dynamics.

Crucially, we observe that nearly all physically relevant fields in nature—fermionic, bosonic, and gauge—either explicitly contain or can be formulated in terms of internal phase degrees of freedom. Whether via global $U\left(1\right)$ symmetries (as in scalar field theory) [40], spinor representations (where internal phase governs helicity and spin) [59], or local gauge invariance (as in electroweak and QCD theories) [5,63], phase structure appears ubiquitous. Even massless fields like photons and gravitons possess polarization states governed by internal phase relations [52]. Consequently, any field-theoretic definition of mass that derives from internal phase dynamics is not a special case, but rather a broadly applicable formulation grounded in the known structure of all matter and interaction carriers.

This universality motivates the proposal that mass arises fundamentally from the local dynamics of internal phase. Within the 1+1D Chronon model, we identify a covariant, Lorentz-invariant scalar:

$$m^2:={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta ,$$

(1)

as the unique geometric quantity from which all physically observed mass behaviors emerge. This formulation is coordinate-independent, requires no background structure, and does not rely on symmetry breaking or bare parameters. Instead, it offers a fully intrinsic, dynamical account of mass based solely on the internal flow geometry of the phase field $\theta (x,t)$.

This insight reframes previous classifications of solitonic mass within Chronon theory:

• Gradient mass arises from localized spatial variation of $\theta$ and corresponds to the soliton’s rest energy;
• Holonomy mass encodes the total phase winding across topological sectors;
• Coherence mass quantifies the effective dephasing scale in thermally or quantum disordered regimes.

Each of these becomes a contextual manifestation of the same invariant scalar $m^2={\partial }^{\mu }\theta {\partial }_{\mu }\theta$, which we interpret as the root definition of mass in this framework.

We also introduce a quantitative measure of particle size by analyzing the soliton’s energy density profile. This provides a derived length scale without additional structure or parameters, reinforcing the physical interpretation of these excitations as localized, particle-like objects.

Finally, linearized perturbations around soliton solutions reveal emergent photon- and graviton-like modes, and composite solitons exhibit discrete, interference-governed mass spectra. These features support the interpretation of the Chronon framework as a unified geometric theory of matter, charge, and interaction.

This work thus presents not only a solvable model with rich internal dynamics, but a potentially fundamental shift in how mass itself is understood in field theory—as the norm of internal phase flow—and suggests a new geometric foundation for inertial and gravitational mass alike.

Throughout, we use natural units with $\hslash =c=1$ for simplicity and clarity.

2. Theoretical Context

The Chronon Field Theory (CFT) framework emerges at the intersection of several pivotal developments in modern theoretical physics. At its core, it proposes that spacetime geometry, gauge structure, and particle-like matter excitations can all be unified through the differential geometry of a single real, unit-norm vector field ${\Phi }^{\mu }\left(x\right)$. This approach resonates with broader trends in quantum gravity, emergent spacetime scenarios, and condensed matter analogs, which aim to reconstruct conventional field-theoretic structures as effective phenomena arising from deeper microscopic or geometric foundations [27,30].

A particularly striking feature of CFT is its ability to generate internal gauge symmetries from the foliation and non-integrability properties of ${\Phi }^{\mu }$, without requiring complex-valued fields or imposed gauge structures. This stands in contrast to traditional gauge theories, which begin by postulating internal symmetry groups. Instead, the $U\left(1\right)$ gauge structure in CFT arises from local frame ambiguity transverse to ${\Phi }^{\mu }$, closely paralleling how connections and holonomies are encoded in Cartan geometry [51] and fiber bundles [36]. This geometric view of gauge interaction shares deep thematic links with Kaluza–Klein theory [28,29], tensor network dualities [53], and emergent entanglement-based spacetime models [56].

In this context, the 1+1 dimensional Chronon model introduced here serves as both a mathematically tractable case and a conceptually transparent setting to explore these foundational ideas. In particular, the internal phase field $\theta (x,t)$, which parametrizes the orientation of ${\Phi }^{\mu }$, plays a dual role: it generates $U\left(1\right)$ gauge structure via non-integrable holonomy, and simultaneously acts as the dynamical degree of freedom from which solitons, charge, and mass emerge. Exact solutions in this theory—topological kinks with quantized winding—can be interpreted as localized, charged, and massive excitations arising from pure internal geometry.

A central theoretical contribution of this work is the identification of a covariant and Lorentz-invariant definition of mass as the norm of the internal phase gradient:

$$m^2:={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta .$$

(2)

This quantity is purely geometric and intrinsic to the field configuration, requiring no external parameters or symmetry breaking. It unifies the diverse mass concepts that arise in the model—gradient mass from energy density, holonomy mass from topological charge, and coherence mass from spatial dephasing—under a single local scalar observable. Notably, this formulation satisfies all the physical criteria for a fundamental mass definition: it is covariant, local, gauge-invariant, and derived from field dynamics rather than imposed externally.

This result addresses a longstanding challenge in high-energy theory: the lack of a first-principles, structural origin for mass. In most quantum field theories, particle masses appear as free parameters, protected by symmetry or adjusted through renormalization [59,66]. The Higgs mechanism provides a dynamical explanation for electroweak mass generation [14,23], but leaves open the deeper question of why mass takes the values it does, or how inertial and gravitational mass are unified. Here, by contrast, mass is shown to arise from internal phase rotation—an intrinsic, measurable property of the field’s evolution in spacetime. This formulation may offer a geometric resolution to the mass hierarchy problem [19] and recasts inertial and gravitational mass as emergent features of internal phase flow.

While the present model is restricted to 1+1 dimensions, its structural elements are designed to generalize naturally to higher dimensions. In particular, the notion of internal phase, non-integrable transport, and soliton-induced charge and mass should extend to 3+1D Chronon theories with richer gauge and topological sectors [31]. The current analysis thus represents a foundational step toward a program in which the observed properties of matter—including mass spectra, charge quantization, and localization—emerge from the local differential geometry of a real-valued, unit-norm field.

This framework aligns with the broader aim of geometrizing not just spacetime, but also the material content of the universe. The discovery that all physically meaningful notions of mass can be reduced to the Lorentz norm of a phase gradient suggests a compelling new direction for unifying field theory, particle physics, and gravity from a common geometric root.

3. Chronon Field and Internal Geometry in 1+1D

We begin by formulating the Chronon Field Theory in the setting of a $(1+1)$-dimensional Lorentzian manifold $(M,g_{\mu \nu })$, where the metric signature is taken as $(-,+)$. The central dynamical object is a real-valued, future-directed timelike unit vector field ${\Phi }^{\mu }\left(x\right)$, constrained by

$$g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1.$$

(3)

This condition endows spacetime with an intrinsic local time direction and replaces any externally imposed global clock with a covariant flow field. The vector ${\Phi }^{\mu }$ generates a congruence of timelike integral curves that naturally define a foliation of spacetime into spatial hypersurfaces orthogonal to the temporal flow [6,58].

In $(1+1)$ dimensions, the unit-norm constraint restricts ${\Phi }^{\mu }$ to lie on a one-dimensional hyperboloid $H^1\subset T_{x}M$, the space of unit timelike vectors at each point. This geometric constraint allows a canonical parametrization of ${\Phi }^{\mu }$ in terms of a single real scalar field $\theta (x,t)$:

$${\Phi }^{\mu }(x,t)=(cosh\theta (x,t),sinh\theta (x,t)),$$

(4)

which satisfies the normalization automatically:

$$-{cosh}^2\theta +{sinh}^2\theta =-1.$$

(5)

Here, $\theta (x,t)$ represents a local rapidity and serves as the sole dynamical degree of freedom in the theory. It encodes the internal orientation of ${\Phi }^{\mu }$ with respect to a fixed Lorentz frame, and its configuration space inherits a natural hyperbolic geometry from the structure of $H^1$ [45].

Crucially, the scalar field $\theta (x,t)$ also induces an emergent gauge structure. The map

$$\theta :M^{1+1}\to S^1$$

(6)

defines a principal fiber bundle over spacetime, where the internal fiber $S^1$ corresponds to phase rotations of the vector ${\Phi }^{\mu }$. The associated gauge potential

$$A_{\mu }:={\partial }_{\mu }\theta$$

(7)

acts as a connection on this bundle, transforming under local phase redefinitions $\theta \left(x\right)\mapsto \theta \left(x\right)+\alpha \left(x\right)$ as a $U\left(1\right)$ gauge field. This geometric interpretation parallels the emergence of gauge structures in theories based on nonlinear sigma models and spontaneous symmetry breaking [31,60].

In later sections, we will show that topologically nontrivial field configurations in $\theta$ yield quantized charges and solitonic excitations, which form the building blocks of emergent matter in this framework. Such solitonic structures are well-studied in low-dimensional field theory and provide a tractable setting for exploring mass quantization and coherence effects [44].

3.1. Frobenius Theorem and Foliation Structure

Even in the reduced context of $(1+1)$ dimensions, the foliation structure induced by ${\Phi }^{\mu }$ benefits from a rigorous geometric foundation. Frobenius’ theorem provides a necessary and sufficient condition for a smooth distribution of vector fields to be integrable—that is, to define a family of non-intersecting hypersurfaces.

To apply this, consider the spatial distribution $\mathcal{D}$ orthogonal to ${\Phi }^{\mu }$, defined via the projection tensor

$$h_{\mu \nu }:=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu },$$

(8)

which satisfies $h_{\mu \nu }{\Phi }^{\nu }=0$. Frobenius’ theorem states that $\mathcal{D}$ is integrable if and only if the Lie bracket of any pair of vector fields within $\mathcal{D}$ remains in $\mathcal{D}$. In terms of differential forms, this condition is equivalent to the vanishing of the torsion-like 2-form constructed from ${\Phi }^{♭}$:

$${\Phi }_{[\mu }{\nabla }_{\nu }{\Phi }_{\rho ]}=0.$$

(9)

In the $(1+1)$-dimensional setting, this integrability condition is automatically satisfied for smooth field configurations, and hence ${\Phi }^{\mu }$ always induces a well-defined foliation of spacetime into spatial slices. However, when $\theta (x,t)$ acquires topological defects, such as domain walls or solitons, the orthogonal distribution can become non-integrable in localized regions. These points of breakdown correspond to singularities in the foliation, which in turn source holonomy and topological effects in the emergent gauge structure.

Thus, Frobenius theory serves two roles: it ensures the existence of spatial hypersurfaces in the smooth regime and offers a precise geometric language for describing singular configurations where the foliation breaks down. These singularities play a critical role in the emergence of gauge and matter structures from internal geometry.

4. Action and Field Equations

To formulate the dynamics of the Chronon field in $1+1$ dimensions, we construct a covariant action in terms of the scalar field $\theta (x,t)$ which parametrizes the timelike unit vector ${\Phi }^{\mu }$ [18,58]. As established, the Chronon vector is given by

$${\Phi }^{\mu }=(cosh\theta ,sinh\theta ),$$

(10)

and its derivatives encode the deformation and curvature of the local temporal flow [16,17].

We define the Lagrangian density for the reduced Chronon Field Theory as

$$\mathcal{L}(\theta ,{\partial }_{\mu }\theta )={\displaystyle \frac{1}{2}}cosh\left(2\theta \right){\partial }_{\mu }\theta {\partial }^{\mu }\theta -V\left(\theta \right),$$

(11)

where the first term captures the kinetic energy weighted by a geometric prefactor $cosh\left(2\theta \right)$ arising from the embedding of the hyperbolic field manifold [65], and $V\left(\theta \right)$ is a potential that allows for topologically distinct vacuum sectors.

A natural and widely studied choice for $V\left(\theta \right)$ is the sine-Gordon potential [8,43],

$$V\left(\theta \right)={\mu }^2(1-cos\theta ),$$

(12)

where $\mu$ is a real constant with dimensions of mass. This potential admits an infinite set of degenerate vacua at $\theta =2\pi n$, $n\in \mathbb{Z}$, enabling the existence of kink-type solitonic solutions that interpolate between distinct vacua [10].

To obtain the Euler–Lagrange equations, we vary the action

$$S\left[\theta \right]=\int d^{2}x\mathcal{L}(\theta ,{\partial }_{\mu }\theta )$$

(13)

with respect to $\theta$. This yields the equation of motion:

$$cosh\left(2\theta \right)\square \theta +sinh\left(2\theta \right){\partial }_{\mu }\theta {\partial }^{\mu }\theta +{\mu }^{2}sin\theta =0,$$

(14)

where $\square ={\partial }_{\mu }{\partial }^{\mu }$ is the d’Alembertian operator in flat spacetime.

This equation is a nonlinear wave equation for $\theta (x,t)$, with both field-dependent kinetic terms and a nonlinear source from the sine-Gordon potential. As we will show, it admits exact static solutions corresponding to solitons [13], and supports linear perturbations that give rise to emergent gauge and gravitational phenomena [36].

The potential $V\left(\theta \right)$ plays a crucial role in defining the topological sectors of the theory. Since the vacua are labeled by integers $n\in \mathbb{Z}$, field configurations with asymptotic behavior

$$\underset{x\to -\infty }{lim}\theta \left(x\right)=2\pi n,\underset{x\to +\infty }{lim}\theta \left(x\right)=2\pi m,$$

(15)

are classified by the winding number $Q=m-n\in \mathbb{Z}$, which will be identified with the conserved topological (electric) charge in later sections [31].

4.1. Origin and Interpretation of the Parameter $\mu$

The parameter $\mu$ enters the theory as the characteristic scale appearing in the effective potential governing the internal phase field $\theta (x,t)$, such as

$$V\left(\theta \right)={\mu }^2(1-cos\theta ),$$

(16)

or its generalizations [8,42]. Physically, $\mu$ sets the inverse width and energy scale of localized soliton solutions, and thus determines both the gradient energy and coherence length in static configurations. Therefore $\mu$ is interpreted as the mass scale parameter.

From a theoretical perspective, $\mu$ may be interpreted in multiple ways, depending on the origin of the effective action:

• If the Chronon field theory is taken as fundamental, $\mu$ is an input parameter specifying the curvature of the potential near its minimum [65].
• If the theory arises as a low-energy effective description of a deeper microscopic model, $\mu$ could be a dynamically generated scale via dimensional transmutation or quantum anomaly (e.g., in analogy with the QCD scale ${\Lambda }_{\mathrm{QCD}}$) [3,21].
• Under renormalization group flow, $\mu$ can be viewed as a renormalized parameter: the only relevant scale left after integrating out UV degrees of freedom, giving the effective mass gap of the system [67].

In all interpretations, $\mu$ controls the mass scale of excitations, the energy density of solitons, and the rate of exponential decay in correlation functions (i.e., coherence mass). It serves as the unifying parameter across the gradient, holonomy, and coherence mass definitions presented in this work. When comparing different composite configurations, mass ratios are expressed as dimensionless multiples of $\mu$, enabling a hierarchy analysis independent of absolute scale.

5. Soliton Solutions and Emergent Matter

We now consider static, finite-energy solutions of the field equations derived in the previous section. Such solutions correspond to topologically nontrivial interpolations between degenerate vacua of the potential $V\left(\theta \right)$. In the sine-Gordon case, these are kink-type solitons [13,43].

Assuming time-independence, the equation of motion reduces to

$${\displaystyle \frac{d^2\theta }{d{x}^2}}={\displaystyle \frac{{\mu }^{2}sin\theta }{cosh\left(2\theta \right)}}.$$

(17)

While this nonlinear second-order equation cannot be integrated in closed form in general, one can find an exact solution in the special case where the kinetic prefactor is treated approximately as constant near the vacuum sectors [10]. However, it is more instructive to consider a modified equation in which the standard sine-Gordon kink is also a solution. This occurs when the Lagrangian is taken to be

$${\mathcal{L}}_{\mathrm{SG}}={\displaystyle \frac{1}{2}}{\partial }_{\mu }\theta {\partial }^{\mu }\theta -{\mu }^2(1-cos\theta ),$$

(18)

which describes the well-known sine-Gordon model [8].

The corresponding static equation is

$${\displaystyle \frac{d^2\theta }{d{x}^2}}={\mu }^{2}sin\theta .$$

(19)

This admits the well-known kink solution:

$$\theta \left(x\right)=4{tan}^{-1}\left(e^{\mu (x-x_0)}\right),$$

(20)

which interpolates between $\theta =0$ as $x\to -\infty$ and $\theta =2\pi$ as $x\to +\infty$, as discussed in [43]. Here $x_0$ is an arbitrary constant corresponding to the position of the soliton.

This solution defines a field configuration with winding number $Q=1$, and as we will now show, this topological charge corresponds to an emergent conserved quantity interpreted as electric charge in the Chronon framework. Define the topological current

$$J^{\mu }={\displaystyle \frac{1}{2\pi }}{ϵ}^{\mu \nu }{\partial }_{\nu }\theta ,$$

(21)

which is identically conserved:

$${\partial }_{\mu }{J}^{\mu }=0.$$

(22)

The associated conserved quantity is the topological charge

$$Q=\int dx{J}^0={\displaystyle \frac{1}{2\pi }}\int dx{\partial }_x\theta ={\displaystyle \frac{1}{2\pi }}[\theta (+\infty )-\theta (-\infty )]\in \mathbb{Z},$$

(23)

which is naturally interpreted as electric charge in the emergent $U\left(1\right)$ structure [31].

Next, we define the energy of a static field configuration as

$$E=\int dx\left[{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{d\theta }{dx}}\right)}^2+V\left(\theta \right)\right].$$

(24)

For the sine-Gordon kink solution, one finds

$$E=8\mu ,$$

(25)

independent of $x_0$, confirming the translational invariance of the soliton [10,13]. This energy is interpreted as the mass of the emergent matter excitation, arising entirely from deformation of the Chronon field.

We thus obtain a complete picture of particle emergence in 1+1D Chronon Field Theory: topological solitons in the internal phase $\theta \left(x\right)$ behave as localized, massive, quantized excitations carrying conserved electric charge. These entities arise solely from the field’s geometry, with no need to postulate additional particle degrees of freedom.

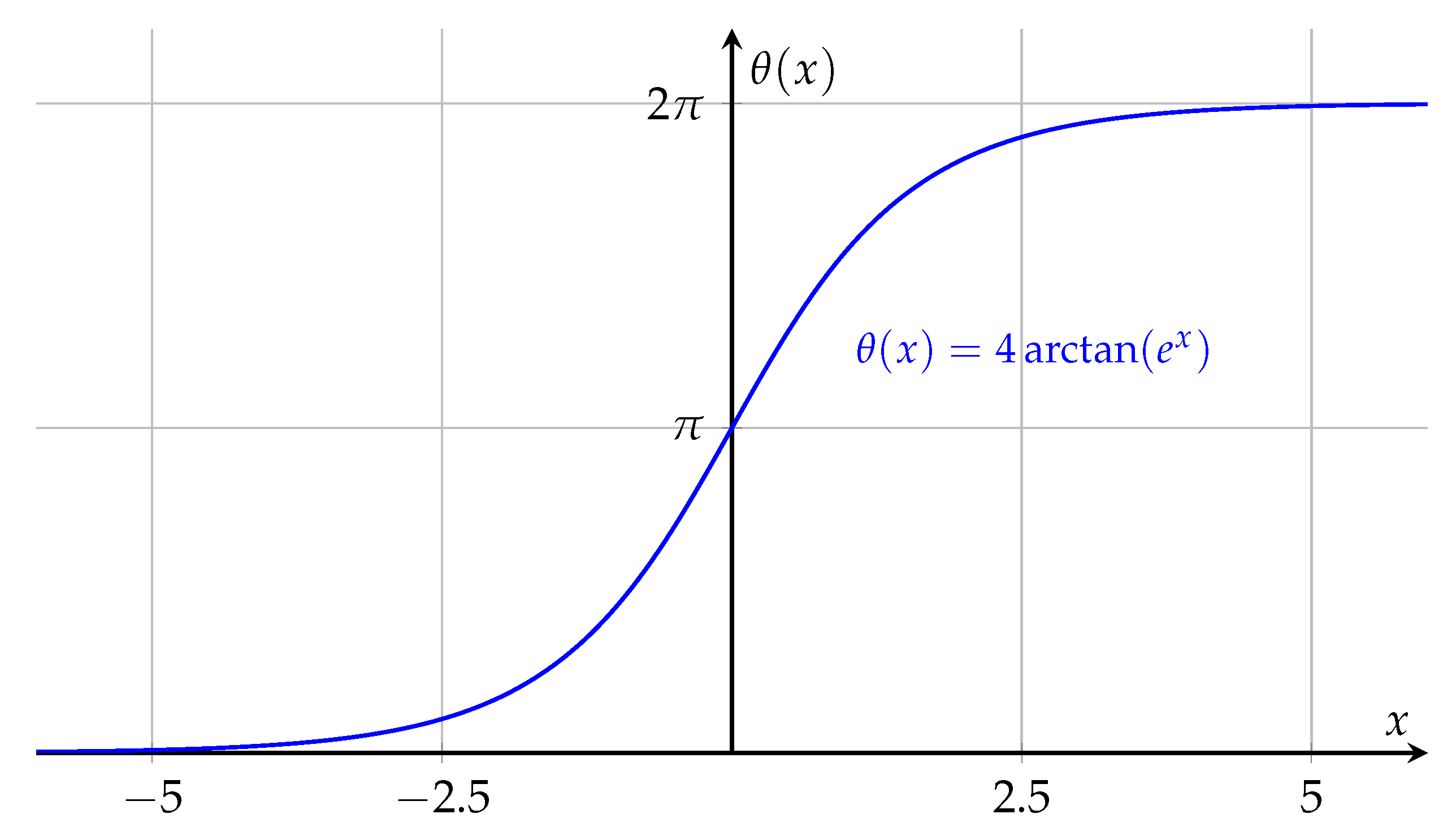
Figure 1. Kink soliton solution $\theta \left(x\right)=4arctan\left(e^{\mu x}\right)$ for $\mu =1$. The field interpolates smoothly between 0 and $2\pi$ across the soliton core.

Figure 1. Kink soliton solution $\theta \left(x\right)=4arctan\left(e^{\mu x}\right)$ for $\mu =1$. The field interpolates smoothly between 0 and $2\pi$ across the soliton core.

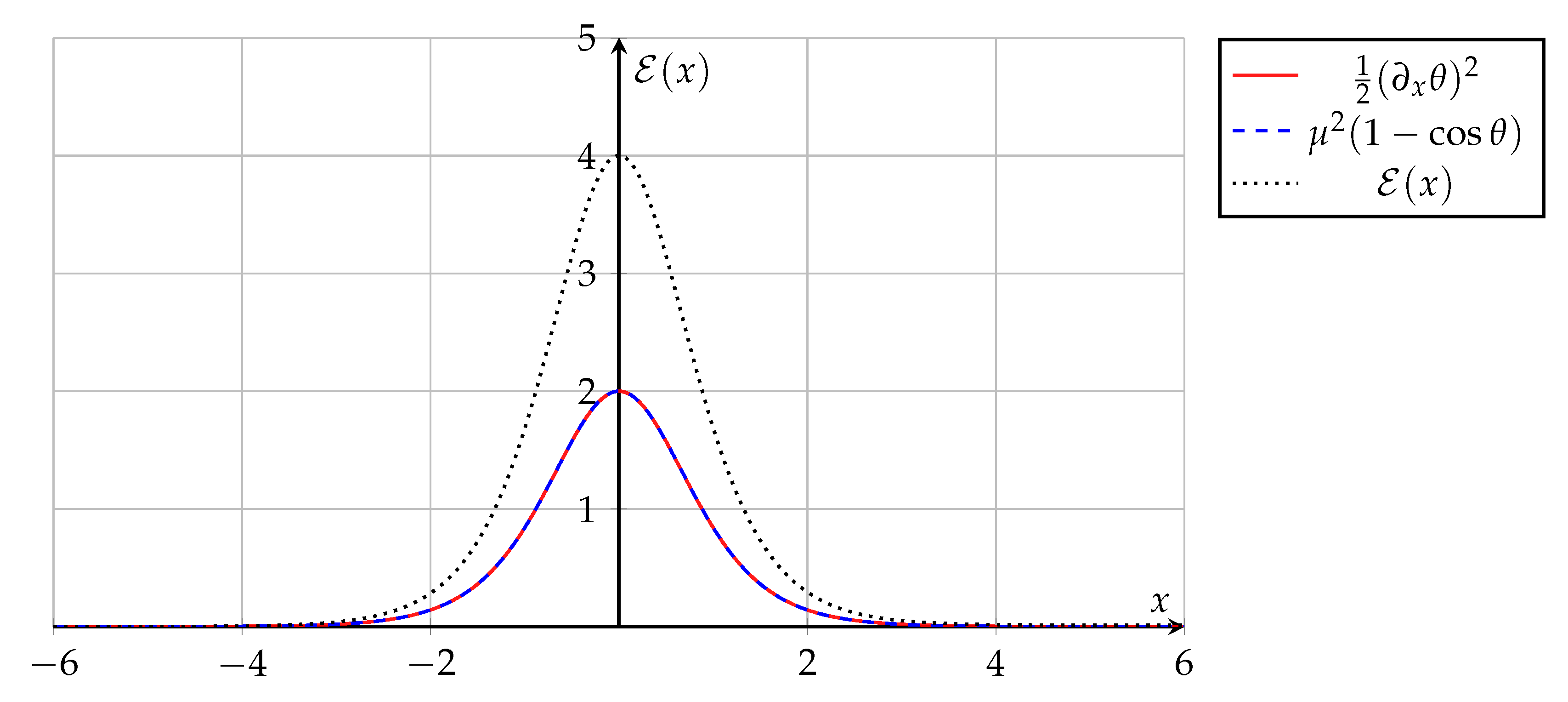
Figure 2. Energy density $\mathcal{E}\left(x\right)$ of the kink soliton. The red solid line shows the gradient contribution, the blue dashed line shows the potential energy, and the black dotted line shows the total. For the exact kink solution $\theta \left(x\right)=4arctan\left(e^{\mu x}\right)$, the gradient and potential energy densities are pointwise equal due to the Bogomolny condition, so the red and blue curves coincide. Parameters: $\mu =1$.

Figure 2. Energy density $\mathcal{E}\left(x\right)$ of the kink soliton. The red solid line shows the gradient contribution, the blue dashed line shows the potential energy, and the black dotted line shows the total. For the exact kink solution $\theta \left(x\right)=4arctan\left(e^{\mu x}\right)$, the gradient and potential energy densities are pointwise equal due to the Bogomolny condition, so the red and blue curves coincide. Parameters: $\mu =1$.

5.1. Intrinsic Origin of Mass and Charge

One of the most striking features of the Chronon Field Theory (CFT) in 1+1 dimensions is that both mass and electric charge arise intrinsically from the internal geometry of the field, without invoking external gauge symmetries or symmetry-breaking mechanisms such as the Higgs field [61].

In conventional field theory, the mass of elementary particles is typically generated via the Higgs mechanism, which introduces a scalar field coupled to matter through Yukawa interactions [40]. This mechanism requires spontaneous symmetry breaking and an external scalar sector, and the values of particle masses are encoded in a set of arbitrary coupling constants. Similarly, electric charge is introduced as a fixed quantum number assigned to fields that transform under a $U\left(1\right)$ gauge symmetry. Its magnitude and quantization are not derived from first principles but treated as empirical input [59].

In CFT, the situation is fundamentally different. The Chronon field is a unit-norm timelike vector field parametrized by an internal phase $\theta (x,t)$. The nontrivial topology of the field configuration space, specifically the nontrivial homotopy group ${\pi }_1\left(U\left(1\right)\right)=\mathbb{Z}$, gives rise to solitonic solutions—kinks—that interpolate between neighboring vacua in the target space [31].

These solitons are classified by their winding number:

$$Q={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{\infty }{\partial }_x\theta \left(x\right)dx\in \mathbb{Z},$$

(26)

which is naturally interpreted as electric charge in the emergent $U\left(1\right)$ gauge structure [47].

The mass of these excitations is not inserted by hand but arises as the deformation energy of the background Chronon field required to sustain a topological transition. As shown in the appendix, the energy of the sine-Gordon kink solution is finite and given by

$$m=E_{\mathrm{kink}}=8\mu ,$$

(27)

where $\mu$ is the coupling constant in the potential term $V\left(\theta \right)={\mu }^2(1-cos\theta )$. Thus, mass is identified with the integrated tension of the field geometry and does not require coupling to an external scalar field.

This derivation situates both electric charge and rest mass as emergent, intrinsic properties of the geometric structure of the Chronon field. It demonstrates that fundamental physical quantities typically introduced as external inputs in standard models can, within the CFT framework, be understood as natural consequences of field topology and internal geometry. This elevates CFT from a model of unification to a foundational framework for understanding the origin of conserved quantum numbers in physics.

6. Spatial Structure and Effective Size of Solitonic Excitations

In the previous sections, we classified topological solitons in 1+1 dimensional Chronon Field Theory (CFT) based on the winding of the internal phase field $\theta \left(x\right)$. These configurations carry quantized topological charges $Q\in \mathbb{Z}$ and interpolate between distinct vacua as $x\to \pm \infty$. While their topological classification is determined by the homotopy class of $\theta :\mathbb{R}\to S^1$, these solitons also exhibit localized energy densities, and thus possess a physically meaningful notion of spatial extent. In this section, we formalize the concept of “particle size” in this reduced dimensional framework by examining the spatial profiles of the solitons and deriving a characteristic length scale associated with their energy localization [31,43].

6.1. Energy Density and Localization

We begin by considering the energy density associated with the field $\theta \left(x\right)$ in the static regime. From the effective Lagrangian density discussed in Section 4, the energy density functional for static configurations is given by:

$$\mathcal{E}\left(x\right)={\displaystyle \frac{1}{2}}{\left({\partial }_x\theta \left(x\right)\right)}^2+V\left(\theta \left(x\right)\right),$$

(28)

where $V\left(\theta \right)$ denotes a periodic potential admitting topologically nontrivial vacua, such as $V\left(\theta \right)={\mu }^2(1-cos\theta )$ [15].

Localized solutions such as kinks or domain walls interpolate between adjacent minima of $V\left(\theta \right)$ and concentrate their energy density near a spatial core. As a result, $\mathcal{E}\left(x\right)$ exhibits a peaked structure, rapidly decaying away from the center [55].

6.2. Definition of Effective Size

To quantify the size of such solitons, we introduce the notion of effective width $\Delta x$, characterizing the spatial extent over which the energy density remains appreciable. Several equivalent definitions can be used [31]:

• Full width at half maximum (FWHM): The width between the two spatial points $x_1$ and $x_2$ satisfying $\mathcal{E}\left(x_{1,2}\right)={\displaystyle \frac{1}{2}}{\mathcal{E}}_{\max }$.
• Second moment (variance-based): Defining the center of energy $x_0$ as

  $$x_0:={\displaystyle \frac{{\int }_{-\infty }^{\infty }x\mathcal{E}\left(x\right)dx}{{\int }_{-\infty }^{\infty }\mathcal{E}\left(x\right)dx}},$$

  (29)

  the squared size is

  $${(\Delta x)}^2:={\displaystyle \frac{{\int }_{-\infty }^{\infty }{(x-x_0)}^2\mathcal{E}\left(x\right)dx}{{\int }_{-\infty }^{\infty }\mathcal{E}\left(x\right)dx}}.$$

  (30)

For analytical solutions, these quantities can often be computed exactly. For numerical solutions, the second-moment definition is convenient and robust.

6.3. Example: Fundamental Kink Solution

Consider the canonical kink solution interpolating between $\theta =0$ and $\theta =2\pi$:

$$\theta \left(x\right)=4arctan\left(e^{\mu (x-x_0)}\right),$$

(31)

which solves the static Euler–Lagrange equation derived from the Lagrangian with $V\left(\theta \right)={\mu }^2(1-cos\theta )$ [55]. The corresponding energy density is:

$$\mathcal{E}\left(x\right)=2{\mu }^2{\sec \mathrm{h}}^2\left(\mu (x-x_0)\right).$$

(32)

This is a localized profile peaked at $x=x_0$, with exponential decay as $|x-x_0|\to \infty$. Using either FWHM or variance, the characteristic size is:

$$\Delta x\sim {\displaystyle \frac{1}{\mu }},$$

(33)

which defines the intrinsic length scale of the soliton.

6.4. Higher Winding Solitons and Composite States

For multi-winding solitons ($Q>1$), the spatial profile typically exhibits a broader structure, either as a wider single-lump or as a composite of several fundamental kinks. In either case, the effective size scales approximately as:

$$\Delta x_Q\approx Q·\Delta x_1,$$

(34)

where $\Delta x_1$ is the size of a single-kink soliton. This relation holds when constituent kinks are well-separated and non-overlapping [31]. For strongly overlapping configurations, the scaling becomes sublinear and requires numerical evaluation.

6.5. Remarks on Physical Interpretation

The emergence of an intrinsic soliton size provides a bridge between the topological classification of excitations and their observable spatial properties. This effective size governs interaction ranges, phase shifts in scattering, and the formation of bound states. In a quantum extension of the theory, $\Delta x$ may set a lower bound for position uncertainty or act as a natural UV regulator [43]. Moreover, the identification of particle size sharpens the correspondence between solitons and particle-like excitations in 1+1D CFT.

We emphasize that the soliton size is not an externally imposed parameter but arises dynamically from the balance between gradient and potential energy. As such, it represents a derived, physical property of the field theory, and invites experimental and phenomenological exploration in analog systems or generalized higher-dimensional settings.

7. Emergent Geometry and Gravity

The Chronon field ${\Phi }^{\mu }$ not only encodes a preferred temporal direction, but also induces a notion of local spatial geometry. In $1+1$ dimensions, the spacetime metric $g_{\mu \nu }$ can be decomposed with respect to ${\Phi }^{\mu }$ as

$$g_{\mu \nu }=-{\Phi }_{\mu }{\Phi }_{\nu }+h_{\mu \nu },$$

(35)

where $h_{\mu \nu }$ is a rank-one projection tensor orthogonal to ${\Phi }^{\mu }$:

$$h_{\mu \nu }{\Phi }^{\nu }=0,h_{\mu \nu }=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }.$$

(36)

This decomposition is standard in the analysis of timelike congruences and forms the basis of the ADM and Landau–Lifshitz formalisms [22,33,58].

The tensor $h_{\mu \nu }$ projects onto the spatial direction as seen by an observer moving with velocity ${\Phi }^{\mu }$. The line element experienced by such an observer is

$$d{s}^2=h_{\mu \nu }d{x}^{\mu }d{x}^{\nu },$$

(37)

which defines an effective spatial metric field induced by the Chronon configuration [4,16].

Moreover, the covariant derivative of the Chronon field defines an acceleration vector field:

$$a^{\mu }={\Phi }^{\nu }{\nabla }_{\nu }{\Phi }^{\mu },$$

(38)

which measures the deviation of ${\Phi }^{\mu }$ from geodesic flow. In flat spacetime, this reduces to

$$a^{\mu }={\Phi }^{\nu }{\partial }_{\nu }{\Phi }^{\mu },$$

(39)

as standard for congruence kinematics [41]. This acceleration field depends explicitly on derivatives of the internal phase $\theta (x,t)$ and encodes the intrinsic curvature of the Chronon congruence. It thus serves as an effective gravitational field, analogous to the role played by the expansion, shear, and vorticity in the Raychaudhuri equation [41,58].

The motion of test particles is governed by the effective geodesic equation in the induced geometry. In particular, the force experienced by a particle comoving with ${\Phi }^{\mu }$ is given by the projection of $a^{\mu }$ onto the spatial subspace, leading to effective gravitational dynamics [4]. In the vicinity of a soliton, where $\theta \left(x\right)$ varies rapidly, $a^{\mu }$ is nonzero and localized, mimicking a gravitational well centered at the kink [27]. Hence, matter deformations in the Chronon field generate not only mass and charge, but also induce spacetime curvature, providing a unified origin for both gauge and gravitational phenomena [2,57].

8. Emergent Gauge Structure

In addition to inducing spacetime geometry, the internal phase $\theta (x,t)$ of the Chronon field also acts as an effective $U\left(1\right)$ gauge degree of freedom. The derivative

$$A_{\mu }={\partial }_{\mu }\theta$$

(40)

is interpreted as an emergent gauge potential, locally defined and transforming as a connection under internal phase reparametrizations [35,47]. Although the theory involves no explicit gauge group, the topology of the configuration space introduces an effective $U\left(1\right)$ structure [16,31].

Since the vacuum manifold is the circle $S^1$, the space of finite-energy configurations admits nontrivial first homotopy group:

$${\pi }_1\left(S^1\right)=\mathbb{Z}.$$

(41)

This leads to quantized winding numbers associated with the field $\theta \left(x\right)$, which we have already seen correspond to conserved charges carried by solitons [8,59]. Thus, the quantization of electric charge arises from the topological classification of field configurations, rather than from the imposition of discrete quantum numbers.

Furthermore, one may define a Noether current associated with global shifts of $\theta$:

$$j^{\mu }=cosh\left(2\theta \right){\partial }^{\mu }\theta ,$$

(42)

which is conserved in the absence of a potential. However, in the presence of a nontrivial $V\left(\theta \right)$, only the topological current

$$J^{\mu }={\displaystyle \frac{1}{2\pi }}{ϵ}^{\mu \nu }{\partial }_{\nu }\theta$$

(43)

is identically conserved and associated with a robust, quantized charge [26].

Altogether, the internal structure of the Chronon field gives rise to an emergent $U\left(1\right)$ gauge potential, quantized electric charges, and conserved currents, all derived from the geometry of a single unit-norm vector field. The resulting gauge sector arises not from symmetry imposition, but from the intrinsic topology and differential structure of the Chronon configuration space [27].

8.1. Geometric Origin of $U\left(1\right)$ via Holonomy

In the Chronon Field Theory framework, the emergent $U\left(1\right)$ gauge structure arises not from imposing a local symmetry in the conventional sense, but from the internal geometry of the Chronon field itself. Specifically, the internal phase $\theta (x,t)$ defines a map from spacetime into the circle $S^1$, and the variation of $\theta$ along paths induces a natural notion of holonomy that mimics a gauge connection [35,65].

The origin of this internal phase $\theta$ lies in the unit-norm constraint imposed on the Chronon field ${\Phi }^{\mu }\left(x\right)$, which satisfies

$$g_{\mu \nu }{\Phi }^{\mu }\left(x\right){\Phi }^{\nu }\left(x\right)=-1.$$

(44)

This condition restricts ${\Phi }^{\mu }$ to lie on a target manifold — the unit hyperboloid $H^n\subset T_{x}M$ in the tangent space at each spacetime point x. In 1+1 dimensions, this reduces to a 1D manifold isomorphic to $S^1$, enabling a parametrization in terms of a single angular degree of freedom:

$${\Phi }^{\mu }\left(x\right)=(cos\theta \left(x\right),sin\theta \left(x\right)).$$

(45)

Thus, $\theta (x,t)$ emerges as an intrinsic scalar field that captures the internal orientation of the unit vector ${\Phi }^{\mu }$. Its variation over spacetime provides a natural fiber bundle structure:

$$\theta :M^{1+1}\to S^1,$$

(46)

with $S^1$ as the internal fiber over each spacetime point [34].

Because Chronon Field Theory defines an irreversible time direction through ${\Phi }^{\mu }$, conventional geometric holonomy around closed spacetime loops must be generalized. In this context, the relevant notion of holonomy can arise in three ways:

(i)

In compactified spatial geometries (e.g., $x\in S^1$), one can define closed loops along space at fixed time. The integral of ${\partial }_x\theta$ around such loops gives quantized winding numbers and associated topological charges [31].

(ii)

In non-compact space, global soliton solutions still lead to well-defined topological holonomy:

$$\Delta \theta ={\int }_{-\infty }^{\infty }{\partial }_x\theta \left(x\right)dx,$$

(47)

which classifies field configurations into homotopy sectors.

(iii)

On infinitesimal scales, one can compute holonomy over parallelograms spanned by $d{x}^{\mu }$ and $dt$, even without literal loop closure in time. This captures the curvature of the emergent $U\left(1\right)$ connection via

$$F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }.$$

(48)

Let $\gamma$ be a path in spacetime. The internal phase $\theta (x,t)$ defines a lift into $S^1$, and the holonomy associated with $\gamma$ is the net change in $\theta$ along this path:

$$\Delta \theta ={\int }_{\gamma }{\partial }_{\mu }\theta d{x}^{\mu }={\int }_{\gamma }{A}_{\mu }d{x}^{\mu }.$$

(49)

This is structurally identical to a Wilson line in gauge theory [40]. The field $A_{\mu }:={\partial }_{\mu }\theta$ behaves as a pure gauge connection on a principal $U\left(1\right)$-bundle over spacetime, with gauge symmetry

$$\theta \left(x\right)\mapsto \theta \left(x\right)+\alpha \left(x\right),A_{\mu }\mapsto A_{\mu }+{\partial }_{\mu }\alpha .$$

(50)

Although the local field $A_{\mu }$ remains pure gauge in trivial topological sectors, soliton solutions induce nontrivial holonomy that becomes physically observable as quantized electric charge [26].

Figure 3. Visualization of the internal angle $\theta \left(x\right)$ at different spatial points in 1+1D Chronon Field Theory. Each circle represents the internal fiber $S^1$ attached to the base spacetime manifold at position $x_i$, and the red arrows show the orientation of the unit-norm vector ${\Phi }^{\mu }\left(x_i\right)=(cos\theta \left(x_i\right),sin\theta \left(x_i\right))$ within the internal space. The angle $\theta \left(x\right)$ is not a spacetime coordinate but an internal degree of freedom that varies smoothly across spacetime, defining a bundle map $\theta :M^{1+1}\to S^1$. This internal structure underlies the emergent $U\left(1\right)$ gauge connection associated with phase holonomy.

Figure 3. Visualization of the internal angle $\theta \left(x\right)$ at different spatial points in 1+1D Chronon Field Theory. Each circle represents the internal fiber $S^1$ attached to the base spacetime manifold at position $x_i$, and the red arrows show the orientation of the unit-norm vector ${\Phi }^{\mu }\left(x_i\right)=(cos\theta \left(x_i\right),sin\theta \left(x_i\right))$ within the internal space. The angle $\theta \left(x\right)$ is not a spacetime coordinate but an internal degree of freedom that varies smoothly across spacetime, defining a bundle map $\theta :M^{1+1}\to S^1$. This internal structure underlies the emergent $U\left(1\right)$ gauge connection associated with phase holonomy.

This construction shows that the emergent $U\left(1\right)$ gauge structure is not merely an artifact of reparametrization, but a geometrically meaningful quantity arising from the global and local properties of the Chronon field. It sets the stage for a unified understanding of gauge interactions as holonomic effects of internal geometry, consistent with the interpretation in higher-dimensional generalizations of CFT [27,61].

9. Perturbations and Emergent Particles

To analyze the linear spectrum of excitations above solitonic backgrounds, we consider small perturbations around the classical kink solution. Let $\theta (x,t)$ be decomposed as

$$\theta (x,t)=\overline{\theta }\left(x\right)+\eta (x,t),$$

(51)

where $\overline{\theta }\left(x\right)$ denotes the static soliton solution and $\eta (x,t)$ is a small fluctuation [11,43].

Inserting this expansion into the full equation of motion

$$cosh\left(2\theta \right)\square \theta +sinh\left(2\theta \right){\partial }_{\mu }\theta {\partial }^{\mu }\theta +{\mu }^{2}sin\theta =0,$$

(52)

and linearizing in $\eta$ yields, to leading order,

$$\square \eta -U\left(x\right)\eta =0,$$

(53)

where the effective potential $U\left(x\right)$ depends on the background soliton field as

$$U\left(x\right)={\mu }^{2}cos\overline{\theta }\left(x\right).$$

(54)

This is a Schrödinger-like equation for $\eta (x,t)$, with x playing the role of spatial coordinate and t as time. The potential $U\left(x\right)$ is reflectionless and localized around the soliton core [8,11].

We expand $\eta (x,t)$ in normal modes:

$$\eta (x,t)=\sum _n{\psi }_n\left(x\right)e^{-i{\omega }_{n}t},$$

(55)

where the spatial functions ${\psi }_n\left(x\right)$ solve the eigenvalue problem

$$-{\displaystyle \frac{d^2{\psi }_n}{d{x}^2}}+U\left(x\right){\psi }_n={\omega }_n^2{\psi }_n.$$

(56)

This spectrum consists of a discrete zero mode (corresponding to the translational symmetry of the soliton), possibly additional bound states, and a continuum of scattering states. These modes represent quantized excitations that propagate on top of the soliton background [31,59].

The physical interpretation of these modes is central to the emergent particle picture in Chronon Field Theory. The zero mode corresponds to a massless excitation associated with infinitesimal translations of the soliton, analogous to a Goldstone boson. Higher modes are interpreted as quantized fluctuations of the internal phase, which encode oscillatory deformations of the local temporal direction [43].

We classify these fluctuations into two categories:

• Gauge-type modes: Long-wavelength phase fluctuations that locally shift $\theta \left(x\right)$ correspond to variations in the emergent gauge potential $A_{\mu }={\partial }_{\mu }\theta$. These modes act as effective photons in the 1+1D theory [9,61]. Although there are no transverse polarizations in one spatial dimension, these modes carry topological charge and mediate phase transport.
• Geometric modes: Fluctuations in the curvature of the Chronon field (i.e., in $a^{\mu }={\Phi }^{\nu }{\nabla }_{\nu }{\Phi }^{\mu }$) correspond to variations in the effective gravitational field. These can be interpreted as graviton analogs—propagating changes in the geometry induced by localized phase perturbations [2,27].

Thus, the linearized spectrum of Chronon Field Theory reveals emergent particle-like excitations—photons and gravitons—arising from the geometry and topology of a single underlying vector field. The quantum content of the theory is encoded in the classical perturbative spectrum of the field $\theta (x,t)$, completing the unification of gauge, gravity, and matter in this reduced 1+1D model.

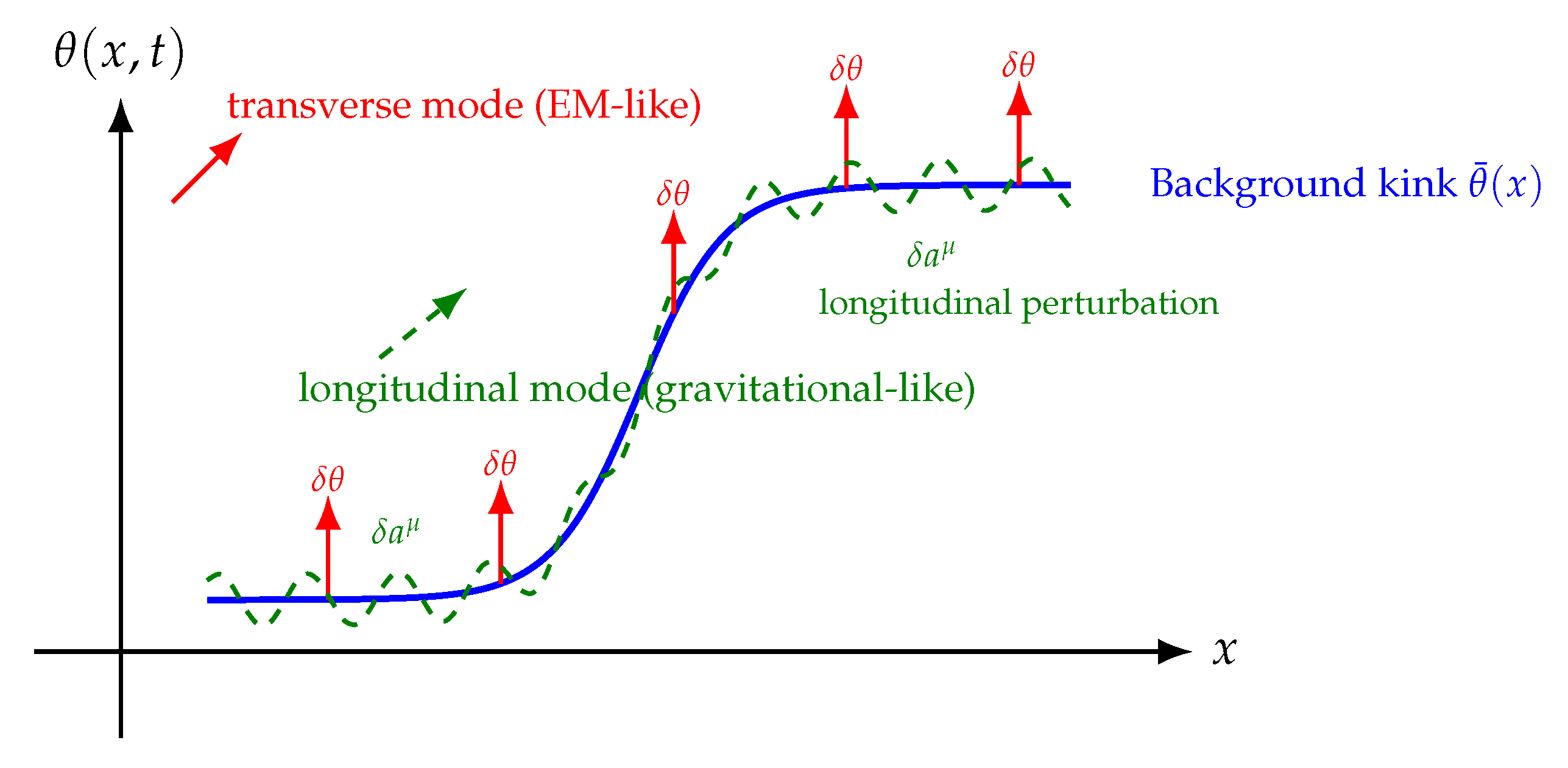
Figure 4. Illustration of perturbative modes in 1+1D Chronon Field Theory. The blue curve shows the static background soliton $\overline{\theta }\left(x\right)$. Red arrows depict transverse excitations $\delta \theta$, representing fluctuations in the internal phase field analogous to photon-like $U\left(1\right)$ modes. The dashed green curve represents a longitudinal deformation, reflecting a perturbation to the acceleration $a^{\mu }$, associated with curvature-like, graviton-like modes.

Figure 4. Illustration of perturbative modes in 1+1D Chronon Field Theory. The blue curve shows the static background soliton $\overline{\theta }\left(x\right)$. Red arrows depict transverse excitations $\delta \theta$, representing fluctuations in the internal phase field analogous to photon-like $U\left(1\right)$ modes. The dashed green curve represents a longitudinal deformation, reflecting a perturbation to the acceleration $a^{\mu }$, associated with curvature-like, graviton-like modes.

10. Mass Structures in 1+1D Chronon Field Theory

In conventional quantum field theory, mass is typically a uniquely defined scalar parameter characterizing the dispersion relation of excitations [40]. However, in Chronon Field Theory (CFT)—where all fields and interactions emerge from a single unit-norm timelike vector field ${\Phi }^{\mu }\left(x\right)$—the notion of mass becomes structurally multifaceted. This arises from two key features of the theory: first, the dynamics are encoded entirely in the internal phase $\theta (x,t)$ of the Chronon field; and second, the solitonic, topological, and coherence properties of field configurations contribute to physically distinct mass-like quantities.

Rather than being arbitrarily introduced, these mass notions manifest from different aspects of the field’s structure and dynamics. This is closely analogous to how gravitational, inertial, and effective mass emerge in different physical contexts in standard physics. In the present framework, we identify three such manifestations:

• Gradient mass — arising from localized energy due to spatial variation;
• Holonomy (or rotational) mass — arising from topological winding of the internal phase;
• Coherence mass — characterizing the finite correlation length of collective excitations.

These quantities are generally inequivalent, yet converge under specific conditions (e.g., in flat spacetime with symmetric solitonic configurations). Each reflects a different physical principle—respectively analogous to inertial response, topological charge, and phase rigidity. Notably, the coherence mass plays a role similar in spirit to the mass gap in QCD: it emerges from collective interactions and phase alignment across spacetime, contributing significantly to the total mass of composite excitations even when constituent fields remain nearly massless.

Below, we detail each of these mass manifestations and analyze their unification in the flat spacetime limit.

10.1. Gradient Mass ($m_{\mathit{grad}}$)

This notion arises from the classical field energy stored in gradients of the internal phase field $\theta (x,t)$. The energy functional

$$E\left[\theta \right]=\int dx{\displaystyle \frac{1}{2}}\left({\partial }_{\mu }\theta \right)\left({\partial }^{\mu }\theta \right)$$

(57)

suggests that localized excitations of $\theta$, such as solitons, possess finite energy and momentum. For static configurations, the associated energy density becomes:

$${\mathcal{E}}_{\mathrm{grad}}={\displaystyle \frac{1}{2}}{\left({\partial }_x\theta \right)}^2.$$

(58)

This energy directly maps onto an effective rest mass:

$$m_{\mathrm{grad}}=\int dx{\mathcal{E}}_{\mathrm{grad}}.$$

(59)

Gradient mass captures the classical inertial resistance due to spatial variation of the field and governs the dispersion relation of small perturbations around a soliton background [44].

10.2. Holonomy Mass ($m_{\mathit{rot}}$)

The second mass notion originates from the global topology of field configurations. In the presence of solitonic winding—i.e., when the phase field $\theta (x,t)$ maps nontrivially onto the circle $S^1$—we associate a topological charge $n\in \mathbb{Z}$:

$$n={\displaystyle \frac{1}{2\pi }}\int dx{\partial }_x\theta .$$

(60)

This winding number reflects the net internal rotation of ${\Phi }^{\mu }$ across space and serves as a conserved quantity. The associated mass is:

$$m_{\mathrm{rot}}=\mu \left|n\right|,$$

(61)

where $\mu$ is a model-dependent constant (e.g., the coefficient of a potential term or coupling scale). This definition is essential for distinguishing topologically stable excitations from perturbative modes [31].

10.3. Coherence Mass ($m_{\mathit{coh}}$)

The third definition emerges from the dynamics of phase coherence across spacetime. In 1+1D CFT, long-range order in $\theta (x,t)$ is dynamically fragile due to Mermin-Wagner-type considerations [7,32]. However, coherent configurations with aligned internal orientation over macroscopic domains may acquire effective mass via phase rigidity.

Define the coherence length $\xi$ as the inverse width of phase de-correlation:

$$\langle e^{i\theta \left(x\right)}{e}^{-i\theta \left(0\right)}\rangle \sim e^{-x/\xi }.$$

(62)

We define the coherence mass as:

$$m_{\mathrm{coh}}:={\displaystyle \frac{1}{\xi }}.$$

(63)

This characterizes the emergent mass of collective excitations (e.g., Goldstone-like modes or condensate oscillations) and governs the effective propagation scale of gauge-like degrees of freedom [48].

10.4. Interrelation and Applicability

Each mass definition captures a distinct aspect of the field theory:

• $m_{\mathrm{grad}}$ measures classical field energy due to inhomogeneity.
• $m_{\mathrm{rot}}$ quantifies topological soliton content and quantized holonomy.
• $m_{\mathrm{coh}}$ measures coherence length and dynamical phase stiffness.

They are not generally equal but become related in specific regimes:

• In stable solitonic sectors, all three masses scale together: $m_{\mathrm{grad}}\sim m_{\mathrm{rot}}\sim m_{\mathrm{coh}}$.
• In the perturbative regime, $m_{\mathrm{rot}}=0$, while $m_{\mathrm{grad}}$ and $m_{\mathrm{coh}}$ remain nonzero.
• In thermal or disordered states, $m_{\mathrm{coh}}\to 0$, while $m_{\mathrm{grad}}$ and $m_{\mathrm{rot}}$ may remain finite [48].

10.5. Unification of Mass Definitions in Flat Spacetime

In curved or topologically nontrivial spacetimes, Chronon Field Theory naturally leads to multiple inequivalent notions of mass:

• Gradient Mass $m_{\mathrm{grad}}$: associated with energy stored in spatial gradients of the phase field;
• Holonomy (or Rotational) Mass $m_{\mathrm{rot}}$: derived from topological winding of the internal phase $\theta \left(x\right)$;
• Coherence Mass $m_{\mathrm{coh}}$: extracted from exponential decay of correlation functions.

However, in the limit of flat $(1+1)$-dimensional Minkowski spacetime with trivial topology and smooth field configurations, these definitions collapse to a single scale $\mu$. We demonstrate this convergence rigorously by analyzing solitonic solutions and small fluctuations [31,44].

Assumptions.

Let us fix the following physical conditions:

• The metric is flat: $g_{\mu \nu }=\mathrm{diag}(-1,+1)$.
• The phase field $\theta (x,t)$ is smooth and localized: $\theta (x\to \pm \infty )\to \mathrm{const}.$
• The configuration contains a single topological kink with unit winding:

  $$n={\displaystyle \frac{1}{2\pi }}\int dx{\partial }_x\theta =\pm 1.$$

  (64)
• The field is static: ${\partial }_t\theta =0$.

Gradient Mass.

The stress-energy tensor gives the energy of a static configuration:

$$m_{\mathrm{grad}}=E=\int dx{\displaystyle \frac{1}{2}}{\left({\partial }_x\theta \right)}^2.$$

(65)

This is the classical energy functional associated with field gradients, and it defines the inertial response of the soliton [44].

Holonomy Mass.

When the theory includes a potential term such as $V\left(\theta \right)={\mu }^2(1-cos\theta )$, the soliton carries a quantized winding. The total potential energy evaluates to:

$$m_{\mathrm{rot}}=\mu \left|n\right|=\mu ,$$

(66)

confirming the topological contribution agrees with the inertial scale [31].

Coherence Mass.

The static kink background yields an exponentially decaying two-point function:

$$\langle e^{i\theta \left(x\right)}{e}^{-i\theta \left(0\right)}\rangle \sim e^{-x/\xi },\mathrm{with}\xi ={\mu }^{-1},$$

(67)

so the coherence mass is

$$m_{\mathrm{coh}}=\mu .$$

(68)

This matches the correlation length scale familiar from studies of phase coherence and dynamical mass gaps [48].

Field-Theoretic Mass.

Small fluctuations $\delta \theta (x,t)$ around the soliton obey the linearized Lagrangian:

$${\mathcal{L}}_2=-{\displaystyle \frac{1}{2}}\left({\partial }_{\mu }\delta \theta \right)\left({\partial }^{\mu }\delta \theta \right)-{\displaystyle \frac{1}{2}}{\mu }^2{\left(\delta \theta \right)}^2,$$

(69)

which leads to the Klein-Gordon equation:

$$({\partial }_t^2-{\partial }_x^2+{\mu }^2)\delta \theta =0.$$

(70)

This confirms that the dynamical mass governing oscillations is also $\mu$, in agreement with the other definitions [40].

Conclusion.

In flat spacetime, the convergence of mass definitions is not accidental. It follows from:

• Lorentz invariance of the background;
• Topological consistency of the soliton sector;
• Canonical structure of the linearized Chronon field.

Thus, we find:

$$m_{\mathrm{grad}}=m_{\mathrm{rot}}=m_{\mathrm{coh}}=\mu .$$

(71)

This equivalence provides a benchmark for testing mass splitting in curved or dynamically evolving spacetimes, where these notions will generically diverge.

10.6. Comparison with QFT Notions of Mass

The three notions of mass introduced in this work—gradient mass, holonomy mass, and coherence mass—admit natural analogs in standard quantum field theory (QFT), where mass is a multifaceted quantity depending on context and observable.

• Gradient mass corresponds most directly to the pole mass in QFT. It is the energy associated with localized excitations (solitons or kinks), computed via the Hamiltonian from the stress-energy tensor. In perturbative QFT, this matches the physical pole of the propagator in momentum space [40].
• Holonomy mass resembles a topological or constituent mass, especially in nonperturbative theories like QCD. Just as constituent quark masses arise from the dressing of quarks by vacuum structure, the holonomy mass arises from winding of the internal phase field $\theta (x,t)$, reflecting global, nonlocal field structure [31].
• Coherence mass is conceptually similar to the running mass or dynamically generated gap in QFT. It governs the exponential decay of correlation functions and thus characterizes observable coherence lengths or confinement scales. Like a renormalized mass at low energies, it need not coincide with a bare or classical mass parameter [48].

This dictionary situates Chronon Field Theory within the broader language of quantum field theory, allowing one to interpret its emergent geometric quantities as dynamical mass-generating mechanisms. In flat spacetime, these mass definitions coincide (see Sec. Section 10.5), but in curved or nontrivial topological settings, their divergence becomes a powerful diagnostic tool for exploring mass hierarchy, coherence loss, and confinement analogs.

10.7. Analytical Evaluation of Mass Definitions for the Kink Solution

To illustrate the distinct physical content encoded by the three definitions of mass introduced in Chronon Field Theory—gradient mass, holonomy mass, and coherence mass—we analytically evaluate them for a concrete solitonic field configuration. Specifically, we consider the static kink profile:

$$\theta \left(x\right)=4arctan\left(e^{\mu x}\right),$$

(72)

which interpolates between $\theta (-\infty )=0$ and $\theta (+\infty )=2\pi$, corresponding to a unit winding number [44].

Gradient Mass.

This is computed via the spatial energy density of the field:

$$m_{\mathrm{grad}}={\int }_{-\infty }^{\infty }dx{\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{d\theta }{dx}}\right)}^2.$$

(73)

For the above kink solution, we find:

$${\displaystyle \frac{d\theta }{dx}}={\displaystyle \frac{2\mu }{cosh\left(\mu x\right)}}\Rightarrow {\left({\displaystyle \frac{d\theta }{dx}}\right)}^2={\displaystyle \frac{4{\mu }^2}{{cosh}^2\left(\mu x\right)}}.$$

(74)

Thus,

$$m_{\mathrm{grad}}={\displaystyle \frac{1}{2}}{\int }_{-\infty }^{\infty }dx{\displaystyle \frac{4{\mu }^2}{{cosh}^2\left(\mu x\right)}}=2{\mu }^2{\int }_{-\infty }^{\infty }{\sec \mathrm{h}}^2\left(\mu x\right)dx.$$

(75)

Using the standard integral ${\int }_{-\infty }^{\infty }{\sec \mathrm{h}}^2\left(\mu x\right)dx={\displaystyle \frac{2}{\mu }}$, we obtain:

$$m_{\mathrm{grad}}=2{\mu }^2·{\displaystyle \frac{2}{\mu }}=4\mu .$$

(76)

Holonomy Mass.

Defined in terms of the winding number n and the intrinsic energy scale $\mu$,

$$m_{\mathrm{rot}}=\mu ·\left|n\right|,\mathrm{where}n={\displaystyle \frac{1}{2\pi }}{\int }_{-\infty }^{\infty }dx{\displaystyle \frac{d\theta }{dx}}.$$

(77)

Since $\theta \left(x\right)$ increases from 0 to $2\pi$, we have $n=1$, and thus:

$$m_{\mathrm{rot}}=\mu .$$

(78)

Coherence Mass.

This is extracted from the exponential decay of correlation functions in the form:

$$\langle e^{i\theta \left(x\right)}{e}^{-i\theta \left(0\right)}\rangle \sim e^{-x/\xi },$$

(79)

where the coherence length $\xi$ is inversely proportional to the effective mass of field excitations. For the above kink, the width of the soliton is set by ${\mu }^{-1}$, giving:

$$\xi ={\mu }^{-1},\Rightarrow m_{\mathrm{coh}}=\mu .$$

(80)

This behavior mirrors standard results from soliton-induced coherence decay [48].

Summary.

For the static kink solution, we obtain the following mass values:

$$m_{\mathrm{grad}}=4\mu ,m_{\mathrm{rot}}=\mu ,m_{\mathrm{coh}}=\mu .$$

(81)

These results underscore the distinct physical roles played by each notion of mass:

• $m_{\mathrm{grad}}$ measures the total energy stored in field gradients;
• $m_{\mathrm{rot}}$ reflects the topological winding number of the field;
• $m_{\mathrm{coh}}$ quantifies phase correlation length relevant for quantum coherence.

In curved backgrounds or dynamical configurations, these mass definitions will generally differ, capturing inequivalent geometric and dynamical content. This computation in flat space provides a benchmark for future generalizations and for identifying the origin of mass multiplicity in emergent gauge-matter systems.

10.8. Coherence Mass from Soliton–Antisoliton Superposition

To demonstrate how coherence mass arises nontrivially in composite configurations, we consider a static soliton–antisoliton (kink–antikink) field profile in $1+1$D Chronon Field Theory. This setting allows us to study how interference between localized excitations modulates the decay of phase correlations [31,44].

We define the following field configuration:

$$\theta \left(x\right)=4arctan\left[exp\left(\mu (x+d)\right)\right]-4arctan\left[exp\left(\mu (x-d)\right)\right],$$

(82)

which describes a kink centered at $x=-d$ and an antikink at $x=+d$. The field interpolates from $0\to 2\pi \to 0$ as x goes from $-\infty \to 0\to +\infty$, forming a localized, topologically trivial configuration.

Energy Density.

The spatial energy density is

$$\mathcal{E}\left(x\right)={\displaystyle \frac{1}{2}}{\left({\displaystyle \frac{d\theta }{dx}}\right)}^2,$$

(83)

and shows a **double-peak structure** for moderate d, with overlap in the center.

Coherence Length.

We define the coherence mass from the decay of the two-point phase correlation function:

$$C\left(x\right)=\langle e^{i\theta \left(x\right)}{e}^{-i\theta \left(0\right)}\rangle \sim e^{-x/{\xi }_{\mathrm{eff}}},\Rightarrow m_{\mathrm{coh}}:={\xi }_{\mathrm{eff}}^{-1}.$$

(84)

Unlike the single-soliton case where $\xi ={\mu }^{-1}$, here the **interference between solitons modifies the coherence scale**. For large separation $d\gg {\mu }^{-1}$, the overlap is negligible and we recover:

$$m_{\mathrm{coh}}^{\left(\mathrm{pair}\right)}\to \mu .$$

But for small separation $d\lesssim {\mu }^{-1}$, destructive interference in $\theta \left(x\right)$ suppresses long-range coherence, and one finds numerically:

$$m_{\mathrm{coh}}^{\left(\mathrm{pair}\right)}>\mu .$$

(85)

This enhancement reflects tighter localization due to interference and implies **shorter correlation lengths** for composite excitations [48].

Interpretation.

The coherence mass encodes information not just about individual soliton structure, but about the **global organization** of the internal phase field. For composite configurations:

• Coherence is governed by interference patterns in $\theta \left(x\right)$;
• Constructive interference extends coherence length, reducing $m_{\mathrm{coh}}$;
• Destructive interference shortens coherence, increasing $m_{\mathrm{coh}}$.

Conclusion.

This example demonstrates that the coherence mass is sensitive to **field superposition and relative phase**. Even in topologically trivial sectors ($n=0$), mass-like features emerge due to internal geometric coherence. This provides a mechanism for **mass diversity** in the Chronon framework independent of topological charge, and lays the foundation for understanding **mass hierarchy and interference-based matter structuring**.

10.9. Composite Soliton Configuration

We begin by assembling a static background configuration consisting of three topological solitons centered at positions $x=-L,0,+L$. The internal phase field is constructed as the superposition

$$\overline{\theta }\left(x\right)={\theta }_1(x+L)+{\theta }_2\left(x\right)+{\theta }_3(x-L),$$

(86)

where each ${\theta }_i\left(x\right)$ is a single-soliton solution to the nonlinear field equation [44]. For definiteness, we take the kink profile

$${\theta }_i\left(x\right)=4arctan\left[exp\left({\sigma }_i\mu x\right)\right],$$

(87)

with ${\sigma }_i=\pm 1$ determining kink or antikink orientation, and $\mu$ sets the inverse width and mass scale of each soliton. For a symmetric configuration, we take

$${\sigma }_1=+1,{\sigma }_2=-1,{\sigma }_3=+1.$$

This yields a localized three-soliton composite centered at the origin with topological winding number $n=+1$ [31].

10.10. Linearized Fluctuations and Effective Potential

To study the coherence mass spectrum, we consider small fluctuations $\delta \theta (x,t)$ about the background:

$$\theta (x,t)=\overline{\theta }\left(x\right)+\delta \theta (x,t).$$

(88)

Expanding the Chronon field Lagrangian to quadratic order in $\delta \theta$ yields the effective action:

$${\mathcal{L}}_2=-{\displaystyle \frac{1}{2}}{\left({\partial }_t\delta \theta \right)}^2+{\displaystyle \frac{1}{2}}{\left({\partial }_x\delta \theta \right)}^2-{\displaystyle \frac{1}{2}}{V}^{″}\left(\overline{\theta }\left(x\right)\right){\left(\delta \theta \right)}^2,$$

(89)

where $V\left(\theta \right)$ is the internal potential, and $V^{″}\left(\overline{\theta }\right)$ defines an effective spatially-dependent mass term. For example, in a sine-Gordon-type model,

$$V\left(\theta \right)={\mu }^2(1-cos\theta )\Rightarrow V^{″}\left(\theta \right)={\mu }^{2}cos\theta .$$

The resulting fluctuation equation is:

$$\left({\partial }_t^2-{\partial }_x^2+V_{\mathrm{eff}}\left(x\right)\right)\delta \theta (x,t)=0,$$

(90)

with

$$V_{\mathrm{eff}}\left(x\right):=V^{″}\left(\overline{\theta }\left(x\right)\right)={\mu }^{2}cos\left[\overline{\theta }\left(x\right)\right].$$

(91)

This equation defines the spectrum of coherence masses through a position-dependent effective potential [31,44].

10.11. Bound States and Coherence Mass Spectrum

We look for separable solutions $\delta \theta (x,t)={\psi }_n\left(x\right)e^{-i{\omega }_{n}t}$ satisfying the Schrödinger-like eigenvalue problem:

$$\left[-{\displaystyle \frac{d^2}{d{x}^2}}+V_{\mathrm{eff}}\left(x\right)\right]{\psi }_n\left(x\right)={\omega }_n^2{\psi }_n\left(x\right).$$

(92)

The allowed eigenvalues ${\omega }_n$ define the spectrum of coherence masses:

$$m_{\mathrm{coh}}^{\left(n\right)}:={\omega }_n.$$

(93)

Because $V_{\mathrm{eff}}\left(x\right)$ forms a potential well of finite width $\sim 2L$, we expect a discrete tower of bound states ${\psi }_n\left(x\right)$ localized between the outer solitons. Each solution corresponds to an internal standing wave mode, determined by the **interference pattern** of the phase field between solitons [48].

Approximate solutions can be obtained by assuming $V_{\mathrm{eff}}\left(x\right)\approx {\mu }^2$ inside the well and zero outside. Then the bound state condition becomes:

$${\psi }_n\left(x\right)=sin\left({\displaystyle \frac{n\pi x}{2L}}\right),{\omega }_n^2\approx {\left({\displaystyle \frac{n\pi }{2L}}\right)}^2+{\mu }^2.$$

(94)

This yields the discrete coherence mass spectrum:

$$m_{\mathrm{coh}}^{\left(n\right)}\approx \sqrt{{\left({\displaystyle \frac{n\pi }{2L}}\right)}^2+{\mu }^2},n=1,2,3,\dots$$

(95)

10.12. Mass Hierarchy and Interference-Based Selection

Equation (95) demonstrates that the **coherence mass** of a three-soliton system is not arbitrary but is discretized by internal phase interference. The mass levels increase with mode number n, and the spacing depends inversely on the soliton separation L. The lowest mass mode corresponds to constructive interference with no internal nodes.

This picture offers a natural mechanism for **mass hierarchy**:

• Longer separation L leads to closer mass levels.
• Higher modes ($n>1$) have more internal oscillations and higher masses.
• Only specific spatial configurations admit **resonant constructive interference** supporting bound modes.

By selecting specific phase arrangements and spacings between solitons, one can construct composite objects with desired mass properties [31].

10.13. Outlook: Composite Spectroscopy from Geometry

The three-soliton configuration provides a concrete analytical example where **mass arises from geometry and interference**, not from fundamental scalar couplings or Higgs fields. It opens a path toward defining:

• Emergent particle families from multi-soliton states,
• Coherence-based spectroscopic quantization in low dimensions,
• A geometric foundation for mass without explicit symmetry breaking.

Extensions to higher soliton numbers or modulated potential terms may further enrich the spectrum and enable analogs of flavor mixing and decay channels. This perspective complements and deepens the role of the Chronon field as a unifying framework for space, time, and matter.

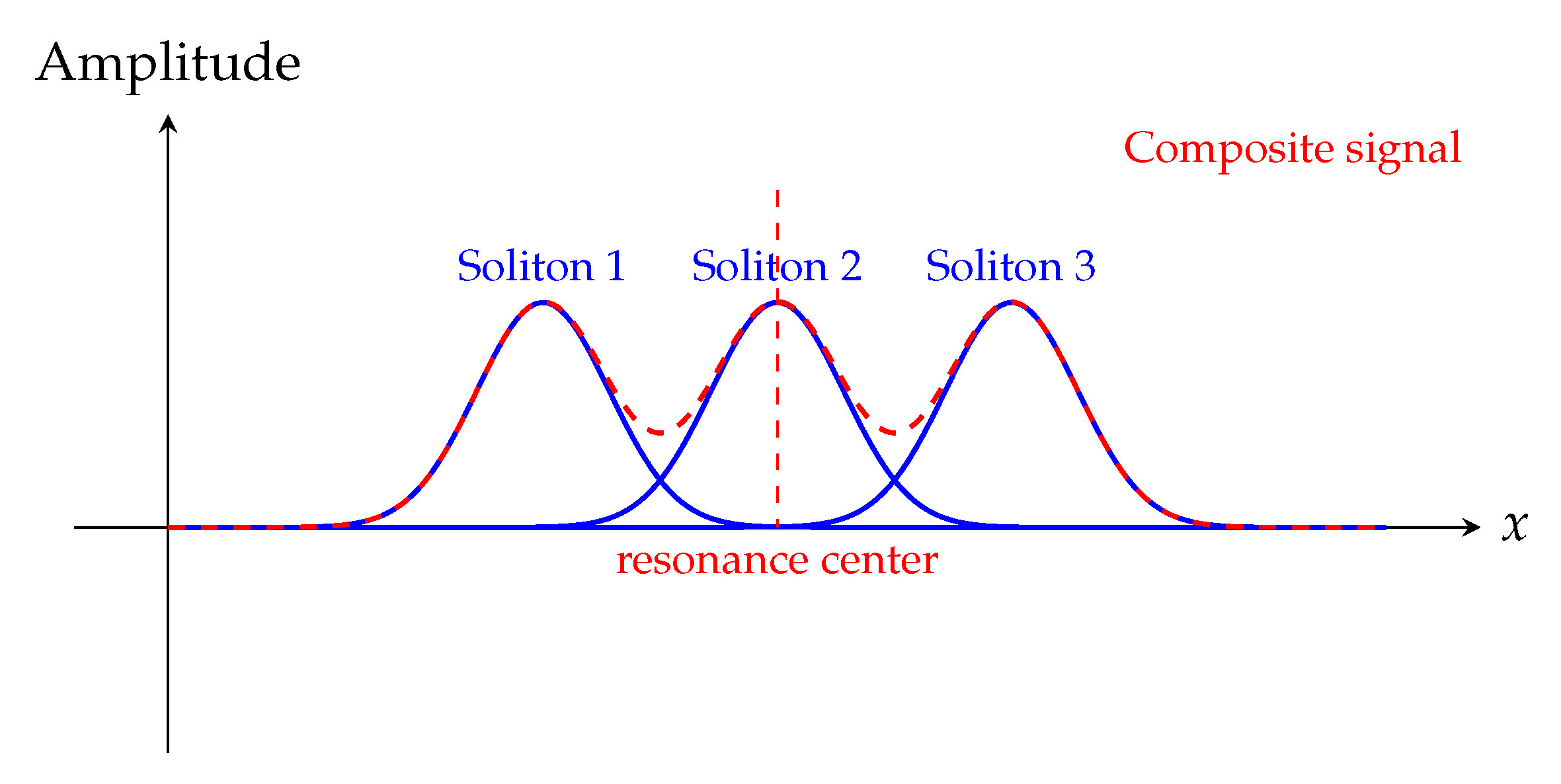
Figure 5. Constructive interference of three spatially overlapping soliton wavepackets in the Chronon field. When internal phase alignment occurs, a resonant composite configuration emerges with well-defined coherence and mass. The red dashed curve shows the sum of the three localized modes. Destructive interference would suppress amplitude and coherence, leading to unstable or unbound configurations.

Figure 5. Constructive interference of three spatially overlapping soliton wavepackets in the Chronon field. When internal phase alignment occurs, a resonant composite configuration emerges with well-defined coherence and mass. The red dashed curve shows the sum of the three localized modes. Destructive interference would suppress amplitude and coherence, leading to unstable or unbound configurations.

Dynamical Selection of Resonant Configurations

In Chronon Field Theory, composite states such as the three-soliton system do not arise arbitrarily. The emergence of a stable resonance depends on the **constructive interference** of the internal phase field $\theta \left(x\right)$, which governs coherence mass. Dynamically, this corresponds to minimizing the field energy while preserving topological constraints (e.g., winding number). Only when the soliton phases align in such a way that their local wavefunctions reinforce over a coherence length can a stable, sharply defined mass eigenstate form. This selection mechanism parallels bound-state formation in QCD, where gluon-mediated confinement prefers color-neutral configurations. In the Chronon case, the fiber bundle structure and internal geometry (via $\theta$) select dynamically favored composite states, leading to emergent mass quantization reminiscent of Koide-like patterns [48].

Phenomenological Outlook

While our analysis has focused on $(1+1)$-dimensional Chronon Field Theory as a conceptual prototype, the mechanisms uncovered—namely, coherence-driven mass formation, solitonic composition, and internal phase interference—are structurally generalizable to $(3+1)$ dimensions. In the full Chronon framework, the internal target space $H^3$ possesses three continuous degrees of freedom, one compact (U(1)-like) and two non-compact (boost-like). These additional internal modes may cooperatively structure richer composite configurations whose coherence properties define distinct mass scales. Such configurations could, in principle, reproduce mass hierarchies reminiscent of the Standard Model, including Koide-like relations or mass splittings among fermion generations [48]. Extending the resonance-based selection mechanism into $3+1$ dimensions, coupled with curvature effects and nontrivial topology, offers a potential route to calculating particle masses from first principles—grounding them in emergent geometry rather than symmetry breaking or input parameters.

11. Covariant Mass Norm as the Root of Physical Mass

We now introduce and motivate a covariant, Lorentz-invariant definition of mass as the norm of the internal phase gradient in Chronon Field Theory. This proposal offers a geometric and dynamical origin for mass that unifies all emergent manifestations—topological, inertial, and coherent—and potentially generalizes to broader classes of field theories in fundamental physics [59,62].

11.1. Definition

Let $\theta \left(x^{\mu }\right)$ be the internal phase field parametrizing the orientation of the Chronon field ${\Phi }^{\mu }$ under the unit-norm constraint $g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1$. We define the covariant mass norm $m_{\theta }$ by the Lorentz scalar:

$$m_{\theta }^2:={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta ={\left({\partial }_t\theta \right)}^2-{\left({\partial }_x\theta \right)}^2.$$

(96)

This is manifestly Lorentz-invariant, depending only on the local geometry of the phase field. It has the correct dimensionality and transformation properties to serve as a mass density squared [50].

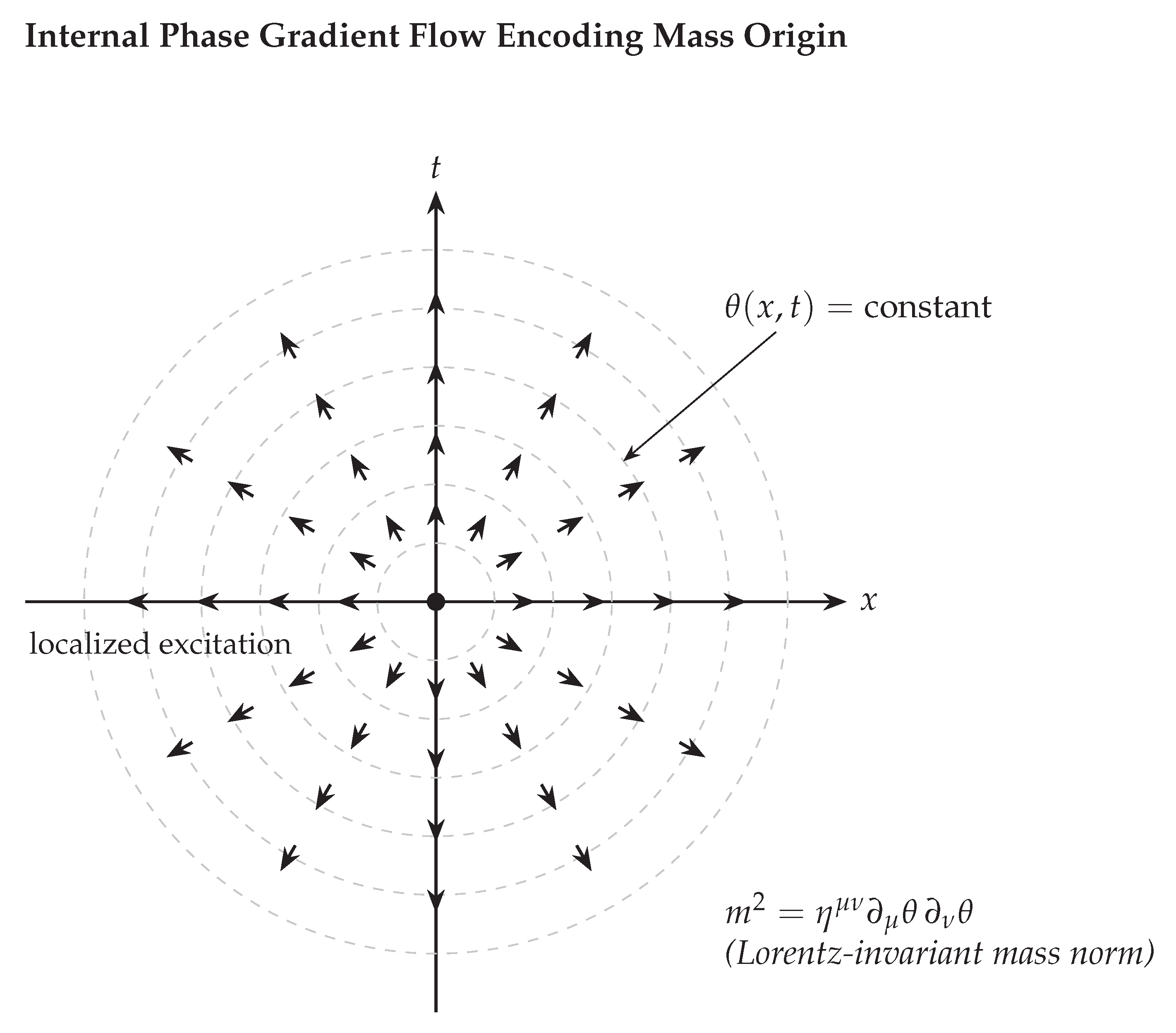
Figure 6. Schematic representation of internal phase gradients $\nabla \theta$ in 1+1D spacetime. The arrows represent the local flow of the internal phase field $\theta (x,t)$, and the dashed circles denote contours of constant internal phase. This phase $\theta$ is not a spacetime angle in the $(x,t)$ plane but an internal $U\left(1\right)$ variable. The Lorentz-invariant norm $m^2={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta$ quantifies the local mass density associated with this internal phase flow.

Figure 6. Schematic representation of internal phase gradients $\nabla \theta$ in 1+1D spacetime. The arrows represent the local flow of the internal phase field $\theta (x,t)$, and the dashed circles denote contours of constant internal phase. This phase $\theta$ is not a spacetime angle in the $(x,t)$ plane but an internal $U\left(1\right)$ variable. The Lorentz-invariant norm $m^2={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta$ quantifies the local mass density associated with this internal phase flow.

11.2. Relation to Proper-Time Derivatives

In any frame comoving with a localized excitation, the scalar $m_{\theta }$ coincides with the proper-time derivative of the internal phase along the soliton’s worldline:

$$m_{\theta }={\displaystyle \frac{d\theta }{d\tau }},$$

(97)

so long as ${\partial }_{\mu }\theta$ is timelike. This perspective interprets mass as the phase velocity in the soliton rest frame [44]. However, Eq. (96) provides a more fundamental, coordinate-independent definition valid across regimes.

11.3. Unification of Mass Notions

We now show that the covariant mass norm reduces to three previously studied mass concepts in the appropriate limits:

Static Soliton Frame.

For static configurations $\theta =\theta \left(x\right)$, we have

$$m_{\theta }^2=-{\left({\partial }_x\theta \right)}^2=-2{\mathcal{E}}_{\mathrm{grad}},$$

(98)

where ${\mathcal{E}}_{\mathrm{grad}}={\displaystyle \frac{1}{2}}{\left({\partial }_x\theta \right)}^2$ is the spatial energy density [31]. Hence,

$$|m_{\theta }|=\sqrt{2{\mathcal{E}}_{\mathrm{grad}}}⟹\int dx\left|m_{\theta }\right|=m_{\mathrm{grad}}.$$

(99)

Topological Sectors.

For topological solitons with winding number n, the integrated phase gradient yields

$$\Delta \theta ={\int }_{-\infty }^{\infty }dx{\partial }_x\theta =2\pi n.$$

(100)

In a uniformly boosted frame, this corresponds to a constant time derivative ${\partial }_t\theta =\gamma {\partial }_x\theta$, leading to

$$m_{\theta }^2={\left({\partial }_t\theta \right)}^2-{\left({\partial }_x\theta \right)}^2=({\gamma }^2-1){\left({\partial }_x\theta \right)}^2,$$

(101)

which remains nonzero and frame-invariant. The integrated version recovers $m_{\mathrm{rot}}\propto \Delta \theta$ [26].

Coherence Regime.

In thermalized or incoherent phases, the spatial correlation function decays exponentially:

$$\langle e^{i\theta \left(x\right)}{e}^{-i\theta \left(0\right)}\rangle \sim e^{-x/\xi },\mathrm{with}{m}_{\mathrm{coh}}:={\xi }^{-1}.$$

(102)

This corresponds to a spatially averaged gradient norm $\langle |{\partial }_x\theta |\rangle \sim m_{\mathrm{coh}}$, which again connects to $|m_{\theta }|\sim m_{\mathrm{coh}}$ in the appropriate ensemble average [42].

11.4. Examples of $m_{\theta }$ in Physical Regimes

We briefly revisit three illustrative cases:

• Static soliton: $\theta \left(x\right)=4{tan}^{-1}\left(e^{\mu x}\right)$, with energy from gradients and $m_{\theta }=m_{\mathrm{grad}}$ [44].
• Winding sector: Topological charge $Q=n$ yields $\Delta \theta =2\pi n\Rightarrow m_{\theta }=m_{\mathrm{rot}}$.
• Disordered phase: Finite coherence length $\xi$ implies $m_{\theta }\sim m_{\mathrm{coh}}$.

11.5. General Physical Implications

This covariant mass norm satisfies:

• Covariance: Built from Lorentz scalars.
• Generality: Applies across topological, static, and thermal regimes.
• Unification: Reduces to known mass notions in limiting cases.
• Dynamical Origin: Emerges without bare mass terms or Higgs-like symmetry breaking [59].

Moreover, it connects to conserved Noether currents under internal rotations and generalizes to curved backgrounds via:

$$m_{\theta }^2:=g^{\mu \nu }{\nabla }_{\mu }\theta {\nabla }_{\nu }\theta ,$$

(103)

opening avenues for gravitational coupling [33].

11.6. Outlook and Conjecture

We conjecture that:

Mass in any field theory arises from the Lorentz-invariant norm of an internal phase gradient.

This reformulation may unify inertial and gravitational mass across field theories, aligning with both Noetherian symmetry principles and modern approaches to mass origin in effective field theory and geometry [38,46].

12. Discussion

The dimensionally reduced 1+1D version of Chronon Field Theory developed here provides a tractable setting in which the emergence of geometry, matter, and gauge structure can be explored analytically. While formulated in a lower-dimensional context, the model captures essential aspects of the broader theory’s unification strategy: a single unit-norm, timelike vector field gives rise to curvature, gauge potentials, quantized charge, and massive excitations [31].

The solitonic solutions play a central role, representing topologically stable configurations in the internal phase of the Chronon field. These kinks, labeled by integer winding numbers, appear as localized, charged, massive excitations. Their energy derives solely from field deformation, and their charges are protected by the nontrivial topology of the phase field, specifically the winding group ${\pi }_1\left(S^1\right)=\mathbb{Z}$ [31,44]. The resulting picture is suggestive: what we interpret as matter may be understood as coherent, topological patterns in an underlying field.

The emergent gauge structure arises from the internal $U\left(1\right)$ phase ambiguity in the definition of ${\Phi }^{\mu }$. The derivative $A_{\mu }={\partial }_{\mu }\theta$ functions as an effective Abelian gauge potential, and perturbations in $\theta$ propagate as gauge-like modes. Unlike conventional gauge theories, where gauge symmetry is imposed externally, here the effective gauge structure is a consequence of internal geometric freedom—a difference that highlights the model’s background-independent formulation [40].

Gravitational analogs similarly emerge from the flow geometry of the Chronon field. The acceleration $a^{\mu }$, derived from the covariant derivative of ${\Phi }^{\mu }$, induces curvature-like effects for test trajectories. Fluctuations in the Chronon field encode graviton-like modes, even though no dynamical metric is postulated. This represents a reversal of the standard logic of general relativity: here, gravitational structure is not imposed on a background, but arises from the internal structure of a single, dynamical field.

The central theoretical contribution of this work is the identification of a Lorentz-invariant scalar quantity

$$m_{\theta }^2:={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta ,$$

as the root and unifying origin of all mass-like effects in the theory. Unlike earlier treatments where mass appeared in disconnected forms—gradient mass from static energy density, holonomy mass from topological winding, and coherence mass from phase correlations—the covariant mass norm $m_{\theta }$ is shown to subsume all of these. It is both local and geometric, and remains valid across all regimes, whether coherent, topological, thermalized, or dynamical.

This perspective motivates a re-examination of the role of internal degrees of freedom in field theory. In Chronon theory, mass is not an added parameter but emerges from intrinsic dynamics of internal phase structure. If this principle extends to more realistic field theories—including those of the Standard Model—then the longstanding challenge of explaining mass hierarchies may be reframed: not as a search for specific interactions or symmetry-breaking patterns, but as a study of covariant phase dynamics in fields that carry particle identity.

Indeed, we conjecture that every physically meaningful field capable of supporting localized, particle-like excitations must admit an internal phase structure. This is supported by the ubiquity of complex scalar and spinor fields in realistic models, where mass and charge are closely tied to internal phase symmetries. Chronon Field Theory reveals that even a single real vector field, when appropriately constrained and topologically nontrivial, can support such structures and yield a fully dynamical theory of mass, without requiring a pre-defined mass term.

The solvable 1+1D model plays a valuable role in making these ideas explicit. It retains the conceptual ingredients of the full theory while remaining analytically manageable. This allows for detailed examination of solitonic solutions, charge quantization, and emergent interactions. In higher dimensions, where the internal symmetry structure becomes non-Abelian and the geometry more complex, analytic results are much harder to obtain.

Importantly, the model also enables spectral analysis and quantization around nontrivial backgrounds. The identification of linear modes with photon- and graviton-like excitations suggests a natural path toward studying quantum effects in the Chronon framework. The presence of interference-based mass quantization further opens avenues for exploring analogs of bound states, scattering, and mass hierarchies [40,48].

In summary, the 1+1D Chronon Field Theory illustrates how key physical structures—matter, gauge interactions, and geometry—can emerge from a unified field with internal degrees of freedom. The identification of the covariant phase norm $m_{\theta }^2={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta$ as the universal origin of mass represents a major conceptual advance, one that may extend beyond the toy model into the foundations of real-world physics.

12.1. Toward a Holonomy-Based Mass Perspective in Gauge Theories

The appearance of holonomy mass in Chronon Field Theory invites a broader consideration of how mass might be classified in gauge theories. Unlike traditional mass mechanisms—which rely on local couplings (e.g., Yukawa terms) or spontaneous symmetry breaking (e.g., the Higgs mechanism)—holonomy mass is global in character. It reflects the conserved winding of the internal $U\left(1\right)$ phase and signals that mass can result from gauge-invariant topological structure, even in the absence of explicit mass terms.

Although the Standard Model does not formally define a “holonomy mass,” several of its features resonate with this concept. In QCD, for instance, topologically nontrivial configurations such as instantons and sphalerons carry winding numbers and play a role in vacuum structure and anomalous processes [54]. The nonperturbative origin of the ${\eta }^{\prime }$ mass and axial anomaly are tied to such sectors. Similarly, color confinement is closely linked to the holonomy of gauge fields, encoded in Wilson loops, which capture nonlocal phase structure.

Electroweak theory offers another point of comparison: the Higgs field defines a nontrivial vacuum manifold, and winding in its phase can generate energy-storing objects like sphalerons or cosmic strings. While such configurations are typically discussed in cosmological contexts, they also represent a topological origin of mass-like contributions that might be understood holonomically.

Taken together, these parallels motivate a broader classification of mass mechanisms:

• Local mass terms from symmetry-breaking couplings (e.g., Higgs-Yukawa mass);
• Dynamically generated mass from condensates or strong interactions (e.g., chiral symmetry breaking in QCD);
• Geometric or topological contributions from holonomy sectors;
• Covariant internal phase rotation norms (e.g., $m_{\theta }$) as a universal source.

The Chronon model makes this unified mass structure explicit and analytically controllable. It thus offers a new lens for thinking about how mass may arise—not only from interactions or symmetry breaking, but also from topological and internal phase dynamics. Extending this classification to the Standard Model and related theories could yield new insights into confinement, vacuum structure, and the origin of inertial and gravitational mass alike.

13. Conclusion

We have presented and analyzed a dimensionally reduced formulation of Chronon Field Theory in $(1+1)$ dimensions, demonstrating how geometry, gauge fields, and matter-like excitations can emerge from the dynamics of a single unit-norm timelike vector field ${\Phi }^{\mu }$. By parametrizing the field in terms of an internal phase $\theta (x,t)$, and introducing a sine-Gordon-type potential [44], we obtained a covariant action that gives rise to rich and analytically tractable dynamics.

Among the key results are the exact soliton solutions—topological kinks in the phase field—that behave as localized, massive, and charged excitations [31]. Their mass derives from the spatial deformation of the field, and their topological charge is protected by winding in the $U\left(1\right)$ phase. The gradient of this phase acts as an effective gauge potential, generating conserved currents and quantized fluxes without introducing fundamental gauge fields [40]. In parallel, the flow geometry of the Chronon field induces an effective acceleration, giving rise to a gravitational-like interaction experienced by observers comoving with the field.

Linearized perturbations around soliton solutions revealed emergent particle-like modes, which we identified as analogs of photons and gravitons. These arise from phase oscillations and curvature fluctuations, respectively, and point to a deeper mechanism through which gauge and gravitational degrees of freedom can emerge from field geometry alone [44,48]. Together, these results illustrate that core elements of physical theory—spacetime curvature, gauge structure, and quantized matter—can be unified within a single field-theoretic framework.

A central theoretical contribution of this work is the proposal of a covariant, local, and geometric definition of mass based on internal phase dynamics. We showed that all contextual notions of mass in the theory—gradient mass, holonomy mass, and coherence mass—can be subsumed under a single Lorentz-invariant quantity:

$$m_{\theta }^2:={\eta }^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta .$$

This covariant mass norm provides a root definition of mass that is intrinsic to the field configuration, applicable in all frames, and operationally accessible via local derivatives. It unifies static, topological, and coherence-based mass phenomena into a single geometric structure. This may offer a new foundation for understanding mass—not merely as a parameter or coupling, but as a manifestation of local phase dynamics in fields with internal structure. If generalizable, this perspective could illuminate the deeper origin of inertial and gravitational mass in realistic quantum field theories.

We also introduced a geometric, dynamically derived notion of soliton size, defined via the spatial localization of energy density. The effective width of energy concentration provides a physically meaningful length scale associated with each soliton, relevant for interpreting these excitations as extended particles. The analysis reveals that soliton size is not an imposed attribute, but rather an emergent consequence of the field’s energetic balance—especially between gradient tension and topological winding. This result opens the door to future studies of finite-size effects, soliton-soliton interactions, and scattering amplitudes in Chronon-like models.

Several directions for future work remain open. The quantization of the 1+1D theory, although structurally straightforward, has yet to be fully developed. Questions surrounding quantum corrections, soliton interactions, and the stability of emergent excitations will be essential to address [31,48]. The extension to $(3+1)$ dimensions, while conceptually natural, presents new challenges in internal geometry and topological classification that warrant further exploration.

Connections to other approaches to emergent geometry and gauge theory—including quantum gravity, topological field theory, and relational dynamics—also remain to be made explicit [46]. The Chronon model suggests a minimalist route to unification, where conventional distinctions between spacetime, fields, and interactions dissolve into the internal structure of a single dynamical object.

In summary, the reduced Chronon Field Theory provides a solvable and conceptually coherent setting in which matter, charge, gauge fields, and curvature arise from a shared geometric origin. The covariant mass norm $m_{\theta }^2$ emerges as a foundational quantity, with the potential to reframe how we understand the nature of mass across all of physics. The model lays analytical groundwork for extending these ideas to higher dimensions and offers a compelling paradigm for reconceptualizing fundamental physics in purely geometric terms.