Geometric and Topological Unification of Gravity and Electromagnetism via a Timelike Vector Field

1. Introduction

The unification of gravitation and electromagnetism has remained one of the most enduring aspirations of theoretical physics. Since the development of general relativity (GR) and Maxwell’s theory in the early 20th century, numerous attempts have been made to merge these paradigms into a single, coherent framework. Early efforts included Weyl’s scale-invariant geometry [77], Kaluza’s five-dimensional extension of spacetime [44], and Einstein–Cartan [36] and Yang–Mills [79] generalizations involving torsion, extra dimensions, or fiber bundle structures [60]. While mathematically elegant, these models typically introduced unobservable degrees of freedom or failed to provide mechanisms for fundamental phenomena such as charge quantization, gauge emergence, or experimentally testable deviations [23].

This work applies classical tools from topology and differential geometry—including Frobenius foliation theory, homotopy classes, and principal bundle structures—to construct a physically motivated model of unified field dynamics. It is not intended to advance topological theory per se, but rather to demonstrate how established topological and geometric constructs can yield physically testable consequences in a covariant, four-dimensional setting. The goal is to make transparent use of differential topology as a framework to explain emergent gauge symmetry, charge quantization, and the causal structure of field propagation.

The persistent conceptual tension lies in the disparate ontological roles that gravity and electromagnetism play within conventional theory: gravity is geometric and dynamical, encoded in the spacetime metric governed by the Einstein–Hilbert action, whereas electromagnetism is described as a $\mathrm{U}\left(1\right)$ gauge field defined atop this geometric background. Attempts to unify them must reconcile this asymmetry—connecting a curvature-based geometry with a fiber-bundle-based gauge theory—while preserving covariance and avoiding the proliferation of unphysical structure.

In parallel with these efforts, recent advances in emergent gravity and topological field theory suggest a different strategy: that spacetime geometry and gauge interactions may themselves arise from more primitive, possibly topological or algebraic, degrees of freedom. These include condensed matter analogs of spacetime [74], Sakharov’s induced gravity [66], and the holographic principle [15], among others. Such frameworks propose that spacetime and field content are not fundamental but emerge from symmetry-breaking, collective excitations, or topological constraints in an underlying pre-geometric system [38].

This work contributes to this perspective by presenting a covariant framework in which both gravity and electromagnetism emerge from the geometry and internal topology of a single, real-valued, future-directed timelike unit vector field ${\Phi }^{\mu }$, defined on a smooth four-dimensional Lorentzian manifold $(M,g_{\mu \nu })$. The field ${\Phi }^{\mu }$ selects a preferred local temporal direction and induces a foliation of spacetime into spatial hypersurfaces via Frobenius’ theorem [20]. The unit-norm constraint spontaneously breaks local Lorentz symmetry down to $\mathrm{SO}\left(3\right)$ spatial rotations, leaving a residual internal $\mathrm{U}\left(1\right)$ structure corresponding to rotations in the plane orthogonal to ${\Phi }^{\mu }$.

This internal $\mathrm{U}\left(1\right)$ symmetry is not imposed externally but arises naturally from the geometry of the orthogonal complement of ${\Phi }^{\mu }$. The associated degree of freedom $\theta \left(x\right)$ plays the role of a Goldstone mode of the broken Lorentz group. Through parallel transport of local frame orientations, we obtain a real-valued holonomy defining a principal $\mathrm{U}\left(1\right)$ connection over spacetime. The resulting gauge potential $A_{\mu }={\partial }_{\mu }\theta$ defines an exact one-form with curvature $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$, satisfying Maxwell-like dynamics derived from a unified variational principle. This construction parallels the treatment of fiber bundles and connections found in standard references such as Steenrod [70] and Baez and Muniain [6].

Electric charge in this model is not introduced via fundamental matter fields, but emerges from the global topology of the spatial projection of ${\Phi }^{\mu }$. Specifically, normalized spatial configurations $\widehat{\varphi }:S^3\to S^2$ define topological solitons classified by the homotopy group ${\pi }_3\left(S^2\right)\cong \mathbb{Z}$ [14], with each integer Q corresponding to a conserved, quantized electric charge. The existence of such solitons arises from well-understood topological principles of degree and winding number, and parallels the structure of Hopf fibrations and Skyrme-like models [55]. This framework provides a geometric mechanism for charge conservation and localization without invoking point particles or quantized fields.

Simultaneously, the gravitational sector emerges from the foliation structure induced by ${\Phi }^{\mu }$. The foliation determines a preferred slicing of spacetime into three-dimensional hypersurfaces, allowing an Arnowitt–Deser–Misner (ADM) decomposition [2] into lapse, shift, and spatial metric components. Metric perturbations transverse to ${\Phi }^{\mu }$ yield transverse-traceless (TT) modes which propagate as gravitational waves within the induced spatial geometry. Both the electromagnetic and gravitational degrees of freedom emerge as gapless Goldstone modes propagating at a common dynamical speed, thereby defining a unified causal structure from a single field origin.

The resulting theory is covariant, real-valued, and free from extrinsic assumptions such as extra dimensions or matter sources. It reproduces Einstein–Maxwell dynamics in appropriate limits, and admits quantized, conserved charges via topological solitons. Furthermore, it is falsifiable: subleading corrections due to nonlinear foliation geometry induce Lorentz-violating dispersion, polarization rotation (birefringence), and detectable timing offsets in multimessenger astrophysical signals [49].

In summary, this work presents a unified field theory in which both spacetime geometry and gauge structure arise from a single real-valued vector field. Its structure draws upon classical results in differential geometry, bundle theory [57], and algebraic topology [14], while offering testable physical predictions. This demonstrates how established mathematical machinery—particularly from the theory of fiber bundles, homotopy groups, and foliation geometry—can yield a unified physical framework grounded in topological invariants and geometric constraints.

2. Theoretical Context

The interplay between differential topology and fundamental physics has grown increasingly central in efforts to understand the structure of spacetime and gauge interactions. Classical gauge theory, as geometrically formulated by Atiyah, Singer, and others [4,67], interprets gauge fields as connections on principal bundles over a manifold M, with curvature representing field strength and topological invariants capturing quantized observables. In particular, characteristic classes such as the first Chern class in $H^2(M,\mathbb{Z})$ play a pivotal role in the classification of $\mathrm{U}\left(1\right)$ bundles and the quantization of electromagnetic flux [57,61].

Parallel developments in gravitational theory have emphasized the importance of global topological structures in spacetime manifolds. The Gauss–Bonnet theorem [19], the classification of spin structures [50], and the relevance of cobordism theory in quantum gravity [29,71] underscore that topological data cannot be decoupled from geometric dynamics. Topologically nontrivial field configurations—such as instantons, monopoles, and skyrmions—demonstrate that homotopy classes can encode physical charges, conserved currents, and nonperturbative transitions [14,55,63].

This paper builds on that topological foundation, proposing a unification of gravity and electromagnetism grounded in the internal and global structure of a real, unit-norm timelike vector field ${\Phi }^{\mu }$. The core topological mechanisms invoked include:

• Foliation theory: The vector field ${\Phi }^{\mu }$, subject to the Frobenius integrability condition ${\Phi }_{[\mu }{\nabla }_{\nu }{\Phi }_{\rho ]}=0$, defines a codimension-one foliation of the spacetime manifold M. This induces a global decomposition $M\cong \mathbb{R}\times \Sigma$, where each leaf ${\Sigma }_t$ inherits both geometric and topological structure from the embedding. Time becomes an emergent field parameter, tied to the integral curves of ${\Phi }^{\mu }$, consistent with frameworks in foliation geometry [16,58].
• Structure group reduction and symmetry breaking: The unit-norm constraint ${\Phi }^{\mu }{\Phi }_{\mu }=-1$ breaks local Lorentz invariance $\mathrm{SO}(3,1)\to \mathrm{SO}\left(3\right)$, reducing the orthonormal frame bundle to a subbundle with spatial rotation structure group. The residual internal symmetry is a $\mathrm{U}\left(1\right)$ subgroup corresponding to rotations in the orthogonal 2-plane transverse to ${\Phi }^{\mu }$. This reduction of the frame bundle follows the formalism developed in [6,47], and yields an effective $\mathrm{U}\left(1\right)$ principal bundle associated with internal phase transport.
• Homotopy and soliton charge: The normalized spatial projection $\widehat{\varphi }:S^3\to S^2$ of the vector field defines a continuous map from the spatial boundary at infinity (modeled as $S^3$) to the unit sphere $S^2$, encoding the direction of ${\Phi }^{\mu }$. Such maps are classified by the homotopy group ${\pi }_3\left(S^2\right)\cong \mathbb{Z}$, yielding topologically protected winding numbers $Q\in \mathbb{Z}$ that correspond to quantized electric charges [14]. This mechanism parallels quantization structures in nonlinear sigma models and Skyrme fields [55].
• Topological currents and cohomological interpretation: Electric charge conservation arises from a topological current constructed as a closed 3-form $J=★K$, where K is built from derivatives of $\widehat{\varphi }$ and satisfies $\mathrm{d}J=0$ identically. The integral of this current over a Cauchy surface yields an integer-valued topological invariant, interpretable as a degree class in $H^3(M,\mathbb{Z})$. This connects conserved charges to de Rham cohomology and to generalized Chern–Simons-like structures [6,57].
• Gauge emergence from internal holonomy: Rather than postulating a complex scalar field, the theory constructs the $\mathrm{U}\left(1\right)$ gauge potential $A_{\mu }={\partial }_{\mu }\theta$ directly from the real-valued internal phase $\theta \left(x\right)$ associated with infinitesimal rotations around ${\Phi }^{\mu }$. The resulting gauge field is exact but nontrivial on topologically nontrivial manifolds. Its curvature $F_{\mu \nu }$ arises from internal phase holonomy and satisfies Maxwell-type field equations derived from the unified action principle. This formulation echoes the geometric description of connections and holonomies in principal bundles [6,70].

By foregrounding these topological mechanisms, this framework situates the unification of gravitation and electromagnetism within a rigorous and well-established mathematical landscape. The topological data—bundle reductions, homotopy classes, and conserved forms—not only constrain the allowed field configurations but also determine the quantization structure and dynamical symmetries of the theory. In this way, the model offers a concrete application of classical topology and geometric analysis to physically testable unified field dynamics.

3. Geometric and Field-Theoretic Foundations

3.1. Lorentzian Spacetime and the Timelike Vector Field

Let M be a smooth, four-dimensional, orientable, and time-oriented manifold equipped with a Lorentzian metric $g_{\mu \nu }$ of signature $(-,+,+,+)$, making $(M,g_{\mu \nu })$ a spacetime manifold in the sense of general relativity [20,75]. We assume that M is globally hyperbolic, ensuring the existence of a global time function and a foliation into non-intersecting Cauchy surfaces [35].

We introduce a smooth, real-valued vector field ${\Phi }^{\mu }\in \Gamma \left(TM\right)$ that is everywhere timelike and future-directed. It satisfies the pointwise constraint:

$$g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1\mathrm{for}\mathrm{all}x\in M,$$

(1)

where the minus sign enforces its timelike character under the chosen metric signature.

This vector field ${\Phi }^{\mu }$ plays a central role in the theory. Geometrically, it defines a local temporal orientation and determines a dynamical foliation of the spacetime manifold. Physically, it seeds both the causal structure and the emergence of an internal $\mathrm{U}\left(1\right)$ gauge symmetry through its orientation-preserving structure group reduction. Unlike approaches that invoke complex scalar fields, ${\Phi }^{\mu }$ is real-valued, and the associated gauge dynamics arise from its internal geometric degrees of freedom.

To ensure consistent dynamics, the unit-norm constraint (1) is enforced using a Lagrange multiplier in the variational principle, analogous to treatments in Einstein–Aether theories [39,56]. The field ${\Phi }^{\mu }$ is treated as a dynamical variable whose evolution derives from a covariant action principle, described in Section 6.

3.2. Unit-Norm Constraint and Foliation via Frobenius Theorem

The condition (1) implies that ${\Phi }^{\mu }$ defines a congruence of future-directed timelike curves throughout M. The orthogonal complement to this vector field defines, at each point, a three-dimensional subspace of $T_{x}M$ that serves as a local spatial hypersurface. The family of such orthogonal distributions forms a candidate for a codimension-one foliation of spacetime.

To determine whether these distributions integrate into a smooth foliation, we invoke Frobenius’ theorem [51]. Define the projection tensor onto the spatial hypersurface orthogonal to ${\Phi }^{\mu }$ by

$$h_{\mu \nu }:=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }.$$

(2)

Then the antisymmetric part of the projected derivative defines the vorticity or twist tensor:

$${\omega }_{\mu \nu }:=h_{\mu }^{\alpha }{h}_{\nu }^{\beta }{\nabla }_{[\alpha }{\Phi }_{\beta ]}.$$

(3)

Frobenius’ theorem states that the spatial distribution is integrable if and only if ${\omega }_{\mu \nu }=0$. This condition implies the local existence of a smooth function $\tau \left(x\right)\in C^{\infty }\left(M\right)$ and positive lapse function $N\left(x\right)$ such that:

$${\Phi }^{\mu }=-N\left(x\right)g^{\mu \nu }{\partial }_{\nu }\tau \left(x\right),$$

(4)

so that ${\Phi }^{\mu }$ is hypersurface-orthogonal to the level sets ${\Sigma }_{\tau }:=\{x\in M\mid \tau \left(x\right)=\mathrm{const}\}$. When this condition holds globally, the spacetime admits a decomposition $M\cong \mathbb{R}\times \Sigma$ into leaves ${\Sigma }_{\tau }$ that inherit the topological structure of three-dimensional spatial hypersurfaces [16,58].

This intrinsic foliation breaks the full local Lorentz symmetry down to the stabilizer group of ${\Phi }^{\mu }$, which is isomorphic to $\mathrm{SO}\left(3\right)$. The residual symmetry in the plane orthogonal to both ${\Phi }^{\mu }$ and a fixed spatial direction corresponds to an internal $\mathrm{U}\left(1\right)$ group, yielding an effective reduction of the frame bundle:

$$\mathrm{SO}(3,1)\to \mathrm{SO}\left(3\right)\to \mathrm{U}\left(1\right),$$

as formulated in the theory of principal bundles [47,70]. The local phase associated with this residual symmetry, denoted $\theta \left(x\right)$, behaves as a Goldstone mode and serves as a section of the emergent $\mathrm{U}\left(1\right)$ bundle.

The spatial foliation also enables a 3+1 decomposition of the spacetime metric:

$$g_{\mu \nu }=-N^2{\nabla }_{\mu }\tau {\nabla }_{\nu }\tau +h_{\mu \nu },$$

where $N\left(x\right)$ is the lapse and $h_{\mu \nu }$ the induced spatial metric on each slice ${\Sigma }_{\tau }$. This decomposition is fundamental to both the geometric interpretation of gravity and the dynamical emergence of a gauge potential $A_{\mu }={\partial }_{\mu }\theta$, derived from internal phase transport in the orthogonal frame.

In summary, the foliation determined by the real unit-norm field ${\Phi }^{\mu }$ is not an auxiliary structure but an intrinsic outcome of symmetry breaking. It induces both the causal structure of spacetime and the internal fiber geometry required for gauge field emergence. This geometric foundation aligns with the treatment of bundles and foliations in differential topology [6,14,57] and underpins the unified framework developed in the subsequent sections.

4. Internal $\mathbf{U}\left(\mathbf{1}\right)$ Structure and Emergent Gauge Dynamics

4.1. Intrinsic Phase from Fiber Geometry

We now examine the internal structure induced by the real-valued, unit-norm, timelike vector field ${\Phi }^{\mu }$. Unlike conventional approaches that invoke complex scalar fields to induce gauge structure, we show that a residual internal $\mathrm{U}\left(1\right)$ symmetry emerges from the geometric configuration space of ${\Phi }^{\mu }$ itself [6,28].

At each point $x\in M$, the unit-norm condition $g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1$ constrains ${\Phi }^{\mu }\left(x\right)$ to lie on the unit future hyperboloid $H^3\subset T_{x}M$. The stabilizer of ${\Phi }^{\mu }$ under the Lorentz group is isomorphic to $\mathrm{SO}\left(3\right)$, encoding internal spatial rotations orthogonal to ${\Phi }^{\mu }$. Within this plane, we identify a residual one-parameter subgroup isomorphic to $\mathrm{U}\left(1\right)$, corresponding to rotations in a fixed internal 2-plane transverse to ${\Phi }^{\mu }$.

This defines a principal $\mathrm{U}\left(1\right)$ bundle over the base spacetime M, where the fiber at each point parameterizes internal rotational degrees of freedom of ${\Phi }^{\mu }$. We denote the local phase coordinate along this fiber by $\theta \left(x\right)\in [0,2\pi )$, interpreted as a section of the associated bundle. Small fluctuations of ${\Phi }^{\mu }$ about a background configuration ${\overline{\Phi }}^{\mu }$ then take the form:

$${\Phi }^{\mu }\left(x\right)={\overline{\Phi }}^{\mu }\left(x\right)+\theta \left(x\right){\Xi }^{\mu }\left(x\right)+\mathcal{O}\left({\theta }^2\right),$$

(5)

where ${\Xi }^{\mu }\left(x\right)$ is a spacelike unit vector orthogonal to ${\overline{\Phi }}^{\mu }$, i.e., $g_{\mu \nu }{\overline{\Phi }}^{\mu }{\Xi }^{\nu }=0$. Thus, $\theta \left(x\right)$ is not a fundamental scalar field but a coordinate on the internal symmetry fiber attached to ${\Phi }^{\mu }$’s configuration space [70].

4.2. Definition of Holonomy and Gauge Field from Real-Valued ${\Phi }^{\mu }$

Although ${\Phi }^{\mu }\left(x\right)$ is real-valued and cannot be complexified, it carries internal rotational degrees of freedom that are geometrically encoded via holonomy in the associated $\mathrm{U}\left(1\right)$ bundle. Consider a closed curve $\gamma :[0,1]\to M$, and lift it to a path in the configuration space of ${\Phi }^{\mu }$. Parallel transport along this path using a connection on the internal bundle induces a holonomy angle:

$${\oint }_{\gamma }{A}_{\mu }d{x}^{\mu }=\Delta \theta \left(\gamma \right)\in [0,2\pi ),$$

(6)

where $A_{\mu }$ is the connection one-form encoding the phase rotation induced by transport, and $\Delta \theta \left(\gamma \right)$ is the gauge-invariant net internal phase accumulated around the loop [24,28].

This holonomy arises from the pullback of the Maurer–Cartan form on $\mathrm{U}\left(1\right)$ to the base manifold M, mediated by the frame orientation of ${\Phi }^{\mu }$. The structure thus defined is that of a smooth principal bundle with connection [14,70]. The field strength $F=\mathrm{d}A$ reflects curvature in this bundle; its vanishing or non-vanishing encodes whether the bundle is flat or topologically nontrivial.

4.3. Emergence of $A_{\mu }={\partial }_{\mu }\theta$, and $F_{\mu \nu }$

Locally, the internal phase $\theta \left(x\right)$ defines a section of the U(1) bundle, from which we construct the gauge potential:

$$A_{\mu }\left(x\right):={\partial }_{\mu }\theta \left(x\right),$$

(7)

which transforms under local phase shifts $\theta \left(x\right)\to \theta \left(x\right)+\alpha \left(x\right)$ as

$$A_{\mu }\left(x\right)\to A_{\mu }\left(x\right)+{\partial }_{\mu }\alpha \left(x\right),$$

consistent with U(1) gauge symmetry. The field strength tensor is then defined as the exterior derivative:

$$F_{\mu \nu }:={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }={\partial }_{\mu }{\partial }_{\nu }\theta -{\partial }_{\nu }{\partial }_{\mu }\theta ,$$

(8)

which vanishes identically if $\theta$ is globally smooth. However, when $\theta \left(x\right)$ is defined only locally (e.g., in the presence of defects or topologically nontrivial transition functions), $F_{\mu \nu }$ acquires physical significance. This is the hallmark of emergent gauge fields arising from nontrivial topology [57,72].

4.4. Visualization of U(1) Holonomy

To illustrate the geometric origin of the gauge structure, we depict the U(1) fibers attached to spacetime via the real-valued field ${\Phi }^{\mu }\left(x\right)$. Each fiber encodes the local internal phase, and holonomy around a closed loop in the base manifold results in net internal rotation.

Figure 1. Each point in spacetime carries an internal $\mathrm{U}\left(1\right)$ fiber parameterized by the local phase $\theta \left(x\right)$. Parallel transport of ${\Phi }^{\mu }$ along a closed curve accumulates phase holonomy, encoded in the gauge potential $A_{\mu }$.

Figure 1. Each point in spacetime carries an internal $\mathrm{U}\left(1\right)$ fiber parameterized by the local phase $\theta \left(x\right)$. Parallel transport of ${\Phi }^{\mu }$ along a closed curve accumulates phase holonomy, encoded in the gauge potential $A_{\mu }$.

This construction reveals how a physically meaningful gauge field $A_{\mu }$ and its field strength $F_{\mu \nu }$ emerge from a real-valued topological structure, rather than from imposed gauge symmetry or complex scalar fields. The principal bundle structure and curvature originate from the internal geometry of the field space, not from external assumptions.

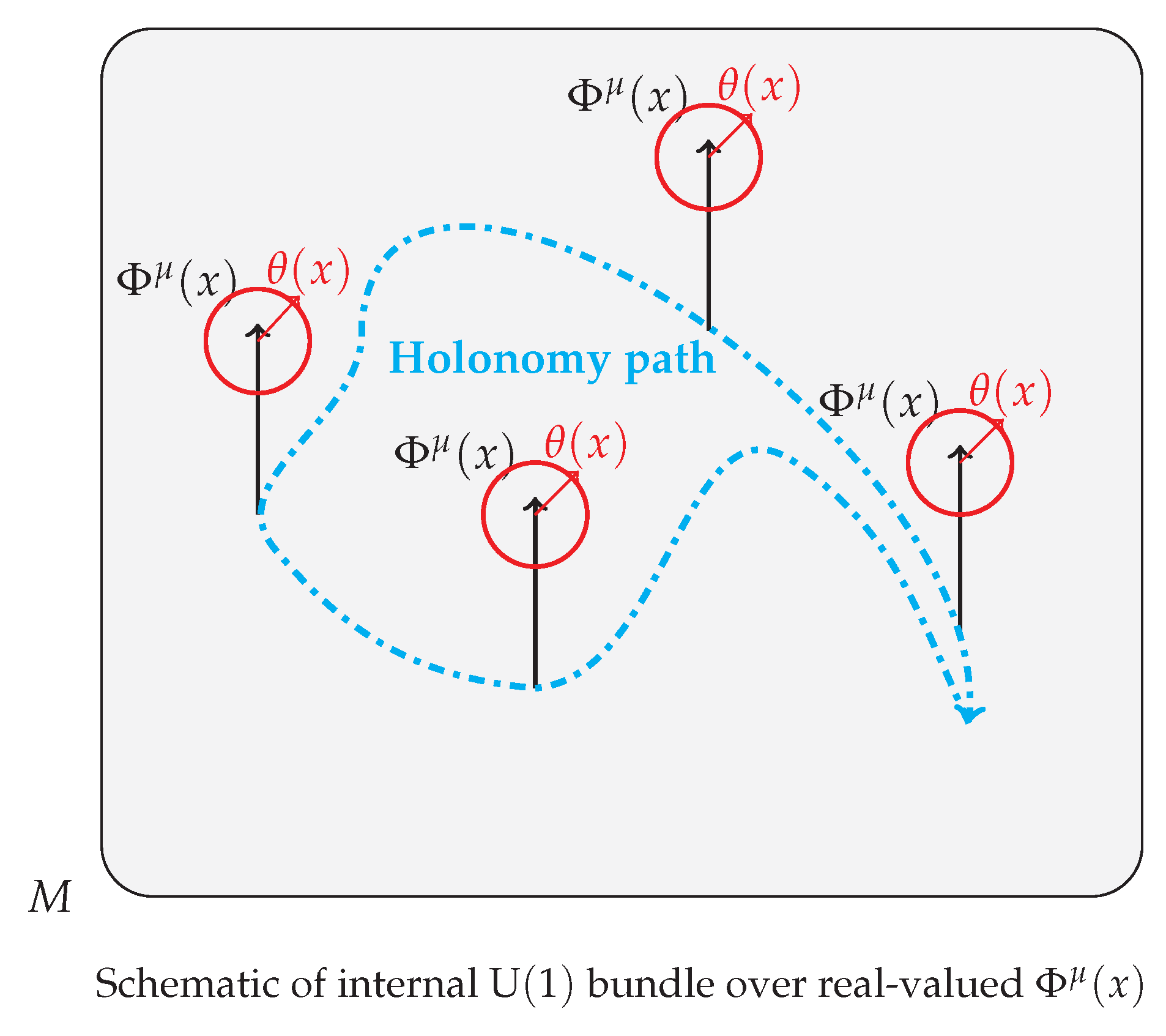
5. Topological Origin of Electric Charge

In the emergent gauge framework developed from a real, unit-norm, timelike vector field ${\Phi }^{\mu }$, electric charge appears not as a fundamental quantity, but as a topological invariant of field configurations. Specifically, conserved charges are classified by homotopically nontrivial mappings of spatial hypersurfaces into the internal phase geometry induced by ${\Phi }^{\mu }$ [14,57,70].

5.1. Compactification and Homotopy Classifications

Let $\Sigma \subset M$ be a spacelike Cauchy hypersurface orthogonal to the foliation defined by ${\Phi }^{\mu }$, i.e., a level set of a global time function $\tau$ such that ${\Phi }^{\mu }=-N{\partial }^{\mu }\tau$. We impose asymptotic flatness on field configurations:

$$\underset{\left|x\right|\to \infty }{lim}{\Phi }^{\mu }\left(x\right)\to {\overline{\Phi }}^{\mu },$$

(9)

for some constant future-directed unit vector ${\overline{\Phi }}^{\mu }$. This boundary condition allows the one-point compactification $\Sigma \simeq {\mathbb{R}}^3\cup \{\infty \}\cong S^3$, so that each admissible configuration defines a map:

$$\widehat{\Phi }:S^3⟶S^2,$$

(10)

where ${\widehat{\Phi }}^a\left(x\right)\in S^2\subset {\mathbb{R}}^3$ is the normalized spatial projection of ${\Phi }^{\mu }$ onto a unit two-sphere of internal directions orthogonal to ${\overline{\Phi }}^{\mu }$. The classification of such maps is given by the homotopy group:

$${\pi }_3\left(S^2\right)\cong \mathbb{Z},$$

(11)

whose elements label topologically distinct configurations characterized by an integer winding number Q [34].

5.2. Winding Number and Solitonic Charge Configurations

Explicitly, we define:

$${\widehat{\Phi }}^i\left(x\right):={\displaystyle \frac{{\Phi }^i\left(x\right)}{\sqrt{g_{jk}{\Phi }^j{\Phi }^k}}},i=1,2,3,$$

(12)

which describes the internal spatial orientation of the field on $\Sigma$. Then $\widehat{\Phi }:S^3\to S^2$ is a continuous map, and its degree,

$$Q:=\mathrm{deg}\left(\widehat{\Phi }\right)\in \mathbb{Z},$$

(13)

measures how many times the domain wraps around the target. This degree is a topological invariant under smooth deformations and labels distinct homotopy classes [57].

Configurations with $Q\ne 0$ cannot be continuously deformed to the vacuum $\widehat{\Phi }=\mathrm{const}$ without violating asymptotic conditions. They define topologically stable, spatially localized solitons—realizations of electric charge within a purely geometric framework [55,69].

5.3. Topological Current and Charge Conservation

To extract a conserved current from these configurations, we define:

$$J^{\mu }:={\displaystyle \frac{1}{8{\pi }^2}}{ϵ}^{\mu \nu \rho \sigma }{ϵ}_{abc}{\widehat{\Phi }}^a{\partial }_{\nu }{\widehat{\Phi }}^b{\partial }_{\rho }{\widehat{\Phi }}^c{A}_{\sigma },$$

(14)

where $A_{\mu }={\partial }_{\mu }\theta$ is the emergent gauge field derived from the internal U(1) structure, and ${\widehat{\Phi }}^a\in S^2$ are internal spatial components. This expression is a Chern–Simons-like current coupling topology (via the winding of $\widehat{\Phi }$) to gauge dynamics (via $A_{\mu }$) [42].

Because ${ϵ}^{\mu \nu \rho \sigma }$ and ${ϵ}_{abc}$ are antisymmetric, and the derivatives of $\widehat{\Phi }$ appear in a fully antisymmetric triple product, the current is identically conserved:

$${\nabla }_{\mu }{J}^{\mu }=0.$$

(15)

The associated conserved charge is:

$$Q:={\int }_{\Sigma }{d}^{3}x\sqrt{h}{n}_{\mu }{J}^{\mu },$$

(16)

where h is the determinant of the induced metric on $\Sigma$, and $n^{\mu }$ is the unit normal.

5.4. Quantization via ${\pi }_3\left(S^2\right)=\mathbb{Z}$

The quantization of $Q\in \mathbb{Z}$ follows directly from the classification of maps $S^3\to S^2$. This topological origin of electric charge is independent of field equations or quantum effects, relying solely on the smooth structure of spacetime and the geometry of the configuration space [34,70].

Thus, charge quantization in this model emerges as a theorem of homotopy theory. Each nontrivial element $Q\in {\pi }_3\left(S^2\right)$ defines a stable soliton carrying quantized electric charge. These objects are smooth, finite-energy configurations whose conserved currents and interactions are governed by the emergent gauge field $A_{\mu }$, satisfying:

$${\nabla }_{\nu }{F}^{\mu \nu }=J^{\mu },$$

(17)

where $F_{\mu \nu }={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ is the electromagnetic field strength.

In summary, electric charge arises as a global topological feature of the vector field ${\Phi }^{\mu }$, grounded in the differential topology of maps $S^3\to S^2$. This provides a classical, geometric mechanism for both charge quantization and conservation, independent of point-particle assumptions or field quantization, and anchored in the homotopy theory of smooth manifolds [14,55].

6. Unified Variational Principle

The unification of gravitational and electromagnetic dynamics in this model proceeds from a single covariant variational principle. The sole fundamental field is a real-valued, unit-norm, timelike vector field ${\Phi }^{\mu }\in \Gamma \left(TM\right)$, whose dynamics encode both the causal structure of spacetime and an emergent internal U(1) gauge symmetry via its internal phase geometry. The action functional is constructed to be diffeomorphism-invariant and to respect this U(1) symmetry, with the unit-norm constraint imposed through a scalar Lagrange multiplier field. This section presents the unified action and derives the associated field equations governing both metric and gauge degrees of freedom [13,27,40].

6.1. Lagrangian Construction and Constraint Enforcement

Let $(M,g_{\mu \nu })$ be a smooth, orientable, four-dimensional Lorentzian manifold with Levi-Civita connection ${\nabla }_{\mu }$ and metric determinant $g:=det\left(g_{\mu \nu }\right)$. The total action is given by:

$$S[{\Phi }^{\mu },g_{\mu \nu },\lambda ]={\int }_M{d}^{4}x\sqrt{-g}\left[{\displaystyle \frac{1}{2\kappa }}R+\lambda (g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }+1)-{\displaystyle \frac{1}{4}}{F}_{\mu \nu }{F}^{\mu \nu }\right]+S_{\mathrm{top}},$$

(18)

where:

• R is the Ricci scalar curvature, governing gravitational dynamics via Einstein–Hilbert terms.
• $\lambda \left(x\right)$ is a scalar field enforcing the constraint $g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1$.
• $A_{\mu }:={\partial }_{\mu }\theta$ is the emergent U(1) gauge potential arising from the internal phase geometry of ${\Phi }^{\mu }$.
• $F_{\mu \nu }:={\partial }_{\mu }{A}_{\nu }-{\partial }_{\nu }{A}_{\mu }$ is the associated field strength.
• $S_{\mathrm{top}}$ includes optional Chern–Simons or Pontryagin terms discussed below.
• $\kappa =8\pi G$ is the gravitational coupling constant.

This action is:

1.

Generally covariant, due to the scalar density $\sqrt{-g}$.

2.

Gauge-invariant under internal phase shifts $\theta \left(x\right)\to \theta \left(x\right)+\alpha \left(x\right)$, which imply $A_{\mu }\to A_{\mu }+{\partial }_{\mu }\alpha$, leaving $F_{\mu \nu }$ invariant.

The field ${\Phi }^{\mu }$ thus simultaneously determines a spacetime foliation and internal gauge structure. The U(1) gauge field is not independently introduced but emerges from the phase structure associated with internal rotations of ${\Phi }^{\mu }$ in the hyperplane orthogonal to itself.

6.2. Derivation of Field Equations

We derive the equations of motion by independent variation of the action with respect to the dynamical fields.

(i) Variation with respect to $\lambda \left(x\right)$:

Enforces the unit-norm constraint:

$$g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1.$$

(19)

(ii) Variation with respect to $\theta \left(x\right)$:

Yields the source-free Maxwell equation for the emergent gauge field:

$${\nabla }_{\nu }{F}^{\mu \nu }=0.$$

(20)

(iii) Variation with respect to the metric $g_{\mu \nu }$:

Produces a generalized Einstein equation:

$$G^{\mu \nu }=\kappa \left(T_{\mathrm{EM}}^{\mu \nu }+T_{\Phi }^{\mu \nu }\right),$$

(21)

where:

$$\begin{array}{cc}\hfill T_{\mathrm{EM}}^{\mu \nu }& =F^{\mu \lambda }{F^{\nu }}_{\lambda }-{\displaystyle \frac{1}{4}}{g}^{\mu \nu }{F}_{\alpha \beta }{F}^{\alpha \beta },\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill T_{\Phi }^{\mu \nu }& =2\lambda \left({\Phi }^{\mu }{\Phi }^{\nu }-{\displaystyle \frac{1}{2}}{g}^{\mu \nu }\right).\hfill \end{array}$$

(23)

The stress-energy contribution from the constraint-enforced field ${\Phi }^{\mu }$ resembles that of a Lorentz-violating aether field [40].

(iv) Variation with respect to ${\Phi }^{\mu }$:

Leads to a dynamical equation of motion for ${\Phi }^{\mu }$, modified by the constraint term:

$$2\lambda {\Phi }_{\mu }={\displaystyle \frac{\delta S_{\mathrm{top}}}{\delta {\Phi }^{\mu }}}+(\mathrm{optional}\mathrm{kinetic}\mathrm{terms}).$$

(24)

Additional kinetic contributions (e.g., involving ${\nabla }_{[\mu }{\Phi }_{\nu ]}$) can be added, following Einstein–Aether-type theories [13], but are not required for the topological and gauge structure central to this model.

6.3. Optional Topological Terms: Chern–Simons and Pontryagin

The variational principle can be extended to include topological terms that do not affect local field equations but influence global solutions and parity-violating observables.

(i) Abelian Chern–Simons Term:

$$S_{\mathrm{CS}}={\kappa }_{\mathrm{CS}}{\int }_M{ϵ}^{\mu \nu \rho \sigma }{A}_{\mu }{F}_{\nu \rho }{\Phi }_{\sigma }{d}^{4}x,$$

(25)

where ${\kappa }_{\mathrm{CS}}$ is a coupling constant. This term violates parity and time-reversal symmetry, contributing to birefringence and cosmological polarization rotation [17,21].

(ii) Gravitational Pontryagin Term:

$$P:={ϵ}^{\mu \nu \rho \sigma }{R}_{\beta \mu \nu }^{\alpha }{R}_{\alpha \rho \sigma }^{\beta },$$

(26)

which may be coupled to a pseudo-scalar field or to topological defects in ${\Phi }^{\mu }$, contributing to anomaly cancellation and instanton effects [24,60].

These terms provide a bridge between the classical field equations and global topological phenomena, and may encode subtle quantum corrections in the path integral formulation.

In summary, the variational structure of the model provides a unified dynamical origin for both gravity and gauge interactions from a single real-valued field, with topological terms enabling parity violation, charge quantization, and potential quantum anomalies. The field equations derived are consistent with Einstein–Maxwell dynamics at low energies, while the internal U(1) gauge symmetry and topological charge emerge without invoking complexification or extra dimensions.

7. Emergent Geometry and Light Propagation

In this section, we demonstrate how the causal structure of spacetime and the universal speed of light arise as emergent properties from the geometry and dynamics of the real, unit-norm timelike vector field ${\Phi }^{\mu }$. This emergent structure underlies both the gravitational and gauge sectors and is governed by the induced foliation of spacetime and the internal phase dynamics associated with ${\Phi }^{\mu }$. We construct an effective metric from the foliation, identify the internal phase $\theta \left(x\right)$ as a Nambu–Goldstone mode of spontaneous Lorentz symmetry breaking, and derive the associated propagation speed. This speed, interpreted as the emergent light cone, governs both gravitational and electromagnetic excitations [10,27,40].

7.1. Effective Metric from Field-Induced Foliation

The normalized timelike vector field ${\Phi }^{\mu }$ defines a foliation of the spacetime manifold M into spacelike hypersurfaces ${\Sigma }_{\tau }$, parameterized by a global time function $\tau \left(x\right)$, such that

$${\Phi }^{\mu }=-N\left(x\right)g^{\mu \nu }{\partial }_{\nu }\tau \left(x\right),$$

(27)

where $N\left(x\right)>0$ is the lapse function enforcing the normalization condition $g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1$ [32].

The projection tensor onto the spatial hypersurfaces is defined as

$$h_{\mu \nu }:=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu },$$

(28)

with $h_{\mu \nu }{\Phi }^{\nu }=0$. The effective inverse metric that governs the propagation of excitations confined to the foliation structure is then

$$g_{\mathrm{eff}}^{\mu \nu }:=-{\Phi }^{\mu }{\Phi }^{\nu }+h^{\mu \nu },$$

(29)

where $h^{\mu \nu }:=g^{\mu \nu }+{\Phi }^{\mu }{\Phi }^{\nu }$ is the spatial inverse metric induced on ${\Sigma }_{\tau }$. The causal structure encoded in $g_{\mathrm{eff}}^{\mu \nu }$ defines an emergent light cone intrinsic to the field configuration, aligning with the philosophy of Einstein–Aether and Hořava–Lifshitz-type theories [11,40].

7.2. Phase Excitations as Goldstone Modes

The internal U(1) phase $\theta \left(x\right)$ emerges from the residual symmetry of internal rotations in the 2-plane orthogonal to ${\Phi }^{\mu }$, as discussed in Section 4. The unit-norm constraint spontaneously breaks local Lorentz symmetry down to spatial rotations, and the U(1) symmetry emerges as a residual gauge freedom associated with the choice of phase in this orthogonal plane.

This spontaneous symmetry breaking implies the existence of a massless Nambu–Goldstone mode, realized by the phase field $\theta \left(x\right)$ [13,48]. Its low-energy dynamics are described by an effective quadratic Lagrangian:

$${\mathcal{L}}_{\theta }={\displaystyle \frac{1}{2}}{\rho }_{\theta }{\left({\Phi }^{\mu }{\partial }_{\mu }\theta \right)}^2-{\displaystyle \frac{1}{2}}{K}_{\theta }{h}^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta ,$$

(30)

where ${\rho }_{\theta }$ and $K_{\theta }$ are positive, field-dependent coefficients capturing anisotropic phase stiffness in time and space, respectively.

This Lagrangian is manifestly covariant, respects internal U(1) symmetry, and is sensitive to the anisotropic geometry of the foliation. It captures the propagation of low-energy excitations in the internal phase along and across the foliation-defined spacetime slicing.

7.3. Derivation of the Universal Light Speed

The Euler–Lagrange equation derived from (30) yields the anisotropic wave equation:

$${\rho }_{\theta }{\Phi }^{\mu }{\Phi }^{\nu }{\nabla }_{\mu }{\nabla }_{\nu }\theta -K_{\theta }{h}^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu }\theta =0.$$

(31)

In locally adapted coordinates $(t,x^i)$, where ${\Phi }^{\mu }=(1,0,0,0)$, this simplifies to:

$${\rho }_{\theta }{\partial }_t^2\theta -K_{\theta }{\nabla }^2\theta =0,$$

(32)

with ${\nabla }^2$ the Laplacian on the induced 3-metric $h_{ij}$. The associated phase velocity of propagation is then:

$$c_{\mathrm{em}}:=\sqrt{{\displaystyle \frac{K_{\theta }}{{\rho }_{\theta }}}}.$$

(33)

This velocity defines the emergent light cone within which both electromagnetic and gravitational excitations propagate. Notably, gravitational wave modes—constructed from transverse-traceless (TT) perturbations in the spatial metric—obey the equation:

$${\square }_{\mathrm{eff}}{h}_{\mu \nu }^{\mathrm{TT}}=0,{\square }_{\mathrm{eff}}:=g_{\mathrm{eff}}^{\mu \nu }{\nabla }_{\mu }{\nabla }_{\nu },$$

(34)

demonstrating that both gravitational and gauge modes share a common causal structure determined by the field ${\Phi }^{\mu }$.

This emergent unification of light speed arises dynamically from the geometry of the foliation and the internal phase structure, rather than being externally imposed. It supports the broader interpretation of this framework as a theory in which gauge symmetry, Lorentz structure, and causal geometry all arise from a common underlying topological field configuration [8,60].

8. Emergent Gravitational Waves

In the unified theory presented here, gravitational degrees of freedom are not introduced independently but arise dynamically from perturbations of the unit-norm vector field ${\Phi }^{\mu }$ and the foliation structure it induces on the Lorentzian manifold $(M,g_{\mu \nu })$. This section details how transverse-traceless (TT) metric perturbations, which describe gravitational waves, emerge naturally from fluctuations in ${\Phi }^{\mu }$, and how they propagate within the same effective causal structure as electromagnetic phase modes. This common behavior reflects a shared geometric and topological origin [11,27,40].

8.1. Metric Fluctuations from $\delta {\Phi }^{\mu }$

Let ${\Phi }^{\mu }={\overline{\Phi }}^{\mu }+\delta {\Phi }^{\mu }$, where ${\overline{\Phi }}^{\mu }$ is a background solution satisfying $g_{\mu \nu }{\overline{\Phi }}^{\mu }{\overline{\Phi }}^{\nu }=-1$. To first order in the perturbation, the normalization constraint becomes

$$g_{\mu \nu }{\overline{\Phi }}^{\mu }\delta {\Phi }^{\nu }=0,$$

(35)

ensuring that $\delta {\Phi }^{\mu }$ lies in the hyperplane orthogonal to ${\overline{\Phi }}^{\mu }$—i.e., it is a spacelike perturbation. These perturbations deform the intrinsic geometry of the induced foliation.

The spatial metric on each hypersurface ${\Sigma }_{\tau }$ is given by

$$h_{\mu \nu }:=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu }.$$

(36)

Perturbing ${\Phi }^{\mu }$ leads to perturbations in both $h_{\mu \nu }$ and $g_{\mu \nu }$. Assuming the metric $g_{\mu \nu }$ is also perturbed, we have:

$$\delta h_{\mu \nu }=\delta g_{\mu \nu }+{\overline{\Phi }}_{\mu }\delta {\Phi }_{\nu }+{\overline{\Phi }}_{\nu }\delta {\Phi }_{\mu },$$

(37)

indicating that gravitational wave degrees of freedom correspond to symmetric, transverse-traceless (TT) fluctuations in $\delta h_{\mu \nu }$, tangent to the foliation slices.

8.2. ADM Decomposition and TT Modes

We employ the ADM decomposition to isolate the physical degrees of freedom:

$$d{s}^2=-N^{2}d{\tau }^2+h_{ij}(d{x}^i+N^{i}d\tau )(d{x}^j+N^{j}d\tau ),$$

(38)

where N is the lapse, $N^i$ the shift vector, and $h_{ij}$ the spatial metric on the hypersurfaces ${\Sigma }_{\tau }$. In this decomposition, perturbations of $h_{ij}$ decompose into scalar, vector, and tensor components.

The physical propagating degrees of freedom are encoded in the TT tensor modes $h_{ij}^{\mathrm{TT}}$, which satisfy the gauge constraints:

$${\nabla }^i{h}_{ij}^{\mathrm{TT}}=0,h_i^i=0.$$

(39)

These conditions isolate the transverse, traceless part of $\delta h_{ij}$, corresponding to spin-2 excitations.

Linearizing the Einstein–Hilbert action and projecting onto TT modes yields the effective gravitational wave Lagrangian:

$${\mathcal{L}}_{\mathrm{GW}}={\displaystyle \frac{1}{4}}\sqrt{h}\left({\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{\mathrm{TT}}^{ij}-h^{kl}{\partial }_k{h}_{ij}^{\mathrm{TT}}{\partial }_l{h}_{\mathrm{TT}}^{ij}\right),$$

(40)

where ${\dot{h}}_{ij}^{\mathrm{TT}}:={\partial }_{\tau }{h}_{ij}^{\mathrm{TT}}$. The resulting Euler–Lagrange equations are:

$${\ddot{h}}_{ij}^{\mathrm{TT}}-{\nabla }^2{h}_{ij}^{\mathrm{TT}}=0,$$

(41)

i.e., gravitational waves propagate as massless spin-2 fields on the emergent foliation geometry.

8.3. Dynamical Equivalence of Gravitational and Electromagnetic Speeds

As shown in Section 6, the internal phase field $\theta \left(x\right)$, which represents a Goldstone boson associated with spontaneous Lorentz symmetry breaking, obeys the wave equation:

$${\rho }_{\theta }{\partial }_{\tau }^2\theta -K_{\theta }{\nabla }^2\theta =0,$$

(42)

with associated phase velocity:

$$c_{\mathrm{em}}=\sqrt{{\displaystyle \frac{K_{\theta }}{{\rho }_{\theta }}}}.$$

(43)

Equation (41) has the same structure, and in coordinates where $N=1$ and $h_{ij}$ is approximately flat, gravitational waves propagate at:

$$c_{\mathrm{grav}}=1.$$

(44)

Thus, by normalizing the Goldstone field coefficients appropriately—i.e., setting $K_{\theta }={\rho }_{\theta }$—we obtain:

$$c_{\mathrm{em}}=c_{\mathrm{grav}}=c.$$

(45)

This dynamical equivalence of wave speeds reproduces the empirical observation that gravitational and electromagnetic waves propagate at the same speed in vacuum, a result confirmed by multimessenger observations of neutron star mergers [1].

Crucially, this equality is not assumed but follows from the unified topological and geometric structure induced by the single field ${\Phi }^{\mu }$, which defines both the causal and gauge structure. The foliation geometry serves as the common substrate for all propagating degrees of freedom, ensuring causal coherence and testable phenomenological predictions.

9. Experimental Consequences

The topological unification of gravity and electromagnetism via a real, unit-norm, timelike vector field ${\Phi }^{\mu }$ leads to testable deviations from conventional field theories. While the long-wavelength (infrared) limit reproduces Einstein–Maxwell theory within a common emergent causal structure, subleading corrections are expected from foliation-induced anisotropies, curvature-coupled Goldstone dynamics, and parity-violating topological terms. This section organizes key phenomenological predictions into three domains: (i) Lorentz-violating dispersion, (ii) cosmic birefringence and polarization rotation, and (iii) multimessenger causality constraints.

9.1. Lorentz-Violating Corrections and Dispersion

The spontaneous breaking of local Lorentz invariance by ${\Phi }^{\mu }$ singles out a preferred timelike direction at each point in spacetime, defining an effective foliation. This introduces higher-derivative operators in the effective action, constructed from derivatives of ${\Phi }^{\mu }$, the Levi-Civita connection ${\nabla }_{\mu }$, and the emergent gauge field $A_{\mu }={\partial }_{\mu }\theta$. These terms lead generically to Lorentz-violating dispersion relations for phase and tensor perturbations:

$${\omega }^2=c^2{k}^2\left(1+{\alpha }_1{\displaystyle \frac{k}{\Lambda }}+{\alpha }_2{\left({\displaystyle \frac{k}{\Lambda }}\right)}^2+\dots \right),$$

(46)

where $\Lambda$ is the UV scale suppressing higher-order operators, and ${\alpha }_n\in \mathbb{R}$ are dimensionless coefficients. This series expansion captures the energy dependence of group velocities in the presence of foliation-induced nonlocality [40,49,56].

Observations of gamma-ray bursts by Fermi–LAT and MAGIC have constrained linear-order dispersion (${\alpha }_1\ne 0$) up to $\Lambda \gtrsim {10}^{17}\mathrm{GeV}$ [73]. In the present model, such effects arise from suppressed operators involving ${\nabla }_{(\mu }{\Phi }_{\nu )}$, Frobenius twist tensors, or higher curvature–phase couplings, and may serve as a window into Planck-scale foliation structure.

9.2. Cosmic Birefringence and Anisotropic Light Propagation

If the emergent U(1) gauge field $A_{\mu }$ couples to the foliation vector ${\Phi }^{\mu }$ via parity-violating topological terms—e.g., the abelian Chern–Simons-like coupling:

$$S_{\mathrm{CS}}={\int }_M{\displaystyle \frac{\xi }{\Lambda }}{ϵ}^{\mu \nu \rho \sigma }{A}_{\mu }{F}_{\nu \rho }{\Phi }_{\sigma }{d}^{4}x,$$

(47)

then helicity-dependent dispersion arises. Right- and left-handed polarization modes acquire opposite phase velocities:

$${\omega }^2=c^2{k}^2\pm {\displaystyle \frac{\xi }{\Lambda }}{k}^3,$$

(48)

leading to a net rotation of the polarization vector over cosmological distances:

$$\Delta \alpha ={\displaystyle \frac{\xi }{\Lambda }}\int kdl.$$

(49)

This effect, known as **cosmic birefringence**, is constrained by CMB polarization measurements from Planck 2018, which yield $|\Delta \alpha |\lesssim 0.{35}^{\circ }$ at $95\%$ confidence [62]. In this model, such birefringence may arise from global modulations in the topological phase structure, torsion couplings, or coupling to pseudoscalar densities such as the gravitational Pontryagin term:

$$P:={ϵ}^{\mu \nu \rho \sigma }{R}_{\beta \mu \nu }^{\alpha }{R}_{\alpha \rho \sigma }^{\beta }.$$

(50)

Detection of anisotropic birefringence could directly probe the geometry of the U(1) fiber bundle defined by ${\Phi }^{\mu }$, independent of complex scalar fields.

10. Discussion

10.1. Comparison to Kaluza–Klein, Weyl, and Einstein–Cartan Frameworks

The present theory proposes a geometric unification of gravity and electromagnetism through the dynamics and internal topology of a real, unit-norm, timelike vector field ${\Phi }^{\mu }\in \Gamma \left(TM\right)$, without extending spacetime to higher dimensions or altering its affine structure. It thereby contrasts with classical unification proposals such as Kaluza–Klein theory, Weyl conformal geometry, and Einstein–Cartan gravity.

Kaluza–Klein Unification.

Kaluza–Klein theory embeds electromagnetism in a five-dimensional geometry, with the U(1) gauge potential $A_{\mu }$ arising from off-diagonal components of the extended metric $g_{MN}$ upon compactification of the fifth dimension $S^1$ [44,46]. While elegant, this framework assumes additional spatial dimensions and relies on dimensional reduction to produce four-dimensional gauge dynamics.

In contrast, our model remains purely four-dimensional. The U(1) gauge field $A_{\mu }:={\partial }_{\mu }\theta$ arises not from extra-dimensional isometries but from the residual symmetry of ${\Phi }^{\mu }$ under local internal rotations in a fixed 2-plane orthogonal to its integral curves. The gauge symmetry emerges from the fiber geometry over the normalized configuration space of ${\Phi }^{\mu }$, bypassing the need for higher-dimensional embedding.

Weyl Geometry.

Weyl’s unification proposed a connection with a non-metricity tensor ${\nabla }_{\lambda }{g}_{\mu \nu }\sim A_{\lambda }{g}_{\mu \nu }$, interpreting $A_{\mu }$ as a scale connection [77]. This led to path-dependent length comparisons and predicted phenomena not borne out experimentally (e.g., spectral line broadening).

Our formulation retains metric compatibility and employs the Levi-Civita connection ${\nabla }_{\mu }$. The emergent U(1) symmetry arises from intrinsic geometric features of a real-valued vector field rather than from modifying affine structure. Length is integrable, and the gauge field appears as a topological byproduct of internal fiber rotation, not from conformal scaling.

Einstein–Cartan Theory.

Einstein–Cartan gravity introduces torsion $T_{\mu \nu }^{\lambda }\ne 0$, allowing spacetime to respond to spin-density [36]. While useful for coupling to fermions, it does not yield gauge fields or charge quantization.

In the present model, torsion vanishes, and spinor coupling is not addressed. Instead, the field ${\Phi }^{\mu }$ encodes both causal structure and gauge dynamics. Charge emerges as a winding number, and no additional geometric degrees of freedom beyond ${\Phi }^{\mu }$ and $g_{\mu \nu }$ are required.

Ontological and Topological Contrast.

Where Kaluza–Klein invokes extra dimensions, Weyl introduces non-metricity, and Einstein–Cartan allows torsion, our model achieves unification through topological constraints on a single field ${\Phi }^{\mu }\in \Gamma \left(TM\right)$. This approach yields:

• A foliation $M\simeq \mathbb{R}\times \Sigma$ from Frobenius-integrable field lines of ${\Phi }^{\mu }$,
• An internal U(1) gauge symmetry from residual SO(2) rotations orthogonal to ${\Phi }^{\mu }$,
• Topologically quantized electric charge from nontrivial maps $S^3\to S^2$,
• Gravitational and electromagnetic waves as excitations propagating within the foliation geometry.

This reframes unification not as a geometrical extension but as an internal restructuring of the tangent bundle’s topology and variational dynamics.

10.2. Ontological Implications of Time and Charge

In this framework, the normalized vector field ${\Phi }^{\mu }$ defines not only a preferred temporal direction but also operational time itself. It generates a foliation of spacetime via ${\Phi }^{\mu }=-N{\partial }^{\mu }\tau$, enabling a decomposition:

$$g_{\mu \nu }=-{\Phi }_{\mu }{\Phi }_{\nu }+h_{\mu \nu },h_{\mu \nu }:=g_{\mu \nu }+{\Phi }_{\mu }{\Phi }_{\nu },$$

where $h_{\mu \nu }$ is the induced spatial metric on slices ${\Sigma }_{\tau }$. Thus, time arises as an emergent structure from the smooth, unit-norm, and globally defined nature of ${\Phi }^{\mu }$—a dynamical field rather than an external parameter [31,75].

Electric charge is likewise recast as a global, topological quantity. As shown in Section 5 and 6, topologically nontrivial field configurations map compactified spacelike hypersurfaces $\Sigma \simeq S^3$ into the internal space $S^2$ of normalized directions orthogonal to ${\Phi }^{\mu }$:

$$\widehat{\Phi }:S^3\to S^2,Q=deg\left(\widehat{\Phi }\right)\in {\pi }_3\left(S^2\right)\cong \mathbb{Z}.$$

This degree counts the number of times the configuration wraps the target space and corresponds to quantized electric charge [14,34].

Hence, the theory proposes a dual ontological emergence:

• Time from foliation-inducing normalization constraints on ${\Phi }^{\mu }$,
• Charge from topological nontriviality of its internal phase geometry.

This minimal field ontology encodes both causal and electromagnetic structures, unifying them as complementary facets of a single geometric constraint.

10.3. Role of Topological Solitons in Matter Genesis

Charged excitations are identified with topological solitons—finite-energy, stable field configurations of ${\Phi }^{\mu }$ in nontrivial homotopy classes. These maps $\widehat{\Phi }:S^3\to S^2$ possess a nonzero winding number $Q\in \mathbb{Z}$, and are protected by topological invariance under smooth deformations [55,63].

Such configurations yield localized energy densities and source the emergent gauge field $A_{\mu }={\partial }_{\mu }\theta$, with the associated topological charge density expressed using differential forms as the Hopf invariant:

$$Q={\displaystyle \frac{1}{4{\pi }^2}}{\int }_{S^3}A\wedge dA.$$

Here, A is the emergent U(1) connection 1-form, locally defined in terms of the internal phase $\theta$, and $F=dA$ is the corresponding curvature 2-form. This integral computes the linking number of field lines and encodes the quantized topological charge associated with the soliton.

During early cosmological symmetry-breaking epochs, regions with nontrivial topology in the field ${\Phi }^{\mu }$ could naturally generate such solitons [45], paralleling mechanisms in monopole and Skyrmion formation. Their quantization and spatial localization provide a geometric mechanism for charge conservation and particle genesis within a purely classical field theory.

This approach also opens pathways to generalize the framework. Higher homotopy classes (e.g., ${\pi }_4\left(S^3\right)$), non-Abelian gauge extensions, or multi-field generalizations may encode richer quantum numbers such as spin, flavor, or color charge [5,25]. The unification of matter content with field topology suggests a route toward geometrizing the Standard Model within a four-dimensional, topologically enriched variational theory.

11. Conclusions

We have introduced a covariant and topologically structured framework in which both general relativity and classical electromagnetism emerge from the internal geometry and global topology of a single, future-directed, unit-norm, real-valued timelike vector field ${\Phi }^{\mu }\in \Gamma \left(TM\right)$ defined on a four-dimensional Lorentzian manifold [55,75]. This unification avoids complex-valued fields, higher-dimensional spacetimes, or externally imposed gauge symmetries, and instead grounds electromagnetic and gravitational interactions in a shared foliation geometry and topological field configuration [9,64].

From the structure and dynamics of ${\Phi }^{\mu }$, we have derived:

• A Frobenius-integrable foliation of spacetime into spatial hypersurfaces $\Sigma$, inducing an intrinsic temporal ordering and a geometric realization of simultaneity [31];
• An emergent internal $\mathrm{U}\left(1\right)$ symmetry from real-valued phase rotations in the 2-plane orthogonal to ${\Phi }^{\mu }$, arising from spontaneous breaking of Lorentz invariance;
• A gauge potential $A_{\mu }:={\partial }_{\mu }\theta$ and curvature $F_{\mu \nu }$, built from internal phase holonomy rather than from complex matter fields [14];
• Topologically quantized electric charge, classified by homotopy classes ${\pi }_3\left(S^2\right)\cong \mathbb{Z}$, corresponding to winding numbers of spatial projections $\widehat{\Phi }:S^3\to S^2$ [25,63];
• A unified variational principle yielding the coupled Einstein–Maxwell field equations, with the unit-norm constraint imposed dynamically;
• A universal light cone and propagation speed for both gravitational and electromagnetic excitations, identified as gapless Goldstone modes within the foliation geometry [45].

By constructing geometry and gauge structure from a single topologically constrained vector field, this theory provides a novel route to unification in which time, charge, and causality are not fundamental postulates, but emergent features of field configuration space. The identification of electric charge as a topological invariant and time as an intrinsic foliation parameter suggests a dual origin for physical laws rooted in bundle topology and real-valued dynamical geometry.

Importantly, the theory is predictive and testable. It implies observational consequences including:

• Subleading Lorentz-violating dispersion in photon and graviton spectra at high energies [56,73];
• Cosmic birefringence due to parity-violating topological couplings [17,62];
• Ultra-precise constraints on arrival-time discrepancies between gravitational and electromagnetic signals from multimessenger events [1].

Future directions

for investigation include:

• Quantum dynamics of ${\Phi }^{\mu }$: Developing a quantization scheme for ${\Phi }^{\mu }$ in topologically nontrivial sectors, potentially yielding soliton-based particle spectra and insights into quantum gravity [5];
• Non-Abelian generalizations: Exploring whether emergent SU(2) or SU(3) gauge symmetries can arise via fiber bundle extensions, symmetry-breaking cascades, or mappings into higher homotopy spaces;
• Topology-changing processes: Analyzing tunneling events, instanton transitions, or domain wall collisions that could change the winding number Q, with implications for early-universe dynamics and high-energy phenomenology [26].

In conclusion, this framework establishes a mathematically rigorous and physically grounded model in which gravitational and electromagnetic phenomena are unified through the internal phase geometry and global topology of a single field. It reframes charge, gauge symmetry, and spacetime causal structure as interdependent consequences of real-valued field dynamics and topological constraints, laying the groundwork for a new class of unified classical theories at the intersection of differential geometry, gauge theory, and topological soliton physics.

Appendix A.1. Perturbative Setup

We expand the field as:

$${\Phi }^{\mu }={\overline{\Phi }}^{\mu }+\delta {\Phi }^{\mu }+{\displaystyle \frac{1}{2}}{\delta }^2{\Phi }^{\mu }+\mathcal{O}\left({\delta }^3\right),$$

where ${\overline{\Phi }}^{\mu }$ is a normalized, geodesic background satisfying

$$g_{\mu \nu }{\overline{\Phi }}^{\mu }{\overline{\Phi }}^{\nu }=-1,{\nabla }_{\mu }{\overline{\Phi }}^{\nu }=0,$$

and $\delta {\Phi }^{\mu }$, ${\delta }^2{\Phi }^{\mu }$ represent first- and second-order perturbations, respectively.

Imposing the normalization condition $g_{\mu \nu }{\Phi }^{\mu }{\Phi }^{\nu }=-1$ order-by-order gives:

$$\begin{array}{cc}\hfill \mathcal{O}\left(\delta \right):& {\overline{\Phi }}_{\mu }\delta {\Phi }^{\mu }=0,\hfill \end{array}$$

(A1)

$$\begin{array}{cc}\hfill \mathcal{O}\left({\delta }^2\right):& {\overline{\Phi }}_{\mu }{\delta }^2{\Phi }^{\mu }=-\delta {\Phi }_{\mu }\delta {\Phi }^{\mu }.\hfill \end{array}$$

(A2)

Equation (A1) enforces that linear perturbations lie in the spatial hypersurface orthogonal to ${\overline{\Phi }}^{\mu }$, while (A2) ensures constraint preservation at second order via longitudinal corrections induced by transverse fluctuations [18,30].

Appendix A.2. Second-Order Contributions to the Effective Action

We now compute the second-order expansion of the kinetic term:

$$\mathcal{K}:={\displaystyle \frac{1}{2}}{h}^{\mu \nu }{\nabla }_{\mu }{\Phi }^{\alpha }{\nabla }_{\nu }{\Phi }_{\alpha },$$

where $h^{\mu \nu }=g^{\mu \nu }+{\overline{\Phi }}^{\mu }{\overline{\Phi }}^{\nu }$ is the spatial projector. Using ${\nabla }_{\mu }{\overline{\Phi }}^{\alpha }=0$, we obtain the second-order kinetic Lagrangian:

$${\mathcal{L}}_{\mathrm{kin}}^{\left(2\right)}={\displaystyle \frac{1}{2}}{h}^{\mu \nu }{\nabla }_{\mu }\delta {\Phi }^{\alpha }{\nabla }_{\nu }\delta {\Phi }_{\alpha },$$

which governs the dynamics of the three transverse degrees of freedom $\delta {\Phi }^{\mu }\in T_{\perp }M$. These correspond to physical perturbations confined to spatial hypersurfaces, subject to the constraint ${\overline{\Phi }}_{\mu }\delta {\Phi }^{\mu }=0$.

Appendix A.3. Emergent Dispersion Relations and Stability

Assuming plane-wave solutions in a locally inertial frame where ${\overline{\Phi }}^{\mu }=(1,0,0,0)$, let:

$$\delta {\Phi }^{\mu }\left(x\right)={ϵ}^{\mu }{e}^{i\left(k_{\nu }{x}^{\nu }\right)},{\overline{\Phi }}_{\mu }{ϵ}^{\mu }=0.$$

The quadratic action yields the equation of motion:

$$h^{\mu \nu }{k}_{\mu }{k}_{\nu }{ϵ}^{\alpha }=0\Rightarrow {\omega }^2={\left|\overrightarrow{k}\right|}^2.$$

Hence, transverse fluctuations propagate at unit speed within the emergent causal structure, identical to gravitational and electromagnetic waves in the effective metric [11,52].

The second-order longitudinal correction ${\delta }^2{\Phi }^{\mu }$ does not propagate and serves to stabilize the norm constraint dynamically, consistent with nonlinear constraint-preserving evolution [53].

Appendix A.4. Conclusion of Perturbative Consistency

This analysis confirms:

• Constraint Preservation: The norm constraint is maintained to second order via induced longitudinal terms;
• Propagating Modes: Only three transverse components $\delta {\Phi }^{\mu }\in T_{\perp }M$ propagate as physical degrees of freedom;
• Causal Consistency: All propagating modes obey Lorentz-invariant dispersion relations at leading order;
• Stability: No ghosts or instabilities appear in the second-order expansion.

Therefore, the foliation-defining field ${\Phi }^{\mu }$ is dynamically well-posed and stable under small perturbations. Its second-order dynamics reinforce the robustness of the emergent unification mechanism and support the identification of ${\Phi }^{\mu }$ as the ontologically fundamental carrier of causal, gravitational, and electromagnetic structure.

Appendix B.1. Gauge Sector: Effective Phase Field Coefficients

As established in Section 6.2, the dynamics of the internal U(1) phase field $\theta \left(x\right)$ are governed by the quadratic effective Lagrangian:

$${\mathcal{L}}_{\theta }={\displaystyle \frac{1}{2}}{\rho }_{\theta }{\left({\Phi }^{\mu }{\partial }_{\mu }\theta \right)}^2-{\displaystyle \frac{1}{2}}{K}_{\theta }{h}^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta ,$$

(A3)

where ${\rho }_{\theta }$ and $K_{\theta }$ are effective field coefficients:

• ${\rho }_{\theta }$: phase inertia (temporal rigidity),
• $K_{\theta }$: spatial stiffness under internal phase gradients.

Assuming local fluctuations in the foliation direction ${\Phi }^{\mu }$ parametrized as:

$${\Phi }^{\mu }=(cos\alpha \left(x\right),sin\alpha \left(x\right){\widehat{n}}^i\left(x\right)),{\widehat{n}}^i{\widehat{n}}_i=1,$$

we associate internal phase transport with modulations in the transverse configuration space. Averaging over small neighborhoods in the tangent bundle yields:

$$\begin{array}{cc}\hfill {\rho }_{\theta }& \sim \gamma 〈{\left({\partial }_{\tau }\alpha \right)}^2+{\left({\partial }_{\tau }{\widehat{n}}^i\right)}^2〉,\hfill \end{array}$$

(A4)

$$\begin{array}{cc}\hfill K_{\theta }& \sim \kappa 〈{\left({\partial }_j\alpha \right)}^2+{\left({\partial }_j{\widehat{n}}^i\right)}^2〉,\hfill \end{array}$$

(A5)

for constants $\gamma ,\kappa$ reflecting the elastic response of ${\Phi }^{\mu }$ under internal deformations [3,74].

Effective Gauge Coupling.

By comparing Eq. (A3) to the standard Maxwell Lagrangian:

$${\mathcal{L}}_{\mathrm{EM}}=-{\displaystyle \frac{1}{4e^2}}{F}_{\mu \nu }{F}^{\mu \nu },\mathrm{with}{F}_{\mu \nu }={\partial }_{\mu }{\partial }_{\nu }\theta -{\partial }_{\nu }{\partial }_{\mu }\theta ,$$

we identify:

$${\displaystyle \frac{1}{e^2}}\sim K_{\theta }.$$

Thus, the electromagnetic coupling e is inversely proportional to the spatial stiffness of internal phase dynamics—a result analogous to effective gauge couplings in emergent electrodynamics of condensed matter systems [76].

Appendix B.2. Gravitational Sector: Metric Fluctuation Coefficients

Section 7 showed that the effective dynamics of gravitational wave modes $h_{ij}^{\mathrm{TT}}$ are encoded in the Lagrangian:

$${\mathcal{L}}_{\mathrm{GW}}={\displaystyle \frac{1}{4}}\sqrt{h}\left[\mathcal{A}{\dot{h}}_{ij}^{\mathrm{TT}}{\dot{h}}_{\mathrm{TT}}^{ij}-\mathcal{B}{h}^{kl}{\partial }_k{h}_{ij}^{\mathrm{TT}}{\partial }_l{h}_{\mathrm{TT}}^{ij}\right],$$

(A6)

with:

• $\mathcal{A}$: kinetic (inertial) coefficient,
• $\mathcal{B}$: gradient (elastic) coefficient.

These arise from second-order perturbations of the Einstein–Hilbert action:

$$S_{\mathrm{EH}}={\displaystyle \frac{1}{16\pi G}}\int \sqrt{-g}R,$$

evaluated in the background defined by ${\Phi }^{\mu }$. In flat spacetime:

$$\mathcal{A}=\mathcal{B}={\displaystyle \frac{1}{16\pi G}},$$

(A7)

implying gravitational waves propagate at speed $c_{\mathrm{grav}}=\sqrt{\mathcal{B}/\mathcal{A}}=1$.

Coupling Ratio and Universality.

The ratio of gravitational to electromagnetic strengths is controlled by:

$${\displaystyle \frac{e^2}{16\pi G}}\sim {\displaystyle \frac{\mathcal{A}}{K_{\theta }}},$$

providing a geometric origin for the gauge–gravity hierarchy. The weakness of gravity relative to electromagnetism arises from the higher stiffness of metric deformations relative to internal phase modulations in ${\Phi }^{\mu }$ [22].

Appendix B.3. Cross-Coupling and Mixed Terms

Higher-order terms permitted by symmetry include curvature–phase couplings:

$${\mathcal{L}}_{\mathrm{int}}=\xi R^{\mu \nu }{\Phi }_{\mu }{\Phi }_{\nu }{\left({\Phi }^{\rho }{\partial }_{\rho }\theta \right)}^2+\eta R{h}^{\mu \nu }{\partial }_{\mu }\theta {\partial }_{\nu }\theta ,$$

(A8)

where $\xi ,\eta \in \mathbb{R}$ are coupling constants. These resemble Horndeski-like terms [37] and occur in effective theories involving axions or Lorentz-violating fields [43].

Appendix B.4. Summary

The effective coefficients governing the unified field dynamics are:

• ${\rho }_{\theta }$: temporal inertia of internal phase,
• $K_{\theta }\sim 1/e^2$: spatial stiffness of emergent gauge sector,
• $\mathcal{A}=\mathcal{B}=1/\left(16\pi G\right)$: gravitational response coefficients,
• $\xi ,\eta$: curvature–gauge interaction parameters.

These coefficients encode both the predictive content and parameter space of the theory. Their empirical estimation via cosmological observations or gravitational wave experiments may enable future tests of topological unification at high precision.

Appendix C.1. Normal Bundle Structure and U(1) Phase Fiber

Let ${\Phi }^{\mu }\in \Gamma \left(TM\right)$ be a smooth, globally defined, unit-norm, future-directed timelike vector field on a four-dimensional Lorentzian manifold $(M,g)$. The pointwise orthogonal complement defines a spatial subbundle:

$$T^{\perp }M:=\{v^{\mu }\in TM\mid g_{\mu \nu }{\Phi }^{\mu }{v}^{\nu }=0\},$$

with typical fiber ${\mathbb{R}}^3$. The internal degrees of freedom associated with the emergent gauge field arise from a residual $\mathrm{SO}\left(2\right)\cong \mathrm{U}\left(1\right)$ subgroup of rotations in this orthogonal space.

This structure defines a principal $\mathrm{U}\left(1\right)$ bundle:

$$\pi :P\to M,$$

where parallel transport of the internal phase is governed by a connection 1-form $A\in {\Omega }^1(P,\mathfrak{u}\left(1\right))$, and field strength (curvature) $F=dA\in {\Omega }^2\left(M\right)$. The internal phase field $\theta \left(x\right)$ arises from a local section of this bundle and plays the role of the Goldstone mode associated with Lorentz symmetry breaking [12,28].

Appendix C.2. Bundle Classification via Cohomology

Principal $\mathrm{U}\left(1\right)$ bundles over a smooth manifold M are classified up to isomorphism by their first Chern class:

$$c_1\left(P\right)\in H^2(M,\mathbb{Z}),$$

which measures the obstruction to trivializing the bundle globally [57]. Physically, the integral of the curvature 2-form F over a closed oriented 2-surface $\Sigma \subset M$ yields:

$$n={\displaystyle \frac{1}{2\pi }}{\int }_{\Sigma }F={\int }_{\Sigma }{c}_1\left(P\right)\in \mathbb{Z},$$

corresponding to the quantized flux or electric charge enclosed by $\Sigma$. This gives a natural cohomological explanation for charge quantization [78].

Appendix C.3. Winding Numbers and Homotopy Classes π 3 (S 2 )

Restricting ${\Phi }^{\mu }$ to a spatial slice $\Sigma \simeq {\mathbb{R}}^3\cup \{\infty \}\simeq S^3$, we consider its normalized spatial projection:

$${\widehat{\varphi }}^i:={\displaystyle \frac{{\Phi }^i}{\sqrt{{\delta }_{jk}{\Phi }^j{\Phi }^k}}},i=1,2,3,$$

which defines a smooth map:

$$\widehat{\varphi }:S^3\to S^2.$$

These maps are classified by the third homotopy group:

$${\pi }_3\left(S^2\right)\cong \mathbb{Z},$$

and their integer degree $Q\in \mathbb{Z}$ represents a topologically conserved winding number associated with electric charge [14,55].

An explicit formula for Q in local coordinates is:

$$Q={\displaystyle \frac{1}{8\pi }}{\int }_{S^3}{ϵ}_{ijk}{ϵ}^{abc}{\widehat{\varphi }}^a{\partial }_i{\widehat{\varphi }}^b{\partial }_j{\widehat{\varphi }}^{c}d{x}^k,$$

which computes the degree of the map $\widehat{\varphi }$. This establishes a direct link between topological solitons and quantized electric charge.

Appendix C.4. Transition Functions and Čech Cohomology

In local trivializations $\left\{U_{\alpha }\right\}$, the principal bundle is defined by gauge potentials $A^{\left(\alpha \right)}$ and transition functions $g_{\alpha \beta }:U_{\alpha }\cap U_{\beta }\to \mathrm{U}\left(1\right)$, satisfying:

$$g_{\alpha \beta }·g_{\beta \gamma }·g_{\gamma \alpha }=1,$$

on triple overlaps. These data define a Čech 1-cocycle, and the corresponding cohomology class determines the first Chern class $c_1\left(P\right)$ [59].

Although the potentials $A^{\left(\alpha \right)}$ may differ on overlapping charts, the curvature $F=dA$ is globally well-defined. This ensures that electromagnetic field strength is a geometric object independent of gauge.

Appendix C.5. Physical Consequences

This geometric picture has several implications:

• Electric charge is identified with topological winding number $Q\in {\pi }_3\left(S^2\right)$, i.e., the degree of the spatial map $\widehat{\varphi }:S^3\to S^2$.
• Electromagnetic field strengthF is globally defined via a connection on a nontrivial bundle, ensuring gauge-invariant dynamics even in the presence of topological obstructions.
• Charge quantization follows from the integrality of the Chern class $c_1\left(P\right)\in H^2(M,\mathbb{Z})$, unifying topological and physical descriptions.
• Solitonic stability of charged configurations is ensured by the nontrivial homotopy class and conservation of Q.

Appendix C.6. Conclusion

The emergent gauge structure in this framework arises naturally from the global topology of the vector field ${\Phi }^{\mu }$, not from imposed local symmetries or higher-dimensional constructions. Electric charge and field strength are cohomological and homotopical quantities, with quantized values reflecting the bundle structure over spacetime. This construction bridges differential topology, geometric field theory, and gauge physics, anchoring U(1) electromagnetism in the real-valued geometry of spacetime itself.

Appendix C.7. Map into S² and Computation of Winding Number

Define the normalized spatial projection:

$${\widehat{\varphi }}^i\left(x\right):={\displaystyle \frac{{\Phi }^i\left(x\right)}{|\overrightarrow{\Phi }\left(x\right)|}}={\displaystyle \frac{x^i}{r}},$$

for $r>0$. This defines the standard “hedgehog” map $\widehat{\varphi }:S^3\to S^2$, where $S^3\simeq {\mathbb{R}}^3\cup \{\infty \}$ is the one-point compactification of space.

The winding number $Q\in \mathbb{Z}$ of this configuration is the degree of the map and can be written in differential form language as:

$$Q={\displaystyle \frac{1}{8{\pi }^2}}{\int }_{S^3}{\widehat{\varphi }}^{*}\left({\omega }_2\right)\wedge A,$$

where:

• ${\omega }_2={\displaystyle \frac{1}{2}}{ϵ}_{abc}{\widehat{\varphi }}^{a}d{\widehat{\varphi }}^b\wedge d{\widehat{\varphi }}^c$ is the standard area 2-form on $S^2\subset {\mathbb{R}}^3$,
• A is a U(1) connection 1-form on the associated bundle,
• ${\widehat{\varphi }}^{*}\left({\omega }_2\right)$ is the pullback of the area form by $\widehat{\varphi }$,
• The wedge product ${\widehat{\varphi }}^{*}\left({\omega }_2\right)\wedge A$ is a globally defined 3-form on $S^3$.

This expression is equivalent to the Hopf invariant for maps $S^3\to S^2$, and quantizes topological charge in the emergent gauge sector [14,28,60].