Submitted:
22 August 2025
Posted:
27 August 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methodology
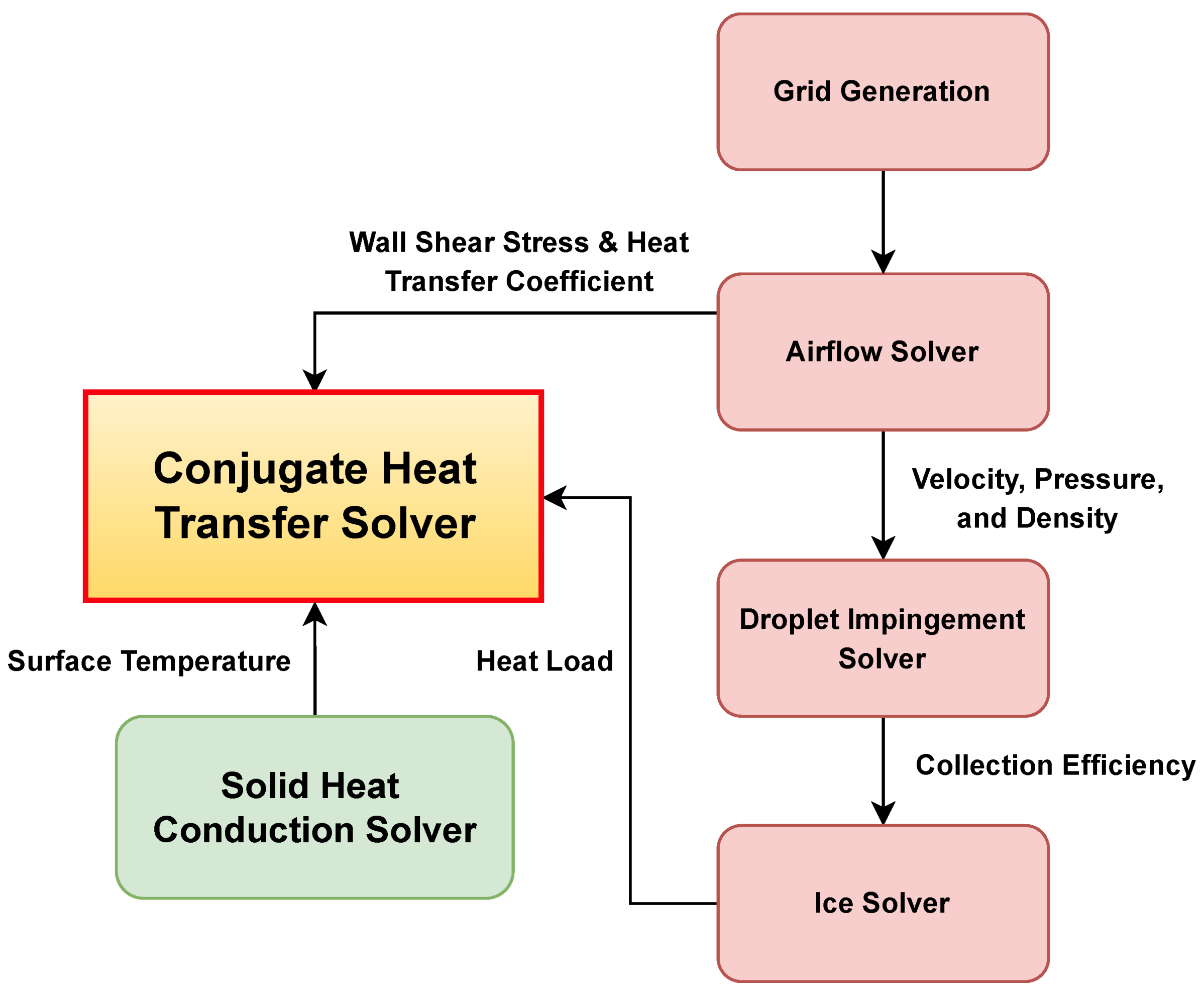
2.1. Governing Equations for the Icing/De-icing Model
2.2. Numerical model setup and validation
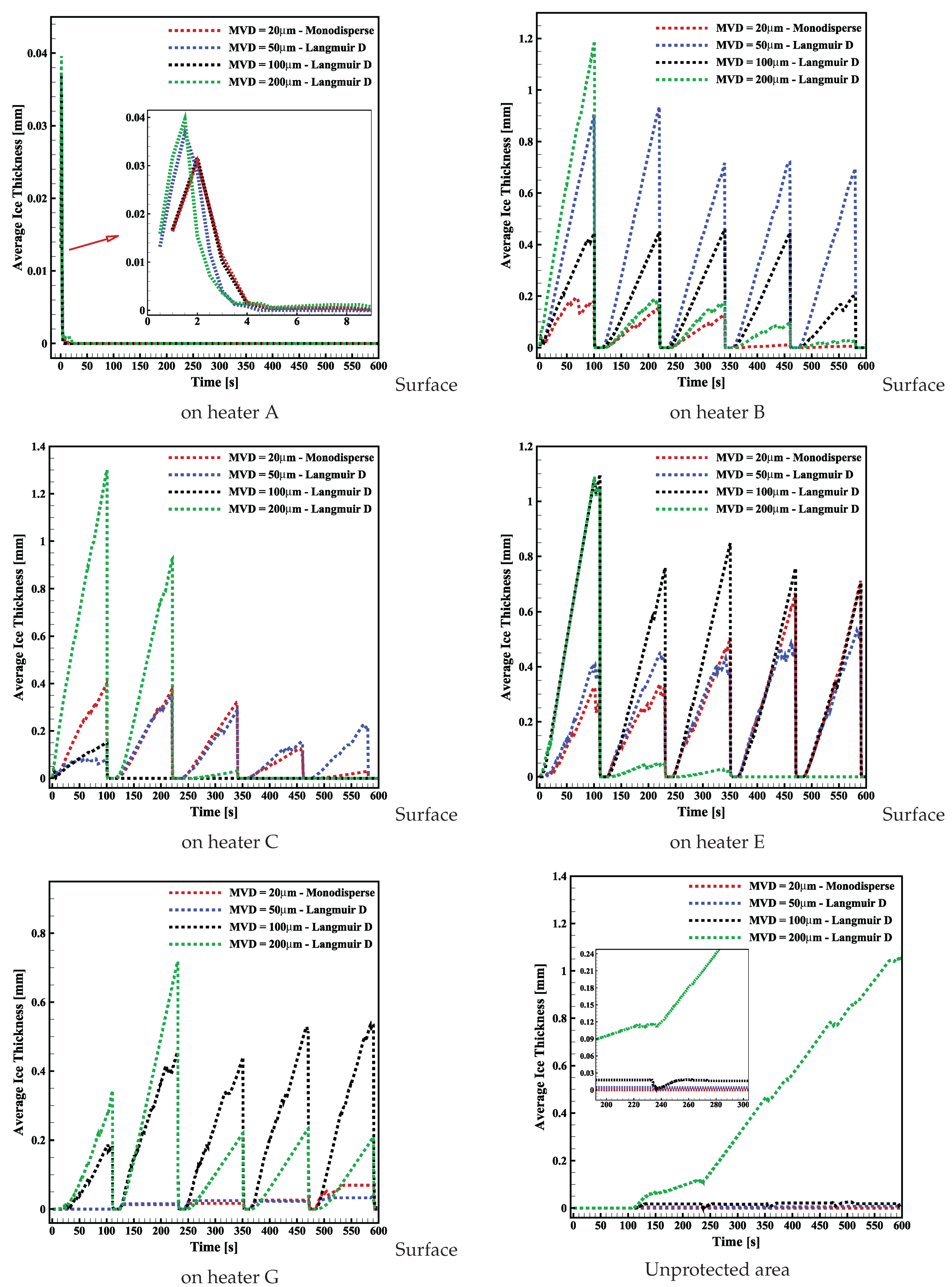
| Class i | Ratio /MVD | Weight Fraction [] (%) |
|---|---|---|
| 1 | 0.31 | 5 |
| 2 | 0.52 | 10 |
| 3 | 0.71 | 20 |
| 4 | 1.00 | 30 |
| 5 | 1.37 | 20 |
| 6 | 1.74 | 10 |
| 7 | 2.22 | 5 |
| Case | LWC | MVD | AOA | Roughness Height | Icing Time | ||
|---|---|---|---|---|---|---|---|
| [K] | [m/s] | [g/m3] | [m] | [deg] | [m] | [min] | |
| Normal Flight Condition | |||||||
| Case 1 | 266.483 | 44.704 | 0.78 | 20 | 0 | 500 | 10 |
| Case 2 | 266.483 | 44.704 | 0.78 | 20 | -4 | 500 | 10 |
| Case 3 | 266.483 | 44.704 | 0.78 | 20 | 4 | 500 | 10 |
| Case 4 | 266.483 | 44.704 | 0.78 | 20 | 8 | 500 | 10 |
| Case 5 | 266.483 | 44.704 | 0.78 | 20 | 12 | 500 | 10 |
| Harsh Flight Condition | |||||||
| Case 6 | 266.483 | 44.704 | 0.78 | 50 | 0 | 500 | 10 |
| Case 7 | 266.483 | 44.704 | 0.78 | 100 | 0 | 500 | 10 |
| Case 8 | 266.483 | 44.704 | 0.78 | 200 | 0 | 500 | 10 |
3. Results and Discussion
3.1. Simulation of Ice Accretion Without De-Icing
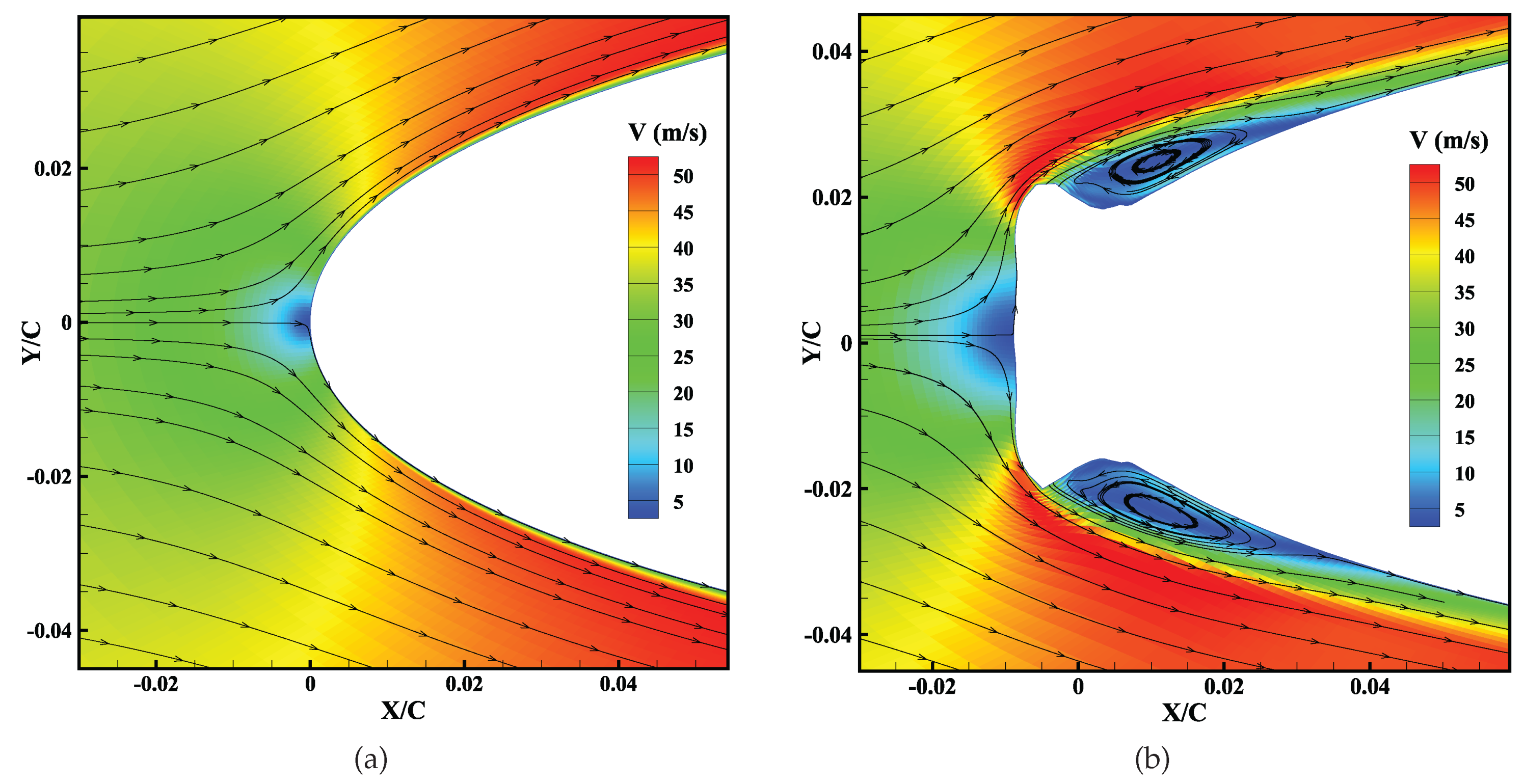
3.2. Aerodynamics Degradation
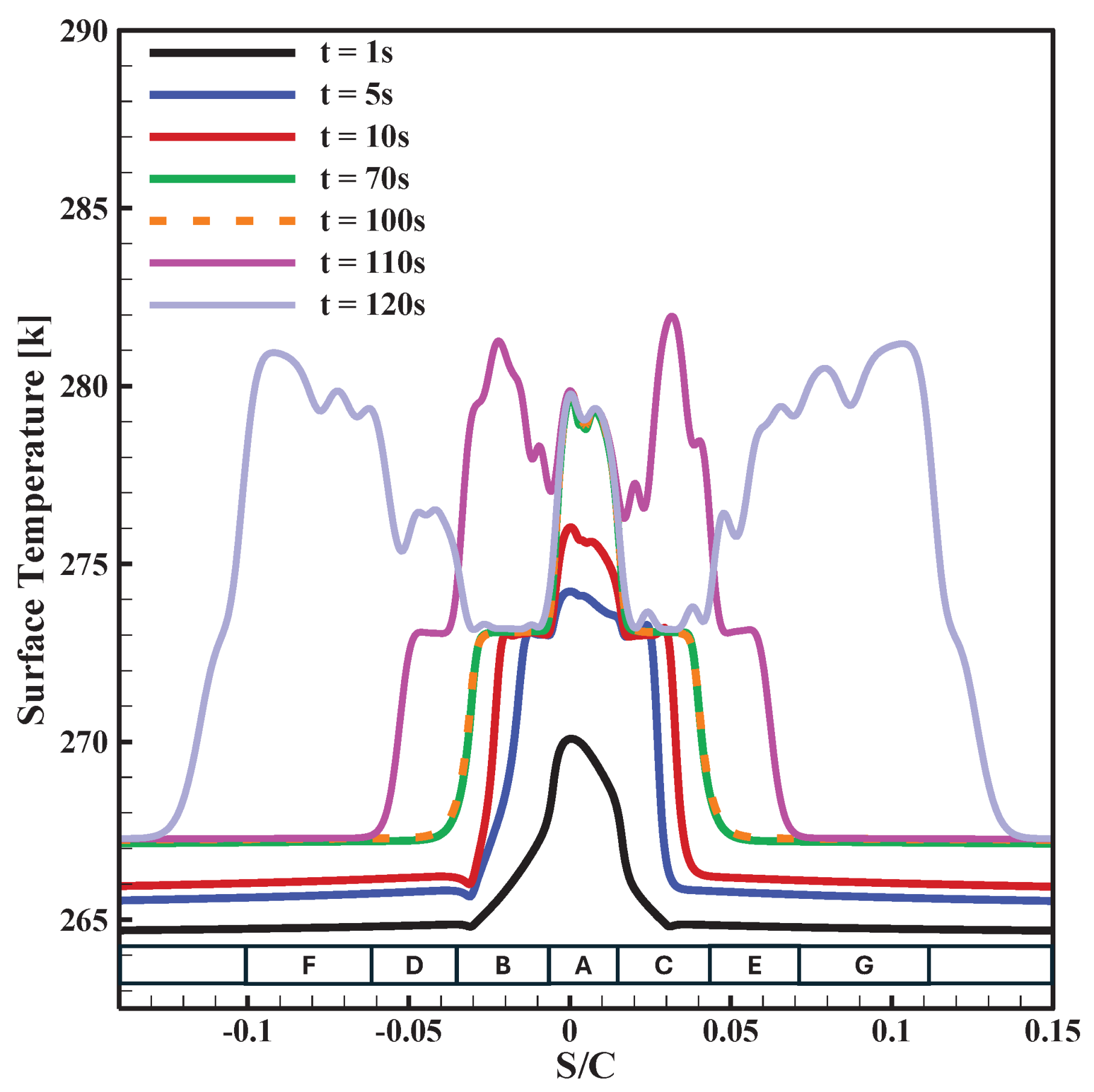
3.3. Analysis of electro-thermal de-icing system in normal icing conditions
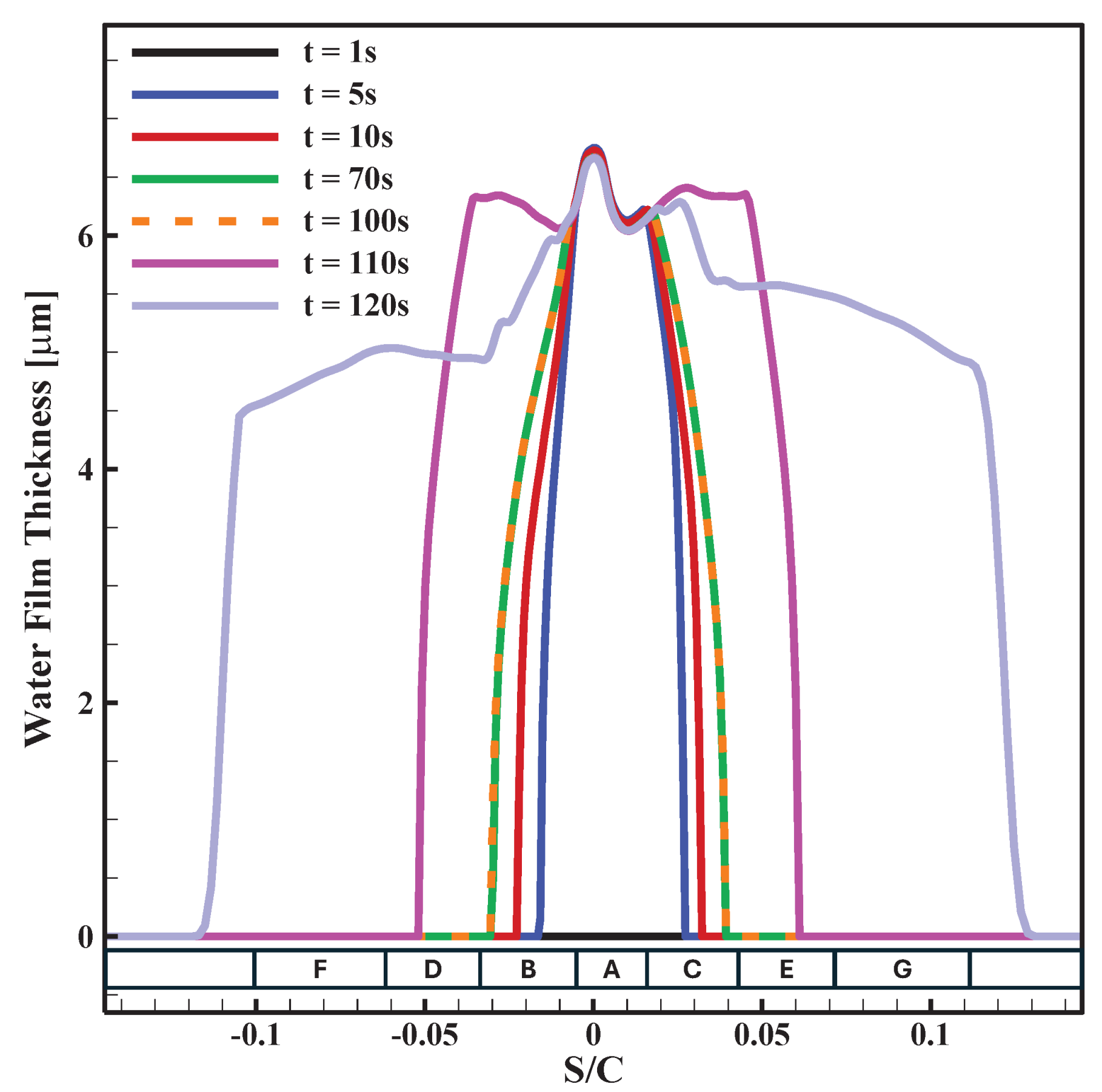
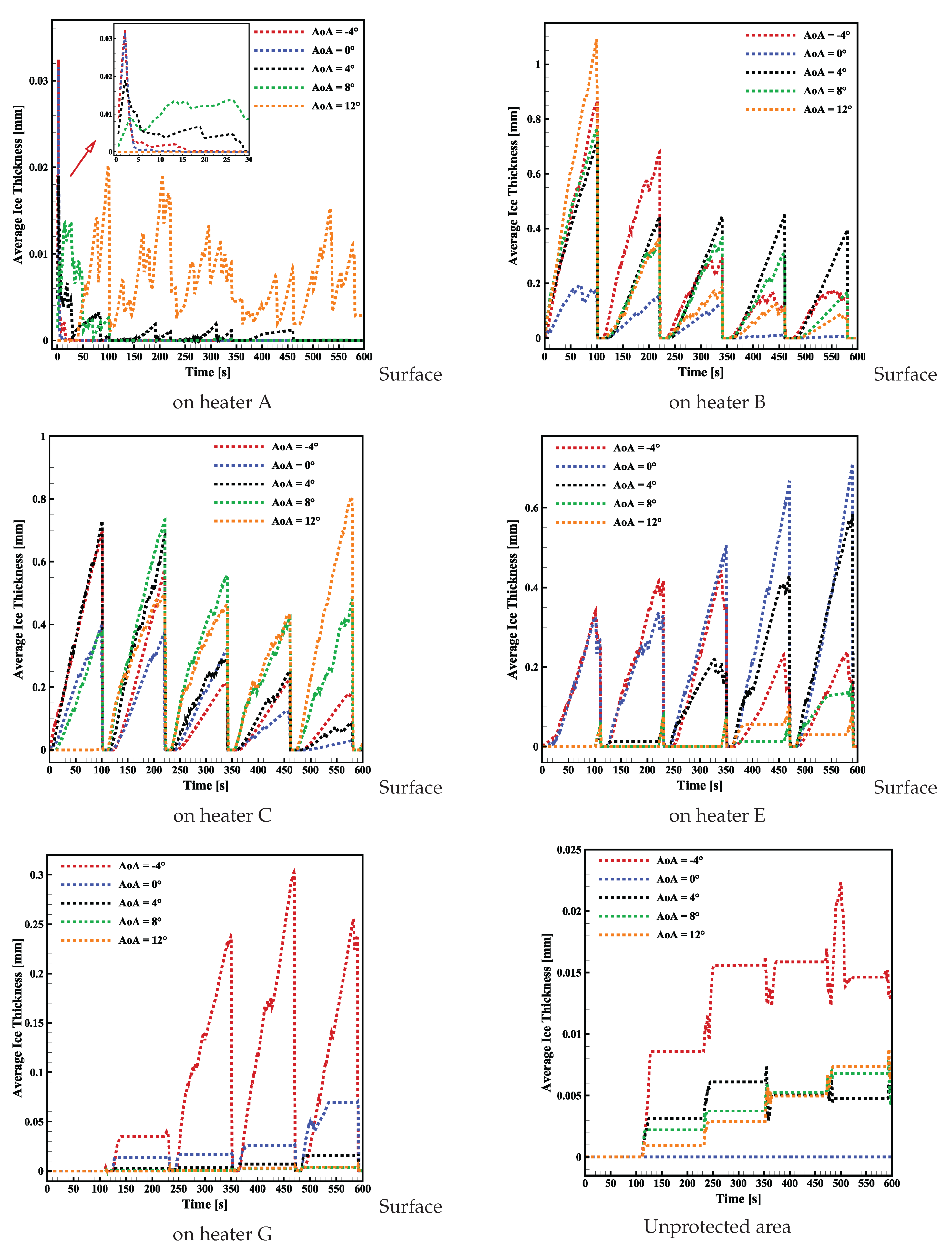
3.4. Analysis of Electro-Thermal De-Icing System at Various Angles of Attack
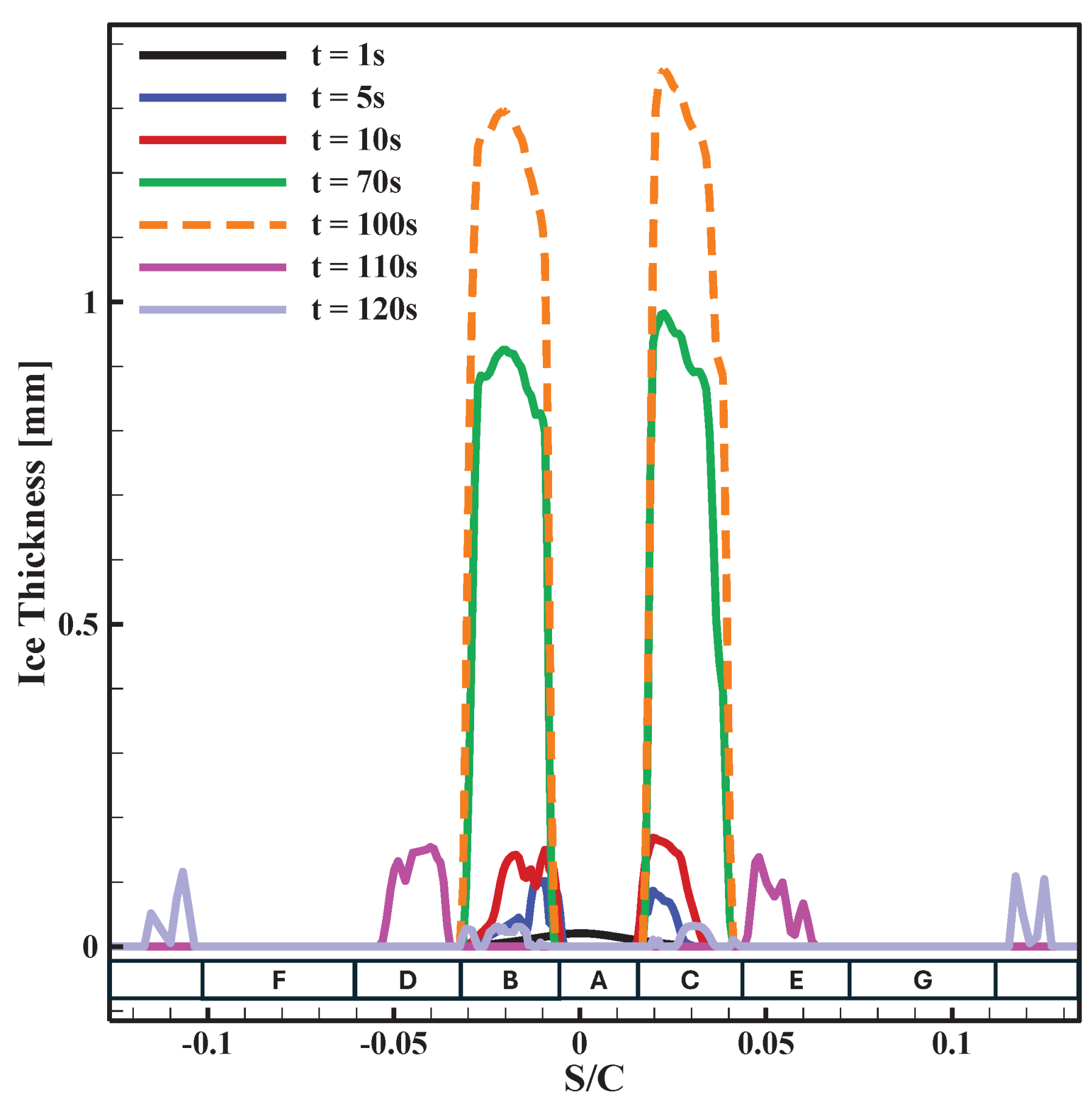
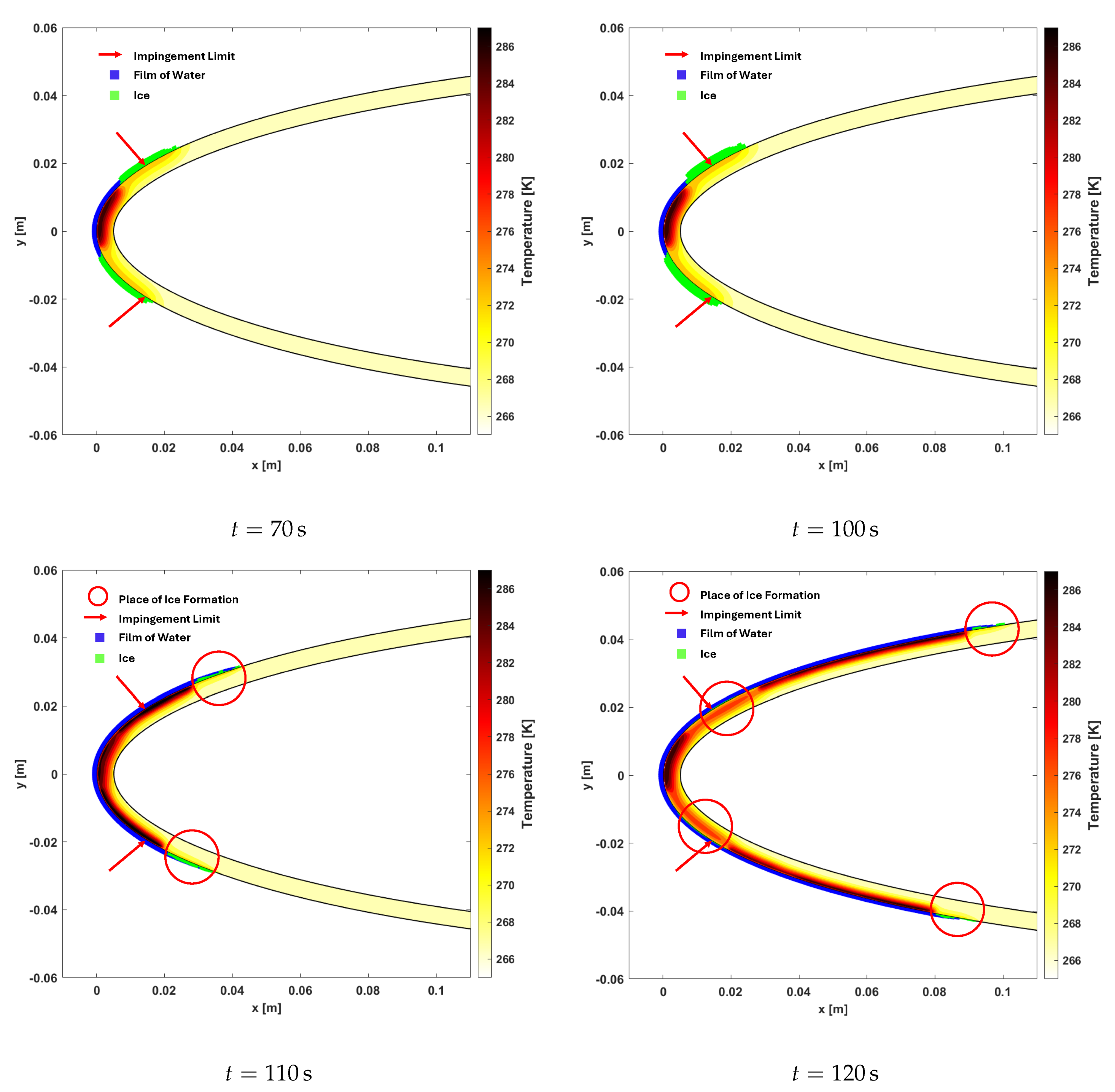
3.5. Analysis of Electro-Thermal De-Icing System in Harsh SLD Condition
4. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameters | |
| Convective heat-transfer coefficient [W ] | |
| Specific heat [J ] | |
| Energy of droplet [J] | |
| h | Thickness [m] |
| L | Latent heat [J kg] |
| LWC | Liquid water content [kg ] |
| Mass transfer rate [kg s] | |
| Q | Heat flux [W m] |
| T | Temperature [K] |
| Mean velocity [m s] | |
| Velocity vector [m ] | |
| Water volume fraction | |
| Weber number | |
| Ohnesorge number | |
| Droplet’s surface tension | |
| Mundo parameter | |
| Cossali parameter | |
| Boltzmann constant [W ] | |
| Solid emissivity | |
| Collection efficiency | |
| Froude Number | |
| Drag coefficient | |
| Droplet Reynolds number | |
| K | Inertial parameter |
| Dynamic viscosity [Pa s] | |
| Wall shear stress [Pa] | |
| Enthalpy change [J] | |
| S | Curvilinear arc length along the airfoil surface from the leading-edge [m] |
| C | Chord length (leading edge to trailing edge) [m] |
| Subscripts | |
| a | Air |
| d | Droplet |
| evap | Evaporation |
| f | Water film |
| rec | Recovery |
| ∞ | Reference (freestream) |
References
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerospace science and technology 2018, 75, 353–385. [Google Scholar] [CrossRef]
- Kong, W.; Liu, H. Unified icing theory based on phase transition of supercooled water on a substrate. International Journal of Heat and Mass Transfer 2018, 123, 896–910. [Google Scholar] [CrossRef]
- Zhao, Y.; Guo, Q.; Lin, T.; Cheng, P. A review of recent literature on icing phenomena: Transport mechanisms, their modulations and controls. International Journal of Heat and Mass Transfer 2020, 159, 120074. [Google Scholar] [CrossRef]
- Bourgault, Y.; Beaugendre, H.; Habashi, W.G. Development of a shallow-water icing model in FENSAP-ICE. Journal of Aircraft 2000, 37, 640–646. [Google Scholar] [CrossRef]
- Nath, P.; Lokanathan, N.; Wang, J.; Benmeddour, A.; Nichman, L.; Ranjbar, K.; Hickey, J.P. Parametric investigation of aerodynamic performance degradation due to icing on a symmetrical airfoil. Physics of Fluids 2024, 36. [Google Scholar] [CrossRef]
- Lu, H.; Xu, Y.; Li, H.; Zhao, W. Numerical study on glaze ice accretion characteristics over time for a NACA 0012 airfoil. Coatings 2023, 14, 55. [Google Scholar] [CrossRef]
- Esmaeilifar, E.; Raj, L.P.; Myong, R. Computational simulation of aircraft electrothermal de-icing using an unsteady formulation of phase change and runback water in a unified framework. Aerospace Science and Technology 2022, 130, 107936. [Google Scholar] [CrossRef]
- Rausa, A.; Guardone, A. Multi-physics simulation of in-flight ice shedding. In Proceedings of the Journal of Physics: Conference Series. IOP Publishing, 2021, Vol. 1730, p. 012024.
- Sengupta, B.; Raj, L.P.; Cho, M.; Son, C.; Yoon, T.; Yee, K.; Myong, R. Computational simulation of ice accretion and shedding trajectory of a rotorcraft in forward flight with strong rotor wakes. Aerospace Science and Technology 2021, 119, 107140. [Google Scholar] [CrossRef]
- Farabello, L.; Scarabino, A.; Bacchi, F. Numerical analysis of ice accretion on an airfoil: A case study. Revista Facultad de Ingeniería Universidad de Antioquia 2025.
- Mousavi, S.M.; Sotoudeh, F.; Chun, B.; Lee, B.J.; Karimi, N.; Faroughi, S.A. The potential for anti-icing wing and aircraft applications of mixed-wettability surfaces-A comprehensive review. Cold Regions Science and Technology 2024, 217, 104042. [Google Scholar] [CrossRef]
- Janjua, Z.A.; Turnbull, B.; Hibberd, S.; Choi, K.S. Mixed ice accretion on aircraft wings. Physics of Fluids 2018, 30. [Google Scholar] [CrossRef]
- Bodoc, V.; Berthoumieu, P.; Déjean, B. Experimental investigation of large droplet impact with application to SLD icing. Microgravity Science and Technology 2021, 33, 59. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, F.; Kong, W.; Liu, H. The Characteristics of SLD icing accretions and aerodynamic effects on high-lift configurations. In Proceedings of the 33rd AIAA Applied Aerodynamics Conference; 2015; p. 3385. [Google Scholar]
- Yamazaki, M.; Jemcov, A.; Sakaue, H. A review on the current status of icing physics and mitigation in aviation. Aerospace 2021, 8, 188. [Google Scholar] [CrossRef]
- Lee, J.W.; Cho, M.Y.; Kim, Y.H.; Yee, K.; Myong, R.S. Current status and prospect of aircraft ice protection systems. Journal of the Korean Society for Aeronautical & Space Sciences 2020, 48, 911–925. [Google Scholar] [CrossRef]
- Gallia, M.; Carnemolla, A.; Premazzi, M.; Guardone, A. Optimisation of a Nacelle Electro-Thermal Ice Protection System for Icing Wind Tunnel Testing. Transactions on Aerospace Research 2023, 2023, 32–44. [Google Scholar] [CrossRef]
- Tormen, D.; Zanon, A.; De Gennaro, M. Ice Protection System Design for the Next Generation Civil Tiltrotor Engine Intake. Technical report, SAE Technical Paper, 2023.
- Hann, R.; Enache, A.; Nielsen, M.C.; Stovner, B.N.; van Beeck, J.; Johansen, T.A.; Borup, K.T. Experimental heat loads for electrothermal anti-icing and de-icing on UAVs. Aerospace 2021, 8, 83. [Google Scholar] [CrossRef]
- Shi, K.; Duan, X. A review of ice protection techniques for structures in the Arctic and offshore harsh environments. Journal of Offshore Mechanics and Arctic Engineering 2021, 143, 064502. [Google Scholar] [CrossRef]
- Pourbagian, M.; Habashi, W. On Optimal Design of Electro-Thermal In-Flight Ice Protection Systems. In Proceedings of the 5th AIAA Atmospheric and Space Environments Conference; 2013; p. 2937. [Google Scholar]
- Gallia, M.; Rausa, A.; Martuffo, A.; Guardone, A. A comprehensive numerical model for numerical simulation of ice accretion and electro-thermal ice protection system in anti-icing and de-icing mode, with an ice shedding analysis. Technical report, SAE Technical Paper, 2023.
- He, Z.; Wang, J. Anti-icing strategies are on the way. The Innovation 2022, 3. [Google Scholar] [CrossRef]
- He, Z.; Xie, H.; Jamil, M.I.; Li, T.; Zhang, Q. Electro-/Photo-Thermal Promoted Anti-Icing Materials: A New Strategy Combined with Passive Anti-Icing and Active De-Icing. Advanced Materials Interfaces 2022, 9, 2200275. [Google Scholar] [CrossRef]
- Mauery, T.; Alonso, J.; Cary, A.; Lee, V.; Malecki, R.; Mavriplis, D.; Medic, G.; Schaefer, J.; Slotnick, J. A guide for aircraft certification by analysis. Technical report, 2021.
- Gutiérrez, B.A.; Della Noce, A.; Gallia, M.; Bellosta, T.; Guardone, A. Numerical simulation of a thermal Ice Protection System including state-of-the-art liquid film model. Journal of Computational and Applied Mathematics 2021, 391, 113454. [Google Scholar] [CrossRef]
- Bennani, L.; Trontin, P.; Radenac, E. Numerical simulation of an electrothermal ice protection system in anti-icing and deicing mode. Aerospace 2023, 10, 75. [Google Scholar] [CrossRef]
- Niu, Y.; Wang, Z.; Su, J.; Yao, J.; Wang, H. Prediction of Airfoil Icing and Evaluation of Hot Air Anti-Icing System Effectiveness Using Computational Fluid Dynamics Simulations. Aerospace 2025, 12. [Google Scholar] [CrossRef]
- Stewart, E.A.; Bartkus, T.P. Computational Icing Analysis on NASA’s SIDRM Geometry to Investigate Collection Efficiency. In Proceedings of the International Conference on Icing of Aircraft, Engines, and Structures; 2023. [Google Scholar]
- Uranai, S.; Fukudome, K.; Mamori, H.; Fukushima, N.; Yamamoto, M. Numerical simulation of the anti-icing performance of electric heaters for icing on the NACA 0012 airfoil. Aerospace 2020, 7, 123. [Google Scholar] [CrossRef]
- Milani, Z.R.; Matida, E.; Razavi, F.; Ronak Sultana, K.; Timothy Patterson, R.; Nichman, L.; Benmeddour, A.; Bala, K. Numerical Icing Simulations of Cylindrical Geometry and Comparisons to Flight Test Results. Journal of Aircraft 2024, pp. 1–11.
- Martini, F.; Ibrahim, H.; Contreras Montoya, L.; Rizk, P.; Ilinca, A. Turbulence modeling of iced wind turbine airfoils. Energies 15 (22): 8325, 2022.
- Esmaeilifar, E.; Sengupta, B.; Raj, L.P.; Myong, R. In-flight anti-icing simulation of electrothermal ice protection systems with inhomogeneous thermal boundary condition. Aerospace Science and Technology 2024, 150, 109210. [Google Scholar] [CrossRef]
- Papadakis, M.; Wong, S.C.; Rachman, A.; Hung, K.E.; Vu, G.T.; Bidwell, C.S. Large and small droplet impingement data on airfoils and two simulated ice shapes. Technical report, 2007.
- Ansys. Ansys FENSAP-ICE User Manual, Release 2022 R2. Ansys, Canonsburg, PA, 2022. 2022.
- Aupoix, B.; Spalart, P. Extensions of the Spalart–Allmaras turbulence model to account for wall roughness. International Journal of Heat and Fluid Flow 2003, 24, 454–462. [Google Scholar] [CrossRef]
- Wright, B.; Al-Khalil, K.; Miller, D. Validation of nasa thermal ice protection computer codes part2-lewice. Thermal, AIAA 1997, pp. 97–0050.
- Zhou, Z.; Li, F.; Li, G.; Sang, W. Icing numerical simulation for single and multi-element airfoils. In Proceedings of the 28th AIAA Applied Aerodynamics Conference; 2010; p. 4232. [Google Scholar]
- Costes, M.; Moens, F.; Brunet, V. Prediction of iced airfoil aerodynamic characteristics. In Proceedings of the 54th AIAA Aerospace Sciences Meeting; 2016; p. 1547. [Google Scholar]
- Shen, X.; Wang, H.; Lin, G.; Bu, X.; Wen, D. Unsteady simulation of aircraft electro-thermal deicing process with temperature-based method. Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering 2020, 234, 388–400. [Google Scholar] [CrossRef]
- Federal Aviation Administration. CFR Part 25 Appendix C. Federal Register Rules and Regulations, 2011.
- Federal Aviation Administration. Airplane and Engine Certification Requirements in Supercooled Large Drop, Mixed Phase, and Ice Crystal Icing Conditions. Federal Register Rules and Regulations, 2014.
- Langmuir, I.; Blodgett, K. A mathematical investigation of water droplet trajectories; Number 5418, Army Air Forces Headquarters, Air Technical Service Command, 1946.
- Yang, X.; Bai, X.; Cao, H. Influence analysis of rime icing on aerodynamic performance and output power of offshore floating wind turbine. Ocean Engineering 2022, 258, 111725. [Google Scholar] [CrossRef]
- Suzzi, N.; Croce, G. Numerical simulation of film instability over low wettability surfaces through lubrication theory. Physics of Fluids 2019, 31. [Google Scholar] [CrossRef]
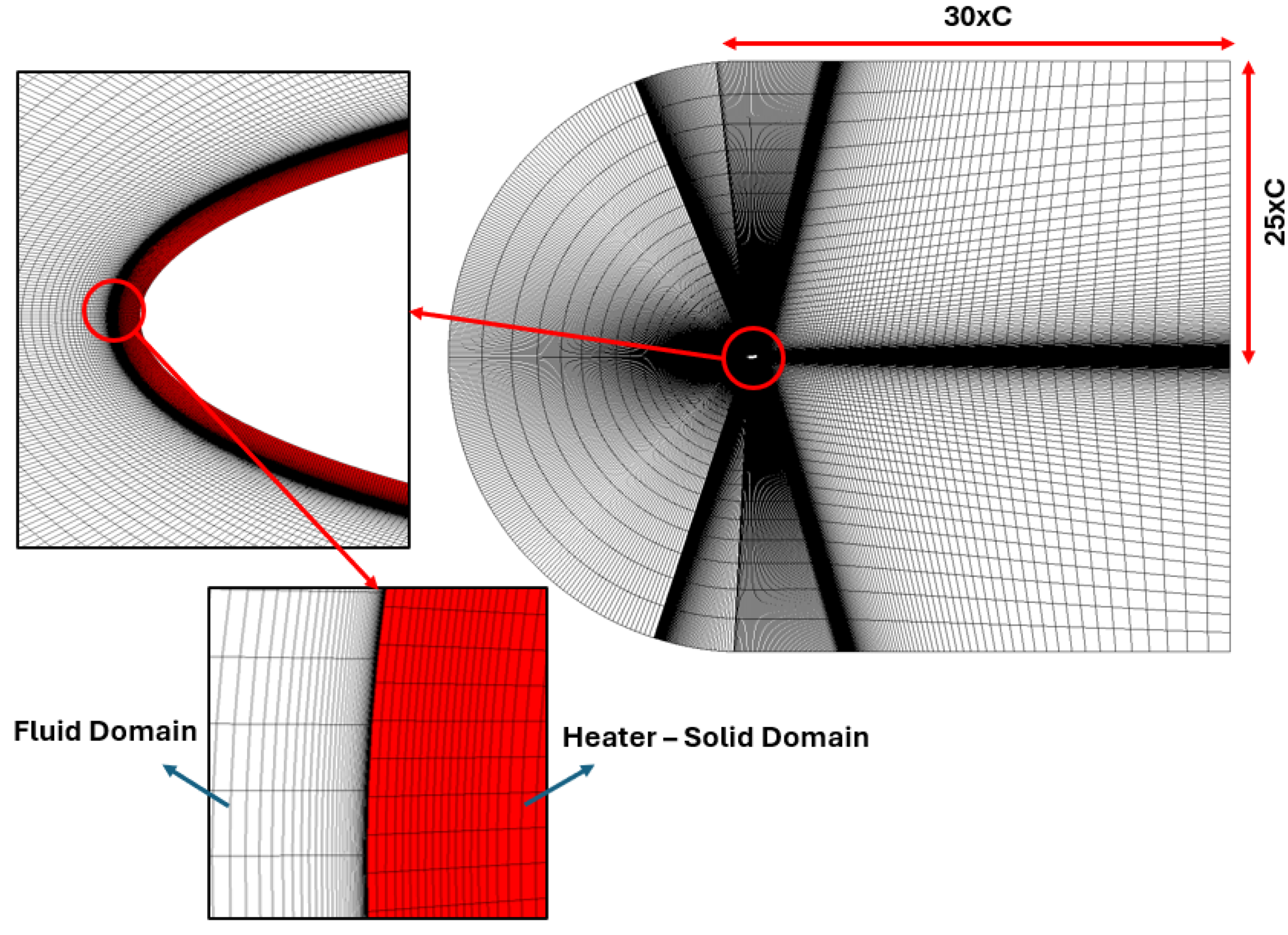
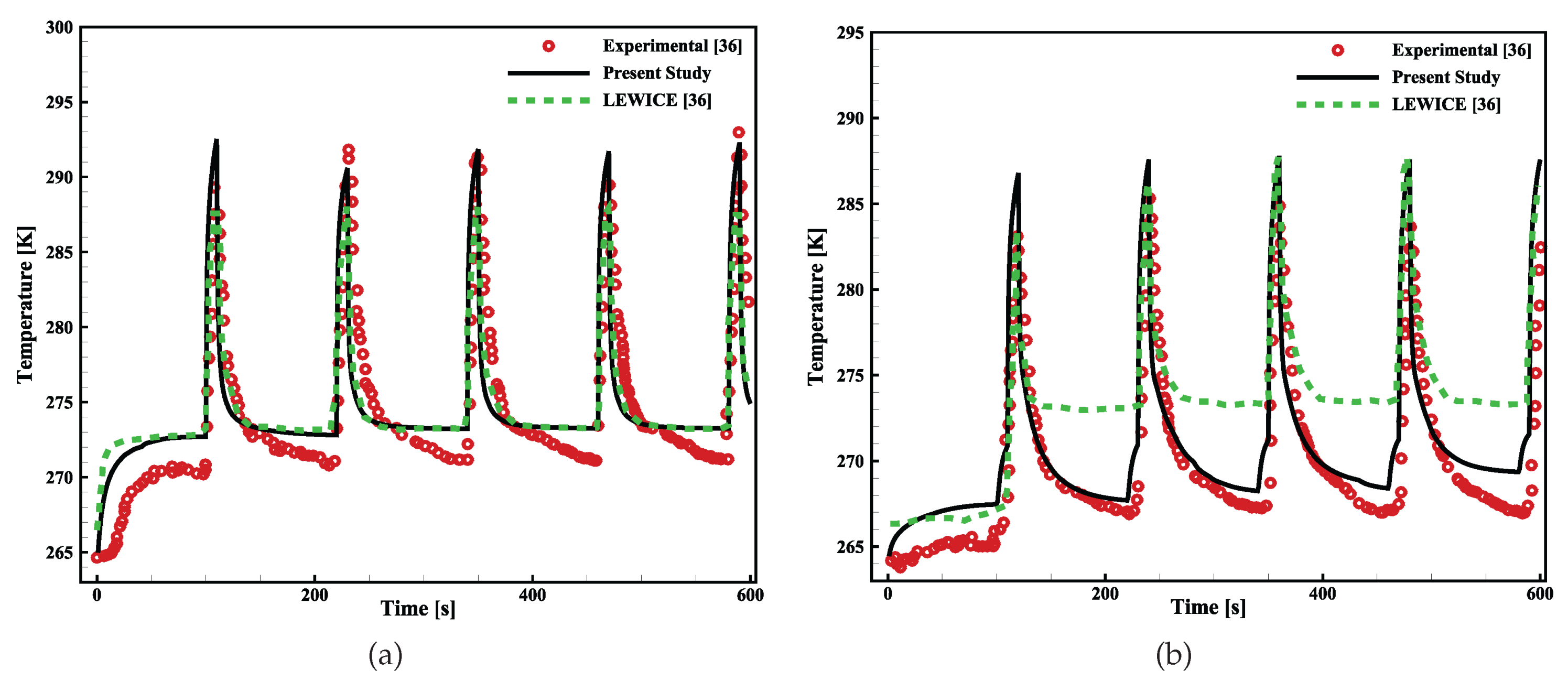
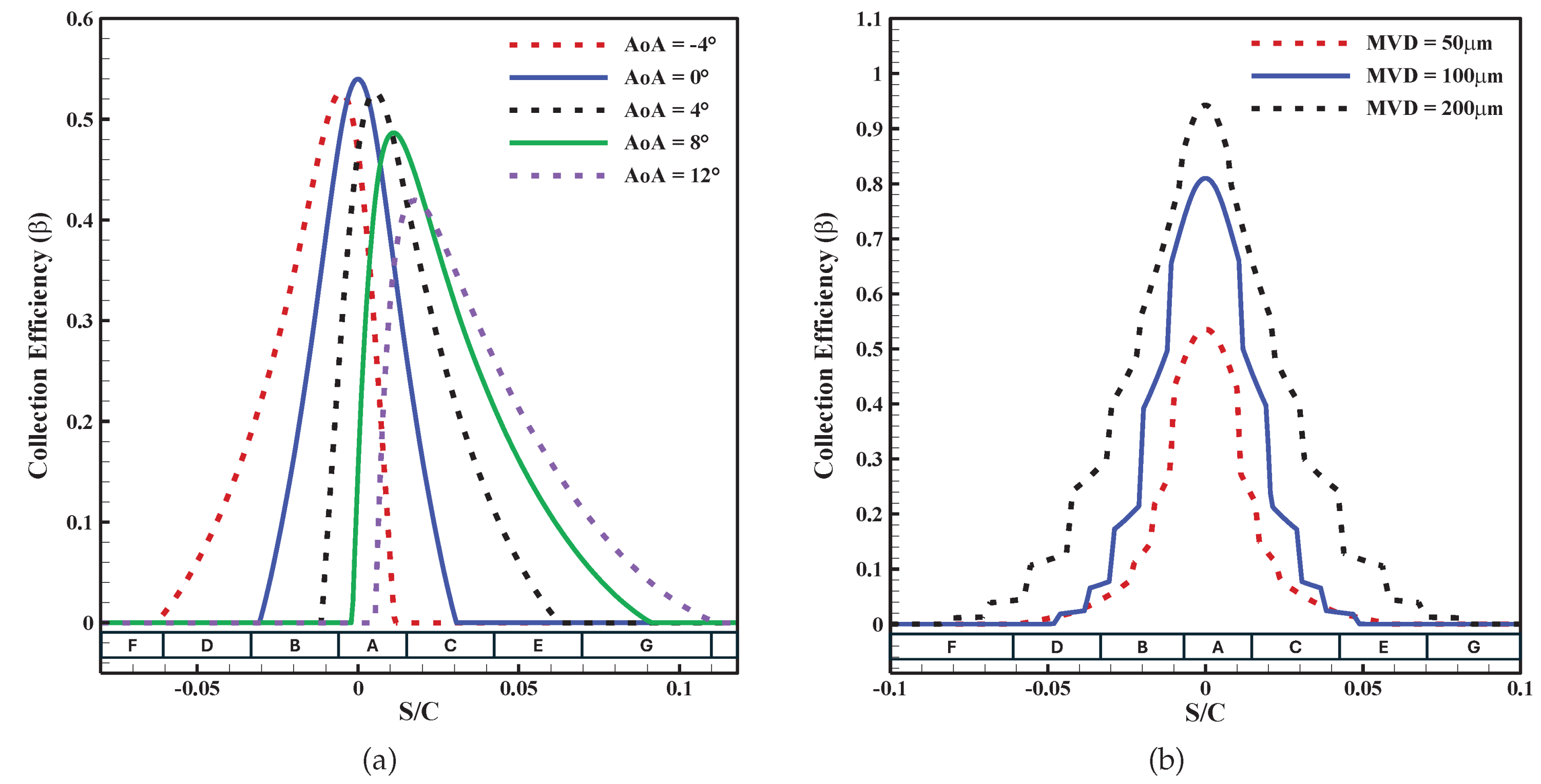
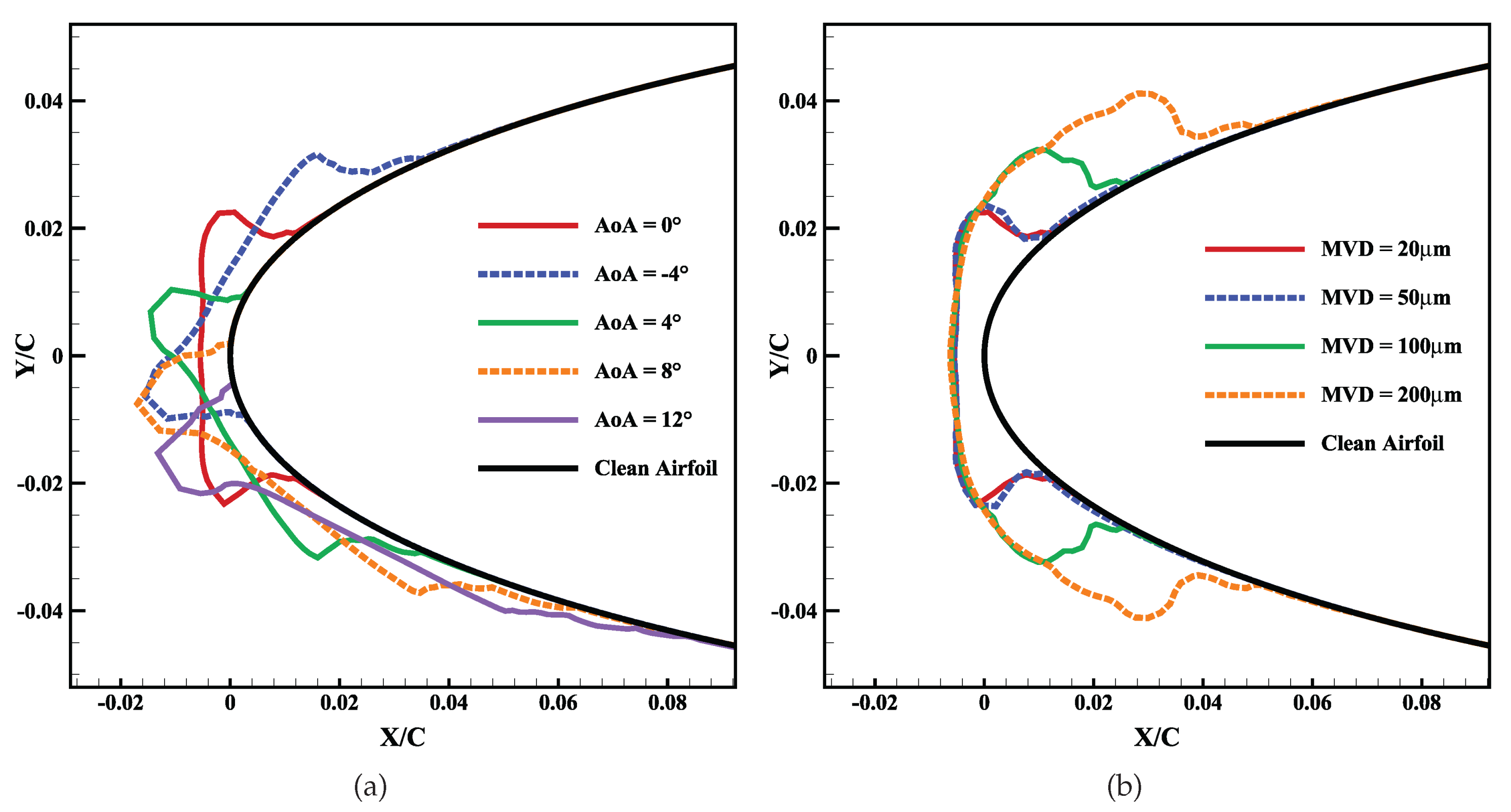
| Computational | Total Number | First Cell | Drag Coefficient | Percentage Change |
|---|---|---|---|---|
| Grid | of Cells | Height [m] | (CD) | Compared to |
| Previous Mesh | ||||
| Coarse | 38,500 | 2.00E-06 | 0.01463 | - |
| Medium | 82,400 | 2.00E-06 | 0.01546 | 5.67% |
| Fine | 161,800 | 2.00E-06 | 0.01587 | 2.48% |
| Very Fine | 310,600 | 2.00E-06 | 0.01598 | 0.69% |
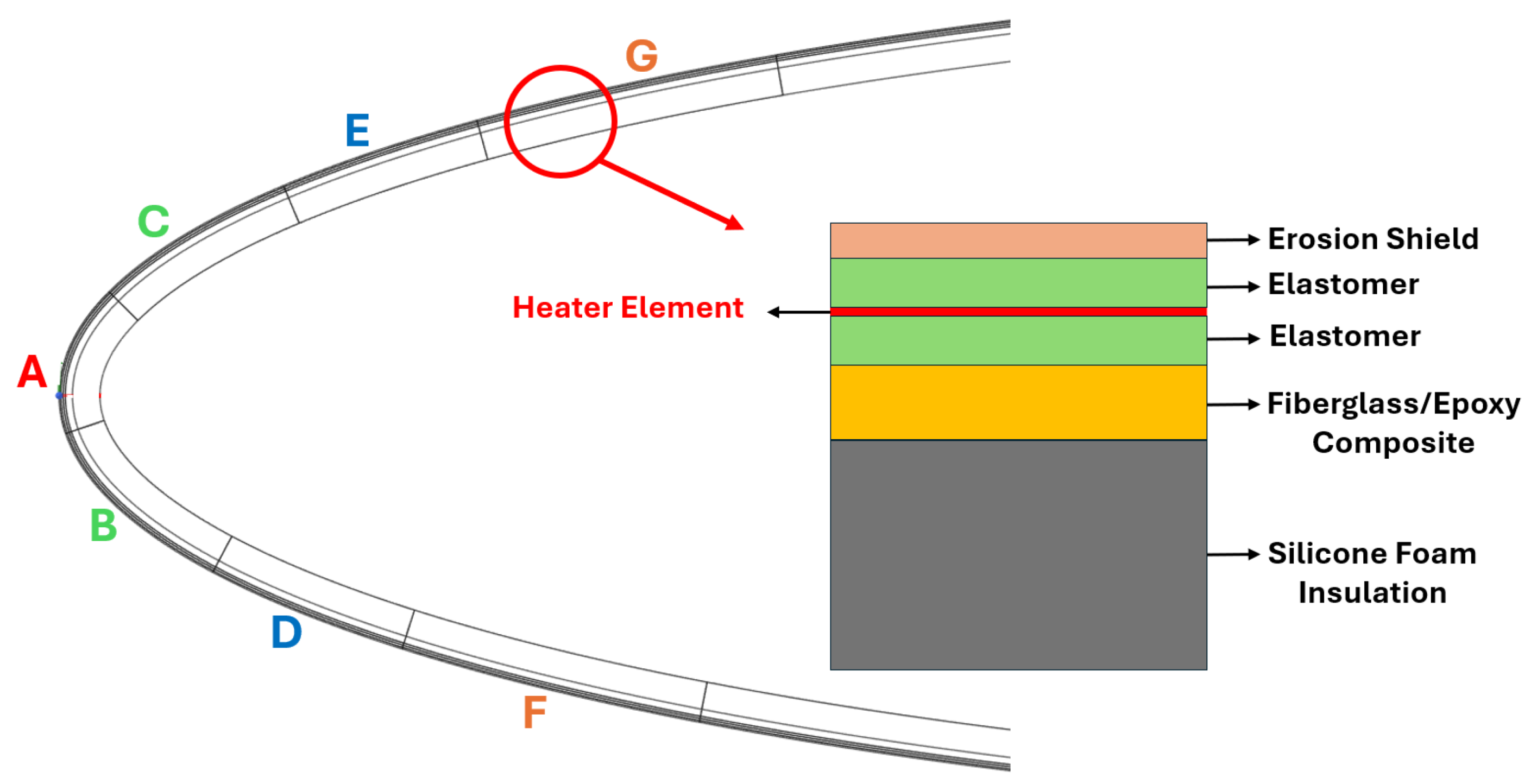
| Material | k [W/m.K] | [kg/] | [J/kg.K] | Thickness [mm] |
|---|---|---|---|---|
| Heating element (alloy 90) | 41.018 | 8906.26 | 385.112 | 0.0127 |
| Erosion shield (SS 301 HH) | 16.269 | 8025.25 | 502.32 | 0.2032 |
| Elastomer (COX 4300) | 0.256 | 1383.99 | 1255.8 | 0.2794 |
| Fiberglass/epoxy composite | 0.294 | 1794.07 | 1569.75 | 0.889 |
| Silicone foam insulation | 0.121 | 648.75 | 1130.22 | 3.429 |
| Heater | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| Start (S/C) | -0.0051 | -0.0329 | 0.0157 | -0.0607 | 0.0435 | -0.1024 | 0.0713 |
| End (S/C) | 0.0157 | -0.0051 | 0.0435 | -0.0329 | 0.0713 | -0.0607 | 0.1129 |
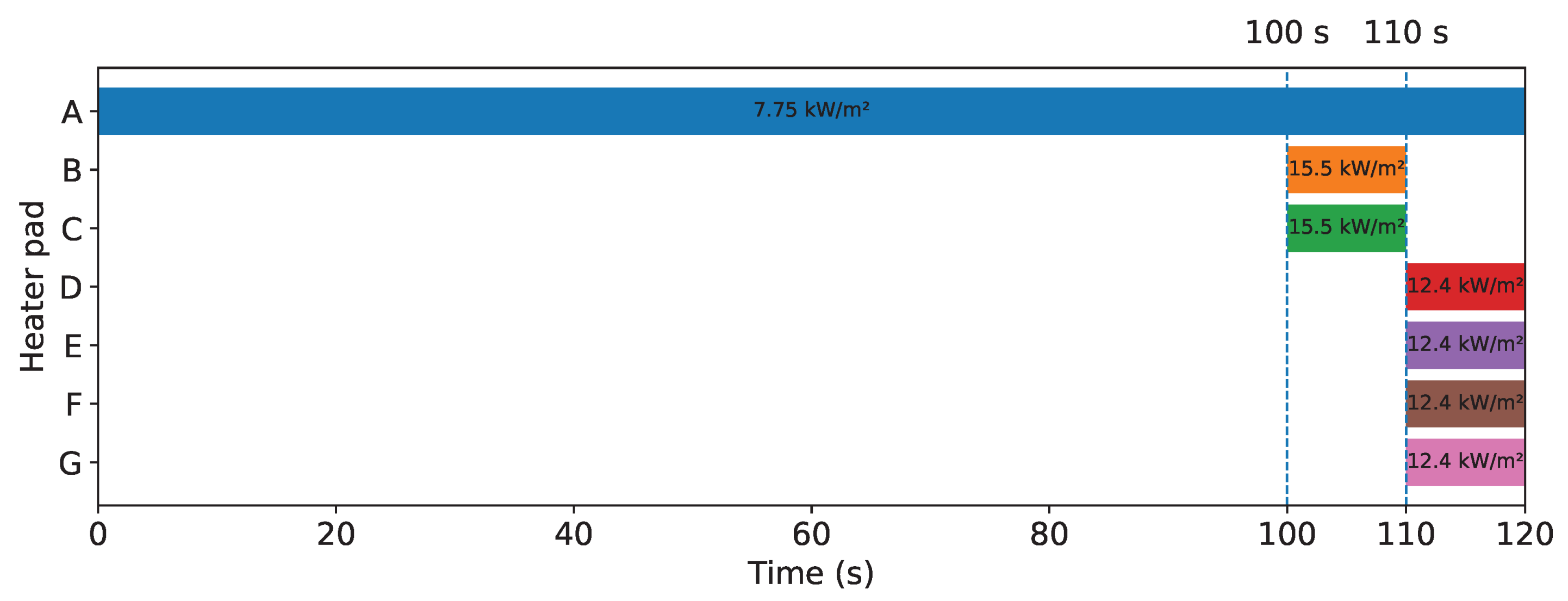
| Heating Element | Power Density [W/] | Duration [s] |
|---|---|---|
| A | 7750 | 0 to 120 |
| B-C | 15500 | 100 to 110 |
| D-E-F-G | 12400 | 110 to 120 |
| Case | Change in | Change in | ||||
|---|---|---|---|---|---|---|
| Case 1 | 0 | 0 | - | 0.01587 | 0.01901 | 19.8% |
| Case 2 | -0.4109 | -0.3993 | -2.8% | 0.01706 | 0.02062 | 20.9% |
| Case 3 | 0.4108 | 0.4036 | -1.8% | 0.01705 | 0.02031 | 19.1% |
| Case 4 | 0.797 | 0.7837 | -1.7% | 0.02233 | 0.02558 | 14.6% |
| Case 5 | 1.104 | 0.9813 | -11.1% | 0.03656 | 0.05420 | 48.2% |
| Case 6 | 0 | 0 | - | 0.01587 | 0.01874 | 18.1% |
| Case 7 | 0 | 0 | - | 0.01587 | 0.02088 | 31.6% |
| Case 8 | 0 | 0 | - | 0.01587 | 0.02166 | 36.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





