Applied Trigonotopology: Defining a Four-Dimensional Function to Collapse the Space between Distant Points

1. Introduction

The paradigm of locality, grounded in the space-time separation of bodies and events, imposes physical limits on movement. This article questions, both conceptually and structurally, several classical foundations of physics, particularly those embedded in the paradigm of relativity and causal locality. The proposed model aims to eliminate time as a parameter and to present the possibility of instantaneous transport between two spatial points. This directly challenges the structure of both special and general relativity, which impose a fundamental speed limit for the propagation of any physical interaction (the speed of light) and require continuity in space-time. In essence, the model seeks to propose a solution that contradicts the continuous and metric nature of space-time and its causal velocity limitations.

In the developed model, space is no longer measured by distance (metric), but through functional equivalence expressed by the Trigonotelary Function, which synthesizes a four-dimensional nonlinear trigonometric structure. The notion that two points may be functionally 'adjacent' despite being spatially distant contradicts the classical view of continuous three-dimensional space, challenging Euclidean/Riemannian geometry and the standard topology based on metric neighborhoods. Furthermore, by adopting the concept of 'ontological simultaneity' proposed by Magalhães (2016), in which events are not connected by temporal succession but by structural implication, the model dismisses the traditional causal-temporal framework of physics. However, this contradiction does not imply direct antagonism, as it emerges from an alternative ontological path.

This article’s central hypothesis is: is it possible to rigorously model the instantaneous transport of a body between two points without time acting as a limiting factor? To investigate this, we adopt the view that the distance between events is not merely a geometric measure, but rather an ontological and structural function, potentially eliminable. Thus, we propose the four-dimensional nonlinear trigonometric function (TTNL), which operates without time as an explicit variable, enabling such a conceptual leap. The complexity of this function incorporates nonconventional mathematical concepts in physics, such as Cantor sets and Perelman's geometric entropy, to describe spatial connectivity, suggesting that space is a functional web of variable density, as described by Strogatz (2003) in his studies on complex networks and continuous spontaneous synchronization. By adopting a view of space as an emergent network of functional topological connections, rather than a fixed stage where events occur, this perspective aligns more closely with complex systems models than with traditional physical frameworks.

2. Theoretical Framework and Methods

Note on AI Use: Portions of the text and structure of this manuscript were developed using artificial intelligence tools (ChatGPT, OpenAI), under the supervision and critical review of the listed author. The use of such tools is documented here in accordance with COPE and Preprints.org guidelines.

2.1. Ontological Simultaneity

The concept of ontological simultaneity challenges the temporal succession model of classical physics by proposing that certain events may occur simultaneously due to structural relationships, rather than temporal causality. This view aligns with Magalhães (2016), who suggests that simultaneity can emerge from the internal architecture of systems rather than from chronological sequencing. In this framework, events are functionally entangled by their positions within a system’s topological configuration, enabling instantaneous connections beyond traditional space-time constraints.

2.2. Perelman's Geometric Entropy

Perelman's concept of geometric entropy, developed within the context of Ricci flow and topology, offers a way to evaluate the structural complexity and deformation of manifolds. Applied here, it allows us to understand how regions of space can condense or expand in functional terms, rather than purely geometric ones. This contributes to the notion of spatial equivalence between distant points when viewed through the lens of informational density and entropy minimization.

2.3. Cantor Sets

Cantor sets serve as a mathematical foundation for modeling discontinuities and fragmented spaces. Their recursive, self-similar structure allows for the representation of non-continuous spatial domains, which is essential to support the TT function. The presence of "gaps" in Cantor sets parallels the idea of instant disconnection or reconnection between spatial points, forming a lattice of potential equivalences.

2.4. Poincaré and Bell

Henri Poincaré’s topological insights, especially concerning the nature of three-dimensional manifolds, provide a framework for understanding global structural transformations in space. Meanwhile, Bell’s theorem from quantum mechanics, which demonstrates the non-locality of entangled particles, reinforces the plausibility of non-local models like the one proposed here. Together, these foundations justify exploring models where distance does not constrain connectivity.

2.5. Complex Systems

Complex systems theory provides tools to analyze emergent patterns from non-linear interactions across a network. Such systems are characterized by self-organization, feedback loops, and dynamic equilibrium. In this article, the spatial field is understood as a complex system in which proximity emerges from synchronization and resonance, rather than from geometric measurement.

2.6. Traditional and Reformulated TT Function (Figure 1)

We begin with the traditional form of the Trigonotelary Function, which explicitly expresses each spatial component and the entanglement parameter:

T(x, y, z, θ) = ∑ₙ αₙ · cos(ωₙₓ·x + ωₙᵧ·y + ωₙz·z + φₙ(θ))

In this formulation:

• - x, y, z ∈ ℝ are spatial coordinates,
• - θ ∈ ℝ is the ontological simultaneity (or entanglement) parameter,
• - ωₙₓ, ωₙᵧ, ωₙz ∈ ℝ are frequency components along each spatial axis,
• - αₙ ∈ ℝ are amplitude coefficients,
• - φₙ(θ) is the phase shift modulated by the entanglement parameter.

This expression defines a nonlinear oscillatory field over a spatial domain modulated by a fourth ontological dimension, without any reference to time as a fundamental parameter.

To generalize this structure and facilitate formal developments in higher-dimensional and topological spaces, we adopt a reformulated notation:

T(P, Θ) = ∑ₙ αₙ · cos(⟨ωₙ, P⟩ + φₙ(Θ))

Where:

• - P = (x, y, z) ∈ ℝ³ is the spatial position vector,
• - ωₙ = (ωₙₓ, ωₙᵧ, ωₙz) ∈ ℝ³ is the frequency vector across spatial dimensions,
• - Θ ∈ ℝ generalizes the entanglement parameter θ,
• - ⟨ωₙ, P⟩ denotes the inner product between frequency and position vectors.

This vector-based formulation provides a more compact and flexible mathematical structure, which serves as the foundation for the generalized formalism presented in Section 3.1. There, the Trigonotelary Function is embedded in a non-Euclidean topological framework, allowing us to describe phase-based equivalences and functional collapses between spatially distant points (Figure 2).

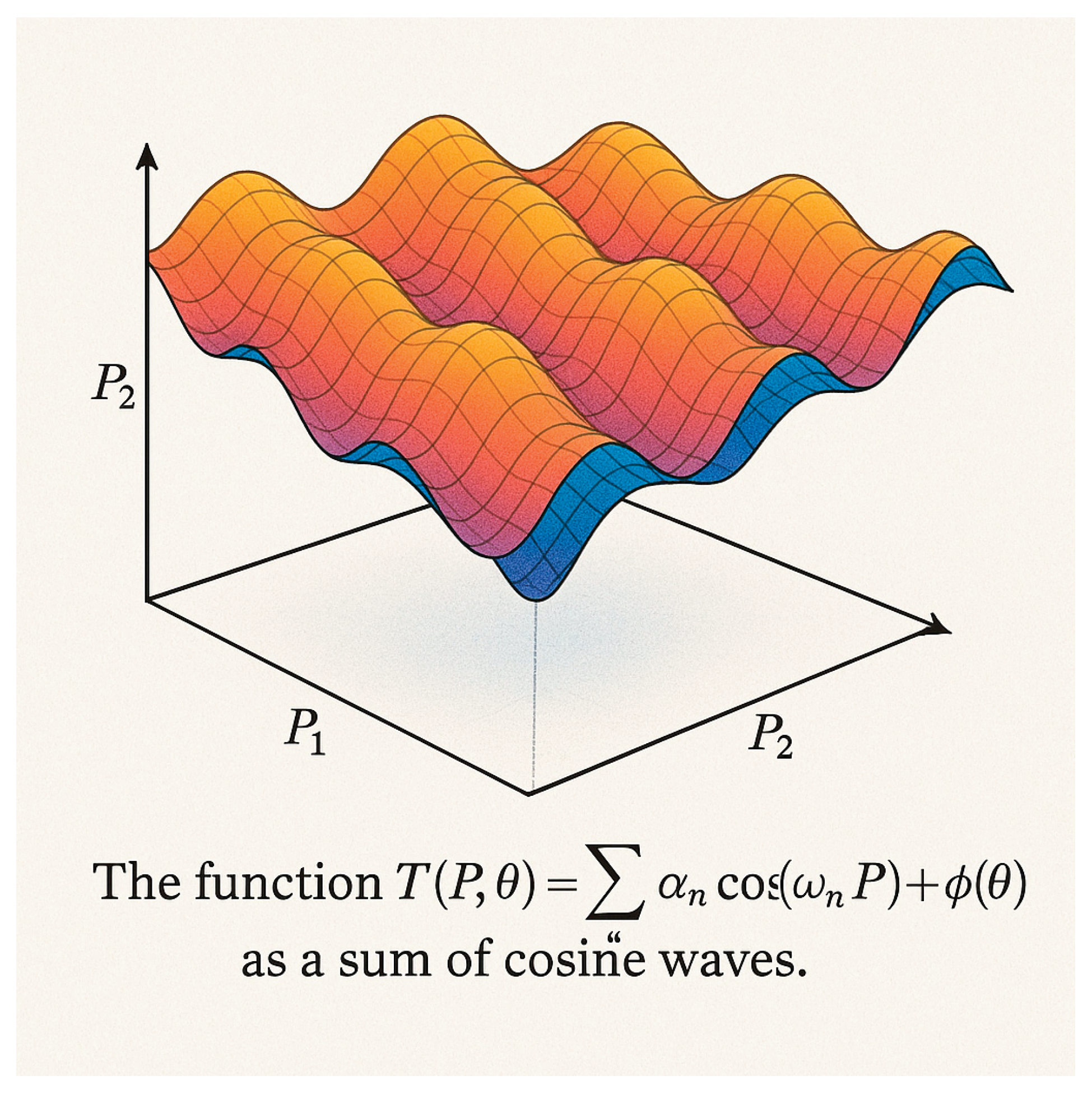
Figure 1. - Geometric Representation of the Trigonotellar Function. Graphical representation of the trigonometric function TT(P,θ) = Σₙ αₙ · cos(⟨ωₙ,P⟩ + φₙ(θ)). The image illustrates the function as a composition of cosine waves in a two-dimensional space, suggesting the wavelike complexity that expands from each spatial dimension with variation of the parameter θ.

Figure 1. - Geometric Representation of the Trigonotellar Function. Graphical representation of the trigonometric function TT(P,θ) = Σₙ αₙ · cos(⟨ωₙ,P⟩ + φₙ(θ)). The image illustrates the function as a composition of cosine waves in a two-dimensional space, suggesting the wavelike complexity that expands from each spatial dimension with variation of the parameter θ.

Figure 2. Artistic rendering of the multidimensional resonant network defined by the TT function.

Figure 2. Artistic rendering of the multidimensional resonant network defined by the TT function.

The image suggests a structure of interconnected wave networks, with multiple layers of spatial propagation, where the fourth dimension (represented by θ) manifests itself as a topological and phase modulation factor, influencing the formation and amplitude of peaks and valleys in the wave field. The interaction between the different planes and colors illustrates the superposition of the multiple harmonic components of the function.

3. Results

Following the formal progression established in the previous sections—where the Trigonotelary Function was reformulated in a compact vector-based structure—we now explore the core theoretical outcomes enabled by this framework.

These results focus on the ontological behavior of the function in a non-Euclidean, topologically entangled space, where phase resonance governs the interaction between spatial nodes. Time, in this context, is not a driving variable. Instead, the parameter Θ plays a central role in mediating simultaneity and enabling instantaneous functional equivalence between distinct points.

We begin by formally expressing the Trigonotelary Function using its generalized formulation. Then, we introduce the concept of functional collapse, a condition in which spatially distant coordinates become indistinguishable through harmonic identity. Lastly, we provide a qualitative and graphical interpretation of the function’s behavior, highlighting zones of resonance, curvature, and entangled topology.

3.1. Formalization of the Trigonotelary Function (Figure 3)

Building on the reformulated expression presented in Section 2.6, we now adopt the vector-based notation of the Trigonotelary Function as a structural foundation for modeling ontological simultaneity and functional equivalence in a non-Euclidean framework:

T(P, Θ) = ∑ₙ αₙ · cos(⟨ωₙ, P⟩ + φₙ(Θ))

Where:

• - P ∈ ℝ³ is the spatial position vector, representing the coordinates (x, y, z),
• - ωₙ ∈ ℝ³ is the frequency vector associated with each mode n,
• - αₙ ∈ ℝ are amplitude coefficients,
• - φₙ(Θ) is a phase shift function modulated by the entanglement parameter Θ ∈ ℝ.

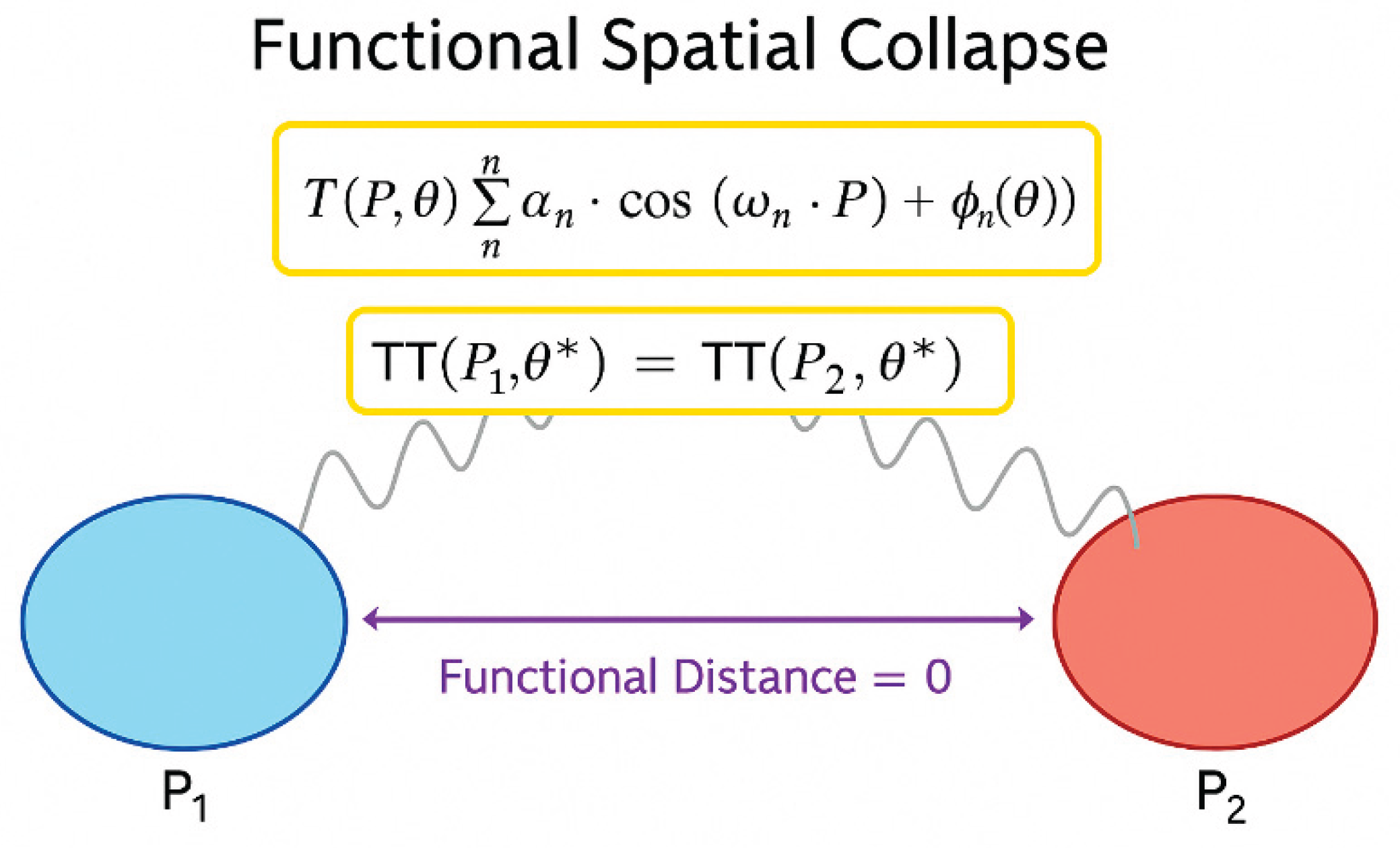
Figure 3. Diagram showing functional collapse between spatially distinct points P₁ and P₂ under resonance alignment at critical parameter Θ*. Blue and red spheres (P₁ and P₂): distinct spatial positions. Gray wavy lines: coupling by the trigonotellar web. Yellow box: equality of the values ​​TT(P₁,θ*) = TT(P₂,θ*). Purple double arrow: nullified functional distance (simultaneous manifestation). θ*: critical parameter that tunes the collapse.

Figure 3. Diagram showing functional collapse between spatially distinct points P₁ and P₂ under resonance alignment at critical parameter Θ*. Blue and red spheres (P₁ and P₂): distinct spatial positions. Gray wavy lines: coupling by the trigonotellar web. Yellow box: equality of the values ​​TT(P₁,θ*) = TT(P₂,θ*). Purple double arrow: nullified functional distance (simultaneous manifestation). θ*: critical parameter that tunes the collapse.

Unlike traditional time-based formulations, the Trigonotelary Function operates within a topological structure where time is not a fundamental parameter. Instead, the function evolves in a space of ontological resonance, governed by phase alignment and spatial-frequency coupling.

This model describes a multidimensional oscillatory field in which points are not separated by Euclidean distances but are instead distinguished—or collapsed—based on their phase resonance states. The parameter Θ encapsulates the entanglement or simultaneity structure, functioning as a mediator of functional identity between spatially distinct nodes.

Thus, the Trigonotelary Function is not merely a spatial wave function, but a resonant phase field where identity between points emerges from harmonic alignment, enabling phenomena such as functional collapse, instantaneous transposition, and topological proximity without geometric contiguity.

3.2. Functional Collapse Condition

The system reaches a functional collapse (instantaneous equivalence between two distinct spatial points Pᵢ and Pⱼ) when:

T(Pᵢ, θ_c) = T(Pⱼ, θ_c) and ∂T/∂θ |_{θ=θ_c} = 0

This critical condition θ_c corresponds to a phase equilibrium state in which two spatially separated points become indistinguishable under the function’s output. Instead of continuity or contiguity, functional identity emerges.

3.3. Graphical Representation and Interpretation (Figure 4)

The TT function generates a multidimensional oscillatory field with locally and globally entangled structures. Under graphical simulations, the TT function reveals:

• - Dense wave interference zones where functional identity is achievable.
• - Curved propagation patterns that reflect non-metric topology.
• - Symmetrical harmonic regions indicating the potential for instant transport between distant nodes.

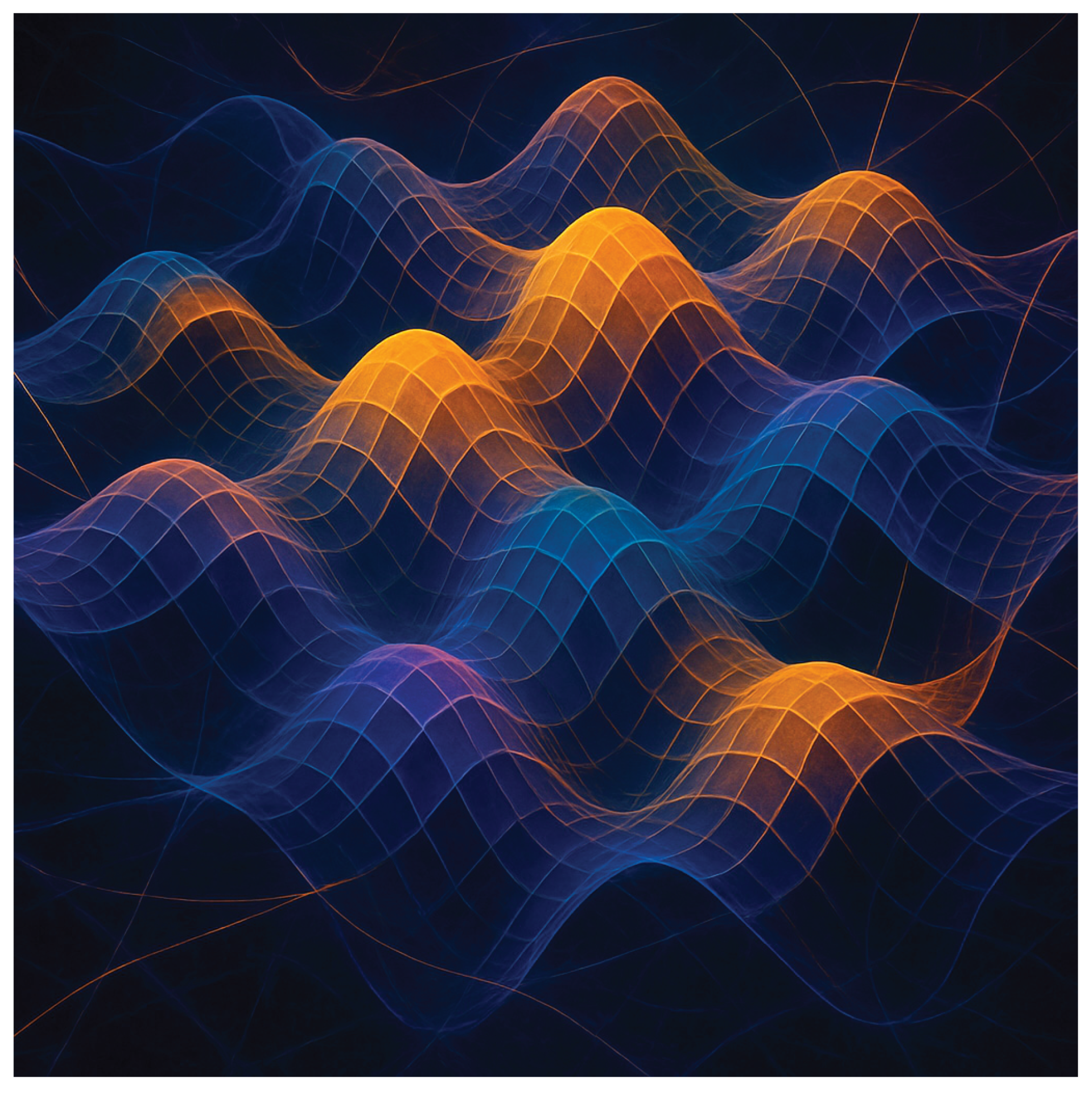
Figure 4. Tetradimensional entanglement mesh illustrating phase synchronization across distant spatial nodes.

Figure 4. Tetradimensional entanglement mesh illustrating phase synchronization across distant spatial nodes.

The image represents an artistic visualization of the trigonotellar function, highlighting the entanglement resulting from the interaction between multiple harmonic components in a nonlinear four-dimensional space. This composition incorporates continuous spatial curvatures that suggest the twisting of space as a function of the parameters ωₙ and the variable phase φₙ(θ), evidencing a complex wave-like topology. The loops and inflections depict the coalescence of multiple dimensions of frequency, amplitude and orientation, implying that each point of the function is functionally connected to all the others, abolishing local separation in space. The image thus symbolizes the functional collapse of traditional space and the emergence of an integrated and curved network that structures the timeless movement between points.

These results are consistent with the theoretical condition of ontological proximity: two points sharing the same resonance state are not merely “close” in geometric terms, but effectively collapsed in the functional topology (Figure 5).

This image integrates the structure of interconnected wave networks and the four-dimensional entanglement. The overlapping of layers, frequencies and spatial orientations suggests a complex topological configuration, where the fourth dimension (θ) acts as a modulation factor, creating a nonlinear pattern of interaction between the components of the wave field. The illustration highlights the simultaneity of multiple phases and the inseparability between the local and global effects of the function.

3.4. Conceptual Consequences

The formal structure suggests that:

• - Space may be emergent from resonance and synchronization patterns.
• - Distance becomes irrelevant where phase and amplitude conditions align.
• - Transport is replaced by instantaneous manifestation, challenging classical continuity and relativistic constraints.

These insights expand the potential for mathematical and physical exploration of non-local interaction fields in cosmology, quantum information, and historiographical models of structural equivalence.

4. Discussion

4.1. Functional Collapse Condition

The central theoretical result derived from the Trigonotelary Function (TT) is the condition of functional collapse. As established in Section 3, this collapse allows two spatially distinct points to become functionally equivalent when their respective TT values coincide under a critical entanglement parameter Θ*:

T(P₁, Θ*) = T(P₂, Θ*) and ∂T/∂Θ|_{Θ=Θ*} = 0

This equation expresses a phase equilibrium where the topological configuration of the space reaches a point of convergence. In this state, the function’s harmonic composition eliminates the spatial separation between P₁ and P₂, causing them to collapse into a single ontological identity within the function’s domain.

This theoretical condition has strong implications: it removes the dependency on metric distance and redefines the notion of connectivity in terms of resonance, frequency, and ontological alignment. It transforms movement from a trajectory to a structural reconfiguration in the phase-space defined by the TT function.

4.2. Mathematical Representations

The reformulated TT function adopts a compact vector form that facilitates analytical manipulation and visualization:

T(P, Θ) = ∑ₙ αₙ · cos(⟨ωₙ, P⟩ + φₙ(Θ))

This expression supports a variety of dynamic and topological configurations, allowing the generation of multidimensional fields of oscillatory influence.

4.3. Analogies with Quantum Experiments

The TT model mirrors quantum entanglement: spatial separation does not prevent instantaneous relational behavior. The critical parameter Θ acts as a tuning variable, aligning distant points as though “entangled.”

Unlike quantum indeterminacy, however, the TT framework is deterministic within its ontological domain, governed by harmonic and phase alignment. This analogy is conceptually valuable for understanding the model’s non-local simultaneity.

4.4. Cosmological and String-Theoretical Implications

The TT functional mesh resonates with cosmological structures such as the cosmic web, where filaments connecting galaxies can be interpreted as resonance strands. Likewise, string theory’s vibrational paradigm finds an ontological parallel: TT envisions space as a phase-based field in which resonance, not geometry, dictates spatial identity.

Thus, the TT field may be viewed as a macroscopic lattice of ontological “strings” whose interactions define proximity, existence, and manifestation.

4.5. Historical Theory and Structural Equivalence

Beyond physics and cosmology, the TT model offers insights for historiography. If resonance—rather than chronological sequence—governs connectivity, historical events may be structurally equivalent despite temporal or geographic separation.

Modeling history via shared resonance patterns (ontological isomorphism across eras) allows rethinking causality, recurrence, and pattern recognition in structural history, with the TT function providing a formal tool for such analysis.

5. Conclusions

This study introduced and formalized the Trigonotelary Function (TT) as a theoretical and mathematical model capable of collapsing spatial distance through harmonic equivalence. The central claim of this work is ontological: the space between two points is not fundamentally defined by metric distance, but by the alignment of resonance, frequency, and phase within a multidimensional functional topology.

Unlike conventional physical models, which rely on geometric continuity and chronological causality, the TT function eliminates time as a fundamental variable and replaces Euclidean separation with functional connectivity. This represents a paradigm shift: from a metric space to a resonant structure; from distance to ontological synchronization.

The notion of functional resonance, expressed through the TT harmonic superposition, allows for the simultaneous manifestation of a body at multiple spatial coordinates when certain conditions are met — notably the tuning of the entanglement parameter Θ to its critical value Θ*. This functional identity breaks the limits imposed by relativity and traditional geometry, offering a non-local mechanism for interaction, transport, and ontological coherence.

Moreover, the TT model suggests that space is not a container but a dynamic mesh of relational intensities. In this mesh, proximity is determined not by position but by phase, and causality emerges from structural equivalence rather than sequential ordering. This ontological perspective opens new possibilities not only for theoretical physics and cosmology but also for historiography, where structural resonance might connect events across distant temporal layers.

In essence, the Trigonotelary Function redefines spatiality and presence. It introduces a non-metric, non-temporal substrate of reality governed by phase resonance — a continuous field where equivalence precedes separation, and manifestation replaces motion. It is a move toward a physics of relational presence, encoded in the harmonics of a multidimensional space.