Submitted:
10 June 2025
Posted:
11 June 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Correlation Analysis Based on FP-Growth Segments
2.1. Theory of FP-Growth Association Rules
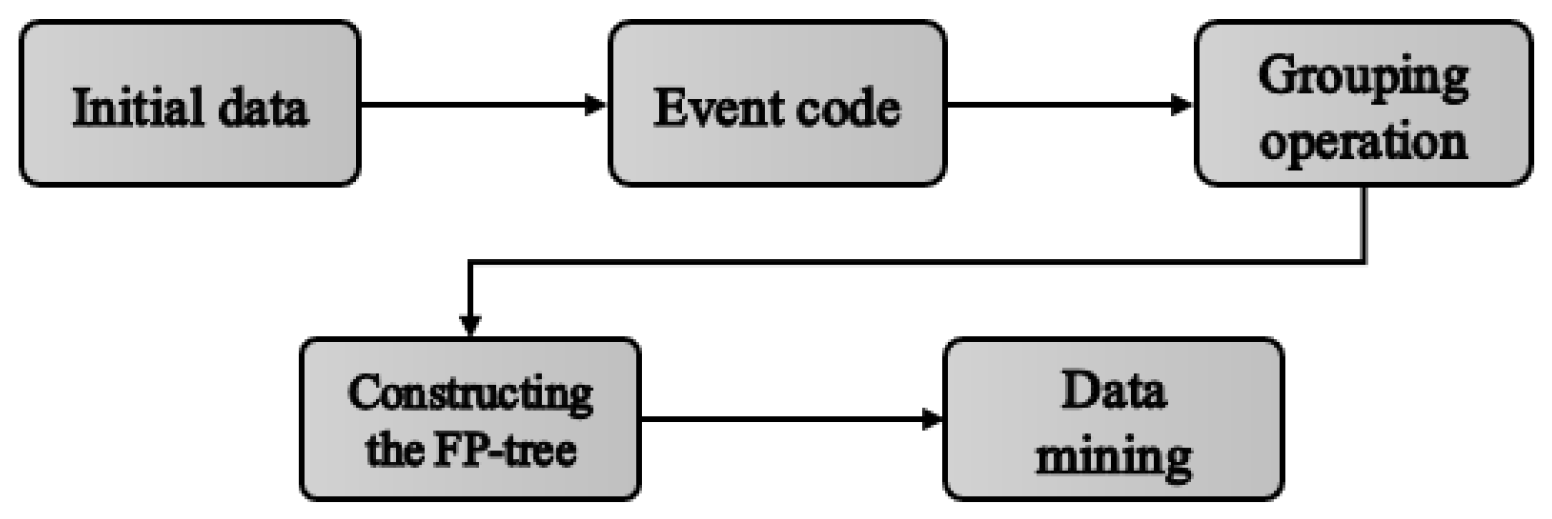
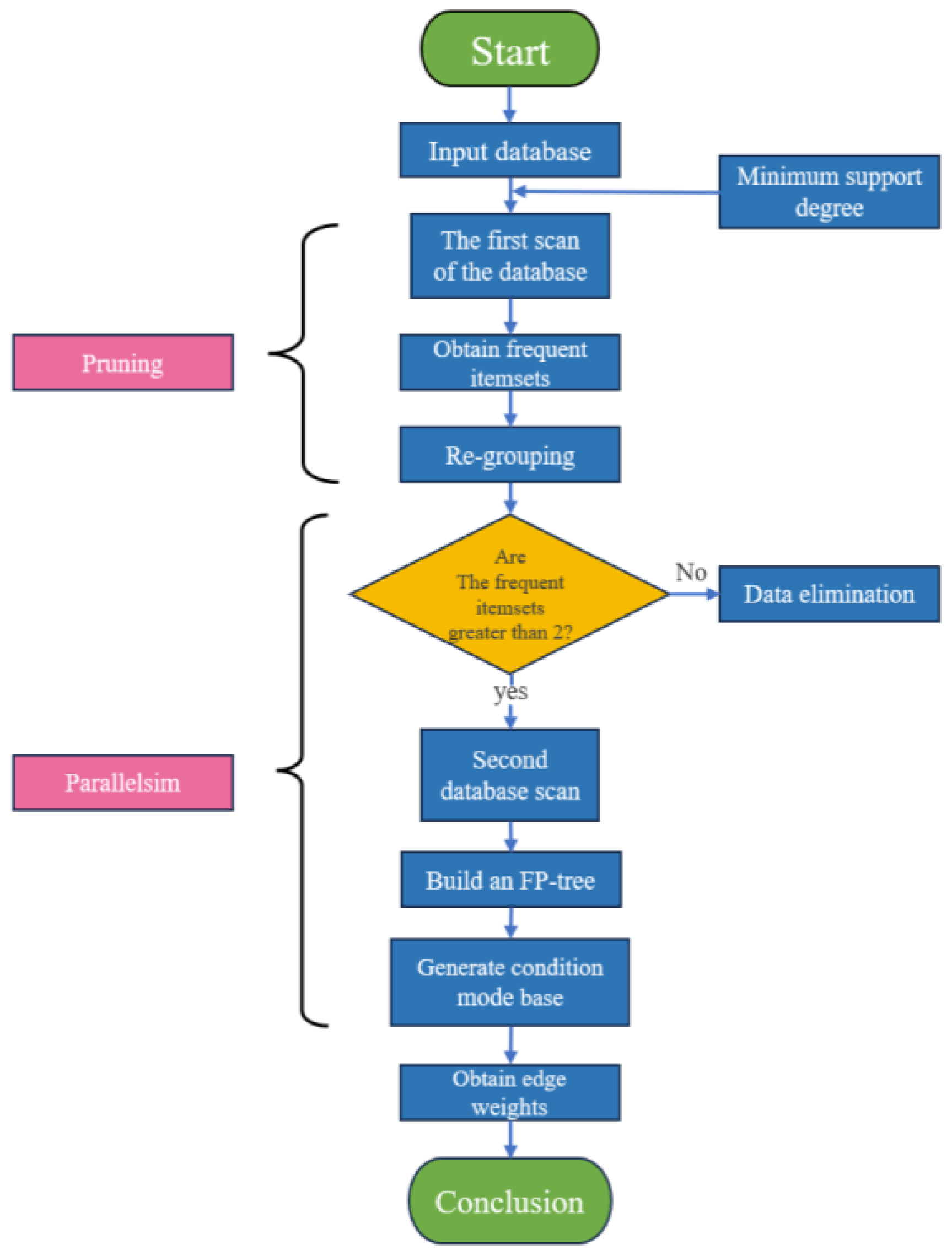
2.2. FP-Growth Algorithm Improvement Process
- Table 2. Airline Network Factor.
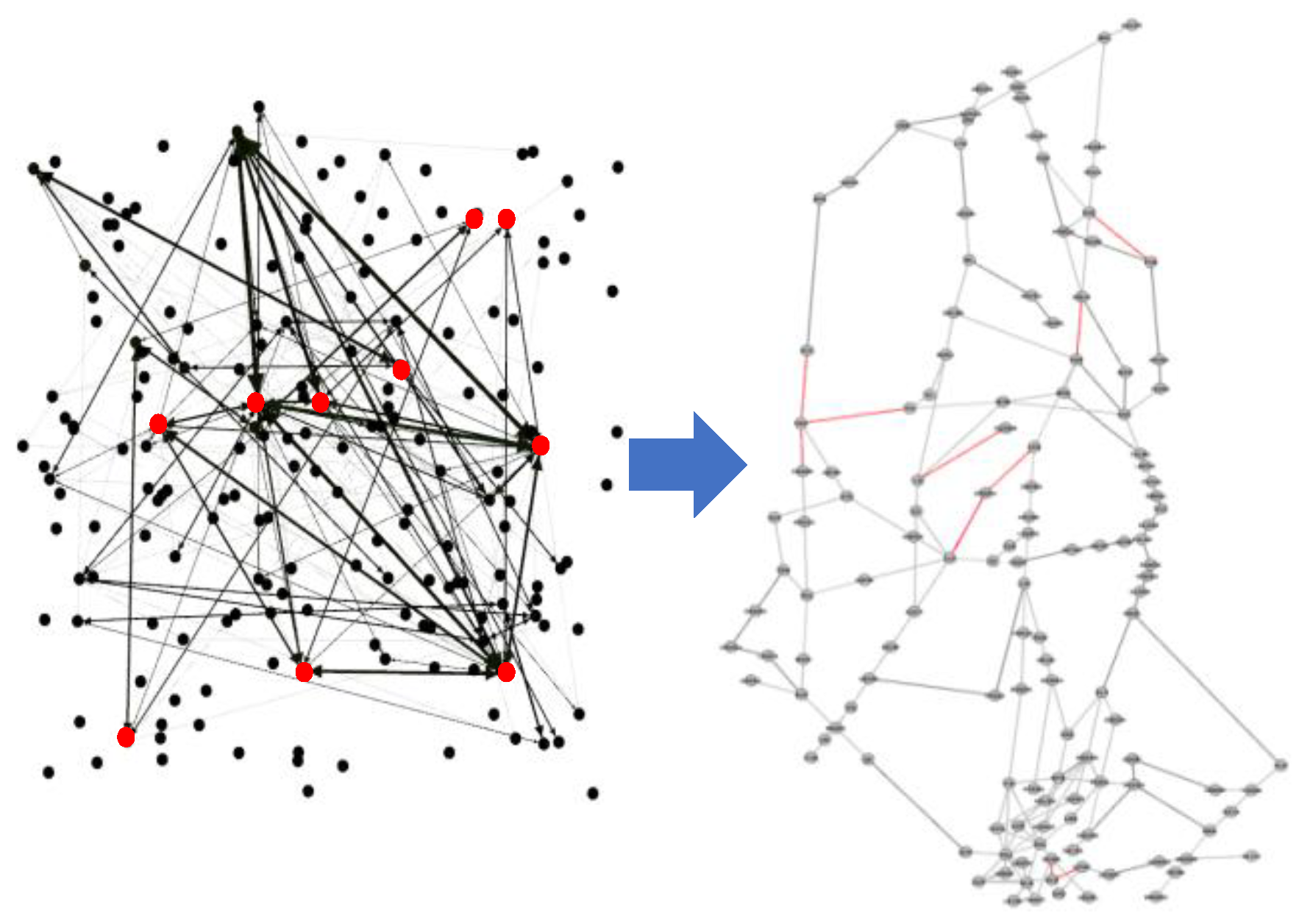
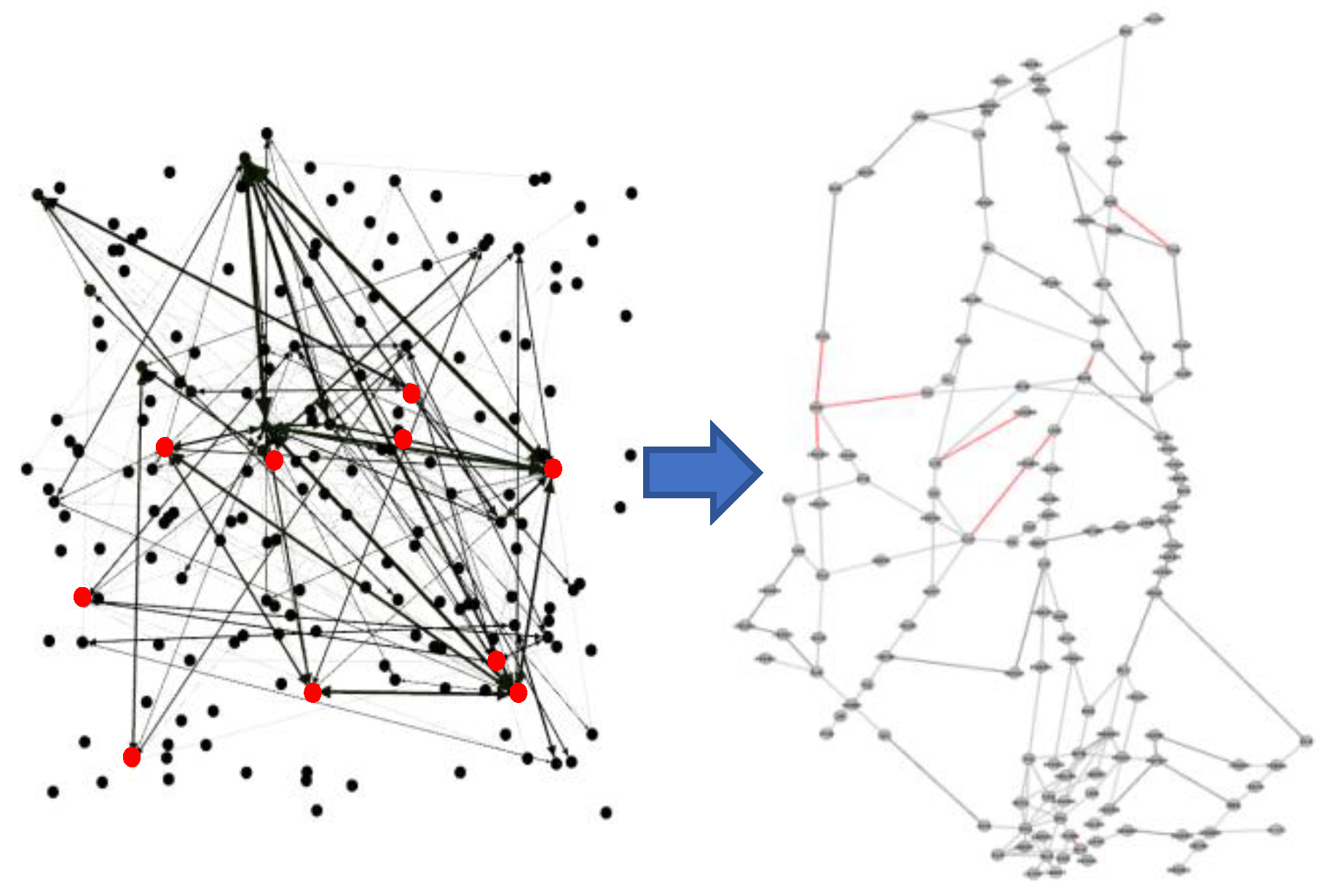
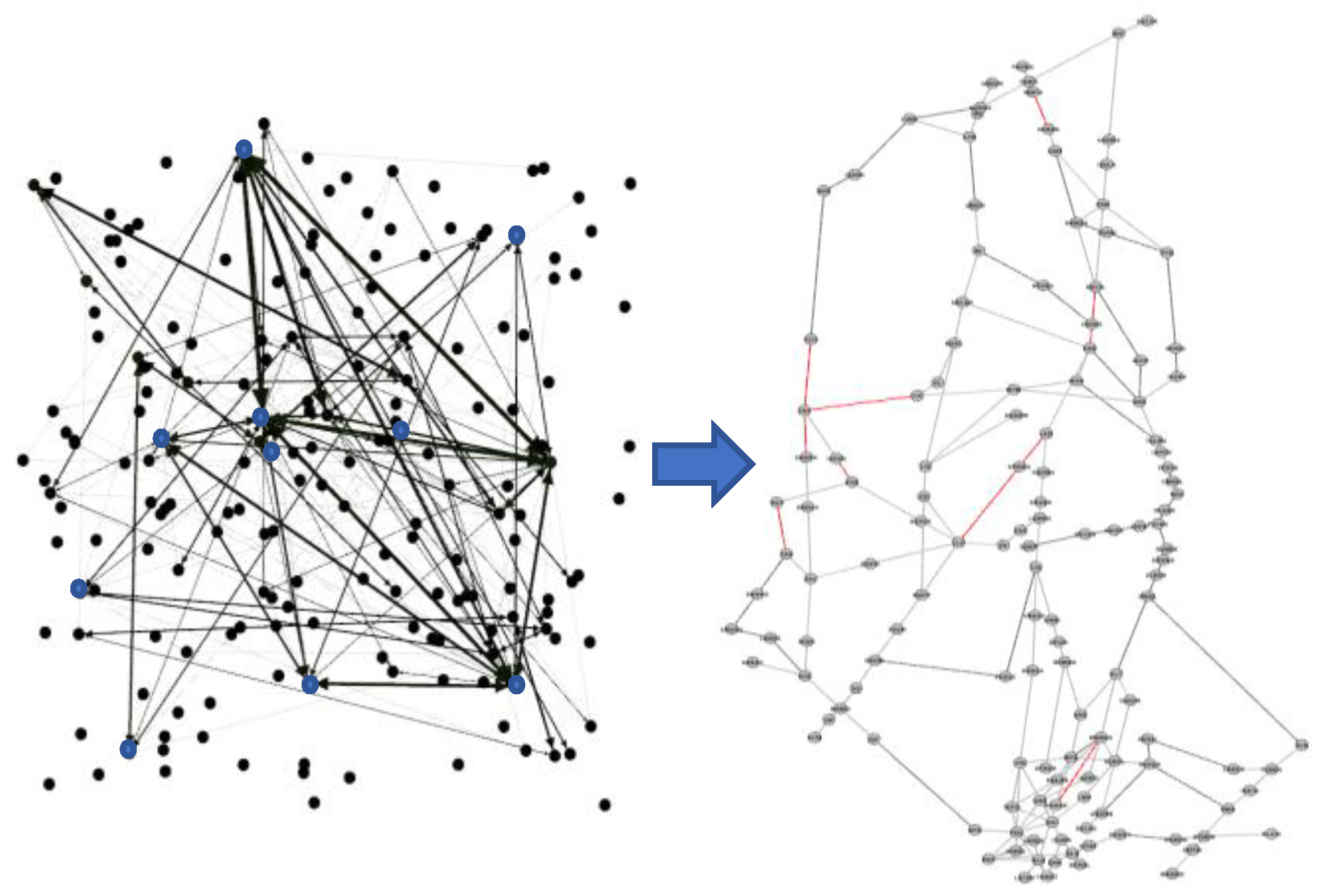
3. Segment Network Correlation Construction and Analysis
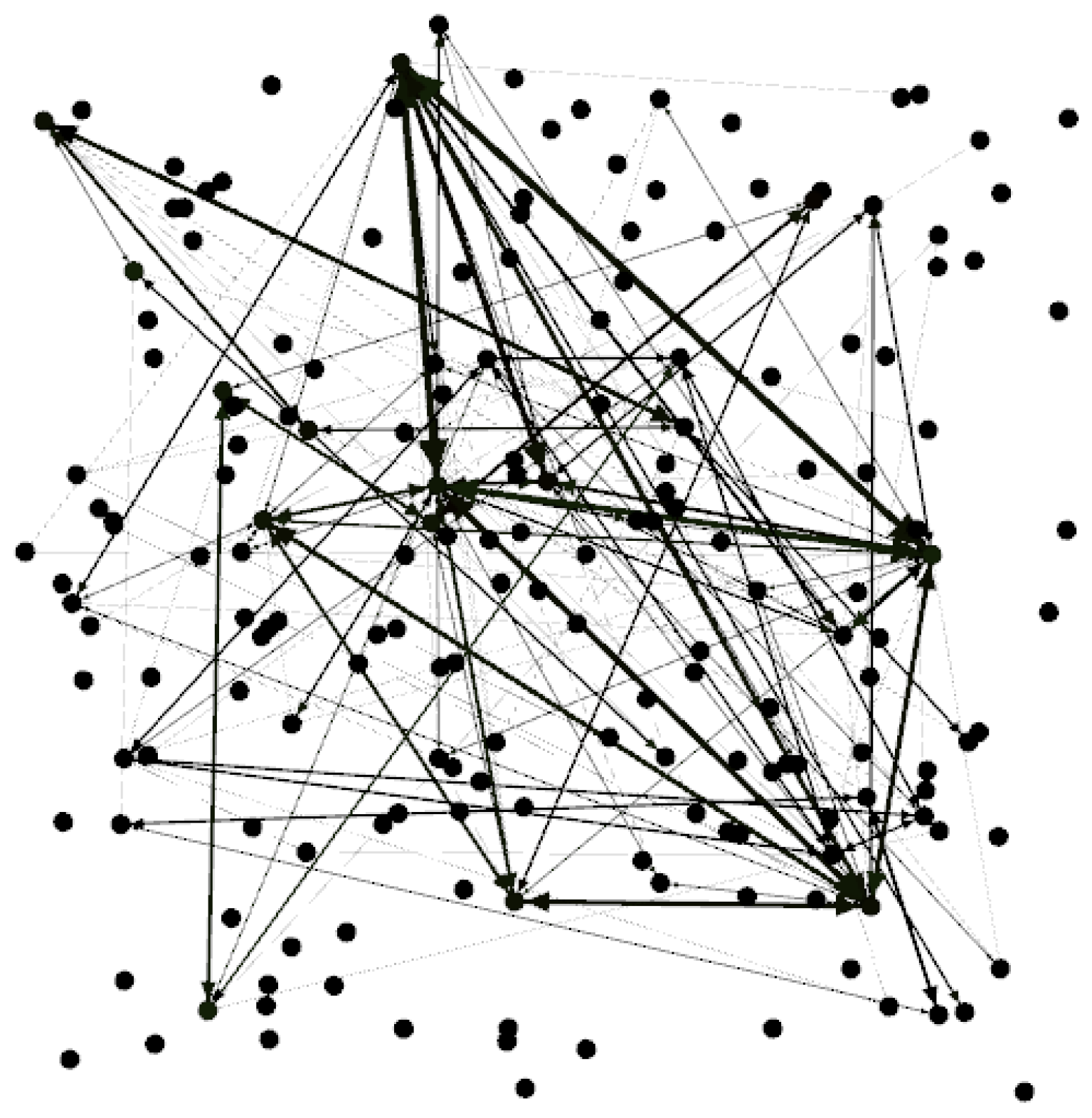
3.1. Construct Segment Network Correlation Models
| Number | Source | Target | Weight |
| 1 | HOK-OBLIK | DAPRO-AKUBA | 0.8438 |
| 2 | DAPRO-AKUBA | IDUMA-GLN | 0.8350 |
| 3 | HOK-OBLIK | P61-ENH | 0.6875 |
| 4 | BIPOP-KD | AKUBA-LUMKO | 0.7174 |
| 5 | BIPOP-KD | P234-P373 | 0.6739 |
| ... | ... | ... | ... |
| 281 | IGOMO-ZK | P159-ZHJ | 0.5258 |
| 282 | AKUBA-LUMKO | FYG-ZHO | 0.53125 |
| 283 | ENH-P373 | P159-ZHJ | 0.5795 |
| 284 | P159-ZHJ | ENH-P373 | 0.5604 |
| 285 | HOK-OBLIK | P159-ZHJ | 0.5667 |
3.2. Indicators of Correlation Topological Properties of the Segment Network
| serial number | numerical value | Corresponding nodes | rankings |
|---|---|---|---|
| 41 | 0.537313433 | YIH-ENH | 1 |
| 40 | 0.507462687 | ENH-P373 | 2 |
| 48 | 0.507462687 | GOSMA-LLC | 3 |
| 42 | 0.47761194 | P61-ENH | 4 |
| 47 | 0.358208955 | GOSMA-LKO | 5 |
| 45 | 0.298507463 | VIPAP-GLN | 6 |
| 46 | 0.298507463 | IDUMA-GLN | 7 |
| 43 | 0.268656716 | FYG-ZHO | 8 |
| 51 | 0.268656716 | GUGAM-LIN | 9 |
| 55 | 0.268656716 | HOK-OBLIK | 10 |
| serial number | numerical value | Corresponding nodes | rankings |
|---|---|---|---|
| 41 | 0.051892546 | YIH-ENH | 1 |
| 40 | 0.050518788 | ENH-P373 | 2 |
| 48 | 0.046513524 | GOSMA-LLC | 3 |
| 42 | 0.04650554 | P61-ENH | 4 |
| 46 | 0.034805308 | IDUMA-GLN | 5 |
| 45 | 0.033696961 | VIPAP-GLN | 6 |
| 47 | 0.032517298 | GOSMA-LKO | 7 |
| 56 | 0.032175325 | WHA-HOK | 8 |
| 43 | 0.031745663 | FYG-ZHO | 9 |
| 51 | 0.030911148 | GUGAM-LIN | 10 |
| serial number | numerical value | Corresponding nodes | rankings |
|---|---|---|---|
| 48 | 0.362698825 | GOSMA-LLC | 1 |
| 41 | 0.361836666 | YIH-ENH | 2 |
| 40 | 0.34975014 | ENH-P373 | 3 |
| 42 | 0.336310779 | P61-ENH | 4 |
| 47 | 0.279491837 | GOSMA-LKO | 5 |
| 97 | 0.252152445 | MABAG-NOMAR | 6 |
| 55 | 0.243061461 | HOK-OBLIK | 7 |
| 59 | 0.2344985 | HUY-TRN | 8 |
| 35 | 0.167105634 | IGPAR-DYG | 9 |
| 31 | 0.166197437 | DUBAG-NOPIN | 10 |
4. Comparative Analysis of Examples
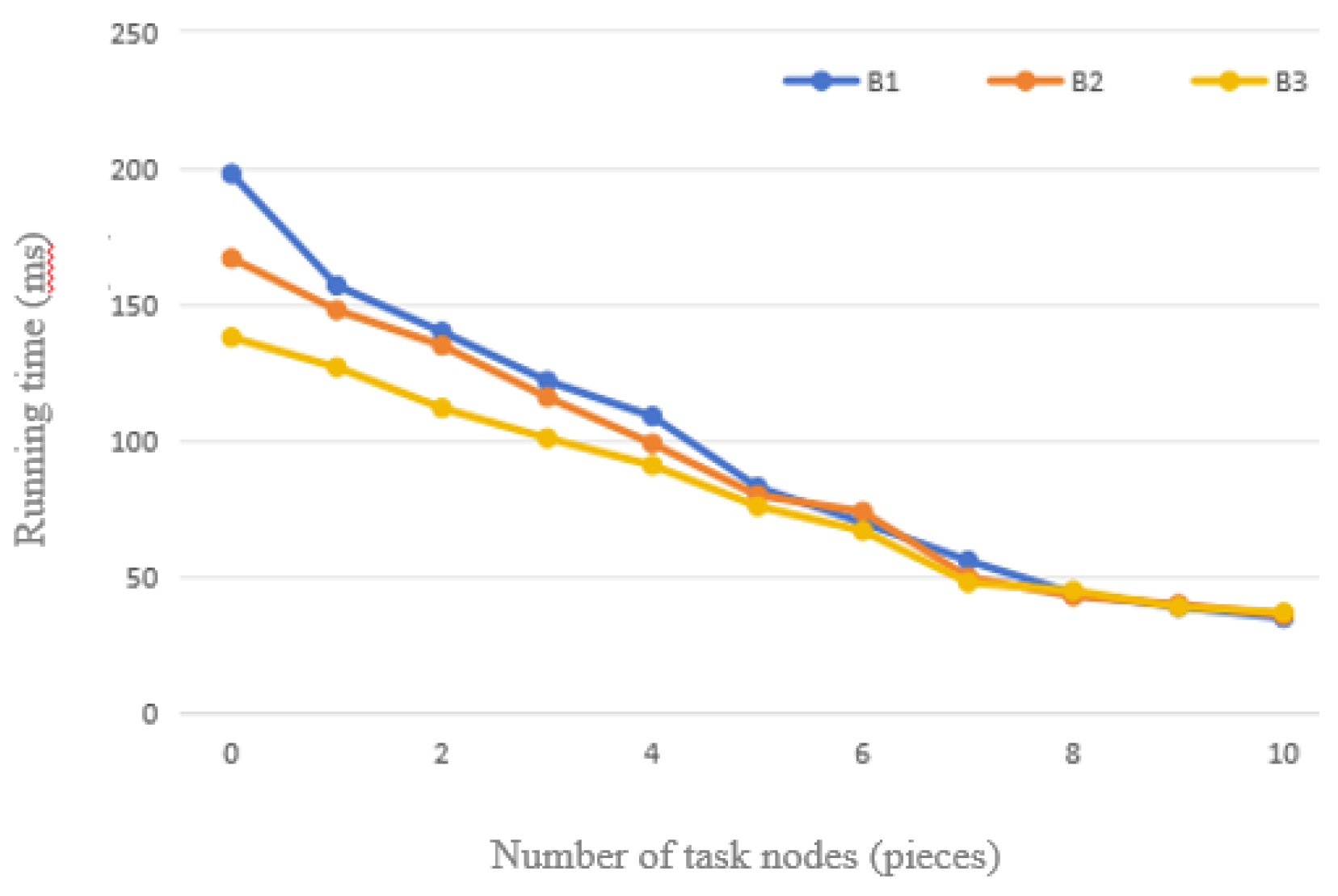
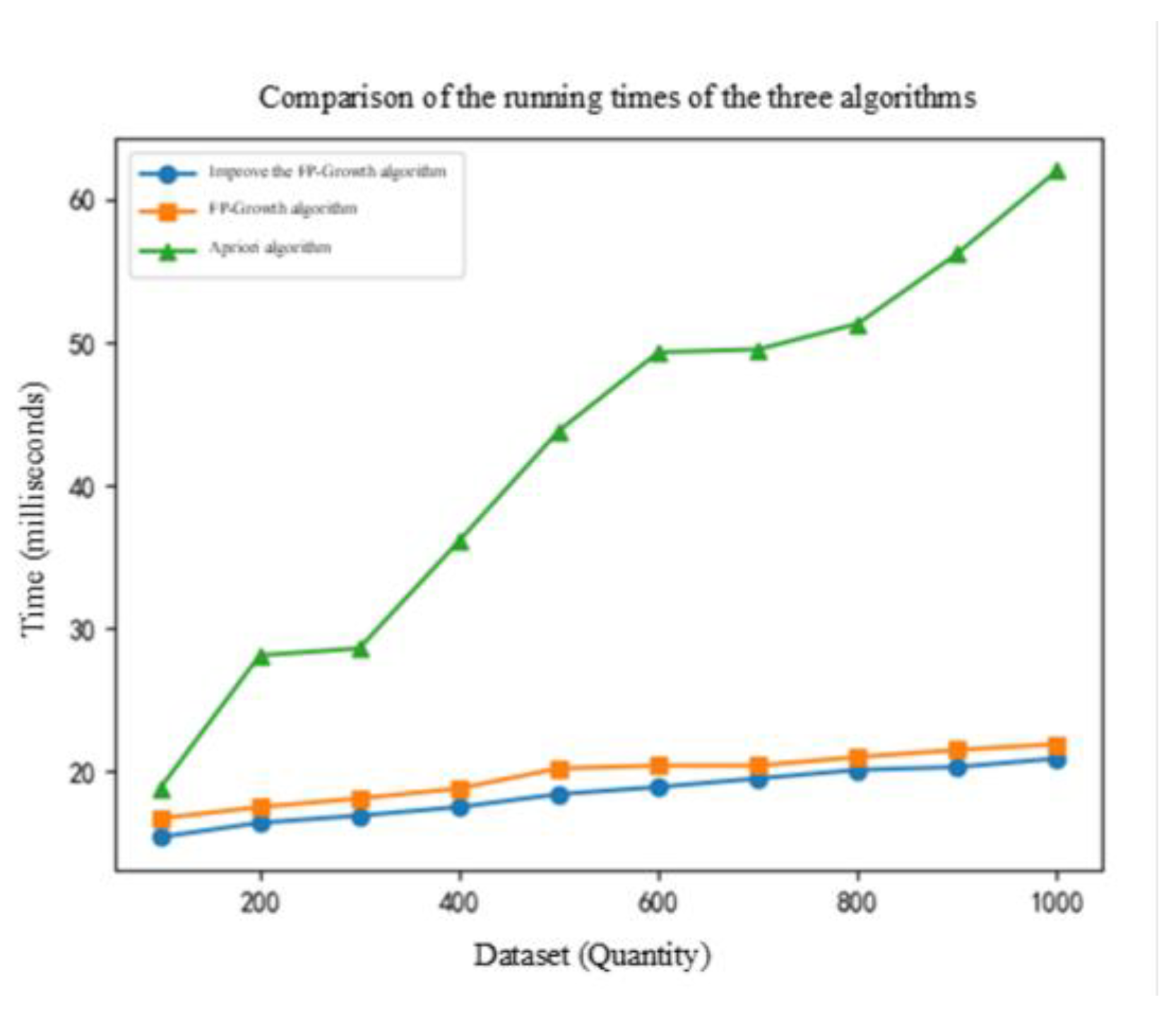
4.1. Algorithm Time Comparison
4.2. Node Performance Testing
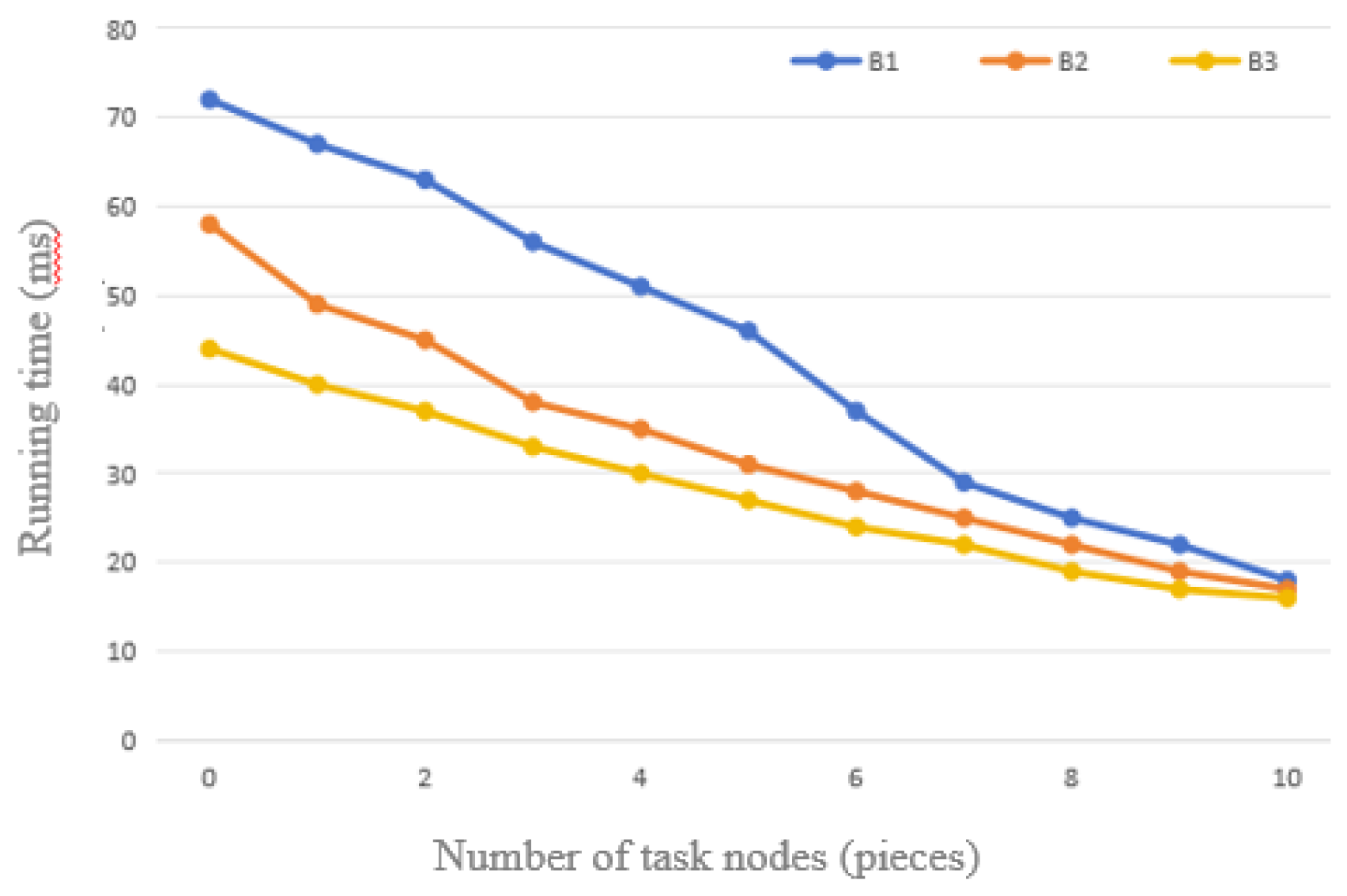
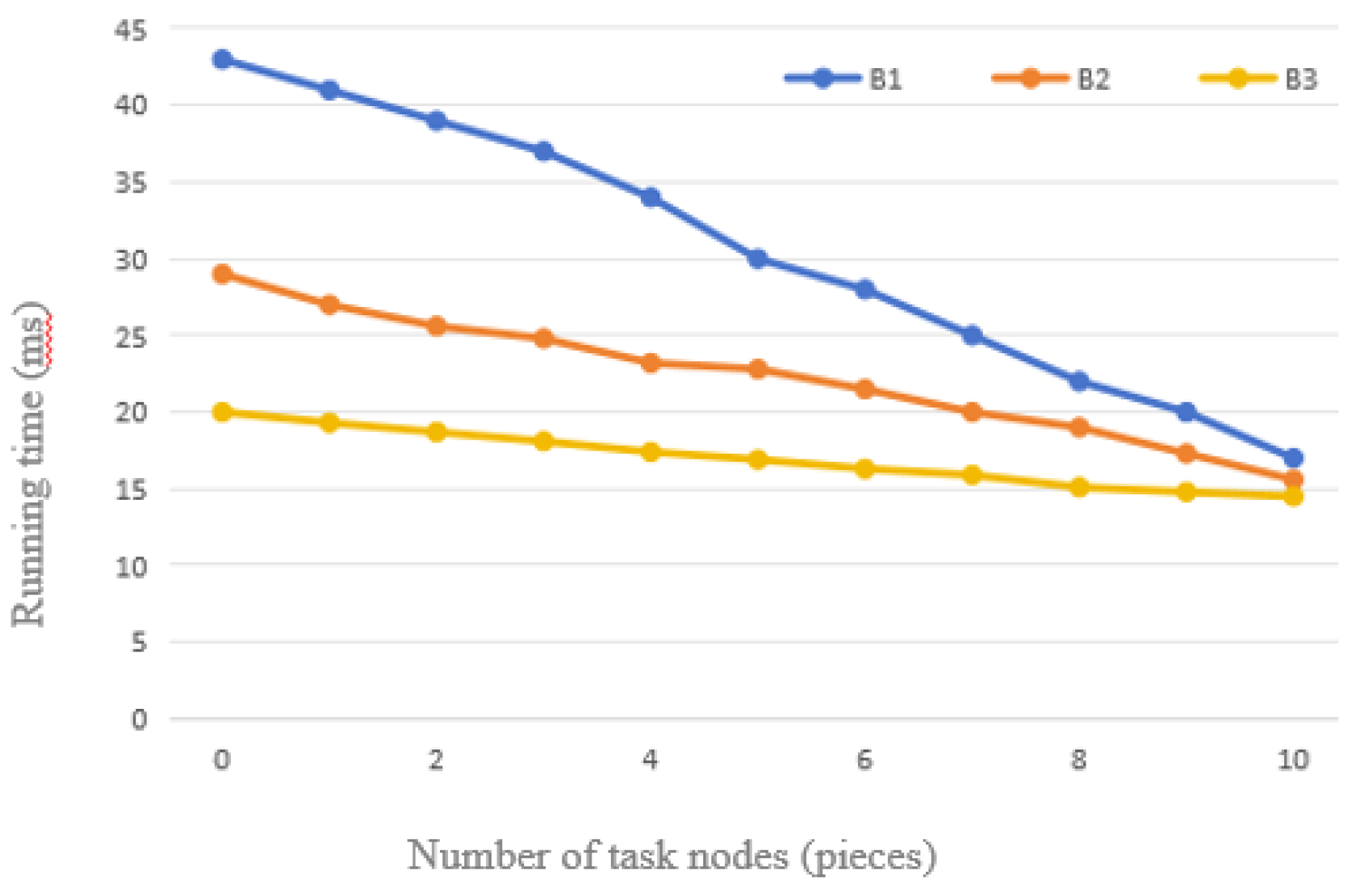
4.3. Reality of Connecting the Edges
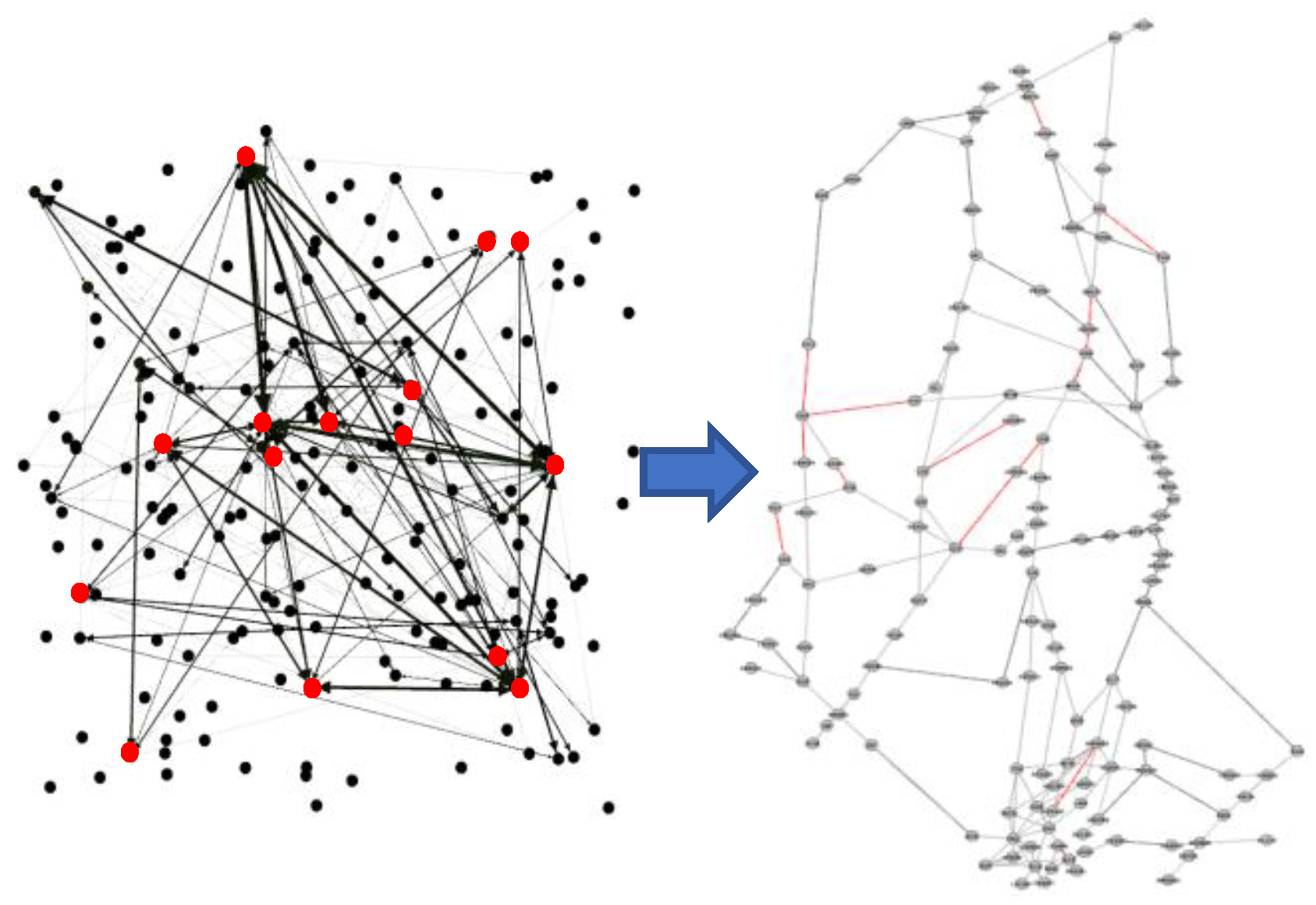
5. Conclusion
References
- Yu Shasha,Chen Xingyu. Key technological innovations and challenges in urban air transportation[J/OL]. Journal of Aviation,1-15[2024-07-05].
- ZHANG Zhaoning,ZHANG Jia. Propagation of large flight delays based on SEIR model[J]. Science, Technology and Engineering,2020,20(08):3356-3361.
- Li Shanmei,Zhou Xiangzhi. Airport departure flight delay prediction based on S2S-CNN-GRU[J]. Chinese Journal of Safety Science,2023,33(08):93-100. [CrossRef]
- LI Ang, ZHAI Wenpeng, AN Qi. Flight time optimization of North China airport cluster for on-time performance improvement[J]. Computer Simulation,2020,37(02):38-40.
- Sun Yue,Ding Jian. Stacking integrated prediction model of flight delays for severe weather[J/OL]. Big Data,1-18[2024-07-05].
- LIU Fei,YU Minjian,LI Jiawei,et al. Flight conflict critical point identification based on complex network theory[J]. Journal of Air Force Engineering University(Natural Science Edition),2019,20(04):19-25.
- Lin He. Impact of optimization and innovation of air transport system on enhancing aviation safety[J]. China Aviation Weekly, 2023,(29):76-78.
- XU Feng,YIN Jia-Nan,YANG Wen-Dong,et al. Reliability analysis of air-rail intermodal super network under flight delay perturbation[J/OL]. Complex Systems and Complexity Science,1-10[2024-07-05].
- Cai, Guan-Wen. On the analysis and solution of aviation communication and navigation interference factors[J]. China Aviation Weekly,2021,(03):58-59.
- WANG Shaopeng,NIU Chaoyu. Clustered frequent pattern mining for time-ordered transaction data[J/OL]. Journal of Software,1-20[2024-07-05].
- LIU Donghua,ZHAO Xing,ZHAO Jiangping. Dynamic association network analysis of tower crane accident causation based on improved Apriori algorithm[J]. Safety and Environmental Engineering,2023,30(06):106-112.
- Qiao Yangyang,Wang Lijuan. Simulation of parallel FP-Growth mining algorithm for data point locations[J]. Computer Simulation,2023,40(05):501-505.
- Xie Zhaoxian,Zou Xingmin,Zhang Wenjing. An efficient decision tree parameter pruning algorithm for large datasets[J]. Computer Engineering,2024,50(01):156-165.
- XU Xianze,TAN Shenghuang,LIU Jing et al. User location prediction based on parallel pattern mining and path matching[J]. Journal of Northeastern University (Natural Science Edition),2020,41(06):767-770+777.
- WANG Yu,WEN Guobing,LEI Di,et al. Optimization design of airport route network under two-layer planning model[J]. Transportation Science and Economy,2023,25(02):24-31.
- Zhang Haoyu. Research on flight delay propagation characteristics based on complex network theory [D]. Nanjing University of Aeronautics and Astronautics, 2018.
- Guan Xiangmin, Zhao Shuazhe. Research on airport risk communication network for aviation network[J/OL]. Journal of Beijing University of Aeronautics and Astronautics,1-14[2023-04-23].
- WANG Xinglong, ZHU Lina, SHI Zongbei. Modeling and correlation analysis of multilayer route aggregation network [J]. Science, Technology and Engineering, 2020, 20(3):1243-1249.
- HU Funian,YANG Weidan,CHEN Jun. Robustness assessment of power infophysical systems based on key nodes[J/OL]. Complex Systems and Complexity Science,1-9[2024-06-30].
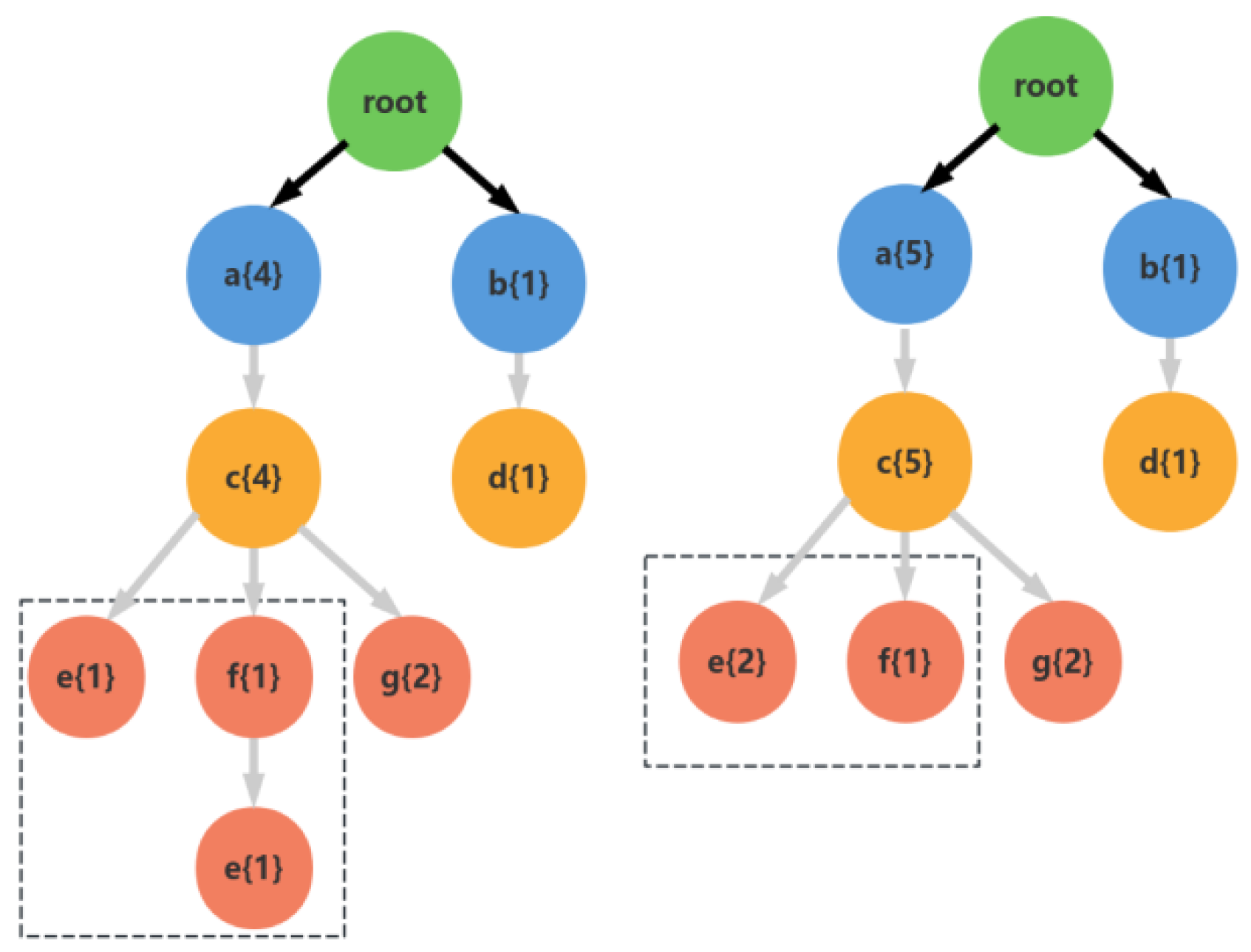
| Basic parameters | average value | maximum values | minimum value |
|---|---|---|---|
| Degree Centrality | 0.1251 | 0.5373 | 0.01493 |
| PageRank | 0.0147 | 0.0519 | 0.0022 |
| Eigenvector Centrality | 0.0999 | 0.3627 | 0.0001 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





