Emergence of Physical Constants from the Informational Ω-Background of Spacetime

1. Introduction

The idea that spacetime and its structure may emerge from a deeper, non-geometric substrate has gained significant traction in theoretical physics. Notable approaches, such as causal set theory, holographic duality, and quantum information geometry, seek to reconstruct continuum physics from primitive, often informational, building blocks [1,2,3]. These models share a core aim: to understand the origin of geometry, fields, and physical law from a more fundamental level. Among the persistent mysteries in physics, the dimensionless fine-structure constant α ≈ 1/137 stands out [4]. It appears across domains, from quantum electrodynamics to atomic structure, yet its value remains unexplained. Why this number unites the quantum of action ℏ, the speed of light c, vacuum impedance (ε₀, μ₀), and the elementary charge e has no established theoretical basis.

The present work builds upon the Ω-dimension framework developed in earlier studies [5,6], in which spacetime and its physical content emerge through constraint-governed projection from a non-metric identity domain Ω. Identity signatures $\sigma \in \mathsf{\Omega }$ represent latent, timeless structures whose realization as fields or particles depends on compatibility with constraint classes C ⊂ ${\mathsf{\Omega }}^n$. Observable entities arise via projection $\mathsf{\Pi }:\mathsf{\Omega }\to \mathrm{M}$, as constraint-satisfying instantiations and not as dynamic evolutions. Unlike causal set theory [1], where causality orders discrete events, the $\mathsf{\Omega }$-framework defines causality as a structural precedence relation among projections, grounded in identity coherence. In contrast to holographic duality [2], no boundary manifold or conformal field theory is assumed. Spacetime structure emerges through projection geometry. While tensor network models [3] link geometry to entanglement, we reinterpret entanglement as a byproduct of non-factorizable constraint structure in $\mathsf{\Omega }$. This study demonstrates that key physical constants, including ℏ, G, ε₀, μ₀, c, e and α, arise as spectral invariants of the projection process. These constants are reframed as geometric and informational consequences of identity realization and not as empirical inputs. The result is a unified ontological account of constants, derived from structural properties of the projection map$\Pi$, and consistent with earlier theoretical and gravitational components of the framework [5,6].

2. The Ontological Vacuum of Fundamental Constants

Fundamental constants play a dual role in physical theory. They mediate between unit systems and define the structural couplings giving form to physical law. Among them, the speed of light c sets the relationship between temporal and spatial measurements, defining the invariant light cone that underlies Lorentzian spacetime geometry. Planck’s constant ℏ links energy and frequency through the quantum relation $E=\hslash \omega$, anchoring the wave-particle duality and setting the scale at which classical mechanics gives way to quantum discreteness. The vacuum permittivity ε₀ and permeability μ₀ define the normalization of electromagnetic fields in Maxwell’s equations and through them, determine the wave impedance and the propagation speed of light in vacuum. Newton’s gravitational constant G sets the coupling strength between energy-momentum and curvature in general relativity, establishing the response of spacetime geometry to mass and energy distributions. The elementary charge e quantizes the interaction strength of electrically charged particles and governs the magnitude of electromagnetic forces.[7]

These constants do not exist in isolation. Their interdependence is captured in dimensionless quantities such as the fine-structure constant $\alpha$, which governs the strength of electromagnetic interactions relative to the quantum and relativistic structure of spacetime. Though the universal constants are fundamental to theoretical physics, their numerical values remain empirical facts. Theories rely on them, are structured around them, and predict within their framework, but offer no account of why they take the values they do, or why they exist at all. There is no formal reason why the speed of light should be approximately $2.997\times {10}^8\hspace{0.17em}\mathrm{m}/\mathrm{s}$, or why the fine-structure constant should hover near 1/137. The standard model of particle physics and general relativity each depend on these constants as externally imposed parameters, fitted to observation rather than derived from first principles.

In this sense, the fundamental constants are the clearest indicators of the incompleteness of current theory. They mark the limits of explanation, the points at which description yields to assumption. The challenge (and the opportunity), is to find a deeper structure in which these constants are not imposed, but instead emerge as necessary features of an underlying architecture. The Ω-framework addresses this challenge by reinterpreting these constants as spectral invariants of projection. They are emergent quantities that arise from the way informational identity is filtered into observable spacetime through constraint-satisfying mappings. In this view, the empirical role of constants is a shadow of their ontological function to quantify the structure and limitation of reality as a projection.

3. Mathematical Framework of the Ω-Theory

The Ω-dimension, as introduced in [5,6], is conceived as a non-metric, non-dynamical and timeless domain encoding all identity structures admissible in the physical universe. In the present formulation, we introduce the minimal mathematical formalism necessary to derive physical constants as structural invariants of projection from Ω to the emergent manifold$M$. We work within a generalized algebraic-topological setting, with emphasis on projection admissibility, constraint class compatibility and curvature-induced informational resistance. A visual overview of the $\mathsf{\Omega }$→ $M$ projection process, including the role of identity signatures, constraint embeddings, and projection latency, is provided in [5], Figures 1, 3–5. These schematics illustrate the structural underpinnings of identity realization and entanglement in the projection-based framework.

3.1. Ontological Preliminaries

Let Ω denote a stratified topological space, whose elements σ ∈ Ω represent identity signatures. Each σ encodes the intrinsic, timeless structure of a potentially realizable physical entity, be it particle, field, or composite configuration, independent of its spacetime trajectory.

A subset C ⊂ ${\mathsf{\Omega }}^n$ is called a constraint class if all n-tuples $({\sigma }_1,\dots ,{\sigma }_{\mathrm{n}})\in C$ are simultaneously projectable to a shared neighborhood in $M$. Such classes formalize the idea of co-projectability and may carry additional structure such as algebraic closure, topological connectedness, or homotopy invariance, depending on the physical domain.

The projection operator $\Pi :\mathsf{\Omega }\to M$ is defined as a surjective, structure-preserving map that instantiates an identity signature σ ∈ Ω into an admissible field configuration $\Pi \left(\mathsf{\sigma }\right)\in {\mathcal{F}}_{\mathcal{x}}\subset \mathcal{F}\left(M\right)$ at point $x\in M$, where $\mathcal{F}\left(M\right)$ is the space of physically admissible field configurations on $M$. Projection is only defined where σ is compatible with the local constraint geometry at x.

3.1.1. Structural Quantities and Emergent Scales

The projection latency $\tau \left(\sigma \right)$ is the minimal interval between two successive compatible instantiations of a signature $\sigma$ in $M$. It is interpreted as an informational delay reflecting projection resistance and gives rise to temporal granularity and inertia.

The projection curvature $\kappa \left(\sigma \right)$quantifies second-order variation of projection admissibility. Let $C_x\subset \mathsf{\Omega }$be the fiber of constraint classes over a neighborhood of $x\in M$, then:

$$\kappa \left(\sigma \right)≔{‖{\nabla }_C{\nabla }_C\mathsf{\Pi }\left(\sigma \right)‖}^2,$$

(1)

which captures the local embedding tension of $\sigma$ in deformable constraint structures.

The projection impedance tensor ${\mathbf{Z}}_{\mu \nu }\left(x\right)$ encodes directional resistance to projection at a point $x\in M$. Formally, for all $\sigma \in {\mathsf{\Omega }}_x$, where ${\mathsf{\Omega }}_x$ ⊂ $\mathsf{\Omega }$ is the set of signatures admissible at $x$, we define:

$${\mathbf{Z}}_{\mu \nu }\left(x\right)≔\sum _{\sigma \in {\mathsf{\Omega }}_x}\left({\displaystyle \frac{{\partial }^2\mathsf{\Pi }\left(\sigma \right)}{\partial x^{\mu }\partial x^{\mathsf{\nu }}}}\right),$$

(2)

This tensor represents the resistance of the projection interface to geometric instantiation along different spacetime directions. Subcomponents ${\mathbf{Z}}_{\mu \nu }^{\left(E\right)}$ and ${\mathbf{Z}}_{\mu \nu }^{\left(B\right)}$ represent electric and magnetic impedance structures respectively. The charactristic projection action associated with a signature $\sigma \in \mathsf{\Omega }$ is given by:

$$\mathcal{S}\left(\sigma \right)≔\tau \left(\sigma \right)\cdot \kappa \left(\sigma \right),$$

(3)

quantifying the effective resistance of $\mathsf{\Omega }$→ $M$ instantiation due to temporal and geometric tension. Planck’s constant ℏ is interpreted as the threshold value of admissible projection action, reflecting the existence of a discrete lower bound on physically stable projection structures:

$$\hslash ≔\underset{\sigma \in \Omega }{\mathit{inf}}\mathcal{S}\left(\sigma \right).$$

(4)

3.1.2. Constraint Topology and Charge Quantization

Beyond local projection structure, the global topological behavior of constraint classes determines the emergence of quantized observables. Let $\mathcal{C}$ denote the bundle of constraint classes over $M$. A closed path $\mathsf{\gamma }\subset \mathcal{C}$ induces a holonomy class $\left[\mathsf{\gamma }\right]\in H^1\left(\mathcal{C},\mathbb{Z}\right)$). The associated charge content of a signature $\sigma \in \mathsf{\Omega }$ is given by:

$$e\left(\sigma \right)≔{\displaystyle \frac{1}{2\pi }}{\oint }_{\gamma }\mathcal{A},$$

(5)

where $\mathcal{A}$ is a U(1)-valued connection over $\mathcal{C}$, encoding phase alignment of projective embeddings. The elementary electric charge $e$ is the minimal non-zero quantized holonomy compatible with projection.

3.2. Geometry Induced by Projection Impedance

The projection impedance tensor ${\mathbf{Z}}_{\mu \nu }\left(x\right)$ encodes the structural resistance to identity realization in different spacetime directions at point $x\in M$. As a symmetric bilinear map over the tangent space $T\times M$, it satisfies ${\mathbf{Z}}_{\mu \nu }={\mathbf{Z}}_{\nu \mu }$ and is assumed to be positive-definite under physically realizable projection regimes. In this section, we formalize the geometric role of ${\mathbf{Z}}_{\mu \nu }$ by interpreting it as an effective metric tensor and define a projection-compatible connection that gives rise to emergent curvature within the projection manifold.

3.2.1. Effective Connection from Projection Impedance

Given that ${\mathbf{Z}}_{\mu \nu }$ plays the role of a structural metric over spacetime induced by projection impedance, we define the associated Levi-Civita–like connection coefficients ${\Gamma }_{\mu \nu }^{\lambda }$ by the usual metric-compatibility and torsion-free conditions:

$${\Gamma }_{\mu \nu }^{\lambda }≔{\displaystyle \frac{1}{2}}{\mathbf{Z}}^{\mathsf{\lambda }\mathsf{\kappa }}\left({\partial }_{\mathsf{\mu }}{\mathbf{Z}}_{\mathsf{\nu }\mathsf{\kappa }}+{\partial }_{\mathsf{\nu }}{\mathbf{Z}}_{\mathsf{\mu }\mathsf{\kappa }}-{\partial }_{\mathsf{\kappa }}{\mathbf{Z}}_{\mathsf{\mu }\mathsf{\nu }}\right),$$

(6)

where ${\mathbf{Z}}^{\lambda \kappa }$ is the inverse of ${\mathbf{Z}}_{\mu \nu }$, satisfying ${\mathbf{Z}}^{\lambda \kappa }{\mathbf{Z}}_{\kappa \rho }={\delta }_{\rho }^{\mathsf{\lambda }}$. This connection enables us to define parallel transport and geodesic deviation directly in terms of projection impedance. The interpretation here is geometric. Projection resistance defines not just limits on realization, but induces a notion of effective distance and curvature. Hence, ${\mathbf{Z}}_{\mu \nu }$ behaves as a pseudo-metric whose Christoffel symbols reflect how projection strain accumulates under coordinate variation in $M$.

3.2.2. Emergent Curvature from Projection Geometry

Using the connection ${\Gamma }_{\mu \nu }^{\lambda }$, we define the corresponding Riemann curvature tensor:

$${\mathcal{R}}_{ \mu \nu \rho }^{\sigma }≔{\partial }_{\nu }{\Gamma }_{\mu \rho }^{\sigma }-{\partial }_{\rho }{\Gamma }_{\mu \nu }^{\sigma }+{\Gamma }_{\nu \lambda }^{\sigma }{\Gamma }_{\mu \rho }^{\lambda }-{\Gamma }_{\rho \lambda }^{\sigma }{\Gamma }_{\mu \nu }^{\lambda }.$$

(7)

From this, the Ricci tensor is obtained by contraction: ${\mathcal{R}}_{\mu \nu }≔{\mathcal{R}}_{ \mu \lambda \nu }^{\lambda },$ and the scalar curvature is defined as:

$$\mathcal{R}≔{\mathbf{Z}}^{\mu \nu }{\mathcal{R}}_{\mu \nu }.$$

(8)

This curvature is interpreted as the second-order resistance of the projection substrate to coherent constraint embedding. Unlike in general relativity, where curvature arises from stress-energy, here it is a measure of the internal structural response of the projection interface.

3.2.3. Emergent Metric and Geodesics

By construction, ${\mathbf{Z}}_{\mu \nu }$ behaves as an effective metric:

$${\mathbf{g}}_{\mu \nu }\left(x\right)≔{\mathbf{Z}}_{\mu \nu }\left(x\right).$$

(9)

This emergent metric determines geodesics as minimal-impedance paths of projection flow:

$${\displaystyle \frac{d^2{x}^{\lambda }}{d{s}^2}}+{\Gamma }_{\mu \nu }^{\lambda }{\displaystyle \frac{d{x}^{\mu }}{ds}}{\displaystyle \frac{d{x}^{\nu }}{ds}}=0.$$

(10)

In the $\mathsf{\Omega }$-framework, this geodesic equation describes the default projection trajectory for an identity signature $\sigma \in \mathsf{\Omega }$ under unperturbed projection into $M$. Curvature in this geometry indicates structural resistance to such realization, and hence aligns with the appearance of gravitational phenomena.

This emergent geometric framework, based entirely on projection-theoretic quantities, will serve as the foundation for deriving Newton’s constant and the gravitational field equations in section 5. The advantage of this approach is that curvature, causal structure and dynamical interaction all emerge from the same primitive: the projection impedance tensor, itself a consequence of constraint geometry in $\mathsf{\Omega }$.

3.3. Axioms of Projection Geometry

To ground the emergence of geometric structure, causal ordering, and quantized observables within a projection-based ontology, we now introduce a minimal set of structural axioms. These formal principles define the admissibility, coherence, and constraint-governed nature of identity projection from the $\mathsf{\Omega }$-domain into the spacetime manifold M. Rather than prescribing dynamics, the axioms characterize how projection conditions give rise to effective temporal structure, embedding resistance, and global topological constraints.

• Timeless identity: Identity signatures in $\mathsf{\Omega }$ are non-evolving and persistent. Time arises solely from ordering relations between projections $\Pi \left({\sigma }_i\right)\prec \Pi \left({\sigma }_j\right)$ where structural compatibility imposes a partial ordering.
• Constraint-governed projection: Projection $\Pi \left(\sigma \right)$ is admissible at $x\in M$ only if $\sigma \in C_x\subset {\mathsf{\Omega }}^{\mathrm{n}}$ for some constraint class compatible with the ambient field structure.
• Projection resistance: The probability amplitude for a projection event is modulated by local projection impedance ${\mathbf{Z}}_{\mu \nu }\left(x\right)$ and decays exponentially with increasing latency–curvature action $\mathcal{S}\left(\sigma \right)$.
• Topological quantization: Holonomy over closed constraint cycles induces discrete topological invariants. Projection is only globally coherent when topological class invariants (e.g., charge) are preserved.

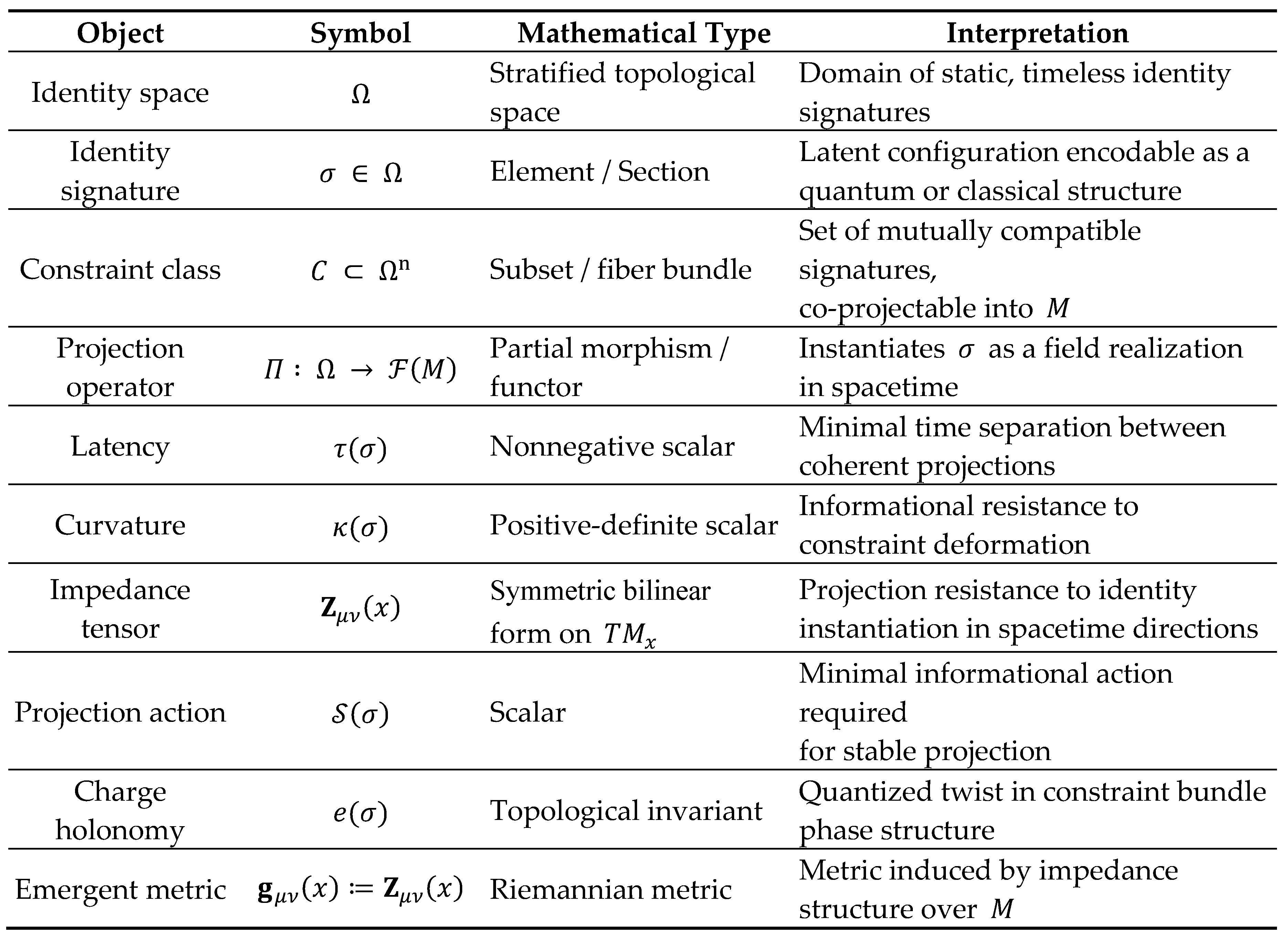
3.4. Core Mathematical Entities

The core mathematical entities introduced above, along with their types and roles within the $\mathsf{\Omega }$-framework, are summarized in the following Table 1 for clarity and reference:

4. Projection Mechanics and the Emergence of Constants

This section reconstructs fundamental constants as structural invariants of admissible identity realization. Each constant appears as a spectral feature of projection mechanics, tied to the geometry and topology of constraint-saturated identity flow into the observable manifold.

4.1. Projection Impedance and the Emergence of Electromagnetic Constants

The electromagnetic vacuum parameters $\epsilon ₀$ and $\mu ₀$, as well as the speed of light $c$, are interpreted in the Ω-framework as structural features of the projection impedance tensor ${\mathbf{Z}}_{\mu \mathsf{\nu }}\left(x\right)$. This tensor, defined over the tangent bundle of spacetime, quantifies the local resistance of the projection interface to directional field instantiation. Its electric and magnetic components, ${\mathbf{Z}}_{\mu \nu }^{\left(E\right)}$ and ${\mathbf{Z}}_{\mu \nu }^{\left(B\right)}$, govern the emergence of Maxwell field structure and give rise to the wave impedance and propagation speed of light:

$$c={\displaystyle \frac{1}{\sqrt{{\epsilon }_0{\mu }_0}}},\hspace{1em}{Z}_0=\sqrt{{\displaystyle \frac{{\mu }_0}{{\epsilon }_0}}}.$$

(11)

We now show how these quantities arise naturally from the tensorial structure of ${\mathbf{Z}}_{\mu \nu }\left(x\right)$ under stable projection regimes.

Electromagnetic observables correspond to antisymmetric field structures which require dual compatibility: both electric and magnetic components must be instantiated coherently. We therefore partition the impedance tensor as

$${\mathbf{Z}}_{\mu \nu }\left(x\right)={\mathbf{Z}}_{\mu \nu }^{\left(E\right)}\left(x\right)+{\mathbf{Z}}_{\mu \nu }^{\left(B\right)}\left(x\right),$$

(12)

where ${\mathbf{Z}}_{\mu \nu }^{\left(E\right)}$ and ${\mathbf{Z}}_{\mu \nu }^{\left(B\right)}$ quantify the projection impedance for electric and magnetic degrees of freedom, respectively. Each term can be understood as a functional over constraint gradients:

$${\mathbf{Z}}_{\mu \nu }^{\left(E\right)}\left(x\right)≔{\int }_{{\mathsf{\Omega }}_E}\mathcal{D}\sigma \hspace{0.17em}\left({\displaystyle \frac{{\mathsf{\delta }}^2\mathsf{\Pi }\left(\sigma \right)}{\mathsf{\delta }{C}^2}}\cdot {\displaystyle \frac{\partial C}{\partial x^{\mu }}}{\displaystyle \frac{\partial C}{\partial x^{\nu }}}\right),$$

(13)

with an analogous expression for ${\mathbf{Z}}_{\mu \nu }^{\left(B\right)}$, where ${\mathsf{\Omega }}_B\subset \mathsf{\Omega }$ denotes the subspace of magnetically active signatures. We define the scalar projection impedances associated with electric and magnetic identity projection as ${\mathcal{Z}}_{\mathcal{E}}≔Tr\left({\mathbf{Z}}_{\mathsf{\mu }\mathsf{\nu }}^{\left(E\right)}\right),{\mathcal{Z}}_{\mathcal{B}}≔Tr\left({\mathbf{Z}}_{\mathsf{\mu }\mathsf{\nu }}^{\left(B\right)}\right),$ where each trace quantifies the resistance of the projection map $\Pi$ to instantiating coherent field structures under the constraints associated with ${\mathsf{\Omega }}_{\mathrm{E}}$ or ${\mathsf{\Omega }}_{\mathrm{B}}$, respectively.

To interpret these quantities in relation to known physical constants, we introduce the associated projection admittances ${\mathcal{A}}_{\mathcal{E}}≔{\mathcal{Z}}_{\mathcal{E}}^{-1}$ and ${\mathcal{A}}_{\mathcal{B}}≔{\mathcal{Z}}_{\mathcal{B}}^{-1}$. These scalars encode the ease with which electric and magnetic identity signatures can be coherently instantiated in the projection interface. We then identify ${\epsilon }_0≔{\mathcal{A}}_{\mathcal{E}}\mathrm{a}\mathrm{n}\mathrm{d}{\mu }_0≔{\mathcal{A}}_{\mathcal{B}},$ where ${\epsilon }_0$ and ${\mu }_0$ are interpreted as structural measures of projection admittance across $\mathsf{\Omega }$-compatible field configurations. This identification preserves the relationship:

$$c={\displaystyle \frac{1}{\sqrt{{\mathsf{\epsilon }}_0{\mathsf{\mu }}_0}}}={\left({\mathcal{Z}}_{\mathcal{E}}\cdot {\mathcal{Z}}_{\mathcal{B}}\right)}^{-1/2},$$

(14)

ensuring that the causal structure of spacetime arises as a derived limit on projection coherence, constrained jointly by electric and magnetic projection resistance.

While the expression for ${\mathcal{Z}}_{\mathcal{E}}$ involves standard second-order variations of $\Pi$ over spatial constraint gradients, the interpretation of ${\mathcal{Z}}_{\mathcal{B}}$ demands further structural clarity. Unlike electric projection, which aligns with directional displacements in constraint gradients, magnetic field instantiation is fundamentally rotational and nonlocal. In classical theory, magnetic fields arise from current loops and are described via the curl of the vector potential, suggesting that magnetic projection requires support for cyclic or closed constraint configurations.

We therefore interpret ${\mathbf{Z}}_{\mu \nu }^{\left(B\right)}$ as encoding rotational projection impedance, which is resistance to embedding loop-consistent constraint transitions. Mathematically, we extend the projection functional to include variation over constraint holonomy. Let $\mathsf{\Gamma }\subset \mathcal{C}$ be a contractible loop in constraint space (or a cycle class in $H_1\left(\mathcal{C},\mathbb{Z}\right)$) corresponding to a projected magnetic flux tube. We then generalize the magnetic projection impedance tensor as:

$${\mathbf{Z}}_{\mu \nu }^{\left(B\right)}\left(x\right)\sim {\int }_{\mathsf{\Gamma }\subset {\mathsf{\Omega }}_B}\mathcal{D}\sigma \left({\displaystyle \frac{{\mathsf{\delta }}^2\Pi \left(\sigma \right)}{\mathsf{\delta }{\Gamma }^2}}\cdot {\displaystyle \frac{\partial \Gamma }{\partial x^{\mu }}}{\displaystyle \frac{\partial \Gamma }{\partial x^{\nu }}}\right),$$

(15)

where ${\displaystyle \frac{{\delta }^2\Pi \left(\sigma \right)}{\delta {\Gamma }^2}}$ denotes a second-order response to holonomy deformation, analogous to curvature in a connection bundle over constraint space.

This construction captures the magnetic field’s resistance to nontrivial loop embedding in the projection structure. It justifies the identification of ${\mu }_0$with ${\mathcal{A}}_{\mathcal{B}}$, where ${\mathcal{Z}}_{\mathcal{B}}$ now includes cyclic and topological projection impedance. This naturally complements the interpretation of electric projection as local, and magnetic projection as nonlocal, aligning with duality principles in gauge theory. The full structure reflects the internal geometry of projection as a curl-divergence dual pair, unified under constraint topology in $\Omega$.

A deeper understanding of this structure will emerge in section 4.4, where charge quantization and the fine-structure constant $\alpha$ are derived from $\Omega$-holonomy. There, the topological quantization of projection cycles will reinforce the interpretation of ${\mu }_0$ as an emergent permeability rooted in closed-loop constraint propagation. In this formulation, ${\epsilon }_0$, ${\mu }_0$ and $c$ appear as derived invariants from the informational geometry of the $\mathsf{\Omega }\to M$mapping. They encode the metric and causal structure of spacetime via projection-resistance across distinct constraint subspaces.

4.2. Projection Granularity and the Origin of Planck’s Constant

Let $\sigma \in \mathsf{\Omega }$denote an identity signature characterized by a set of invariant structural features. We define a projection sequence as an ordered chain $\{{\Pi }_i\left(\sigma \right){\}}_{i\in \mathbb{N}}\subset \mathcal{F}\left(M\right)$ such that each element corresponds to a locally admissible realization of $\sigma$ under successive constraint configurations. This sequence is assumed to be locally coherent if the associated field instantiations satisfy compatibility conditions imposed by $\mathsf{\Omega }$-derived constraint classes.

Following its introduction in 3.1.1., we define the projection latency $\tau \left(\sigma \right)$as the infimum temporal interval between two successive realizations of $\sigma$ that preserve structural coherence:

$$\tau \left(\sigma \right)≔\inf \left\{t_{\mathrm{i}+1}-t_i\hspace{0.17em}|\hspace{0.17em}{\Pi }_{\mathrm{i}}\left(\sigma \right)\prec {\Pi }_{\mathrm{i}+1}\left(\sigma \right),\mathrm{ }{\Pi }_{\mathrm{i}+1}\left(\sigma \right)\in \mathrm{Adm}\left(C\right),\mathrm{ }C\subset {\mathsf{\Omega }}^{\mathrm{n}}\right\},$$

(16)

where ≺ denotes structural precedence in projection order, and $\mathrm{Adm}\left(C\right)$ denotes the set of projections compatible with constraint class $C$.

To relate projection latency to energy, we introduce the notion of projection curvature, denoted $\kappa \left(\sigma \right)$, defined as the informational deviation induced in a local constraint manifold by the instantiation of $\sigma$. Let $C\left(x\right)\subset \Omega$ denote the constraint fiber above $x\in M$. Then $\kappa \left(\sigma \right)≔ {‖{\nabla }_C{\nabla }_C\Pi \left(\sigma \right)‖}^2 is defined as shown in 3.1.1.,$with ${\nabla }_C$ denoting the derivative along directions of constraint deformation in $\Omega$-space. The quantity $\kappa$ measures the tension required to embed $\sigma$ in local field geometry.

We now define the minimal projection action associated with a signature $\sigma \in \mathsf{\Omega }$as: $\mathcal{S}\left(\sigma \right)≔\tau \left(\sigma \right)\cdot \kappa \left(\sigma \right).$ This quantity reflects the minimal informational area required to support coherent projection of $\sigma$ across its local realization domain. We postulate that Planck’s constant arises as the infimum action over all projectable signatures:

$$\hslash ≔\underset{\sigma \in \mathsf{\Omega }}{\inf }\mathcal{S}\left(\sigma \right)=\underset{\sigma \in \mathsf{\Omega }}{\inf }\left[\tau \left(\sigma \right)\cdot \kappa \left(\sigma \right)\right].$$

(17)

This definition gives $\mathrm{\hslash }$ a precise structural meaning. Planck’s constant ℏ is the smallest possible product of latency and curvature that allows a signature to be coherently projected into spacetime. In this context, ℏ is a fundamental quantum of projection coherence. It sets the lower bound on the informational complexity of any realizable identity transformation within spacetime. Projection events violating this lower bound either fragment structurally or fail to stabilize.

The canonical commutation relation $[x, p]=\mathrm{i}\mathrm{\hslash }$is reinterpreted as a non-commutativity of projection orderings within $\mathsf{\Omega }$-constrained configurations. Specifically, position-like observables correspond to projection localization in configuration space, while momentum-like observables correspond to projection curvature in constraint space. Their non-commutativity reflects the fact that the sequential instantiation of position and curvature-dependent projections leads to path-dependent informational structures. Thus, ℏ governs the non-commutative algebra of identity realization.

Furthermore, the Heisenberg uncertainty principle follows from the structure of projection latency itself. For a signature $\mathsf{\sigma }\in \mathsf{\Omega }$, the minimal resolvable energy-time window follows as ΔE ⋅ Δt ≥ ℏ, with Δt ≥ τ(σ) and ΔE ∼ κ(σ) interpreted as the minimal curvature modulation needed to support a localized excitation. In this sense, the uncertainty principle reflects a hard limit on informational resolution in the $\mathsf{\Omega }\to M$ mapping, rather than a statistical indeterminacy intrinsic to state vectors. Planck’s constant appears as the foundational granularity of the projection architecture. It encodes the irreducible action-area required for coherent identity instantiation and reveals the minimal scale at which information can structure spacetime without decohering or fragmenting.

4.3. Constraint Curvature and the Emergence of Newton’s Constant

Let us consider a region $U\subset M$of the emergent spacetime manifold populated by projections $\Pi \left({\sigma }_{\mathrm{i}}\right)$of identity signatures ${\sigma }_{\mathrm{i}}\in \mathsf{\Omega }$. As these projections instantiate, they deform the local informational environment, modifying the constraint topology that governs further projection. This deformation is encoded directly in the projection resistance structure. We interpret this resistance as the source of an emergent curvature over the projection bundle, reflecting informational deformation of constraint geometry.

As previously developed in Section 3.2, the symmetric projection impedance tensor ${\mathbf{Z}}_{\mu \nu }\left(x\right)$ defines an effective impedance metric ${\mathbf{g}}_{\mu \nu }\left(x\right)\propto {\mathbf{Z}}_{\mu \nu }\left(x\right)$ over spacetime, by quantifying directional resistance to field instantiation. To define curvature, we consider the second variation of projection compatibility under constraint deformation. The projection curvature tensor ${\mathcal{R}}_{\mathrm{ }\mu \nu \rho }^{\sigma }$ is defined by analogy with the Riemann tensor, constructed from the impedance connection coefficients ${\mathsf{\Gamma }}_{\mu \nu }^{\lambda }$ derived from ${\mathbf{Z}}_{\mu \nu }$. Contraction yields the Ricci tensor ${\mathcal{R}}_{\mu \nu }$, which quantifies projection curvature as experienced by compatible identity chains. The scalar curvature, $\mathcal{R}≔{\mathbf{Z}}^{\mu \nu }{\mathcal{R}}_{\mu \nu }$, defines the net strain induced by constraint saturation over a region.

Projection strain arises when a region of M experiences dense, latency-synchronized identity realization. To quantify this, we define the projection strain tensor as the directional informational flux at point $x\in M$:

$${\mathbf{T}}_{\mu \nu }^{\left(\mathsf{\Pi }\right)}\left(x\right)≔\sum _{\sigma \in {\mathsf{\Omega }}_x}\left({\partial }_{\mu }\Pi \left(\sigma \right)\left(x\right)\right)\left({\partial }_{\nu }\Pi \left(\sigma \right)\left(x\right)\right),$$

(18)

where $\Pi \left(\sigma \right)\left(x\right)$ denotes the projected field value of identity signature $\sigma$ at point x. This tensor captures how constraint-saturated regions induce curvature in the impedance geometry and serves as a structural analogue of the energy–momentum tensor, independent of matter fields or dynamics.

We now postulate that the balance between curvature and strain is given by a structural field equation:

$${\mathcal{G}}_{\mu \nu }≔{\mathcal{R}}_{\mu \nu }-{\displaystyle \frac{1}{2}}{\mathbf{Z}}_{\mu \nu }\mathcal{R}=G\cdot {\mathbf{T}}_{\mu \nu }^{\left(\Pi \right)}.$$

(19)

Here, ${\mathcal{G}}_{\mu \nu }$ is the $\mathsf{\Omega }$-Einstein tensor, and $G$ emerges as a scaling coefficient quantifying the projection coupling strength between curvature and informational stress. This equation expresses a geometric equilibrium between curvature induced by projection impedance and the structural strain of constraint-saturated identity realization. This follows the fact that regions with high projection strain, like dense, coherent constraint configurations, necessarily exhibit high curvature in the projection impedance landscape. The resulting field equation mirrors the form of Einstein’s equations but offers a different ontology. Curvature and “stress” are no longer fundamental entities but emerge from the geometry of constraint compatibility and the density of coherent projection.

We interpret $G$ as an informational elasticity modulus of the projection manifold. Newton’s constant $G$ quantifies the ratio of curvature induction to projection strain — effectively, the compliance of the projection manifold. Its smallness reflects the high structural stiffness of the $\mathsf{\Omega }\to M$ mapping: only the collective effect of many coherent, low-latency projections can yield measurable curvature. Moreover, because mass and inertia have already been identified with projection latency in earlier work, the equivalence of inertial and gravitational mass follows directly. Both types of mass reflect resistance to reconfiguration within the constraint topology of $\mathsf{\Omega }$. Gravitational effects occur when such latency gradients modulate impedance curvature. There is no need for a field-based graviton or metric quantization.

Finally, the universality of $G$ across all forms of matter reflects the universality of constraint geometry itself. All identity signatures that satisfy projection conditions do so within the same $\mathsf{\Omega }$-defined topology. In this view, Newton’s constant is not a parameter of gravitational interaction, but a structural invariant of informational geometry, encoding the universal stiffness of the spacetime projection substrate.

4.4. Topological Quantization and the Emergence of Charge and the Fine-Structure Constant

In conventional field theory, electric charge is treated as a fundamental conserved quantity and the fine-structure constant $\alpha$ is a dimensionless empirical input governing electromagnetic interaction strength. Within the $\mathsf{\Omega }$-framework, both quantities arise from topological invariants of identity signatures and constraint class geometry under projection.

Let $\sigma \in \mathsf{\Omega }$ be an identity signature characterized by the tuple $\sigma =(\omega , ϵ,\mathcal{l},\varphi , C)$, where $C\subset {\mathsf{\Omega }}^{\mathrm{n}}$ is the minimal constraint class required for admissible projection. A projection $\Pi \left(\sigma \right)\in {\mathcal{F}}_{\mathcal{x}}$ is allowed at $x\in M$only if the local compatibility conditions imposed by $C$ are met.

We define the charge content of a signature $\sigma$ as a topological invariant associated with the obstruction to trivial factorization of its constraint embedding. Let $\pi :\mathsf{\Omega }\to \mathcal{C}$denote the projection to the space of constraint classes and let $\gamma \subset \mathcal{C}$be a closed loop generated by adiabatic variation of environmental projection conditions. Then, we define the net topological charge of $\sigma$ as the holonomy class:

$$\eta \left(\sigma \right)≔{\displaystyle \frac{1}{2\mathsf{\pi }}}{\oint }_{\gamma }\mathcal{A},$$

(20)

where $\mathcal{A}$ is a $U\left(1\right)$-valued connection over $\mathcal{C}$ that encodes phase rotation symmetry in $\mathsf{\Omega }$-signature projection. This expression mirrors the Berry phase formalism but is defined over structural constraint space rather than Hilbert space. The quantization of $\eta$ arises from the requirement that the holonomy group be compact and discrete under projection compatibility.

The elementary charge $e$ is then defined as the minimal non-zero holonomy among projectable identity signatures:

$$e≔\underset{\sigma \in \mathsf{\Omega }\setminus {\mathsf{\Omega }}_0}{\min }\left|\eta \left(\sigma \right)\right|,$$

(21)

where ${\mathsf{\Omega }}_0$ denotes the set of projection-neutral (trivial-holonomy) signatures.

To explore how topological tension interacts with the geometric structure of projection, we introduce a dimensionless structural action ratio $\Xi$ within the $\mathsf{\Omega }$-framework. The ratio $\Xi$ is a structural necessity. In any projection-based ontology with quantized topology, impedance-limited realization, and minimal action thresholds, a dimensionless measure of projection-limited topological embedding must exist [8,9]. This ratio is constructed from quantities that capture three key aspects of projection behavior:

• The topological cost of charged projection (via discontinuities in constraint class embeddings);
• The geometric permeability of the projection interface;
• The minimal action required to stably instantiate charged identity signatures.

We define:

$$\Xi ≔{\displaystyle \frac{{\left(\mathsf{\Delta }C\right)}^2}{{\mathcal{Z}}_{\mathcal{E}}\cdot {\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}}\cdot \kappa ·v_{\mathrm{m}\mathrm{a}\mathrm{x}}}},$$

(22)

where $\mathsf{\Delta }C$ corresponds to the topological tension introduced by projecting a non-neutral signature, while ${\mathcal{Z}}_{\mathcal{E}},{\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}}\cdot \kappa$and $v_{\mathrm{m}\mathrm{a}\mathrm{x}}$ describe the permeability, minimal projection action, and causal admissibility of the projection substrate. Together, they define a normalized measure of projection efficiency for embedding charged identity. The inclusion of $\kappa$ alongside ${\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}}$reflects the fact that minimal projection action involves not only a temporal threshold, but also a structural curvature cost. Whereas ${\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}}$captures the time-scale resolution of projection events, $\kappa$accounts for the intrinsic geometric tension required to instantiate topologically nontrivial configurations. Their product defines the projection grain ${\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}}\cdot \kappa \sim \hslash$, which governs the minimal coherent action scale in the $\mathsf{\Omega }\to M$interface. A more mathematically detailed derivation is shown in Appendix A.

We now show how the structural ratio $\Xi$ in the $\mathsf{\Omega }$-topology translates into observable reality in spacetime. We have already established that:

• $\mathsf{\Delta }{C}^2\sim e^2$, the square of the minimal holonomy class defect;
• ${\mathcal{Z}}_{{\mathcal{E}}^{-1}}\sim {\epsilon }_0$, electric vacuum admittance;
• ${\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}}\cdot \kappa \sim \mathrm{\hslash }$, projection action threshold;
• $v_{\mathrm{m}\mathrm{a}\mathrm{x}}\sim c$, the maximal propagation speed.

Substituting these identifications into Equation (22), the structural ratio $\Xi$ collapses into the standard expression:

$$\Xi ={\displaystyle \frac{{\left(\mathsf{\Delta }C\right)}^2}{{\mathcal{Z}}_{\mathcal{E}}\cdot {\tau }_{\mathrm{m}\mathrm{i}\mathrm{n}}\cdot \kappa \cdot v_{\mathrm{m}\mathrm{a}\mathrm{x}}}}\hspace{1em}\stackrel{\mathrm{substitution}}{\to }\hspace{1em}{\displaystyle \frac{e^2}{{\epsilon }_0\mathrm{\hslash }c}}\approx \alpha ,$$

(23)

demonstrating that the fine-structure constant emerges as a necessary ratio of projection-theoretic quantities.

In this view, $\alpha$ quantifies the normalized informational cost of embedding non-neutral topologies into spacetime. Its small value (~1/137) reflects the high selectivity of the projection interface for topologically charged configurations. It encodes the fine balance between topological tension and impedance-permitted realization, and thereby explains the relative weakness of electromagnetic interaction and the high coherence required for charge-bearing states to persist.

Charge conservation follows directly. The constraint cohomology ${\mathrm{H}}^1\left(\mathcal{C},\mathbb{Z}\right)$ is invariant under continuous $\mathsf{\Omega }$-projection morphisms, and hence the topological class $\left[\mathsf{\eta }\left(\mathsf{\sigma }\right)\right]\in {\mathrm{H}}^1\left(\mathcal{C},\mathbb{Z}\right)$ is conserved. This yields a structural explanation for Gauss’s law and charge conservation in the projection framework.

Finally, the local $U\left(1\right)$gauge symmetry of electrodynamics arises naturally from the automorphism group of phase-rotation-preserving transformations of constraint classes. Gauge freedom corresponds to fiberwise equivalence classes of projections under internal $U\left(1\right)$-rotation, consistent with the $\mathsf{\Omega }$-framework’s foundational ontology.

In summary, electric charge emerges as a quantized topological obstruction to constraint trivialization, and the fine-structure constant quantifies the normalized projection cost of embedding such obstructions into a causal, impedance-limited geometric substrate. Both are derived, not assumed, and are fixed by the global structure of the $\mathsf{\Omega }\to M$projection map.

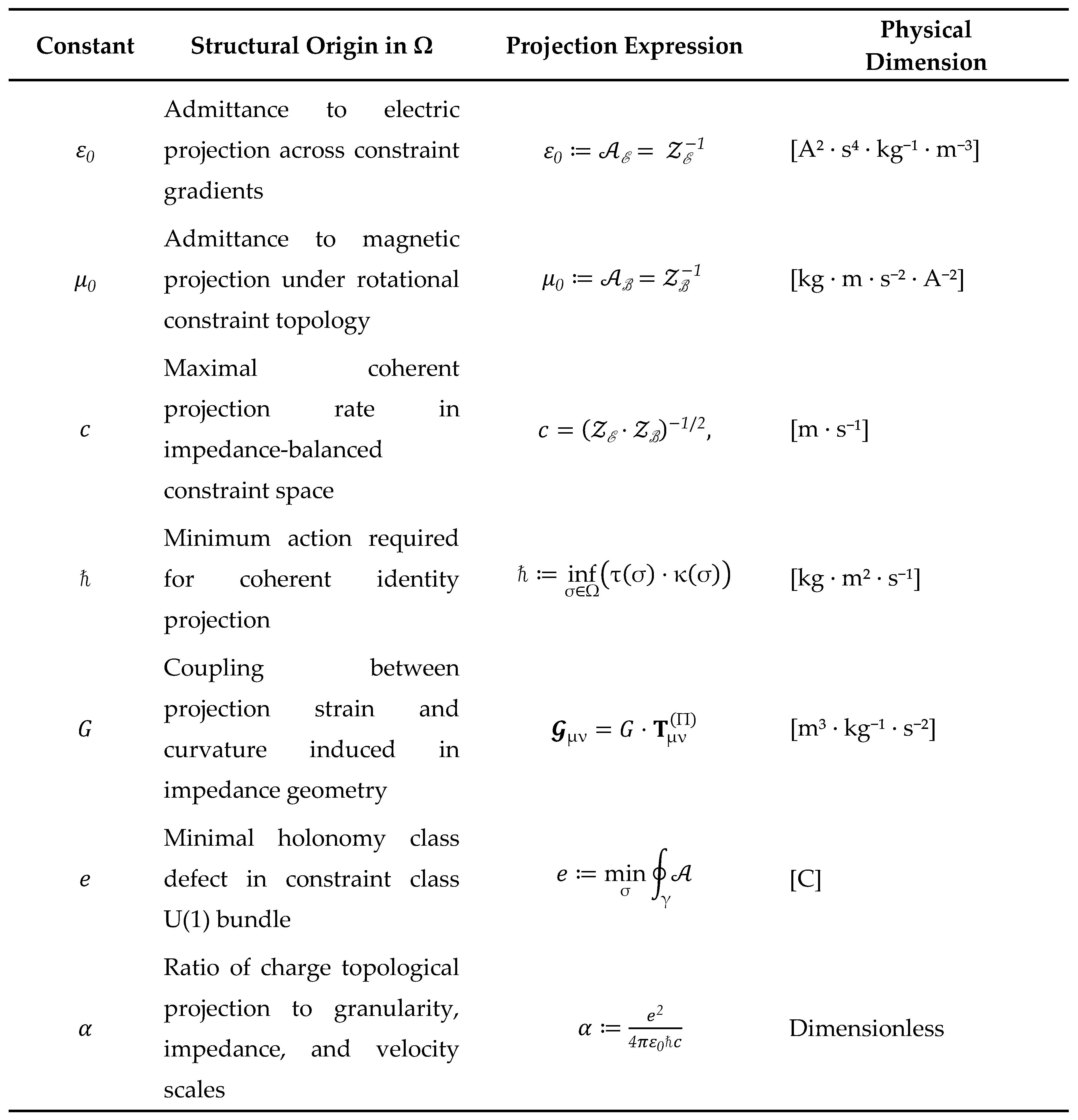
4.5. Constants as Projection Invariants: Structure and Dimensional Analysis

The preceding sections have demonstrated that the constants fundamental to physical theory, ε₀, μ₀, c, ℏ, G, e, and α, emerge in the Ω-framework. They arise from the interplay between projection geometry, constraint topology and informational granularity as structural invariants. Their values, roles, and dimensional structure can now be reinterpreted as expressions of deeper projection-theoretic properties.

We summarize the origin, interpretation, and dimensional form of each constant in the table below, which also serves to unify the derivations from Chapters 4.1 to 4.4.

Table 2. Projection-theoretic origins and dimensional structure of fundamental constants.

Table 2. Projection-theoretic origins and dimensional structure of fundamental constants.

Each constant is rendered as the projection-invariant output of a single informational architecture and not as a free-standing input to physical law. The projection latency τ, curvature κ, and constraint topology $C$ together yield a closed system from which the constants’ dimensions and relations arise necessarily.

This unification reveals the fundamental constants as spectral signatures of identity coherence under projection. They emerge from the algebraic and topological structure of constraint geometry, encoding how informational identity becomes stable, measurable structure in spacetime.

5. Structural Universality of $\mathit{\alpha }$ Across Theoretical Frameworks

The fine-structure constant $\alpha$ derived in Section 4.4, occupies a special position among the constants emerging from the $\mathsf{\Omega }$-framework. As a dimensionless invariant, it encapsulates the normalized projection cost of topologically charged identity realization. Its structure, balancing constraint discontinuity against geometric latency, impedance, and causal limit, provides a template for interpreting other coupling constants as emergent features of the projection interface. In this chapter, we examine how this interpretation of $\alpha$ contrasts with its treatment in other major frameworks and what this implies for the structural role of physical constants more broadly.

5.1. Contrast with Holographic Duality

In AdS/CFT correspondence, coupling constants such as α are typically encoded in boundary correlation functions, often appearing as prefactors in the Lagrangian of the boundary theory. For example, the Yang–Mills coupling $g_{\mathrm{Y}\mathrm{M}}^2\sim \mathsf{\alpha }$ governs interaction strength in the conformal field theory, with its scale-dependence captured by the renormalization group [10].

In the $\mathsf{\Omega }$-framework, by contrast, $\mathsf{\alpha }$ is not a dynamical coupling in the Lagrangian sense. It is an emergent invariant, independent of scale transformations and defined without reference to variational principles. Rather than arising from boundary correlators, it emerges from the internal structure of the projection map as a measure of the impedance-weighted cost of embedding topologically charged signatures. Its constancy follows from the stability of the projection geometry itself and not from renormalization invariance.

Mathematically, this distinction may be formalized by treating the projection interface $\Pi :\mathsf{\Omega }\to M$as an operator algebra homomorphism, with $\mathsf{\Omega }$-constraint classes representing structural operator families and their realizations in $M$ acting as bulk observables. In this analogy, $\mathsf{\alpha }$ corresponds to the spectral norm of a transfer operator encoding the obstruction to unitarity during identity propagation with constraint torsion, being a deviation from symmetry-preserving realization under projection.

5.2. Contrast with Causal Set Theory

Causal set theory introduces discreteness at the level of spacetime events, with causal order encoded in a partially ordered set. While this structure naturally reproduces Lorentzian causality and volume measures, dimensionless coupling constants such as $\mathsf{\alpha }$ are not derived but must be inserted phenomenologically [11].

In the $\mathsf{\Omega }$-framework, time-ordering arises from the partial ordering of admissible projections, and interaction strength emerges from the topology of constraint embeddings. Rather than counting elements or links, we interpret $\mathsf{\alpha }$ as a cohomological threshold on admissibility, a minimal projection tension required for non-neutral configurations to stabilize. Formally, one may define a mapping $\mathrm{f}:\mathcal{C}\to \mathsf{\Pi }\left(\mathsf{\Omega }\right)$ such that ${\mathrm{x}}_{\mathrm{i}}\prec {\mathrm{x}}_{\mathrm{j}}\hspace{0.25em}\iff \hspace{0.25em}\mathsf{\Pi }\left({\mathsf{\sigma }}_{\mathrm{i}}\right)\prec \mathsf{\Pi }\left({\mathsf{\sigma }}_{\mathrm{j}}\right),$ and identify the projection latency $\tau \left(\sigma \right)$ with the minimum temporal separation needed to maintain coherence along such chains. In this setting, $\mathsf{\alpha }$ appears as a universal bound on the informational load per causal link — not a function of graph connectivity, but a quantized threshold in constraint cohomology.

5.3. Contrast with Quantum Information Geometry

Tensor network approaches, such as MERA or PEPS, model spatial geometry and quantum correlations via entanglement structure. Coupling constants in these models reflect bond dimensions, network depth, and information flows [12].

In the $\mathsf{\Omega }$-framework, this logic is reversed. Entanglement is not a primitive construct but an emergent consequence of shared constraint compatibility. The fine-structure constant does not track entanglement strength but rather the resistance to embedding non-factorizable constraint overlaps. A larger $\mathsf{\alpha }$ would indicate easier co-projection of charged identities. A smaller $\mathsf{\alpha }$, as observed in nature, reflects the high structural selectivity for such instantiation.

Projection fidelity can be defined via:

$$\mathcal{F}\left(C\right)≔{\displaystyle \frac{{\mathit{dim}}_{\sigma \in C}\Pi \left(\sigma \right)}{{\mathit{dim}}_{\sigma \in C}\mathsf{\Omega }}},$$

(24)

measuring the coherence fraction of projectable configurations within a constraint class. In tensor network terms, this aligns with the minimal bond coherence necessary to realize topologically nontrivial projections. The fine-structure constant then emerges as the lowest $\mathcal{F}\left(C\right)$ for which electromagnetically charged identities can stably exist.

5.4. Structural Universality of α

Within the $\mathsf{\Omega }$-framework, $\mathsf{\alpha }$ acts as a structural selector, a dimensionless equilibrium ratio that balances topological twist, impedance resistance, projection latency, and causal admissibility. Its small magnitude reflects the exceptionally high informational cost of realizing topologically charged states and the delicate coherence required for their persistence in spacetime.

Unlike in field-theoretic models, where changes in $\mathsf{\alpha }$ suggest altered interaction strengths, variations in $\mathsf{\alpha }$ here would imply deformation of the projection substrate itself — such as changes in the topology, impedance tensor, or cohomological structure of $C$. The empirical constancy of $\mathsf{\alpha }$ thus signifies the global stability of the $\mathsf{\Omega }\to M$projection architecture.

This reframes $\mathsf{\alpha }$ as a geometric and cohomological invariant: a fixed point in the interplay between constraint class topology, projection granularity, and identity realization bandwidth. In this capacity, $\mathsf{\alpha }$ plays a role analogous to a moduli index, characterizing the admissible structure of reality itself.

6. Discussion

This work has developed a structural derivation of the fundamental constants of nature from an informational ontology rooted in projection from a non-spatiotemporal identity space, $\mathsf{\Omega }$. By formalizing projection latency, constraint curvature, and impedance geometry, we have shown how constants such as $\hslash , G, e, {\epsilon }_0, {\mu }_0,$ and $\alpha$ emerge as invariant quantities within the mapping$\Pi :\mathsf{\Omega }\to M$, where $M$ denotes the observable spacetime manifold.

Each constant corresponds to a distinct structural feature of this projection process: latency and curvature give rise to the quantum of action; impedance tensors determine electromagnetic response and causal limits; constraint holonomy induces charge quantization and the fine-structure constant appears as a dimensionless ratio unifying these features. These constants are consequences of deeper algebraic and topological constraints on projection and not free parameters. The Ω-framework thus reframes the constants of physics as structural invariants at the interface between informational identity and spacetime realization. Rather than modifying physical law, it offers an ontological foundation in which both the constants and the spacetime framework they inhabit arise as emergent phenomena.

The results presented here do not merely suggest that physical constants might be emergent but demonstrate this emergence explicitly. The Ω-framework stands as a mathematically structured, conceptually coherent foundation in which spacetime and its constants arise as necessary projections of informational identity.