Reconciling Discreteness and Continuity as Complementary Spectral Projections of Complex-Time Geometry in the Single Monad Model

1. Introduction

From the paradoxes of Zeno [1,2] to the debates between Leibniz and Newton on the nature of infinitesimals [3], the question of whether reality is fundamentally discrete or continuous has remained unresolved. In modern physics this tension has re-emerged with greater urgency. Quantum mechanics enforces quantization of energy, spin, and other observables [4], while relativity requires smooth spacetime manifolds and differentiable fields [5]. The discreteness–continuity dichotomy is therefore a central obstacle in unifying quantum theory with general relativity.

Canonical approaches to quantum gravity typically emphasize either discreteness or continuity, often at the expense of the other. For instance, loop quantum gravity predicts discrete spectra for geometric operators but struggles to recover smooth continuum dynamics at macroscopic scales [6,7]. Causal set theory imposes discreteness at a fundamental level, yet encounters significant challenges in reproducing Lorentz invariance and differentiable manifold structure [8,9]. Conversely, string theory assumes a continuous background spacetime while introducing discrete excitations through string modes, leaving the origin of discreteness and its relation to continuity unresolved [10]. Non-commutative geometry encodes discreteness algebraically via operator algebras, but does not derive it dynamically from fundamental principles [11]. Consequently, none of these frameworks provides a unified mechanism in which discreteness and continuity emerge as complementary manifestations of a single underlying structure. In Section 2, we will compare between the different approaches to the discreteness–continuity duality and highlight their limitations.

In this work, we propose a novel resolution grounded in the primacy of time over space. Rather than privileging space as the fundamental arena or treating time and space on equal footing, we introduce a dual-time structure consisting of two hyperbolically orthogonal levels: a compact inner time governing the discrete re-creation of spatial dimensions, and an unbounded outer time corresponding to the continuous evolution experienced by the observer. In Section 3.2, this split-complex “time–time” geometry will be formally derived and justified, demonstrating that the compact and discrete character of inner time arises from its cyclic topology, whereas the outer time appears linear and continuous due to its unbounded extension within the observer’s frame.

This original formulation is founded on the ontological principles of the Single Monad Model (SMM) [12], which posits that all physical multiplicity and evolution originate from the iterative unfolding of one indivisible entity—the Single Monad. The associated Duality of Time Theory (DTT) [13] provides the mathematical realization of this principle, yielding a rigorous formalism for physical and geometric analysis based on the dual-time structure. In Section 3, we will elaborate further on the ontological and metaphysical foundations of this model and show how they can be connected directly with measurable physical phenomena.

Mathematically, the SMM/DTT framework naturally admits a non-commutative operator algebra acting on a temporally structured Hilbert space. In spectral terms, this can be expressed as a triple $(\mathcal{A},\mathcal{H},D)$, where $\mathcal{A}$ encodes projection operators associated with inner cycles, $\mathcal{H}$ represents the space of temporal states, and D is the Dirac operator governing the interplay between discrete and continuous evolution. As will be demonstrated in Section 5, this geometric–algebraic structure yields discrete spectra while preserving Lorentz invariance and the differentiable manifold of the outer (imaginary) time.

At the level of physical multiplicity, entities must appear either discrete or continuous—there is no third alternative. A truly foundational theory must therefore explain how this apparent duality arises from a single, indivisible substrate. This perspective aligns with recent efforts to reconstruct space-time from quantum mechanical postulates [14], emphasizing the need to root physical geometry in a deeper underlying reality. By bridging foundational metaphysical and ontological insights with realistic physical modeling and rigorous mathematical formalism, the SMM/DTT framework derives the entire structure of physical reality from a unified origin, realized through discrete split-complex dual-time dynamics.

2. Limitations of Existing Approaches

In classical mechanics and general relativity, physical quantities vary smoothly and continuously: position and momentum are modeled as real-valued functions on differentiable manifolds, and fields such as the electromagnetic tensor or the metric tensor are defined over continuous spacetime. General relativity, in particular [5], assumes a $C^{\infty }$-differentiable manifold equipped with a Lorentzian metric, ensuring smooth curvature and geodesic structure.

In contrast, quantum theory introduces inherent discreteness. Spectra of observables such as angular momentum, energy levels in bound systems, and electric charge are quantized [4,15]. On the other hand, although the wavefunction evolves continuously under the Schrödinger equation, measurement collapses it discontinuously, yielding discrete outcomes according to the Born rule. This juxtaposition between continuous evolution and discrete observation underlies many foundational paradoxes in quantum theory [16].

Efforts to unify quantum theory with general relativity aggravate the tension between discreteness and continuity. Various quantum gravity programs attempt to address this duality, but each tends to emphasize one side while approximating or struggling to recover the other.

• Loop Quantum Gravity (LQG) predicts discrete spectra for geometric operators such as area and volume [6,7], implying fundamental quantization of spacetime. However, recovering smooth classical geometry and Lorentz symmetry in the semiclassical limit remains an open challenge:
• Causal Set Theory (CST) models spacetime as a discrete partially ordered set of causal elements [8,9]. While discreteness is fundamental, deriving a smooth manifold with general relativistic properties has proven difficult.
• String Theory maintains a continuous spacetime background, while discreteness emerges from quantized vibrational modes of strings [10]. The theory does not offer a first-principles explanation for either the emergence of continuity or the origin of quantization.
• Non-commutative Geometry (NCG) encodes discreteness algebraically via operator algebras and spectral triples [11,17]. Though mathematically elegant, discreteness is imposed rather than dynamically derived from geometric or physical principles.
• Asymptotic Safety proposes a nontrivial ultraviolet fixed point of the renormalization group to resolve quantum gravity divergences [18,19]. While spacetime is treated as continuous at all scales, the theory does not offer a foundational account of discreteness or its relation to geometry.
• Causal Dynamical Triangulations (CDT) uses path integrals over simplicial manifolds to recover smooth 4D geometry from discrete elements [20,21]. However, its discreteness is a computational regularization tool, not a fundamental ontological feature.
• Holography and AdS–CFT relate a continuous gravitational bulk to a discrete operator spectrum in boundary CFTs [22]. Yet the origin of both continuity and quantization remains unaddressed within this duality.
• Relational and Quantum Time Theories, such as Rovelli’s relational time [23] and the Montevideo interpretation [24], propose that time is not fundamental but emergent or observer-dependent. These models suggest temporal fuzziness but do not offer a geometric structure that unifies discreteness and continuity.

While existing frameworks have provided important insights, none offers a unified mechanism in which discreteness and continuity emerge as complementary aspects of a single underlying structure. Most formulations treat one as fundamental and attempt to recover the other through approximation, coarse-graining, or limiting procedures. This gap motivates the search for a framework in which both properties follow simultaneously from a single geometric principle.

In the SMM/DTT framework, discreteness and continuity arise together from a split-complex temporal geometry. The compact inner-time $t_{\mathrm{real}}\in S^1$ encodes quantized re-creation cycles, analogous to the discrete quanta of causal-set or spin-network approaches, whereas the unbounded outer-time $t_{\mathrm{imag}}\in \mathbb{R}$ supports continuous Lorentzian propagation. Unlike other models, this framework provides a unifying perspective in which discreteness and continuity—and related dualities such as locality and nonlocality—arise as complementary manifestations of a single hyperbolic temporal geometry.

To establish this unification on firm conceptual grounds, we now turn to the ontological foundations of the SMM/DTT framework and explain how they can be rigorously connected with mathematical modeling and physical observations.

3. The Ontological Foundations of SMM/DTT

The Single Monad Model (SMM) [12] and its formal extension, the Duality of Time Theory (DTT) [13], arise from the ontological worldview of the “Oneness of Being” articulated by Muhyiddin Ibn al-Arabi [25]. This foundation interprets physical reality as the continuous self-manifestation of a single indivisible source—the Monad. Through successive temporal unfoldings, this primordial unity generates all multiplicity and change. By linking this metaphysical principle to a dual-temporal geometry, the SMM/DTT framework offers a coherent route to reconcile quantum discreteness with relativistic continuity.

The Monad functions as an ontological singularity—zero-dimensional, atemporal, and of maximal informational density—that creates the dimensions rather than existing within them. Each compact cycle of the inner (real) time produces an elementary unit of geometry or energy, while the unbounded outer (imaginary) time orders these discrete acts into the continuous evolution observed in nature. Thus, space is not a pre-existing background but the cumulative manifestation of structured temporal recurrence. Conventional differential geometry arises only when this generative process is coarse-grained into a continuous manifold.

Philosophically, this temporal ontology parallels process-based views of reality, such as Whitehead’s actual occasions [26] and Bohm’s implicate order [27], but here it is formalized within a precise dual-time geometry. The nested temporal hierarchy maps potential unity (the Monad) to archetypal inner-time cycles and finally to empirical outer-time evolution, providing a continuous bridge from metaphysics to measurable physics [28,29].

A central insight of SMM/DTT is its inversion of reductionism: complexity emerges from a temporally structured simplicity. Continuous fields and differential geometry are effective descriptions of a deeper stratified temporal architecture. This ontological reformulation thus redefines the foundations of physics as the emergent dynamics of a self-renewing temporal unity.

3.1. The Main SMM/DTT Postulates

The central postulate of the Duality of Time Theory (DTT) may be stated as follows:

At every instant of the outer (imaginary) level of time, the spatial dimensions are continuously re-created through a precise chronological sequence of inner (real) time layers, forming nested temporal hierarchies embedded within each lower dimension.

This principle establishes the fundamental asymmetry between the two levels of time. The inner (real) time governs the discrete act of re-creation that generates existence, while the outer (imaginary) time governs the continuous flow of events perceived by observers. Each instant of outer time thus corresponds to a complete renewal of the cosmos through a finite sequence of inner-time cycles.

From this structure, the emergence of spatial dimensions follows naturally. Each spatial dimension arises from the coupling of two successive inner temporal cycles, producing six compact layers of real time. Combined with the unbounded outer (imaginary) time, these form a septenary hierarchy of intertwined temporal degrees of freedom whose collective projection manifests as the observed $(3+1)$-dimensional spacetime.

The ontological and physical content of this principle can be summarized in four foundational postulates defining the SMM/DTT framework:

• Unity of Being: All multiplicity and change arise from a single ontological source—the Monad—which possesses neither spatial extension nor temporal duration but manifests the totality of existence through perpetual re-creation.
• Duality of Time: Time unfolds across two orthogonal levels: a compact, discrete inner time $t_{\mathrm{real}}$ responsible for quantized re-creation, and an unbounded, continuous outer time$t_{\mathrm{imag}}$ responsible for causal propagation and relativistic evolution. Their split-complex synthesis, as defined in Equation (1), forms the geometric and algebraic foundation of physical dynamics.
• Re-Creation Principle: Physical reality is renewed through successive cycles of inner time. Each cycle represents an indivisible temporal quantum, whose sequential manifestation gives rise to discrete spectra and quantized physical observables.
• Emergence of Dimensions: Spatial dimensions and physical structures develop hierarchically from nested inner-time layers. Each pair of coupled inner cycles produces one spatial dimension, yielding the observed $(3+1)$ spacetime as the outer projection of seven interwoven temporal degrees of freedom.

Together, these postulates define a unified temporal ontology in which discreteness and continuity, circularity and linearity, and the metaphysical and physical domains emerge as complementary aspects of one self-consistent dual-time geometry. The cosmos is thus a single, perpetually renewed entity—discrete in its generative essence yet continuous in its manifested evolution.

3.2. The Hyperbolic Split-Complex Dual-Time Geometry

Within the SMM/DTT framework, time is represented as a split-complex variable composed of two hyperbolically orthogonal components with distinct physical roles:

• Inner (real) time ($t_{\mathrm{real}}$): compact and cyclic, governing discrete acts of re-creation that generate quantized spectra of physical observables such as energy, spin, and charge.
• Outer (imaginary) time ($t_{\mathrm{imag}}$): unbounded and continuous, sequencing inner cycles into extended evolution and supporting Lorentzian spacetime dynamics.

The inner component encodes quantization through cyclic recurrence, while the outer ensures smooth relativistic propagation. Together they define a dual-temporal structure in which discreteness and continuity are complementary aspects of a single hyperbolic geometry. The formal definition is

$$t_{\mathrm{complex}}=t_{\mathrm{real}}+j{t}_{\mathrm{imag}},j^2=+1,$$

(1)

where j is the hyperbolic unit ensuring orthogonality between the two components. The compactness of $t_{\mathrm{real}}$ leads naturally to discrete spectra via Fourier decomposition on the inner temporal circle, while the unboundedness of $t_{\mathrm{imag}}$ preserves continuous relativistic evolution.

3.2.1. Justification of the Split-Complex Structure

The choice of split-complex numbers arises from the intrinsic asymmetry and orthogonality between the two temporal levels. The inner time $t_{\mathrm{real}}$ represents closed and periodic re-creation cycles, whereas the outer time $t_{\mathrm{imag}}$ denotes open and directional evolution. Their relation is therefore hyperbolic, not Euclidean.

Unlike the circular symmetry of standard complex numbers, the hyperbolic metric

$$t_{\mathrm{real}}^2-t_{\mathrm{imag}}^2=\mathrm{constant}$$

reflects the causal and directional structure of reality: each act of inner re-creation ($t_{\mathrm{real}}$) is interrupted and reprojected through an outer temporal instant ($t_{\mathrm{imag}}$). This form parallels the Minkowskian signature of relativistic spacetime, where temporal and spatial coordinates combine under a hyperbolic invariant.

Hence, the split-complex representation is not merely mathematical—it expresses the ontological duality of creation and observation. The compact generative inner time and the unbounded observational outer time are orthogonal yet inseparable, forming a single hyperbolic manifold that unifies discrete creation with continuous evolution.

3.2.2. Discrete Change and the Illusion of Motion

In the SMM/DTT view, change occurs only through successive acts of re-creation; there is no infinitesimal transition between states. Each entity is annihilated and re-created in a new configuration at every inner-time cycle. Thus, at any instant of outer time, the universe is perfectly static: apparent motion arises from the sequential re-creation of static states over continuous outer flow.

Formally, let each spatial point alternate between two primordial phases—existence and non-existence. During the re-creative (inner) phase, the point attains the real velocity of creation $v_r=c$, effectively infinite since it occurs in compact inner time $t_{\mathrm{real}}$ where no measurable interval elapses. During the manifest (outer) phase, it rests at $v_i=0$, having been projected into the observer’s frame. The apparent motion thus corresponds to the temporal averaging of these two complementary states:

$$\left|v\right|={\displaystyle \frac{1}{N}}\sum _N\langle 0|c\rangle ,0\le \left|v\right|\le c.$$

Light represents the limiting case of continuous existence: it is never interrupted by re-creation and therefore experiences no inner temporal delay. Its intrinsic speed is indefinite, but for observers embedded in outer time—who themselves undergo discrete re-creation—it appears as the finite, invariant constant c. Hence, c measures the projection ratio between absolute re-creation in inner time and the observer’s temporal perception.

In this way, the DTT framework resolves Zeno’s paradox of motion: nothing physically “moves” between positions; existence itself is discretely renewed at each inner cycle. The observed constancy of light speed emerges as a perceptual projection of this infinite re-creative rate, linking relativity’s invariant c directly to the fundamental discreteness of time.

3.2.3. Illustrating the Split-Complex Temporal Geometry

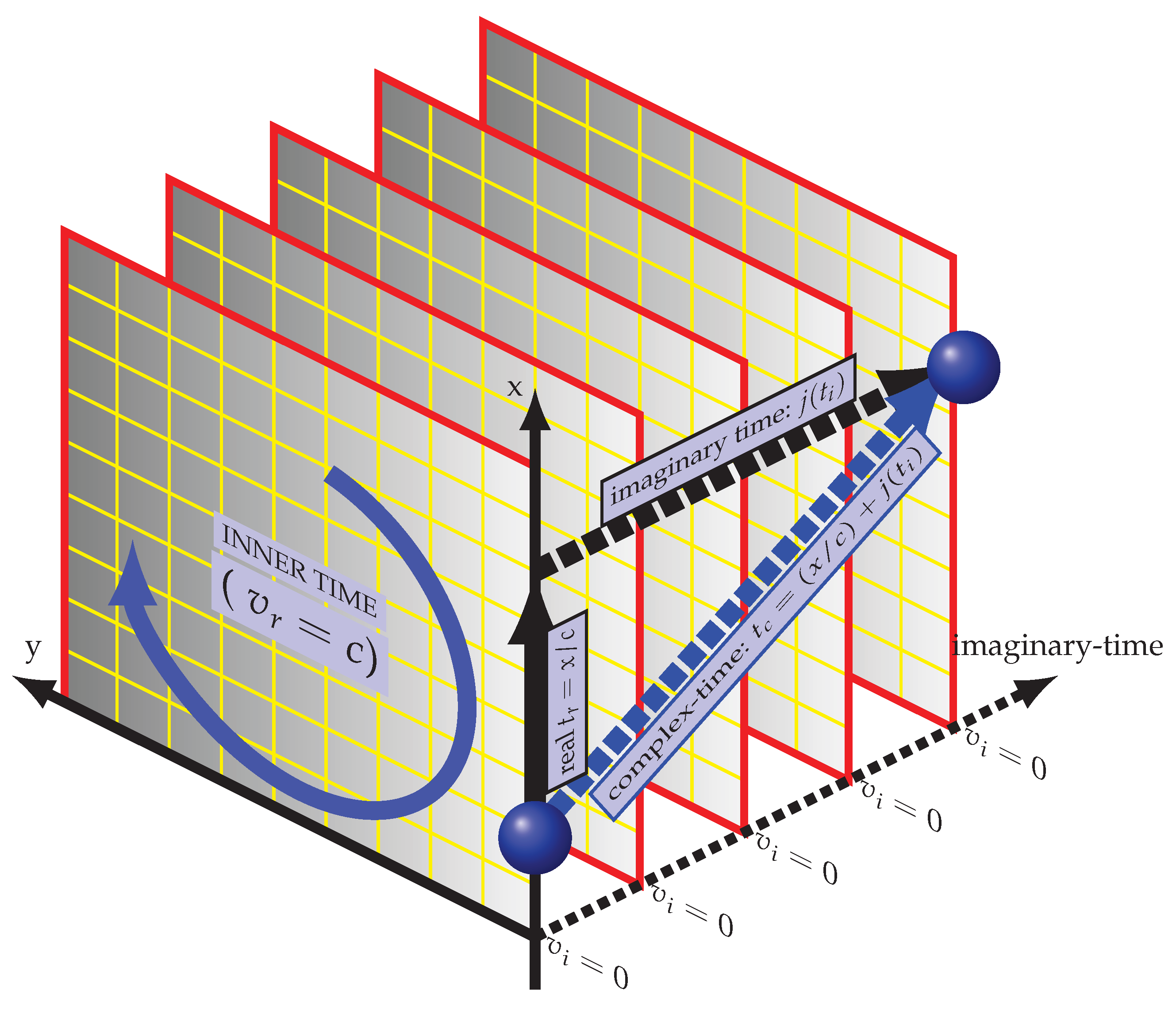
Figure 1 schematically depicts the genuinely complex time–time geometry. Space is shown in two dimensions $(x,y)$, while dynamics are simplified along the x-axis to illustrate how discrete inner-time frames unfold continuously along the outer temporal flow, forming the total complex-time manifold $t_{\mathrm{complex}}=t_{\mathrm{real}}+j{t}_{\mathrm{imag}}$.

3.2.4. The Discrete Nature of Time

In this framework, “time” is not an absolute physical quantity but an abstract ordering parameter enumerating the sequential manifestations—or re-creation events—of the Single Monad. It is therefore intrinsically discrete, arising from a countable succession of ontological acts of creation. Each event marks a distinct re-creative instance, and the perceived continuity of time is merely the projection of this discrete sequence.

Formally, the inner temporal sequence is expressed as

$$t_n=n{\tau }_0,n\in \mathbb{N},$$

where each step represents a fundamental re-creation cycle of duration ${\tau }_0$. When the number of events becomes exceedingly large ($n\to \infty$), the discrete index can be approximated by a continuous variable,

$$t=\underset{n\to \infty }{lim}{\displaystyle \frac{n}{N}}{\tau }_0,N\to \infty ,$$

so that $t\in \mathbb{R}$ may take any real or infinitesimal value. Hence, continuity arises only as an idealized mathematical limit of an inherently discrete temporal process.

In this formulation, the total (complexified) time coordinate of Equation (1) expresses two complementary aspects of a single ontological process. The distinction between the “real” and “imaginary” components is not ontological but perspectival, reflecting the observer’s position within the dual-time hierarchy. For an observer embedded in the outer, physically extended level of time, the cyclic sequence of inner re-creation appears as the “real” component, while their continuous experience of evolution corresponds to the “imaginary” component. This distinction therefore arises from observational perspective rather than from any inherent asymmetry between the two temporal modes.

3.2.5. The Circular Nature of Time

Beyond its discrete character, time in this framework is also intrinsically circular. This circularity follows from the reductionist ontology of the SMM, in which all multiplicity and change reduce to successive self-manifestations of a single indivisible reality. Since all transformation is fundamentally temporal—representing transitions between states of manifestation rather than motion through space—the total process of existence must be cyclic. Each act of manifestation by the Single Monad returns to its origin, ensuring conservation and recurrence across the totality of existence. Time is thus compactified rather than open-ended, expressing the self-consistent closure of the cosmic process.

This intrinsic circularity resonates with known principles in physics. Poincaré’s recurrence theorem implies that any finite, closed system eventually returns arbitrarily close to its initial state, while cosmological models such as the cyclic or conformal universe [30,31,32] describe large-scale evolution through successive phases of expansion and contraction. The SMM generalizes these recurrence principles ontologically: not merely as cycles of configuration within spacetime, but as cycles of re-creation of spacetime itself. Thus, the compactification of inner time provides a metaphysical basis for nature’s empirical tendencies toward periodicity and conservation.

Mathematically, the inner temporal coordinate resides on a compact manifold,

$$t_{\mathrm{inner}}\in S^1,$$

where each revolution represents a complete cycle of creation and annihilation at the fundamental level. This compactness guarantees global self-consistency and dynamic conservation of the total state of existence.

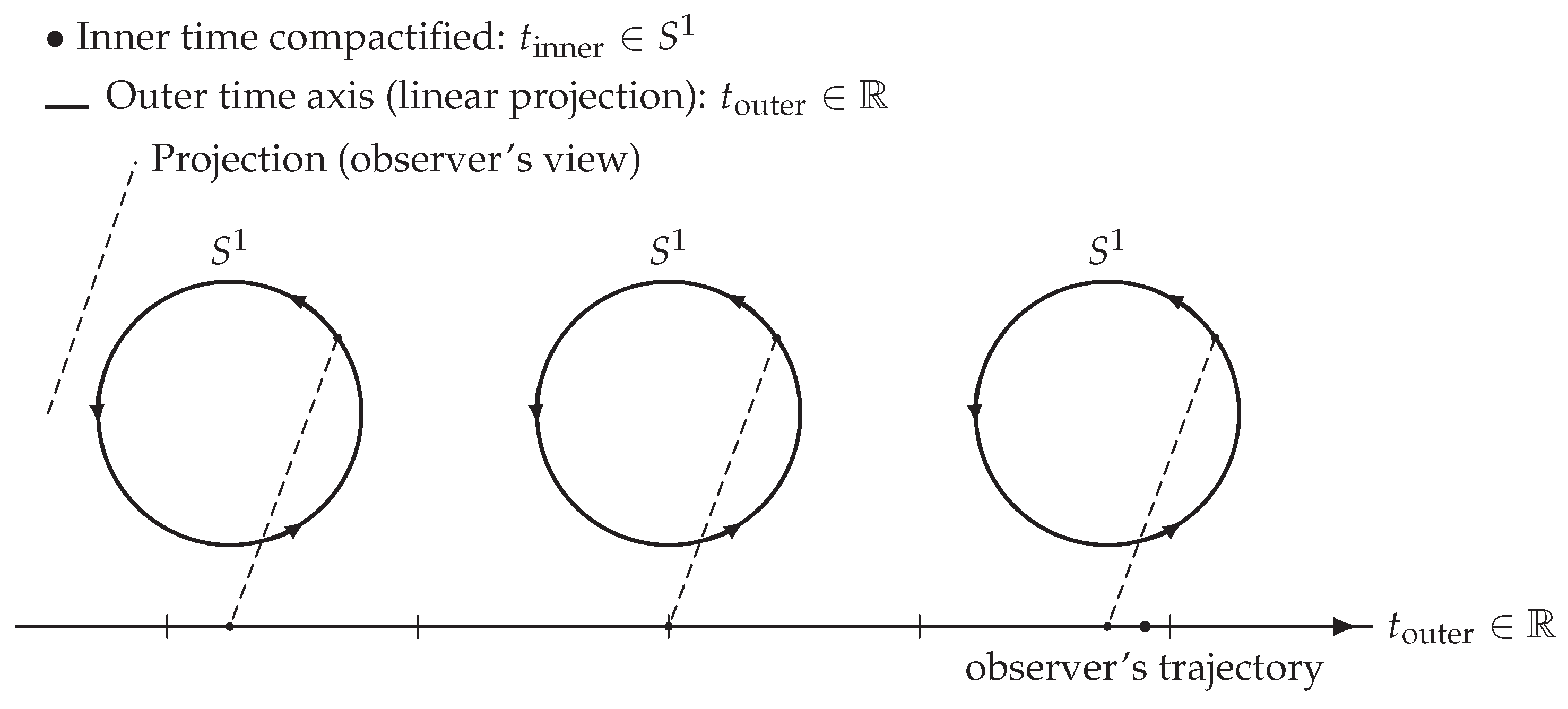
For an observer situated within the outer, continuous flow of time, however, these inner cycles appear as a linear progression,

$$t_{\mathrm{outer}}\in \mathbb{R},$$

where apparent continuity emerges from the projection and superposition of infinitely repeated inner cycles (see Figure 2). The arrow of time thus reflects the observer’s embeddedness within the unidirectional projection of an underlying cyclic process. While the inner structure of time is compact and reversible, its outer manifestation appears linear and irreversible due to the cumulative sequencing of successive cycles.

This dual description reconciles the circular ontology of existence with the linear phenomenology of experience. The cosmos evolves through perpetual renewal—cyclic in its intrinsic structure yet linear in its observed unfolding.

3.3. From Metaphysical Ontology to Measurable Physics

Although the dual-time framework originates from a metaphysical foundation—namely, the Single Monad and the structured re-creation of reality—it also yields a formalism directly connected to measurable physical phenomena. In what follows, the key metaphysical constructs, such as the dual temporal components and the process of re-creation, are given explicit operational and physical meaning. This translation from ontology to physics ensures empirical accessibility and opens the possibility of testable predictions rooted in a deeper temporal architecture.

In metaphysical terms, existence arises from the interplay between essence (potential being) and existence (manifest being). Within the DTT framework, these correspond respectively to the compact inner time $t_{\mathrm{real}}$ and the extended outer time $t_{\mathrm{imag}}$. The Monad represents their synthesis—the ontological point where potentiality and actuality coincide. Through this mapping, principles such as unity, causation, and renewal acquire measurable counterparts: discreteness, evolution, and conservation.

3.3.1. Monad as a Dynamical Boundary Condition

The generative entity of layered creation is the Single Monad, conceived as a zero-dimensional, atemporal source of maximal informational density. It serves as the ontological fixed point from which all multiplicity and physical structure emerge through sequential re-creation across nested temporal layers.

Formally, the Monad can be represented as the fixed point of a recurrence operator $R\left(\tau \right)$ acting on a temporally structured Hilbert space:

$$\underset{\tau \to 0}{lim}R\left(\tau \right)\psi \left(t\right)=\psi \left(t\right),$$

(2)

implying that the Monad functions as a boundary condition initiating all real-time cycles. Analogous to the “no-boundary” condition in quantum cosmology, it can also be viewed as an initial temporal vacuum state ${|0\rangle }_{\mathrm{inner}}$ from which re-creation cycles emerge.

Physically, the Monad enforces global causal coherence across all temporal layers, just as the quantum vacuum constrains field excitations. It thus embodies the metaphysical unity of existence, operationalized as a universal constraint on local dynamics—a precursor to gauge invariance and background independence.

3.3.2. Re-Creation as Discrete Temporal Modulation

The process of “re-creation” denotes the sequential reconstruction of physical states along the compact real-time direction $t_{\mathrm{real}}$, expressible as a discrete Fourier structure:

$$\mathsf{\Psi }(t_{\mathrm{imag}},t_{\mathrm{real}},x)=\sum _{n\in \mathbb{Z}}{\psi }_n(t_{\mathrm{imag}},x)e^{in{t}_{\mathrm{real}}/\ell }.$$

(3)

Each mode n represents a re-creation cycle, giving rise to observable phenomena such as:

• Discrete spectra in energy and charge,
• Quantized holonomies and geometric phases,
• Universal decoherence scaling $\mathsf{\Gamma }\propto {\omega }^2{\tau }_i.$

Physically, this corresponds to a discrete temporal sampling underlying continuous evolution, analogous to stroboscopic quantization or Floquet systems. Thus, “re-creation” attains measurable significance through periodic phase modulation and spectral recurrence.

3.3.3. Operational Meaning of Dual Time

The dual-time variable

$$t_{\mathrm{complex}}=t_{\mathrm{real}}+j{t}_{\mathrm{imag}},j^2=+1,$$

encodes orthogonal components of temporal evolution:

• $t_{\mathrm{imag}}\in \mathbb{R}$: the unbounded outer time responsible for continuous propagation and relativistic invariance;
• $t_{\mathrm{real}}\in S^1$: the compact inner time introducing quantization through boundary conditions and spectral decomposition.

Although $t_{\mathrm{real}}$ is not directly observable, its influence appears as quantized phase shifts, discrete frequency towers, and periodic modulations in measurable quantities. Effective energy levels, for instance, may include real-time contributions of the form

$$E_{n,k}=E_k^{\left(0\right)}+\alpha {\displaystyle \frac{n}{\ell }},n\in \mathbb{Z},k\in {\mathbb{N}}_0,$$

(4)

where $\alpha$ is a coupling constant determined by the inner-time scale.

The coexistence of compact and unbounded temporal components introduces a fundamental complementarity: the inner-time structure yields quantization, while the outer-time flow guarantees continuity and causality. The discreteness–continuity paradox is thus resolved ontologically rather than empirically, as both arise from projections of the same dual-time manifold.

3.3.4. Physical Postulates of the DTT Framework

By reformulating the metaphysical concepts—Monad, re-creation, and dual time—in terms of spectral structures and operator dynamics, the framework acquires direct physical relevance. The real-time cycles correspond to quantized modes affecting observable spectra, while the imaginary-time flow supports continuous relativistic propagation. Together, they define a coherent operator-based foundation for measurable physics.

The main physical postulates can be summarized as follows:

• Complex-Time Geometry: Physical reality is embedded in a split-complex manifold $t_{\mathrm{complex}}=t_{\mathrm{real}}+j{t}_{\mathrm{imag}}$, with $j^2=+1$, where the compact real component introduces discreteness and the unbounded imaginary component yields continuous evolution.
• Spectral Compactification: Quantization of energy, charge, and spin arises from the compact topology $t_{\mathrm{real}}\in S^1$, whose periodic boundary conditions produce discrete Fourier modes ${\lambda }_n=n/\ell$.
• Continuous Lorentz Propagation: The outer time $t_{\mathrm{imag}}\in \mathbb{R}$ governs smooth unitary evolution consistent with Lorentz symmetry. The interaction between discrete inner cycles and continuous outer flow manifests as wave–particle complementarity.
• Non-Commutative Temporal Algebra: Operators generating discrete shifts in $t_{\mathrm{real}}$ and translations in $t_{\mathrm{imag}}$ satisfy $[U,T]\ne 0$, defining a spectral triple $(\mathcal{A},\mathcal{H},D)$ in the sense of non-commutative geometry.
• Observable Projections: Inner-time dynamics project into measurable quantities as discrete spectra, geometric phases, and frequency modulations. Observable effects include quantized holonomies, fine-structure shifts, and universal decoherence scaling $\mathsf{\Gamma }\sim {\omega }^2{\tau }_i$.

These postulates establish the measurable counterpart of the SMM/DTT ontology. Discreteness and continuity, though metaphysically complementary, appear in physics as coherent operator dynamics within a single dual-time geometry.

4. Spectral Triple Construction

The dual-time manifold admits a natural spectral representation $(\mathcal{A},\mathcal{H},D)$ in the sense of non-commutative geometry, providing the rigorous algebraic formulation of the DTT framework. Here, the algebra $\mathcal{A}$ encodes temporal quantization through compact inner cycles, the Hilbert space $\mathcal{H}$ represents the field of states evolving in outer time, and the Dirac operator D links them via hyperbolic differentiation. Together, these elements capture both the algebraic and geometric content of dual-time dynamics and constitute the foundation of the emergent spectral geometry developed in the following sections.

4.1. Algebra $\mathcal{A}$

We define the unital *-algebra

$$\mathcal{A}:=\mathrm{Alg}\{T,U,U^{†},H,U_n\},$$

where:

• T generates translations in the compact inner (real) time, representing discrete re-creation cycles;
• H generates evolution along the unbounded outer (imaginary) time, analogous to the Hamiltonian;
• U and $U^{†}$ act as shift operators between inner-time modes;
• $U_n:=e^{i{\theta }_n}{P}_n$ are phase operators encoding local holonomies, with $P_n=|n\rangle \langle n|$ and phases ${\theta }_n\in \mathbb{R}$.

Because H and T are unbounded, they are treated as affiliated with the enveloping von Neumann algebra of bounded operators on $\mathcal{H}$, with all domain subtleties handled on a common dense subspace.

4.2. Hilbert Space $\mathcal{H}$

We take

$$\mathcal{H}={\ell }^2\left(\mathbb{Z}\right)\otimes L^2\left(\mathbb{R}\right)\otimes {\mathbb{C}}^2,$$

where:

• ${\ell }^2\left(\mathbb{Z}\right)$ represents the discrete spectrum of inner-time modes;
• $L^2\left(\mathbb{R}\right)$ represents continuous evolution along outer time;
• ${\mathbb{C}}^2$ supports a Clifford representation associated with the hyperbolic signature of the dual-time metric.

The dense invariant domain

$${\mathcal{D}}_0:=\mathrm{span}\left\{|n\rangle \otimes \phi \left(t\right)\otimes \chi |\phi \in \mathcal{S}\left(\mathbb{R}\right),\chi \in {\mathbb{C}}^2\right\}$$

is stable under all generators and under the action of D.

4.3. Dirac Operator D

The Dirac operator is defined as

$$D:={\gamma }_{0}H+{\gamma }_{1}T+{\gamma }_2(U+U^{†}),$$

(5)

where ${\gamma }_{\mu }\in \mathrm{End}\left({\mathbb{C}}^2\right)$ satisfy the Clifford relations

$$\{{\gamma }_{\mu },{\gamma }_{\nu }\}=2{\eta }_{\mu \nu },{\eta }_{\mu \nu }=\mathrm{diag}(-1,1,1).$$

We use the Pauli matrices

$${\gamma }_0={\sigma }_3,{\gamma }_1={\sigma }_1,{\gamma }_2={\sigma }_2,$$

to represent the hyperbolic (split-signature) Clifford structure.

Physical interpretation. H generates outer-time evolution, T encodes discrete inner-time shifts, and $U+U^{†}$ describes bounded transitions between re-creation modes. The Clifford structure ensures hyperbolic orthogonality between discrete and continuous components.

4.4. Spectral Triple Properties

Proposition 1. 

The Dirac operator D is symmetric and essentially self-adjoint on the dense domain ${\mathcal{D}}_0\subset \mathcal{H}$.

Sketch. 

Each unbounded summand ($H,T$) is essentially self-adjoint on ${\mathcal{D}}_0$; $U+U^{†}$ is bounded. By standard results (e.g., Nelson’s commutator theorem), D is essentially self-adjoint on ${\mathcal{D}}_0$. □

Proposition 2. 

D has compact resolvent, and $[D,a]$ is bounded for all $a\in \mathcal{A}$.

Sketch. 

The resolvent ${(D-i)}^{-1}$ is compact under spectral truncation. Commutators $[D,a]$ involve only bounded shifts and phase operators, ensuring boundedness for all $a\in \mathcal{A}$. □

4.5. Summary

The spectral triple $(\mathcal{A},\mathcal{H},D)$ satisfies:

• D is self-adjoint with compact resolvent;
• $[D,a]$ is bounded for all $a\in \mathcal{A}$;
• $\mathcal{A}$ acts by bounded operators on a dense, invariant domain of D.

This construction captures the operator-algebraic essence of dual-time geometry:

• Discreteness arises from the compact inner-time operator T;
• Continuity arises from the unbounded outer-time generator H;
• Their non-commutativity establishes a unified spectral framework where discreteness and continuity emerge as complementary aspects of one operator structure.

Although presented heuristically, this dual-time spectral triple satisfies the principal axioms of non-commutative geometry and provides a rigorous foundation for the DTT framework. A complete treatment would include verification of summability and dimension axioms and computation of spectral invariants. Nevertheless, the present construction demonstrates that discreteness and continuity naturally coexist within a single operator algebra, unifying quantum discreteness and relativistic continuity under one spectral geometry.

5. The Geometric–Algebraic Resolution

Building upon the Duality-of-Time Postulate introduced in Section 3.1 and the split-complex geometry formulated in Section 3.2, we now construct the corresponding geometric and algebraic framework that unifies discrete re-creation with continuous evolution. 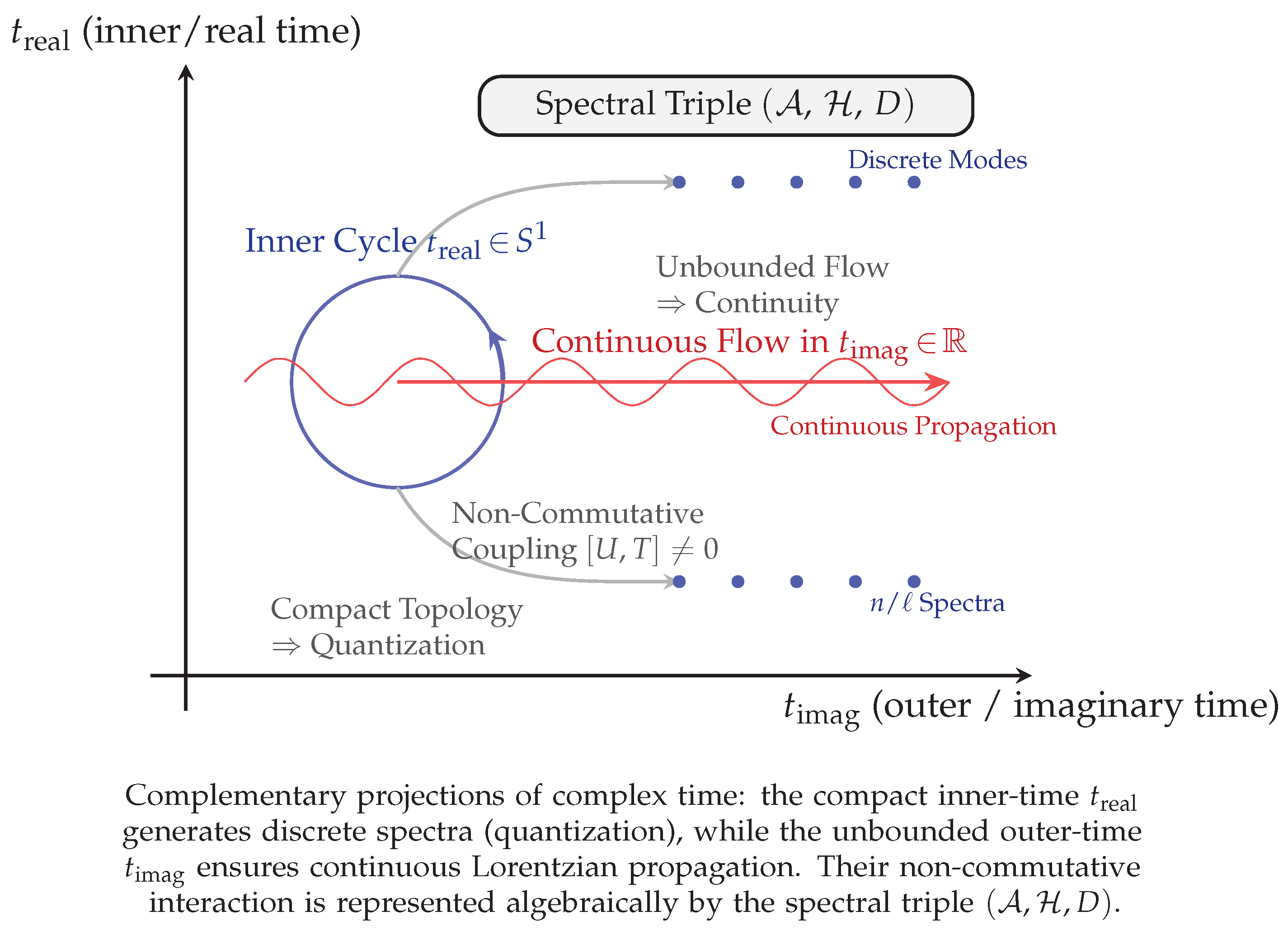The apparent tension between quantum discreteness and classical continuity dissolves once time itself is recognized as a dual entity composed of two hyperbolically orthogonal components: the compact, cyclic inner time $t_{\mathrm{real}}$, governing the discrete renewal of existence, and the unbounded outer time $t_{\mathrm{imag}}$, representing the continuous flow experienced by observers. Every physical process therefore consists of quantized inner cycles projected through a continuous outer dimension, so that discreteness and continuity emerge as complementary aspects of one temporal manifold rather than competing ontological features (see Figure 3).

The compact inner level of time satisfies the periodic boundary condition

$$t_{\mathrm{real}}\left(0\right)\equiv t_{\mathrm{real}}\left(T\right),$$

forming a closed temporal manifold $S^1$ that enforces spectral quantization through its cyclic topology. By contrast, the outer level extends without bound, $t_{\mathrm{imag}}\in \mathbb{R}$, generating the smooth evolution of classical phenomena. Together they define the split-complex coordinate in Equation (1), whose hyperbolic metric

$$\parallel t_{\mathrm{complex}}{\parallel }^2=t_{\mathrm{real}}^2-t_{\mathrm{imag}}^2$$

captures the intrinsic asymmetry between the generative (inner) and observational (outer) modes of time.

In what follows, we formalize this structure algebraically and geometrically, showing that their non-commutative coupling provides a natural resolution of the discreteness–continuity paradox while preserving Lorentz invariance, energy conservation, and dimensional stability.

5.1. Algebraic Coupling of Inner and Outer Time

As established in Section 3.2.5 and Section 3.2.4, the compact and discrete character of the inner time $t_{\mathrm{real}}$ arises from its circular topology: each act of re-creation terminates at its ontological origin, forming a closed temporal loop. In contrast, the outer time $t_{\mathrm{imag}}$ is unbounded and continuous, describing the linear progression of events perceived by observers. These two temporal domains are intrinsically coupled, forming the dynamic interface between absolute re-creation and observed evolution.

The algebraic structure of the split-complex time, expressed by Equation (1), admits the hyperbolic metric

$$\parallel t_{\mathrm{complex}}{\parallel }^2=t_{\mathrm{real}}^2-t_{\mathrm{imag}}^2,$$

reflecting the orthogonality and asymmetry between the two flows of time. Compactness implies a discrete spectrum,

$$t_{\mathrm{real}}=n{\tau }_0,n\in \mathbb{Z},$$

where ${\tau }_0$ denotes the fundamental period of re-creation. Meanwhile, $t_{\mathrm{imag}}\in \mathbb{R}$ allows differentiable evolution over this discrete basis. Physical processes thus correspond to smooth projections of quantized temporal cycles, each representing an elementary act of manifestation by the Single Monad.

The interplay between these levels is encoded in their non-commutative coupling,

$$[t_{\mathrm{real}},t_{\mathrm{imag}}]=j{\tau }_0,$$

which formalizes the ontological ordering of re-creation: the inner cycle must complete before outer progression occurs. This relation serves as the temporal analogue of the canonical time–energy conjugacy in quantum mechanics, ensuring that discrete renewal and continuous evolution are dynamically conjugate rather than independent. The resulting hyperbolic algebra unifies quantization and smooth propagation within a single dual-temporal framework.

5.2. Geometric Resolution of Discreteness and Continuity

The circular compactification of $t_{\mathrm{real}}$ and the open extension of $t_{\mathrm{imag}}$ together form a hybrid temporal manifold that supports both discrete spectra and continuous dynamics. Each complete inner cycle produces one quantized increment of outer evolution, so that continuity on the outer level emerges as the cumulative effect of successive discrete renewals on the inner level. The world thus appears smooth to an observer situated within $t_{\mathrm{imag}}$, even though it is ontologically re-created in finite temporal quanta governed by $t_{\mathrm{real}}$.

Formally, let $\psi \left(t_{\mathrm{imag}}\right)$ denote a physical state evolving along the outer time. Its periodic regeneration through the inner cycle introduces a discrete phase factor,

$$\psi (t_{\mathrm{imag}}+{\tau }_0)=e^{j{\omega }_0{\tau }_0}\psi \left(t_{\mathrm{imag}}\right),$$

where ${\omega }_0=2\pi /{\tau }_0$ defines the fundamental frequency of re-creation. The observable continuity of motion then results from the smooth modulation of this periodic structure across the extended outer time. Thus, continuity is not the negation of discreteness but its perpetual unfolding along an unbounded temporal axis.

Consequently, the hyperbolic coupling

$$t_{\mathrm{complex}}=t_{\mathrm{real}}+j{t}_{\mathrm{imag}}$$

provides a geometric–algebraic resolution of the discreteness–continuity paradox. The compact inner time ensures spectral quantization and recurrence, while the unbounded outer time guarantees differentiable propagation and Lorentz invariance. Both arise from the same dual-temporal manifold, confirming that discreteness and continuity are complementary projections of one unified temporal geometry.

5.3. Lorentz Invariance and Spectral Quantization

The hyperbolic metric

$$\parallel t_c{\parallel }^2=t_{\mathrm{real}}^2-t_{\mathrm{imag}}^2$$

naturally induces a Lorentzian signature when projected into the physical spacetime manifold. Since $t_{\mathrm{real}}$ and $t_{\mathrm{imag}}$ are hyperbolically orthogonal, the transformation

$$t_{\mathrm{real}}^{\prime }=\gamma (t_{\mathrm{real}}-\beta t_{\mathrm{imag}}),t_{\mathrm{imag}}^{\prime }=\gamma (t_{\mathrm{imag}}-\beta t_{\mathrm{real}}),$$

with $\gamma ={(1-{\beta }^2)}^{-1/2}$, preserves the norm $\parallel t_{\mathrm{complex}}^{\prime }{\parallel }^2={\parallel t_{\mathrm{complex}}\parallel }^2$. The Lorentz group therefore emerges directly as the symmetry group of the dual-time metric, and the invariant speed c corresponds to the fundamental ratio between the inner and outer temporal rates. The constancy of the speed of light thus reflects the geometric invariance of the hyperbolic temporal manifold rather than an empirical postulate.

The compact inner time supports discrete eigenfrequencies,

$${\omega }_n={\displaystyle \frac{2\pi n}{{\tau }_0}},n\in \mathbb{Z},$$

associated with the re-creation cycles of the Monad. Each eigenmode defines a quantized energy level via the dual-time analogue of Planck’s relation,

$$E_n=\hslash {\omega }_n={\displaystyle \frac{2\pi \hslash n}{{\tau }_0}},$$

where ${\tau }_0$ sets the fundamental scale of quantization. Continuous evolution along $t_{\mathrm{imag}}$ allows these discrete modes to interfere and superpose, producing the smooth propagation of energy and information observed in classical dynamics. The spectrum of observable phenomena thus arises from the interplay between the cyclic discreteness of $t_{\mathrm{real}}$ and the continuous extension of $t_{\mathrm{imag}}$.

Light represents the limiting case in which propagation occurs purely within the inner-time domain, without outer re-creation. Because its dynamics are confined to $t_{\mathrm{real}}$, it is perceived by observers—who evolve along $t_{\mathrm{imag}}$—as moving at the invariant speed c. Hence, Lorentz invariance emerges as a direct geometric consequence of the hyperbolic dual-time structure.

5.4. Energy–Momentum Relation and Conservation Laws

The split-complex representation $t_c=t_{\mathrm{real}}+j{t}_{\mathrm{imag}}$, with $j^2=+1$, establishes the foundation for energy–momentum conservation. The inner component generates quantized energy levels, while the outer extension corresponds to momentum and spatial propagation.

Let the temporal phase be defined as

$$\mathsf{\Phi }={\omega }_r{t}_{\mathrm{real}}+j{\omega }_i{t}_{\mathrm{imag}},$$

where ${\omega }_r$ and ${\omega }_i$ denote the inner and outer frequencies, respectively. Invariance of the hyperbolic norm,

$${\parallel \mathsf{\Phi }\parallel }^2={\omega }_r^2{t}_{\mathrm{real}}^2-{\omega }_i^2{t}_{\mathrm{imag}}^2=\mathrm{constant},$$

implies conservation of the associated physical quantity,

$$E^2-{\left(pc\right)}^2={\left(m{c}^2\right)}^2,$$

upon identifying $E=\hslash {\omega }_i$, $p=\hslash {\omega }_r/c$, and $m{c}^2=\hslash /{\tau }_0$. The relativistic energy–momentum relation thus follows directly from the invariance of the dual-time metric. The re-creation period ${\tau }_0$ acts as the fundamental temporal unit linking mass to the compact inner cycle.

Moreover, the commutation relation

$$[t_{\mathrm{real}},t_{\mathrm{imag}}]=j{\tau }_0$$

ensures conservation of total temporal flux across the dual manifold: every increment in continuous outer evolution is balanced by a discrete contribution from inner re-creation. This dual balance underlies all conservation laws—energy, momentum, and charge—interpreting them as consequences of the Monad’s self-consistent re-creation rather than imposed symmetries of spacetime.

Therefore, the fundamental invariant

$$E^2-{\left(pc\right)}^2={\left(m{c}^2\right)}^2$$

represents the macroscopic projection of a deeper temporal symmetry: the constancy of the hyperbolic norm $\parallel t_c{\parallel }^2=t_{\mathrm{real}}^2-t_{\mathrm{imag}}^2$. Conservation laws thus express the stability of the dual-time manifold itself, linking persistence and motion to the perpetual renewal of existence.

5.5. Minimal Stability and Dimensional Balance

The synthesis of discrete inner time and continuous outer time naturally imposes constraints on spatial dimensionality. Since each spatial dimension arises from coupling two orthogonal temporal generators, the number of stable spatial degrees of freedom is limited by the algebraic consistency of these couplings under

$$[t_{\mathrm{real}},t_{\mathrm{imag}}]=j{\tau }_0.$$

Each additional spatial dimension requires an independent pair of orthogonal temporal generators, but beyond three such pairs, associativity and non-commutativity cannot both be preserved. This defines a minimal stability criterion for spatial dimensionality.

Formally, the temporal algebra

$${\mathcal{A}}_T=\{1,t_{\mathrm{real}},t_{\mathrm{imag}},t_{\mathrm{real}}{t}_{\mathrm{imag}}\}$$

is closed under hyperbolic multiplication and yields three spatially independent directions. Higher-order extensions introduce non-associative terms, destabilizing the re-creation sequence. The three-dimensionality of space therefore follows from the requirement that the temporal algebra remain closed and self-consistent under cyclic renewal.

Dynamically, a balanced interplay between discrete inner cycles (quantization) and continuous outer evolution (propagation) is achievable only in three orthogonal directions. Fewer dimensions cannot sustain complete re-creation loops, while higher ones fragment the coherence of the cyclic manifold. The observed $3+1$ spacetime structure thus represents the lowest-order stable projection of the dual-time geometry.

This minimal stability principle explains why the universe manifests three extended spatial dimensions and a single continuous temporal flow. Dimensionality emerges as an algebraic equilibrium between associativity and non-commutativity in the cyclic process of re-creation.

Summary of the Geometric–Algebraic Resolution

The dual-time framework establishes a coherent synthesis wherein quantized inner cycles and continuous outer evolution are unified through a hyperbolic temporal geometry. The compact inner time $t_{\mathrm{real}}$ yields discrete spectra and recurrence; the unbounded outer time $t_{\mathrm{imag}}$ ensures continuous propagation and relativistic invariance. Their non-commutative coupling generates energy–momentum conservation and the Lorentz metric, while algebraic closure under cyclic renewal accounts for the stability of three spatial dimensions.

Hence, the discreteness–continuity paradox is resolved not by dual ontologies but by recognizing them as complementary projections of one self-consistent temporal manifold. Within this unified geometry, quantization, relativity, and dimensionality arise from the same principle of perpetual re-creation. This synthesis completes the transition from metaphysical ontology to formal physics and sets the stage for the worked example in Section 5.6, as illustrated schematically in Figure 3.

5.6. Worked Example: Spectral Quantization

To illustrate how discrete physical spectra emerge naturally from the compact inner-time geometry, consider a field $\mathsf{\Psi }(t_{\mathrm{real}},t_{\mathrm{imag}})$ defined on the dual-time manifold introduced in Section 3.2. The compactness of the real temporal component $t_{\mathrm{real}}\in [0,{\tau }_0)$ enforces the periodic boundary condition

$$\mathsf{\Psi }(t_{\mathrm{real}}+{\tau }_0,t_{\mathrm{imag}})=\mathsf{\Psi }(t_{\mathrm{real}},t_{\mathrm{imag}}),$$

(6)

where ${\tau }_0$ denotes the fundamental period of re-creation.

Expanding $\mathsf{\Psi }$ in a Fourier basis along the compact inner-time coordinate yields

$$\mathsf{\Psi }(t_{\mathrm{real}},t_{\mathrm{imag}})=\sum _{n\in \mathbb{Z}}{\psi }_n\left(t_{\mathrm{imag}}\right)e^{in2\pi t_{\mathrm{real}}/{\tau }_0},$$

(7)

so that each Fourier mode ${\psi }_n\left(t_{\mathrm{imag}}\right)$ evolves continuously along the unbounded outer time. The cyclic nature of $t_{\mathrm{real}}$ quantizes the corresponding eigenfrequencies,

$${\omega }_n={\displaystyle \frac{2\pi n}{{\tau }_0}},n\in \mathbb{Z},$$

(8)

and thus the energy levels,

$$E_n=\hslash {\omega }_n={\displaystyle \frac{2\pi \hslash n}{{\tau }_0}}.$$

(9)

Hence, spectral quantization follows directly from the compact topology of the inner-time circle $S^1$ without invoking an external quantization postulate.

The continuous flow along $t_{\mathrm{imag}}$ allows superposition and interference between discrete modes, producing the smooth dynamics observed in classical evolution. In the limiting case ${\tau }_0\to 0$, the spacing between eigenvalues vanishes, and the discrete spectrum becomes dense, recovering the classical continuum.

Therefore, quantization appears as a purely geometric consequence of the compactification of inner time, while continuity arises from the unbounded extension of outer time. This example demonstrates concretely how the Duality-of-Time framework reconciles discrete and continuous behavior within a single temporal geometry.

This example provides the explicit operational realization of the geometric–algebraic synthesis developed in Section 5. The discrete Fourier modes arising from the compact inner-time circle $t_{\mathrm{real}}\in S^1$ embody the quantized re-creation cycles of the Single Monad, while their continuous evolution along the unbounded outer time $t_{\mathrm{imag}}\in \mathbb{R}$ manifests as the smooth propagation of physical processes. Thus, spectral quantization and classical continuity are not separate regimes but complementary expressions of one dual-temporal geometry, confirming the Duality-of-Time Theory as a coherent resolution of the discreteness–continuity paradox.

6. Theoretical and Empirical Implications

The dual-time framework introduced in this work provides a unified conceptual and mathematical resolution to the longstanding discreteness–continuity paradox that underlies quantum theory, relativity, and cosmology. By treating discrete and continuous dynamics as complementary projections of a complex-temporal manifold, the framework offers a geometric ontology in which quantized spectra, smooth propagation, and temporal irreversibility all emerge from a single dynamical structure.

6.1. Quantum Theory and Measurement

In conventional quantum mechanics, discrete spectra are postulated axiomatically, while wavefunctions evolve continuously under the Schrödinger equation [4]. The measurement problem stems from the disjunction between unitary evolution and discontinuous collapse [33,34]. Within the dual-time formalism:

• Outer (imaginary) time $t_{\mathrm{imag}}$ governs continuous evolution in Hilbert space, reproducing standard quantum dynamics.
• Inner (real) time $t_{\mathrm{real}}$, being compact, generates a tower of discrete modes interpreted as quantized energy, spin, or charge levels.
• Measurement corresponds to projection between temporal layers—not a fundamental collapse, but synchronization of discrete and continuous time modes.

This provides a geometric reinterpretation of quantum collapse and links naturally to time-symmetric and relational formulations [35,36], where apparent discontinuity arises from changes in temporal frame.

6.2. Relativity, Gauge Structure, and Quantum Gravity

General relativity assumes a smooth Lorentzian manifold, while quantum theories demand a discrete substrate. The dual-time framework reconciles these:

• Lorentz invariance is preserved through smooth evolution along $t_{\mathrm{imag}}$, maintaining macroscopic relativistic structure.
• Discreteness enters through compact real-time cycles $t_{\mathrm{real}}$, embedding Planck-scale microstructure.
• The invariant spacetime interval is reinterpreted as a projection from complex-temporal curvature:

  $$d{s}^2=c^{2}d{t}_{\mathrm{imag}}^2-c^{2}d{t}_{\mathrm{real}}^2.$$

Gauge symmetries also acquire geometric meaning. Compact inner-time loops induce quantized phase rotations analogous to $U\left(1\right)$, while multidimensional projections of the temporal manifold relate to higher gauge structures. Coupling constants may emerge from geometric ratios between temporal frequencies. Unlike purely algebraic approaches [17,37], this grounds gauge structure in physical time.

In quantum gravity, the dual-time picture offers a synthesis:

• Loop quantum gravity’s discreteness arises from real-time compactification.
• Diffeomorphism invariance and continuous propagation from string theory are preserved via $t_{\mathrm{imag}}$.
• The fundamental commutation $[T_r,T_i]\ne 0$ defines a non-trivial temporal phase space, making geometry itself a spectral consequence of time duality.

6.3. Entropy, Information, and Computation

Thermodynamic irreversibility emerges when phase coherence between inner and outer time modes breaks down. This produces an effective entropy gradient and a direction of time, without invoking probabilistic coarse-graining [38,39]. Decoherence corresponds to loss of synchronization between $t_{\mathrm{real}}$ cycles and continuous evolution.

At the informational level, quantum entanglement may be viewed as inner-time phase alignment across systems, resembling nonlocal temporal correlations in path-integral formulations [40,41]. This dual-time view provides a geometric understanding of measurement, computation, and entropy within a single temporal framework.

6.4. Cosmological Implications

Cosmology reflects the dual structure of time:

• Vacuum energy: Averaged inner-time fluctuations manifest as residual vacuum energy, potentially addressing the cosmological constant problem [42].
• Inflation: Rapid real-time cycles generate effective exponential expansion, possibly eliminating the need for a separate inflaton field.
• Late-time smoothness: At cosmic scales, continuous outer-time evolution dominates, while inner-time discreteness leaves subtle imprints.

Nested cycles in the early universe may generate the observed isotropy via geometric averaging, offering a new foundation for inflation and dark energy.

6.5. Empirical Signatures and Testability

Although $t_{\mathrm{real}}$ is not directly observable, its effects project into $t_{\mathrm{imag}}$ and yield testable predictions:

Quantum Decoherence Scaling.

Real-time discreteness predicts universal decoherence scaling with square of the frequency:

$$\mathsf{\Gamma }\sim {\omega }^2{\tau }_i,$$

where ${\tau }_i$ is the inner cycle period. This deviates from environmental decoherence and may be tested via interferometry in atomic and optical systems [43,44].

Atomic Clock Stability.

Optical lattice clocks with $<{10}^{-18}$ uncertainty may detect subtle, frequency-dependent drifts due to inner-time fluctuations [45,46].

Gravitational-Wave Background.

Nested cycles may induce a stochastic $f^2$ background distinguishable from astrophysical sources. Future detectors (LISA, Cosmic Explorer) may be sensitive to this signature [47,48].

Cosmological Observables.

Fluctuations in inner-time cycles could imprint:

• Modified inflationary spectra in the CMB [49],
• Residual inhomogeneities at large scales,
• A vacuum energy scale $\mathsf{\Lambda }\sim 1/{\ell }^2$, linking Planck discreteness to dark energy.

High-Energy Physics.

If couplings arise from inner-time holonomies, small anomalies in renormalization-group running may be observable at collider energies.

In all cases, the predictions differ qualitatively from standard theories, making the dual-time model empirically falsifiable and physically meaningful.

7. Outlook and Future Work

The framework developed here opens multiple directions for further investigation, both theoretical and experimental.

7.1. Mathematical Development

Future work will aim to refine the spectral triple $(\mathcal{A},\mathcal{H},D)$, extend it to include gauge groups and interactions, and derive non-perturbative structures analogous to the Standard Model [17]. Explicit Lagrangian or Hamiltonian formulations incorporating real-time cycles will enable comparison with canonical quantization approaches.

7.2. Field Theory and Particle Physics

Inner-time holonomies may underlie:

• Charge quantization and coupling constants,
• Mass hierarchies and generation structure via winding numbers,
• Modifications to coupling running in QED/QCD.

These possibilities suggest that dual-time geometry could inform beyond-Standard-Model physics.

7.3. Quantum Gravity and Spacetime Structure

Bridges with existing approaches can be further explored:

• Mapping real-time eigenmodes to loop quantum gravity spin-network labels,
• Emergence of causal set orderings from nested cycles,
• Extending the spectral action to dual-time manifolds.

7.4. Cosmological Simulations

Simulating early-universe dynamics under nested real-time cycles may clarify:

• Inflationary behavior without scalar fields,
• The cosmological constant as a time-averaged projection,
• Discrete structure in the CMB and large-scale surveys.

7.5. Experimental Design

On the experimental front, targeted probes are feasible:

• Interferometric platforms for ${\omega }^2$ decoherence signatures,
• Atomic clock networks to detect inner-time-induced drifts,
• Gravitational-wave detectors for stochastic projection noise,
• Particle colliders for signs of temporal holonomy effects.

Closing Perspective. In unifying quantum discreteness and relativistic continuity within a single temporal geometry, the dual-time framework transforms foundational paradoxes into consequences of a deeper temporal ontology. Whether real-time compactification is a feature of nature is an empirical question—one that upcoming technologies are increasingly capable of answering.