New Demonstration of the Presence of Errors 1 and 2 in Michelson’s Analysis of His MMX, Based on the Symmetry of TSC Contest, Contradicting the Solution in Physics Textbooks, Which Therefore Require Correction

1. Introduction

In this article, initially we present, within New Interpretation NI96 of Michelson’s analysis of experiments from 1881/87 (MMX) [1,2,3,4,5,6,7,8,9,10,11,12,13], a new demonstration of the existence of Errors 1 and 2 (ER12) in TSC actual Analysis, which is widely recognized as a faithful model of Michelson’s interferometer experiments of 1881/87 (MMX), based on the symmetry of the paths and on the symmetry/equality of the associated times.

We recall here, that Error 1 refers in the case of MMX to the wrong transverse path of ray 2, and Error 2 refers to the wrong calculation of the transverse time t₂ of ray 2, and similarly ER12 applies to TSC [11,14]. It is very important to note that ER12 refers exclusively to Michelson’s Analysis and not to the MMX physical experiment in the laboratory or in the field, carried out impeccably [1,2,3,4,5,6,7,8,9,10,11,12,13].

For this, in Sec. 2 we present a new mathematical demonstration of the existence of ER12, in Michelson’s Analysis, as a new complement to NI96, based on the symmetric character of the paths and associated times, in TSC analyzed in river bank (BF) frame.

The new calculations are based on the special scheme of paths and speeds for the transverse path in TSC, starting from the initial Phase 0 scheme, for the case of a perfectly symmetrical stationary river. In the subsequent Phase 1 with an arbitrary water v speed in the longitudinal direction, the preservation of the symmetry of the longitudinal and transverse total times, that is, their equality t_1t=t_2t was analytically demonstrated precisely.

This result of times equality t₁=t₂ constitutes an new additional confirmation of the NI96 correctness, and of the existence of ER12 in Michelson’s analysis, discovered by us, then corrected [1,2,3,4,5,6,7,8,9,10,11,12,13], and as a consequence, physics textbooks require corrections in order to obtain there also the equality of times t₁=t₂ in MMX, and in TSC, swimmer SW2 should not win, but TSC ends in a tie.

2. A New Demonstration of the Presence of Errors 1 and 2 in Michelson’s Analysis of MMX Based on the Symmetrical Character of TSC

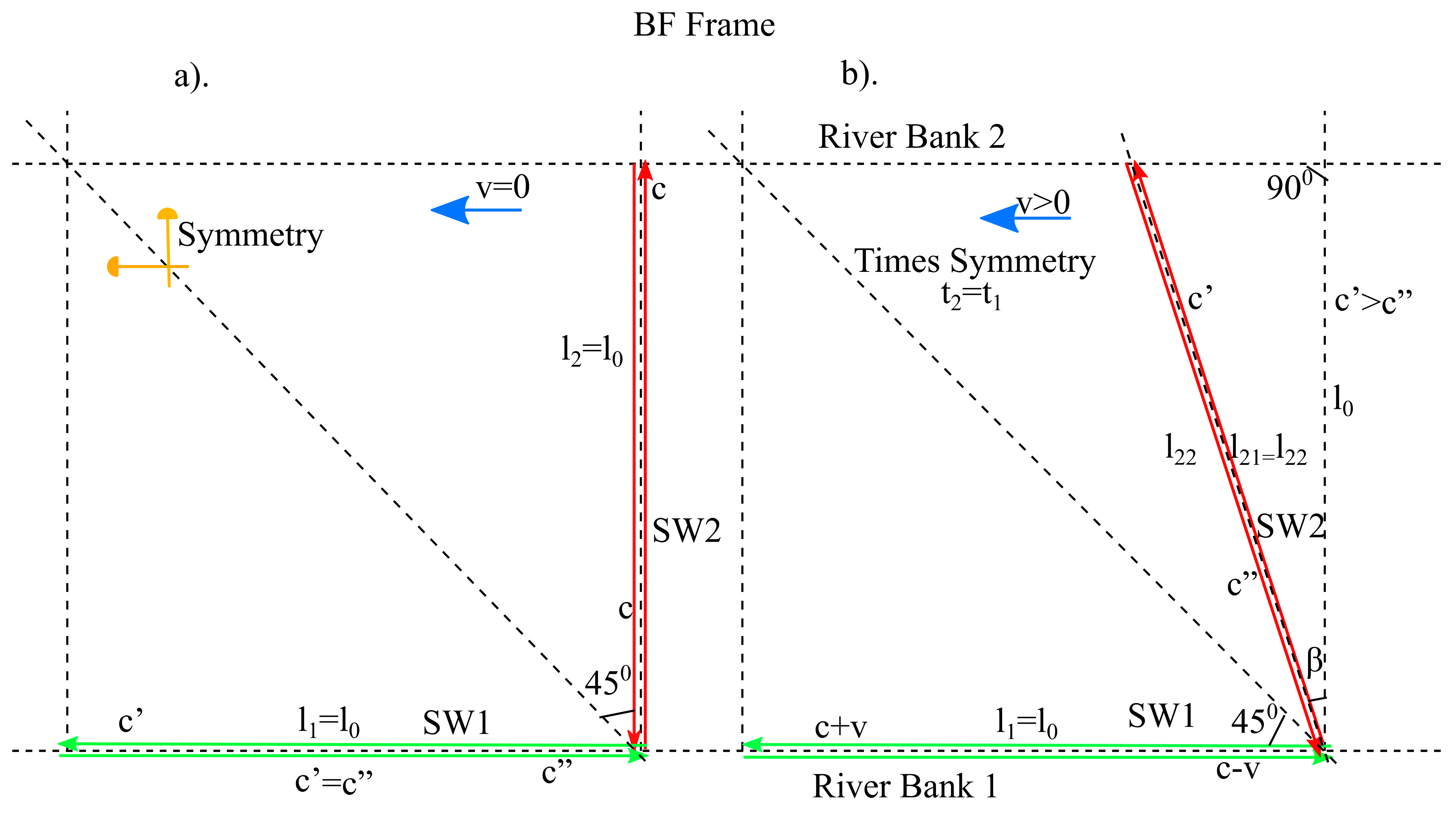
We start from the observation that the TSC contest in its simplest form can be considered by the situation in which the water is stationary so that the speed of the water/ether current is v=0 everywhere (Figure 1a).

In this initial case, noted with Phase 0 of TSC, the paths of the two swimmers/boats, which respect the rules of a correct, fair play contest TSC, indicated in detail in Sec.3 of [11], are fulfilled and respected exactly.

The initial situation of TSC is represented in Figure 1.a). where the Bank frame/referential (BF) is used, in which the two swimmers start simultaneously, with their speed c in the water, having their contest paths perpendicular to each other.

It is found that in the Phase 0 of the TSC, the round-trip paths on both initial distances and directions l₀ of swimmers SW1 and SW2 starting simultaneously from the same Block-Start (BS) at time t=0 are symmetrical with respect to the diagonal of quadrant II in which the TSC race takes place, in the BF reference frame.

And according to Figure 1a. the total round-trip times, t₁₀ and t₂₀ will be as follows for swimmers SW1 and SW2:

$$t_{10}={\displaystyle \frac{2l_0}{c}}$$

(1)

$$t_{20}={\displaystyle \frac{2l_0}{c}}$$

(2)

From (1) and (2) the following results:

$$t_{10}=t_{20}$$

(3)

From (3) it is found that the two times are equal, and the TSC contest ends in a tie, so that the symmetry of the times of the two swimmers in Phase 0, t₁₀ and t₂₀ is also preserved.

Now in the usual contest, noted Phase 1, we will consider the occurrence of a water movement in the direction of the riverbed slope, here to the left with water speed v >0, as in Figure 1b. but the rest of conditions in the TSC from Phase 0, remain unchanged. The representation is also given in the BF reference frame.

We will evaluate in Phase 1 the influence of the new factor, the water speed v, on the path/trajectory of the two swimmers as well as on the times t₁ and t₂ for their round trips, in order to demonstrate the effect of the symmetry property on these times in the TSC, highlighted in Phase 0.

The total time t_1t related to swimmer SW1 for the complete round trip Figure 1.b. will be easily calculable directly with the classical formulas:

$$t_{1t}=t_{11}+t_{12}={\displaystyle \frac{l_0}{\left(c+v\right)}}+{\displaystyle \frac{l_0}{\left(c-v\right)}}={\displaystyle \frac{2c{l}_0}{c^2-v^2}}={\displaystyle \frac{2l_0}{c}}{\displaystyle \frac{1}{1-\raisebox{1ex}{$v^2$}\!\left/ \!\raisebox{-1ex}{$c^2$}\right.}}={\displaystyle \frac{2l_0}{c}}{\displaystyle \frac{1}{{\propto }^2}}$$

(4)

With coefficient:

$$\propto =\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}$$

(4b)

Now the total time t_2t for swimmer SW2 for the complete round trip (Figure 1.b.) will be given by the following more complicated expressions, that cannot be calculated directly:

$$t_{2t}=t_{21}+t_{22}={\displaystyle \frac{l_{21}}{c’}}+{\displaystyle \frac{l_{22}}{c”}}$$

(5)

In (5) the terms l₂₁ , c’ , l₂₁ , l₂₂ and c” (Figure 2) will have to be evaluated by mathematical procedures and calculations, which are presented below.

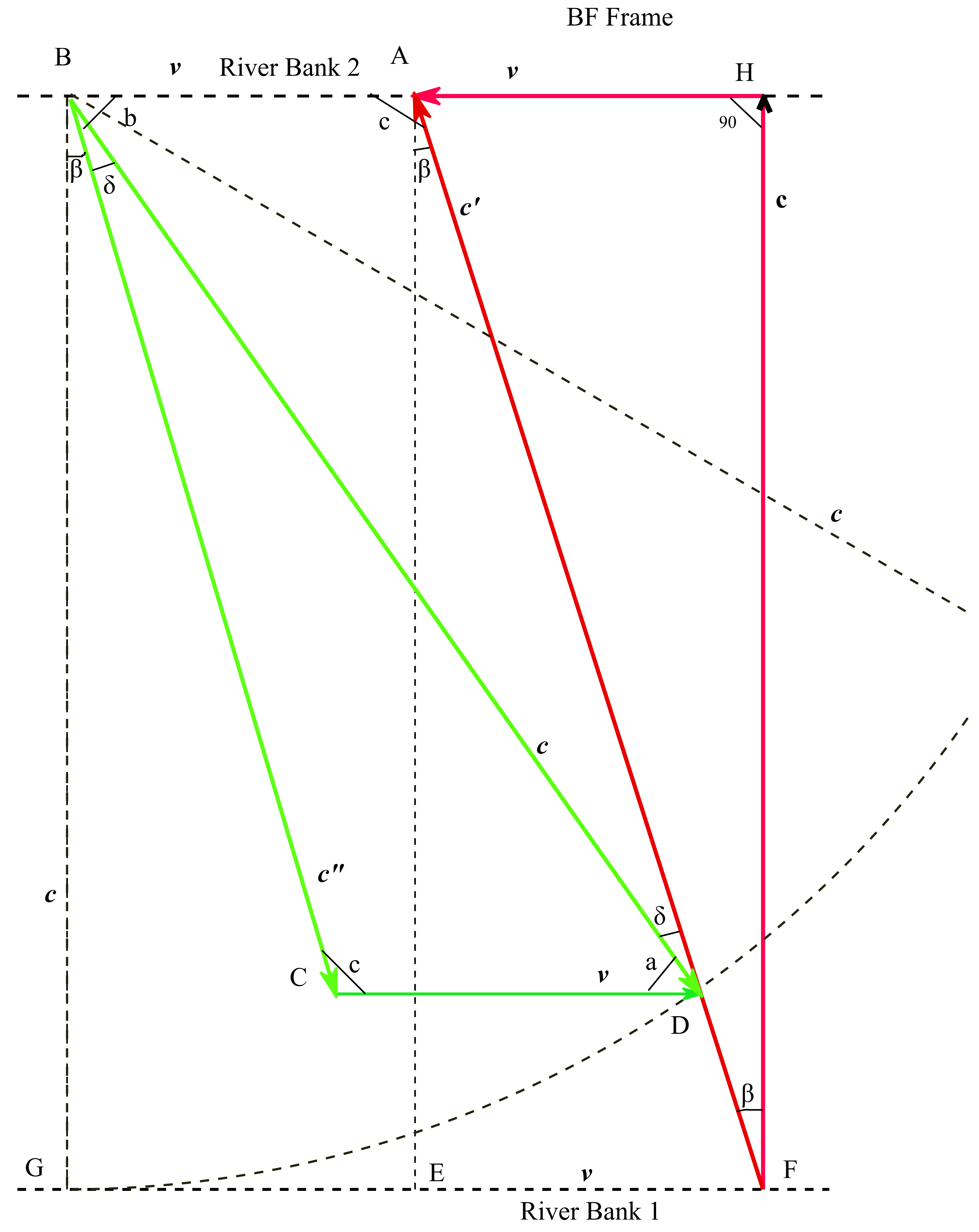
For this purpose, the paths of SW2 forward and backward will be detailed as in Figure 2, using the BF reference frame, based on the real velocities c’ and c” whose determination in BF will prove to be more complicated than in the WF reference frame, used in [11].

In Figure 2., the speed polygons including the speed c’ at departure through the right triangle AEF and the speed at return c” through the obtuse triangle BCD are initially represented here on a convenient scale.

Now, to represent the speed c’’ when SW2 returns, we will have to make an auxiliary geometric construction consisting of drawing a circle of radius c, with the center at point B (Figure 2).

And at the intersection of the circle with the line AF we find point D. In triangle ABD, the line BD has exactly the size c.

Then through point D we draw a parallel to the side EF, with a segment whose length is exactly v, where we find point C. And in the obtuse triangle BCD, the line CD has exactly the size v, and the line BC has exactly the size of the speed c’’ of the return path (in the BF frame of reference).

In Figure 2 in right triangle AEF we note the angle EAF with β which has the well-known classical expression:

$$tg\beta ={\displaystyle \frac{v}{c}}$$

(6)

We also denote the newly formed angle CBD (Figure 2) with the letter δ, and the remaining newly formed angles with the lowercase letters a, b, c, which are still of unknown sizes that will be determined geometrically and trigonometrically below.

In triangle ABD (Figure 2) we write the sine theorem as follows:

$${\displaystyle \frac{sin\delta }{v}}={\displaystyle \frac{sin\left({90}^0+\beta \right)}{c}}$$

(7)

$$sin\delta ={\displaystyle \frac{v}{c}}sin\left({90}^0+\beta \right)=tg\beta sin\left({90}^0+\beta \right)=tg\beta cos\beta =sin\beta$$

(8)

So we find the relationship:

$$\delta =\beta$$

(9)

Now in triangle BCD (Figure 2) we write the theorem of sines as follows:

$${\displaystyle \frac{sin\delta }{v}}={\displaystyle \frac{sin\left({90}^0-\beta +\delta \right) }{c”}}$$

(10)

Resulting:

$$c”=v{\displaystyle \frac{sin\left({90}^0-\beta -\delta \right)}{sin\delta }}=v{\displaystyle \frac{sin\left({90}^0-\beta -\delta \right)}{tg\beta sin\left({90}^0+\beta \right)}}={\displaystyle \frac{v}{\frac{v}{c}}}{\displaystyle \frac{sin\left({90}^0-\beta -\delta \right)}{sin\left({90}^0+\beta \right)}}=c{\displaystyle \frac{sin\left({90}^0-\beta -\delta \right)}{sin\left({90}^0+\beta \right)}}$$

(11)

Using the formula for the sum of two angles from trigonometry in (10) we have:

$$sin\left({90}^0-\beta -\delta \right)=sin\left({90}^0-\beta \right)cos\delta -cos\left({90}^0-\beta \right)sin\delta =cos\beta cos\delta -sin\beta sin\delta$$

(12)

Introducing (12) into (11) and simplifying with cosβ we obtain:

$$c”=c\left(cos\delta -tg\beta sin\delta \right)$$

(13)

Inserting (9) into (11) we obtain:

$$c”=c\left(cos\beta -tg\beta sin\beta \right)=c{\displaystyle \frac{co{s}^2\beta -si{n}^2\beta }{cos\beta }}=c{\displaystyle \frac{1-2si{n}^2\beta }{cos\beta }}$$

(14)

We use in (14) the relations from trigonometry:

$$cos\beta ={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{1+t{g}^2\beta }$}\right.} and sin\beta ={\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\sqrt{1+ct{g}^2\beta }$}\right.}$$

(15)

and we get:

$$c”=c{\displaystyle \frac{1-2\frac{t{g}^2\beta }{1+t{g}^2\beta }}{\frac{1}{\sqrt{1+t{g}^2\beta }}}}=c{\displaystyle \frac{\frac{1-t{g}^2\beta }{1+t{g}^2\beta }}{\frac{1}{\sqrt{1+t{g}^2\beta }}}}=c{\displaystyle \frac{1-t{g}^2\beta }{\sqrt{1+t{g}^2\beta }}}$$

(16)

But the time t₂₁ required for SW2 to travel the path at departure (Figure 2) according to (5) will be:

$$t_{21}={\displaystyle \frac{l_{21}}{c^{\prime }}}={\displaystyle \frac{l_0}{c}}$$

(17)

And the time t₂₂ required for SW2 to travel the return path (Figure 2), according to (5), will be:

$$t_{22}={\displaystyle \frac{l_{22}}{c”}}={\displaystyle \frac{l_0}{c”cos\beta }}={\displaystyle \frac{l_0}{cos\beta .c\frac{1-t{g}^2\beta }{\sqrt{1+t{g}^2\beta }} }}={\displaystyle \frac{l_0}{c.\frac{1}{\sqrt{1+t{g}^2\beta }}.\frac{1-t{g}^2\beta }{\sqrt{1+t{g}^2\beta }} }}={\displaystyle \frac{l_0}{c.\frac{1-t{g}^2\beta }{1+t{g}^2\beta } }}={\displaystyle \frac{l_0}{c}}{\displaystyle \frac{1+t{g}^2\beta }{1-t{g}^2\beta }}={\displaystyle \frac{l_0}{c}}{\displaystyle \frac{1+\frac{v^2}{c^2}}{1-\frac{v^2}{c^2}}}={\displaystyle \frac{l_0}{c}}{\displaystyle \frac{c^2+v^2}{c^2-v^2}}$$

(18)

And the total time t_2t required for SW2 to travel the round trip (Figure 1., Figure 2) from (17) and (18) will be:

$$t_{2t}={\displaystyle \frac{l_0}{c}}+{\displaystyle \frac{l_0}{c}}{\displaystyle \frac{c^2+v^2}{c^2-v^2}}={\displaystyle \frac{l_0{c}^2-l_0{v}^2+l_0{v}^2+l_0{c}^2}{c\left(c^2-v^2\right)}}={\displaystyle \frac{2l_0}{c}}{\displaystyle \frac{1}{1-\frac{v^2}{c^2}}}$$

(19)

Or using the established notation with letter α from (4b), it results:

$$t_{2t}={\displaystyle \frac{2l_0}{c}}{\displaystyle \frac{1}{{\propto }^2}}$$

(20)

From (19) and (20) it follows that for the total time of SW2 t_2t we obtained the same value as for the time t_1t of SW1 from (4), or t_2t= t_1t, so the symmetry of times is preserved in the situation of the TSC contest in Phase 1 above, so confirming the presence of ER12 in the Michelson’s MMX and in TSC [11,14].

But in [11] we demonstrated that the equality of the times of the two swimmers t_2t= t_1t, is preserved also in the most general case when the departure direction of SW1 is at any angle u_i to the Ox axis (SW2 also departs orthogonally to SW1).

In the present case, if we consider various Phases i, of the contest in which the direction of the water velocity v, is inclined with some angle u_i, different from zero, to the Ox direction (as in Figure 1b, Figure 2), we will also obtain in these cases, the equality of the times t_2t= t_1t, of the two swimmers SW1 and SW2 , so in these cases the symmetry of their times is preserved (Figure 2).

In this case of Phase 1, the existence of Errors 1 and 2 in Michelson’s Analysis of MMX is reconfirmed.

It also results that the original symmetry in Phase 0 of times t₁ and t₂ in the TSC is not affected by the presence of a water current with speed v, not only longitudinally but in any direction u_i, so that the equality of times t₁=t₂ in Phase 1 of the TSC is also justified [11], contradicting the result t₁>t₂ supported/present in all physics textbooks [14], which will all have to be corrected, and the admission of all the resulting consequences, including the admission of the existence of the ether and the consequences of its presence.

3. Conclusions and Consequences

From the above results for the TSC type contest analysis, first performed in the BF referential, we obtained the correct times for SW1 and SW2, t₁=t₂, also proving the symmetry of the TSC contest, utilizing the rules from our works in NI96, starting from 1996._.

However, this result does not coincide with the times provided by Physics Textbooks, which give the times t₁>t₂, stating that SW2 wins the contest, so resulting even the existence of ER12 in Physics Textbooks, which comes from Michelson’s erroneous analysis in MMX, containing ER12, as we demonstrated.

At the same time, it also results that applying a velocity v in any direction u_i, to the water in TSC, does not affect the symmetry of times t₁ and t₂, nor their equality t₁=t₂, which confirms the presence of ER12 in the TSC and therefore also in the MMX.

From the above result, of times symmetry/equality t₂=t₁ from TSC, which was also applied to the analysis of Michelson for his experiments MMX from 1881/87, by discovering and then correcting ER12, it follows that the ether should no longer be eliminated from physics, as Einstein did in 1905, based precisely on MMX whose Analysis contained ER12.

By readmitting by us, the existence of the ether in physics, multiple related consequences emerged, including the elaboration and development of the HM16 ether model. The new principles and consequences of ether existence were then derived, the start of which was given by the new theory of gravitation (NTG16), followed by a new theory of physics (NTP16), theories that will be permanently developed within all branches of science.

However, the our above result of equality of the two times t₂=t₁ and their symmetry of the two swimmers from the TSC contest, compared with the result of the times t₁>t₂, values resulting from treatment in Physics Textbooks, respectively of the two times of the two light rays from the MMX interferometer, was predicted, justified and demonstrated by us in NI96, through the work started since 1996. All starting from the existence and the discovery of ER12 in Michelson’s Analysis in MMX, and as a consequence, all Physics textbooks require the corresponding corrections to ER12.