Introduction
In the article, we initially refer to a numerical calculations for the well-known contest of two Boats/Swimmers (TSC), here for one Motorboat (BO), at the first crossing of a river (RC1), which is presented as numerical Example 1 (EX1), in the academic platform/website Physics Classroom (TPC) on the internet [
1], for the use and guidance/tutorial, of Physics students/teachers. In TPC, the calculation of the times is performed only for RC1 from the TSC but the applied rules are general, so they are also valid for the return trip of BO, from TSC, which is widely recognized as a faithful model of Michelson's interferometer experiments of 1881/87 (MMX - ME1881/87).
However, this calculation in TPC it is a new one in TSC (even in MMX), that does not respect the solution described in all Physics Textbooks (PTBs) which actually contains Errors 1 and 2 from Michelson's analysis (ER12), as we have discovered and demonstrated since 1996, when we elaborated a New Interpretation (NI96) of Michelson’s Analysis of MMX. However, the calculations and results of TPC, which were performed for EX1, are mathematically correct and are in agreement with our previous research (NI96), relating to discovery and demonstration of the existence of ER12.
Therefore, even TPC via EX1, confirms the existence of ER12 in Michelson's analysis, which we discovered in NI96.
Therefore, in the present article, we expand the area of application of the correct numerical calculus and procedures used in EX1 from TPC and analyze BO's second river crossing (RC2) from TSC, to provide additional arguments in support of the existence of ER12 in Michelson's analysis.
In
Section 2, the calculations from EX1 for the first river crossing RC1 [
1] are presented in detail, for easier reference in the article. We mention that in the TPC tutorial, the calculation in EX1 is reported/referred to as the riverbank frame (BF) reference frame, but without the authors mention this important aspect for the correctness of the analysis.
But the accuracy of the calculation in EX1 is reduced because of the inclination angle θ
1 of the starting/forward path is calculated numerically with only one decimal place. Therefore, in this article, we redid in
Section 3 the calculation from EX1 from TPC for RC1, with the angle θ
1 having a precision increased to 5 decimal places, reported/referred to BF.
However, in Sec. 4, we continued the EX1 contest by performing a complex geometric procedure for establishing also the return path of BO2 consisting of the return journey RC2 of BO2 to its starting point O, resulting in an inverse diagonal path MO, reported in BF Fame, similar to the corrected light ray 2 in MMX, when reported to Device Frame (DF).
In Sec. 5, we continued the contest of EX1 by performing the numerical calculation of the time t
2b for the second river crossing (RC2) of the contest, when we applied the same mathematical and logical rules as those applied in EX1 [
1], reported also in BF Frame, but included a complex trigonometric procedure, resulting in t
2b=71.428571s; thus, the total time of BO2 resulted in t
2= 91.428571s.
To complete the contest, it was necessary to perform the calculation of the total time for BO1, which travels the same length of the round trip but is oriented parallel to the direction of the river current. This calculation performed in Sec. 6 was the classic, simpler calculation, which does not involve ambiguities/controversies in the BF frame and results in a total time of BO1 of t1= 91.428571s.
Practically, the equality of the two times t
1 and t
2 was obtained, using the logical rules and mathematical procedures proposed in EX1 from the TPC website [
1], officially recognized as guidance of Physics teachers and students, so that the claims in the Physics textbooks (PTB) that BO2 (SW2, etc.) wins the competition are wrong because the contest, if conducted correctly, ends in a tie.
In the article, for confirming the equality of the results of times t1 and t2 in the two frames/referentials, BF frame and water frame (WF), we presented in Sec. 7 the complete paths schemes of BO2 and BO1, reported in the WF frame, on the basis of which paths, the times t1=t2=2 l/c*1/α2 were correctly calculated. These calculations were performed via our mathematical and logical procedures proposed since 1996 in NI96, which admit the existence of ER12 in Michelson's Analysis of MMX, errors that have been corrected.
This result of times equality t1=t2 obtained also under the rules of the TPC, a platform/website generally agreed upon in current scholar physics, constitutes an additional confirmation of the NI96 correctness, and of the existence of ER12 in Michelson's analysis, discovered by us, then corrected, and as a consequence, also physics textbooks require corrections in order to obtain also here the equality of times t1=t2 in MMX, and in TSC, Agent 2 should not win, but end in a tie.
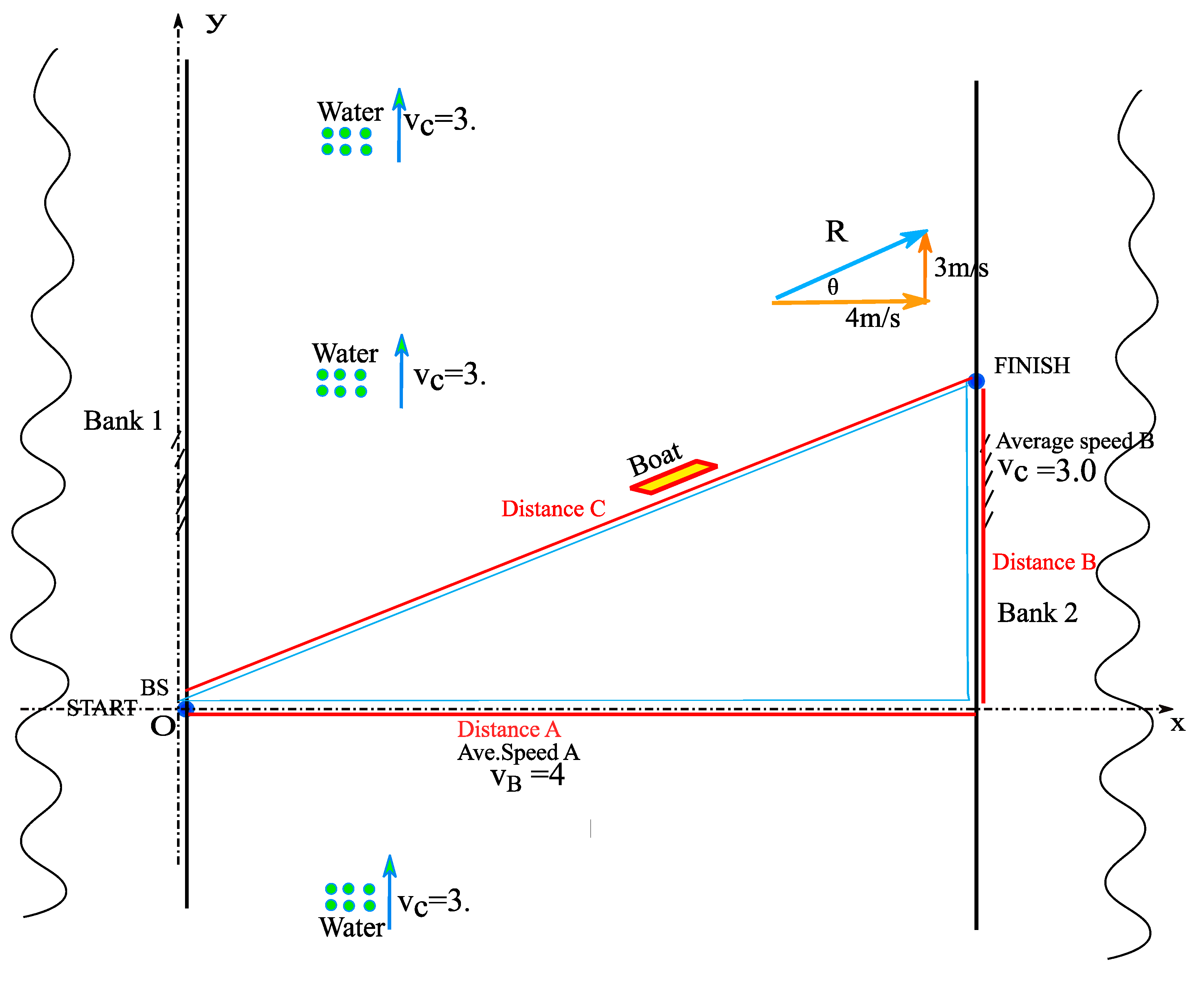
2. Presentation of Example 1 from the TPC Tutorial, with Boat 2 on the First River Crossing
We start this article from the appearance in the TPC academic platform/website for the use of Physics students/teachers, of a written material consisting of a logical reasoning, applying the rules of composition of vectors in the plane, but completed only by the numerical calculation of the time t
2a, without final formulas, presented in the text form of EX1 [
1], only for the first part of the contest model TSC (
Figure 1), of two motorboats (BO), a calculation that was developed theoretically/mathematically accurate/correct and based on correct/deep logical reasoning.
We mention that this competition TSC, is generally recognized as a faithful model for Michelson's interferometer experiment of 1881/87 (MMX, or ME1881/87).
EX1 although it is only numerically calculated, is important because for the first time, in an article published in the Scholar/Academic literature, it is logically justified and mathematically correctly calculates the time t2a and correctly drawn the BO2 path, for the first crossing of the river by BO2 (equivalent to the path at departure of the light ray 2’ in MMX), but which solution contradicts the path and time results of treating this experiment in the specialized literature in Physics and in Physics Textbooks.
However, at the same time, this solution to the problem of the first crossing of the river by BO2 coincides with the correct solution indicated by us since 1996 [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12],
However, the accuracy of the calculation in EX1 is reduced because the angle θ
1 (
Figure 1), of the forward path is evaluated with only one decimal place, a precision insufficient for future comparisons.
Initially, we reproduce below in extenso, for easier documentation, comparison and analysis, EX1 from TPC Tutorial [
1].
”Example 1
1. The resulting speed of the Motorboat (MB2)
2. The time required to cross the river bank with a width of l=80.0m
3. The distance downstream on the opposite bank that the MB2t will reach.
It is assumed that the MB2 will cross the river straight (will aim straight for the opposite bank), so it will not reach the opposite bank at the point directly opposite the starting point because the river current, that will carry MB2 downstream (Figure 1). As a result, the resultant speed of MB2, R, relative to an observer on the bank, will be greater than 4.0 m/s. and inclined downstream.
1. Solution to point 1.
The Pythagorean theorem is applied to the resulting speeds:
R2=42+3225; R=5 m/s
2.a. Solution to point 2a.
Direction. The angle θ1 is determined trigonometrically:
tan θ1=3.0/4.0; θ1=36.9° (36.86989)
2.b. Solution to point 2b.
The time to cross 80.0m:
time=distance/speed.
From the known speeds, vB=4.0m/s was chosen (by logical judgments), and the time results were as follows:
t1=80/4=20s
3. Solution to point 3.
The distance downstream is shown in Figure 1
. The same equation from point 2b is applied. From the known speeds, vC=3.0m/s was chosen (by logical judgments), and the time results were as follows:
distance=speed*time=3.0x20.0=60.0 m.
Therefore, MB2 will be carried downstream at a distance of 60.0m while the river crosses”.
These were the ideas in the text of EX1 from TPC, viewed in December 2024 and in January 2025, briefly presented [
1]
3. Redoing the Calculation of Times from EX1 for BO2 at the First Crossing of the River, with Increased Precision
We find that EX1 from Tutorial TPC [
1], correctly and justifiably, mathematically but also correctly logically, describes, the first half of the route of BO2, only the first crossing of the river of BO2, which constitutes only the first part of the TSC, is well known as a contest of double crossing a river in Physics Textbooks.
We mention that designed similarly to TSC, there are other Examples with topics similar to MO2 from EX1 (planes, boats, etc.) that benefit from the same methods of solving the situation and reach similar results regarding the diagonal path and the crossing/travel time.
However, the size of the angle θ1= 36.90, which is indicated in the Tutorial to be remembered from EX1, is not very precise, but we will have to consider this size in the following calculations with a precision of at least 5 decimal places: θ1= 36.869890 to ensure satisfactory precision and correctness for clear conclusions in future calculations.
Fortunately, the rest of the results from EX1 are correct and accurate, including the diagonal/inclined path and the time of the first crossing of the river by BO2: t2a=20s.
The downstream travel distance of BO2 is B=60.0m, which is also consistent with the theoretical solution we proposed starting from [
2,
3,
4,
5,
6]. Thus, from [
3] eq. (4.7), or from [
10], eq. (1), we obtain the same time as EX1:
However, from all the examples in Physics Textbooks Chapters regarding river crossing by Boats/Planes/Swimmers, for the same time t
2a at departure, other values of times accepted today result. Thus, from [
13] eq (26.2), we find:
However, according to [
13], for the return of the same time results:
The total transverse time from [
13] results as follows:
This is obviously less than the total longitudinal time t
1, which, according to simple classical calculus, is also in accordance with eq (16) from Sec. 6:
This result is exactly the same as that of Michelson's analysis but is incorrect because Michelson's analysis within MEE1881/87 contains Errors 1 and 2, as we have demonstrated.
However, EX1 from the tutorial TSC, for unexplained reasons, unfortunately does not analyze the second part of the BO2/TSC competition.
However, in
Section 3, where the correct solution of this return route of BO2 is presented, this calculation presents a series of new mathematical/theoretical difficulties, especially logical difficulties (some of which are also mentioned in EX1/pg.1).
Notably, if the Author of EX1 of the TPC Tutorial had treated and solved correctly similar to part 1, also part 2 of EX1, namely, the problem of the reverse crossing of the river by BO2, he should have obtained the same result as us in [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12], which we obtained theoretically, starting from 1996 and which we will also obtain numerically in
Section 3, i.e., a reverse crossing time of>t
2b=71.428571s, resulting in the total correct crossing time of BO2:
In (7), for t
2 resulted in the same size of time as in t
1. If the Author of EX1 had correctly calculated the total time t
1 of the round trip of BO1, which moves parallel to the direction of the river current (this calculus is without mathematical or logical difficulties, according to Sec. 4) over the same distance l
1=80.0m (
Figure 1), he should have obtained t
1=91.428571s and thus could observe the coincidence of the two values of the times practically: t
1 = t
2; However, such a result was in flagrant contradiction with the results indicated by all the Textbooks as in eq. (6) of Michelson.
However, this result of equality of the times of the two competitors from (7) was also in flagrant contradiction with the result taught in the Physics Course, in the Michelson Interferometer Experiment Section, or in contradiction with the TSC result indicated by all Textbooks, from eq. (6), which always stated t2<t1, thus justifying the eventual displacement of the fringes in the MMX apparatus by rotation and, respectively, the winning of the contest by SW2/BO2.
When, in fact, practically no displacement of the fringes in the MMX Interferometer was observed and the contest of the two SWs/BOs ends in a tie, according to Sec. 4, but never the victory of SW2 or of BO2, was reported/obtained experimentally.
Under these complicated circumstances of second part of two MBOs contests, the abandonment by the Author of EX1 of solving the 2nd part of the return of MBO2 in the Contest is not totally surprising, but it just was not motivated.
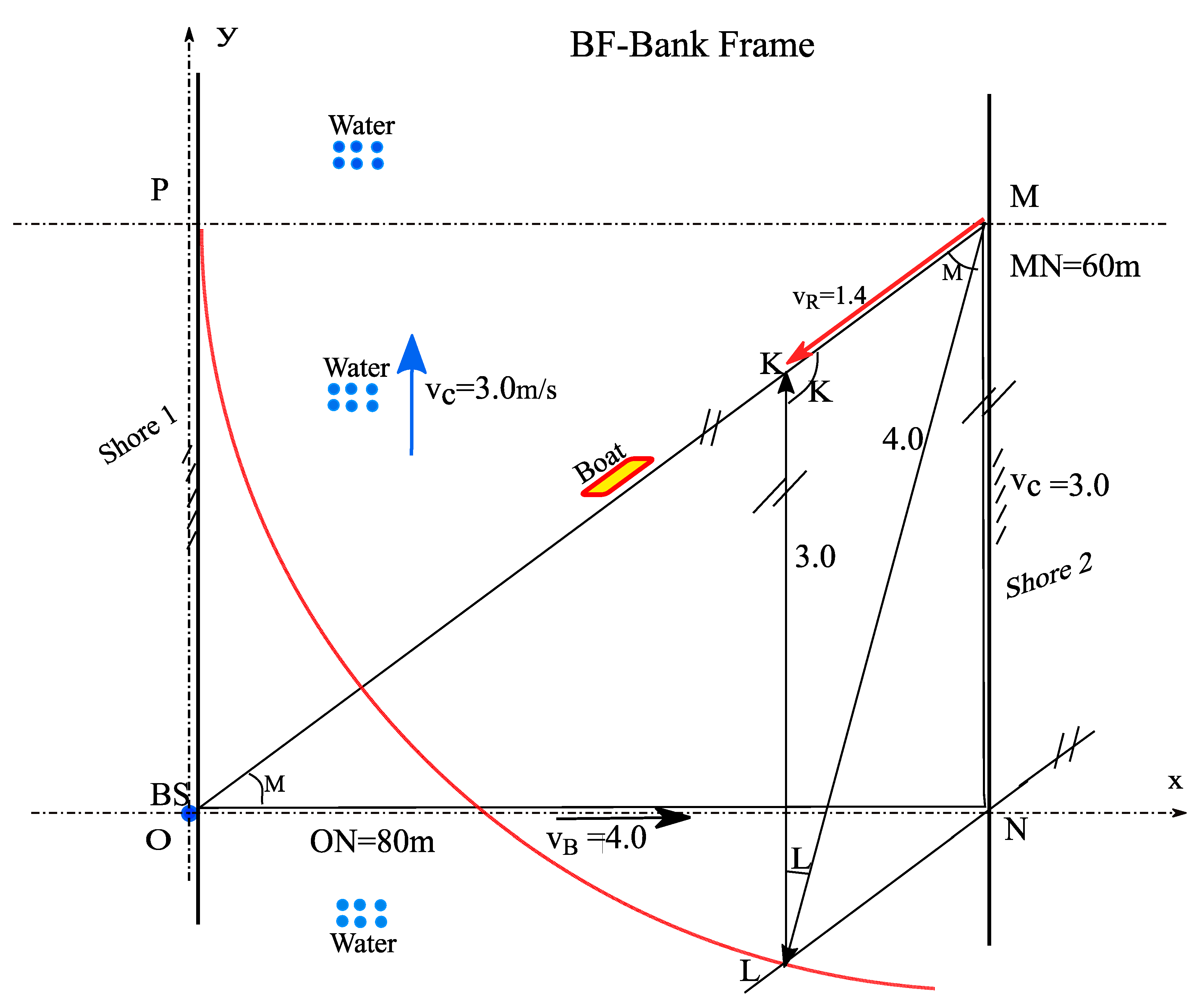
4. Presentation of the Correct Path Back to the BS of BO2 (in the BF Frame)
However, below, we analyze the conditions of the return path of BO2 to its initial starting point O/BS (
Figure 2).
However, here, we rely on the theoretical results previously obtained by us in this problem of MMX and TSC [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12].
At the same time, here, we will apply practically the same rules of mathematical calculation and principles of correct logical judgment used in EX1 (Tutorial) by the author (and a lot of logic –Sec 2).
We calculate the related data for the second half of the competition, namely, the return path of BO2 from point M on the opposite bank to its starting point O/SB.
However, here, we also apply the basic rule from our previous articles [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12], namely, the precise establishment of a reference frame for reporting the displacements of the points of the mobile objects, in the problem.
In this case, we adopt a reference frame Oxy attached to the river bank (BF), with the origin O fixed at the starting point of the BOs on the first bank of the river, coinciding with the official block start (BS) of the competition
Figure 2). In
Figure 2, we note the degree of the angles (e.g., L
0) with the same capital letter as that of the point of the vertex of the main angle (L
0≈L).
Therefore, for its return, BO2 will have to retrace the same route MO (in BF - Frame), diagonally in reverse sense or route C from Ex.1 (
Figure 1,
Figure 2), to return to O/BS, but which is also the shortest return path to point O.
However, when the situation is analyzed logically, we find that BO2 will have to maintain the same proper speed of the Boat engine, v
B =4m/s in relation to the water, but correctly oriented from the beginning of the return at the M point so that the resulting vector of the boat's speed v
Cb=v
R (
Figure 1,
Figure 2), from the composition in the plane of its own speed vector v
B with the water current speed vector v
c (v
Cb =v
R =v
B+v
C), has the diagonal direction C/MO (
Figure 1,
Figure 2).
Therefore, the resultant velocity vector v
Cb=v
R will have to be inclined with the same angle as that of the resultant vector v
Ca of BO2, from the forward path, of magnitude θ
1=M (
Figure 2), to ensure the return of Boat 2 to the starting point O/BS (containing BS) but v
R oriented/directed against the river current (
Figure 2).
Obviously, the resultant magnitude of the return velocity vector vCb results in a different magnitude than the forward velocity vCa because the vectors vB and vC have different directions in the two situations.
To obtain this inclination θ
1 with respect to the normal to the river bank/axis of the resultant velocity vector v
Cb of BO2 when turning, Boatman2 will only have to aim his gaze at the moment BO2 turns at point M, exactly point O/BS (
Figure 2), but without needing to know the size of the angle θ
1, is an action that does not violate Fair Play rules.
Thus, by the plane vector composition of the velocity of BO2, vB=3m/s oriented toward point O/BS with the current velocity vc =4m/s oriented parallel to the bank/current, a resultant velocity VCb will result just after the direction θ1=M=36.869890.
NOTE 1. Under these conditions, we observe that the driver of BO2 does not need/benefit from precise information regarding the size of the angle M=θ1 or regarding the speed of the water current vC. On the contrary, the boatman/pilot/swimmer in all the cases presented in all Physics Textbooks benefited of this information right from leaving the BS, so this was an inadmissible action in a fair-play competition. from which Boatman 2 in EX1 did not benefit.
However, in the new plane vector composition, the two speeds are no longer orthogonal, and the Pythagorean theorem cannot be applied here, as in the case of the first crossing in EX1. This is because the composition of the speeds is still vectorial, but in the plane, according to the directions and senses mentioned above of the two speed vectors: vB of BO2, which is 4.0m/s with the inclination at angles θ1, and speed vC of the river, which is 3.0m/s with the inclination of 900 to the bank.
In this way, the KLM triangle (
Figure 2) is completely defined/determined, for which we know the magnitude of the vector v
C=3.0m/s, the direction of the vector v
C of the current speed, oriented according to KL, which is parallel to the Axis Oy, or to MN and the direction of the resultant speed v
R according to the direction MK, or MO.
Therefore, in the KLM triangle, we know the magnitude of one side and two directions of the sides, so the triangle is determined.
However, to determine other elements of the triangle, necessary for calculating the reverse crossing time t2b, the following mathematical/geometric operations are needed, as shown in Fig. 2.
-Initially, in
Figure 2, we can position point M by the two vectors ON=v
C=3m/s and NM=v
B=4,0m/s represented at the same scale and by known directions (
Figure 2).
Then in the future triangle KLM, we can simultaneously position point L and point K as follows:
-We initially draw the circle with the center at point M having the radius (
Figure 2), MP=v
B=4.0m/s. Then:
-Variant V1:
- Point L will be located at the intersection of the circle of radius ON=MP, with the center at point M passing through P and parallel to the side OM drawn through point N (
Figure 2).
- Point K will be located at the intersection parallel to the side MN drawn through point L, with the side OM, at point K.
- Variant V2.
- Point K and point L will be on a line parallel to line MN, which we position at the point where it intercepts a segment of size KL=3, measured at the same scale of the drawing, between line OM and the drawn circle of radius MP, parallel line on which point K and point L will be found (Fig. 2).
- This results in the triangle KLM being completely known/determined.
We find that at point M and at the moment of BO2 return, for Boatman 2, it will be necessary to perform a simple operation, namely, Boatman 2, to aim with the line of BO2, precisely the starting point of the block-start O/BS on the opposite bank, toward which to direct the course/speed v
B=4.0m/s of BO2, which will thus constantly follow the route MO, but with the resulting speed v
R=MK=1.4m/s according to Sec. 5 (
Figure 2), and BO2 will return to starting point O/BS after time t
2b, which will be calculated in Sec. 5.
5. Calculation of the Return Time of Boat 2 to the BS in the BF Frame
---In the triangle KLM (
Figure 2), we can find the angle K as follows:
K=180-(-36.86989+90)=180--53.13001=126.869890
----We also know the sides KL=3.0m/s and ML=4.0m/s.
In the triangle KLM, we can find the size of the side MK as follows:
From the sines theorem, we have (
Figure 2):
Therefore, we can also write:
However, we have: sin K=sin126.869890=0.80000
From the first equality of (8), we obtain:
sinM=KL×sinK/ML=3.0×sinK/KL=3.0×0.80000/4=0.60000
The angles M and L result as follows:
M=arcsin 0.60000=36.8698970
L=180-(K+M)=180--126.86989--36.869897=16.260210
sinL=sin16.260210=0.28000
From the second equality in (8), we have:
0.28000/KM=0.6000/3.
The resulting speed will be as follows:
vRb=MK=0.28000×3/0.6000=1.40000 m/s
Now, we can calculate the time t
2b of BO2's turn as follows (
Figure 2):
t2b=OM/vRb=OM/KM;
However, according to the classical notations from the MMX experiment and the equivalent contest of TSC, we have:
The total round trip time of BO2 is as follows:
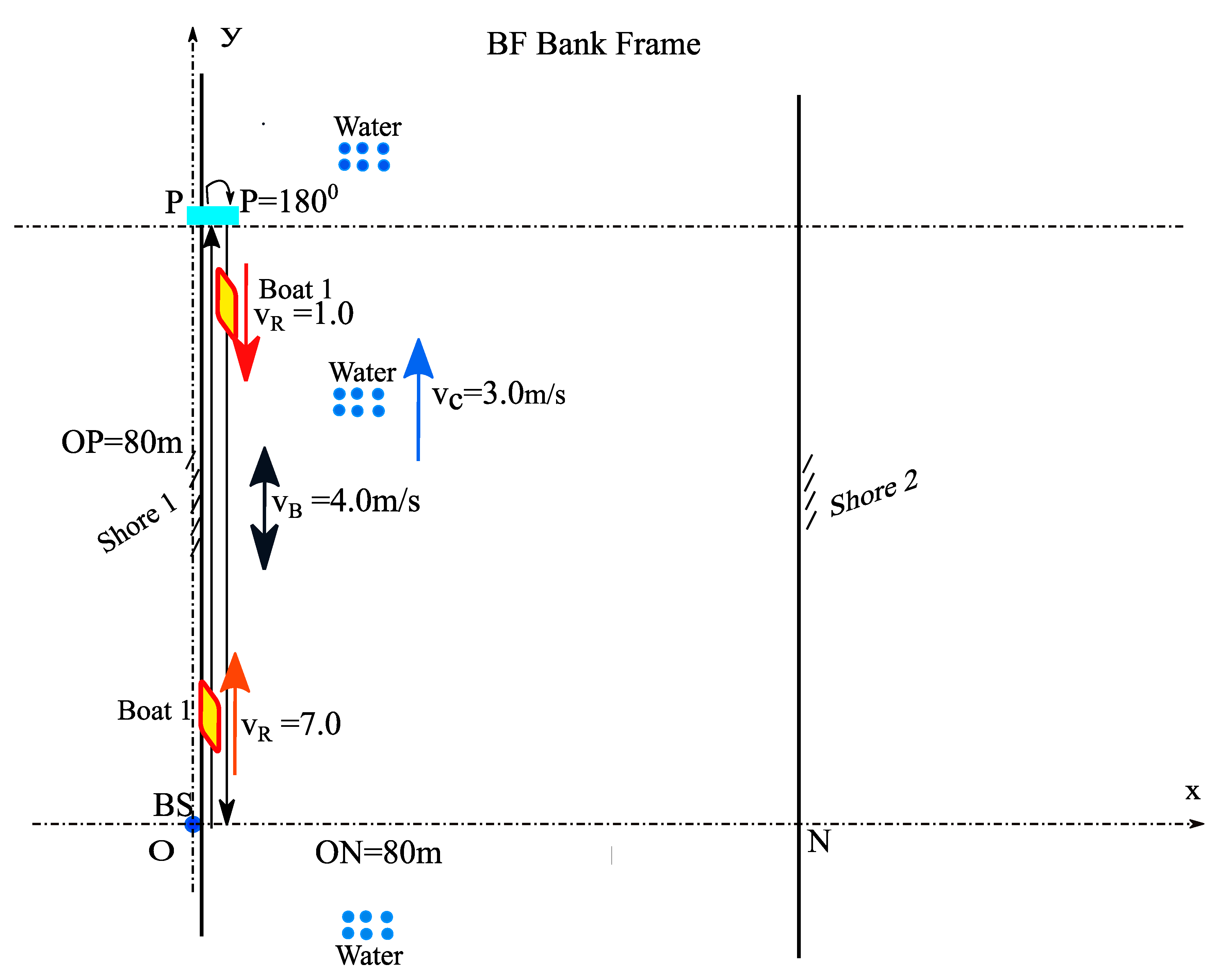
6. Calculation of the Total Round-Trip Distance to the BS of BO1 in the BF Frame
We will now calculate the time required for BO1 for the two round trips, each of length denoted by l
1a, l
1b, but in the BF Frame, we have l
1a =l
1b. (
Figure 3)
In
Figure 3, we also use the BF reference frame [
3,
4,
5,
6,
7,
8,
9,
10,
11,
12,
15]:
The speed on the outgoing trip of BP1, the one in the direction of the current, will be the resultant speed v
R1 of the two parallel speeds by simple addition of their vectors (
Figure 3):
vRa=vB+vC=4.0+3.0=7.0m/s.
The time corresponding to the outgoing trip is as follows:
The speed on the return trip of BO1, the one in the opposite direction to the current, will be the resultant speed v
Rb by simple subtraction of their vectors (
Figure 3):
The time corresponding to the return trip is as follows:
The total round trip time of BO1 is as follows:
Therefore, if the two arms are equal, l
2=l
1=80m from (10), (12) and (16), the equality of the two times are as follows:
Moreover, numerically, from (12) and (16), we obtain:
We mention that from our theoretical analysis of the contest of the two Boats, in the BF frame, eq. (4.1) was used in [
3]. (4.18) or in [
10], eqs. (26), (27), the same times t
1 and t
2 resulted as for the WF frame calculated below in Sec. 7. :
We mention that from our theoretical analysis of the contest of the two Boats also in BF Frame, in [
3], eqs. (4.1), (4.18) or in [
10], eqs. (26), (27), the same times t
1 and t
2 resulted as for WF Frame calculated below in Sec.7:
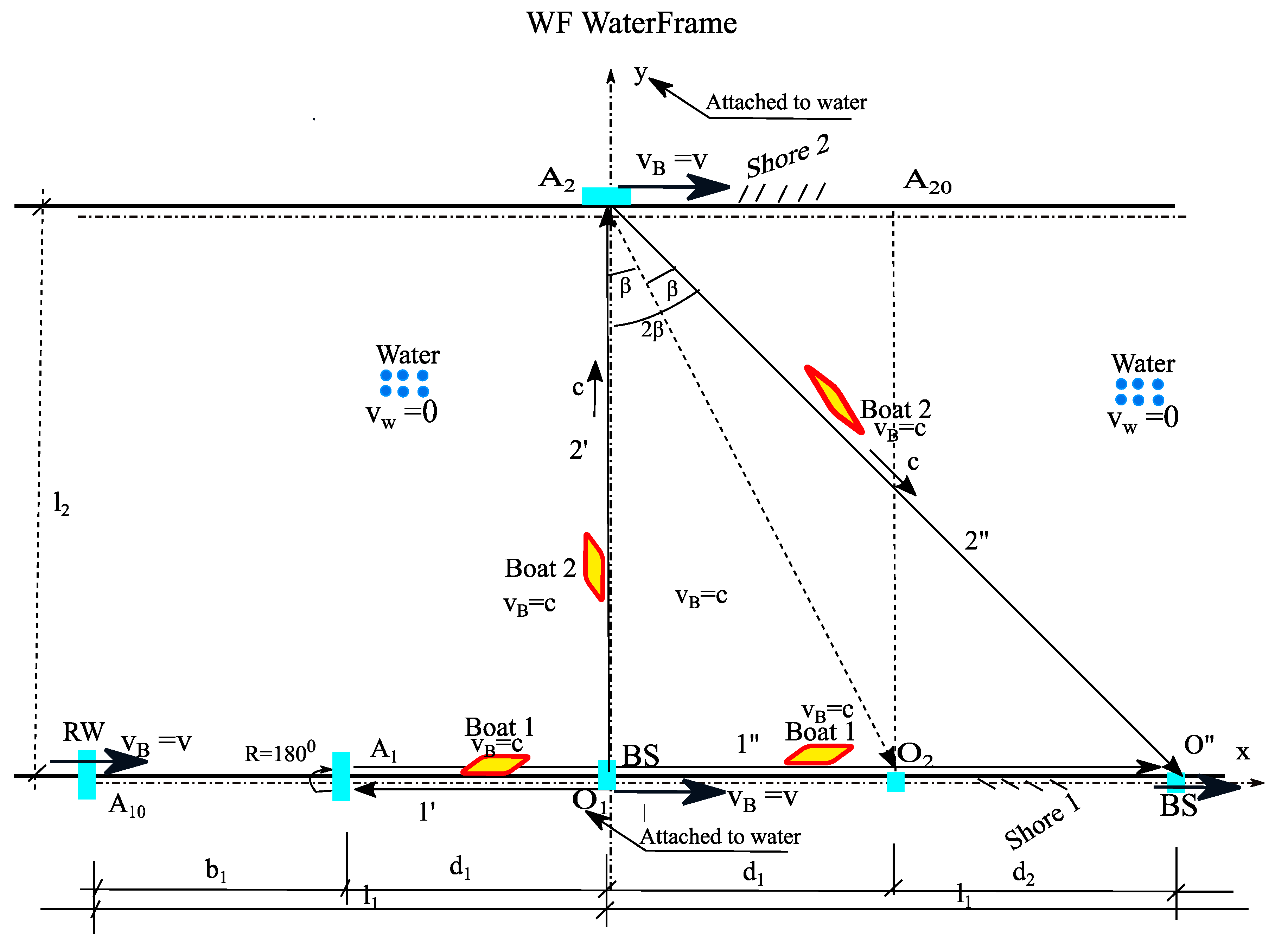
7. Calculation of the Total Travel Times of Boats 1 and 2 in the WF Frame
In our previous articles [
2,
3,
4,
5,
6,
7,
8,
9,
10,
11,
12] concerning the competition of the two BOs, we applied and performed parallel analyses in the BF frame and calculations in the WF frame (water/ether) to establish the correct paths and finally calculate the times t
1 and t
2 in the two orthogonal directions of movement of BO1 and BO2 (
Figure 4).
The results of times t
1 and t
2 in the WF reference [
11,
15] were as follows:
Therefore, if l
2=l
1 from (20) and (21), it results in the end of our analysis of the two BOs contest, including in the BF frame:
Therefore, it follows from (22) that the contest of the two BOs ends in a tie and that the displacement of the fringes in the MMX interferometer should not have occurred at all.
This result also proves that ME81/87 could not determine the relative speed of the Earth and ether, so the ether should not have been eliminated from Physics by Einstein starting in 1905.
But to confirm this result we will perform below, the calculation also of the time of the boat BO1, t
1 and the time of the BO2 t
2, as round trips over a river with width l
2 longitudinal road of length l
1 both BOs with speed c, and the river having speed v, both roads being represented in BF Frame (
Figure 1,
Figure 2 and
Figure 3).
For BO2, the path traveled is represented by the hypotenuse/diagonal AC of the triangle ABC in
Figure 1 or by the hypotenuse/diagonal OM of the triangle ONM in
Figure 2 with the forward path OM, for which we can write (
Figure 2):
The resulting speed of BO2 when going forward is as follows:
However, the travel time t
2 is obtained most simply for the path ON traveling at speed c:
For BO2, the return path is represented by the hypotenuse/diagonal MO of the triangle ONM in
Figure 2, for which we can write from the right triangle ONM (
Figure 2):
From the KLM triangle, we can write (
Figure 2):
Inserting (25) into (27) results in:
From (26), we can also write (
Figure 2):
Now, from (8), we can write:
The projection of KM on NO (Ox axis) will be (
Figure 2)
The time to return on the real/correct road MO (
Figure 2) is equal to the time on the road on route NO, which travels here with the projection of the resulting speed onto it: cos β×V
R. resulting in the time:
With the relations from trigonometry:
sin(90+β)=cosβ and cos2β=2cos2β-1;
from (34), the following results:
With the relations from trigonometry:
cos
2 β =1/[1+tg
2 β ] from (35) results:
Now, the time to return will be as follows:
The total travel time of BO2 in the two river crossings is as follows:
In (39), we noted classically:
Equation (39) shows that the total time t
2 of the double crossing of BO2 in the BF frame is obtained, which is equal to the total time t
2 of the crossing of BO2 in the WF frame from [
11,
15].
Moreover, the times t2 in both the BF frame and WF frame are equal to the corresponding times t1 and t2= t1 in the same Frames.
These results suggest that Micheson's analysis in MMX contained Error 1 and Error 2, as they were identified and corrected, including Ether reintroduction by us, since 1996.
8. Conclusions
From the above results for the TSC type contest, we obtained with the rules from our demonstration NI96 starting from 1996 and partially with the rules of EX1 from the TPC Physics platform/website for training Physics teachers and students, the correct times for BO1 and BO2, t1=t2.. However, this result does not coincide with the times provided by Physics Textbooks, which give the times t1>t2, indicating the existence of ER12 in Physics Textbooks, which comes from Michelson's wrong/erroneous analysis, as we demonstrated.
This result of times t1=t2 was obtained partially also with the rules of EX1 from the TPC Physics platform/website for training Physics teachers and students, and so it constitutes a reconfirmation of the correctness of our demonstration NI96 from 1996 for the correct result t1=t2 and for the existence of ER12 in Michelson analysis.
From this result, of times equality t2=t1 from BOs contest or from TSC, which was also applied to the analysis of Michelson for his experiments MMX from 1881/87, by discovering and then correcting ER12, it follows that the ether should no longer be eliminated from physics, as Einstein did in 1905, which was based precisely on MMX. By readmitting by us, the existence of the ether in physics, multiple related consequences emerged, including the elaboration and development of the HM16 ether model. The new principles and consequences of ether existence were then derived, the start of which was given by the new theory of gravitation (NTG16), followed by a new theory of physics (NTP16), theories that will be permanently developed within all branches of science.
However, the our above result of equality of the two times t2=t1 of the paths of the two boats/swimmers, from the TSC contest, (a problem treated similarly in EX1 from TPC), compared with the result of the times t1>t2, values resulting from treatment in Physics Textbooks, respectively, of the two times of the two light rays from the MMX interferometer, was predicted, justified and demonstrated by us in NI96, through the work started since 1996, all starting from the existence and the discovery of ER12 in Michelson's Analysis, and as a consequence, all Physics textbooks require corrections, except EX1 from TPC.
Funding
No funds, grants, or other support was received for this article.
Acknowledgments
The first author gratefully acknowledges initial advice on the subject and encouragement from his late professor N. Barbulescu, a follower of Sommerfeld. He is also sincerely grateful to the late Prof. P. Mazilu from TUCB Bucharest for his rigorous lessons on rationality and is indebted to Gen. Prof. G. Barsan, Col. Prof. Al. Babos from LFA Sibiu, Prof. D. Stoicescu from ULBS Sibiu, Prof. D. Siposan from MTA Bucharest, and Ms. Veronica Has, from Bucharest, for their support.
Authors Contributions
All authors contributed to the study conception and design. Material preparation, data collection and analysis were performed by Ioan Has. The first draft of the manuscript was written by Ioan Has, and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Data Availability
All data generated or analysed during this study are included in this published article.
Competing interests
The authors have no competing interests to declare that are relevant to the content of this article.
References
- Physics classroom (TPC). (2025). An online, free to use physics website https://www.physicsclassroom.com/class/vectors/Lesson-1/Relative-Velocity-and-Riverboat-Problems.
- Has I, (1996) A reconsideration of the illustrative example of Michelson’s experiment (in Romanian), Rev. Fizica & Chimie. XXXI/11-12, Bucharest pp 14-18.
- Has I, (1997) Considerations about motion phenomena starting from a model for relativity theory. In Volume the IVth Congress of "S. Odobleja" Academy, Ed. Europa Nova, Bucharest, pp 51-65.
- Has I, (1997) A new interpretation of Michelson’s experiment (in Romanian). Rev. Fizica & Chimie. XXXII/6-7-8, Bucharest pp 1-5.
- Has I, Has A, (2000) Light paths analysis in classic interferometer conditions. Balkan Phys. Lett. (proc. Suppl. BPL-4) pp 67-70.
- Has, I. (2000). ‘The analysis of an alternative light path in Michelson’s experiment’, Romanian Reports in Physics, 52, pp. 775–789.
- Has, I., Miclaus, S., Has, A. (2010). ‘An alternative light path analysis in Michelson’s experiment’, Physics Essays, 23, pp. 248–257.
- Has, I., Miclaus, S., Has, A. (2014). ‘A reanalysis of the theory of interferometer experiment demonstrating that Michelson’s analysis contains an error, including the boat model analysis, so readmitting the ether presence’, Optics 3(4), pp. 24–32. http://www.sciencepublishinggroup.com/j/optics.
- Has, I., Miclaus, S., Has, A. (2018). ‘A reanalysis of the two swimmers problem, as frequent model of Michelson’s interferometric experiment demonstrating that transversal path is not an isosceles but a right triangle and the race will end in a tie’, Journal of Applied Mathematics and Physics, 6(4), pp. 1507–1521. www.scirp.org/journal/jamp.
- Has, I., Miclaus, S., Has, A. (2019). ‘Reanalysis of Michelson’s interferometric experiment in relation to the two swimmers’, Journal of Physics, Conference Series, 1251(012020), pp. 1–24. [CrossRef]
- Has, I., (2020). ‘Identification of Michelson’s errors in his 1881/87 experiments and their reanalysis’, Research and Reviews: Journal of Pure and Applied Physics, 8(4), pp. 1–15. https://www.rroij.com/open-access/identification-of-michelsons-errors-in-his-188187-experimentsand-their-reanalysis.pdf.
- Has, I., Miclaus, S., Has, A. (2022). ‘Michelson’s analysis of errors in his 1881/87 experiments of the two swimmers contest; Necessity of correcting college textbooks, Journal of Physics, Conference Series, 2197(2022)(012012), pp. 1–27. [CrossRef]
- Serway, R. et al (2007). Physics for scientists and engineers. Vol. 2. Cengage Learny, p.1117.
- Has, I., Miclaus, S. Has, A. (2021). ‘An actualized presentation of a new physics theory based on the HM16 model of ether’, Buletin Stiintific Suplimentar, Official Catalog of Salon Cadet INOVA–LFA, Sibiu 6/2021, pp. 106–126. https://www.cadetinova.ro/index.php/ro/organizare/catalog/catalog-inova-21.
- Has, I., Miclaus, S., Has, A. (2022). Presentation of a new physics theory based on the HM16 model of the ether, Journal of Physics, Conference Series, 2197(2022)(012014), pp. 1–19. [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).