Time-Entropy Mapping; Mass-Gravity Duality; Metric-Frequency Mirroring: A Two-Layer Fiber Bundle Model with Topologically Invariant Space Configuration

1. Preparatory assumptions:

1.1. The universe is expanding.

1.2. The universe operates under the Law of Energy Conservation and the Law of Entropy Increase.

1.3. The universe consists of SEQ, discrete Planck-scale units, forming a topologically homeomorphic 3D structure (adjacency relations remain preserved while individual SEQ energy states may vary). Importantly, this polycrystalline structure necessarily contains primordial Periodic or Random Topological Dislocation to ensure physical isotropy, yet maintains strict 3D topological homeomorphism as these defects are cosmologically frozen and adjacency-preserving since the birth of the universe. The distortion of light around black holes demonstrates that gravitational and electromagnetic field quanta are coupled, suggesting they originate from the same quantum field in different excited states—leading to the SEQ hypothesis. The spacing and tension between adjacent SEQ can be modulated by gravitational or equivalent gravitational fields.

1.4. All field quanta and elementary particles represent different energy excitation states of SEQ, expressible as 3D dynamic structural matrices of SEQ .

1.5. SEQ possess a ground state energy (e.g., ground-state spin or vibrational modes). If ground-state spin chirality is fixed, this may explain parity violation. The ground-state energy of SEQ could also account for the cosmological constant in General Relativity. This framework shows strong alignment with Loop Quantum Gravity theory.

1.6. Adjacent SEQ maintain a dynamic equilibrium spacing interconnected via spring-like bonds in their ground state. SEQ are fundamental, indivisible Planck-scale entities—their structure remains intact under any deformation or energy fluctuations.

The sub-Planckian regime governs the spatial elasticity of the network (including elastic potential storage and release), while quantized energy transfer occurs exclusively through interactions between SEQ. Within this framework:

• The spin degrees of freedom of SEQ and their elastic bonds remain decoupled, preserving independent dynamical regimes.
• Under perturbation, the system responds by modifying SEQ resonant frequencies while generating compressive/tensile forces.
• This elastic response is nonlinear and asymmetric.
• SEQ are stable, indivisible structures composed of sub-Planckian components. SEQ’ spin emerges from collective space transformations at the sub-Planck level. This ensures the spin degrees of freedom do not interfere with elastic deformations in the SEQ network. This architecture naturally protects spin dynamics from elastic disturbances.
• At the sub-Planckian scale, the elastic properties of the underlying substrate impose an upper bound on the spacing modulation and tension between adjacent SEQ. This fundamental limit ensures that extreme deformations (e.g., near black hole singularities) cannot disrupt the topological integrity of the SEQ network.
• In this model, the harmonic oscillation intervals of SEQ are integer multiples of Planck time(tₚ). Consequently, all dynamic processes—including elastic strain interactions, harmonic conduction, as well as scalar, spinor field transmissions and other energy conduction mode induced by rotational axis dynamics—are fundamentally constrained by the discrete Planck-time intervals. This property inherently ensures the model’s consistency with the discrete-time hypothesis in quantum mechanics and quantum gravity theories.
• Any discrete model of spacetime must confront the challenge of restoring spatial isotropy so as to remain compatible with the Lorentz-covariant rules established by observation. Beyond the isotropy mechanism tied to the topologically dislocated configuration discussed in §1.3, an alternative is to let the SEQ lattice spacing be sufficiently large for sub-Planckian elastic constituents—whose characteristic scale is far below the Planck length—to fill the network uniformly. Provided that, within the precision accessible to cosmological observations, the statistical distribution of these constituents yields a dispersion relation that is effectively Lorentz-covariant, macroscopic isotropy emerges naturally and remains consistent with all current observational data.

1.7. If matter truly traversed space, it would require modification of spacetime’s adjacency relations. Yet black holes—despite their extreme mass—preserve local spacetime topology (as evidenced by smooth light bending). This implies that apparent particle motion must instead represent propagating excitations of spacetime itself, consistent with GR. The speed of light (c) constitutes the maximum excitation propagation rate in space.

From another perspective, gravity propagates through space, and since no material can shield gravity, it suggests that matter should be a certain excitation of space itself, inherently part of space.

1.8. Algebra derivation:Matter-Spacetime Unity| Matter is a part of space

General Relativity tells us that matter affects the metric of space, and the metric of space in turn determines the motion of matter along geodesics. In other words, matter and space influence each other.

Algebra module theory and category theory further reveal that two entities capable of mutual interaction must share part of the same algebraic structure. In categorical terms, relations are morphisms and interactions are structural.

Expressed in physical language, this means that matter and space must share a common underlying basis — hence, matter and space-time are one.

1.9. Quantum-Elastic Two-Layer Fiber Bundle Model | Common Base Space Platform for General Relativity and Quantum Field Theory

This quantum-elastic base space model, where the underlying structure consists of elastic space components at sub-Planckian scales, forming a topologically homeomorphic spatial network. Within this network, structurally stable space elementary quanta (SEQ) and nodal quantized spatial networks are constructed from sub-Planckian components. The SEQ are interconnected via sub-Planckian elastic components, forming a dual-layer fiber bundle base space structure, where the sub-Planckian components serve as the foundational substrate and the space elementary quanta form the secondary layer.

On this base space, due to the fact that the space elementary quanta themselves are composed of sub-Planckian components, the spin of these quanta is essentially a topologically protected spin excitation conduction wave on the sub-Planckian topological network. This allows for the decoupling of spin and elasticity without altering the fundamental spatial topology. Matter is fundamentally a compressed excitation state of space, and the motion of matter is essentially a topologically protected excitation wave on space. The motion at each level is essentially a wave on the substrate of the lower level, thus enabling the coexistence of quantum spin and axial rotational degrees of freedom with spatial elastic degrees of freedom, without disrupting the topological homeomorphism structure.

Based on this structure, it becomes straightforward to define two fundamental connections: the gauge group of quantum field theory (QFT) and the metric tensor of general relativity (GR). This enables the model to simultaneously accommodate the mathematical frameworks and phenomenological interpretations of both quantum field theory and general relativity.

Between these two connections, there also exists a categorical morphism: the geometry-frequency mirror, which will be discussed in Section 13.

In this quantum-elastic spatial network model, the energy carried by space elementary quanta can represent the quantum spin-resonance energy of space. Additionally, the elastic potential energy of space can be decomposed and calculated across relevant regions of the space elementary quanta with the mirroring principle between geometric deformation and quantum resonance frequency introduced in section 13. Thus, the entire spatial energy distribution can be represented solely by the energy carried by the space elementary quanta.

Although the Space Elementary Quanta (SEQ) are composed of sub-Planckian elastic components, they are termed “space elementary quanta” because their energy states can represent the spatial energy distribution, including the elastic potential energy distribution at the sub-Planckian level.

Once the energy distribution across space is constructed using the energy carried by the space elementary quanta, each step in the dynamic energy distribution of this quantum-elastic space corresponds to each step of spatial transformation. The second law of thermodynamics manifests as a process of energy distribution homogenization. Based on this, multiplicative entropy can be used to define the entropy value of each spatial transformation, which can then be mapped onto the time set. This provides a clear definition of cosmic time and embeds the thermodynamic time arrow of the second law of thermodynamics into the models of general relativity and quantum field theory.

The core premise of this model is that the entire space is topologically homeomorphic and fixed: its connectivity graph never changes. All motion and change amount to a dynamic redistribution of energy across this immutable network. This built-in topological invariance—an unalterable graph structure—serves as the model’s fundamental invariant. It furnishes an intuitive physical picture for the constancy of the speed of light, supplies a concrete mechanism for global energy conservation that general relativity does not provide, and also simplifies the Hamiltonian mathematics of the model.

The consistent coexistence of quantum spin and axial degrees of freedom with spacetime elasticity—under the constraint of topological invariance—is only possible within the two-layer base space framework introduced here.

1.10. Derivation of the Spatial Topological Invariance Postulate in This Model

From a phenomenological perspective, the light around massive astrophysical objects such as black holes exhibits a highly smooth distribution of spacetime curvature, with no observed evidence of topological tearing or singular connectivity structures. This characteristic suggests that space possesses a certain degree of structural stability at macroscopic scales—meaning that the global connectedness and neighborhood relations of space remain invariant.

From a theoretical standpoint, the validity of the Feynman path integral method further supports the stability of spatial topology. This approach requires a weighted integration over all possible paths between two points, a procedure that presupposes the existence of a well-defined measure on the space of paths. If the spatial topology were to vary dynamically over time—altering its connectivity, adjacency structure,—the set of paths would no longer admit a consistent measure, rendering integration ill-defined. Given that the path integral formulation has been extensively validated in quantum field theory and experimental predictions, this implies, by inference, that the underlying spacetime background must operate within a stable topological class.

Therefore, we propose that the postulate—”the topological homeomorphic structure of space remains invariant throughout physical evolution”—is a justified foundational assumption within the framework of this model. This postulate not only ensures mathematical consistency (such as the validity of path integrals and the Schrödinger equation), but also aligns with observational facts such as the geometric smoothness near black holes.

2. Time as a counting process of spacetime network transformations:

2.1. SEQ serve as the electromagnetic wave conducting medium. Matter with mass and its motion are waves in this medium. In this framework, nothing truly moves through space - light speed c is the maximum conduction speed c, preventing velocity stacking beyond c. All physical phenomena correspond to specific energy state configurations, establishing SEQ as the universal substrate.

2.2. The universe’s composition: Energy conservation and quantization imply a finite number N of SEQ, each with M possible energy states,(where each energy state $m_i$is an integer multiple of Planck’s constant h, ) allowing up to $M^N$ transformations. These M energy states form an algebraic system incorporating translational, spinning and rotational operations connecting to standard model. Energy conservation and entropy increase constraints reduce possible transformations significantly below $M^N$.

2.3. Time definition:

2.3.1. Let J be the possible universe transformations (J <<$M^N$).

2.3.2. The Planck time (tₚ) interval separates adjacent transformations as the minimal time unit.

2.3.3. Time’s arrow follows entropy increase.

2.3.4. Transformations map non-bijectively to entropy values (k distinct values partition J transformations into K classes). Parallel transformations share the same entropy values, but only one can occur. The entropy set maps to possible time values - each moment corresponds to one universe transformation. Non-uniform entropy increase means only a subset of possible time values actually occur.

2.3.5. Each space transformation (state transition of the SEQ network) can be assigned a unique entropy value calculated via the multiplicative energy distribution across this space transformation’s matrix.

2.3.6. Finite transformations ensure discrete, limited time in this model.

(Note:this derivation is a speculative exploration within the discrete framework and does not imply reality.)

3. Definition and analysis formula of entropy In this definition of entropy, the entropy value of a closed system at a given moment (i.e., during a specific state transition) is calculated as the multiplicative product of the energy norms of all SEQ involved in that transition(that moment’s space transformation).

Entropy value of closed system S=

$\prod _{i=1}^n{m}_i,i\in N$ ①

Energy of closed system=constant=${\sum }_{i=1}^n{m}_i,i\in N$ ②

${\mathrm{S}}_{\mathbf{m}\mathbf{a}\mathbf{x}}\le$ ${{\mathit{m}}_{\mathit{i}}}^{\mathit{n}}$, When all $m_i$ are equal or differ only by Planck’s constant h

(Where $m_i$ refers to the energy carried by the ith SEQ during a single transformation of the closed system, where each energy state $m_i$is an integer multiple of Planck’s constant h, $m_i$=$n_i$h, $n_i\in N$)

Each SEQ carries energy mᵢ = the resonant kinetic energy of this SEQ+its spin kinetic energy+the elastic potential energy of the local space surrounding the SEQ, calculated based on the gradient of resonance frequency shift relative to the Planck frequency of the SEQ, as will be elaborated in Section 9.1 and Section13.

Under this setup, the total energy of the entire space can indeed be represented solely by mᵢ, without the need to separately calculate the elastic potential energy within the sub-Planckian components.

3.1. Energy transfer rules and triggering conditions:

Energy exchange occurs between adjacent SEQ (i,j) if and only if the following thermodynamic gradient exists:$m_i>m_j+h$, Energy transfer occurs only in discrete quanta of Planck’s constant h, $m_i$ →$m_i$ −h; $m_j$→$m_j$+h (Planck’s constant:h)

3.2. Numerical Example: System States and Entropy Evolution

Table 1. Simplified Entropy Increase Demonstration.

System State	SEQ Energy Distribution $\sum _{i=i}^n{m}_i$=12	Entropy ${\prod }_{i=1}^n{m}_i$	Remarks
Initial non-equilibrium state	[3, 1, 5, 3]	45	-
Intermediate state	PathA:[3, 1, 4, 4]; PathB:[3, 2, 4, 3];	PathA:48; PathB:72;	-
Final state	PathA:[3, 2, 3, 4]; PathB:[3, 3, 3, 3];	PathA:72; PathB:81;	Due to adjacent energy transfer with minimal quanta h, this system cannot reach maximum entropy in case A

Note: The above analysis demonstrates that different entropy-increasing pathways exhibit distinct sequences of entropy variation.

Table 1. Simplified Entropy Increase Demonstration.

System State	SEQ Energy Distribution $\sum _{i=i}^n{m}_i$=12	Entropy ${\prod }_{i=1}^n{m}_i$	Remarks
Initial non-equilibrium state	[3, 1, 5, 3]	45	-
Intermediate state	PathA:[3, 1, 4, 4]; PathB:[3, 2, 4, 3];	PathA:48; PathB:72;	-
Final state	PathA:[3, 2, 3, 4]; PathB:[3, 3, 3, 3];	PathA:72; PathB:81;	Due to adjacent energy transfer with minimal quanta h, this system cannot reach maximum entropy in case A

Note: The above analysis demonstrates that different entropy-increasing pathways exhibit distinct sequences of entropy variation.

3.3. Logarithmic Relation:

After logarithmic transformation, lnS aligns with the conventional Boltzmann entropy form, while the multiplicative formulation naturally suits discrete systems.

3.4. Proof of Spontaneous Entropy Increase

Spontaneity Theoremof entropy increase (Second Law of Thermodynamics):

For every possible energy transfer process, the total entropy change satisfies ΔS≥0.

Proof Outline: Let the pre-transfer states be $m_i$=a, $m_j$=b (a$>$b+h);

The post-transfer entropy ratio is:

$S_{t2}$/$S_{t1}$=(a−h)(b+h)/ab=1+h(a−b−h)/ab$>$1 (Planck’s constant h)

3.5. The definition conserves energy, has an entropy ceiling, ensures spontaneous increase, and logarithmically aligns with classical entropy.

Indeed, this model establishes a novel analytic quantum thermodynamic framework where coarse-graining automatically enforces the quantum indistinguishability of quantized homogeneous invariant network in physical properties while simultaneously characterizing the entropy-increasing process of energy homogenization. These properties collectively confirm the validity of this entropy definition. At this point, a clear multiple mapping can be established:

One space transformation$\to$one entropy value$\to$One possible moment

Figure 1. : Space-Time-Entropy Mapping Diagram.

Figure 1. : Space-Time-Entropy Mapping Diagram.

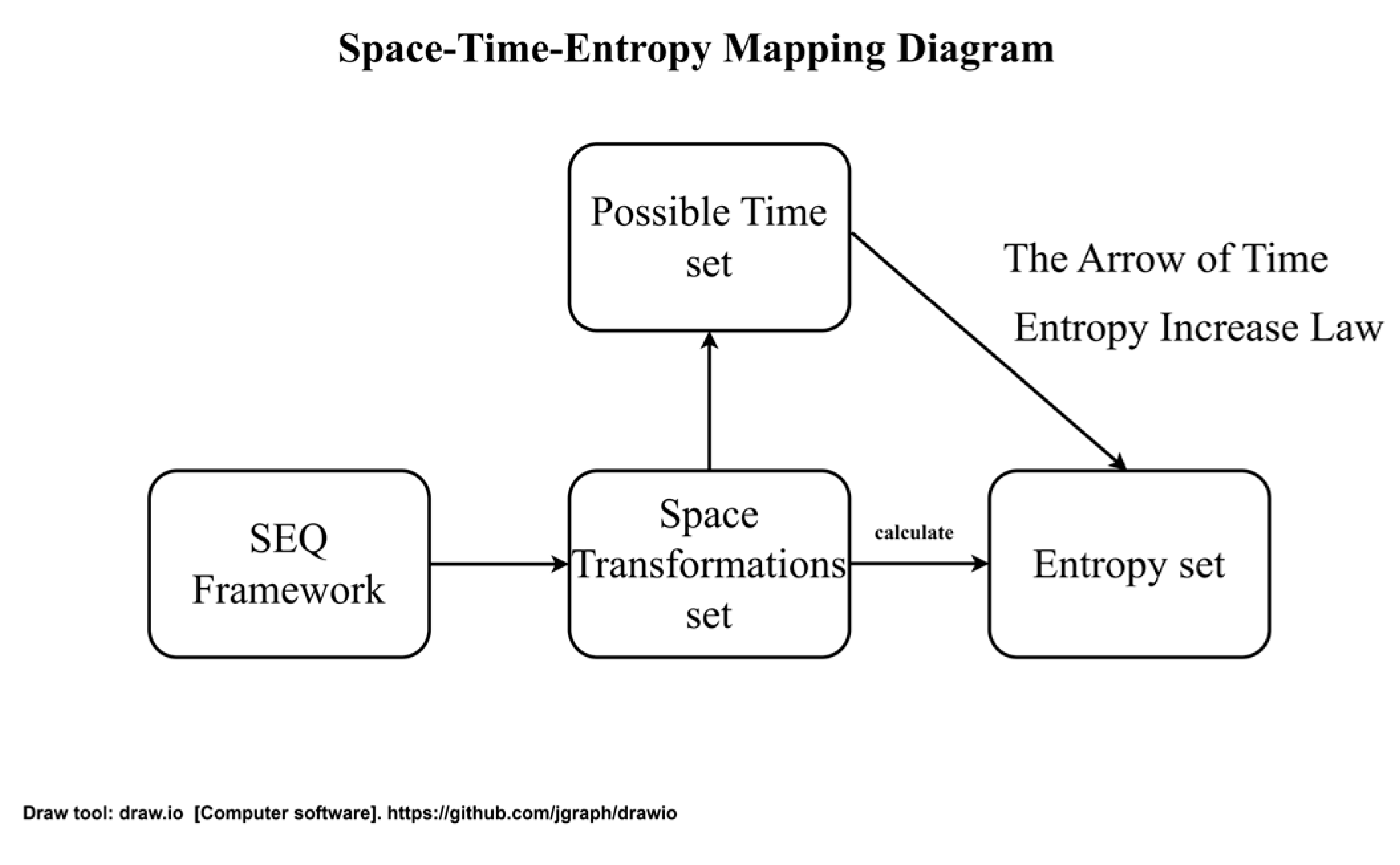
3.6. The Spontaneous Entropy Increase is Causality.

The existence of isoentropic transformations and different entropy-increasing pathways imply that even with the constraint of the least action principle further limiting the degrees of freedom in future spatial transformation paths, the potential spacetime evolution trajectories are not necessarily unique. Within this model’s framework, multiple solutions may satisfy the least action condition, indicating that while causality adheres to Markov properties, with a certain dynamic freedom persists.

3.7. Why Analytic multiplicative Entropy is Adopted: Within this model’s framework, physical states at Planck-time scales exhibit deterministic characteristics. Although current experimental conditions cannot directly measure them, traditional statistical entropy can be reduced to analytic expressions at this scale. This perspective not only reveals the microscopic essence of statistical quantities but also provides a new analytic foundation for quantum thermodynamics—unifying macroscopic statistical behaviors with deterministic dynamics at the Planck scale.

Multiplicative analytic entropy corresponds to each step of energy homogenization in a system. With every step toward a more uniform energy distribution, the multiplicative analytic entropy increases, offering a clearer and more detailed characterization of the process compared to traditional statistical entropy.

Multiplicative Entropy vs. Traditional Statistical Entropy

Comparison Dimension	Multiplicative Entropy	Traditional Statistical Entropy
Process Explicitness	Explicitly records energy homogenization steps via product sequences (e.g., ∏ᵢ mᵢ), preserving microstate transition details	Describes only macro-state differences via logarithmic state-count (ln Ω), erasing intermediate dynamics
Physical Intuitiveness	Entropy increase directly reflects irreversible energy redistribution; time asymmetry emerges from dynamics	Relies on probabilistic assumptions (e.g., molecular disorder) and requires ad hoc low-entropy past boundary
Process Resolution	Tracks Planck-timescale (tₚ) energy transfers;	Limited to ensemble averages, incapable of resolving quantum fluctuations or short-timescale entropy production

3.8. Analysis of the Maximum Entropy Principle

In the SEQ model, the maximum entropy principle is manifested through the driving tendency of entropy increase: energy not only flows from a higher-energy SEQ to an adjacent lower-energy SEQ, but it also follows the path with the largest energy difference.

For example, consider an SEQ i, which is adjacent to two other SEQ j and k. The energies carried by nodes i, j, and k are A, B, and C respectively, where A > B > C. In this case, there are two possible energy transfer paths from SEQ i according to the principle of entropy increase: path i→j or path i→k. We will analyze the entropy change for each path separately.

Under the constraint of energy conservation (i.e., A + B + C = constant), the entropy of the local system composed of these three SEQ before energy transfer is:S = A×B×C

Path i→j: transferring energy to node j (which has relatively higher energy):

S′= (A − 1)(B + 1)C = (A − 1)(BC + C)

Path i → k: transferring energy to node k (which has lower energy):

S″= (A − 1)B(C + 1) = (A − 1)(BC + B)

Here, “1” represents one unit of Planck constant h. Since B > C ⇒ BC + B > BC + C ⇒ S″> S′, the entropy increases more along the i→k path—that is, the path with the larger energy difference leads to a greater increase in entropy.

This deduction can be easily generalized to cases where the number of adjacent nodes is greater than two, so a detailed proof is omitted here.

However, it should be emphasized that the path with the maximum energy difference is not necessarily unique. Therefore, for states that have not yet occurred, the future still retains sufficient degrees of freedom — the evolution is not entirely deterministic.

3.9. In section 9.1.1, we will continue to discuss the decomposition of energy carried by SEQ {mᵢ=Kresonant (Kspin) +Uelastic assigned to this SEQ from its adjacent elastic bonds manifested as frequency suppression.}, the relational expressions, and the supplementary description of the initial low-entropy state of the universe. Chapter 13 will provide a detailed explanation of the metric-SEQ resonance frequency mirror relationship under this model. With this setting, there is no need to observe the sub-Planckian constituent-level elastic potential energy or the metric tensor; instead, the regional elastic potential energy can be directly represented by the SEQ resonance frequency. Chapter 14 will mention that SEQ spin and resonance frequency mutually excite each other and change synchronously; therefore, SEQ spin kinetic energy can also be represented by SEQ resonant kinetic energy.

4. Analysis of Action

The dimension of the action quantity is consistent with that of Planck constant, so the action quantity can be the number of units of quantum energy (Planck constant).

The total number of unit quantum conduction energy of a physical process involves two parameters, one is the number n of SEQ involved in the physical process wave conduction, and the other is the conduction times$k_i$of the ith SEQ involved in the conduction, in which the maximum number of conduction count $k_i$ of all single SEQ is less than or equal to times of local spatial transformations in this process. h is Planck constant. Then the action amount can also be written as

${\sum }_{i=1}^{n}h{k}_i,i\in N$ ③

The law of the principle of least action reveals that the path selected by physics process is the path that the total amount of energy conduction involved SEQ is the least. It involves two parameters, as mentioned above. If the number of SEQ involved remains the same and the conduction times of each SEQ are the same, (1)Fermat’s principle of the shortest time of optical path and (2)the principle of the steepest descent line can be directly derived, because in these two examples, the number of SEQ involved in the physical process and the rolling spherical rigid body in the steepest descent line remain the same, and the conduction times of each SEQ are also approximately the same, then time (the number of local space transformations) is the only variable for the calculation of action, so using time to divide the wave forms of different paths is equivalent to using action to divide the wave forms of different paths. Time here refers to the transformation times of local space. From this point of view, we can probably understand why the analysis of action amount proposed in different periods is different, but it can explain some phenomena.

The model assumes that each transmission of SEQ can only carry energy in discrete units of Planck’s constant h, where the principle of least action corresponds to minimizing the number of transmission steps. When spacetime is curved, the stretched regions exhibit lower SEQ density, requiring fewer quanta for energy propagation. However, as discussed in later sections, deformation modulates the resonant frequencies of SEQs, and the elastic properties differ between compressed and stretched phases. This necessitates a comprehensive consideration of transmission pathways through both compressed and stretched regions.

Crucially, the stretched path with reduced SEQ density remains the dominant route for minimal action propagation. In this model framework, Planck time defines the fundamental-minimum period of SEQ harmonic oscillation (corresponding to the maximum resonant frequency). Both compression and stretching deformations increase the SEQ harmonic period (reducing frequency and slowing spacetime transformation rates), though with different modulation strengths. Despite this asymmetry, the stretched path’s advantage in requiring fewer transmission steps persists, consistent with the observed convex trajectory of light around black holes.

Quantitative implementation of this model requires future development of discrete formulations of general relativistic field equations and variational principles to properly account for the asymmetric effects of spacetime deformation on SEQ network propagation. The current conceptual framework demonstrates self-consistency while providing a novel discrete approach to understanding spacetime dynamics at quantum scales.

Comparison with Hamiltonian and Lagrangian:

Compared with the Lagrangian and Hamiltonian, the analytical expression herein does not explicitly contain a potential energy term. In subsequent sections (section 9 to section 10), it will be mentioned that any form of metric change in space leads to a decrease in SEQ resonance frequency - resonance frequency modulation.

Thus, the actual analytical expression in this chapter has already implicitly included the potential energy term. Conversely, under this model, the essence of the potential energy term in the analytical expressions of the Hamiltonian and Lagrangian is the modulation of the number of energy transmissions. Under this model, gravitational potential energy, electromagnetic potential energy, weak interaction potential energy, and strong interaction potential energy are essentially the elastic potential energy of tensor or twist distortion of space.

To elaborate further:

• The absence of an explicit potential energy term in the analytical herein expression is compensated by the concept that any form of metric change in space results in a reduction of SEQ resonance frequency. This implies that the potential energy term is inherently embedded within the formulation via resonance frequency modulation.
• The essence of the potential energy terms in both the Hamiltonian and Lagrangian formulations, under this model, can be understood as modulations in the frequency of energy transmission events.
• Gravitational potential energy, electromagnetic potential energy, weak interaction potential energy, and strong interaction potential energy are all fundamentally manifestations of the elastic potential energy resulting from distortions in the spatial tensors or twists.
• The essence of potential energy release is the reduction of spatial distortion, which is accompanied by an increase in SEQ resonance frequency.

A Brief Discussion on Causality:

Within the ontological framework of quantum spacetime, the law of causality is determined by three fundamental principles: the second law of entropy increase, the principle of maximum entropy path selection, and the principle of least action (minimum action path selection).

At the microscopic scale, the discrete evolution of SEQ network is governed by a Markov process — each state transformation at the Planck time unit depends only on the immediately preceding state. However, open possibilities are preserved through nonlinear energy redistribution.

At the macroscopic scale, the cumulative effect of such microscopic causal interactions gives rise to a quasi-deterministic picture under the multiple constraints of entropy increase, maximum entropy path selection, and the principle of least action.

Thus, the second law of entropy, the maximum entropy path principle, and the minimum action path principle together constitute the foundational logic of cosmic causality: the former provides the arrow of irreversibility in evolution, while the latter two ensure the optimality of path selection. Together, they determine a unified causal network spanning from the quantum microscopic level to the observable macroscopic world.

However, since the path of least action is not necessarily unique, nor is the maximum entropy path, and the rate of entropy increase also has degrees of freedom (as will be discussed in Chapter 13 in relation to the duality between spatial deformation and SEQ resonance frequency), the future still retains uncertainty — it is not strictly deterministic.

5. Local time , the proper time and relative time in Relativity

5.1. local time. As previously established, global time is defined by the transformations of the universe. This work introduces local time as an operational concept that: (1) provides correspondence with special relativistic time notions; and (2) enables precise specification of time scales for localized physical processes. Crucially, any measurable time parameter in physical calculations necessarily corresponds to transformations within a specific local space. This operational concept is designated as local time.

The local space scope must be unambiguously specified: either as the SEQ network along the physical process path or the connected region within the observer’s light cone. This distinction mirrors the complementarity between Feynman’s path-integral formulation and relativistic theory, avoiding conceptual confusion in prior works.

Local time: it can specify the time set corresponding to the transformations within a specific spatial range. In fact, from the perspective of this framework, the existing equations with t parameter in textbooks are actually the local time by default.

One example: the clock slowness effect in Relativity manifests as different transformation times in different local spaces.

Every local space transformation constitutes a part of the universal evolution. Global time progression (${\mathsf{\Delta }\mathrm{T}}_{\mathrm{g}\mathrm{l}\mathrm{o}\mathrm{b}\mathrm{a}\mathrm{l}}$) does not necessitate synchronous local transformations, the state matrix of a given local space may remain invariant despite cosmic-scale changes ( ${\mathsf{\Delta }\mathsf{\tau }}_{\mathrm{l}\mathrm{o}\mathrm{c}\mathrm{a}\mathrm{l}}$≈ 0) when this local space undergoes no state transition.

5.2. The proper time in General Relativity is related to local transformations count of physics process entities. (Section 9.1,Section9.5.6 present the physical mechanism underlying proper time dilation in GR.)

5.3. Understanding on Lorentz-covariant rules in Special Relativity theory: The time perception of physical processes across distinct reference frames fundamentally corresponds to the observation of transformation counts. The observation time discrepancy between frames derives from the accumulated difference in their frame SEQ transformation counts. An observer measures another frame’s time evolution through the differential transformation count ΔN, while he can’t perceive their own transformation count N0. The observed ΔN is fundamentally governed by the dynamic light-path difference between the observer’s frame and the moving reference frame of the measured object. Under the principle of non-additivity of light speed (c-invariance), this formulation naturally derives Lorentz-covariant rules through counting operations.

• Key Distinction from GR Effects

While the mathematical derivation process aligns with standard special relativity textbooks—replacing continuous spacetime metrics with discrete counting operations—the physical interpretation differs substantially in conceptualization:

• SR Effects as Perceptual Phenomena

Time dilation and length contraction emerge purely as observer-dependent measurement consequences

Originate from information transmission constraints via discrete light-signal counting

• Contrast with GR Mechanisms

Gravitational time dilation involves actual deformation of the SEQ network’s transformation frequency

Equivalence principle effects require space compression as well (see §9.5)

5.4. Physical Meaning of Planck Time

In this framework, the Planck time (${\mathrm{t}}_{\mathrm{p}}$) corresponds to the fundamental-minimum harmonic period of the SEQ network in its equilibrium state—the duration for a complete energy transfer (or harmonic oscillation period) between adjacent SEQ. This period defines the theoretical minimum transformation cycle (i.e., maximum transformation frequency) of the universe as a whole.

While gravitational fields or equivalent interactions can locally modulate the harmonic frequency by deforming the SEQ network (e.g., compression/stretching, as in gravitational time dilation), the global maximum theoretical transformation frequency remains anchored by $t_p$in the equilibrium state. However, due to the omnipresence of gravitational effects, the empirically observable maximum transformation frequency of space may marginally less than this theoretical limit.

6. Basic physical quantities in this framework

Time: the count of the transformations of universe or specific local space.

Length: the count of SEQ in adjacent space. The source of transformation is the change of energy state, and the minimal transformation is the adjacent energy transmission. For example, after of N transformations, the number of SEQ that the farthest conduction of gravitational wave passes through is also N. This example vividly shows the concept of the integration of time and space.

Energy: integer multiple of the minimum energy unit(the Planck constant).

Entropy: the cumulative multiplication of energy on the SEQ in a whole or a locally closed space.

Time, energy, length and entropy are dimensionless integers.

7. Phenomenological consistency checks

7.1. Why can’t the speed of light stack up?

As established above(Refer to Section1), the speed of light (c) constitutes the maximum excitation propagation rate in space, wherein all observed motion fundamentally represents state transitions within SEQ network rather than physical traversal through space.

7.2. Uncertainty Relation and Wave-particle Duality.

The Uncertainty Principle naturally arises from wave propagation through discrete SEQ: precise position inherently limits determination of conduction speed (wave dynamics), and vice versa.

Wave-particle Duality. The wave nature is fundamental, while the particle nature emerges from the discreteness of spacetime itself.

7.3. Double-slit experiment.

The interference pattern observed in repeated single-electron or single-photon double-slit experiments can be interpreted as a statistical accumulation of distinct trajectories, each corresponding to a different realization of initial excitation conditions and local environmental fluctuations. Each individual particle effectively follows a path of stationary action — that is, a trajectory that extremizes the action functional according to the principle of least action (In reality, multipath disturbances are still present—they’re just too small to be noticeable). The high-density arrival regions in the double-slit interference pattern emerge as overlapping zones of these individual stationary-action paths across successive trials, reflecting the probabilistic distribution predicted by the quantum path integral formalism.[1,2]

Note:While this framework strictly enforces time ordering along entropy increase, it currently does not provide an interpretation for delayed-choice experiments. This remains an open question requiring further development in this framework.

Nonlocality may exist in nature, I prefer to focus on what is computable, evolvable, and causal. This model assumes that quantum phenomena arise from the coherent superposition of real paths, which evolve under local interactions. This approach avoids the complexity and unpredictability introduced by nonlocality, while still being able to explain interference and decoherence.

7.4. Non-conservation of parity

With the assumption above, if SEQ ground state spin chirality is fixed, that could be one possible explanation of the non conservation of parity.

Is dark matter potentially explained by high-density SEQ ground-state clusters under gravity? And is the ground state energy carried by the SEQ the so-called dark energy?

7.5. Conjecture on Muon Decay experiment [3]

Within this framework, accelerated muon motion induces local SEQ spacing variation, lowering local spacetime transformation frequency—manifesting as time dilation. Particle decay arises from the destabilization of their 3D structural matrices when interaction forces(EM/weak/strong) can no longer sustain equilibrium. Crucially, this destabilization exhibits transformation-frequency dependence, explaining observed variations in Muon Decay experiment.

8. Experiment to verify or falsify the hypotheses proposed

A prediction of a difference in the magnetic moments of the positron and electron.

Given the isotropic nature of the electric field generated by electrons, this framework hypothesizes that electrons possess an Spatially Symmetric dynamic structure composed of SEQ. Under the SEQ framework, all charged microscopic particles including electrons and quarks possess 3D structures that preserve spherical symmetry in space.

If a statistically significant discrepancy is measured between the magnetic moment of the positron and that of the electron, it would strengthen the credibility of the hypothesis 1)the SEQ’s chiral ground state and 2)the structured nature of electrons .This difference arises because the positron’s structural matrix rotates with opposite chirality to the electron’s, resulting in distinct coupling configurations with the SEQ’s fixed-chirality ground-state spin. Based on this, it can be inferred that the magnetic moments of the positron and electron should exhibit a slight discrepancy.

9. Gravitational Interaction, General Relativity and Cosmic Evolution Model

9.1. Gravitational interaction is modeled as a translational action described by matrices that alter the equilibrium spacing between SEQ. SEQ are interconnected via spring-like bonds in their ground state(Refer to the basic setting in Section 1.6, page2). Gravity modifies this spacing, creating tension with finite potential energy. This system behaves like a loaded spring: under gravitational fields, oscillation frequencies decrease, reducing local spacetime transformation rates and causing time dilation - matching general relativity’s predictions while revealing its mechanism. Mass-generated gravity acts as a spherically divergent translation with inverse-square density, curving flat spacetime topologically to produce general relativistic metric changes.

Within this discrete framework, the singularity paradox of black holes is naturally resolved because the tension between SEQ has a upper limit.

Macroscopically, (1)It explains metric variations and gravitational time dilation predicted by general relativity, while remaining compatible with its continuity assumption, (2)The ground-state energy of SEQ can also give a depiction of the cosmological constant in general relativity. (3)At the cosmic edge, adjacent SEQ lack outward coordination sites, creating an expansion tendency from interior with the initial kinetic energy released during the birth of the universe—a potential mechanism for cosmic expansion.

9.1.1. Under this model, a detailed deduction of the process of cosmic expansion.

Stage-Phase	Stage Name	Process	Universe State	Thermodynamic Characteristics
0-Compression	Pre-Big Bang Initial State	The universe’s SEQ network is highly compressed, with resonant frequencies close to zero. The initial low-entropy state may be reflected in a part of local SEQ network having particularly high energy, while most have low energy.	High-energy Aggregation State	Low entropy
1-Compression	Compression Potential Energy → Kinetic Energy	Elastic compression potential energy is released and converted into cosmic expansion kinetic energy	Accelerating Expansion	Low entropy, high energy concentration, rapid entropy increase
2-Stretching	Kinetic Energy → Tension Potential Energy	Expansion kinetic energy is converted into tension potential energy	Decelerating Expansion	Increasing entropy
3-Stretching	Tension Potential Energy → Kinetic Energy	Tension potential energy is released and converted into contraction kinetic energy	Accelerating Contraction	Entropy continues to increase
4-compression	Kinetic Energy → Compression Potential Energy	Contraction kinetic energy is converted into compression potential energy	Decelerating Contraction	Entropy continues to increase
repeated Oscillation → Equilibrium Oscillation	Energy Homogenization → Equilibrium Oscillation	In each cycle, the energy distribution becomes more uniform, with no obvious concentrated states remaining	Approaching Equilibrium State	Entropy approaches maximum, oscillating universe in thermal equilibrium
This process does not collapse back to the initial birth configuration of universe, nor does it reduce entropy—since the entropy increasing trend remains invariant under expansion or contraction, the homogenization of energy distribution is an irreversible process, until entropy reaches its maximum value.

• E global SEQ network =Kresonant (K spin) +Uelastic;
• Uelastic=U compress-stretch +U twistor(Space network spinor);
• Utwistor(Space network spinor) converts into Kresonant(Kspin) ; embodied as space network spinor

Among them, the conversion of twistor potential energy into resonant kinetic energy corresponds to the Kerr metric. However, since the Kerr metric distortion is not completely radial, the conversion of Kerr metric distortion potential energy into resonant kinetic energy simultaneously alters both the resonant frequency and the resonant axis vector ( generalized coordinates in the model mentioned in Section 13.4). Further mathematical formalization requires rigorous derivation by professional physicists based on observational data; here, only a rough model can be proposed.

• Ucompress-stretch converts into Kresonant (Kspin)

1	Potential energy is stored in elastic bonds composed of sub-Planck scale components.
2	In this model the energy of SEQ mᵢ equals the SEQ resonant kinetic energy plus the elastic potential energy assigned to this SEQ from its adjacent elastic bonds manifested as frequency suppression. Chapter 14 will mention that SEQ spin and resonance frequency mutually excite each other and change synchronously; therefore, SEQ spin kinetic energy can also be represented by SEQ resonant kinetic energy.
3	Chapter 10 will discuss that mass formation is mainly due to spin locking the spatial compression state and the key factor is the coupling confinement potential between the network spinor and the SEQ fixed chirality spin.

Supplementary description of the initial low-entropy state of the universe

Before the Big Bang, the universe was in a highly compressed state. The elastic potential energy was divided into two components: one was spatial compression potential energy, and the other was spatial twistor potential energy(Space network spinor). The spatial twistor potential energy was concentrated in some local regions of space — this constituted the initial low-entropy state. After the Big Bang, the twistor potential energy from this tiny region was released through conversion into SEQ resonant kinetic energy and SEQ spin kinetic energy, and this energy was then conducted to other regions of space. This process represents the specific mechanism of entropy increase.

9.1.2. The mass formation and matter-energy conversion mechanisms in different stages of cosmic evolution:

• First stage of cosmic expansion: mass generation dominates.

According to this quantized elastic space-time model, mass is formed when compressed states are locked by the coupling of SEQ network spinors and the fixed chirality spin of SEQ . The formation of mass states depends on the degree of spatial compression and the intensity of SEQ network spinor. Since the universe as a whole is in a highly compressed phase during this stage, and SEQ network spinor is concentrated on a local zone, it is consistent that mass is formed. In the first stage, the entire cosmic space is generally in a highly compressed state, and during the initial inflationary period, the compression is even more pronounced. Due to the space network spinor--SEQ fixed chirality coupling locking mechanism (similar to the Higgs mechanism, introduced in Chapter 10), the highly concentrated spinor of local zone causes certain compressed spatial states to be locked into mass states. Therefore, mass generation dominates in this stage, especially during the early inflationary phase, when the spatial compression level is higher and better matches the compression required for mass state formation.

• Second and third stages of cosmic evolution:

transformation from mass states to energy states dominates, with possible new mass state formation during the process.

In these stages, the universe as a whole enters a stretched phase. According to this model, mass states become unstable due to the stretching of the space itself. The conditions for mass state become weaker, leading to more mass states breaking down. During this phase, new elements—mass states—may be generated within massive celestial bodies.

• Fourth stage of cosmic evolution : the universe re-enters a compressed phase.

However, at this stage, the distribution of SEQ network spinor distribution has become more uniform, and the effect of the Higgs-like mechanism is weaker. Although new mass states may still form, the overall rate of mass generation is significantly lower than in the first stage.

• Fifth stage of cosmic evolution:

repeated oscillations leading into thermal equilibrium oscillation.

As the network energy becomes increasingly uniformly distributed—an irreversible entropy increase process—the proportion of mass states in the universe gradually decreases through repeated oscillations. Eventually, all mass states are transformed into energy states, meaning the spin kinetic energy distribution of the SEQ network becomes uniform, and the universe enters oscillation in a thermal equilibrium state.

This mechanism, in which high spatial compression collaborates with space network spinor to generate mass, may also explain the observed anomalies in galaxy rotation curves. Specifically, the early universe featured a high concentration of network spinor. This intense network spinor concentration, coupled with the extreme spatial compression, facilitated the formation of mass. Consequently, the resulting mass structures and their surrounding space likely retain higher-than-expected spinor, which could account for the observed rotational dynamics in galaxies.

Dark matter formation is also dominated by a synergistic locking mechanism involving spatial compression states and a Higgs-like mechanism (space network spinor and SEQ fixed-chirality spin coupling), similar to the mass generation mechanism in the early stages of cosmic expansion. However, dark matter formed at a later stage than ordinary mass. The spatial compression level during this phase was insufficient to reach the threshold required for mass generation. Moreover, by this time, the increase in entropy had led to a more uniform distribution of space network spinor, reducing the strength of the spinor field in the Higgs-like mechanism to a level insufficient to lock high-compression states. This is the fundamental difference between dark matter and mass states. In essence, dark matter is also a form of locked spatial compression state, but with a much lower compression strength compared to mass states. Nevertheless, it still exerts a stretching effect on the surrounding space, manifesting as a gravitational field.

Why is there a global gravitational tension-restoring potential in the first stage of cosmic expansion, even though the entire space is in a compressed phase? Because the compression level within mass structures is significantly higher than that of the surrounding space, leading to a large gradient in spatial deformation, which gives rise to a relative tension-restoring potential — the gravitational potential.

This explanation is self-consistent and visually clear, especially in providing a concrete physical image and mechanism for the large-scale generation of mass states in the early inflationary universe.

9.2. Consistent with general relativity, high-velocity or accelerated transformations of localized matter compress space, thereby inducing tensile stretching of surrounding space (equivalent gravitational effects). This process not only induces spacetime curvature but also modulates the conduction frequency of waves.

In relativity theory, equivalent gravitational fields from velocity/acceleration (1) share the same core mechanism as mass-generated gravity—local SEQ compression (reduced spacing) inducing spacetime stretching, but (2) exhibit vector-directional dependence (anisotropic compression) instead of spherical symmetry, and (3) reflect inertial-SEQ lattice coupling through their non-spherical divergence and preferred orientation alignment in quantum spacetime structure.

9.3. Detailed Correspondence with Newton’s law of universal gravitation

“The number of sub-Planck substrate on the surface of a mass source corresponds to the number of gravitational flux lines (i.e., the count of gravitational transmission paths). As the gravitational field diverges spherically, the density of these flux lines becomes inversely proportional to the surface area at any given radius, thus exhibiting an inverse-square relationship with distance. This result directly coincides with Newton’s law of universal gravitation.”

9.4. Correspondence with Newton’s First Law—the Law of Inertia

In this framework, the compressed space at the front and the stretched space at the rear—both caused by the object’s motion at Constant Velocity—are always the interfacial boundary between the matter wave and the surrounding SEQ. Beyond this boundary, there is no compression or stretching induced by the object’s motion at Constant Velocity, only a shift in the harmonic vibration phase of the SEQ , the system reaches equilibrium at Constant Velocity.

The work input during acceleration establishes interfacial strain energy in the SEQ network, which then sustains uniform motion through elastic potential equilibration.

9.5. Understanding on General Relativity

9.5.1. Under gravitational and equivalent gravitational interactions, the dynamic deformation of 3D space structural matrix and variation in local SEQ density distribution corresponds to Metric field in General Relativity.

9.5.2. Minimum cumulative conduction count path adjustment along with the cumulative dynamic paths connecting every two-points with the minimal count of adjacent SEQ through spacetime distortion corresponds to geodesic path in general relativity. (Principle of least action)

9.5.3. Global topological homeomorphic transformation in SEQ framework corresponds to Diffeomorphism invariance in General Relativity.

9.5.4. The continuity assumption in general relativity, analogous to the continuum medium framework in fluid mechanics, constitutes a necessary and effective computational framework.

9.5.5. Black hole event horizon:

Inside the event horizon of a black hole, due to intense gravitational forces, the spacing between SEQ is compressed to its limit. This extreme compression approximately and locally halts: (1)Energy conduction (2) space transformations (3)Entropy increase step (Neglecting black hole accretion).

9.5.6. Gravitational and Kinematic Time Dilation

All factors that induce metric variation, including mass (gravity), velocity, and acceleration(equivalence principle), compress or stretch spacetime locally, thereby modulating the transformation frequency of related space. This frequency suppression constitutes the fundamental mechanism of time dilation.

10. Mass, Gravity, SU(3) and Higgs field in Quantum Field Theory

10.1. SU(3) as the Origin of Mass Derivation

10.1.1. General Relativity establishes that gravitational fields manifest as metric perturbations→spacetime curvature.

10.1.2 Mass must therefore induce localized spacetime distortion→creating the observed gravitational potential.

10.1.3 This implies mass itself represents a condensed form of spacetime deformation →self-consistent with stress-energy sourcing curvature.

10.1.4 Within hadrons, quark-gluon dynamics are governed by SU(3) color interactions→the dominant force compressing SEQ network.

10.1.5. Thus, SU(3)-mediated compression of SEQ network → generates both quark confinement energy (mass) and external spacetime stretching (gravity).

10.1.6 Generalizing this mechanism→ equivalent effects (velocity/acceleration) anisotropically compress local space→inducing equivalent gravitational attraction via adjacent SEQ tension.

Note:The phase in SU(3):compression or stretching shift between SEQ.

10.2. U(1): Electromagnetic Interaction

10.3. SU(2): Adjustments of Rotational Axes, spin and encoding chirality in Charged Microscopic Particle Structural Matrices.Encoding Rotational chirality of Charged Microscopic Particle Structural Matrices as the Origin of Weak Interaction Symmetry Breaking. because the rotational Structural Matrices with different chirality have different coupling mode with the fixed chirality of SEQ’s ground-state spin. Although SU(2) lacks a chirality modulation parameter, its definition as adjusting rotation axes and spin for charged particles with specific chirality intrinsically encodes chiral variables.

10.4. SU(3):

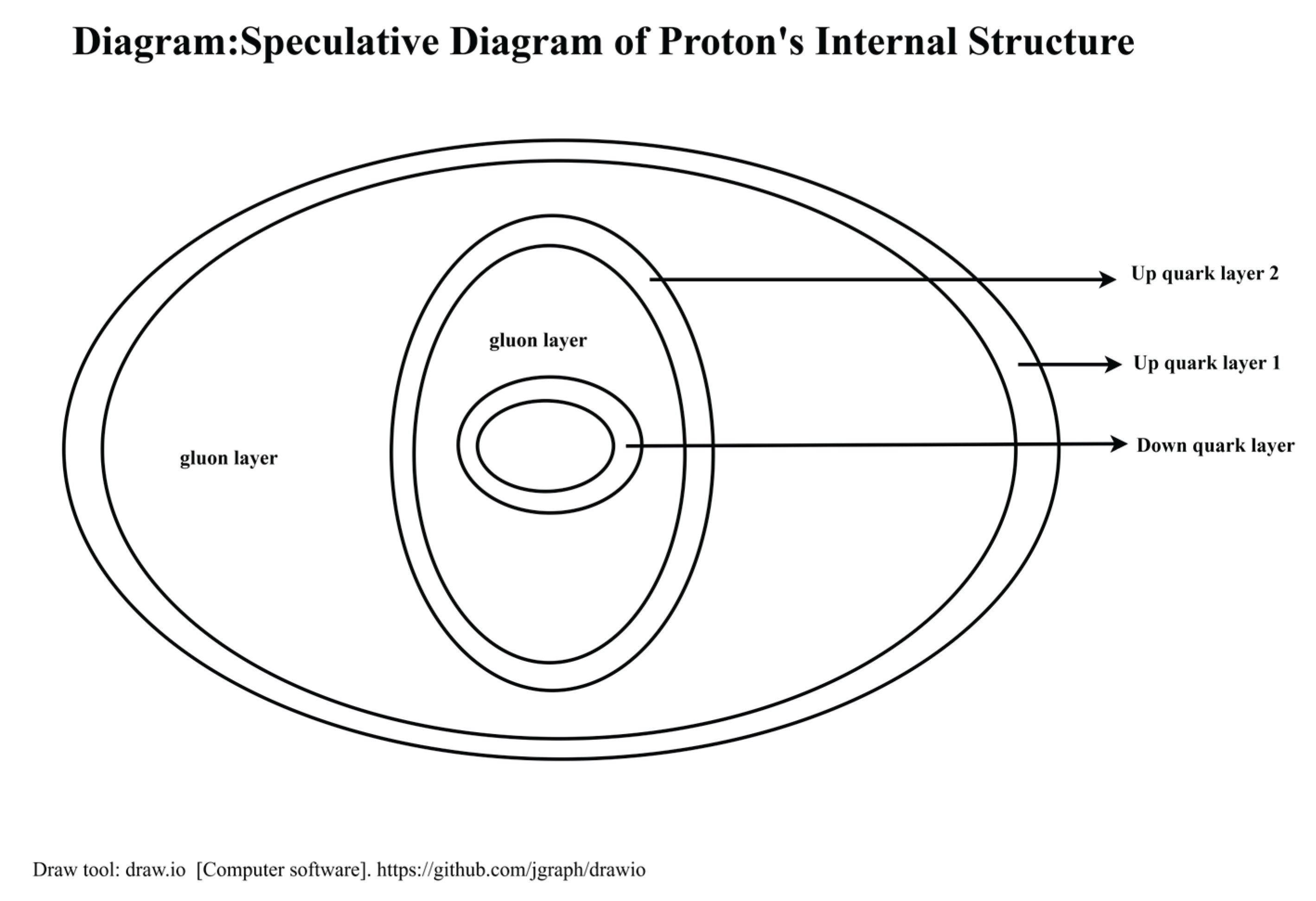
10.4.1. Imagine the 3D dynamic quasi-spherical matrix structure of quarks as a multi-layered and multi-axial rotational configuration. Due to the high-energy concentration within the structure, the SEQ within the structure remain in a dynamic equilibrium of compression or stretching, while the interactions between layers also maintain a dynamic equilibrium of compression or stretching.

10.4.2. Fractional quark charges emerge from stratified SEQ layers in proton/neutron matrices, with 2/3-charged quarks occupying twice the layers of 1/3-charged quarks. The multi-layered structure well explains the observed differences between high-energy(uniform angular distribution) and medium-energy regimes in electron-proton scattering experiments.

10.4.3. The color property of quarks corresponds to the long axis of their dynamic structural matrix, specifically the axis with the highest energy density distribution within the quark’s structural configuration. The color neutrality of protons and neutrons corresponds to the global spatial symmetry, the isotropy of the electric field (protons)and structural stability exhibited by their spatial structural matrices.

10.4.4. Antiquarks correspond to the handedness reverse representation of structural matrix rotational transformation of their corresponding quarks.

10.4.5. The 8 generators of SU(3) correspond to 8 distinct interactions mediated by different gluons dynamics manner. Among them, the 6 non-diagonal matrices represent combinations of color exchange operations, stretching and compression phase transformations with phase variations(3*2); while the 2 diagonal matrices correspond to scaling transformations across the three color dimensions. These gluons and their 8 distinct interaction types operate within the interlayer regions of the multi-layered structural matrices of protons or neutrons.

The dynamic color exchange corresponding to the generators of SU(3) and the three-dimensional color distribution modulation are fundamentally linked to the translational action of gravity. Therefore, the color modulation and exchange interactions of SU(3) could constitute one of the origin of mass.

10.4.6. Gluons mediate compression and tensile stresses between quarks or interlayer SEQ. Gluons can be understood as a kind of quasi-structure of highly condensed SEQ, akin to a rotational high-density array of springs.

10.4.7. Quark asymptotic freedom and color confinement originated from nonlinear variations in compression-tensile tensions among SEQ.

10.4.8. The three-quark point-like configuration inherently fails to achieve spatial symmetry, contradicting the observed spherical charge distribution of protons, whereas this hypothesis of a layered arrangement in a quasi-spherical structure of up and down quarks within the proton offers a more plausible explanation for the integer charge of the proton and the isotropic nature of the electric field as well.

10.4.9. The discrepancy in the proton’s g-factor from theoretical models stems from an underestimation of the gluon field’s spinor contribution. If the effect of the rapidly rotating gluon field were properly accounted for, this deviation would significantly diminish. Moreover, the conventional three-point-quark distribution framework fundamentally cannot accommodate a proportionally substantial gluon field spinor component. The layered structure proposed in this model presents a viable architectural framework worthy of serious consideration.

10.5. How SU(3) Generators Mediate Mass Formation

They compress local space while performing 3D modulation, axis transformations, and compression-phase adjustments to ensure the compressed space remains approximately spherically symmetric. As a result, the gravitational field generated by mass (the stretching of external space due to local compression) is also spherically divergent, guaranteeing the isotropy of mass-induced gravity. The physical picture is now clear.

10.6. The essence of mass is the storage of gravitational (spatial elastic) potential energy under the interaction of SU(3) corresponding to the compression of space.

10.6.1. Dimensional analysis dictates that the relationship between mass and energy must satisfy [E]/[m][$v^2$], with the proportionality coefficient determined by the fundamental constants of spacetime (the speed of light, c).

10.6.2. The compressed potential energy of mass in localized space is inherently mainly released as gravitational waves with radiation, which propagate at speed c , thus directly yielding $∆$E=$∆$m$c^2$.

10.7. Complementary Role of the Higgs Field: Symmetry Breaking and “Locking” Mechanism:

10.7.1. The Higgs field plays a crucial yet subtle role in this framework by acting as a stabilizing “quantum chiral lock” that preserves the compression effects mediated by the SU(3) gluon field on the local SEQ network. While the SU(3) color force actively compresses the local space to generate mass-energy through spatial deformation, the Higgs mechanism serves to maintain this compressed configuration in a stable equilibrium state. This locking function is particularly vital for quark confinement, as it prevents the rapid dissipation of the gluon field’s compressive energy that would otherwise lead to deconfinement. The Higgs field’s symmetry-breaking properties thus complement the SU(3) compression mechanism by providing an additional interaction of stability to the mass-generating structure. In essence, if the SU(3) mediated compression is likened to a tensed spring storing potential energy, the Higgs field acts as the catch mechanism that keeps the spring compressed, ensuring the persistence of the mass effect. This dual mechanism - active compression by color forces and passive stabilization by the Higgs field - offers a more complete picture of mass generation that bridges quantum chromodynamics with electroweak theory while remaining consistent with the discrete spacetime framework proposed in the paper. The interplay between these mechanisms may also help explain why certain particles (like quarks) exhibit both confinement and mass properties, while others (like leptons) primarily acquire mass through Higgs interactions alone(like a preloaded torsional spring energy storage combined with a ratchet).

This dual mechanism—where the QCD color interaction-SU(3) acts as a compressive spring system, while the Higgs mechanism functions like a preloaded torsional spring combined with a ratchet (enabling unidirectional energy storage while preventing reversal)- provides a vivid mechanical analogy for how fundamental particles maintain their mass stability in the quantum spacetime fabric. Just as a ratchet’s teeth enforce unidirectional motion through asymmetric geometry, the Higgs’ chiral coupling to the SEQ ground state spin with fixed chirality may similarly lock the gluon field’s compressive energy in an metastable configuration.

10.7.2. Origin and Physical Picture of the Higgs Mechanism

In this model, the Higgs mechanism is fundamentally a synergistic effect of gauge fields (U(1), SU(2), SU(3)) rather than an independent field. The torsional-spring-like vorticity of the Higgs mechanism originates from the vorticity coupling of U(1), SU(2), and SU(3), while the ratchet-like locking arises from symmetry breaking induced by the fixed chiral spin of SEQ.

According to the model specification in Section 1.6, the spin degrees of freedom of SEQ and higher-level spinors are decoupled from the elastic bonds between SEQ and their sub-Planckian components. This decoupling mechanism naturally explains the vorticity disparity between the gravitational field (emerging from macroscopic SEQ network stretching) and the gluon field (originating from localized SU(3) compression of SEQ).

10.7.3. Therefore, quark confinement may arise from the combined effects of the Higgs field’s quantum chiral lock and the nonlinear response of spatial elasticity(QCD).

10.8. A fundamental duality emerges between the SU(3)-driven compression of matter at quantum scales and the emergent gravitational field: The mass of hadrons arises from intense color-force compaction within subnuclear volumes, whereas gravity manifests as the coherent stretching of the finite SEQ fabric. This stark contrast in interaction ranges—from quark confinement to system-wide SEQ deformation—naturally explains the hierarchical strength difference between nuclear and gravitational forces.

In simple terms, the elastic coefficients and deformation ratios differ between the compressive phase (QCD) and the tensile phase (gravity). The deformation of gravity is distributed across the entire space, whereas QCD’s deformation is more localized. This difference leads to the distinct energy scales of QCD and gravity.

10.9. In nuclear reactions, the release of kinetic energy primarily corresponds to the elastic potential energy-kinetic energy of the QCD dynamic spring array, while the breaking of the Higgs mechanism mainly releases stored Fermionic Spinor energy-akin to torsional spring energy storage in the form of radiation. This explains the energy type distribution in nuclear reactions and the radiative phenomena in QED.

A Hypothetical Qualitative Analysis:

In light-nuclei fusion reactions (e.g., D-T fusion), the simple nuclear structure and low mass of light nuclei result in a relatively minor contribution from the “spinor-twisted spacetime structure” (analogous to a torsion-spring energy storage mechanism) induced by Higgs field coupling. Consequently, the proportion of radiative energy release in total reaction energy remains notably small. In contrast, heavy nuclei (e.g., ²³⁵U) possess significantly higher nucleon number density, wherein the Higgs-mediated spinor distortion effects become more dominant. This leads to a markedly increased share of radiative energy release through β-decay chains during fission processes. The observed disparity may reflect enhanced synergy between Higgs field and QCD confinement potential in heavy nuclear structures.

10.10. According to my personal understanding, the tensor description in standard General Relativity (GR) represents the compression and stretching of space in different directions. In fact, the synthesis of such compression-stretching tensors across different directions can generate structures similar to spinors, and the Kerr metric is essentially doing this kind of work.

On the other hand, ECT (Einstein-Cartan Theory) directly introduces a spinor-defined connection by adding it to the affine connection.

In other words, the Kerr metric can be expressed using the tensors of standard GR, while the spinors in ECT are defined separately as part of the connection, and this connection can in fact be directly applied to the quantum spinor in quantum field theory.

However, my understanding is that in order to unify General Relativity with quantum field theory, at the quantum level, spin must decouple from spatial elasticity; otherwise, mutual interference would contradict observed phenomena. Of course, ECT should mainly define the coupling between quantum spin and spatial tensors under high-energy conditions, while in low-energy states, it should still exhibit a behavior similar to such a decoupling.

From the perspective of my personal proposed model, the combined effect of the Kerr metric and ECT actually corresponds to the essence of the Higgs mechanism, making it easier to describe how spatial spinors and fixed-chirality quantum spin lock spatial compression or stretching.

11. Thoughts on the 3D Spatial Arrangement Matrix of Microscopic Particles

11.1. Spatial Arrangement Matrix Representation of Electrons:

To ensure the observed spherical symmetry of the electron’s electric field, its structure must comprise at least four or more SEQ in a 3D (possibly multi-layered) configuration. Additionally, the electron’s structural matrix may undergo rapid multi-axis rotation. Estimates based on electron mass suggest this matrix contains a large number of SEQ.

11.2. Representation of Electric Charge:

Electric charge may correspond to the intrinsic multi-layered, multi-axis rotational dynamics of the structural matrix governing microscopic particles. All electric charged microscopic particles are embedded with analogous substructures.

11.3. Fractional Charges of Quarks:

Fractional charges cannot exist in isolation but depend on SU(3)-mediated collective effects of quark confinement. The underlying mechanism suggests that when gluons between quarks disintegrate, the quarks must either likewise disintegrate or undergo reintegration.

11.4. Annihilation and Decay of Microscopic Particles:

The annihilation or decay of microscopic particles fundamentally arises from the disintegration or reintegration of their spatial structural arrangement matrices.

11.5. Mechanism Analysis of Positron and other types of Antiparticle Scarcity:

The intrinsic spin of an electron is essentially the orbital rotation of SEQ in the electron’s structure around the electron’s center.

Positron and other types of Antiparticle scarcity emerges from their interaction with the fixed-chirality ground-state spin of SEQ, inducing instability of their structural matrices, a mechanism that simultaneously explains parity violation.

11.6. Geometric intuition for the half-integer spin of electrons:

It is imaginable that the spin axis of an electron undergoes a flipping motion, with the flipping period synchronized with the spin period. This would allow for a 4π reset, while also providing a geometric intuition for the SU(2) double covering of SO(3). In fact, this combination of spin and axis-flipping corresponds to the mechanism required to explain the spherically symmetric and divergent electric field of the electron.

SU(2) double covers SO(3), meaning that the double covering is a homomorphism where the preimage set contains twice as many elements as the image set. My intuitive understanding of this is in terms of a “double rotational degree of freedom”. This double rotational freedom could be interpreted as a combination of spin and axis rotation. How can a 4π reset be realized? When the spin period and the axis-flipping period are synchronized, a reset after two flips of the axis corresponds precisely to a 4π spin reset.

This geometric intuition is consistent with the observed physical phenomena.

11.7. The Nature and Origin of Lepton Mass:

In this model, the electron possesses an internal structure, and its spin arises from the field excitation of this structural rotation. Such a spinorial field excitation can distort spacetime, while the near-light-speed tangential velocity of the electron’s rotation corresponds to a spatial twist that generates a spherically divergent gravitational field. The mass of the electron is fundamentally the result of the external spacetime stretching—manifested as a gravitational field—induced by this rotating spinorial distortion. This can equivalently be understood as the inertial mass described by relativity.

From this perspective, the electron mass calculated in this theoretical model is inherently inertial mass, and the speed-of-light constraint applies equally to the tangential excitation wave velocity at the electron’s surface. Under this understanding and constraint, recalculating the electron’s radius yields a self-consistent result where the tangential velocity never exceeds the speed of light.

The flaw in traditional theoretical calculations lies in their presupposition that the electron’s mass is rest mass, thereby underestimating the relativistic inertial mass. This leads to an overestimated radius and, consequently, a paradoxical derivation of superluminal tangential velocity. In contrast, this model eliminates the paradox: the electron’s rest mass approaches zero, is not governed by chromodynamics, and is instead dominated purely by the dynamic spinorial field excitation of the Higgs mechanism—an inertial mass framework free of contradictions.

12. Quantum Gravity, Graviton and Space Elastic Response Frequency

12.1. Gravity fundamentally stems from its mediation by elastic bonds(sub-Planckian constituents) between SEQ rather than direct SEQ interactions.

12.2. When the resonant frequency of SEQ significantly exceeds the elastic response frequency of inter-SEQ bonds, gravitational field mediation does not encode SEQ’s spectral fingerprints.

12.3. The method of gravitational wave frequency detection implies that the detected frequency range should fall within the spatial elastic response frequency range. As our understanding of gravitational wave frequencies expands, so too will our knowledge of the spatial elastic response frequency range.

The sub-Planckian spacetime constituents mediating gravitational interactions may correspond to the graviton , as they are the fundamental units responsible for conducting spatial elasticity and gravitational effects.

13. Space Deformation(Geometry) - SEQ Resonant Frequency Modulation Duality:-Connecting GR to QFT

In Section 4, we discussed the action and mentioned that spatial deformation corresponds to frequency modulation. In this chapter, we will further explore this topic. Furthermore, the subsequent mathematical formalization of this model does not require a specific characterization of spatial deformation. Instead, it maps spatial deformation onto the corresponding region’s frequency domain of SEQ network while distinguishing between compression phases, stretching phases, and twistors. Frequency modulation is used to characterize spatial deformation and potential energy changes.

13.1. Frequency Modulation as an Essential Description of Spatial Deformation

• The model suggests that any metric change in space, such as curvature caused by gravitational fields, modulates the resonant frequency of SEQ. Compression and stretching phases influence frequency domain modulation through asymmetric elastic coefficients. This frequency modulation directly encodes the geometric information of spatial deformation, eliminating the need for additional Riemann geometry descriptions.
• The traditional concept of potential energy terms (gravitational, electromagnetic, or quantum field potentials) is reinterpreted as frequency modulation of SEQ resonance. For instance, a decrease in gravitational potential energy corresponds to a frequency domain offset, while the release of potential energy manifests as dynamic modulation restoring the frequency to its high-frequency ground state. This mapping enables a unified frequency-domain representation of the metric field in general relativity and potential energy terms in quantum field theory.
• Entropy Increase Rate: In addition, since the conduction frequency within a local space directly determines the local entropy increase rate of the system, there also exists a dualistic modulation mechanism between space geometry deformation and the rate of entropy increase. This relationship is self-consistent and analytically derivable under the SEQ quantized space model.

Simplified Pathway for Mathematical Formalization:

13.2. Classification of Spatial Deformations: First, classify spatial deformations into 4 types (specific classifications can be refined based on future research):

• Stretching Phase
• Compression Phase
• Left-handed Twistor
• Right-handed Twistor

Since the model assumes that SEQ have a fixed chirality spin in their ground state, the frequency modulation caused by left-handed and right-handed twistors is not entirely symmetric. Based on QCD and cosmological observations, the elastic coefficients and frequency modulation of space should be nonlinear functions. Therefore, according to existing QCD, electromagnetism, and cosmological observations, preliminary modeling of the operator functions for these 4 deformations to SEQ frequency modulation can be established. Embedding these operators into the action function or other equations allows the analytic expression of action from Chapter 4 to represent the modulation of transmission frequency due to deformation.

13.3. Construction of Discrete Functional Framework:

By defining the local frequency response function of the SEQ network, continuous spatial deformation can be transformed into a parametric problem on discrete frequency lattice points. This model converts the geometrical dynamics of spatial tensor-twistor deformation into frequency dynamics, providing a new mathematical framework for unifying gravity and quantum theory. Its formal simplicity may offer new tools for physics. Future research should focus on developing specific algorithms for discrete functional equations and establishing mappings with parameters of the Standard Model. However, it should be noted that the specific mathematical modeling of this discrete model depends on the adjacency topology of the space SEQ network, which remains undetermined at present. Therefore, the mathematical phenomenological fitting is only approximate.

13.4. Generalized Coordinates in This Model:

Preliminary Discussion on the Lagrangian and Hamiltonian Analytical Mechanics Framework Based on This Model:

In the topologically homeomorphic space field of this quantized elastic spacetime model, each SEQ (Space Elementary Quantum) has a fixed spatial coordinate and fixed adjacency relations. The generalized coordinates of each SEQ are its resonance frequency and resonance axis vector(ωᵢ,n̂(i)). These two quantities, combined with the dynamic structural matrix of matter, can generate physical quantities such as mass, momentum, velocity, acceleration, force, kinetic energy, and potential energy—all expressed as polynomials of the generalized coordinates or their differentials (partial derivatives or integrals). Based on this framework, conservation equations can be constructed.

13.5. Under the topologically homeomorphic setting, the spatial coordinates of each SEQ serve as its structural label and constitute important topological invariants. These coordinates remain fixed during dynamical evolution (i.e., they do not change over time), and therefore are not subjected to time differentiation. Nevertheless, they play a crucial role in constructing conservation equations, such as defining local gradients and adjacency relations. Hence, they should be regarded as background structural parameters rather than components of generalized coordinates.13.6. Mass, Mass represents a spatial compression state that cannot be characterized by a single SEQ. Instead, it requires a local description in terms of the local spatial compression rate — the degree of deformation, which can be quantitatively expressed as the average frequency shift within that local space. Frequency directly reflects the extent of spatial deformation.

Since this model does not incorporate the conventional concept of volume, the notion of compression is inherently tied to the topologically homeomorphic SEQ network. Whether compressed or not, the structure remains a SEQ grid, and thus, spatial compression must be described through either:

A general relativistic tensor representation of the compression rate, or

The average resonance frequency of the SEQs contained within the mass-bearing object, which captures the spatial deformation effect.

Therefore, mass can be effectively represented by the number of SEQs within the object and their collective resonance frequency. This leads to the following formulation:

m = K×N×(ωₚ/ω̄)

Where:

• m: mass
• K: a dimensional conversion constant (can be dimensionless or carry traditional mass dimensions)
• N: number of SEQs contained in the mass-bearing object
• ω̄ : average resonance frequency (relative to Planck frequency shift)
• ωₚ : Planck frequency
• (ωₚ/ω̄): represents the degree of spatial deformation

13.7. Force — next, we discuss F = ma. Acceleration can be understood as the rate of change of spatial deformation gradient between a mass-bearing object and its external environment. This gradient of deformation induces the object to maintain structural synchronization during acceleration, resulting in additional spatial deformation — compression at the front end of acceleration and stretching at the back end. In this framework, m represents the structural response barrier (mass), and F is the deformation action required to induce an additional gradient of spatial deformation in an object of mass m. The essence of F = m a is: in order to cause a change in the spatial deformation gradient (acceleration) of an object that possesses a structural response barrier (mass), a corresponding deformation action (force) must be applied.

13.8. Other conceptual constructions of classical physical quantities — the following are only examples and not strict mathematical formalizations:

Starting from the perspective of spatial deformation — local frequency duality, we define the phase φ = Δω / ω₀, where Δω is the local frequency shift and ω₀ is the reference frequency. From this, we construct the wave vector k = ∇φ. Then, we define momentum of generalized coordinate-SEQ Frequency as p = ħk, where ħ is the reduced Planck constant, ħ = h / (2π).

The resonance frequency and resonance axis vector of each SEQ — which are the generalized coordinates — correspond to two different sets of analytical expressions for generalized momentum. The generalized momentum of the SEQ resonance axis needs to be further developed in future work. According to this model, the direction of the SEQ resonance axis depends on the adjacency configuration, which is discrete and finite, thus making the direction quantized as well.

In the analytical expression of the generalized momentum of the SEQ resonance frequency as a generalized coordinate, the reduced Planck constant ħ is not used to characterize the quantization of angular momentum, but rather to describe phase quantization in the harmonic oscillation of SEQ (this is only a conceptual analysis tool — the actual phase variation may not necessarily be quantized). This allows for a formal description of the phase gradient between matter and its surrounding SEQ in the process of material wave formation.

Velocity is then defined as v = p / m, acceleration as a = dv / dt, force as F = dp / dt, and so on.

13.9. In this model, the spatial field is a topologically homeomorphic structural field, and the motion of matter corresponds to the propagation of excitation waves on this field. Therefore, when constructing conservation equations, they may differ from the traditional conservation equations in analytical mechanics, but they should be able to derive equivalent forms corresponding to the classical ones. Here, I can only propose a rough framework, and the specific rigorous mathematical formalization likely still requires the work of professional physicists to complete.

Although Einstein adopted the geometric description based on the metric tensor in his General Relativity, he had already noticed the significant influence of gravity on light frequency shifts. The ‘Deformation-Frequency Equivalence Principle’ proposed in this paper can be regarded as a continuation of this unification vision—it reinterprets the variation of spacetime tensor structure as a frequency modulation process of SEQ, thereby establishing a new unified descriptive paradigm between the microscopic and macroscopic scales.

Deriving a metric-quantum frequency function from cosmological gravitational redshift measurements and QCD-level interactions could establish a functional mapping(ω_QFT = f(g_μν)_GR) between GR’s spacetime geometry and QFT’s quantum observables, offering a mathematically tractable and empirically testable tool for unifying gravity and quantum theory.

13.10. Hamiltonian, Schrödinger Equation, and General Relativity Equations from the Perspective of This Model

13.10.1. From the perspective of this model, the Hamiltonian is an energy function defined in terms of the generalized coordinates (resonance frequency and resonance axis vector of Space Elementary Quanta, SEQ) and their corresponding generalized momenta. It fully characterizes the current local spatial configuration of energy distribution and acts as the generator of time evolution, determining the subsequent energy distribution and its evolutionary trend at the next moment. In this framework, the traditional notions of kinetic and potential energy terms are both manifested as different modes of frequency modulation of SEQ. The so-called “potential energy” fundamentally arises from elastic potential energy associated with spatial tensor deformations or twistor structures.

13.10.2. Schrödinger Equation: In this model’s interpretation, the Schrödinger equation describes how the current energy distribution, along with its gradients—such as phase gradients (encoded in the Hamiltonian)—determines the probabilistic evolution of the next moment’s energy distribution and its gradients. The origin of probabilistic randomness lies in the non-uniqueness of maximum entropy paths within the system’s dynamical evolution. Thus, quantum probability emerges not from intrinsic indeterminism, but from the multiplicity of valid pathways that satisfy thermodynamic and variational principles under constrained initial conditions.

13.10.3. Einstein’s field equations of General Relativity—the metric tensor equation—and the geodesic equation essentially describe the same class of evolutionary dynamics as the Schrödinger equation: namely, that the present state of energy distribution and its gradient determines the future path of energy distribution evolution. The difference lies only in the encoding language: General Relativity formulates this law geometrically through spacetime curvature and affine connections, while the Schrödinger equation expresses it through quantum phase dynamics and probability amplitudes. Despite their distinct mathematical formulations and interpretive frameworks, both reflect a unified underlying principle—the causal propagation of energy configurations governed by extremal principles such as least action and entropy increase.

13.11. Due to the topological invariance of the spatial field in this model, the spatial coordinates of each field quantum are fixed (the space may deform, but the connectivity and adjacency relations remain unchanged). Each Space Elementary Quantum (SEQ) carries only two generalized coordinates: the field quantum resonance frequency (associated with field quantum spin and mutual spin synchronization, representing elastic potential energy at sub-Planckian elastic scales) and the field quantum resonance axis vector, denoted as (ωᵢ, n̂(i)). Consequently, the Hamiltonian formulation of this model is simpler, more intuitive, and more consistent with the physical process of energy redistribution and energy gradient configurations than those of traditional quantum field theory or general relativity, while naturally preserving global energy conservation and embedding thermodynamic arrow of time.

14. Preliminary Exploration of the Electromagnetic Interaction Physical Picture:

A GR Reformulation of Electromagnetic Interactions within the Quantized Elastic Spacetime Framework.

The following discussion may not be rigorous or entirely accurate but represents an attempt to describe the electromagnetic interaction within the framework of this model.

14.1. Electromagnetic Waves:

The SEQ resonance generates an electric field, which induces a spin magnetic moment orthogonal to the resonance direction. The spin and resonance of SEQ mutually excite and synchronize with each other. The phase of this magnetic moment aligns with the SEQ resonance phase. The SEQ resonance drives adjacent elastic bonds in the network. Given the model’s assumption of symmetrically arranged elastic bonds around each SEQ, the resulting wave propagates spherically. Since the elastic bonds in the plane orthogonal to the resonance axis are more significantly perturbed, the transverse plane wave dominates.

The magnetic field of an electromagnetic wave fundamentally arises from the spatial twist (twistor) generated by SEQ spin. As noted in Chapter 1’s foundational postulates, the twist induced by SEQ spin is decoupled from spatial elasticity. Thus, magnetic twist propagation relies on the electric field’s propagation and cannot be mediated by sub-Planckian elastic components.

14.2. Closed Magnetic Fields of Charged Particles:

In this model, all charged particles possess a dynamic quasi-spherical structure composed of SEQ. The electric field diverges spherically, while the resonance axes of the SEQ within the structure radiate outward from the center. Since the magnetic field is orthogonal to the electric field, the induced magnetic field must form closed spherical surfaces. Macroscopically, this results in a closed magnetic field topology.

14.3. Spin-Generated Magnetic Moment Mechanism:

The twist-induced magnetic moment generated by the structural spin of charged particles and the SEQ spin magnetic moment are distinct concepts at different levels. Further work is needed to analyze the structural spin magnetic moment of charged particles.

14.4. Magnetic Field of Moving Charges:

In an electron’s structure, SEQ are spherically distributed, with their resonance axes radiating from the center. The electron’s motion introduces spatial deformation along its acceleration direction, which reduces the resonance frequency of SEQ. The frequency suppression is most pronounced when the SEQ resonance axis aligns with the acceleration direction (smaller angle), weakening the induced magnetic field.

Due to the electron’s high velocity and acceleration, frequency modulation effects are highly significant. When the SEQ resonance axis is perpendicular to the acceleration direction, the deformation projection is minimized, preserving the magnetic field response. Thus, only SEQ with resonance axes orthogonal to the acceleration direction contribute dominantly to the observed magnetic field, resulting in a toroidal (ring-shaped) field around the motion direction.

14.5. Theoretical Integration:

This electromagnetic physical picture inherits the core ideas of Maxwell’s vortex model while incorporating the SEQ framework. It synthesizes general relativistic effects and the metric-frequency mirror model, providing a microscopic explanation for electromagnetic wave generation and magnetic field formation within this paradigm.

15. Discussion:

15.1. During the expansion of the universe, would the Planck constant have subtle changes?

15.2. Can a discrete differential geometry model, a spacetime nonlinear elastic coefficient function, and QCD simulations model be constructed to be compatible with this framework?

15.3 What would be the real emergent physical picture and interaction topology of electromagnetism ?

15.4 The next stage of this model could employ an algebra system to explore the closed transformations of M energy states on SEQ—encompassing (1) inter-SEQ translation effect (stress modulation), (2) spin, and (3) axial rotation—ultimately embedding this algebraic structure with the Standard Model.

15.5 Quark confinement and asymptotic freedom characterize the nonlinearity and asymmetry of spacetime’s elastic modulus at microscopic QCD scales. This behavior may extend to cosmic scales, potentially linking to variations in dark energy distribution density. QCD as an Intrinsic Property of Elastic Spacetime.

15.6 This framework suggests that the essence of QCD may ultimately reside in the elastic spacetime paradigm. Specifically, the non-perturbative features of quark confinement and asymptotic freedom could emerge from the topological connectivity patterns of adjacent SEQ - implying that studying Planck-scale SEQ adjacency configurations represents a fundamental pathway for deeper understanding of QCD dynamics beyond current effective field theories.

15.7 This framework is restricted to local interactions; non-local quantum entanglement falls outside its current scope.

15.8. The discrete field equations and discrete functionals in this model need to be built on a clear spatial adjacency topology. However, since the configuration of spatial adjacency topology remains undetermined at present, an exact mathematically formalized model cannot be provided. Therefore, the model can only remain at a conceptual stage for now.

16. Summary:

16.1. While this framework currently lacks complete mathematical formalization due to its foundational nature, the proposed quantization of spacetime provides a compelling new paradigm for offering a novel perspective to understand cosmic structure, time evolution, and thermodynamic principles.

This speculative framework requires rigorous validation by professional physicists.

16.2. If a computer model of the universe is developed with this framework, the first and second laws of thermodynamics and Principle of least action would be the main factors to drive the simulation, treating entropy as a dynamical coordinate for spontaneous system evolution’s simulation. The mathematical simplicity of our model reflects a deeper truth: the universe itself operates on fundamental rules that generate complexity through iteration. If the nonlinear and asymmetric elastic modulus between SEQ is modeled, such a computer-based physical simulation could further embed General Relativity and QCD, evolving into a more comprehensive physical simulation framework.

For computational modeling of the SEQ network, three polycrystalline adjacency configurations could be considered as candidate lattice structures:

• Cubic
• Face-Centered Cubic (FCC)
• Hexagonal Close-Packed (HCP)

16.3. The analysis of entropy and action in the text operates at the Planck scale, where observable-level practical computability is unachievable, but this work provides a perspective to understand the concrete mechanisms of entropy and action from the Planck-scale .

16.4. This framework achieves a profound synthesis by embedding the Standard Model within Einstein’s elastic spacetime paradigm, revealing their unified geometric essence: (i) The SU(3) color symmetry corresponds physically to spherical compression modes of the spacetime quantum network, where gluon-mediated interactions preserve perfect 3D isotropy during local space compaction, while the resultant outward stretching generates the characteristic 1/r²gravitational field. (ii) The Higgs field operates as a chiral locking mechanism - its symmetry-breaking role emerges from how it pins compressed spacetime quanta to their deformation states, like a cosmic ratchet preventing elastic recoil. (iii) This framework proposes a hypothetical 3D multi-layered symmetric architecture for leptons: Different lepton generations manifest distinct charge and mass properties due to their varying layered configurations within the SEQ matrix. (iv) Dark matter and energy find natural explanations as topological defect vibrations and the ground-state tension of this crystalline spacetime fabric, respectively - no exotic particles required. Crucially, these phenomena all derive from a single principle: quantum spacetime compressible, defect-laden, yet topologically preserved nature.

16.5. In this framework, quantum superposition arises from the dynamic resonating, multi-layer, multi-axis rotation of a particle’s internal SEQ structure—a high-dimensional phase space of possible configurations prior to measurement. The eigenstates correspond to metastable solutions of this system, determined by its intrinsic parameters: mass distribution (gravitational potential storage), electromagnetic coupling, chiral symmetry constraints (e.g., Higgs locking), and initial conditions. Measurement collapses the rotating structure into one of these allowed states.

Within this framework, all statistical quantities at the Planck time scale can be reduced to analytical determinants, and probabilistic functions are fully reducible to exact analytical formulations—reflecting the intrinsic determinism of SEQ dynamics. In other words, this model is fundamentally a quasi Deterministic Framework operating at the Planck time scale, where all apparent randomness emerges from higher-level interactions of these discrete deterministic units.

As discussed in Section 3.8 and Section 4, although the past and present states are deterministic, the future still retains degrees of freedom under the joint constraints of entropy increase and the least action principle. The Markov property dictates that the future depends solely on the immediately preceding state, implying a non-deterministic evolutionary process. This aligns with the model’s framework where multiple valid paths may satisfy the minimum action condition.

Affirming the Planck time as the minimal temporal unit is equivalent to accepting the determined state of this current moment at this scale, whereas insisting on probabilistic behavior beneath the Planck time inherently negates its status as the fundamental limit of temporal divisibility.

16.6. This work originates from a profound reflection on the nature of time. With no theory of time, definitions of physical processes would be fundamentally ambiguous.16.7. If the human observation is regarded as a physical interaction, then indeed it can lead to a change in quantum states. However, human observation is not fundamentally different from other physical interactions such as electromagnetic or other types of forces. We are, in the grand scheme of the universe, merely a small and fleeting process. Humility, therefore, should be our fundamental attitude towards the cosmos and our place within it.

17. Statement:

While this framework provides a physical picture of discrete spacetime (SEQ network) and its interaction with QCD/Higgs fields, it currently does not include a fully formalized discrete generalization of Einstein’s field equations. This is because constructing such a mathematical structure—while feasible—would require deep expertise in discrete differential geometry and lattice QCD simulations, areas where specialists could likely derive rigorous formulations far more efficiently than the author. The primary focus of this work is to establish the conceptual linkage between spacetime elasticity, SU(3) compression, and emergent gravity, leaving the formal discretization of GR as an open task for collaboration. Researchers with relevant expertise are warmly invited to develop this aspect further.

The interpretation of mass-gravity-color interactions in this paper is not my original creation. In fact, Einstein’s elastic spacetime paradigm proposed a century ago had already elucidated this fundamental principle.

The above framework and its speculative explanation can be consistent with most known physical phenomena(can’t explain delayed-choice experiments), give another angle to understand physics process, but it just put forward a different analytical perspective, not a negation of the existing theory.

Some may critique this model appears overly mechanistic, but what we perceive as ‘mechanical’ might be self-organization’s extension of Planck level interaction rules.

The elastic spacetime paradigm, pioneered by Einstein’s geometric intuition (Einstein, 1916)[4] has been profoundly developed by subsequent physicists through both theoretical refinements and experimental verification. The model proposed herein builds upon the elastic spacetime paradigm, reinterpreting its continuum-based foundations through a discrete quantum framework.

As is widely known, Einstein established General Relativity; Planck’s discoveries ignited the discussion and development of quantum theory; and Dirac laid the foundational framework for Quantum Field Theory. Throughout this process, numerous esteemed physicists have developed and refined these frameworks.

Murray Gell-Mann; George Zweig; Harald Fritzsch; Heinrich Leutwyler; David Gross[5]; Frank Wilczek[5]; Hugh Politzer[6] These physicists studying the SU(3) strong interaction not only integrated algebraic structures with complex physical phenomena but also uncovered intricate phenomena such as quark confinement and asymptotic freedom. Their work has significantly advanced the understanding of the fundamental forces governing particle interactions. Anthony Zee[7] actually proposed the physical intuition of spring networks decades ago in his renowned textbook Quantum Field Theory in a Nutshell (2003). Jacobson, Theodore’ study[8] of thermodynamics has provided profound insights into The Einstein Equation . Gerard ‘t Hooft[9] has made groundbreaking advances in quantum gravity, advocating for deterministic, discrete structures underlying quantum mechanics and general relativity. Carlo Rovelli [10]and Lee Smolin[11] have made significant contributions through their development of loop quantum gravity in the realm of quantum gravity. Notably, the ground-state spin postulate of SEQ framework exhibits remarkable consistency with the fundamental assumptions of loop quantum gravity, particularly regarding the discrete quantum structure of spacetime. Rafael Sorkin[12] is renowned for his foundational work on causal set theory, which posits that spacetime is fundamentally discrete and described by a partially ordered set of events. Edward Witten[13] has made transformative contributions to string theory and quantum field theory. Michael Turner[14] is celebrated for his pioneering research in cosmology, especially his work on dark energy and the accelerating universe. Xiao-Gang Wen’s[15] has made pioneering work on topological order and string-net condensation demonstrates. John Wheeler’s[16] visionary concept of quantum foam-a fluctuating discrete spacetime at the Planck scale foundational supports to the framework. Fotini Markopoulou’s[17] Quantum Graphity model describes spacetime as a dynamical quantum network. David Finkelstein,[18] a pioneer in discrete spacetime physics, proposed that time and space emerge from algebraic operations on fundamental quantum units, directly prefiguring modern quantum gravity models. Wayne C. Myrvold’s[19] seminal work to the philosophical foundations of thermodynamics have significantly deepened our understanding of its role as a fundamental driver of the universe. Recently, I noticed that Perez Felipe Sergio’s[20] might have earlier recognized how the compression of space by massive objects leads to external stretching. Ali H. Chamseddine,Viatcheslav Mukhanov[21] develop a discrete differential geometry framework, where spacetime curvature and connections emerge from elementary Planck-scale cells, bridging discrete and continuous spacetime. Dmitry Chelkak, Alexander Glazman, Stanislav Smirnov [22]developed a discrete version of the stress-energy tensor for lattice models, rigorously connecting it to continuum field theory. A precision measurement of the positron magnetic moment, currently underway by the Fan-Myers-Sukra-Gabrielse collaboration [23], could test two key hypotheses of the SEQ framework: (1) the fixed chirality of SEQ ground-state spin, and (2) the spatially symmetric SEQ structure of charged leptons as proposed herein. Manoelito M. de Souza[24]presents a rigorous theoretical framework for discrete scalar fields in spacetime. The diagrams in this work were created using the free online drawing tool provided by JGraph [25]

I recently discovered through search engines that Gudrun Kalmbach H.E. (2021) [26] and C. G. Sim (2021)[27] reported the relationship between gravity and color charge interactions in their respective papers before me, although our theoretical frameworks differ fundamentally. This work builds upon Wolfram’s foundational insight[28] that simple computational rules can give rise to complex emergent behavior. Usha Raut had pointed out the connection between QCD and gravity in the paper[30] in 2023. Recently, I found that the idea of mass as a compressed state of space was previously explored by Ethan Richards[31], who presented this concept earlier than my own contribution. The latest experiment by Holger F. Hofmann’s team has verified that photons physically exist in multiple wave paths during the double-slit experiment[32], I believe this experiment is of great significance, as it verifies the simultaneous existence of multiple equivalent paths of least action. Maxwell’s vortex model provided significant inspiration for the electromagnetic field physical picture under the SEQ framework in Chapter 14 [33] .David Cornberg emphasized early on in his work that matter is a form of space and provided many insightful perspectives on the nature of space[34]. John Duffield has shared many critical opinions and historical insights on physics on his blog, especially regarding the understanding of time and the structure of space, offering original and thought-provoking perspectives[35]. Louis de Broglie [36]was the first to systematically propose the concept of matter waves, which inspired numerous subsequent studies on the nature of matter and its motion, including my own research. In The Universe in a Helium Droplet [37], Volovik regards the vacuum as a continuous topological quantum liquid, unifying particles, gauge fields, and gravity through the order parameter field and its topological defects in momentum space. Miguel O. Katanaev and Igor V. Volovich modeled the universe as an elastic medium and incorporated dislocation mechanisms, providing a reformulation of Einstein–Cartan theory within a three-dimensional framework using elasticity theory[38]. The term “Elastic Quantized Space” was used by Leonov Vladimir (1996) in his work[39], a fact that came to our attention through systematic keyword-based literature searches, while our conceptual and theoretical framework is distinct. I have benefited greatly from the extensive summary of analogue gravity models presented by Barceló, Liberati, and Visser [40], which helped clarify the landscape of related approaches.

Similar ideas may exist in earlier literature. I strive to properly cite the relevant prior work as I know them through ongoing research.

Appendix A.1 Speculative Diagram of Proton’s Internal Structure with Quarks and Gluons.

Diagram.2:Speculative Diagram of Proton’s Internal Structure with Quarks and Gluons. Online Draw tool [25]

Appendix A.2. Degrees of Freedom in the Future and The essence of life in This Model:

The essence of life: Life is a spontaneously evolved cumulative entropy maximization path-planning system within a thermodynamic context.

Organisms record historically efficient multi-step high-entropy-output pathways through genetic and experiential mechanisms, encoding them into functional modules that are storable, composable, and extrapolatable. By performing fractal recognition and pattern matching on the topological structure of spatial energy distribution, these templates are selectively and batch-invoked to maximize cumulative entropy production across extended time scales. The more advanced the organism, the stronger its capacity for long-term sequential planning, the more refined its fractal identification of energy landscape topology, and the higher its efficiency in recording and encoding historical high-entropy-output pathways. Intelligent beings such as humans do not rely solely on passive genetic memory to store modularized pathways; instead, they extend this capability externally—through written records, evolving into electronic media storage, and further materializing these high-entropy-output pathways into tools and engineered devices that embody and automate their operation.

In section 13.10, we mentioned that from the perspective of this model, the probabilistic randomness in the Schrödinger equation arises because there is more than one maximum entropy path available at the next moment.

Within this model, although equivalent maximum entropy paths may exist for the next moment, different choices among these equivalent paths lead to divergent evolutionary trajectories over extended time sequences. This divergence constitutes the essence of biological path selection. While immediate next-step choices may be thermodynamically equivalent, their long-term consequences differ significantly in terms of cumulative entropy production. Thus, biological decision-making is fundamentally a forward-looking process. Genetic memory and experiential memory equip organisms with the capacity to anticipate future path developments, going beyond mere Markovian decisions based solely on the present state.

For example, for an organism, placing wood either to the left by the river or to the right beside a fire might represent equally probable maximum entropy transitions in the immediate next step. However, their subsequent entropy production over time will differ substantially. Therefore, the organism performs a prospective evaluation—selecting, among several equivalent maximum entropy paths at each instant, the one that leads to the greatest cumulative entropy increase over multiple future steps. This evaluation relies on genetic and experiential memory, which essentially encode previously successful cumulative high-entropy-production pathways and extrapolate them into the future.

Even in the choice of whether or not to freeze food in a cold storage facility, the act of refrigeration—though seemingly entropy-reducing—can be understood from a broader thermodynamic perspective. When considering the local system as a whole, including both the refrigerator and its external environment, the thermodynamic evolution at the next moment may follow an equivalent maximum entropy production path compared to leaving the food unrefrigerated and allowing it to decay naturally. In other words, the instantaneous rate of entropy production may not differ significantly between the two choices. The refrigeration process itself consumes energy and releases waste heat, and the total entropy generated during this process is sufficient to ensure that the global entropy increase is no less than—and possibly even exceeds—that of natural decomposition. Thus, the maximum entropy paths at the immediate next moment are effectively equivalent.

However, the crucial difference emerges over multi-step temporal evolution and the resulting trajectory of cumulative entropy production. Although the two choices exhibit thermodynamic equivalence at the initial moment, the decision to refrigerate opens up a distinct future path topology. By delaying the inefficient breakdown of organic matter, refrigeration preserves food resources with high chemical potential energy, thereby enabling individuals or societies to sustain metabolic activity over longer timescales, engage in complex labor, operate advanced technologies, and drive organizational expansion. These subsequent activities—whether agricultural reproduction, industrial manufacturing, transportation, or information processing—are all high-entropy-producing processes.

This once again confirms a central insight: the decisions made by living organisms, and especially intelligent civilizations, are not based merely on Markovian choices that maximize instantaneous entropy production at each moment. Rather, they are guided by a forward-looking path evaluation mechanism that integrates historical experience and future modeling. What intelligent beings optimize is not just the immediate step, but the long-term cumulative entropy production, operating within the constraint of selecting among maximum entropy paths available at each successive moment.

Genetic and especially experiential memory are most effectively formalized through mathematical structures—that is, encoding experience via mathematical representations to ensure precise storage and retrieval.

Feature	Advantages of Mathematical Formalization
Compression	Abstracts vast amounts of concrete experience into concise rules (e.g., “fire heats objects”)
Generalization	Applicable to novel situations (e.g., inferring combustibility of new materials)
Composability and Extensibility	Multiple rules can be combined to simulate complex behaviors (heat → steam → motion → tools)
Transmissibility	Easily shared across individuals (via language, symbols, education)
Predictability	Enables forward simulation: logical chains such as “if A, then B”

The essence of science and technology in intelligent life is the encoding of past experiences that successfully opened cumulative high-speed entropy-increasing pathways into tools, machines, and code—transforming them into pre-established routes that do not need to be rediscovered. These modular structures enable intelligent agents to transcend the Markov limitation of making decisions based only on the current state for the next immediate step. Instead, they allow pursuit of maximal cumulative entropy production over multiple time steps—not resisting entropy increase, but actively guiding and amplifying it.

In the framework of SEQ network dynamics, technological behavior in intelligent organisms can be viewed as an optimized control process for maximizing cumulative entropy production. Given the current spatial energy distribution {Eᵢ(t)}, the system does not simply select the path that maximizes instantaneous entropy rate Ṡ(t) in the next moment. Rather, drawing upon genetic and experiential memory, it activates a set of pre-encoded multi-step entropy-increasing path templates Γₖ = {ΔSₖ⁽¹⁾, ΔSₖ⁽²⁾, ..., ΔSₖ⁽ⁿ⁾}, and physically implements them through tools, devices, or algorithms.

These templates, once encapsulated programmatically and combined modularly, form stable high-entropy-production channels, significantly enhancing long-term efficiency of entropy flow. This establishes life as an active participant in cosmic evolution. From this perspective, living systems can be understood as units optimized for discovering and following paths of maximal cumulative entropy increase.

Human civilization as a whole can thus be seen as a large-scale network dedicated to discovering, optimizing, and solidifying such maximal cumulative entropy-increasing pathways:

• Power systems → enabling long chains from fossil fuels to electricity, mechanical work, and information processing;
• The Internet → accelerating knowledge diffusion, improving societal responsiveness and adaptive efficiency;
• Space exploration → probing new energy sources and novel topological configurations of space;

All of these continuously expand the available pathways for generating greater entropy, representing a collective, intentional alignment with the universe’s fundamental tendency toward increasing disorder—not by opposing it, but by channeling it more effectively.

From fossil energy to nuclear energy utilization, representing an upgrade in the freedom of energy levels; from power grids to the internet; from small electronic components such as resistors and capacitors to large-scale integrated circuits; from personal computers to artificial intelligence; from steam engines to electrical automation systems; and from geographical exploration on Earth to venturing into outer space—these developments continuously expand new pathways for achieving greater cumulative entropy production. The essence of realizing all this lies in recording, classifying, summarizing, and extrapolating previously successful cumulative entropy-increasing paths, transforming them into modularized and hardware-embodied forms, thereby enabling more efficient reproduction of past high-entropy-production pathways and facilitating the discovery of novel patterns that maximize cumulative entropy production in subsequent path selections

The specific optimization of cumulative entropy production pathways is as follows:

1.Record previous cumulative entropy-increasing pathways, and systematically summarize, structure, and mathematically formalize them. This process transforms historically successful energy-dissipation sequences into reusable and analyzable models.

2.Expand the degrees of freedom in energy levels—for instance, by harnessing nuclear energy—thereby accessing higher-density energy sources that enable a qualitative leap in entropy production rates.

3.Use tools or engineered systems to modularize and encapsulate these optimized entropy-increasing pathways. Devices such as power grids, automation systems, and integrated circuits serve as physical embodiment of high-efficiency dissipation routes.

4.Store the optimized pathways in durable media—such as books, digital databases, or electronic storage—to preserve collective knowledge across time and facilitate transmission between generations or networks.

5.Discover new entropy-maximizing pathways through reasoning or computational methods, including deduction, induction, and exhaustive trial-and-error exploration. Artificial intelligence and simulation tools significantly enhance this discovery process by enabling predictive modeling before physical implementation.

6.Continuously improve the identification of the topological fractal structure of environmental conditions, thereby enhancing the adaptability and efficiency of pre-optimized entropy-increasing modules when deployed in varying contexts.

7.After completing one full cycle from step 1 to step 6, the newly refined pathway Γₖ₊₁ is written back into the memory repository. Subsequent iterations can then proceed via minor adjustments to existing templates, leading to progressively higher overall entropy production efficiency. If a breakthrough in energy-level degrees of freedom occurs, the cumulative entropy production efficiency may increase exponentially.

In this framework, civilization can be understood as an automaton driven by the principle of cumulative entropy maximization, while the SEQ framework provides an operational language spanning from the Planck scale to engineering scales.