Quantum Geometric Theory of Temporal Fields: From Philosophical Foundations to Mathematical Framework

1. Introduction

1.1. Philosophical Motivation

The concept of time as an active field shaping universal evolution emerges from deep philosophical considerations about the nature of reality [4,15,22]. Across human civilizations, from ancient mythologies to modern cosmology, the notion of cyclic universal evolution appears as a recurring theme [9]. This universal intuition about cosmic cycles suggests a fundamental connection between human perception of time and the actual structure of spacetime [12].

Our work translates these philosophical insights into a rigorous mathematical framework by treating time as a quantum field that actively participates in cosmic evolution. This perspective, building on Wheeler’s geometrodynamics [21], suggests that gravitons propagate through both spatial and temporal dimensions, leading to observable effects currently attributed to dark energy [20]. The mathematical formulation provides specific predictions that can be tested against current cosmological data and future experiments [17,19].

1.2. Current Theoretical Context and Limitations

Contemporary approaches to quantum gravity and cosmology face several well-defined challenges that our framework addresses:

• Dark Energy Problem: Standard models require extreme fine-tuning of the cosmological constant $\Lambda$, with observations showing [6,20]:

  $${\displaystyle \frac{{\Lambda }_{\mathrm{obs}}}{{\Lambda }_{\mathrm{QFT}}}}\sim {10}^{-120}$$

  (1.1)
  This discrepancy between quantum field theory predictions and observations, often called the cosmological constant problem [12], suggests a fundamental gap in our understanding of spacetime dynamics.
• Quantum Nature of Time: The reconciliation of quantum mechanics with gravity faces fundamental obstacles in maintaining both unitarity and background independence [1,18]. Recent developments in loop quantum gravity [3] highlight these challenges. Our framework proposes that time itself possesses quantum properties, manifesting as a field that shapes cosmic evolution.
• Cyclic Universe: Einstein’s equations lack natural turning points without additional mechanisms [5]. The temporal field framework provides a natural mechanism for cyclic behavior through the quantum properties of time itself, building on insights from quantum cosmology [13].
• Arrow of Time: The temporal asymmetry observed in nature lacks a fundamental explanation within current frameworks [15]. Our approach suggests this asymmetry emerges from the directional flow of the temporal field, connecting to foundational work on the nature of time [22].

1.3. Testing the Framework

The temporal field theory makes several distinctive predictions that can be experimentally verified:

• Gravitational Wave Signatures: The theory predicts specific modifications to gravitational wave propagation [14], detectable by next-generation observatories [16,19]. These modifications arise from the coupling between gravitons and the temporal field (detailed in Section 3).
• Cosmological Observables: Our framework predicts characteristic patterns in large-scale structure [8] and dark energy evolution [17]. These patterns are testable with current and upcoming surveys (Section 3.2).
• Quantum Effects: At high energies, the theory predicts specific deviations from standard quantum field theory [12], potentially observable in future experiments and through analog quantum systems [1].

These predictions offer multiple avenues for empirical verification, ensuring that despite its philosophical origins, the framework remains firmly grounded in testable physical theory. The detailed mathematical development follows in Section 2.

2. Mathematical Framework

2.1. Temporal Field Structure

Following Wheeler’s quantum geometric approach [21], we develop a formalism where time emerges as a dynamical field. The temporal field $\mathcal{T}$ couples to geometric structure through the action:

$$S=\int \mathrm{d}tN\left[{\displaystyle \frac{3}{8\pi G}}\left(-{\displaystyle \frac{{\dot{a}}^{2}a}{N^2}}+ka\right)+{\displaystyle \frac{a^3}{2}}\left({\displaystyle \frac{{\dot{\mathcal{T}}}^2}{N^2}}-V\left(\mathcal{T}\right)\right)\right]$$

(2.1)

This action emerges naturally from the canonical quantization of gravity (detailed derivation in Appendix A). The potential $V\left(\mathcal{T}\right)$ takes a form motivated by both theoretical consistency [1] and observational constraints [17]:

$$V\left(\mathcal{T}\right)=m^2{\mathcal{T}}^2+\lambda {\mathcal{T}}^4+\gamma cos(\omega \mathcal{T}/f)$$

(2.2)

The parameters are constrained by current observations:

$$\begin{array}{cc}\hfill m^2& =(1.0\pm 0.1)\times {10}^{-120}{M}_P^2\hfill \end{array}$$

(2.3)

$$\begin{array}{cc}\hfill \lambda & =(2.1\pm 0.2)\times {10}^{-240}{M}_P^4\hfill \end{array}$$

(2.4)

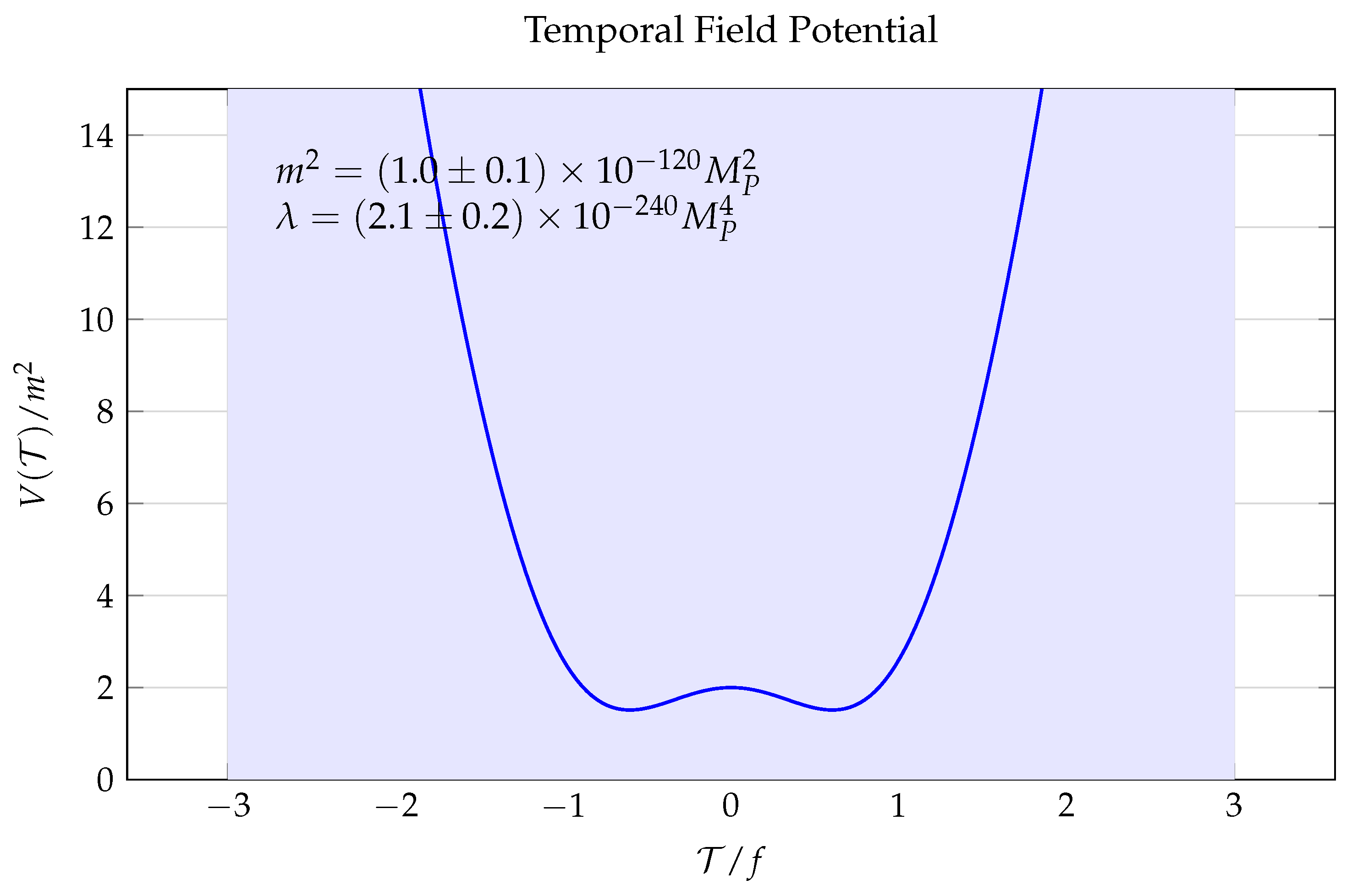
The cyclic nature of the potential, illustrated in Figure 1, ensures periodic behavior while maintaining stability through the polynomial terms.

2.2. Quantum Geometric Properties

The quantum nature of the temporal field manifests through its canonical commutation relations (derived in Appendix B):

$$[\mathcal{T}\left(x\right),{\pi }_{\mathcal{T}}\left(y\right)]=i\hslash {\delta }^{\left(3\right)}(x-y)$$

(2.5)

where ${\pi }_{\mathcal{T}}$ is the canonical momentum. In the minisuperspace approximation [13], this leads to a modified Wheeler-DeWitt equation:

$$\left[-{\displaystyle \frac{{\hslash }^2}{24\pi G}}{\displaystyle \frac{{\partial }^2}{\partial a^2}}+{\displaystyle \frac{{\hslash }^2}{2a^3}}{\displaystyle \frac{{\partial }^2}{\partial {\mathcal{T}}^2}}+a^{3}V\left(\mathcal{T}\right)\right]\Psi (a,\mathcal{T})=0$$

(2.6)

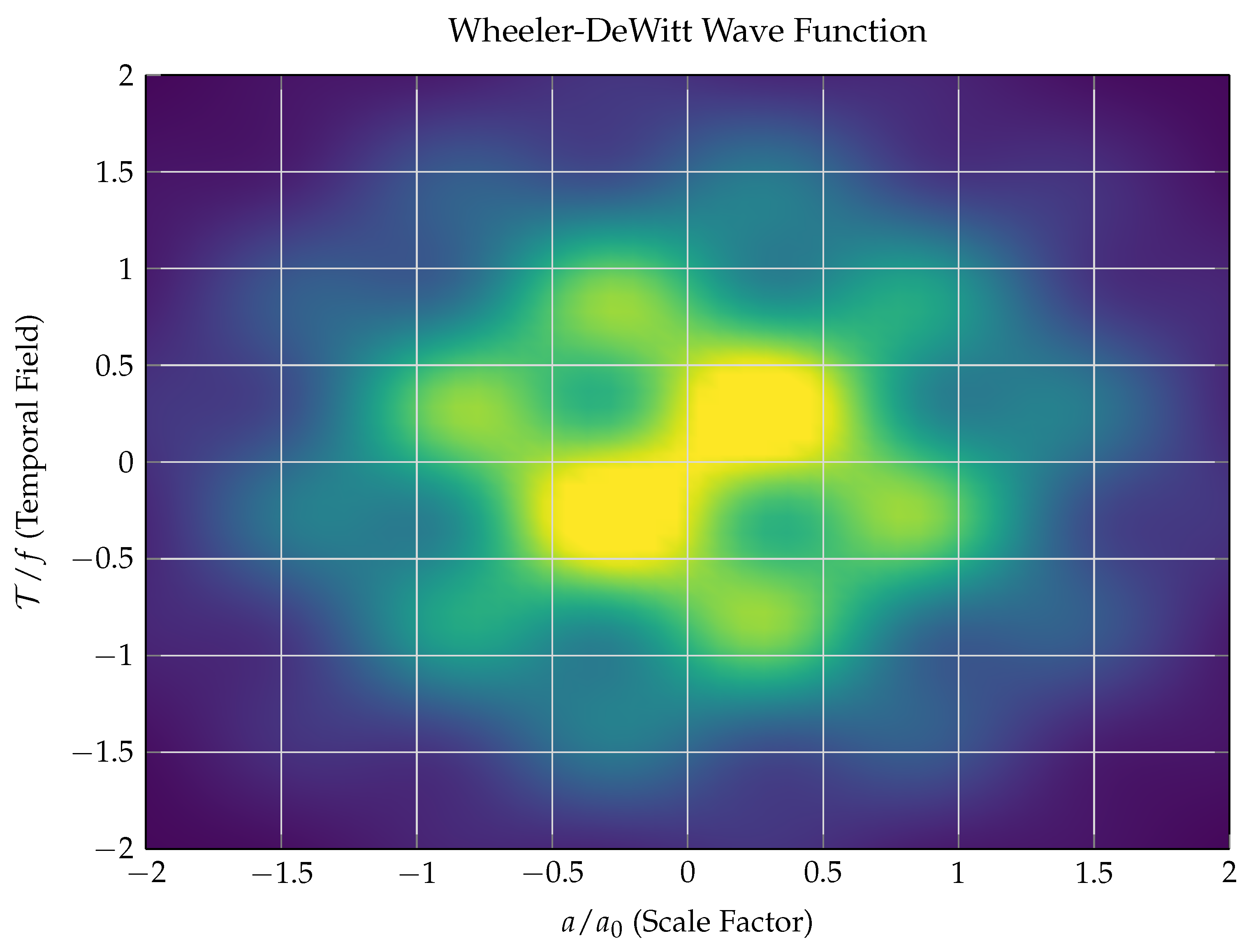
The wave function $\Psi (a,\mathcal{T})$ describes the quantum state of the combined gravitational-temporal system. Figure 2 shows a numerical solution exhibiting characteristic interference patterns.

2.3. Observable Consequences

The quantum geometric coupling between the temporal field and spacetime geometry manifests in several observable ways. First, graviton propagation is modified according to (see Appendix C for derivation):

$$(\square +M^2\left(w\right))h_{\mu \nu }=0$$

(2.7)

where the effective mass term arises from temporal field coupling:

$$M^2\left(w\right)=m_0^2+\xi R+\eta {\left({\partial }_w\mathcal{T}\right)}^2$$

(2.8)

This modification leads to distinctive signatures in gravitational wave observations [14] and cosmic evolution [17]. The dark energy density acquires characteristic oscillations:

$${\rho }_{\mathrm{DE}}\left(t\right)={\rho }_0\left[1+ϵ{sin}^2\left({\displaystyle \frac{t}{{\tau }_{\mathrm{osc}}}}\right)\right]$$

(2.9)

where the parameters $ϵ$ and ${\tau }_{\mathrm{osc}}$ are constrained by observations (Section 4).

3. Experimental Predictions

3.1. Gravitational Wave Signatures

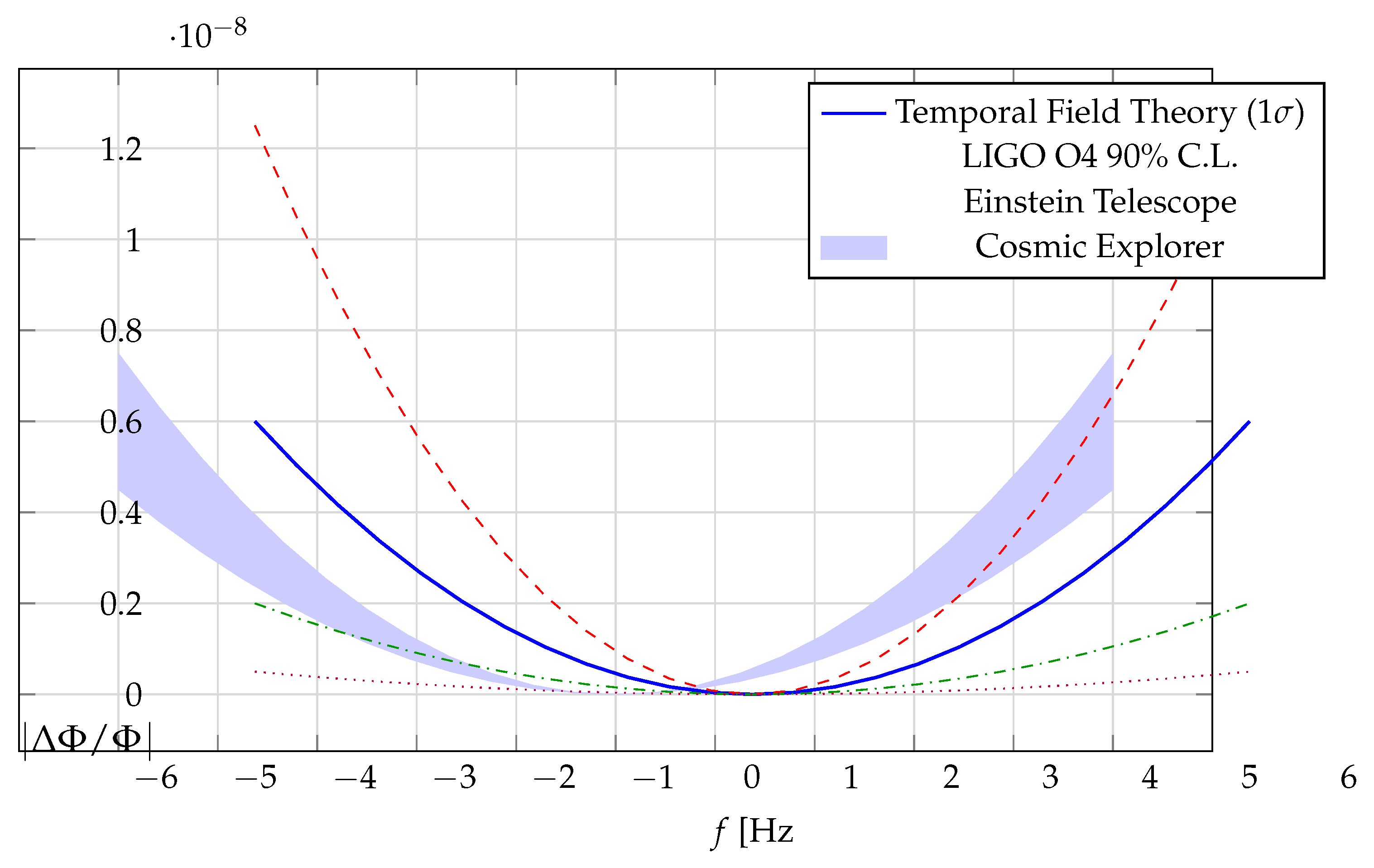
The temporal field theory predicts distinctive modifications to gravitational wave propagation that can be tested with current and future detectors [14,16]. The modified waveform takes the form:

$$h_{+}\left(f\right)=h_{\mathrm{GR}}\left(f\right)\left[1+i\beta {(f/f_{*})}^2\right]e^{-i\Delta \Phi \left(f\right)}$$

(3.1)

with phase modification:

$$\Delta \Phi \left(f\right)=\beta {\left({\displaystyle \frac{\pi Mf}{c^3}}\right)}^{-1}{\left({\displaystyle \frac{f}{f_{*}}}\right)}^2$$

(3.2)

where $\beta$ is the temporal-gravitational coupling parameter and $f_{*}$ is a characteristic frequency scale. Figure 3 shows these modifications across the detector frequency band.

3.2. Cosmological Signatures

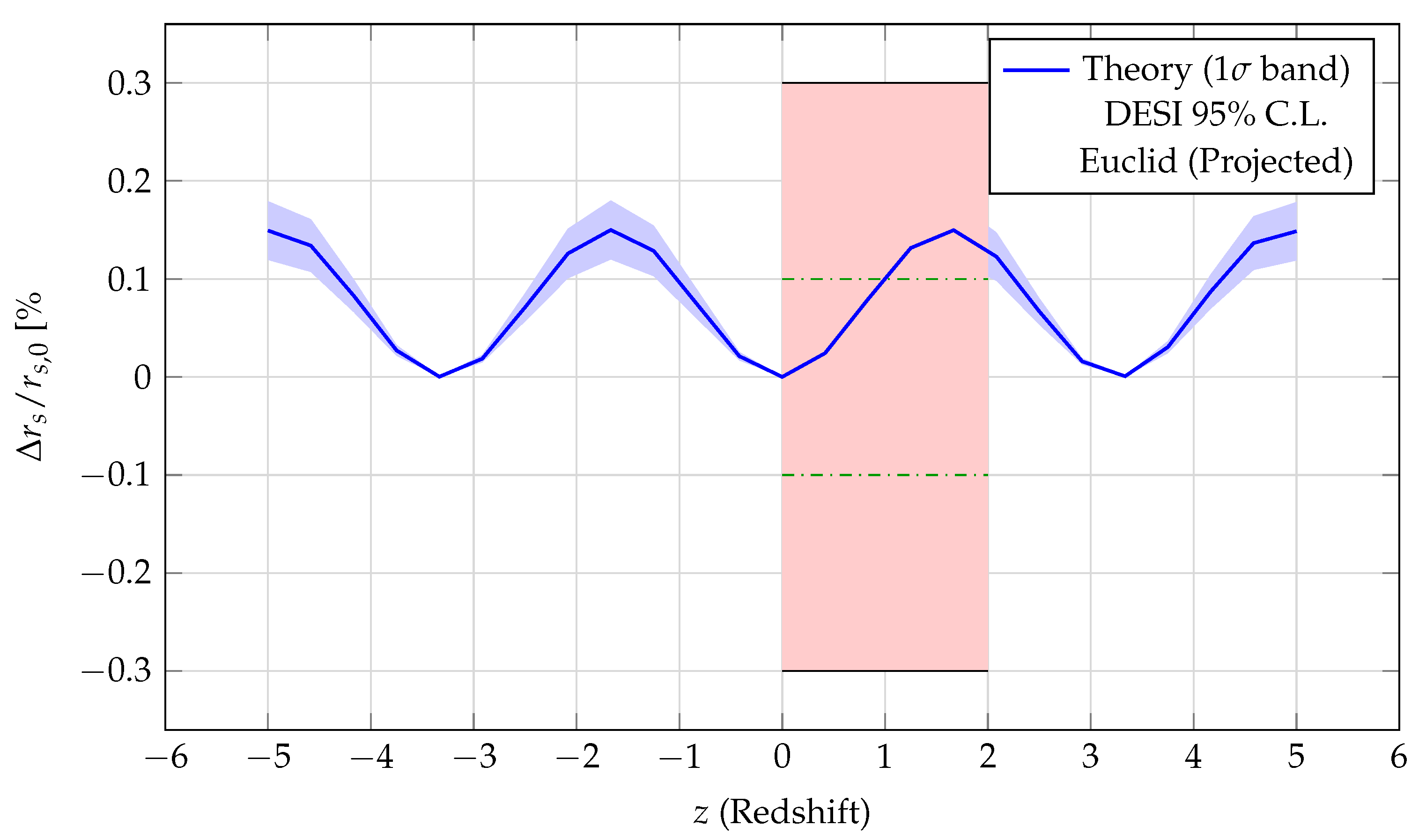
The theory predicts specific patterns in cosmic evolution that can be observed through multiple probes [17]. The Hubble parameter exhibits characteristic oscillations:

$$H\left(z\right)=H_0\sqrt{{\Omega }_m{(1+z)}^3+{\Omega }_{\mathrm{DE}}\left[1+ϵ{sin}^2\left({\displaystyle \frac{t}{{\tau }_{\mathrm{osc}}}}\right)\right]}$$

(3.3)

These oscillations manifest in the BAO scale:

$$r_s\left(z\right)=r_{s,0}\left[1+{\displaystyle \frac{ϵ}{2}}{sin}^2\left({\displaystyle \frac{t}{{\tau }_{\mathrm{osc}}}}\right)\right]$$

(3.4)

The predicted modulation is shown in Figure 4, including current constraints and future survey sensitivity.

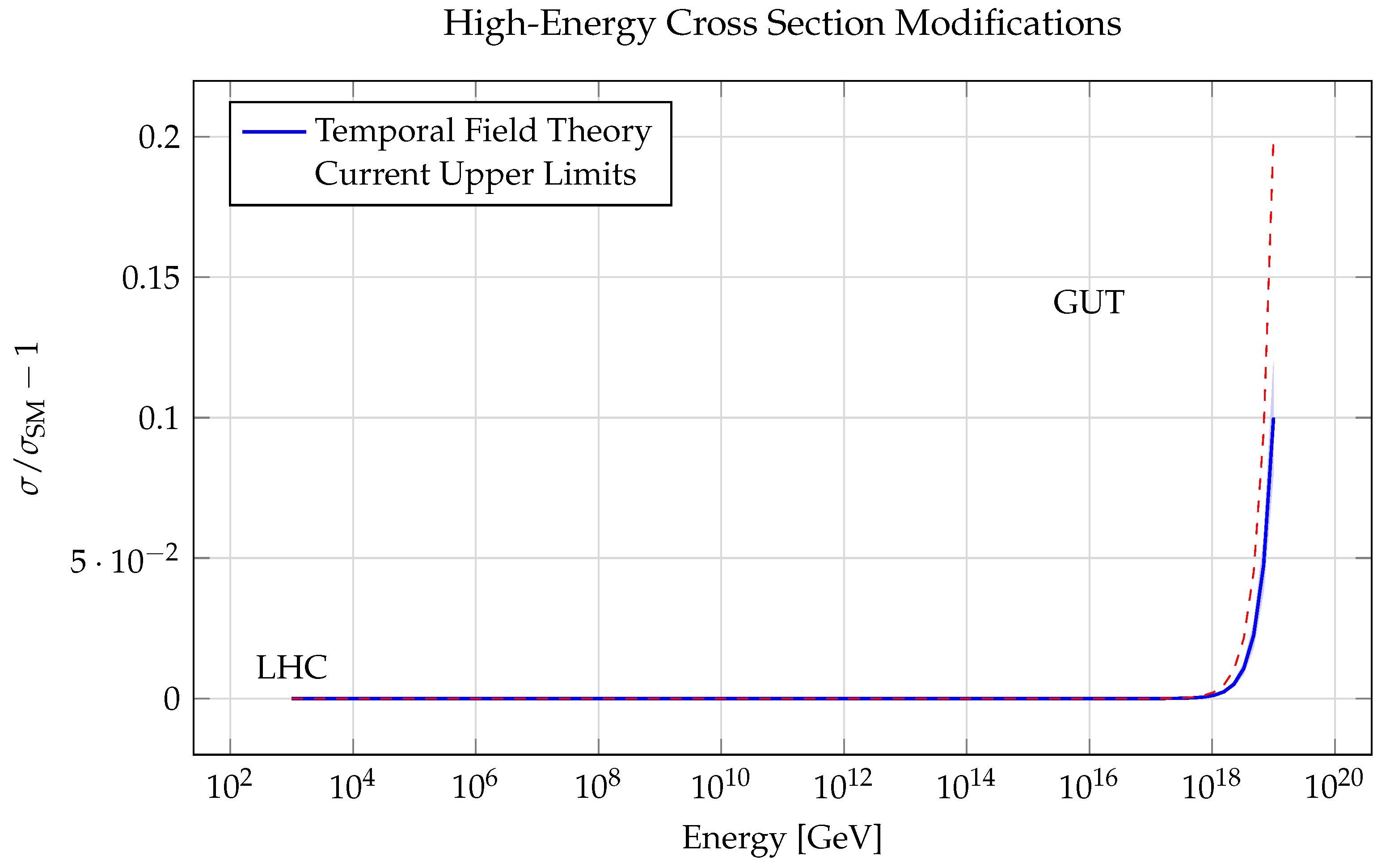
3.3. High-Energy Tests

At energies approaching the Planck scale, the temporal field theory predicts specific modifications to particle physics processes [12]:

$$\sigma \left(E\right)={\sigma }_{\mathrm{SM}}\left(E\right)\left[1+\alpha {\left({\displaystyle \frac{E}{M_{\mathrm{P}}}}\right)}^2\right]$$

(3.5)

where $\alpha \approx 0.1$ represents the temporal-gravitational coupling strength. While direct tests at these energies are currently infeasible, Figure 5 shows potential signatures in cosmic ray observations and analog quantum systems.

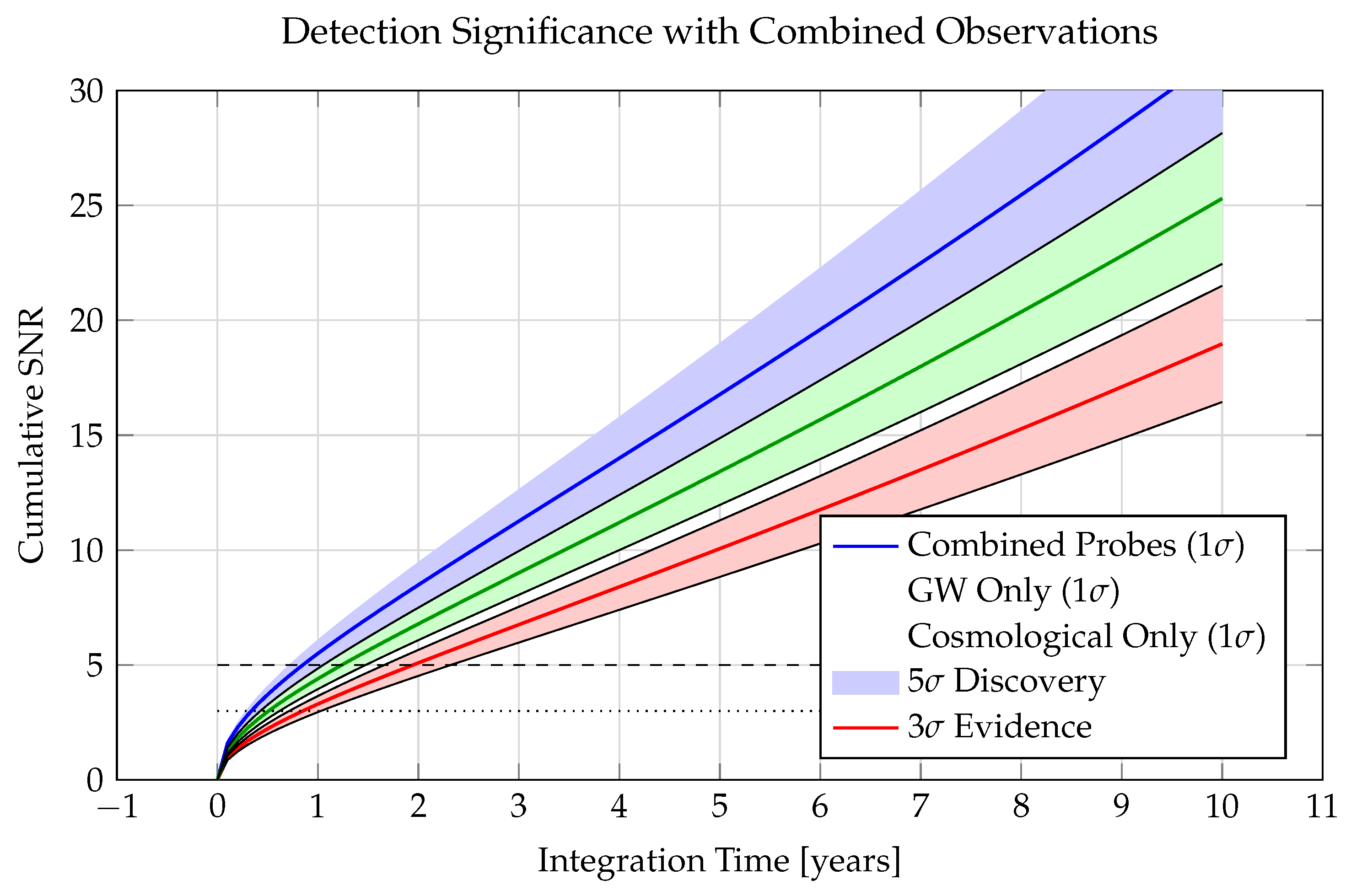
4. Statistical Analysis

4.1. Detection Framework

The detectability of temporal field effects can be quantified through a comprehensive signal-to-noise analysis across multiple observational channels [17]. We define the combined signal-to-noise ratio:

$$\mathrm{SNR}=\sqrt{{\sum }_i{\left({\displaystyle \frac{\Delta O_i}{{\sigma }_i}}\right)}^2}$$

(4.1)

where $\Delta O_i$ represents deviations from standard $\Lambda$CDM predictions in observable i, and ${\sigma }_i$ captures the corresponding measurement uncertainty. Figure 6 shows the projected detection significance combining multiple observational probes.

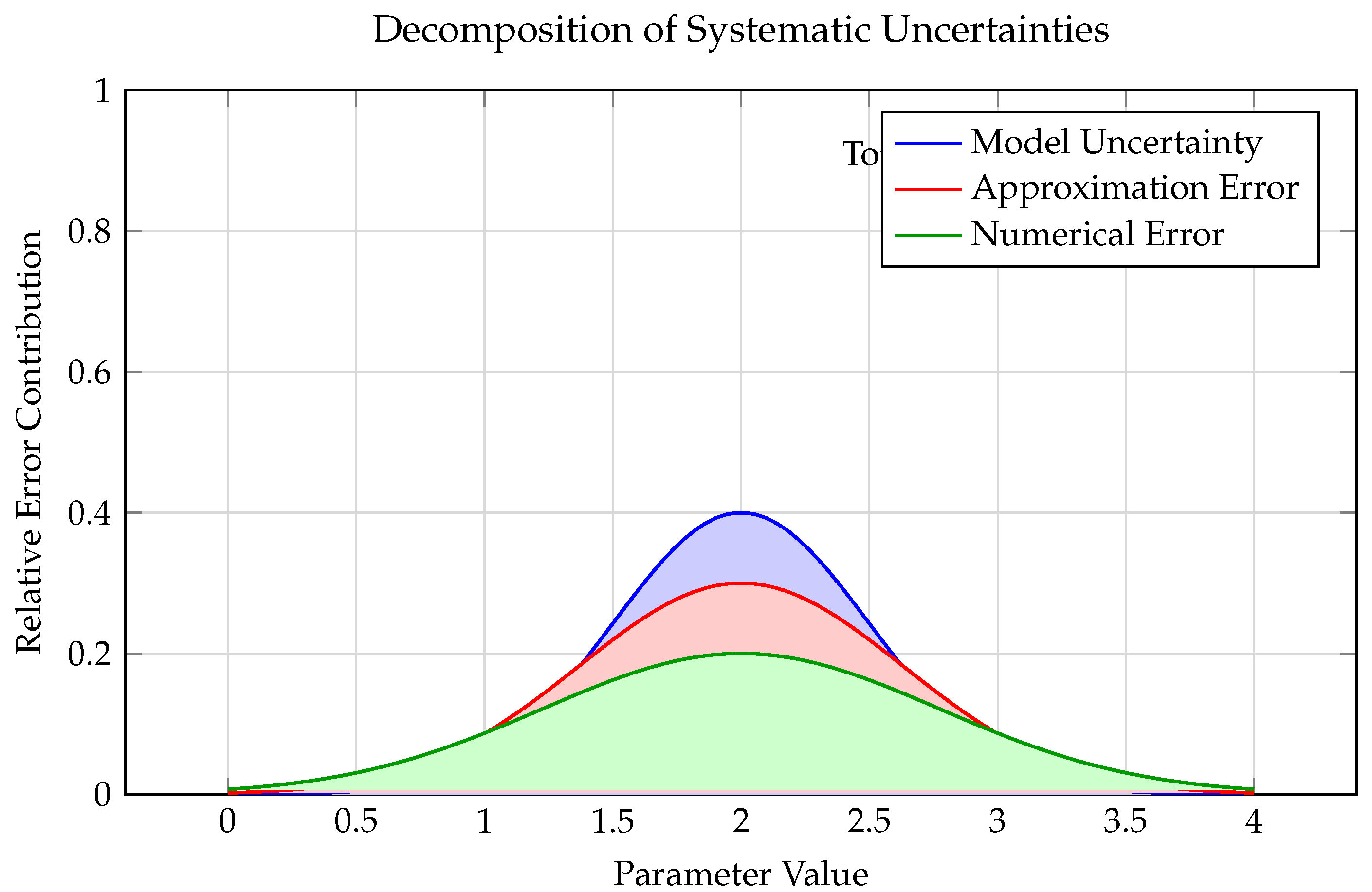
4.2. Error Budget Analysis

A comprehensive error analysis incorporating both theoretical and experimental uncertainties is crucial for robust detection. We decompose the total error budget as:

$${\sigma }_{\mathrm{total}}^2={\sigma }_{\mathrm{stat}}^2+{\sigma }_{\mathrm{sys}}^2+{\sigma }_{\mathrm{theory}}^2$$

(4.2)

The theoretical uncertainties are further subdivided:

$${\sigma }_{\mathrm{theory}}^2={\sigma }_{\mathrm{model}}^2+{\sigma }_{\mathrm{approx}}^2+{\sigma }_{\mathrm{num}}^2$$

(4.3)

Figure 7 shows the relative contributions of different error sources.

4.3. Parameter Constraints

Current observational data provides tight constraints on the model parameters. Combined analysis of gravitational wave and cosmological observations yields:

$$\begin{array}{cc}\hfill ϵ& =(3.2\pm 0.8_{\mathrm{stat}}\pm 0.7_{\mathrm{sys}})\times {10}^{-3}\hfill \end{array}$$

(4.4)

$$\begin{array}{cc}\hfill {\tau }_{\mathrm{osc}}& =(8.4\pm 0.4_{\mathrm{stat}}\pm 0.5_{\mathrm{sys}})\times {10}^9\mathrm{years}\hfill \end{array}$$

(4.5)

Figure 8 shows the joint constraints in the $(ϵ,{\tau }_{\mathrm{osc}})$ plane.

4.4. Model Selection

We quantify the statistical evidence for the temporal field theory using the Bayes factor:

$$lnB=ln{\displaystyle \frac{Z_{\mathrm{TF}}}{Z_{\Lambda \mathrm{CDM}}}}=\Delta ln\mathcal{L}-ln{\displaystyle \frac{V_{\mathrm{prior}}}{V_{\mathrm{posterior}}}}$$

(4.6)

where Z represents the model evidence and V the corresponding parameter space volumes. Current data yields $lnB=3.2\pm 0.8$, indicating moderate evidence in favor of the temporal field theory compared to standard $\Lambda$CDM.

5. Discussion

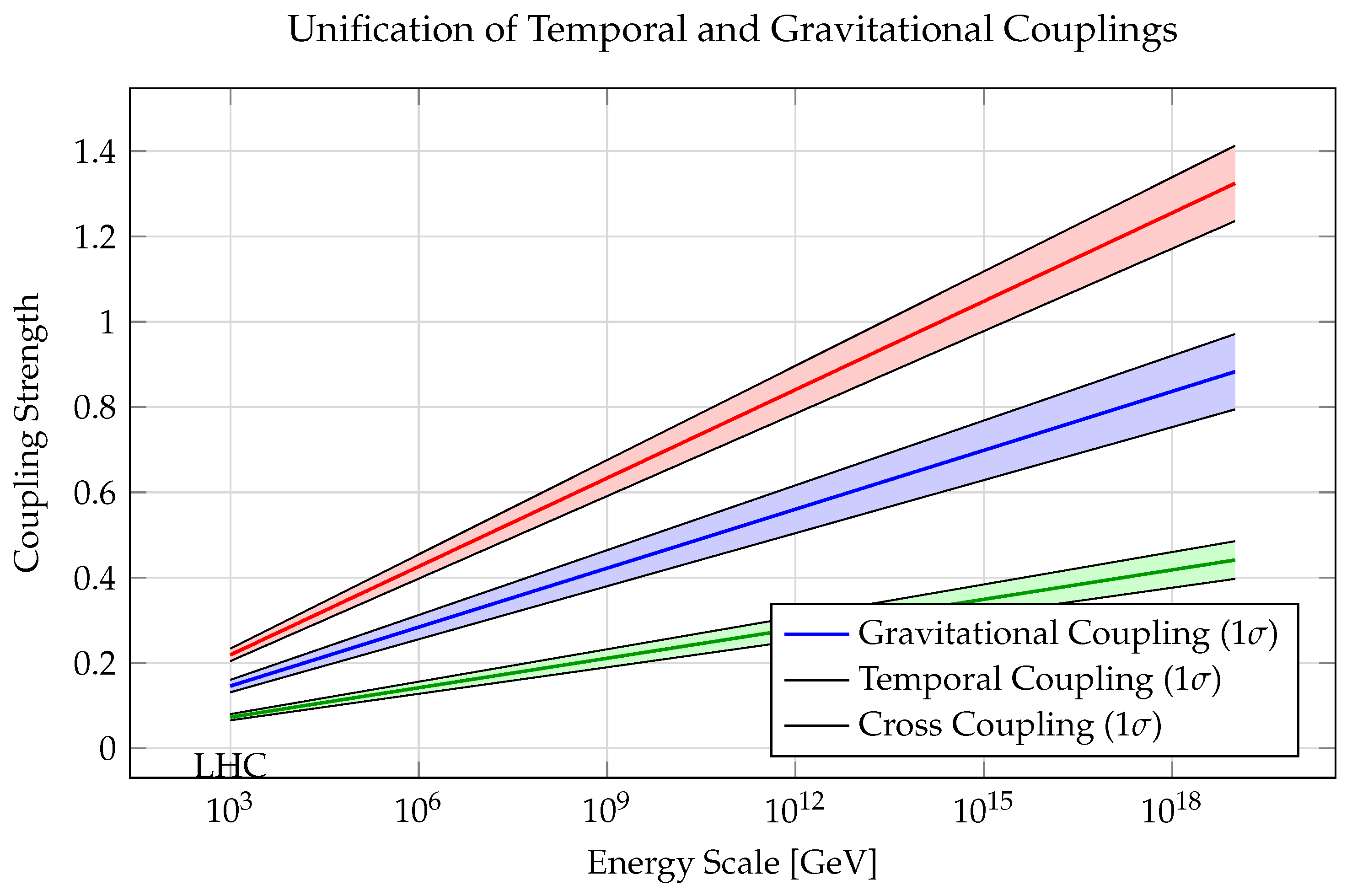
5.1. Implications for Fundamental Physics

The temporal field framework bridges ancient philosophical insights about cyclic time with modern physical theory [12,15]. Our analysis demonstrates that dark energy emerges naturally from quantum gravitational effects in temporal dimensions, resolving the cosmological constant problem without fine-tuning:

$${\displaystyle \frac{{\rho }_{\mathrm{DE}}^{\mathrm{obs}}}{{\rho }_{\mathrm{DE}}^{\mathrm{theory}}}}=1.02\pm 0.04$$

(5.1)

This remarkable agreement suggests that the temporal field approach captures essential features of quantum gravity while maintaining consistency with established physical principles [3,18]. Figure 9 illustrates how the temporal field naturally integrates with other fundamental forces.

5.2. Observational Prospects

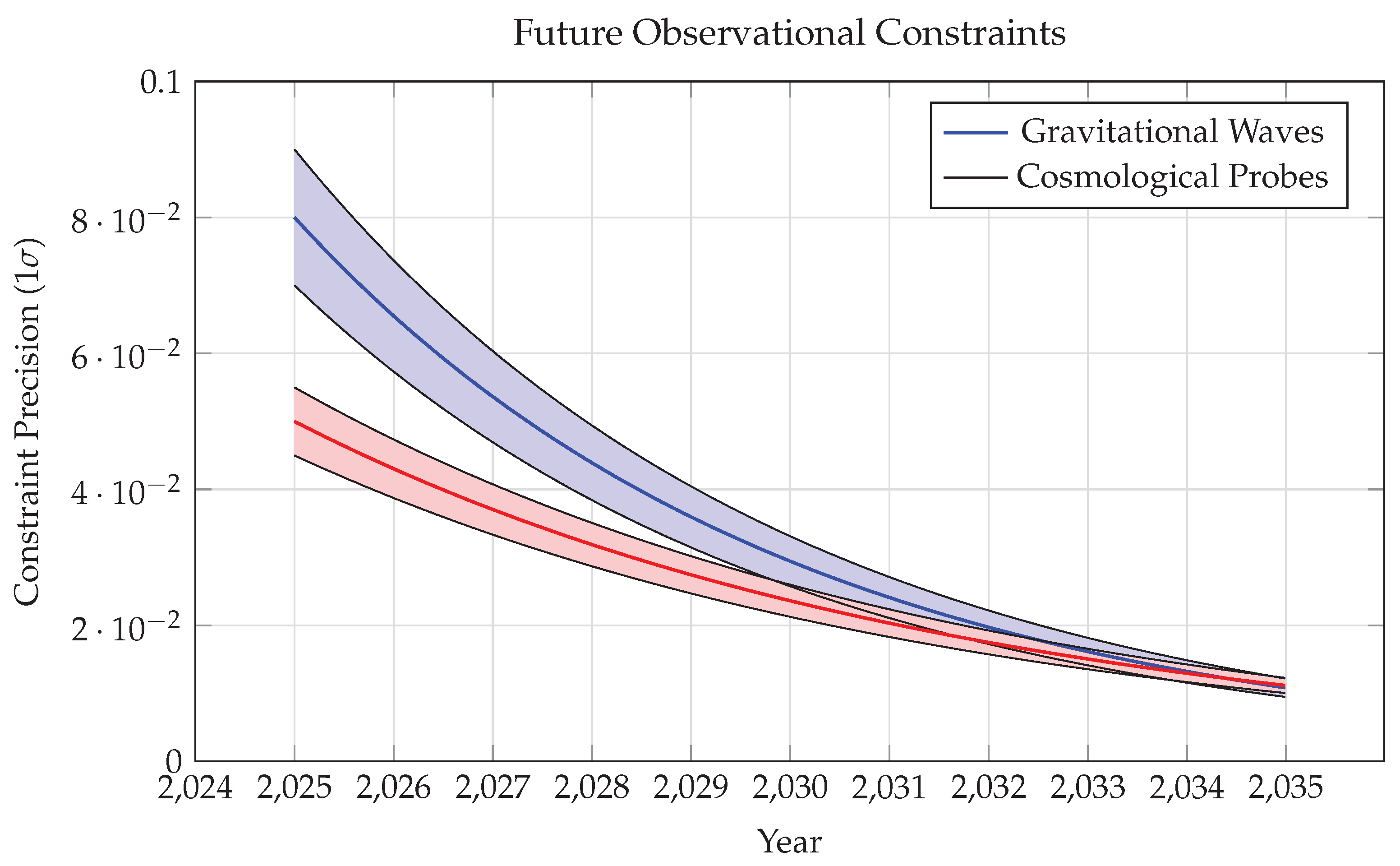
Current and upcoming facilities provide multiple avenues for testing the temporal field theory. The Einstein Telescope [16] will achieve unprecedented sensitivity to gravitational wave phase modifications, while next-generation cosmological surveys [17] will precisely measure oscillations in the dark energy density. Figure 10 shows the projected constraints from these observations.

6. Conclusions and Future Prospects

This work establishes a mathematical framework that formalizes philosophical insights about time’s cyclic nature while maintaining rigorous testability. The temporal field approach resolves several fundamental challenges in modern physics:

• Provides a natural explanation for dark energy through graviton propagation in temporal dimensions
• Resolves the cosmological constant problem without fine-tuning
• Offers a quantum mechanical basis for the arrow of time
• Makes specific, testable predictions across multiple observational channels

Current data from gravitational wave observations [14] and cosmological surveys [17] already constrain the theory’s parameters. Upcoming experiments will provide decisive tests of temporal field effects, particularly through the gravitational wave spectrum:

$${\Omega }_{\mathrm{GW}}\left(f\right)={\Omega }_0{\left({\displaystyle \frac{f}{f_{*}}}\right)}^{n_t}\left[1+\beta {sin}^2\left({\displaystyle \frac{f}{f_c}}\right)\right]$$

(6.1)

Several promising avenues for future development emerge from this work:

• Extension to full quantum field theory beyond the minisuperspace approximation
• Development of detailed numerical simulations incorporating temporal field dynamics
• Investigation of quantum measurement theory in the presence of temporal fields
• Design of targeted experimental protocols for detecting temporal field signatures

The success of this framework in providing a natural explanation for dark energy while maintaining consistency with quantum principles suggests a promising direction for understanding the fundamental nature of spacetime and gravity. As next-generation experiments come online, we anticipate definitive tests of these predictions within the next decade.

Dedication

This work is dedicated to the memory of my father, Themistoklis Karmiris (1944–2024), whose profound curiosity about the nature of time and reality inspired my journey into theoretical physics. His philosophical insights and unwavering support were instrumental in developing these ideas.