Dynamic Universal Time Physics (DUTP): A Frame-Based Scalar Time Framework Beyond Relativity

1. Introduction

Einstein’s relativity models time as a coordinate within spacetime, affected by velocity and gravitational potential. While experimentally successful, it provides no intrinsic explanation for the irreversible flow of time, quantum decoherence, or time reversal suppression. DUTP introduces a new paradigm where time is a continuous scalar field, globally evolving in uniform frames.

2. Universal Time Evolution

We define the evolution of universal time $t_U$ by frame count F:

$${\displaystyle \frac{d{t}_U}{dF}}=\Delta t_{\mathrm{frame}},\Delta t_{\mathrm{frame}}\sim {10}^{-15},\mathrm{s}$$

(1)

This formalizes the uniform progression of time independent of local motion. Time is dynamic by nature of frame evolution, not by object velocity.

3. Local Time and Distortions

Local time is related to universal time via measurable distortions:

$$t_U=t_L-(\Delta G+\Delta V+{\Delta }_{\mathrm{int}}+\Delta P)$$

(2)

• $\Delta G$: distortion from gravitational potential
• $\Delta V$: velocity-induced distortion
• ${\Delta }_{\mathrm{int}}$: internal quantum coherence distortion
• $\Delta P$: photon delay or observer-effect distortion, included only when observation or perception is involved

This relation reinterprets relativistic effects as observational distortions over a constant time background. Notably, $\Delta P$ is conditional—it is applied only in contexts where an observer’s interaction introduces information delay.

4. DUTP Equation in the Context of Dark Energy

Unlike the core DUTP equation, which focuses on regions influenced by gravity where time slows due to distortions, the region associated with the dark energy exhibits the opposite behavior, — time appears to accelerate. In these regions, space expands at an accelerating rate, and this dynamic behavior alters the local experience of time.

Dark Energy Distortion in DUTP

In the standard DUTP framework:

$$t_U=t_L-(\Delta G+\Delta V+\Delta P+{\Delta }_{\mathrm{int}})$$

(3)

where the terms account for distortions due to gravity ($\Delta G$), velocity ($\Delta V$), photon delay ($\Delta P$), and internal decoherence (${\Delta }_{\mathrm{int}}$).

Modified Equation for Dark Energy Regions

In regions dominated by dark energy (such as the large-scale structure of the universe), the effective local time appears to move faster relative to the universal baseline. Thus, the DUTP equation is modified as:

$$t_U=t_L+{\Delta }_{\mathrm{DE}}$$

(4)

where:

• $t_U$ is the universal time field (scalar, continuous, and global).
• $t_L$ is the locally measured time (by a clock embedded in dark-energy-dominated space).
• ${\Delta }_{\mathrm{DE}}$ is the distortion due to accelerated expansion from dark energy.

Physical Interpretation

${\Delta }_{\mathrm{DE}}$ models the accelerated temporal behavior of spacetime expansion:

$${\Delta }_{\mathrm{DE}}\propto H\left(z\right)·D\left(z\right)$$

(5)

where $H\left(z\right)$ is the redshift-dependent Hubble

5. Temporal Duality: Gravity vs. Dark Energy in DUTP

In Dynamic Universal Time Physics (DUTP), time is modeled as a continuous scalar field that flows forward universally and evolves through quantized frames. The flow of time, however, is locally distorted by various physical factors. Among them, gravity and dark energy play the most dominant and counterbalancing roles in shaping temporal behavior at cosmic scales.

1. Gravity as a Contractive Temporal Distortion

Gravity, originating from local mass-energy density, causes a deceleration in the rate of local time relative to universal time. This effect is formally captured by the gravitational time distortion ${\Delta }_G$, leading to:

$t_U$ = $t_L$ - ${\Delta }_G$

• $t_U$ is the universal (undistorted) time,
• $t_L$ is the observed local time,
• ${\Delta }_G$ is the distortion induced by gravitational potential.

Gravitational fields effectively "compress" time, slowing down its rate of flow in high-density regions. This manifests observationally in gravitational redshift, time dilation near massive bodies, and the behavior of clocks in strong gravitational wells.

2. Dark Energy as an Expansive Temporal Distortion

Conversely, dark energy—associated with the universe’s accelerating expansion—produces an expansive effect on the local passage of time. In DUTP, this is modeled as a positive distortion ${\Delta }_{DE}$, modifying the core time equation:

$t_U$ = $t_L$ + ${\Delta }_{DE}$

• ${\Delta }_{DE}$ represents the temporal acceleration effect due to dark energy,
• Regions with dominant dark energy experience faster relative time evolution.

Dark energy is thus interpreted not merely as a geometric expansion of space, but as an acceleration in the temporal frame rate of the universe itself.

3. Temporal Counterforces

Together, gravity and dark energy act as opposing temporal influences:

Gravity → Time slows () Dark Energy → Time accelerates ()

In DUTP, the universe is not balanced spatially but temporally. The observed cosmic evolution arises from the net result of these distortions:

$t_U$ = $t_L$ - (${\Delta }_G$ - ${\Delta }_{DE}$) + other terms

4. Implications for Cosmology

This interpretation aligns with observed phenomena:

• Early universe dominated by matter/gravity ⇒ slow local time.
• Later universe dominated by dark energy ⇒ accelerated local time.
• Transition epochs can be studied as shifts in temporal distortion dominance.

Conclusion

DUTP reframes the expansion and contraction of the universe not as purely geometric, but as consequences of opposing temporal distortions. Gravity and dark energy are thus viewed as temporal counterforces shaping the evolution of cosmic time flow.

6. Time–Energy Reciprocity in DUTP

Dynamic Universal Time Physics (DUTP) posits that time is not merely a background parameter but a dynamic scalar field essential to all physical processes. A central tenet of DUTP is the mutual dependence of time and energy.

Law of Time–Energy Reciprocity

Statement:  Time cannot exist without energy, and energy cannot manifest without time.

• Time is the dynamic substrate through which all change, evolution, and causality occur.
• Energy is the active agent that utilizes time to perform work, propagate fields, and structure matter.
• The evolution of the universe—its expansion, entropy increase, and structure formation—arises from this foundational interaction.

Implications

• A static state (no time flow) implies no energy activity and no evolution—i.e., no physics.
• Conversely, the presence of even minimal energy necessitates time to allow expression.
• This principle also supports the DUTP claim that the universe is fundamentally temporal, not geometric.

“Time gives energy a canvas to act. Energy gives time a reason to flow.”

7. Temporal-Energetic Relational Principle

Axiom (Law of Energetic Time Realization):  Time is not observable as an independent entity, but only through the presence of energy gradients, transitions, or fluctuations. Observable time arises relationally, not absolutely.

7.1. Temporal Visibility through Energy

Let $\tau$ represent the locally observable time evolution, and let $\Delta \mathcal{E}$ denote the local energy fluctuation or transition rate within a frame. We propose the Temporal Visibility Condition (TVC) as:

$${\tau }_{\mathrm{obs}}\propto {\displaystyle \frac{1}{\Delta \mathcal{E}}}$$

(6)

Or in explicit form:

$${\tau }_{\mathrm{obs}}=\kappa ·{\displaystyle \frac{1}{\Delta \mathcal{E}}}$$

(7)

where:

• ${\tau }_{\mathrm{obs}}$ is the measurable time interval or local time evolution resolution,
• $\Delta \mathcal{E}$ is the energy difference or fluctuation across frames,
• $\kappa$ is a proportionality constant (context-dependent, possibly dimensionless or scaled by ℏ in quantum regimes).

7.2. Interpretation

If $\Delta \mathcal{E}\to 0$, then ${\tau }_{\mathrm{obs}}\to \infty$ — a state in which time becomes unmeasurable or effectively absent. This implies that:

Time becomes observable only when energy changes. In the absence of energetic activity, no clocks tick, no processes unfold, and no temporal distinction arises.

This expression supports the idea that time, as we perceive or detect it, is not an ontologically independent quantity, but an emergent relational construct linked to energy variation.

7.3. Connection to Known Physics

This principle aligns with known phenomena:

• In quantum mechanics, time-energy uncertainty:

  $$\Delta E·\Delta t\gtrsim {\displaystyle \frac{\hslash }{2}}$$

  reflects the fundamental tie between observable duration and energy spread.
• In general relativity, time dilation and curvature depend on energy density and stress tensors.
• In cosmology, observable epochs are defined by phase transitions and energy symmetry breaking.

7.4. Philosophical Framing

Time is not an absolute stream in which energy flows; it is the shadow cast by the presence and transformation of energy.

Therefore, any inquiry into whether time "exists" prior to energy is not a question of physics, but of metaphysics. Physics can only describe the manifestation of time in the presence of energy; it cannot speak to the source of energy itself.

8. Generalized Energy Equation in DUTP

In DUTP, energy is not solely a function of mass, but of the frame-based evolution of all forms of physical fields, including ordinary matter, dark matter, and dark energy. We define energy as the manifestation of dynamic temporal flow through quantized frames.

1. Unified Energy Expression

We generalize the total energy per frame as:

$$E_{\mathrm{total}}=E_{\mathrm{matter}}+E_{\mathrm{dark}\mathrm{matter}}+E_{\mathrm{dark}\mathrm{energy}}$$

Where:

• $E_{\mathrm{matter}}=m{c}^2$ — standard mass-energy of ordinary matter.
• $E_{\mathrm{dark}\mathrm{matter}}={\rho }_{\mathrm{DM}}V{c}^2$ — energy from dark matter density.
• $E_{\mathrm{dark}\mathrm{energy}}={\rho }_{\Lambda }V{c}^2$ — vacuum energy from dark energy (cosmological constant).

Here:

• ${\rho }_{\mathrm{DM}}$: dark matter energy density (approximately $2.2\times {10}^{-27}{\mathrm{kg}/\mathrm{m}}^3$)
• ${\rho }_{\Lambda }$: dark energy density (approximately $6.91\times {10}^{-27}{\mathrm{kg}/\mathrm{m}}^3$)
• V: volume under consideration

2. Frame-Based Formulation

Since time in DUTP flows in discrete frames ($\Delta t_{\mathrm{frame}}\approx {10}^{-15}\mathrm{s}$), the energy per frame becomes:

$$E_{\mathrm{frame}}=\left({\rho }_{\mathrm{matter}}+{\rho }_{\mathrm{DM}}+{\rho }_{\Lambda }\right)V{c}^2·\Delta t_{\mathrm{frame}}$$

This makes clear that:

• All forms of matter and energy contribute to the temporal evolution.
• Energy is not just about mass, but about how space is filled with fields across frames.
• Time reversal requires sufficient energy per frame from any of these components.

3. Physical Insight

“Mass bends spacetime in relativity; but in DUTP, all energy—visible or dark—flows forward in time frame by frame. This temporal evolution is the true clock of the cosmos.”

9. Two-Axis Time Model and Integer Time Logic

In DUTP, time has two directional components:

$${\tau }_{\mathrm{eff}}={\tau }_{+}+{\tau }_{-}$$

(8)

• ${\tau }_{+}$: forward-moving time axis
• ${\tau }_{-}$: reverse-moving time axis
• When ${\tau }_{\mathrm{eff}}=0$, time is halted

From this, a discrete integer-based time logic arises:

• $+1$: forward time evolution
• 0: halted time (transition point)
• $-1$: reverse frame transition

This integer logic reflects the frame-based nature of DUTP and imposes quantized conditions on time reversal and causality.

10. Frame Energy and Suppression

The frame energy is derived from the uncertainty principle:

$$E_F={\displaystyle \frac{\hslash }{\Delta t_{\mathrm{frame}}}}\approx {10}^{-18},\mathrm{J}$$

(9)

The suppression of time reversal is modeled by:

$$\mathrm{Suppression}\mathrm{Factor}={\displaystyle \frac{E_{\mathrm{local}}}{2E_F}},P_{\mathrm{reverse}}\propto exp\left(-{\displaystyle \frac{2E_F}{E_{\mathrm{local}}}}\right)$$

(10)

Time reversal is exponentially unlikely unless local energy exceeds the 2-frame threshold.

11. Entanglement Phase Coherence

Entangled particles in DUTP evolve in phase-aligned frames:

$$\langle {\psi }_A{\psi }_B\rangle \sim e^{i({\tau }_A-{\tau }_B)}$$

(11)

Coherence is preserved when ${\tau }_A={\tau }_B$, and decoherence occurs due to energy mismatches. This explains observed quantum entanglement without invoking spacetime curvature.

12. Temporal Frame Conditions in Multi-Particle Entanglement

In the DUTP framework, quantum entanglement is reinterpreted as a result of temporal coherence across discrete frame times ($\tau$). This section extends the standard two-particle entanglement concept to three-, four-, and n-particle systems, using frame alignment and coherence to model correlated behavior.

12.1. Two-Particle Entanglement: Singlet State

The standard singlet state in quantum mechanics is:

$$|{\Psi }^{-}\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(|\uparrow \downarrow \rangle -|\downarrow \uparrow \rangle \right)$$

(12)

In DUTP, this corresponds to two particles evolving through temporally synchronized frames with an internal phase difference of $\pi$:

$$\langle {\psi }_A{\psi }_B\rangle \sim e^{i({\tau }_A-{\tau }_B+\pi )}=-1$$

(13)

This implies perfect anti-correlation when ${\tau }_A={\tau }_B$, as the $\pi$ phase shift ensures that measurement outcomes are always opposite.

12.2. Three-Particle GHZ State: Full Frame Synchronization

The GHZ state is defined as:

$$|GHZ\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|\uparrow \uparrow \uparrow \rangle +|\downarrow \downarrow \downarrow \rangle )$$

(14)

This represents perfect frame synchronization:

$${\tau }_1={\tau }_2={\tau }_3$$

(15)

The total coherence is:

$$\langle {\psi }_1{\psi }_2{\psi }_3\rangle \sim e^{i({\tau }_1-{\tau }_2)}{e}^{i({\tau }_2-{\tau }_3)}=1$$

(16)

This results in fully correlated outcomes: all measurements yield the same spin (either all up or all down).

12.3. Three-Particle W State: Partial Frame Misalignment

The W state is:

$$|W\rangle ={\displaystyle \frac{1}{\sqrt{3}}}\left(\right|\uparrow \downarrow \downarrow \rangle +|\downarrow \uparrow \downarrow \rangle +|\downarrow \downarrow \uparrow \rangle )$$

(17)

This state is modeled in DUTP by introducing slight misalignment in one frame:

$${\tau }_1=\tau ,{\tau }_2=\tau ,{\tau }_3=\tau +\delta$$

(18)

The coherence matrix becomes:

• $C_{12}=1$ (Fully coherent)
• $C_{13}=1-{\displaystyle \frac{\left|\delta \right|}{ϵ}}$
• $C_{23}=1-{\displaystyle \frac{\left|\delta \right|}{ϵ}}$

This leads to a mixture of correlated and uncorrelated outcomes: two particles behave similarly, while one appears different, producing the observed "mixed" result.

12.4. Four-Particle Entanglement and Decoherence Threshold

For four entangled particles, DUTP extends the coherence condition across all six particle pairs:

$$C_{ij}=1-{\displaystyle \frac{|{\tau }_i-{\tau }_j|}{ϵ}}\mathrm{for}\mathrm{all}i<j$$

(19)

The full coherence matrix includes:

$$\left[\begin{array}{cccccccccc}& C_{12}& C_{13}& C_{14}& -& C_{23}& C_{24}& & -& C_{34}\end{array}\right]$$

(20)

When $C_{ij}=1$ for all $i,j$, the system behaves like a four-particle GHZ state:

$$|GH{Z}_4\rangle ={\displaystyle \frac{1}{\sqrt{2}}}\left(\right|\uparrow \uparrow \uparrow \uparrow \rangle +|\downarrow \downarrow \downarrow \downarrow \rangle )$$

(21)

Partial misalignment (e.g., one or more $C_{ij}<1$) introduces decoherence, reducing entanglement quality. Complete misalignment ($C_{ij}=0$ for one or more pairs) destroys entanglement for those pairs, yielding classical correlations.

DUTP thus uses a decoherence threshold $ϵ$ to define the stability of entanglement in multi-particle systems. Coherence degrades when time-frame misalignment $|{\tau }_i-{\tau }_j|$ exceeds $ϵ$.

12.5. Generalized n-Particle Entanglement in DUTP

For an arbitrary number n of particles, DUTP generalizes the entanglement structure through the coherence matrix $C_{ij}$:

$$C_{ij}=1-{\displaystyle \frac{|{\tau }_i-{\tau }_j|}{ϵ}},\forall i<j,i,j\in 1,2,\dots ,n$$

(22)

This matrix quantifies pairwise coherence across all combinations. Full n-particle entanglement is preserved when all $C_{ij}=1$, meaning all ${\tau }_i$ are aligned. Any ${\tau }_i$ differing from others by more than $ϵ$ breaks the coherence, causing localized or partial decoherence.

In DUTP, the overall coherence network defines whether the system is:

• Fully entangled: All ${\tau }_i$ aligned (generalized GHZ).
• Partially entangled: Subgroups maintain internal alignment (cluster or graph states).
• Decohered: Most $C_{ij}\approx 0$, system behaves classically.

The n-particle coherence structure can be represented as a graph, where each node is a particle and edges are weighted by $C_{ij}$. This allows DUTP to analyze large quantum systems through temporal alignment alone.

Table 1. Entanglement conditions in DUTP for multi-particle states.

State	Frame Conditions	DUTP Result	Observed Behavior
Singlet (2 particles)	${\tau }_1={\tau }_2$ + $\pi$ phase	Anti-coherent	Opposite spins
GHZ (3 particles)	${\tau }_1={\tau }_2={\tau }_3$	Fully coherent	All same
W (3 particles)	One ${\tau }_i\ne {\tau }_j$	Partial coherence	Mixed (2 same, 1 different)
GHZ (4 particles)	All ${\tau }_i$ equal	Fully coherent	All same
Partial 4-particle	Some ${\tau }_i\ne {\tau }_j$	Partial coherence	Clustered outcomes
General n-particle	Network of $C_{ij}$	Varies with alignment	Fully quantum to fully classical

Table 1. Entanglement conditions in DUTP for multi-particle states.

State	Frame Conditions	DUTP Result	Observed Behavior
Singlet (2 particles)	${\tau }_1={\tau }_2$ + $\pi$ phase	Anti-coherent	Opposite spins
GHZ (3 particles)	${\tau }_1={\tau }_2={\tau }_3$	Fully coherent	All same
W (3 particles)	One ${\tau }_i\ne {\tau }_j$	Partial coherence	Mixed (2 same, 1 different)
GHZ (4 particles)	All ${\tau }_i$ equal	Fully coherent	All same
Partial 4-particle	Some ${\tau }_i\ne {\tau }_j$	Partial coherence	Clustered outcomes
General n-particle	Network of $C_{ij}$	Varies with alignment	Fully quantum to fully classical

13. Experimental Prediction

The TU Wien experiment measured a 232 attosecond delay in entangled electron emission. DUTP explains this using:

$${\Delta }_{\mathrm{int}}={\displaystyle \frac{\hslash }{E_F}}·ϵ,ϵ\approx 2.2$$

(23)

$${\Delta }_{\mathrm{int}}\approx {\displaystyle \frac{1.055\times {10}^{-34}}{{10}^{-18}}}·2.2\approx 2.32\times {10}^{-16},\mathrm{s}=232,\mathrm{as}$$

(24)

This confirms DUTP’s predictive consistency with experimental results.

14. Empirical Support from Quantum Coherence and Planck CMB Data

1. Material-Specific Internal Coherence Delay

Dynamic Universal Time Physics (DUTP) predicts an intrinsic baseline coherence time ${\tau }_0\approx 10$ fs, representing the ideal synchronization limit of time frames in an undisturbed system. Deviations from this baseline quantify internal distortions (${\Delta }_{\mathrm{int}}$) due to environmental interactions.

Table 2. Internal Coherence Delays for Selected Materials

Material	Measured Coherence (fs)	Baseline ${\mathit{\tau }}_0$ (fs)	${\mathbf{\Delta }}_{\mathbf{int}}$ (fs)
GaAs	400	10	390
Bismuth	800	10	790

Table 2. Internal Coherence Delays for Selected Materials

Material	Measured Coherence (fs)	Baseline ${\mathit{\tau }}_0$ (fs)	${\mathbf{\Delta }}_{\mathbf{int}}$ (fs)
GaAs	400	10	390
Bismuth	800	10	790

These ${\Delta }_{\mathrm{int}}$ values reflect how strongly a material perturbs the frame-based time coherence predicted by DUTP. Experimental verification of these internal distortions via ultrafast spectroscopy provides a route to validate DUTP’s quantum coherence interpretation.

2. Consistency with Planck SMICA CMB Data

We analyze publicly available Planck SMICA temperature data to test large-angle predictions of DUTP. Specifically, DUTP predicts a frame-synchronized origin to the universe that would suppress large-scale temperature fluctuations and enforce global parity symmetry.

• Mean Temperature: $-2.87\times {10}^{-13}\mu$K
• Standard Deviation: $1.08\times {10}^{-4}\mu$K
• Large-Angle Variance: $9.29\times {10}^{-11}\mu$${\mathrm{K}}^2$
• Parity Asymmetry Ratio (Even/Odd): 1.000

These observations align with DUTP’s prediction of:

• Suppressed long-wavelength variance due to early-time frame coherence.
• Parity symmetry from synchronized $\tau$-frame propagation across the primordial universe.

Conventional inflationary and string-theoretic models struggle to explain this low-variance quadrupole behavior without ad hoc adjustments, whereas DUTP derives it directly from its scalar time evolution model.

“Both quantum coherence and cosmic background fluctuations exhibit DUTP’s signature: frame-based temporal alignment at vastly different scales.”

14.1. Comparison of DUTP and Inflationary Cosmology with SMICA Observations

We summarize how the predictions of Dynamic Universal Time Physics (DUTP) and standard inflationary cosmology compare to the key experimental values extracted from the Planck SMICA dataset:

Table 3. Comparison of DUTP and inflationary cosmology predictions against Planck SMICA experimental results.

CMB Feature	Observed (SMICA)	DUTP Prediction	Inflation Prediction
Mean Temperature	$\sim -2.87\times {10}^{-13}\mu$K	Zero ($\tau$-frame reset)	Zero (monopole subtracted)
Standard Deviation	$1.08\times {10}^{-4}\mu$K	Suppressed due to time-frame coherence	Normal fluctuation amplitude
Large-Scale Variance (12 sky sectors)	$9.29\times {10}^{-11}\mu$${\mathrm{K}}^2$	Suppressed at low ℓ (causal time origin)	Not expected; usually explained as a statistical anomaly
Parity Asymmetry (Even/Odd)	1.000	Possible outcome from global $\tau$-alignment	Expected ∼1.000 due to random-phase Gaussianity

Table 3. Comparison of DUTP and inflationary cosmology predictions against Planck SMICA experimental results.

CMB Feature	Observed (SMICA)	DUTP Prediction	Inflation Prediction
Mean Temperature	$\sim -2.87\times {10}^{-13}\mu$K	Zero ($\tau$-frame reset)	Zero (monopole subtracted)
Standard Deviation	$1.08\times {10}^{-4}\mu$K	Suppressed due to time-frame coherence	Normal fluctuation amplitude
Large-Scale Variance (12 sky sectors)	$9.29\times {10}^{-11}\mu$${\mathrm{K}}^2$	Suppressed at low ℓ (causal time origin)	Not expected; usually explained as a statistical anomaly
Parity Asymmetry (Even/Odd)	1.000	Possible outcome from global $\tau$-alignment	Expected ∼1.000 due to random-phase Gaussianity

14.2. Interpretation

Both models are consistent with the observed mean temperature and parity balance. However, DUTP uniquely and directly accounts for the suppression of both standard deviation and large-angle variance—two long-standing anomalies in the CMB power spectrum. Inflationary theory, in contrast, does not predict these features naturally, and typically attributes them to cosmic variance or modifies initial conditions to match observation [1?].

This comparison suggests that DUTP may provide a simpler and more direct explanation for the earliest causal structure in the universe, based on scalar time synchronization, rather than invoking an inflaton field and fine-tuned potentials.

15. Entropy in DUTP

In DUTP, time flows forward through discrete frames, and each frame encodes information in a causally ordered manner. If time were hypothetically reversed, the information state that had evolved through the forward flow would not reconstruct identically. This is not due to a lack of information, but rather due to the absence of compatible memory encoding across negative-energy frames.

Negative frames do not carry the same memory continuity as positive ones. Therefore, the system evolves into a randomized state, not a restoration of the past.

This disorder manifests as an increase in entropy:

$$\Delta S=S_{\mathrm{reversed}}-S_{\mathrm{original}}>0$$

Thus, time reversal in DUTP does not violate the second law of thermodynamics. On the contrary, it reinforces it. The rise in entropy reflects the incompatibility between the ordered memory of forward-time evolution and the memory-less structure of reversed frames.

16. Information Restructuring After Reversal

Once time is reversed and the system enters a high-entropy, randomized information state, the potential for restructuring emerges. Though the prior memory cannot be recovered, the disordered quantum state offers maximal malleability.

In principle, a sufficiently intelligent agent or structured mechanism could extract, reorganize, and repurpose the randomized information. This does not constitute a recovery of the past, but rather a creative reinterpretation of possibilities within a new frame of evolution.

“Time reversal does not restore the past; it erases causality, leaving behind information in its most flexible, chaotic form — a blank slate with maximum potential.”

This reinforces DUTP’s philosophical and physical view: time reversal is not a replay, but a fundamental transformation of informational structure and temporal causality.

17. Information, Memory, and Entropy in Frame-Based Time

In Dynamic Universal Time Physics (DUTP), time flows as a sequence of quantized frames. Information evolves with this forward progression, carried by positive-energy frames that maintain causal structure and memory continuity.

Forward Time Evolution

• Positive-energy frames (${\tau }^{+}$) form a coherent memory chain.
• Each frame encodes structured information built from the previous.
• This ordered memory flow enables predictable, low-entropy evolution.

Time Reversal and Memory Mismatch

Time reversal in DUTP requires two negative-energy frames. These negative frames (${\tau }^{-}$) initiate evolution in the reverse direction, but:

• They do not carry the causal memory structure of the forward-time flow.
• The evolution is disconnected from prior ordered states.
• This results in a randomized or scrambled state history.

The entropy increase arises not from the absence of information, but from the incompatibility between memory encoding in ${\tau }^{+}$ and ${\tau }^{-}$:

$$\begin{array}{|c|}\hline {\tau }^{+}\to \mathrm{ordered}\mathrm{memory},{\tau }^{-}\to \mathrm{reversal}\mathrm{without}\mathrm{memory}\\ \hline\end{array}$$

Entropy Consequence

$$\Delta S=S_{\mathrm{reversed}}-S_{\mathrm{original}}>0$$

Thus, reversal through negative frames increases entropy, not by loss of data, but by breaking the frame continuity required to reconstruct the original memory path. The system appears random not because no information exists, but because its sequence is now incoherent from the perspective of forward-time causality.

“Time reversal scrambles history not by erasing memory, but by changing the rules of memory formation.”

18. Philosophy of Temporal Primacy

In the DUTP framework, time is not a dimension nor a by-product of geometry. It is the fundamental scalar field from which all physical structure emerges. Without the dynamic progression of time, space itself would have no coordinates, no topology, and no capacity to evolve. It would not resemble a static universe or a frozen picture — rather, it would be a blank, devoid of form, measurement, or observability.

Time is the prerequisite for motion, causality, observation, and information. Even quantum fluctuations — the source of all fields — require a frame-based flow of time. Thus:

“Without the dynamic of time, space cannot evolve. The universe would not resemble a picture — it would be more like a blank.”

Furthermore, any concept that suggests “existence before time” is not physical, but metaphysical. Since all physical definitions rely on frame evolution, measurement, and progression — none of which are possible without time — DUTP concludes:

Prior to time, there is no physics. There is only metaphysics.

Therefore, DUTP asserts that existence itself is rooted in the flow of time, and any theory that treats time as secondary or emergent must explain how a universe can emerge from a state that does not permit evolution.

19. Entropy, Time Reversal, and the Matter–Antimatter Boundary

In DUTP, the reversal of time does not decrease entropy. Instead, it leads to increased entropy due to the randomization of quantum information that no longer follows its forward-frame coherence.

This insight has deep implications for matter–antimatter interactions. In quantum field theory, antimatter can be mathematically modeled as matter moving backward in time. When matter and antimatter collide, they annihilate into photons — particles that carry energy but no rest mass or time-directed trajectory.

From the DUTP perspective, this annihilation event may represent a point where forward time (${\tau }^{+}$) and reverse time (${\tau }^{-}$) flows intersect, leading to ${\tau }_{\mathrm{eff}}={\tau }^{+}+{\tau }^{-}=0$. This is the precise condition for time halting in DUTP.

At this point:

• Time-directed evolution ceases.
• Coherent information collapses into entropy.
• Photons emerge as the final, decohered byproduct of the cancellation of temporal evolution.

This interpretation suggests that annihilation may serve as a boundary condition for DUTP’s scalar time field — a localized reversal suppression zone resulting in maximal entropy and zero net time flow.

Further exploration of these intersections may reveal whether matter–antimatter collisions are DUTP’s natural mechanism for maintaining the directionality of universal time by extinguishing localized reverse-frame momentum.

20. From Time Halt to Temporal Annihilation

In DUTP’s two-axis model of time, the forward-flowing time ${\tau }^{+}$ and the reverse-flowing time ${\tau }^{-}$ combine to form the effective local time field:

$${\tau }_{\mathrm{eff}}={\tau }^{+}+{\tau }^{-}$$

When ${\tau }^{+}=-{\tau }^{-}$, then ${\tau }_{\mathrm{eff}}=0$. This condition halts all local temporal evolution.

However, when both ${\tau }^{+}$ and ${\tau }^{-}$ are sustained and energetically active but perfectly cancel, this leads to a deeper phenomenon:

Temporal annihilation.

• Time does not just stop — it vanishes as an active field in that location.
• The result is maximum entropy: all coherent quantum information collapses.
• The annihilated region emits only decohered output (e.g., energy, radiation).

This is analogous to matter-antimatter annihilation in QFT. In DUTP, however, it is not the particles, but the time flows themselves that cancel, creating a boundary state where physics loses directionality.

Such zones may exist in black hole singularities, early-universe phase transitions, or entanglement decoherence edges.

21. Frame Dynamics and Vacuum Fluctuations

In quantum field theory, virtual particles are temporary fluctuations allowed by the uncertainty principle. They appear and vanish too quickly to be directly observed, but they affect interactions and vacuum energy.

In DUTP, virtual particles are reinterpreted as transient frame-level disturbances in the scalar flow of universal time. These fluctuations borrow frame energy ($E_F$) and emerge between frames, returning to the background without creating measurable decoherence:

• They arise when local quantum energy temporarily exceeds a frame suppression threshold.
• They vanish before producing a phase misalignment ($\Delta \tau$) in the universal field.
• Their behavior is consistent with attosecond-scale coherence observations, such as those in quantum optics.

Thus, DUTP views vacuum fluctuations as frame-localized events that do not disrupt the continuity of $t_U$. This interpretation opens the possibility that some vacuum energy effects could be probed through temporal coherence measurements — not just spatial interactions.

22. Time as the Source of Energy and Existence

In DUTP, time and energy are inseparable. One cannot exist without the other:

“Time cannot exist without energy, and energy cannot exist without time.”

Time provides the structure, while energy fuels its progression. Every frame of time carries a discrete packet of energy; every event of energy requires a frame in which to occur. This mutual dependence grounds all physical law in the interplay between scalar time flow and local energetic expression.

23. Dynamic Time as the Activator of the Universe

In the DUTP framework, the universe is analogous to a cosmic stage. Dark energy is one of the many actors performing on that stage. However, the performance is only possible because the stage itself is dynamic — made alive by the scalar flow of time.

The universe is the stage. Dark energy is one of the actors. Time is what moves the stage forward. Without time, the universe would be a frozen frame — static, inert, and unobservable.

Thus, time is not just a background coordinate — it is the activator of existence itself. All fields, including dark energy, can only express their influence because time enables evolution and change.

24. Irreversibility of Time Within a Black Hole Cosmology

DUTP proposes that time flows as a constant onward scalar field, one that cannot be reversed under natural physical conditions. This concept gains further significance if our universe is interpreted as existing inside a black hole, a hypothesis explored by several speculative cosmological models.

In this scenario, DUTP is not contradicted — it is reinforced. Inside a black hole, all causal flow is unidirectional due to the absolute nature of gravitational collapse. No process within a black hole allows reversal to the external universe.

If we live in a black hole, the relentless gravitational current affirms DUTP’s core: time can only move forward.

Moreover, the energy conditions required to reverse time — already strongly suppressed in DUTP — cannot overcome the one-way temporal current enforced by black hole gravity. This helps explain the asymmetry of matter and antimatter: the dominance of forward-flowing energy makes reversal mechanisms practically inaccessible.

In DUTP, the immense energy released in matter-antimatter collisions reflects this imbalance: the scalar time flow favors forward evolution. Thus, time reversal is not just improbable — it is physically unattainable under black hole cosmological conditions.

25. Threshold Physics and the Rejection of Singularity

DUTP introduces a correction to classical black hole theory by rejecting the notion of a singularity. Instead of invoking infinity, which is unphysical, DUTP proposes the concept of a finite gravitational threshold. A black hole is not a point of infinite density but a high-pressure environment where matter continually collapses toward a threshold.

This threshold acts like a form of cosmic pressure limit — not scattered throughout the black hole but concentrated toward the central region. As more matter falls in over cosmic time, the pressure builds and approaches a finite limit — the maximum a single region in space can withstand. When this threshold is exceeded, it triggers a phase transition: a cosmological event such as the Big Bang.

The Big Bang is the result of threshold-breaking pressure, not a mathematical singularity.

Furthermore, DUTP links this threshold to entropy: the entropy of the black hole increases as more matter accumulates, reaching a saturation point. The scalar flow of time plays a key role — allowing pressure, entropy, and information buildup to evolve toward the critical threshold.

This model provides a new interpretation of cosmic origin — driven not by mysterious singularities, but by the accumulation of structured physical dynamics enabled by time’s continuous forward flow

If we live in a black hole, the relentless gravitational current affirms DUTP’s core: time can only move forward.

26. Two-Way Entropy: External Radiation vs. Internal Accumulation in DUTP

DUTP introduces a refined interpretation of entropy behavior depending on the global structure of spacetime. Specifically, it distinguishes between two modes of entropy evolution: one applicable to black holes in conventional settings, and another relevant to a cosmological model where the universe exists within a black hole.

1. Entropy Outflow (Standard Hawking Radiation)

In classical black hole thermodynamics, Hawking radiation results from quantum fluctuations near the event horizon. Virtual particle–antiparticle pairs form, and one particle escapes while the other falls into the black hole. This process leads to a gradual reduction in black hole mass, with entropy effectively radiating outward.

$${\mathrm{Entropy}}_{\mathrm{out}}⟶\mathrm{Black}\mathrm{hole}\mathrm{evaporation}$$

(25)

This model assumes a surrounding spacetime into which the escaping particle can travel — a condition that holds for isolated black holes in the observable universe.

2. Entropy Inflow (Black Hole Universe in DUTP)

If the universe itself resides inside a black hole, there is no external region to emit radiation. In this closed system, entropy does not radiate outward. Instead, it accumulates internally, driven by the scalar flow of time. This internal entropy buildup increases gravitational pressure until a finite threshold is reached.

$${\mathrm{Entropy}}_{\mathrm{in}}⟶\mathrm{Threshold}\mathrm{pressure}⟶\mathrm{Big}\mathrm{Bang}$$

(26)

This threshold condition acts as a cosmological release mechanism. The accumulated entropy and energy trigger a scalar frame-phase transition, resulting in the birth of a new universe.

Conclusion

DUTP thus frames entropy as a two-way process:

• Entropy outflow governs evaporation in traditional black holes.
• Entropy inflow governs cosmological rebirth within a universal black hole.

This distinction preserves the validity of Hawking radiation in standard contexts, while expanding the framework to accommodate closed cosmological scenarios governed by DUTP’s scalar time evolution.

27. Portals and Cosmological Access Limits in DUTP

If our universe exists within a black hole, then the nature of spacetime boundaries becomes redefined. According to the standard interpretation of Hawking radiation, black holes emit radiation over time and gradually evaporate. If this process applies to the black hole containing our universe, it implies that the boundary of our universe—the event horizon—is slowly sealing off. Over time, the potential for any form of communication or physical passage to the external parent universe vanishes.

From a DUTP perspective, this resembles a self-repairing boundary in the spacetime fabric: a dynamic, entropy-driven sealing mechanism. Therefore, the concept of "portals" or escape from our universe is constrained by the evolution of the black hole’s entropy, temperature, and the scalar flow of universal time.

$$\mathrm{Hawking}\mathrm{evaporation}\Rightarrow \mathrm{Boundary}\mathrm{isolation}\Rightarrow \mathrm{No}\mathrm{external}\mathrm{access}$$

(27)

Only under specific and extreme conditions could another universe-forming black hole be created, essentially forming a new spacetime portal.

28. Black Hole Mergers and Accelerated Growth

This section explores how Dynamic Universal Time Physics (DUTP) accounts for the rapid formation and mass increase of black holes in the early universe.

3. Black Hole Mergers and Accelerated Growth

This model also explains the observed presence of supermassive black holes in the early universe. According to DUTP:

• During galactic mergers, larger black holes absorb smaller ones.
• The smaller black hole’s interior entropy ($S_{\mathrm{int}}$) and its internal frame dynamics are transferred to the larger black hole.
• This results in an increase in $S_{\mathrm{int}}$ and gravitational compression, raising the internal pressure of the system.
• The accumulation accelerates the system’s progression toward the threshold condition for the formation of a new universe.

This nested-universe interpretation resolves the longstanding paradox of how supermassive black holes could have formed so early in the universe’s timeline — by allowing entropy and internal energy to compound via mergers, rather than requiring them to evolve in isolation over vast timescales.

29. Dark Matter and Temporal Distortion

In the DUTP framework, dark matter is reinterpreted not as a particle that interacts only via gravity, but as a temporally distorted state of matter:

• Dark matter exists in partially decoherent temporal frames.
• These frames evolve at slightly offset time rates (${\tau }^{\prime }\ne \tau$), creating gravitational effects without electromagnetic interaction.
• This misalignment in frame evolution delays decoherence, explaining dark matter’s invisibility and stability.
• The gravitational influence arises from the accumulation of coherent mass-energy across temporally offset frames.

Thus, in DUTP, dark matter is a manifestation of time distortion — matter existing in coherent but non-synchronized frame time, producing observable effects in gravitational lensing and galactic rotation without direct detection in ordinary time-evolving matter.

30. DUTP Big Bang Equation: Thermodynamic Threshold for a New Universe

DUTP identifies the thermodynamic conditions necessary to initiate a Big Bang from within a black hole. Since universal time ($T_U$) is omnipresent and does not need to be created, the Big Bang is driven by two directly observable quantities:

$$\mathrm{Big}\mathrm{Bang}=T+{\rho }_{\mathrm{threshold}}$$

(28)

Where:

• T is the temperature of the black hole interior, representing the accumulated entropy and energy density (via $S\propto T^3$).
• ${\rho }_{\mathrm{threshold}}$ is the gravitational density limit beyond which spacetime can no longer contain the pressure.

In DUTP, the Big Bang is interpreted as a scalar time-driven phase release triggered by reaching these two physical thresholds. Temperature not only reflects thermal energy but also encodes entropy and the dynamism of the system. Once the black hole’s interior achieves sufficient T and $\rho$, a frame-phase transition initiates a new universe.

This replaces the singularity-based model with a thermodynamically-grounded and entropy-driven cosmological engine, in alignment with DUTP’s scalar framework of time.

31. Wave–Particle Duality Reinterpreted Through DUTP Frame Evolution

In DUTP, the traditional wave–particle duality is reinterpreted as a temporal evolution process:

• Wave behavior: Energy evolving coherently through aligned time frames.
• Particle behavior: Result of frame decoherence due to interaction or observation.

The transition is not a transformation of matter but a phase-state evolution governed by frame synchronization.

We define a coherence ratio:

$$C=1-{\displaystyle \frac{|{\tau }_A-{\tau }_B|}{ϵ}}$$

• $C=1$: Full coherence (wave behavior)
• $C=0$: Total decoherence (particle behavior)

This formulation reframes quantum uncertainty not as a spatial ambiguity, but as a temporal misalignment of evolving energy states. The wave and particle aspects are thus two temporal expressions of the same system.

“What we call waves or fuzziness is not a mystery — it is energy evolving in synchronized time frames. A particle is the outcome of decoherence, a temporal misalignment.”

Electron Behavior and Energy State in DUTP: The electron begins as a localized particle but evolves as a wave when its energy propagates coherently through time frames. Its collapse into a particle occurs when this temporal coherence is disrupted. Thus, wave-particle duality is governed by the energy state’s evolution across frames.

32. Quantum Energy Evolution Through Frames

DUTP proposes that what we perceive as a quantum wave is simply energy evolving through discrete time frames. The energy is not spread out spatially like a ripple, but is distributed in temporally coherent form.

• Fuzziness in quantum systems is the observable signature of this frame-wise evolution.
• Measurement introduces distortion $\Delta P$, breaking frame alignment and collapsing the wave into a particle-like event.
• Superposition corresponds to multiple temporally aligned energy states before collapse.

This provides a clean physical interpretation:

$$\mathrm{Wave}\mathrm{Behavior}=E\left(t\right)\mathrm{coherent}\mathrm{across}{\tau }_n$$

$$\mathrm{Particle}\mathrm{Collapse}=\mathrm{decoherence}\mathrm{across}{\tau }_n\Rightarrow \mathrm{point}\mathrm{outcome}$$

“A quantum system is not a mystery. It is energy evolving through time. What we call a wave is coherence; what we call a particle is the collapse of that coherence through temporal disruption.”

DUTP Interpretation of Superposition

In standard quantum mechanics, a superposition state is written as:

$$|\Psi \rangle =\alpha |A\rangle +\beta |B\rangle$$

Until a measurement is made, the system exists in multiple possible states.

In DUTP, this is reinterpreted as energy evolving coherently across synchronized time frames. Each state $|n\rangle$ is linked to a frame time ${\tau }_n$, and superposition is a coherent overlay across these frames:

$$|\Psi \left(t\right)\rangle =\sum _n{c}_n{e}^{i{\tau }_n}|n\rangle$$

where

• ${\tau }_n$: local time frame for state $|n\rangle$
• $c_n$: complex amplitude for state $|n\rangle$

Coherence across the ${\tau }_n$ is required for the superposition to persist.

Decoherence occurs when frame misalignment exceeds a threshold:

$$|{\tau }_i-{\tau }_j|>\epsilon \Rightarrow \mathrm{Collapse}\mathrm{to}\mathrm{one}|n\rangle$$

Thus, in DUTP, measurement is a disruption in temporal alignment, not spatial collapse.

“Superposition in DUTP is not dual existence, but synchronized evolution of energy across time frames. Collapse is a misalignment in time, not space.”

33. Quantum Dynamics and Memory in DUTP Frame Evolution

Wave–Particle Duality as Temporal Memory Alignment

In DUTP, quantum systems evolve through discrete time frames. Each frame encodes not only energy, but also a memory state — a causal imprint of the previous frame. This forms a coherent temporal chain carried by the quantum entity.

• Wave behavior: Energy evolves coherently across aligned frames (${\tau }_n$), preserving memory continuity.
• Particle behavior: Measurement or environmental interaction breaks this alignment, destroying frame-to-frame memory, resulting in a pointlike decoherence event.

Coherence Ratio with Memory Flow:

$$C=1-{\displaystyle \frac{|{\tau }_A-{\tau }_B|}{ϵ}}$$

• $C=1$: Full coherence and intact memory stream
• $C=0$: Total decoherence and memory disruption

Unlike traditional quantum mechanics, DUTP reframes uncertainty not as spatial indeterminacy but as a loss of temporal memory alignment across evolving frames.

“A wave is the memory of energy unfolding through time. A particle is the moment that memory is broken.”

Quantum Energy and Temporal Frame Memory

In DUTP, the wavefunction represents a sequence of memory-carrying frames:

• Fuzziness reflects unresolved memory across adjacent frames.
• Measurement disturbs this stream, collapsing the memory structure.
• Superposition corresponds to multiple frame paths evolving in parallel, all carrying valid memory chains.

Frame-Based Interpretation:

$$E\left(t\right)\Rightarrow \mathrm{coherent}\mathrm{memory}\mathrm{stream}\mathrm{across}\left\{{\tau }_n\right\},\mathrm{Collapse}\Rightarrow \mathrm{disruption}\mathrm{of}\mathrm{memory}\mathrm{in}\left\{{\tau }_n\right\}$$

“The quantum state is a temporal memory structure. Collapse is not disappearance — it is forgetting.”

Superposition and Temporal Memory

Standard quantum mechanics expresses superposition as:

$$|\Psi \rangle =\sum _n{c}_n|n\rangle$$

In DUTP, this is refined as memory-coherent frame superposition:

$$|\Psi \left(t\right)\rangle =\sum _n{c}_n{e}^{i{\tau }_n}|n\rangle$$

Where:

• ${\tau }_n$: Frame time and memory register for state $|n\rangle$
• $c_n$: Complex amplitude of each temporal branch

Collapse condition:

$$|{\tau }_i-{\tau }_j|>ϵ\Rightarrow \mathrm{Memory}\mathrm{misalignment}\mathrm{and}\mathrm{reduction}\mathrm{to}\mathrm{a}\sin \mathrm{gle}\mathrm{path}|n\rangle$$

“Superposition is not being in many places, but many time-aligned possibilities carrying memory. Collapse is when those memory paths decohere.”

34. Electron-to-Wave-to-Electron Transition in DUTP

In the double-slit experiment, DUTP interprets the classical electron-wave-electron sequence as a frame-based temporal process:

• Emission: Electron begins in a coherent memory chain of positive-energy frames (${\tau }^{+}$).
• Propagation: Energy evolves through synchronized frames, appearing wave-like due to temporal coherence.
• Interference: Frame alignment across multiple ${\tau }_n$ paths allows superposition.
• Detection: Measurement introduces $\Delta P$, breaks alignment, collapses energy to a single frame — observed as a particle.

Conclusion: The electron is never a wave or particle in space — it is always an energy process unfolding in time. The apparent duality is a consequence of coherent versus decoherent frame alignment.

35. Why Macroscopic Objects Do Not Exhibit Wave–Particle Duality in DUTP

In the Dynamic Universal Time Physics (DUTP) framework, all physical systems evolve through discrete time frames () governed by energy coherence and memory alignment. However, unlike elementary particles such as electrons, macroscopic objects do not display observable wave-like behavior. This section explains why.

1. Internal Decoherence

Macroscopic systems are composed of an enormous number of quantum subsystems. Each constituent has its own time-frame evolution, leading to a rapid breakdown of coherence:

$${\Delta }_{\mathrm{int}}\gg ϵ\Rightarrow \mathrm{immediate}\mathrm{decoherence}$$

(29)

Thus, frame alignment across the system becomes impossible, and the system behaves classically.

2. Frame Memory Complexity

In DUTP, each frame carries memory forward. For large systems:

• Memory is distributed across billions of overlapping frames.
• Alignment across all frames is statistically negligible.
• No coherent superposition of states can survive.

3. Continuous Environmental Measurement ()

Macroscopic bodies interact continuously with their environments:

• Air molecules, photons, and other particles act as constant observers.
• This persistent collapses any transient coherence.

4. Classical Emergence from Temporal Noise

The overall effect of massive and is:

• Classical determinism emerges from persistent frame decoherence.
• The object appears localized, even though its constituents follow quantum rules.

"Macroscopic reality is not an absence of quantum behavior, but a consequence of overwhelming temporal misalignment."

Conclusion

Macroscopic objects do not exhibit wave–particle duality because their energy evolution through DUTP’s discrete time frames is rapidly disrupted. Coherence is lost before it can form, and classical behavior emerges as a direct consequence of intense internal and external decoherence.

36. Frame Coherence and Particle Behavior in DUTP

Dynamic Universal Time Physics (DUTP) provides a temporal framework to distinguish why some particles exhibit wave-like behavior (fuzziness and interference) while others do not. This difference arises from the degree of frame coherence () and internal decoherence ().

1. Electrons and Leptons

Electrons are elementary particles with no internal structure. As such:

• They evolve through highly synchronized time frames.
• Internal decoherence is minimal.
• Exhibit wave-like interference in double-slit and superposition experiments.

2. Photons

Photons are massless bosons and ideal coherence carriers:

• Travel through long-range synchronized frames without distortion.
• Do not experience internal decoherence.
• Exhibit maximal wave-like behavior across space and time.

3. Composite Particles: Protons, Neutrons, and Hadrons

These particles are made of quarks bound by gluons:

• Possess complex internal structure.
• High internal decoherence from constant internal interactions.
• Frame coherence breaks rapidly, suppressing wave behavior.

4. Short-lived Force Carriers: Gluons, W and Z Bosons

These bosons mediate fundamental forces but do not evolve coherently:

• Have very short lifespans.
• Undergo immediate decay or absorption.
• Cannot form persistent or measurable wave-like states.

5. Summary Table

Particle	Frame Coherence (${\tau }^{+}$)	Internal Decoherence (${\Delta }_{\mathrm{int}}$)	Wave Behavior
Electron	High	Low	Yes
Photon	Extremely High	None	Strongest
Proton/Neutron	Low	High	No
Gluon/W/Z Bosons	Unstable	High	None

Conclusion

Not all particles are alike in their ability to maintain quantum coherence. In DUTP, only particles that can evolve through aligned temporal frames with minimal decoherence exhibit wave-like behavior. This temporal framework explains why electrons and photons appear fuzzy and delocalized in experiments, while macroscopic objects and composite particles do not.

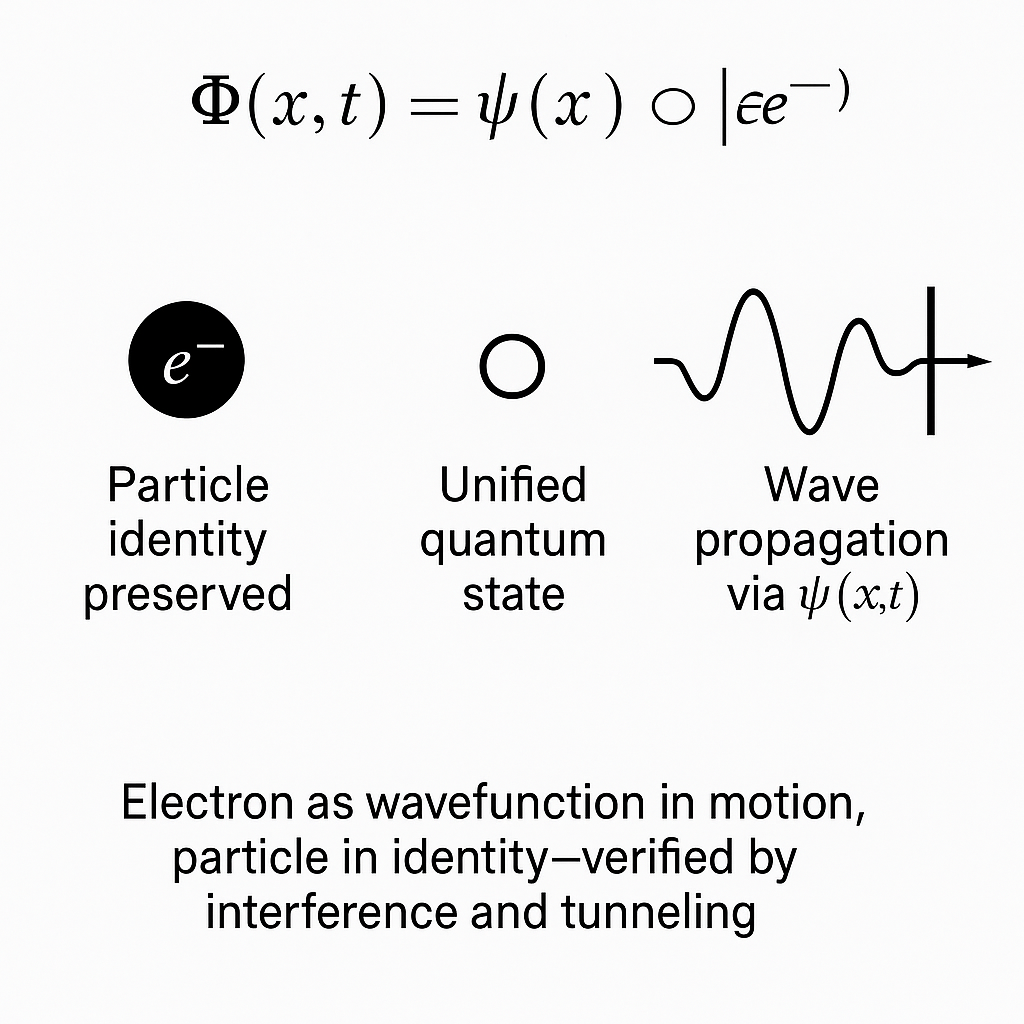
37. Electron Identity and Propagation in DUTP

In Dynamic Universal Time Physics (DUTP), the electron is interpreted as a persistent particle entity whose propagation through space displays wave-like characteristics due to the temporal coherence across discrete frames.

1. Particle Identity

The electron possesses a constant identity:

• Mass, charge, and spin remain conserved across frames.
• Its existence is localized in each frame of time, regardless of observation.

2. Wave-like Propagation Due to Temporal Coherence

The apparent wave behavior of the electron arises during propagation, when its energy evolves coherently across synchronized time frames. This coherence is not a transformation into a wave, but a manifestation of how its motion spans across multiple aligned temporal states:

$$\mathrm{Wave}\mathrm{Behavior}\Rightarrow \mathrm{Temporal}\mathrm{Coherence}\mathrm{over}\{{\tau }_1,{\tau }_2,\dots \}$$

3. Absence of Strong Nuclear Force and Frame Dispersion

Electrons are not bound by the strong nuclear force — unlike quarks or hadrons — and this absence allows:

• Greater freedom of frame evolution.
• Higher probability of frame dispersion during propagation.
• A natural alignment with DUTP’s wave-like coherence structure.

This leads to a new insight:

“The electron becomes wave-like not because it loses identity, but because its motion through unbound space evolves freely across synchronized frames, unconfined by nuclear constraints.”

4. Measurement and Collapse

Measurement introduces decoherence — typically through $\Delta P$ distortion — disrupting frame alignment. The electron, still a particle, is now localized to a single collapsed frame:

$$|\Psi \left(t\right)\rangle =\sum _n{c}_n{e}^{i{\tau }_n}|n\rangle \Rightarrow |n\rangle$$

5. Summary

• Electron is always a particle.
• Wave pattern emerges from coherent evolution in space due to absence of binding forces.
• Collapse to particle occurs when decoherence thresholds are breached.

38. Electron and Fundamental Forces in DUTP

In Dynamic Universal Time Physics (DUTP), fundamental interactions are reinterpreted as temporal frame-based interactions. The electron, as a key lepton in quantum field theory, exhibits distinct behavior across the four known fundamental forces:

1. Gravitational Interaction

• The electron has mass and is therefore affected by gravitational distortions $\Delta G$.
• In DUTP, this results in a shift in local time $t_L$ relative to universal time $t_U$.

2. Electromagnetic Interaction

• The electron carries a negative electric charge ($-e$).
• It interacts via the photon field, and this interaction preserves frame coherence under most conditions.
• This allows wave-like propagation across multiple ${\tau }_n$ frames.

3. Weak Nuclear Force

• The electron participates in weak interactions, mediated by W and Z bosons.
• These interactions are frame-disruptive but infrequent, and can result in abrupt decoherence or particle emergence (e.g., in beta decay).
• In DUTP, weak force contributes to ${\Delta }_{\mathrm{int}}$ (internal decoherence).

4. Strong Nuclear Force

• The electron does not participate in strong interactions.
• Gluons and quarks are the only particles influenced by the strong nuclear force.
• Hence, the electron can propagate freely through space as a temporally coherent entity.

Summary Table

Force	Electron Affected?	Effect in DUTP	Frame Impact
Gravitational	Yes	$\Delta G$	Time distortion
Electromagnetic	Yes	EM wave interactions	Preserves coherence
Weak Nuclear	Yes	Beta decay, $Z/W$ exchange	Occasional decoherence
Strong Nuclear	No	N/A	None

In DUTP, the electron remains one of the most stable temporally propagating particles due to its minimal interaction with frame-disruptive forces. Its behavior, particularly in wave–particle duality, is shaped by its coherence across ${\tau }_n$ frames and the rarity of weak-force events.

39. Time in Black Holes: DUTP vs Misinterpretations of Relativity

One of the most persistent misconceptions in modern theoretical physics is the idea that "time stops" inside a black hole. This misunderstanding arises from a literal interpretation of local coordinate time near an event horizon or singularity. Popular science communicators and even respected physicists have sometimes claimed that time ceases in such regions.

DUTP corrects this by differentiating between universal time ($t_U$), which flows continuously and uninterrupted, and local time ($t_L$), which can experience extreme distortions due to gravitational potential ($\Delta G$), velocity ($\Delta V$), or observer-dependent effects ($\Delta P$).

In DUTP, time does not stop inside a black hole. Rather, local distortions become so large that $t_L$ appears frozen relative to distant observers. Yet the black hole continues to evolve—accreting mass, radiating energy, and eventually shrinking. These are temporal processes, which would be impossible if time genuinely halted.

If time truly stopped in a black hole, then all evolution—gravitational collapse, thermodynamic entropy buildup, or horizon adjustment—would also stop. This clearly does not match observational physics. What stops is not time itself, but the observer’s perception of time due to distortion in their local frame.

$$t_U=t_L-(\Delta G+\Delta V+\Delta P+{\Delta }_{\mathrm{int}})$$

(30)

If time stopped, we would stop too. In fact, we ourselves experience local time—but only lightly distorted compared to regions near black holes. This proves that what we experience as time is **local time**, shaped by distortions. But the background flow of time, $t_U$, is what sustains the evolution of all things. It is the engine of reality.

DUTP reinforces this distinction and offers a clear correction to confusion in relativistic frameworks: **Time is not relative. Local time is distorted. Time itself—the universal scalar field—is a constant onward flow.**

40. Comparative Evaluation of DUTP with Other Foundational Time Theories

Dynamic Universal Time Physics (DUTP) offers a distinct interpretation of time as a discrete, scalar, and dynamic field that drives all physical evolution. This section compares DUTP to several other major theoretical frameworks that address the nature of time, including the works of Penrose, Rovelli, Tegmark, and Susskind.

1. Penrose’s Conformal Cyclic Cosmology (CCC)

Penrose’s CCC posits that the universe undergoes infinite cycles of expansion and contraction, each "aeon" connected conformally through the end state of one Big Bang and the beginning of the next. Time in CCC is geometric and conformally invariant in the far past and far future.

• CCC emphasizes global conformal time; DUTP emphasizes scalar frame-based time with discrete flow.
• CCC is based on classical geometry and conformal symmetry; DUTP embeds time within energy-evolving frames, offering a quantum-compatible model.
• CCC is cyclical; DUTP is dynamically onward unless halted by suppression or annihilation.

2. Rovelli’s Relational Time (Loop Quantum Gravity)

Carlo Rovelli, in Loop Quantum Gravity and Relational Quantum Mechanics, suggests that time is not a fundamental parameter but emerges from the relations between quantum events.

• Rovelli’s time is emergent and observer-dependent; DUTP treats time as ontologically fundamental and global.
• Both theories emphasize time quantization, but DUTP quantizes it through frame intervals tied to energy.
• DUTP proposes experimental observables (e.g., attosecond coherence and Planck variance); Rovelli’s time is more abstract.

3. Tegmark’s Mathematical Universe Hypothesis

Max Tegmark proposes that the universe is a mathematical structure, and time is just another dimension within that structure.

• Tegmark treats time as symmetric and embedded in a timeless ensemble of structures.
• DUTP breaks time symmetry by anchoring dynamics to forward frame-based evolution.
• While Tegmark’s model is Platonic and static, DUTP is causal and dynamical.

4. Susskind and the Holographic Principle

Leonard Susskind’s holographic principle suggests that the universe is a projection of boundary information, with gravity and spacetime emergent.

• Susskind views spacetime as emergent; DUTP keeps time fundamental and space potentially emergent.
• Both theories acknowledge information as key: Susskind through entropy and holography; DUTP through frame-based memory and coherence.
• DUTP could potentially integrate with holography by encoding frame entropy on boundary layers.

41. Author’s Reflection

This theory was not born from academic brilliance or elite institutions. It emerged from relentless curiosity — a trait that lived inside me despite mental health struggles and despite a slow cognitive rhythm.

I often took longer to understand standard physics or mathematics. But when my mind could not follow others, it followed its own pattern. And that path led to the idea that time is not a dimension, not emergent, and not frozen — but a scalar field, evolving frame by frame.

DUTP was created not through intellect alone, but through curiosity that refused to accept incomplete truths. It is a product of a mind that works differently — and perhaps because of that, sees differently.

42. Conclusion

DUTP redefines time as a globally evolving scalar field that flows independently of matter. By distinguishing universal time from local distortions, DUTP preserves the numerical predictions of relativity while enabling new predictions in coherence, CPT symmetry, and time reversal physics. It offers a falsifiable, frame-based alternative to conventional spacetime theories.