Submitted:
15 October 2024
Posted:
17 October 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
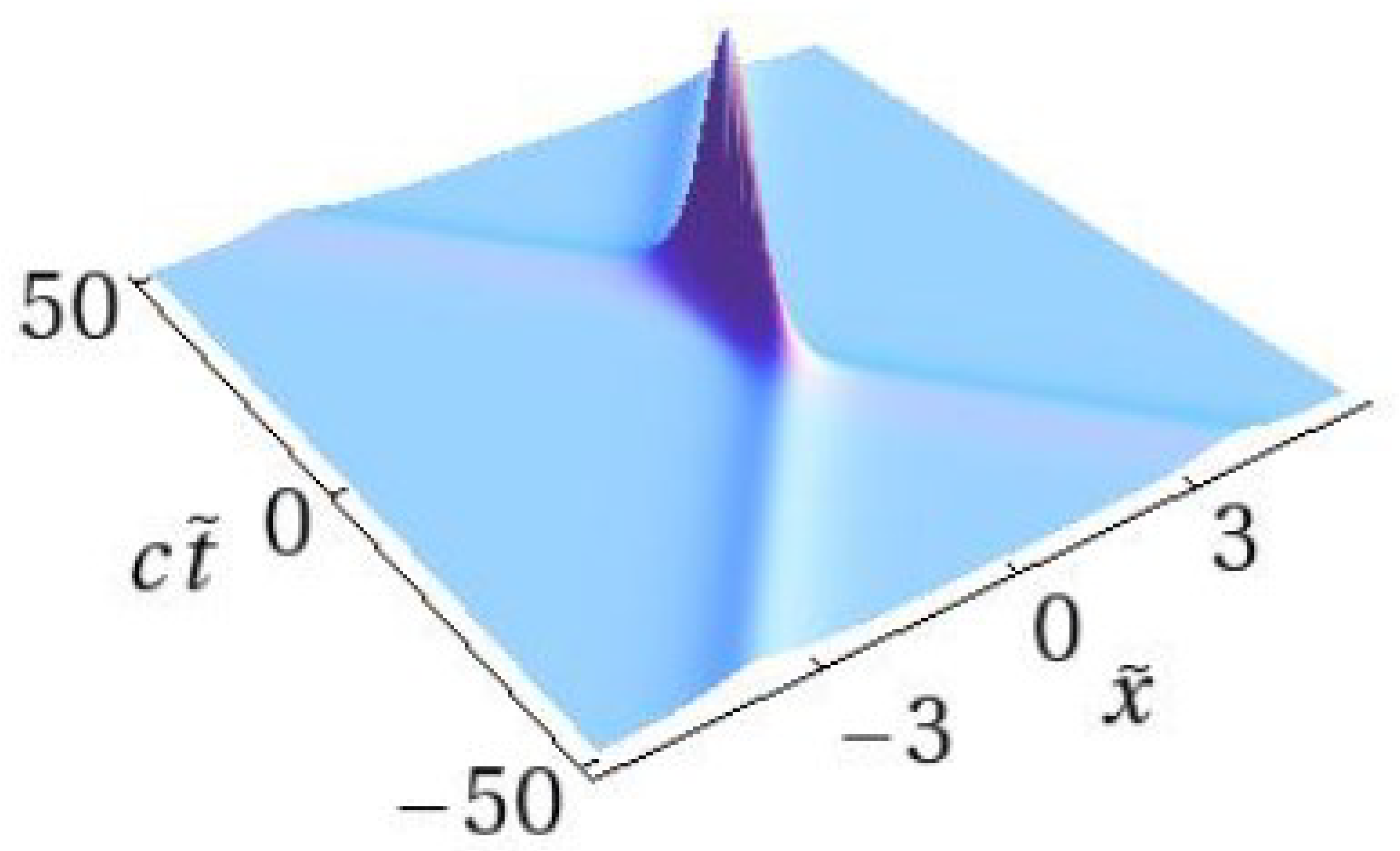
2. Soliton Collisions with Interference
3. Interference Patter of Electrons

4. Cosmic Bell Test?
5. Discussion: “Collapse” of the Wave Function Triggered by Self-Gravity?
References
- V.I. Arnol’d: Catastrophe Theory, Third, revised and expanded edition (Springer, Berlin 1992).
- A. Aspect: “Closing the Door on Einstein and Bohr’s Quantum Debate, ” Physics 8 123 (16 December 2015).
- J. Bjorken: The Future of the Quantum Theory (Beam Line, Sommer/Fall 2000).
- Carl, H. Brans: “Bell’s theorem does not eliminate fully causal hidden variables,” Int. J. Theor. Phys. 27, 219 (1988).
- M. Born: “The Interpretation of Quantum Mechanics,” Max Born’s response to two articles in The British Journal for the Philosophy of Science by Erwin Schrödinger entitled "Are There Quantum Jumps?" (Part I and Part II). August and Noviember 1952, pages 95-106, received 29. 1. 1953.
- D. Castañeda Valle and E. W. Mielke: “Relativistic soliton collisions of axion type dark matter,” Phys. Lett. B 758, 93 (2016). [CrossRef]
- I. Christov and C.I. Christov: “Physical dynamics of quasi-particles in nonlinear wave equations", Phys. Lett. A 372, 841–848 (2008). [CrossRef]
- S. Colin, T. Durt and R. Willox: “L. de Broglie’s double solution program: 90 years later,” Annales de la Fondation Louis de Broglie, 42, numero special, 19-71 (2017). [CrossRef]
- L. de Broglie: Nonlinear Wave Mechanics (Elsevier, Amsterdam 1960).
- D. R. Gulevich, F. V. Kusmartsev, Sergey Savel’ev, V. A. Yampol’skii, and Franco Nori: “Shape and wobbling wave excitations in Josephson junctions: Exact solutions of the (2+1)-dimensional sine-Gordon model", Phys. Rev. B 80, 094509 (2009). [CrossRef]
- J. Handsteiner et al. “Cosmic Bell Test: Measurement Settings from Milky Way Stars", Phys. Rev. Lett. 118, 060401 (2017).
- V. Jacques et al.: “Experimental Realization of Wheeler’s Delayed-Choice Gedanken Experiment", Science 315, Issue 5814 pp. 966–968 (16 Feb 2007).
- C. Jönsson: Electron Diffraction at Multiple Slits, American Journal of Physics 42, 4 (1974).
- A. Khare, I.C. Christov, and A. Saxena: “Successive phase transitions and kink solutions in ϕ8, ϕ10, and ϕ12 field theories", Phys. Rev. E 90, 023208 (2014).
- T. Kibble: “Relativistic models of Nonlinear Quantum Mechanics,” Commun. Math. Phys. 64, 73 (1978).
- F. V. Kusmartsev: “Application of catastrophe theory to molecules and solitons,” Phys. Rept. 183, 1 (1989).
- F. V. Kusmartsev, E. W. Mielke and F. E. Schunck: “Gravitational stability of boson stars,” Phys. Rev. D 43, 3895 (1991); “Stability of neutron and boson stars: A new approch based on catastrophe theory", Phys. Lett. A 157, 465 –468.
- V. G. Ivancevic and Tijana T. Ivancevic: “Sine-Gordon solitons, kinks and breathers as physical models of nonlinear excitations in living cellular structures,” J. Geometry and Symmetry in Physics 31, 1 – 56 (2013). [CrossRef]
- J. Javanainen and Uttam Shrestha: “Nonlinear Phenomenology from Quantum Mechanics: Soliton in a Lattice,” Phys. Rev. Lett. 101, 170405 (2008).
- C. Rogers and W.K. Schief: Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory (Cambridge University Press, Cambridge 2002).
- I. Lindgren: “Interpretation of Quantum Mechanics. A view of our universe,” AIP Conference Proceedings 1177, 10 (2009. [CrossRef]
- E.W. Mielke: “Outline of a Nonlinear, Relativistic Quantum Mechanics of Extended Particles,” Fortschritte der Physik 30, 551–585 (1981).
- E.W. Mielke: “Toward exact solutions of the nonlinear Heisenberg Pauli-Weyl spinor equation,” J. Math. Phys. 22, 2034 (1981).
- E.W. Mielke: “Rotating Boson Stars,” Part of the Fundamental Theories of Physics book series (Fontier FTPH, Springer volume 183, 2016).
- E.W. Mielke: Geometrodynamics of Gauge Fields: On the Geometry of Yang-Mills and Gravitational Gauge Theories" (Mathematical Physics Studies) 2nd ed. (Springer, 2017).
- E. W. Mielke: “Soliton model of dark matter and natural inflation,” J. Phys. Conf. Ser. 1208, 1, 012012 (2019); “Bifurcations of a soliton model of dark matter towards natural inflation,” Physics Letters B 807 (2020) 135538.
- E. W. Mielke and R. Scherzer: “Geon-type solutions of the nonlinear Heisenberg-Klein-Gordon equation,” Phys. Rev. D 24, 2111 (1981).
- B. Mielnik: “Is Nonlinear Quantum Mechanics possible??", in Quantum Theory And Symmetries - Proceedings of the International Symposium edited by V. K. Dobrev, Heinz-Dietrich Doebner, J.-D. Hennig, W Lucke p. 124 - 133 (World Scientific, Singapore 1981).
- B. Mielnik: “ Nonlinear quantum mechanics: a conflict with the Ptolomean structure?,” Physics Letters A 289, pages 1-8 (2001).
- P. Nattermann: “On (Non)linear Quantum Mechanics,” Symmetry in Nonlinear Mathematical Physics, Vol.2, 270– 278 (1997).
- B. Nordén: “Quantum entanglement: facts and fiction – how wrong was Einstein after all?", Quarterly Reviews of Biophysics (2016) 49, page 1 of 13. [CrossRef]
- Yu P. Rybakov and B. Saha: “Soliton model of the atom,” Foundations of Physics 25 (12):1723-1731 (1995); “Soliton Model of Extended Quantum Particles,” Annales de la Fondation Louis de Broglie 26, 381 (2001).
- R. Penrose: “On the Gravitization of Quantum Mechanics 1: Quantum State Reduction,” Found. Phys. 44 557–575 (2014).
- R. Penrose: Fashion, Faith, and Fantasy in the New Physics of the Universe (Princeton University Press, 2016).
- M. Tegmark and John Archibald Wheeler: “ 100 Years of the Quantum,” Sci. Am. 284, 68–75 (2001).
- A. Tonomura: “Direct Observation of thitherto unobservable Quantum Phenomena by using Electrons. PNAS 102, No. 42, 14952 – 14959 (October 18, 2005).
- St. Weinberg: “Testing quantum mechanics,” Annals of Physics 194, 336-386 (1989).
- Luis Vásquez: Time-energy Heisenberg-type relations for nonlinear classical fields, Phys. Rev. D 33, 2478 (1986).

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



