Submitted:
08 October 2023
Posted:
09 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The metric
3. The methods
3.1. Wave-like equation and boundary conditions
3.2. Higher order WKB method
3.3. Time-domain integration
3.4. Frobenius method
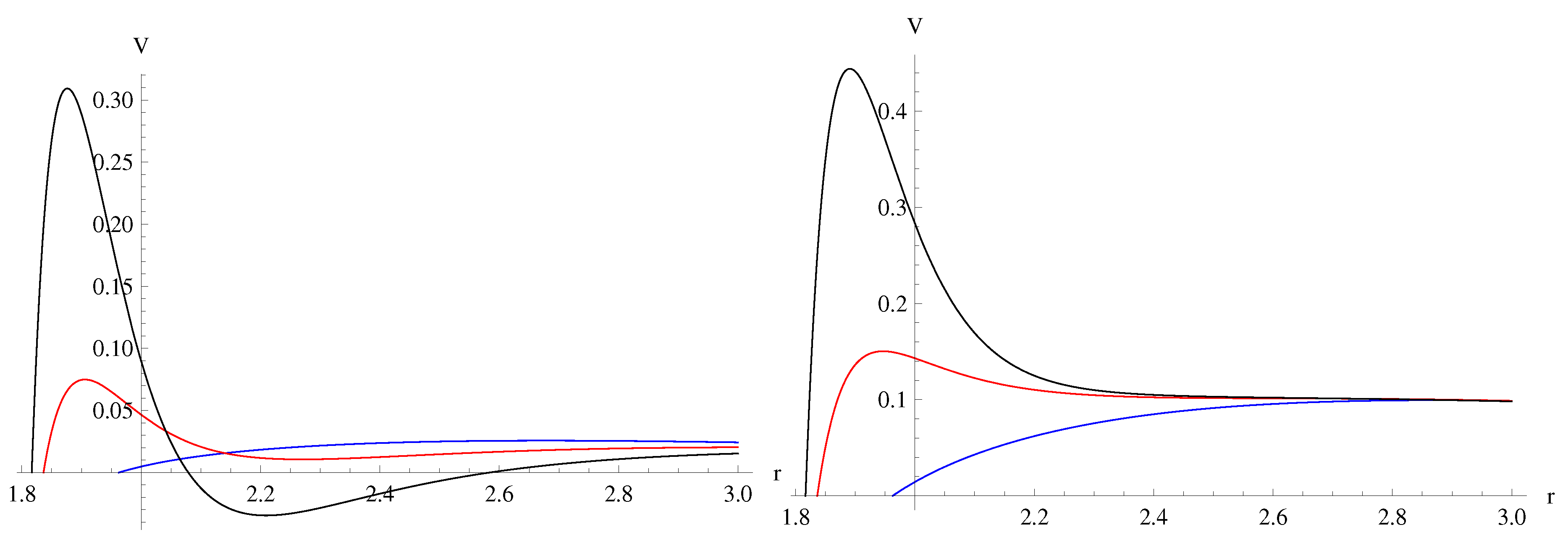
4. The threshold of instability
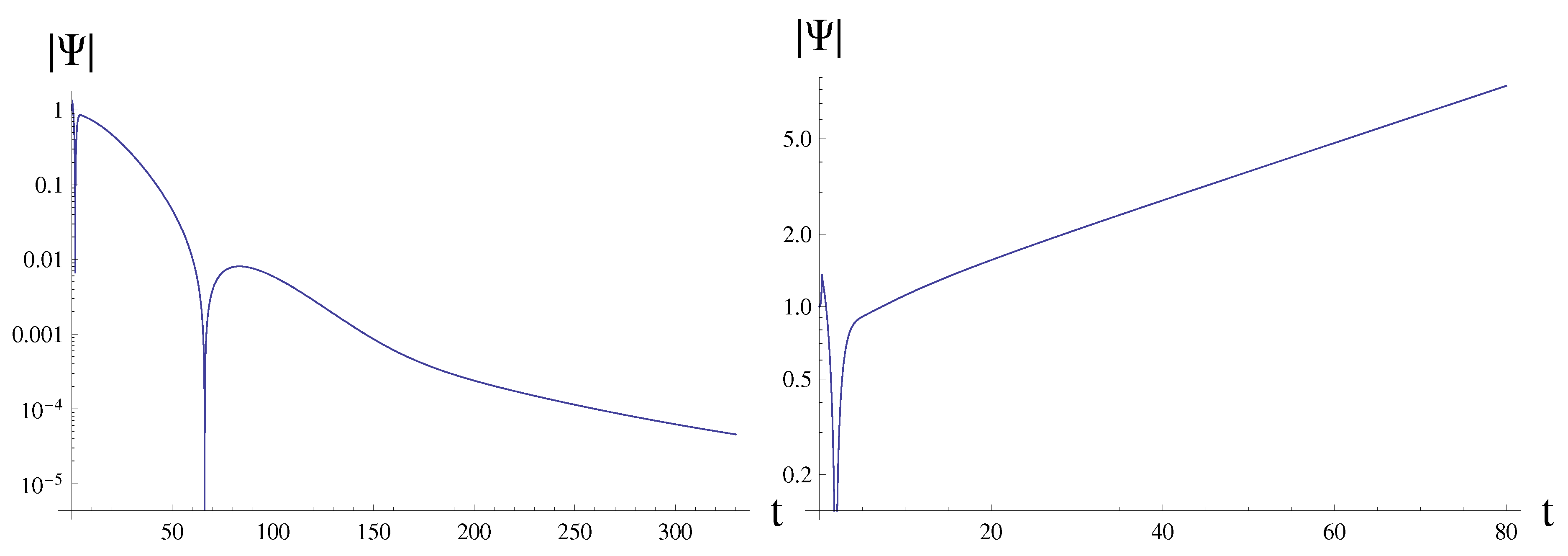
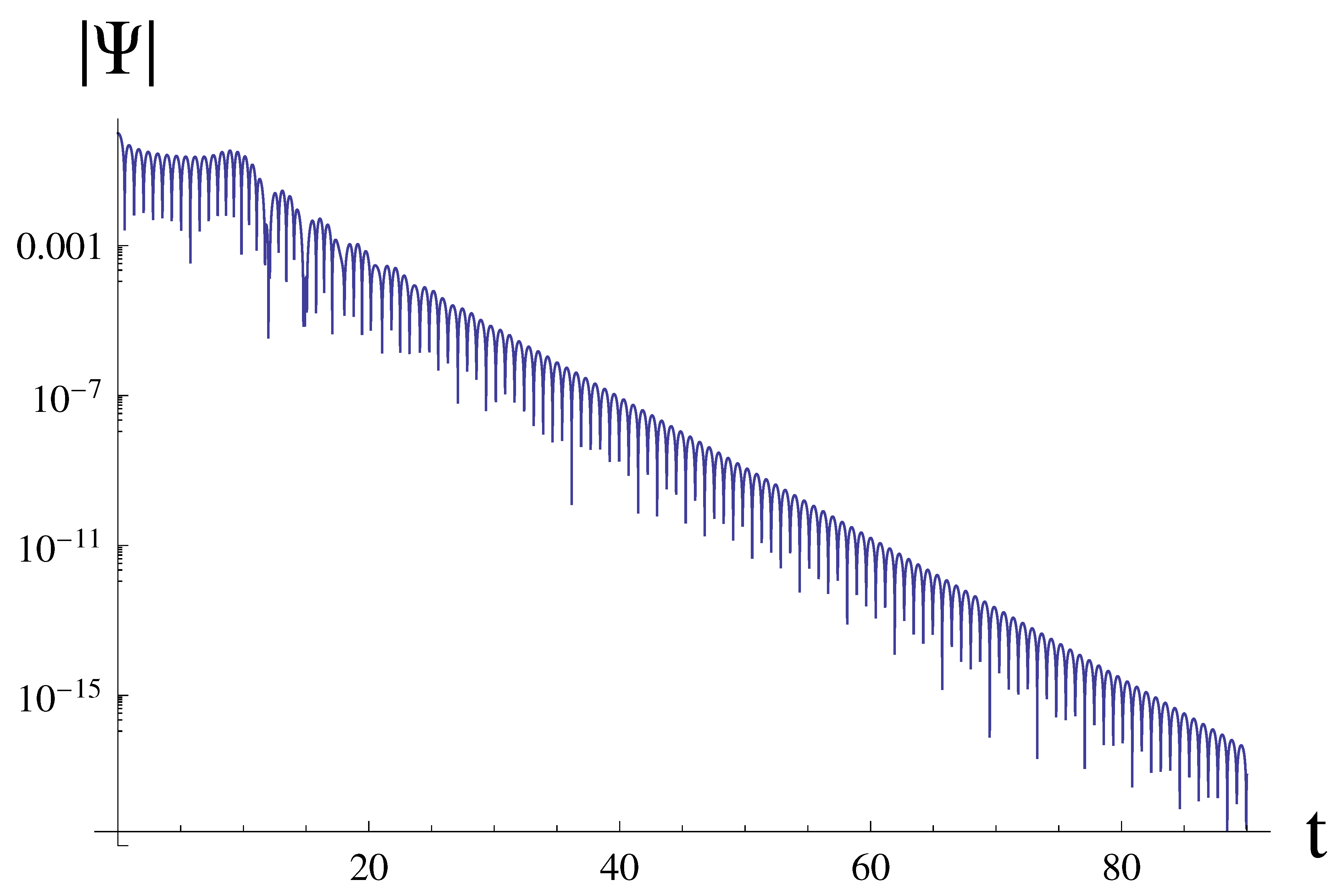
5. Quasinormal frequencies in the stable sector
| Time-domain | WKB | |
| 0.110022 - 0.105870 i | 0.109460 - 0.103417 i | |
| 0.110119- 0.105857 i | 0.109426 - 0.103701 i | |
| 0.110244 - 0.105843 i | 0.109436 - 0.103135 i | |
| 0.110766 - 0.105798 i | 0.083291 - 0.094837 i | |
| 0.111322 - 0.105778 i | 0.091824 - 0.129149 i | |
| 0.111892 - 0.105784 i | 0.086486 - 0.138424 i | |
| 0.112733 - 0.105896 i | 0.032663 - 0.143389 i | |
| 0.121337 - 0.115261 i | – |
| Time-domain | WKB | |
| 0.293003 - 0.097665 i | 0.292990 - 0.097690 i | |
| 0.293090 - 0.097568 i | 0.293246 - 0.097705 i | |
| 0.293202- 0.097447 i | 0.293569 - 0.097658 i | |
| 0.293430- 0.097203 i | 0.294184 - 0.097428 i | |
| 0.293667- 0.096956 i | 0.294743 - 0.097104 i | |
| 0.293912 - 0.096706 i | 0.295266 - 0.096741 i | |
| 0.294166 - 0.096453 i | 0.295776 - 0.096360 i | |
| 0.295543 - 0.095136 i | 0.299002 - 0.094337 i | |
| 0.304555 - 0.091160 i | 0.279144 - 0.059728 i | |
| 0.315643 - 0.093030 i | 0.278248 - 0.138408 i | |
| 0.323746 - 0.099017 i | 0.006171 - 0.042030 i | |
| 0.330159 - 0.109229 i | 0.082300 - 0.106786 i |
6. Conclusions
- At unphysically large values of the parameter of compactification it produces instability, while the regime of small is free from instability
- In the eikonal limit the correspondence breaks down, because it reproduces only part of the eikonal spectrum, but, unlike [58], this breakdown is for an asymptotically flat space.
- The ringing consists of the two stages at each of which different modes dominate. This could be well seen in the regime of large ℓ.
Acknowledgments
References
- Kokkotas, K.D.; Schmidt, B.G. Quasinormal modes of stars and black holes. Living Rev. Rel. 1999, 2, 2. [Google Scholar] [CrossRef]
- Nollert, H.P. TOPICAL REVIEW: Quasinormal modes: the characteristic `sound’ of black holes and neutron stars. Class. Quant. Grav. 1999, 16, R159–R216. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Quasinormal modes of black holes: From astrophysics to string theory. Rev. Mod. Phys. 2011, arXiv:gr-qc/1102.4014]83, 793–836. [Google Scholar] [CrossRef]
- Berti, E.; Cardoso, V.; Starinets, A.O. Quasinormal modes of black holes and black branes. Class. Quant. Grav. 2009, arXiv:gr-qc/0905.2975]26, 163001. [Google Scholar] [CrossRef]
- Barack, L.; others. Black holes, gravitational waves and fundamental physics: a roadmap. Class. Quant. Grav. 2019, arXiv:gr-qc/1806.05195]36, 143001. [Google Scholar] [CrossRef]
- Akiyama, K.; others. First Sagittarius A* Event Horizon Telescope Results. VI. Testing the Black Hole Metric. Astrophys. J. Lett. 2022, 930, L17. [Google Scholar] [CrossRef]
- Goddi, C.; others. BlackHoleCam: Fundamental physics of the galactic center. Int. J. Mod. Phys. D 2016, arXiv:astro-ph.HE/1606.08879]26, 1730001. [Google Scholar] [CrossRef]
- Konoplya, R.; Zhidenko, A. Detection of gravitational waves from black holes: Is there a window for alternative theories? Phys. Lett. B 2016, arXiv:gr-qc/1602.04738]756, 350–353. [Google Scholar] [CrossRef]
- Yunes, N.; Yagi, K.; Pretorius, F. Theoretical Physics Implications of the Binary Black-Hole Mergers GW150914 and GW151226. Phys. Rev. D 2016, arXiv:gr-qc/1603.08955]94, 084002. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Spectrum of relict gravitational radiation and the early state of the universe. JETP Lett. 1979, 30, 682–685. [Google Scholar]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Ivanov, V.R.; Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. Analytic extensions of Starobinsky model of inflation. JCAP 2022, arXiv:gr-qc/2111.09058]03, 058. [Google Scholar] [CrossRef]
- Ketov, S.V. Starobinsky–Bel–Robinson Gravity. Universe 2022, arXiv:gr-qc/2205.13172]8, 351. [Google Scholar] [CrossRef]
- Campos Delgado, R.; Ketov, S.V. Schwarzschild-type black holes in Starobinsky-Bel-Robinson gravity. Phys. Lett. B 2023, arXiv:gr-qc/2209.01574]838, 137690. [Google Scholar] [CrossRef]
- Ketov, S.V.; Pozdeeva, E.O.; Vernov, S.Y. On the superstring-inspired quantum correction to the Starobinsky model of inflation. JCAP 2022, arXiv:gr-qc/2211.01546]12, 032. [Google Scholar] [CrossRef]
- Do, T.Q.; Nguyen, D.H.; Pham, T.M. Stability investigations of isotropic and anisotropic exponential inflation in the Starobinsky-Bel-Robinson gravity 2023. arXiv:gr-qc/2303.17283.
- Pozdeeva, E.; Ketov, S.; Vernov, S. String-Inspired Correction to R2 Inflation. Phys. Sci. Forum 2023, 7, 2. [Google Scholar] [CrossRef]
- Belhaj, A.; Belmahi, H.; Benali, M.; Hassouni, Y.; Sedra, M.B. Deflection angle and Shadows by Black Holes in Starobinsky-Bel-Robinson Gravity from M-theory 2023. arXiv:hep-th/2304.03883.
- Arora, D.; Molla, N.U.; Chaudhary, H.; Debnath, U.; Atamurotov, F.; Mustafa, G. Exploring Tidal Force Effects and Shadow Constraints for Schwarzschild-like Black Hole in Starobinsky-Bel-Robinson Gravity 2023. arXiv:gr-qc/2308.13901.
- Whiting, B.F. Mode Stability of the Kerr Black Hole. J. Math. Phys. 1989, 30, 1301. [Google Scholar] [CrossRef]
- Dias, O.J.C.; Santos, J.E. Origin of the Reissner-Nordström–de Sitter instability. Phys. Rev. D 2020, arXiv:hep-th/2005.03673]102, 124039. [Google Scholar] [CrossRef]
- Ishihara, H.; Kimura, M.; Konoplya, R.A.; Murata, K.; Soda, J.; Zhidenko, A. Evolution of perturbations of squashed Kaluza-Klein black holes: escape from instability. Phys. Rev. D 2008, arXiv:hep-th/0802.0655]77, 084019. [Google Scholar] [CrossRef]
- Kodama, H.; Konoplya, R.A.; Zhidenko, A. Gravitational stability of simply rotating Myers-Perry black holes: Tensorial perturbations. Phys. Rev. D 2010, arXiv:gr-qc/0904.2154]81, 044007. [Google Scholar] [CrossRef]
- Cardoso, V.; Lemos, M.; Marques, M. On the instability of Reissner-Nordstrom black holes in de Sitter backgrounds. Phys. Rev. D 2009, arXiv:gr-qc/1001.0019]80, 127502. [Google Scholar] [CrossRef]
- Takahashi, T.; Soda, J. Catastrophic Instability of Small Lovelock Black Holes. Prog. Theor. Phys. 2010, arXiv:gr-qc/1008.1618]124, 711–729. [Google Scholar] [CrossRef]
- Cuyubamba, M.A.; Konoplya, R.A.; Zhidenko, A. Quasinormal modes and a new instability of Einstein-Gauss-Bonnet black holes in the de Sitter world. Phys. Rev. D 2016, arXiv:gr-qc/1604.03604]93, 104053. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, S.J.; Pellicer, C.E.; Wang, B.; Abdalla, E. Stability of Reissner-Nordström black hole in de Sitter background under charged scalar perturbation. Phys. Rev. D 2014, arXiv:hep-th/1405.4931]. [Addendum: Phys.Rev90, 044042. [Google Scholar] [CrossRef]
- Ohashi, A.; Sakagami, M.a. Massive quasi-normal mode. Class. Quant. Grav. 2004, 21, 3973–3984. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Stability and quasinormal modes of the massive scalar field around Kerr black holes. Phys. Rev. D 2006, 73, 124040. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Massive charged scalar field in the Kerr-Newman background I: quasinormal modes, late-time tails and stability. Phys. Rev. D 2013, arXiv:gr-qc/1307.1812]88, 024054. [Google Scholar] [CrossRef]
- Schutz, B.F.; Will, C.M. Black Hole Normal Modes: A semianalytic approach. Astrophys. J. Lett. 1985, 291, L33–L36. [Google Scholar] [CrossRef]
- Iyer, S.; Will, C.M. Black Hole Normal Modes: A WKB Approach. 1. Foundations and Application of a Higher Order WKB Analysis of Potential Barrier Scattering. Phys. Rev. D 1987, 35, 3621. [Google Scholar] [CrossRef] [PubMed]
- Konoplya, R.A. Quasinormal behavior of the d-dimensional Schwarzschild black hole and higher order WKB approach. Phys. Rev. D 2003, 68, 024018. [Google Scholar] [CrossRef]
- Matyjasek, J.; Opala, M. Quasinormal modes of black holes. The improved semianalytic approach. Phys. Rev. D 2017, arXiv:gr-qc/1704.00361]96, 024011. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A.; Zinhailo, A.F. Higher order WKB formula for quasinormal modes and grey-body factors: recipes for quick and accurate calculations. Class. Quant. Grav. 2019, arXiv:gr-qc/1904.10333]36, 155002. [Google Scholar] [CrossRef]
- Matyjasek, J. Accurate quasinormal modes of the five-dimensional Schwarzschild-Tangherlini black holes. Phys. Rev. D 2021, arXiv:gr-qc/2107.04815]104, 084066. [Google Scholar] [CrossRef]
- Guo, G.; Wang, P.; Wu, H.; Yang, H. Superradiance instabilities of charged black holes in Einstein-Maxwell-scalar theory. JHEP 2023, arXiv:gr-qc/2301.06483]07, 070. [Google Scholar] [CrossRef]
- Matyjasek, J. Quasinormal modes of dirty black holes in the effective theory of gravity with a third order curvature term. Phys. Rev. D 2020, arXiv:gr-qc/2009.10793]102, 124046. [Google Scholar] [CrossRef]
- Konoplya, R.A. Quantum corrected black holes: quasinormal modes, scattering, shadows. Phys. Lett. B 2020, arXiv:gr-qc/1912.10582]804, 135363. [Google Scholar] [CrossRef]
- Gundlach, C.; Price, R.H.; Pullin, J. Late time behavior of stellar collapse and explosions: 1. Linearized perturbations. Phys. Rev. D 1994, 49, 883–889. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Konoplya, R.A. Echoes in brane worlds: ringing at a black hole–wormhole transition. Phys. Rev. D 2020, arXiv:gr-qc/1912.05315]101, 064004. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F.; Stuchlik, Z. Quasinormal modes and Hawking radiation of black holes in cubic gravity. Phys. Rev. D 2020, arXiv:gr-qc/2006.10462]102, 044023. [Google Scholar] [CrossRef]
- Leaver, E.W. An Analytic representation for the quasi normal modes of Kerr black holes. Proc. Roy. Soc. Lond. A 1985, 402, 285–298. [Google Scholar] [CrossRef]
- Leaver, E.W. Spectral decomposition of the perturbation response of the Schwarzschild geometry. Phys. Rev. D 1986, 34, 384–408. [Google Scholar] [CrossRef] [PubMed]
- Nollert, H.P. Quasinormal modes of Schwarzschild black holes: The determination of quasinormal frequencies with very large imaginary parts. Phys. Rev. D 1993, 47, 5253–5258. [Google Scholar] [CrossRef]
- Zhidenko, A. Massive scalar field quasi-normal modes of higher dimensional black holes. Phys. Rev. D 2006, 74, 064017. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. The portrait of eikonal instability in Lovelock theories. JCAP 2017, arXiv:hep-th/1705.01656]05, 050. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Murata, K.; Soda, J.; Zhidenko, A. Looking at the Gregory-Laflamme instability through quasi-normal modes. Phys. Rev. D 2008, arXiv:hep-th/0807.1897]78, 084012. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Analytic expressions for quasinormal modes and grey-body factors in the eikonal limit and beyond, arXiv: 2309.02560. 2023, arXiv:gr-qc/2309.02560. [Google Scholar]
- Cardoso, V.; Miranda, A.S.; Berti, E.; Witek, H.; Zanchin, V.T. Geodesic stability, Lyapunov exponents and quasinormal modes. Phys. Rev. D 2009, arXiv:hep-th/0812.1806]79, 064016. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Stuchlík, Z. Are eikonal quasinormal modes linked to the unstable circular null geodesics? Phys. Lett. B 2017, arXiv:gr-qc/1705.05928]771, 597–602. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F. Quasinormal modes, stability and shadows of a black hole in the 4D Einstein–Gauss–Bonnet gravity. Eur. Phys. J. C 2020, arXiv:gr-qc/2003.01188]80, 1049. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F.; Stuchlík, Z. Quasinormal modes, scattering, and Hawking radiation in the vicinity of an Einstein-dilaton-Gauss-Bonnet black hole. Phys. Rev. D 2019, arXiv:gr-qc/1903.03483]99, 124042. [Google Scholar] [CrossRef]
- Zhidenko, A. Quasinormal modes of Schwarzschild de Sitter black holes. Class. Quant. Grav. 2004, 21, 273–280. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. High overtones of Schwarzschild-de Sitter quasinormal spectrum. JHEP 2004, 06, 037. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zhidenko, A. Nonoscillatory gravitational quasinormal modes and telling tails for Schwarzschild–de Sitter black holes. Phys. Rev. D 2022, arXiv:gr-qc/2209.12058]106, 124004. [Google Scholar] [CrossRef]
- Cardoso, V.; Costa, J.a.L.; Destounis, K.; Hintz, P.; Jansen, A. Quasinormal modes and Strong Cosmic Censorship. Phys. Rev. Lett. 2018, arXiv:gr-qc/1711.10502]120, 031103. [Google Scholar] [CrossRef]
- Konoplya, R.A. Further clarification on quasinormal modes/circular null geodesics correspondence. Phys. Lett. B 2023, arXiv:gr-qc/2210.08373]838, 137674. [Google Scholar] [CrossRef]
- Jusufi, K. Quasinormal Modes of Black Holes Surrounded by Dark Matter and Their Connection with the Shadow Radius. Phys. Rev. D 2020, arXiv:gr-qc/1912.13320]101, 084055. [Google Scholar] [CrossRef]
- Jafarzade, K.; Kord Zangeneh, M.; Lobo, F.S.N. Shadow, deflection angle and quasinormal modes of Born-Infeld charged black holes. JCAP 2021, arXiv:gr-qc/2010.05755]04, 008. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





