Long Lived Quasinormal Modes and Telling Oscillatory Tails of the Bardeen Spacetime

1. Introduction

The Einstein theory of gravity raises a number of crucial problems in cosmology and physics of compact objects. One of such problems is existence of the Schwarzschild singularity which means reaching the limits of a classical gravitational theory. In this context the Bardeen metric is the first historically important model of a regular black hole [1]. Decades after the Bardeen’s report [1], an interpretation of the Bardeen metric was put forward in the context of a specific nonlinear electrodynamics in curved spacetime, suggesting it as a massive gravitating magnetic monopole [2]. However, as the weak field limit is constrained to the usual Maxwell electrodynamics, the electric charge must disappear, as required by the Bronnikov theorem [3]. Despite such a defect of the interpretation of the Bardeen metric, numerous investigations have been dedicated to exploring various effects around such giant magnetic monopoles, particularly their characteristic oscillation frequencies ([4,5,6,7]). These (quasinormal) frequencies have been studied for the above and similar non-linear electrodynamics in great number of works [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28].

We will be studying here the Bardeen spacetime in a completely different context, namely, as a quantum-corrected solution to the Schwarzschild metric. Within this framework, the parameter that previously denoted the magnetic charge now governs the scale of the quantum correction of a neutral black hole. Stringy correction to the Schwarzschild spacetime coming from the string T-duality was proposed by Nicolini et. al. [29]. There, the intrinsic non-perturbative nature of stringy corrections introducing an ultraviolet cutoff resulted in a consistent spherically symmetric, asymptotically flat and regular black-hole metric. The metric is equivalent to the Bardeen spacetime after the appropriate redefinition of constants [29]. It is interesting that the Bardeen metric can also be deduced as an effective one that reproduces the black-hole thermodynamics within the so called Generalized Uncertainty Principle [30], representing another, more speculative approach to construction of quantum correction to the classical black-hole spacetime.

One of the facets that captures our interest concerns the behavior of the first few higher overtones within the quasinormal spectrum. While the prevailing notion suggests that the fundamental mode alone describes the geometry of the black hole, this perspective is not entirely accurate. The fundamental mode remains impervious to the event horizon’s geometry and is primarily dictated by the geometry near the maximum of the effective potential. Consequently, if a black hole were to be substituted with a distorted black hole (or even an alternative entity, such as a wormhole) possessing a matching geometry around the potential’s peak, the fundamental mode would change only minimally [31]. To discern the behavior in proximity to the horizon, it becomes imperative to contemplate multiple overtones which demonstrate a high degree of sensitivity to even the slightest deformations in the vicinity of the event horizon [32]. Furthermore, these overtones play a pivotal role in describing the early phase of the ringdown [33]. Hence, delving into the first several overtones of the spectrum equips us to probe the black hole’s geometry near the event horizon.

Quasinormal modes of the Bardeen black holes, construed as quantum corrections to Schwarzschild gravity, have recently been computed for massless fields in [34] utilizing the precise Leaver method. The analysis revealed that the higher overtones deviate from their Schwarzschild counterparts at a substantially higher pace compared to the fundamental mode, and this deviation can be traced back to the metric’s deformation around the event horizon [32]. Analogous deviations have been recently detected in the context of black holes within theories involving higher curvature corrections and asymptotically safe gravity [35,36,37,38].

Here we will make the next step and study the quasinormal modes for a massive scalar field in the Bardeen spacetime. This way we can see how the phenomenon of arbitrarily long lived modes, which also includes complex behavior of overtones, overlaps with the expected outburst of overtones.

There exist various motivations for delving into the study of massive fields. The inclusion of a mass term brings about qualitative shifts within the black hole spectrum: distinct modes, known as quasi-resonances [39,40], with arbitrarily extended lifetimes emerge in the spectrum. The occurrence of quasi-resonances is a pervasive phenomenon, manifesting not only in the context of scalar fields within the Schwarzschild background, but also for massive fields of varying spins [41], axially-symmetric Kerr and Kerr-Newman backgrounds [42,43], and other objects such as wormholes [44]. It also takes place within diverse alternative theories of gravity [45,46,47]. In addition, a massless field acquires an effective massive term when the black hole is immersed in a magnetic field [48,49,50]. The effective massive term appears also in the spectra of higher dimensional theories of gravity [51,52]. After all, the massive term changes the evolution of the signal in time-domain, the period of quasinormal ringing is changed not by power-law asymptotic tails, but by slowly decaying oscillatory tails studied in a great number of works [53,54,55,56,57,58]. Recently it was suggested [59] that these oscillatory tails may contribute into the very long waves detected by the pulsar timing array observations [60].

We will show that the quasinormal spectrum of the massive scalar field in the Bardeen background is qualitatively different from the massless one. First of all, the damping rate is decreasing, once the mass of the field grows, leading to the arbitrarily long lived modes. At asymptotically late times, the oscillatory tails are observed whose decay law is different from those in the Schwarzschild or Reinssner-Nordström spacetimes.

The structure of the paper is outlined as follows. In Section II, we suggest a concise overview of the Bardeen solution along with the associated wave-like equations providing effective potentials. Section III encompasses the numerical techniques used for the computation of quasinormal modes. Within Section IV, we discuss the found quasinormal modes of a massive scalar field and the emergence of the outburst of overtones. Lastly, the Conclusions section encapsulates a summary of the attained outcomes and highlights future perspectives.

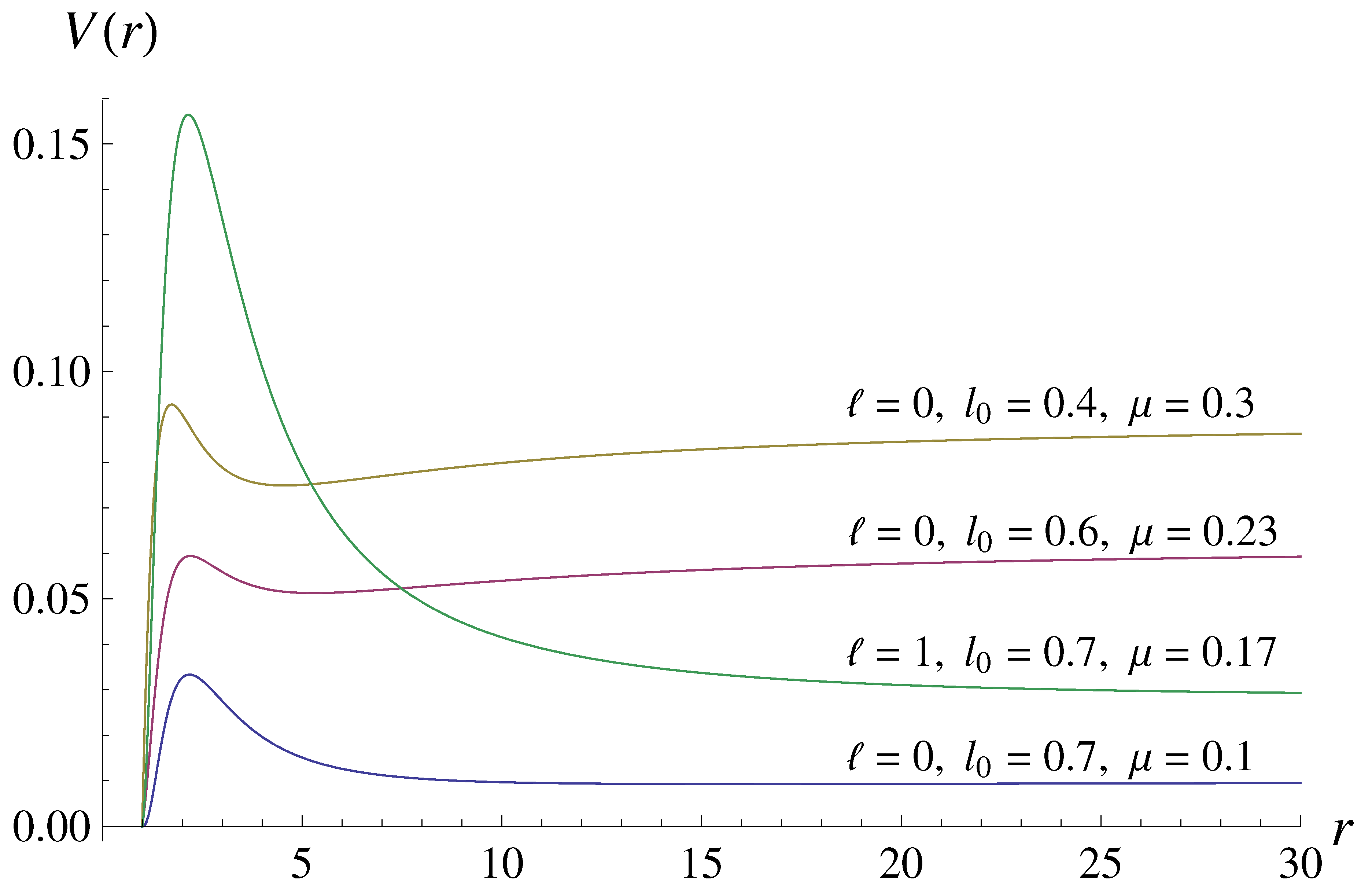
2. The black hole background and wavelike equations

The spherically symmetric metric is given by the following line element

$$d{s}^2=-f\left(r\right)d{t}^2+f^{-1}\left(r\right)d{r}^2+r^2(d{\theta }^2+{sin}^2\theta d{\phi }^2),$$

(1)

where for the Bardeen spacetime we have

$$f\left(r\right)=1-\frac{2M{r}^2}{{(r^2+l_0^2)}^{3/2}}.$$

(2)

The horizon exists if,

$$|l_0|\le \frac{4M}{3\sqrt{3}},$$

as it was shown in [61]. The parameter $l_0$ is related to the Regge slope:

$$\sqrt{{\alpha }^{\prime }}=\frac{l_0}{2\pi }\approx 0.117l_P,$$

(3)

where $l_P$ is the Plank mass, so that, as in [62], we have: $l_0\sim l_P$. Instead of the central singularity the Bardeen spacetime has a de Sitter core in the origin, since for $r\ll l_0$ we have

$$f\left(r\right)\to 1-\frac{{\mathrm{\Lambda }}_{\mathrm{eff}}{r}^2}{3},$$

(4)

where ${\mathrm{\Lambda }}_{\mathrm{eff}}=6M/l_0^3$ can be considered as an effective cosmological constant.

When using the Frobenius method we will utilize the expansion of the above full metric in terms of the small parameter $l_0$:

$$\begin{array}{ccc}\hfill f\left(r\right)& =& \left(1-\frac{2M}{r}\right)+\frac{3l_0^{2}M}{r^3}-\frac{15l_0^{4}M}{4r^5}+\frac{35l_0^{6}M}{8r^7}\hfill \\ & -& \frac{315l_0^{8}M}{64r^9}+\frac{693l_0^{10}M}{128r^{11}}-\frac{3003l_0^{12}M}{512r^{13}}+\frac{6435l_0^{14}M}{1024r^{15}}\hfill \\ & -& \frac{109395l_0^{16}M}{16384r^{17}}+\frac{230945l_0^{18}M}{32768r^{19}}-\frac{969969l_0^{20}M}{131072r^{21}}\hfill \\ & +& \frac{2028117l_0^{22}M}{262144r^{23}}-\frac{16900975l_0^{24}M}{2097152r^{25}}+O\left(l_0^{26}\right),\hfill \end{array}$$

(5)

which is a very good approximation to the full metric as can be seen on comparison for quasinormal modes calculated for the full metric and for the above approximation in [34].

The general relativistic Klein-Gordon equations for the scalar field can be written as follows:

$$\begin{array}{ccc}\hfill \frac{1}{\sqrt{-g}}{\partial }_{\mu }\left(\sqrt{-g}{g}^{\mu \nu }{\partial }_{\nu }\mathrm{\Phi }\right)+{\mu }^2\mathrm{\Phi }& =& 0.\hfill \end{array}$$

(6)

Here $\mu$ is the mass of the scalar field. After separation of variables Equation (6) take the wave-like form:

$${\displaystyle \frac{d^2\mathrm{\Psi }}{d{r}_{*}^2}}+({\omega }^2-V\left(r\right))\mathrm{\Psi }=0,$$

(7)

where the “tortoise coordinate” $r_{*}$ is defined as follows:

$$d{r}_{*}\equiv \frac{dr}{f\left(r\right)}.$$

(8)

The effective potential for the scalar field has the form

$$V\left(r\right)=f\left(r\right)\left(\frac{\ell (\ell +1)}{r^2}+\frac{1}{r}\frac{df\left(r\right)}{dr}+{\mu }^2\right),$$

(9)

where $\ell =0,1,2,\dots$ are the multipole numbers.

Figure 1. Effective potentials of a massive scalar field in the Bardeen background for various values of $l_0$, ℓ and $\mu$; $r_0=1$.

Figure 1. Effective potentials of a massive scalar field in the Bardeen background for various values of $l_0$, ℓ and $\mu$; $r_0=1$.

3. Methods for finding of quasinormal modes

Quasinormal modes are eigenfrequencies of the master wave-like equation Equation (7) satisfying specific boundary conditions. Namely, it is required that only purely incoming waves either to the event horizon or to infinity are allowed. Thus, the waves coming from either infinity or the event horizon to the peak of the effective potential are forbidden and the observer considers proper frequencies when the source of perturbations stopped acting. A number of methods for determining quasinormal frequencies have been discussed in a lot of papers (see a review [7]), so that we will only briefly summarize the three methods which we used: the WKB method with the application of the Padé approximants, the Leaver or Frobenius method, and the Price-Pullin time-domain integration scheme.

3.1. WKB approach

We will apply the semi-analytic WKB approach developed at the first WKB order by Will and Schutz [63] and generalized to 13th order [64,65,66]. Recently it has been improved by implementing the Padé approximants [66,67], so that with this last improvement the accuracy of the WKB method is frequently sufficient even for finding $\ell =n$ modes.

The general WKB formula can be written as follows [68]:

$$\begin{array}{ccc}\hfill {\omega }^2& =& V_0+A_2\left({\mathcal{K}}^2\right)+A_4\left({\mathcal{K}}^2\right)+A_6\left({\mathcal{K}}^2\right)+\dots \hfill \\ \hfill & -& i\mathcal{K}\sqrt{-2V_2}\left(1+A_3\left({\mathcal{K}}^2\right)+A_5\left({\mathcal{K}}^2\right)+A_7\left({\mathcal{K}}^2\right)+\dots \right),\hfill \end{array}$$

(10)

where for the quasinormal modes boundary conditions $\mathcal{K}=n+1/2$ is a half-integer. The corrections $A_k\left({\mathcal{K}}^2\right)$, of order k, are polynomials of ${\mathcal{K}}^2$ with some rational coefficients, which depend higher derivatives of the effective potential $V\left(r\right)$ in the maximum, $V_j,(j=0,1,2,...$). We also used the Matyjasek-Opala improvement [66] with Padé approximants as follows: we use the sixth-order WKB formula with Pade approximants with $\tilde{m}=4,5$, where the parameter $\tilde{m}$ defines corresponding polynomial degrees in the expressions for Padé approximants [66,68]. This choice yields the best accuracy in the Schwarzschild limit and is also appropriate for the Bardeen black hole, as confirmed by comparisons with accurate data in [34]. The WKB series converges only asymptotically, not guaranteeing better accuracy at each order. That is why, the WKB method will be applied here only as an additional way to check the Leaver method in the range of its validity. In addition, the WKB method is useful here for providing initial guess for quasinormal modes when further applying the Frobenius method.

3.2. Leaver method

The Frobenius or Leaver method is our main method here, which is based on the convergent procedure and let us attain precise values of quasinormal modes, including higher overtones with $\ell <n$, we will utilize the Frobenius method, also known as the Leaver method [69]. The differential wave-like equation consistently exhibits a regular singular point at the event horizon, located at $r=r_0$, and an irregular singular point at spatial infinity, denoted as $r=\infty$. Following a similar approach as in [70], we introduce a novel function:

$$\mathrm{\Psi }\left(r\right)=P(r,\omega ){\left(1-\frac{r_0}{r}\right)}^{-i\omega /F^{\prime }\left(r_0\right)}y\left(r\right),$$

(11)

where the choice of $P(r,\omega )$ is made such that $y\left(r\right)$ maintains regularity within the interval $r_0\le r<\infty$, ensuring that $\mathrm{\Psi }\left(r\right)$ complies with the quasinormal mode boundary condition. Subsequently, we represent $y\left(r\right)$ in the form of a Frobenius series:

$$y\left(r\right)=\sum _{k=0}^{\infty }{a}_k{\left(1-\frac{r_0}{r}\right)}^k.$$

(12)

By applying Gaussian elimination to the recurrence relation governing the expansion coefficients, we simplify the problem to solving an algebraic equation. To expedite convergence, we will also incorporate the Nollert improvement [71] in the general n-term recurrence relation form suggested in [72]. We see that for the first tens overtones the method converges very quickly and only two or three terms of the Nollert expansion are sufficient. When the singular points of the wave-like equation fall within the unit circle $\left|x\right|<1$, we employ a sequence of positive real midpoints according to [73]. We also used the data from the WKB method for the initial guess of the low laying modes.

3.3. Time-domain integration

For finding not only quasinormal modes, but also analysis of the evolution of the signal with time including the asymptotic tails, we use the time-domain integration method based on integration of the wave-like equation in terms of the null-cone variables $u=t-r_{*}$ and $v=t+r_{*}$. As a discretization scheme, we will apply the Gundlach-Price-Pullin procedure [74]:

$$\mathrm{\Psi }\left(N\right)=\mathrm{\Psi }\left(W\right)+\mathrm{\Psi }\left(E\right)-\mathrm{\Psi }\left(S\right)$$

$$-{\mathrm{\Delta }}^{2}V\left(S\right)\frac{\mathrm{\Psi }\left(W\right)+\mathrm{\Psi }\left(E\right)}{4}+\mathcal{O}\left({\mathrm{\Delta }}^4\right).$$

(13)

Here, the points are: $N\equiv \left(u+\mathrm{\Delta },v+\mathrm{\Delta }\right)$, $W\equiv \left(u+\mathrm{\Delta },v\right)$, $E\equiv \left(u,v+\mathrm{\Delta }\right)$, and $S\equiv \left(u,v\right)$. Gaussian initial wave package are imposed on the two null surfaces $u=u_0$ and $v=v_0$ and it is well-known that the frequencies do not depend on the parameters of this initial incident wave package. The low-lying quasinormal frequencies can be extracted from the time-domain profile using the Prony method, if the profile is built with sufficiently high accuracy.

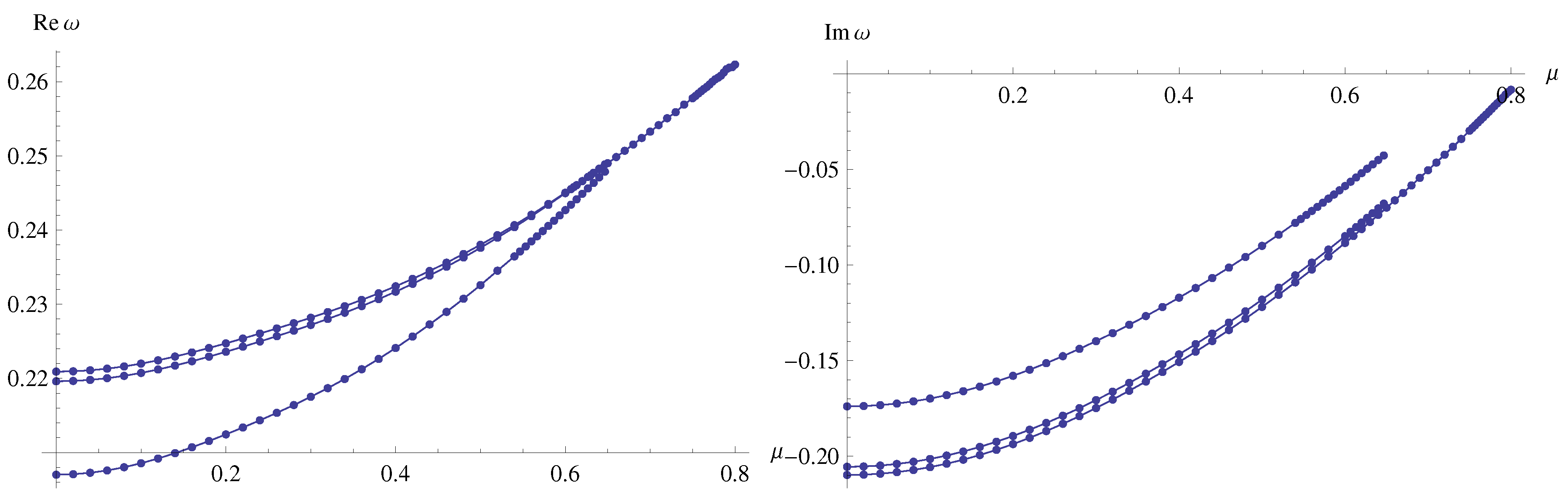
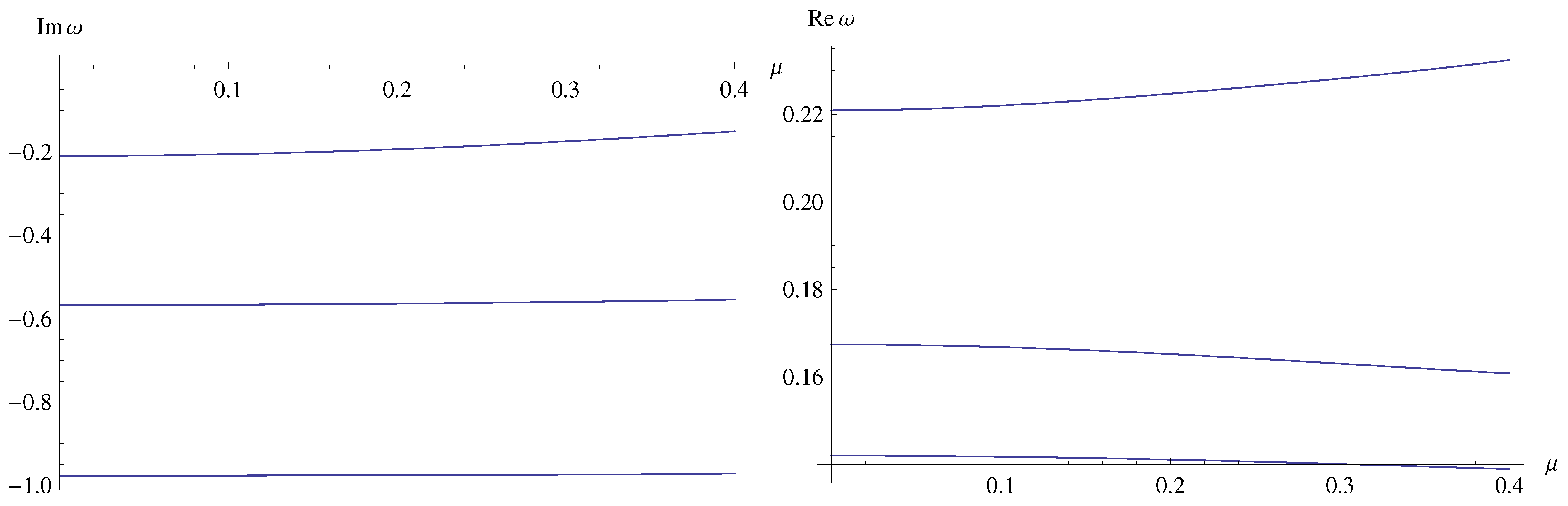
4. Quasi-resonances and outburst of overtones

We will find quasinormal frequencies in units of the fixed radius of the event horizon, $r_0=1$, instead of fixing the mass of the black hole, M. The mass and radius of the event horizon are related as follows:

$$M=\frac{{(r_0^2+l_0^2)}^{3/2}}{2r_0^2}.$$

(14)

This equation allows us to switch between the units $r_0=1$ and $M=1$. The units of the fixed event horizon are more convenient when using the Frobenius method, because it requires analysis of the singular points of the master differential wave equation.

From Figure 2 from accurate data obtained by the Frobenius method we see that when the mass of the field $\mu$ increases, the real oscillations frequency increases monotonically, while the damping rate decreases and the extrapolation to larger values of $\mu$ indicates that the modes go over into the arbitrarily long lived modes (quasi-resonances). This is illustrated for the Bardeen black hole with $l_0=0.1$ and $l_0=0.3$ in Figure 2. We see that the quantum deformation parameter $l_0$ suppresses both $\mathrm{Re}\omega$ and $\mathrm{Im}\omega$. Notice that in order to reach the regime of very small damping rates, much longer Frobenius expansion is necessary for achieving convergence and the whole computational procedure is many times lengthier for the expanded Bardeen metric given by Equation (5). Therefore, the modes for the Bardeen case are calculated until smaller values of $\mu$ than those for the Schwarzschild limit in Figure 2. However, extrapolation to larger $\mu$ clearly indicates the appearance of the quasi-resonances.

In Table 1, Table 2, Table 3, Table 4 and Table 5 the quasinormal modes of a massive scalar field obtained with the 6th order WKB method with Padé approximants are shown. There we can see that once the mass $\mu$ is relatively small, the WKB provides reasonable accuracy with the accurate Frobenius data. For example, the 6th order WKB with Padé for $\ell =0$ (which is the worst case) aand $\mu =0.1$ gives $\omega =0.214506-0.182665i$. This value differs from the accurate Frobenius data $\omega =0.214580-0.183725i$ by less than one percent, while the usual 6th order WKB gives $\omega =0.221975-0.197486i$ producing a relative error of several percents.

However, the larger $\mu$, the larger is the descripancy with the accurate results, which is expected since the massive term produce a second peak in the far region. When $\mu =0$ we reproduce the results presented in [34], while at both $\mu =0$ and $l_0=0$, the data for the Schwarzschild case are reproduced [40].

From Figure 3 we see that the fundamental mode changes at a much higher rate than the overtones, when the mass of the field is increased. This concerns more the real oscillation frequency than the damping rate. The mass term vanishes at the event horizon and represents a kind of deformation of the spacetime in far zone. Thus, this is another demonstration, in addition to that made in [32], that the deformation at a distance from the black hole does not produce the outburst of overtones. Nevertheless we observe the outburst of overtones relatively the Schwarzschild spacetime, if we consider $l_0$ as a deformation of the Schwarzschild metric. Then second and third modes deviate from the Schwarzschild limit at a greater rate than the fundamental mode at the same value of $\mu$.

At asymptotically late times, the quasinormal ringing of a massless scalar or gravitational field is suppressed by power-law tails which do not oscillate and the Price decay law [75] is fulfilled. The situation is different for the massive scalar field in the Schwarzschild or Reinssner-Nordström backgrounds [54,58], where the asymptotic tail is oscillatory and does not depend on ℓ:

$$\left|\mathrm{\Psi }\right|\sim t^{-5/6}sin\left(\mu t\right),t\to \infty .$$

(15)

This decay law dominates at times

$$\frac{t}{M}>{\left(\mu M\right)}^{-3}.$$

(16)

This law was observed for a number of other backgrounds and fields. For example, it was observed for a massive scalar filed in the dilatonic black hole background [55], for a massive vector field in the Schwarzschild spacetime [76], for the massive Dirac field [53], for gravitational field in the Randall-Sundrum-type models [51] and others. Thus it would be highly expected to observe the same behavior for the Bardeen black hole. However, as can be seen from Figure 5, the decay law is different now:

$$\left|\mathrm{\Psi }\right|\sim t^{-1}sin\left(A\left(\mu \right)t\right),t\to \infty .$$

(17)

At the intermediate times the tails could be observed if one choose relatively small value of $\mu M$ (see Figure 4). The decay law is

$$\left|\mathrm{\Psi }\right|\sim t^{-(\frac{8}{6}+\ell )}sin\left(A\left(\mu \right)t\right).$$

(18)

Here $A\left(\mu \right)$ is some function, which, in principle, could be found via fitting numerical data for various values of $\mu$.

5. Conclusions

The spacetime structure of the Bardeen solution defines a regular black hole with a de Sitter core instead of a central singularity. Considering this spacetime as the metric describing a black hole that incorporates quantum corrections through the string T-duality [29], an exhaustive examination of the quasinormal spectrum a massive scalar field was undertaken. We have shown that:

• The decay rate of a given mode decreases while the mass of the field grows, which leads to appearance of the arbitrarily long lived quasinormal modes, called quasi-resonances [39,42].
• The outburst of overtones, i.e. the deviation of the overtones from their Schwarzschild limits at a much higher rate than it happens for the fundamental mode, occurs also for the massive field when the quantum deformation parameter $l_0$ is considered as a near-horizon deformation that induces the outburst.
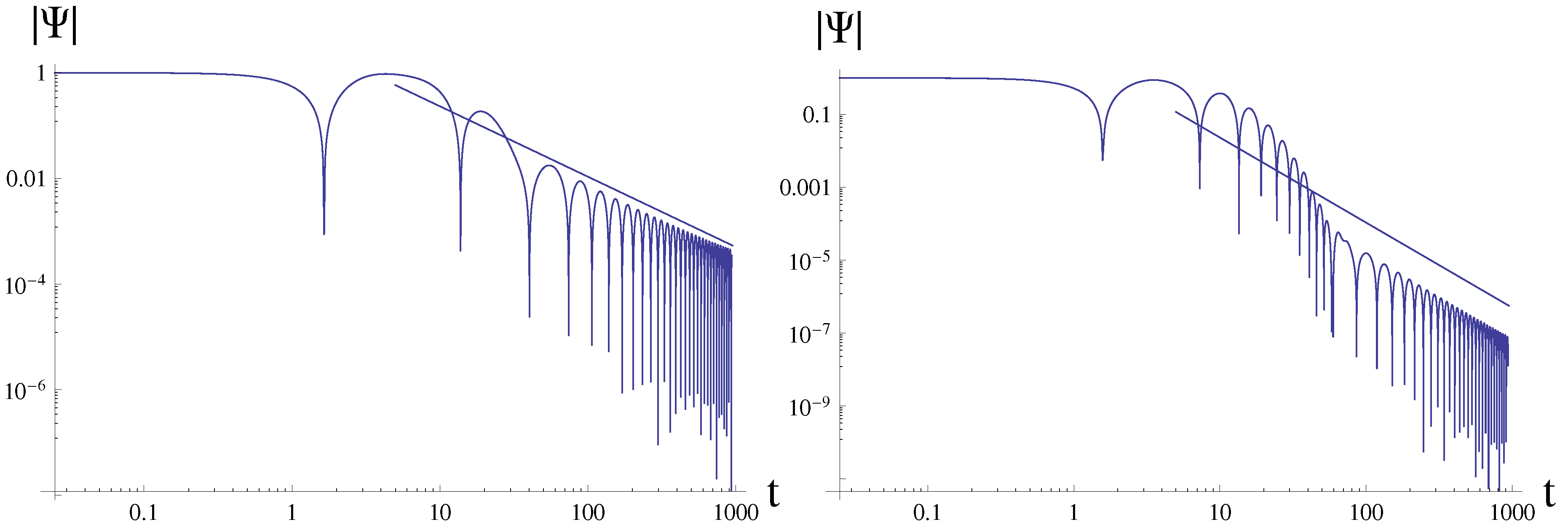
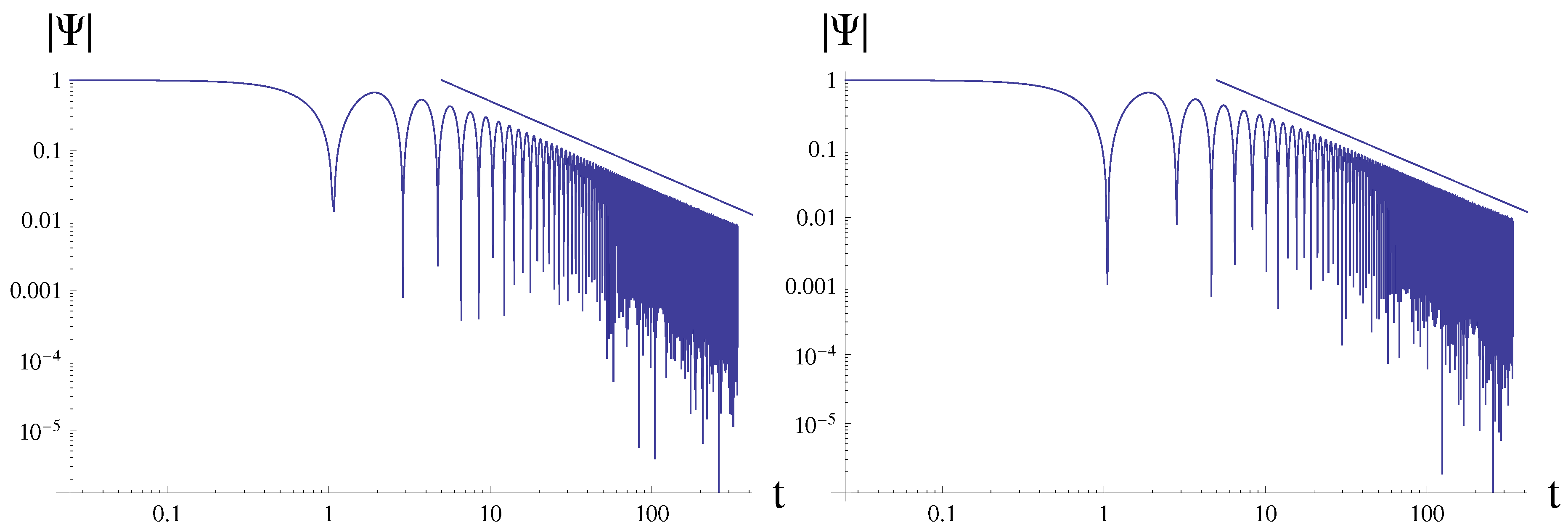
• At asymptotically late time the oscillatory tails dominate and the decay law is different from those for the Schwarzschild, Reissner-Nordström and a number of other spacetimes both at intermediate and asymptotic times.
• The quasinormal frequencies were found precisely with the help of the convergent Frobenius method and checked with the higher order WKB method and time-domain integration. Comparison with the accurate Frobenius data shows that the WKB approach with Padé approximants is more accurate than the usual WKB method. Nevertheless, the error of the WKB method grows as $\mu$ is increased.

Our work could be extended in various ways. First of all, as the asymptotic decay law differs from the Reissner-Nordström case, it is tempting to consider massive fields of other spin such as vector and Dirac in order to see whether the decay law is universal or depends on the spin of the field. Finally, if a convincing axially-symmetric generalization of the Bardeen spacetime will be obtained within the T-duality approach, our analysis could, in principle, be extended to rotating black holes.