Submitted:
30 December 2022
Posted:
04 January 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. 4D EGB Model
3. The Black Hole Thermodynamics
4. Black Holes Shadows
5. Black Holes Energy Emission Rate
6. Quasinormal Modes
7. Summary
Appendix A
References
- T. Clifton, P. G. Ferreira, A. Padilla, and C. Skordis. Modified Gravity and Cosmology, Phys. Rept. 513, 1 (2012). arXiv:1106.2476.
- C. M. Will. The Confrontation between General Relativity and Experiment. Living Rev. Rel. 2014, 17, 4. [CrossRef] [PubMed]
- Lanczos, C. Elektromagnetismus als natürliche eigenschaft der riemannschen geometrie. Zeitschrift für Physik 1932, 73, 147. [Google Scholar] [CrossRef]
- Lanczos, C. A remarkable property of the riemann-christoffel tensor in four dimensions. Annals of Mathematics 1938, 842–850. [Google Scholar] [CrossRef]
- Lovelock, D. Divergence-free tensorial concomitants. Aequationes mathematicae 1970, 4, 127. [Google Scholar] [CrossRef]
- Lovelock, D. The Einstein tensor and its generalizations. J. Math. Phys. 1971; 12, 498. [Google Scholar]
- Ostrogradsky, M. Mémoires sur leséquations différentielles, relatives au problème des isopérimètres. Mem. Acad. St. Petersbourg, 1850; 6, 385. [Google Scholar]
- Gross, D.J.; Witten, E. Superstring modifications of Einstein’s equations. Nucl. Phys. B 1986, 277, 1. [Google Scholar] [CrossRef]
- Gross, D.J.; Sloan, J.H. The quartic effective action for the heterotic string. Nucl. Phys. B 1987, 291, 41. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Two-loop β-function for the generalized bosonic sigma model. Phys. Lett. B 1987, 191, 354. [Google Scholar] [CrossRef]
- Metsaev, R.R.; Tseytlin, A.A. Order α’ (two-loop) equivalence of the string equations of motion and the σ-model Weyl invariance conditions: Dependence on the dilaton and the antisymmetric tensor. Nucl. Phys. B 1987, 293, 385. [Google Scholar] [CrossRef]
- Zwiebach, B. Curvature squared terms and string theories. Phys. Lett. B 1985, 156, 315. [Google Scholar] [CrossRef]
- Glavan, D.; Lin, C. Einstein-Gauss-Bonnet gravity in four-dimensional spacetime, Phys. Rev. Lett 2020, arXiv:1905.03601124, 081301. [Google Scholar] [CrossRef]
- Aoki, K.; Gorji, M.A.; Mukohyama, S. A consistent theory of D→4 Einstein–Gauss–Bonnet gravity. Phys. Lett. B 2020, arXiv:2005.03859810, 135843. [Google Scholar] [CrossRef]
- Aoki, K.; Gorji, M.A.; Mukohyama, S. Inflationary gravitational waves in consistent D→4 Einstein–Gauss–Bonnet gravity. JCAP 2020, arXiv:2005.084289, 14. [Google Scholar] [CrossRef]
- Aoki, K.; Gorji, M.A.; Mizuno, S.; Mukohyama, S. Inflationary gravitational waves in consistent D→4 Einstein–Gauss–Bonnet gravity. JCAP 2021, arXiv:2010.03973]1, E01. [Google Scholar] [CrossRef]
- Jafarzade, K.; Zangeneh, M.K.; Lobo, F.S.N. Shadow, deflection angle and quasinormal modes of Born–Infeld charged black holes. JCAP 2021, arXiv:2010.057554, 008. [Google Scholar] [CrossRef]
- Fernandes, P.G.; Carrilho, P.; Clifton, T.; Mulryne, D.J. The 4D Einstein-–Gauss–-Bonnet theory of gravity: a review. Class. Quant. Grav 2022, 39, 063001. [Google Scholar] [CrossRef]
- Alexeyev, S.; Sendyuk, M. Black Holes and Wormholes in Extended Gravity, Universe. Universe 2020, 6, 25. [Google Scholar] [CrossRef]
- Kruglov, S.I. Magnetic black holes in AdS space with nonlinear electrodynamics, extended phase space thermodynamics and Joule-–Thomson expansion. Int. J. Geom. Meth. Mod. Phys. 2023, arXiv:2210.1062720, 2350008. [Google Scholar] [CrossRef]
- Soleng, H.H. Charged black points in General Relativity coupled to the logarithmic U(1) gauge theory. Phys. Rev. D 1995, arXiv:hep-th/950903352, 6178. [Google Scholar] [CrossRef] [PubMed]
- Kruglov, S.I. On Generalized Logarithmic Electrodynamics. Eur. Phys. J. C 2015, arXiv:1411.774175, 88. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F. Quasinormal modes, stability and shadows of a black hole in the 4D Einstein-Gauss-Bonnet gravity. Eur. Phys. J. C 2020, arXiv:2003.0118880, 1049. [Google Scholar] [CrossRef]
- Konoplya, R.A.; Zinhailo, A.F. 4D Einstein–Lovelock black holes: Hierarchy of orders in curvature. Phys. Lett. B 2020, 807, 135607. [Google Scholar] [CrossRef]
- Belhaj, A.; Benali, M.; El Balali, A.; El Moumni, H.; Ennadifi, S.E. Deflection Angle and Shadow Behaviors of Quintessential Black Holes in arbitrary Dimensions. Class. Quant. Grav, 2020; 37, 215004arXiv:2006.01078. [Google Scholar]
- Konoplya, R.A.; Stuchlik, Z. Are eikonal quasinormal modes linked to the unstable circular null geodesics. Phys. Lett. B 2017, arXiv:1705.05928771, 597. [Google Scholar] [CrossRef]
- Stefanov, I.Z.; Yazadjiev, S.S.; Gyulchev, G.G. Connection between black-hole quasinormal modes and lensing in the strong deflection limit. Phys. Rev. Lett. 2010, arXiv:1003.1609104, 251103. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Miao, Y.G. Null geodesics, quasinormal modes and the correspondence with shadows in high-dimensional Einstein-Yang-Mills spacetimes. Phys. Rev. D 2020, arXiv:2007.08227102, 084057. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Null geodesics, quasinormal modes, and thermodynamic phase transition for charged black holes in asymptotically flat and dS spacetimes. Chin. Phys. C 2020, arXiv:1909.11911]44, 115103. [Google Scholar] [CrossRef]
- Birkhoff, G.D. Relativity and Modern Physics (Harvard University Press, Cambrige, USA, 1923), p. 253.
- Mignemi, S.; Stewart, N.R. Charged black holes in effective string theory. Phys. Rev. D 1993, 47, 5259. [Google Scholar] [CrossRef]
- Medved, A.J.M.; Vagenas, E.C. When conceptual worlds collide: The GUP and the BH entropy. Phys. Rev. D 2004, arXiv:hep-th/041102270, 124021. [Google Scholar] [CrossRef]
- Kruglov, S.I. Einstein–Gauss–Bonnet gravity with nonlinear electrodynamics. Ann. Phys. 2021, arXiv:2104.08099428, 168449. [Google Scholar] [CrossRef]
- Kruglov, S.I. Einstein–-Gauss–-Bonnet Gravity with Nonlinear Electrodynamics: Entropy, Energy Emission, Quasinormal Modes and Deflection Angle. Symmetry 2021, 13, 944. [Google Scholar] [CrossRef]
- Kruglov, S.I. Einstein–Gauss–Bonnet gravity with rational nonlinear electrodynamics. EPL 2021, arXiv:2106.00586133, 6. [Google Scholar] [CrossRef]
- Akiyama, K.; et al. First M87 Event Horizon Telescope Results. Astrophys. J. 2019, arXiv:1906.11241875, L1. [Google Scholar]
- Synge, J.L. The escape of photons from gravitationally intense stars 131, 463 (1966). Mon. Not. Roy. Astron. Soc. 1966, 131, 463. [Google Scholar] [CrossRef]
- Kruglov, S.I. 4D Einstein–-Gauss–-Bonnet Gravity Coupled with Nonlinear Electrodynamics. Symmetry 2021, 13, 204. [Google Scholar] [CrossRef]
- Wei, S.W.; Liu, Y.X. Observing the shadow of Einstein-Maxwell-Dilaton-Axion black hole. JCAP 2013, arXiv:1311.425111, 063. [Google Scholar] [CrossRef]
- Jusufi, K. Quasinormal Modes of Black Holes Surrounded by Dark Matter and Their Connection with the Shadow Radius. Phys. Rev. D 2020, arXiv:1912.13320101, 084055. [Google Scholar] [CrossRef]
- Jusufi, K. Connection Between the Shadow Radius and Quasinormal Modes in Rotating Spacetimes. Phys. Rev. D 2020, arXiv:2004.04664101, 124063. [Google Scholar] [CrossRef]
- Dymnikova, I. Regular electrically charged vacuum structures with de Sitter centre in nonlinear electrodynamics coupled to general relativity. Class. Quant. Grav. 2004, arXiv:gr-qc/040707221, 4417. [Google Scholar] [CrossRef]
- Hawking, S.W.; Ellis, G.F.R. The large scale structure of space-time; Cambridge Univ. Press: Cambridge, UK, 1973. [Google Scholar]
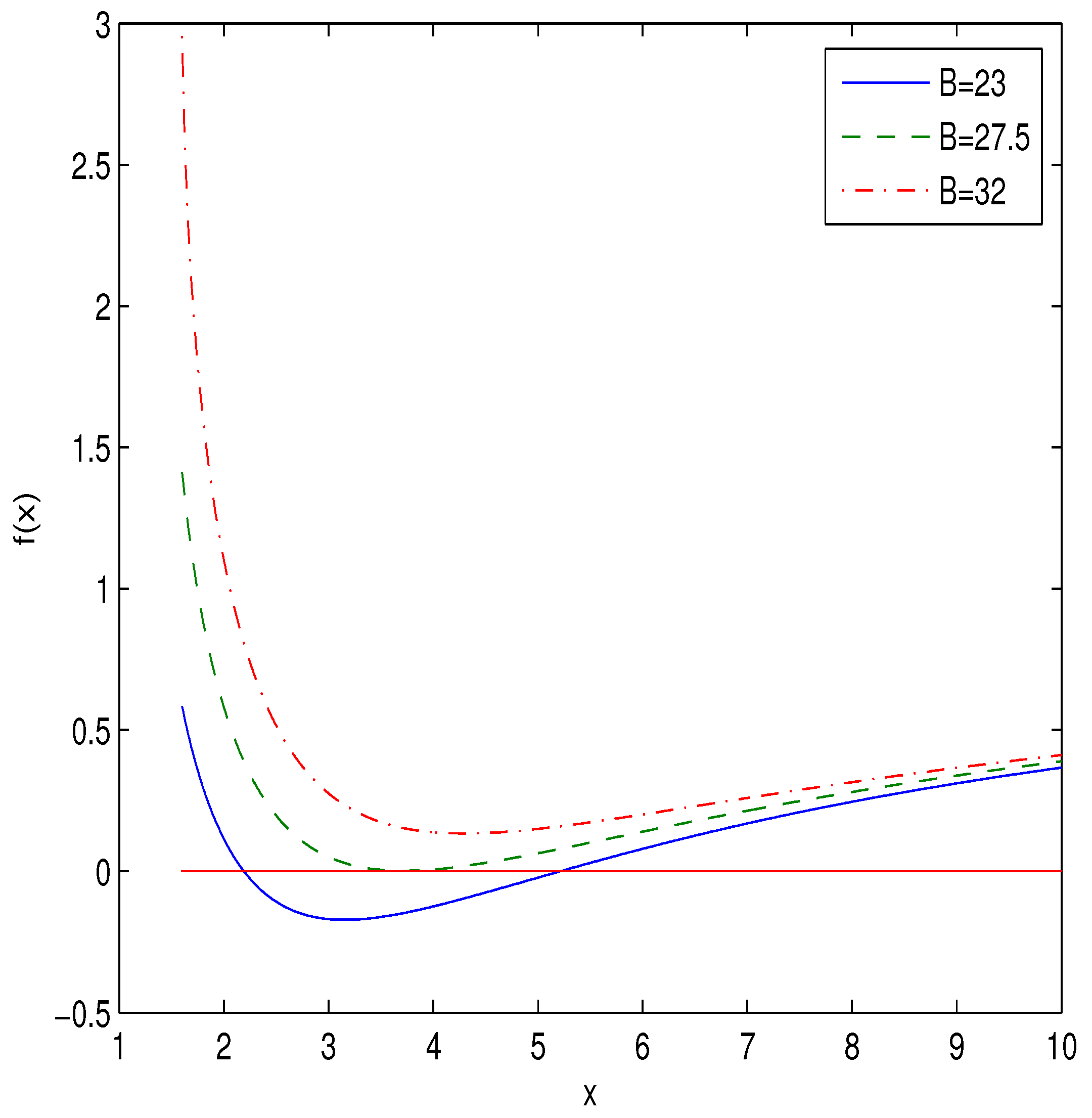
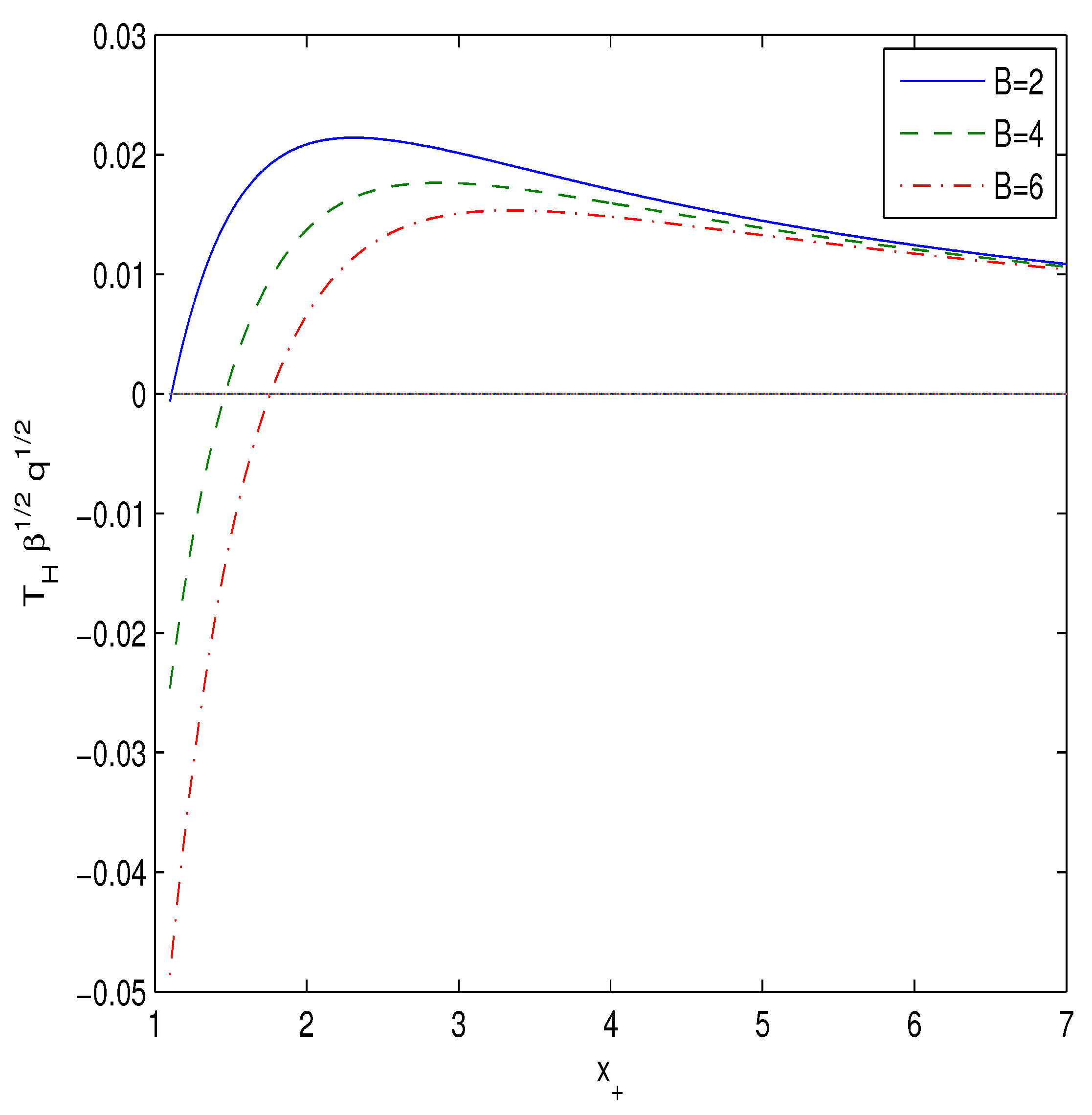
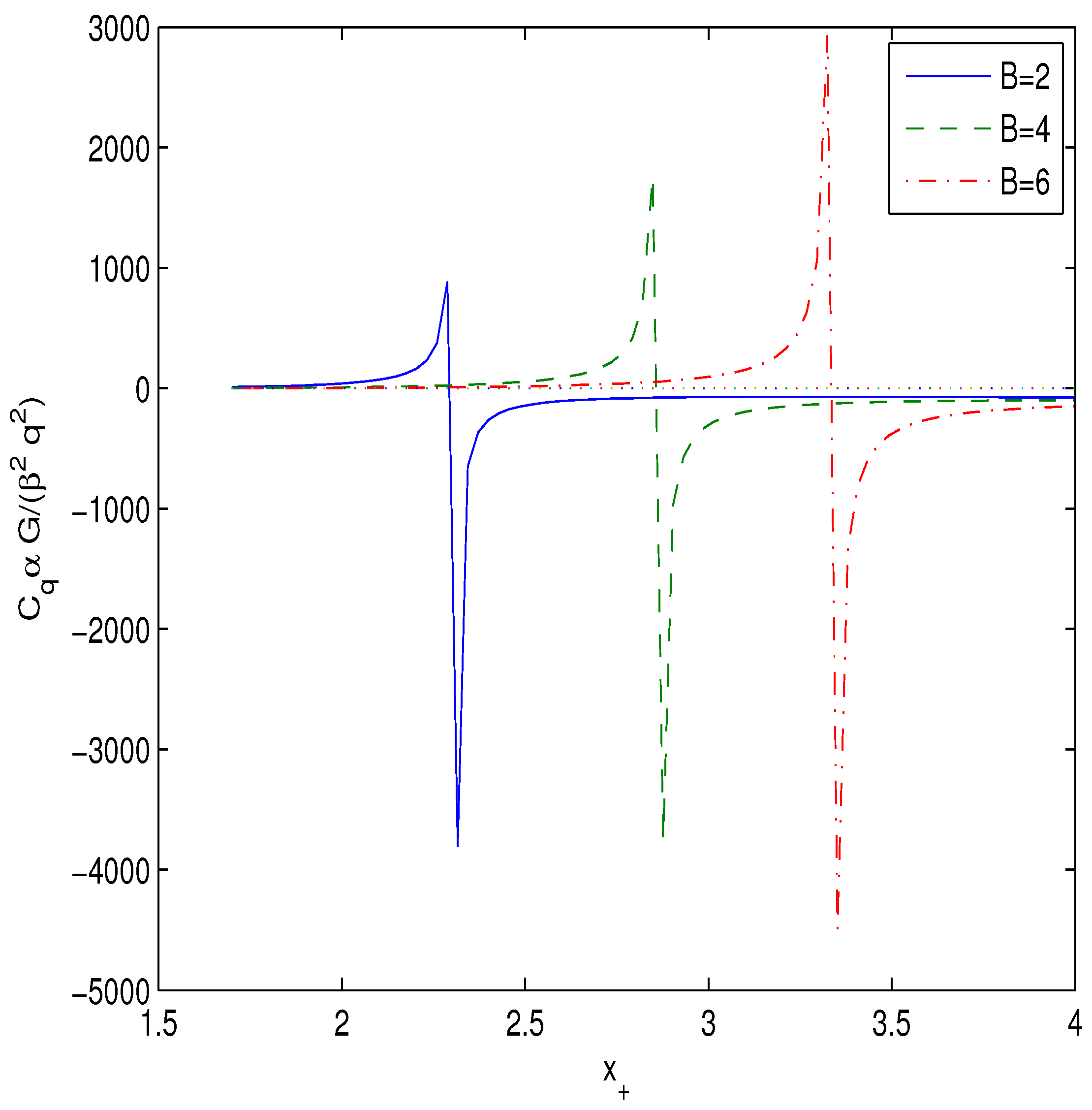
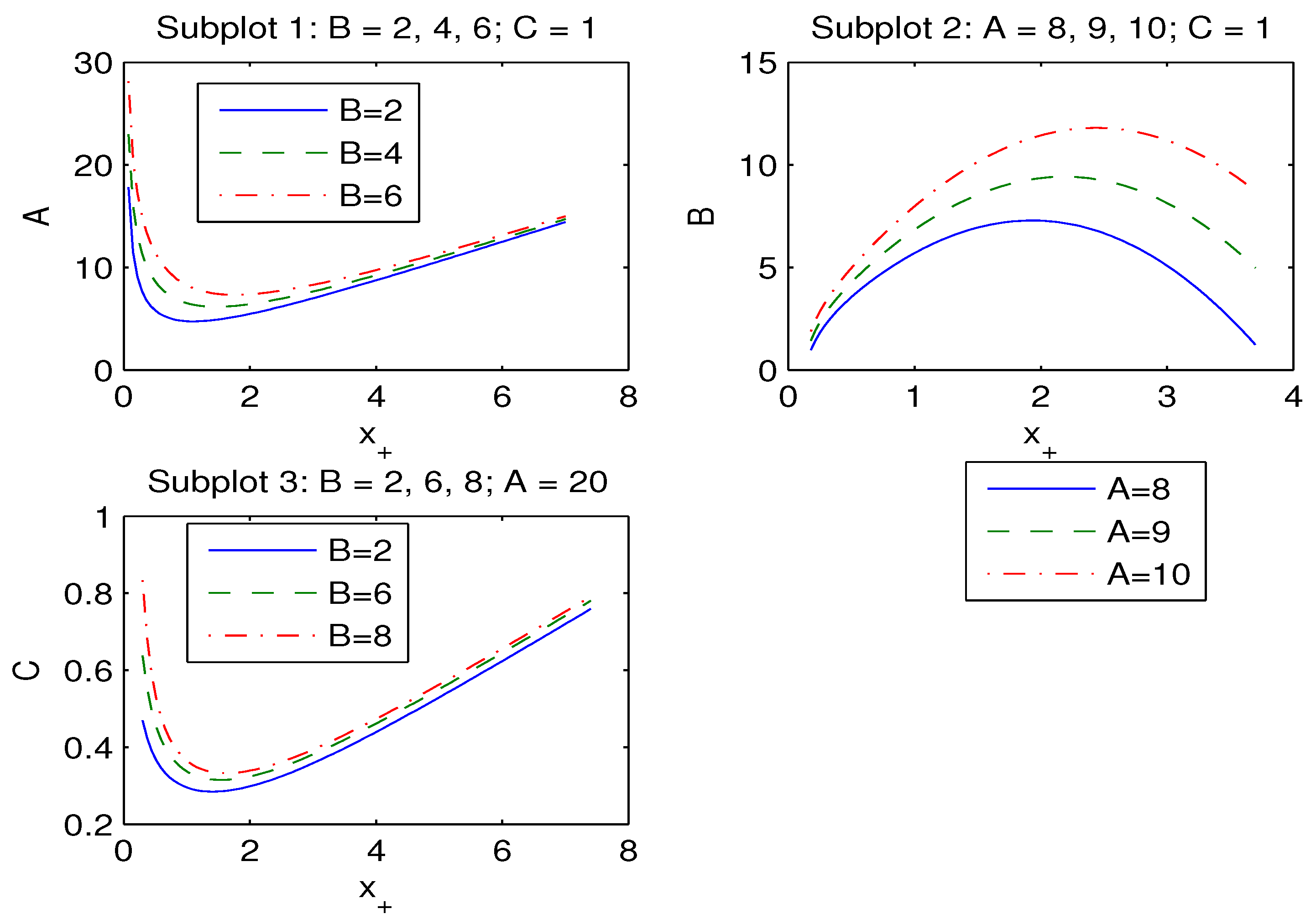
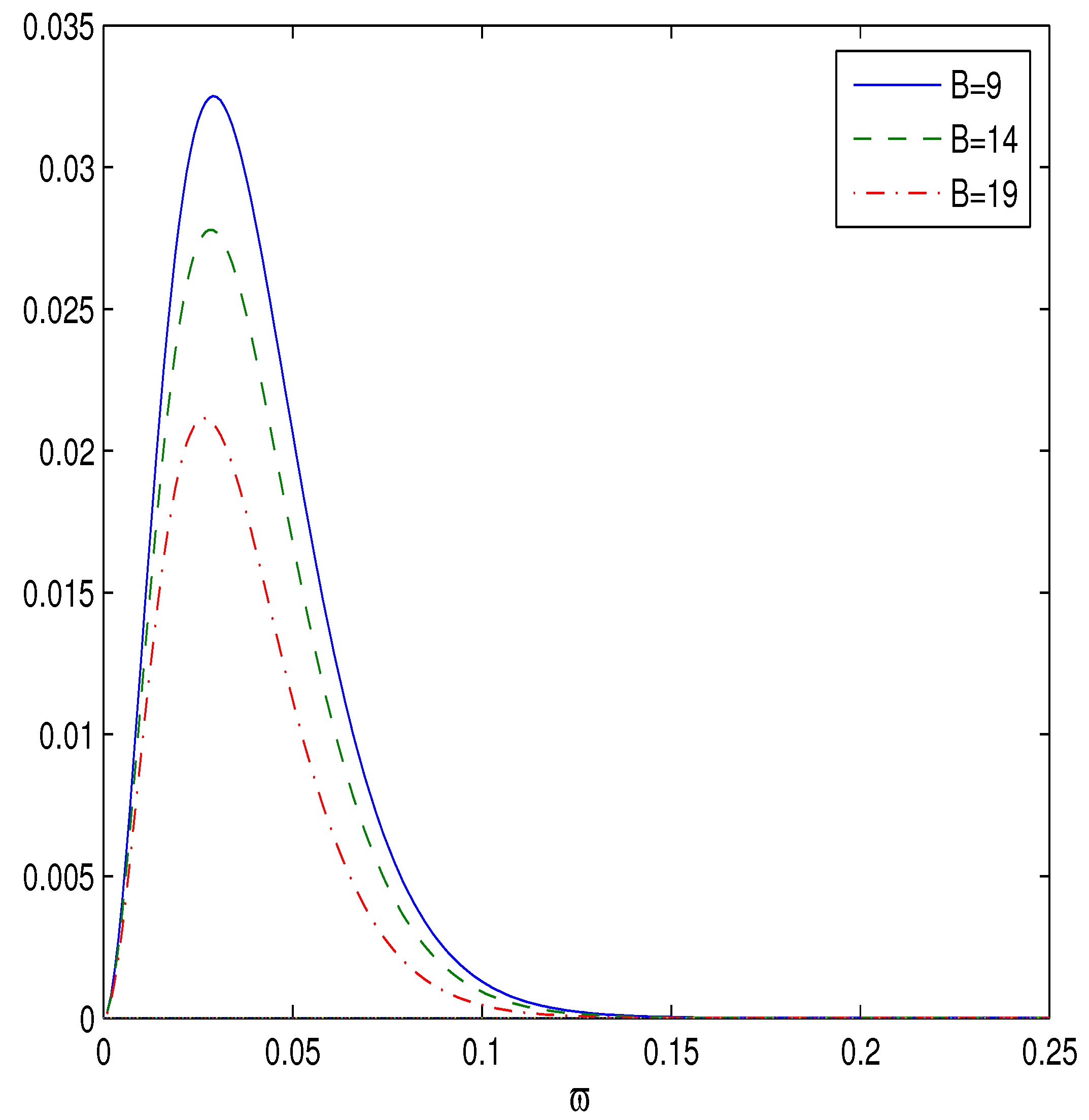
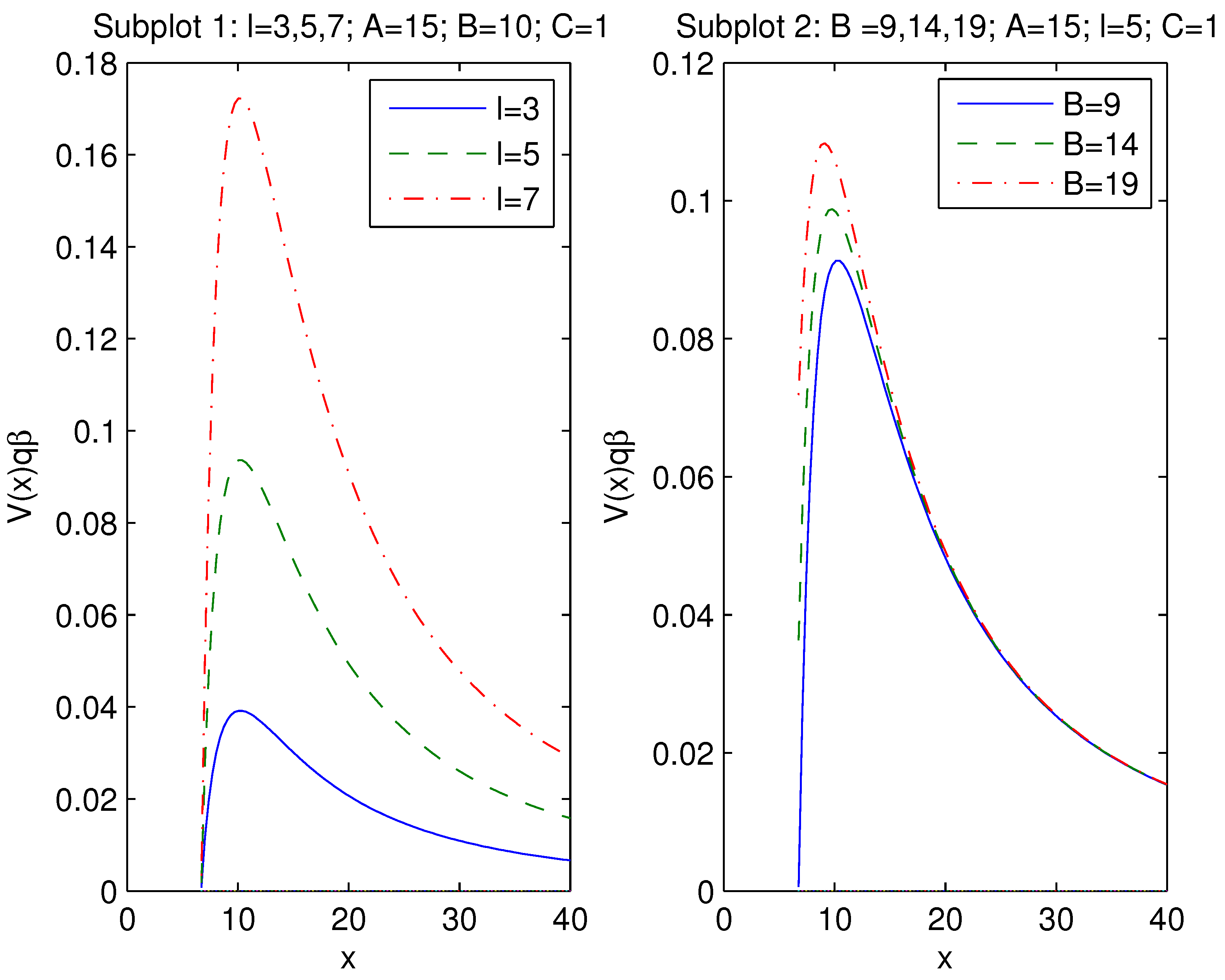
| B | 9 | 13.5 | 14 | 15 | 16.5 | 17.5 | 18 | 19 |
|---|---|---|---|---|---|---|---|---|
| 6.763 | 6.365 | 6.317 | 6.219 | 6.063 | 5.953 | 5.896 | 5.777 | |
| 10.313 | 9.806 | 9.746 | 9.623 | 9.431 | 9.298 | 9.229 | 9.088 | |
| 18.311 | 17.677 | 17.603 | 17.451 | 17.216 | 17.054 | 16.971 | 16.802 |
| B | 14 | 15 | 16.5 | 17.5 | 18 | 19 |
|---|---|---|---|---|---|---|
| 0.568 | 0.573 | 0.581 | 0.586 | 0.589 | 0.595 | |
| 0.2853 | 0.2852 | 0.2849 | 0.2845 | 0.2842 | 0.2835 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





