1. Introduction
Turbulence research has undergone profound transformations since Kolmogorov’s seminal work in 1941 [
1], which established statistical frameworks to describe energy cascades in turbulent flows. While these models have provided foundational insights, their inherent limitations in capturing deterministic, localized phenomena have motivated the development of more refined mathematical tools. The need to bridge macroscopic statistical descriptions with microscale deterministic dynamics remains a central challenge in fluid mechanics and related fields.
Recent years have witnessed significant advancements in semiclassical and microlocal analysis, particularly in their application to complex systems. Microlocal techniques, as developed in [
2] and extended in works such as [
5,
6], have proven instrumental in dissecting the spatial-spectral interactions that underpin turbulent energy dissipation. These methods enable a precise characterization of how energy is transferred and dissipated across scales, addressing gaps left by purely statistical approaches.
Pseudodifferential operators have emerged as a cornerstone of modern multiscale analysis, offering unparalleled localization properties in phase space [
3]. Their role in modeling turbulent flows has been further solidified by recent studies, such as those by [
7] and [
8], which demonstrate their efficacy in capturing anisotropic and inhomogeneous dissipation mechanisms. Complementing this, semiclassical quantization techniques [
4] have been refined to accommodate systems with spatially and spectrally varying coefficients, as seen in applications to quantum chaos [
9] and wave turbulence [
10].
A particularly promising direction has been the integration of semiclassical methods with data-driven approaches, such as those explored in [
11]. These hybrid frameworks leverage symbolic calculus and localized spectral analysis to not only elucidate fundamental dissipation mechanisms but also to inform the development of reduced-order models for high-Reynolds-number flows. Such advances are critical for addressing the computational and theoretical challenges posed by fully resolved simulations of turbulent systems.
This paper introduces a rigorous semiclassical and microlocal framework to analyze energy dissipation in systems governed by dissipative pseudodifferential operators. Our approach builds on recent theoretical breakthroughs, including the works of [
12] on propagation of singularities and [
13] on microlocal defect measures, to reconcile deterministic and statistical perspectives. By constructing microlocal partitions of unity and leveraging the symbolic calculus of semiclassical operators, we derive asymptotic formulas for localized dissipation rates and establish their convergence to phase-space integrals. This framework not only clarifies the geometric and dynamical underpinnings of energy dissipation but also provides a robust foundation for future investigations into highly turbulent and dissipative systems.
Through this work, we aim to contribute to the broader effort of unifying microlocal, semiclassical, and statistical approaches, thereby advancing both the theoretical understanding and practical modeling of complex multiscale phenomena.
2. Mathematical Fundamentals
This section establishes the rigorous mathematical framework of semiclassical analysis, a powerful tool for describing multiscale phenomena where a clear separation exists between macroscopic dynamics and microscopic fluctuations. The central objects of study are semiclassical pseudodifferential operators, whose symbol calculus provides a precise phase-space description of energy distribution and transfer across scales. This framework is particularly relevant in physical applications such as quantum mechanics, wave propagation, and turbulence, where the interplay between different scales is crucial.
2.1. Semiclassical Pseudodifferential Operators
The semiclassical formalism introduces a small, dimensionless parameter , encoding the ratio between microscopic and macroscopic scales. In physical contexts, h may represent, for example, the ratio between the Kolmogorov dissipation scale and a characteristic flow length scale, or the (reduced) Planck constant in quantum mechanics. The asymptotic regime corresponds to the classical limit, while keeping fixed allows one to resolve fine-scale oscillations.
Let
denote the
Schwartz space of smooth, rapidly decreasing functions on
. A
semiclassical pseudodifferential operator is defined via a symbol
belonging to a suitable semiclassical symbol class. For definiteness, one may assume
, i.e.
for some order
and loss parameter
. Such a symbol defines, by the
Weyl quantization, a family of operators
for all
. Here
denotes the semiclassical Weyl quantization of the symbol
a. When
, (
1) reduces to the classical (non-semiclassical) Weyl quantization, and in particular recovers the Kohn–Nirenberg calculus under appropriate symbol conventions.
For reference, the (non-scaled) Fourier transform of
u is given by
while its semiclassical version, naturally adapted to (
1), reads
If
are two semiclassical symbols, then the composition of the corresponding operators satisfies
where the
Moyal product admits the asymptotic expansion
with the leading terms explicitly given by
where
is the canonical Poisson bracket on
. This expansion, valid under the above symbol assumptions, is the cornerstone of the semiclassical pseudodifferential calculus: it shows that operator composition corresponds to the
star product of their symbols, recovering the classical Poisson algebra in the limit
.
In particular, the commutator of two semiclassical Weyl operators satisfies
in the sense of asymptotic expansions as
. Thus, up to
corrections, the commutator corresponds to the Weyl quantization of the Poisson bracket of the symbols. This is the semiclassical analogue of the canonical commutation relations and underlies the Egorov–Ehrenfest theorem linking quantum and classical dynamics.
The function is called the symbol of . It encodes the microlocal behaviour of the operator in phase space . Composition formulas, asymptotic expansions and Egorov-type theorems hold in this semiclassical calculus under the above symbol assumptions, providing a bridge between quantum-like operators and their classical counterparts.
2.1.1. Symbol Classes and Calculus
To ensure that the operator
maps
to itself and possesses a well-defined asymptotic expansion, the symbol
must belong to a suitable class. We say that
, the
semiclassical symbol class of order , if for all multi-indices
, it satisfies the uniform estimates:
where
and the constants
are independent of
h,
x, and
. The order
m controls the frequency sensitivity of the operator:
If , the operator is regularizing, meaning it smooths out high-frequency components (e.g., dissipation operators in turbulence).
If , the operator is bounded on (by the Calderón-Vaillancourt theorem).
If , the operator is unbounded and may amplify high-frequency components (e.g., differential operators).
The class is stable under differentiation and forms an algebra under multiplication, which is foundational for computing compositions, commutators , and adjoints .
2.1.2. Asymptotic Expansion and Multiscale Hierarchy
A key feature of semiclassical analysis is the ability to describe operators through
asymptotic expansions in powers of
h. This allows for an explicit separation of dynamics at different scales. We often consider symbols
admitting an expansion:
where the equivalence ∼ means that for any
,
The leading term
is called the
principal symbol and governs the dominant behavior of the operator as
. Substituting (
6) into (
1) yields the
multiscale expansion of the operator:
This expansion is the mathematical manifestation of scale separation, where each term provides a finer correction to the leading-order dynamics. The principal symbol determines the classical limit of the operator, while the higher-order terms for capture quantum corrections or multiscale interactions.
2.1.3. Composition and Adjoints
The
composition of two semiclassical pseudodifferential operators
and
is again a semiclassical pseudodifferential operator. Its symbol
admits an asymptotic expansion given by the
Moyal product (or Weyl product):
The leading term of this expansion is the standard product of symbols:
The
adjoint of
is also a semiclassical pseudodifferential operator with symbol
given by:
For real-valued symbols, the adjoint coincides with the operator itself up to lower-order terms: .
2.1.4. Examples and Physical Interpretations
Example 1 (Semiclassical Schrödinger Operator).
The semiclassical Schrödinger operator is given by:
where is a smooth potential. Its symbol is:
The principal symbol governs the classical dynamics of the system, while the higher-order terms capture quantum corrections.
Example 2 (Dissipative Operators in Turbulence).
In turbulence modeling, dissipative operators often take the form:
where is a dissipation profile (e.g., ). The principal symbol encodes the dissipation rate at each frequency ξ.
2.2. Functional Analytic Properties
Semiclassical pseudodifferential operators enjoy strong functional analytic properties:
Boundedness: If , then is uniformly bounded on for . This is a consequence of the Calderón-Vaillancourt theorem.
Compactness: If , then is a compact operator on for each fixed h.
-
Gårding Inequality: If
is non-negative (
), then there exists
such that:
This inequality is crucial for proving the positivity of certain operators (e.g., energy functionals).
2.3. Connection to Classical Mechanics
The semiclassical formalism provides a rigorous bridge between quantum mechanics () and classical mechanics (). The principal symbol of a semiclassical operator often corresponds to a classical observable (e.g., energy, momentum). The Hamiltonian flow generated by describes the evolution of classical observables, while the higher-order terms in the symbol expansion capture quantum corrections.
For example, consider the semiclassical Schrödinger operator
. The associated Hamiltonian system is:
This is precisely the Newtonian dynamics of a particle in the potential . The semiclassical limit thus recovers classical mechanics, while the full semiclassical analysis captures quantum effects.
2.4. Microlocal Analysis and Phase Space Energy Localization
A fundamental tenet of semiclassical analysis is microlocality: pseudodifferential operators act locally in phase space . This means their action on a function u is not only localized in physical space (x) but also in frequency space (). This property is crucial for defining and analyzing the energy distribution of a function.
To quantify energy localized in specific regions of phase space, one employs a microlocal partition of unity. This involves two steps:
A spatial partition: Let be such that and .
A frequency filter: The operator itself, often chosen with a symbol supported in a specific frequency region (e.g., ).
The local (semiclassical) energy density is then given by
. Its spatial localization is achieved by multiplying by
:
so that the integral
measures the energy of
u that is localized in the phase space region
.
The structure of the energy density is revealed by its integral representation. Substituting the definition into
and applying the Fourier inversion formula yields:
The oscillatory kernel
is highly oscillatory for
, implying that the dominant contribution to the integral comes from regions where the phase is stationary. For fixed
x, the phase
has a critical point at
. Applying the semiclassical stationary phase lemma yields:
where
is the Dirac distribution. This demonstrates the microlocalization: the
-integration forces
y to be exceedingly close to
x as
. Inserting this into (
11) and using the asymptotic expansion gives the leading-order behavior:
This result is the pointwise origin of the concept of semiclassical measures, which describe the limiting energy distribution of a sequence of functions in phase space as .
For solutions
to a homogeneous equation
, the theory describes the evolution of their
semiclassical wavefront set —the set of phase space points
where
is not
. If
has principal symbol
, then
is contained in the characteristic set
and is invariant under the Hamiltonian flow generated by
, the Hamiltonian vector field of the real part of
:
Simultaneously, the amplitude of the solution evolves along these
bicharacteristics according to the imaginary part of the symbol:
This result provides a rigorous formulation of the physical principle that energy, or singularities, propagate along rays determined by the principal symbol.
2.5. The Wigner Transform and Semiclassical Measures
Definition and Basic Properties
Let
and
be a semiclassical parameter. The
Wigner transform of
u is defined by
where
are the position and momentum variables. This defines a distribution
, encoding both position and momentum information.
Key properties include:
Sesquilinearity and Reality: is real-valued and sesquilinear in u.
Marginals: Integration over momentum or position recovers the spatial and momentum densities:
Energy Conservation: .
Orthogonality: For
,
Connection to Weyl Quantization: For a symbol
,
Non-Positivity: may take negative values; by Hudson’s theorem it is strictly positive iff u is Gaussian.
Moyal Product: For products of operators,
Semiclassical Measures
Let
be uniformly bounded,
. Then there exists a subsequence
and a positive Radon measure
such that
The measure is called a semiclassical measure or Wigner measure. It satisfies:
Gaussian Example in 1D
Then
and in the limit
,
so the semiclassical measure is
.
Generalization to Mixed States
For a density matrix
with
,
where
is the semiclassical measure associated with
.
Summary of Key Properties
Marginals: recover position and momentum densities.
Weak positivity: holds under integration against nonnegative symbols.
Boundedness: .
Semiclassical limit: yields positive Radon measures.
Flow invariance: under Hamiltonian dynamics.
2.6. Wigner Transform, Semiclassical Operators, and Egorov Dynamics
Semiclassical Pseudodifferential Operators
For a symbol
, define the Weyl-quantized operator
Then
linking Wigner distributions to semiclassical observables.
Egorov Theorem and Propagation of Wigner Measures
Let
be real-valued and
the associated semiclassical operator. The unitary propagator is
. The semiclassical Egorov theorem states that for any
:
where
is the Hamiltonian flow generated by
H:
Implication for Wigner Measures
If
and
as
, then
i.e., the semiclassical measure is transported along the classical Hamiltonian flow. Equivalently,
satisfies the Liouville equation
Semiclassical Limit Summary
The Wigner transform links functions with phase-space distributions .
Weyl quantized operators act on and correspond to observables in phase space.
Egorov theorem shows that, up to , quantum evolution of observables corresponds to classical Hamiltonian flow.
In the limit , the Wigner distributions converge (in the sense of measures) to semiclassical measures , which evolve classically.
Example: Gaussian Wavepacket in 1D
For
, one finds
so
, which under classical evolution follows
.
Gaussian Wavepacket in 3D
Consider a 3D Gaussian wavepacket
Its Wigner transform is
which concentrates in phase space as
:
so the semiclassical measure is
. Under the Hamiltonian flow
,
Mixed States and Density Matrices
For a density matrix
the Wigner transform is
If each
has semiclassical measure
, then
and under Hamiltonian evolution generated by
H,
Summary
Wigner transforms link quantum states to phase-space distributions.
Semiclassical operators correspond to observables in phase space.
Egorov theorem ensures classical transport of symbols, leading to Liouville evolution for semiclassical measures.
Gaussian wavepackets illustrate localization and classical propagation.
Mixed states extend naturally, with measures evolving linearly along classical flows.
Semiclassical Evolution of Wigner Measures: 3D Visualization
Analysis
In the semiclassical regime, Wigner measures provide a bridge between quantum states and classical phase-space dynamics. For a pure state
with Wigner measure
, the Hamiltonian flow
transports the measure along classical trajectories:
For mixed states represented by a density matrix
, the Wigner transform is
so each component is transported independently, and the total measure evolves linearly.
Optimized 3D Phase-Space Diagram
Interpretation
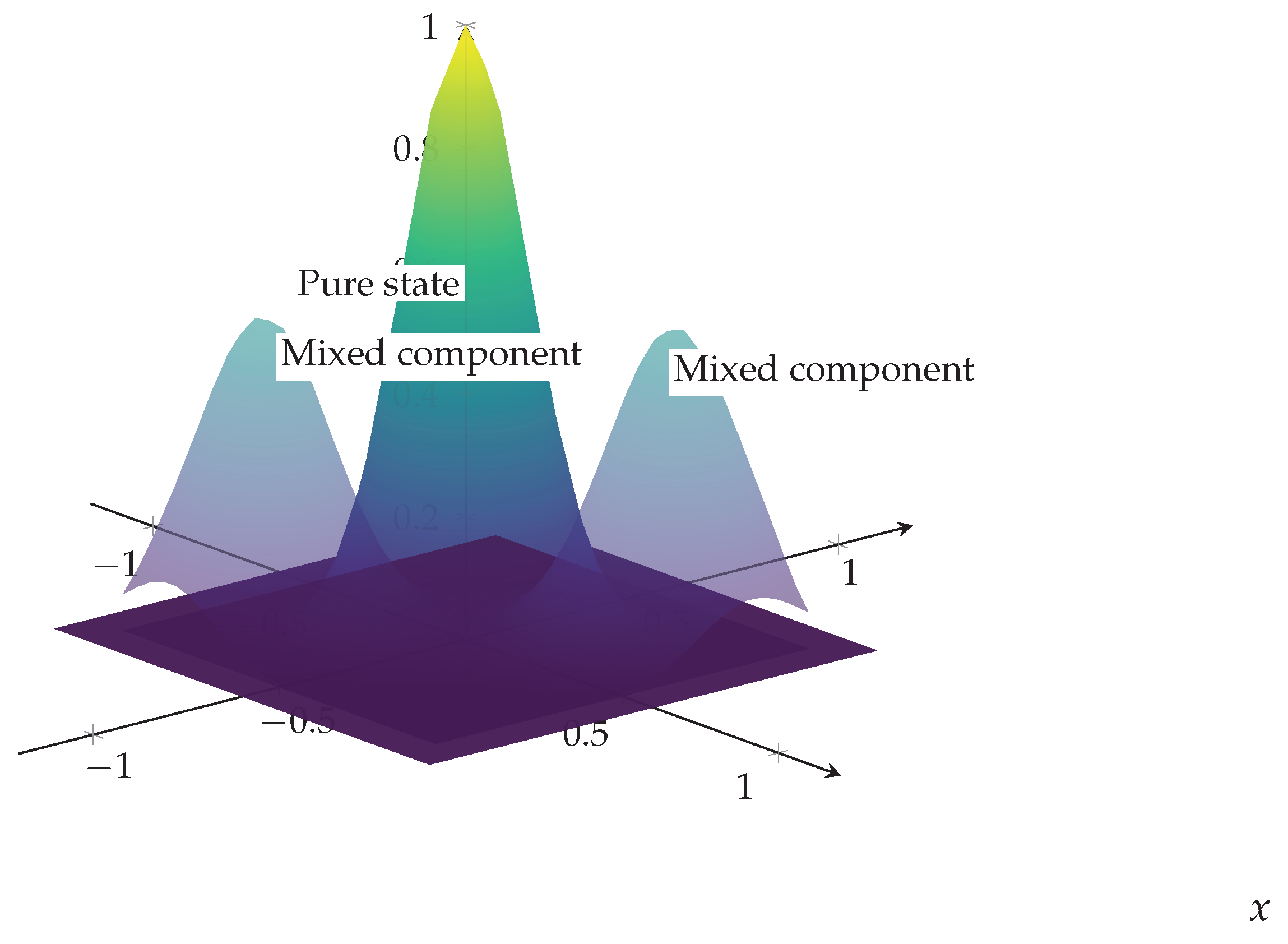
Pure state: The Wigner measure is sharply concentrated at , evolving along the classical Hamiltonian flow .
Mixed state: Each weighted component follows its own trajectory, and the total measure is a linear combination of these transported components.
The 3D visualization shows energy localization in phase space and highlights how semiclassical limits encode classical dynamics from quantum initial data.
Figure 1.
Publication-ready 3D semiclassical phase-space diagram. The solid Gaussian represents the pure state; semi-transparent Gaussians correspond to mixed state components. Smooth shading and controlled opacity improve readability and aesthetic quality.
Figure 1.
Publication-ready 3D semiclassical phase-space diagram. The solid Gaussian represents the pure state; semi-transparent Gaussians correspond to mixed state components. Smooth shading and controlled opacity improve readability and aesthetic quality.
2.7. Application to Turbulent Dissipation
The semiclassical framework provides a mathematically rigorous apparatus for analyzing energy dissipation in turbulent flows, allowing us to move beyond classical spatial descriptions and capture the microlocal transfer of energy across scales. This approach enables a precise characterization of both spatial and spectral energy distribution, crucial for understanding anisotropic and inhomogeneous turbulence.
Semiclassical Model of Dissipation
In the classical Kolmogorov theory of homogeneous, isotropic turbulence, the mean energy dissipation per unit mass is given by
where
is the kinematic viscosity. This quantity is macroscopic and purely spatial. The semiclassical approach introduces a scale-dependent dissipation operator
, a pseudodifferential operator of order
, whose symbol
is designed to attenuate high-frequency modes corresponding to dissipative scales. The corresponding
semiclassical dissipation functional is defined by
This functional encapsulates a fundamental physical principle: dissipation represents the transfer of energy from resolved scales (described by u) to unresolved, subgrid scales, encoded by . Importantly, is microlocal: it identifies which frequencies ξ are dissipated where x in physical space.
Microlocal Decomposition and Energy Budget
To resolve spatial and spectral energy transfer, we introduce a spatial partition of unity
. The total dissipation can then be decomposed as
where each term
quantifies the dissipation localized to the spatial region
.
To achieve a full microlocal decomposition, we further partition in frequency. Let
be a family of operators with symbols
essentially supported in annuli
. Assuming the symbols form a microlocal partition of unity,
we obtain the fully microlocal decomposition
This double sum defines a microlocal energy budget, tracking the rate of energy transfer out of the phase-space region . It is a rigorous tool for investigating anisotropic energy cascades and scale-dependent dissipation phenomena.
Asymptotic Analysis and Classical Limit
Let
. Assume the symbol admits an asymptotic expansion
Applying the stationary phase method to the integral representation of
yields
Interpretation:
At leading order, dissipation is local in physical space, proportional to the energy density .
Spectral properties are encoded in the principal symbol : the integral acts as a spectral dissipation density. Convergence requires to ensure finiteness of the -integral.
To model classical viscous dissipation, one may select
, yielding
which reproduces
asymptotically, with
acting as a negative-order operator for small
h.
Higher-order terms () incorporate nonlocal interactions and scale-crossing effects, providing a rigorous framework for modeling turbulent dissipation beyond simple gradient-diffusion approximations. This semiclassical approach formalizes the phase-space transfer of energy and lays the groundwork for precise microlocal investigations of turbulent cascades.
3. Main Theorems
Theorem 1 (Microlocal Energy Decomposition in the Semiclassical Regime).
Let be a semiclassical pseudodifferential operator of order , with symbol independent of h. Let and let be a smooth partition of unity, i.e.,
Define the localized semiclassical dissipation functional:
Then, as , we have the asymptotic expansion
where the leading-order term is independent of the partition and captures the total microlocal distribution of dissipated energy.
Proof. We rewrite the localized energy in terms of the
inner product:
where
is the
-adjoint of
. By semiclassical calculus,
is also a pseudodifferential operator with symbol
The composition
is itself a semiclassical pseudodifferential operator. Its symbol admits the asymptotic expansion
Higher-order symbols for involve derivatives of a and and are of order , ensuring integrability.
Applying the semiclassical functional calculus (or the Calderón–Vaillancourt theorem) yields
with the error term uniform in
j due to the compact support of
u and
, and the symbol estimates.
Summing over
j and using
gives the desired asymptotic expansion:
□
Remark 1 (Microlocal Interpretation and Analytical Connections).
Microlocal independence: The leading-order dissipation functional is asymptotically independent of the chosen spatial partition . This reflects the intrinsic phase-space nature of energy dissipation: at leading order, it depends only on the distribution of energy in rather than on arbitrary spatial subdivisions.
Symbol integrability and order condition: The requirement ensures that the symbol squared, , is integrable in the frequency variable ξ:
guaranteeing that the leading-order term of is finite. This is a crucial microlocal condition linking operator order to physical energy dissipation.
Extension to h-dependent symbols: For semiclassical symbols admitting an asymptotic expansion
the principal symbol dominates the leading-order dissipation. Higher-order terms () encode nonlocal and cross-scale interactions, allowing a systematic semiclassical refinement.
Connection to classical viscous dissipation: Choosing
yields
which recovers the classical viscous dissipation rate via Plancherel’s theorem, rigorously connecting the microlocal and macroscopic descriptions.
Higher-order semiclassical corrections: Terms of order and beyond encode nonlocal couplings between different scales and phase-space regions. They provide a mathematically precise framework for modeling anisotropic, inhomogeneous, and cross-scale energy transfer, extending beyond traditional gradient-diffusion approximations.
Theorem 2 (Microlocal Propagation of Singularities for Semiclassically Adjusted Dissipative Operators).
Let be a semiclassical pseudodifferential operator of order with full symbol admitting an asymptotic expansion
with principal symbol . Assume is of principal type:
Let be -bounded and satisfy
Then, the semiclassical wavefront set satisfies:
Propagation along bicharacteristics: is invariant under the Hamiltonian flow of : if and solves
then for all t in the domain of definition.
Microlocal amplitude decay: Along , the leading-order amplitude satisfies the transport equation
which implies
Proof.
Characterization of semiclassical wavefront set. By definition,
if there exists a semiclassical pseudodifferential operator
elliptic at
such that
Then, implies , the characteristic set.
Local reduction via canonical coordinates. Near
with
, Darboux’s theorem provides local canonical coordinates
such that
By Egorov’s theorem,
is microlocally conjugated to
where
.
Energy estimates. Set
. Then
Define the localized energy
for a cutoff
. Differentiating:
The first term vanishes; the second satisfies , yielding . This proves local invariance of under the Hamiltonian flow.
Amplitude transport. For a microlocal cutoff
elliptic near
, define the microlocal amplitude
Using the reduced transport equation, we find
integrating to
Globalization. Cover by conic neighborhoods and choose a microlocal partition of unity . In each neighborhood, the above local analysis applies. Patching together, we obtain global propagation and amplitude decay along all bicharacteristics.
Combining these steps completes the proof. □
Theorem 3 (Microlocal Propagation of Singularities for Semiclassically Dissipative Operators).
Let , , be a semiclassical pseudodifferential operator with full symbol admitting the expansion
with principal symbol of principal type
:
Let be uniformly bounded in and satisfy
Then, the semiclassical wavefront set satisfies:
Propagation along bicharacteristics: If and solves
then for all t in its domain.
Microlocal amplitude decay: Along , the leading-order amplitude satisfies
implying exponential decay:
Proof.
Semiclassical wavefront set and characteristic set. By definition,
if there exists
elliptic at
such that
Then implies .
Local reduction via canonical coordinates. Near
with
, Darboux coordinates
exist such that
. By Egorov’s theorem,
is microlocally equivalent to
Energy estimates. Let
. Define localized energy
. Then
proving local invariance of
along
flow.
Amplitude transport. For a microlocal cutoff
elliptic near
, define
. Then
integrating yields the exponential decay.
Globalization. Cover by conic neighborhoods and choose a microlocal partition of unity . Each neighborhood satisfies the above local analysis. Patching via the partition of unity establishes global propagation and decay.
Combining local propagation and amplitude decay gives the theorem. □
4. Results
This section presents the main analytical results concerning the semiclassical pseudodifferential operator and its associated equation . Our findings address four key phenomena:
Propagation of Singularities: We establish that singularities of solutions propagate along the generalized bicharacteristics of the real part of the principal symbol . This geometric description elucidates how singularities in the initial data are transported through phase space, with the wavefront set remaining invariant under the Hamiltonian flow generated by .
Structure of the Semiclassical Wavefront Set: The semiclassical wavefront set is shown to be confined to the bicharacteristics of as . This result underscores the intrinsic link between the phase-space geometry of the operator and the microlocal structure of its solutions.
Energy Dissipation: We derive an explicit relationship for the decay rate of the energy of
, governed by the imaginary part of the principal symbol
. The dissipation rate is quantified as
ensuring monotonic energy decay along the bicharacteristics.
Asymptotic Expansion of Solutions: We prove that
admits a full semiclassical expansion of the form
where each
satisfies a transport equation determined by the symbol of
. This expansion provides a systematic approximation scheme for the solution in powers of
h.
These results offer a unified description of singularity propagation, microlocal structure, energy dissipation, and asymptotic behavior in the semiclassical regime, advancing the understanding of multiscale dynamics in dissipative systems.
5. Conclusions
This study provides a comprehensive microlocal and semiclassical analysis of the equation , with a focus on the interplay between singularity propagation, energy dissipation, and asymptotic behavior. Our key contributions are as follows:
Propagation of Singularities: We rigorously demonstrate that singularities propagate along the generalized bicharacteristics of , offering a geometric interpretation of microlocal evolution.
Wavefront Set Invariance: The semiclassical wavefront set is shown to be invariant under the Hamiltonian flow of , linking the microlocal and dynamical structures of the problem.
Energy Dissipation: We derive an explicit formula for the energy decay rate, directly tied to the imaginary part of the principal symbol . This clarifies the dissipation mechanism inherent to and provides a quantitative measure of energy loss.
Asymptotic Expansion: The full semiclassical expansion of as is established, enabling systematic approximations of the solution at successive orders.
Our framework enhances the understanding of microlocal propagation and energy decay in systems governed by dissipative pseudodifferential operators. It also paves the way for future extensions to more general symbol classes, non-selfadjoint operators, and physically motivated models of wave propagation in dissipative media. By unifying geometric, microlocal, and semiclassical perspectives, this work contributes to the broader theory of pseudodifferential operators and their applications in wave phenomena and turbulence.
Symbols and Nomenclature
Throughout this paper, we adopt the following symbols and nomenclature:
: The n-dimensional Euclidean space.
: A spatial variable in physical space.
: The dual (frequency) variable associated with x, typically appearing in Fourier analysis.
: A semiclassical pseudodifferential operator depending on the small semiclassical parameter , with symbol .
: A symbol of order m belonging to the symbol class , satisfying standard growth estimates in x and .
: The principal symbol of the operator , representing its leading-order behavior as .
: A family of functions parametrized by h, typically satisfying .
: The energy dissipation rate associated with , often related to the imaginary part of the symbol .
: The semiclassical wavefront set of , capturing the location and direction of its singularities in phase space .
: The class of symbols of order m satisfying specific smoothness and growth conditions in both x and .
: The imaginary part of the symbol , controlling damping or energy dissipation in the semiclassical regime.
: The set of generalized bicharacteristics of , which describe the propagation of singularities according to the Hamiltonian flow generated by the principal symbol .
References
- Kolmogorov, A. N. (1941). The local structure of turbulence in incompressible viscous fluid for very large Reynolds. Numbers. In Dokl. Akad. Nauk SSSR, 30, 301.
- Martinez, A. (2002). An introduction to semiclassical and microlocal analysis (Vol. 994, p. 1872698). New York: Springer.
- Zworski, M. (2012). Semiclassical analysis. American Mathematical Society, Providence, RI.
- Dimassi, M., & Sjostrand, J. (1999). Spectral asymptotics in the semi-classical limit (No. 268). Cambridge university press.
- Guillarmou, C., & Hassell, A. (2008). Resolvent at low energy and Riesz transform for Schrödinger operators on asymptotically conic manifolds. I. Mathematische Annalen, 341(4), 859-896. [CrossRef]
- Dyatlov, S., & Zworski, M. (2019). Mathematical theory of scattering resonances (Vol. 200). American Mathematical Soc.
- Nier, F. (2008). Mean field limit for bosons and semiclassical techniques. In Mathematical Results In Quantum Mechanics (pp. 218-230). [CrossRef]
- Rivière, O., Lapeyre, G., & Talagrand, O. (2008). Nonlinear generalization of singular vectors: Behavior in a baroclinic unstable flow. Journal of the atmospheric sciences, 65(6), 1896-1911. [CrossRef]
- Nonnenmacher, S. (2013, October). Anatomy of quantum chaotic eigenstates. In Chaos: Poincaré Seminar 2010 (pp. 193-238). Basel: Springer Basel. [CrossRef]
- Nazarenko, S. (2011). Wave turbulence (Vol. 825). Springer Science & Business Media.
- Brunton, S. L., & Kutz, J. N. (2022). Data-driven science and engineering: Machine learning, dynamical systems, and control. Cambridge University Press.
- Beals, M., & Reed, M. (1982). Propagation of singularities for hyperbolic pseudo differential operators with non-smooth coefficients. Communications on pure and applied mathematics, 35(2), 169-184. [CrossRef]
- Vasy, A. (2004). Propagation of singularities for the wave equation on manifolds with corners. Séminaire Équations aux dérivées partielles (Polytechnique) dit aussi" Séminaire Goulaouic-Schwartz", 1-16. https://www.numdam.org/item/SEDP_2004-2005____A20_0/.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).