Research on Multi‐Objective Optimization Design of Traditional Soil Dwelling Renovation Based on AHPQFD‐ NSGA‐II: A Case Study of Tuyugou Village in Turpan, Xinjiang

1. Introduction

Over 8,000 years ago, during the Neolithic era, earth was widely used as a primary building material, serving as a precursor to modern construction. Today, approximately 30% of the global population still utilizes earthen materials in buildings [1] (Figure 1), with over 100 million people in China residing in earthen houses [2] (Figure 2). The traditional earthen structures of Tuyugou Village, Turpan, are a key part of the region’s architectural heritage. While these buildings reflect the historical lifestyle of local inhabitants and offer cultural value, modernization has become necessary due to changing resident needs and safety concerns. Moreover, the growing interest in cultural heritage tourism supports their continued development [3]. However, the modernization process presents challenges: it requires preserving cultural significance while adapting to modern living standards, introducing new architectural considerations [4,5].

In recent years, traditional dwellings, as vital carriers of regional culture, have attracted increasing attention. Numerous studies have explored various approaches to optimizing and modernizing these buildings from different angles. For instance, Luo and Wu studied the preservation and transmission of regional cultural heritage in five traditional villages in northwestern Jiangxi. They examined the cultural significance and modernization challenges of these dwellings, proposing renovation strategies that integrate modern construction techniques with traditional craftsmanship, focusing on functionality, durability, and aesthetic preservation [6]. Jiang and Li used village genetic data and spatial texture with the CityEngine platform to digitize and visualize traditional Xiaoxi villages in western Hunan, offering a new perspective and scientific framework for spatial evolution analysis [7]. Fu and Zhou applied spatial databases, remote sensing (RS), and GPS technology to evaluate seven traditional villages in western Hunan, developing restoration strategies based on the entropy weighting method [8]. Layla Iskandar et al. assessed the cooling efficiency and thermal comfort of natural ventilation strategies in a historic San Antonio residence, validating CFD and energy models. Their findings demonstrated that all strategies saved energy while preserving historical architecture [9]. Guilherme B.A and colleagues evaluated energy consumption and costs for three setpoints, emphasizing the positive effects of passive retrofits on energy savings and artifact preservation, though they noted climate-specific variations in effectiveness [10].

Most renovation strategies for traditional dwellings, as reviewed in domestic and international studies, focus on specific groups or single objectives, such as energy efficiency, comfort, structural safety, or cultural preservation. However, a comprehensive renovation must balance multiple objectives, including modern living standards, cultural preservation, environmental sustainability, and economic viability [11]. Furthermore, renovations involve a variety of stakeholders, such as government agencies, residents, tourists, and industry experts. Current efforts often lack systematic methodologies and objective data, relying heavily on architects' subjective decisions [12].

To address these challenges, this research applied the QFD model and NSGA-II algorithm to optimize the renovation of traditional earth dwellings in Turpan, ensuring a balance between traditional aesthetics and modern standards. This approach enhances the functionality of Tuyugou Village’s dwellings while providing theoretical and practical references for similar projects. The Analytic Hierarchy Process (AHP) was first used to prioritize user needs, assigning weights through expert evaluation from four key stakeholders [13]: homeowners, tourists, construction experts, and government officials. Next, the QFD method translated these needs into design attributes via the House of Quality [14]. Finally, the NSGA-II algorithm performed multi-objective optimization, generating Pareto-optimal solutions to balance conflicting renovation goals and support informed decision-making [15].

2. Theoretical Background

2.1. Analytic Hierarchy Process (AHP)

The Analytic Hierarchy Process (AHP), introduced by Saaty in the 1970s, is a multi-criteria decision-making tool that breaks complex problems into hierarchical levels, allowing experts to assign weights and facilitate comprehensive evaluations. AHP’s strengths lie in its simplicity and ability to handle both qualitative and quantitative data [13]. Its use in construction has grown recently, with applications like Kamaruzzaman's weighted system for Malaysia's sustainability assessment program [16] and Saman Aminbakhsh’s safety risk assessment framework for prioritizing risks within budget constraints [17].

2.2. Quality Function Deployment (QFD)

Quality Function Deployment (QFD) is a customer-focused method that translates customer needs into product design characteristics and quality requirements by establishing a relationship matrix between the two [14]. Its key tool, the "House of Quality," links customer requirements with product features to guide design and improvement. QFD is effective in capturing customer needs [14], improving product quality, and boosting competitiveness. In architecture, Adinyira and Kwofie identified the top five energy efficiency requirements for housing using QFD [18], while Singhaputtangkul developed an automated fuzzy decision support tool (KBDSS-QFD) to evaluate building materials in high-rise residential projects [19].

2.3. Non-Dominated Sorting Genetic Algorithm II (NSGA-II)

NSGA-II, introduced by Kalyanmoy Deb et al. in 2000, is an evolutionary algorithm designed to solve multi-objective optimization problems by addressing computational complexity, accuracy, and diversity in selection [20]. It improves upon earlier genetic algorithms by reducing complexity, increasing computational speed, and enhancing optimization precision[20]. Yao et al. used genetic algorithms to optimize prefabricated building site layouts, improving solution quality and reducing time [21]. Zhu and Song applied an enhanced genetic algorithm for project scheduling in prefabricated buildings, aiding strategy formulation in uncertain conditions [22]. Yu et al. employed a multi-objective genetic algorithm to optimize energy consumption and thermal comfort, offering sustainable building design solutions [23].

Each methodology—AHP, QFD, and NSGA-II—brings unique advantages, and their combination creates an effective multi-objective optimization framework that enhances decision-making. AHP breaks down complex decisions, prioritizing and weighting user needs, which are then used in QFD to translate these needs into design attributes [18]. QFD serves as an intermediary, linking abstract requirements to specific design targets, laying the groundwork for NSGA-II. NSGA-II, in turn, balances multiple objectives, generating a set of non-dominated solutions that address factors like cultural preservation, energy efficiency, and comfort [22]. The integration of AHP, QFD, and NSGA-II strengthens the optimization process, making it both scientifically rigorous and flexible enough for real-world applications. The framework of this study is shown in Figure 3.

3. Case Study

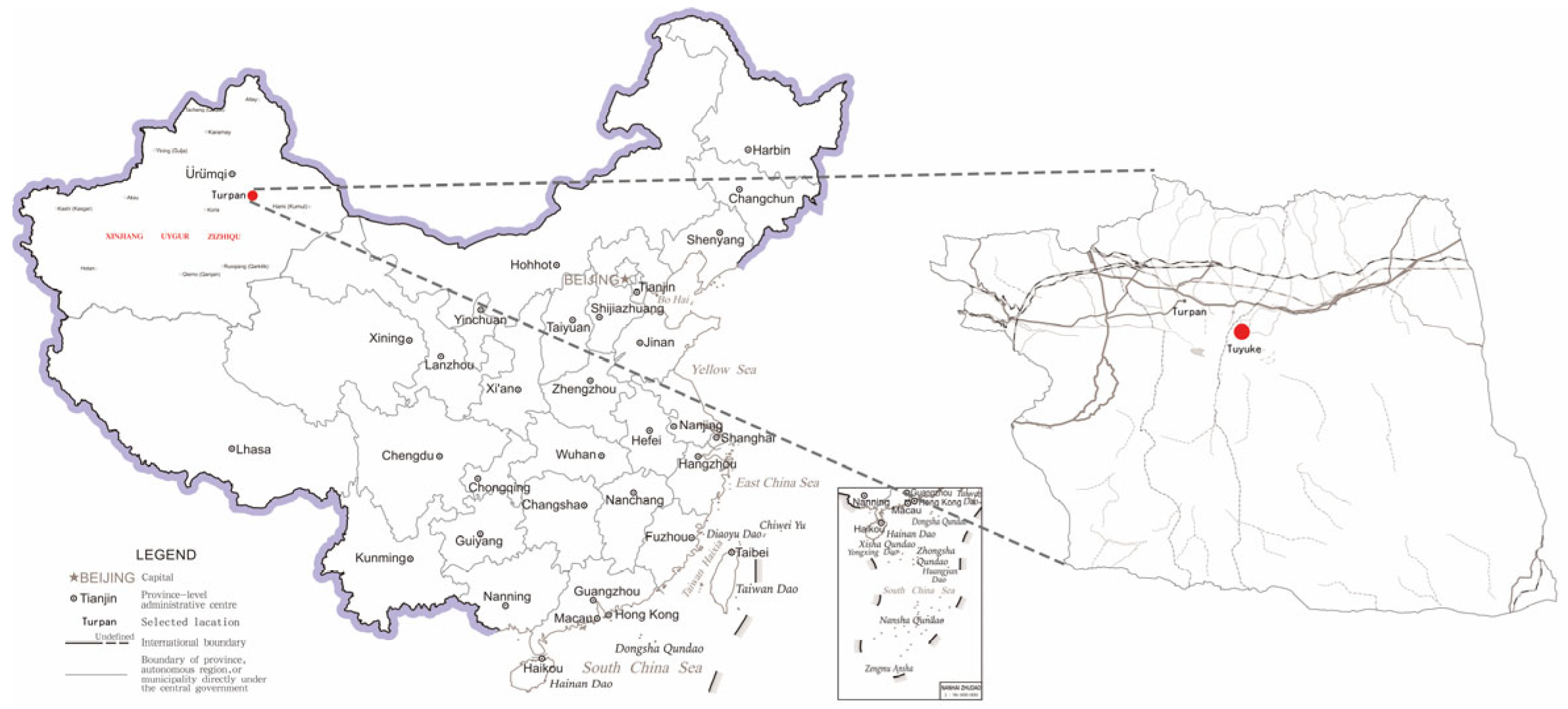
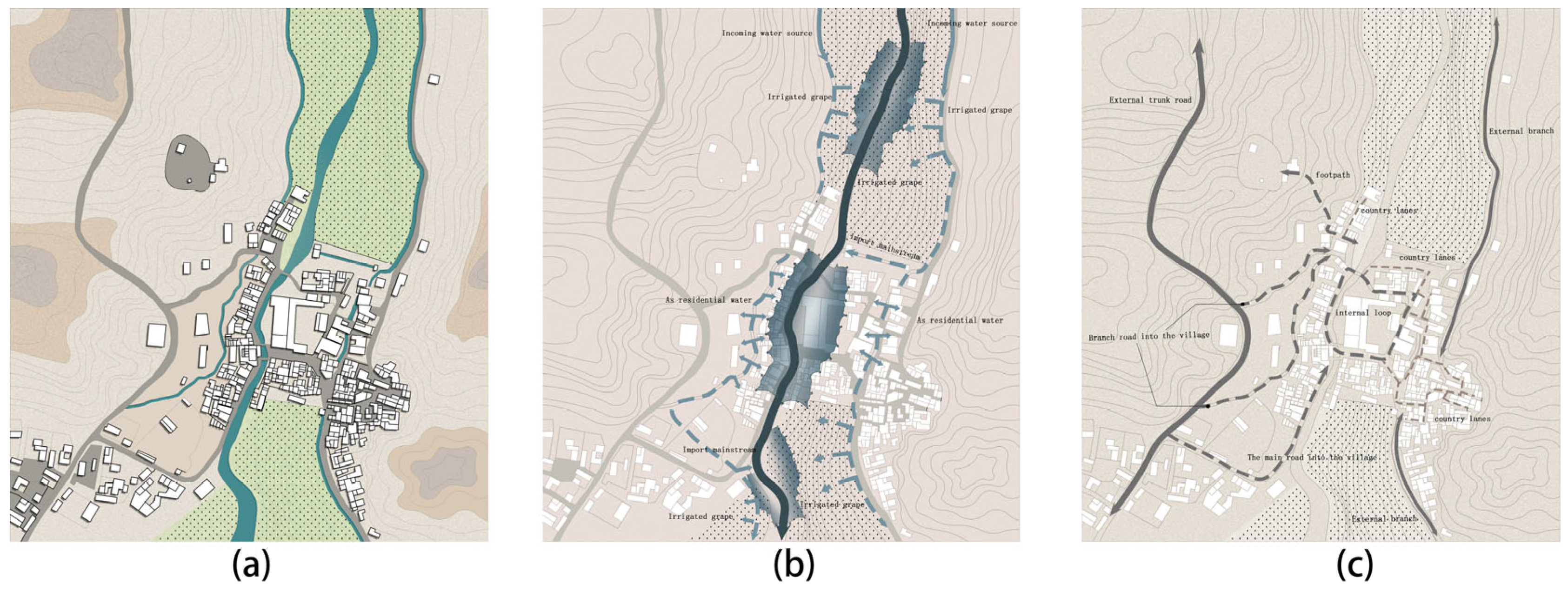
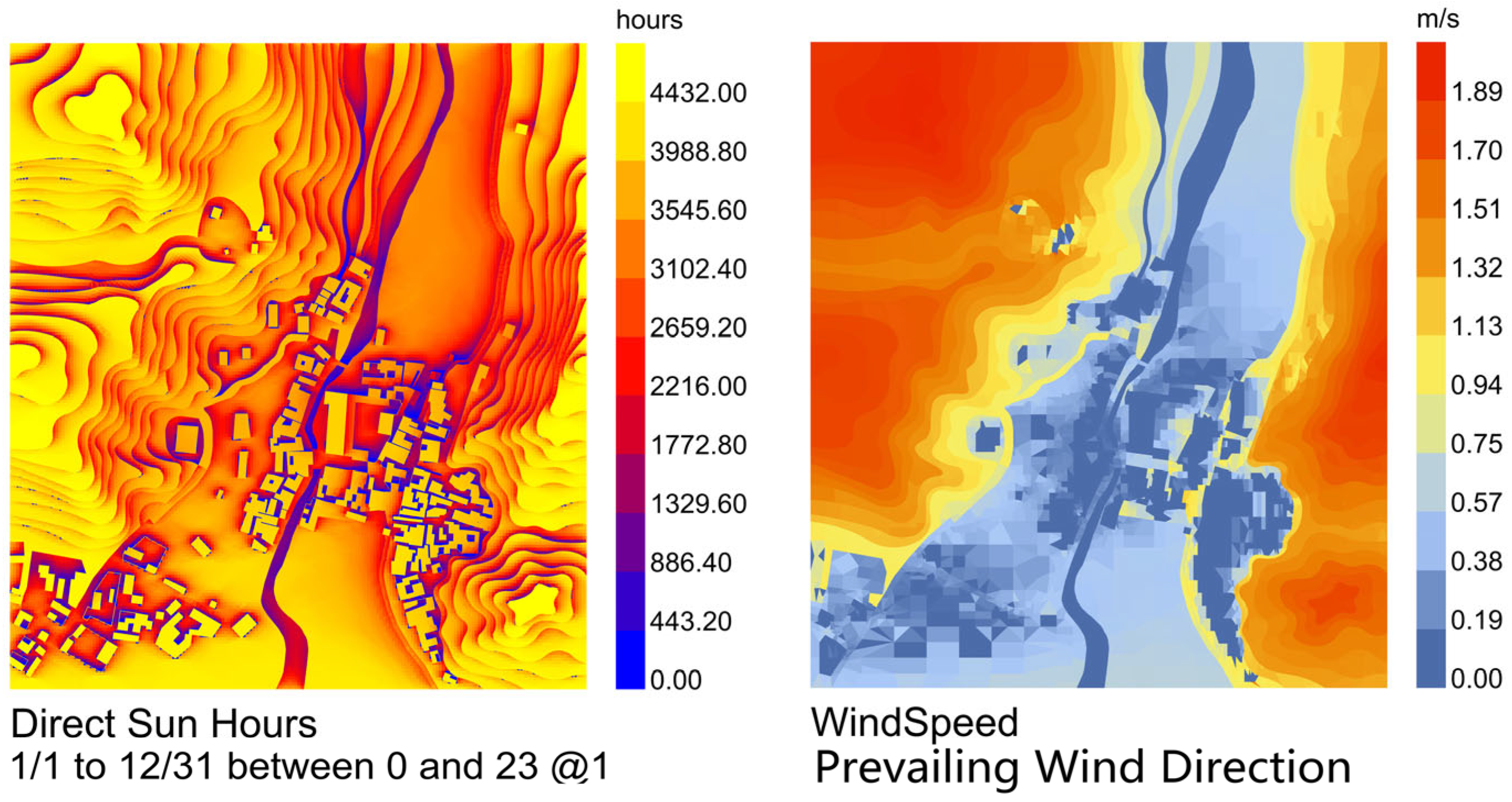
3.1. Overview of Tuyugou Village

Tuyugou Village, situated in the Turpan region of Xinjiang (see Figure 4), is depicted in Figure 5. Extending from north to south, the village encompasses the Subashi Ruins, the Thousand Buddha Caves, and ancient tombs. In 2005, the village was designated as a national historical and cultural site, making it the first of its kind in Xinjiang [4]. The layout of the village maximizes the natural terrain, seamlessly integrating mountains, waterways, dwellings, and roads—a characteristic trait of oasis settlements [5]. Water from a branch of the Tianshan system irrigates surrounding fields via channels along the river, while buildings are harmoniously integrated with the surrounding hills and farmland. The primary water system creates a "川"-shaped configuration, merging natural and cultural features [4]. To conserve farmland, the village expands outward from its central structures, with houses positioned to optimize sunlight and protect against wind. The road network, intersecting with the water system, consists of primary roads, a central ring road, and smaller paths, all tailored to the terrain and designed to meet residents' transportation needs [24,25].

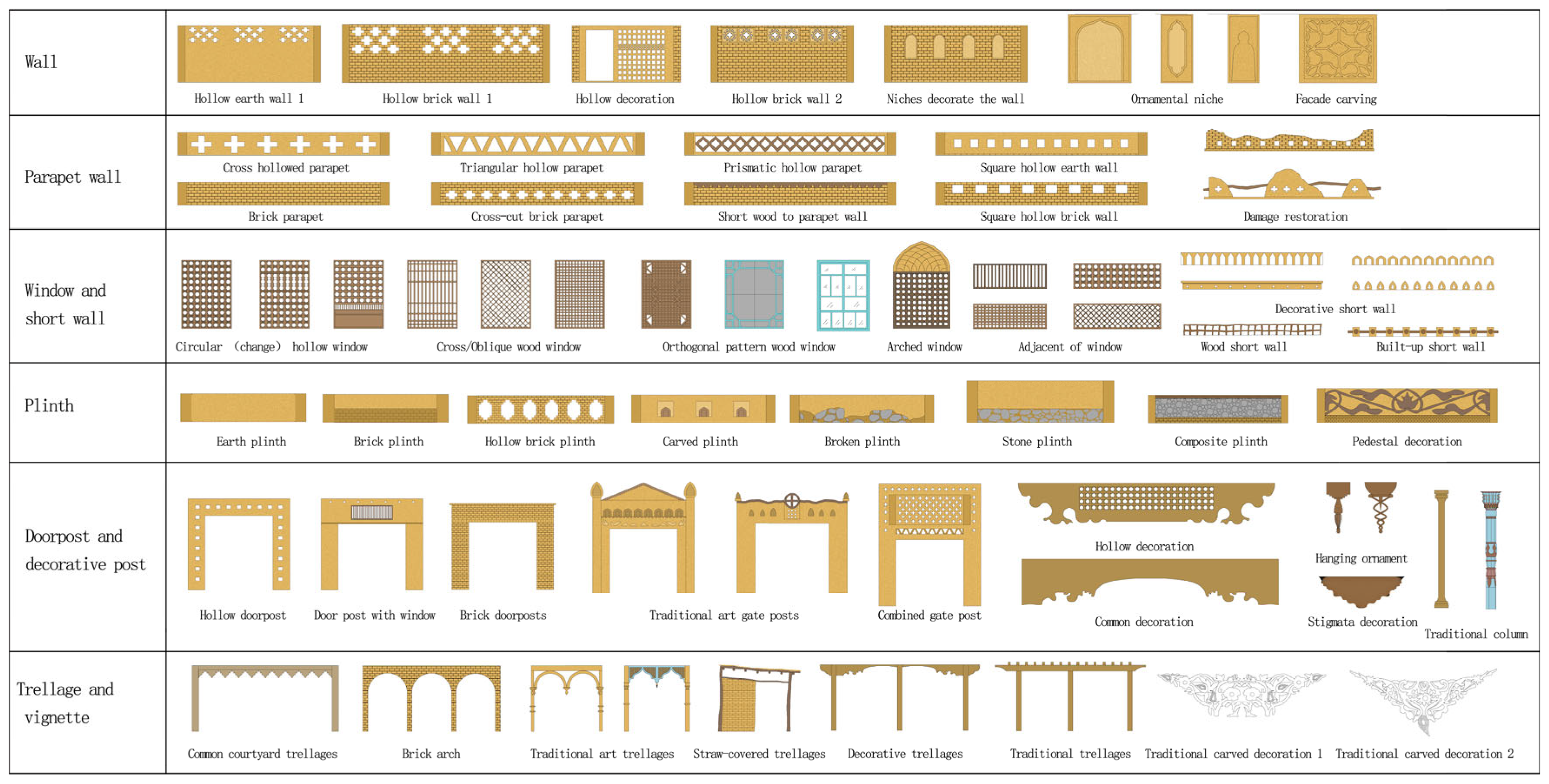
3.2. Ecological and Cultural Aspects of Tuyugou Village

In line with the hot-summer and cold-winter climate typical of Xinjiang, the site selection for Tuyugou Village adheres to traditional Chinese principles, specifically: "Avoid constructing high on ridges with limited water and avoid building low near water to reduce ditch construction effort." [4] The village is situated between two mountains in the heart of a valley, which serves to shield it from cold winter monsoons and reduces direct solar exposure during the summer months. The majority of the buildings are oriented toward the water, capitalizing on evaporative cooling that reduces the temperature by approximately 2°C while increasing humidity relative to the surrounding mountains. During the night, wind speeds toward the valley decrease, and in winter, temperatures within the valley are typically 2–3°C warmer than those outside [26]. To evaluate Tuyugou Village's ecological adaptability, we utilized Ladybug simulation software on the Rhino and Grasshopper platforms to model annual sunshine hours and prevailing wind patterns. The results, presented in Figure 6, reveal that the village experiences reduced sunlight exposure and lower wind speeds compared to the surrounding mountains, showcasing its exceptional ecological adaptability to extreme environments.

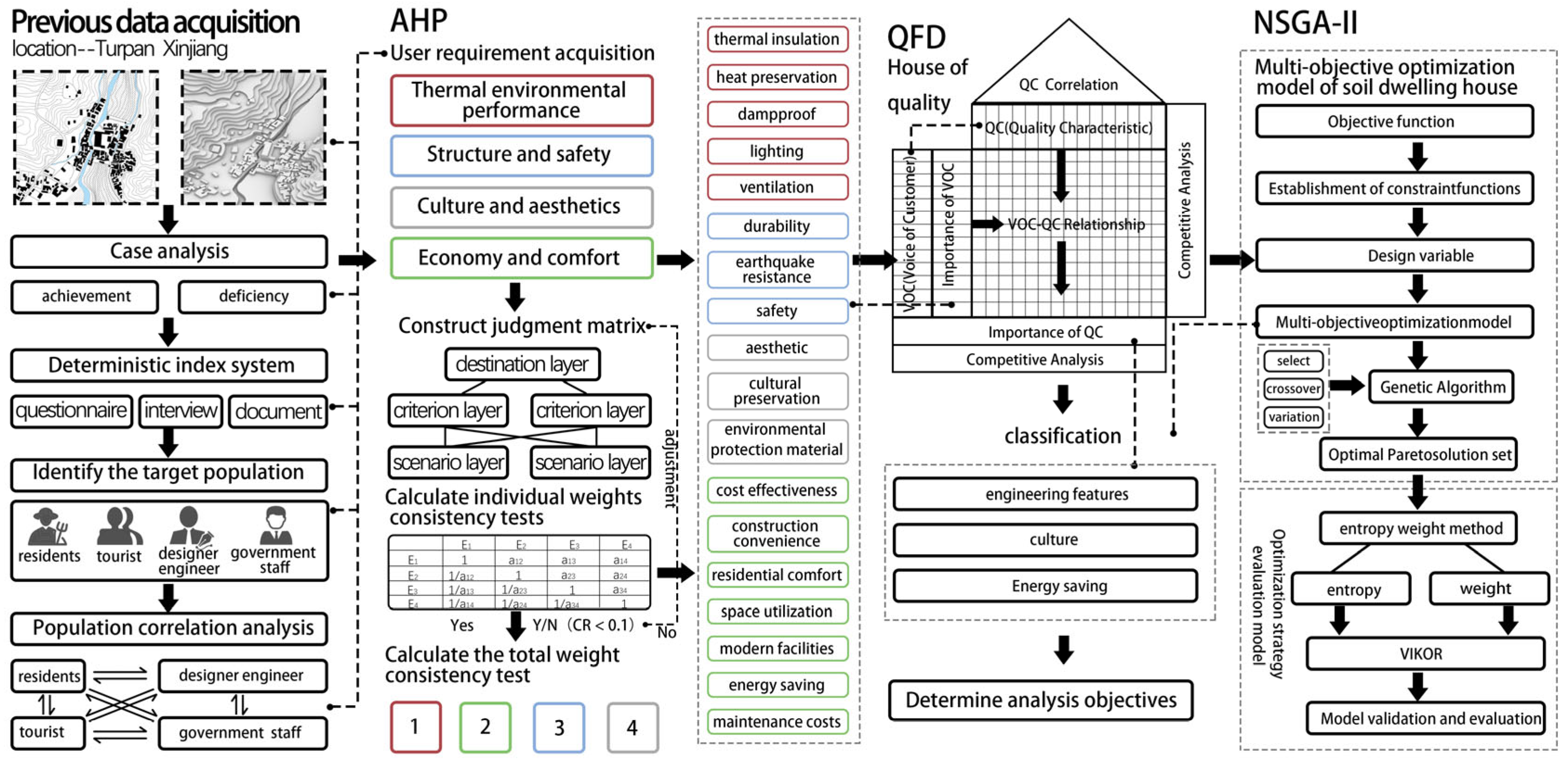
4. Research Design

This research examined the developmental context of Tuyugou Village to identify the needs of various stakeholders, particularly those involved in the refurbishment and modernization of earthen dwellings. The primary stakeholders in this process included local residents, visiting tourists, construction experts (including architects and engineers), and governmental bodies responsible for the region. To systematically gather and interpret the perspectives, expectations, and priorities of these groups, the study utilized structured surveys, focus group discussions, and comprehensive interviews (Table 1) [27]. This method not only uncovered critical stakeholder requirements but also highlighted the initial relationships between the differing priorities of these groups. These insights were instrumental in formulating design criteria that were more specific and tailored to the renovation of Tuyugou Village’s traditional earthen architecture.

4.2. Priority Ranking Using the AHP Method

The restoration of traditional earthen dwellings in Tuyugou Village requires addressing the diverse needs of various stakeholders. Data collection was divided into two stages to define the design criteria. The first stage involved fieldwork, which assessed the physical and environmental conditions of the dwellings to identify key renovation requirements. Additionally, data were collected from similar renovation projects, climate studies, and relevant policies. In the second phase, 200 questionnaires were distributed(See Appendix Table A1), with 177 valid responses received. These responses helped the research team understand stakeholder demands. From this analysis, four primary needs were identified: thermal performance, structural safety, cultural and aesthetic values, and economic/comfort considerations, in addition to 18 secondary needs.

To prioritize these needs, the team employed Saaty’s 1-9 scale to assign relative weights. Judgment matrices were constructed from the survey responses, allowing comparison of indicators to assess their relative importance [16]. The geometric mean method was applied to calculate the weight of each criterion, thereby establishing a hierarchy for the renovation strategy [28].

The AHP method addressed challenges in traditional QFD models, particularly in managing subjectivity and integrating both qualitative and quantitative data [29]. Utilizing Saaty’s 1-9 rating system, the team conducted pairwise comparisons across four secondary and 19 tertiary user needs specific to Tuyugou Village. In this system, a score of 1 indicates equal importance, while a score of 9 signifies that one factor is considerably more important than another. Weight calculations were performed using judgment matrices, which compared factors on a 1-9 scale [28].

$$\mathrm{A}=\left[\begin{array}{cccc}1& a_{12}& \cdots & a_{1n}\\ {\displaystyle \frac{1}{a_{12}}}& 1& \cdots & a_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ {\displaystyle \frac{1}{a_{1n}}}& {\displaystyle \frac{1}{a_{2n}}}& \cdots & 1\end{array}\right]$$

(1)

In the formula, $a_{ij}={\displaystyle \frac{1}{a_{ij}}}$ and$a_{ij}=1$.

The ranking weights for each factor are extracted from the judgment matrix. To estimate the eigenvector, known as M, the square root method is applied. The corresponding normalized vector, symbolized as ω, indicates the relative significance of user needs. Each element within ω represents the weight allocated to a particular need at the current level, using the needs from the preceding level as a reference. To ensure the results are consistent, the maximum eigenvalue, λmax, of the judgment matrix is computed. The procedure for this calculation is outlined in the following steps [28]:

$$M_i=\sqrt[n]{\prod _{j=1}^n{a}_{ij}}$$

(2)

$${\omega }_i={\displaystyle \frac{M_i}{\sum _{i=1}^n{M}_i}}$$

(3)

$${\lambda }_{max}=\sum _{i=1}^n\left(\sum _{j=q}^n{a}_{ij}·{\omega }_j\right)/{\omega }_i$$

(4)

To ensure the judgment matrix is accurate and free of bias, a consistency validation is conducted. This involves calculating the consistency index (CI) and consistency ratio (CR). The CI measures the alignment within the matrix, while the random index (RI) acts as a comparison benchmark. A CI of zero indicates perfect consistency [28].

Once the CI is calculated, the CR accounts for random variations affecting reliability. If the CR is below 0.1, the matrix is deemed consistent, validating the weight rankings. If it exceeds 0.1, revisions are needed. Together, the CI and CR offer a comprehensive check of the matrix's consistency, ensuring reliable data.

$$CI={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}$$

(5)

$$R={\displaystyle \frac{CI}{RI}}$$

(6)

After performing data calculations using the software, the weight matrix W=[0.4787, 0.1865, 0.1183, 0.2165] was obtained. Specifically, the weight for thermal performance is 0.4787, the weight for structure and safety is 0.1865, the weight for culture and aesthetics is 0.1183, and the weight for economics and comfort is 0.2165. The calculated maximum eigenvalue λmax​=4.0934, CR = 0.0346, CI = 0.0311, and with CR = 0.0346 < 0.1, it indicates that the judgment matrix has high reliability. Similarly, by combining the primary indicator weights, the weights for the secondary indicators are calculated, and the comprehensive weights for the secondary indicators are derived as a reference for the optimization design of earthen dwellings. See Table 2 for details.

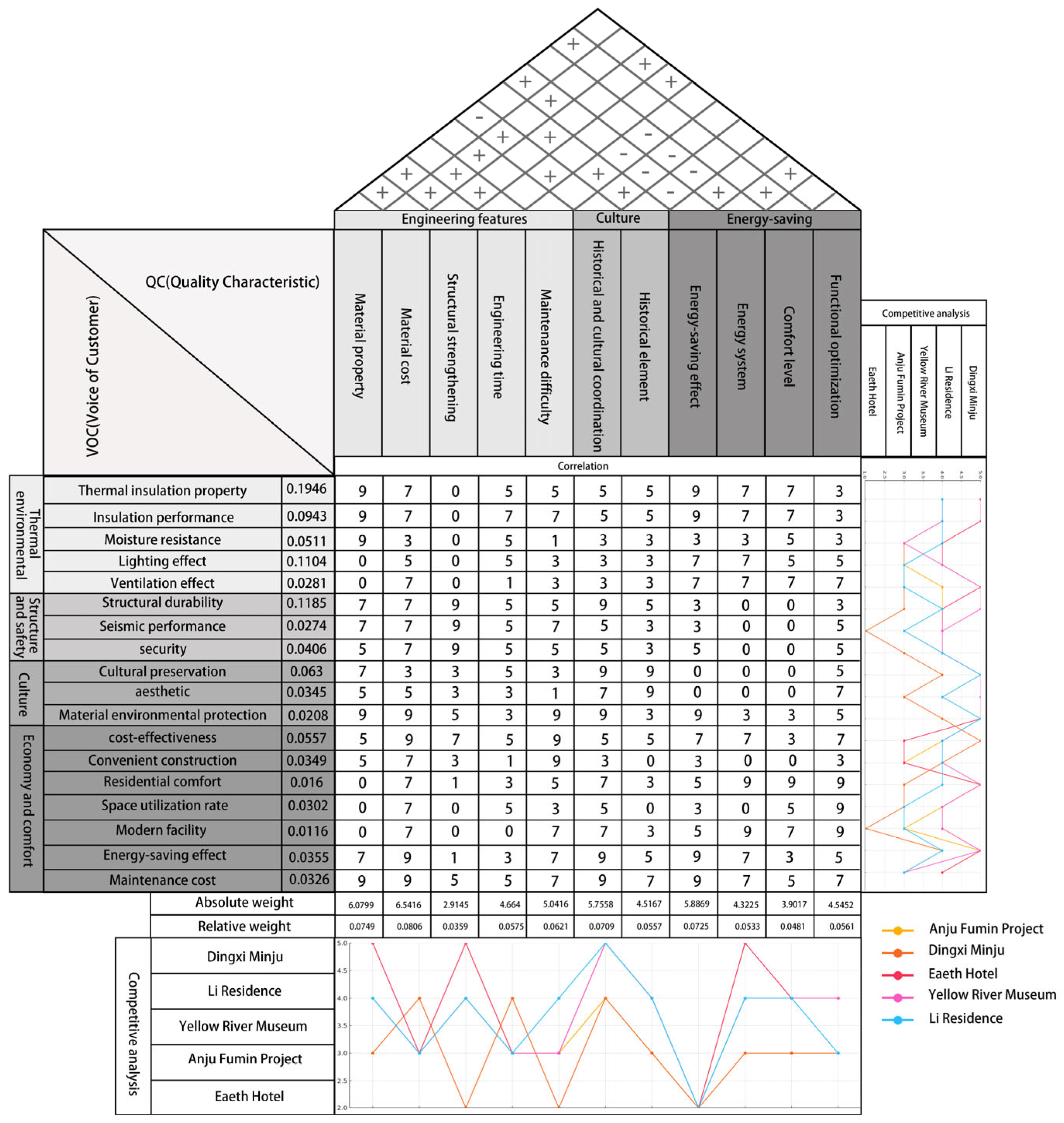
4.3. Determination of Quality Characteristics

Using the weights of user needs derived from the AHP analysis, the research team translated these into precise quality characteristics. To maintain scientific rigor and objectivity, the team collected feedback from a wide range of stakeholders. The participants included five local residents, five craftsmen specializing in earthen construction, five cultural preservation officials, ten architectural designers, and five professors from the Civil Engineering Department of Xinjiang University. A comprehensive review of these discussions allowed the team to pinpoint 11 key design quality characteristics. By incorporating expert input alongside a multidimensional analytical approach, the renovation design was crafted to address diverse stakeholder needs, ensuring both practical feasibility and scientific validity.

4.4. Constructing the Relationship Matrix

After identifying user needs and design quality characteristics, the team established their relationship by assigning values: 9 (very strong correlation), 7 (strong correlation), 5 (moderate correlation), 3 (weak correlation), 1 (very weak correlation), and 0 (no correlation) [29]. This matrix enabled the association between the quality characteristics of Tuyugou earthen dwellings and user needs, facilitating the calculation of the weight scores for each characteristic.

4.5. Determining the Priority of Quality Characteristics

The bottom part of the Quality House evaluates the importance of each quality characteristic by taking into account its difficulty coefficient, overall benefits, and associated trade-offs to establish its priority. Characteristics with higher priority are those that should be addressed first, as they have a greater impact on boosting customer satisfaction, loyalty, competitiveness, and profitability of earthen dwellings. The formula used for this calculation is as follows:

$$S_i=\sum _{j=1}^n(W_j·R_{ij})$$

(7)

In the formula, ${\mathrm{S}}_{\mathrm{i}}$​ represents the total score of design quality characteristic i. ${\mathrm{W}}_{\mathrm{j}}$​ represents the weight of user need j. ${\mathrm{R}}_{\mathrm{i}\mathrm{j}}$ represents the strength of the relationship between user need j and design quality characteristic ${\mathrm{Q}}_{\mathrm{i}}$​, typically expressed using 9, 7, 5, 3, 1, or 0 to indicate the degree of association. n is the total number of user needs.

4.7. Competitive Analysis:

To assess the design's industry competitiveness, the project team integrated competitive analysis modules into the right and bottom sections of the Quality House. These modules enabled a comprehensive evaluation of the strengths and weaknesses of each project, emphasizing specific design attributes. Five prominent earthen architecture projects in China were selected, representing key industry trends. The selected projects were the "Anju Fumin" demonstration [1], the Tongwei County residence renovation (Dingxi) [30], the Urho earthen hotel in Karamay [31], the Yellow River Loess Geological Museum [32], and the Li family earthen house renovation [33]. A symbolic scoring matrix evaluated each project’s design indicators. The resulting scores offered insights into each project's performance across different design attributes and their alignment with client expectations [31]. Through the analysis of these results, the team developed a Quality House model, facilitating a detailed comparison of each design’s competitive positioning, as illustrated in Figure 7.

4.8. Converting Quality Characteristics into Optimization Objective Functions

In the context of multi-objective optimization, the objective function organizes quality attributes into three primary categories, each comprising several sub-objectives [11](See Appendix Table A2). Through the integration of engineering parameters, a robust and practical evaluation framework is developed. This systematic approach effectively balances trade-offs between competing project objectives, resulting in design solutions that are both efficient and feasible.

4.8.1. Developing the Optimization Objective Model for Engineering Characteristics

In construction projects, evaluating key quality factors, including building materials, scheduling, and construction methods, is crucial. These factors are optimized through the application of established engineering principles. Key considerations such as cost management, ease of maintenance, construction speed, and budget control are closely linked to material selection and project timelines. Consequently, these factors form the foundation for assessing the economic viability of a project, taking into account material costs and scheduling (see Table 3 and Table 4). By assigning suitable weights to these variables, costs related to materials, maintenance, and construction, alongside project timelines, can be effectively managed, shaping the final optimization outcomes.

$${f_1=C}_{total}=\sum _{i=1}^n(C_{mi}{·Q}_i)+(C_{li}·{\displaystyle \frac{100}{P_m}}+C_{labor}·T)·e^{-\lambda \cdot T}$$

(8)

Among them, the material cost ${\mathrm{C}}_{\mathrm{m}\mathrm{i}}$​ is the unit price of the i-th material, and ${\mathrm{Q}}_{\mathrm{i}}$ is the quantity of material used. This part reflects the cost of the selected material. ${\mathrm{C}}_{\mathrm{l}\mathrm{i}}$ is the annual maintenance cost of the material. ${\mathrm{P}}_{\mathrm{m}}$ is the maintenance cycle, ${\mathrm{C}}_{\mathrm{l}\mathrm{a}\mathrm{b}\mathrm{o}\mathrm{r}}$​ is the labor cost, T is the project duration, and ${\mathrm{e}}^{-\mathsf{\lambda }\cdot \mathrm{T}}$ is the exponential decay term, which reflects the gradual decline in overall project economics as the project duration increases. The value of λ can be adjusted to fit different engineering scenarios. The specific material parameters are shown in Table 3; The relevant parameters of construction labor cost and construction period are shown in Table 4.

4.8.2. Stablishing the Cultural Optimization Objective Model:

Traditional earthen dwellings are built from rammed yellow clay, featuring essential components such as boundary and courtyard walls, partition walls, short fences, gates, corridors, high sheds, storage rooms, hearths, grape-drying rooms, toilets, and livestock pens [35]. Decorative elements were added to the walls of these structures to enhance their artistic value. Unique geometric patterns were created by strategically placing bricks on door pillars and hollowing out sections of the short fences. Certain buildings highlighted their significance through the use of brick arches [36]. Intricately carved columns with distinctive shapes and vibrant colors enhanced the artistic appeal within the courtyards. Sheds were classified into inner courtyard sheds, external support sheds, roof sheds, built-in sheds, and corridor sheds. Windows, often adorned with hollow carvings, were available in square, arched, or strip shapes. These decorative techniques were employed to beautify the environment, enhance the architectural facade, and emphasize the building's overall theme. As illustrated in Figure 8, the exterior elements are divided into five major categories and 69 individual components.

The cultural adaptability of materials is assessed by examining their composition, traditional relevance, and proportional use in construction. This assessment considers how well each material aligns with the cultural heritage of the project, offering a balanced evaluation of both functional and cultural significance. The calculation formula for this adaptability is provided below：

$$f_2(x)=\sum _{i=1}^n(Q_i·C_{cultural})·{\displaystyle \frac{{\mathrm{M}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{d}}}{{\mathrm{H}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}}}·{\displaystyle \frac{{\mathrm{E}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{d}}}{69}}$$

(9)

Among them, ${\mathrm{M}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{d}}$​ represents the total amount of traditional materials. ${\mathrm{H}}_{\mathrm{t}\mathrm{o}\mathrm{t}\mathrm{a}\mathrm{l}}$​ represents the total amount of materials (including all materials), and ${\mathrm{Q}}_{\mathrm{i}}$ is the quantity of material used. ${\mathrm{C}}_{\mathrm{c}\mathrm{u}\mathrm{l}\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{a}\mathrm{l}}$ is the cultural adaptability score of the material, representing its coherence and adaptability in historical culture. ${\mathrm{E}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{d}}$​ is the number of traditional elements used, and 69 represents the total summarized traditional elements.

4.8.3. Establishing the Energy-Saving Optimization Objective Model

Energy efficiency refers to the amount of energy required by a building and its systems to meet specific load demands. In both building design and equipment selection, enhancing energy efficiency not only minimizes energy consumption and operational costs but also promotes environmental sustainability and improves the overall comfort of the building. The energy efficiency optimization method presented in this paper integrates the thermal properties of building materials with equipment selection and operational control strategies. The equipment involved in the transformation process is shown in Table 5.

Given that building loads and equipment performance fluctuate in a dynamic environment, real-time adjustments to equipment operations and optimization of thermal management are essential for maximizing energy efficiency [41]. Building load demands vary according to factors such as time of day, seasonal changes, and equipment operating conditions. To effectively capture these fluctuations, this study utilizes day-night load models, seasonal load models, and equipment load models. The variation in daily and nightly loads is modeled using a sine function, as demonstrated in the day-night load model described below.

$$L_{day-night}\left(t\right)=L_{avg}+L_{amp}·sin({\displaystyle \frac{2\pi }{24}}·t)$$

(10)

where: $L_{avg}$ is the daily average load (unit: kW), $L_{amp}$ is the load amplitude (unit: kW), and t is the time (unit: hours).

The load of each device varies with time and load demand. The equipment load model is as follows:

$$L_{device}\left(t\right)=C_{load}·P_{rated}·l_{operating}\left(t\right)$$

(11)

where: $C_{load}$ is the load factor (unit: 0-1), representing the ratio of the actual working load to the rated load of the equipment. $P_{rated}$ is the rated power of the equipment (unit: kW), and $l_{operating}$ is the indicator function, used to describe whether the equipment is in operation at time t.

Based on the above information, the equipment operation time for the local traditional soil dwellings is shown in Figure 9 (a), and the power output distribution is shown in Figure 9 (b). This indicates that, due to Turpan's extreme climate conditions, the power consumption of air conditioning and heating fluctuates significantly. Their usage frequency is concentrated during specific climate conditions, while the power consumption of lighting and water heaters remains relatively stable. However, there are some fluctuations as the seasonal climate changes.

Based on the dynamic load, the selection and operation control of equipment is another crucial step. The operational efficiency of equipment is closely related to the load. Therefore, by dynamically adjusting the start-stop operation and power output of the equipment, energy consumption can be effectively controlled and system efficiency improved.

$$P_{device}\left(t\right)=C_{load}\left(t\right)+P_{rated}·l_{operating}\left(t\right)$$

(12)

where $C_{load}\left(t\right)$ is the load factor, representing the load ratio of the equipment at the current time. $P_{rated}$ is the rated power of the equipment, and $l_{operating}\left(t\right)$ is the indicator function for the equipment's start-stop status.

Based on the above, in a discrete-time model, the total energy consumption of the equipment combined with the load model at different time periods can be expressed as:

$$E_{device}=\sum _{t=1}^T{P}_{device}\left(t\right)·\Delta t$$

(13)

Based on the dynamic load, equipment selection, and thermal storage system, the heat transfer process of the building envelope also incurs energy consumption. Considering factors such as material density, specific heat, thermal conductivity, and thickness, the building’s energy consumption is related to heat transfer, temperature differences, and thermal storage characteristics, based on the principles of heat transfer and energy conservation. The heat transfer through the building envelope can be described using Fourier's law:

$$Q_{dynamic}={\displaystyle \frac{A\cdot \lambda \cdot \Delta T\cdot t}{d}}$$

(14)

In the formula, Q is the heat transferred through the building envelope, measured in joules (J) or kilowatt-hours (kWh). A is the area of the building envelope, measured in square meters (m²). ΔT is the temperature difference between the interior and exterior, measured in kelvins (K). t is the time, measured in seconds or hours. λ is the thermal conductivity of the material, measured in watts per meter-kelvin (W/m·K). d is the thickness of the material.

The heat storage coefficient (S) determines a material's ability to retain and release heat, influencing a building's thermal performance. Materials with higher S values stabilize indoor temperatures by absorbing and releasing heat over time, which is beneficial in fluctuating climates [38]. Calculating S involves specific heat capacity, density, and thickness, with higher values indicating improved energy efficiency.

$$Q_{heat}=S\cdot A\cdot \Delta T$$

(15)

where ${\mathrm{Q}}_{h\mathrm{e}\mathrm{a}\mathrm{t}}$ is the heat absorbed or released by the material, measured in joules (J). S is the heat storage coefficient of the material, measured in watts per square meter-kelvin (W/(m²·K)). A is the area of the building envelope, measured in square meters (m²). ΔT represents the temperature change, measured in kelvins (K). The specific material parameters are shown in Table 6.

Taking into account the heat transfer and thermal storage characteristics of materials, the building's energy consumption can be expressed as the sum of the heat transfer energy consumption and the thermal storage energy consumption of the building envelope.

$$E_{total}=Q_{heat}+Q_{dynamic}$$

(16)

By omitting considerations like solar radiation gains, ventilation energy usage, and internal heat contributions, the energy consumption of both the building and its energy system is calculated. The final formula for this calculation is formulated by integrating the economic benefits of the energy system with its energy-saving advantages.

$$f_3(x)=\sum _{i=1}^n({\displaystyle \frac{C_{device}}{E_{device}}}+{\displaystyle \frac{C_{mi}{·Q}_i}{E_{total}}})$$

(17)

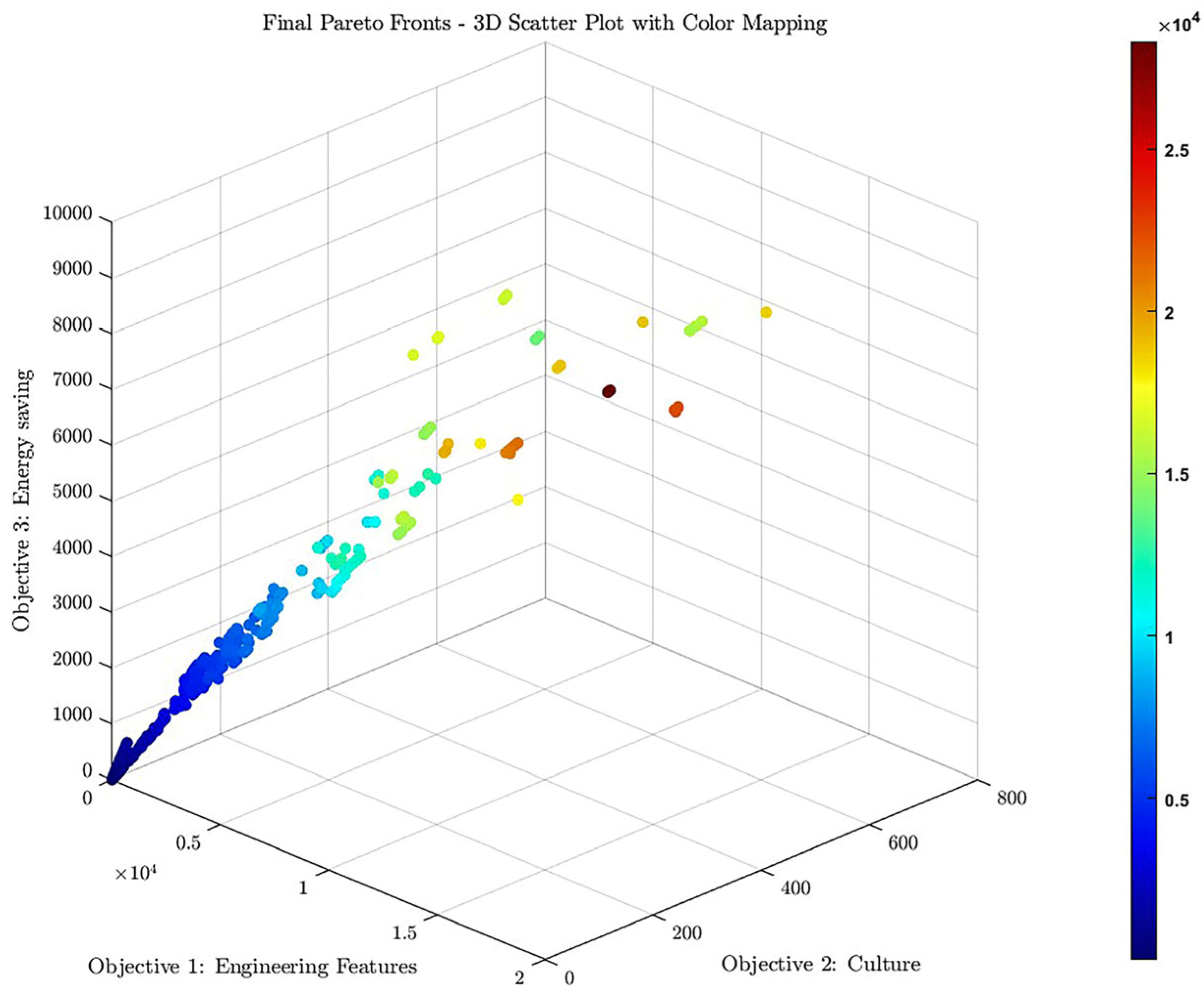
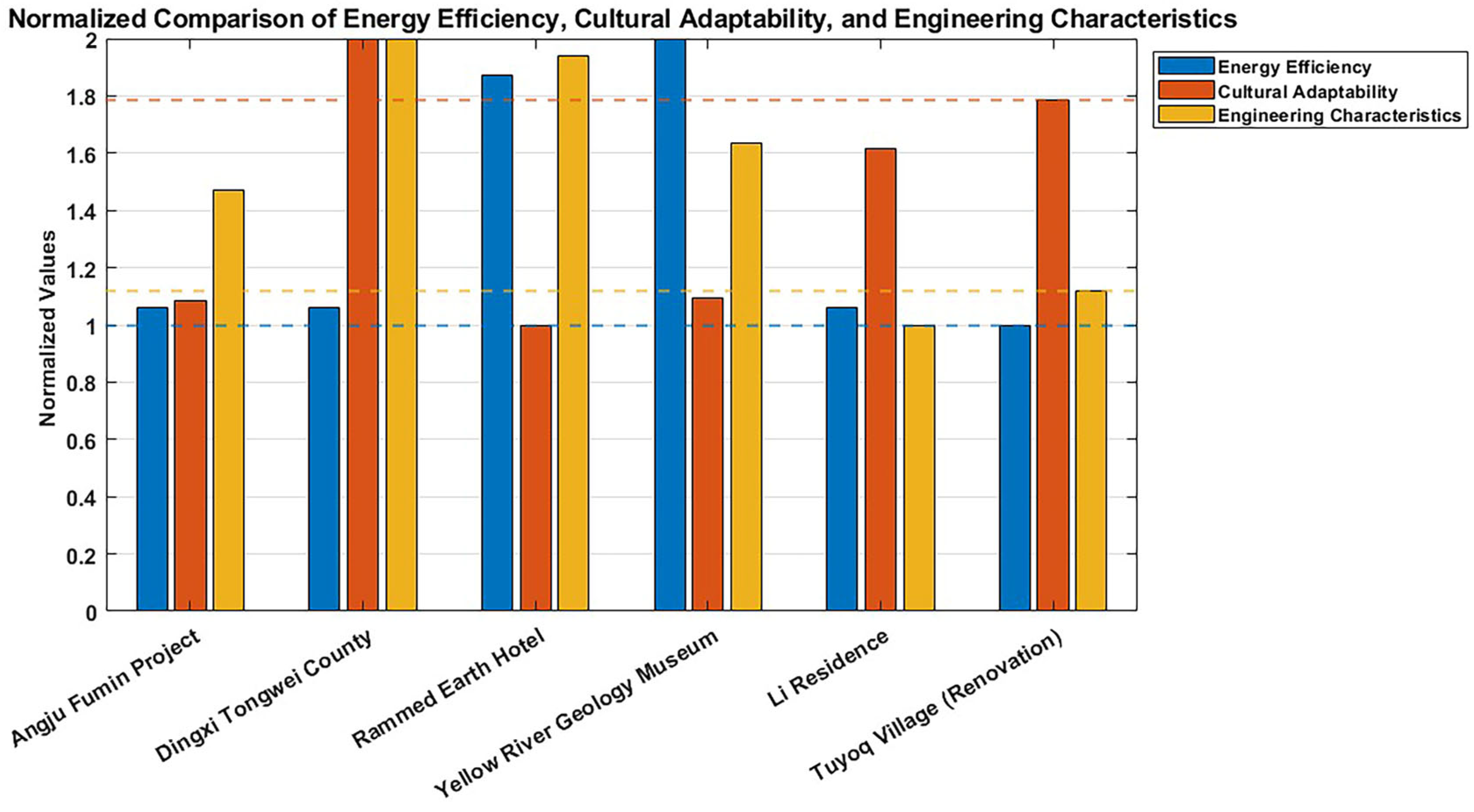
5. Design Results

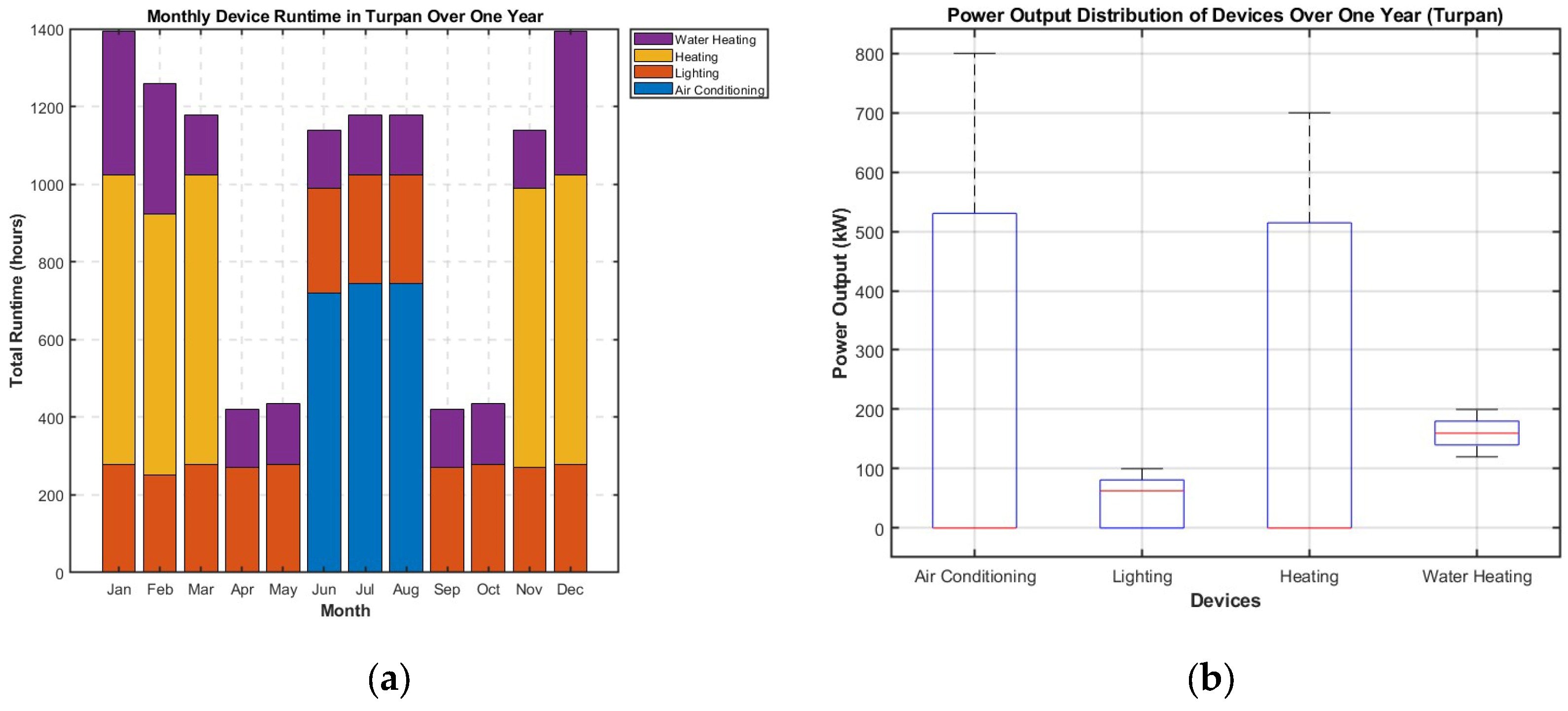
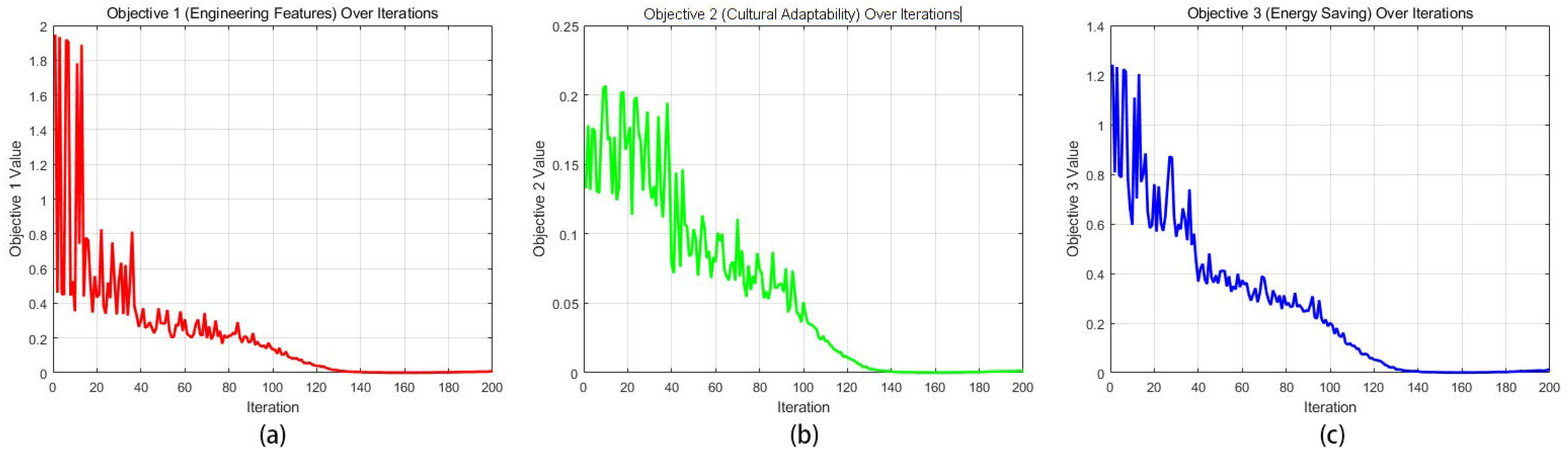
5.1. Parameter Settings

This research employed Matlab to develop the necessary scripts and functions for the analysis. In the main script, several key parameters were defined: a population size (N) of 100, a maximum of 200 iterations, a crossover probability of 0.8, and a mutation probability of 0.2. Figure 10 illustrates the Pareto optimal solution set generated after applying the NSGA-II algorithm to solve the multi-objective optimization problem. Additionally, Figures 10a-c present the iteration diagrams for each objective derived from the NSGA-II model.

Once the algorithm reaches the predefined limit for iterations, it halts, producing a set of Pareto-optimal solutions that conform to the established constraints. These solutions, depicted in Figure 11, represent distinct construction strategies, each specifically designed to align with the various objectives outlined during the optimization. By taking into account factors such as cost-effectiveness, preservation of cultural heritage, and energy efficiency, these solutions offer a diverse array of alternatives for decision-makers to assess [39]. The range of strategies demonstrates the algorithm’s capability to balance conflicting priorities, thereby making it a powerful tool for resolving complex construction challenges within the specified parameters.

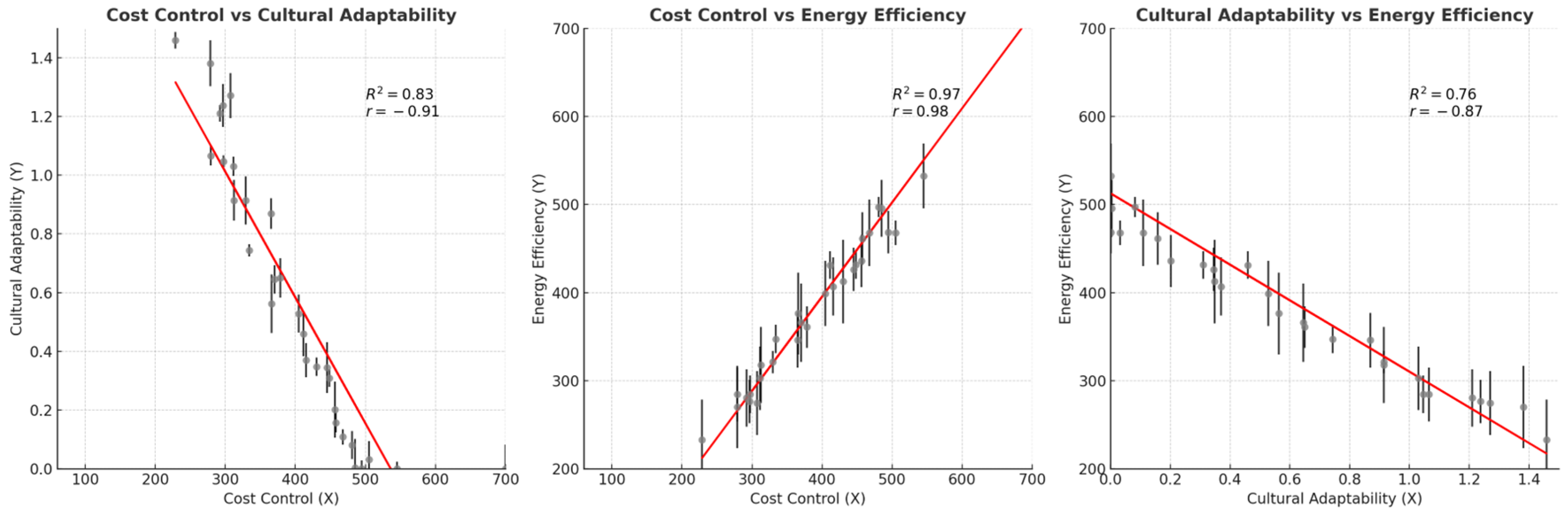
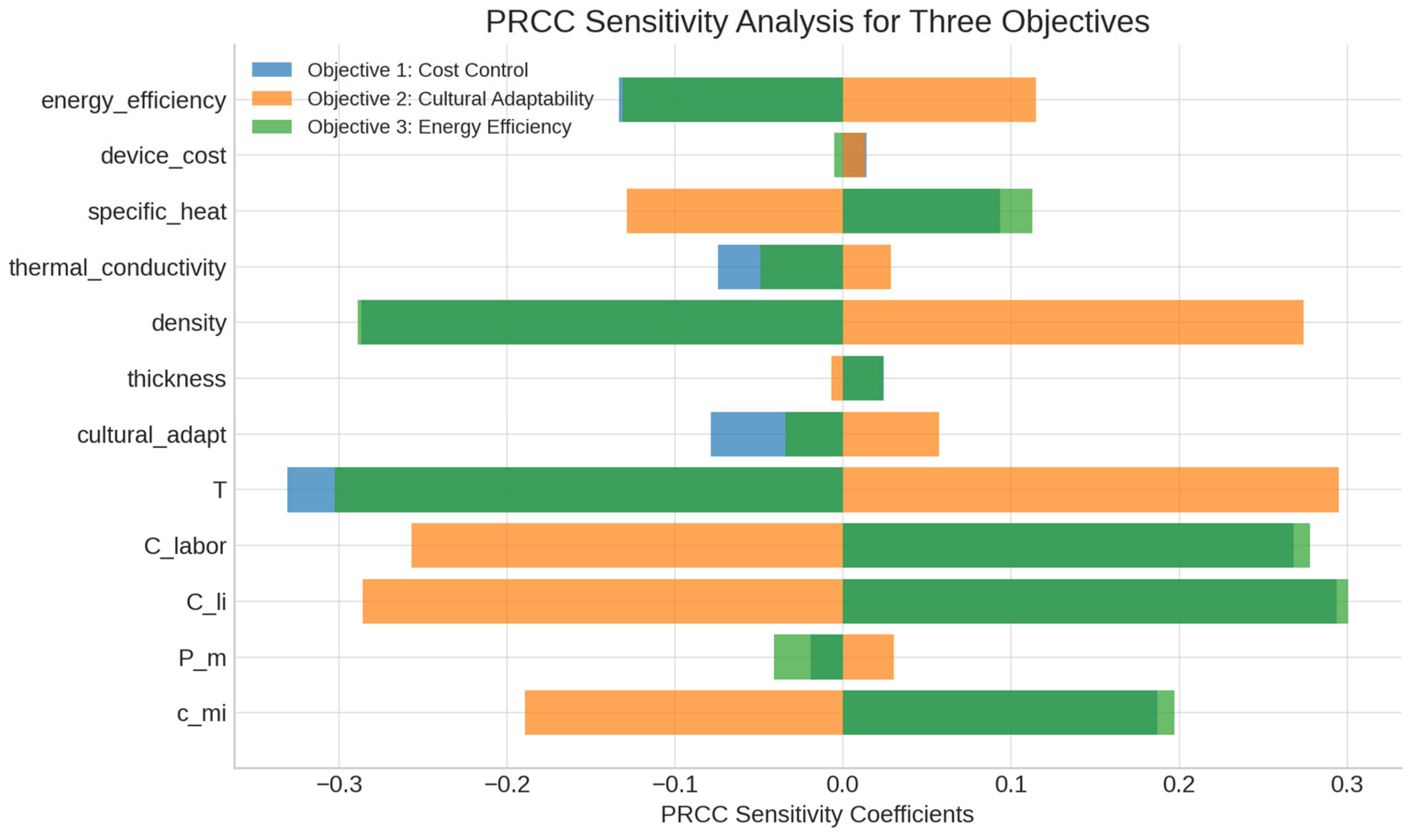
5.2. PRCC Sensitivity Analysis

To achieve an appropriate balance among multiple objectives while fulfilling overall design requirements, this paper performs a trade-off analysis of the Pareto-optimal solutions [40], as illustrated in Figure 12. A clear trade-off exists among cost control, cultural adaptability, and energy efficiency.

First, cost control and cultural adaptability exhibit a negative correlation (r = −0.91, R² = 0.83), indicating that cost reduction often compromises cultural preservation. A balance must be achieved between these two factors.

Second, cost control and energy efficiency demonstrate a positive correlation (r = 0.98, R² = 0.97), suggesting that enhancements in energy efficiency typically entail increased costs.

Finally, cultural adaptability and energy efficiency exhibit a negative correlation (r = −0.87, R² = 0.76), implying that the preservation of traditional culture may diminish energy efficiency. Therefore, prior to decision-making, it is essential to balance these three objectives and conduct a sensitivity analysis of the design variables.

The sensitivity analysis results, as shown in Figure 13, reveal the varying effects of different input parameters on cost control, cultural adaptability, and energy efficiency. The analysis shows that labor costs and project duration significantly impact all objectives, making them key factors that require close attention. Annual maintenance costs and material types play a crucial role in energy efficiency and long-term cost control. To achieve a balance among the three objectives, optimizing labor costs and construction duration is a core strategy. Moreover, a thoughtful selection of material types is needed to balance cultural preservation and energy-saving requirements between cultural adaptability and energy efficiency. Overall, decision-makers can achieve the optimal combination of cost and performance by flexibly adjusting key parameters while meeting project goals [41].

Based on the above analysis, this paper selects 10 solutions from the Pareto optimal set as reference solutions. These solutions made reasonable selections of material types and screened labor costs and construction duration. Specific data are shown in Table 7.

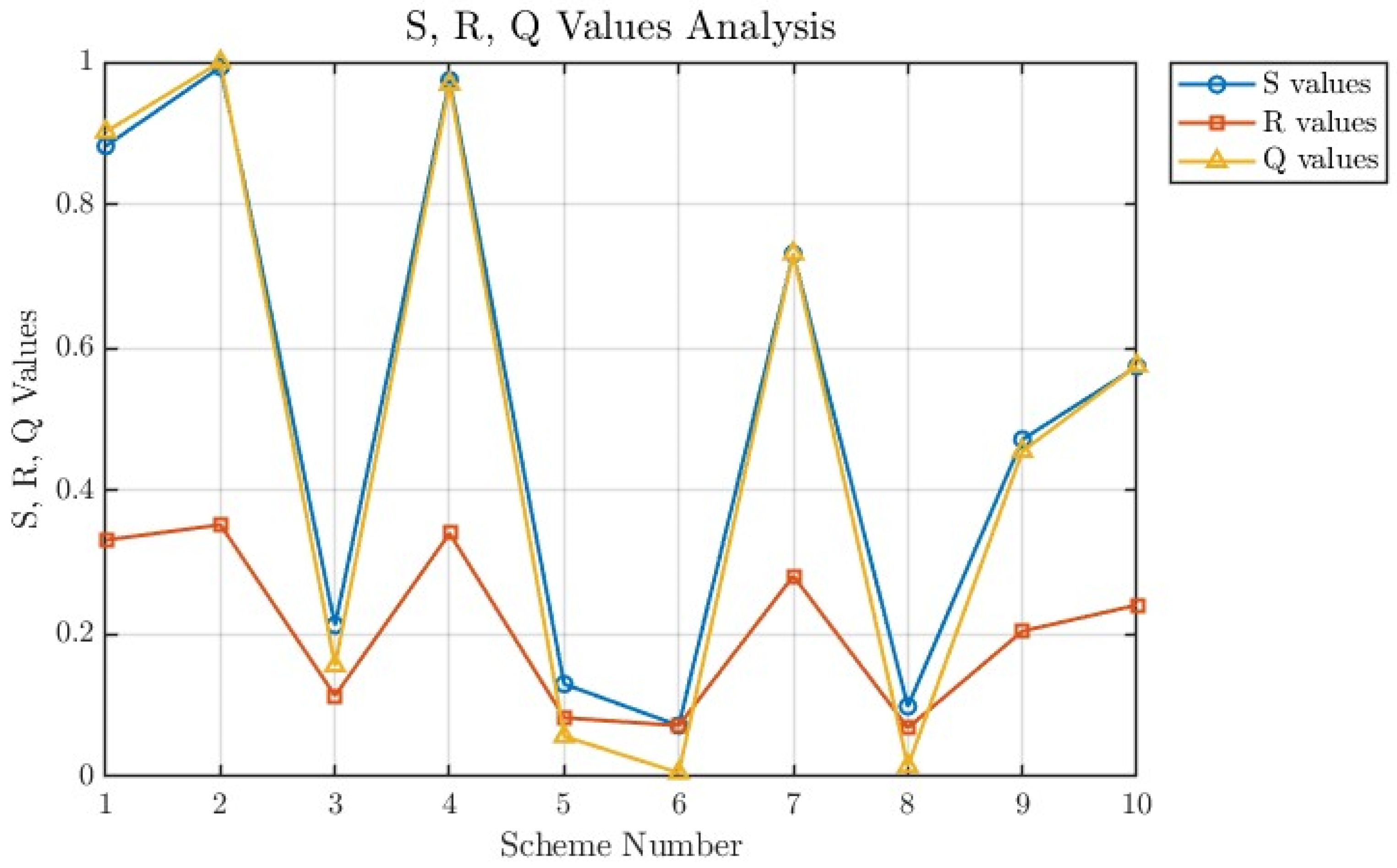
5.3. Entropy Weight -VIKOR Method

To minimize external influences on decision-making, this study adopts an objective approach by combining the entropy weight method with the VIKOR technique [42]. This integrated method addresses limitations in other multi-criteria decision-making techniques, such as AHP's subjectivity and TOPSIS's emphasis on a single criterion. The process starts by applying the entropy weight method to calculate objective weights, ensuring a fair and rational distribution. After determining the weights, the VIKOR method is employed to comprehensively evaluate and rank the objectives, selecting the optimal solution. This combined approach offers a scientifically grounded and balanced selection of Pareto-optimal solutions, ensuring fairness and consistency throughout the decision-making process [43]. The detailed steps for entropy method calculation include evaluating 10 decision alternatives (m = 10) and 3 criteria (n = 3), constructing an initial matrix to represent these parameters.

$$x=\left[\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& \cdots & x_{23}\\ ⋮& \ddots & ⋮\\ x_{\mathrm{10,1}}& \cdots & x_{\mathrm{10,3}}\end{array}\right]$$

(18)

To make the scores under different criteria comparable, the data needs to be normalized. For positive criteria (such as culture), where higher scores are better, normalization is performed using the following formula:

$$r_{ij}={\displaystyle \frac{x_{ij}-min\left(x_j\right)}{max\left(x_j\right)-min\left(x_j\right)}}$$

(19)

For negative criteria (such as engineering features and energy-saving effects), where lower scores are better, the following formula is used for normalization:

$$r_{ij}={\displaystyle \frac{max\left(x_j\right)-x_{ij}}{max\left(x_j\right)-min\left(x_j\right)}}$$

(20)

After normalization, the percentage of each score is further calculated:

$$R_{ij}={\displaystyle \frac{r_{ij}}{\sum _{j=1}^m{r}_{ij}}}$$

(21)

The final normalized matrix R is obtained:

$$R=\left[\begin{array}{ccc}{R}_{11}& R_{12}& R_{13}\\ R_{21}& \cdots & R_{23}\\ ⋮& \ddots & ⋮\\ R_{\mathrm{10,1}}& \cdots & R_{\mathrm{10,3}}\end{array}\right]$$

(22)

Next, the entropy method is used to calculate the entropy value for each evaluation criterion:

$$e_j={\displaystyle \frac{1}{\ln m}}·\sum _{i=1}^m{R}_{ij}\ln R_{ij}$$

(23)

$$R{w}_j={\displaystyle \frac{1-e_j}{\sum _{j=1}^n(1-e_j)}}$$

(24)

Here, $R_{ij}$​ represents the normalized score value, m is the number of decision options, and to avoid the situation where ln(0) appears, the 0 values in $R_{ij}$​ can be replaced with a very small value, such as ${1\mathrm{e}}^{-10}$, during calculation. Finally, the entropy values and weights for each objective are obtained, as shown in Table 8:

After determining the weights for each criterion, the VIKOR method is used to rank the solutions. During the VIKOR method process, we will calculate the S, R, and Q values for each solution through the following steps, and ultimately select the optimal solution.

Ideal Solution (Best) and Anti-Ideal Solution (Worst) [42]:

The ideal solution $f_j^{\mathrm{*}}$​ is the best value for each criterion (for positive criteria, take the maximum value; for negative criteria, take the minimum value).

The anti-ideal solution $f_j^{-}$​ is the best value for each criterion (for positive criteria, take the maximum value; for negative criteria, take the minimum value) [42].

S Value: Represents the weighted distance between each solution and the ideal solution [44]. The calculation formula is as follows:

$$S_j=\sum _{i=1}^m{W}_j\left({\displaystyle \frac{f_j^{\mathrm{*}}-f_{ij}^{-}}{f_j^{\mathrm{*}}-f_j^{-}}}\right)$$

(25)

R Value: The maximum weighted distance in each solution:

$$R_i={MAX}_j\left(W_j·{\displaystyle \frac{f_j^{\mathrm{*}}-f_{ij}^{-}}{f_j^{\mathrm{*}}-f_j^{-}}}\right)$$

(26)

Q Value: A weighted calculation that combines the S and R values, with the compromise coefficient v generally set to 0.5.

$$Q_i=v·{\displaystyle \frac{S_i-S^{\mathrm{*}}}{S^{-}-S^{\mathrm{*}}}}+(1-v){\displaystyle \frac{R_i-R^{\mathrm{*}}}{R^{-}-R^{\mathrm{*}}}}$$

(27)

After analyzing the final S, R, and Q values, Figure 14 is obtained.

Based on the analysis of the S, R, and Q value graph obtained above, the researchers found that the values are relatively close. To ensure the final evaluation results are more scientifically authoritative, a weighted comprehensive score incorporating the weights is used for ranking:

Using the S, R, and Q values along with their respective weights, a comprehensive score is calculated, and then the solutions are ranked based on this score.

The formula for the comprehensive score is: Score=$w_Q$⋅Q+$w_R$⋅R+$w_S$⋅S, where $w_Q$​, $w_R$​, and $w_S$​ are the weights for Q, R, and S, with $w_Q$=0.6, $w_R$=0.3, and $w_S$=0.1. After calculating the comprehensive score [42], the solutions are ranked from lowest to highest, as shown in Table 9:

The 6th optimization plan stands out as the most optimal solution, excelling in areas such as cost control, cultural adaptability, and energy efficiency. The unit construction cost is 340.566 yuan, reflecting its economic feasibility. With a cultural adaptability score of 1.5364, this plan effectively integrates local historical and cultural features by modernizing the architecture without compromising its traditional aesthetic and building techniques. In terms of energy performance, the plan achieves an energy cost of 352.793 yuan/kWh. Through improvements to the building envelope and the implementation of efficient energy systems, it successfully reduces energy consumption while addressing daily operational demands.

To assess the effectiveness of the renovation plan, five case study buildings were evaluated across three key areas: engineering features, cultural adaptability, and energy efficiency. The materials and related equipment were rated and then compared to the renovation plan. The results are shown in Figure 15: Tuyugou Village project outperformed the others in energy efficiency, with an energy cost of 352.793 yuan/kWh. In contrast, the energy costs for the Tongwei County residential project and Li’s house were 26% to 27% higher. The rammed-earth hotel and Yellow River Geology Museum exhibited even greater energy costs, with increases of 381% and 436%, respectively, likely due to their reliance on more energy-intensive systems or materials.

Regarding cultural adaptability, the Tuyugou Village project showed strong integration with local traditions, second only to the Tongwei County residential project, which had a 16% higher cultural adaptability score. On the other hand, the Anju Fumin Demonstration Project, the rammed-earth hotel, and the Yellow River Geology Museum demonstrated significantly lower cultural adaptability, with reductions ranging from 55% to 60%.

In terms of engineering features, the Tuyugou Village renovation had a unit cost of 340.566 yuan/m², reflecting reasonable construction costs. The Anju Fumin Demonstration Project and Li’s house had even lower costs, reduced by 32% and 11%, respectively. However, the Tongwei County residential project and the rammed-earth hotel experienced substantial cost increases, of 80% and 75%, respectively, due to the use of more expensive materials and more intricate designs.

In summary, the Tuyugou Village renovation project achieved a well-balanced combination of cost control, cultural adaptability, and energy efficiency, positioning it as a strong example of sustainable development. Future renovation efforts should continue to focus on harmonizing traditional values with modern efficiency to ensure long-term viability.

6. Conclusion

The optimization of traditional earthen dwellings in Tuyugou Village, Turpan, integrates engineering performance, cultural preservation, and energy efficiency. This study employs AHP, QFD, and NSGA-II to address the needs of residents, tourists, architects, and government officials. By balancing modern living standards with cultural heritage, it provides a data-driven strategy tailored for arid regions.

Through AHP, the research identified key priorities such as thermal efficiency, structural integrity, cultural preservation, and economic feasibility. These priorities were transformed into actionable design features using QFD, which were then optimized using NSGA-II to find an equilibrium between cost, cultural value, and energy performance. The VIKOR method further refined and ranked these solutions to facilitate objective decision-making.

The sixth design was identified as the optimal choice, excelling in managing costs, cultural integration, and energy performance. With an engineering cost of 340.566 yuan and a cultural adaptability score of 1.5364, it successfully blended traditional architectural elements with modern technology. Its energy efficiency, at 352.793 yuan/kWh, contributed to sustainability and improved living conditions.

This research presents a framework for renovating traditional rural dwellings in arid environments, effectively balancing cultural preservation and modernization. It offers both theoretical guidance and practical solutions for developing sustainable housing in regions where cultural and environmental sensitivities are critical.