Assembly Theory of Binary Messages

Szymon Łukaszyk; Wawrzyniec Bieniawski

doi:10.20944/preprints202401.1113.v11

Preprint

Article

Assembly Theory of Binary Messages

This version is not peer-reviewed.

Szymon Łukaszyk^*

Wawrzyniec Bieniawski

Szymon Łukaszyk^*

Wawrzyniec Bieniawski

This version is not peer-reviewed.

Downloads

797

Views

363

Comments

Submitted:

14 May 2024

Posted:

15 May 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract

Using assembly theory, we investigate the assembly pathways of binary strings (bitstrings) of length N formed by joining bits present in the assembly pool and the bitstrings that entered the pool as a result of previous joining operations. We show that the bitstring assembly index is bounded from below by the shortest addition chain for N, and we conjecture about the form of the upper bound. We define the degree of causation for the minimum assembly index and show that for certain N it has regularities that can be used to determine the length of the shortest addition chain for N. We show that a bitstring with the smallest assembly index for N can be assembled by a binary program of length equal to this index if the length of this bitstring is expressible as a product of Fibonacci numbers. Knowing that the problem of determining the assembly index is at least NP-complete, we conjecture that this problem is NP-complete, while the problem of creating the bitstring so that it would have a predetermined largest assembly index is NP-hard. The proof of this conjecture would imply P ≠ NP, since every computable problem and every computable solution can be encoded as a finite bitstring.

Keywords:

assembly theory

;

emergent dimensionality

;

shortest addition chains

;

P versus NP problem

;

mathematical physics

Subject:

Physical Sciences - Mathematical Physics

1. Introduction

Assembly Theory (AT) [1,2,3,4,5,6,7] provides a distinctive complexity measure, superior to established complexity measures used in information theory, such as Shannon entropy or Kolmogorov complexity [1,5]. AT does not alter the fundamental laws of physics [6]. Instead, it redefines objects on which these laws operate. In AT, objects are not considered sets of point particles (as in most physics), but instead are defined by the histories of their formation (assembly pathways) as an intrinsic property, where, in general, there are multiple assembly pathways to create a given object.

AT explains and quantifies selection and evolution, capturing the amount of memory necessary to produce a given object [6] (this memory is the object [8]). This is because the more complex a given object is, the less likely an identical copy can be observed without the selection of some information-driven mechanism that generated that object. Formalizing assembly pathways as sequences of joining operations, AT begins with basic units (such as chemical bonds) and ends with a final object. This conceptual shift captures evidence of selection in objects [1,2,6].

The assembly index of an object corresponds to the smallest number of steps required to assemble this object, and - in general - increases with the object’s size but decreases with symmetry, so large objects with repeating substructures may have a smaller assembly index than smaller objects with greater heterogeneity [1]. The copy number specifies the observed number of copies of an object. Only these two quantities describe the evolutionary concept of selection by showing how many alternatives were excluded to assemble a given object [6,8].

AT has been experimentally confirmed in the case of molecules and has been probed directly experimentally with high accuracy with spectroscopy techniques, including mass spectroscopy, IR, and NMR spectroscopy [6,7]. It is a versatile concept with applications in various domains. Beyond its application in the field of biology and chemistry [7], its adaptability to different data structures, such as text, graphs, groups, music notations, image files, compression algorithms, human languages, memes, etc., showcases its potential in diverse fields [2].

In this study, we investigate the assembly pathways of binary strings (bitstrings) by joining individual bits present in the assembly pool and bitstrings that entered the pool as a result of previous joining operations.

Bit is the smallest amount and the quantum of information. Perceivable information about any object can be encoded by a bitstring [9,10] but this does not imply that a bitstring defines an object. Information that defines a chemical compound, a virus, a computer program, etc. can be encoded by a bitstring. However, a dissipative structure [11] such as a living biological cell (or its conglomerate such as a human, for example) cannot be represented by a bitstring (even if its genome can). This information can only be perceived (so this is not an object defining information). Therefore, we use the emphasis for the object in this paper as this term, understood as a collection of matter, is a misnomer, as it neglects the (quantum) nonlocality [12]. The nonlocality is independent of the entanglement among particles [13], as well as the quantum contextuality [14], and increases as the number of particles [15] grows [16,17]. Furthermore, the ugly duckling theorem [9,10] asserts that every two objects we perceive are equally similar (or equally dissimilar).

Furthermore, a bitstring, as such is neither dissipative nor creative. It is its assembly process that can be dissipative or creative. The perceivable universe is not big enough to contain the future; it is deterministic going back in time and non-deterministic going forward in time [18]. But we know [2,11,19,20,21,22,23,24,25,26,27,28,29] that it has evolved to the present since the Big Bang. Evolution is about assembling a novel structure of information and optimizing its assembly process until it reaches the assembly index. Once the new information is assembled (by a dissipative structure operating far from thermodynamic equilibrium, including humans), it enters the realm of the 2^nd law of thermodynamics, and nature seeks how to optimize its assembly pathway.

At first, the newly assembled structure of information is discovered by groping [19] and its assembly pathway does not attain its most economical or efficient form at once. For a certain period of time, its evolution gropes about within itself. The try-out follows the try-out, not being finally adopted. Then finally perfection comes within sight, and from that moment the rhythm of change slows down [19]. The new information, having reached the limit of its potentialities, enters the phase of conquest. Stronger now than its less perfected neighbours, the new information multiplies and consolidates. When the assembly index is reached, new information attains equilibrium, and its evolution terminates. It becomes stable.

"Thanks to its characteristic additive power, living matter (unlike the matter of the physicists) finds itself ’ballasted’ with complications and instability. It falls, or rather rises, towards forms that are more and more improbable. Without orthogenesis life would only have spread; with it there is an ascent of life that is invincible." [19]

The paper is structured as follows. Section 2 introduces basic concepts and definitions used in the paper. Section 3 shows that the bitstring assembly index is bounded from below and provides the form of this bound. Section 4 defines the degree of causation for the smallest assembly index bitstrings. Section 5 shows that the bitstring assembly index is bounded from above and conjectures about the exact form of this bound. Section 6 introduces the concept of a binary assembling program and shows that, in general, the trivial assembling program assembles the smallest assembly index bitstrings. Section 7 discusses and concludes the findings of this study.

2. Preliminaries

For K subunits of an objectO the assembly index

a_{O}

of this object is bounded [1] from below by

min (a_{O}) = {log}_{2} (K),

(1)

and from above by

max (a_{O}) = K - 1,

(2)

The lower bound (1) represents the fact that the simplest way to increase the size of a subunit in a pathway is to take the largest subunit assembled so far and join it to itself [1] and, in the case of the upper bound (2), subunits must be distinct so that they cannot be reused from the pool, decreasing the index.

Here, we consider bitstrings

C_{k}^{(N)}

containing bits

{1, 0}

, with

N_{0}

zeros and

N_{1}

ones, having length

N = N_{0} + N_{1}

N_{1}

is called the binary Hamming weight or bit summation of a bitstring. Bitstrings are our basic AT objects [2] and we consider the process of their formation within the AT framework. Where the bit value can be either 1 or 0, we write

* = {1, 0}

with * being the same within the bitstring

C_{k}^{(N)}

. If we allow for the 2^nd possibility that can be the same as or different from *, we write

★ = {1, 0}

. Thus,

C_{k}^{(2)} = [* ★]

, for example, is a placeholder for all four 2-bit strings.

We consider bitstrings

C_{k}^{(N)}

to be messages transmitted through a communication channel between a source and a receiver, similarly to the Claude Shannon approach [30] used in the derivation of binary information entropy

H (C_{k}^{(N)}) = - p_{0} {log}_{2} (p_{0}) - p_{1} {log}_{2} (p_{1}),

(3)

where

p_{0} = \frac{N_{0}}{N} and p_{1} = \frac{N_{1}}{N},

(4)

are the ratios of occurrences of zeros and ones within the bitstring

C_{k}^{(N)}

and the unit of entropy (3) is bit.

Definition 1.

A bitstring assembly index

a^{(N)}

is the smallest number of steps s required to assemble a bitstring

C_{k}^{(N)}

of length N by joining two distinct bits contained in the initial assembly pool

P = {1, 0}

and bitstrings assembled in previous steps that were added to the assembly pool. Therefore, the assembly index

a^{(N)} (C_{k})

is a function of the bitstring

C_{k}^{(N)}

For example, the 8-bit string

C_{k}^{(8)} = [01010101]

(5)

can be assembled in at most seven steps:

join 0 with 1 to form $C_{k}^{(2)} = [01]$ , adding $[01]$ to $P = {1, 0, 01}$ ,
join $C_{k}^{(2)} = [01]$ with 0 to form $C_{k}^{(3)} = [010]$ , adding $[010]$ to $P = {1, 0, 01, 010}$ ,
...
join $C_{k}^{(7)} = [0101010]$ with 1 to form $C_{k}^{(8)} = [01010101]$

(i.e. not using the assembly pool P), six, five, or four steps:

join 0 with 1 to form $C_{k}^{(2)} = [01]$ , adding $[01]$ to P,
join $C_{k}^{(2)} = [01]$ with $[01]$ taken from P to form $C_{k}^{(4)} = [0101]$ , adding $[0101]$ to P,
join $C_{k}^{(4)} = [0101]$ with $[01]$ taken from P to form $C_{k}^{(6)} = [010101]$ , adding $[010101]$ to P,
join $C_{k}^{(6)} = [010101]$ with $[01]$ taken from P to form $C_{k}^{(8)} = [01010101]$ ,

or at least three steps:

join 0 with 1 to form $C_{k}^{(2)} = [01]$ , adding $[01]$ to P,
join $C_{k}^{(2)} = [01]$ with $[01]$ taken from P to form $C_{k}^{(4)} = [0101]$ , adding $[0101]$ to P,
join $C_{k}^{(4)} = [0101]$ with $[0101]$ taken from P to form $C_{k}^{(8)} = [01010101]$ ,

while the 8-bit string

C_{l}^{(8)} = [00010111]

(6)

can be assembled in at least six steps:

join 0 with 1 to form $C_{l}^{(2)} = [01]$ , adding $[01]$ to P,
join $C_{l}^{(2)} = [01]$ with $[01]$ taken from P to form $C_{l}^{(4)} = [0101]$ , adding $[0101]$ to P,
join 0 with 0 adding $[00]$ to P,
join $C_{l}^{(4)} = [0101]$ with $[00]$ taken from P to form $C_{l}^{(6)} = [000101]$ , adding $[000101]$ to P,
join $C_{l}^{(6)} = [000101]$ with 1 to form $C_{l}^{(7)} = [0001011]$ , adding $[0001011]$ to P,
join $C_{l}^{(7)} = [0001011]$ with 1 to form $C_{l}^{(8)} = [00010111]$ ,

as only the doublet

[01]

can be reused from the pool. Therefore, bitstrings (5) and (6), despite having the same length

N = 8

, Hamming weight

N_{1} = 4

, and Shannon entropy (3), have respective assembly indices

a^{(8)} (C_{k}) = 3

and

a^{(8)} (C_{l}) = 6

that represent the lengths of their shortest assembly pathways, which in turn ensures that their assembly pools P are distinct sets for a given assembly pathway.

Table 1 and Table A5–Table A12 (Appendix C) show the distributions of the assembly indices among

2^{N}

bitstrings for

4 \leq N \leq 12

taking into account the number of ones

N_{1}

. The sums of each column form Pascal’s triangle read by rows (OEIS A007318).

The following definition is commonly known, but we provide it here for clarity.

Definition 2.

A bitstring

B_{k}^{(N)}

is a balanced string if its Hamming weight

N_{1} = ⌊N / 2⌋

N_{1} = ⌈N / 2⌉

Without loss of generality, we shall assume that if N is odd,

N_{1} < N_{0}

(e.g., for

N = 5

N_{1} = 2

, and

N_{0} = 3

). However, our results are equivalently applicable if we assume the opposite (i.e. a larger number of ones for an odd N). The number

| B^{(N)} |

of balanced bitstrings among all

2^{N}

bitstrings is1

\begin{matrix} | B^{(N)} | & = (\binom{N}{⌊N / 2⌋}) = (\binom{N}{⌈N / 2⌉}) \approx \sqrt{\frac{2}{π N}} 2^{N} . \end{matrix}

(7)

This is the OEIS A001405 sequence, the maximal number of subsets of an N-set such that no one contains another, as asserted by Sperner’s theorem, and approximated using Stirling’s approximation for large N. Balanced and even length bitstrings

B_{k}^{(N)}

have natural binary entropies (3)

H (B_{k}^{(N)}) = {0, 1}

. Conversely, non-balanced and/or odd-length bitstrings

C_{k}^{(N)}

have binary entropies

0 < H (C_{k}^{(N)}) < 1

Theorem 1.

N = 4

-bit string is the shortest string having more than one bitstring assembly index 1.

Proof.

The proof is trivial. For

N = 1

the assembly index

a^{(1)} (C) = 0

, as all basis objects have a pathway assembly index of 0 [2] (they are not assembled).

N = 2

provides four available bitstrings with

a^{(2)} (C) = 1

N = 3

provides eight available bitstrings with

a^{(3)} (C) = 2

. Only

N = 4

provides 16 bitstrings that include four stings with

a^{(4)} (C) = 2

and twelve bitstrings with

a^{(4)} (C) = 3

including

| B^{(4)} | = 6

balanced bitstrings, as shown in Table 1 and Table 2. For example, to assemble the bitstring

B_{1} = [0101]

, we need to assemble the bitstring

[01]

and reuse it. Therefore,

a^{(N)} (C_{k}) = N - 1

for

0 < N < 4

\forall k = {1, 2, \dots, 2^{N}}

and

min_{k} ({a^{(N)} (C_{k})}) < N - 1

for

N \geq 4

, where

{a^{(N)} (C_{k})}

denotes a set of assembly indices of all

2^{N}

bitstrings. □

Interestingly, Theorem 1 strengthens the meaning of

N = 4

as the minimum information capacity that provides a minimum thermodynamic black hole entropy [31,32,33]. There is no disorder or uncertainty in an object that can be assembled in the same number of steps

s \leq 2

The following definition, taking into account the cyclic order of bitstrings, is also provided for the sake of clarity.

Definition 3.

A bitstring

R_{k}^{(N)}

is a ringed bitstring if a ring formed with this string by joining its beginning with its end is unique among the rings formed from the other ringed strings

R_{l}^{(N)}, l \neq k

There are at least two and at most N forms of a ringed bitstring

R_{k}^{(N)}

that differ in the position of the starting bit. For example for

| B^{(4)} | = 6

balanced bitstrings, shown in Table 2, two augmented strings with

a^{(4)} = 2

correspond to each other if we change the starting bit

\begin{matrix} [\dots 1 | 0101 | 0101 | 01 \dots] = \\ [\dots 10 | 1010 | 1010 | 1 \dots] . \end{matrix}

(8)

Similarly, four augmented bitstrings with

a^{(4)} = 3

correspond to each other

\begin{matrix} [\dots | 0110 | 0110 | 011 \dots] = \\ [\dots 0 | 1100 | 1100 | 11] = \\ [\dots 01 | 1001 | 1001 | 1 \dots] = \\ [\dots 011 | 0011 | 0011 | \dots], \end{matrix}

(9)

after a change in the position of the starting bit. Thus, there are only two balanced ringed bitstrings

E_{k}^{(4)}

The number of ringed bitstrings

| R_{k}^{(N)} |

among all

2^{N}

bitstrings is given by the OEIS sequence A000031. In general (for

N \geq 3

), the number

| R_{k}^{(N)} |

of ringed bitstrings is much lower than the number

| B_{k}^{(N)} |

of balanced bitstrings.

By neglecting the notion of the beginning and end of a string, we focus on its length and content. In Yoda’s language,

"complete, no matter where it begins. A message is".

The numbers of the balanced

| B_{k}^{(N)} |

, ringed

| R_{k}^{(N)} |

, and balanced ringed2

| E_{k}^{(N)} |

bitstrings are shown in Table 3 and Figure 1. The formula for

| E_{k}^{(N)} |

remains to be researched.

We note that, in general, the starting bit is relevant for the assembly index. Thus, different forms of a ringed bitstring may have different assembly indices. For example, for

N = 7

balanced bitstrings

B_{34}

and

B_{35}

, shown in Table A15 have

a^{(7)} = 6

. However, these bitstrings are not ringed, since they correspond to each other and to the balanced bitstrings

B_{13}

B_{18}

B_{20}

B_{28}

, and

B_{30}

with

a^{(7)} = 5

. They all have the same triplet of adjoining ones.

Definition 4.

The assembly index of a ringed bitstring

R_{k}^{(N)}

is the smallest assembly index among all forms of this string.

Thus, if different forms of a ringed bitstring have different assembly indices, we assign the smallest assembly index to this string. In other words, we assume that the smallest number of steps

a^{(N)} (R_{k}) = min_{l} ({a^{(N)} {(R_{k})}_{l}}), {(R_{k})}_{l} \in R_{k},

(10)

where

{(R_{k})}_{l}

denotes a particular

l^{th}

form of a ringed bitstring

R_{k}

, is the bitstring assembly index of this ringed string. We assume that if an object that can be represented by a ringed bitstring can be assembled in fewer steps, this procedure will be preferred by nature.

The distribution of the assembly indices of the balanced ringed bitstrings

E_{k}

is shown in Table 4.

3. Minimum Bitstring Assembly Index

In the following, we derive the tight lower bound of the set of different bitstring assembly indices.

Theorem 2

(Tight lower bound on the bitstring assembly index). The smallest bitstring assembly index

a^{(N)} (C_{\min})

as a function of N corresponds to the shortest addition chain for N (OEIS A003313).

Proof.

Bitstrings

C_{\min}

for which

a^{(N)} (C_{\min}) = min_{k} ({a^{(N)} (C_{k})})

\forall k = {1, 2, \dots, 2^{N}}

can be formed in subsequent steps s by joining the longest bitstring assembled so far with itself until

N = 2^{s}

is reached [1]. Therefore, if

N = 2^{s}

, then

min_{k} ({a_{(2^{s})} (C_{k})}) = s = {log}_{2} (N)

. Only four bitstrings

C_{\min_{1}}^{(2^{s})} = [00 \dots], C_{\min_{2}}^{(2^{s})} = [11 \dots], C_{\min_{3}}^{(2^{s})} = [0101 \dots], and C_{\min_{4}}^{(2^{s})} = [1010 \dots]

(11)

have such an assembly index in this case.

An addition chain for

N \in N

having the shortest length

s \in N

(commonly denoted as

l (N)

) is defined as a sequence

1 = b_{0} < b_{1} < \dots < b_{s} = N

of integers such that for each

j \geq 1

b_{j} = b_{k} + b_{l}

for

l \leq k < j

. The first step in creating an addition chain for N is always

b_{1} = 1 + 1 = 2

and this corresponds to assembling a doublet

[* ★]

from the initial assembly pool P. Thus, the lower bound for s of the addition chain for N,

s \geq {log}_{2} (N)

is achieved for

N = 2^{s}

. In our case, this bound is achieved by the bitstrings (11). The second step in creating an addition chain can be

b_{2} = 1 + 1 = 2

b_{2} = 1 + 2 = 3

Thus, finding the shortest addition chain for N corresponds to finding an assembly index of a bitstring containing bits and/or doublets and/or triplets generated by these doublets for

N \neq 2^{s}

since due to Theorem 1 only they provide the same assembly indices

{0, 1, 2}

. Such strings correspond to linear molecules made of carbons [4]. □

The smallest assembly indices

a_{\min}^{(N)}

are shown in Table 5 for

1 \leq N \leq 21

. Calculating the minimum length of the addition chain for N, as well as finding the shortest assembly pathway for a chemical molecule, have been shown to be at least as hard as NP-complete [4,34].

4. Degree of Causation for Minimum Assembly Index Bitstrings

Using the difference between the general AT lower bound (1) and the smallest bitstring assembly index (OEIS A003313) we can define the quantity

D_{C} (N) 2^{({log}_{2} (N) - a_{\min}^{(N)})} = N 2^{- a_{\min}^{(N)}},

(12)

capturing a degree of causation [6] of assembling the bitstrings of length N with the smallest assembly index, as shown in Figure 2. For

N = 2^{s}

, the degree of causation

D_{C} (N) = 1

, as all bitstrings (11) can be assembled along a single pathway only; their assembly is entirely causal. However, for

N \neq 2^{s}

D_{C} (N) < 1

, since some bitstrings

C_{\min}^{(N)}

can be assembled along different pathways. For example, there are two pathways for the bitstring

[001]

: (a)

[00] + 1

and (b)

0 + [01]

leaving different subunits (respectively

[00]

and

[01]

) in their assembly pools and resulting in lower values of

D_{C} (N)

Equation (12) naturally divides the set of natural numbers into sections

2^{s} \leq N < 2^{s + 1}

and shows regularities that for certain values of N can be used to determine the smallest assembly index (i.e. the shortest addition chain for N) as

a_{\min}^{(N)} = {log}_{2} (N) - {log}_{2} (D_{C} (N))

. For each

N = 2^{s} \Leftrightarrow a_{\min}^{(2^{s})} = s

and for each

\hat{N}

being the sum of two powers of 2 (OEIS A048645)

\hat{N} 2^{s} + 1 \cdot 2^{l}, l = 0, 1, \dots, s - 1 \Leftrightarrow a_{\min}^{(\hat{N})} = s + 1,

(13)

while for the remaining

\tilde{N}

not being the sum of two powers of 2 (OEIS A072823)

2^{s} < \tilde{N} < 2^{s + 1}, \tilde{N} \neq \hat{N} \Leftrightarrow a_{\min}^{(\tilde{N})} = s + k, k \geq 2,

(14)

where

k = 2

for

\tilde{N} = {7, 11, 13 - 15, 19, 21 - 23, 25 - 28, \dots}

, while some

\tilde{N}

’s generate exceptions to this general rule (cf. OEIS A230528). For example,

k = 3

for

\tilde{N} = {29, 31, 47, 53, 55, 57 - 59, 61 - 63, \dots}

k = 4

for

\tilde{N} = {127, 191, 235, 237, 239, 247, 251, 253, 254, \dots}

, etc. The first exception,

k = 3

is for

{\tilde{N}}_{13} = 29

. The first double exception,

k = 4

is for

{\tilde{N}}_{63} = 127

. However, in particular, for

{\tilde{N}}_{3} = 2^{s} + 3 \cdot 2^{l}, l = 0, 1, \dots, s - 2 \Leftrightarrow a_{\min}^{({\tilde{N}}_{3})} = s + 2, and

(15)

{\tilde{N}}_{7, s - 3} = 2^{s} + 7 \cdot 2^{s - 3} = {15, 30, 60, \dots}, s \geq 3 \Leftrightarrow a_{\min}^{({\tilde{N}}_{7, s - 3})} = s + 2,

(16)

so the number of Ns within each section, not included in the set of general rules

2^{s}

, (13), (15), and (16), is

| N_{ngr} | = | 2^{s} - 1 - s - (s - 1) - 1 | = | 2^{s} - 2 s - 1 |

. Furthermore,

lim_{s \to \infty} (min D_{C} (\hat{N})) = lim_{s \to \infty} (\frac{1}{2} (1 + \frac{1}{2^{s}})) = \frac{1}{2}, lim_{s \to \infty} (max D_{C} (\tilde{N})) = D_{C} ({\tilde{N}}_{7, s - 3}) = \frac{15}{32} .

(17)

The shortest addition chain sequence generating factors for

1 \leq s \leq 5

are listed in Table 6, where the subsequent odd numbers of the form

m_{k}

generate sequences

N = 2^{s} + m_{k} \cdot 2^{l}

, where

l = 0, 1, \dots, k - 1

, while the

m_{k}

numbers in red indicate that certain

\tilde{N}

s within the sequences they generate are exceptions to the general

a_{\min}^{(\tilde{N})} = s + 2

rule. For example, if

s = 4

then

a_{\min}^{(16)} = 4

and

\begin{matrix} \hat{N} = 2^{4} + 2^{l} = {17, 18, 20, 24} & \Leftrightarrow a_{\min}^{(\hat{N})} = 4 + 1 = 5, \\ {\tilde{N}}_{3} = 2^{4} + 3 \cdot 2^{l} = {19, 22, 28} & \Leftrightarrow a_{\min}^{({\tilde{N}}_{3})} = 4 + 2 = 6, \\ {\tilde{N}}_{5} = 2^{4} + 5 \cdot 2^{l} = {21, 26} & \Leftrightarrow a_{\min}^{({\tilde{N}}_{5})} = 4 + 2 = 6, \\ {\tilde{N}}_{7} = 2^{4} + 7 \cdot 2^{l} = {23, 30} & \Leftrightarrow a_{\min}^{({\tilde{N}}_{7})} = 4 + 2 = 6, \\ {\tilde{N}}_{9} = 2^{4} + 9 \cdot 2^{l} = 25 & \Leftrightarrow a_{\min}^{({\tilde{N}}_{9})} = 4 + 2 = 6, \\ {\tilde{N}}_{11} = 2^{4} + 11 \cdot 2^{l} = 27 & \Leftrightarrow a_{\min}^{({\tilde{N}}_{11})} = 4 + 2 = 6, \\ {\tilde{N}}_{13} = 2^{4} + 13 \cdot 2^{l} = 29 & \Leftrightarrow a_{\min}^{({\tilde{N}}_{13})} = 4 + 3 = 7, \\ {\tilde{N}}_{15} = 2^{4} + 15 \cdot 2^{l} = 31 & \Leftrightarrow a_{\min}^{({\tilde{N}}_{15})} = 4 + 3 = 7, \end{matrix}

(18)

where the last two values

a_{\min}^{(\tilde{N})}

are higher than those given by the general rule. Based on the OEIS A003313 sequence for

N \leq 10^{5}

, we have determined the number of exceptions, that is

| N_{exc} |

such that

a_{\min}^{(N_{exc})} \neq {s, s + 1, s + 2}

for

0 \leq s \leq 15

as shown in Table 7, where

min (m_{k})

is the minimal generating factor

m_{k}

shown in Table 6 that generates the exceptional

a_{\min}^{(N_{exc})}

. For all

s \geq 4

max (m_{k}) = 2^{s} - 1

. The fact that

| N_{ngr} | > | N_{exc} |, \forall s \geq 3

hints at the existence of general rules other than

2^{s}

, (13), (15), and (16).

Furthermore, for

4 \leq s \leq 6

| N_{exc} | = 2^{s} - s^{2} + 2

and for

s \geq 7

| N_{exc} | = 2^{s} - s^{2} + 1

(OEIS A024012) [35]. As shown in Figure 3(a), for all s,

| N_{exc} |

asymptotically approaches

2^{s}

available in a given section as

s \to \infty

, as shown in Figure 3(b) For

s = 6

this ratio has a deflection point

| N_{exc} | / 2^{6} = 15 / 32

Only living systems have been found to be capable of producing abundant molecules with an assembly index greater than an experimentally determined value of 15 steps [3,8]. The cut-off between 13 and 15 is sharp, which means that molecules made by random processes cannot have assembly indices exceeding 13 steps [3,8]. In particular,

N = 15

is the length of the shortest addition chain for N which is smaller than the number of multiplications to compute

N^{th}

power by the Chandah-sutra method (OEIS A014701, OEIS A371894). Furthermore, the values of the sequence A014701 are larger than the shortest addition chain for

N \notin 2^{2} + 2^{l}

. These values (OEIS A371894) are not given by equation (15) but equation (16) provides their subset. Their Hamming weight is at least 4 in binary representation [36]. Furthermore, the exceptional

a_{\min}^{(N_{exc})}

values bear similarity to the atomic numbers Z of chemical elements that violate the Aufbau rule [15] that correctly predicts the electron configurations of most elements. Only about twenty elements within

24 \leq Z \leq 103

(with only two non-doubleton sets of consecutive ones) violate the Aufbau rule.

5. Maximum Bitstring Assembly Index

In the following, we conjecture the form of the upper bound of the set of different bitstring assembly indices. In general, of all bitstrings

C_{k}

having a given assembly index, shown in Table 1 and Table A5–Table A12 (Appendix C), most have

N_{1} = ⌊N / 2⌋

, though we have found a few exceptions, mostly for non-maximal assembly indices, namely for

a^{(8)} = 4

(

4 < 8

) and for

a^{(8)} = 6

(

24 < 26

), for

a^{(10)} = 4

(

2 < 5

) and for

a^{(10)} = 5

(

32 < 33

), and for

a^{(12)} = 4

(

2 < 3

). These observations allow us to restrict the search space of possible bitstrings with the largest assembly indices to balanced bitstrings only: with the exception of

N = 8

, of all bitstrings

C_{k}^{(N)}

having a largest assembly index, most are balanced. We can further restrict the search space to ringed bitstrings (Definition 3). If a bitstring

C_{\min}

for which

a^{(N)} (C_{\min}) = min_{k} ({a^{(N)} (C_{k})})

is constructed from repeating patterns, then a bitstring

C_{\max}

for which

a^{(N)} (C_{\max}) = max_{k} ({a^{(N)} (C_{k})})

must be the most patternless. The bitstring assembly index must be bounded from above and

a^{(N)} (C_{\max})

must be a monotonically nondecreasing function of N that can increase at most by one between N and

N + 1

. Certain heuristic rules apply in our binary case. For example,

for $N = 7$ we cannot avoid two doublets (e.g. $2 \times [00]$ ) within a ringed bitstring $E_{28}^{(7)} = [0011100]$ and thus $a^{(7)} (C_{\max}) = 5 < 6$ ,
for $N = 8$ we cannot avoid two pairs of doublets (e.g. $2 \times [00]$ and $2 \times [11]$ ) within a ringed bitstring $E_{7}^{(8)} = [00001111]$ and thus $a^{(8)} (C_{\max}) = 5 < 6$ ,
for $N = 12$ we cannot avoid three pairs of doublets (e.g. $2 \times [00]$ , $2 \times [10]$ , and $2 \times [11]$ ) within a ringed bitstring $E_{k}^{(12)} = [111000101100]$ and thus $a^{(12)} (C_{\max}) = 8 < 9$ ,
for $N = 14$ we cannot avoid two pairs of doublets and one doublet three times (e.g. $2 \times [00]$ , $2 \times [11]$ , and $3 \times [01]$ , and thus $a^{(14)} (C_{\max}) = 9 < 10$ ,
etc.

Table 8 shows the exemplary balanced bitstrings

B_{\max}

having the largest assembly indices that we assembled (cf. also Appendix A). To determine the assembly index

a^{(18)} = 11

of the bitstring

E_{k}^{(18)} = [1 (001) (11) (110) (110) (00) (001) 0],

(19)

for example, we look for the longest patterns that appear at least twice within the string, and we look for the largest number of these patterns. Here, we find that each of the two triplets

[001]

and

[110]

appear twice in

E_{k}^{(18)}

and are based on the doublets

[00]

and

[11]

also appearing in

E_{k}^{(18)}

. Thus, we start with the assembly pool

{1, 0, [00], [001], [11], [110]}

made in four steps and join the elements of the pool in the following seven steps to arrive at

a^{(18)} (E_{k}) = 11

. On the other hand, another form of this balanced ringed string

E_{l}^{(18)} = [(01) (11) (110) (110) 00 (001) (01) 0],

(20)

has

a^{(18)} (E_{l}) = 12

These results allow us to formulate the following conjecture.

Conjecture 1

(Tight upper bound on a bitstring assembly index). With exceptions for small N the largest bitstring assembly index

a^{(N)} (C_{\max})

is given by a sequence formed by

{+ 1, + 1, k \times 0, + 1, + 1, k \times 0}

for

k \in N_{0}

, where

+ 1

denotes increasing

a^{(N)} (C_{\max})

by one, and 0 denotes maintaining it at the same level, and

a^{(0)} = - 1

However, at this moment, we cannot state whether this conjecture applies to ringed or non-ringed bitstrings. The assembly indices for

N < 3

are the same for a given N, whereas the assembly indices for

4 \leq N \leq 10

were discussed above and are calculated in Appendix C for balanced and balanced ringed bitstrings.

The conjectured sequence is shown in Figure 4 and Figure 5 starting with

a^{(0)} = - 1

(we note in passing that

n = - 1

is a dimension of the void, the empty set ∅, or (-1)-simplex). Subsequent terms are given by

{0, 1, 2, 3, 4, 5, 5, 6, 7, 7, 8, 9, 9, 9, 10, \dots}

, which is periodic for

N = k (k + 3)

and defines plateaus of a constant bitstring assembly index at

a^{(N)} (C_{\max}) = 4 k - 3

, and

a^{(N)} (C_{\max}) = 4 k - 1

k \in N

k > 1

This sequence can be generated using the following procedure

We note the similarity of this bound to the monotonically nondecreasing Shannon entropy of chemical elements, including observable ones [15]. Perhaps the exceptions in the sequence of Conjecture 1 vanish as N increases.

6. Binputation

So far we have assembled bitstrings "manually". Now we shall automatize this process using other bitstrings as assembling programs.

Definition 5.

The binary assembling program

Q_{B}

is a bitstring of length

s_{Q}

that acts on the assembly pool P and outputs the assembled bitstrings, adding them to the pool.

Definition 6.

The trivial assembling program Q is a binary assembling program with consecutive bits denoting the following commands:

0: ⇔ take the last element from P, join it with itself, and output,
1: ⇔ take the last two elements from P, join them with each other, and output.

As the assembly pool P is a distinct set to which bitstrings are added in subsequent assembly steps, only these two commands apply to the initial assembly pool

P = {1, 0}

containing only two bits, regardless of the starting command.

Theorem 3 ()If a bitstring

C_{\min}^{(N)}

can be assembled by an elegant trivial program of length

s_{Q} = a^{(N)} (C_{\min})

then N is expressible as a product of Fibonacci numbers (OEIS A065108) and the length

s_{Q}

of any trivial program Q is not shorter than the assembly index of the string that this trivial assembling program assembles.

Proof.

An elegant program is the shortest program that produces a given output [37,38]. Furthermore, no program P shorter than an elegant program Q can find this elegant program Q [37]. If it could, it could also generate the Q’s output. But if P is shorter than Q, then Q would not be elegant, which leads to a contradiction.

The

1^{st}

bit of the trivial assembling program Q is irrelevant as

Q = 0

assembles

C_{\min_{1}}^{(2)} = [00]

and

Q = 1

assembles

C_{\min_{4}}^{(2)} = [10]

, so

Q = *

assembles

C_{\min_{1, 4}}^{(2)} = [* 0]

. Then the programs

Q = * 0 \dots 0

assemble the

2^{s_{Q}}

-bit strings

C_{\min_{1, 4}}^{(2^{s})} = [* 0 * 0 \dots]

having the assembly index

a_{\min}^{(2^{s_{Q}})} = s_{Q}

, while bitstrings

C_{\min_{2, 3}}^{2^{s_{Q}}}

with the smallest assembly index

a_{\min}^{(2^{s_{Q}})} = s_{Q}

can be assembled with the same two programs starting with the reversed assembly pool

P = {0, 1}

The remaining

2^{s_{Q} - 1} - 2

programs will assemble some of the shorter bitstrings with the assembly index

a_{\min}^{(N)} = s_{Q}

. In general, all programs Q assemble bitstrings having lengths expressible as a product of Fibonacci numbers (OEIS A065108) as shown in Table A1 (Appendix B), wherein out of

2^{s_{Q} - 1}

programs (cf. Table A4 and Table A1):

$2^{s_{Q} - 2}$ programs $Q = * 0 ★ \dots$ assemble even length balanced bitstrings $B = [* 0 * 0 \dots]$ having natural binary entropies (3) $H (C) = {0, 1}$ , including bitstrings $C_{\min_{1, 4}}^{(2^{s_{Q}})}$ (11),
$2^{s_{Q} - 3}$ programs $Q = * 10 ★ \dots$ assemble $[0 * 00 * 0 \dots]$ bitstrings having lengths divisible by three and entropies $H (C) \approx {0, 0.9183}$ ,
$2^{s_{Q} - 4}$ programs $Q = * 110 ★ \dots$ assemble $[* 00 * 0 * 00 * 0 \dots]$ bitstrings having lengths divisible by five and entropies $H (C) \approx {0, 0.9710}$ ,
$2^{s_{Q} - 5}$ programs $Q = * 1110 ★ \dots$ assemble $[0 * 0 * 00 * 0 \dots]$ bitstrings having lengths divisible by eight, entropies $H (C) \approx {0, 0.9544}$ , and assembly indices $a^{(N)} = s_{Q} - 1$ if $* = 1$ ,
⋯,
the program $Q = * 1 \dots 0$ joins two shortest bitstrings assembled in a previous step into a bitstring of length being twice the Fibonacci sequence (OEIS A055389), and finally
the program $Q = * 1 \dots 1$ assembles the shortest bitstring that has length belonging to the set of Fibonacci numbers.

Thus, for

* = 1

, binary assembling programs Q assemble subsequent

2^{s_{Q} - 1} = 2^{s_{Q} - 2} + 2^{s_{Q} - 3} + \dots + 2^{0} + 1

Fibonacci words and their concatenations having entropies (3) with ratios (4)

p_{1, m} = \frac{F_{m}}{F_{m + 2}} and p_{0, m} = \frac{F_{m + 1}}{F_{m + 2}},

(21)

where

m = {1, 2, \dots s_{Q}}

, and F is the Fibonacci sequence starting from 1. Ratios (21) rapidly converge to

lim_{s_{Q} \to \infty} p_{0, m} = φ - 1 \approx 0.618033989 and lim_{s_{Q} \to \infty} p_{1, m} = 2 - φ \approx 0.381966011

(22)

where

φ

is the golden ratio. Therefore,

{lim}_{s_{Q} \to \infty} H_{m} \approx 0.9594

is the binary entropy of the Fibonacci word limit. The Fibonacci sequence can be expressed through the golden ratio, which corresponds to the smallest Pythagorean triple

{- 3, 4, 5}

[39,40].

However, for

s_{Q} \geq 4

, some of the programs are no longer elegant if

* = 0

and some of the assembled bitstrings are not

C_{\min}

* = 1

For

s_{Q} \geq 4

Q = 111100 \dots

assembles a bitstring

C_{non - \min}^{(2^{s_{Q} - 1})} = [01010010 \dots]

(23)

with an assembly index

a^{(2^{s_{Q} - 1})} = s_{Q}

which is not the minimum for this length of the bitstring. For example, the 4-bit program

Q = * 111

assembles the bitstring

C^{(8)} = [0 * 0 * 00 * 0]

, but if

* = 0

this string can be assembled by a shorter 3-bit program

Q = * 00

, and if

* = 1

this string does not have the smallest assembly index

a^{(8)} (C_{\min}) = 3

but

a^{(8)} (C_{non - \min}) = 4

For

s_{Q} = {4, 7}

and

s_{Q} \geq 10

and for the shortest bitstring assembled by the program Q the program Q is not elegant for

* = 0

and the shortest bitstring assembled by the program is not

C_{\min}

for

* = 1

However, the length

s_{Q}

of any program Q is not shorter than the assembly index of the bitstring that this program assembles. □

The trivial assembly programs Q and the bitstrings they assemble are listed in Table 9 and Table A2–Table A4 (Appendix B) for one version of the assembly pool and for

1 \leq s_{Q} \leq 6

We note in passing that there are other mathematical results on bitstrings and the Fibonacci sequence. For example, it was shown [41] that having two concentric circles with radii

{F_{n}, F_{n + 2}}

and drawing two pairs of parallel lines orthogonal to each other and tangent to the inner circle, one obtains an octagon defined by the points of intersection of those lines with the outer circle, which comes very close to the regular octagon with

n \to \infty

. Furthermore, each of these octagons defines a Sturmian binary word (a cutting sequence for lines of irrational slope) except in the case of

n = 5

[41].

Perhaps the smallest assembly index given by Theorem 2 and the bitstrings of Theorem 3 are related to the Collatz conjecture, as the lengths of the strings (11) for

N = 2^{2 k}

correspond to the numbers to which the Collatz conjecture converges, from

N = (2^{2 k} - 1) / 3

k \in N

(OEIS A002450).

Theorem 3 is also related to Gödel’s incompleteness theorems and the halting problem. N cases of the halting problem correspond only to

{log}_{2} (N)

, not to N bits of information [42] and therefore, complexity is more fundamental to incompleteness than self-reference of Gödel’s sentence [43]. Any formal axiomatic system only enables provable theorems to be proved. If a theorem can be proved by an automatic theorem prover, the prover will halt after proving this theorem. Thus, proving a theorem equals halting. If we assume that the axioms of the trivial program given by Definition 6 define the formal axiomatic system, then the bitstrings having lengths expressible as a product of Fibonacci numbers assembled by this program would represent provable theorems.

If we wanted to define a binary assembling program

Q_{B}

that would use specific bitstrings other than the last one or two bitstrings in the assembly pool, we would have to index the bitstrings in the pool. However, at the beginning of the assembly process, we cannot predict in advance how many bitstrings will enter the assembly pool. Thus, we do not know how many bits will be needed to encode the indices of the strings in the pool. Therefore, we state the following conjecture.

Conjecture 2.

There is no binary assembling program (Definition 5) that has a length shorter than the length of the bitstring having the largest assembly index that could assemble this string.

Theorem 3 would be violated if in Definition 6 we specified the command "0" e.g. as "take the last element from the assembly pool, join it with itself, join with what you have already assembled (say at "the right"), and output". Then, the 2-bit program "00" would produce the 6-bit string

[000000]

with the assembly index

a^{(6)} = 3

. However, such a one-step command would violate the axioms of assembly theory, since it would perform two assembly steps in one program step. An elegant program to output the gigabyte bitstring of all zeros would take a few bits of code and would have a low Kolmogorov complexity [44]. However, such a bitstring would be outputted, not assembled. Furthermore, the length of such a program that outputs the bitstring

[0 \dots]

would be shorter than the length of the program that outputs the string

[10 \dots]

, while in AT, the lengths of these programs must be the same if the strings have the same assembly indices. Definitions 5, 6 and Theorem 3 are about binputation, about bitstrings assembling other bitstrings.

In particular, Theorem 3 confirms that the assembly index is related to the amount of physical memory required to store the information to direct the assembly of an object (a bitstring in our case) and set a directionality in time from the simple to the complex [8]:

s_{Q}

-bit long trivial assembling programs (i.e., with

s_{Q}

-bits of memory) can assemble

2^{s_{Q}}

-bit strings with minimal assembly indices

s_{Q}

and, for

s_{Q} \geq 4

, some shorter but more complex bitstrings with non-minimal assembly indices

s_{Q}

. The memory defines the object [8].

7. Discussion and Conclusions

Consider the SARS-CoV-2 genome sequence defined by 29903 nucleobases

{A, C, G, T}

, its initial version MN9089473 collected in December 2019 in Wuhan and its sample OL3513704 collected in Egypt nearly two years after the Wuhan outbreak, on October 23, 2021. In the MN version, the nucleobases are distributed as

| A | = 8954

| C | = 5492

| G | = 5863

, and

| T | = 9594

and in the OL version as

| A | = 8954

| C | = 5470

| G | = 5856

, and

| T | = 9623

, following Chargaff’s parity rules with the same count of adenines. We can convert these sequences into bitstrings by assigning two bits per nucleobase. For such

N = 59806

, not being the sum of two powers of 2, with the degree of causation [6] given by equation (14), the assembly index is bounded by

21 \leq a^{(59806)} (C_{k}) ≪ 971 .

(24)

Interestingly, if a bitstring

C^{(N)}

were to encode four DNA/RNA nucleobases, then the smallest assembly index bitstrings (as well as the strings generated by trivial assembly programs Q according to Definition 6) would not encode all nucleobases. For example, the bitstring

C_{\min}^{(10)} = [1001010010]

with

a_{\min}^{(10)} = 4

and encoding A=00, C=01, G=10, and T=11, cannot encode T=11. Therefore, we increased the lower bound (24), given by Theorem 2, by one. The upper bound (24) was estimated by finding the smallest k that satisfies

k (k + 3) \geq N

and using the relation

a^{(N)} (C_{\max}) = 4 ⌈k⌉ - 1

of Conjecture 1. We do not know the actual assembly indices of the MN and OL sequences. Their determination is an NP-complete problem, as we conjecture. There are twelve possible assignments of two bits per one nucleobase with twelve different Hamming weights and six different Shannon entropies (3)

\begin{matrix} N_{1} (C_{M N}^{(59806)}) & = {25801, 26172, 26441, 26812, 29263, 29532, 30274, 30543, 32994, 33365, 33634, 34005}, \\ N_{1} (C_{O L}^{(59806)}) & = {25750, 26136, 26419, 26805, 29234, 29517, 30289, 30572, 33001, 33387, 33670, 34056}, \\ H (C_{M N}^{(59806)}) & = {0.9864, 0.9887, 0.9903, 0.9923, 0.9997, 0.99989}, \\ H (C_{O L}^{(59806)}) & = {0.9860, 0.9885, 0.9902, 0.9922, 0.9996, 0.99988} . \end{matrix}

(25)

All sequences (25) are almost balanced (

N / 2 = 29903

). However, the later OL versions are less balanced, producing lower Shannon entropies and showcasing the existence of an entopic force that governs genetic mutations [25]. We conjecture that the assembly index of the OL sequence is higher than that of the MN one - the evolution of information tends to increase the assembly index.

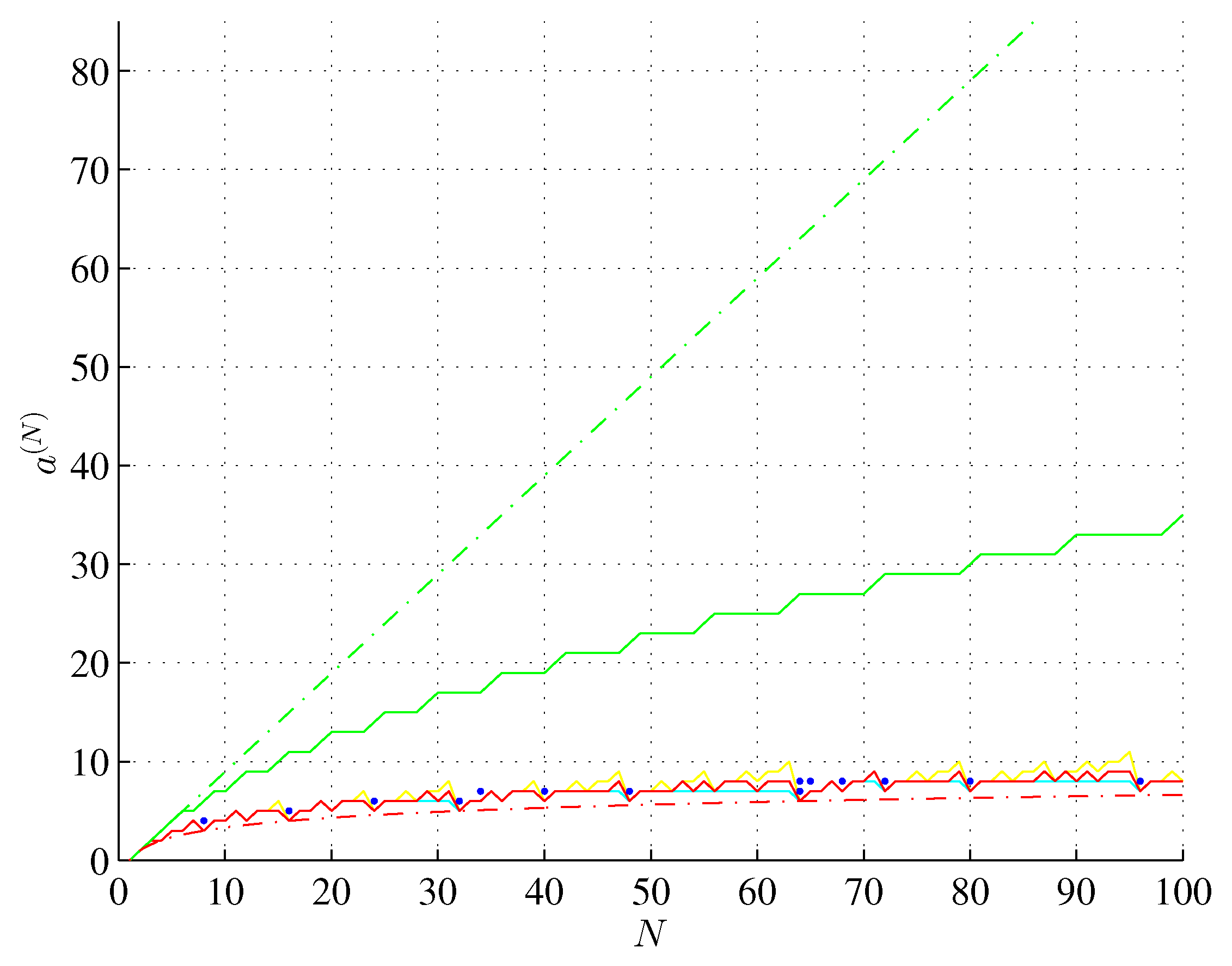
The bounds of Theorem 2 and Conjecture 1 are shown in Table 5 and Table 8 and are illustrated in Figure 4 and Figure 5. No bitstring can be assembled in a smaller number of steps than is given by a lower bound of Theorem 2. However, some bitstrings cannot be assembled in a smaller number of steps than given by an upper bound.

We found it much easier to determine the assembly index of a given bitstring

C_{k}^{(N)}

than to assemble a bitstring so that it would have the largest assembly index. Similarly, a trivial bitstring with the smallest assembly index for N can have the form

C_{\min_{1 - 4}}^{(N)} = [* ★ \dots]

(11) or the form of a Fibonacci word generated by the trivial assembling program (Definition 6). Therefore, we state the following conjecture.

Conjecture 3.

The problem of determining the assembly index of any bitstring

C_{k}^{(N)}

is NP-complete. The problem of assembling the bitstring so that it would have the largest assembly index for large N is NP-hard. This corresponds to determining the largest assembly index value for large N.

A proof of conjecture 3 would also be the proof of the following known conjecture.

Conjecture 4.

P \neq NP

Every computable problem and every computable solution can be encoded as a finite bitstring. Here, determining whether the assembly index of a given bitstring has its known maximal value corresponds to checking the solution to a problem for correctness, whereas assembling such a bitstring corresponds to solving the problem. Thus, AT would solve the P versus NP problem in theoretical computer science. There is ample pragmatic justification for adding

P \neq NP

as a new axiom [42]; rather than attempting to prove this conjecture, mathematicians should accept that it may not be provable and simply accept it as an axiom [45].

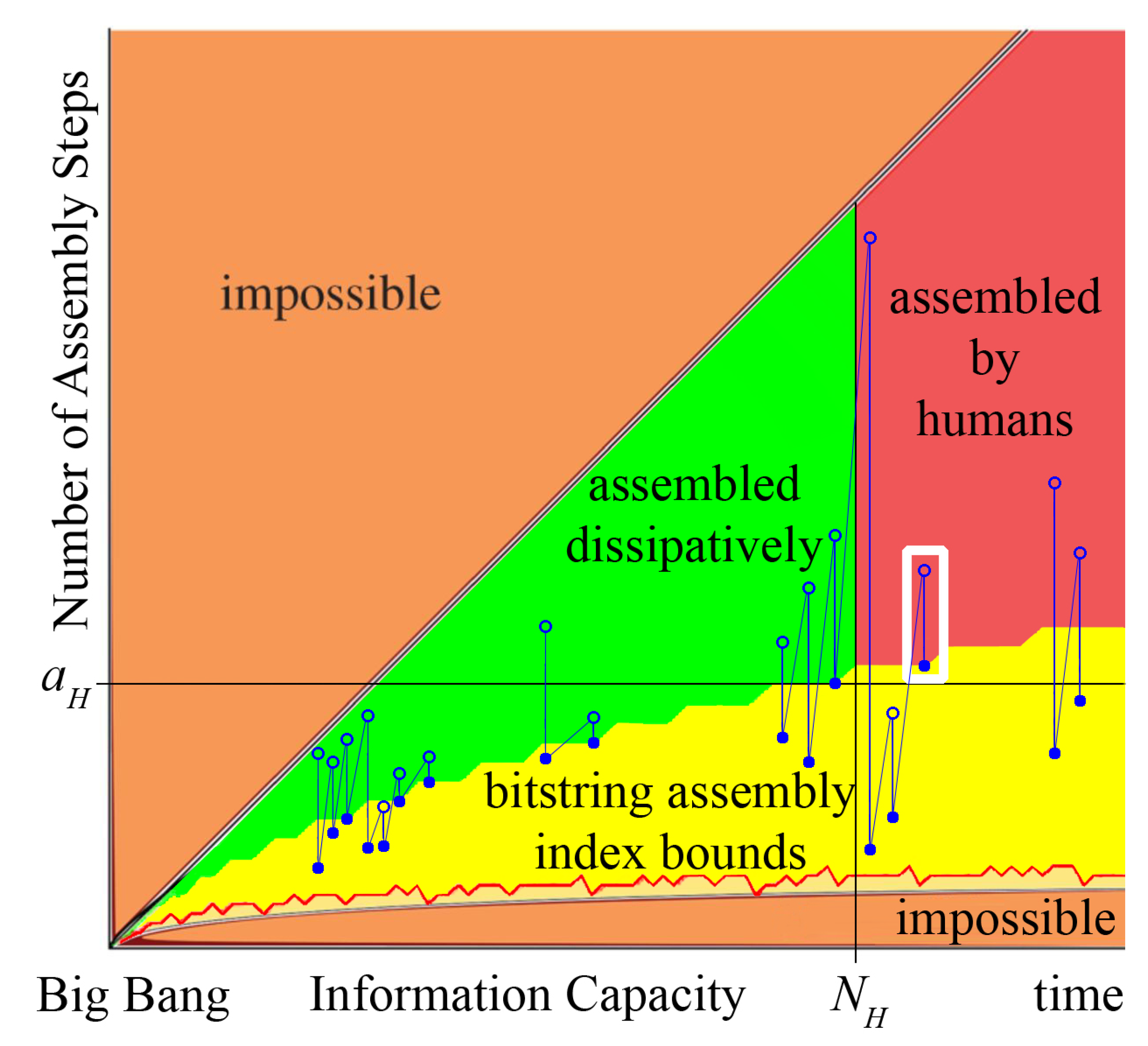
The bounds on the bitstring assembly index given by Theorem 2 and Conjecture 1, and the general bounds (1), and (2) on the assembly index [1] are illustrated in Figure 6 (adopted from [1] and modified; not to scale). The lower bound on the bitstring assembly index implies two paths of evolution:

creative path (slanting lines in Figure 6), and
optimization path (vertical lines in Figure 6),

as for some bitstrings

C_{m}

of length

N > 3

it admits the possible region of their assembly steps

a_{\min}^{(N)} (C_{m}) < s \leq N - 1

. For

1 \leq N \leq 3

only the creative path is available as there is nothing to optimize:

a^{(1 \leq N \leq 3)} = N - 1

. The 2^nd path becomes available already at

N = 4

, where the suboptimal number of 3 steps used to assemble a bitstring

[0101]

can be optimized to

a_{\min}^{(4)} = 2

. The evolution becomes interesting for

N \geq 7

(

N > 7

for ringed strings; cf. Table 8) due to an upper bound on the bitstring assembly index. For each (

N \geq 7

)-bit string

C_{m}

suboptimally assembled in

a^{(N \geq 7)} (C_{m}) < s \leq N - 1

steps, the search space is recursively explored to optimize the number of steps until the assembly index

a^{(N \geq 7)} (C_{m})

of this bitstring is reached, where

a_{\min}^{(N \geq 7)} \leq a^{(N \geq 7)} (C_{m}) \leq a_{\max}^{(N \geq 7)}

We conjecture that, in general, the assembly of a novel, nontrivial bitstring

C_{m}^{(N + l)}

, for

l \in N

, with a longer length

N + l

using the 1^st path of evolution is NP-hard, requires access to noncomputability, and, thus, is available only to dissipative structures, including life, including humans. This path represents "true" creativity. However, once this new bitstring is assembled, it is unlikely that it will be assembled optimally in s steps corresponding to its assembly index. This implies the 2^nd path of minimizing the number of steps s required to assemble this newly found nontrivial bitstring

C_{m}^{(N + l)}

towards its assembly index, which is only NP-complete. The bitstring

C_{m}^{(N + l)}

is reassembled in a simpler way, but such a reassembly is no longer creative. The 2^nd path represents "generative creativity" available both to dissipative structures and to artificial intelligence.

To illustrate this process, consider two examples: one from biological evolution (the emergence of amphibians from fish) and another from technological evolution (the invention of an airplane). The fish began to evolve around 541 million years ago, forming a plethora of fish species and exploring the available search space, optimizing the fish assembly index and increasing the information capacity within the range delimited by the same upper bound fish plateau (cf. Conjecture 1). Around 400 million years ago, some species of fish began using areas with fluctuating water levels, where occasionally water was scarce. The next amphibian plateau of a larger assembly index was within sight. By groping [19], protolungs developed, allowing fish to obtain oxygen from air instead of water. The breakthrough was made and amphibians were formed, exploring the subsequent amphibian plateau and optimizing this evolutionary gain. Many inventions led to the first airplane: the invention of airfoil (George Cayley), its use in gliders (Otto Lilienthal), propeller,... Again, the search space was well explored, and the airplane plateau of a larger assembly index was close. Finally, it was the Wright brothers, bicycle retailers, who realized the importance of combining roll and yaw control in their first suboptimal Wright Flyer foreplane configuration. Once it was shown that it can be done, other people began to optimize this invention, minimizing the number of steps required to recreate it.

AT captures the notion of intelligence, understood as a degree of ability to reach the same goal through different means (assembly pathways) [46], where a fundamental aspect of intelligence is collective behavior [47]. Once the search space is saturated, the fish collectively explore it to develop lungs, just as humans, starting at least in the nineteenth century, began to think collectively about heavier-than-air flying machines. We assume that only dissipative structures can assemble novel structures of information and define life as a dissipative structure provided with choice (ability to select [6]) and human as a living dissipative structure provided with abstract, modality-independent language. As shown in Figure 6, we predict a limit on complexity or maximum assembly index

a_{H}

achievable by non-human dissipative structures. These structures do not use an abstract, modality-independent language required for advanced human creativity. A human creative work also needs a certain minimum amount of information

N_{H}

. We take it for granted that presently only Homo sapiens has a gift of creativity that exceeds

a_{H}

. Any creation is required to be shaped by the unique personality of its human creator(s) to such an extent that it is statistically one-time in nature [48]; it is an imprint of the author’s personality. Subsequent plateaus of

a_{\max}^{(N)} > a_{H}

can also be thought of as scientific paradigms [49] defining coherent traditions of investigation.

Any structure of information assembled by a dissipative structure in s steps can belong to one of the four regions shown in Figure 6:

1.	$N < N_{H}$ and $a_{\max}^{(N)} < s < N - 1$ ,	suboptimally assembled by dissipative structures (green region),
2.	$a_{\min}^{(N)} < s < max (a_{\max}^{(N)}, a_{H})$ ,	optimally assembled by dissipative structures,
3.	$N > N_{H}$ and $a_{H} < s < a_{\max}^{(N)}$ ,	optimally assembled by humans, and
4.	$N > N_{H}$ and $a_{\max}^{(N)} < s < N - 1$ ,	suboptimally assembled by humans (red region).

We do not exclude that non-human dissipative structures are capable of suboptimally assembling structures C above

a_{H}

, provided that their assembly indices satisfy

a^{(N)} (C) < a_{H}

. Thus, the optimization path shown in the white rectangle in Figure 6 is available only to humans.

The results reported here can be applied in the fields of cryptography, data compression methods, stream ciphers, approximation algorithms [50], reinforcement learning algorithms [51], information-theoretically secure algorithms, etc. Another possible application of the results of this study could be molecular physics and crystallography. Overall, the results reported here support the AT, emergent dimensionality [12,15,22,23,24,26,27,28,40], the second law of infodynamics [25,29], and invite further research.

Author Contributions

WB: Conjecture concerning the diversification of bitstrings in Theorem 1; partitioning conjecture for

N \geq 16

resulting in the flattening of the maximum bitstring assembly index; observation that the maximum bitstring assembly index should be monotonically nondecreasing; prior-art search; numerous clarity corrections and improvements; SŁ: The remaining part of the study.

Data Availability Statement

The public repository for the code written in MATLAB computational environment is given under the link https://github.com/szluk/Evolution_of_Information (accessed on November 23, 2023).

Acknowledgments

The authors thank Piotr Masierak for his research on the general strategy for determining the bitstring assembly indices and creating the

E_{k}^{(18)}

bitstring (Peter’s rock), Andrzej Tomski for clarity corrections, Michael Orr for his note on the role of choice, and Mariola Bala for noting that "this is logical". SŁ thanks his wife Magdalena Bartocha for her unwavering support and motivation and his partner and friend, Renata Sobajda, for her prayers.

Abbreviations

The following abbreviations are used in this manuscript:

AT	assembly theory;
N	length of a bitstring;
$N_{0}$	number of 0’s in the bitstring;
$N_{1}$	binary Hamming weight of the bitstring;
$C_{k}^{(N)}$	bitstring of length N;
$B_{k}^{(N)}$	balanced bitstring of length N;
$R_{k}^{(N)}$	ringed bitstring of length N;
$E_{k}^{(N)}$	balanced ringed bitstring of length N;
$\| C^{(N)} \|$	number of bitstrings of length N ( $2^{N}$ );
$\| B^{(N)} \|$	number of balanced bitstrings of length N (OEIS A001405);
$\| R^{(N)} \|$	number of ringed bitstrings of length N (OEIS A000031);
$\| E^{(N)} \|$	number of balanced ringed bitstrings of length N ;
$a^{(N)}$	assembly index of a bitstring of length N;
$P = {1, 0}$	initial assembly pool;
s	assembly step;
Q	binary assembling program;
$s_{Q}$	length of the binary assembling program;
F	Fibonacci sequence.

Appendix A. Exemplary Maximal Assembly Index Bitstrings

For the exemplary balanced ringed bitstrings

E_{\max}

, shown in Table 8:

all forms of $E_{k}^{(4)} = [0011]$ have $a^{(4)} = 3$ ,
all forms of $E_{6}^{(5)} = [00011]$ have $a^{(5)} = 4$ ,
all forms of $E_{16}^{(6)} = [000111]$ have $a^{(6)} = 5$ ,
the form $E_{28}^{(7)} = [0011100]$ has $a^{(7)} = 5$ but the form $E_{34}^{(7)} = [0001110]$ has $a^{(7)} = 6$ ,
all forms of $E_{45}^{(8)} = [00010111]$ have $a^{(8)} = 6$ ,
all forms of $E_{13}^{(9)} = [000011101]$ have $a^{(9)} = 7$ ,
the form $E_{22}^{(10)} = [0000111101]$ has $a^{(10)} = 7$ but the form $E_{l}^{(10)} = [0111101000]$ has $a^{(10)} = 8$ ,
all forms of $E_{7}^{(11)} = [00000101111]$ have $a^{(11)} = 8$ ,
all forms of $E_{9}^{(12)} = [111000101100]$ have $a^{(12)} = 8$ ,
all forms of $E_{8}^{(13)} = [0000001011111]$ have $a^{(13)} = 9$ ,
all forms of $E_{k}^{(14)} = [00000101011111]$ have $a^{(14)} = 9$ ,
all forms of $E_{k}^{(15)} = [000001010111110]$ have $a^{(15)} = 10$ ,
all forms of $E_{k}^{(16)} = [1000000101011111]$ have $a^{(16)} = 10$ ,
all forms of $E_{k}^{(17)} = [00000010101111110]$ have $a^{(17)} = 11$ ,
all forms of $E_{k}^{(18)} = [000000101010111111]$ have $a^{(18)} = 11$ ,
some forms of $E_{k}^{(19)} = [1000010101001111101]$ have $a^{(19)} = 12$ ,
some forms of $E_{k}^{(20)} = [10100111110110000010]$ have $a^{(20)} = 13$ .

Appendix B. Trivial Assembling Programs

Table A1 shows the lengths of the bitstrings assembled by the trivial assembling program introduced in Section 6 for

1 \leq s_{Q} \leq 7

. The table is divided into sections corresponding to sets of assembled bitstrings having the same form but different lengths. For example, thirty two 7-bit programs in the bottom section assemble bitstrings

C = [* 1 * 1 \dots]

. The boxed symbols denote program commands, not the bitstring lengths.

Table A1. Lengths of the bitstrings assembled by trivial assembly programs Qs (OEIS A065108).

$a^{(N)}$	0	1	2	3	3,4	4,5	5,6	6,7
$s_{Q}$		1	2	3	4	5	6	7
1	1	2	3	5	$8^{‡}$	13	21	$34^{‡}$
		\|	\|	\|	\|	\|	$\begin{matrix} ★ \end{matrix}$	42
		\|	\|	\|	\|	$\begin{matrix} 0 \end{matrix}$	26	39
		\|	\|	\|	\|		$\begin{matrix} ★ \end{matrix}$	52
		\|	\|	\|	$\begin{matrix} 0 \end{matrix}$	$16^{‡}$	$24^{‡}$	$40^{‡}$
		\|	\|	\|		\|	$\begin{matrix} ★ \end{matrix}$	$48^{‡}$
		\|	\|	\|		$\begin{matrix} ★ \end{matrix}$	$32^{‡}$	$48^{‡}$
		\|	\|	\|			$\begin{matrix} ★ \end{matrix}$	$64^{‡}$
		\|	\|	$\begin{matrix} 0 \end{matrix}$	10	15	25	$40^{‡}$
		\|	\|		\|	\|	$\begin{matrix} ★ \end{matrix}$	50
		\|	\|		\|	$\begin{matrix} ★ \end{matrix}$	30	45
		\|	\|		\|		$\begin{matrix} ★ \end{matrix}$	60
		\|	\|		$\begin{matrix} ★ \end{matrix}$	20	30	50
		\|	\|			\|	$\begin{matrix} ★ \end{matrix}$	60
		\|	\|			$\begin{matrix} ★ \end{matrix}$	40	60
		\|	\|				$\begin{matrix} ★ \end{matrix}$	80
		\|	$\begin{matrix} 0 \end{matrix}$	6	9	15	$24^{†}$	39
		\|		\|	\|	\|	$\begin{matrix} ★ \end{matrix}$	$48^{†}$
		\|		\|	\|	$\begin{matrix} ★ \end{matrix}$	30	45
		\|		\|	\|		$\begin{matrix} ★ \end{matrix}$	60
		\|		\|	$\begin{matrix} ★ \end{matrix}$	18	27	45
		\|		\|		\|	$\begin{matrix} ★ \end{matrix}$	54
		\|		\|		$\begin{matrix} ★ \end{matrix}$	36	54
		\|		\|			$\begin{matrix} ★ \end{matrix}$	72
		\|		$\begin{matrix} ★ \end{matrix}$	12	18	30	$48^{†}$
		\|			\|	\|	$\begin{matrix} ★ \end{matrix}$	60
		\|			\|	$\begin{matrix} ★ \end{matrix}$	36	54
		\|			\|		$\begin{matrix} ★ \end{matrix}$	72
		\|			$\begin{matrix} ★ \end{matrix}$	24	36	60
		\|				\|	$\begin{matrix} ★ \end{matrix}$	72
		\|				$\begin{matrix} ★ \end{matrix}$	48	72
		\|					$\begin{matrix} ★ \end{matrix}$	96
		$\begin{matrix} 0 \end{matrix}$	4	6	10	$16^{†}$	26	42
			\|	\|	\|	\|	$\begin{matrix} ★ \end{matrix}$	52
			\|	\|	\|	$\begin{matrix} ★ \end{matrix}$	$32^{†}$	$48^{†}$
			\|	\|	\|		$\begin{matrix} ★ \end{matrix}$	$64^{†}$
			\|	\|	$\begin{matrix} ★ \end{matrix}$	20	30	50
			\|	\|		\|	$\begin{matrix} ★ \end{matrix}$	60
			\|	\|		$\begin{matrix} ★ \end{matrix}$	40	60
			\|	\|			$\begin{matrix} ★ \end{matrix}$	80
			\|	$\begin{matrix} ★ \end{matrix}$	12	18	30	$48^{†}$
			\|		\|	\|	$\begin{matrix} ★ \end{matrix}$	60
			\|		\|	$\begin{matrix} ★ \end{matrix}$	36	54
			\|		\|		$\begin{matrix} ★ \end{matrix}$	72
			\|		$\begin{matrix} ★ \end{matrix}$	24	36	60
			\|			\|	$\begin{matrix} ★ \end{matrix}$	72
			\|			$\begin{matrix} ★ \end{matrix}$	48	72
			\|				$\begin{matrix} ★ \end{matrix}$	96
			$\begin{matrix} ★ \end{matrix}$	8	12	20	$32^{†}$	52
				\|	\|	\|	$\begin{matrix} ★ \end{matrix}$	$64^{†}$
				\|	\|	$\begin{matrix} ★ \end{matrix}$	40	60
				\|	\|		$\begin{matrix} ★ \end{matrix}$	80
				\|	$\begin{matrix} ★ \end{matrix}$	24	36	60
				\|		\|	$\begin{matrix} ★ \end{matrix}$	72
				\|		$\begin{matrix} ★ \end{matrix}$	48	72
				\|			$\begin{matrix} ★ \end{matrix}$	96
				$\begin{matrix} ★ \end{matrix}$	16	24	40	$64^{†}$
					\|	\|	$\begin{matrix} ★ \end{matrix}$	80
					\|	$\begin{matrix} ★ \end{matrix}$	48	72
					\|		$\begin{matrix} ★ \end{matrix}$	96
					$\begin{matrix} ★ \end{matrix}$	32	48	80
						\|	$\begin{matrix} ★ \end{matrix}$	96
						$\begin{matrix} ★ \end{matrix}$	64	96
							$\begin{matrix} ★ \end{matrix}$	128

Table A2. 4-bit programs assembling bitstrings with

a^{(N)} = {3, 4}

Table A2. 4-bit programs assembling bitstrings with

a^{(N)} = {3, 4}

Q	$C (s = 3)$	$C (s_{Q} = 4)$	N
$* 111$	$* 00 * 0$	$0 * 0 * 00 * 0$	$8^{‡}$
$* 110$	$* 00 * 0$	$* 00 * 0 \dots$	10
$* 101$	$0 * 0 \dots$	$0 * 0 \dots$	9
$* 100$	$0 * 0 \dots$	$0 * 0 \dots$	12
$* 011$	$* 0 \dots$	$* 0 \dots$	10
$* 010$	$* 0 \dots$	$* 0 \dots$	12
$* 001$	$* 0 \dots$	$* 0 \dots$	12
$* 000$	$* 0 \dots$	$* 0 \dots$	16

14.1cm ^‡. This program is not elegant if

* = 0

and the assembled bitstring is not

C_{\min}

* = 1

Table A3. 5-bit programs assembling bitstrings with

a^{(N)} = {4, 5}

Table A3. 5-bit programs assembling bitstrings with

a^{(N)} = {4, 5}

Q	$C (s = 4)$	$C (s_{Q} = 5)$	N
$* 1111$	$0 * 0 * 00 * 0$	$* 00 * 00 * 0 * 00 * 0$	13
$* 1110$	$0 * 0 * 00 * 0$	$0 * 0 * 00 * 0 \dots$	$16^{‡}$
$* 1101$	$* 00 * 0 \dots$	$* 00 * 0 \dots$	15
$* 1100$	$* 00 * 0 \dots$	$* 00 * 0 \dots$	20
$* 1011$	$0 * 0 \dots$	$0 * 0 \dots$	15
$* 1010$	$0 * 0 \dots$	$0 * 0 \dots$	18
$* 1001$	$0 * 0 \dots$	$0 * 0 \dots$	18
$* 1000$	$0 * 0 \dots$	$0 * 0 \dots$	24
$* 0111$	$* 0 \dots$	$* 0 \dots$	$16^{†}$
$* 0110$	$* 0 \dots$	$* 0 \dots$	20
$* 0101$	$* 0 \dots$	$* 0 \dots$	18
$* 0100$	$* 0 \dots$	$* 0 \dots$	24
$* 0011$	$* 0 \dots$	$* 0 \dots$	20
$* 0010$	$* 0 \dots$	$* 0 \dots$	24
$* 0001$	$* 0 \dots$	$* 0 \dots$	24
$* 0000$	$* 0 \dots$	$* 0 \dots$	32

14.1cm ^†. This program is not elegant (the same bitstring can be assembled using the shorter 4-bit program

* 000

). ^‡. This program is not elegant if

* = 0

and the assembled bitstring is not

C_{\min}

* = 1

Table A4. 6-bit programs assembling bitstrings with

a^{(N)} = {5, 6}

Table A4. 6-bit programs assembling bitstrings with

a^{(N)} = {5, 6}

Q	$C (s_{Q} = 6)$	N
$* 11111$	$0 * 0 * 00 * 0 * 00 * 00 * 0 * 00 * 0$	21
$* 11110$	$* 00 * 00 * 0 * 00 * 0 \dots$	26
$* 1110 ★$	$0 * 0 * 00 * 0 \dots$	$24^{‡}, 32^{‡}$
$* 110 ★ ★$	$* 00 * 0 \dots$	$25, 30, 40$
$* 10 ★ ★ ★$	$0 * 0 \dots$	$24^{†}, \dots, 48$
$* 0 ★ ★ ★ ★$	$* 0 \dots$	$26, 32^{†}, \dots, 64$

14.1cm ^†. This program is not elegant. ^‡. This program is not elegant if

* = 0

and the assembled bitstring is not

C_{\min}

* = 1

Appendix C. Bitstrings and Their Assembly Indices

Table A1 show the lengths of the bitstrings assembled by programs Fs having the smallest assembly indices. Table A5-Table A12 show distributions of the assembly indices for

5 \leq N \leq 12

. Table A13-Table A17 show balanced bitstrings

B^{(N)}

and their assembly indices for

5 \leq N \leq 8

. Table A18-Table A23 show the balanced ringed bitstrings

E^{(N)}

and their assembly indices for

5 \leq N \leq 10

. Table A24-Table A26 show selected balanced ringed bitstrings

E^{(N)}

and their assembly indices for

11 \leq N \leq 13

Table A5. Distribution of the assembly indices for

N = 5

Table A5. Distribution of the assembly indices for

N = 5

		$N_{1}$
$a^{(5)} (C)$	$\| a^{(5} (C) \|$	0	1	2	3	4	5
3	18	1	3	5	5	3	1
4	14		2	5	5	2
32		1	5	10	10	5	1

Table A6. Distribution of the assembly indices for

N = 6

Table A6. Distribution of the assembly indices for

N = 6

		$N_{1}$
$a^{(6)} (C)$	$\| a^{(6)} (C) \|$	0	1	2	3	4	5	6
3	10	1		3	2	3		1
4	44		6	10	12	10	6
5	10			2	6	2
64		1	6	15	20	15	6	1

Table A7. Distribution of the assembly indices for

N = 7

Table A7. Distribution of the assembly indices for

N = 7

		$N_{1}$
$a^{(7)} (C)$	$\| a^{(7)} (C) \|$	0	1	2	3	4	5	6	7
4	50	1	5	7	12	12	7	5	1
5	74		2	14	21	21	14	2
6	4				2	2
128		1	7	21	35	35	21	7	1

Table A8. Distribution of the assembly indices for

N = 8

Table A8. Distribution of the assembly indices for

N = 8

		$N_{1}$
$a^{(8)} (C)$	$\| a^{(8)} (C) \|$	0	1	2	3	4	5	6	7	8
3	4	1				2				1
4	38			9	8	4	8	9
5	132		8	17	22	40	22	17	8
6	82			2	26	24	26	2
256		1	8	28	56	70	56	28	8	1

Table A9. Distribution of the assembly indices for

N = 9

Table A9. Distribution of the assembly indices for

N = 9

		$N_{1}$
$a^{(9)} (C)$	$\| a^{(9)} (C) \|$	0	1	2	3	4	5	6	7	8	9
4	24	1	3		3	5	5	3		3	1
5	184		4	17	35	36	36	35	17	4
6	248		2	19	42	61	61	42	19	2
7	56				4	24	24	4
512		1	9	36	84	126	126	84	36	9	1

Table A10. Distribution of the assembly indices for

N = 10

Table A10. Distribution of the assembly indices for

N = 10

		$N_{1}$
$a^{(10)} (C)$	$\| a^{(10)} (C) \|$	0	1	2	3	4	5	6	7	8	9	10
4	20	1		3		5	2	5		3		1
5	198		8	22	20	33	32	33	20	22	8
6	502		2	18	68	108	110	108	68	18	2
7	288			2	32	62	96	62	32	2
8	16					2	12	2
1024		1	10	45	120	210	252	210	120	45	10

Table A11. Distribution of the assembly indices for

N = 11

Table A11. Distribution of the assembly indices for

N = 11

		$N_{1}$
$a^{(11)} (C)$	$\| a^{(11)} (C) \|$	0	1	2	3	4	5	6	7	8	9	10	11
5	184	1	7	14	23	18	29	29	18	23	14	7	1
6	686		4	32	69	104	134	134	104	69	32	4
7	970			9	69	178	229	229	178	69	9
8	208				4	30	70	70	30	4
2048		1	11	55	165	330	462	462	330	165	55	11

Table A12. Distribution of the assembly indices for

N = 12

Table A12. Distribution of the assembly indices for

N = 12

		$N_{1}$
$a^{(12)}$	$\| a^{(12)} \|$	0	1	2	3	4	5	6	7	8	9	10	11	12
4	10	1				3		2		3				1
5	94			13	4	10	12	16	12	10	4	13
6	1034		12	42	94	141	130	196	130	141	94	42	12
7	1688			11	106	196	354	354	354	196	106	11
8	1180				16	143	282	298	282	143	16
9	90					2	14	58	14	2
4096		1	12	66	220	495	792	924	792	495	220	66	12	1

Table A13.

| B^{(5)} | = 10

balanced bitstrings.

Table A13.

| B^{(5)} | = 10

balanced bitstrings.

k	$B_{k}^{(5)}$					$a^{(5)} (B_{k})$
1	0	(0	1)	(0	1)	3
2	(0	1)	0	(0	1)	3
3	(0	1)	(0	1)	0	3
4	(1	0)	0	(1	0)	3
5	(1	0)	(1	0)	0	3
6	0	0	0	1	1	4
7	0	0	1	1	0	4
8	0	1	1	0	0	4
9	1	0	0	0	1	4
10	1	1	0	0	0	4

Table A14.

| B^{(6)} | = 20

balanced bitstrings.

Table A14.

| B^{(6)} | = 20

balanced bitstrings.

k	$B_{k}^{(6)}$						$a^{(6)} (B_{k})$
1	(0	1)	(0	1)	(0	1)	3
2	(1	0)	(1	0)	(1	0)	3
3	0	(0	1)	(0	1)	1	4
4	0	(0	1)	1	(0	1)	4
5	(0	1)	0	(0	1)	1	4
6	(0	1)	(0	1)	1	0	4
7	(0	1)	1	0	(0	1)	4
8	(0	1)	1	(0	1)	0	4
9	(1	0)	0	(1	0)	1	4
10	(1	0)	0	1	(1	0)	4
11	(1	0)	(1	0)	0	1	4
12	(1	0)	1	(1	0)	0	4
13	1	(1	0)	0	(1	0)	4
14	1	(1	0)	(1	0)	0	4
15	0	0	1	1	1	0	5
16	0	0	0	1	1	1	5
17	0	1	1	1	0	0	5
18	1	0	0	0	1	1	5
19	1	1	0	0	0	1	5
20	1	1	1	0	0	0	5

Table A15.

| B^{(7)} | = 35

balanced bitstrings.

Table A15.

| B^{(7)} | = 35

balanced bitstrings.

k	$B_{k}^{(7)}$							$a^{(7)} (B_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
2	(0	1)	(0	1)	(0	1)	0	4
3	(1	0)	(1	0)	(1	0)	0	4
4	(0	1)	(0	1)	0	(0	1)	4
5	(1	0)	(1	0)	0	(1	0)	4
6	(0	1)	0	(0	1)	(0	1)	4
7	(1	0)	0	(1	0)	(1	0)	4
8	(1	0	0)	(1	0	0)	1	4
9	(1	0	0)	1	(1	0	0)	4
10	1	(1	0	0)	(1	0	0)	4
11	(0	0	1)	1	(0	0	1)	4
12	(0	0	1)	(0	0	1)	1	4
13	1	(0	0)	(0	0)	1	1	5
14	1	0	0	(0	1)	(0	1)	5
15	(1	0)	0	0	1	(1	0)	5
16	(1	0)	(1	0)	0	0	1	5
17	(1	0)	1	(1	0)	0	0	5
18	1	1	(0	0)	(0	0)	1	5
19	1	(1	0)	(1	0)	0	0	5
20	1	1	1	(0	0)	(0	0)	5
21	(0	1)	(0	1)	1	0	0	5
22	(0	1)	1	0	0	(0	1)	5
23	(0	1)	1	0	(0	1)	0	5
24	(0	1)	1	(0	1)	0	0	5
25	(0	1)	0	(0	1)	1	0	5
26	0	(0	1)	(0	1)	1	0	5
27	0	(0	1)	1	(0	1)	0	5
28	(0	0)	1	1	1	(0	0)	5
29	(0	1)	0	0	(0	1)	1	5
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5
33	1	(1	0)	0	0	(1	0)	5
34	0	0	0	1	1	1	0	6
35	0	1	1	1	0	0	0	6

Table A16.

| B^{(8)} | = 70

balanced bitstrings (1^st part).

Table A16.

| B^{(8)} | = 70

balanced bitstrings (1^st part).

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
2	((1	0)	(1	0))	((1	0)	(1	0))	3
3	((0	0)	(1	1))	((0	0)	(1	1))	4
4	((0	1)	(1	0))	((0	1)	(1	0))	4
5	((1	0)	(0	1))	((1	0)	(0	1))	4
6	((1	1)	(0	0))	((1	1)	(0	0))	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	(0	0	1)	(0	0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
12	(0	0	1)	1	1	(0	0	1)	5
13	(0	0)	(1	1)	(1	1)	(0	0)	5
14	(0	1)	0	(0	1)	(0	1)	1	5
15	(0	1)	0	(0	1)	1	(0	1)	5
16	(0	1)	(0	1)	0	(0	1)	1	5
17	(0	1)	(0	1)	(0	1)	1	0	5
18	(0	1)	(0	1)	1	0	(0	1)	5
19	(0	1)	(0	1)	1	(0	1)	0	5
20	(0	1	1)	0	0	(0	1	1)	5
21	(0	1)	1	0	(0	1)	(0	1)	5
22	(0	1)	1	(0	1)	0	(0	1)	5
23	(0	1)	1	(0	1)	(0	1)	0	5
24	(0	1	1)	(0	1	1)	0	0	5
25	(1	0	0)	(1	0	0)	1	1	5
26	1	0	(0	1)	(0	1)	(0	1)	5
27	(1	0)	0	(1	0)	1	(1	0)	5
28	(1	0)	0	1	(1	0)	(1	0)	5
29	(1	0	0)	1	1	(1	0	0)	5
30	(1	0	1)	0	0	(1	0	1)	5
31	(1	0)	(1	0)	0	1	(1	0)	5
32	(1	0)	(1	0)	(1	0)	0	1	5
33	(1	0)	(1	0)	1	(1	0)	0	5
34	(1	0)	1	(1	0)	0	(1	0)	5
35	(1	0)	1	(1	0)	(1	0)	0	5
36	(1	1)	(0	0)	(0	0)	(1	1)	5
37	(1	1	0)	0	0	(1	1	0)	5
38	1	1	(0	0	1)	(0	0	1)	5
39	1	1	0	0	1	0	1	0	5
40	1	(1	0)	(1	0)	0	(1	0)	5
41	(1	1	0)	(1	1	0)	0	0	5
42	1	1	0	1	0	1	0	0	5
43	1	1	(1	0	0)	(1	0	0)	5
44	(1	1)	(1	1)	(0	0)	(0	0)	5
45	0	0	(0	1	1)	(0	1	1)	5
46	0	(0	1	1)	(0	1	1)	0	5

Table A17.

| B^{(8)} | = 70

balanced bitstrings (2^nd part).

Table A17.

| B^{(8)} | = 70

balanced bitstrings (2^nd part).

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
47	0	0	(0	1)	(0	1)	1	1	6
48	0	0	(0	1)	1	1	(0	1)	6
49	0	0	0	(1	1)	(1	1)	0	6
50	0	(0	1)	(0	1)	1	1	0	6
51	0	0	1	1	(1	0)	(1	0)	6
52	(0	1)	0	0	(0	1)	1	1	6
53	(0	1)	0	(0	1)	1	1	0	6
54	(0	1)	(0	1)	1	1	0	0	6
55	(0	1)	1	1	0	0	(0	1)	6
56	(0	1)	1	1	0	(0	1)	0	6
57	(0	1)	1	1	(0	1)	0	0	6
58	0	(1	1)	(1	1)	0	0	0	6
59	1	(0	0)	(0	0)	1	1	1	6
60	(1	0)	0	0	(1	0)	1	1	6
61	1	0	0	(0	1)	1	(0	1)	6
62	(1	0)	0	0	1	1	(1	0)	6
63	(1	0)	(1	0)	0	0	1	1	6
64	(1	0)	1	(1	0)	0	0	1	6
65	(1	0)	1	1	(1	0)	0	0	6
66	1	(1	0)	0	0	(1	0)	1	6
67	1	1	(0	1)	0	0	(0	1)	6
68	1	1	1	(0	0)	(0	0)	1	6
69	1	1	(1	0)	0	0	(1	0)	6
70	1	1	(1	0)	(1	0)	0	0	6

Table A18.

| E^{(5)} | = 2

balanced ringed bitstrings.

Table A18.

| E^{(5)} | = 2

balanced ringed bitstrings.

k	$E_{k}^{(5)}$					$a^{(5)} (E_{k})$
1	0	(0	1)	(0	1)	3
6	0	0	0	1	1	4

Table A19.

| E^{(6)} | = 4

balanced ringed bitstrings.

Table A19.

| E^{(6)} | = 4

balanced ringed bitstrings.

k	$E_{k}^{(6)}$						$a^{(6)} (E_{k})$
1	(0	1)	(0	1)	(0	1)	3
3	0	(0	1)	(0	1)	1	4
4	0	(0	1)	1	(0	1)	4
16	0	0	0	1	1	1	5

Table A20.

| E^{(7)} | = 5

balanced ringed bitstrings.

Table A20.

| E^{(7)} | = 5

balanced ringed bitstrings.

k	$E_{k}^{(7)}$							$a^{(7)} (E_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
12	(0	0	1)	(0	0	1)	1	4
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5

Table A21.

| E^{(8)} | = 10

balanced ringed bitstrings.

Table A21.

| E^{(8)} | = 10

balanced ringed bitstrings.

k	$E_{k}^{(8)}$								$a^{(8)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
3	(0	0)	(1	1)	(0	0)	(1	1)	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	0	(0	1)	0	(0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
46	0	0	(0	1	1)	(0	1	1)	5
45	0	0	(0	1)	(0	1)	1	1	6
47	0	0	(0	1)	1	1	(0	1)	6

Table A22. Selected balanced ringed bitstrings

| E^{(9)} | = 14

Table A22. Selected balanced ringed bitstrings

| E^{(9)} | = 14

k	$E_{k}^{(9)}$									$a^{(9)} (E_{k})$
1	0	((0	1)	(0	1))	((0	1)	(0	1))	4
2	0	((0	0)	(1	1))	((0	0)	(1	1))	5
3	(0	(0	1))	(0	1)	(0	0	1)	1	5
4	(0	(0	1))	(0	0	1)	1	(0	1)	5
5	(0	(0	1))	(0	0	1)	(0	1)	1	5
6	0	(0	0	1)	1	1	(0	0	1)	6
7	0	0	(0	1)	1	(0	1)	(0	1)	6
8	0	0	(0	1)	(0	1)	1	(0	1)	6
9	0	0	(0	1)	(0	1)	(0	1)	1	6
10	0	(0	0	1)	(0	0	1)	1	1	6
11	(0	0)	(0	0)	(1	1)	0	(1	1)	6
12	0	(0	0)	(0	0)	(1	1)	(1	1)	6
13	(0	0)	(0	0)	1	1	1	0	1	7
14	(0	0)	(0	0)	1	0	1	1	1	7

Table A23.

| E^{(10)} | = 26

balanced ringed bitstrings.

Table A23.

| E^{(10)} | = 26

balanced ringed bitstrings.

k	$E_{k}^{(10)}$										$a^{(10)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	(0	1)	4
2	0	((0	1)	(0	1))	((0	1)	(0	1))	1	5
3	(0	1)	(1	(0	1)	0)	(1	(0	1)	0)	5
4	(0	(0	1)	1)	(0	0	1	1)	(0	1)	5
5	0	((0	1)	0	1)	1	(0	1	0	1)	5
6	0	((1	0)	1	0)	1	(1	0	1	0)	5
7	(0	1)	((0	1)	1	0)	(0	1	1	0)	5
8	(0	(0	1))	(0	1)	(0	0	1)	1	1	6
9	(0	(0	1))	(0	0	1)	1	1	(0	1)	6
10	(0	(0	1))	(0	0	1)	1	(0	1)	1	6
11	(0	(0	1))	(0	0	1)	(0	1)	1	1	6
14	0	(0	0	1	1)	1	(0	0	1	1)	6
15	0	0	((0	1)	1)	(0	1	1)	(0	1)	6
16	0	0	((0	1)	1)	(0	1)	(0	1	1)	6
17	0	(0	0	1	1)	(0	0	1	1)	1	6
19	0	0	(0	1)	((0	1)	1)	(0	1	1)	6
12	(0	0)	0	(1	1)	(1	1)	(0	0)	1	7
13	0	0	(0	1)	1	1	(0	1)	(0	1)	7
18	0	0	(0	1)	(0	1)	1	1	(0	1)	7
20	0	0	(0	1)	(0	1)	(0	1)	1	1	7
21	(0	0)	0	1	(0	0)	(1	1)	(1	1)	7
22	(0	0)	(0	0)	(1	1)	(1	1)	0	1	7
23	(0	0)	(0	0)	(1	1)	1	0	(1	1)	7
24	(0	0)	(0	0)	(1	1)	0	(1	1)	1	7
25	(0	0)	(0	0)	1	0	(1	1)	(1	1)	7
26	(0	0)	(0	0)	0	1	(1	1)	(1	1)	7

Table A24. Selected balanced ringed bitstrings

E^{(11)}

Table A24. Selected balanced ringed bitstrings

E^{(11)}

k	$E_{k}^{(11)}$											$a^{(11)} (E_{k})$
1	0	(0	1)	((0	1))	(0	1))	(0	1	0	1)	5
2	(0	(0	1)	(0	1))	(0	0	1	0	1)	1	5
3	(0	0)	((0	0)	1	1)	(1	0	0	1	1)	6
4	(0	(0	1))	(0	1)	(0	1)	(0	0	1)	1	6
5	(0	0)	(0	0)	(0	0)	(1	1)	(1	1)	1	7
6	(0	0)	(1	1	0)	1	(0	0)	(1	1	0)	7
7	(0	0)	(0	0)	(0	1)	(0	1)	1	1	1	8

Table A25. Selected balanced ringed bitstrings

E^{(12)}

Table A25. Selected balanced ringed bitstrings

E^{(12)}

k	$E_{k}^{(12)}$												$a^{(12)} (E_{k})$
1	((0	1)	(0	1))	(0	1	0	1)	(0	1	0	1)	4
2	(0	(0	1)	1	(0	1))	(0	0	1	1	0	1)	5
3	((0	1)	1	(0	(0	1)))	((0	1)	1	(0	0	1))	5
4	(0	(0	1)	1)	(0	0	1	1)	(0	1)	(0	1)	6
5	((0	1)	0	(0	1))	(0	1	0	0	1)	1	1	6
6	(0	0	1)	(0	0	1)	(0	0	1)	1	1	1	7
7	(0	0)	(0	0)	(0	0)	(1	1)	(1	1)	(1	1)	7
8	(0	0)	(0	0)	(1	1)	(1	1)	1	(0	0)	1	8
9	(0	0)	(1	0)	(1	1)	(0	0)	(1	1)	(1	0)	8
10	(1	1)	(1	1)	(0	1)	(0	1)	(0	0)	(0	0)	8
11	(1	1)	(1	1)	(0	0)	(0	0)	(1	0)	(1	0)	8

Table A26. Selected balanced ringed bitstrings

E^{(13)}

Table A26. Selected balanced ringed bitstrings

E^{(13)}

k	$E_{k}^{(13)}$													$a^{(13)} (E_{k})$
1	0	((0	1)	(0	1))	(0	1	0	1)	(0	1	0	1)	5
2	0	((1	0)	0	1	(1	0))	(1	0	0	1	1	0)	6
3	(0	((0	1)	(0	1))	(0	0	1	0	1)	(0	1)	1	6
4	0	(0	0)	((0	0)	(1	1))	(0	0	1	1)	(1	1)	7
5	(0	0)	((0	0)	(1	1))	(0	0	1	1)	0	(1	1)	7
6	(0	0)	(0	0)	(0	0)	0	(1	1)	(1	1)	(1	1)	8
7	(0	0	(0	1))	(0	0	0	1)	(0	1)	1	1	1	8
8	(0	0)	(0	0)	(0	0)	1	0	(1	1)	(1	1)	1	9

Notes

1	" $⌊x⌋$ " is the floor function that yields the greatest integer less than or equal to x and " $⌈x⌉$ " is the ceiling function that yields the least integer greater than or equal to x.
2	$\| E_{k}^{(N)} \|$ is close to OEIS A000014 up to the eleventh term.
3	Available online at https://www.ncbi.nlm.nih.gov/nuccore/MN908947.
4	Available online at https://www.ncbi.nlm.nih.gov/nuccore/OL351370.

References

Marshall, S.M.; Murray, A.R.G.; Cronin, L. A probabilistic framework for identifying biosignatures using Pathway Complexity. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 2017, 375, 20160342. [Google Scholar] [CrossRef]
Murray, A.; Marshall, S.; Cronin, L. Defining Pathway Assembly and Exploring its Applications, 2018. arXiv:1804.06972 [cs, math].
Marshall, S.M.; Mathis, C.; Carrick, E.; Keenan, G.; Cooper, G.J.T.; Graham, H.; Craven, M.; Gromski, P.S.; Moore, D.G.; Walker, S.I.; Cronin, L. Identifying molecules as biosignatures with assembly theory and mass spectrometry. Nature Communications 2021, 12, 3033. [Google Scholar] [CrossRef]
Liu, Y.; Mathis, C.; Bajczyk, M.D.; Marshall, S.M.; Wilbraham, L.; Cronin, L. Exploring and mapping chemical space with molecular assembly trees. Science Advances 2021, 7, eabj2465. [Google Scholar] [CrossRef]
Marshall, S.M.; Moore, D.G.; Murray, A.R.G.; Walker, S.I.; Cronin, L. Formalising the Pathways to Life Using Assembly Spaces. Entropy 2022, 24, 884. [Google Scholar] [CrossRef]
Sharma, A.; Czégel, D.; Lachmann, M.; Kempes, C.P.; Walker, S.I.; Cronin, L. Assembly theory explains and quantifies selection and evolution. Nature 2023, 622, 321–328. [Google Scholar] [CrossRef]
Jirasek, M.; Sharma, A.; Bame, J.R.; Mehr, S.H.M.; Bell, N.; Marshall, S.M.; Mathis, C.; MacLeod, A.; Cooper, G.J.T.; Swart, M.; Mollfulleda, R.; Cronin, L. Investigating and Quantifying Molecular Complexity Using Assembly Theory and Spectroscopy. ACS Central Science. [CrossRef]
Walker, S.; Cronin, L. Time is an object (Not a backdrop, an illusion or an emergent phenomenon, time has a physical size that can be measured in laboratories), 2023.
Watanabe, S. Knowing and Guessing: A Quantitative Study of Inference and Information; Wiley, 1969.
Watanabe, S. Epistemological Relativity. Annals of the Japan Association for Philosophy of Science 1986, 7, 1–14. [Google Scholar] [CrossRef]
Prigogine, I.; Stengers, I. Order out of Chaos: Man’s New Dialogue with Nature; Bantam Books, 1984.
Łukaszyk, S. A No-go Theorem for Superposed Actions (Making Schrödinger’s Cat Quantum Nonlocal). In New Frontiers in Physical Science Research Vol. 3; Purenovic, D.J., Ed.; Book Publisher International (a part of SCIENCEDOMAIN International), 2022; pp. 137–151. [CrossRef]
Qian, K.; Wang, K.; Chen, L.; Hou, Z.; Krenn, M.; Zhu, S.; Ma, X.s. Multiphoton non-local quantum interference controlled by an undetected photon. Nature Communications 2023, 14, 1480. [Google Scholar] [CrossRef]
Xue, P.; Xiao, L.; Ruffolo, G.; Mazzari, A.; Temistocles, T.; Cunha, M.T.; Rabelo, R. Synchronous Observation of Bell Nonlocality and State-Dependent Contextuality. Physical Review Letters 2023, 130, 040201. [Google Scholar] [CrossRef]
Łukaszyk, S. Shannon Entropy of Chemical Elements. European Journal of Applied Sciences 2024, 11, 443–458. [Google Scholar] [CrossRef]
Tran, D.M.; Nguyen, V.D.; Ho, L.B.; Nguyen, H.Q. Increased success probability in Hardy’s nonlocality: Theory and demonstration. Phys. Rev. A 2023, 107, 042210. [Google Scholar] [CrossRef]
Colciaghi, P.; Li, Y.; Treutlein, P.; Zibold, T. Einstein-Podolsky-Rosen Experiment with Two Bose-Einstein Condensates. Phys. Rev. X 2023, 13, 021031. [Google Scholar] [CrossRef]
Cronin, Leroy. Lee Cronin: Controversial Nature Paper on Evolution of Life and Universe | Lex Fridman Podcast #404, 2023. Accessed: 2023-12-18.
de Chardin, P.T. The Phenomenon of Man; Harper, New York, 1959.
Melamede, R. Dissipative Structures and the Origins of Life. Unifying Themes in Complex Systems IV; Minai, A.A., Bar-Yam, Y., Eds.; Springer Berlin Heidelberg: Berlin, Heidelberg, 2008; pp. 80–87. [Google Scholar]
Vedral, V. Decoding Reality: The Universe as Quantum Information; Oxford University Press, 2010. [CrossRef]
Łukaszyk, S. Life as the Explanation of the Measurement Problem. Journal of Physics: Conference Series 2024, 2701, 012124. [Google Scholar] [CrossRef]
Łukaszyk, S., Black Hole Horizons as Patternless Binary Messages and Markers of Dimensionality. In Future Relativity, Gravitation, Cosmology; Nova Science Publishers, 2023; chapter 15, pp. 317–374. [CrossRef]
Łukaszyk, S. Four Cubes, 2020. [CrossRef]
Vopson, M.M.; Lepadatu, S. Second law of information dynamics. AIP Advances 2022, 12, 075310. [Google Scholar] [CrossRef]
Łukaszyk, S. Novel Recurrence Relations for Volumes and Surfaces of n-Balls, Regular n-Simplices, and n-Orthoplices in Real Dimensions. Mathematics 2022, 10. [Google Scholar] [CrossRef]
Łukaszyk, S.; Tomski, A. Omnidimensional Convex Polytopes. Symmetry 2023, 15. [Google Scholar] [CrossRef]
Łukaszyk, S. The Imaginary Universe. preprint, PHYSICAL SCIENCES, 2023.
Vopson, M.M. The second law of infodynamics and its implications for the simulated universe hypothesis. AIP Advances 2023, 13, 105308. [Google Scholar] [CrossRef]
Shannon, C.E. A Mathematical Theory of Communication. Bell System Technical Journal 1948, 27, 379–423. [Google Scholar] [CrossRef]
Bekenstein, J.D. Black holes and the second law. Lettere Al Nuovo Cimento Series 2 1972, 4, 737–740. [Google Scholar] [CrossRef]
Bekenstein, J.D. Black Holes and Entropy. Phys. Rev. D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
Hawking, S.W. Particle creation by black holes. Communications In Mathematical Physics 1975, 43, 199–220. [Google Scholar] [CrossRef]
Downey, P.; Leong, B.; Sethi, R. Computing Sequences with Addition Chains. SIAM Journal on Computing 1981, 10, 638–646. [Google Scholar] [CrossRef]
Hugo Pfoertner observation during draft edits for A372152 discusson., 2024.
Kevin Ryde observation during draft edits for A371894 discusson., 2024.
Chaitin, G.J. Randomness and Mathematical Proof. Scientific American 1975, 232, 47–52. [Google Scholar] [CrossRef]
Chaitin, G.J. The unknowable; Springer series in discrete mathematics and theoretical computer science, Springer: Singapore ; New York, 1999.
Rajput, C. Metallic Ratios in Primitive Pythagorean Triples : Metallic Means embedded in Pythagorean Triangles and other Right Triangles. JOURNAL OF ADVANCES IN MATHEMATICS 2021, 20, 312–344. [Google Scholar] [CrossRef]
Łukaszyk, S. Metallic Ratios and Angles of a Real Argument. IPI Letters 2024, pp. 26–33. [CrossRef]
Caldarola, F.; d’Atri, G.; Maiolo, M.; Pirillo, G. New algebraic and geometric constructs arising from Fibonacci numbers: In honor of Masami Ito. Soft Computing 2020, 24, 17497–17508. [Google Scholar] [CrossRef]
Chaitin, G. From Philosophy to Program Size: Key Ideas and Methods : Lecture Notes on Algorithmic Information Theory from the 8th Estonian Winter School in Computer Science, EWSCS’03 : [2-7 March]; Institute of Cybernetics at Tallinn Technical University, 2003.
Chaitin, G.J. Computational complexity and Gödel’s incompleteness theorem. ACM SIGACT News 1971, pp. 11–12. [CrossRef]
Kolmogorov, A. On tables of random numbers. Theoretical Computer Science 1998, 207, 387–395. [Google Scholar] [CrossRef]
Chaitin, G. Omega and why maths has no TOEs, 2023.
The principles of psychology; Henry Holt and company, 1890.
McMillen, P.; Levin, M. Collective intelligence: A unifying concept for integrating biology across scales and substrates. Communications Biology 2024, 7, 378. [Google Scholar] [CrossRef]
Barta, J.; Markiewicz, R. (Eds.) Prawo autorskie: przepisy, orzecznictwo, umowy miedzynarodowe, wyd. 4., rozsz. i zaktualizowane ed.; Dom Wydawniczy ABC: Warszawa, 2002. [Google Scholar]
Kuhn, T.S. The structure of scientific revolutions, 3rd ed ed.; University of Chicago Press: Chicago, IL, 1996. [Google Scholar]
Łukaszyk, S. A new concept of probability metric and its applications in approximation of scattered data sets. Computational Mechanics 2004, 33, 299–304. [Google Scholar] [CrossRef]
Castro, P.S.; Kastner, T.; Panangaden, P.; Rowland, M. MICo: Improved representations via sampling-based state similarity for Markov decision processes. Advances in Neural Information Processing Systems 2021, 34, 30113–30126. [Google Scholar] [CrossRef]

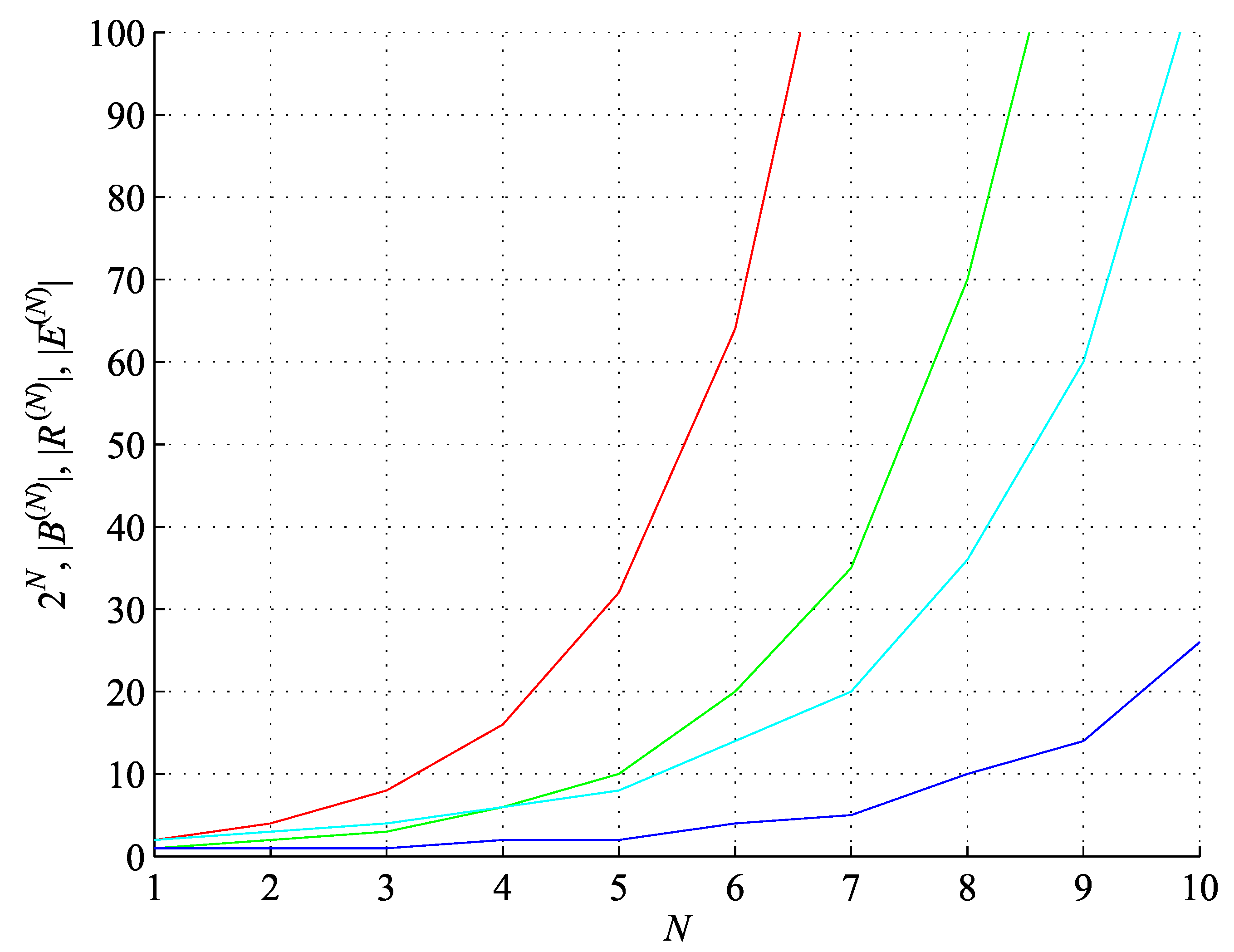
Figure 1. Numbers of all

2^{N}

bitstrings (red), balanced bitstrings

| B_{k}^{(N)} |

(green), ringed bitstrings

| R_{k}^{(N)} |

(cyan), and balanced ringed bitstrings

| E_{k}^{(N)} |

(blue) as a function of the bitstring length N.

Figure 1. Numbers of all

2^{N}

bitstrings (red), balanced bitstrings

| B_{k}^{(N)} |

(green), ringed bitstrings

| R_{k}^{(N)} |

(cyan), and balanced ringed bitstrings

| E_{k}^{(N)} |

(blue) as a function of the bitstring length N.

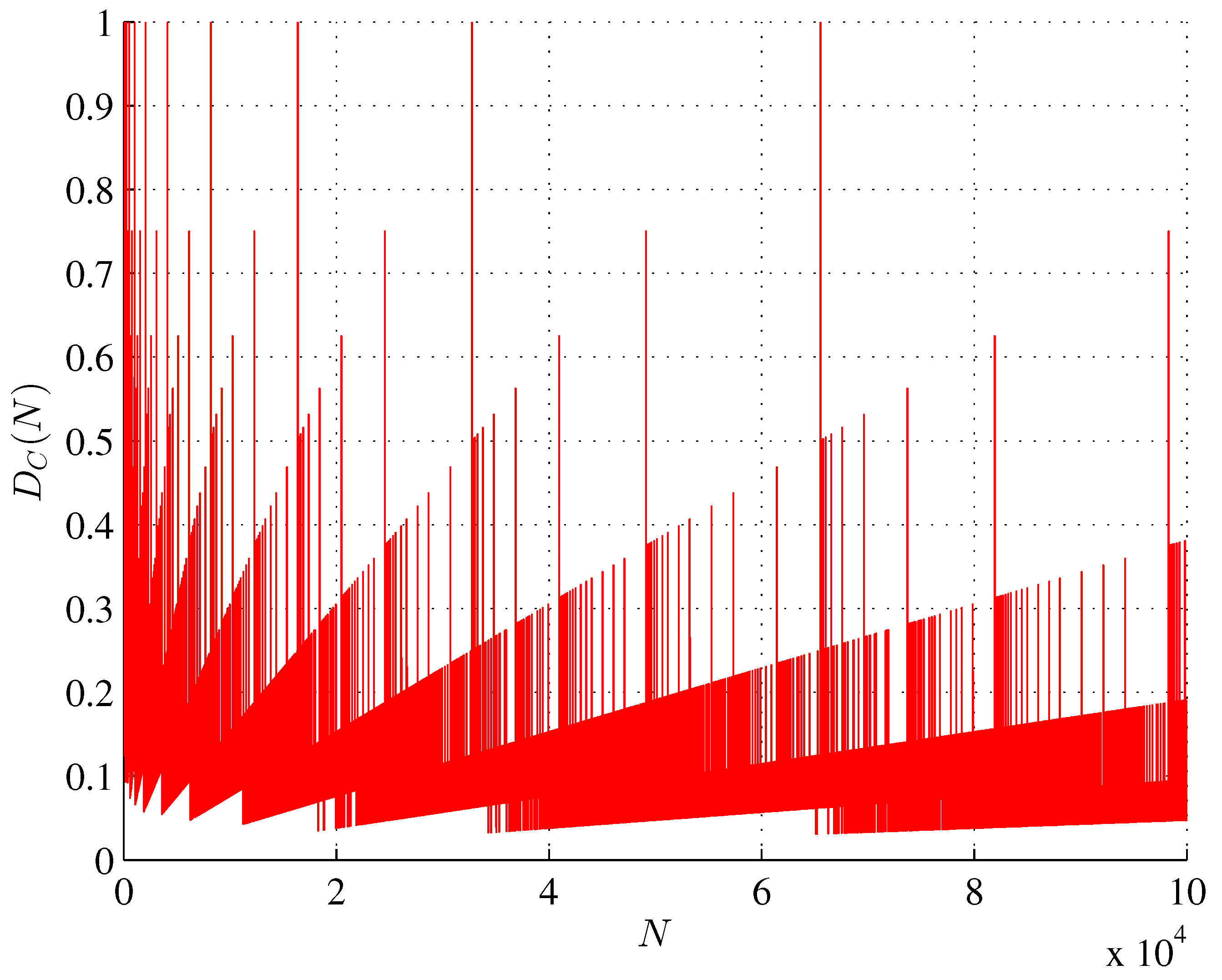
Figure 2. Degree of causation as a function of

1 \leq N \leq 10^{5}

Figure 2. Degree of causation as a function of

1 \leq N \leq 10^{5}

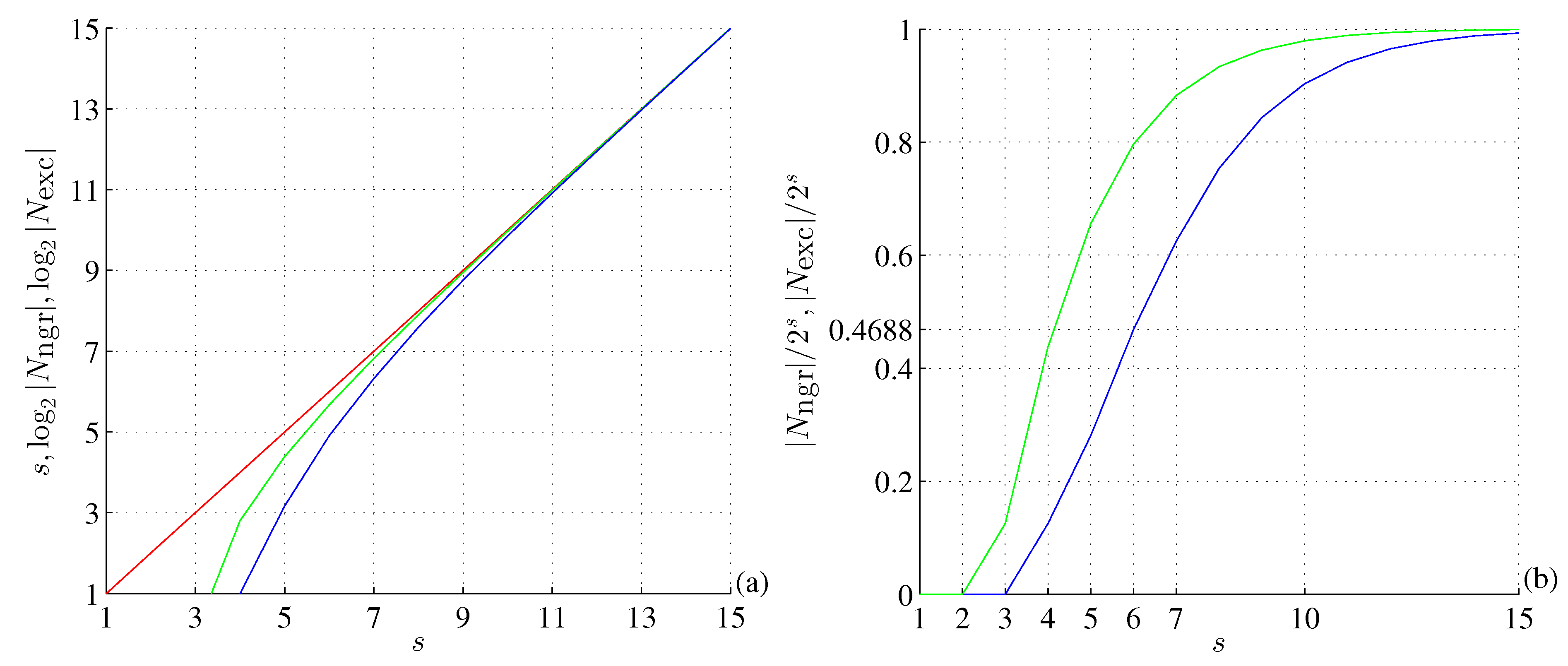
Figure 3. (a) Semi-log plot of

2^{s}

(red),

| N_{ngr} |

(green), and

| N_{exc} |

(blue). (b) Fractions of

| N_{ngr} |

(green) and

| N_{exc} |

(blue) to

2^{s}

, showing the deflection point for

s = 6

(see text for details).

Figure 3. (a) Semi-log plot of

2^{s}

(red),

| N_{ngr} |

(green), and

| N_{exc} |

(blue). (b) Fractions of

| N_{ngr} |

(green) and

| N_{exc} |

(blue) to

2^{s}

, showing the deflection point for

s = 6

(see text for details).

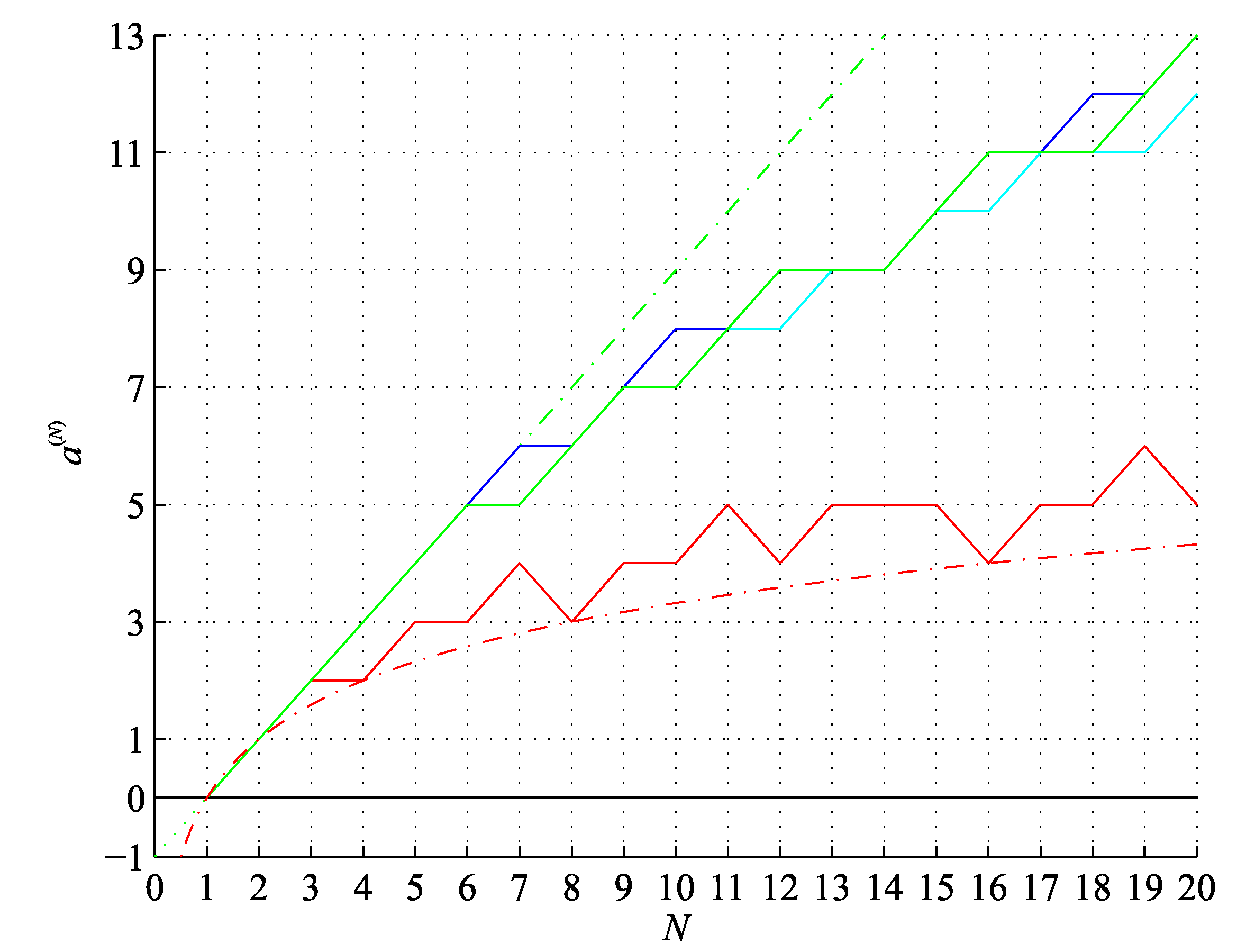
Figure 4. Lower bound on the bitstring assembly index 2 (red) and

{log}_{2} (N)

(red, dash-dot), conjectured upper bound on the bitstring assembly index 1 (green), factual values of the bitstring assembly index (blue) and the ringed bitstring assembly index (cyan) and

N - 1

(green, dash-dot), for the bitstring length

0 \leq N \leq 20

Figure 4. Lower bound on the bitstring assembly index 2 (red) and

{log}_{2} (N)

(red, dash-dot), conjectured upper bound on the bitstring assembly index 1 (green), factual values of the bitstring assembly index (blue) and the ringed bitstring assembly index (cyan) and

N - 1

(green, dash-dot), for the bitstring length

0 \leq N \leq 20

Figure 5. Lower bound on the bitstring assembly index (red),

{log}_{2} (N)

(red, dash-dot), general rule

a_{\min}^{({2^{s}, \hat{N}, \tilde{N}})} = {s, s + 1, s + 2}

(cyan), and OEIS A014701 (yellow); conjectured upper bound on the bitstring assembly index (green) and

N - 1

(green, dash-dot); and assembly indices of

C_{non - \min}^{(N)}

bitstrings assembled by trivial assembling programs (blue); for the bitstring length

0 \leq N \leq 100

(see text for details).

Figure 5. Lower bound on the bitstring assembly index (red),

{log}_{2} (N)

(red, dash-dot), general rule

a_{\min}^{({2^{s}, \hat{N}, \tilde{N}})} = {s, s + 1, s + 2}

(cyan), and OEIS A014701 (yellow); conjectured upper bound on the bitstring assembly index (green) and

N - 1

(green, dash-dot); and assembly indices of

C_{non - \min}^{(N)}

bitstrings assembled by trivial assembling programs (blue); for the bitstring length

0 \leq N \leq 100

(see text for details).

Figure 6. An illustrative graph of complexity against information capacity: orange regions are impossible, as they are above or below the assembly index general bounds, yellow region indicates the bitstring assembly index bounds, green region contains structures that can be assembled by dissipative structures of nature, red region contains structures that can only be assembled by humans, blue circles and dots denote, respectively, the number of steps of suboptimally assembled bitstrings and their assembly indices, blue slanting and vertical lines denote, respectively, creative and optimization paths of evolution of information (figure not to scale; see text for details).

Table 1. Distribution of the assembly indices for

N = 4

Table 1. Distribution of the assembly indices for

N = 4

		$N_{1}$
$a^{(4)} (C)$	$\| a^{(4)} (C) \|$	0	1	2	3	4
2	4	1		2		1
3	12		4	4	4
16		1	4	$\| B^{(4)} \| = 6$	4	1

Table 2.

| B^{(4)} | = 6

balanced bitstrings

B_{k}^{(4)}

Table 2.

| B^{(4)} | = 6

balanced bitstrings

B_{k}^{(4)}

k	$B_{k}^{(4)}$				$a^{(4)} (B_{k})$
1	(0	1)	(0	1)	2
2	(1	0)	(1	0)	2
3	0	1	1	0	3
4	1	1	0	0	3
5	1	0	0	1	3
6	0	0	1	1	3

Table 3. Bitstring length N, number of all bitstrings

2^{N}

, number of balanced bitstrings

B_{k}^{(N)}

, number of ringed bitstrings

R_{k}^{(N)}

, and number of balanced ringed bitstrings

E_{k}^{(N)}

Table 3. Bitstring length N, number of all bitstrings

2^{N}

, number of balanced bitstrings

B_{k}^{(N)}

, number of ringed bitstrings

R_{k}^{(N)}

, and number of balanced ringed bitstrings

E_{k}^{(N)}

N	$2^{N}$	$\| B_{k}^{(N)} \|$	$\| R_{k}^{(N)} \|$	$\| E_{k}^{(N)} \|$	$\| B_{k}^{(N)} \| / \| E_{k}^{(N)} \|$
1	2	1	2	1	1
2	4	2	3	1	2
3	8	3	4	1	3
4	16	6	6	2	3
5	32	10	8	2	5
6	64	20	14	4	5
7	128	35	20	5	7
8	256	70	36	10	7
9	512	126	60	14	9
10	1024	252	108	26	$9.6923 \dots$
11	2048	462	188	42	11
12	4096	924	352	80	11.55
13	8192	1716	632	132	13
14	16384	3432	1182	246	$13.9512 \dots$
15	32768	6435	2192	429	15

Table 4. Distribution of assembly indices among balanced ringed bitstrings

E^{(N)}

for

4 \leq N \leq 11

Table 4. Distribution of assembly indices among balanced ringed bitstrings

E^{(N)}

for

4 \leq N \leq 11

N	$\| E^{(N)} \|$	$a^{(N)} = 2$	$a^{(N)} = 3$	$a^{(N)} = 4$	$a^{(N)} = 5$	$a^{(N)} = 6$	$a^{(N)} = 7$	$a^{(N)} = 8$
4	2	1	1
5	2		1	1
6	4		1	2	1
7	5			2	3
8	10		1	1	6	2
9	14			1	4	7	2
10	26			1	6	9	10
11	42				2	14	20	6

Table 5. The lower bound on the bitstring assembly index (OEIS A003313).

N	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
$a_{\min}^{(N)}$	0	1	2	2	3	3	4	3	4	4	5	4	5	5	5	4	5	5	6	5	6

Table 6. List of the shortest addition chain sequence generating factors for

1 \leq s \leq 5

Table 6. List of the shortest addition chain sequence generating factors for

1 \leq s \leq 5

s	$2^{s}$	The shortest addition chain sequence generating factors
1	2	$1_{1}$
2	4	$1_{2}$	$3_{1}$
3	8	$1_{3}$	$3_{2}$	$5_{1}$	$7_{1}$
4	16	$1_{4}$	$3_{3}$	$5_{2}$	$7_{2}$	$9_{1}$	$11_{1}$	$13_{1}$	$15_{1}$
5	32	$1_{5}$	$3_{4}$	$5_{3}$	$7_{3}$	$9_{2}$	$11_{2}$	$13_{2}$	$15_{2}$	$17_{1}$	$19_{1}$	$21_{1}$	$23_{1}$	$25_{1}$	$27_{1}$	$29_{1}$	$31_{1}$

Table 7. Number of exceptional

a_{\min}^{(N_{exc})}

values

| N_{exc} |

, and the number

| N_{ngr} |

a_{\min}^{(N_{ngr})}

not generated by general rules for

0 \leq s \leq 15

Table 7. Number of exceptional

a_{\min}^{(N_{exc})}

values

| N_{exc} |

, and the number

| N_{ngr} |

a_{\min}^{(N_{ngr})}

not generated by general rules for

0 \leq s \leq 15

s	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
$\| N_{exc} \|$	0	0	0	0	2	9	30	80	193	432	925	1928	3953	8024	16189	32544
$2^{s}$	1	2	4	8	16	32	64	128	256	512	1024	2048	4096	8192	16384	32768
$\| N_{ngr} \|$	0	0	0	1	7	21	51	113	239	493	1003	2025	4071	8165	16355	32737
$min (m_{k})$					13	13	7	7	7	7	7	7	7	7	7	7

Table 8. Exemplary balanced bitstrings

B_{\max}^{(N)}

that have a largest assembly index. Conjectured (

a_{conj}^{(N)}

) form of the largest assembly index and its factual values for ringed (

a_{rng}^{(N)}

) and non-ringed (

a_{nrng}^{(N)}

) bitstrings (red if below the conjectured value, green if above).

Table 8. Exemplary balanced bitstrings

B_{\max}^{(N)}

that have a largest assembly index. Conjectured (

a_{conj}^{(N)}

) form of the largest assembly index and its factual values for ringed (

a_{rng}^{(N)}

) and non-ringed (

a_{nrng}^{(N)}

) bitstrings (red if below the conjectured value, green if above).

N	$B_{\max}^{(N)}$																				$a_{conj}^{(N)}$	$a_{rng}^{(N)}$	$a_{nrng}^{(N)}$
1	0																				0	0	0
2	1	0																			1	1	1
3	0	0	1																		2	2	2
4	0	0	1	1																	3	3	3
5	0	0	0	1	1																4	4	4
6	0	0	0	1	1	1															5	5	5
7	0	0	1	1	1	0	0														5	5	6
8	0	0	0	1	0	1	1	1													6	6	6
9	0	0	0	0	1	1	1	0	1												7	7	7
10	0	0	0	0	1	1	1	1	0	1											7	7	8
11	0	0	0	0	0	1	0	1	1	1	1										8	8	8
12	1	1	1	0	0	0	1	0	1	1	0	0									9	8	8
13	0	0	0	0	0	0	1	0	1	1	1	1	1								9	9	9
14	0	0	0	0	0	1	0	1	0	1	1	1	1	1							9	9	9
15	0	0	0	0	0	1	0	1	0	1	1	1	1	1	0						10	10	10
16	1	0	0	0	0	0	0	1	0	1	0	1	1	1	1	1					11	10	10
17	0	0	0	0	0	0	1	0	1	0	1	1	1	1	1	1	0				11	11	11
18	1	0	0	1	1	1	1	1	0	1	1	0	0	0	0	0	1	0			11	11	12
19	1	0	0	0	0	1	0	1	0	1	0	0	1	1	1	1	1	0	1		12	11	12
20	1	0	1	0	0	1	1	1	1	1	0	1	1	0	0	0	0	0	1	0	13	12	13

Table 9. 3-bit elegant programs assembling bitstrings with

a^{(N)} = 3

Table 9. 3-bit elegant programs assembling bitstrings with

a^{(N)} = 3

Q	$C (s = 1)$	$C (s = 2)$	$C (s_{Q} = 3)$	N
$* 11$	$* 0$	$0 * 0$	$* 00 * 0$	5
$* 10$	$* 0$	$0 * 0$	$0 * 00 * 0$	6
$* 01$	$* 0$	$* 0 * 0$	$* 0 * 0 * 0$	6
$* 00$	$* 0$	$* 0 * 0$	$* 0 * 0 * 0 * 0$	8

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

797

Views

363

Comments

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

k	$B_{k}^{(5)}$					$a^{(5)} (B_{k})$
1	0	(0	1)	(0	1)	3
2	(0	1)	0	(0	1)	3
3	(0	1)	(0	1)	0	3
4	(1	0)	0	(1	0)	3
5	(1	0)	(1	0)	0	3
6	0	0	0	1	1	4
7	0	0	1	1	0	4
8	0	1	1	0	0	4
9	1	0	0	0	1	4
10	1	1	0	0	0	4

k	$B_{k}^{(6)}$						$a^{(6)} (B_{k})$
1	(0	1)	(0	1)	(0	1)	3
2	(1	0)	(1	0)	(1	0)	3
3	0	(0	1)	(0	1)	1	4
4	0	(0	1)	1	(0	1)	4
5	(0	1)	0	(0	1)	1	4
6	(0	1)	(0	1)	1	0	4
7	(0	1)	1	0	(0	1)	4
8	(0	1)	1	(0	1)	0	4
9	(1	0)	0	(1	0)	1	4
10	(1	0)	0	1	(1	0)	4
11	(1	0)	(1	0)	0	1	4
12	(1	0)	1	(1	0)	0	4
13	1	(1	0)	0	(1	0)	4
14	1	(1	0)	(1	0)	0	4
15	0	0	1	1	1	0	5
16	0	0	0	1	1	1	5
17	0	1	1	1	0	0	5
18	1	0	0	0	1	1	5
19	1	1	0	0	0	1	5
20	1	1	1	0	0	0	5

k	$B_{k}^{(7)}$							$a^{(7)} (B_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
2	(0	1)	(0	1)	(0	1)	0	4
3	(1	0)	(1	0)	(1	0)	0	4
4	(0	1)	(0	1)	0	(0	1)	4
5	(1	0)	(1	0)	0	(1	0)	4
6	(0	1)	0	(0	1)	(0	1)	4
7	(1	0)	0	(1	0)	(1	0)	4
8	(1	0	0)	(1	0	0)	1	4
9	(1	0	0)	1	(1	0	0)	4
10	1	(1	0	0)	(1	0	0)	4
11	(0	0	1)	1	(0	0	1)	4
12	(0	0	1)	(0	0	1)	1	4
13	1	(0	0)	(0	0)	1	1	5
14	1	0	0	(0	1)	(0	1)	5
15	(1	0)	0	0	1	(1	0)	5
16	(1	0)	(1	0)	0	0	1	5
17	(1	0)	1	(1	0)	0	0	5
18	1	1	(0	0)	(0	0)	1	5
19	1	(1	0)	(1	0)	0	0	5
20	1	1	1	(0	0)	(0	0)	5
21	(0	1)	(0	1)	1	0	0	5
22	(0	1)	1	0	0	(0	1)	5
23	(0	1)	1	0	(0	1)	0	5
24	(0	1)	1	(0	1)	0	0	5
25	(0	1)	0	(0	1)	1	0	5
26	0	(0	1)	(0	1)	1	0	5
27	0	(0	1)	1	(0	1)	0	5
28	(0	0)	1	1	1	(0	0)	5
29	(0	1)	0	0	(0	1)	1	5
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5
33	1	(1	0)	0	0	(1	0)	5
34	0	0	0	1	1	1	0	6
35	0	1	1	1	0	0	0	6

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
2	((1	0)	(1	0))	((1	0)	(1	0))	3
3	((0	0)	(1	1))	((0	0)	(1	1))	4
4	((0	1)	(1	0))	((0	1)	(1	0))	4
5	((1	0)	(0	1))	((1	0)	(0	1))	4
6	((1	1)	(0	0))	((1	1)	(0	0))	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	(0	0	1)	(0	0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
12	(0	0	1)	1	1	(0	0	1)	5
13	(0	0)	(1	1)	(1	1)	(0	0)	5
14	(0	1)	0	(0	1)	(0	1)	1	5
15	(0	1)	0	(0	1)	1	(0	1)	5
16	(0	1)	(0	1)	0	(0	1)	1	5
17	(0	1)	(0	1)	(0	1)	1	0	5
18	(0	1)	(0	1)	1	0	(0	1)	5
19	(0	1)	(0	1)	1	(0	1)	0	5
20	(0	1	1)	0	0	(0	1	1)	5
21	(0	1)	1	0	(0	1)	(0	1)	5
22	(0	1)	1	(0	1)	0	(0	1)	5
23	(0	1)	1	(0	1)	(0	1)	0	5
24	(0	1	1)	(0	1	1)	0	0	5
25	(1	0	0)	(1	0	0)	1	1	5
26	1	0	(0	1)	(0	1)	(0	1)	5
27	(1	0)	0	(1	0)	1	(1	0)	5
28	(1	0)	0	1	(1	0)	(1	0)	5
29	(1	0	0)	1	1	(1	0	0)	5
30	(1	0	1)	0	0	(1	0	1)	5
31	(1	0)	(1	0)	0	1	(1	0)	5
32	(1	0)	(1	0)	(1	0)	0	1	5
33	(1	0)	(1	0)	1	(1	0)	0	5
34	(1	0)	1	(1	0)	0	(1	0)	5
35	(1	0)	1	(1	0)	(1	0)	0	5
36	(1	1)	(0	0)	(0	0)	(1	1)	5
37	(1	1	0)	0	0	(1	1	0)	5
38	1	1	(0	0	1)	(0	0	1)	5
39	1	1	0	0	1	0	1	0	5
40	1	(1	0)	(1	0)	0	(1	0)	5
41	(1	1	0)	(1	1	0)	0	0	5
42	1	1	0	1	0	1	0	0	5
43	1	1	(1	0	0)	(1	0	0)	5
44	(1	1)	(1	1)	(0	0)	(0	0)	5
45	0	0	(0	1	1)	(0	1	1)	5
46	0	(0	1	1)	(0	1	1)	0	5

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
47	0	0	(0	1)	(0	1)	1	1	6
48	0	0	(0	1)	1	1	(0	1)	6
49	0	0	0	(1	1)	(1	1)	0	6
50	0	(0	1)	(0	1)	1	1	0	6
51	0	0	1	1	(1	0)	(1	0)	6
52	(0	1)	0	0	(0	1)	1	1	6
53	(0	1)	0	(0	1)	1	1	0	6
54	(0	1)	(0	1)	1	1	0	0	6
55	(0	1)	1	1	0	0	(0	1)	6
56	(0	1)	1	1	0	(0	1)	0	6
57	(0	1)	1	1	(0	1)	0	0	6
58	0	(1	1)	(1	1)	0	0	0	6
59	1	(0	0)	(0	0)	1	1	1	6
60	(1	0)	0	0	(1	0)	1	1	6
61	1	0	0	(0	1)	1	(0	1)	6
62	(1	0)	0	0	1	1	(1	0)	6
63	(1	0)	(1	0)	0	0	1	1	6
64	(1	0)	1	(1	0)	0	0	1	6
65	(1	0)	1	1	(1	0)	0	0	6
66	1	(1	0)	0	0	(1	0)	1	6
67	1	1	(0	1)	0	0	(0	1)	6
68	1	1	1	(0	0)	(0	0)	1	6
69	1	1	(1	0)	0	0	(1	0)	6
70	1	1	(1	0)	(1	0)	0	0	6

k	$E_{k}^{(7)}$							$a^{(7)} (E_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
12	(0	0	1)	(0	0	1)	1	4
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5

k	$E_{k}^{(8)}$								$a^{(8)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
3	(0	0)	(1	1)	(0	0)	(1	1)	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	0	(0	1)	0	(0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
46	0	0	(0	1	1)	(0	1	1)	5
45	0	0	(0	1)	(0	1)	1	1	6
47	0	0	(0	1)	1	1	(0	1)	6

k	$E_{k}^{(9)}$									$a^{(9)} (E_{k})$
1	0	((0	1)	(0	1))	((0	1)	(0	1))	4
2	0	((0	0)	(1	1))	((0	0)	(1	1))	5
3	(0	(0	1))	(0	1)	(0	0	1)	1	5
4	(0	(0	1))	(0	0	1)	1	(0	1)	5
5	(0	(0	1))	(0	0	1)	(0	1)	1	5
6	0	(0	0	1)	1	1	(0	0	1)	6
7	0	0	(0	1)	1	(0	1)	(0	1)	6
8	0	0	(0	1)	(0	1)	1	(0	1)	6
9	0	0	(0	1)	(0	1)	(0	1)	1	6
10	0	(0	0	1)	(0	0	1)	1	1	6
11	(0	0)	(0	0)	(1	1)	0	(1	1)	6
12	0	(0	0)	(0	0)	(1	1)	(1	1)	6
13	(0	0)	(0	0)	1	1	1	0	1	7
14	(0	0)	(0	0)	1	0	1	1	1	7

k	$E_{k}^{(10)}$										$a^{(10)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	(0	1)	4
2	0	((0	1)	(0	1))	((0	1)	(0	1))	1	5
3	(0	1)	(1	(0	1)	0)	(1	(0	1)	0)	5
4	(0	(0	1)	1)	(0	0	1	1)	(0	1)	5
5	0	((0	1)	0	1)	1	(0	1	0	1)	5
6	0	((1	0)	1	0)	1	(1	0	1	0)	5
7	(0	1)	((0	1)	1	0)	(0	1	1	0)	5
8	(0	(0	1))	(0	1)	(0	0	1)	1	1	6
9	(0	(0	1))	(0	0	1)	1	1	(0	1)	6
10	(0	(0	1))	(0	0	1)	1	(0	1)	1	6
11	(0	(0	1))	(0	0	1)	(0	1)	1	1	6
14	0	(0	0	1	1)	1	(0	0	1	1)	6
15	0	0	((0	1)	1)	(0	1	1)	(0	1)	6
16	0	0	((0	1)	1)	(0	1)	(0	1	1)	6
17	0	(0	0	1	1)	(0	0	1	1)	1	6
19	0	0	(0	1)	((0	1)	1)	(0	1	1)	6
12	(0	0)	0	(1	1)	(1	1)	(0	0)	1	7
13	0	0	(0	1)	1	1	(0	1)	(0	1)	7
18	0	0	(0	1)	(0	1)	1	1	(0	1)	7
20	0	0	(0	1)	(0	1)	(0	1)	1	1	7
21	(0	0)	0	1	(0	0)	(1	1)	(1	1)	7
22	(0	0)	(0	0)	(1	1)	(1	1)	0	1	7
23	(0	0)	(0	0)	(1	1)	1	0	(1	1)	7
24	(0	0)	(0	0)	(1	1)	0	(1	1)	1	7
25	(0	0)	(0	0)	1	0	(1	1)	(1	1)	7
26	(0	0)	(0	0)	0	1	(1	1)	(1	1)	7

k	$E_{k}^{(11)}$											$a^{(11)} (E_{k})$
1	0	(0	1)	((0	1))	(0	1))	(0	1	0	1)	5
2	(0	(0	1)	(0	1))	(0	0	1	0	1)	1	5
3	(0	0)	((0	0)	1	1)	(1	0	0	1	1)	6
4	(0	(0	1))	(0	1)	(0	1)	(0	0	1)	1	6
5	(0	0)	(0	0)	(0	0)	(1	1)	(1	1)	1	7
6	(0	0)	(1	1	0)	1	(0	0)	(1	1	0)	7
7	(0	0)	(0	0)	(0	1)	(0	1)	1	1	1	8

k	$B_{k}^{(5)}$					$a^{(5)} (B_{k})$
1	0	(0	1)	(0	1)	3
2	(0	1)	0	(0	1)	3
3	(0	1)	(0	1)	0	3
4	(1	0)	0	(1	0)	3
5	(1	0)	(1	0)	0	3
6	0	0	0	1	1	4
7	0	0	1	1	0	4
8	0	1	1	0	0	4
9	1	0	0	0	1	4
10	1	1	0	0	0	4

k	$B_{k}^{(6)}$						$a^{(6)} (B_{k})$
1	(0	1)	(0	1)	(0	1)	3
2	(1	0)	(1	0)	(1	0)	3
3	0	(0	1)	(0	1)	1	4
4	0	(0	1)	1	(0	1)	4
5	(0	1)	0	(0	1)	1	4
6	(0	1)	(0	1)	1	0	4
7	(0	1)	1	0	(0	1)	4
8	(0	1)	1	(0	1)	0	4
9	(1	0)	0	(1	0)	1	4
10	(1	0)	0	1	(1	0)	4
11	(1	0)	(1	0)	0	1	4
12	(1	0)	1	(1	0)	0	4
13	1	(1	0)	0	(1	0)	4
14	1	(1	0)	(1	0)	0	4
15	0	0	1	1	1	0	5
16	0	0	0	1	1	1	5
17	0	1	1	1	0	0	5
18	1	0	0	0	1	1	5
19	1	1	0	0	0	1	5
20	1	1	1	0	0	0	5

k	$B_{k}^{(7)}$							$a^{(7)} (B_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
2	(0	1)	(0	1)	(0	1)	0	4
3	(1	0)	(1	0)	(1	0)	0	4
4	(0	1)	(0	1)	0	(0	1)	4
5	(1	0)	(1	0)	0	(1	0)	4
6	(0	1)	0	(0	1)	(0	1)	4
7	(1	0)	0	(1	0)	(1	0)	4
8	(1	0	0)	(1	0	0)	1	4
9	(1	0	0)	1	(1	0	0)	4
10	1	(1	0	0)	(1	0	0)	4
11	(0	0	1)	1	(0	0	1)	4
12	(0	0	1)	(0	0	1)	1	4
13	1	(0	0)	(0	0)	1	1	5
14	1	0	0	(0	1)	(0	1)	5
15	(1	0)	0	0	1	(1	0)	5
16	(1	0)	(1	0)	0	0	1	5
17	(1	0)	1	(1	0)	0	0	5
18	1	1	(0	0)	(0	0)	1	5
19	1	(1	0)	(1	0)	0	0	5
20	1	1	1	(0	0)	(0	0)	5
21	(0	1)	(0	1)	1	0	0	5
22	(0	1)	1	0	0	(0	1)	5
23	(0	1)	1	0	(0	1)	0	5
24	(0	1)	1	(0	1)	0	0	5
25	(0	1)	0	(0	1)	1	0	5
26	0	(0	1)	(0	1)	1	0	5
27	0	(0	1)	1	(0	1)	0	5
28	(0	0)	1	1	1	(0	0)	5
29	(0	1)	0	0	(0	1)	1	5
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5
33	1	(1	0)	0	0	(1	0)	5
34	0	0	0	1	1	1	0	6
35	0	1	1	1	0	0	0	6

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
2	((1	0)	(1	0))	((1	0)	(1	0))	3
3	((0	0)	(1	1))	((0	0)	(1	1))	4
4	((0	1)	(1	0))	((0	1)	(1	0))	4
5	((1	0)	(0	1))	((1	0)	(0	1))	4
6	((1	1)	(0	0))	((1	1)	(0	0))	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	(0	0	1)	(0	0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
12	(0	0	1)	1	1	(0	0	1)	5
13	(0	0)	(1	1)	(1	1)	(0	0)	5
14	(0	1)	0	(0	1)	(0	1)	1	5
15	(0	1)	0	(0	1)	1	(0	1)	5
16	(0	1)	(0	1)	0	(0	1)	1	5
17	(0	1)	(0	1)	(0	1)	1	0	5
18	(0	1)	(0	1)	1	0	(0	1)	5
19	(0	1)	(0	1)	1	(0	1)	0	5
20	(0	1	1)	0	0	(0	1	1)	5
21	(0	1)	1	0	(0	1)	(0	1)	5
22	(0	1)	1	(0	1)	0	(0	1)	5
23	(0	1)	1	(0	1)	(0	1)	0	5
24	(0	1	1)	(0	1	1)	0	0	5
25	(1	0	0)	(1	0	0)	1	1	5
26	1	0	(0	1)	(0	1)	(0	1)	5
27	(1	0)	0	(1	0)	1	(1	0)	5
28	(1	0)	0	1	(1	0)	(1	0)	5
29	(1	0	0)	1	1	(1	0	0)	5
30	(1	0	1)	0	0	(1	0	1)	5
31	(1	0)	(1	0)	0	1	(1	0)	5
32	(1	0)	(1	0)	(1	0)	0	1	5
33	(1	0)	(1	0)	1	(1	0)	0	5
34	(1	0)	1	(1	0)	0	(1	0)	5
35	(1	0)	1	(1	0)	(1	0)	0	5
36	(1	1)	(0	0)	(0	0)	(1	1)	5
37	(1	1	0)	0	0	(1	1	0)	5
38	1	1	(0	0	1)	(0	0	1)	5
39	1	1	0	0	1	0	1	0	5
40	1	(1	0)	(1	0)	0	(1	0)	5
41	(1	1	0)	(1	1	0)	0	0	5
42	1	1	0	1	0	1	0	0	5
43	1	1	(1	0	0)	(1	0	0)	5
44	(1	1)	(1	1)	(0	0)	(0	0)	5
45	0	0	(0	1	1)	(0	1	1)	5
46	0	(0	1	1)	(0	1	1)	0	5

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
47	0	0	(0	1)	(0	1)	1	1	6
48	0	0	(0	1)	1	1	(0	1)	6
49	0	0	0	(1	1)	(1	1)	0	6
50	0	(0	1)	(0	1)	1	1	0	6
51	0	0	1	1	(1	0)	(1	0)	6
52	(0	1)	0	0	(0	1)	1	1	6
53	(0	1)	0	(0	1)	1	1	0	6
54	(0	1)	(0	1)	1	1	0	0	6
55	(0	1)	1	1	0	0	(0	1)	6
56	(0	1)	1	1	0	(0	1)	0	6
57	(0	1)	1	1	(0	1)	0	0	6
58	0	(1	1)	(1	1)	0	0	0	6
59	1	(0	0)	(0	0)	1	1	1	6
60	(1	0)	0	0	(1	0)	1	1	6
61	1	0	0	(0	1)	1	(0	1)	6
62	(1	0)	0	0	1	1	(1	0)	6
63	(1	0)	(1	0)	0	0	1	1	6
64	(1	0)	1	(1	0)	0	0	1	6
65	(1	0)	1	1	(1	0)	0	0	6
66	1	(1	0)	0	0	(1	0)	1	6
67	1	1	(0	1)	0	0	(0	1)	6
68	1	1	1	(0	0)	(0	0)	1	6
69	1	1	(1	0)	0	0	(1	0)	6
70	1	1	(1	0)	(1	0)	0	0	6

k	$E_{k}^{(7)}$							$a^{(7)} (E_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
12	(0	0	1)	(0	0	1)	1	4
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5

k	$E_{k}^{(8)}$								$a^{(8)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
3	(0	0)	(1	1)	(0	0)	(1	1)	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	0	(0	1)	0	(0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
46	0	0	(0	1	1)	(0	1	1)	5
45	0	0	(0	1)	(0	1)	1	1	6
47	0	0	(0	1)	1	1	(0	1)	6

k	$E_{k}^{(9)}$									$a^{(9)} (E_{k})$
1	0	((0	1)	(0	1))	((0	1)	(0	1))	4
2	0	((0	0)	(1	1))	((0	0)	(1	1))	5
3	(0	(0	1))	(0	1)	(0	0	1)	1	5
4	(0	(0	1))	(0	0	1)	1	(0	1)	5
5	(0	(0	1))	(0	0	1)	(0	1)	1	5
6	0	(0	0	1)	1	1	(0	0	1)	6
7	0	0	(0	1)	1	(0	1)	(0	1)	6
8	0	0	(0	1)	(0	1)	1	(0	1)	6
9	0	0	(0	1)	(0	1)	(0	1)	1	6
10	0	(0	0	1)	(0	0	1)	1	1	6
11	(0	0)	(0	0)	(1	1)	0	(1	1)	6
12	0	(0	0)	(0	0)	(1	1)	(1	1)	6
13	(0	0)	(0	0)	1	1	1	0	1	7
14	(0	0)	(0	0)	1	0	1	1	1	7

k	$E_{k}^{(10)}$										$a^{(10)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	(0	1)	4
2	0	((0	1)	(0	1))	((0	1)	(0	1))	1	5
3	(0	1)	(1	(0	1)	0)	(1	(0	1)	0)	5
4	(0	(0	1)	1)	(0	0	1	1)	(0	1)	5
5	0	((0	1)	0	1)	1	(0	1	0	1)	5
6	0	((1	0)	1	0)	1	(1	0	1	0)	5
7	(0	1)	((0	1)	1	0)	(0	1	1	0)	5
8	(0	(0	1))	(0	1)	(0	0	1)	1	1	6
9	(0	(0	1))	(0	0	1)	1	1	(0	1)	6
10	(0	(0	1))	(0	0	1)	1	(0	1)	1	6
11	(0	(0	1))	(0	0	1)	(0	1)	1	1	6
14	0	(0	0	1	1)	1	(0	0	1	1)	6
15	0	0	((0	1)	1)	(0	1	1)	(0	1)	6
16	0	0	((0	1)	1)	(0	1)	(0	1	1)	6
17	0	(0	0	1	1)	(0	0	1	1)	1	6
19	0	0	(0	1)	((0	1)	1)	(0	1	1)	6
12	(0	0)	0	(1	1)	(1	1)	(0	0)	1	7
13	0	0	(0	1)	1	1	(0	1)	(0	1)	7
18	0	0	(0	1)	(0	1)	1	1	(0	1)	7
20	0	0	(0	1)	(0	1)	(0	1)	1	1	7
21	(0	0)	0	1	(0	0)	(1	1)	(1	1)	7
22	(0	0)	(0	0)	(1	1)	(1	1)	0	1	7
23	(0	0)	(0	0)	(1	1)	1	0	(1	1)	7
24	(0	0)	(0	0)	(1	1)	0	(1	1)	1	7
25	(0	0)	(0	0)	1	0	(1	1)	(1	1)	7
26	(0	0)	(0	0)	0	1	(1	1)	(1	1)	7

k	$E_{k}^{(11)}$											$a^{(11)} (E_{k})$
1	0	(0	1)	((0	1))	(0	1))	(0	1	0	1)	5
2	(0	(0	1)	(0	1))	(0	0	1	0	1)	1	5
3	(0	0)	((0	0)	1	1)	(1	0	0	1	1)	6
4	(0	(0	1))	(0	1)	(0	1)	(0	0	1)	1	6
5	(0	0)	(0	0)	(0	0)	(1	1)	(1	1)	1	7
6	(0	0)	(1	1	0)	1	(0	0)	(1	1	0)	7
7	(0	0)	(0	0)	(0	1)	(0	1)	1	1	1	8

Assembly Theory of Binary Messages

Abstract

Keywords:

Subject:

1. Introduction

2. Preliminaries

3. Minimum Bitstring Assembly Index

4. Degree of Causation for Minimum Assembly Index Bitstrings

5. Maximum Bitstring Assembly Index

6. Binputation

7. Discussion and Conclusions

Author Contributions

Data Availability Statement

Acknowledgments

Abbreviations

Appendix A. Exemplary Maximal Assembly Index Bitstrings

Appendix B. Trivial Assembling Programs

Appendix C. Bitstrings and Their Assembly Indices

Notes

References

MDPI Initiatives

Important Links

Subscribe

k	$B_{k}^{(5)}$					$a^{(5)} (B_{k})$
1	0	(0	1)	(0	1)	3
2	(0	1)	0	(0	1)	3
3	(0	1)	(0	1)	0	3
4	(1	0)	0	(1	0)	3
5	(1	0)	(1	0)	0	3
6	0	0	0	1	1	4
7	0	0	1	1	0	4
8	0	1	1	0	0	4
9	1	0	0	0	1	4
10	1	1	0	0	0	4

k	$B_{k}^{(6)}$						$a^{(6)} (B_{k})$
1	(0	1)	(0	1)	(0	1)	3
2	(1	0)	(1	0)	(1	0)	3
3	0	(0	1)	(0	1)	1	4
4	0	(0	1)	1	(0	1)	4
5	(0	1)	0	(0	1)	1	4
6	(0	1)	(0	1)	1	0	4
7	(0	1)	1	0	(0	1)	4
8	(0	1)	1	(0	1)	0	4
9	(1	0)	0	(1	0)	1	4
10	(1	0)	0	1	(1	0)	4
11	(1	0)	(1	0)	0	1	4
12	(1	0)	1	(1	0)	0	4
13	1	(1	0)	0	(1	0)	4
14	1	(1	0)	(1	0)	0	4
15	0	0	1	1	1	0	5
16	0	0	0	1	1	1	5
17	0	1	1	1	0	0	5
18	1	0	0	0	1	1	5
19	1	1	0	0	0	1	5
20	1	1	1	0	0	0	5

k	$B_{k}^{(7)}$							$a^{(7)} (B_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
2	(0	1)	(0	1)	(0	1)	0	4
3	(1	0)	(1	0)	(1	0)	0	4
4	(0	1)	(0	1)	0	(0	1)	4
5	(1	0)	(1	0)	0	(1	0)	4
6	(0	1)	0	(0	1)	(0	1)	4
7	(1	0)	0	(1	0)	(1	0)	4
8	(1	0	0)	(1	0	0)	1	4
9	(1	0	0)	1	(1	0	0)	4
10	1	(1	0	0)	(1	0	0)	4
11	(0	0	1)	1	(0	0	1)	4
12	(0	0	1)	(0	0	1)	1	4
13	1	(0	0)	(0	0)	1	1	5
14	1	0	0	(0	1)	(0	1)	5
15	(1	0)	0	0	1	(1	0)	5
16	(1	0)	(1	0)	0	0	1	5
17	(1	0)	1	(1	0)	0	0	5
18	1	1	(0	0)	(0	0)	1	5
19	1	(1	0)	(1	0)	0	0	5
20	1	1	1	(0	0)	(0	0)	5
21	(0	1)	(0	1)	1	0	0	5
22	(0	1)	1	0	0	(0	1)	5
23	(0	1)	1	0	(0	1)	0	5
24	(0	1)	1	(0	1)	0	0	5
25	(0	1)	0	(0	1)	1	0	5
26	0	(0	1)	(0	1)	1	0	5
27	0	(0	1)	1	(0	1)	0	5
28	(0	0)	1	1	1	(0	0)	5
29	(0	1)	0	0	(0	1)	1	5
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5
33	1	(1	0)	0	0	(1	0)	5
34	0	0	0	1	1	1	0	6
35	0	1	1	1	0	0	0	6

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
2	((1	0)	(1	0))	((1	0)	(1	0))	3
3	((0	0)	(1	1))	((0	0)	(1	1))	4
4	((0	1)	(1	0))	((0	1)	(1	0))	4
5	((1	0)	(0	1))	((1	0)	(0	1))	4
6	((1	1)	(0	0))	((1	1)	(0	0))	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	(0	0	1)	(0	0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
12	(0	0	1)	1	1	(0	0	1)	5
13	(0	0)	(1	1)	(1	1)	(0	0)	5
14	(0	1)	0	(0	1)	(0	1)	1	5
15	(0	1)	0	(0	1)	1	(0	1)	5
16	(0	1)	(0	1)	0	(0	1)	1	5
17	(0	1)	(0	1)	(0	1)	1	0	5
18	(0	1)	(0	1)	1	0	(0	1)	5
19	(0	1)	(0	1)	1	(0	1)	0	5
20	(0	1	1)	0	0	(0	1	1)	5
21	(0	1)	1	0	(0	1)	(0	1)	5
22	(0	1)	1	(0	1)	0	(0	1)	5
23	(0	1)	1	(0	1)	(0	1)	0	5
24	(0	1	1)	(0	1	1)	0	0	5
25	(1	0	0)	(1	0	0)	1	1	5
26	1	0	(0	1)	(0	1)	(0	1)	5
27	(1	0)	0	(1	0)	1	(1	0)	5
28	(1	0)	0	1	(1	0)	(1	0)	5
29	(1	0	0)	1	1	(1	0	0)	5
30	(1	0	1)	0	0	(1	0	1)	5
31	(1	0)	(1	0)	0	1	(1	0)	5
32	(1	0)	(1	0)	(1	0)	0	1	5
33	(1	0)	(1	0)	1	(1	0)	0	5
34	(1	0)	1	(1	0)	0	(1	0)	5
35	(1	0)	1	(1	0)	(1	0)	0	5
36	(1	1)	(0	0)	(0	0)	(1	1)	5
37	(1	1	0)	0	0	(1	1	0)	5
38	1	1	(0	0	1)	(0	0	1)	5
39	1	1	0	0	1	0	1	0	5
40	1	(1	0)	(1	0)	0	(1	0)	5
41	(1	1	0)	(1	1	0)	0	0	5
42	1	1	0	1	0	1	0	0	5
43	1	1	(1	0	0)	(1	0	0)	5
44	(1	1)	(1	1)	(0	0)	(0	0)	5
45	0	0	(0	1	1)	(0	1	1)	5
46	0	(0	1	1)	(0	1	1)	0	5

k	$B_{k}^{(8)}$								$a^{(8)} (B_{k})$
47	0	0	(0	1)	(0	1)	1	1	6
48	0	0	(0	1)	1	1	(0	1)	6
49	0	0	0	(1	1)	(1	1)	0	6
50	0	(0	1)	(0	1)	1	1	0	6
51	0	0	1	1	(1	0)	(1	0)	6
52	(0	1)	0	0	(0	1)	1	1	6
53	(0	1)	0	(0	1)	1	1	0	6
54	(0	1)	(0	1)	1	1	0	0	6
55	(0	1)	1	1	0	0	(0	1)	6
56	(0	1)	1	1	0	(0	1)	0	6
57	(0	1)	1	1	(0	1)	0	0	6
58	0	(1	1)	(1	1)	0	0	0	6
59	1	(0	0)	(0	0)	1	1	1	6
60	(1	0)	0	0	(1	0)	1	1	6
61	1	0	0	(0	1)	1	(0	1)	6
62	(1	0)	0	0	1	1	(1	0)	6
63	(1	0)	(1	0)	0	0	1	1	6
64	(1	0)	1	(1	0)	0	0	1	6
65	(1	0)	1	1	(1	0)	0	0	6
66	1	(1	0)	0	0	(1	0)	1	6
67	1	1	(0	1)	0	0	(0	1)	6
68	1	1	1	(0	0)	(0	0)	1	6
69	1	1	(1	0)	0	0	(1	0)	6
70	1	1	(1	0)	(1	0)	0	0	6

k	$E_{k}^{(7)}$							$a^{(7)} (E_{k})$
1	0	(0	1)	(0	1)	(0	1)	4
12	(0	0	1)	(0	0	1)	1	4
30	(0	0)	(0	0)	1	1	1	5
31	0	0	(0	1)	(0	1)	1	5
32	0	0	(0	1)	1	(0	1)	5

k	$E_{k}^{(8)}$								$a^{(8)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	3
3	(0	0)	(1	1)	(0	0)	(1	1)	4
7	(0	0)	(0	0)	(1	1)	(1	1)	5
8	0	(0	1)	0	(0	1)	1	1	5
9	0	(0	1)	(0	1)	(0	1)	1	5
10	0	(0	1)	(0	1)	1	(0	1)	5
11	0	(0	1)	1	(0	1)	(0	1)	5
46	0	0	(0	1	1)	(0	1	1)	5
45	0	0	(0	1)	(0	1)	1	1	6
47	0	0	(0	1)	1	1	(0	1)	6

k	$E_{k}^{(9)}$									$a^{(9)} (E_{k})$
1	0	((0	1)	(0	1))	((0	1)	(0	1))	4
2	0	((0	0)	(1	1))	((0	0)	(1	1))	5
3	(0	(0	1))	(0	1)	(0	0	1)	1	5
4	(0	(0	1))	(0	0	1)	1	(0	1)	5
5	(0	(0	1))	(0	0	1)	(0	1)	1	5
6	0	(0	0	1)	1	1	(0	0	1)	6
7	0	0	(0	1)	1	(0	1)	(0	1)	6
8	0	0	(0	1)	(0	1)	1	(0	1)	6
9	0	0	(0	1)	(0	1)	(0	1)	1	6
10	0	(0	0	1)	(0	0	1)	1	1	6
11	(0	0)	(0	0)	(1	1)	0	(1	1)	6
12	0	(0	0)	(0	0)	(1	1)	(1	1)	6
13	(0	0)	(0	0)	1	1	1	0	1	7
14	(0	0)	(0	0)	1	0	1	1	1	7

k	$E_{k}^{(10)}$										$a^{(10)} (E_{k})$
1	((0	1)	(0	1))	((0	1)	(0	1))	(0	1)	4
2	0	((0	1)	(0	1))	((0	1)	(0	1))	1	5
3	(0	1)	(1	(0	1)	0)	(1	(0	1)	0)	5
4	(0	(0	1)	1)	(0	0	1	1)	(0	1)	5
5	0	((0	1)	0	1)	1	(0	1	0	1)	5
6	0	((1	0)	1	0)	1	(1	0	1	0)	5
7	(0	1)	((0	1)	1	0)	(0	1	1	0)	5
8	(0	(0	1))	(0	1)	(0	0	1)	1	1	6
9	(0	(0	1))	(0	0	1)	1	1	(0	1)	6
10	(0	(0	1))	(0	0	1)	1	(0	1)	1	6
11	(0	(0	1))	(0	0	1)	(0	1)	1	1	6
14	0	(0	0	1	1)	1	(0	0	1	1)	6
15	0	0	((0	1)	1)	(0	1	1)	(0	1)	6
16	0	0	((0	1)	1)	(0	1)	(0	1	1)	6
17	0	(0	0	1	1)	(0	0	1	1)	1	6
19	0	0	(0	1)	((0	1)	1)	(0	1	1)	6
12	(0	0)	0	(1	1)	(1	1)	(0	0)	1	7
13	0	0	(0	1)	1	1	(0	1)	(0	1)	7
18	0	0	(0	1)	(0	1)	1	1	(0	1)	7
20	0	0	(0	1)	(0	1)	(0	1)	1	1	7
21	(0	0)	0	1	(0	0)	(1	1)	(1	1)	7
22	(0	0)	(0	0)	(1	1)	(1	1)	0	1	7
23	(0	0)	(0	0)	(1	1)	1	0	(1	1)	7
24	(0	0)	(0	0)	(1	1)	0	(1	1)	1	7
25	(0	0)	(0	0)	1	0	(1	1)	(1	1)	7
26	(0	0)	(0	0)	0	1	(1	1)	(1	1)	7

k	$E_{k}^{(11)}$											$a^{(11)} (E_{k})$
1	0	(0	1)	((0	1))	(0	1))	(0	1	0	1)	5
2	(0	(0	1)	(0	1))	(0	0	1	0	1)	1	5
3	(0	0)	((0	0)	1	1)	(1	0	0	1	1)	6
4	(0	(0	1))	(0	1)	(0	1)	(0	0	1)	1	6
5	(0	0)	(0	0)	(0	0)	(1	1)	(1	1)	1	7
6	(0	0)	(1	1	0)	1	(0	0)	(1	1	0)	7
7	(0	0)	(0	0)	(0	1)	(0	1)	1	1	1	8