1. Introduction
Assembly Theory (AT) [
1,
2,
3,
4,
5,
6,
7] provides a distinctive complexity measure, superior to established complexity measures used in information theory, such as Shannon entropy or Kolmogorov complexity [
1,
5]. AT does not alter the fundamental laws of physics [
6]. Instead, it redefines
objects on which these laws operate. In AT,
objects are not considered as sets of point
particles (as in most physics), but instead are defined by the histories of their formation (assembly pathways) as an intrinsic property, where, in general, there are multiple assembly pathways to create a given
object.
AT explains and quantifies selection and evolution, capturing the amount of memory necessary to produce a given
object [
6]. This is because the more complex a given
object is, the less likely an identical copy can be observed without the selection of some information-driven mechanism that generated that
object. Formalizing assembly pathways as sequences of joining operations, AT begins with basic units (such as chemical bonds) and concludes with a final
object. This conceptual shift captures evidence of selection in
objects [
1,
2,
6].
The Assembly Index, which represents the length of the shortest assembly pathway leading to an
object, facilitates the quantification of the minimum memory required for its construction. In general, it increases with the
object’s size, but decreases with symmetry, so large
objects with repeating substructures may have lower complexity than smaller
objects with greater heterogeneity [
1]. The copy number specifies the number of copies of an
object, essential for assessing its structural complexity.
AT has been experimentally confirmed in the case of molecules and probed directly experimentally with high accuracy with spectroscopy techniques, including mass spectroscopy, IR, and NMR spectroscopy [
6]. It is a versatile concept with applications in various domains. Beyond its application in the field of biology and chemistry [
7], its adaptability to different data structures, such as text, graphs, groups, music notations, image files, compression algorithms, etc., showcases its potential in diverse fields [
2].
In this study, we investigate the assembly pathways of binary strings by joining individual bits present in the assembly pool [
6] and strings that entered the pool as a result of previous joining operations.
In particular, we investigate the assembly of black-body objects (BBs: black holes (BHs), white dwarfs, and neutron stars) considered binary strings [
8,
9,
10]. It is known [
2,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19] that information in the universe evolves toward increased structural complexity, decreasing information entropy.
We use emphasis for
object as this term, understood as a collection of
matter, is a misnomer, as it neglects the (quantum) nonlocality [
20]. Nonlocality is independent of the entanglement among
particles [
21], as well as the quantum contextuality [
22], and increases as the number of
particles [
23] grows [
24,
25]. Furthermore, the ugly duckling theorem [
26,
27] asserts that every two
objects we perceive are equally similar (or equally dissimilar).
This study extends the findings of previous research [
8,
9,
10,
23] within the framework of AT and emergent dimensionality [
8,
9,
10,
15,
17,
18,
20,
23,
28]. However, our results generally apply to information theory. Therefore, we put the BB-related content in frames like this one. The reader not interested in BBs may skip the text in these frames and the additional results presented in
Section 7.
The paper is structured as follows.
Section 2 introduces the basic definitions used in the paper.
Section 3 shows that the assembly index of binary strings is bounded from below and provides the form of this bound.
Section 4 shows that the assembly index of binary strings is bounded from above and conjectures about the exact form of this bound.
Section 6 introduces the concept of binary assembling program and shows that the trivial assembling program assembles binary strings that have a minimum assembly index.
Section 7 discusses additional results of this research in the context of BBs.
Section 8 concludes the findings of this study.
2. Preliminaries
For
K subunits of an
object O the assembly index
of AT is bounded [
1] from below by
and from above by
The lower bound (
1) represents the fact that the simplest way to increase the size of a subunit in a pathway is to take the largest subunit so far and join it to itself [
1] and, in the case of the upper bound (
2), subunits must be distinct so that they cannot be reused from the pool, decreasing the index.
Here we consider binary strings
containing bits
, which are our basis AT
objects [
2], with
zeros and
ones (
is called binary Hamming weight or bit summation of a string
.), having a fixed length
.
Where the bit value can be either 1 or 0, we write with * being the same within the string . If we allow for the 2nd possibility that can be the same as or different from *, we write . Thus, , for example, is a placeholder for all four 2-bit strings.
We consider strings to be
messages transmitted through a communication channel between a source and a receiver, similarly to the Claude Shannon approach [
29] used in the derivation of binary information entropy
where
are the ratios of occurrences of zeros and ones within the string
and the unit of entropy (
3) is bit.
Here, we consider the process of formation of binary strings within the AT framework.
Definition 1. A string assembly index is the smallest number of steps s required to assemble a binary string of length N by joining two distinct bits contained in the initial assembly pool and strings joined in previous steps that are added to the assembly pool. Therefore, the assembly index is a function of the string .
For example, the 8-bit string
can be assembled in at most seven steps:
- 1.
join 0 with 1 to form , adding to ,
- 3.
join with 0 to form , adding to ,
- 3.
...
- 7.
join with 1 to form
(i.e., not using the pool), six, five, or four steps:
join 0 with 1 to form , adding to P,
join with taken from P to form , adding to P,
join with taken from P to form , adding to P,
join with taken from P to form ,
or at least three steps:
join 0 with 1 to form , adding to P,
join with taken from P to form , adding to P,
join with taken from P to form ,
while the 8-bit string
can be assembled in at least six steps:
join 0 with 1 to form , adding to P,
join with taken from P to form , adding to P,
join 0 with 0 adding to P,
join with taken from P to form , adding to P,
join with 1 to form , adding to P,
join with 1 to form ,
as only the doublet
can be reused from the pool. Therefore, strings (
5) and (
6) have respective assembly indices
and
that represent the lengths of their shortest assembly pathways, which in turn ensures that the assembly pool
P is a distinct set.
Theorem 1. A string having length is the shortest string having more than one string assembly index 1.
Proof. The proof is trivial. For
the assembly index
, as all basis
objects have a pathway assembly index of 0 [
2] (they are not
assembled).
provides four available strings with
.
provides eight available strings with
. Only
provides 16 strings that include four stings with
and twelve strings with
including
balanced strings, as shown in
Table 1 and
Table 2.
For example, to assemble the string we need to assemble the string and reuse it. Therefore, for and for , where denotes a set of different assembly indices. □
Table 1.
Distribution of the assembly indices for .
Table 1.
Distribution of the assembly indices for .
| |
|
|
|
0 |
1 |
2 |
3 |
4 |
| 2 |
4 |
1 |
|
2 |
|
1 |
| 3 |
12 |
|
4 |
4 |
4 |
|
| 16 |
1 |
4 |
|
4 |
1 |
Table 2.
balanced strings .
Table 2.
balanced strings .
| k |
|
|
| 1 |
(0 |
1) |
(0 |
1) |
2 |
| 2 |
(1 |
0) |
(1 |
0) |
2 |
| 3 |
0 |
1 |
1 |
0 |
3 |
| 4 |
1 |
1 |
0 |
0 |
3 |
| 5 |
1 |
0 |
0 |
1 |
3 |
| 6 |
0 |
0 |
1 |
1 |
3 |
Interestingly, Theorem 1 strengthens the meaning of
as the minimum information capacity that provides a minimum thermodynamic (BH) entropy [
30,
31,
32].
There is no disorder or uncertainty in an object that can be assembled in the same number of steps .
Definition 2. A string is a balanced string if it has the same number of bits, where or if N is odd.
Without loss of generality, we assume that if N is odd, (e.g., for , , and ). However, our results are equivalently applicable if we assume the opposite (i.e., a larger number of ones for an odd N).
Considered as messages [
29], only balanced and even length strings
have binary entropies
, i.e., natural numbers. Conversely, only non-balanced and/or odd length strings
have binary entropies
.
The number
of balanced strings among all
strings is ("
" is the floor function that yields the greatest integer less than or equal to
x and "
" is the ceiling function that yields the least integer greater than or equal to
x.)
This is the OEIS A001405 sequence, the maximal number of subsets of an
N-set such that no one contains another, as asserted by Sperner’s theorem, and approximated using Stirling’s approximation for large
N.
BBs emit Hawking black-body radiation having a continuous spectrum that depends only on one factor, the BB temperature
corresponding to the BB diameter
, where
and
denotes respectively the Planck length and temperature [
8].
Triangulated BB surfaces contain a balanced number of Planck area triangles, each having binary potential
, where
c denotes speed of light in vacuum, as has been shown [
8,
10], based on the Bekenstein-Hawking entropy [
30,
31,
32]
. Here
is the Boltzmann constant and
is the information capacity of the BB surface, i.e., the
Planck triangles corresponding to bits of information [
8,
9,
10,
31,
33,
34], and the fractional part triangle(s) having the area
too small to carry a single bit of information [
8,
9].
Therefore, a balanced string
represents a BB surface comprising
active Planck triangles (APTs) with binary potential
and energy
[
9].
Definition 3. A string is a distinct string if a ring formed with this string by joining its beginning with its end is unique among the rings formed from the other distinct strings .
There are at least two and at most
N forms of a distinct string
that differ in the position of the starting bit. For example for
balanced strings, shown in
Table 2, two augmented strings with
correspond to each other if we change the starting bit
Similarly, four augmented strings with
correspond to each other
after a change in the position of the starting bit. Thus, there are only two balanced distinct strings
.
The number of distinct strings among all strings is given by the OEIS sequence A000031. In general (for ), the number of distinct strings is much lower than the number of balanced strings.
As asserted by the no-hair theorem [
35], BH is characterized only by three parameters: mass, electric charge, and angular momentum.
However, BHs are fundamentally uncharged and non-rotating, since the parameters of any conceivable BH, that is, charged (Reissner-Nordström), rotating (Kerr) and charged rotating (Kerr-Newman), can be arbitrarily altered, provided that the area of a BH surface does not decrease [
36] using Penrose processes [
37,
38] to extract electrostatic and/or rotational energy of a BH [
39].
Thus, a BH is defined by a single real number, and no Planck triangle is distinct on a BH surface. We can define neither a beginning nor an end of a balanced distinct string that represents a given BH.
By neglecting the notion of the beginning and end of a string, we focus on its length and content. In Yoda’s language,
"complete, no matter where it begins. A message is".
The numbers of the balanced
, distinct
, and balanced distinct (
is close to OEIS A000014 up to the eleventh term.)
strings are shown in
Table 3 and
Figure 1. The formula for
remains to be researched.
We note that, in general, the starting bit is relevant for the assembly index. Thus, different forms of a distinct string may have different assembly indices. For example, for
balanced strings
and
, shown in
Table A16 have
. However, these strings are not distinct, since they correspond to each other and to the balanced strings
,
,
,
, and
with
. They all have the same triplet of adjoining ones.
Definition 4. The assembly index of a distinct string is the smallest assembly index among all forms of this string.
Thus, if different forms of a distinct string have different assembly indices, we assign the smallest assembly index to this string. In other words, we assume that the smallest number of steps
where
denotes a particular form of a distinct string
, is the string assembly index of this distinct string.
If an object that can be represented by a distinct string (a BB in particular) can be assembled in fewer steps, this procedure will be preferred by nature.
The distribution of the assembly indices of the balanced distinct strings
is shown in
Table 4.
4. Maximum Assembly Index
In the following, we conjecture the form of the upper bound of the set of different string assembly indices 1.
In general, of all strings
having a given assembly index, shown in
Table 1,
Table A6,
Table A7,
Table A8,
Table A9,
Table A10,
Table A11,
Table A12 and
Table A13 (
Appendix D), most are those having
. The only exceptions we found are
for
(
) and for
(
),
for
(
) and for
(
), and
for
(
).
Introducing the definition 2 of a balanced string allows us to reduce the search space of possible strings with maximal assembly indices to balanced strings only. With the exception of , of all strings having a maximum assembly index, most are balanced. We can further restrict the search space to distinct strings 3.
If a string for which is constructed from repeating patterns, then a string for which must be the most patternless. The string assembly index must be bounded from above and must be a monotonically nondecreasing function of N that can increase at most by one between N and .
Identifying the shortest pathway is known to be computationally challenging [
3]. This problem has been proven to be at least as hard as NP-complete [
4]. However, certain heuristic rules apply in our binary case. For example,
for we cannot avoid two doublets (e.g., ) within a distinct string and thus ,
for we cannot avoid two pairs of doublets (e.g., and ) within a distinct string and thus ,
for we cannot avoid three pairs of doublets (e.g., , , and ) within a distinct string and thus ,
for we cannot avoid two pairs of doublets and one doublet three times (e.g., , , and , and thus ,
etc.
Table 6 shows the exemplary balanced strings
having maximal assembly indices that we assembled (cf. also
Appendix B). To determine the assembly index
of the string
we look for the longest patterns that appear at least twice within the string, and we look for the largest number of these patterns. Here, we find that each of the two triplets
and
appear twice in
and are based on the doublets
and
also appearing in
. Thus, we start with the assembly pool
made in four steps and join the elements of the pool in the following seven steps to arrive at
. On the other hand, another form of this balanced distinct string
has
.
Conjecture 3 (Tight upper bound on a string assembly index). With exceptions for small N the largest string assembly index of a binary string as a function of N is given by a sequence formed by strings for , where denotes increasing by one, and 0 denotes maintaining it at the same level, and .
However, at this moment, we cannot state whether this conjecture applies to distinct or non-distinct strings. The assembly indices for
are the same for a given
N, whereas the assembly indices for
were discussed above and are calculated in
Appendix D for balanced and balanced distinct strings.
The conjectured sequence is shown in
Figure 2 and
Figure 3 starting with
(we note in passing that
is a dimension of the void, the empty set ∅, or (-1)-simplex). Subsequent terms are given by
, which is periodic for
and flattens at
, and
,
,
.
This sequence can be generated using the following procedure
step=1; % step flag
run =1; % run flag
flat=0; % flat counter
Nk = 0;
aub= -1; % the upper bound
while Nk < N
if step < 3
Nk = Nk+1; % next Nk
aub= aub + 1; % increment the bound
else % step==3
for k=1:flat
if flat > 0
Nk = Nk+1; % next Nk
end
end
run = run+1; % increment run flag
if run > 2
run = 1; % reset run flag
flat = flat+1; % increment flat counter
end
end
step = step+1; % increment step flag
if step > 3
step=1; % reset step flag
end
end
We note the similarity of this bound to the Aufbau rule (Only about twenty chemical elements (with only two non-doubleton sets of consecutive ones) violate the Aufbau rule.), the Janet sequence (OEIS A167268) and the monotonically non-decreasing Shannon entropy of chemical elements, including observable ones [
23]. Perhaps the exceptions in the sequence 3 vanish as
N increases.
6. Binputation
Definition 5. The binary assembling program is a binary string of length that acts on the assembly pool P and outputs the assembled strings, adding them to the pool.
Definition 6. The trivial assembling program Q is a binary assembling program 5 with particular bits denoting
-
0
take the last element from P, join it with itself, and output.
-
1
take the last two elements from P, join them with each other, and output; and
As the assembly pool P is a distinct set to which strings are added in subsequent assembly steps, only these two commands are applicable to the initial assembly pool containing only two bits.
Theorem 5. A string can be assembled by an elegant trivial program of length iff N is expressible as a product of Fibonacci numbers (OEIS A065108).
Proof. An elegant program is the shortest program that produces a given output [
41,
42].
The bit of the program Q is irrelevant as assembles and assembles , so assembles . Then the programs assemble the -bit strings having the assembly index , while strings with the smallest assembly index can be assembled with the same two programs starting with the pool .
The remaining
programs will assemble some of the shorter strings with the assembly index
. In general, all programs
Q assemble strings having lengths expressible as a product of Fibonacci numbers (OEIS A065108) as shown in
Table A2 (
Appendix C), wherein out of
programs (cf.
Table A5 and
Table A2):
programs
assemble even length balanced strings
having natural binary entropies (
3)
, including strings
(
11),
programs assemble strings having lengths divisible by three and entropies ,
programs assemble strings having lengths divisible by five and entropies ,
programs assemble strings having lengths divisible by eight, entropies , and assembly indices if ,
⋯,
the program joins two shortest strings joined in a previous step into a string of length being twice the Fibonacci sequence (OEIS A055389), and finally
the program assembles the shortest string that has length belonging to the set of Fibonacci numbers.
Thus, for
, binary assembling programs
Q assemble subsequent
Fibonacci words and their concatenations having entropies (
3) with ratios (
4)
where
, and
F is the Fibonacci sequence starting from 1 that rapidly converge to
where
is the golden ratio. Therefore,
is the binary entropy of the Fibonacci word limit. The Fibonacci sequence can be expressed through the golden ratio, which corresponds to the smallest Pythagorean triple
[
28,
43].
Furthermore, for , some of the programs are no longer elegant if and some of the assembled strings are not if .
For
,
assembles a string
with an assembly index
which is not the minimum for this length of the string. For example, 4-bit program
assembles the string
, but if
this string can be assembled by a shorter, 3-bit program
, and if
this string does not have the minimal assembly index
but
.
For and and for the shortest string assembled by the program Q the program Q is not elegant for and the shortest string assembled by the program is not for .
However, the length of any program Q is not shorter than the assembly index of the string that this program assembles. □
The trivial assembly programs
Q and the strings they assemble are listed in
Table 7,
Table A3,
Table A4 and
Table A5 (
Appendix C) for one version of the assembly pool and for
. If a binary string
were to code four DNA nucleobases, (for example as, A
, G
, C
, and T
) then we note that the nucleobase encoded by 11 (or 00 for
) would not be present in the strings generated by trivial assembly programs
Q defined by 6.
Perhaps the minimum assembly index 2 and Theorem 5 are related to the Collatz conjecture, as the lengths of the strings (
11)
correspond to the numbers to which the Collatz conjecture converges, from
,
(OEIS A002450).
Theorem 5 is related to Gödel’s incompleteness theorems and the halting problem.
N cases of the halting problem correspond only to
, not to
N bits of information [
44]. Therefore,
-bit elegant programs assemble all four strings
with
(with two versions of the assembly pool). Furthermore, we could consider all strings assembled by the
-bit assembly program as corresponding to provable theorems. Any formal axiomatic system (such as our trivial program; Definition 6) only enables proving provable theorems. Thus, proving a theorem equals halting. There is a more fundamental path to incompleteness that involves complexity, rather than self-reference [
45].
Theorem 5 would be violated if we defined the command "0" e.g., as "take the last element from the assembly pool, join it with itself, join with what you have already assembled (say at "the right"), and output". Then the 2-bit program "00" would produce
with the assembly index
. However, such a one-step command would violate the axioms of assembly theory since it would perform two assembly steps in one program step. An elegant program to output the gigabyte binary string of all zeros would take a few bits of code and would have a low Kolmogorov complexity [
46]. However, such a string would be
outputted, not
assembled. Furthermore, the length of such a program that outputs the string
would be shorter than the length of the program that outputs the string
, while in AT, the lengths of these programs must be the same if the strings have the same assembly indices. Theorem 5 is about
binputation (As an analog to chemputation, where assembly theory is applied in digital chemistry.) of binary strings.
Conjecture 6. There is no binary assembling program 5 that has a length shorter than the length of the string having the largest assembly index that could assemble this string.
Partial Proof. When assembling the string having the largest assembly index (the largest complexity), we cannot rely solely on the last or two last strings in the assembly pool. Thus, we need to index the strings in the pool. However, we cannot predict in advance how many strings there will be in the assembly pool. Thus, we do not know how many bits will be needed to encode the indices.
Furthermore, no program P (for a Turing machine) shorter than an elegant program Q can find Q. If it could, it could also generate Q’s output. But if P is shorter than Q, then Q would not be elegant. Contradiction.
Conjecture 7. The problem of determining the assembly index of a given binary string and the problem of assembling a non-trivial string so that it would have a minimum assembly index (Theorem 2) for N are NP-complete. The problem of assembling the string so that it would have a maximum assembly index for N is NP-hard.
Partial Proof. We found it much easier to determine an assembly index of a given binary string than to assemble a string so that it would have a maximum assembly index. Similarly, a trivial string with a minimum assembly index for N can have the form or the form of a Fibonacci word generated by the trivial program 6.
A proof of conjecture 7 would also be the proof of the following conjecture.
Proof. Every computable problem and every computable solution can be encoded as a finite binary string. Here, determining whether the assembly index of a given string has its known maximal value corresponds to checking the solution to a problem for correctness, whereas assembling such a string corresponds to solving the problem.
Thus, AT would solve the P versus NP problem in theoretical computer science. There is ample pragmatic justification for adding
as a new axiom [
44].
7. Additional Results
The [perceivable] universe is not big enough to contain the future; it is deterministic going back in time and non-deterministic going forward in time [
47]. But we know [
2,
8,
9,
10,
11,
12,
13,
14,
15,
16,
17,
18,
19] that it has evolved to the present since the Big Bang.
Perceivable information about any
object can be encoded by a binary string [
26,
27]. This does not imply that a binary string defines an
object. Information that defines a chemical compound, a virus, a computer program, etc. can be encoded by a binary string. However, a dissipative structure [
12] such as a living biological cell (or its conglomerate such as a human, for example) cannot be represented by a binary string (even if its genome can). This information can only be perceived (so this is not an
object defining information). Each of us is given to ourselves as a mystery [
48]. Therefore, since one bit is the smallest amount and the quantum of information, the lower bound and the upper bound of the string assembly index define the allowed region of the assembly indices for binary strings.
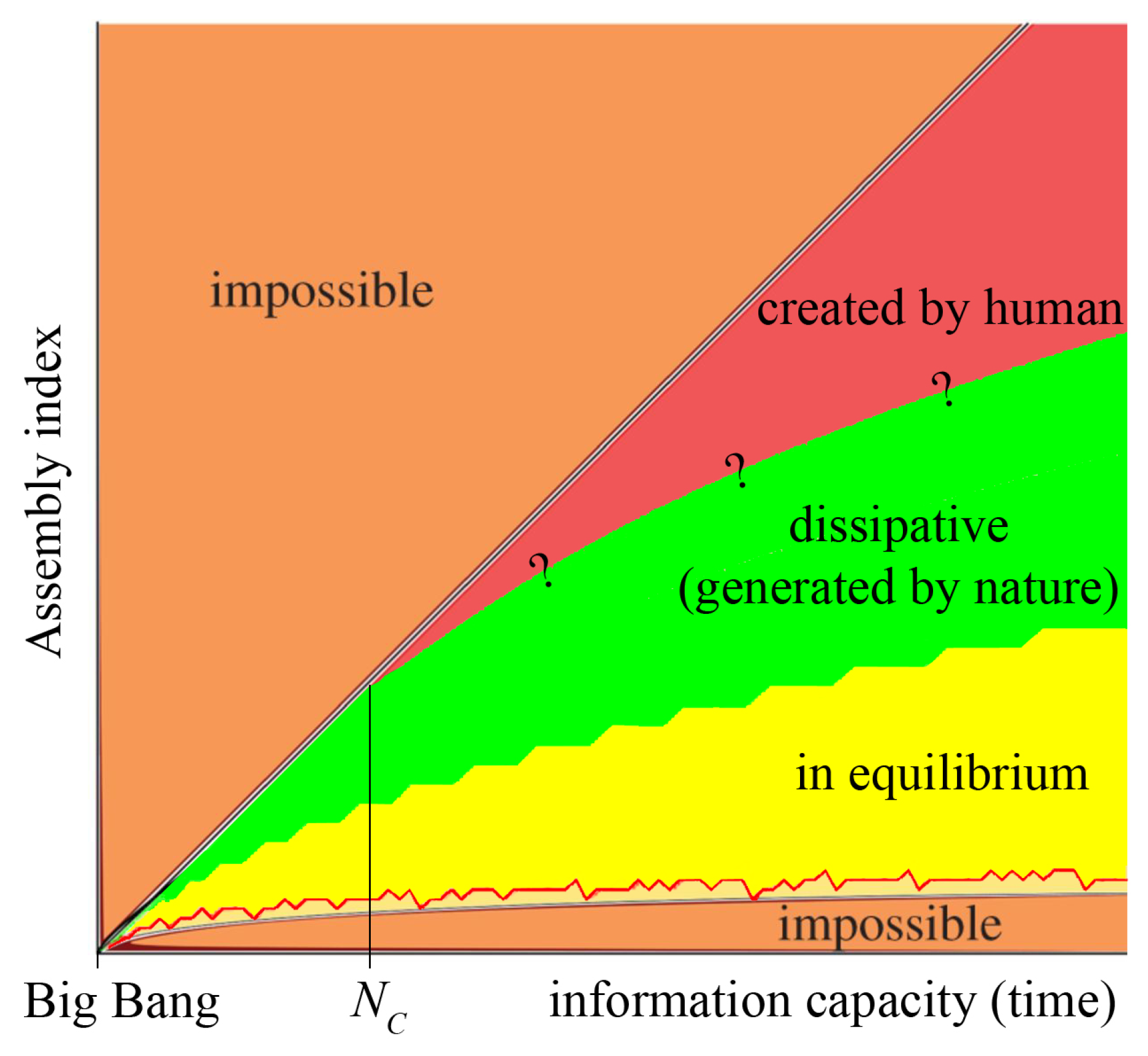
The bounds 2, 3, (
1), and (
2) on the assembly index are shown also in
Figure 4 (adopted from [
1] and modified). According to the authors of [
1], the "green portion of the figure is illustrative of the location in the complexity space where life might reasonably be found. Regions below can be thought of as being potentially naturally occurring, and regions above being so complex that even living systems might have been unlikely to create them. This is because they represent structures with limited internal structure and symmetries, which would require vast amounts of effort to faithfully reproduce." [
1].
We disagree with this statement. It is obvious that a binary string itself is neither dissipative nor creative. It is its assembly process that can be dissipative or creative. Evolution is about assembling new information and optimizing it until it reaches its assembly index.
That is why, we found determining the assembly index of a given binary string
is easier than creating a string with a maximum assembly index for this length of the string (Conjecture 7). Once the new information is assembled (by a dissipative structure operating far from thermodynamic equilibrium, or created by humans) increasing the information entropy according to the 2
nd law of infodynamics [
16], it enters the realm of the 2
nd law of thermodynamics, and nature seeks how to optimize its assembly pathway decreasing information entropy. And only humans are gifted with creativity. Any creation is required to be shaped by the unique personality of the creator to such an extent that it is statistically one-time in nature [
49]; it is an imprint of the author’s personality.
The total entropy of the universe
S is constant and is the sum of the information entropy
and the physical entropy
. Therefore, over time [
19]
The time corresponds to an increasing information capacity. Bit by bit:
At first, the newly assembled information corresponds to the discovery by groping [
11]. However, its assembly pathway does not attain its most economical or efficient form all at once. For a certain period of time, its evolution gropes about within itself. The try-out follows the try-out, not being finally adopted. Then finally perfection comes within sight, and from that moment the rhythm of change slows down [
11]. The new information, having reached the limit of its potentialities, enters the phase of conquest. Stronger now than its less perfected neighbours, the new information multiplies and consolidates. When the assembly index is reached, new information attains its equilibrium (not necessarily a BH equilibrium) and its evolution terminates. It becomes stable.
There is a certain minimum amount of information
required to establish a creation, as shown in
Figure 4. Sixteen possibilities provided by the minimum of thermodynamic entropy [
30,
31,
32] bifurcate the assembly pathways (cf. Theorem 1) but none of these possibilities can be considered a
creation. However, the boundary between the green region of dissipative structures [
12] and the red region of human creativity remains to be discovered.
"Thanks to its characteristic additive power, living matter (unlike the matter of the physicists) finds itself ’ballasted’ with complications and instability. It falls, or rather rises, towards forms that are more and more improbable. Without orthogenesis life would only have spread; with it there is an ascent of life that is invincible." [
11]
BB having the energy given by mass-energy equivalence
where
,
denote the BB mass, and
,
denote the Planck energy and mass,
is the fine-structure constant and
is the
fine-structure constant related to
by
, and
k is the BB size-to-mass ratio (STM) [
10] (
if BB is BH).
It was shown [
9] based on the Mandelstam-Tamm [
50], Margolus–Levitin [
51], and Levitin-Toffoli [
52] theorems on the quantum orthogonalization interval that BBs generate (or rather
assemble) a pattern forming nonequilibrium shell (VS) through the solid-angle correspondence, as shown in
Figure 5. The BB entropic work
is the work done by all APTs of a BB. It is the product of the BB entropy [
30,
31,
32] and the general, complex BB temperature
which in modulus and for a BH (
) reduces [
10] to Hawking temperature
where
is the reduced Planck constant,
G is the gravitational constant, and
is the Planck temperature. In particular [
10]
where
is the energy equilibrium STM.
A VS has the information capacity bounded by
where
l is a VS defining factor. The number of APTs is bounded by
as shown in
Figure 6, and thus its binary potential
[
8,
9] is bounded by
and the theoretical probability
for a triangle on a VS to be an active Planck triangle is also bounded [
9] by
which is satisfied by the ratio
(
17) of the trivial assembling program 6 for
. On the other hand, the entropy variation [
8,
53]
so that for
the lower bound (
31) is negative and the upper bound (
30) is positive (
in this range). The Planck triangle of VS is located
somewhere on the VS surface defined by a solid angle
that corresponds to the BB Planck triangle.
The BB information capacity is dictated by its diameter and the BB energy (
21) as a function of its diameter is the same for all BBs (it is independent on
k). However, the BB mass and density
are not.
Based on the orbiting condition
, where
is the orbital, and
is the escape speed of an orbiting
object,
is the average distance from the center of the central
object to the center of the orbiting
object, and
is the mass of the central
object, the bounds
containing the velocity term
,
were also derived [
9]. Plugging
from the bounds (
28) into the bounds (
34) we arrive at
which is satisfied by real and imaginary (but not complex) velocities (for example, for
by
,
,
, and
). Taking the square root of the bounds (
35), using
,
[
9], and squaring again, we arrive at
The bounds (
35) and (
36), shown in
Figure 7, meet at
, where de Broglie and Compton wavelengths of mass
M are the same
where
p is the relativistic momentum. The same is the ratio of orbital to escape speed:
.
Furthermore, the bounds (
35) and (
36) do not overlap only for
. Therefore,
defines the dissipativity or the assembly range. Furthermore, the intersection of the bounds (
35) and (
36) is the common region for both velocities. If
is within this region, then
is as well. We note that the average orbital velocity of each orbiting
object only slightly exceeds its orbital speed
. This implies that the average VS defining factor
in (
28) for a VS orbiting
object (cf.
Appendix A).
BBs define a perfect thermodynamic equilibrium, and the bounds (
28) and (
29) show that nature uses optimally assembled information (cf. Conjecture 4) to assemble new information.
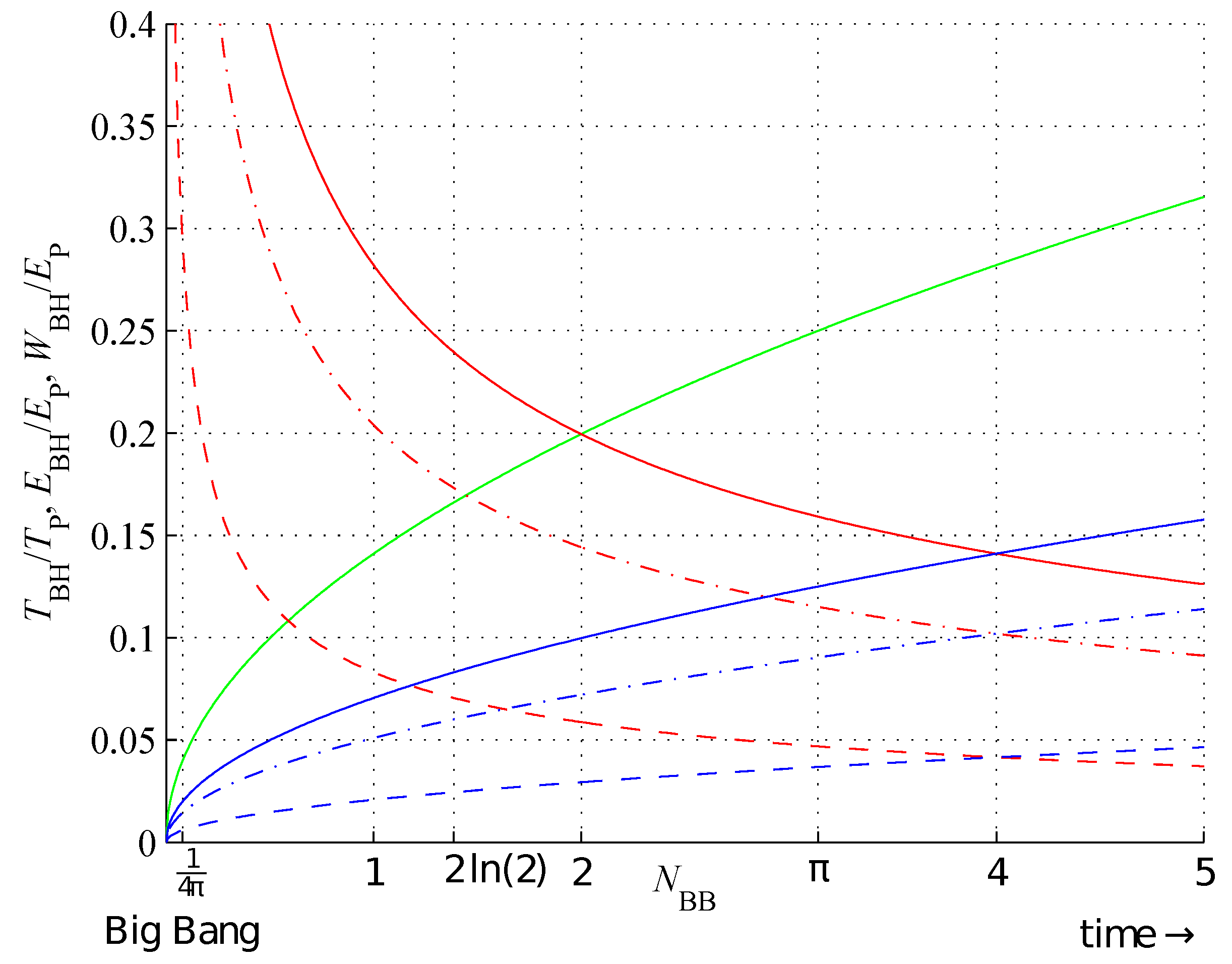
Figure 8 shows the bounds on the string assembly indices and
Figure 9 shows the BB temperature (
24), energy (
21), and entropic work (
22) for
.
is a rational number for natural
. Furthermore,
for
and
.
Let us examine this process starting from the Big Bang during the Planck epoch and shortly thereafter, and for continuous (i.e., including fractional Planck triangle(s)).
-
There is nothing to talk about. It is a mystery.
-
The Big Bang has occurred, forming the 1
st BB. At
the BB temperature (
24) and subsequently at
the BH temperature (
24) become equal to the Planck temperature, but any BB in this range is still too small to carry a single bit of information and cannot be triangulated. However, independent BBs merge [
9,
10] summing their entropies and increasing the information capacity.
-
The first bit (a degree of freedom [
9]) becomes available and APTs on BBs begin to fluctuate providing the initial assembly pool
. The BH energy reaches the limit of the equipartition theorem for one bit (
). However, the bounds (
29) make them unable to generate any APTs on a VS (
).
-
This is the only range in which the lower AT bound (
1) is greater than the upper AT bound (
2).
The BH temperature (
24) exceeds its energy (
21) (
) [
9]. At
the BH energy (
21) is equal to the Landauer limit
[
54]. Shortly thereafter, at
, the BH density reaches the level of the Planck density For a BB [
10] Still
. Merging BBs expand fractional Planck triangle(s) to form the 2
nd bit.
-
The first nonvanishing
becomes available on a VS generated by a BB. The BH temperature (
24) is equal to its energy (
21) (
).
-
At
the BH entropic work (
22) is equal to the Landauer limit (
). At
the density of the least dense BB (
) decreases below the modulus of its temperature.
.
-
With
BBs can finally be triangulated. Yet, containing only one APT (
), they are not ergodic [
9].
At
the BH surface gravity
decreases below the Planck acceleration and the tangential acceleration [
8,
9] becomes real (
).
-
The BB assembly index bifurcates, minimal thermodynamic entropy [
31] is reached, and the relation (
29) provides the second bit on a VS (
). At this moment BB can be assembled in a different number of steps and nature seeks to minimize this number following the dynamics induced by the relation (
20). The BH temperature (
24) is equal to its entropic work (
22) (
).
-
The BH temperature (
24) finally decreases below the entropic work (
22) limit and
.
-
A BB reaches the upper bound on distinct assembly index.
-
The imaginary Planck time appears at the BH surface [
8] heralding the end of the Planck epoch. After crossing this threshold, the VSs begin to operate with
on
, and the first dissipative structures can be assembled.
Nature enters a directed exploration phase (
) and selectivity emerges, limiting the discovery of new objects [
6].
-
A BB reaches the upper bound on nondistinct assembly index.
⋯
-
At
a first precise diameter relation can be established between the vertices of the BB surface. Furthermore, for
, the solid angle (
32) equals one steradian.
⋯
-
The onset of human creativity.
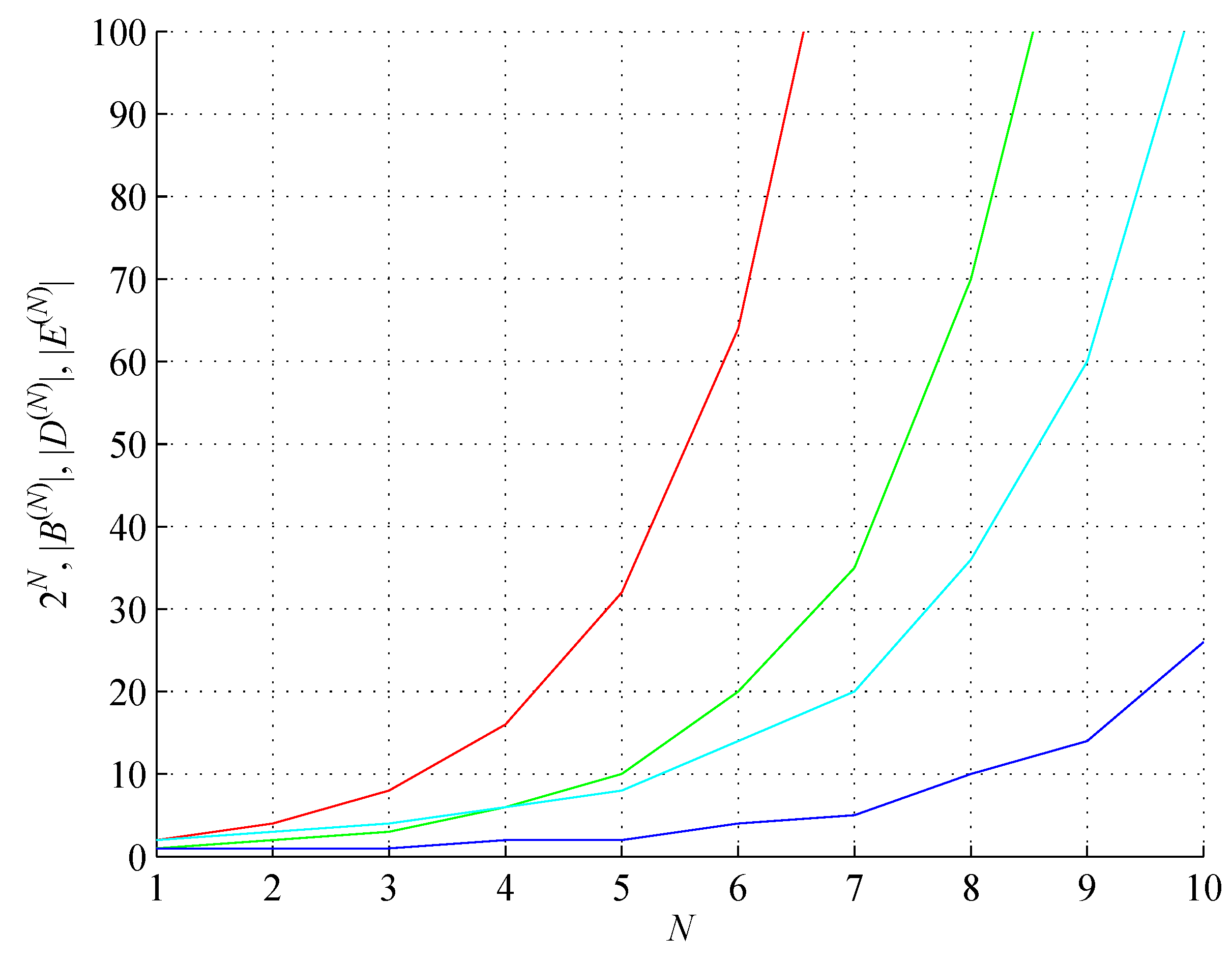
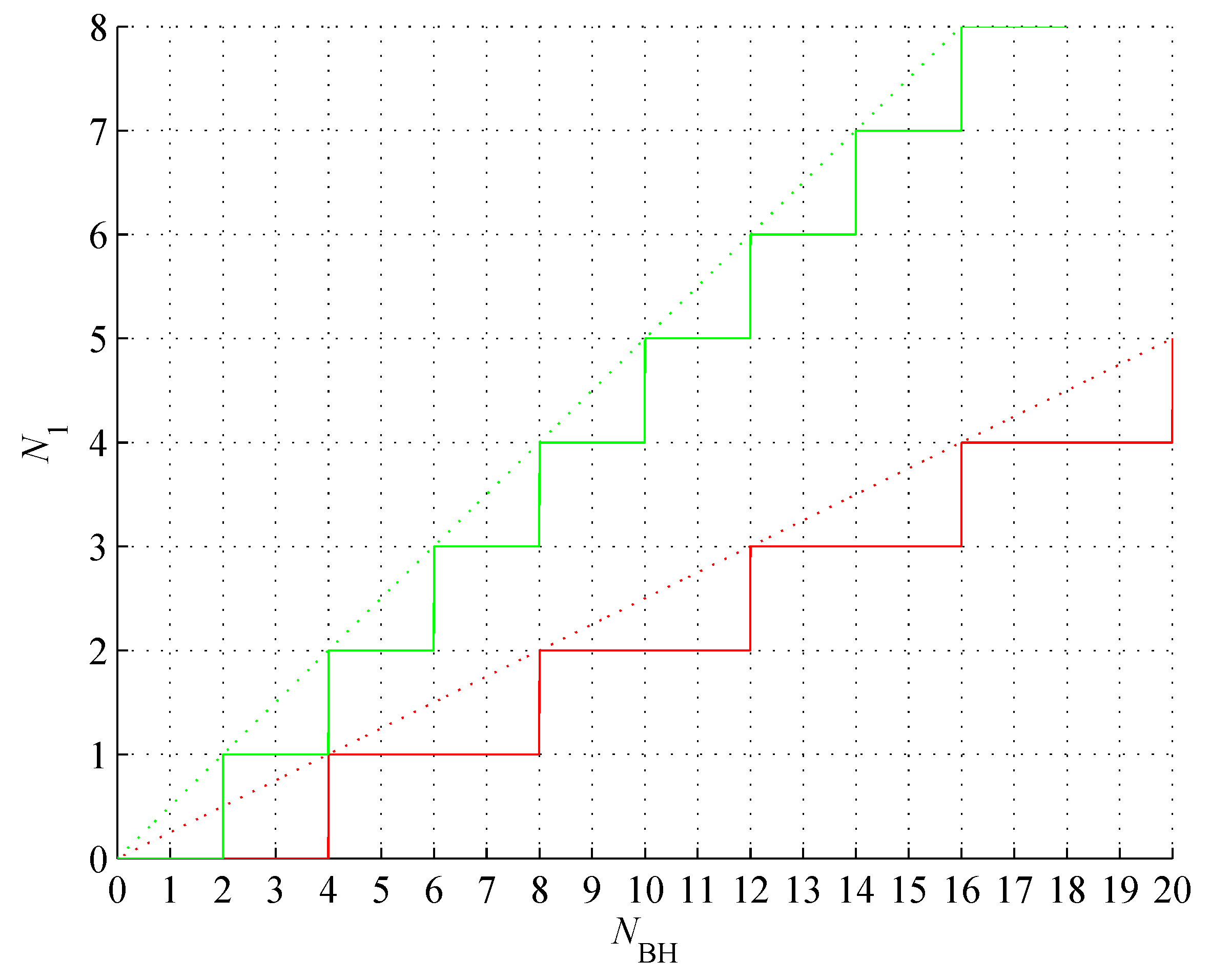
Figure 1.
Numbers of all strings (red), balanced strings (green), distinct strings (cyan), and balanced distinct strings (blue) as a function of the string length N.
Figure 1.
Numbers of all strings (red), balanced strings (green), distinct strings (cyan), and balanced distinct strings (blue) as a function of the string length N.
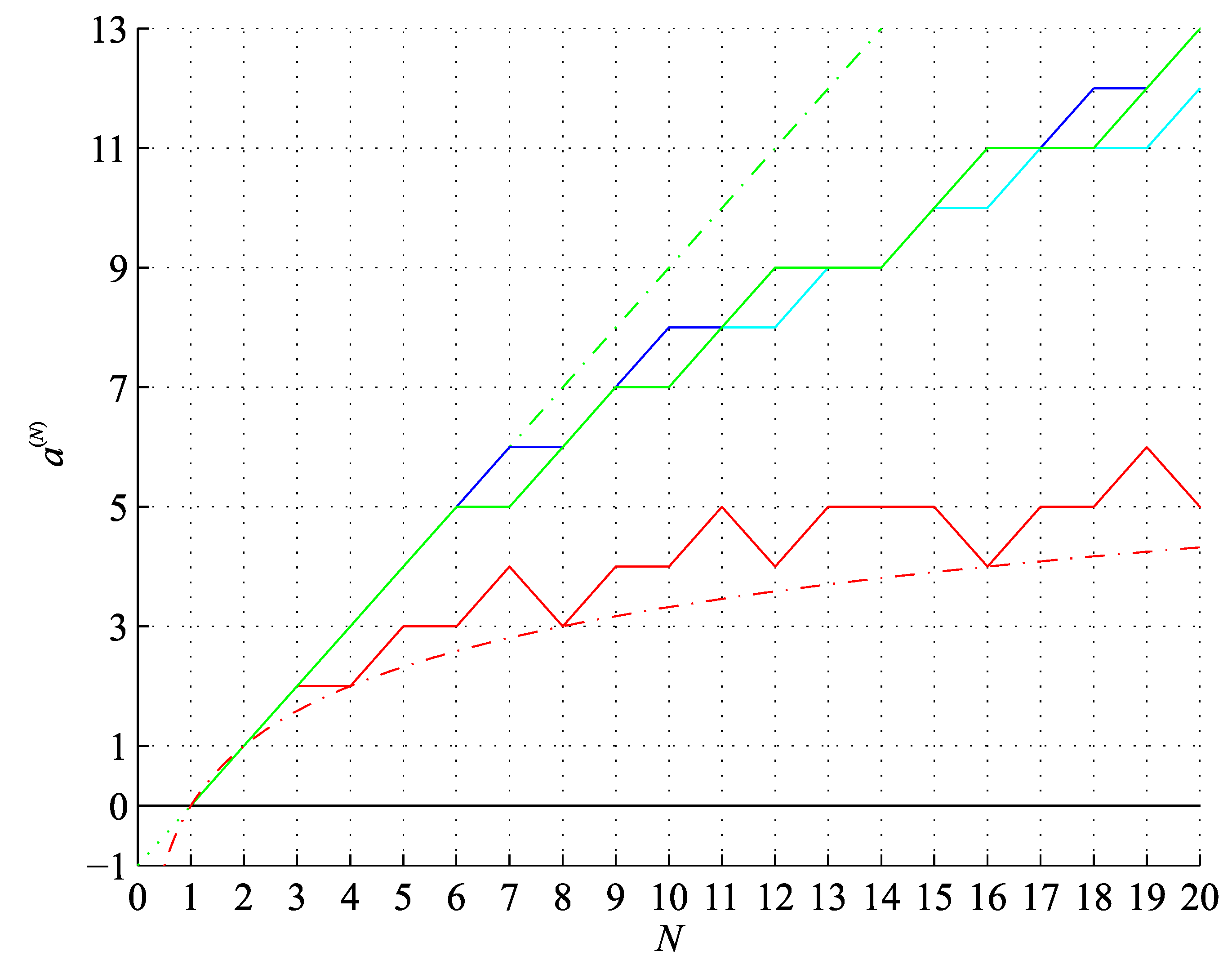
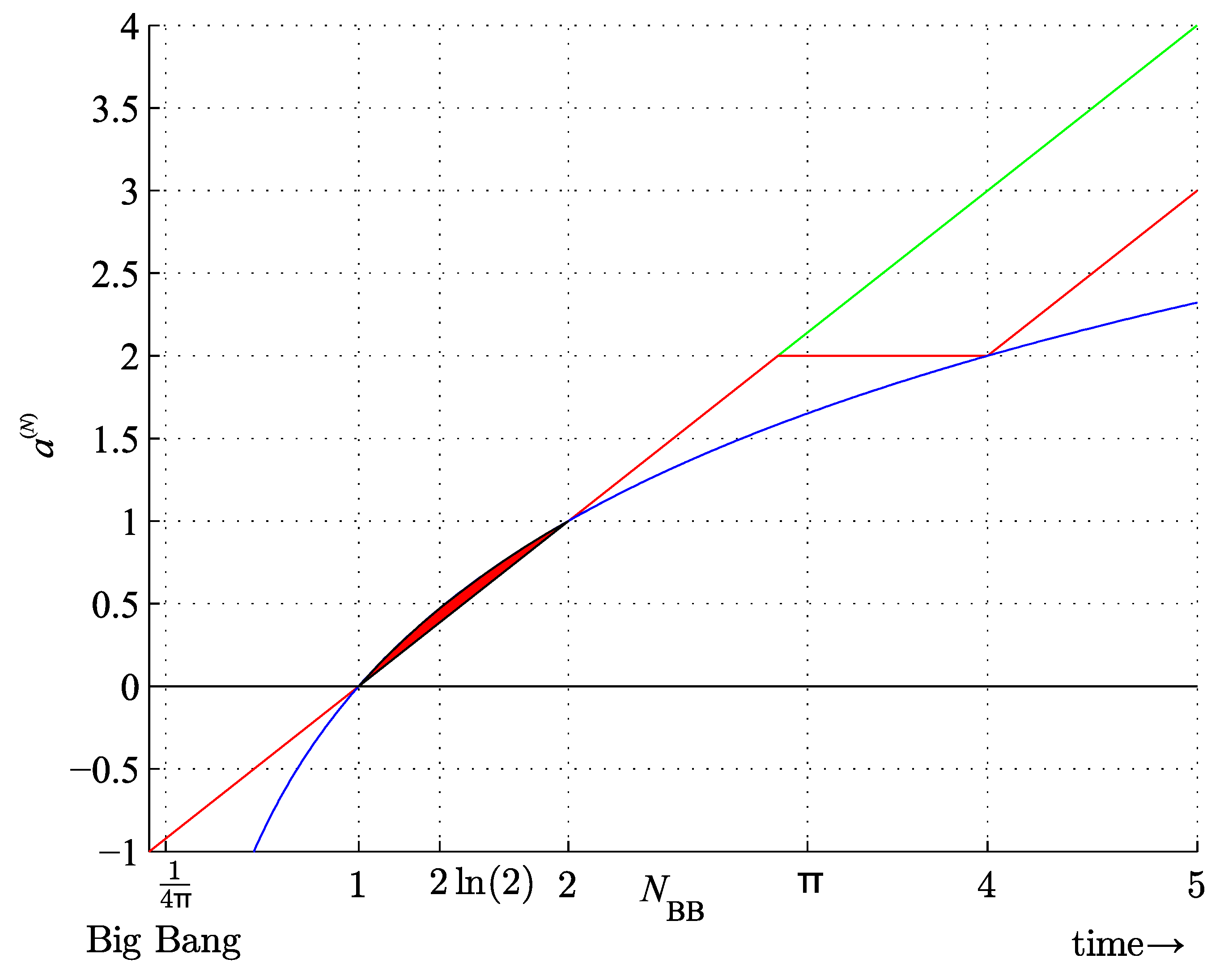
Figure 2.
Lower bound on the binary string assembly index 2 (red) and (red, dash-dot), conjectured upper bound on the binary string assembly index 3 (green), factual values of the string assembly index (blue) and the distinct string assembly index (cyan) and (green, dash-dot), for the string length .
Figure 2.
Lower bound on the binary string assembly index 2 (red) and (red, dash-dot), conjectured upper bound on the binary string assembly index 3 (green), factual values of the string assembly index (blue) and the distinct string assembly index (cyan) and (green, dash-dot), for the string length .
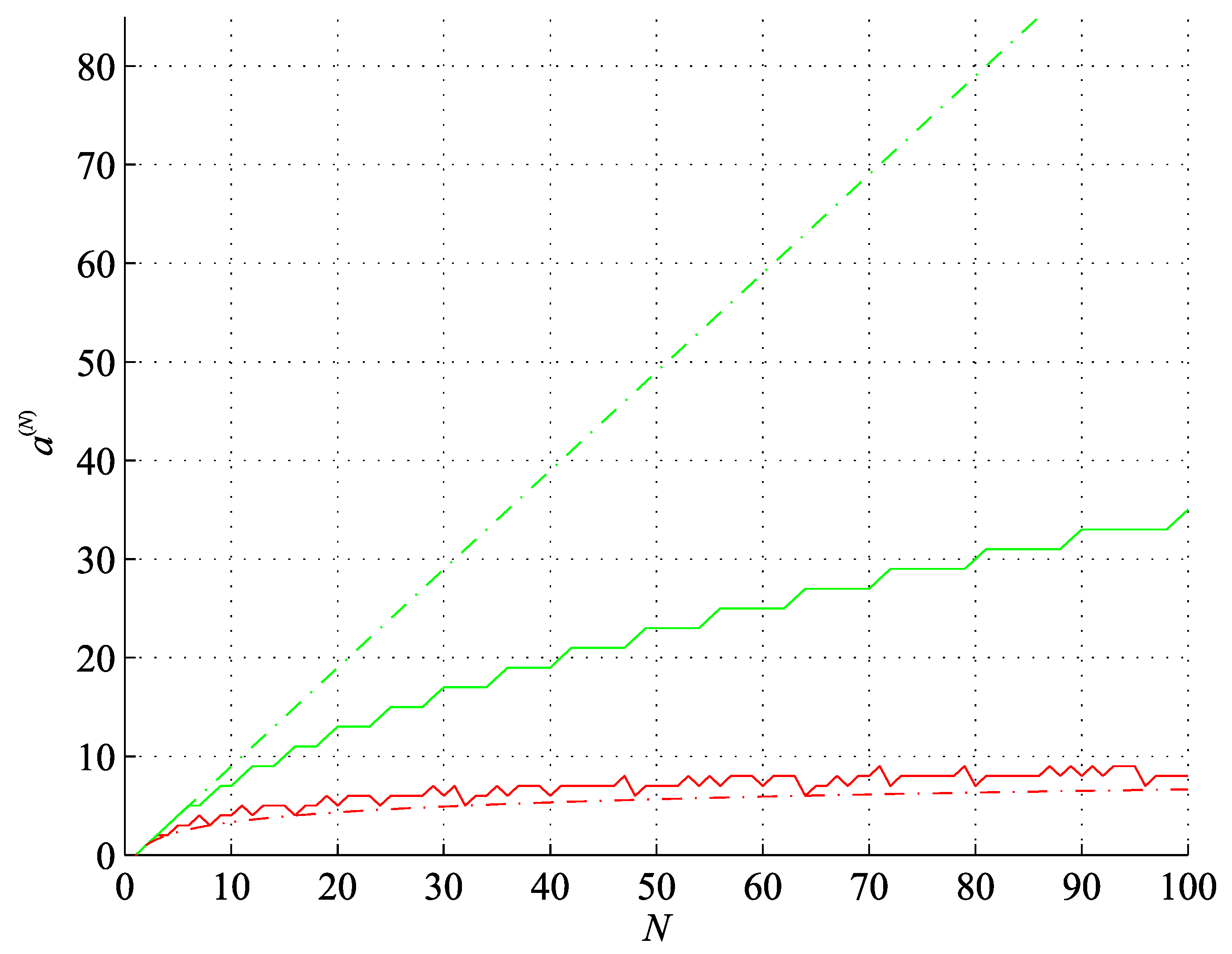
Figure 3.
Lower bound on the binary string assembly index (red) and (red, dash-dot), conjectured upper bound on the string assembly index (green) and (green, dash-dot), for the binary string length .
Figure 3.
Lower bound on the binary string assembly index (red) and (red, dash-dot), conjectured upper bound on the string assembly index (green) and (green, dash-dot), for the binary string length .
Figure 4.
An illustrative graph of complexity against information capacity: orange regions are impossible, as they are above or below the assembly bounds; yellow region contains structures optimally assembled (in equilibrium); green region contains dissipative structures; and red region is the region of human creativity (figure not to scale).
Figure 4.
An illustrative graph of complexity against information capacity: orange regions are impossible, as they are above or below the assembly bounds; yellow region contains structures optimally assembled (in equilibrium); green region contains dissipative structures; and red region is the region of human creativity (figure not to scale).
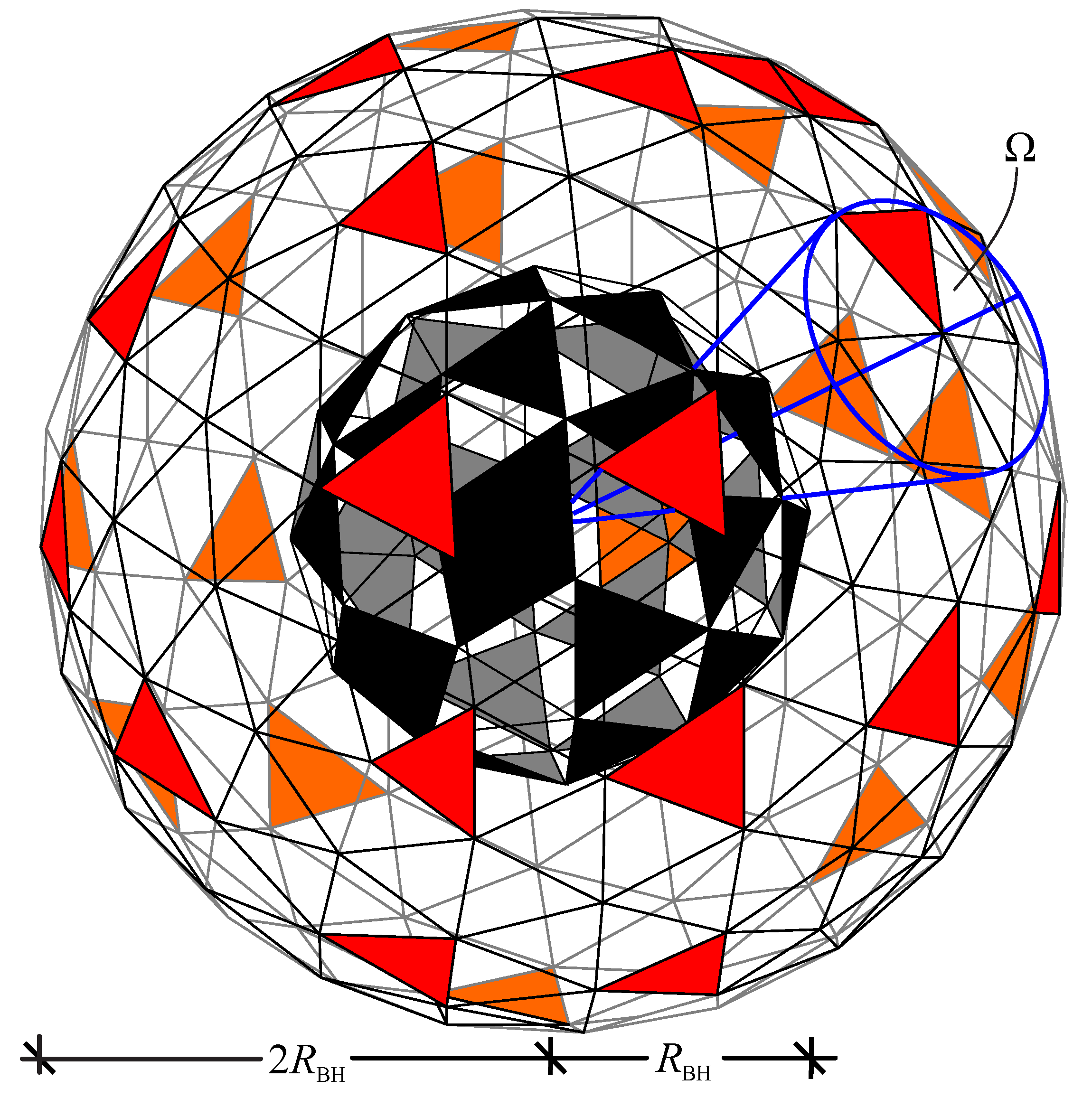
Figure 5.
A black body object as a generator of an entropy variation shell (VS) through the solid angle correspondence.
Figure 5.
A black body object as a generator of an entropy variation shell (VS) through the solid angle correspondence.
Figure 6.
Lower (red) and upper (green) bound on the number of APTs
on a VS as a function of the information capacity of the generating BB [
9].
Figure 6.
Lower (red) and upper (green) bound on the number of APTs
on a VS as a function of the information capacity of the generating BB [
9].
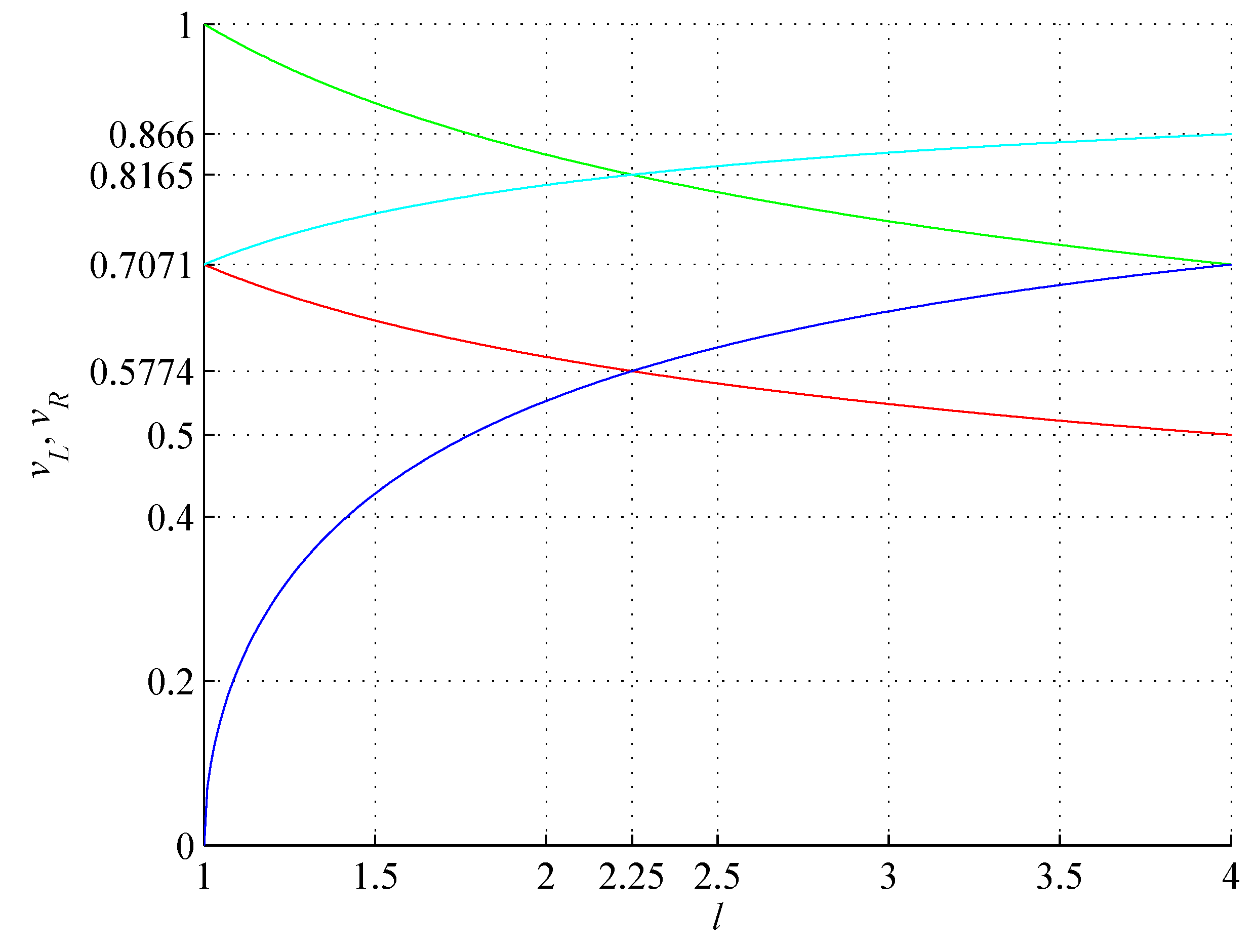
Figure 7.
Lower (red) and upper (green) bounds on and lower (blue) and upper (cyan) bounds on as a function of l defining VS. Characteristic velocities are , .
Figure 7.
Lower (red) and upper (green) bounds on and lower (blue) and upper (cyan) bounds on as a function of l defining VS. Characteristic velocities are , .
Figure 8.
Lower (red) and upper (green) bounds on the binary string assembly index of length and (blue), for .
Figure 8.
Lower (red) and upper (green) bounds on the binary string assembly index of length and (blue), for .
Figure 9.
Black body object energy (green); temperature (red), (red, dash-dot), (red, dash); and work (blue), (blue, dash-dot), (blue, dash),as a function of its information capacity in terms of Planck units, for .
Figure 9.
Black body object energy (green); temperature (red), (red, dash-dot), (red, dash); and work (blue), (blue, dash-dot), (blue, dash),as a function of its information capacity in terms of Planck units, for .
Table 3.
String length N, number of all strings , number of balanced strings , number of distinct strings , and number of balanced distinct strings .
Table 3.
String length N, number of all strings , number of balanced strings , number of distinct strings , and number of balanced distinct strings .
| N |
|
|
|
|
|
| 1 |
2 |
1 |
2 |
1 |
1 |
| 2 |
4 |
2 |
3 |
1 |
2 |
| 3 |
8 |
3 |
4 |
1 |
3 |
| 4 |
16 |
6 |
6 |
2 |
3 |
| 5 |
32 |
10 |
8 |
2 |
5 |
| 6 |
64 |
20 |
14 |
4 |
5 |
| 7 |
128 |
35 |
20 |
5 |
7 |
| 8 |
256 |
70 |
36 |
10 |
7 |
| 9 |
512 |
126 |
60 |
14 |
9 |
| 10 |
1024 |
252 |
108 |
26 |
|
| 11 |
2048 |
462 |
188 |
42 |
11 |
| 12 |
4096 |
924 |
352 |
80 |
11.55 |
| 13 |
8192 |
1716 |
632 |
132 |
13 |
| 14 |
16384 |
3432 |
1182 |
246 |
|
| 15 |
32768 |
6435 |
2192 |
429 |
15 |
Table 4.
Distribution of assembly indices among balanced distinct strings for .
Table 4.
Distribution of assembly indices among balanced distinct strings for .
| N |
|
|
|
|
|
|
|
|
| 4 |
2 |
1 |
1 |
|
|
|
|
|
| 5 |
2 |
|
1 |
1 |
|
|
|
|
| 6 |
4 |
|
1 |
2 |
1 |
|
|
|
| 7 |
5 |
|
|
2 |
3 |
|
|
|
| 8 |
10 |
|
1 |
1 |
6 |
2 |
|
|
| 9 |
14 |
|
|
1 |
4 |
7 |
2 |
|
| 10 |
26 |
|
|
1 |
6 |
9 |
10 |
|
| 11 |
42 |
|
|
|
2 |
14 |
20 |
6 |
Table 5.
The lower bound on the binary string assembly index (OEIS A003313).
Table 5.
The lower bound on the binary string assembly index (OEIS A003313).
| N |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
|
0 |
1 |
2 |
2 |
3 |
3 |
4 |
3 |
4 |
4 |
5 |
4 |
5 |
5 |
5 |
4 |
5 |
5 |
6 |
5 |
6 |
Table 6.
Exemplary balanced strings having a maximum assembly index. Conjectured () form of the maximum assembly index and its factual values for distinct () and non-distinct () strings (red if below the conjectured value, green - if above).
Table 6.
Exemplary balanced strings having a maximum assembly index. Conjectured () form of the maximum assembly index and its factual values for distinct () and non-distinct () strings (red if below the conjectured value, green - if above).
| N |
|
|
|
|
| 1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
| 2 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
| 3 |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
| 4 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
3 |
| 5 |
0 |
0 |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
4 |
4 |
| 6 |
0 |
0 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
5 |
| 7 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
5 |
6 |
| 8 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
6 |
6 |
| 9 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
7 |
7 |
7 |
| 10 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
7 |
7 |
8 |
| 11 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
8 |
8 |
8 |
| 12 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
9 |
8 |
8 |
| 13 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
9 |
9 |
9 |
| 14 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
9 |
9 |
9 |
| 15 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
|
|
|
10 |
10 |
10 |
| 16 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
11 |
10 |
10 |
| 17 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
|
|
11 |
11 |
11 |
| 18 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
|
11 |
11 |
12 |
| 19 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
|
12 |
11 |
12 |
| 20 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
13 |
12 |
13 |
Table 7.
3-bit elegant programs assembling strings with .
Table 7.
3-bit elegant programs assembling strings with .
| Q |
|
|
|
N |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
6 |
|
|
|
|
8 |