Submitted:
11 January 2024
Posted:
11 January 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Problem formulation
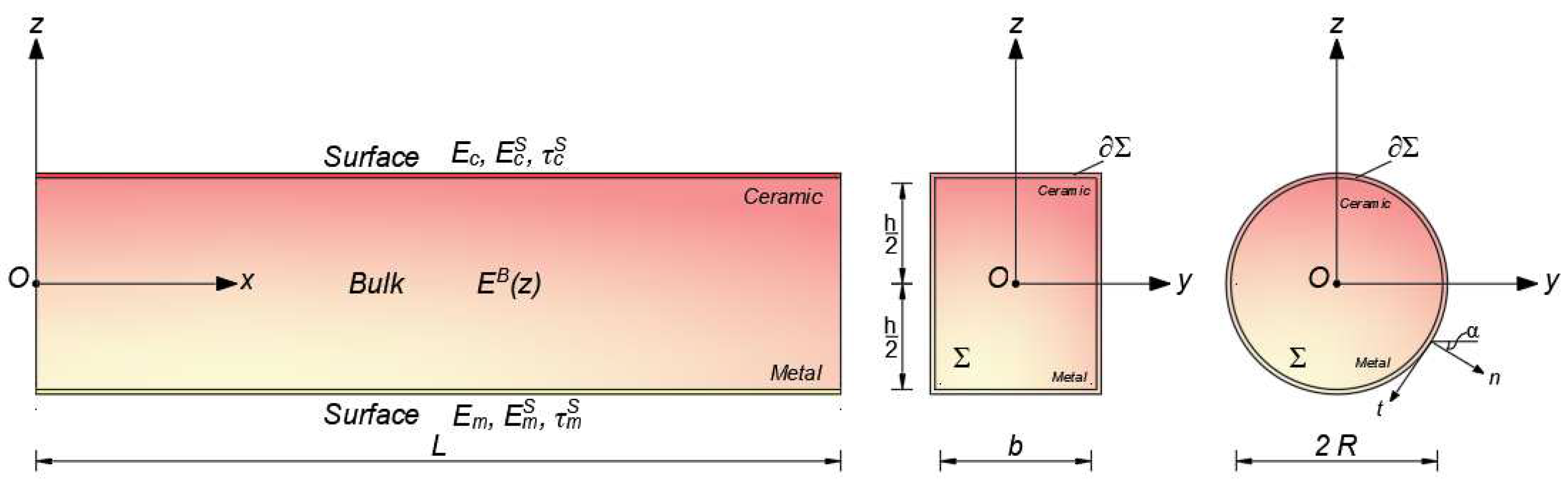
2.1. Kinematic
2.2. Governing equations

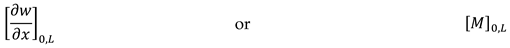
3. Surface stress-driven model for free vibrations analysis
3.1. A brief outline of the surface stress-driven nonlocal model
3.2. Size-dependent governing equation
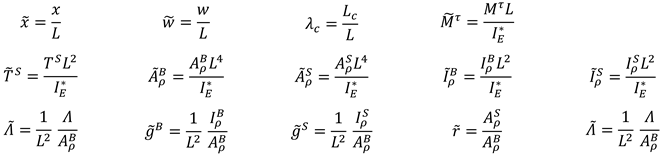

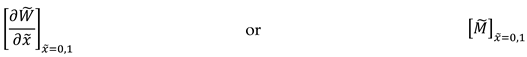
4. Results and discussion
5. Conclusions
- -
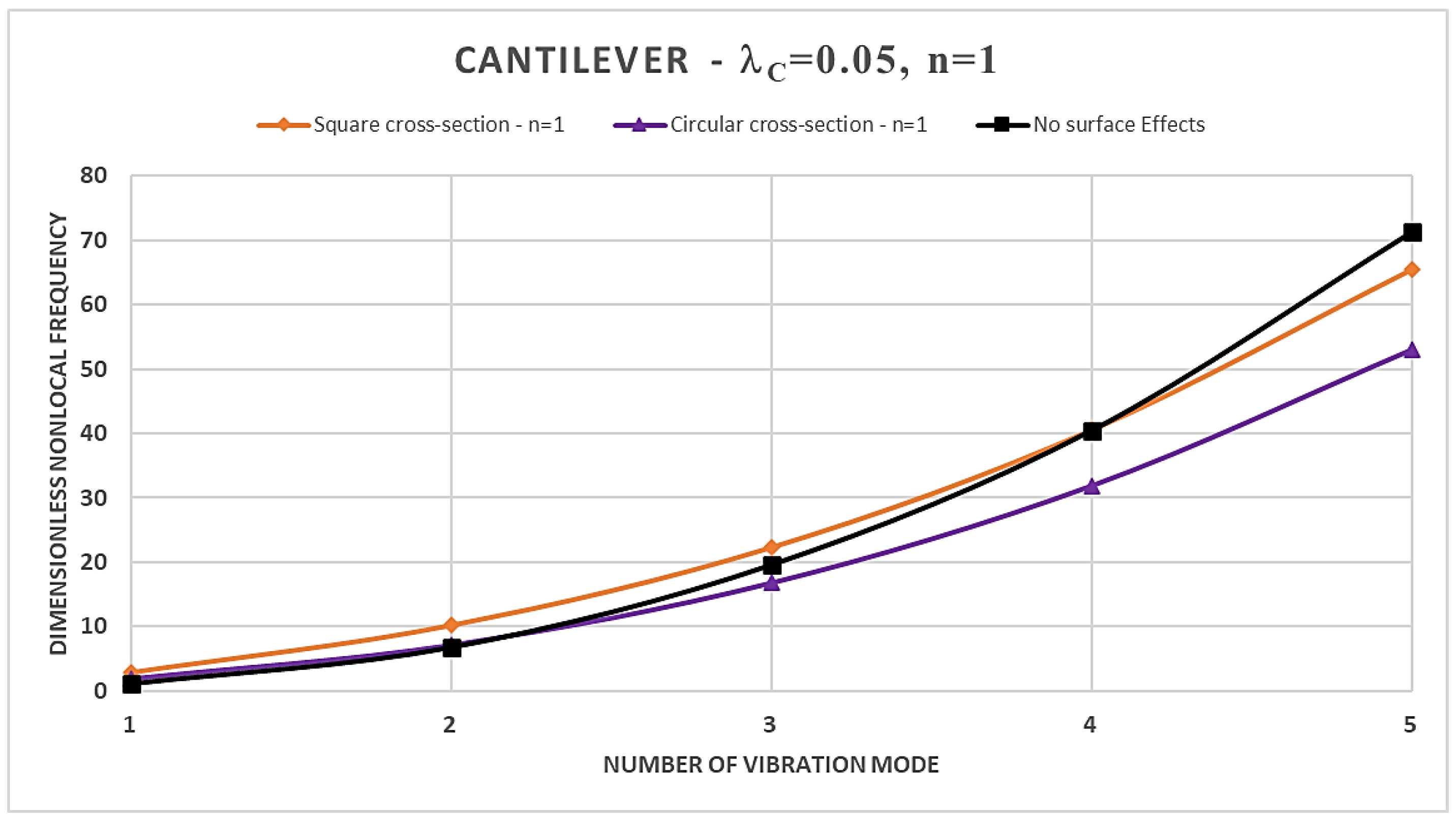
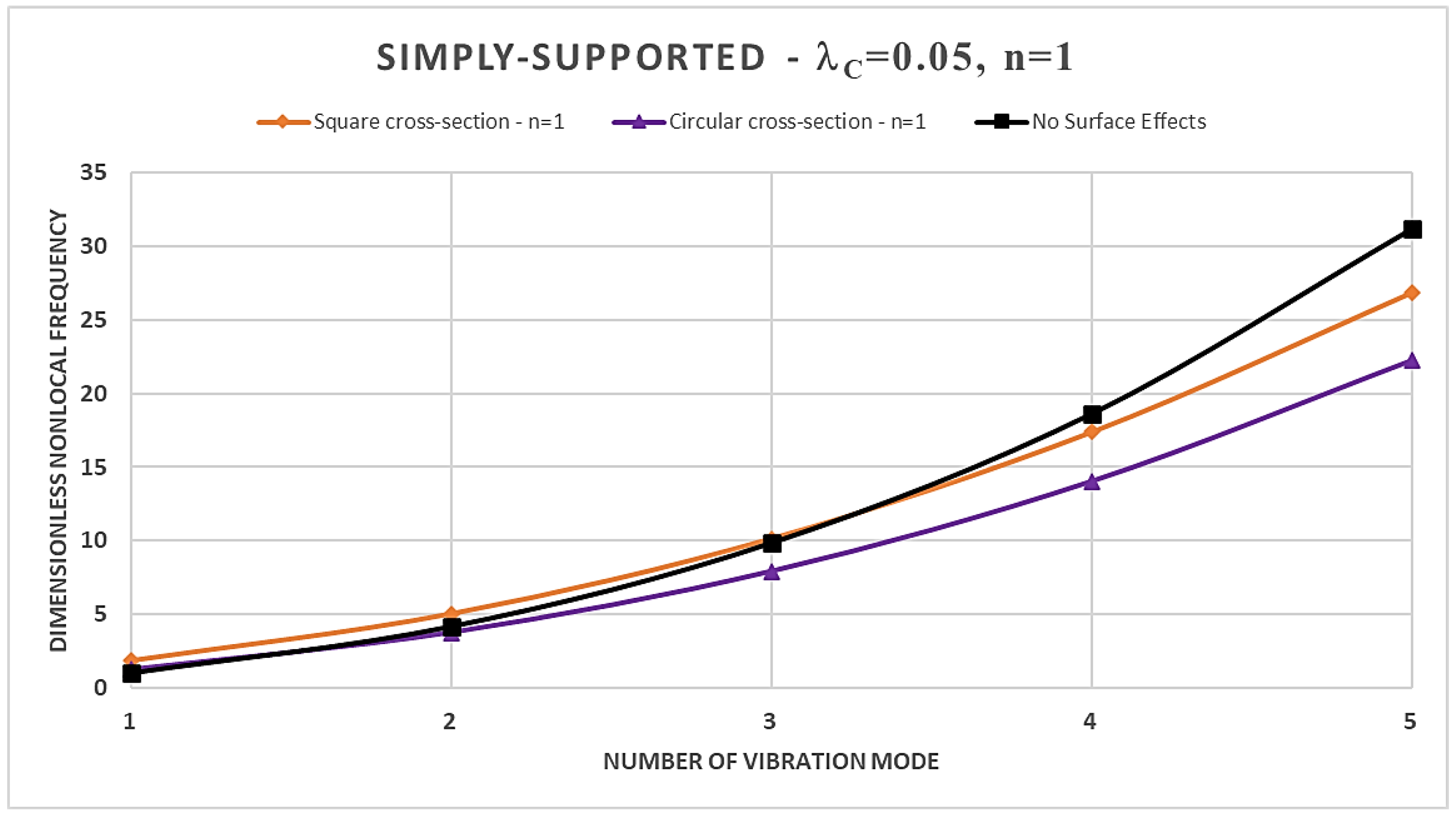
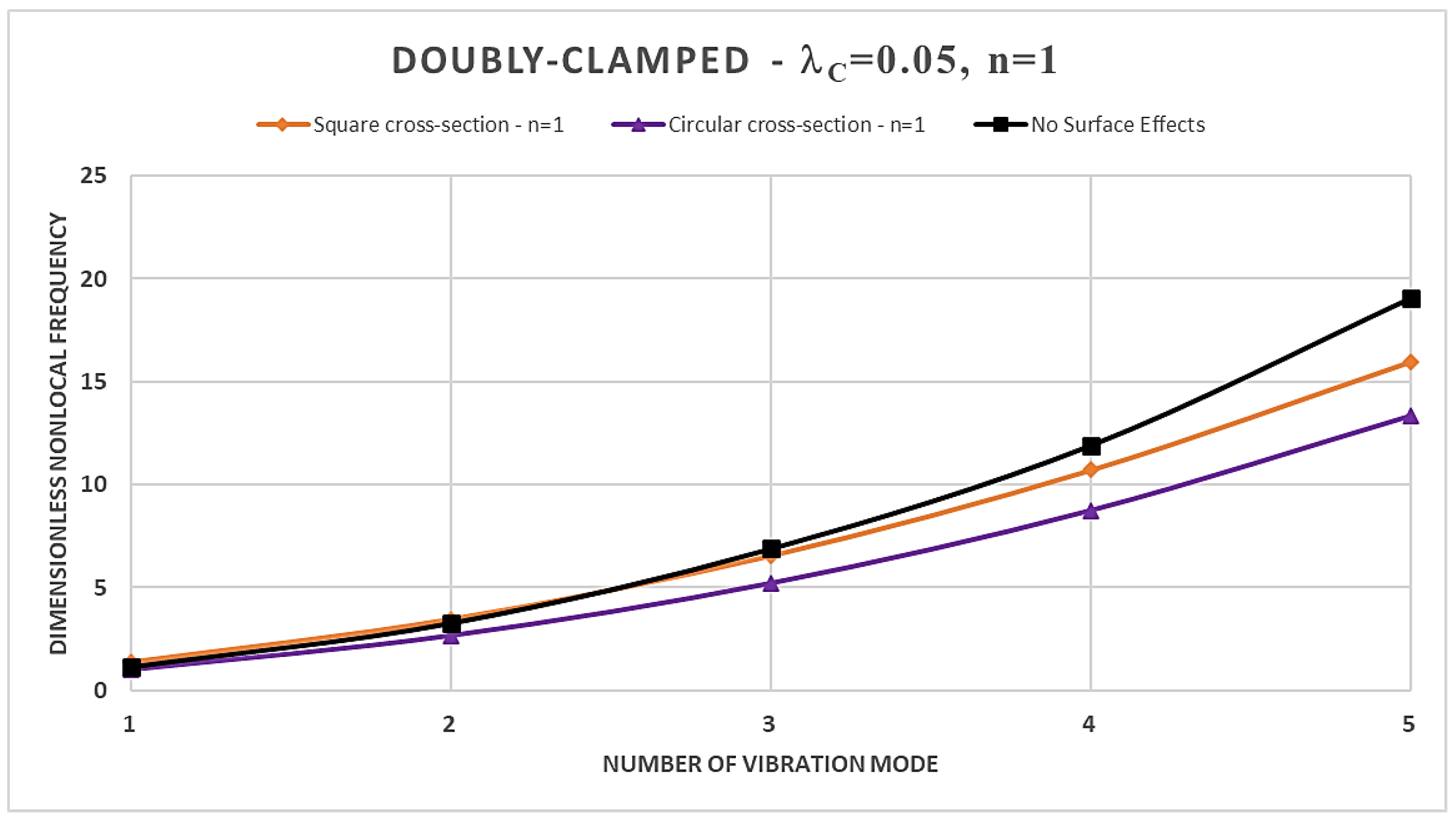
- an increase in the material gradient index consistently results in an increase in the normalized nonlocal frequencies in the case of square cross-section, regardless of the boundary constrains are considered; while, for the case of the circular cross-section the trend is conditioned by the specific static scheme considered;
- -
- the normalized nonlocal frequencies increase by increasing the order of the vibration modes for each static schemes considered;
- -
- the dimensionless nonlocal frequencies reach their maximum value in the case of the C-F nanobeam and the minimum one in the case of C-C nanobeam for each vibration mode, regardless of the cross-sectional shapes chosen;
- -
- the nonlocality strongly influences the dimensionless frequencies, and its effects are stronger for higher vibration modes;
- -
- by increasing the nonlocal parameter, the SSDM formulation always shows an increase in the normalized nonlocal frequencies;
- -
- as the number of vibration modes increases the SSDM model always provides a stiffening behavior;
- -
- in the case of a square cross-section, the presence of surface effects results in additional stiffness, leading to an increase in the dimensionless normalized nonlocal frequencies for the first three vibration modes compared to the model without surface effects; however, the surface energy causes a reduction in dimensionless nonlocal frequencies for the fourth and fifth vibration modes;
- -
- finally, the dynamic behavior of circular FG nanobeams is influenced by the coupled effects of the material gradient index and the nonlocal parameter, as well as by the boundary conditions at the nanobeams ends, and, therefore, it is not possible to define a specific trend.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| λc | Nonlocal parameter | |||
| vB, vS | Poisson’s ratios of the bulk and surface layer | |||
| E | Euclidean space | n | material gradient index | |
| L | Length of FG nanobeam | Ec | Young’s modulus ceramic | |
| Σ | Generic cross-section | Em | Young’s modulus metal | |
| ∂Σ | Perimeter of Σ | ρc | Mass density of ceramic | |
| {O, X, Y, Z} | Cartesian coordinate system | ρm | Mass density of metal | |
| O | Geometric center of Σ | Surface Young modulus of ceramic | ||
| x | Axis of FG nanobeam | Surface Young modulus of metal | ||
| y, z | Principal axes of geometric inertia of Σ | Surface mass density of ceramic | ||
| b, h | Width and thickness Σ | Surface mass density of metal | ||
| R | Radius of Σ | Residual surface stress of ceramic | ||
| B, S | Bulk and surface layers of FG material | Residual surface stress of metal | ||
References
- Ö. Civalek, B. Uzun, M. Ö. Yaylı, “On nonlinear stability analysis of saturated embedded porous nanobeams”, International Journal of Engineering Science, vol. 190, no. 103898, May 2023. [CrossRef]
- F. Cornacchia, F. Fabbrocino, N. Fantuzzi, R. Luciano, R. Penna, “Analytical solution of cross- and angle-ply nano plates with strain gradient theory for linear vibrations and buckling”, Mech. Adv. Mater. Struct, vol. 28, no. 12, pp. 1201-1215, September 2019. [CrossRef]
- X. Xu, D. Shahsavari, B. Karami, “On the forced mechanics of doubly-curved nanoshells”, International Journal of Engineering Science,vol. 168, no. 103538, November 2021. [CrossRef]
- A. Gholipour, M. H. Ghayesh, “Nonlinear coupled mechanics of functionally graded nanobeams”, International Journal of Engineering Science, vol. 150, no. 103221, May 2020. [CrossRef]
- B. Karami, M. Janghorban, “On the mechanics of functionally graded nanoshells”, International Journal of Engineering Science, vol. 153, no. 103309, August 2020. [CrossRef]
- M. H. Ghayesh, A. Farajpour, “A review on the mechanics of functionally graded nanoscale and microscale structures”, International Journal of Engineering Science, vol. 137, pp. 8-36, April 2019. [CrossRef]
- A. Farajpour, M. H. Ghayesh, H. Farokhi, ”A review on the mechanics of nanostructures”, International Journal of Engineering Science, vol. 133, pp. 231-263, December 2018. [CrossRef]
- H. Akhavan, M. Ghadiri, A. Zajkani, “A new model for the cantilever MEMS actuator in magnetorheological elastomer cored sandwich form considering the fringing field and casimir effects”, Mechanical Systems and Signal Processing, vol. 121, pp. 551-561, April 2019. [CrossRef]
- D.C.C. Lam, F. Yang, A.C.M. Chong, J. Wang, P. Tong, “Experiments and theory in strain gradient elasticity”, Journal of the Mechanics and Physics of Solids, vol. 51, no. 8, pp. 1477-1508, August 2003). [CrossRef]
- S. J. L. Billinge, I. Levin, “The Problem with Determining Atomic Structure at the Nanoscale”, Science, vol. 316, no. 5824, pp. 561-565, April 2007. [CrossRef]
- A. Eringen, “Linear theory of nonlocal elasticity and dispersion of plane waves”, Int J. Eng Sci, vol. 10, no. 5, pp. 425–435, May 1972. [CrossRef]
- A. Eringen, “On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves”, J. Appl. Phys., vol. 54, pp. 4703-4710, September 1983. [CrossRef]
- Eringen A.C., 1987. Theory of nonlocal elasticity and some applications, Res Mechanica 21, 313-342.
- C. Lim, G. Zhang, J.N. Reddy, “A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation”, J. Mech. Phys. Solids, vol. 78, pp. 298-313, May 2015. [CrossRef]
- R. Mindlin, “Micro-structure in linear elasticity”, Archive for Rational Mechanics and Analysis, vol.16, no. 1, pp. 51–78, January 1964.
- M. Gurtin, A. Murdoch, “A continuum theory of elastic material surfaces”, Archive for Rational Mechanics and Analysis, vol. 57, no. 4, pp.291–323, December 1975. [CrossRef]
- M. Gurtin, A. Murdoch, “Surface stress in solids”, International Journal of Solids and Structures, vol. 14, no. 6, pp. 431–440, November 1977. 19 November. [CrossRef]
- J. Fernández-Sáez, R. Zaera, J. Loya, J. Reddy, “Bending of Euler–Bernoulli beams using Eringen’s integral formulation: A paradox resolved”, International Journal of Engineering Science, vol. 99, pp. 107-116, February 2016. [CrossRef]
- C. Li, L. Yao, W. Chen, S. Li, “Comments on nonlocal effects in nano-cantilever beams”, International Journal of Engineering Science, vol. 87, pp. 47-57, February 2015. [CrossRef]
- G. Romano, R. Barretta, R, “Comment on the paper ‘‘Exact solution of Eringen’s nonlocal integral model for bending of Euler–Bernoulli and Timoshenko beams by Meral Tuna & Mesut Kirca’’, International Journal of Engineering Science, vol. 109, pp. 240–242, December 2016. [CrossRef]
- G. Romano, R. Barretta, M. Diaco, F. Marotti de Sciarra, “Constitutive boundary conditions and paradoxes in nonlocal elastic nano-beams”, International Journal of Mechanical Sciences, vol. 121, pp. 151–156, August 2017. [CrossRef]
- G. Romano and R. Barretta R., “Nonlocal elasticity in nanobeams: The stress-driven integral model”, Int. J. Eng. Sci., vol. 115, pp. 14-27, June 2017. [CrossRef]
- R. Penna, L. Feo, G. Lovisi, “Hygro-thermal bending behavior of porous FG nano-beams via local/nonlocal strain and stress gradient theories of elasticity”, Composite Structures, vol. 263, no. 113627, May 2021. [CrossRef]
- R. Penna, L. Feo, G. Lovisi, F. Fabbrocino, “Hygro-Thermal Vibrations of Porous FG Nano-Beams Based on Local/Nonlocal Stress Gradient Theory of Elasticity”, Nanomaterials, vol. 11, no. 910, March 2021. [CrossRef]
- R. Penna, A. Lambiase, G. Lovisi and L. Feo, “Investigating hygrothermal bending behavior of FG nanobeams via local/nonlocal stress gradient theory of elasticity with general boundary conditions”, Mech. Adv. Mater. Struct, October 2023. [CrossRef]
- H. Darban, F. Fabbrocino, L. Feo, R. Luciano, “Size-dependent buckling analysis of nanobeams resting on two-parameter elastic foundation through stress-driven nonlocal elasticity model”, Mech. Adv. Mater. Struct, vol. 28, March 2020. [CrossRef]
- A. Apuzzo, R. Barretta, R. Luciano, F. Marotti de Sciarra, R. Penna, “Free vibrations of Bernoulli-Euler nano-beams by the stress-driven nonlocal integral model”, Composites Part B: Engineering, vol. 123, pp. 105-111, August 2017. [CrossRef]
- Caporale, H. Darban, and R. Luciano, Exact closed-form solutions for nonlocal beams with loading discontinuities, Mech. Adv. Mater. Struct., vol. 29, no. 5, pp. 694–704, 2022. [CrossRef]
- Y. Tang, and H. Qing, Bi-Helmholtz kernel based stress-driven nonlocal integral model with discontinuity for size-dependent fracture analysis of edge-cracked nanobeam, Mech. Adv. Mater. Struct., pp. 1–11, 2023. [CrossRef]
- R. Barretta, L. Feo, L., R. Luciano, F. Marotti de Sciarra, R. Penna, "Nano-beams under torsion: a stress-driven nonlocal approach", PSU Research Review, vol. 1, no. 2, pp. 164-169, May 2017. [CrossRef]
- R. Penna, G. Lovisi, L. Feo, “Dynamic Response of Multilayered Polymer Functionally Graded Carbon Nanotube Reinforced Composite (FG-CNTRC) Nano-Beams in Hygro-Thermal Environment”, Polymers, vol. 13, no. 2340, July 2021. [CrossRef]
- Francesco Fabbrocino, Marco Francesco Funari, Fabrizio Greco, Paolo Lonetti, Raimondo Luciano, Rosa Penna, Dynamic crack growth based on moving mesh method,Composites Part B: Engineering, Volume 174, 2019, 107053. [CrossRef]
- Andrea Apuzzo, Chiara Bartolomeo, Raimondo Luciano, Daniela Scorza, Novel local/nonlocal formulation of the stress-driven model through closed form solution for higher vibrations modes, Composite Structures, Volume 252, 2020, 112688. [CrossRef]
- Raimondo Luciano, Hossein Darban, Chiara Bartolomeo, Francesco Fabbrocino, Daniela Scorza, Free flexural vibrations of nanobeams with non-classical boundary conditions using stress-driven nonlocal model, Mechanics Research Communications, Volume 107, 2020, 103536. [CrossRef]
- R. Penna, “Bending analysis of functionally graded nanobeams based on stress-driven nonlocal model incorporating surface energy effects”, International Journal of Engineering Science, vol. 189, no. 103887, August 2023. [CrossRef]
- L. Feo, G. Lovisi and R. Penna, “Free vibration analysis of functionally graded nanobeams based on surface stress-driven nonlocal model”, Mech. Adv. Mater. Struct, December 2023. [CrossRef]
- Rosa Penna, Luciano Feo, Giuseppe Lovisi, Arturo Pascuzzo, A stress-driven model incorporating surface energy effects for the bending analysis of functionally graded nanobeams with loading discontinuities, Procedia Structural Integrity, Volume 47, 2023, Pages 789-799, ISSN 2452-3216. [CrossRef]
- G. Lovisi, “Application of the surface stress-driven nonlocal theory of elasticity for the study of the bending response of FG cracked nanobeams”, Composite Structures, vol. 324, no. 117549, November 2023. [CrossRef]
- S. Saffari, M. Hashemian, D. Toghraie, “Dynamic stability of functionally graded nanobeam based on nonlocal Timoshenko theory considering surface effects”, Physica B: Condensed Matter, vol. 520, pp. 97–105, September 2017. [CrossRef]
| Material | Parameters | Values | Unit |
| Ceramic (Si) |
210 | [GPa] | |
| -10.6543 | [N/m] | ||
| 0.6048 | [N/m] | ||
| 2370 | [kg/m3] | ||
| 3.1688 10-7 | [kg/m2] | ||
| Metal (Al) |
70 | [GPa] | |
| 5.1882 | [N/m] | ||
| 2700 | [kg/m3] | ||
| 0.9108 | [N/m] | ||
| 5.4610 10-7 | [kg/m2] |
| Mode | No Surface Effects | Square Cross-Section | Circular Cross-Section | ||||||
| Present | Ref. [34] | ||||||||
| 0.00+ | 1.0000 | 1.0000 | 2.2799 | 2.7626 | 3.0027 | 1.4981 | 1.7904 | 1.8865 | |
| 6.2669 | 6.2669 | 8.5112 | 9.7142 | 10.3436 | 5.9107 | 6.7299 | 6.9369 | ||
| 17.5475 | 17.5475 | 19.1051 | 20.4685 | 21.2408 | 13.9919 | 15.2841 | 15.4319 | ||
| 34.3860 | - | 33.8579 | 35.1898 | 35.9955 | 25.6689 | 27.4754 | 27.5037 | ||
| 56.8427 | - | 51.8652 | 53.0981 | 53.9124 | 40.5012 | 42.7677 | 42.6559 | ||
| 0.01 | 1.0101 | - | 2.2946 | 2.7797 | 3.0209 | 1.5081 | 1.8020 | 1.8985 | |
| 6.3357 | - | 8.5816 | 9.7884 | 10.4201 | 5.9625 | 6.7859 | 6.9931 | ||
| 17.7713 | - | 19.3130 | 20.6764 | 21.4494 | 14.1515 | 15.4522 | 15.5981 | ||
| 34.9207 | - | 34.3280 | 35.6554 | 36.4594 | 26.0392 | 27.8616 | 27.8852 | ||
| 57.9402 | - | 52.7813 | 54.0042 | 54.8148 | 41.2392 | 43.5319 | 43.4113 | ||
| 0.03 | 1.0309 | - | 2.3244 | 2.8137 | 3.0569 | 1.5284 | 1.8254 | 1.9228 | |
| 6.5093 | - | 8.7539 | 9.9674 | 10.6034 | 6.0897 | 6.9227 | 7.1298 | ||
| 18.5002 | - | 19.9871 | 21.3409 | 22.1109 | 14.6669 | 15.9929 | 16.1306 | ||
| 37.0797 | - | 36.2703 | 37.5626 | 38.3510 | 27.5482 | 29.4378 | 29.4370 | ||
| 63.0858 | - | 57.2474 | 58.4058 | 59.1879 | 44.7714 | 47.2065 | 45.1013 | ||
| 0.05 | 1.0524 | 1.0524 | 2.3545 | 2.8477 | 3.0926 | 1.5490 | 1.8491 | 1.9471 | |
| 6.7278 | 6.7278 | 8.9646 | 10.1836 | 10.8232 | 6.2460 | 7.0897 | 7.2959 | ||
| 19.5634 | 19.5634 | 20.9672 | 22.2996 | 23.0608 | 15.4154 | 16.7767 | 16.9002 | ||
| 40.4580 | - | 39.3323 | 40.5640 | 41.3229 | 29.9179 | 31.9145 | 31.8738 | ||
| 71.3062 | - | 64.4541 | 65.5116 | 66.2479 | 50.4474 | 53.1200 | 52.8692 | ||
| 0.10 | 1.1087 | 1.1087 | 2.4306 | 2.9331 | 3.1817 | 1.6011 | 1.9090 | 2.0088 | |
| 7.4325 | 7.4325 | 9.6210 | 10.8467 | 11.4935 | 6.7369 | 7.6095 | 7.8101 | ||
| 23.2560 | 23.2560 | 24.3703 | 25.6113 | 26.3313 | 18.0146 | 19.4950 | 19.5662 | ||
| 52.1914 | - | 50.0444 | 51.0811 | 51.7429 | 38.1909 | 40.5729 | 40.3977 | ||
| 99.0703 | - | 88.9574 | 89.7452 | 90.3647 | 69.7106 | 73.2203 | 72.7155 | ||
| Mode | No Surface Effects | Square Cross-Section | Circular Cross-Section | ||||||
| Present | Ref. [34] | ||||||||
| 0.00+ | 1.0000 | 1.0000 | 1.5375 | 1.8218 | 1.9718 | 1.0416 | 1.2124 | 1.2649 | |
| 4.0000 | 4.0000 | 4.4988 | 4.8850 | 5.1033 | 3.2633 | 3.5906 | 3.6395 | ||
| 9.0000 | 9.0000 | 9.0110 | 9.4167 | 9.6589 | 6.7903 | 7.2932 | 7.3111 | ||
| 16.0000 | - | 14.7940 | 15.1850 | 15.4386 | 11.4929 | 12.1644 | 12.1399 | ||
| 24.9999 | - | 21.5186 | 21.8782 | 22.1411 | 17.1945 | 17.9903 | 17.9198 | ||
| 0.01 | 1.0005 | - | 1.5379 | 1.8221 | 1.9721 | 1.0419 | 1.2127 | 1.2651 | |
| 4.0077 | - | 4.5052 | 4.8909 | 5.1090 | 3.2684 | 3.5953 | 3.6445 | ||
| 9.0391 | - | 9.0449 | 9.4485 | 9.6905 | 6.8170 | 7.3206 | 7.3380 | ||
| 16.1233 | - | 14.8988 | 15.2869 | 15.5391 | 11.5764 | 12.2508 | 12.2248 | ||
| 25.3003 | - | 21.7635 | 22.1185 | 22.3792 | 17.3934 | 18.2228 | 18.1220 | ||
| 0.03 | 1.0042 | - | 1.5402 | 1.8240 | 1.9739 | 1.0438 | 1.2146 | 1.2669 | |
| 4.0662 | - | 4.5541 | 4.9359 | 5.1521 | 3.3068 | 3.6349 | 3.6824 | ||
| 9.3321 | - | 9.2994 | 9.6921 | 9.9285 | 7.0167 | 7.5272 | 7.5399 | ||
| 17.0355 | - | 15.6762 | 16.0440 | 16.2860 | 12.1951 | 12.8912 | 12.8545 | ||
| 27.4868 | - | 23.5495 | 23.8728 | 24.1196 | 18.8430 | 19.6904 | 19.5969 | ||
| 0.05 | 1.0110 | 1.0110 | 1.5446 | 1.8278 | 1.9774 | 1.0474 | 1.2181 | 1.2702 | |
| 4.1740 | 4.1740 | 4.6445 | 5.0194 | 5.2322 | 3.3779 | 3.7440 | 3.7525 | ||
| 9.8598 | 9.8598 | 9.7601 | 10.1345 | 10.3614 | 7.3780 | 7.9012 | 7.9060 | ||
| 18.6338 | - | 17.0446 | 17.3809 | 17.6073 | 13.2832 | 14.0186 | 13.9640 | ||
| 31.2018 | - | 26.5951 | 26.8736 | 27.1016 | 21.3127 | 22.2403 | 22.1147 | ||
| 0.10 | 1.0389 | 1.0389 | 1.5628 | 1.8431 | 1.9916 | 1.0623 | 1.2326 | 1.2838 | |
| 4.5952 | 4.5952 | 5.0033 | 5.3532 | 5.5536 | 3.6588 | 3.9955 | 4.0315 | ||
| 11.8266 | 11.8266 | 11.4990 | 11.8171 | 12.0146 | 8.7368 | 9.3128 | 9.2904 | ||
| 24.3000 | - | 21.9395 | 22.1933 | 22.3809 | 17.1639 | 18.0516 | 17.9408 | ||
| 43.7693 | - | 36.9613 | 37.1361 | 37.3285 | 29.7045 | 30.9210 | 30.6978 | ||
| Mode | No Surface Effects | Square Cross-Section | Circular Cross-Section | ||||||
| Present | Ref. [34] | ||||||||
| 0.00+ | 1.0000 | 1.0000 | 1.2776 | 1.4411 | 1.5296 | 0.8955 | 1.0101 | 1.0362 | |
| 3.2406 | 3.2406 | 3.4794 | 3.7020 | 3.8302 | 2.5552 | 2.7816 | 2.8020 | ||
| 6.7614 | 6.7614 | 6.6373 | 6.8740 | 7.0185 | 5.0325 | 5.3803 | 5.3797 | ||
| 11.5623 | - | 10.5625 | 10.7930 | 10.9466 | 8.2399 | 8.6987 | 8.6705 | ||
| 17.6435 | - | 15.0470 | 15.2594 | 15.4214 | 12.0630 | 12.5991 | 12.5415 | ||
| 0.01 | 1.0108 | - | 1.2883 | 1.4520 | 1.5407 | 0.9035 | 1.0186 | 1.0447 | |
| 3.2813 | - | 3.5167 | 3.7389 | 3.8670 | 2.5840 | 2.8118 | 2.8318 | ||
| 6.8644 | - | 6.7266 | 6.9619 | 7.1059 | 5.1033 | 5.4539 | 5.4523 | ||
| 11.7807 | - | 10.7415 | 10.9692 | 11.1219 | 8.3852 | 8.8487 | 8.8187 | ||
| 18.0579 | - | 15.3677 | 15.5760 | 15.7366 | 12.3295 | 12.8723 | 12.8117 | ||
| 0.03 | 1.0375 | - | 1.3129 | 1.4763 | 1.5651 | 0.9221 | 1.0381 | 1.0639 | |
| 3.4104 | - | 3.6320 | 3.8504 | 3.9766 | 2.6734 | 2.9048 | 2.9230 | ||
| 7.2715 | - | 7.0827 | 7.3084 | 7.4476 | 5.3834 | 5.7448 | 5.7382 | ||
| 12.7887 | - | 11.5928 | 11.8040 | 11.9489 | 9.0666 | 9.5542 | 9.5140 | ||
| 20.1774 | - | 17.0764 | 17.2602 | 17.4109 | 13.8938 | 14.3097 | 14.2316 | ||
| 0.05 | 1.0703 | 1.0703 | 1.3416 | 1.5041 | 1.5925 | 0.9442 | 1.0611 | 1.0864 | |
| 3.5967 | 3.5967 | 3.7972 | 4.0084 | 4.1311 | 2.8017 | 3.0378 | 3.0528 | ||
| 7.9066 | 7.9066 | 7.6426 | 7.8527 | 7.9839 | 5.8222 | 6.2008 | 6.1861 | ||
| 14.4028 | - | 12.9725 | 13.1593 | 13.2927 | 10.1653 | 10.6941 | 10.6379 | ||
| 23.5687 | - | 19.8429 | 19.9935 | 20.1319 | 15.9729 | 16.6313 | 16.5260 | ||
| 0.10 | 1.1749 | 1.1749 | 1.4304 | 1.5875 | 1.6737 | 1.0131 | 1.1318 | 1.1418 | |
| 4.2468 | 4.2468 | 4.3784 | 4.5650 | 4.6750 | 3.2517 | 3.5049 | 3.5094 | ||
| 10.1365 | 10.1365 | 9.6348 | 9.8008 | 9.9094 | 7.3762 | 7.8211 | 7.7804 | ||
| 19.9215 | - | 17.7410 | 17.8691 | 17.9770 | 13.9492 | 14.6302 | 14.5244 | ||
| 34.7602 | - | 29.0444 | 29.1236 | 29.2425 | 23.4328 | 24.3488 | 24.1620 | ||
| Mode | No Surface Effects | Square Cross-Section | Circular Cross-Section | ||||||
| Present | Ref. [34] | ||||||||
| 0.00+ | 1.0000 | 1.0000 | 1.1448 | 1.2397 | 1.2927 | 0.8225 | 0.9067 | 0.9181 | |
| 2.7565 | 2.7565 | 2.8670 | 3.0045 | 3.0849 | 2.1245 | 2.2952 | 2.3016 | ||
| 5.4039 | 5.4039 | 5.2236 | 5.3724 | 5.4652 | 3.9804 | 4.2402 | 4.2136 | ||
| 8.9329 | - | 8.0769 | 8.2231 | 8.3237 | 6.3237 | 6.6614 | 6.6334 | ||
| 13.3443 | - | 11.2860 | 11.4210 | 11.5289 | 9.0751 | 9.4637 | 9.4155 | ||
| 0.01 | 1.0214 | - | 1.1656 | 1.2606 | 1.3137 | 0.8382 | 0.9233 | 0.9345 | |
| 2.8211 | - | 2.9263 | 3.0633 | 3.1436 | 2.1703 | 2.3433 | 2.3491 | ||
| 5.5464 | - | 5.3466 | 5.4941 | 5.5864 | 4.0783 | 4.3420 | 4.3320 | ||
| 9.2036 | - | 8.2957 | 8.4395 | 8.5393 | 6.5027 | 6.8459 | 6.8158 | ||
| 13.8141 | - | 11.6416 | 11.7729 | 11.8798 | 9.3734 | 9.7689 | 9.7176 | ||
| 0.03 | 1.0726 | - | 1.2135 | 1.3075 | 1.3603 | 0.8745 | 0.9615 | 0.9720 | |
| 3.0062 | - | 3.0942 | 3.2271 | 3.3054 | 2.3001 | 2.4789 | 2.4823 | ||
| 6.0329 | - | 5.7732 | 5.9120 | 6.0001 | 4.4141 | 4.6914 | 4.6761 | ||
| 10.2718 | - | 9.1936 | 9.3233 | 9.4169 | 7.2234 | 7.5923 | 7.5524 | ||
| 15.8833 | - | 13.2967 | 13.4079 | 13.5077 | 10.5476 | 11.1652 | 11.0979 | ||
| 0.05 | 1.1349 | 1.1349 | 1.2701 | 1.3620 | 1.4138 | 0.9178 | 1.0066 | 1.0161 | |
| 3.2614 | 3.2614 | 3.3252 | 3.4508 | 3.5253 | 2.4786 | 2.6649 | 2.6648 | ||
| 6.8814 | 6.8814 | 6.4143 | 6.5396 | 6.6208 | 4.9160 | 5.2143 | 5.1908 | ||
| 11.9129 | - | 10.5959 | 10.7059 | 10.7909 | 8.3411 | 8.7528 | 8.6978 | ||
| 19.0851 | - | 15.9012 | 15.9867 | 16.0780 | 12.8489 | 13.3540 | 13.2626 | ||
| 0.10 | 1.1766 | 1.1766 | 1.4485 | 1.5316 | 1.5790 | 1.0549 | 1.1487 | 1.1546 | |
| 4.1322 | 4.1322 | 4.1225 | 4.2251 | 4.2875 | 3.0922 | 3.3059 | 3.2939 | ||
| 9.2325 | 9.2325 | 8.6431 | 8.7337 | 8.7977 | 6.6519 | 7.0286 | 6.9793 | ||
| 17.4074 | - | 15.3466 | 15.4132 | 15.4815 | 12.1120 | 12.6785 | 12.5778 | ||
| 29.4704 | - | 24.4213 | 24.4545 | 24.5363 | 19.7635 | 20.5082 | 20.3449 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





