Submitted:
06 May 2023
Posted:
08 May 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Running Vacuum in the Universe
3. Type I: Running Vacuum Interacting with Dark Matter
3.1. Background Equations
3.2. Perturbation Equations
3.3. Type I with Threshold
4. Type II: Running Vacuum with Running
4.1. Background Equations
4.2. Perturbation Equations
| Survey | z | Observable | Measurement | References |
|---|---|---|---|---|
| 6dFGS+SDSS MGS | [Mpc] | [Mpc] | [122] | |
| DR12 BOSS | [123] | |||
| WiggleZ | [Mpc] | [Mpc] | [124] | |
| [Mpc] | [Mpc] | |||
| [Mpc] | [Mpc] | |||
| DESY3 | [125] | |||
| eBOSS Quasar | [126] | |||
| Ly-Forests | [127] | |||
| z | [km/s/Mpc] | References |
|---|---|---|
| [128] | ||
| [129] | ||
| [128] | ||
| [130] | ||
| [131] | ||
| [131] | ||
| [128] | ||
| [130] | ||
| [128] | ||
| [131] | ||
| [132] | ||
| [130] | ||
| [132] | ||
| [132] | ||
| [132] | ||
| [133] | ||
| [132] | ||
| [134] | ||
| [131] | ||
| [131] | ||
| [135] | ||
| [131] | ||
| [131] | ||
| [134] | ||
| [130] | ||
| [131] | ||
| [130] | ||
| [136] | ||
| [130] | ||
| [130] | ||
| [130] | ||
| [136] |
5. Data and Methodology
- Baseline: In our Baseline dataset we consider the string SNIa+BAO++LSS+CMB. Notice that here we do not include the SH0ES data.
- Baseline+SH0ES: The Baseline dataset is in this case complemented with the apparent magnitudes of the SNIa in the host galaxies and their distance moduli employed by SH0ES.
- Baseline (No pol.): The same as in the Baseline case, but now removing the high-ℓ polarization data from the CMB likelihood. That is to say, we have replaced the “CMB” dataset with “CMB (No pol.)”.
- Baseline (No pol.)+SH0ES: The same as in “Baseline (No pol.)”, but including also the data from SH0ES.
| Baseline | |||||
|---|---|---|---|---|---|
| Parameter | CDM | type-I RRVM | type-I RRVM | type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| DIC | - | -2.04 | +15.34 | -4.18 | |
| Baseline +SH0ES | |||||
|---|---|---|---|---|---|
| Parameter | CDM | type-I RRVM | type-I RRVM | type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| - | |||||
6. Discussion of the Results
| Baseline (No pol.) | |||||
|---|---|---|---|---|---|
| Parameter | CDM | type-I RRVM | type-I RRVM | type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| - | |||||
| Baseline (No pol.) +SH0ES | |||||
|---|---|---|---|---|---|
| Parameter | CDM | type-I RRVM | type-I RRVM | type-II RRVM | XCDM |
| (km/s/Mpc) | |||||
| - | - | ||||
| - | - | - | - | ||
| - | - | - | - | ||
| M | |||||
| (Mpc) | |||||
| - | |||||
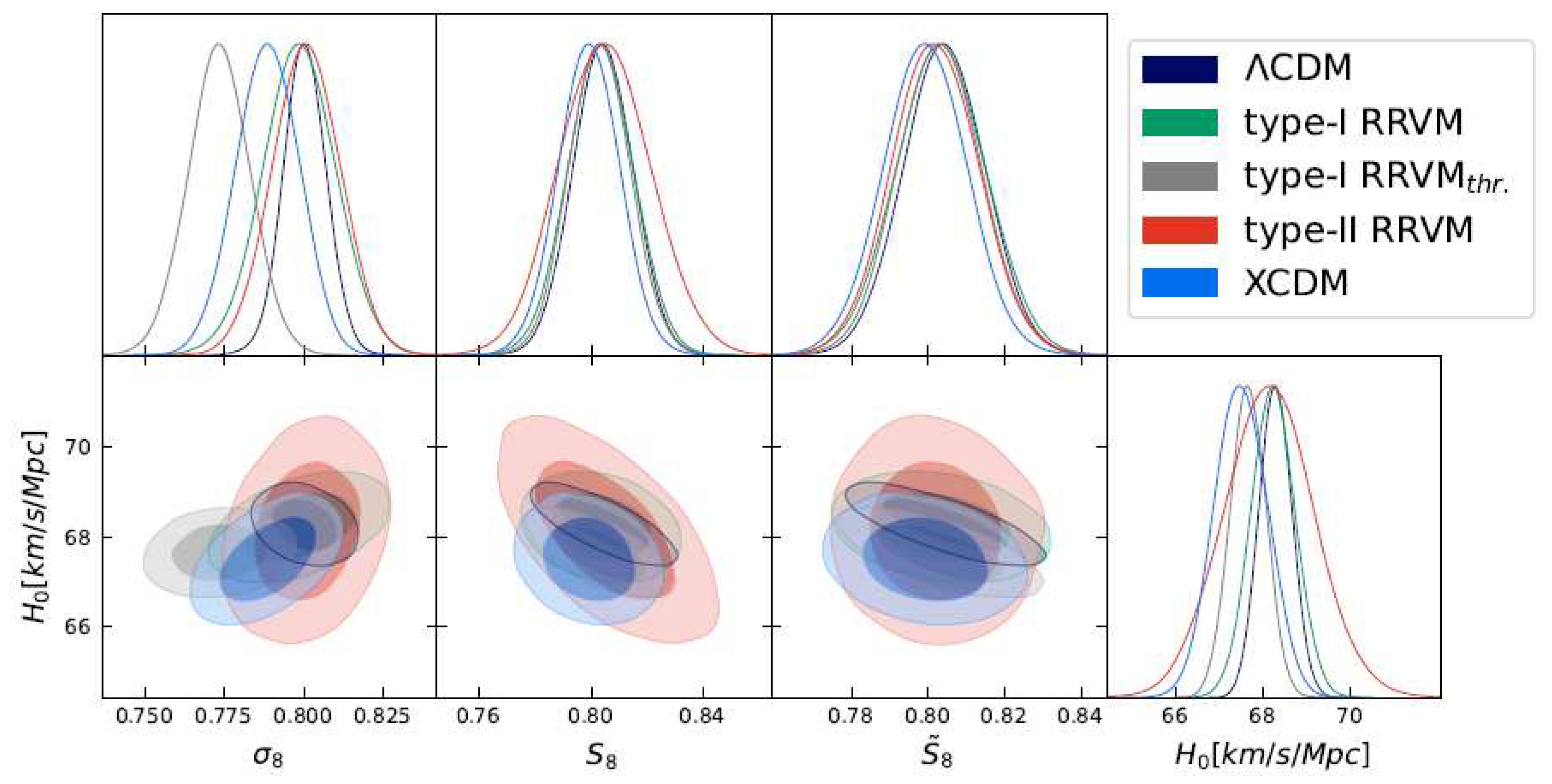
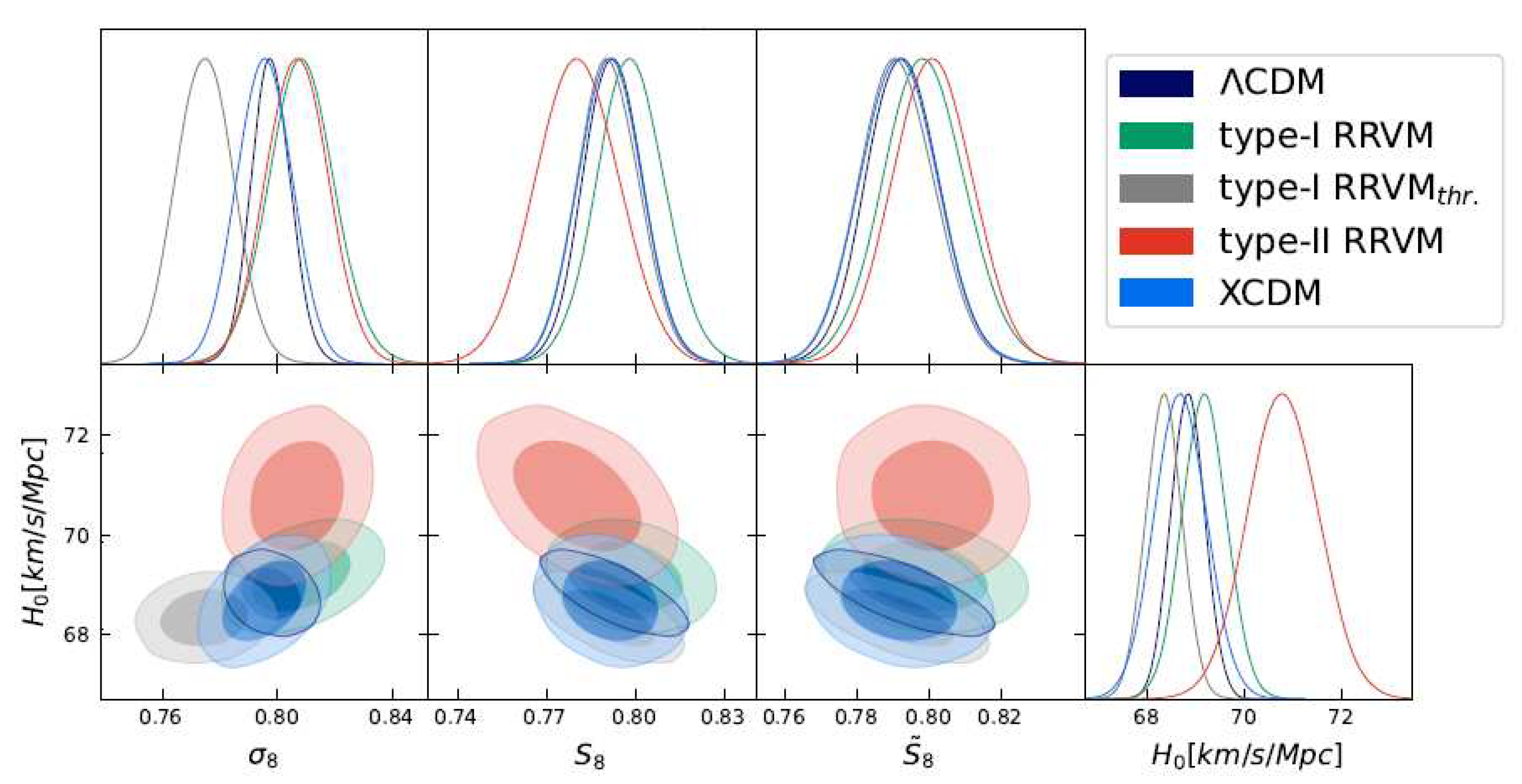
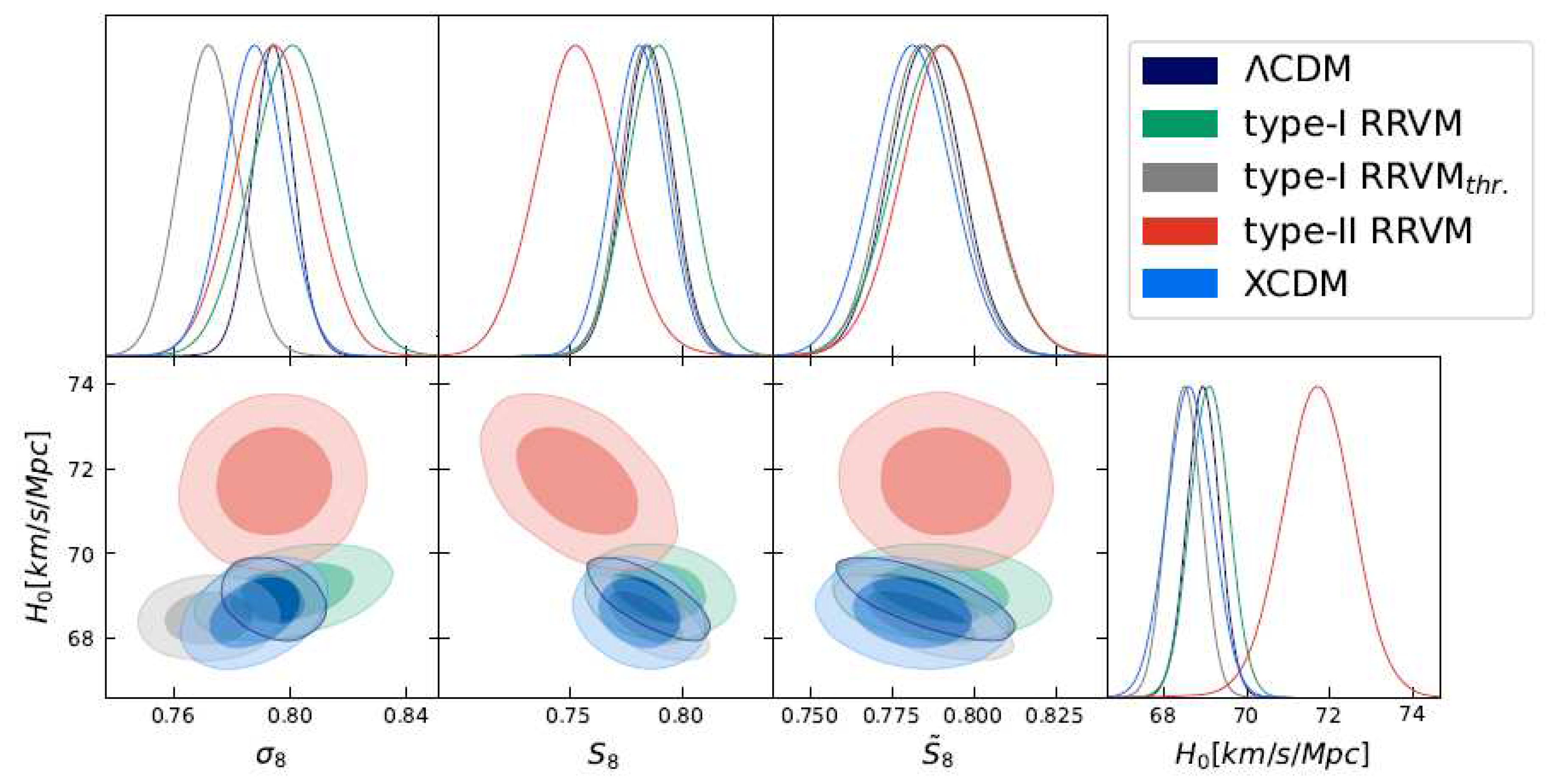
7. Conclusions
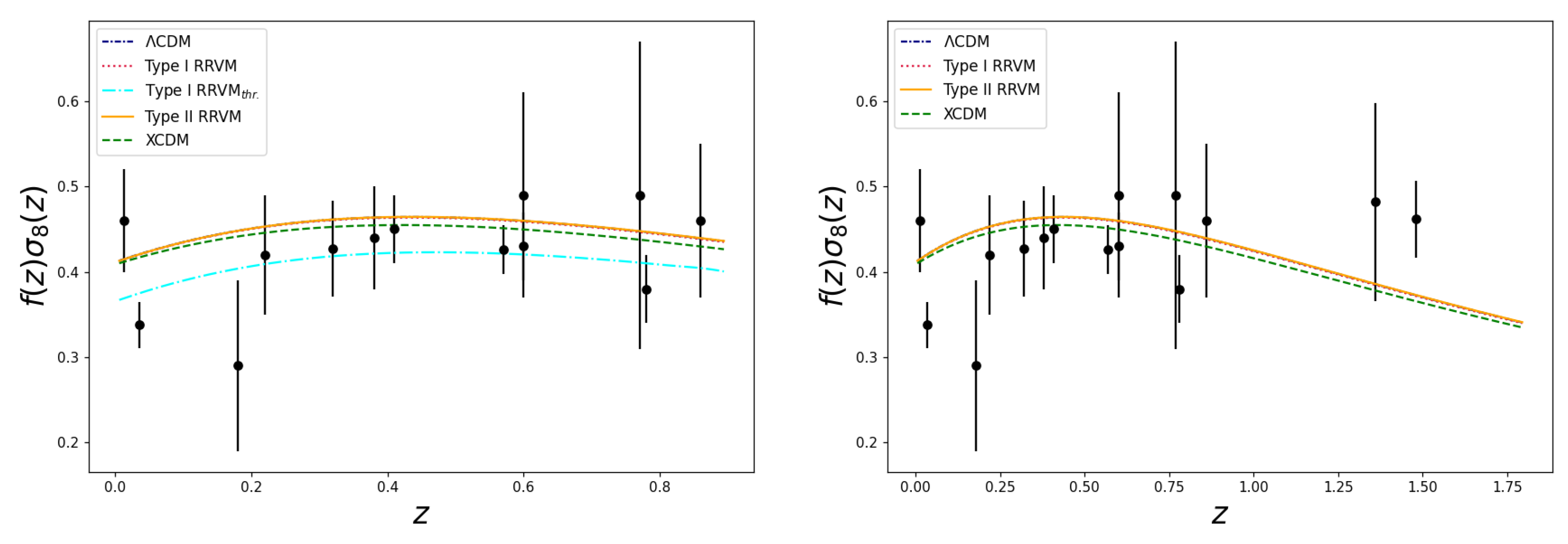
Acknowledgments
Appendix A. Additional Tables
| Baseline | |||||
|---|---|---|---|---|---|
| Experiment | CDM | type-I RRVM | type-I RRVM | type-II RRVM | XCDM |
| CMB | |||||
| SNIa | |||||
| BAO- (correl.) | |||||
| BAO | |||||
| Baseline+SH0ES | |||||
|---|---|---|---|---|---|
| Experiment | CDM | type-I RRVM | type-I RRVM | type-II RRVM | XCDM |
| CMB | |||||
| SNIa | |||||
| BAO- (correl.) | |||||
| BAO | |||||
| Baseline (No pol.) | |||||
|---|---|---|---|---|---|
| Experiment | CDM | type-I RRVM | type-I RRVM | type-II RRVM | XCDM |
| CMB | |||||
| SNIa | |||||
| BAO- (correl.) | |||||
| BAO | |||||
References
- P. J. E. Peebles, Principles of physical cosmology. Princeton University Press, 1993.
- P. J. E. Peebles, “Tests of Cosmological Models Constrained by Inflation”, Astrophys. J., vol. 284, pp. 439–444, 1984.
- M. S. Turner, “The Road to Precision Cosmology”, 2201.04741 [astro-ph.CO] (to appear in Annu. Rev. Nucl. Part. Sci. 2022; arXiv:2201.04741.
- L. Amendola and S. Tsujikawa, Dark Energy: Theory and Observations. Cambridge University Press, 2015.
- P. J. E. Peebles and B. Ratra, “The Cosmological Constant and Dark Energy”, Rev. Mod. Phys., vol. 75, pp. 559–606, 2003, astro-ph/0207347.
- T. Padmanabhan, “Cosmological constant: The Weight of the vacuum”, Phys. Rept., vol. 380, pp. 235–320, 2003, hep-th/0212290.
- A. G. Riess et al., “Observational evidence from supernovae for an accelerating universe and a cosmological constant”, Astron. J., vol. 116, pp. 1009–1038, 1998, astro-ph/9805201.
- S. Perlmutter et al., “Measurements of Ω and Λ from 42 high redshift supernovae”, Astrophys. J., vol. 517, pp. 565–586, 1999, astro-ph/9812133.
- P. de Bernardis et al., “A Flat universe from high resolution maps of the cosmic microwave background radiation”, Nature, vol. 404, pp. 955–959, 2000, astro-ph/0004404.
- D. J. Eisenstein et al., “Detection of the Baryon Acoustic Peak in the Large-Scale Correlation Function of SDSS Luminous Red Galaxies”, Astrophys. J., vol. 633, pp. 560–574, 2005, astro-ph/0501171.
- M. Tegmark et al., “Cosmological Constraints from the SDSS Luminous Red Galaxies”, Phys. Rev. D, vol. 74, p. 123507, 2006, astro-ph/0608632.
- E. Komatsu et al., “Five-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation”, Astrophys. J. Suppl., vol. 180, pp. 330–376, 2009. arXiv:0803.0547.
- A. G. Riess, L. Macri, S. Casertano, H. Lampeitl, H. C. Ferguson, A. V. Filippenko, S. W. Jha, W. Li, and R. Chornock, “A 3% Solution: Determination of the Hubble Constant with the Hubble Space Telescope and Wide Field Camera 3”, Astrophys. J., vol. 730, p. 119, 2011, arXiv:1103.2976 [Erratum: Astrophys. J., vol. 732, p. 129, 2011].
- P. A. R. Ade et al., “Planck 2015 results. XIII. Cosmological parameters”, Astron. Astrophys., vol. 594, p. A13, 2016. arXiv:1502.01589.
- N. Aghanim et al., “Planck 2018 results. VI. Cosmological parameters”, Astron. Astrophys., vol. 641, p. A6, 2020. arXiv:1807.06209.
- S. Weinberg, “The Cosmological Constant Problem”, Rev. Mod. Phys., vol. 61, pp. 1–23, 1989.
- J. Solà, “Cosmological constant and vacuum energy: old and new ideas”, J. Phys. Conf. Ser., vol. 453, p. 012015, 2013. arXiv:1306.1527.
- P. J. Steinhardt, “A quintessential introduction to dark energy”, Phil. Trans. Roy. Soc. Lond. A, vol. 361, pp. 2497–2513, 2003.
- J. Solà and A. Gómez-Valent, “The Λ¯CDM cosmology: From inflation to dark energy through running Λ”, Int. J. Mod. Phys. D, vol. 24, p. 1541003, 2015. arXiv:1501.03832.
- J. Solà Peracaula, “The cosmological constant problem and running vacuum in the expanding universe”, Phil. Trans. Roy. Soc. Lond. A, vol. 380, p. 20210182, 2022. arXiv:2203.13757.
- Y. Zel’dovich, “Cosmological constant and elementary particles”, Sov. Phys. JETP. Lett., vol. 6, p. 3167, 1967.
- E. J. Copeland, M. Sami, and S. Tsujikawa, “Dynamics of dark energy”, Int. J. Mod. Phys. D, vol. 15, pp. 1753–1936, 2006, hep-th/0603057.
- S. Tsujikawa, “Quintessence: A Review”, Class. Quant. Grav., vol. 30, p. 214003, 2013. arXiv:1304.1961.
- C. Moreno-Pulido and J. Solà, “Running vacuum in quantum field theory in curved spacetime: renormalizing ρvac without ∼m4 terms”, Eur. Phys. J. C, vol. 80, no. 8, p. 692, 2020. arXiv:2005.03164.
- C. Moreno-Pulido and J. Solà Peracaula, “Renormalizing the vacuum energy in cosmological spacetime: implications for the cosmological constant problem”, Eur. Phys. J. C, vol. 82, no. 6, p. 551, 2022. arXiv:2201.05827.
- C. Moreno-Pulido and J. Solà Peracaula, “Equation of state of the running vacuum”, Eur. Phys. J. C, vol. 82, no. 12, p. 1137, 2022. arXiv:2207.07111.
- C. Moreno-Pulido, J. Solà Peracaula, and S. Cheraghchi, “Running vacuum in QFT in FLRW spacetime: The dynamics of ρvac(H) from the quantized matter fields”, 2023. arXiv:2301.05205.
- L. Perivolaropoulos and F. Skara, “Challenges for ΛCDM: An update”, New Astron. Rev., vol. 95, p. 101659, 2022. arXiv:2105.05208.
- E. Di Valentino et al., “Snowmass2021 - Letter of interest cosmology intertwined II: The hubble constant tension”, Astropart. Phys., vol. 131, p. 102605, 2021. arXiv:2008.11284.
- C. Krishnan, E. O. Colgáin, M. M. Sheikh-Jabbari, and T. Yang, “Running Hubble Tension and a H0 Diagnostic”, Phys. Rev. D, vol. 103, no. 10, p. 103509, 2021. arXiv:2011.02858.
- M. G. Dainotti, B. De Simone, T. Schiavone, G. Montani, E. Rinaldi, and G. Lambiase, “On the Hubble constant tension in the SNe Ia Pantheon sample”, Astrophys. J., vol. 912, no. 2, p. 150, 2021. arXiv:2103.02117.
- E. Di Valentino et al., “Cosmology Intertwined III: fσ8 and S8”, Astropart. Phys., vol. 131, p. 102604, 2021. arXiv:2008.11285.
- E. Macaulay, I. K. Wehus, and H. K. Eriksen, “Lower Growth Rate from Recent Redshift Space Distortion Measurements than Expected from Planck”, Phys. Rev. Lett., vol. 111, no. 16, p. 161301, 2013. arXiv:1303.6583.
- S. Nesseris, G. Pantazis, and L. Perivolaropoulos, “Tension and constraints on modified gravity parametrizations of Geff(z) from growth rate and Planck data”, Phys. Rev. D, vol. 96, no. 2, p. 023542, 2017. arXiv:1703.10538.
- W. Lin and M. Ishak, “Cosmological discordances II: Hubble constant, Planck and large-scale-structure data sets”, Phys. Rev. D, vol. 96, no. 8, p. 083532, 2017. arXiv:1708.09813.
- A. Gómez-Valent and J. Solà Peracaula, “Density perturbations for running vacuum: a successful approach to structure formation and to the σ8-tension”, Mon. Not. Roy. Astron. Soc., vol. 478, no. 1, pp. 126–145, 2018. arXiv:1801.08501.
- C. Garcia-Quintero, M. Ishak, L. Fox, and W. Lin, “Cosmological discordances. III. More on measure properties, large-scale-structure constraints, the Hubble constant and Planck data”, Phys. Rev. D, vol. 100, no. 12, p. 123538, 2019. arXiv:1910.01608.
- M. Asgari et al., “KiDS-1000 Cosmology: Cosmic shear constraints and comparison between two point statistics”, Astron. Astrophys., vol. 645, p. A104, 2021. arXiv:2007.15633.
- T. M. C. Abbott et al., “Dark Energy Survey Year 3 results: Cosmological constraints from galaxy clustering and weak lensing”, Phys. Rev. D, vol. 105, no. 2, p. 023520, 2022. arXiv:2105.13549.
- N.-M. Nguyen, D. Huterer, and Y. Wen, “Evidence for suppression of structure growth in the concordance cosmological model”, 2023. arXiv:2302.01331.
- S. A. Adil, O. Akarsu, M. Malekjani, E. O. Colgáin, S. Pourojaghi, A. A. Sen, and M. M. Sheikh-Jabbari, “S8 increases with effective redshift in ΛCDM cosmology”, 2023. arXiv:2303.06928.
- L. Heisenberg, H. Villarrubia-Rojo, and J. Zosso, “Can late-time extensions solve the H0 and σ8 tensions?”, Phys. Rev. D, vol. 106, p. 043503, 2022. arXiv:2202.01202.
- V. Marra and L. Perivolaropoulos, “Rapid transition of Geff at zt≃0.01 as a possible solution of the Hubble and growth tensions”,Phys. Rev. D vol. 104 , no. 2, p. L021303, 2021. arXiv:2102.06012.
- G. Alestas, L. Kazantzidis and L. Perivolaropoulos, “w-M phantom transition at zt<0.1 as a resolution of the Hubble tension”, Phys. Rev. D vol. 103, no. 8, p. 083517, 2020. arXiv:2012.13932.
- L. Perivolaropoulos and F. Skara, “Hubble tension or a transition of the Cepheid SnIa calibrator parameters?”, Phys. Rev. D vol. 104, no. 12, p. 123511, 2021. arXiv:2109.04406.
- G. Alestas, D. G. Alestas, D. Camarena, E. Di Valentino, L. Kazantzidis, V. Marra, S. Nesseris and L. Perivolaropoulos, “Late-transition versus smooth H(z)-deformation models for the resolution of the Hubble crisis”, Phys. Rev. D, vol. 105, no. 6, p. 6. 2022; arXiv:2110.04336. [Google Scholar]
- L. Perivolaropoulos and F. Skara, “A Reanalysis of the Latest SH0ES Data for H0: Effects of New Degrees of Freedom on the Hubble Tension”, Universe, vol. 8, no. 10, p. 502, 2022. arXiv:2208.11169.
- J. Grande, J. J. Grande, J. Solà, and H. Stefancic, “LXCDM: A Cosmon model solution to the cosmological coincidence problem?”, JCAP, vol. 08, p. 011, 2006, gr-qc/0604057.
- J. Grande, A. Pelinson, and J. Solà, “Dark energy perturbations and cosmic coincidence”, Phys. Rev. D, vol. 79, p. 043006, 2009. arXiv:0809.3462.
- E. Abdalla et al., “Cosmology intertwined: A review of the particle physics, astrophysics, and cosmology associated with the cosmological tensions and anomalies”, JHEAp, vol. 34, pp. 49–211, 2022. arXiv:2203.06142.
- M. Dainotti, B. De Simone, G. Montani, T. Schiavone, and G. Lambiase, “The Hubble constant tension: current status and future perspectives through new cosmological probes”, 2023. arXiv:2301.10572.
- I. L. Shapiro and J. Solà, “Scaling behavior of the cosmological constant: Interface between quantum field theory and cosmology”, JHEP, vol. 02, p. 006, 2002, hep-th/0012227.
- A. Babic, B. Guberina, R. Horvat, and H. Stefancic, “Renormalization-group running cosmologies. A Scale-setting procedure”, Phys. Rev. D, vol. 71, p. 124041, 2005, astro-ph/0407572.
- P. D. Alvarez, B. P. D. Alvarez, B. Koch, C. Laporte, and A. Rincón, “Can scale-dependent cosmology alleviate the H0 tension?”, JCAP, vol. 06, p. 019, 2021. arXiv:2009.02311.
- M. Ozer and M. Taha, “A Solution to the Main Cosmological Problems”, Phys. Lett. B, vol. 171, pp. 363–365, 1986.
- O. Bertolami, “Time dependent cosmological term”, Nuovo Cim. B, vol. 93, pp. 36–42, 1986.
- K. Freese, F. C. K. Freese, F. C. Adams, J. A. Frieman, and E. Mottola, “Cosmology with Decaying Vacuum Energy”, Nucl. Phys. B, vol. 287, pp. 797–814, 1987.
- P. J. E. Peebles and B. Ratra, “Cosmology with a Time Variable Cosmological Constant”, Astrophys. J., vol. 325, p. L17, 1988.
- W. Chen and Y. S. Wu, “Implications of a cosmological constant varying as R-2”, Phys. Rev. D, vol. 41, pp. 695–698, 1990 [Erratum: Phys.Rev.D, vol. 45, p. 4728, 1992].
- A. M. M. Abdel-Rahman, “Singularity - free decaying vacuum cosmologies”, Phys. Rev. D, vol. 45, pp. 3497–3511, 1992.
- J. Carvalho, J. J. Carvalho, J. Lima, and I. Waga, “On the cosmological consequences of a time dependent lambda term”, Phys. Rev. D, vol. 46, pp. 2404–2407, 1992.
- R. C. Arcuri and I. Waga, “Growth of density inhomogeneities in Newtonian cosmological models with variable Lambda”, Phys. Rev. D, vol. 50, pp. 2928–2931, 1994.
- I. Waga, “Decaying vacuum flat cosmological models: Expressions for some observable quantities and their properties”, Astrophys. J., vol. 414, pp. 436–448, 1993.
- J. A. S. Lima and J. M. F. Maia, “Deflationary cosmology with decaying vacuum energy density”, Phys. Rev. D, vol. 49, pp. 5597–5600, 1994.
- J. A. S. Lima and M. Trodden, “Decaying vacuum energy and deflationary cosmology in open and closed universes”, Phys. Rev. D, vol. 53, pp. 4280–4286, 1996, astro-ph/9508049.
- A. I. Arbab, “Cosmological models with variable cosmological and gravitational constants and bulk viscous models”, Gen. Rel. Grav., vol. 29, pp. 61–74, 1997.
- C. Espana-Bonet et al, “Testing the running of the cosmological constant with type Ia supernovae at high z”, JCAP, vol. 02, p. 006, 2004, hep-ph/0311171.
- P. Wang and X.-H. Meng, “Can vacuum decay in our universe?”, Class. Quant. Grav., vol. 22, pp. 283–294, 2005, astro-ph/0408495.
- H. A. Borges and S. Carneiro, “Friedmann cosmology with decaying vacuum density”, Gen. Rel. Grav., vol. 37, pp. 1385–1394, 2005, gr-qc/0503037.
- J. S. Alcaniz and J. A. S. Lima, “Interpreting cosmological vacuum decay”, Phys. Rev. D, vol. 72, p. 063516, 2005, astro-ph/0507372.
- J. D. Barrow and T. Clifton, “Cosmologies with energy exchange”, Phys. Rev. D, vol. 73, p. 103520, 2006, astro-ph/0604063.
- F. E. M. Costa and J. S. Alcaniz, “Cosmological consequences of a possible Λ-dark matter interaction”, Phys. Rev. D, vol. 81, p. 043506, 2010. arXiv:0908.4251.
- D. Bessada and O. D. Miranda, “Probing a cosmological model with a Λ=Λ0+3βH2 decaying vacuum”, Phys. Rev. D, vol. 88, no. 8, p. 083530, 2013. arXiv:1310.8571.
- A. Gómez-Valent and J. Solà, “Vacuum models with a linear and a quadratic term in H: structure formation and number counts analysis”, Mon. Not. Roy. Astron. Soc., vol. 448, pp. 2810–2821, 2015. arXiv:1412.3785.
- J. Overduin and F. Cooperstock, “Evolution of the scale factor with a variable cosmological term”, Phys. Rev. D, vol. 58, p. 043506, 1998, astro-ph/9805260.
- S. Basilakos, N. E. Mavromatos, and J. Solà Peracaula, “Gravitational and Chiral Anomalies in the Running Vacuum Universe and Matter-Antimatter Asymmetry”, Phys. Rev. D, vol. 101, no. 4, p. 045001, 2020. arXiv:1907.04890.
- S. Basilakos, N. E. Mavromatos, and J. Solà Peracaula, “Quantum Anomalies in String-Inspired Running Vacuum Universe: Inflation and Axion Dark Matter”, Phys. Lett. B, vol. 803, p. 135342, 2020. arXiv:2001.03465.
- N. E. Mavromatos and J. Solà Peracaula, “Stringy-running-vacuum-model inflation: from primordial gravitational waves and stiff axion matter to dynamical dark energy”, Eur. Phys. J. ST, vol. 230, no. 9, pp. 2077–2110, 2021. arXiv:2012.07971.
- N. E. Mavromatos and J. Solà Peracaula, “Inflationary physics and trans-Planckian conjecture in the stringy running vacuum model: from the phantom vacuum to the true vacuum”, Eur. Phys. J. Plus, vol. 136, no. 11, p. 1152, 2021. arXiv:2105.02659.
- J. Solà Peracaula, A. Gómez-Valent, J. de Cruz Pérez, and C. Moreno-Pulido, “Running vacuum against the H0 and σ8 tensions”, EPL, vol. 134, no. 1, p. 19001, 2021. arXiv:2102.12758.
- J. Solà Peracaula, A. Gómez-Valent, and J. de Cruz Pérez, “The H0 tension in light of vacuum dynamics in the Universe”, Phys. Lett. B, vol. 774, pp. 317–324, 2017. arXiv:1705.06723.
- A. Gómez-Valent and J. Solà, “Relaxing the σ8-tension through running vacuum in the Universe”, EPL, vol. 120, no. 3, p. 39001, 2017. arXiv:1711.00692.
- J. Solà Peracaula, J. de Cruz Pérez, and A. Gómez-Valent, “Dynamical dark energy vs. Λ = const in light of observations”, EPL, vol. 121, no. 3, p. 39001, 2018. arXiv:1606.00450.
- J. Solà, “Cosmological constant vis-a-vis dynamical vacuum: bold challenging the ΛCDM”, Int. J. Mod. Phys. A, vol. 31, no. 23, p. 1630035, 2016. arXiv:1612.02449.
- J. Solà, A. J. Solà, A. Gómez-Valent, and J. de Cruz Pérez, “First evidence of running cosmic vacuum: challenging the concordance model”, Astrophys. J., vol. 836, no. 1, p. 43, 2017. arXiv:1602.02103.
- J. Solà Peracaula, J. de Cruz Pérez, and A. Gómez-Valent, “Possible signals of vacuum dynamics in the Universe”, Mon. Not. Roy. Astron. Soc., vol. 478, no. 4, pp. 4357–4373, 2018. arXiv:1703.08218.
- J. Solà, A. J. Solà, A. Gómez-Valent, and J. de Cruz Pérez, “Hints of dynamical vacuum energy in the expanding Universe”, Astrophys. J., vol. 811, p. L14, 2015. arXiv:1506.05793.
- A. Gómez-Valent, J. A. Gómez-Valent, J. Solà, and S. Basilakos, “Dynamical vacuum energy in the expanding Universe confronted with observations: a dedicated study”, JCAP, vol. 01, p. 004, 2015. arXiv:1409.7048.
- J. Solà Peracaula, “Running Vacuum and the ΛCDM tensions”, PoS, vol. CORFU2021, p. 106, 2022. [CrossRef]
- J. Solà Peracaula, “Tensions in the ΛCDM and vacuum dynamics”, Int. J. Mod. Phys. A, vol. 33, no. 31, p. 1844009, 2018.
- J. Solà, “Dark energy: A Quantum fossil from the inflationary Universe?”, J. Phys. A, vol. 41, p. 164066, 2008. arXiv:0710.4151.
- S. Basilakos, D. Polarski, and J. Solà, “Generalizing the running vacuum energy model and comparing with the entropic-force models”, Phys. Rev. D, vol. 86, p. 043010, 2012. arXiv:1204.4806.
- S. Basilakos and J. Solà, “Entropic-force dark energy reconsidered”, Phys. Rev. D, vol. 90, no. 2, p. 023008, 2014. arXiv:1402.6594.
- A. Gómez-Valent, E. Karimkhani, and J. Solà, “Background history and cosmic perturbations for a general system of self-conserved dynamical dark energy and matter”, JCAP, vol. 12, p. 048, 2015. arXiv:1509.03298.
- M. Rezaei, M. Malekjani, and J. Solà, “Can dark energy be expressed as a power series of the Hubble parameter?”, Phys. Rev. D, vol. 100, no. 2, p. 023539, 2019. arXiv:1905.00100.
- M. Rezaei and J. Solà Peracaula, “Running vacuum versus holographic dark energy: a cosmographic comparison”, Eur. Phys. J. C, vol. 82, p. 765, 2022. arXiv:2207.14250.
- J. Solà, A. Gómez-Valent, J. de Cruz Pérez, and C. Moreno-Pulido, “Running vacuum against the H0 and σ8 tensions”, EPL, vol. 134, no. 1, p. 19001, 2021. arXiv:2102.12758.
- C. W. Misner, K. S. C. W. Misner, K. S. Thorn, and J. A. Wheeler, Gravitation. San Francisco: Freeman, 1974.
- J. Lesgourgues, “The Cosmic Linear Anisotropy Solving System (CLASS) I: Overview”, 2011. arXiv:1104.2932.
- D. Blas, J. D. Blas, J. Lesgourgues, and T. Tram, “The Cosmic Linear Anisotropy Solving System (CLASS) II: Approximation schemes”, JCAP, vol. 1107, p. 034, 2011. arXiv:1104.2933.
- C.-P. Ma and E. Bertschinger, “Cosmological perturbation theory in the synchronous and conformal Newtonian gauges”, Astrophys. J., vol. 455, pp. 7–25, 1995, astro-ph/9506072.
- Y. Wang, D. Wands, L. Xu, J. De-Santiago, and A. Hojjati, “Cosmological constraints on a decomposed Chaplygin gas”, Phys. Rev. D, vol. 87, no. 8, p. 083503, 2013. arXiv:1301.5315.
- Y. Wang, D. Y. Wang, D. Wands, G.-B. Zhao, and L. Xu, “Post-Planck constraints on interacting vacuum energy”, Phys. Rev. D, vol. 90, no. 2, p. 023502, 2014. arXiv:1404.5706.
- V. Salvatelli, N. Said, M. Bruni, A. Melchiorri, and D. Wands, “Indications of a late-time interaction in the dark sector”, Phys. Rev. Lett., vol. 113, no. 18, p. 181301, 2014. arXiv:1406.7297.
- M. Martinelli, N. B. Hogg, S. Peirone, M. Bruni, and D. Wands, “Constraints on the interacting vacuum–geodesic CDM scenario”, Mon. Not. Roy. Astron. Soc., vol. 488, no. 3, pp. 3423–3438, 2019. arXiv:1902.10694.
- N. B. Hogg, M. Bruni, R. Crittenden, M. Martinelli, and S. Peirone, “Latest evidence for a late time vacuum–geodesic CDM interaction”, Phys. Dark Univ., vol. 29, p. 100583, 2020. arXiv:2002.10449.
- L. W. K. Goh, A. Gómez-Valent, V. Pettorino, and M. Kilbinger, “Constraining constant and tomographic coupled dark energy with low-redshift and high-redshift probes”, Phys. Rev. D, vol. 107, no. 8, p. 083503, 2023. arXiv:2211.13588.
- H. Fritzsch and J. Solà, “Matter Non-conservation in the Universe and Dynamical Dark Energy”, Class. Quant. Grav., vol. 29, p. 215002, 2012. arXiv:1202.5097.
- H. Fritzsch and J. Solà, “Fundamental constants and cosmic vacuum: the micro and macro connection”, Mod. Phys. Lett. A, vol. 30, no. 22, p. 1540034, 2015. arXiv:1502.01411.
- C. Brans and R. Dicke, “Mach’s principle and a relativistic theory of gravitation”, Phys. Rev, vol. 124, p. 925, 1961.
- J.-P. Uzan, “Varying Constants, Gravitation and Cosmology”, Living Rev. Rel., vol. 14, p. 2, 2011. arXiv:1009.5514.
- M. Kramer et al., “Strong-Field Gravity Tests with the Double Pulsar”, Phys. Rev. X, vol. 11, no. 4, p. 041050, 2021. arXiv:2112.06795.
- W. W. Zhu et al., “Tests of Gravitational Symmetries with Pulsar Binary J1713+0747”, Mon. Not. Roy. Astron. Soc., vol. 482, no. 3, pp. 3249–3260, 2018. arXiv:1802.09206.
- A. Genova et al., “Solar system expansion and strong equivalence principle as seen by the NASA MESSENGER mission”, Nat Commun 9, 289, 2018.
- J. Solà Peracaula, A. J. Solà Peracaula, A. Gómez-Valent, J. de Cruz Pérez, and C. Moreno-Pulido, “Brans–Dicke Gravity with a Cosmological Constant Smoothes Out ΛCDM Tensions”, Astrophys. J. Lett., vol. 886, no. 1, p. L6, 2019. arXiv:1909.02554.
- J. Solà Peracaula, A. Gómez-Valent, J. de Cruz Pérez, and C. Moreno-Pulido, “Brans–Dicke cosmology with a Λ-term: a possible solution to ΛCDM tensions”, Class. Quant. Grav., vol. 37, no. 24, p. 245003, 2020. arXiv:2006.04273.
- J. de Cruz Pérez, J. Solà Peracaula, and C. P. Singh, “Running vacuum in Brans-Dicke theory: a possible cure for the σ8 and H0 tensions”, 2023. arXiv:2302.04807.
- T. Clifton, P. G. T. Clifton, P. G. Ferreira, A. Padilla, and C. Skordis, “Modified Gravity and Cosmology”, Phys. Rept., vol. 513, pp. 1–189, 2012. arXiv:1106.2476.
- A. Avilez and C. Skordis, “Cosmological constraints on Brans-Dicke theory”, Phys. Rev. Lett., vol. 113, no. 1, p. 011101, 2014. arXiv:1303.4330.
- A. Gómez-Valent and P. Hassan Puttasiddappa, “Difficulties in reconciling non-negligible differences between the local and cosmological values of the gravitational coupling in extended Brans-Dicke theories”, JCAP, vol. 09, p. 040, 2021. arXiv:2105.14819.
- I. L. Shapiro, J. I. L. Shapiro, J. Sola, and H. Stefancic, “Running G and Lambda at low energies from physics at M(X): Possible cosmological and astrophysical implications”, JCAP, vol. 01, p. 012, 2004, hep-ph/0410095.
- P. Carter, F. Beutler, W. J. Percival, C. Blake, J. Koda, and A. J. Ross, “Low Redshift Baryon Acoustic Oscillation Measurement from the Reconstructed 6-degree Field Galaxy Survey”, Mon. Not. Roy. Astron. Soc., vol. 481, no. 2, pp. 2371–2383, 2018. arXiv:1803.01746.
- H. Gil-Marín, W. J. Percival, L. Verde, J. R. Brownstein, C.-H. Chuang, F.-S. Kitaura, S. A. Rodríguez-Torres, and M. D. Olmstead, “The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: RSD measurement from the power spectrum and bispectrum of the DR12 BOSS galaxies”, Mon. Not. Roy. Astron. Soc., vol. 465, no. 2, pp. 1757–1788, 2017. arXiv:1606.00439.
- E. A. Kazin et al., “The WiggleZ Dark Energy Survey: improved distance measurements to z = 1 with reconstruction of the baryonic acoustic feature”, Mon. Not. Roy. Astron. Soc., vol. 441, no. 4, pp. 3524–3542, 2014. arXiv:1401.0358.
- T. M. C. Abbott et al., “Dark Energy Survey Year 3 results: A 2.7% measurement of baryon acoustic oscillation distance scale at redshift 0.835”, Phys. Rev. D, vol. 105, no. 4, p. 043512, 2022. arXiv:2107.04646.
- J. Hou et al., “The Completed SDSS-IV extended Baryon Oscillation Spectroscopic Survey: BAO and RSD measurements from anisotropic clustering analysis of the Quasar Sample in configuration space between redshift 0.8 and 2.2”, Mon. Not. Roy. Astron. Soc., vol. 500, no. 1, pp. 1201–1221, 2020. arXiv:2007.08998.
- H. du Mas des Bourboux et al., “The Completed SDSS-IV Extended Baryon Oscillation Spectroscopic Survey: Baryon Acoustic Oscillations with Lyα Forests”, Astrophys. J., vol. 901, no. 2, p. 153, 2020. arXiv:2007.08995.
- C. Zhang, H. Zhang, S. Yuan, T.-J. Zhang, and Y.-C. Sun, “Four new observational H(z) data from luminous red galaxies in the Sloan Digital Sky Survey data release seven”, Res. Astron. Astrophys., vol. 14, no. 10, pp. 1221–1233, 2014. arXiv:1207.4541.
- R. Jiménez, L. R. Jiménez, L. Verde, T. Treu, and D. Stern, “Constraints on the equation of state of dark energy and the Hubble constant from stellar ages and the CMB”, Astrophys. J., vol. 593, pp. 622–629, 2003, astro-ph/0302560.
- J. Simon, L. Verde, and R. Jiménez, “Constraints on the redshift dependence of the dark energy potential”, Phys. Rev. D, vol. 71, p. 123001, 2005, astro-ph/0412269.
- M. Moresco et al., “Improved constraints on the expansion rate of the Universe up to z 1.1 from the spectroscopic evolution of cosmic chronometers”, JCAP, vol. 1208, p. 006, 2012. arXiv:1201.3609.
- M. Moresco, L. M. Moresco, L. Pozzetti, A. Cimatti, R. Jiménez, C. Maraston, L. Verde, D. Thomas, A. Citro, R. Tojeiro, and D. Wilkinson, “A 6% measurement of the Hubble parameter at z∼0.45: direct evidence of the epoch of cosmic re-acceleration”, JCAP, vol. 1605, no. 05, p. 014, 2016. arXiv:1601.01701.
- A. Ratsimbazafy, S. Loubser, S. Crawford, C. Cress, B. Bassett, R. Nichol, and P. Väisänen, “Age-dating Luminous Red Galaxies observed with the Southern African Large Telescope”, Mon. Not. Roy. Astron. Soc., vol. 467, no. 3, pp. 3239–3254, 2017. arXiv:1702.00418.
- D. Stern, R. Jiménez, L. Verde, M. Kamionkowski, and S. A. Stanford, “Cosmic Chronometers: Constraining the Equation of State of Dark Energy. I: H(z) Measurements”, JCAP, vol. 1002, p. 008, 2010. arXiv:0907.3149.
- N. Borghi, M. N. Borghi, M. Moresco, and A. Cimatti, “Toward a Better Understanding of Cosmic Chronometers: A New Measurement of H(z) at z ∼ 0.7”, Astrophys. J. Lett., vol. 928, no. 1, p. L4. arXiv:2110.04304.
- M. Moresco, “Raising the bar: new constraints on the Hubble parameter with cosmic chronometers at z∼2”, Mon. Not. Roy. Astron. Soc., vol. 450, no. 1, pp. L16–L20. 2015; arXiv:1503.01116.
- M. Moresco, R. Jimenez, L. Verde, A. Cimatti, and L. Pozzetti, “Setting the Stage for Cosmic Chronometers. II. Impact of Stellar Population Synthesis Models Systematics and Full Covariance Matrix”, Astrophys. J., vol. 898, no. 1, p. 82, 2020. arXiv:2003.07362.
- F. Avila, A. Bernui, E. de Carvalho, and C. P. Novaes, “The growth rate of cosmic structures in the local Universe with the ALFALFA survey”, Mon. Not. Roy. Astron. Soc., vol. 505, no. 3, pp. 3404–3413, 2021. arXiv:2105.10583.
- K. Said, M. Colless, C. Magoulas, J. R. Lucey, and M. J. Hudson, “Joint analysis of 6dFGS and SDSS peculiar velocities for the growth rate of cosmic structure and tests of gravity”, Mon. Not. Roy. Astron. Soc., vol. 497, no. 1, pp. 1275–1293, 2020. arXiv:2007.04993.
- F. Simpson, C. Blake, J. A. Peacock, I. Baldry, J. Bland-Hawthorn, A. Heavens, C. Heymans, J. Loveday, and P. Norberg, “Galaxy and mass assembly: Redshift space distortions from the clipped galaxy field”, Phys. Rev. D, vol. 93, no. 2, p. 023525, 2016. arXiv:1505.03865.
- C. Blake et al., “Galaxy And Mass Assembly (GAMA): improved cosmic growth measurements using multiple tracers of large-scale structure”, Mon. Not. Roy. Astron. Soc., vol. 436, p. 3089, 2013. arXiv:1309.5556.
- C. Blake et al., “The WiggleZ Dark Energy Survey: the growth rate of cosmic structure since redshift z=0.9”, Mon. Not. Roy. Astron. Soc., vol. 415, p. 2876, 2011. arXiv:1104.2948.
- F. G. Mohammad et al., “The VIMOS Public Extragalactic Redshift Survey (VIPERS): Unbiased clustering estimate with VIPERS slit assignment”, Astron. Astrophys., vol. 619, p. A17, 2018. arXiv:1807.05999.
- L. Guzzo et al., “A test of the nature of cosmic acceleration using galaxy redshift distortions”, Nature, vol. 451, pp. 541–545, 2008. arXiv:0802.1944.
- Y.-S. Song and W. J. Percival, “Reconstructing the history of structure formation using Redshift Distortions”, JCAP, vol. 0910, p. 004, 2009. arXiv:0807.0810.
- T. Okumura et al., “The Subaru FMOS galaxy redshift survey (FastSound). IV. New constraint on gravity theory from redshift space distortions at z∼1.4”, Publ. Astron. Soc. Jap., vol. 68, no. 3, p. 38, 2016. arXiv:1511.08083.
- M. S. Turner and M. J. White, “CDM models with a smooth component”, Phys. Rev. D, vol. 56, no. 8, p. R4439, 1997, astro-ph/9701138.
- D. Scolnic et al., “The Pantheon+ Analysis: The Full Data Set and Light-curve Release”, Astrophys. J., vol. 938, no. 2, p. 113, 2022. arXiv:2112.03863.
- A. Favale, A. Gómez-Valent, and M. Migliaccio, “Cosmic chronometers to calibrate the ladders and measure the curvature of the Universe. A model-independent study”, 2023. arXiv:2301.09591.
- A. G. Riess et al., “A Comprehensive Measurement of the Local Value of the Hubble Constant with 1 km/s/Mpc Uncertainty from the Hubble Space Telescope and the SH0ES Team”, Astrophys. J. Lett., vol. 934, no. 1, p. L7, 2022. arXiv:2112.04510.
- D. Brout et al., “The Pantheon+ Analysis: Cosmological Constraints”, Astrophys. J., vol. 938, no. 2, p. 110, 2022. arXiv:2202.04077.
- N. Aghanim et al., “Planck 2018 results. VIII. Gravitational lensing”, Astron. Astrophys., vol. 641, p. A8, 2020. arXiv:1807.06210.
- R. Jiménez and A. Loeb, “Constraining cosmological parameters based on relative galaxy ages”, Astrophys. J., vol. 573, pp. 37–42, 2002, astro-ph/0106145.
- W. L. Freedman et al., “The Carnegie-Chicago Hubble Program. VIII. An Independent Determination of the Hubble Constant Based on the Tip of the Red Giant Branch”, Astrophys. J., vol. 882, p. 34, 2019. arXiv:1907.05922.
- W. L. Freedman, “Measurements of the Hubble Constant: Tensions in Perspective”, Astrophys. J., vol. 919, no. 1, p. 16, 2021. arXiv:2106.15656.
- S. Cao and B. Ratra, “H0=69.8±1.3kms-1Mpc-1, Ωm0=0.288±0.017, and other constraints from lower-redshift, non-CMB and non-distance-ladder, expansion-rate data”, 2023. arXiv:2302.14203.
- W. Yuan, A. G. Riess, L. M. Macri, S. Casertano, and D. Scolnic, “Consistent Calibration of the Tip of the Red Giant Branch in the Large Magellanic Cloud on the Hubble Space Telescope Photometric System and a Re-determination of the Hubble Constant”, Astrophys. J., vol. 886, p. 61, 2019. arXiv:1908.00993.
- J. Soltis, S. Casertano, and A. G. Riess, “The Parallax of ω Centauri Measured from Gaia EDR3 and a Direct, Geometric Calibration of the Tip of the Red Giant Branch and the Hubble Constant”, Astrophys. J. Lett., vol. 908, no. 1, p. L5, 2021. arXiv:2012.09196.
- G. S. Anand, R. B. G. S. Anand, R. B. Tully, L. Rizzi, A. G. Riess, and W. Yuan, “Comparing Tip of the Red Giant Branch Distance Scales: An Independent Reduction of the Carnegie-Chicago Hubble Program and the Value of the Hubble Constant”, Astrophys. J., vol. 932, no. 1, p. 15, 2022. arXiv:2108.00007.
- D. Scolnic, A. G. Riess, J. Wu, S. Li, G. S. Anand, R. Beaton, S. Casertano, R. Anderson, S. Dhawan, and X. Ke, “CATS: The Hubble Constant from Standardized TRGB and Type Ia Supernova Measurements”, 2023. arXiv:2304.06693.
- N. Metropolis, A. W. N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller, and E. Teller, “Equation of state calculations by fast computing machines”, J. Chem. Phys., vol. 21, pp. 1087–1092, 1953.
- W. Hastings, “Monte Carlo Sampling Methods Using Markov Chains and Their Applications”, Biometrika, vol. 57, pp. 97–109, 1970.
- B. Audren, J. Lesgourgues, K. Benabed, and S. Prunet, “Conservative Constraints on Early Cosmology: an illustration of the Monte Python cosmological parameter inference code”, JCAP, vol. 02, p. 001, 2013. arXiv:1210.7183.
- T. Brinckmann and J. Lesgourgues, “MontePython 3: boosted MCMC sampler and other features”, Phys. Dark Univ., vol. 24, p. 100260, 2019, arXiv:1804.07261, "https://baudren.github.io/montepython.html".
- S. Brooks and A. Gelman, “General Methods for Monitoring Convergence of Iterative Simulations”, Journal of Computational and Graphical Statistics, vol. 7, p. 434, 1997.
- A. Gelman and D. Rubin, “Inference from Iterative Simulation Using Multiple Sequences”, Statistical Science, vol. 7, p. 457, 1992.
- A. Lewis, “GetDist: a Python package for analysing Monte Carlo samples”, 2019, arXiv:1910.13970,https://getdist.readthedocs.io.
- D. J. Fixsen, “The Temperature of the Cosmic Microwave Background”, Astrophys. J., vol. 707, pp. 916–920, 2009. arXiv:0911.1955.
- D. J. Spiegelhalter, N. G. D. J. Spiegelhalter, N. G. Best, B. P. Carlin, and A. van der Linde, “Bayesian measures of model complexity and fit”, J. Roy. Stat. Soc., vol. 64, p. 583, 2002.
- A. R. Liddle, “Information criteria for astrophysical model selection”, Mon. Not. Roy. Astron. Soc., vol. 377, pp. L74–L78, 2007, astro-ph/0701113.
- H. Akaike, “A new look at the statistical model identification”, IEEE Trans. Autom. Control, vol. 19, pp. 716–723, 1974.
- A. Gómez-Valent, Z. Zheng, L. Amendola, V. Pettorino, and C. Wetterich, “Early dark energy in the pre- and postrecombination epochs”, Phys. Rev. D, vol. 104, no. 8, p. 083536, 2021. arXiv:2107.11065.
- V. Poulin, J. L. Bernal, E. Kovetz, and M. Kamionkowski, “The Sigma-8 Tension is a Drag”, 2022. arXiv:2209.06217.
- A. Gómez-Valent, “Measuring the sound horizon and absolute magnitude of SNIa by maximizing the consistency between low-redshift data sets”, Phys. Rev. D, vol. 105, no. 4, p. 043528, 2022. arXiv:2111.15450.
- G. Benevento, J.A. G. Benevento, J.A. Kable, G. E. Addison and C. L. Bennett, “An Exploration of an Early Gravity Transition in Light of Cosmological Tensions”, Astrophys. J., vol. 935, p. 156, 2022. arXiv:2202.09356.
- G. Ballesteros, A. Notari and F. Rompineve, “The H0 tension: ΔGN vs. ΔNeff”, JCAP, vol. 11, p. 024, 2020. arXiv:2004.05049.
- M. Braglia et al., “Larger value for H0 by an evolving gravitational constant”, Phys.Rev. D vol. 102, p. 023529, 2020. arXiv:2004.11161.
- J. Solà Peracaula, A. Gómez-Valent, and J. de Cruz Pérez, “Dynamical dark energy: scalar fields and running vacuum”, Mod. Phys. Lett. A, vol. 32, no. 9, p. 1750054, 2017. arXiv:1610.08965.
- J. Solà Peracaula, A. Gómez-Valent, and J. de Cruz Pérez, “Signs of Dynamical Dark Energy in Current Observations”, Phys. Dark Univ., vol. 25, p. 100311, 2019. arXiv:1811.03505.
- J. Solà, “Cosmologies with a time dependent vacuum”, J. Phys. Conf. Ser., vol. 283, p. 012033, 2011. arXiv:1102.1815.
- J. Solà, “Vacuum energy and cosmological evolution”, AIP Conf. Proc., vol. 1606, no. 1, pp. 19–37, 2015. arXiv:1402.7049.
| 1 | We use the geometric sign convention (+, +, +) in the popular classification by Misner, Thorne and Wheeler [98]. |
| 2 | |
| 3 | In practice this means that we have first fitted the value of as one more free parameter in our analysis. Subsequently we have assumed that the threshold point remains fixed at that point. See also [104,105,106,107] for a binned/tomographic approach to the DE. In our case we have just one threshold whose existence might be motivated by QFT calculations [25,26]. |
| 4 | If (dark) matter is not conserved, but G remains constant, we retrieve of course our previous scenario (14). In general, we may expect a mixture of both situations, but we shall refrain from dealing with the general case since it would introduce extra parameters. See, however, [108,109] for additional discussions that can be relevant for studies on the possible variation of the fundamental constants of Nature. |
| 5 | It should be clear that is not a dynamical degree of freedom, in contradistinction to Brans-Dicke type theories of gravitation [110], and therefore does not mediate any sort of long-range interaction that should be subdued by screening mechanisms. |
| 6 | Let us emphasize that Eq. (54) is valid only in the MDE, and we have also pointed out that const. in the DE epoch. This means that G gets more and more rigid when it transits from the MDE to the DE epoch, and therefore the actual limits on are weaker than those that we have roughly estimated. This works on our benefit, of course. In fact, a detailed calculation would require computing in the DE epoch, but it proves unnecessary once we have shown that even in the most unfavorable case (i.e. when evolves more rapidly than it actually does in the DE epoch) the obtained limits on are nonetheless preserved by our fits. Notice that type-I models are totally unaffected by these limits since G is in this case constant, so can be, in principle, larger for them. |
| 7 | |
| 8 | This region is also preferred by late-time dynamical DE models when fitted to a very wide variety of background data that are independent from the direct cosmic distance ladder and CMB, km/s/Mpc [156]. See, however, [157,158,159,160] for measurements of more in accordance with SH0ES obtained also with the tip of the red giant branch method. |
| 9 | |
| 10 | |
| 11 | See Section 3.3 for the practical implementation. |
| 12 | |
| 13 | |
| 14 | Noticeably, the central values of , and the absolute magnitude of SNIa, M, obtained for the type-II RRVM when the CMB polarization data are excluded in the fitting analysis are in very good agreement with the model-independent measurements from low-z data reported in [149], which are also independent from the main drivers of the tension. For the Hubble constant these authors find km/s/Mpc. However, these measurements have still large uncertainties and cannot arbitrate the Hubble tension yet. See also [174]. |
| 15 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





