Submitted:
04 January 2026
Posted:
09 January 2026
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
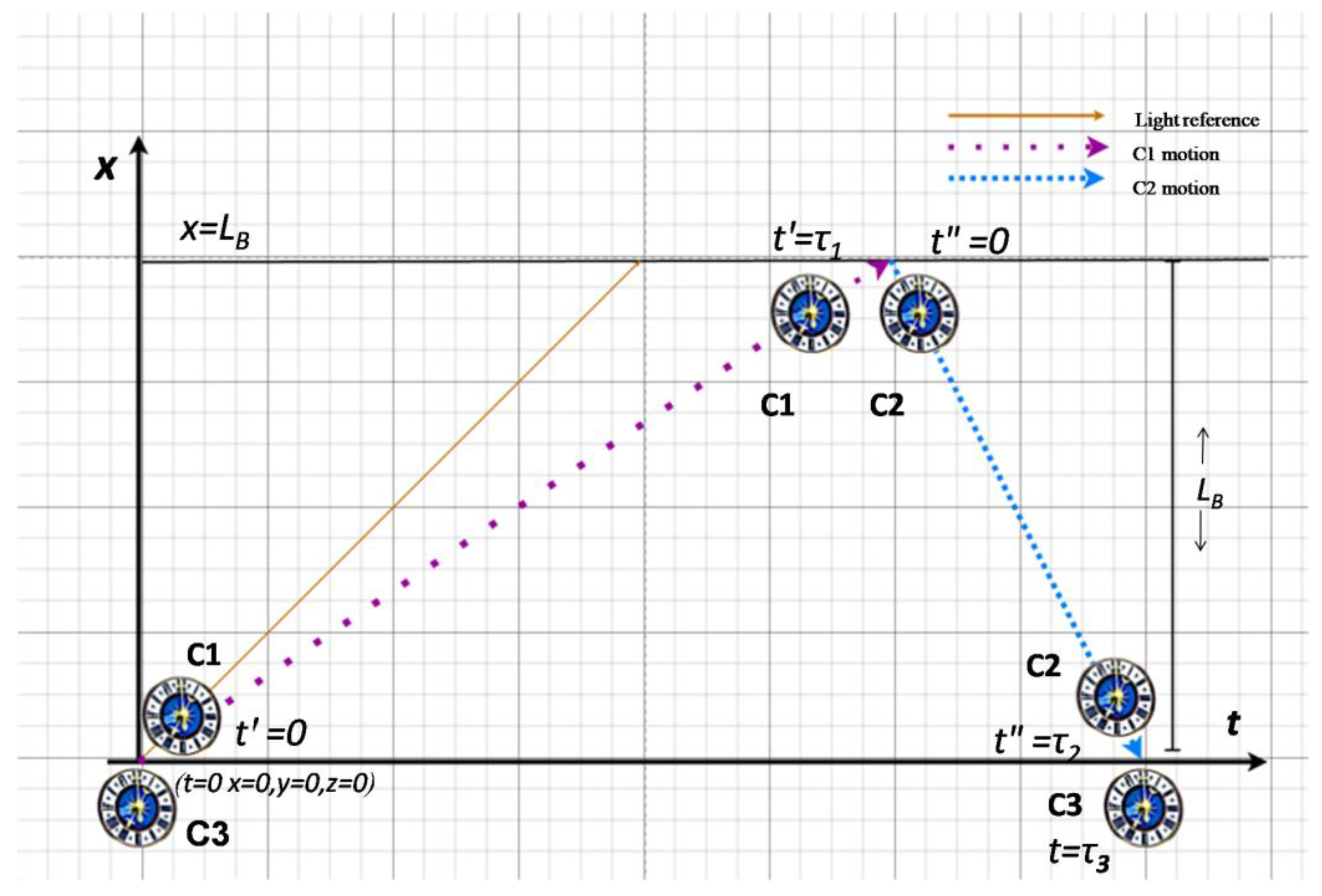
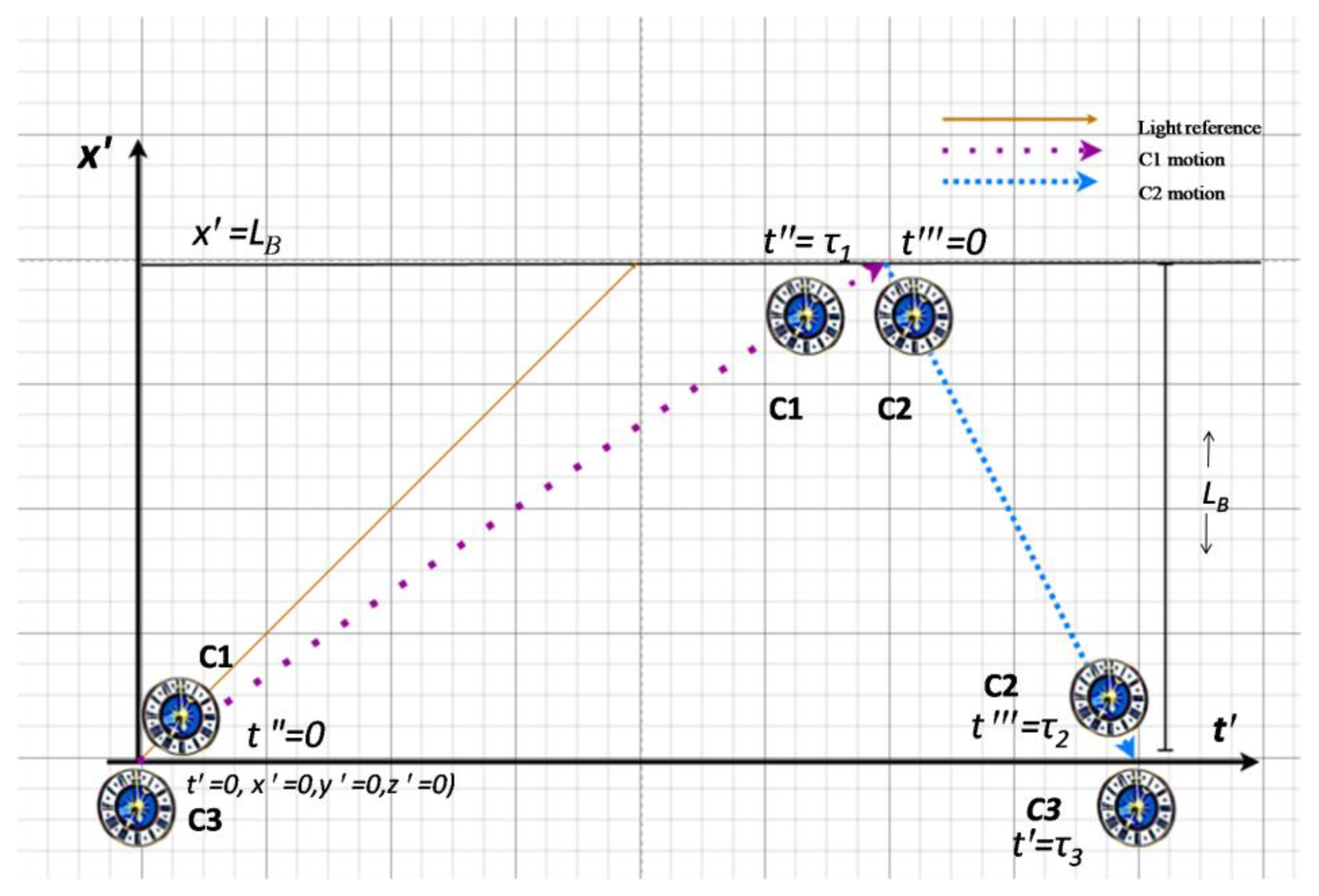
- The stationary system is named ‘System B’ as the Base platform lab for the thought experiment.
- Clock C1arrives from the negative part of the x-axis at constant yet unknown velocity v1 and resets itself to tꞌ=0.
- The stationary clock C3 also resets itself to 0 at the C1 departure event.
- Clock C2 is launched with velocity v2 from far positive side on the x-axis, on a collision course with C1 with a negligible y offset in order to continue its motion towards the origin after the close encounter with C1 during which C2 is reset to tꞌꞌ= 0.
- This round trip arrangement is maintained for compatibility with the Minkowski space triangular arrangement in the original [1] helping geometric reasoning. However, in practice, each trip can be executed sequentially because durations are independent of specific times the motions start.
- Upon the encounter with C2, C1 broadcasts the time tꞌ= to the Base origin for future reckoning.
- Clock C2 arrives to the C3 origin and communicates the time tꞌꞌ = to the Base for future reckoning.
- The stationary C3 clock Base, records the local time of arrival of C2 as t= which is the duration of the round trip between x=0 and x= LB (which is unknown) then back to x=0.
- We have sufficient data to determine not only the unknown LB. but also equally unknown velocities v1 and v2.
2. Distance and Velocities Calculation in Minkowski Spacetime
3. Three Clocks in Tangherlini Spacetime
3.1. Three Clocks Experiment in the Tangherlini 4D Spacetime
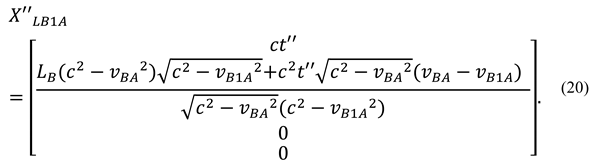
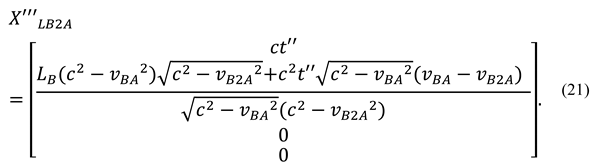
3.2. Finding Analytical Solutions

3.2.1. Verification of Results by Checking Numerical Consistency
3.2.2. Verification of Results via Back-Substitution
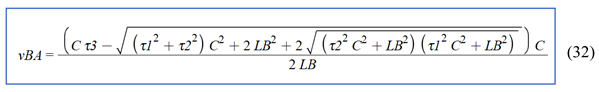


3.3. The Evaluation of the Results
- The algebraic proof of the solution correctness using Maple, has been achieved. Numerical test at a very high precision of 256 digits return exact expected results within the minimum of 64 digits precision for the calculated velocities.
- Furthermore, analytical validation was achieved by substituting solutions to the system of equations (31).
- Traceable derivations of equations from established theories.
- We are therefore convinced that the reality of absolute rest frame and absolute velocity is in principle proven pending 3D generalisation and experimental confirmation in the future.
- The fact that this is only verified for one special case in x-boost configuration does not put in doubt the general nature of our finding. The existence of this analytical solution implies a general solution for arbitrary velocity vector orientations, because this special case is the manifestation of laws of a general, nature acting in all axes configurations no matter how difficult is to obtain general solution in Tangherlini framework. It is hard to imagine that the absolute velocity solutions may exist only on axes aligned with absolute velocity vectors and not elsewhere. This is by analogy to the LT heavily exploited using x-boost configuration for education purposes, but there is no doubt any axes configuration that is more difficult to handle mathematically, would make relativistic effects disappear. A rigorous proof of this should be provided in the future for a full closure.
4. Discussion and Conclusions
4.1. Historical Perspective of the Absolute Velocity Problem
4.2. Conclusions
- Tangherlini prediction of the possibility of detecting absolute velocity were confirmed by our solution because the three clocks scenario did not require separated synchronized clocks to define the velocity which was not “in the usual manner”.
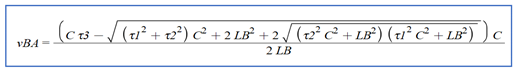
- 2.
- The special case solution we obtained from equations (31), is a manifestation of a general law of nature like Einstein’s simplified SRT’s first findings were the manifestation of GR laws. This yielded relatively simple expression for absolute velocity of the base platform:
- 3.
- Although finding absolute velocity may appear to undermine the STR, this is not the case. The Einstein’s convention is consistent with the underlying fundamental laws by which the average speed of round trip of light is constant and the theory is verifiable within the Einstein - Poincaré synchronized clock ensembles, but not necessary reflecting the synchrony perceived by humans, deemed absolute. The convention takes absolute velocity out of scope, by but it cannot deny or confirm its existence ruled out by definition, so no contradiction with Tangherlini theory. However, some relativistic narratives in literature having no real effect on scientific results may not be accurate. In this view the Poincaré formulation of the Postulate of Relativity was an unproven inference and now becomes obsolete; however, it was ‘mostly right’, reflecting the state of knowledge in early 20th century. Einstein’s postulates appear to be not affected by our findings.
- 4.
- The results presented here demonstrate that nature did not conspire but the absolute velocity of an inertial frame is not hidden but at least is a mathematically accessible quantity when using a three-clock measurement protocol advocated by Matsas et al. [1] , we have shown that Tangherlini’s 1958 theory is both testable and internally consistent. The single, elegant analytical solution represents a significant simplification of the kinematics of preferred frames. Future experimental verification and extension of the presented model could resolve the debate regarding the existence of a preferred frame, moving it from the realm of philosophical interpretation into the domain of empirical measurement."
- 5.
- We hope the results of this work will trigger additional research leading to finding a practical method to measure absolute velocities with high accuracy, which this special case cannot support due to the unknown orientation of the absolute velocity vector needed to be aligned with the coordinate system x-axis.
- 6.
- The unusual nature of the discovery of absolute velocity reflects the long standing view of late Jose G. Vargas [18]: ” there is more to structure in special relativity than meets the eye.”
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ALT | Absolute Lorentz Transformation |
| AR | Absolute Rest |
| ARF | Absolute Rest Frame |
| EOM | Equation of Motion |
| GR | General Relativity |
| LT | Lorentz Transformation |
| STR | Special Theory of Relativity |
| TT | Tangherlini Transformation |
Appendix A. Comments on Absolute Rest, Absolute Velocity and Tangherlini Transformation
References
- Matsas, G.E.A.; Pleitez, V.; Saa, A.; Vanzella, D.A.T. The number of fundamental constants from a spacetime-based perspective. Sci. Rep. 2024, 14, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Tangherlini, F.R. The Velocity of Light in Uniformly Moving Frame- PhD Disertation Stanford University1958. The Abraham Zelmanov Journal 2009, vol. 2, 44–110. [Google Scholar]
- Einstein, A. On the Electrodynamics of Moving Bodies," in The Collected Papers of Albert Einstein. (English). Princeton: Princeton University Press. 1989, Volume 2, 140. Available online: https://einsteinpapers.press.princeton.edu/vol2-trans/154.
- Canales, J. Einstein, Bergson, and the Experiment that Failed: Intellectual Cooperation at the League of Nations. MLN 2005, 120, 1168–1191. [Google Scholar] [CrossRef]
- Einstein, A. Physics and reality. J. Frankl. Inst. 1936, 221, 349–382. [Google Scholar] [CrossRef]
- Einstein, A. ""Discussion" Following Lecture Version of "Theory of Relativity"," in The Collected Papers of Albert Einstein. In The Swiss Years Writings 1909-1911 (English translation supplement); Princeton University Press: Princeton, 1994; Volume 3, p. 353. Available online: https://einsteinpapers.press.princeton.edu/vol3-doc/478.
- Einstein, A. Zur Elektrodynamik bewegter Körper. Annalen der Physik, Band 17 1905, vol. 17, 1905. Available online: https://dn790008.ca.archive.org/0/items/zurelektrodynami00aein/zurelektrodynami00aein.pdf. [CrossRef]
- Eddington, A.S. The Nature of the Physical World; Cambridge University Press: Cambridge, 1929; Available online: https://www.gutenberg.org/cache/epub/72963/pg72963-images.html.
- Jammer, M. Concepts of Simultaneity: From Antiquity to Einstein and Beyond; Johns Hopkins University Press: Baltimore, 2006. [Google Scholar]
- Bell, J.S. On the Einstein Podolsky Rosen paradox. Phys. Phys. Fiz. 1964, 1, 195–200. [Google Scholar] [CrossRef]
- Michelson, A.A.; Morley, E.W. On the relative motion of the Earth and the luminiferous ether. Am. J. Sci. 1887, s3-34, 333–345. [Google Scholar] [CrossRef]
- Poincaré, H. Sur la dynamique de l'électron. Rendiconti del Circolo Matematico di Palermo 21, 1906, 129–176 1906, vol. 21, 129–176. [Google Scholar] [CrossRef]
- Mansouri, R.; Sexl, R.U. A test theory of special relativity: I. Simultaneity and clock synchronization. Gen. Relativ. Gravit. 1977, 8, 497–513. [Google Scholar] [CrossRef]
- Selleri, F. Noninvariant one-way speed of light and locally equivalent reference frames. Found. Phys. Lett. 1997, 10, 73–83. [Google Scholar] [CrossRef]
- Selleri, F. Noninvariant one-way velocity of light. Found. Phys. 1996, 26, 641–664. [Google Scholar] [CrossRef]
- Tangherlini, F.R. Galilean-Like Transformation Allowed by General Covariance and Consistent with Special Relativity. J. Mod. Phys. 2014, 05, 230–243. [Google Scholar] [CrossRef]
- Spavieri, G.; Gillies, G.T.; Haug, E.G. The Sagnac effect and the role of simultaneity in relativity theory. J. Mod. Opt. 2021, 68, 202–216. [Google Scholar] [CrossRef]
- Vargas, J.G. U(1) ×SU(2) from the tangent bundle. In J. Phys.: Conference Series 474, 2013 doi:10.1088/1742-6596/474/1/012032, pp. 1-17.
- Poincaré, H. The Value of Science; Science Press: New York, 1907. [Google Scholar]
[1] Translation from [12] by Google Translate. |
[2] Bill Unruh undisclosed private communication according to [1]. |
[3] We used the observation of Poincare that absolute space is not definable and has no features with coordinates so the only way to bootstrap the derivation is to assume that at time 0 some abstract coordinate system in A is momentarily aligned with the moving one: “absolute space is nonsense, and it is necessary for us to begin by referring space to a system of axes invariably bound to our body (which we must always suppose put back in the initial attitude).” [19] Absolute space then has no role other than being a container of inertial systems only as far as this simple linear algebra model is concerned. |
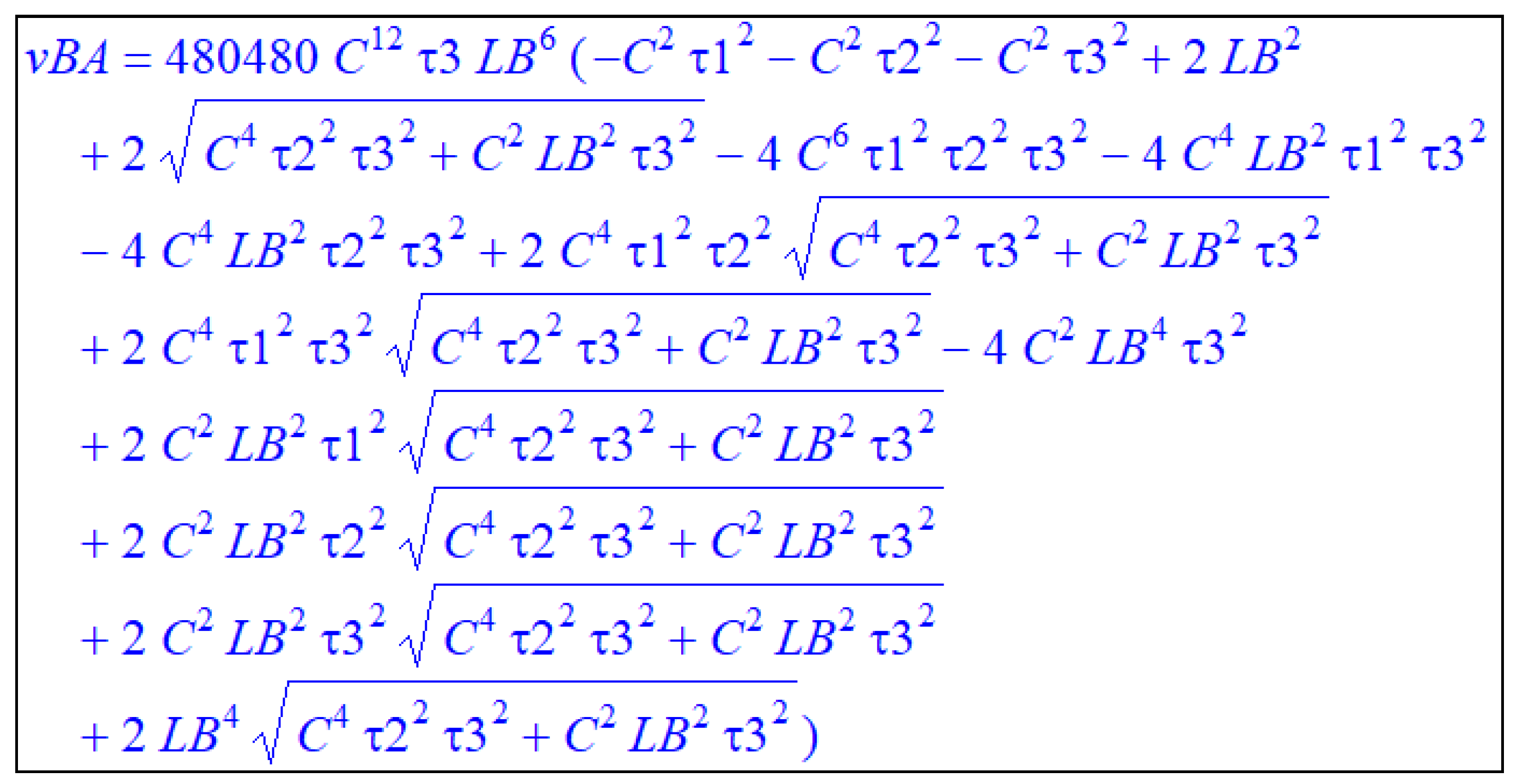

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.




