Refreshing the Theory of Relativity

1. Introduction

The theory of relativity must be revisited¹. Quite simply because it does not properly address the question of time. It avoids confronting it, taking its object for granted, hidden as it is in punctual clocks that don't exist. However, it's not a question of getting rid of it, nor fundamentally modifying its mathematical formalism: it has proved its effectiveness, having been constructed, polished and used by so many researchers. We should even consider it as expressing the general structure of our understanding of space and time, extending beyond the realm of physics and into the humanities and social sciences. It points the way to a close relationship between time and space. But it remains at the level of measurements (the links between time and space are those of clock and ruler readings), and we need speeds close to that of light to have effects that count. It is not more profoundly situated at the level of concepts. In the current situation, the weight of relativity has isolated physics from the human and social sciences; it has created a damaging disconnect, to the point where we sometimes struggle to find a common meaning for physical and human time.

We need to reread the theory of relativity, open it up to other ways of reasoning, and modify the mental images on which it is built. It must accompany the development of the concept of time, associating it with space and movement, rather than taking it as already established. It must therefore be independent of any pre-existing framework, or background independent². This re-reading offers solutions to the more or less significant difficulties (of a mathematical or interpretative nature) that have arisen since its foundation. It makes it capable of fulfilling new functions and restoring the link between the physical sciences and the human and social sciences on the question of time.

We shall adopt the following plan. In the first part, we will list the reasons why we need to get back to the drawing board in the field of physics. In a parallel approach for the time being, we'll take a look at the humanities and social sciences, highlighting some of their own difficulties, or aporias, when it comes to time. We will then propose (Part 2) two major solutions to the problems posed: one that emphasizes a relational rationality, undeveloped at the time of the founding of relativity (we used a substantial rationality); the other based on the conviction that theoretical developments cannot free themselves from embodied cognition, as phenomenology reminds us. We then turn (Part 3) to our approach to relativity, with the concept of motion at its core, and briefly touch on the status of the "speed" of light. In the fourth part, we review some of the solid contributions of our re-reading of relativity theory (validated by peers in peer-reviewed journals), or currently being examined by the scientific community, in the various fields cited, from both the natural sciences and the human and social sciences (the details of these contributions will be deferred to two appendices³ ). We will then put our approach into perspective (Part 5): others have proposed different approaches (scale relativity, constructivism): do they answer the questions we are asking? What original insights do they offer? We conclude (part 6) with a few concluding words. Given the pivotal role of the theory of relativity, we will tend to identify the two expressions - rereading relativity and - deepening the links between time and space, without necessarily mentioning physical theory.

2. Why It's Worth Revisiting the Theory of Relativity and Its Understanding of Time and Space

2.1. Reminder: The Theory of Relativity as We Know It

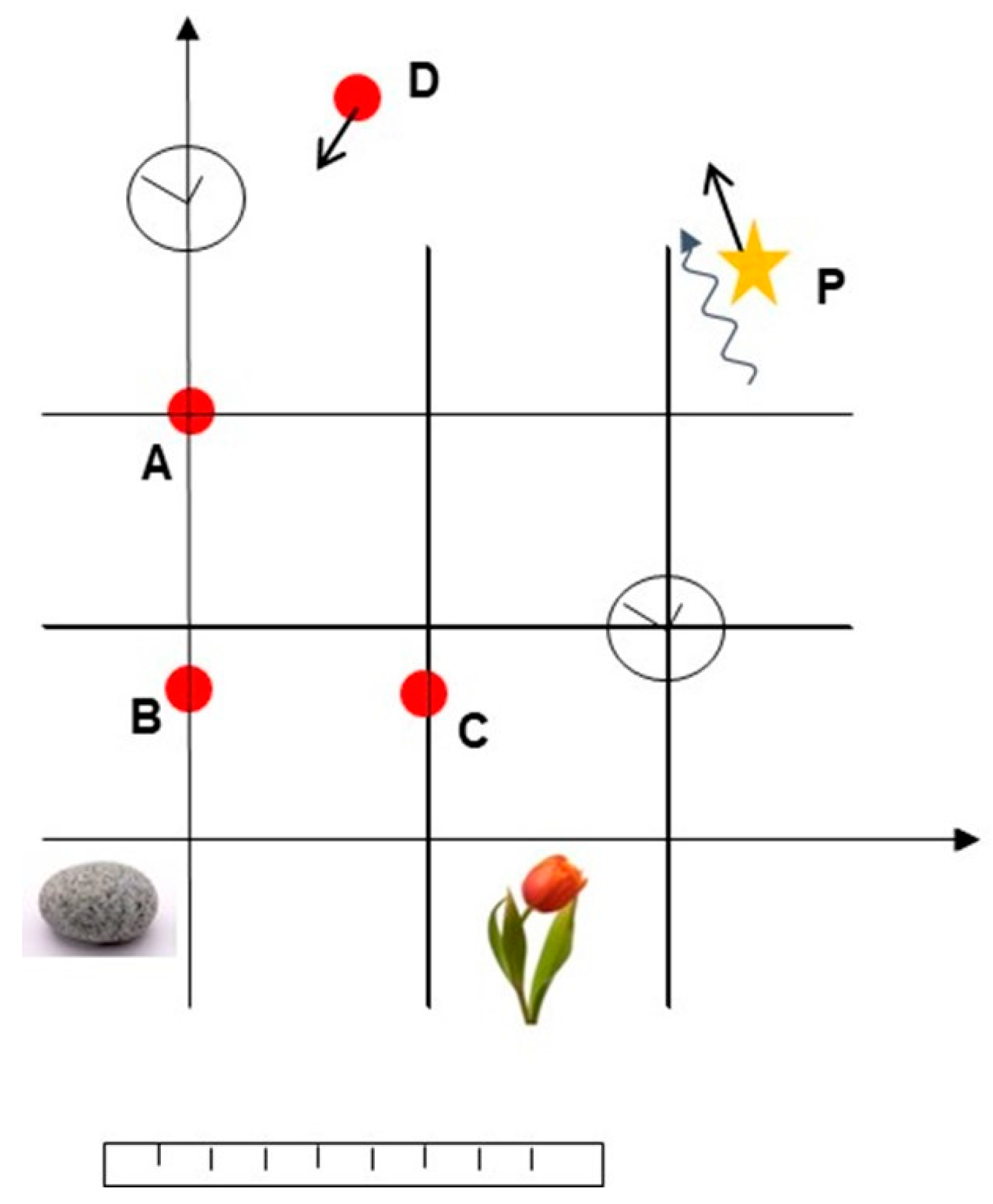
In a few words, the theory of relativity goes beyond the Newtonian use of absolute space and time. By defining spatial reference frames, and under the constraint of various postulates, it associates space and time variables with each reference frame, and shows the relations of transition from one to the other (Lorentz transformations), thereby demonstrating the loss of absolute character. Special relativity is limited to the case without gravitation, while general relativity extends the results of the former to any case, subject to the use of non-Euclidean spaces (the metric is a function of the local mass-energy content). Depending on the author, the various postulates may change (identity of laws in different reference frames, constancy of the speed of light, group structure, etc.), none of them going so far as to call into question the initial use of spatial and temporal variables, which are there without discussion. For example, the⁴ mental image that the researcher creates within the standard framework when writing his equations comprises two elements (Figure 1): - a regular grid defining the spatial reference frame (in general relativity, this grid can be deformed by the bodies immersed in it); - punctual clocks, often assumed to be synchronized (from all eternity?) located at the various nodes of this grid and enabling the (mysterious) flow of time to be evaluated (the caption to the figure provides further details on the foundations of this representation).

Let's now review a number of points that appear to us to be unsatisfactory in the current handling of relativity theory. For further details, please refer to our work (e.g. Guy, 2011, 2019a), as well as that of the many authors cited therein.

2.2. Relativity Takes Time for Granted

The overriding reason for taking things up again is that the theory does not address the question of the existence of time. Yet this concept is not self-evident. It is the subject of much debate, among philosophers and physicists alike. Without denying the useful operation of equations containing the parameter t, which is meaningful in its own right, we need to try to move upstream and co-construct the corresponding concept. When it comes to answering the question of time, a symptom of this overlooked difficulty is the "circular" appeal to clocks ("time is what you read on a good clock"). And clocks are considered to be punctual. Proper time is also widely used ("it's the time read on a clock attached to the object under study"). None of this corresponds to anything concrete. What's inside a clock? If you open it up, you'll find that the time you read on it is a point of view on a movement.

Another way for physicists to answer the question of time is to refer to a frequency, offered by a particular atom⁵ , as isolated from the rest and measuring pure time (and not drifting over billions of years!). This approach is equally unsatisfactory. H. Poincaré pointed out the circular nature of the definition (who decides the constancy of the frequency defining time?). And how can we consider the atom as a point, whose "vibrations" involve interactions between its components (electrons, protons and neutrons)? Predicting the frequencies that define time involves solving Schrödinger's equation, where spatial and temporal variables are associated. Frequency is not "alone" and then transmitted (after it has been "made") by a wave. It is the frequency of the wave associated with the photon that recovers the energy of the electron passing from one level of the atom to another (via the relationship between frequency and energy E = hν). This frequency is therefore inseparable from the wave's propagation (motion) at speed c. The energy levels E_i are among the first results of solving Schrödinger's equation, and involve the quantum numbers associated with the various wave functions (principal, secondary quantum number, etc.). Atomic clocks also take account of possible Doppler effects, another way of saying that atomic motion and its variations are taken into account. All in all, the separation of frequency from the propagation of the wave that transmits it to us is a pure convenience of the mind that corresponds to nothing possible. It's like creating a fictional time⁶ that's useful for thinking, but that doesn't do away with the concrete time that's always associated with movement...

In short, we'd say: no, it's not a trivial approximation to consider punctual clocks and continue on our way as if nothing had happened. It's a convenient way of avoiding the question of time.

2.3. Relativity Maintains Two Distinct Concepts of Space and Time

The previous comment extends to space. Relativity postulates the existence of graduated rulers, whose constituent points are rigidly linked to one another. They are used to define a three-dimensional grid of points in space. In so doing, we are once again relying on objects that correspond to nothing concrete: who knows of a rigid graduated ruler 150 million kilometers long? Talking about rigidity implies situations in which it would not be satisfied. - In which space can we observe the rigidity, or non-rigidity, of the scaffolding that defines space? We need to imagine a second scaffolding, encompassing the first (the fictional character of which is revealed...). - How can we avoid appealing to time when examining a possible deformation of the rulers? The property of rigidity doesn't exist (any more than the punctuality of clocks); it refers to a conventional space of reference whose status needs to be clarified, in association with that of time.

When relativity announces the study of a space-time continuum, it links the values of the associated quantities, but keeps two concepts separate, supported by two distinct types of tools, rulers and clocks⁷ . A more appropriate approach would unite the two concepts in the concept of motion (as announced). The punctuality of clocks and the rigidity of rulers: it's true that, at some point, we have to create a fictional representation of the world; but the fiction must be an outcome, not an a priori statement. If we fail to identify our assumptions correctly, we risk missing the real world altogether.

2.4. Relativity Does not Address the Questions and Objections of Critical Physicists

From the earliest days of the formulation of the theory of relativity, some physicists, known as critics, expressed reservations and pointed out the difficulties they saw in its exposition and development. Dingle (1972) was one of the first; he was well known as a physicist, having initially espoused the theory, before departing from it for reasons set out in his book⁸ . Today, there are countless researchers, associations, seminars, congresses, magazines, books, blogs and press releases disputing various points of the theory and its variants. There is no unanimity, with some calling for relativity to be rejected outright, and others calling for it to be modified along lines that may be considered more or less sensible. A full-time job wouldn't be enough to explore this constellation! The few we know of include: the PIRT (Physical Interpretations of the Relativity Theory) conferences, the NPA (Natural Philosophy Alliance) association and its epigones, the journal Galilean Electrodynamics, compilations of "alternative" theories by various researchers, and so on.

The general public is unaware of these families of thought. Institutional physicists are sometimes aware of them, but look the other way and pretend there's no problem. Without underestimating the effort it would take to examine these works, and get an idea of their value, we feel that their total ignorance is unsatisfactory. For one thing, it's not in line with scientific ethics, or ethics at all: we're dealing with men of good faith. Certainly, some are old, acrimonious, aggressive and, to put it bluntly, impossible: should we imitate them? On the other hand, ignorance leads us to deprive ourselves of the potential contributions of researchers who have given the question some thought; in return, they can reinforce our truths or make us look at this or that point in a new way (knowledge needs contradictory debate; let's remember Blaise Pascal: "look at the opposite truth").

There's a long list of topics discussed in the forums we've mentioned. In a nutshell: the twins paradox, the paradox of non-Galilean velocity addition relations, the difficulties posed by the composition of non-collinear Lorentz transformations... to name just a few of the points we know about; this is just the tip of the iceberg. We'll take up some of the points below, claiming that we can seek an overhanging point of view that could reconcile the essentials of the standard development and the criticisms it elicits, sometimes with slight modifications to the formalism and/or its interpretation. We're in favor of deepening and consolidating the theory (in the sense of saying space = time...), not rejecting it and returning to a supposed Galilean golden age.

2.5. Difficulties Encountered in the Humanities and Social Sciences When It Comes to Time

In the humanities and social sciences, various difficulties, or aporias, of time are enunciated, a priori independent of the physical side. In his "Aporetics of temporality", Paul Ricoeur (1985) lists three of them. The first is the split between an external time, found in the world (the time of the cosmos), and an internal time, seen by the subject, whose reason would be the true locus of the construction of time (cf. also Saint Augustine). The second is the totalization of the past/present/future trilogy into a single concept: time. The third is the irrepresentability of time: we can only use metaphors. We should also mention Plato, Aristotle, Husserl, Heidegger and many others when discussing time and its difficulties (see Dubar, 2008, for a discussion of temporalities). In our work (Guy, 2019a), we have spoken of the "dilation" of Poincaré - Bergson - Boscovich ("the world could swell while the velocities of movements would increase in proportion: we would see nothing of it"). We could also mention the proposition that time stops and then starts again, without this being detected either...

Discussing the embarrassments of thinking about time in the humanities (including philosophy) is a continent we can only see from a distance. But we believe that a renewed understanding of the whole, based on a fresh look at the theory of relativity, will lead to solutions. Physical theory, by seeing as incomparable scientific time, supported by proven instruments, declared objective, and human time, referring to the experience of consciousness difficult to control, declared subjective (why the same word for time?) has made the cut damaging.

3. Two Thinking Tools to Put Movement First

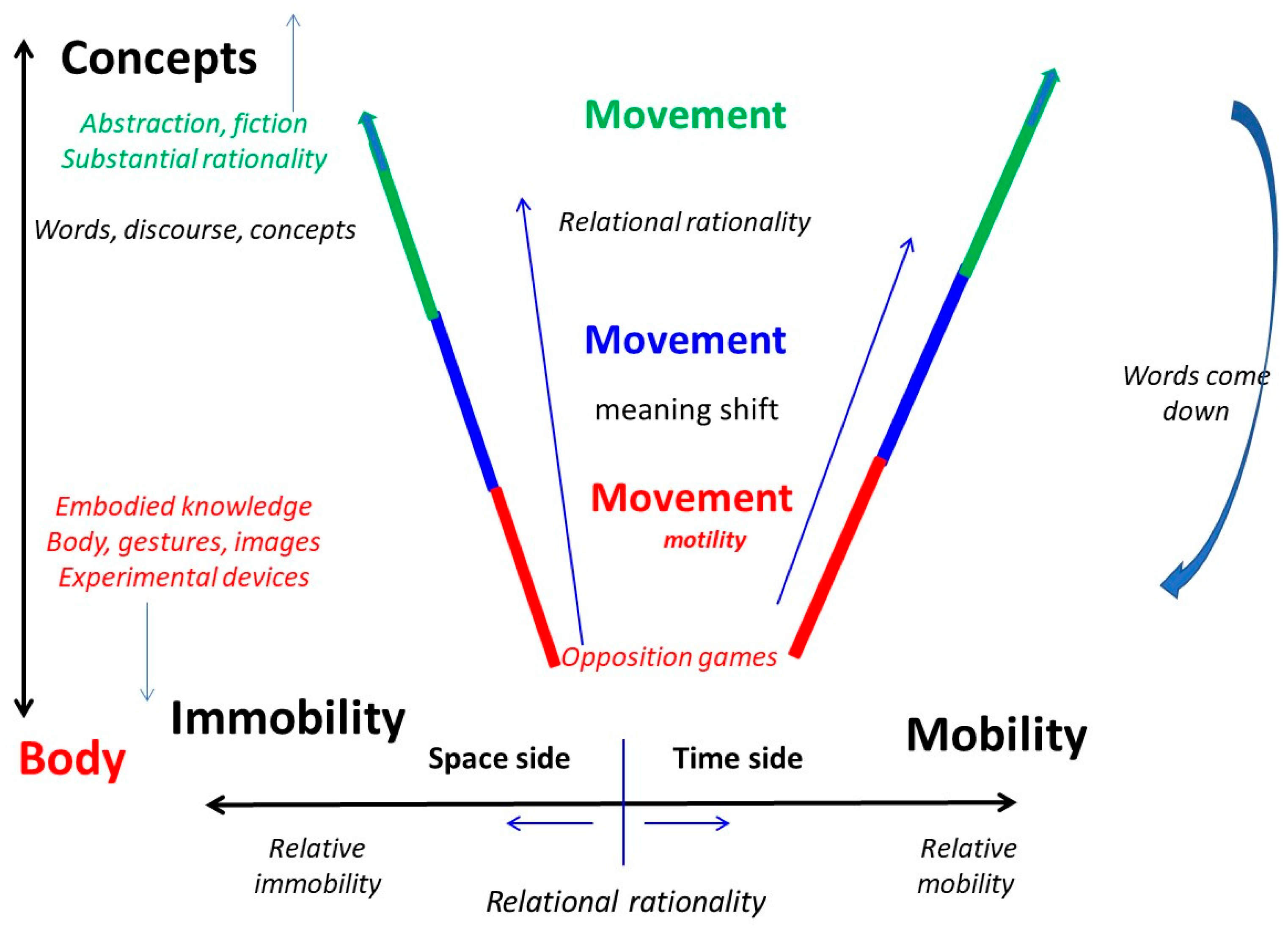
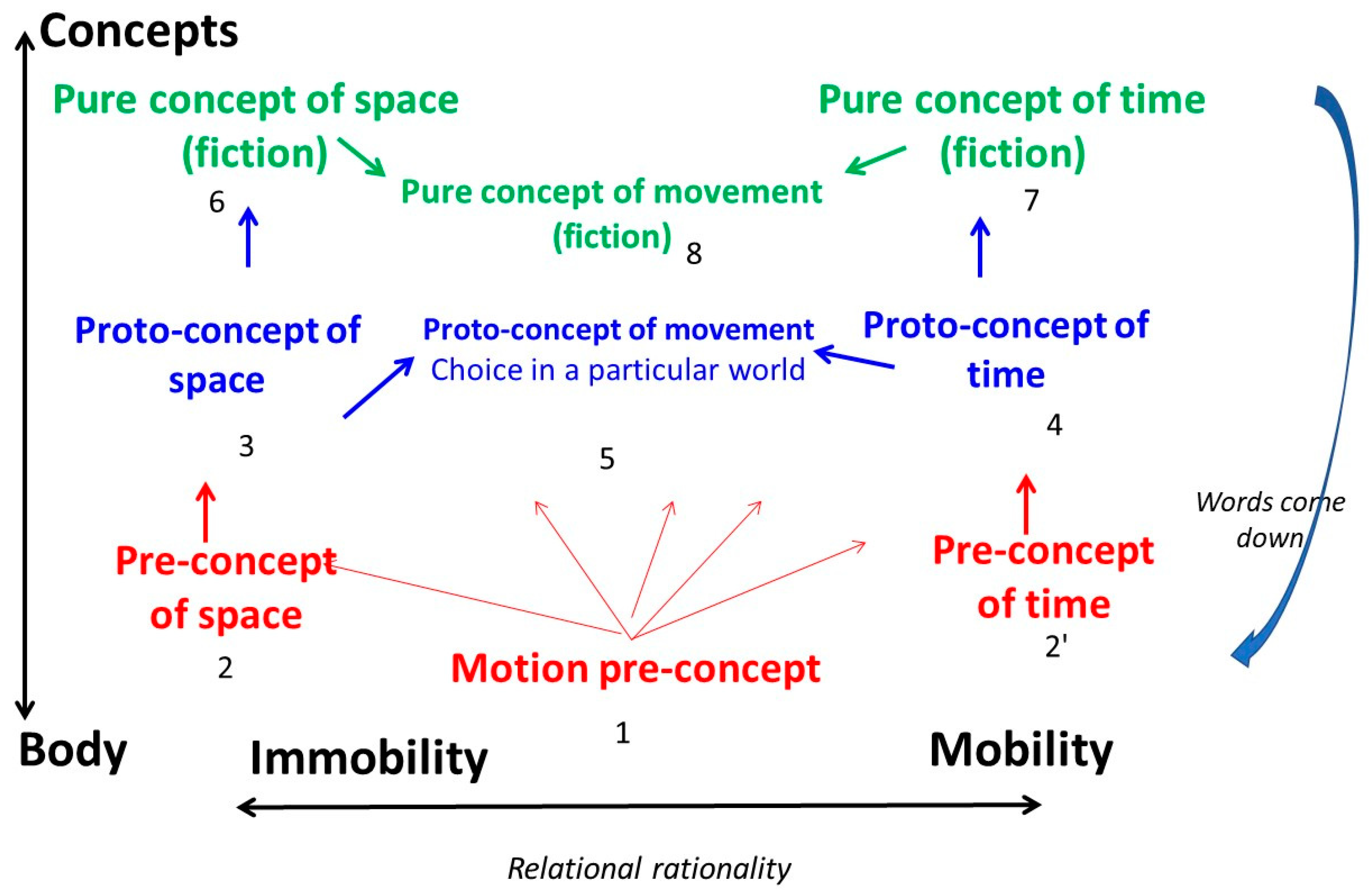
We seek to highlight an approach in which neither time nor space is acquired from the outset, but, on the contrary, is constructed as scholarly knowledge progresses, starting from the movement to which we give a foundational value. The revival we propose (Guy, 2021b, referring to numerous authors⁹ ) is founded on two pillars: - embodied cognition s.l.; - relational rationality (movement is relationship; comparisons of movements help define space and time). We present these two essential dimensions graphically (Figure 2a,b); both argue for the primacy of movement over space and time. Let's take a closer look.

The first dimension, along a vertical axis, opposes two poles, which epistemologists, psychologists, etc., have identified in our appropriation of the world. We take this duality for granted here; among many references, see for example Dahan-Gaida (2020), Lobo (2021)¹⁰, Merleau-Ponty (1945), Vaihinger (1923), Virole (2009), and those cited in Guy (2020b, 2021b). On the one hand, towards the bottom, we're talking about apprehension through the body, gestures, images and the imaginary, before words; a mode that includes, by extension, experimental devices and their implementation in measures¹¹. And on the other, upwards, the use of words, concepts and all discursive formalism and its processes of abstraction and fiction, right up to mathematics. This dimension, contrasting images with words, is just as much that which opposes the singular to the universal, the part to the whole, the proper noun to the common noun, the physical to the philosophical, World 3.0 to World 3.1 (in the sense of Karl Popper, 1984, revisited, cf. Guy, 2021a¹²), and so on. For example, is the movement (space, time, etc.) we're talking about shown, experienced, etc., or defined by a mathematical formula? There is continuity between the two extremes (with a whole series of stages: gestures, sign language, ideograms, emoticons¹³ ! ...), with the words time, space and movement moving along the axis, gradually changing meaning as the context changes.

Highlighting the first dimension means asserting, against what we are sometimes tempted to think (and the temptation always comes back), that there are no pure and true concepts in physics, in good correspondence with reality, that would be cut off from knowledge of the body and its movements, before they are stated as such.

The second dimension is marked by a horizontal axis featuring the relational mode of rationality, fundamental to our business: we are inside the world, we can only compare phenomena (another name for movements) with each other, without stepping out of it or qualifying its objects in themselves in any substantial way¹⁴ (on the relational aspect see, for example: Morin, 1990, 2013; Pascal, 1662; Poincaré, 1905; in his own way Granger, 1992). We will thus contrast mobility with immobility: these words have a concrete character, without prejudging the existence, or meaning, of concepts such as time and space¹⁵. The last two terms themselves do not appear to be paired, unlike the mobility/immobility pair. The latter can be grasped on the basis of human experience, extended in various ways by conceptual generalizations. Mobility and immobility are described as relative, to underline, if need be, the comparative point of view, at a certain scale of speeds. In a given context, we speak of movements of lower mobility, lower speed (let's call speed a way of comparing movements) or stopped, as the basis for constructing concrete space; and, by comparison, movements of higher mobility, higher speed, or continued, as the basis for constructing concrete time. A whole domain stretches out where to put the limit between the "concrete" times and spaces envisaged, variable according to what we can or want to look at (cf. Guy, 2019a).

Highlighting the second dimension means asserting, against what we often tend to think (and the temptation always comes back!), that reality doesn't impose words on us to describe it; we can't avoid going round in circles and making conventions (such as that of dividing concrete time and space along the horizontal axis). Words have relative meanings, depending on context, etc., with inevitable uncertainties and fragilities.

Certainly, along both the first and second dimensions, there are aspects of circularity¹⁶, according to Morin's "complex circle" (show ↔ tell). They can be visualized graphically here: in the ascending path, meaning goes from things to words. Words are not given a priori; they arrive a posteriori, having already been elaborated from the body, etc., passing from proper nouns to common nouns. To "close" the circle, we need to mention another, descending path, which goes from words to things: after having been made, words go back down, as the tools of thought they have become, and enable us to name things, experiences, etc., as we commonly do.

The independence of the two dimensions is not perfect, and is accompanied by shifts in meaning (Figure 2a,b): the further you "climb" away from the body, the more substantial the expression of thought, in words, appears to be, and the further it moves away from its relational character (it separates more and unites less); and the full meaning of concepts also depends on the boundary that has been decided between concrete time and space (the relational aspect has more weight in the lower, more "human" part of the diagram). But in this representation, everything remains relational, both above and below, by definition of the horizontal axis (valid for all space). What is substantial (abstract, fictional in the strict sense) escapes the figure; the escape is from the top, made possible by words that are isolated from one another. At the top, we write relational rationality. In the lower part, we can still use the word relational by "redescending" the words; but, to mark a differentiation, without speaking of rationality, and by insisting on the rooting in knowledge of the body, we could use other terms: play of oppositions, synaptic thought (with a meaning close to physiology). Substantiality is less important to us in the lower part, as this is the level of concrete reality, before words, where everything is connected (but it's still hidden in the relational, see comments in Appendix 3). As for the shift in meaning of the word movement, we can underline it, using for the most elementary (bottom), the term motility¹⁷ (in a primary biological sense).

To promote these two dimensions is, in essence, to say that relativity has not taken them on board, and has not followed a sound path of rationality. This overall criticism will become clearer later on. It's that of insufficient hindsight on the proportion, in any theory, between elements in direct correspondence with reality, and those which are tools of thought, constructed by means of a certain leap from reality: correspondence with it is no longer guaranteed. Their justification is their effectiveness. Every theory makes use of fictions, but these must be created in the course of the research process, not parachuted in from the outset. They must be accounted for in a way that rises above concrete experience.

As a partial conclusion to this second part, we feel it is essential to take up the question of time and space in relativity theory, and place it within a broader problematic in which motion is central.

4. An Interpretation of the Theory of Relativity

4.1. A New Mental Image: A Space of Comparative Movements

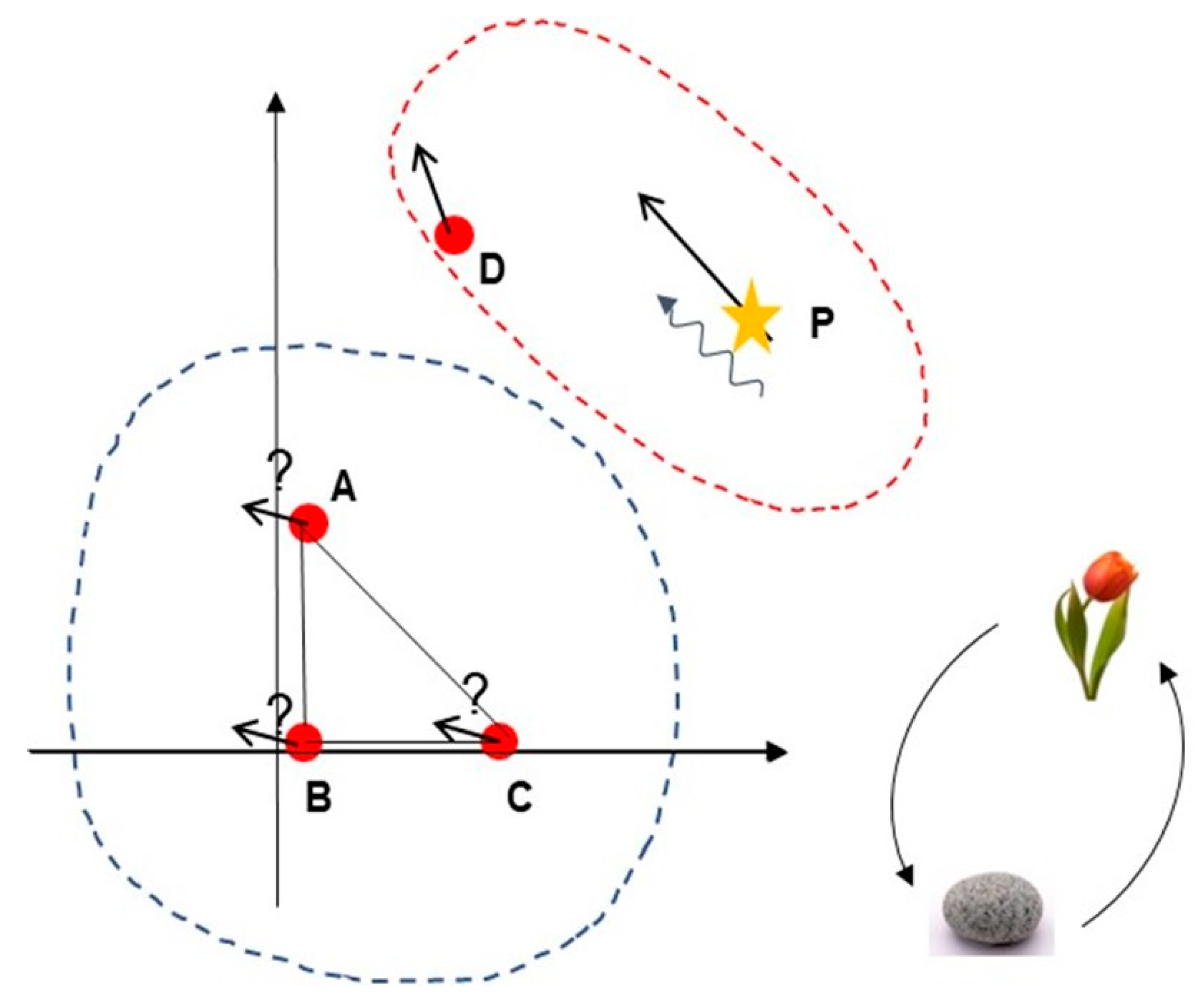
In short, we need to use a new paradigm, based on new mental images, founded on comparisons of movements (Figure 3). So, to replace the image of the grid (more or less distorted) and punctual clocks, we imagine a space of movements from which we construct, by means of revisable conventions stopping endless regressions, space markers (points whose relative movements are negligible/neglected) and clocks (a moving point whose movement is taken as a standard). We understand the genesis of fictional space-time from the first representation (cf. Figure 1 and Section 1.1), at the limit, at the end of the road, but still rooted in the body and relational thought. To speak of a single time, we needed to agree on a standard movement of social value. In physics, the quantitative approach was expressed in Lorentz transformations. In the humanities and social sciences, the consequences of this pre-eminence of motion are expressed in a qualitative relativity that doesn't need excessive speeds! In short, a theory of relativity, whether understood from the perspective of the "hard" sciences or that of the humanities and social sciences, combines the construction of a framework of space and time, anchored in comparative motion, with the choice of a standard mobile to fix this framework (for a minimum of quantitative coordination).

4.2. Lorentz Transformation in the New Frame

The Lorentz transformation is the basis of the theory of relativity. In the present context of "rereading", we can ask a few questions¹⁸ . - How can we derive the Lorentz transformation following a relational rationality, especially if space and time don't pre-exist and have to be understood in the process, on the basis of compared movements? - Can we express the Second Postulate in terms of the speed of light, as we usually do, given that the latter is used to define space and time standards? - Can we write the Lorentz transformation simply in terms of comparisons of v/c ratios (c is the speed of light; v denotes other, non-electromagnetic speeds, such as gravitational)? - More fundamentally, what do we want to express, what need do we have to formalize in equations the progress of phenomena envisaged in reference frames in relative motion? How can we do this, and on what basis?

The answer to this last question is rooted in the need for communication between observers with different points of view on the world; it translates into saying that the laws of physics must be the same in all frames of reference (first postulate). To achieve this, we need to properly define such reference frames, and use one or more phenomena as a point of comparison, or standard(s), for a quantitative approach. This is the meaning of the second postulate, usually particularized by taking light and its "speed" as the basis. We can reformulate the latter in a broader way, encompassing the first: "only comparisons of phenomena (comparisons of movements) between themselves are our point of solidity"? This is in line with Poincaré's remarks (1902, 1905). Lee & Kalotas (1975) and Lévy-Leblond (1976) have each, in their own way, proposed a coalescence of the two postulates. The relational aspect encompasses laws, speeds, confrontations of phenomena, etc. (see Guy 2010a, 2015, 2019b). To discuss quantitatively the various movements offered to our investigation, everything derives from the relational necessity of momentarily (provisionally) choosing a basis of comparison to speak from, deciding to fix the numerator or denominator of a v/c ratio. To the question "Is c constant?", we answer: "We don't know, but we're obliged to assert it, at least locally".

From a technical point of view, are we going to be able to derive the Lorentz transformation without time nor space, simply by relying on a motion ratio of the v/c type? No, not directly. Because, from the moment we formulate discursive propositions or equations, we dissociate space from time. So we're obliged to go through the process several times, in recursions that we can't escape during derivation. We begin by acting as if we had separated space from time, focusing on one of the two terms in a v/c relationship. We give it a fictional meaning in m/s, proclaiming "c = cst". We then realize that space and time are linked, and that c is not the only factor involved in the v/c relationship. In short, we retrace our steps to interpret what we've done: "no, they were just v/c ratios". In the standard derivation, the v/c appears early and we're embarrassed when the test light ray is perpendicular to the vector v of the relative motion of the two reference frames (Guy, 2019a). The γ factor of the Lorentz transformation is expressed in terms of v/c: in Guy (2019b), we express motion ratios vectorially, after opening the clocks that were themselves hiding motion of particular direction. In short, the Lorentz transformation captures the moment when we separate space from time, linked in the comparison of movements.

In addition to, and thanks to, its algebraic aspects, only just mentioned, the theory of relativity (with or without a renewed interpretation), and its expression in the equations of space-time transformations, brings a number of essential qualitative results to mind: - physical quantities are expressed in pairs, such as {electric field, magnetic field} or {energy, momentum}, formalized in four-vectors, or pairs of 3D vectors; - transformations of these coupled quantities enable mass and energy quantities to be linked; - space and time, in the pair (r, t), can be put on the same plane as other physical quantities (cf. Guy, 2016a); etc.

4.3. What Status for the Speed of Light?

What first changes is the meaning given to the word speed: it's a ratio of movements, one of which is chosen as the standard. The speed of light is no exception to this rule, the other motions being gravitational in nature (see historical measurements of the speed of light). The speed c is often taken as a structural constant, but this is in a second stage that does not dispense with its initial construction. Today, this "speed" is no longer a "speed" in the sense that we already have independent space and time standards with which to measure it. On the contrary, it's the propagation of light that today provides the standards of space and time (which return to the same standard via the postulate c = cst). Compared with earlier practices, there is thus a twofold change: 1) a change in order of priority: the propagation of light "precedes" the space and time standards; 2) a change in the number of standards: we move from two standards (space and time) to a single one. Is there continuity between these practices? Yes, and to demonstrate this, we can equate the meter and the second in their ancient definition with portions of light's movement, thus evaluating two quantities of a priori different natures by the same gauge. The "speed" of light then has two values: 299,792,458 m/s, expressing the ratio (fixed by decree) between the two old standards, as two particular "objects" of our world and designated as such; and c = 1, frequently used in physics, expressing today that it has no number, it's what allows us to measure. To speak of the "constancy of the speed of light" is to express a tautology, but to be able to "observe" the latter reassures us as to the remarkable know-how of physicists, and the efficiency of the loop between practices and the choices made in writing equations. In this context, it's more appropriate to say that there are no longer any standards of space or time, and that the second is the standard of motion. And to say that a velocity is the ratio of a movement to the standard of movement (there is still continuity between the old and new definitions of velocity)¹⁹ .

Finally, let's come back to the relationships r = v/c in a slightly different way: we've mentioned their founding role in relation to the two terms v and c that seem to make them up, in particular with regard to the Lorentz transformation and its derivation. Qualitatively speaking, these ratios express, first and foremost, the confrontation or comparison of two phenomena perceived as dissimilar by our senses: we would like to assign them different values from a quantitative point of view (giving one the value v, the other the value c). But what we need to add is that r numbers are not generally obtained by algebraically dividing two other numbers v and c already available to us, as measured separately. In reality, the r value is obtained by a single measurement. And it's only at a later stage that we allow ourselves to "cut" it in two and express it as a ratio (taking one of the two phenomena involved as a reference, or possibly reducing it to a third phenomenon...). It's this inevitable duality of moments that we expressed in our "trial and error" with the Lorentz transformation. To be able to say, we need to separate through fiction what was united in reality. This nuances our view of the concept of "relation", omnipresent in this work: it can mean the facing of entities defined independently of each other, or, more profoundly, the expression of a link such that it contributes to the definition of each of the two terms it unites (Th. Berns, pers. comm. 2023). While we have received it as established on concepts acquired once and for all, the theory of relativity must be placed in this circular movement: it presents itself as using concepts of time and space that are already there, but it produces an operation that shakes up their starting points and opens up a field of novelty.

5. First Fruits?

The previous interpretative framework unites the physical sciences in the broadest sense of the term, on the one hand, and the humanities and social sciences on the other, saying: there is an identity between spatial and temporal relations; space and time are comparisons of movements. To put knowledge into words, we need conventions of a social nature (such as the assumption that a standard is constant). We find this necessity on both sides. Let's take a look at the fruits of our re-reading on both sides. They demonstrate the fruitfulness of the mental representations described in Section 2 and Section 3, and the interest of the announced revival.

5.1. Fruits in Physics

Several physics questions seem to us to be illuminated by a better coupling between the concepts of time and space, and by the primacy of motion. They constitute so many chapters of what could be called a physical theory based on the identity of spatial and temporal relations, or even on the single category of "motion" (cf. Guy, 2016a). A slightly more detailed review is offered in Appendix 1 (with useful references). Let's take a look at a few.

In thermodynamics, the coupling between gradients of quantities (in space) and their temporal derivatives is a way of looking at the fundamental association between space and time, giving the arrow of time a character that is not restricted to this parameter alone: it reflects the tendency of systems left to their own devices to achieve spatial homogeneity. The boundaries between equilibrium and disequilibrium, reversibility and irreversibility, heat and work, and the opening and closing of systems, are not provided by nature, but are determined by where the observer places the boundary between time and space. The entropy function appears naturally in the description of systems at a given scale, freezing their organization at a smaller scale in its most probable state (Guy, 2020d).

The composition of non-collinear Lorentz transformations is a place where our proposals provide a solution to problems that appeared inextricable: the time parameter, constructed from the position of a moving body, is affected by geometric transformations (rotations), brought into play in compositions, in the same way as spatial coordinates. This re-establishes a symmetry between spatial and temporal variables, the lack of which was responsible for a number of difficulties.

As far as the twin paradox is concerned, the important point is to understand time as given by the position of a mobile: the assumption of constancy in the speed of light translates into the decision to attribute the same behavior to a single moving point seen from two different reference points. The result is a variability of possible situations in terms of which twin comes back younger or older than the other, and by how much. We can see the role of interpretation, in this case the choice of direction of movement marking time in clocks.

This is a way of looking at the γ factor of the Lorentz transformation, and its expression as a function of the direction of photon motion in the atomic clocks in use today. We have opened the clocks located in each of the two reference frames in relative displacement, and discovered such motions. We propose new equations where the factor γ depends not only on the velocity ratio β = v/c (v velocity of the relative displacement of the markers, c "speed" of light) but on an angle δ between motions. They relate to various results in the literature.

In other work, we highlight basic physics relations. We call them degree-zero relations, combining temporal and spatial derivatives, and Lorentz invariants. We can add or derive from them relations of epistemic uncertainty (we don't know the standards!) or a-certainty.

If we look at chance and its relational understanding, we can say: we don't know what is random, we contrast what is more certain with what is less certain. Probabilities are given by measures of spatial and temporal amplitudes. Time and space are themselves subject to uncertainty in composition with the various physical quantities. The relationship between quantum mechanics and general relativity is therefore very close, although the former does not have a monopoly on quantization (it must be understood in terms of the comparison of two classes of phenomena in a probabilistic vision), nor does the latter have a monopoly on space and time: we must see their possible composition and not their opposition in terms of space and time (the former would be dependent on the external space-time frame, whereas the latter would not), taking space and time as a pair of associated quantities in composition with the pairs of other physical quantities.

Finally, in cosmology, we emphasize the role of v/c ratios in determining the speed of distant objects²⁰ (a general "relational" necessity). On this basis, we are encouraged to postulate a slower speed of light on the cosmological scale: this avoids the need for dark matter and dark energy, while at the same time extending the age of the universe (a way of getting around the problem of impossible galaxies discovered by the James Webb Space Telescope?).

What did we do to achieve all these results? What recipes did we use? There are many, and they all reflect a relational approach to comparing movements. For example, the variable t refers to a movement and can be understood as the position of a standard mobile. Under these conditions, passing through a point with three coordinates can render a happy symmetry between spatial and temporal variables. These variables can also be balanced by symmetrizing the derivatives $\partial /\partial t_i$ and $\partial /\partial x_i$ and expressing the basic equations as conservation relations. This can also be seen, as we said, by noting that the pair (r, t), where r and t are a priori two vectors of dimension 3, is to be placed on the same footing as the pairs of conjugate quantities in physics. Light is no exception to the relational approach, and we generalize the apprehension of v/c ratios.

5.2. Fruits in the Humanities and Social Sciences

In the humanities and social sciences, a deeper connection between time and space seems fruitful. We spoke earlier of the aporias of time enumerated by Paul Ricoeur; what can we say about them? Is the duality between cosmic time and human time unsurpassable? No, they're merely comparative movements, with the sky having no pre-eminence over the movements of nerve impulses that follow consciousness. With regard to the fusion of past, present and future into a single "time", there are two possible answers. According to the first, it would be a mistake to try to apprehend time alone; language deals with the whole, which is the association of space + time. Time is just one part of it. And according to the second, we're reminded of the relational nature of the space/time tandem, each defined by the negation of the other. The present is as much in the cloud that makes and breaks, as in the peaceful mountain that never changes. Time passes beside the mountain (we're not going to say that the mountain constantly disappears and reappears, that's absurd; see Guy 2011; see also our reflections on the "specious present", Guy, 2019c). The present is particular, not that it constantly flees, but it is not on the same footing as the past and the future: it is underpinned by the direct experience of all the senses in a presence of space, unlike the past and the future, which are embedded in an intellectual fiction²¹. Finally, as regards the need for images, we would say: yes, they have a foundational role, as underlined above, prior to the formulation of discursive knowledge.

In Guy (2019a) we discussed other issues, such as the motor of time (time has no motor because it doesn't exist!), ancestrality (time didn't exist 100 million years ago, but it doesn't exist today either): history is a gear of movements. The division between space and time can take place in different places, depending on the movements we perceive or attach importance to in a given context. There is a multiplicity of spaces and times, with the physicists' unique time and space playing a special role in accommodating broad communication within the social group. The space and time (spaces and times) we construct are based on what makes up our world, from the stones and markers of our monuments and streets, to the men and women with whom we live. In certain situations, the separation between space and time, linked in movement, is not made, or is made more difficult.

How do these first elements manifest themselves in the diversity of the humanities and social sciences? Rather than taking a tedious tour of these sciences, or at least the ones we've tackled or simply come into contact with, we've taken another angle of attack in Guy (2020a): one directly linked to our approach, consisting of identifying which new articulations between space and time are made possible by our point of view, and finding them in the various disciplines. We follow the progression of thought and formulations, from the "original" situation where time and space are welded together in movement, to that where a single, separate time and space are proposed as the reference bases for society. We can distinguish, more or less artificially, several stages, like so many original reading keys, punctuated by digressions on the various modalities of spatio-temporal assemblages (see details in Appendix 2).

The first stage is the nomadic moment, when we wander without seeing a clear separation between space and time, apprehended in movement. You don't look back. In a second stage, we see the beginnings of a separation, with the first conventions, the first hypotheses; but we retain a multiplicity of times (and spaces). The time of each person's story lies somewhere between the first two stages, demonstrating the importance of space in the construction of identity, and not just time (cf. Abravanel, 2013). The next step is to choose a unique time and space of broad social value.

To separate space from time is to artificially separate man from the world: with Descartes, the time elaborated/situated in consciousness is opposed to the expanse of the world around the subject. Separated from the world, his identity lies in his thought (cogito ergo sum). On the contrary, we understand that man's identity is constructed by all the movements (all the relationships) that link him to the world, space and time forming an indissociable whole.

New points of view on the arrangements of space and time shed light on the workings of different areas of the humanities and social sciences. The stages and stops on our journey are another way of looking at the variety of the humanities and social sciences, and the possibility of classifying them: today's accepted boundaries are questionable or subject to variation, such as that between history and geography (or anthropology and sociology).

5.3. Comparison of Contributions from Both Fields (Physics, Humanities and Social Sciences)

In general, what we bring to the table, and what favors a rapprochement between physics and the humanities and social sciences from the point of view of space and time, is first and foremost a motivation to change interpretation: to recognize complexity, to set thought and knowledge in motion, to accept a loss of stability, to dare to go round in circles, to resolve to stop endless regressions at the cost of a lack, of an unknown remainder (cf. Vaudène, 2021). This leads to new, "trans-scientific" mental representations. The link between time, space and movement brings us back to the concrete, offering us new angles of attack for the study of time, but also of space, and concerns all sciences.

One might have wondered a priori how work that cultivates the theory of relativity in physics could also apply to fields whose practitioners don't particularly move around like photons of light! Reconciling the humanities and social sciences with physics! Some will object: "What link do you see between the Lorentz transformation, the mainstay of the theory of relativity (one of the fundamental aspects of the scientific revolution of the early 20th century), and common experience? This is the acute question posed by American pragmatists, in particular Mead (2012) (see also Leclerc-Olive, 2012). For these philosophers, the task was to link science to life, to find "ordinary notions of ordinary people" (Mead), to bring the humanities and social sciences into dialogue with physics. This was at a time when scientific discoveries (in this case, relativity) seemed counter-intuitive. It had worked for Newton, but we had to find a way through for Einstein.

In our work (Guy, 2015b, 2019a), we have proposed a situation where the mathematical structure of Lorentz transformations can be found (somewhat hidden!) in human experience. This is what we call the Phileas Fogg effect (Jules Verne's hero). Let's imagine that the only clock we have is a sundial; to measure time, we rely on the sun's movements; for days, we count the sun's passages at its culmination point in the sky at midday (a way of attributing to the star a movement of constant "speed"). A similarly equipped twin travels east-west or west-east around the earth, while his brother remains sedentary. When they are reunited, there will be a discrepancy in the way they count time. The problem is the same if we replace the sun with a photon in an atomic clock. Time (and space) lose their absolute character. This is not just a thought experiment: Phileas Fogg certainly experienced it (to his advantage) after long tribulations; but today, with the development of air travel, time shifts are felt without waiting 80 days. Depending on the speed of the plane in relation to the path of the sun, time speeds up, slows down or even stops in relation to that of our friends on the ground (see the correspondence with relativistic formulation in the works cited²² ).

All in all, we have noted the omnipresent interest of the²³ relational approach to knowledge, another way of saying that the discussion on space and time is to be conducted, not in terms of ontologies, but of "dynamics"²⁴ . The fruits are somewhat different between physics on the one hand, and the humanities and social sciences on the other, but they do contribute to reviewing, or even contesting, their boundaries, by giving full scope to the co-construction of concepts of space and time. Because movement is first and foremost human, and the construction of concepts is rooted in human experience, it is on the SHS side that the stages of this construction are best followed. This is where we come face to face with the multiplicity of time and space. By contrast, in physics, we go straight to the single social time that has proved its effectiveness in the duality of time (variable t) / space (variables x, y, z). Without radically contesting this duality in this field (that's not the first subject), we're now becoming more lucid about the parameter t: it doesn't refer to a unique substance of the world, it requires conventions; there are possible transformations between space and time depending on points of view, etc. The spatial representation of time is made more lucid by the fact that it's not just a question of time, but also of space. Spatial representation of time is made easier by rebalancing with space coordinates. As shown in Appendix 1, new avenues are opening up.

6. Let's Look Elsewhere

Let's conclude with a few remarks on two ways, among countless others that we don't pretend to know, of taking the theory of relativity, represented by two articles in the current issue of Intentio.

6.1. Scale Relativity

What we have to say about this is based solely on a reading of Nottale (1998). The rationale behind this author's proposal lies mainly in a generalization of the principle of relativity to characteristics of reference frames that go beyond their mere relative velocity, and in the solution it may provide to the disjunction between quantum mechanics and general relativity. In the light of the foregoing developments, let us make a few remarks, tempered by our widespread ignorance of L. Nottale's work.

The first concerns the relative or relational aspect consistently emphasized by this author in his book (op. cit.): we don't know things in themselves, we only know relationships or differences. It doesn't seem to us that this primordial aspect has been pushed to the limit in current physical theory, nor in scale relativity. For example, we could have pointed out that the principle of relativity itself, if restricted to saying c = cst, escapes the relational mindset: what are we comparing the speed of light to? So too it seems to us that the relational mind must be applied in quantum mechanics to explain quantization (or discretization) as we did in Guy (2016a).

It remains interesting to compare the uncertainties of space and time, Feynman's stories and the possible fractal character of space-time. The extension of the principle of relativity to qualities such as the gauge (cf. the fractal character) could be similar to what we say about the convention of separation between space and time: we place ourselves at a scale where we decide, in sum, the precision of space and time measurements (we don't try to find out what happens below this scale).

In contrast to the relativity of scale, we can see that, in the field of thermodynamics, for example, the laws are not the same at different scales (Newton's laws at particle scale; Fick's or Fourier's laws at population scale). The question of the existence and universality of laws is related to the previous ones.

Finally, and quite fundamentally, neither the concept of time nor that of space is criticized by L. Nottale, who takes them for granted, at least at the stage of scale relativity. Yet he speaks of a beyond?

6.2. A Constructivist Approach

A constructivist approach applied to some of the above questions (relations between relativity theory and quantum mechanics, the place of time, etc.) is outlined by Giorgio Quadranti (2023). It leads him to some original results. For example, the primacy given to quantum mechanics and the second nature of relativity, as deduced from the former. Or the pre-eminent place given to time, with space appearing to be derived from it. Or the importance given to processes. We won't comment on these results in detail: they are part of a fundamental reflection on the construction of any theory from reality (with his book Le monde comme texte, 2020, G. Quadranti presents himself in the wake of J. Piaget). There appear to be numerous points of articulation with our own work, such as the convergence of diagnoses on the symmetry problems posed by the Lorentz transformation when the displacements of landmarks and clock-photons are of any direction (Guy, 2019a; G. Quadranti, pers. com. 2021).

Without claiming to have understood everything there is to know about the constructivist approach, let us nonetheless note, with regard to G. Quadranti's work, a few possible points for discussion in relation to our own reflections: - in the constructivist approach, what place is there for complex thinking that confronts circularities and conventions? - How can we take time as a given, without trying to define or construct it? - And how can we accept that clocks are already there?

7. A Few Concluding Words

In the title of our text, we wanted to refresh the theory of relativity. For us, this means reviving its full colors, breathing life into it, humanizing it. Let's turn for a moment to Kurt Gödel: after a life-long quest to lay the foundations of mathematics independently and autonomously, this author came to the conclusion: mathematics cannot do without man and his intuition (Cassou-Noguès, 2004). In a similar way, by giving full rein to movement, as it is first perceived and inhabited by man, we give relativity theory a new openness and its ability to bring together the two branches of the hard sciences and the human and social sciences²⁵ . We can lessen the divide between them; the question of time was a major point of division.