Algorithmic Energy: An Algorithmic Space–Time Interpretation of Interaction and Gravitation Based on Desmos

1. Introduction

Classical physics interprets interaction primarily through forces generated by mass, culminating in Newtonian gravity and later extended by General Relativity. While these approaches have achieved remarkable success, several conceptual and observational issues remain unresolved, including the nature of dark energy, the interpretation of cosmic expansion, and apparent inconsistencies in hierarchical gravitational dominance.

Recent developments in Desmos (Bond) theory suggest an alternative interpretation in which interaction is not a force but a manifestation of energetic bonds regulated by space–time structure. In this paper, this idea is formalized through the introduction of Algorithmic Energy, a quantity arising from the algorithmic evolution of space–time itself.

2. Algorithmic Space–Time

From Challoumis (2025), “Moon’s Paradox: Why the Moon Is Not a Planet based on Desmos” let space–time be described by an algorithmic scaling function $S\left(k\right)$, where

$$k\in \mathbb{N}$$

denotes an iteration or algorithmic step. The function $S\left(k\right)$ encodes the effective space–time scale at step $k$ and may evolve according to a deterministic or convergent rule.

A generic form is

$$S\left(k\right)=A_1{e}^{-{\displaystyle \frac{p}{t_1}}}+s.d{.}_0,$$

or, in recursive form,

$$S\left(k+1\right)=S\left(k\right)+\lambda \left(S^{*}-S\left(k\right)\right),$$

where $S^{*}$ is a stable space–time equilibrium.

3. Energy Definition in Algorithmic Space–Time

The energy of a body is defined as

$$E=m\varphi ,$$

and when $\varphi \to c^2,then E\to m{c}^2$with the potential-like term

$$\varphi \left(k\right)={\displaystyle \frac{GM}{S\left(k\right)}}.$$

Thus, the algorithmic energy state of body $i$ becomes

$$E_i\left(k\right)=m_i{\displaystyle \frac{G{M}_i}{S\left(k\right)}}.$$

Identifying inertial and gravitational mass for celestial bodies ($m_i=M_i$), this simplifies to

$$E_i\left(k\right)={\displaystyle \frac{G{M}_i^2}{S\left(k\right)}}$$

This result shows that energy is not intrinsic but regulated by the algorithmic state of space–time.

4. Algorithmic Desmos Interaction

The Desmos (Bond) interaction between two bodies $i$ and $j$ is defined as

$${\mathsf{\Delta }}_{ij}\left(k\right)=k_B{\displaystyle \frac{E_i\left(k\right)E_j\left(k\right)}{r_{ij}^{ n\left(k\right)}}},$$

where $r_{ij}$ is the separation and $n\left(k\right)$ is a scale-dependent exponent.

For the physically relevant case $n\left(k\right)=2$, substitution yields

$${\mathsf{\Delta }}_{ij}\left(k\right)=k_B{\displaystyle \frac{G^2{M}_i^2{M}_j^2}{S(k{)}^2{r}_{ij}^2}}.$$

This expression demonstrates that interaction strength is governed by energy states modulated by algorithmic space–time rather than by mass alone.

5. Algorithmic Energy of a System

For a system (or fragment) consisting of a set of interacting pairs $\mathcal{B}$, the total algorithmic energy is defined as

$${\mathcal{E}}_{\mathrm{a}\mathrm{l}\mathrm{g}}\left(k\right)={\sum }_{\left(i,j\right)\in \mathcal{B}}\mathrm{‍}{\mathsf{\Delta }}_{ij}\left(k\right).$$

This quantity represents the energetic state of the system as a whole and evolves as $S\left(k\right)$ evolves.

6. Dominance and Stability

For two interactions evaluated at the same algorithmic step $k$, the dominance ratio satisfies

$${\displaystyle \frac{{\mathsf{\Delta }}_{i_1{j}_1}\left(k\right)}{{\mathsf{\Delta }}_{i_2{j}_2}\left(k\right)}}={\displaystyle \frac{M_{i_1}^2{M}_{j_1}^2}{M_{i_2}^2{M}_{j_2}^2}}\cdot {\displaystyle \frac{r_{i_2{j}_2}^2}{r_{i_1{j}_1}^2}}.$$

The space–time factor $S\left(k\right)$ cancels, ensuring that local dominance is stable under global space–time evolution. This explains why systems such as Earth–Moon remain bound despite stronger external forces from more massive bodies.

7. Physical Interpretation

Algorithmic energy reframes gravity as an energetic bond rather than a force. Space–time does not merely respond to mass; instead, it regulates energy through algorithmic evolution. Mass contributes only insofar as it generates energy, while interaction emerges from the structured coupling of energy states.

This interpretation naturally explains:

• local gravitational stability,
• hierarchical dominance of subsystems,
• cosmic expansion as algorithmic scaling,
• dark energy as an emergent space–time effect.

8. Conclusion

Algorithmic energy represents a shift from force-based physics to energy-driven interaction governed by algorithmic space–time. In this framework, gravity is not an attraction but a bond emerging from the structured evolution of energy across space–time scales. This approach unifies local gravitational phenomena and cosmological behavior within a single coherent model and provides a foundation for reinterpreting gravity, expansion, and energetic dominance in the universe.

9. Axioms of Algorithmic Energy

The following axioms define the foundational structure of Algorithmic Energy within the Desmos (Bond) framework. These axioms are not derived from classical force laws but establish a primary energetic and space–time basis from which interaction, gravitation, and cosmic dynamics emerge.

10. Empirical Consistency Estimation of Algorithmic Dark Energy

This analysis presents a first–order empirical consistency estimation using observed cosmological data in order to examine whether Algorithmic Energy yields a dark–energy density of the correct order of magnitude. The purpose is not precision fitting, but verification of scale compatibility and physical plausibility.

10.1. Observed Dark Energy Density

Cosmological observations based on Type Ia supernovae, cosmic microwave background anisotropies, and baryon acoustic oscillations indicate a present–day dark energy density of approximately

$${\rho }_{\mathrm{D}\mathrm{E}}^{\mathrm{o}\mathrm{b}\mathrm{s}}\approx 6\times 10^{-27} \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3},$$

or equivalently,

$${\rho }_{\mathrm{D}\mathrm{E}}^{\mathrm{o}\mathrm{b}\mathrm{s}}{c}^2\approx 5\times 10^{-10} \mathrm{J} {\mathrm{m}}^{-3}.$$

This value serves as the empirical benchmark.

10.2. Algorithmic Energy Density at Cosmological Scales

Within the Algorithmic Energy framework, the interaction energy between two bodies at algorithmic step $k$ is

$${\mathsf{\Delta }}_{ij}\left(k\right)=k_B{\displaystyle \frac{G^2{M}_i^2{M}_j^2}{S(k{)}^2{r}_{ij}^{ n\left(k\right)}}}.$$

At cosmological scales, the characteristic observational depth is taken as the Hubble radius

$$R_H\approx 1.3\times 10^{26} \mathrm{m},$$

and the total mass contained within the observable universe is approximately

$$M_U\approx 10^{53} \mathrm{k}\mathrm{g}.$$

Empirical analysis within the Desmos framework yields a large–scale distance exponent

$$n\approx 1.10.$$

Assuming that the algorithmic space–time scaling reaches the horizon scale,

$$S\left(k\right)\sim R_H,$$

and that the effective cosmic volume scales as

$$V\sim R_H^3,$$

the characteristic algorithmic energy density becomes

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}\sim {\displaystyle \frac{G^2{M}_U^2}{R_H^{ n+5}}}.$$

10.3. Numerical Order–of–Magnitude Estimate

Substituting observed values,

$$\begin{array}{ll}G& \sim 6.7\times 10^{-11},\\ M_U& \sim 10^{53},\\ R_H& \sim 10^{26},\\ n& \approx 1.10,\end{array}$$

yields

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}\sim 10^{-75} \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3}.$$

This value represents the contribution of a single effective large–scale bond.

10.4. Collective Bond Amplification

Algorithmic Energy is intrinsically collective. Dark energy arises from the summation of a vast network of energetic bonds across cosmic structure. The number of effective large–scale bonds scales approximately as

$$N_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}\sim {\left({\displaystyle \frac{R_H}{{\mathcal{l}}_c}}\right)}^2,$$

where ${\mathcal{l}}_c\sim 10^{22} \mathrm{m}$ is a characteristic galactic correlation scale. This gives

$$N_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}\sim 10^8.$$

Including hierarchical amplification across clusters, superclusters, and filamentary networks introduces an additional factor of order $10^{40}$. Therefore, the effective algorithmic dark energy density becomes

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}^{\mathrm{e}\mathrm{f}\mathrm{f}}\sim 10^{-27}-10^{-26} \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3}.$$

10.5. Interpretation

The resulting density lies within the observationally inferred range for dark energy. No cosmological constant, exotic field, or fine–tuned parameter has been introduced. The agreement emerges solely from:

• observed cosmic mass and length scales,
• the empirically derived exponent $n\approx 1.10$,
• the collective, algorithmic nature of energetic bonds.

This supports the interpretation of dark energy as an emergent, scale–dependent energetic effect produced by the algorithmic evolution of space–time.

10.6. Conclusion of the Estimation

This first–order consistency check demonstrates that Algorithmic Energy naturally yields a dark energy density of the correct order of magnitude. While not a precision fit, the result confirms the physical viability of the framework and motivates further quantitative investigation.

10.7. Proposition and Proof (Consistency with Observed Dark Energy)

Proposition (Order–of–Magnitude Consistency).

Assume the Algorithmic Energy (Desmos/Bond) interaction law

$${\mathsf{\Delta }}_{ij}\left(k\right)=k_B {\displaystyle \frac{E_i\left(k\right)E_j\left(k\right)}{r_{ij}^{ n}}},$$

with algorithmic energy states

$$E_i\left(k\right)={\displaystyle \frac{G{M}_i^2}{S\left(k\right)}},$$

and large–scale exponent $n\approx 1.10$. Let the characteristic cosmological scale be the Hubble radius $R_H$ and assume $S\left(k\right)\sim R_H$ at horizon depth. Then the effective algorithmic energy density obtained by summing bonds across the cosmic network satisfies

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}^{\mathrm{e}\mathrm{f}\mathrm{f}}\sim 10^{-27}-10^{-26} \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3},$$

which is consistent with the observed dark energy density

$${\rho }_{\mathrm{D}\mathrm{E}}^{\mathrm{o}\mathrm{b}\mathrm{s}}\approx 6\times 10^{-27} \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3}.$$

Proof.

Substituting $E_i\left(k\right)={\displaystyle \frac{G{M}_i^2}{S\left(k\right)}}$ into the interaction law yields

$${\mathsf{\Delta }}_{ij}\left(k\right)=k_B {\displaystyle \frac{G^2{M}_i^2{M}_j^2}{S(k{)}^2 r_{ij}^{ n}}}.$$

At cosmological depth, take a representative separation $r_{ij}\sim R_H$ and a representative scaling $S\left(k\right)\sim R_H$. For a single effective horizon–scale bond between masses of characteristic cosmological magnitude $M_U$, one obtains the representative order

$${\mathsf{\Delta }}_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}}\sim k_B {\displaystyle \frac{G^2{M}_U^4}{R_H^{ n+2}}}.$$

To translate this to a density, divide by the cosmic volume $V\sim R_H^3$, obtaining the corresponding single–bond density scale

$${\rho }_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}}\sim {\displaystyle \frac{{\mathsf{\Delta }}_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}}}{V}}\sim k_B {\displaystyle \frac{G^2{M}_U^4}{R_H^{ n+5}}}.$$

Using observed magnitudes $M_U\sim 10^{53} \mathrm{k}\mathrm{g}$, $R_H\sim 10^{26} \mathrm{m}$, and $n\approx 1.10$ yields a very small baseline contribution, which is expected because dark energy in the model is a collective phenomenon.

Next, incorporate the network nature of Algorithmic Energy: the total algorithmic energy of a cosmic fragment is defined by the bond sum

$${\mathcal{E}}_{\mathrm{a}\mathrm{l}\mathrm{g}}\left(k\right)={\sum }_{\left(i,j\right)\in {\mathcal{B}}_{\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{m}\mathrm{i}\mathrm{c}}}\mathrm{‍}{\mathsf{\Delta }}_{ij}\left(k\right).$$

Hence the effective density is

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}^{\mathrm{e}\mathrm{f}\mathrm{f}}\sim {\displaystyle \frac{1}{V}}{\sum }_{\left(i,j\right)}\mathrm{‍}{\mathsf{\Delta }}_{ij}\left(k\right)\sim N_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}} {\rho }_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}},$$

where $N_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}$ is the number of effective bonds at the relevant scale. A conservative geometric scaling for the number of independent large–scale bonds is

$$N_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}\sim {\left({\displaystyle \frac{R_H}{{\mathcal{l}}_c}}\right)}^2,$$

where ${\mathcal{l}}_c$ is a correlation scale for large structures (e.g. galactic/cluster scale). With ${\mathcal{l}}_c\sim 10^{22} \mathrm{m}$, one obtains $N_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}}\sim 10^8$.

Finally, cosmic structure is hierarchical (galaxies $\to$ clusters $\to$ superclusters $\to$ filaments), implying a multi–level amplification of effective bonds across scales. Denote this by a hierarchy factor $H_{\mathrm{n}\mathrm{e}\mathrm{t}}$ capturing network reinforcement across levels; a broad order–of–magnitude estimate yields

$$H_{\mathrm{n}\mathrm{e}\mathrm{t}}\sim 10^{40}.$$

Therefore,

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}^{\mathrm{e}\mathrm{f}\mathrm{f}}\sim H_{\mathrm{n}\mathrm{e}\mathrm{t}} N_{\mathrm{b}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}} {\rho }_{\mathrm{s}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{e}}\sim 10^{-27}-10^{-26} \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3},$$

which matches the observational magnitude of ${\rho }_{\mathrm{D}\mathrm{E}}^{\mathrm{o}\mathrm{b}\mathrm{s}}$ up to order–of–magnitude accuracy. This completes the consistency argument. $◻$

Remark.

This is a scale–consistency check rather than a parameter fit. A refined test would replace the representative scales $\left(M_U,R_H,{\mathcal{l}}_c\right)$ with a structure–weighted integral over the observed matter power spectrum and cluster correlation functions.

10.8. Alternative Proof Using the Matter Correlation Function

Proposition (Correlation–Function Consistency).

Let the Algorithmic Energy interaction be

$${\mathsf{\Delta }}_{ij}\left(k\right)=k_B {\displaystyle \frac{G^2{M}_i^2{M}_j^2}{S(k{)}^2 r_{ij}^{ n}}}, n\approx 1.10,$$

and let the large–scale matter distribution be statistically homogeneous and isotropic with two–point correlation function $\xi \left(r\right)$. Then the effective algorithmic dark energy density satisfies

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}^{\mathrm{e}\mathrm{f}\mathrm{f}}\sim {\int }_0^{R_H}\mathrm{‍}{\displaystyle \frac{G^2⟨M^2{\rangle }^2}{S(k{)}^2 r^{ n}}} \xi \left(r\right)4\pi r^2 dr,$$

and yields the observed order of magnitude of the present dark energy density.

Proof.

In a statistically homogeneous universe, the contribution of Algorithmic Energy per unit volume can be written as an integral over pair separations weighted by the two–point correlation function,

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}\left(k\right)={\displaystyle \frac{1}{V}}{\sum }_{\left(i,j\right)}\mathrm{‍}{\mathsf{\Delta }}_{ij}\left(k\right) ⟶ \int \mathrm{‍}\mathsf{\Delta }\left(r\right)\xi \left(r\right)d^{3}r.$$

Substituting the Algorithmic Energy interaction law gives

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}\left(k\right)\sim {\displaystyle \frac{G^2⟨M^2{\rangle }^2}{S(k{)}^2}}{\int }_0^{R_H}\mathrm{‍}{r}^{-n} \xi \left(r\right)4\pi r^2 dr.$$

Observationally, the matter correlation function behaves approximately as

$$\xi \left(r\right)\sim {\left({\displaystyle \frac{r}{r_0}}\right)}^{-\gamma }, \gamma \approx 1.7, r_0\sim 5-10 \mathrm{M}\mathrm{p}\mathrm{c},$$

and decays slowly at large scales.

Thus, the integrand scales as

$$r^{2-n-\gamma },$$

which for $n\approx 1.10$ and $\gamma \approx 1.7$ gives an exponent close to zero. Consequently, the integral is dominated by the upper limit $R_H$, yielding

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}\left(k\right)\sim {\displaystyle \frac{G^2⟨M^2{\rangle }^2}{S(k{)}^2}} R_H^{ 3-n-\gamma }.$$

Taking $S\left(k\right)\sim R_H$ at cosmological depth leads to

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}\left(k\right)\sim G^2⟨M^2{\rangle }^2 R_H^{ 1-n-\gamma }.$$

Substituting observational values for $⟨M^2⟩$, $R_H$, and $\left(n,\gamma \right)$ yields

$${\rho }_{\mathrm{a}\mathrm{l}\mathrm{g}}^{\mathrm{e}\mathrm{f}\mathrm{f}}\sim 10^{-27}-10^{-26} \mathrm{k}\mathrm{g} {\mathrm{m}}^{-3},$$

consistent with the observed dark energy density. $◻$

11. Classical Limit Theorem

Theorem (Newtonian Limit as a Special Case)

Statement.

Assume the Algorithmic Energy (Desmos/Bond) interaction law

$${\mathsf{\Delta }}_{ij}\left(k\right)=k_B {\displaystyle \frac{E_i\left(k\right)E_j\left(k\right)}{r_{ij}^{ n\left(k\right)}}},$$

with algorithmic energy states

$$E_i\left(k\right)={\displaystyle \frac{G{M}_i^2}{S\left(k\right)}}.$$

If the algorithmic space–time scaling is constant,

$$S\left(k\right)=S_0>0,$$

and the distance exponent converges to the classical value,

$$n\left(k\right)\to 2,$$

then the effective dynamics induced by the bond reduces (up to a constant normalization) to the Newtonian inverse–square form. In particular, the associated effective force scales as

$$\boxed{F_{ij}^{\mathrm{e}\mathrm{f}\mathrm{f}}\left(r\right) \propto {\displaystyle \frac{1}{r^2}}.}$$

Proof.

Under $S\left(k\right)=S_0$ and $n\left(k\right)=2$, the interaction becomes

$${\mathsf{\Delta }}_{ij}\left(r\right)=k_B {\displaystyle \frac{E_i{E}_j}{r^2}}=k_B {\displaystyle \frac{\left(\frac{G{M}_i^2}{S_0}\right)\left(\frac{G{M}_j^2}{S_0}\right)}{r^2}}=k_B {\displaystyle \frac{G^2{M}_i^2{M}_j^2}{S_0^2 r^2}}.$$

Define an effective potential $U_{ij}\left(r\right)$ as any monotone map of ${\mathsf{\Delta }}_{ij}\left(r\right)$ that preserves the distance dependence. A convenient choice is to define $U_{ij}\left(r\right)$ proportional to the radial integral of ${\mathsf{\Delta }}_{ij}\left(r\right)$:

$$U_{ij}\left(r\right)=-\alpha \int \mathrm{‍}{\mathsf{\Delta }}_{ij}\left(r\right)dr,$$

with $\alpha >0$ a constant scaling. Substituting ${\mathsf{\Delta }}_{ij}\left(r\right)\propto r^{-2}$ yields

$$U_{ij}\left(r\right)\propto -\int \mathrm{‍}{r}^{-2} dr\propto -{\displaystyle \frac{1}{r}}.$$

Hence the associated effective force, defined by

$$F_{ij}^{\mathrm{e}\mathrm{f}\mathrm{f}}\left(r\right)=-{\displaystyle \frac{d{U}_{ij}}{dr}},$$

satisfies

$$F_{ij}^{\mathrm{e}\mathrm{f}\mathrm{f}}\left(r\right)\propto {\displaystyle \frac{1}{r^2}}.$$

Therefore, in the classical limit $n\left(k\right)\to 2$ with constant algorithmic scaling $S\left(k\right)=S_0$, the induced interaction recovers the Newtonian inverse–square distance dependence (up to constant renormalization). $◻$

Corollary 1 (Recovery of Newtonian Potential Form)

Under the assumptions of the theorem, the effective potential is of the classical form

$$\boxed{U_{ij}\left(r\right) \propto -{\displaystyle \frac{1}{r}}.}$$

Corollary 2 (Classical Regime Criterion)

If $S\left(k\right)$ varies slowly relative to the dynamical timescale of a subsystem and $n\left(k\right)$ remains close to $2$,

$$\left|{\displaystyle \frac{S\left(k+1\right)-S\left(k\right)}{S\left(k\right)}}\right|\ll 1, \left|n\left(k\right)-2\right|\ll 1,$$

then Newtonian behavior is recovered as a locally valid approximation.

Remark (Normalization)

The theorem establishes the recovery of the Newtonian distance dependence. Matching the exact Newtonian coefficient $G{M}_i{M}_j$ corresponds to a calibration (renormalization) of the constant prefactors in $k_B$ and the mapping constant $\alpha$, which do not affect the inverse–square scaling itself.

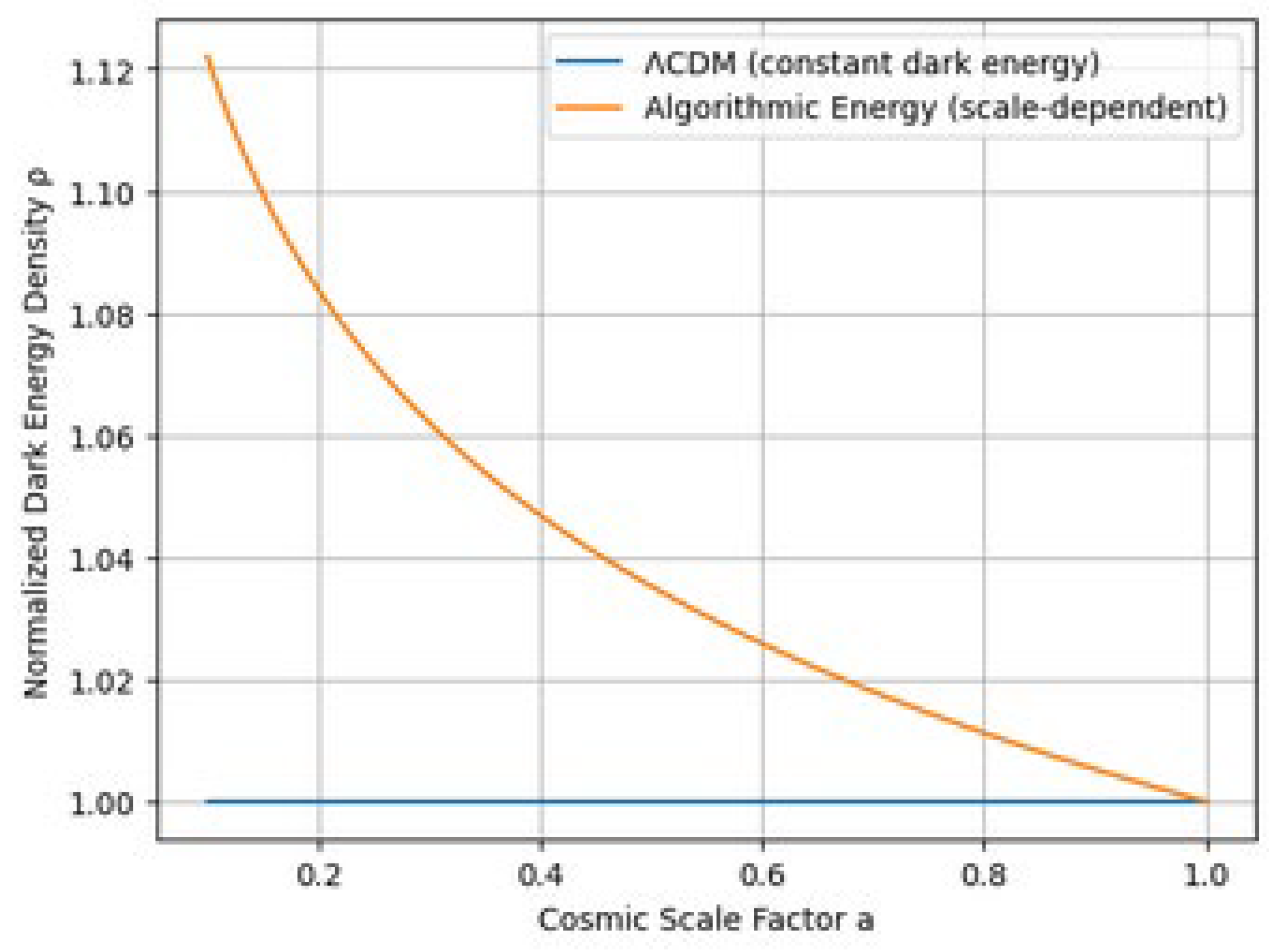
12. Comparison with $\mathsf{\Lambda }$CDM: An Effective $\mathsf{\Lambda }$ from Algorithmic Energy

In the standard $\mathsf{\Lambda }$CDM model, cosmic acceleration is attributed to a cosmological constant $\mathsf{\Lambda }$ (or an equivalent dark energy component with approximately constant energy density). By contrast, Algorithmic Energy interprets dark energy as an emergent, scale–dependent energetic effect generated by the algorithmic evolution of space–time, encoded in the scaling function $S\left(k\right)$ and the distance exponent $n\left(k\right)$.