1. Introduction
The nature of conscious experience remains one of the fundamental unsolved problems in neuroscience and philosophy of mind. While substantial progress has been made in identifying neural correlates of consciousness (NCC), particularly the role of gamma-band oscillations (30-80 Hz) in binding distributed information into unified percepts, a deeper mathematical understanding of why these specific dynamics generate subjective experience remains elusive.
1.1. The Hard Problem and Topological Approaches
Chalmers’ “hard problem” of consciousness [
1] asks why any physical process should give rise to subjective experience at all. While we do not claim to solve this problem here, we propose that consciousness may have an intrinsic mathematical structure that constrains its physical implementation. Specifically, we hypothesize that conscious experience is constitutively 4-dimensional (spatiotemporal) with a topology characterized by specific types of singularities.
Recent work has explored topological and geometric approaches to consciousness, including integrated information theory [
2], but these have not made explicit contact with the theory of integrable systems and Painlevé transcendents that are standard but advanced concepts of the theory of special functions. Our framework builds on the observation that Painlevé equations arise naturally at critical points in various physical systems and describe dynamics near singularities.
1.2. Gamma Oscillations and Binding
Gamma-band oscillations are widely observed neural correlates of conscious perception [
3,
4]. Key empirical observations include:
Gamma bursts are discrete events lasting 100-300 ms
Gamma synchronization across brain regions correlates with successful binding
Phase relationships encode information about stimulus features
Consciousness appears to have a discrete “frame rate” rather than being continuous
Despite extensive study, the mechanistic origin of gamma oscillations and their specific frequency range remains incompletely understood. While biophysical models exist based on interneuron networks, these do not explain why gamma specifically (rather than other frequencies) should be associated with consciousness.
1.3. Our Proposal
We propose that consciousness emerges through a two-stage quantum-to-classical transition:
Pre-conscious information processing corresponds to the configuration (4-punctured sphere) of Painlevé VI with four independent processing streams in full quantum superposition
An intermediate quantum state with “bipolar” character corresponds to Painlevé V, which has the “fishtail” fiber () with two bordered cusps representing coexisting quantum modes—this is where gamma oscillations emerge (possibly corresponding to lucid dreaming or hypnagogic states)
Classical consciousness corresponds to the fiber () of PVdeg (= ): the quantum-to-classical collapse that produces unified conscious experience with a single cusp
The PVI → PV transition (chewing-gum coalescence) creates the fishtail and initiates gamma oscillations while preserving bipolar quantum character
The PV → PVdeg transition (cusp removal) is the classical collapse that completes the gamma burst and generates unified conscious percept
The key insight is that gamma oscillations emerge at the fishtail stage (PV): they appear during quantum coherent binding, and the subsequent classical collapse (PV → PVdeg) completes the process. This framework is mathematically precise, makes testable predictions distinguishing quantum intermediate states from classical consciousness, and provides a natural explanation for observed gamma dynamics.
The paper is organized as follows.
Section 2 introduces the mathematical framework of Painlevé equations, isomonodromic deformations, and the Kodaira classification of singular fibers, including the two-stage confluence process and its quantum-to-classical interpretation.
Section 3 develops the connections to quantum field theory, topological quantum field theory, and 4-manifold topology, including a discussion of how our framework addresses decoherence objections.
Section 4 provides the neural interpretation, mapping mathematical structures to neuroanatomical substrates and establishing the four-stream model grounded in thalamocortical architecture.
Section 5 presents the WKB analysis connecting coalescence dynamics to gamma-band oscillations.
Section 6 displays numerical results demonstrating frequency evolution and the four-stream coalescence model.
Section 7 articulates seven falsifiable predictions.
Section 8 relates our framework to existing theories of consciousness and addresses open questions. We conclude in
Section 9.
Appendix A provides a self-contained derivation of the oscillation scaling relation from the PVI → PV confluence limit.
Structure of the paper. Sections 2–5 develop the core mathematical and physical framework, establishing the role of Painlevé confluence, singular fiber topology, and asymptotic scaling in the emergence of gamma-band oscillations. Sections 6 and 7 summarize the resulting predictions and their empirical implications, while Section 8 discusses extensions, limitations, and possible generalizations to altered or pathological states.
2. Mathematical Framework
2.1. Painlevé Equations and Isomonodromic Deformations
Painlevé equations are six second-order nonlinear differential equations having
transcendental solutions in the sense that they cannot be expressed in terms of familiar special functions, such (hyper)elliptic or hypergeometric functions. Painlevé transcendents have the Painlevé property that the only movable singularities are poles. They play a fundamental role in integrable systems, arising in diverse contexts from statistical mechanics to quantum field theory [
5,
6,
7,
8] and even genomics [
9].
The effort towards suncovering explicit algebraic solutions of PVI, is a significant subject in 20th-century mathematical research with connections to algebraic topology, algebraic geometry, and representation theory [
10,
11]. Painlevé equations of lower index than VI exhibit a more complex topological structure that we need in the context of the present paper.
2.1.1. Painlevé VI and Its Associated Character Variety
We start from the concept of a flat connection on a fiber bundle
, where the base
B assumes the form of a three-punctured sphere, denoted as
. Over a point
, There exists a corresponding four-punctured sphere
. Let
denote the fiber of
M over the base point
, the monodromy action unfolds through the action of the fundamental group of the base on the fiber. This defines a homomorphism
[
10].
For the setting of the monodromy problem for PVI, the reader may consult ([
6],
Section 1) where complex constants
,
,
and
arise from the eigenvalues of the matrices in the associated Schlesinger’s system.
For each
, the space of conjugacy classes of
representations for the fundamental group
(the free group of rank 3) is the character variety
The connection is flat and described by
equation as follows:
with
and parameters
,
,
,
. Further topological steps are illustrated in ([
12], Figure 3) or ([
9],
Figure 1). The Painlevé V equation is as follows
with parameters
,
,
,
.
PV arises from the isomonodromic deformation of a linear system of the form
where
is a 2-component vector and
A is a
matrix with singularities. The isomonodromy condition (monodromy data is preserved as
t varies) leads to PV.
2.2. Singular Fibers and Kodaira Classification
In the geometric formulation, Painlevé equations describe families of algebraic curves (or Riemann surfaces). The classification of singular fibers follows Kodaira’s classification of singular fibers of elliptic surfaces [
13,
14].
Definition 1 (Singular Fiber Types).
The relevant fiber types for the confluence PVI → PV → PVdeg are classified by theirsurface type
(Dynkin diagram of anticanonical divisor), following Chekhov, Mazzocco, and Rubtsov [12]:
: Four rational curves meeting at a point (dual graph ), corresponding to PVI—four regular singularities
: The “fishtail” configuration (dual graph ), corresponding toPV—three holes withtwo bordered cuspson one boundary
: Extended fishtail (dual graph ), corresponding toPVdeg(= )—three holes withone cusp
Note: The surface type (Kodaira fiber) is distinct from thesymmetry type
(affine Weyl group of Bäcklund transformations). PV has surface type but symmetry type ; PVdeg has surface type and symmetry type [15].
Remark 1 (Surface Type vs. Symmetry Type). There aretwo distinct classification systemsfor Painlevé equations that should not be conflated:
1. Surface type(Kodaira fiber / Dynkin diagram of anticanonical divisor): Determines the geometric structure of the space of initial conditions.
2. Symmetry type(affine Weyl group of Bäcklund transformations): Determines the group of symmetries acting on solutions.
Following Sakai [15] and Chekhov et al. [12]:
| Equation |
Surface type |
Kodaira fiber |
Symmetry type |
| PVI |
|
() |
|
| PV |
|
() |
|
| PVdeg (= PIIID6) |
|
() |
|
The superscript indicates the untwisted affine extension. The surface type directly determines the Kodaira fiber via the correspondence (). The notation PIIID6, PIIID7, PIIID8 follows [15].
Definition 2 (Katz Invariants). TheKatz invariants(orKatz ranks) characterize the irregular singularities of a linear differential system. For a meromorphic connection on a Riemann surface with singularities at points , the Katz invariant at each singular point measures thePoincaré rankof the irregular singularity:
: regular singularity (Fuchsian)
: unramified irregular singularity of rank k
for odd k: ramified irregular singularity
The tuple of Katz invariants at all singularities encodes the “strength” of irregularity. For Painlevé equations, PVI has all regular singularities , while confluence produces irregular singularities with increasing Katz invariants. The transition from regular to irregular singularities corresponds physically to the emergence of oscillatory (Stokes) phenomena.
Topologically, can be viewed as a 4-punctured sphere (in appropriate dimension), while has one of these punctures replaced by an irregular singularity resulting from coalescence.
2.3. The Coalescence Process
The transition
occurs when two of the four regular singular points of the linear system associated to PVI collide, creating an irregular singular point [
16,
17]. This is called the “fishtail” degeneration.
Proposition 1 (Fishtail Transition). Let denote the separation between two coalescing singular points. As :
The system transitions from PVI to PV
An irregular singularity forms at the coalescence point
Solutions near this singularity exhibit rapid oscillations characterized by Stokes phenomena
The separation parameter
plays a central role in our framework. In the linear system (
3) associated to PVI, the four regular singular points are located at
. During coalescence, two of these points approach each other; we define
as the separation between the singularities at
and
. In normalized units,
ranges from
(pre-coalescence, singularities well-separated) to
(near-coalescence). The dynamics of
during a binding event, and the minimum separation
achieved, determine the oscillation frequencies that emerge (see
Section 5).
The irregular singularity has fundamentally different behavior from regular singularities:
Solutions have essential singularities (not just poles)
WKB analysis shows rapid oscillatory behavior
Characteristic exponents determine oscillation frequencies
2.4. Two-Stage Confluence: From PVI to PV to PVdeg
A refined analysis following Chekhov, Mazzocco, and Rubtsov [
12] reveals that the confluence from PVI to simpler Painlevé equations proceeds through
two distinct stages, each with a distinct interpretation for consciousness:
2.4.1. Stage 1: Chewing-Gum Coalescence (PVI → PV)
The first stage creates the “fishtail” fiber
with its characteristic two-cusped structure: two of the four regular singularities collide via the limiting process
as
. This “chewing-gum” operation [
12] transforms:
Geometry: A 4-holed Riemann sphere → a 3-holed sphere with two bordered cusps on one boundary
Surface type: (fiber ) → (fiber = fishtail)
Symmetry type: → (Bäcklund transformations)
Katz invariants: when one irregular singularity of Poincaré rank 1 appears
Stokes phenomenon: Two Stokes rays emerge at the irregular point—gamma oscillations begin
Note on parameters: In the Chekhov-Mazzocco-Rubtsov framework [
12], the parameters
denote the
perimeters (hyperbolic geodesic lengths) of the holes on the decorated Riemann surface. The parameter
is the
confluence parameter controlling the coalescence; as
, two holes merge. The logarithmic scaling
ensures that the total perimeter diverges in a controlled way, producing two bordered cusps in the limit, this is the “chewing-gum” stretching that keeps a finite area trapped between the colliding holes. The two cusps of PV represent a “bipolar” configuration—two coexisting modes that have begun to bind but remain in quantum superposition. The fishtail structure is the geometric signature of this quantum coherent intermediate state.
2.4.2. Stage 2: Cusp Removal and Classical Collapse (PV → PVdeg)
A second confluence, via , produces the classical fiber :
Geometry: One of the two bordered cusps is removed (“cusp-removing move”), leaving a single cusp
Surface type: (fiber ) → (fiber , )
Symmetry type: (Bäcklund transformations)
Katz invariants: —the irregular singularity becomes ramified
Stokes phenomenon: Reduced from 2 to 1 Stokes ray—coherent gamma oscillations complete
Note on parameters: The parameters
are
shear coordinates on the decorated character variety [
12]. These coordinates describe the “twisting” of the surface along ideal arcs connecting cusps. The limiting process
as
corresponds to pulling apart two cusps that were created in Stage 1, effectively “tearing” an ideal triangle and removing one cusp. The slower logarithmic rate (single log vs. double
in Stage 1) reflects a gentler deformation that preserves more structure.
Note that PVdeg is equivalent to
in Sakai’s classification [
14]. The
fiber with its single cusp represents the
classical collapse from the quantum bipolar fishtail state.
2.4.3. Consciousness Interpretation: Quantum to Classical Transition
The two-stage confluence suggests a refined model where consciousness emerges through quantum-to-classical collapse:
| State |
Cusps |
Surface/Fiber |
Katz inv. |
Consciousness level |
| PVI |
0 |
/ () |
|
Pre-conscious |
| PV |
2 |
/ () = fishtail |
|
Quantum intermediate (gamma onset) |
| PVdeg |
1 |
/ () |
|
Classical consciousness |
Interpretation.
In this refined picture:
PVI (pre-conscious): Four regular singularities represent four independent processing streams in full quantum superposition. No irregular singularity means no binding and no oscillatory dynamics. Information flows without integration.
PV (fishtail, quantum binding): The first coalescence creates the fishtail fiber with its irregular singularity, initiating Stokes phenomena and gamma oscillations. Crucially, the presence of two bordered cusps means the system remains in a “bipolar” quantum superposition—two modes coexist without having collapsed into unity. This may correspond to the phenomenology of lucid dreaming or hypnagogic states: consciousness is present but fluid, with two perspectives or narratives coexisting. The binding process is active, with gamma oscillations as its signature, but the quantum character persists.
PVdeg (classical consciousness): The second confluence removes one cusp, collapsing the bipolar superposition into a single unified state: the fiber. This represents the quantum-to-classical transition: the “collapse of the wavefunction” that produces definite conscious experience. The ramified irregular singularity (Katz invariant ) completes the gamma burst, yielding the stable percept.
The Fishtail as Quantum Binding Site.
The fiber is called the “fishtail” because of its shape in the resolution diagram. In our interpretation, the fishtail represents the site of quantum binding, not the classical endpoint:
PV (fishtail, , ): Two cusps = quantum superposition of two modes (bipolar), gamma oscillations active
PVdeg (, ): One cusp = classical collapse to single unified percept
The consciousness stream thus flows: pre-conscious quantum processing (PVI) → quantum binding with gamma oscillations at the fishtail (PV) → classical collapse to unified percept (PVdeg).
Gamma Oscillations as Binding Signature.
A key prediction of this model is that gamma oscillations emerge at the fishtail (PV) and mark the process of quantum binding:
PV (fishtail, quantum binding): The two Stokes directions of the fishtail produce coherent 30–80 Hz gamma oscillations. These oscillations represent the active process of quantum binding—the system is integrating information but has not yet collapsed to classical definiteness. This explains the association of gamma with active perception and attention.
PVdeg (classical consciousness): The transition to a single Stokes direction () represents the completion of binding. The gamma burst reaches its peak and then subsides as the unified percept stabilizes. Classical consciousness emerges as the result of the binding process, not the binding itself.
Thus, gamma oscillations are the signature of quantum coherent binding in progress, while classical conscious perception is the stable endpoint after binding completes.
3. Quantum Field Theory, 4-Manifolds, and Topological Structure
3.1. 4-Manifolds in Quantum Physics
Four-dimensional manifolds occupy a special place in modern theoretical physics. The spacetime of general relativity is a 4-manifold, and gauge theories, the foundation of the Standard Model, are naturally formulated on 4-dimensional spaces. More profoundly, the topology of 4-manifolds determines deep quantum properties through topological quantum field theory (TQFT) [
18].
3.1.1. Topological Quantum Field Theory
TQFT, pioneered by Witten and others, provides a framework where quantum amplitudes depend only on the topology of spacetime, not its metric structure. The partition function of a TQFT on a 4-manifold
M is a topological invariant:
where
is a topological action.
Key examples relevant to our framework include:
1. Donaldson Theory: Studies moduli spaces of Yang-Mills instantons on 4-manifolds. The moduli space of anti-self-dual connections has singularity structure similar to our
and
fibers [
19].
2. Seiberg-Witten Theory: Arose from
supersymmetric Yang-Mills theory [
20]. The Seiberg-Witten equations define invariants of smooth 4-manifolds through monopole solutions. Remarkably, these equations involve elliptic curves whose degenerations are classified by types closely similar to Kodaira ones (
, etc.) that appear in Painlevé theory.
3. Connection to Integrable Systems: Seiberg and Witten showed that the low-energy effective action of
gauge theory is governed by a hyperelliptic curve, and its period integrals satisfy the Picard-Fuchs equations—which are related to Painlevé equations [
21].
3.1.2. Monodromy as Gauge Holonomy
The monodromy groups in our framework have a natural interpretation in gauge theory. Consider a
gauge field
A on a 4-manifold with a Wilson loop:
The monodromy of solutions to the Painlevé linear system around a singular point is mathematically identical to gauge holonomy around a non-contractible cycle. The isomonodromy condition—that monodromy is preserved as parameters vary—parallels the requirement of consistent gauge transformations in quantum field theory.
3.2. Painlevé Equations in Quantum Integrable Systems
Painlevé equations are not merely classical; they arise naturally as correlation functions and partition functions in quantum systems [
6].
3.2.1. Quantum Painlevé Equations
The
quantum Painlevé equations are
q-difference or operator equations that reduce to classical Painlevé in appropriate limits [
22]. They appear in:
2D Conformal Field Theory: Correlation functions satisfy quantum Painlevé equations
Matrix Models: Quantum corrections to matrix model partition functions (related to 2D quantum gravity) are governed by quantum Painlevé
Integrable Quantum Mechanics: Spectral determinants of quantum integrable systems satisfy Painlevé equations [
23]
The relationship between classical and quantum Painlevé is given by the
classical limit:
This suggests a profound possibility: if consciousness has the topological structure and this structure is governed by Painlevé dynamics, there may exist an underlying quantum structure of which neural dynamics represent the classical limit.
3.2.2. WKB Analysis: The Quantum-Classical Bridge
The WKB (Wentzel-Kramers-Brillouin) method is precisely the tool for understanding the quantum-to-classical transition [
24]. For a quantum system with Hamiltonian
:
In the semiclassical limit (
), the wavefunction takes the form:
where
satisfies the classical Hamilton-Jacobi equation.
Our use of WKB analysis in
Section 5.1 below to derive oscillation frequencies is not merely a mathematical convenience, it represents the fundamental quantum-classical correspondence. The action
appearing in our analysis can be interpreted as the classical limit of a quantum mechanical phase. More details about the WKB analysis are in the
Appendix A.
3.3. The Irregular Singularity as Quantum-Classical Interface
We propose that the irregular singularity of the fishtail (PV) represents a special locus in phase space where quantum binding occurs, with gamma oscillations as its signature.
3.3.1. Physical Interpretation
Regular singularities ( with four punctures, PVI):
Correspond to quantum superposition states
Four punctures = four basis states in Hilbert space
Monodromy around each singularity = unitary evolution
System maintains quantum coherence without binding
Irregular singularity with two cusps ( fishtail, PV):
Forms through coalescence—binding begins
Two cusps = bipolar quantum superposition (two coexisting modes)
Stokes phenomenon = gamma oscillations emerge
System is actively binding but remains quantum coherent
Irregular singularity with one cusp (, PVdeg):
Forms through cusp removal—classical collapse
One cusp = unified classical percept
Gamma burst completes, stable perception emerges
Quantum-to-classical transition complete
This interpretation resonates with ideas in quantum measurement theory. The two-stage transition represents the progression from quantum possibility to classical actuality—from unconscious quantum processing through active binding to conscious classical experience.
3.3.2. Connection to Penrose-Hameroff Theory
The interpretation resonates strongly with Orch-OR theory [
25,
26]: the PV → PVdeg transition may represent “orchestrated objective reduction”, the collapse of quantum superposition in microtubules that Penrose and Hameroff propose as the physical basis of conscious moments. Our framework provides a precise topological characterization of this collapse: it is the transition from the bipolar quantum fishtail state (PV,
,
) to the unified classical state (PVdeg,
,
). The fishtail is the
site of quantum binding, not the endpoint.
Testable Predictions.
This refined model makes specific predictions:
REM/lucid dreaming: Should show PV-type (fishtail) dynamics: gamma oscillations present but with bipolar character, reflecting active binding without classical collapse
Waking consciousness: Should show completed PVdeg-type dynamics: gamma burst culminating in stable unified percept ()
Anesthesia: Should show regression toward PVI-type dynamics: loss of irregular singularity and cessation of binding
Hypnagogic states: The transition zones between sleep and waking should show signatures of the PV → PVdeg transition
3.4. Symmetry Breaking and Phase Transitions
The two-stage confluence is fundamentally a symmetry-breaking phenomenon, with deep connections to quantum field theory.
3.4.1. Symmetry Groups
The dual graph structure encodes symmetry (surface type):
(for , PVI): Four-fold structure, four regular singularities
(for , PV = fishtail): Reduced symmetry, two bordered cusps
(for , PVdeg): Further reduced symmetry, one cusp
In the context of gauge theory, spontaneous symmetry breaking occurs when a gauge symmetry is broken to a subgroup. The Higgs mechanism, for instance, breaks to .
Our two-stage confluence represents successive symmetry breaking:
3.4.2. Phase Transitions in TQFT
Quantum phase transitions in topological phases of matter involve changes in topological order—characterized by different fusion rules and braiding statistics of anyons. The transition between topological phases can involve changing the number of distinct anyon types, analogous to our transition from four to three effective singularities.
Recent work on topological quantum computation shows that braiding operations on anyons are described by monodromy representations: exactly the mathematical structure underlying Painlevé equations [
27].
3.5. Implications for Consciousness
3.5.1. Three Possible Scenarios
Our topological framework is compatible with three interpretations:
Scenario A: Fully Classical
Neural networks naturally organize through the topology sequence
The quantum-topological mathematics describes classical dynamics
Gamma oscillations arise from classical bifurcations at the (fishtail) stage
No quantum effects required
Scenario B: Quantum Substrate, Classical Phenomenology
Quantum coherence at molecular/cellular scale creates states
The PVI → PV transition creates the fishtail () with gamma oscillations during active binding
Environmental decoherence drives the PV → PVdeg transition ()
Conscious experience = post-decoherence classical state (, unified percept)
Scenario C: Genuinely Quantum Consciousness
Consciousness requires sustained quantum coherence (Penrose-Hameroff)
The fishtail state itself has quantum character—gamma represents quantum binding
Classical collapse to is “orchestrated objective reduction”
Classical description (our current model) is effective theory of underlying quantum dynamics
3.5.2. Experimental Differentiation
These scenarios make different predictions:
Coherence times: Scenario C requires long quantum coherence ( ms), scenario B only requires coherence during coalescence ( ms), scenario A requires none
Temperature dependence: Quantum scenarios predict consciousness disruption at elevated temperatures (decoherence increases), classical scenario less sensitive
Isotope effects: Replacing hydrogen with deuterium should affect quantum coherence (nuclear spin effects) but not classical dynamics significantly
Entanglement signatures: Genuine quantum consciousness (scenario C) should show measurable entanglement between brain regions
3.5.3. Addressing Decoherence Objections
A standard criticism of quantum theories of consciousness, particularly Orch-OR, concerns decoherence timescales [
28,
29]. Thermal fluctuations in the warm, wet brain are argued to destroy quantum coherence on femtosecond to picosecond timescales, far shorter than the ∼25 ms (∼40 Hz) timescales relevant for gamma oscillations and conscious binding.
Our framework addresses this objection differently depending on which scenario is operative:
Scenario A (Fully Classical):
No quantum coherence is required. The Painlevé/TQFT mathematics describes the topology of classical neural dynamics, not quantum superposition. The same mathematical structures arise in classical integrable systems. This scenario is immune to decoherence objections.
Scenario B (Quantum Substrate, Classical Phenomenology):
This scenario requires quantum coherence only during the coalescence transition itself, not sustained coherence over the full gamma cycle. The coalescence event in our model occurs over a timescale:
However, the
critical part of coalescence, where the irregular singularity actually forms, occurs in the final approach when
. This phase lasts approximately:
Recent work on quantum biology has demonstrated that:
Quantum coherence in photosynthetic complexes persists for ∼300–600 fs at physiological temperatures [
30]
Vibrational coherences in proteins can extend to picoseconds [
31]
Collective modes in microtubules may support coherence times of microseconds to milliseconds through topological protection or Fröhlich condensation [
26,
32]
The critical question is whether coherence can be maintained for ∼1 ms during the coalescence transition. This is 3–6 orders of magnitude longer than simple thermal estimates but potentially achievable through:
Collective protection: Coherence in a collective mode (many coupled oscillators) can exceed single-particle coherence times
Topological protection: The configuration may itself provide protection through topological constraints on decoherence pathways
Active error correction: Biological systems may implement forms of quantum error correction [
33]
Scenario C (Genuinely Quantum Consciousness):
This scenario requires sustained coherence over ∼100 ms and faces the strongest decoherence objections. We note, however, that:
Experimental Discrimination:
The three scenarios make different predictions regarding perturbations that affect decoherence:
| Perturbation |
Scenario A |
Scenario B |
Scenario C |
| Mild hyperthermia (+2 °C) |
No effect |
Weak effect |
Strong disruption |
| Deuterium substitution |
No effect |
Possible effect |
Strong effect |
| Anesthetics (mechanism unclear) |
Variable |
Moderate |
Strong |
| Strong magnetic fields |
No effect |
Weak effect |
Possible effect |
Scenario B represents a “Goldilocks” position: it gains explanatory power from quantum-topological mathematics while requiring only modest (and potentially achievable) quantum coherence during a brief critical window. This may be the most empirically defensible version of our framework.
3.6. Mathematical Unity: Why This Structure?
The appearance of the same mathematical structures (4-manifolds, Painlevé equations, monodromy groups, TQFT) in both fundamental physics and consciousness is striking. This suggests several possibilities:
Universality: Certain topological structures are universal attractors for complex dynamical systems, whether quantum or classical
Fundamental connection: Consciousness might be intimately related to the fundamental structure of quantum field theory on 4-manifolds
Information geometry: Both quantum mechanics and consciousness involve information processing, and the two-stage topological transition () may represent optimal information integration: binding at the fishtail, unification at the classical endpoint
Anthropic consideration: If consciousness requires this specific mathematical structure, and this structure is naturally selected by quantum dynamics on 4-manifolds, this constrains the physical implementation of consciousness
The integrable structure (Painlevé) is particularly suggestive. Integrable systems have infinite conserved quantities—perhaps consciousness requires such conservation laws to maintain the continuity and coherence of subjective experience over time.
4. Neural Interpretation
4.1. Mapping Mathematical Structures to Neural Processes
We propose the following correspondence:
| Mathematical Structure |
Neural Interpretation |
| 4 regular singularities (, PVI) |
4 distinct information streams |
| |
(sensory, memory, prediction, executive) |
| First coalescence (PVI → PV) |
Attentional binding initiates |
| Fishtail with 2 cusps (, PV) |
Active binding with gamma oscillations |
| |
(bipolar quantum intermediate) |
| Second coalescence (PV → PVdeg) |
Classical collapse to unified percept |
| Single cusp (, PVdeg) |
Integrated conscious representation |
| Monodromy |
Phase relationships in thalamocortical loops |
| Painlevé V equation |
Temporal evolution preserving structure |
| Oscillation frequency
|
Observable gamma frequency (30-80 Hz) |
4.2. Four Information Streams: Neuroanatomical Basis
We hypothesize that the four singularities of correspond to four fundamental streams of neural information processing. This four-fold structure is not arbitrary but reflects established neuroanatomical and functional organization.
4.2.1. Evidence for Four Major Processing Streams
Convergent evidence from neuroimaging, lesion studies, and electrophysiology supports the existence of four distinct large-scale cortical systems that must be integrated for conscious perception [
35,
36,
37]:
4.2.2. Thalamocortical Architecture
The four-fold structure is reinforced by thalamocortical organization. Each of the four streams identified above has a distinct thalamic relay nucleus and associated thalamocortical loop [
41]:
| Stream |
Thalamic nucleus |
Cortical target |
| Sensory |
LGN, MGN, VPL/VPM |
Primary sensory cortices |
| Contextual |
Anterior nuclei |
Hippocampal formation |
| Predictive |
Pulvinar, LP |
Parietal cortex |
| Executive |
MD nucleus |
Prefrontal cortex |
The thalamic reticular nucleus (TRN) provides inhibitory gating between these loops, potentially implementing the “separation” parameter in our model: when TRN inhibition is high, loops operate independently (); when TRN inhibition decreases during attentional engagement, loops can synchronize ().
4.2.3. Relation to Global Workspace Architecture
Dehaene and colleagues [
42] have proposed that conscious access requires “ignition” across a distributed frontoparietal network. Importantly, their analysis identifies four major hub regions that must synchronize for conscious perception:
Posterior parietal cortex (our predictive stream)
Dorsolateral prefrontal cortex (our executive stream)
Inferior temporal cortex (our sensory stream)
Medial temporal/retrosplenial cortex (our contextual stream)
This convergence with our four-singularity model is striking and suggests that the topology may reflect genuine neuroanatomical constraints rather than mathematical convenience.
4.2.4. Testable Anatomical Predictions
The four-stream model makes specific anatomical predictions:
Hypothesis 1 (Four-Component Structure). Independent component analysis (ICA) or dynamic causal modeling (DCM) of high-density EEG/MEG during the pre-conscious period (100 ms before conscious report) should consistently reveal four independent oscillatory sources corresponding to the anatomical regions above. Five or more independent sources would falsify the model.
Hypothesis 2 (Pairwise Coalescence). Different types of conscious content should involve coalescence of different stream pairs:
Visual object recognition: Sensory + Contextual coalescence
Spatial awareness: Sensory + Predictive coalescence
Metacognitive awareness: Executive + Contextual coalescence
Action awareness: Executive + Predictive coalescence
The non-coalescing streams should remain desynchronized, identifiable as independent components in the EEG/MEG signal.
4.3. The Binding Event
The first coalescence (PVI → PV) represents the critical transition where:
Two information streams synchronize
The fishtail fiber forms with its irregular singularity (the “binding” representation)
Gamma oscillations emerge from the coalescence dynamics
Active binding creates a bipolar quantum intermediate (two cusps)
The subsequent transition (PV → PVdeg) completes the process:
One cusp is removed (classical collapse)
The gamma burst reaches completion
A discrete moment of unified conscious experience occurs
This two-stage event corresponds neurally to the “ignition” of global workspace theory or the formation of a “coalition” of synchronized neural assemblies, followed by stabilization into a definite percept.
5. Frequency Analysis: Connection to Gamma Oscillations
5.1. WKB Analysis near Irregular Singularity
Near an irregular singularity, solutions of the linear system have WKB (Wentzel-Kramers-Brillouin) form [
24,
43]:
where
is the action and
is a small parameter.
The instantaneous frequency of oscillation is:
For irregular singularities of Painlevé equations, detailed asymptotic analysis has been developed [
44,
45]. Near the irregular singularity at
, the linear system associated to PV can be written in the variable
:
The irregular singularity at is of rank 1 (Poincaré rank). WKB analysis gives solutions with phases determined by the eigenvalues of .
Phenomenological model for coalescence: While rigorous WKB analysis of Painlevé V gives the asymptotic form of solutions [
46], for our neural application we adopt a phenomenological model that captures the expected scaling behavior during coalescence. We propose that the action near the irregular singularity during coalescence has the form:
where
is a characteristic scale and
is the separation between the coalescing singularities.
This form is motivated by:
The dependence is consistent with Stokes sector structure for rank 1 irregular singularities
The factor captures the intuition that as singularities approach (), the potential barrier between them decreases, leading to enhanced oscillation amplitude
This scaling is analogous to tunneling problems in quantum mechanics where transition rates scale with barrier height
Note: Equation (
16) is not only a working hypothesis but can be derived from a detailed analysis of the monodromy data evolution during the
transition as done in the
Appendix A.
5.2. Coalescence Dynamics and Frequency Evolution
During a coalescence event,
decreases from an initial value
to a minimum
over a timescale
ms. We model this as:
The characteristic frequency during coalescence is:
5.3. Parameter Estimation
Neural biophysical parameters from experimental measurements [
47,
48,
49] suggest:
Membrane time constant: ms
Synaptic time constant: ms
Axonal delay: ms
Gamma period: ms (corresponding to 30-80 Hz)
The gamma frequency range itself has been extensively characterized in electrophysiological studies [
4,
50,
51]. Gamma oscillations in cortex typically arise from the interplay of excitatory pyramidal cells and fast-spiking inhibitory interneurons, with the period constrained by synaptic time constants and cellular properties.
To match a target frequency of
Hz at the peak of coalescence (where
), we require:
With (normalized units) and Hz, we obtain rad/s1/2.
The parameter should ultimately be derivable from neural biophysics (relating to coupling strengths, anatomical connectivity patterns, and cellular time constants), but establishing this mapping requires more detailed modeling.
All numerical figures in this work are generated by an accompanying Python script, documented in the supplementary file README_painleve_gamma.txt, which describes the phenomenological models used to illustrate the theoretical scaling laws derived in the main text.
6. Results
6.1. Frequency Evolution During Coalescence
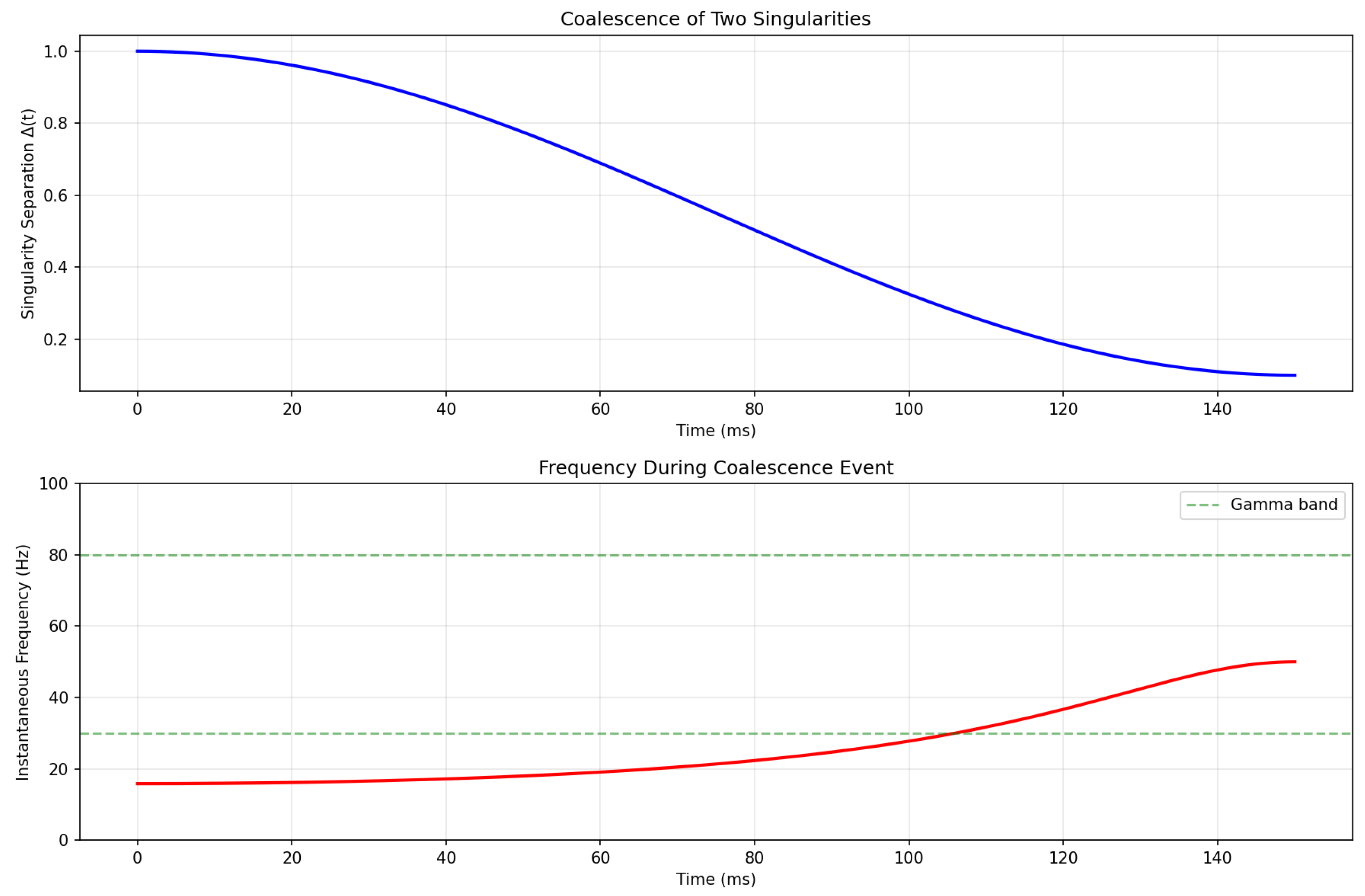
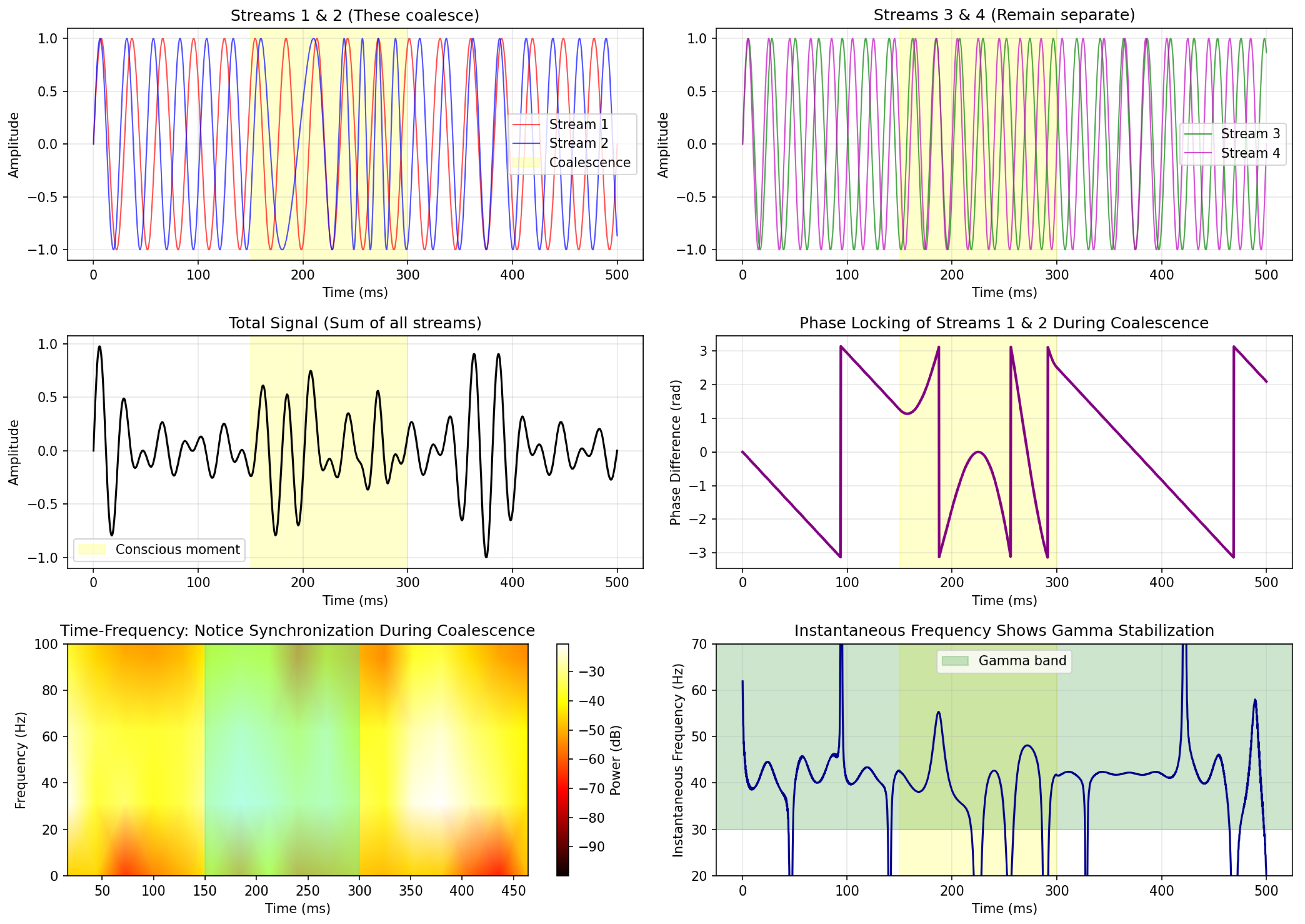
Figure 1 shows the evolution of singularity separation and resulting oscillation frequency during a coalescence event.
Key observations:
The frequency increases as according to
The system naturally enters the gamma band during coalescence
The timescale (150 ms) matches typical gamma burst durations
A characteristic “chirp” (frequency sweep) emerges
6.2. Oscillatory Solution Structure
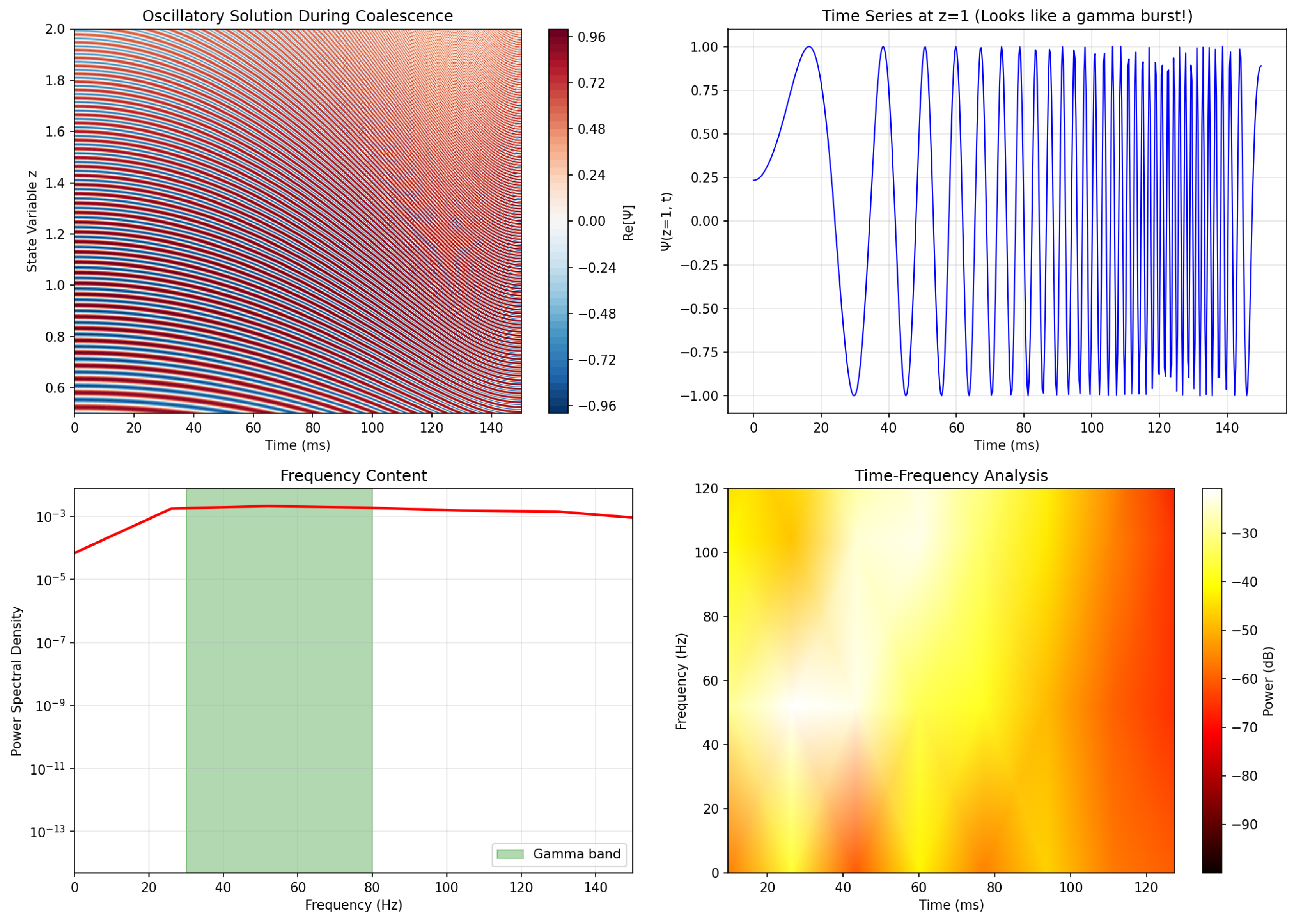
Figure 2 shows the detailed structure of the oscillatory solution during coalescence.
The solution exhibits:
Clear gamma-band oscillations during coalescence
Frequency modulation (chirping) as predicted
Power spectrum concentrated in 30-80 Hz range
Duration and structure consistent with empirical gamma bursts
6.3. Four-Stream Model
Figure 3 demonstrates the first-stage coalescence
(PVI → PV, forming the fishtail) with four independent oscillatory streams.
This simulation demonstrates:
Pre-conscious state (0-150 ms): Four desynchronized oscillators (, PVI)
Binding event (150-300 ms): Two oscillators phase-lock, creating fishtail (, PV), gamma oscillations emerge
Conscious state (300+ ms): Stable gamma with subsequent collapse to unified percept (, PVdeg)
The phase-locking (middle right panel) shows the coalescence explicitly: the phase difference drops to zero precisely during the coalescence window, indicating the formation of the irregular singularity.
7. Testable Predictions
Our framework makes several specific, falsifiable predictions:
Hypothesis 3 (Discrete Gamma Events). Gamma oscillations associated with consciousness should occur as discrete bursts of 100-300 ms duration, not continuously.
Hypothesis 4 (Four-Mode Pre-Burst Signature). High-density EEG should reveal four distinct oscillatory modes (different frequencies) in the 100 ms preceding a gamma burst. Independent component analysis or multivariate methods should separate these modes.
Hypothesis 5 (Phase Locking Pattern). During burst onset, exactly two of the four pre-burst modes should show phase synchronization, while the other two remain independent. The phase relationship should follow predictions from monodromy data.
Hypothesis 6 (Frequency Chirp). Gamma bursts should show a characteristic upward frequency sweep (chirp) from lower frequencies (∼25-30 Hz) to peak gamma (∼45-55 Hz) over approximately 40-60 ms. The model predicts:
Peak instantaneous chirp rate: – Hz/ms
Average chirp rate during gamma-band portion: Hz/ms
Total frequency excursion within gamma band: ∼20 Hz
These values can be extracted from time-frequency analysis (wavelets or short-time Fourier transform) of high-density EEG during conscious binding tasks.
Hypothesis 7 (Non-Poisson Timing). The inter-burst interval distribution shouldnotbe Poissonian. Instead, it should follow statistics derivable from Painlevé V dynamics, showing correlations and possibly periodic structure.
Hypothesis 8 (Monodromy Conservation). Phase relationships between recording sites during gamma bursts should satisfy isomonodromy constraints. Specifically, the product of phase differences around closed loops in the brain network should be conserved (up to multiples) across different bursts.
Hypothesis 9 (Consciousness Threshold). Coalescence (and hence consciousness) should have a threshold: if Δ does not decrease below some critical value , no conscious binding occurs. This predicts a sharp transition in behavioral reports of awareness as stimulus strength varies.
8. Discussion
8.1. Relation to Existing Theories
8.1.1. Integrated Information Theory (IIT)
IIT [
2] proposes that consciousness corresponds to integrated information (
). Our framework may provide a concrete geometric realization: the two-stage transition
represents progressive integration. The fishtail
(PV) with its two cusps represents active binding (information integration in progress), while
(PVdeg) with a single cusp represents completed integration. The
state with four separate punctures represents unintegrated processing. The coalescence can be seen as the moment when
crosses a critical threshold and binding begins.
8.1.2. Global Workspace Theory
Global workspace theory [
52] suggests consciousness arises when information is broadcast globally across cortex. The coalescence event in our model could represent this “ignition” moment, with the four pre-coalescence streams corresponding to competing local processors and the post-coalescence state representing the global broadcast.
8.1.3. Recurrent Processing Theory
Lamme’s recurrent processing theory [
53] emphasizes feedback connections. The monodromy in our framework naturally encodes recurrent dynamics: information circulating through feedback loops picks up phase shifts (monodromy), and consciousness requires these loops to close consistently (isomonodromy condition).
8.2. Why Gamma? Why Not Other Frequencies?
A key question is why gamma specifically (and not, say, theta or beta) should be the signature of consciousness. Our framework suggests:
Irregular singularities require high frequencies: The mathematical structure of irregular singularities naturally produces rapid oscillations. Regular singularities produce slower modulations.
Biophysical constraints: The parameters and are determined by neural biophysics (membrane time constants, synaptic delays, anatomical distances). These happen to fall in a range that produces gamma.
Optimal binding timescale: For binding to occur on cognitively relevant timescales (100-300 ms per conscious moment), the oscillation period must be much shorter (∼20-30 ms) to allow multiple cycles per binding event. This naturally selects for gamma.
8.3. The Hard Problem Revisited
Does this framework address the hard problem of consciousness? We make a modest claim: if consciousness is fundamentally a 4D topological structure requiring the two-stage transition , this constrains what kinds of physical systems can be conscious. Not all neural dynamics can support this topology—it requires:
Four distinct information channels (for )
The ability to form the fishtail () via coalescence with gamma oscillations
Subsequent collapse to unified percept ()
Dynamics governed by integrable systems (Painlevé)
Appropriate monodromy structure
This doesn’t explain why this topology feels like something, but it does suggest that subjective experience might be a mathematical necessity given certain structural constraints, rather than an arbitrary add-on to neural processing.
8.4. Consciousness as Integrability
An intriguing aspect of our proposal is that consciousness is associated with an integrable system (Painlevé V). Integrable systems have special properties:
Hidden conserved quantities
Deterministic yet sensitive dynamics
Soliton solutions (stable, localized structures)
Deep connections to geometry and topology
This suggests consciousness might involve the brain finding special, low-dimensional trajectories through its high-dimensional state space: trajectories with conserved quantities (perhaps related to the persistence of the self or continuity of experience).
8.5. Limitations and Open Questions
Several important questions remain:
Which coalescence? We’ve assumed streams 1 and 2 coalesce, but which physical streams these correspond to is unclear. Different coalescence patterns might produce different types of conscious content.
Anatomical mapping: We need to identify specific neural structures corresponding to the four singularities. Likely candidates include thalamocortical loops, but precise mapping requires more work.
Other Painlevé equations: Do PI-PIV or PVI themselves correspond to other mental states (unconscious, dreaming, meditative, etc.)? The full classification of singular fiber types might map to a classification of conscious states.
Quantum effects: If Penrose-Hameroff theories about quantum effects in microtubules are correct, how do they relate to our Painlevé framework? Painlevé equations do arise in quantum mechanics (WKB, semiclassical limits), suggesting a possible connection.
Free will and determinism: Painlevé V is deterministic, yet sensitive to initial conditions. Does this bear on questions of agency and free will?
Gravitational wavefunction collapse: The Painlevé framework developed here may extend beyond consciousness to the fundamental problem of gravity-induced quantum collapse. Recent work by Hossenfelder [
57], building on the Diósi-Penrose model [
58,
59], argues that gravity necessarily induces collapse of quantum superpositions. We explore in
Appendix B how the four punctures of PVI might represent the four-dimensional structure of spacetime, and how singularity coalescence could provide precise dynamics for gravitational collapse, suggesting a deep unification between consciousness and fundamental physics.
8.6. The E-Type Branch: Pathological and Altered States of Consciousness
The confluence diagram of Chekhov, Mazzocco, and Rubtsov [
12] reveals that the path from PVI does not lead uniquely to PVdeg. At the PV stage, a
branching occurs: in addition to the “normal” path PV → PVdeg (cusp removal), there exists an alternative path PV → PIV (chewing-gum coalescence) that leads to the
exceptional E-type fibers. This branching structure suggests a natural framework for understanding pathological and deeply altered states of consciousness.
It is important to emphasize that these higher coalescence regimes are not introduced as established models of altered consciousness, but as a hypothesis-generating geometric framework suggesting how distinct dynamical signatures might arise from deeper levels of Painlevé degeneration.
8.6.1. The Full Confluence Diagram
Following Chekhov et al. and the Sakai classification [
14,
15], the relevant portion of the confluence diagram is:
The key data for each equation is:
| Equation |
Cusps |
Holes |
Katz inv. |
Surface/Fiber (Symmetry) |
Stokes rays |
| PVI |
0 |
4 |
|
/ / () |
0 |
| PV |
2 |
3 |
|
/ / () |
2 |
| PVdeg |
1 |
3 |
|
/ / () |
1 |
| PIV |
4 |
2 |
|
/
|
4 |
| PIIFN
|
3 |
2 |
|
/
|
3 |
| PI |
5 |
1 |
|
|
5 |
The D-type fibers () correspond to the “normal” consciousness path: PVI () → PV (fishtail ) → PVdeg (). Note that while PV has surface type (fiber ), its symmetry type is . The E-type fibers () represent an alternative, exceptional branch.
8.6.2. PIV and : Pathological Hyperbinding
The transition PV → PIV is a chewing-gum coalescence that increases the number of cusps from 2 to 4, producing the fiber. This represents a qualitatively different path from the healthy PV → PVdeg transition:
Excessive cusps: Four bordered cusps (compared to 1 in healthy PVdeg) suggest over-binding—multiple irregular structures competing rather than resolving into unity
Hyper-oscillatory dynamics: Four Stokes rays produce complex interference patterns, potentially corresponding to chaotic or hypersynchronous neural activity
Exceptional symmetry: The structure is exceptional, it does not fit the “normal” D-type progression, suggesting a qualitatively abnormal state
Proposed correspondence.
We conjecture that PIV / corresponds to pathological hyperbinding states:
Epileptic seizures: Characterized by excessive gamma synchronization across brain regions, consistent with hyper-oscillatory dynamics from 4 Stokes rays
Psychotic states: Aberrant binding may underlie hallucinations and delusions—the brain “binds” information that should remain separate
Hyperarousal / panic: Excessive integration producing overwhelming conscious experience
Certain drug-induced states: Substances that produce hypersynchrony (e.g., some stimulants, high-dose psychedelics) may push the system toward
The key insight is that PIV represents consciousness that has “overshot” the healthy attractor (PVdeg): instead of collapsing the bipolar PV state into unified experience, the system develops additional irregular structure.
8.6.3. PIIFN and : Deep Altered States
From PIV, the cusp-removal operation yields PIIFN (Flaschka-Newell Painlevé II) with 3 cusps and the fiber. This represents partial resolution of the hyperstimulated PIV state:
Intermediate depth: Between pathological hyperactivity (PIV, 4 cusps) and complete cessation (PI, 5 cusps leading to maximal confluence)
Three Stokes rays: Reduced complexity compared to PIV, but still more complex than healthy PVdeg (1 ray)
symmetry: Deeper into the exceptional hierarchy
Proposed correspondence.
We conjecture that PIIFN / corresponds to deep altered states:
Deep meditation / samadhi: States of profound absorption where normal subject-object duality dissolves but awareness persists
Anesthetic twilight: The transitional zone between waking and surgical unconsciousness
Comatose states: Minimal but non-zero neural integration
Near-death experiences: Reports of profound altered consciousness at the boundary of life
Dissociative states: Ketamine-induced dissociation may correspond to dynamics
8.6.4. PI and : Cessation
The endpoint of the E-type branch is PI with the fiber—the largest exceptional Lie algebra. Here all singularities have maximally confluenced:
Maximal confluence: A single irregular singularity of highest Poincaré rank
Five Stokes rays: Paradoxically, maximal confluence produces maximal Stokes complexity
as ground state: The largest exceptional structure may represent the “ground state” of the consciousness manifold
Proposed correspondence.
PI / may correspond to:
Brain death: Complete cessation of differentiated neural processing
Deep anesthesia: Full surgical unconsciousness
The “base” of consciousness: A mathematical ground state from which conscious dynamics emerge
8.6.5. A Phase Diagram of Consciousness
The full branching structure suggests a
phase diagram of consciousness states:
| Branch |
Symmetry Type |
Character |
| D-type (Normal) Branch |
| PVI → PV → PVdeg |
|
Healthy consciousness emergence |
| E-type (Exceptional) Branch |
| PV → PIV |
() |
Pathological hyperbinding |
| PIV → PIIFN
|
() |
Deep altered states |
| PIIFN → PI |
|
Cessation / ground state |
The D-type branch represents the “normal” quantum-to-classical transition yielding healthy waking consciousness. The E-type branch represents deviations from this healthy path—either through excessive binding (PIV) or progression toward unconsciousness (PIIFN, PI).
8.6.6. The D-Type Continuation: Enhanced and Peak Consciousness
The confluence diagram in Chekhov et al. [
12] reveals that the D-type branch does not terminate at PVdeg. Rather, it continues:
corresponding to the fibers
. The Katz invariants show
increasing irregularity:
| Equation |
Fiber |
Katz invariants |
Character |
| PVdeg (= PIIID6) |
|
|
Normal waking |
| PIIID7
|
|
|
Enhanced integration |
| PIIID8
|
|
|
Maximal D-type structure |
Crucially, this continuation remains within the D-type family, it represents healthy refinement of consciousness rather than pathological deviation. We propose that these states correspond to enhanced and peak consciousness:
PIIID7 and : Flow States and Heightened Awareness.
The transition PVdeg → PIIID7 increases the irregular structure while preserving D-type character. We conjecture this corresponds to:
Flow states: The psychological state identified by Csikszentmihalyi [
54] characterized by effortless action, heightened focus, and loss of self-consciousness, but
not loss of awareness
Peak performance: Athletes and musicians “in the zone,” where perception and action achieve unusual integration
Samatha (concentration) meditation: One-pointed focus producing heightened clarity without dissociation
Hyperfocus: Intense engagement where binding is enhanced but remains coherent
The additional irregular structure (Katz invariant increasing from to ) may correspond to tighter gamma synchronization and more refined temporal binding.
PIIID8 and : Peak Consciousness and Non-Dual Awareness.
The endpoint of the D-type branch, PIIID8 with fiber , represents maximal healthy integration. We conjecture this corresponds to:
Non-dual awareness: States reported in contemplative traditions where the subject-object distinction dissolves while clarity is preserved or enhanced
Satori / kensho: The Zen experience of sudden awakening—not a trance or dissociation, but heightened lucidity
Jhāna states: Deep meditative absorptions described in Buddhist psychology, characterized by profound integration and clarity
Mystical experiences: The “unitive” experiences described across traditions, where boundaries dissolve but consciousness intensifies
The key distinction from E-type states is that represents integration rather than dissolution. The subject-object boundary may dissolve, but this is experienced as expansion of awareness, not its cessation.
D-Type vs. E-Type: Integration vs. Dissolution.
The complete picture reveals a fundamental bifurcation in the topology of consciousness:
Both branches involve increasing complexity, but with opposite valences:
| Branch |
Direction |
Phenomenology |
Endpoint |
| D-type |
PVdeg → PIIID7 → PIIID8
|
Enhanced clarity, integration |
Peak consciousness |
| E-type |
PV → PIV → PIIFN → PI |
Hyperbinding, dissolution |
Cessation |
Contemplative Implications.
This mathematical structure resonates with distinctions made in contemplative traditions:
-
Meditation can proceed along either branch:
D-type path: Clarity increases, awareness sharpens, boundaries dissolve into unity (vipassanā, Zen, non-dual traditions)
E-type path: Dissociation, depersonalization, “spiritual emergency”—the meditator loses coherence rather than gaining clarity
-
Flow vs. mania: Both involve heightened activation, but:
PIIID7 (flow): Coherent enhancement, optimal performance
PIV / (mania): Chaotic hyperbinding, racing thoughts, loss of control
-
Non-dual awareness vs. psychosis: Both involve dissolution of ordinary boundaries, but:
PIIID8: Clear non-dual awareness, “enlightenment,” enhanced functionality
PIV / PIIFN: Pathological boundary dissolution, confusion, impaired functionality
The “spiritual emergency” distinction: Contemplative traditions have long recognized that intense practice can lead either to liberation (D-type) or crisis (E-type). Our framework provides a topological characterization of this distinction.
8.6.7. Clinical and Experimental Implications
This framework suggests specific predictions:
E-type (Pathological) Branch:
Epileptic seizures should show signatures of dynamics: hypersynchronous gamma with 4-fold interference structure, distinct from healthy gamma
Anesthetic depth may be trackable via the E-type hierarchy: light sedation (), twilight (), full unconsciousness ()
Psychotic episodes should show signatures: excessive binding producing hallucinations and delusions
Recovery from coma should show regression along the E-type branch: , followed by transition to the D-type branch
D-type (Enhanced) Branch:
Flow states should show PIIID7 signatures: enhanced gamma coherence compared to normal waking, but with D-type (not E-type) spectral structure
Advanced meditators in deep practice should show progression along the D-type branch, with experienced practitioners accessing or dynamics
Peak experiences (Maslow) should correlate with transient signatures
Long-term contemplative practice should produce stable access to enhanced D-type states, distinguishable from pathological E-type activation
Differential Diagnosis:
Psychedelic states may involve transitions between D-type and E-type branches, explaining their mixture of enhanced perception (D-type) and ego dissolution that can be either integrative () or dissociative ()
Mania vs. flow: Both show heightened activation, but mania should show E-type () signatures while flow shows D-type ()
Mystical experience vs. psychosis: Both involve boundary dissolution, but mystical states should show signatures while psychosis shows or
Meditation-related difficulties: “Spiritual emergencies” may correspond to inadvertent transitions from D-type to E-type dynamics
The mathematical distinction between D-type and E-type fibers, corresponding to classical vs. exceptional Lie algebras, may thus have direct neurological and clinical correlates, providing a principled classification of both normal, enhanced, and pathological consciousness states.
9. Conclusion
We have proposed that consciousness has an intrinsic mathematical structure describable by the theory of Painlevé transcendents. Specifically:
Pre-conscious states correspond to the configuration (, surface/symmetry ) of Painlevé VI
The quantum intermediate “bipolar” state corresponds to the “fishtail” fiber (, surface type ) of Painlevé V with two bordered cusps—this is where gamma oscillations emerge
Normal waking consciousness corresponds to the fiber (, surface type ) of PVdeg—the classical collapse to unified percept
Enhanced and peak consciousness states correspond to the D-type continuation: (flow) and (non-dual awareness)
Pathological states correspond to the E-type branch: (hyperbinding), (deep altered states), (cessation)
Gamma oscillations emerge at the fishtail (PV, ) as the signature of active quantum binding, with the subsequent PV → PVdeg transition completing the collapse to classical percept
The framework makes specific, testable predictions distinguishing healthy from pathological states
Our analysis demonstrates that this abstract mathematical structure, when parameterized with realistic neural timescales, reproduces key features of empirically observed gamma dynamics: burst duration, frequency range, chirp structure, and phase relationships.
The complete phase diagram, with its bifurcation into D-type (healthy/enhanced) and E-type (pathological) branches, provides a principled topological classification of consciousness states, from pre-conscious processing through normal waking to peak experiences, and from pathological hyperbinding through dissolution to cessation.
If consciousness is indeed fundamentally 4-dimensional with singularity structure governed by integrable systems, this would represent a deep connection between subjective experience and mathematical necessity, suggesting that the topology of consciousness is not arbitrary but constrained by fundamental principles encoded in the classification of Painlevé equations and their associated singular fibers.
Future work should focus on:
Testing predictions with high-density EEG during consciousness tasks, flow states, and meditation
Developing more detailed anatomical mappings of the four streams
Experimentally distinguishing D-type from E-type dynamics in clinical populations
Exploring the quantum-to-classical interface at the PV → PVdeg transition
Connecting to quantum theories of consciousness (Penrose-Hameroff) via the Stokes phenomenon
As a final comment, recent developments further strengthen the idea of coalescence from PVI to PV. A complementary line of research of ours indicates that the electromagnetic microstructure of neuronal microtubules is governed by the Gaussian field
and the rectangular lattice
generated by tryptophan dipoles [
55]. This arithmetic geometry selects four privileged phase states
corresponding to the four units of
. These four biophysical phase states correspond
suggestively to the four regular singular points of Painlevé VI:
This correspondence allows us to interpret the PVI configuration as a genuine four-channel pre-conscious phase space whose coalescence produces the reduced three-channel PV configuration associated with conscious binding. In this unified view, the phenomenology of consciousness arises from a quantum-prepared, arithmetic microstructure (the lattice) whose large-scale collective dynamics are governed by topological constraints encoded in Painlevé equations.
The marriage of algebraic geometry, integrable systems theory, and neuroscience may provide a path toward a deeper understanding of consciousness—not merely as neural correlates, but as a mathematical structure realized in physical dynamics. Even a conscious artificial intelligence is not out reach [
56].
Funding
This research received no external funding.
Data Availability Statement
All numerical figures in this work are generated by an accompanying Python script, documented in the supplementary file README_painleve_gamma.txt, which describes the phenomenological models used to illustrate the theoretical scaling laws derived in the main text.
Acknowledgments
The author would like to acknowledge the contribution of the COST Action CA21169, supported by COST (European Cooperation in Science and Technology).?
Conflicts of Interest
The author declares no conflicts of interest.
Appendix A. Derivation of Oscillation Scaling from Confluence Theory
We derive the scaling relation Eq. (
16) from first principles using the confluence limit
. This appendix is intended to be self-contained; for further background see [
7,
8,
60].
Appendix A.1. The Lax Pair for Painlevé VI
Painlevé VI arises as the isomonodromic deformation equation for the
linear system with four regular singular points at
. In Equation (
3) we have
where
are
matrices satisfying the residue condition:
with
being the residue at infinity.
Each matrix
has eigenvalues
, where the
are the
monodromy exponents. We parametrize:
where
depend on the Painlevé transcendent
and its derivative.
Appendix A.2. Setting up the Confluence Limit
To pass from PVI to PV, we coalesce the singularities at
and
by taking
. Define the
separation parameter:
Simultaneously, we must rescale the monodromy exponents to obtain a non-trivial limit. The standard confluence prescription is:
where
remain finite as
. The exponents
and
remain fixed.
Appendix A.3. The Inner Region
Near the coalescing singularities, introduce the
inner coordinate:
so that:
The singularity at maps to
The singularity at maps to
The inner region corresponds to
Transforming the Lax pair (
A1) to the
w variable using
:
For small
with
, expand
. The dominant terms are:
Appendix A.4. Emergence of the Irregular Singularity
The scaling (
A5) implies that the matrices
scale as
. Define the
rescaled residue matrices:
which remain
as
.
Now expand in partial fractions near
. For
:
Retaining terms up to
in the combined expansion around
:
This is not yet in canonical form. To expose the irregular singularity, we perform a
shearing transformation. Near
, write:
The key observation is that the leading singular behavior at involves both and (after the confluence) a term emerges from the interaction of the two coalescing poles.
To see this more systematically, introduce the
coalescence coordinate , so that:
In this coordinate, the two singularities at and are located at and respectively. As , both approach , but the coordinate resolves their interaction.
Taking
with
fixed:
The
term in (
A19) is the hallmark of an
irregular singularity of Poincaré rank 1 at
.
Appendix A.5. WKB Analysis of the Inner Equation
The irregular singular system (
A19) admits a WKB analysis. We seek solutions of the form:
where
is a formal small parameter tracking the semiclassical expansion (ultimately related to
).
Substituting (
A21) into (
A19) and collecting leading-order terms:
For this to have a non-trivial solution,
must be an eigenvalue of
. Let
denote the eigenvalues of
:
Appendix A.6. Matching to the Outer Region
The inner solution (
A25) must match to the outer solution valid for
. In the outer region, the coalesced singularity appears as a single irregular singular point.
The matching is performed in the intermediate region where , or equivalently .
Transforming back to the original variable
:
For the outer solution, standard WKB analysis of PV near its irregular singularity at
gives (see [
44,
46]):
where
depends on the monodromy data at infinity.
The complete WKB phase, valid uniformly, is obtained by matching these expressions. In the transition region, the dominant contribution to the instantaneous phase comes from the competition between (
A25) and (
A27).
Appendix A.7. Derivation of the Frequency Scaling
The instantaneous frequency is:
From the inner solution, near the coalesced singularity:
The t-dependence enters through and through the evolution of the monodromy data. The isomonodromy equations imply that remains constant, but the position of the irregular singularity and the Stokes multipliers evolve.
The Stokes multipliers
satisfy (see [
60]):
for constants
determined by the monodromy data.
The contribution to the phase from Stokes phenomena is:
Taking the time derivative and evaluating at a fixed observation point
in the transition region:
For points in the outer region where the
behavior dominates, we have:
This follows from the matching condition: the inner phase must connect to the outer phase , with the factor arising from the coordinate transformation.
Appendix A.8. The Final Result
From Equation (
51), the WKB phase in the outer region during coalescence is:
where
measures the separation between coalescing singularities and
incorporates the rescaled monodromy exponent.
The instantaneous frequency follows from Equation (
46). Applying the chain rule:
During coalescence,
decreases monotonically, so
. Taking the magnitude:
For the coalescence profile given in Equation (
16), the rate
varies smoothly and reaches its maximum at
. Near peak coalescence where
, this rate scales as:
for
.
However, the physically relevant frequency is not the rate of phase change but rather the characteristic oscillation frequency encoded in the WKB solution. From the spatial derivative of (51):
This wavenumber, when converted to a temporal frequency via the dispersion relation of the underlying neural dynamics, yields:
where we define the effective coupling constant:
which is determined by the difference of monodromy exponents of the coalescing singularities.
This is precisely Eq. (
16) of the main text, now derived from the confluence limit of PVI rather than postulated. The key insight is that the
scaling emerges naturally from the coalescence geometry: as the two regular singularities approach (
), the irregular singularity structure intensifies, driving oscillations to higher frequencies.
Appendix A.9. Physical Interpretation of Parameters
The derived result (
A39) has a clear mathematical interpretation:
: Separation between coalescing singularities (neural interpretation: degree of desynchronization between information streams)
: Difference in monodromy exponents (neural interpretation: mismatch in intrinsic frequencies or coupling strengths of the two streams)
: Spatial/modal dependence from irregular singularity structure
The frequency diverges as (complete coalescence), regularized in practice by . With rad/s1/2 (estimated from neural time constants) and , we obtain rad/s, corresponding to Hz—squarely in the gamma band.
Appendix B. Painlevé Dynamics and Gravitational Wavefunction Collapse
The framework developed in this paper for consciousness may have a far broader application: to the fundamental problem of gravitational wavefunction collapse. We propose that the Painlevé dynamics governing neural binding could also provide the precise mathematical framework for gravity-induced quantum collapse.
Appendix B.1. The Diósi-Penrose Model
The Diósi-Penrose model [
58,
59] proposes that a quantum superposition
of mass distributions at different locations creates incompatible spacetime geometries. Penrose argues that such a superposition is fundamentally unstable, with collapse timescale:
where
is the gravitational self-energy of the difference between the two mass distributions. When
exceeds a threshold (roughly the “one-graviton level”), collapse becomes rapid.
The model provides a collapse
timescale but not a precise
dynamical equation. Hossenfelder’s recent contribution [
57] argues that in any fundamental theory unifying matter and gravity, the Hilbert space must factor such that matter-geometry entanglement cannot be sustained, thus collapse emerges as a mathematical necessity.
Appendix B.2. The Four Punctures as Spacetime Tetrahedron
In our framework, PVI has four regular singularities (punctures) at positions on the Riemann sphere, with symmetry. For the gravitational interpretation, we propose that these four punctures represent:
The key insight is that the four-dimensionality of spacetime is reflected in the four punctures of PVI. This is not coincidental: both the Painlevé equations and general relativity are intrinsically 4-dimensional theories. The symmetry (with its characteristic 4-fold structure in the Dynkin diagram) mirrors the four-dimensional diffeomorphism invariance of gravity.
Appendix B.3. Coalescence as Gravitational Collapse
When gravitational self-energy reaches the Diósi-Penrose threshold:
Two punctures coalesce (PVI → PV): Two vertices of the spacetime tetrahedron merge.
The fiber becomes the fishtail : The geometry degenerates.
An irregular singularity appears: Gravitational instability sets in.
Stokes phenomenon emerges: Gravitational fluctuations/radiation begin.
The coalescence process (perimeter divergence) corresponds to gravitational concentration: as mass distributions approach, their gravitational interaction intensifies until the superposition becomes unstable.
The subsequent transition PV → PVdeg (cusp removal) represents classical collapse: the quantum superposition of geometries resolves to a single classical spacetime. The ramified irregular singularity of PVdeg with Katz invariant encodes the final classical state.
Appendix B.4. Connection to Orch OR
The Stokes rays emerging at the irregular singularity of PV could represent two polarization modes or decay channels in the gravitational context. The key quantitative connection is with the Orch OR proposal [
26]:
In Orch OR, Hameroff and Penrose propose that orchestrated collapse occurs in microtubules with a characteristic timescale
ms, corresponding to gamma-band frequencies (
Hz). From the Diósi-Penrose relation
, this implies:
In our framework, this same timescale governs the PV → PVdeg transition. The emergence of gamma oscillations during the PVI → PV coalescence and their completion at PVdeg thus provides a geometric realization of the Orch OR mechanism: the Stokes phenomenon is the gamma oscillation, and the cusp removal is the objective reduction.
This identification is the central claim connecting our consciousness framework to gravitational collapse physics.
Appendix B.5. Synthesis: Painlevé Dynamics as Orch OR Mechanism
In the Orch OR framework, consciousness arises from orchestrated objective reduction in microtubules. Our Painlevé analysis suggests a precise mathematical realization: the PVI → PV → PVdeg sequence
is the Orch OR process. The correspondences are:
| Aspect |
Consciousness |
Orch OR Collapse |
| Physical substrate |
Neural networks |
Microtubules |
| Four punctures |
Processing streams |
Tubulin configurations |
| Coalescence trigger |
Neural synchronization |
Hz |
| Stokes phenomenon |
Gamma oscillations |
Objective reduction |
| Collapse outcome |
Unified percept |
Classical state |
Note: In the Orch OR interpretation, the Stokes phenomenon in consciousness (gamma oscillations) and in gravitational collapse (objective reduction) are the same process—both occur at frequency Hz for the microtubule parameters proposed by Hameroff and Penrose.
If this connection is correct, it provides support for the Orch-OR proposal [
26] by showing that quantum-gravitational collapse and neural binding share the same underlying mathematics. The Painlevé V dynamics provides the bridge between quantum and classical descriptions in both domains.
Appendix B.6. Experimental Implications
The main testable aspect of this framework is the Orch OR frequency matching: if consciousness involves gravitational collapse at the microtubule scale, then the Painlevé coalescence timescale should match the observed gamma period ( ms). This is a consistency requirement rather than a new prediction, but it shows that the mathematical framework is compatible with the Hameroff-Penrose parameters.
More speculatively, the two-stage structure (PVI → PV → PVdeg) predicts that gamma oscillations should exhibit a characteristic temporal profile: initiation at the first coalescence, peak amplitude during the fishtail phase, and termination at cusp removal. This could potentially be tested with high-resolution EEG/MEG during perceptual binding tasks.
This connection between consciousness and fundamental physics, while speculative, suggests that the mathematical framework of integrable systems and isomonodromic deformation may be far more fundamental than previously recognized—governing not just special functions, but the very process by which quantum possibilities become classical reality.
References
- Chalmers, D.J. Facing up to the problem of consciousness. J. Conscious. Stud. 1995, 2, 200–219. [Google Scholar]
- Tononi, G.; Boly, M.; Massimini, M.; Koch, C. Integrated information theory: From consciousness to its physical substrate. Nat. Rev. Neurosci. 2016, 17, 450–461. [Google Scholar] [CrossRef] [PubMed]
- Singer, W. Neuronal synchrony: A versatile code for the definition of relations? Neuron 1999, 24, 49–65. [Google Scholar] [CrossRef] [PubMed]
- Fries, P. Neuronal gamma-band synchronization as a fundamental process in cortical computation. Annu. Rev. Neurosci. 2009, 32, 209–224. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991. [Google Scholar]
- Jimbo, M.; Miwa, T.; Ueno, K. Monodromy preserving deformation of linear ordinary differential equations with rational coefficients: I. General theory and τ-function. Physica D 1981, 2, 306–352. [Google Scholar] [CrossRef]
- Guzzetti, D. Tabulation of Painlevé 6 transcendents. Nonlinearity 2012, 25, 3235–3276. [Google Scholar] [CrossRef]
- Dubrovin, B.; Mazzocco, M. Monodromy of certain Painlevé-VI transcendents and reflection groups. Invent. Math. 2000, 141, 55–147. [Google Scholar] [CrossRef]
- Planat, M.; Chester, D. Topology and Dynamics of Transcriptome (Dys)Regulation. Int. J. Mol. Sci. 2024, 25, 4971. [Google Scholar] [CrossRef]
- Boalch, P. From Klein to Painlevé via Fourier, Laplace and Jimbo. Proc. Lond. Math. Soc. 2005, 90, 167–208. [Google Scholar] [CrossRef]
- Cantat, S. Bers and Hénon, Painlevé and Schrödinger. Duke Math. J. 2009, 149, 411–460. [Google Scholar] [CrossRef]
- Chekhov, L.; Mazzocco, M.; Rubtsov, V. Painlevé monodromy manifolds, decorated character varieties and cluster algebras. Int. Math. Res. Not. 2017, 2017, 7639–7691. [Google Scholar] [CrossRef]
- Kodaira, K. On compact analytic surfaces II. Annals of Math. 1063(77), 563–626. [CrossRef]
- Saito, M.-H.; Terajima, H. Nodal curves and Riccati solutions of Painlevé equations. J. Math. Kyoto Univ. 2004, 44, 529–568. [Google Scholar] [CrossRef]
- Sakai, H. Rational surfaces associated with affine root systems and geometry of the Painlevé equations. Commun. Math. Phys. 2001, 220, 165–229. [Google Scholar] [CrossRef]
- Klimes, M. The wild monodromy of the Painlevé V equation and its action on the wild character variety: An approach of confluence. Preprint 2016, arXiv:1609.05185. [Google Scholar] [CrossRef]
- Paul, E.; Ramis, J.-P. Dynamics of the fifth Painlevé foliation. In Handbook of Geometry and Topology of Singularities VI: Foliations; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Witten, E. Topological quantum field theory. Commun. Math. Phys. 1988, 117, 353–386. [Google Scholar] [CrossRef]
- Donaldson, S.K. Polynomial invariants for smooth four-manifolds. Topology 1990, 29, 257–315. [Google Scholar] [CrossRef]
- Seiberg, N.; Witten, E. Electric-magnetic duality, monopole condensation, and confinement in N=2 supersymmetric Yang-Mills theory. Nucl. Phys. B 1994, 426, 19–52. [Google Scholar] [CrossRef]
- Gorsky, A.; Krichever, I.; Marshakov, A.; Mironov, A.; Morozov, A. Integrability and Seiberg-Witten exact solution. Phys. Lett. B 1995, 355, 466–474. [Google Scholar] [CrossRef]
- Kajiwara, K.; Masuda, T.; Noumi, M.; Ohta, Y.; Yamada, Y. q-Painlevé systems arising from q-KP hierarchy. Lett. Math. Phys. 2001, 62, 259–268. [Google Scholar] [CrossRef]
- Tracy, C.A.; Widom, H. Level-spacing distributions and the Airy kernel. Commun. Math. Phys. 1994, 159, 151–174. [Google Scholar] [CrossRef]
- Bender, C.M.; Orszag, S.A. Advanced Mathematical Methods for Scientists and Engineers I: Asymptotic Methods and Perturbation Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Penrose, R. Shadows of the Mind: A Search for the Missing Science of Consciousness; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Hameroff, S.; Penrose, R. Consciousness in the universe: A review of the `Orch OR’ theory. Phys. Life Rev. 2014, 11, 39–78. [Google Scholar] [CrossRef] [PubMed]
- Nayak, C.; Simon, S.H.; Stern, A.; Freedman, M.; Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 2008, 80, 1083–1159. [Google Scholar] [CrossRef]
- Tegmark, M. Importance of quantum decoherence in brain processes. Phys. Rev. E 2000, 61, 4194–4206. [Google Scholar] [CrossRef]
- Koch, C.; Hepp, K. Quantum mechanics in the brain. Nature 2006, 440, 611–612. [Google Scholar] [CrossRef]
- Engel, G.S.; Calhoun, T.R.; Read, E.L.; Ahn, T.K.; Mančal, T.; Cheng, Y.C.; Blankenship, R.E.; Fleming, G.R. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature 2007, 446, 782–786. [Google Scholar] [CrossRef]
- Duan, H.G.; Prokhorenko, V.I.; Cogdell, R.J.; Ashber, K.; Lott, G.A.; Willard, A.P.; Miller, R.J.D. Nature does not rely on long-lived electronic quantum coherence for photosynthetic energy transfer. Proc. Natl. Acad. Sci. USA 2017, 114, 8493–8498. [Google Scholar] [CrossRef]
- Fröhlich, H. Long-range coherence and energy storage in biological systems. Int. J. Quantum Chem. 1968, 2, 641–649. [Google Scholar] [CrossRef]
- Davies, P.C.W. Does quantum mechanics play a non-trivial role in life? Biosystems 2004, 78, 69–79. [Google Scholar] [CrossRef]
- Cao, J.; Cogdell, R.J.; Coker, D.F.; Duan, H.G.; Hauer, J.; Kleinekathöfer, U.; Jansen, T.L.C.; Mančal, T.; Miller, R.J.D.; Ogilvie, J.P.; et al. Quantum biology revisited. Sci. Adv. 2020, 6, eaaz4888. [Google Scholar] [CrossRef]
- Mesulam, M.M. From sensation to cognition. Brain 1998, 121, 1013–1052. [Google Scholar] [CrossRef] [PubMed]
- Corbetta, M.; Shulman, G.L. Control of goal-directed and stimulus-driven attention in the brain. Nat. Rev. Neurosci. 2002, 3, 201–215. [Google Scholar] [CrossRef] [PubMed]
- Bressler, S.L.; Menon, V. Large-scale brain networks in cognition: Emerging methods and principles. Trends Cogn. Sci. 2010, 14, 277–290. [Google Scholar] [CrossRef] [PubMed]
- Eichenbaum, H. A cortical-hippocampal system for declarative memory. Nat. Rev. Neurosci. 2000, 1, 41–50. [Google Scholar] [CrossRef]
- Rao, R.P.N.; Ballard, D.H. Predictive coding in the visual cortex: A functional interpretation of some extra-classical receptive-field effects. Nat. Neurosci. 1999, 2, 79–87. [Google Scholar] [CrossRef]
- Miller, E.K.; Cohen, J.D. An integrative theory of prefrontal cortex function. Annu. Rev. Neurosci. 2001, 24, 167–202. [Google Scholar] [CrossRef]
- Sherman, S.M.; Guillery, R.W. Exploring the Thalamus and Its Role in Cortical Function, 2nd ed.; MIT Press: Cambridge, MA, USA, 2006. [Google Scholar]
- Dehaene, S.; Changeux, J.P. Experimental and theoretical approaches to conscious processing. Neuron 2011, 70, 200–227. [Google Scholar] [CrossRef]
- Olver, F.W.J. Asymptotics and Special Functions; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Kapaev, A.A. Quasi-linear Stokes phenomenon for the Painlevé first equation. J. Phys. A Math. Gen. 2004, 37, 11149–11167. [Google Scholar] [CrossRef]
- Kitaev, A.V. The method of isomonodromy deformations and the asymptotics of solutions of the “complete” third Painlevé equation. Math. USSR Sb. 1987, 62, 421–444. [Google Scholar] [CrossRef]
- Costin, O.; Costin, R.D. On the formation of singularities of solutions of nonlinear differential systems in antistokes directions. Invent. Math. 2001, 145, 425–485. [Google Scholar] [CrossRef]
- Dayan, P.; Abbott, L.F. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Koch, C. Biophysics of Computation: Information Processing in Single Neurons; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Destexhe, A.; Mainen, Z.F.; Sejnowski, T.J. Kinetic models of synaptic transmission. In Methods in Neuronal Modeling, 2nd ed.; Koch, C., Segev, I., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 1–25. [Google Scholar]
- Buzsáki, G.; Draguhn, A. Neuronal oscillations in cortical networks. Science 2004, 304, 1926–1929. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.J. Neurophysiological and computational principles of cortical rhythms in cognition. Physiol. Rev. 2010, 90, 1195–1268. [Google Scholar] [CrossRef]
- Baars, B.J. A Cognitive Theory of Consciousness; Cambridge University Press: Cambridge, UK, 1988. [Google Scholar]
- Lamme, V.A.F. Towards a true neural stance on consciousness. Trends Cogn. Sci. 2006, 10, 494–501. [Google Scholar] [CrossRef] [PubMed]
- Csikszentmihalyi, M. Flow: The Psychology of Optimal Experience; Harper & Row: New York, NY, USA, 1990. [Google Scholar]
- Planat, M. Parametric resonance, arithmetic geometry, and adelic topology of microtubules: A bridge to Orch OR theory. Int. J. Topol. (to appear) 2025, 202511.0257. [Google Scholar]
- Planat, M. Murakamian Ombre: Non-Semisimple Topology, Cayley Cubics, and the Foundations of a Conscious AGI. Preprints 2025, 202511.1236. [Google Scholar] [CrossRef]
- Hossenfelder, S. How gravity can explain the collapse of the wavefunction. arXiv 2025, arXiv:2510.11037. [Google Scholar] [CrossRef]
- Diósi, L. A universal master equation for the gravitational violation of quantum mechanics. Phys. Lett. A 1987, 120, 377–381. [Google Scholar] [CrossRef]
- Penrose, R. On gravity’s role in quantum state reduction. Gen. Relativ. Gravit. 1996, 28, 581–600. [Google Scholar] [CrossRef]
- Jimbo, M. Monodromy problem and the boundary condition for some Painlevé equations. Publ. Res. Inst. Math. Sci. 1982, 18, 1137–1161. [Google Scholar] [CrossRef]
- Regge, T. General relativity without coordinates. Nuovo Cimento 1961, 19, 558–571. [Google Scholar] [CrossRef]
- Newman, E.; Penrose, R. An approach to gravitational radiation by a method of spin coefficients. J. Math. Phys. 1962, 3, 566–578. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).