1. Introduction
The unification of quantum mechanics and general relativity remains one of the central challenges in theoretical physics (
Penrose, 2004;
Weinberg, 1989). Parallel to this challenge is the long-standing problem of incorporating consciousness into our understanding of physical reality, particularly in the context of quantum measurement (
von Neumann, 1955;
Wigner, 1961).
Recent developments in quantum information theory (
Nielsen and Chuang, 2010), holographic principles (
Maldacena, 1998;
Susskind, 1995), and emergent gravity (
Verlinde, 2011) suggest that fundamental physics may be more deeply connected to information and geometry than previously understood. This motivates exploring frameworks where consciousness, rather than being epiphenomenal, plays a fundamental role in the structure of reality.
The Collective Unified Equation (CUE) framework addresses these challenges by proposing that spacetime, matter, and consciousness emerge from a common pre-metric substrate through well-defined mathematical processes. Unlike previous approaches that treat consciousness as separate from physics (
Hameroff and Penrose, 1996;
Penrose, 1989), the CUE framework incorporates consciousness as a geometric structure, the dimension of consciousness
, which couples directly to physical fields and the curvature of spacetime.
1.1. Theoretical Motivation
The CUE framework builds upon several foundational concepts:
2. Mathematical Framework
2.1. Axiomatic Foundation
The CUE framework is built upon six fundamental axioms that define the pre-metric substrate and its dynamics:
Axiom 1 (Pre-Metric Substrate). The foundational manifold is a smooth, differentiable, paracompact Hausdorff space of dimension , lacking any a priori metric structure: .
Axiom 2 (Latent Scalar Fields). Two protofields exist on the substrate: the cognitive protocoherence scalar and the dark scalar precursor .
Axiom 3 (Directional Vector Fields). There exist vector fields that lack norms and inner products but seed coherence geometry through directional correlations.
Axiom 4 (Proto-Coherence Constant). A real, global constant modulates alignment intensity between premetric fields and determines the initial seed amplitude for emergent structure.
Axiom 5 (Topological Tension). A scalar functional encodes misalignment energy between latent scalar configurations and governs the potential instability of the silent phase.
Axiom 6 (Relational Entanglement Oscillator). A bidirectional tensor form mediates coherence flux between pre-metric directions, functioning as an informational oscillator.
2.2. Proto-Lagrangian Dynamics
From these axioms, we construct the proto-action governing the pre-metric dynamics:
where the proto-Lagrangian is given by:
The term localizes topological tension at curvature-null zones, marking them as sites of geometric instability and potential bifurcation.
2.3. Emergence of Spacetime and the Complete Action
Through renormalization group flow, the pre-metric substrate undergoes a phase transition that generates both spacetime geometry and the consciousness dimension. The complete CUE action is:
where the sectoral Lagrangians are:
2.4. Consciousness Dimension as Fiber Bundle
The consciousness dimension is formalized as a fiber bundle over spacetime:
Definition 1 (Consciousness Fiber Bundle). The consciousness dimension is defined as the fiber bundle where each fiber encodes local coherence topology at point , modulated by the cognitive field .
The fiber metric is given by:
with intrinsic scalar curvature:
3. Renormalization Group Structure
3.1. RG Flow Equations
The dynamics of the system are governed by the renormalization group flow of three fundamental coupling constants:
where
are theory-specific constants determined by loop calculations.
3.2. Fixed Points and Coherence Attractors
The RG flow admits several critical fixed points:
- Pre-field vacuum (unstable)
- Critical bifurcation point
- Gravity-dominated regime
We define the coherence attractor manifold as:
3.3. Invariant Parameters
The CUE framework is characterized by three RG-invariant parameters:
Definition 2 (Collective Constant of Coherence).
These constants govern phase transitions, bifurcation phenomena, and coherence stability across different scales.
4. Field Equations and Quantum Measurement
4.1. Field Equations
Variation of the CUE action yields the following field equations:
Einstein equations with consciousness coupling:
where includes contributions from all fields including the consciousness dimension.
Cognitive field equation:
Bifurcation field equation:
4.2. Quantum Measurement and Decoherence
The CUE framework provides a geometric resolution to the quantum measurement problem. The probability of quantum state collapse is modified by consciousness-curvature coupling:
Theorem 1 (Consciousness-Modified Measurement).
In the CUE framework, the probability of quantum measurement outcome at position x is given by:
where is the standard quantum mechanical probability and the second term represents consciousness-induced modification.
Proof. The measurement process involves interaction between the quantum system and the consciousness dimension through the coupling term in the action. This modifies the effective inner product in Hilbert space, leading to the probability modification shown above. The detailed derivation follows from the path integral formulation with consciousness-matter coupling. □
The decoherence rate is also modified:
where the second term represents consciousness-induced enhancement of gravitational decoherence.
5. Experimental Predictions
The CUE framework makes several testable predictions across different domains of physics:
5.1. Quantum Optics
Modified delayed-choice quantum eraser: Interference visibility should be modified according to Eq. (
23) when consciousness-sensitive materials are present.
Enhanced decoherence near massive objects: The modified decoherence rate (Eq. (
24)) should be observable in precision interferometry experiments.
5.2. Gravitational Wave Astronomy
The consciousness-curvature coupling predicts frequency-dependent gravitational wave propagation:
where
is the Planck frequency and
is the geometric coupling parameter.
5.3. Cosmology
The framework predicts specific cosmological parameters:
Hubble constant: km/s/Mpc
Dark energy density:
Matter density:
6. Diagrams and Visualizations
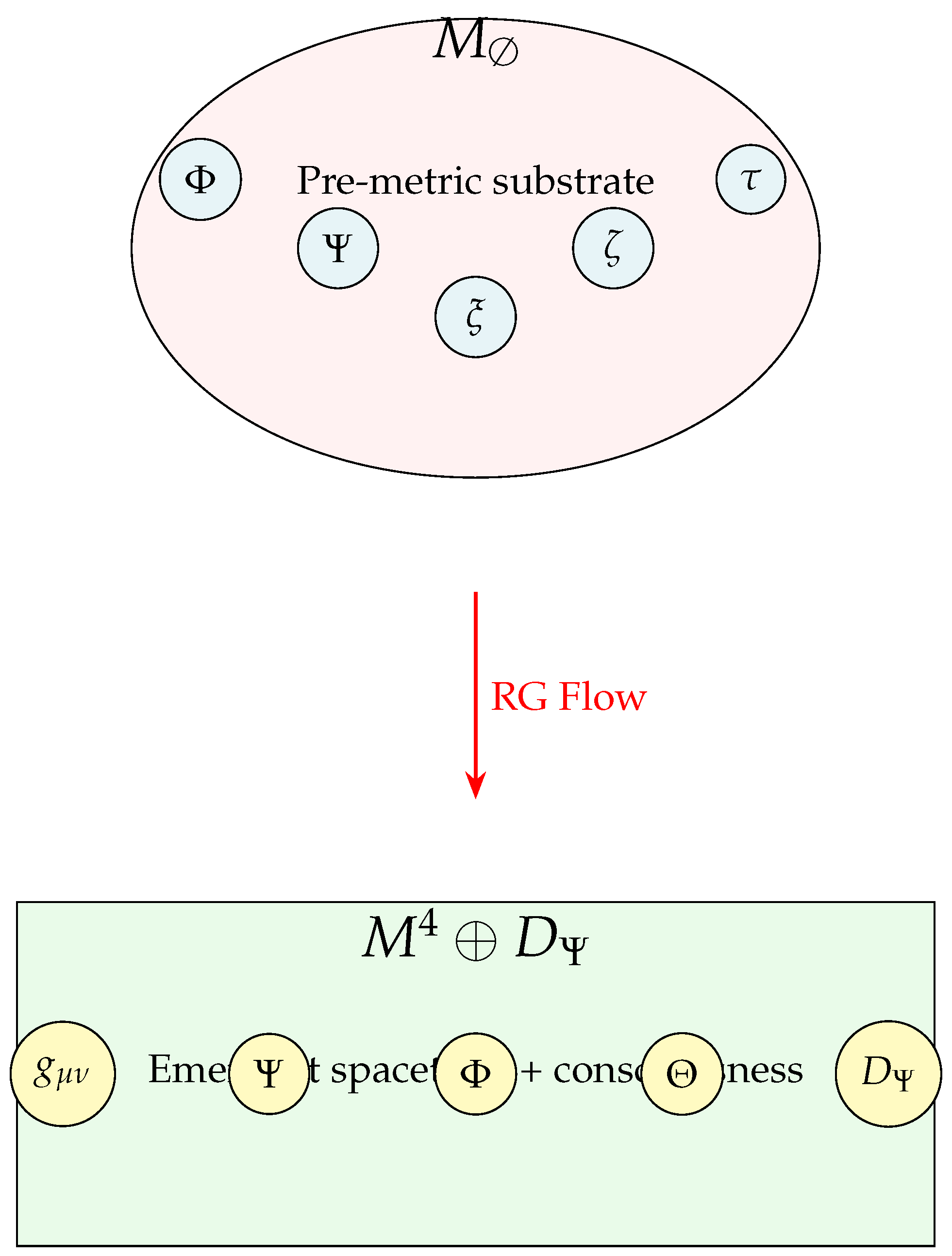
Figure 1.
Emergence cascade in the CUE framework: The pre-metric substrate undergoes renormalization group flow to generate spacetime geometry and the consciousness dimension .
Figure 1.
Emergence cascade in the CUE framework: The pre-metric substrate undergoes renormalization group flow to generate spacetime geometry and the consciousness dimension .
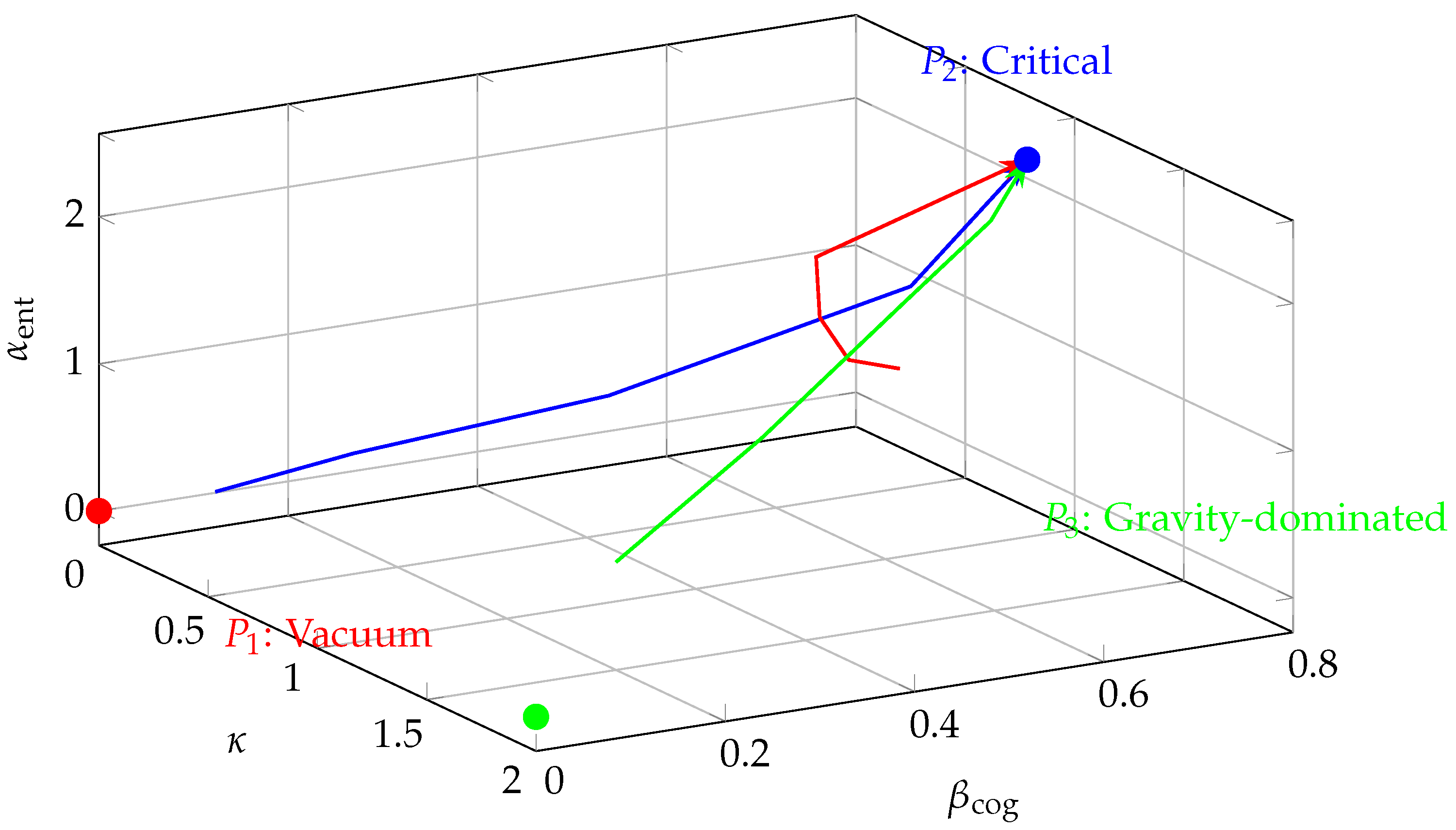
Figure 2.
Renormalization group flow in the coupling space . Trajectories converge toward the coherence attractor manifold .
Figure 2.
Renormalization group flow in the coupling space . Trajectories converge toward the coherence attractor manifold .
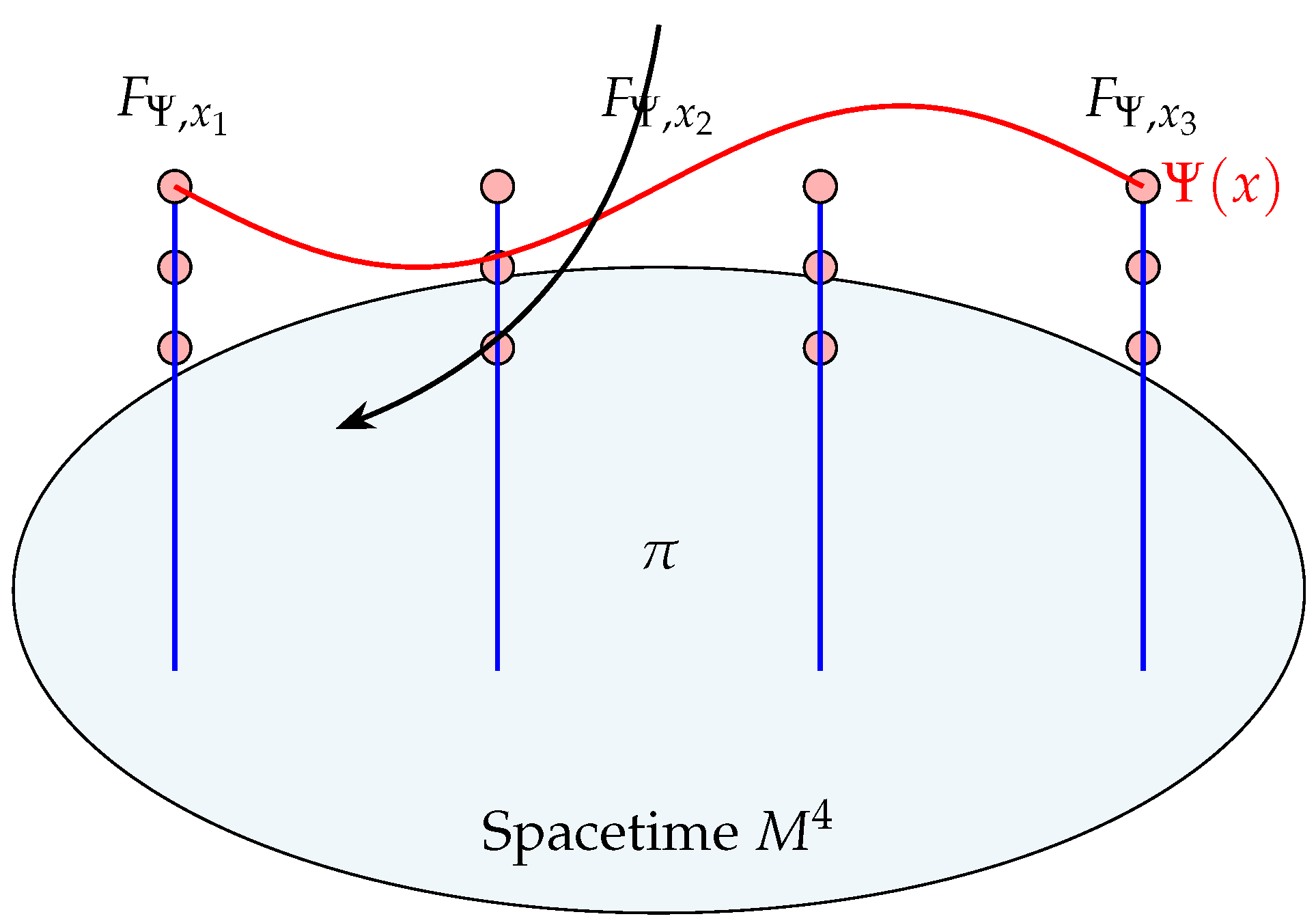
Figure 3.
The consciousness dimension as a fiber bundle over spacetime . Each fiber encodes local coherence topology modulated by the cognitive field .
Figure 3.
The consciousness dimension as a fiber bundle over spacetime . Each fiber encodes local coherence topology modulated by the cognitive field .
7. Discussion and Implications
7.1. Resolution of the Measurement Problem
The CUE framework provides a novel resolution to the quantum measurement problem through geometric mechanisms. Rather than invoking consciousness as a non-physical entity that collapses the wavefunction, the framework treats consciousness as a geometric structure that couples to physical fields through well-defined mathematical relationships.
The consciousness dimension acts as a "geometric witness" to quantum measurements, with its fiber curvature modulating collapse probabilities. This provides a deterministic underpinning to apparent quantum randomness while preserving the empirical success of quantum mechanics.
7.2. Relationship to Existing Theories
The CUE framework maintains compatibility with established physics in appropriate limits:
When , the framework reduces to standard general relativity plus matter fields
When , consciousness effects decouple and standard quantum mechanics is recovered
The holographic sector naturally incorporates AdS/CFT correspondence (
Maldacena, 1998)
7.3. Philosophical Implications
The framework suggests a form of geometric panpsychism where consciousness is fundamental but emerges through the same geometric processes that generate spacetime and matter. This addresses the combination problem in panpsychism by providing a mathematical framework for consciousness aggregation through fiber bundle topology.
8. Conclusions and Future Directions
The Collective Unified Equation framework presents a mathematically rigorous approach to unifying quantum mechanics, general relativity, and consciousness. Key achievements include:
A complete action functional that unifies all fundamental interactions including consciousness
Geometric resolution of the quantum measurement problem
Testable predictions across multiple domains of physics
Mathematical consistency through renormalization group methods
Future research directions include:
Detailed computation of loop corrections and renormalization constants
Numerical simulations of the coupled field equations
Experimental tests of the predicted quantum optical effects
Cosmological parameter fitting using observational data
Extension to incorporate quantum gravity effects in the deep Planck regime
The framework opens new avenues for understanding the fundamental nature of reality by treating consciousness not as an emergent property of complex matter arrangements, but as a geometric structure fundamental to the fabric of spacetime itself.
Acknowledgments
The author thanks the theoretical physics community for ongoing discussions about consciousness and quantum mechanics.
References
- Bekenstein, J. D. 1973. Black holes and entropy. Physical Review D 7, 8: 2333–2346. [Google Scholar] [CrossRef]
- Hameroff, S., and R. Penrose. 1996. Orchestrated reduction of quantum coherence in brain microtubules: A model for consciousness. Mathematics and Computers in Simulation 40, 3-4: 453–480. [Google Scholar] [CrossRef]
- Hawking, S. W. 1975. Particle creation by black holes. Communications in Mathematical Physics 43, 3: 199–220. [Google Scholar] [CrossRef]
- Maldacena, J. 1998. The large N limit of superconformal field theories and supergravity. Advances in Theoretical and Mathematical Physics 2, 2: 231–252. [Google Scholar] [CrossRef]
- Nielsen, M. A., and I. L. Chuang. 2010. Quantum Computation and Quantum Information. Cambridge University Press: Cambridge. [Google Scholar]
- Penrose, R. 1989. The Emperor’s New Mind. Oxford University Press: Oxford. [Google Scholar]
- Penrose, R. 2004. The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape, London. [Google Scholar]
- Polchinski, J. 1992. Effective field theory and the Fermi surface. In Proceedings of TASI 1992; pp. 235–274. [Google Scholar]
- Susskind, L. 1995. The world as a hologram. Journal of Mathematical Physics 36, 11: 6377–6396. [Google Scholar] [CrossRef]
- Verlinde, E. 2011. On the origin of gravity and the laws of Newton. Journal of High Energy Physics 2011, 4: 29. [Google Scholar] [CrossRef]
- von Neumann, J. 1955. Mathematical Foundations of Quantum Mechanics. Princeton University Press: Princeton. [Google Scholar]
- Weinberg, S. 1989. The cosmological constant problem. Reviews of Modern Physics 61, 1: 1–23. [Google Scholar] [CrossRef]
- Wheeler, J. A. 1962. Geometrodynamics. New York: Academic Press. [Google Scholar]
- Wigner, E. P. 1961. Remarks on the mind-body question. In The Scientist Speculates. London: Heinemann, pp. 284–302. [Google Scholar]
- Wilson, K. G. 1974. The renormalization group: Critical phenomena and the Kondo problem. Reviews of Modern Physics 47, 4: 773–840. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).