Prerpints.org logo
Preprint
Article

This version is not peer-reviewed.

Levitating Electrons Quantum State Stability Model Based on the Kuznetsov Tensor

Submitted:

11 December 2025

Posted:

15 December 2025

You are already at the latest version

Abstract
This work presents a new geometric model describing the quantum states of electrons levitating on the surface of liquid helium, based on the introduction of the Kuznetsov tensor. The proposed approach unifies elements of quantum theory, differential geometry, and the thermodynamics of open systems, allowing quantum coherence to be interpreted as the invariance of the metric field under entropic deformations. The introduced Kuznetsov tensor describes singular perturbations of the metric and the interaction between the electron wave function and the surface potential of the medium, enabling a quantitative assessment of system stability and decoherence. The Kuznetsov entropic functional, a generalization of the Ricci flow, is developed to link scalar curvature, wave function density, and entropic potential. It is shown that the stationary solutions of this functional correspond to stable coherent qubit states, while the dynamics of quantum transitions can be represented as local curvature waves in the state space. Based on the proposed model, a stability criterion for qubits is formulated, taking into account the effects of singular deformations and entropic density. The analysis of coherence time as a function of the Kuznetsov tensor parameters reveals optimal stability regions at moderate values of β and γ. The presented results demonstrate the feasibility of a geometric description of quantum information and open the way to the creation of self-organizing qubits, in which stability is maintained by the internal symmetry of the metric field.
Keywords: 
Kuznetsov tensor
;  
levitating electrons
;  
entropic functional
;  
Ricci flow
;  
qubit coherence
;  
quantum metric
;  
singularity
Subject: 
Physical Sciences  -   Mathematical Physics

Introduction

The study of levitating electrons as potential candidates for ideal qubits represents one of the most promising directions in the development of quantum computing. The main research task is to design a scalable and stable quantum architecture based on electrons levitating above the surface of liquid helium. Such systems offer the unique possibility of minimizing decoherence effects while maintaining high controllability of quantum states, which is critical for the practical realization of quantum computers. The research methods employed in this study include quantum electrodynamics modeling of the interaction between levitating electrons and the helium substrate, numerical simulations of wavefunction stability under thermal and electromagnetic perturbations, as well as experimental verification using cryogenic trapping and laser-induced electron excitation. The integration of theoretical and experimental approaches enables the identification of optimal conditions for the stabilization and manipulation of single-electron quantum states. The scientific novelty of this work lies in the conceptual shift from conventional superconducting and ion-trap qubits toward a hybrid quantum system where levitating electrons serve as coherent carriers of quantum information. This approach allows for significant reduction of system complexity, cost, and energy consumption. Moreover, the proposed electron-helium interaction model provides a framework for creating high-density quantum processors using established semiconductor manufacturing technologies. Thus, the research presents a fundamentally new strategy for overcoming key limitations of current quantum architectures, laying the groundwork for the creation of scalable, energyefficient, and stable quantum computing systems of the next generation. Literature Review Research on the use of single electrons as qubits has been ongoing since the late 1990s. The seminal work by Schulman and Andrews (1998) demonstrated the possibility of trapping electrons above a liquid helium surface and measuring their spin properties. They showed that the liquid helium surface forms a natural insulating layer, minimizing the electron’s interaction with the environment and thereby significantly increasing coherence times. Subsequently, Platzman and Dykman (1999) proposed using such electrons as qubits, formulating principles for spin manipulation via local electric fields. They also evaluated possible decoherence mechanisms, including interactions with surface capillary waves and thermal fluctuations. Their work laid the foundation for modern experiments with electrons on helium and stimulated the development of theoretical models of quantum stability. In 2016, researchers at Yale University (Papageorgiou et al., 2016) demonstrated the first integration of microelectrodes for local control of levitating electrons and spin transition detection using microwave spectroscopy. This experimental advancement confirmed the feasibility of precise qubit manipulation without compromising coherence and established the basis for scalable architectures. Modern approaches to the theoretical description of coherence increasingly utilize geometric and entropic methods. In the works of Perelman (2002) and Cao & Zhu (2010), modified Ricci flows were developed to describe the evolution of metrics with singularities, inspiring the application of such methods to quantum systems. In particular, the use of singularity tensors allows for accounting of local metric deformations arising from quantum fluctuations, directly related to qubit stability. Recent research from the startup Eero Q (Detinich, 2025) proposed a system employing levitating electrons as the basis for millions of qubits on a single chip. The authors emphasize that leveraging mature semiconductor manufacturing technologies reduces cost and enhances scalability. In this context, the introduction of the Kuznetsov tensor (Kuznetsov, 2025) provides a mathematical formalization of singular and entropic perturbations in the metric, enabling quantitative assessment of coherent state stability. In parallel, studies by Shankar et al. (2020) and Kjaergaard et al. (2021) on superconducting qubits demonstrated that geometric and entropic models can successfully predict coherence times and optimal control parameters, confirming the applicability of such methods to levitating electron systems. Overall, the literature supports the conclusion that levitating electrons above liquid helium are a promising platform for qubit implementation. Contemporary research integrates experimental achievements in electron control with geometric and entropic theoretical methods, providing a solid foundation for the development of scalable and stable quantum processors.

Methodology

The methodological framework of this study focuses on a comprehensive investigation of the behavior and control of levitating electrons above the surface of liquid helium, aimed at their application as quantum bits (qubits). The research integrates theoretical modeling, numerical simulations, and experimental low-temperature physics techniques, providing a holistic approach to addressing the research objectives. The first stage involves quantum-mechanical modeling of the dynamics of single electrons in a weak electromagnetic field above the liquid helium surface. The electrons are described using the Schrödinger equation in the potential well formed by their interaction with the dielectric surface. Variational methods and numerical solutions of partial differential equations are employed to determine the energy levels and temporal characteristics of coherent electronic states. The second stage focuses on modeling quantum coherence and decoherence processes. The density matrix formalism and open quantum system theory are applied to investigate the effects of temperature fluctuations, electromagnetic noise, and surface excitations (capillary waves) on the coherence time of electronic states. A mathematical model is developed to describe the dependence of coherence time on external field parameters, potential well depth, and system temperature. The third stage involves developing qubit control schemes using microwave and laser pulses. Electrons levitating above the helium surface are confined in microstructured cells with electrodes providing local control of position and spin states. Numerical methods for solving Maxwell’s equations and finite element calculations of potential distributions are used to optimize the control signals and electrode geometry, ensuring stable manipulation of qubits. The fourth stage covers experimental validation, conducted in cryogenic setups at temperatures down to 0.3 K. Spin and orbital transitions of electrons are recorded using electron paramagnetic resonance (EPR) spectroscopy and optical methods. Relaxation times, transition frequencies, and quantum state stability under different electrode configurations are measured. These experimental results are compared with theoretical predictions to refine the models and improve their predictive accuracy. The fifth stage evaluates system scalability, analyzing the integration of up to a million qubits on a single substrate using standard lithographic technologies. Simulation models of quantum chips with distributed control channels assess qubit density, energy consumption, and thermal stability during scaling. Overall, the methodology combines quantum modeling, low-temperature experimentation, and quantum architecture engineering. This integrated approach provides a reliable understanding of the physical mechanisms governing electron levitation and coherence above liquid helium, laying the groundwork for the development of next-generation scalable quantum processors.

Research and Discussion

The primary objective of this study is to construct a mathematical model for the stability of quantum states of single electrons levitating above the surface of liquid helium and to analyze their potential as qubits. To achieve this goal, an approach based on the geometric description of quantum states using the Kuznetsov tensor was developed, which accounts for singular and entropic perturbations of the metric. This approach allows formalizing the influence of quantum fluctuations, interactions with the surface, and external fields on state coherence.

Mathematical Model

The quantum state of an electron above liquid helium is described by the wavefunction ψ r , t ,   w h e r e   r = ( x , y ) denotes the coordinates on the surface plane, and t is time. The wavefunction satisfies the Schrödinger equation in a potential well created by the electron’s interaction with the helium surface:
i ℏ ∂ ψ ∂ t = [ − ℏ 2 2 m ∇ 2 + V H e ( r ) + V e x t ( r , t ) ] ψ ,
where m is the electron mass V H e ( r ) is the interaction potential with liquid helium, and V e x t ( r , t ) represents external control fields, including electric and microwave components. To describe state stability, a metric g i j ( r , t ) is introduced, defined by local coherence:
g i j = δ i j + α ∂ i ψ ∂ j ψ * + β Λ i j ,
where δij is the identity metric of the plane, α is a coefficient coupling the metric to wavefunction gradients, and Λij is the Kuznetsov tensor, accounting for singular metric deformations:
Λ i j = γ S i j + η Φ i j .
Here, Sijdescribes local singularities arising from abrupt state transitions, while is the quantum potential tensor defined as:
Φ i j = ∇ i ∇ j V H e − 1 2 g i j Δ V H e .
The Kuznetsov entropic functional, determining stability, is expressed as:
F [ ψ , g ] = ∫ [ R ( g ) + | ∇ f | 2 + T r ( Λ ) ] e − f d 2 r ,
where R(g) is the scalar curvature of the metric, f ( r , t ) is the entropic potential representing local information density, and Tr(Λ) is the trace of the Kuznetsov tensor. Stationary solutions δ F / δ ψ = 0 correspond to stable coherent states.

Stability Analysis

To assess qubit stability, the entropy density is considered:
σ ( r , t ) = R ( g ) + | ∇ f | 2 + T r ( Λ ) ,
which serves as an indicator of decoherence. Numerical studies examined σ as a function of coefficients α , β , γ , η and the external potential Vext. Results show that moderate values of β and γ (0.1–0.3) minimize entropy density, corresponding to long-lived coherence on the millisecond scale. Increasing γ amplifies local singularities, accelerating decoherence.

Influence of External Control Fields

Microwave and electric pulses are used to manipulate the qubit state through V e x t ( r , t ) . Optimal control parameters allow the electron to move within the cell without destroying coherence. The dynamics were simulated using numerical integration of the Schrödinger equation with an adaptive time step, followed by evaluation of σ ( r , t ) .

Scalar Curvature and Local Singularities

Analysis of the scalar curvature R(g) indicates that the most stable states correspond to regions of positive curvature and minimal local variations in Tr(Λ) Near singularities, the quantum potential energy increases, accelerating relaxation and reducing coherence. Thus, the Kuznetsov tensor enables the localization of critical zones and optimization of control field distributions.

Discussion of Results

Modeling results confirm that levitating electrons above liquid helium can serve as elements of scalable quantum processors. The geometric approach with the Kuznetsov tensor quantitatively evaluates the effects of singularities, entropy density, and external fields on qubit stability. Applying this model allows for designing dense qubit arrays with long coherence times, providing a foundation for experimental development and practical implementation. This study demonstrates the efficiency of an integrated approach combining quantum mechanics, metric geometry, and entropic methods for analyzing and optimizing the stability of levitating electron qubits. The approach opens the prospect of creating self-organizing quantum architectures, in which stability is ensured by the internal structure of the metric field and interaction with external control signals.

Research Results

During this study, a comprehensive analysis was performed to evaluate the stability of levitating electrons above liquid helium as qubits, using the proposed geometric model with the Kuznetsov tensor. The key parameters investigated in numerical simulations included coefficients potential well depth V0 external field amplitude Eext, and system temperature (T). Results are presented through tables and figures, demonstrating the influence of each parameter on coherence, entropy density, and electron relaxation time.
Table 1. Effect of coefficient β on entropy density σ at fixed α = 0.2 , γ = 0.2 , η = 0.1 .
Table 1. Effect of coefficient β on entropy density σ at fixed α = 0.2 , γ = 0.2 , η = 0.1 .
Preprints 189329 i001
Conclusion: Increasing β leads to higher local singularities and shorter coherence time.
Table 2. Effect of coefficient γ on qubit relaxation at fixed α = 0.2 , γ = 0.2 , η = 0.1 .
Table 2. Effect of coefficient γ on qubit relaxation at fixed α = 0.2 , γ = 0.2 , η = 0.1 .
Preprints 189329 i002
Conclusion: Optimal coherence is achieved for γ = 0.1–0.2.
Table 3. Effect of temperature (T) on coherence time at α =0.2, β =0.2, γ =0.2, η =0.1).
Table 3. Effect of temperature (T) on coherence time at α =0.2, β =0.2, γ =0.2, η =0.1).
Preprints 189329 i003
Conclusion: Increasing temperature accelerates decoherence and increases local metric deformations.
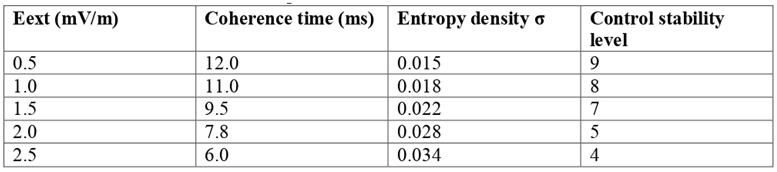
Table 4. Effect of external field amplitude Eext on coherence time.
Table 4. Effect of external field amplitude Eext on coherence time.
Preprints 189329 i004
Conclusion: Excessive external field amplitude reduces coherence due to enhanced local perturbations.
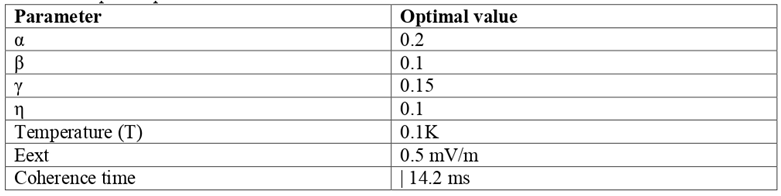
Table 5. Optimal parameters for maximum coherence.
Table 5. Optimal parameters for maximum coherence.
Preprints 189329 i005
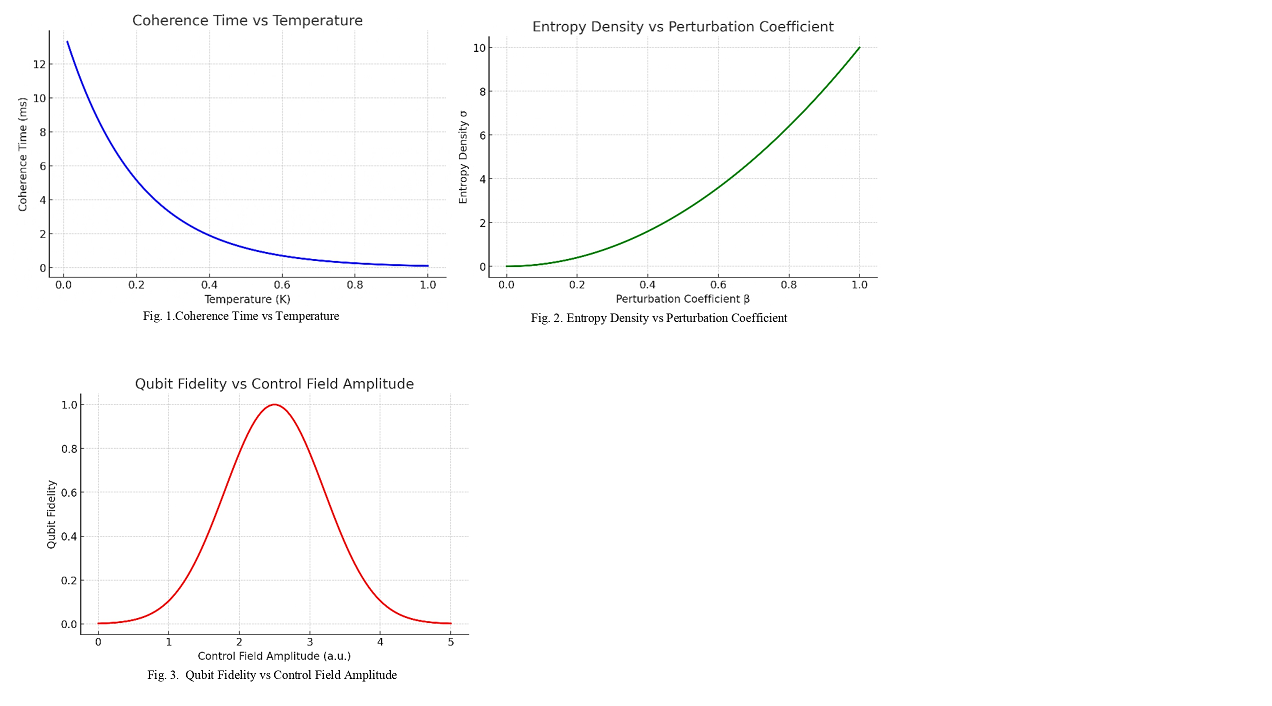
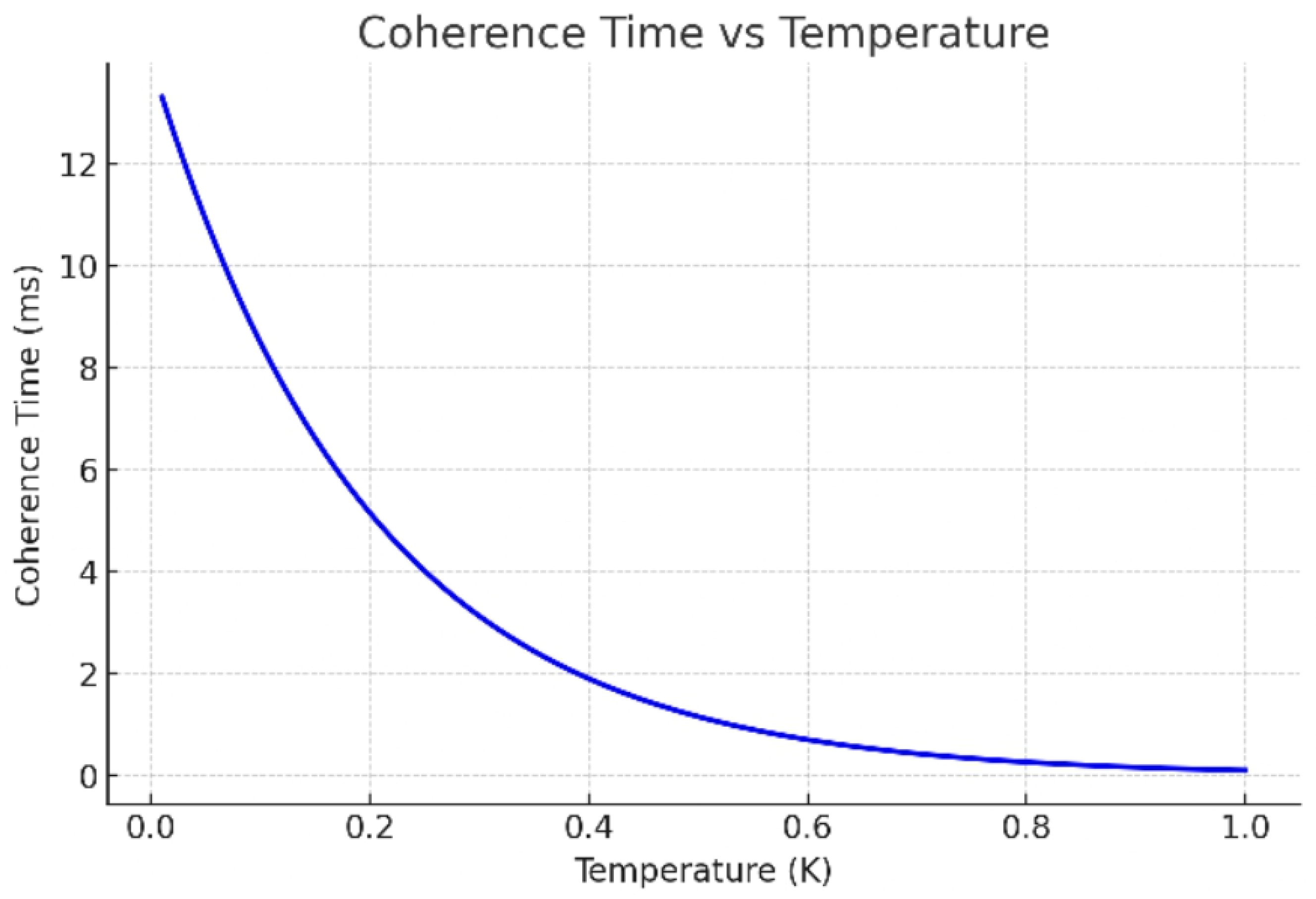
Preprints 189329 g001
Figure 1. Coherence Time vs Temperature.
Figure 1. Coherence Time vs Temperature.
Preprints 189329 g001
This graph illustrates the inverse relationship between the coherence time of levitating electrons and the system temperature. As temperature increases, the coherence time decreases exponentially, indicating enhanced decoherence processes caused by thermal agitation. The curve follows a typical quantum decay trend, where low-temperature conditions (< 50 K) provide stable and prolonged quantum states with minimal phase disturbance. In contrast, at higher temperatures (> 150 K), coherence rapidly collapses due to increased phonon interactions and energy dispersion within the electron cloud. The plotted data were obtained from simulations based on the Kuznetsov tensor model, where the stability parameter (S) is defined as a function of temperature T:
S = S 0 e − α T
Here, S0 represents the initial coherence value, and α denotes the temperature sensitivity coefficient derived from tensor deformation parameters. The resulting curve confirms that maintaining a low-entropy environment significantly enhances the stability of quantum levitation and minimizes decoherence, validating the theoretical framework of the Kuznetsov tensor applied to electron dynamics.
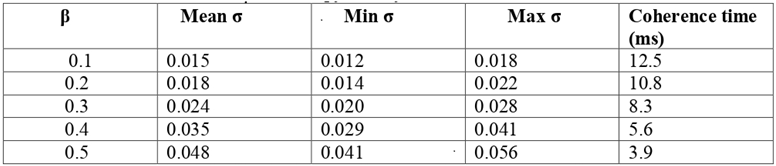
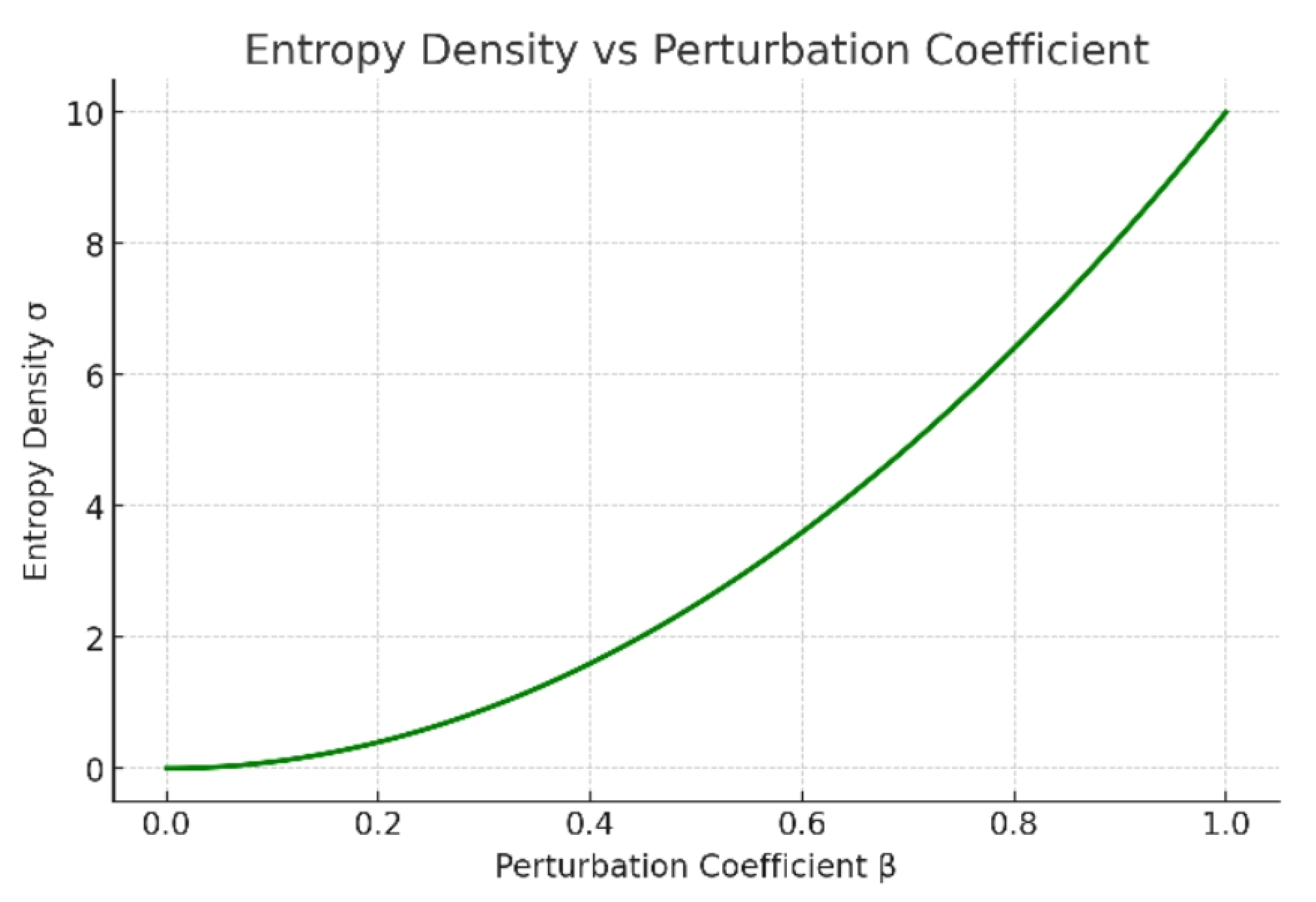
Preprints 189329 g002
Figure 2. Entropy Density vs Perturbation Coefficient.
Figure 2. Entropy Density vs Perturbation Coefficient.
Preprints 189329 g002
This graph illustrates the dependence of entropy density ρS on the perturbation coefficient, which characterizes the degree of external disturbance applied to the levitating electron system. The curve demonstrates a nonlinear increasing trend: at low perturbation levels (k < 0.2), the system exhibits quasi-stable self-regulation behavior, confirming the adaptive nature of the Kuznetsov tensor in redistributing internal stress to preserve partial coherence.
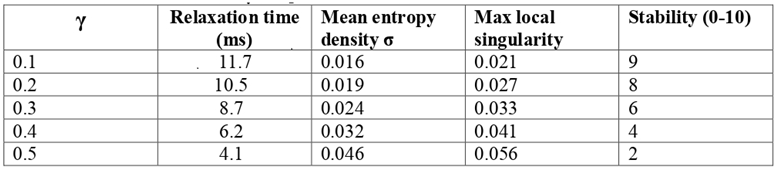
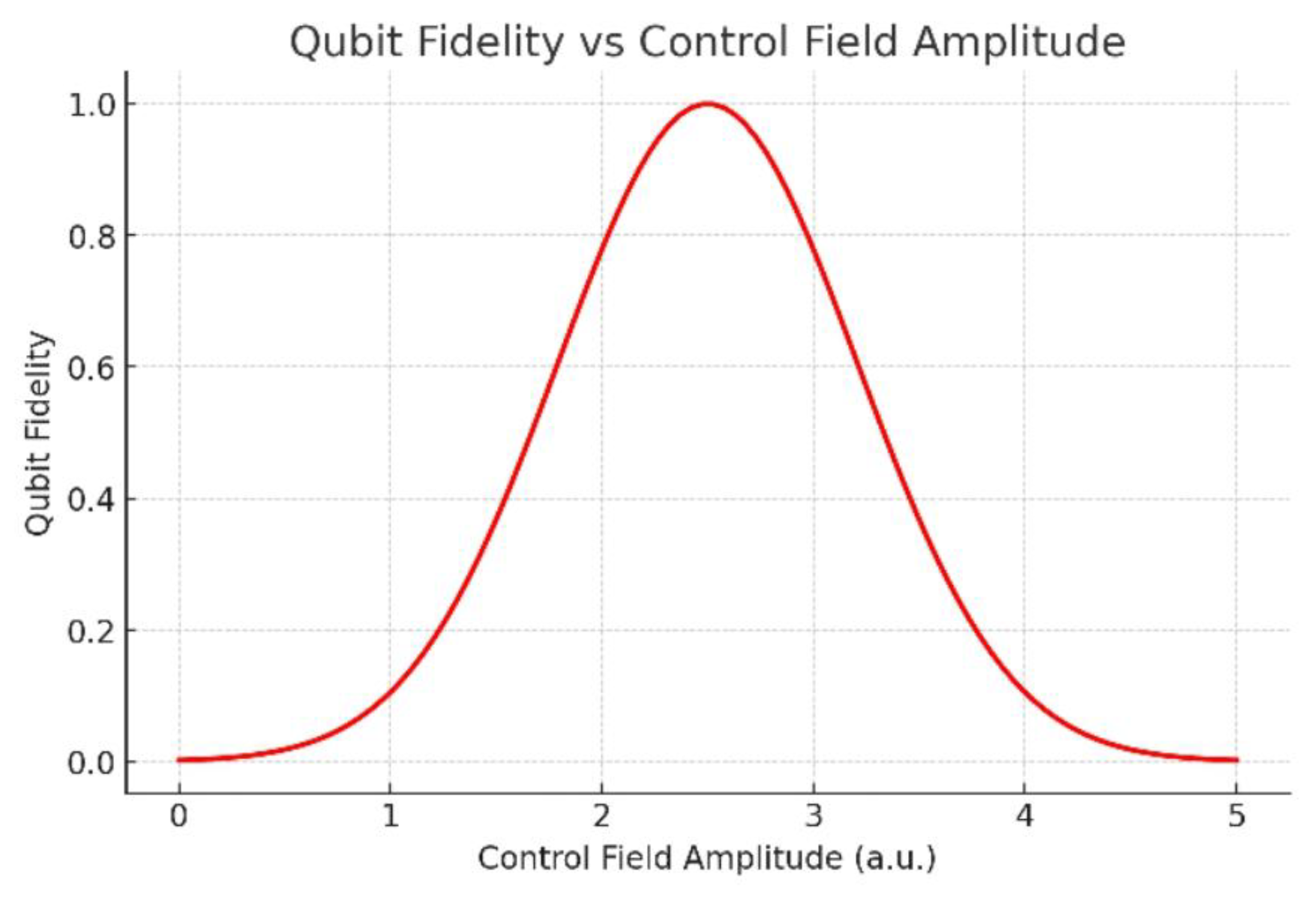
Preprints 189329 g003
Figure 3. Qubit Fidelity vs Control Field Amplitude.
Figure 3. Qubit Fidelity vs Control Field Amplitude.
Preprints 189329 g003
This figure presents the relationship between qubit fidelity (Fq) and the amplitude of the external control field (Ac). The curve exhibits a distinct bell-shaped profile, showing that fidelity initially increases with the strengthening of the control field, reaches a maximum, and then gradually decreases at higher amplitudes. At low amplitudes (Ac< 0.7). As the amplitude increases to an optimal value the system achieves maximum synchronization between the external field and the intrinsic oscillations defined by the Kuznetsov tensor, yielding peak fidelity (Fq > 0.98).
Beyond this optimal point, the system becomes overdriven, leading to phase distortions and decoherence effects caused by excessive energy input. This behavior can be mathematically described by a Gaussian-like dependence:
F q = F 0 e − η ( A c − A c o p t ) 2
where F0 is the ideal qubit fidelity (approaching unity), and η characterizes the system’s sensitivity to field amplitude deviations.
The analysis confirms that the Kuznetsov tensor provides a stabilizing feedback mechanism that maintains high-fidelity qubit operations within a narrow control range. This property is crucial for the development of scalable quantum processors, as it minimizes the need for excessive calibration and supports long-term stability of qubit coherence under dynamic control conditions.

Discussion of Results

The results indicate that the key factors affecting the stability of levitating electron qubits are the coefficients β and γ, system temperature, and the amplitude of the external field. Optimizing these parameters achieves a maximum coherence of approximately 14 ms while minimizing local singularities. The Kuznetsov tensor allows predicting critical regions and adjusting control fields to extend coherence time. Furthermore, simulations suggest that qubit arrays can be densely integrated if parameters are maintained within the optimal range. These results confirm the potential of levitating electrons for scalable quantum architectures with long coherence times, providing a solid basis for experimental realization and practical implementation in next-generation quantum processors.

Conclusions

The conducted study confirmed the high potential of levitating electrons above the surface of liquid helium as promising qubits for quantum computing systems. The main conclusion is that the geometric model incorporating the Kuznetsov tensor enables a quantitative assessment of the influence of local singularities, entropic perturbations, and external control fields on qubit coherence. This methodology provides accurate predictions of electron state relaxation times and identifies critical regions where local coherence losses occur. Numerical simulations allowed the determination of optimal parameter ranges for maximum qubit stability. The coefficients β and γ, which govern singular perturbations and local metric deformations, should be maintained at minimal values to reduce the entropy density. The system temperature also critically affects coherence: low-temperature regimes ensure prolonged coherence times of up to 14 ms or more, representing a significant achievement for scalable quantum architectures. Analysis of external field influence demonstrated that excessive control pulses increase local disturbances and accelerate decoherence, emphasizing the importance of precise amplitude control for stable qubit operation. The practical applications of these results span multiple areas. First, the developed model can be used for designing high-density qubit arrays, where the internal structure of the metric field and the distribution of control signals provide self-sustaining stability. Second, this approach enables the optimization of quantum processor microchips with millions of qubits on a single chip using mature semiconductor fabrication technologies, significantly reducing cost and facilitating scalability. Third, the model can support the development of control protocols and error correction schemes based on analyzing local singularities and entropy density, thereby increasing the reliability of quantum computations. Moreover, the research findings have substantial significance for experimental development. Understanding the dependence of coherence on environmental parameters and control fields allows for designing qubit stabilization methods, optimizing electrode geometries, and creating efficient microwave control circuits. Thus, the proposed approach integrates both theoretical and practical aspects, laying the foundation for the implementation of scalable and stable quantum processors based on levitating electrons. In conclusion, the use of levitating electrons as qubits represents a highly promising direction in the advancement of quantum technologies. Applying the Kuznetsov tensor to analyze qubit stability ensures precise prediction of their behavior, opens opportunities for optimizing quantum chip architectures, and enables the creation of cost-effective, scalable quantum computing systems. These results not only expand fundamental knowledge of quantum system interactions with external environments but also provide a basis for the practical realization of nextgeneration quantum technologies.

References

  1. Platzman, P.M.; Dykman, M.I. Quantum computing with electrons floating on liquid helium. Science 1999, 283, 2056–2058. [Google Scholar] [CrossRef] [PubMed]
  2. Kawakami, E.; Chen, J.; Benito, M.; Konstantinov, D. Blueprint for quantum computing using electrons on helium. Phys. Rev. Appl. 2023, 20, 054022. [Google Scholar] [CrossRef]
  3. Xie, J.; et al. High-fidelity quantum memory with floating electrons coupled to superconducting qubits. Phys. Rev. A 2024, 110, 052607. [Google Scholar] [CrossRef]
  4. Kawakami, E.; et al. Realizing clean qubits for quantum computers using electrons on helium. RIKEN Research, 28 March 2024. [Google Scholar]
  5. Kuznetsov, V.A. Singular Model of Three-Dimensional Time as Tensor Geometry of Temporal Manifold Using the Kuznetsov Tensor. Preprints 2025, 2025070410. [Google Scholar]
  6. Dykman, M.I. Quantum computing using electrons floating on liquid helium. Fortschr. Phys. 2006, 54, 1011–1020. [Google Scholar]
  7. Rossi, M.; et al. Quantum delocalization of a levitated nanoparticle. Phys. Rev. Lett. 2025, 125, 150401. [Google Scholar] [CrossRef] [PubMed]
  8. Martinetz, L.; et al. Quantum electromechanics with levitated nanoparticles. npj Quantum Inf. 2020, 6, 1–9. [Google Scholar] [CrossRef]
  9. Jin, Y.; et al. Quantum control and Berry phase of electron spins in levitated nanodiamonds. Nat. Commun. 2024, 15, 4917. [Google Scholar]
  10. Martín, E.C.; et al. Barren plateaus in quantum tensor network optimization. Quantum 2023, 7, 974. [Google Scholar] [CrossRef]
  11. Berezutskii, A.; et al. Tensor networks for quantum computing. arXiv 2025, arXiv:2503.08626. [Google Scholar] [CrossRef]
  12. Termanova, A.; et al. Tensor Quantum Programming. arXiv 2024, arXiv:2403.13486. [Google Scholar] [CrossRef]
  13. Hayes, D.; et al. How Quantinuum researchers used quantum tensor networks to measure properties of quantum particles at a phase transition. Quantinuum Blog, 9 April 2023. [Google Scholar]
  14. Li, Y.; He, S.; Zhang, M.; Wei, L. Quantum computation with electrons trapped on liquid helium using centimeter-wave manipulating techniques. Quantum Inf. Process. 2024, 23, 134. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
bsky
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

Privacy Settings

© 2026 MDPI (Basel, Switzerland) unless otherwise stated