Sextuple-Q Spin States in Centrosymmetric Hexagonal Magnets

1. Introduction

Multiple-Q magnetic states, characterized by the superposition of spin modulations with several symmetry-related ordering wave vectors, have attracted considerable attention as a fertile platform for emergent spin textures and topological phenomena [1,2,3,4,5,6,7,8,9,10,11]. In particular, the interference among distinct magnetic modulations can generate noncoplanar spin textures with finite scalar spin chirality, which act as emergent magnetic fields for itinerant electrons and give rise to unconventional transport phenomena such as the topological Hall effect [12,13,14,15,16,17,18,19] and the topological Nernst effect [20,21,22,23,24]. The stabilization of such nontrivial spin configurations has been extensively explored in both localized and itinerant magnets [25,26,27,28], where competing exchange interactions [29,30,31,32,33], magnetic anisotropies [34,35,36,37,38,39,40,41], sublattice-dependent couplings [42,43], and higher-order spin interactions [44,45,46,47,48,49,50] play essential roles in lifting degeneracies among single-Q states with symmery-related wave vectors.

Consequently, a wide variety of multiple-Q magnetic structures have been identified across diverse lattice geometries. Noncoplanar triple-Q orderings have been reported in two-dimensional hexagonal systems [51,52,53,54,55,56,57,58,59,60,61] and in three-dimensional cubic systems [62,63,64,65,66,67], where geometrical frustration and competing interactions stabilize complex noncollinear and noncoplanar spin textures. Moreover, since the discovery of the skyrmion crystal (SkX) phase in MnSi [68], research on multiple-Q magnetic states has rapidly expanded, bridging theoretical and experimental investigations [25,45,69,70,71,72,73,74,75,76,77,78]. The SkX discovery provided a real-space realization of a topological spin texture and stimulated intensive studies on multiple-Q magnetism.

In centrosymmetric systems, the absence of Dzyaloshinskii–Moriya interaction [79,80] necessitates alternative stabilization mechanisms for multiple-Q states. Previous theoretical studies have revealed that the coupling among spin density waves at different wave vectors, arising from biquadratic and higher-order spin interactions, can naturally stabilize triple-Q skyrmion crystal phases even in centrosymmetric magnets [27]. These interactions often emerge as effective higher-order terms in itinerant electron systems, where conduction electrons mediate multiple spin couplings via the Fermi surface topology and nesting geometry [81]. In frustrated localized spin systems, similar multi-spin couplings can also arise through higher-order perturbations of Heisenberg exchange interactions [82,83,84], leading to similar noncoplanar orderings.

Experimentally, a variety of multiple-Q spin textures have been observed in hexagonal and tetragonal magnets. In particular, noncoplanar triple-Q structures have been identified in itinerant hexagonal magnets such as ${\mathrm{Y}}_3$${\mathrm{Co}}_8$${\mathrm{Sn}}_4$ [85], ${\mathrm{Gd}}_2$Pd${\mathrm{Si}}_3$ [86,87,88,89,90,91,92], and ${\mathrm{Gd}}_3$${\mathrm{Ru}}_4$${\mathrm{Al}}_{12}$ [38,93,94,95,96], while noncoplanar double-Q structures have been reported in itinerant tetragonal magnets such as Gd${\mathrm{Ru}}_2$${\mathrm{Si}}_2$ [97,98,99,100]. Furthermore, neutron scattering and Lorentz transmission electron microscopy have revealed that these multiple-Q orderings often form a hierarchical sequence from single-Q to multiple-Q phases as functions of magnetic field, temperature, or magnetic anisotropy. These experimental findings underscore the crucial roles of crystalline symmetry and magnetic interactions in stabilizing complex noncoplanar spin textures.

Despite these advances, the possibility of realizing higher-order multiple-Q instabilities, such as sextuple-Q states associated with sixfold rotational symmetry, has remained unexplored [101]. In hexagonal systems, six ordering wave vectors at general wave-vector points in the Brillouin zone can be connected through sixfold rotational and mirror operations. The interference among the six ordering wave vectors may give rise to new types of magnetic superstructures with the scalar spin chirality degree of freedom. These sextuple-Q condensations represent a natural extension of triple-Q mechanisms and provide a promising route toward understanding hierarchical multiple-Q instabilities in frustrated itinerant magnets.

In this study, we theoretically investigate sextuple-Q spin states in centrosymmetric hexagonal magnets by formulating a minimal spin model that incorporates both bilinear and biquadratic exchange interactions together with Zeeman coupling in an external magnetic field. Using extensive simulated annealing calculations, we construct a comprehensive phase diagram as functions of magnetic field and biquadratic interaction strength, identifying single-Q, double-Q, triple-Q, and sextuple-Q phases, as well as SkX phases with distinct skyrmion numbers. We further analyze the real-space spin configurations, scalar spin chiralities, and spin structure factors to elucidate the microscopic characteristics of each phase. Our results demonstrate that the coupling among multiple ordering wave vectors inherent to sixfold- and mirror-symmetric lattices provides a universal mechanism for realizing sextuple-Q instabilities and complex noncoplanar magnetism in centrosymmetric hexagonal systems.

The remainder of this paper is organized as follows. In Sec. 2, we introduce the spin model and outline the computational methods employed in this study. Section 3 presents the numerical results, including the magnetic phase diagram, real-space spin configurations, scalar spin chiralities, and spin structure factors, which reveal the nature of the single-Q, double-Q, triple-Q, and sextuple-Q phases as well as the SkX phases. Finally, Sec. 4 summarizes our findings and provides perspectives for future studies on multiple-Q magnetism in hexagonal systems.

2. Model and Method

We start from the Kondo lattice model on a two-dimensional triangular lattice, which serves as a prototypical framework for itinerant magnets [102]:

$$\begin{array}{c}\hfill {\mathcal{H}}_{\mathrm{KLM}}=-t\sum _{\langle i,j\rangle ,\sigma }{c}_{i\sigma }^{†}{c}_{j\sigma }+J_{\mathrm{K}}\sum _{i,\sigma ,{\sigma }^{\prime }}{c}_{i\sigma }^{†}{\mathit{\sigma }}_{\sigma {\sigma }^{\prime }}·{\mathit{S}}_i{c}_{i{\sigma }^{\prime }},\end{array}$$

(1)

where $c_{i\sigma }^{†}$ ($c_{i\sigma }$) creates (annihilates) an itinerant electron with spin $\sigma$ at site i, and ${\mathit{S}}_i$ denotes a localized classical spin with $|{\mathit{S}}_i|=1$. The first term represents the nearest-neighbor hopping of itinerant electrons, while the second term describes the on-site exchange interaction between localized spins and itinerant-electron spins with the coupling constant $J_{\mathrm{K}}$. Because the triangular lattice considered here is centrosymmetric, no antisymmetric spin–orbit coupling appears in Eq. (1).

When $J_{\mathrm{K}}$ is much smaller than the electronic bandwidth, integrating out the itinerant electron degrees of freedom yields an effective spin model involving bilinear and higher-order multi-spin interactions [81]. Up to the four-spin term, the effective Hamiltonian can be expressed as

$$\begin{array}{c}\hfill {\mathcal{H}}_{\mathrm{eff}}=-\sum _{\mathit{q}}{J}_{\mathit{q}}{\mathit{S}}_{\mathit{q}}·{\mathit{S}}_{-\mathit{q}}+{\displaystyle \frac{1}{N}}\sum _{\left\{{\mathit{q}}_i\right\}}{K}_{{\mathit{q}}_1,{\mathit{q}}_2,{\mathit{q}}_3,{\mathit{q}}_4}({\mathit{S}}_{{\mathit{q}}_1}·{\mathit{S}}_{{\mathit{q}}_2})({\mathit{S}}_{{\mathit{q}}_3}·{\mathit{S}}_{{\mathit{q}}_4}){\delta }_{{\mathit{q}}_1+{\mathit{q}}_2+{\mathit{q}}_3+{\mathit{q}}_4,l\mathit{G}},\end{array}$$

(2)

where N is the total number of lattice sites, ${\mathit{S}}_{\mathit{q}}$ is the Fourier component of the spin, and $\mathit{G}$ is a reciprocal lattice vector (l is an integer). The first term represents the Ruderman-Kittel-Kasuya-Yosida (RKKY) interaction proportional to $J_{\mathrm{K}}^2$ [103,104,105], while the second term describes effective four-spin couplings proportional to $J_{\mathrm{K}}^4$.

To capture the essential features of multiple-Q instabilities inherent to hexagonal lattices, we simplify Eq. (2) by focusing on six symmetry-related ordering wave vectors $\pm {\mathit{Q}}_{\nu }$ ($\nu =1$–6) connected by sixfold rotational and mirror symmetries in the Brillouin zone, as illustrated in Figure 1; we set ${\mathit{Q}}_1=(\pi /3,\sqrt{3}\pi /18)$, ${\mathit{Q}}_2=(-\pi /4,5\sqrt{3}\pi /36)$, ${\mathit{Q}}_3=(-\pi /12,-7\sqrt{3}\pi /36)$, ${\mathit{Q}}_4=(\pi /3,-\sqrt{3}\pi /18)$, ${\mathit{Q}}_5=(-\pi /12,7\sqrt{3}\pi /36)$, and ${\mathit{Q}}_6=(-\pi /4,-5\sqrt{3}\pi /36)$. Restricting to the dominant bilinear and biquadratic contributions and adding the effect of the magnetic field as the Zeeman coupling, we arrive at a minimal spin model:

$$\begin{array}{c}\hfill \mathcal{H}=-2J\sum _{\nu }{\mathit{S}}_{{\mathit{Q}}_{\nu }}·{\mathit{S}}_{-{\mathit{Q}}_{\nu }}+{\displaystyle \frac{2K}{N}}\sum _{\nu }{({\mathit{S}}_{{\mathit{Q}}_{\nu }}·{\mathit{S}}_{-{\mathit{Q}}_{\nu }})}^2-H\sum _i{S}_i^z,\end{array}$$

(3)

where J and K denote the bilinear and biquadratic coupling constants, respectively, and H represents the magnitude of the external magnetic field. Here, we consider only the biquadratic-type interaction in the four-spin term by supposing that the bare susceptibility shows a peak structure at ${\mathit{Q}}_1$–${\mathit{Q}}_6$ owing to the nesting of the Fermi surfaces [81]. The prefactor 2 in the first and second terms denotes the contribution from $-{\mathit{Q}}_{\nu }$. This model captures the essential momentum-space competition among multiple ordering wave-vector channels that can stabilize single-Q, double-Q, triple-Q, and sextuple-Q spin textures. For example, the effective spin model is used to reproduce the experimental phase diagram of EuPtSi [106,107,108,109], where field-direction sensitive nanometric SkX consisting of triple-Q spin density waves is realized [110].

We explore the ground-state phase diagram of Eq. (3) by performing simulated annealing combined with Monte Carlo sampling based on the standard single-spin-flip Metropolis algorithm. We set the system size consisting of $N=24\times 24$ spins under the periodic boundary conditions. Starting from a high temperature $T_0=1$, the temperature is gradually reduced according to $T_{n+1}=\alpha T_n$ with $\alpha =0.999999$ until a final temperature $T=0.0001$ is reached. At each temperature, ${10}^5$–${10}^6$ Monte Carlo sweeps are performed to ensure thermal equilibration and statistical accuracy.

The real-space spin configurations obtained from these simulations are analyzed via the spin structure factor,

$$\begin{array}{c}\hfill S_s^{\eta }\left(\mathit{q}\right)={\displaystyle \frac{1}{N}}\sum _{i,j}{S}_i^{\eta }{S}_j^{\eta }{e}^{i\mathit{q}·({\mathit{r}}_i-{\mathit{r}}_j)}.\end{array}$$

(4)

The $xy$ component of the spin structure factor is denoted as $S_s^{xy}\left(\mathit{q}\right)=S_s^x\left(\mathit{q}\right)+S_s^y\left(\mathit{q}\right)$ and its total component is denoted as $S_s\left(\mathit{q}\right)=S_s^x\left(\mathit{q}\right)+S_s^y\left(\mathit{q}\right)+S_s^z\left(\mathit{q}\right)$. The square root of the spin structure factor corresponds to the momentum-resolved magnetic moments as $m_{\mathit{q}}=\sqrt{S_s\left(\mathit{q}\right)/N}$. We also calculate the magnetization along the magnetic-field direction, $M^z=(1/N){\sum }_i{S}_i^z$. The scalar spin chirality is calculated as

$$\begin{array}{c}\hfill {\chi }^{\mathrm{sc}}={\displaystyle \frac{1}{N}}\sum _{▵}{\mathit{S}}_j·({\mathit{S}}_k\times {\mathit{S}}_l),\end{array}$$

(5)

where the summation is taken over all elementary triangles with sites j, k, and l in the counterclockwise order. The scalar spin chirality serves as a measure of the topological nature of the spin textures and is directly related to the emergence of the topological Hall effect.

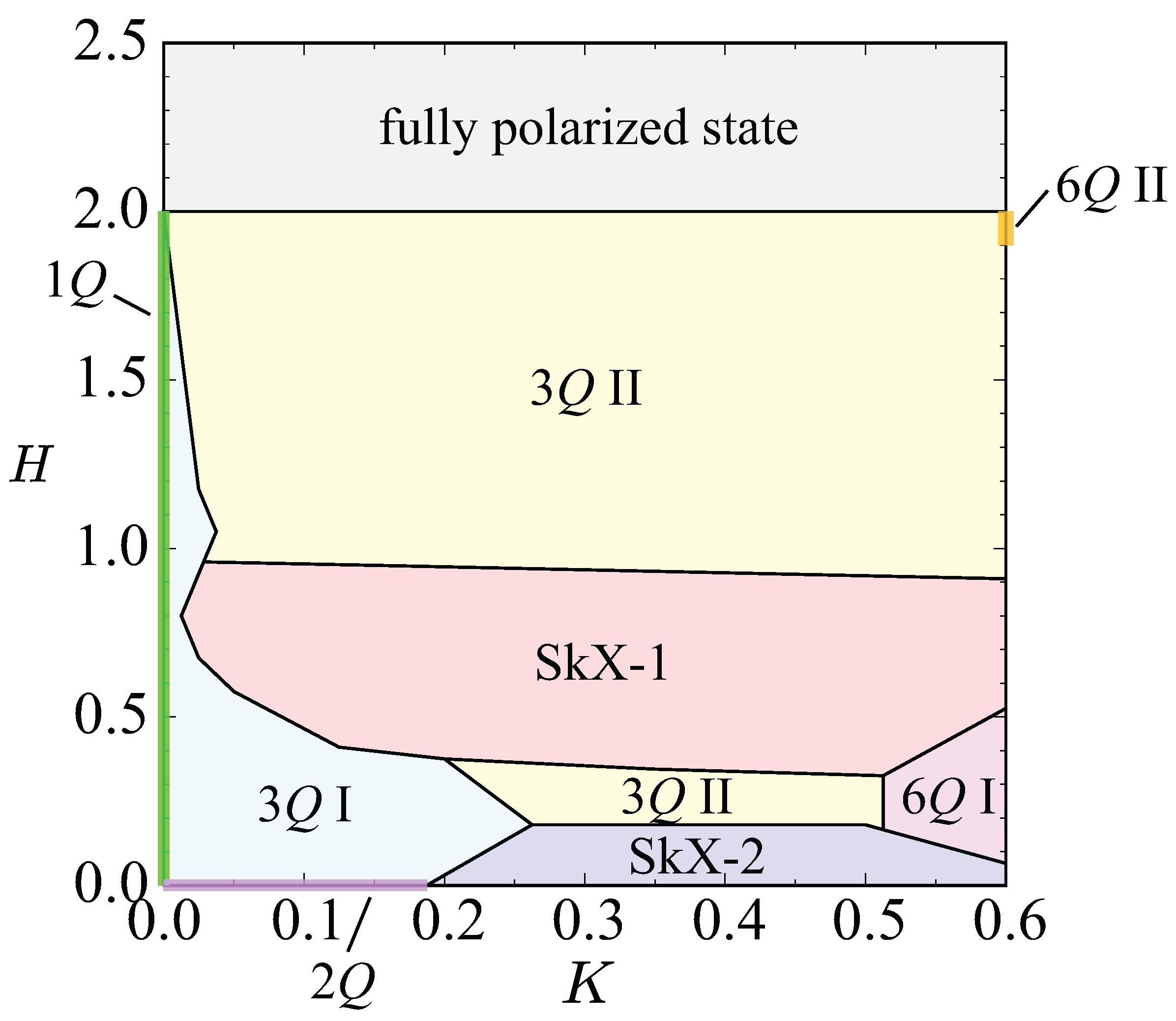
3. Results

Figure 2 summarizes the low-temperature phase diagram on the $(K,H)$ plane for the minimal model in Eq. (3). We identify the following sequence of phases upon increasing H and/or K: single-Q (1Q) state, double-Q (2Q) state, triple-Q I (3Q I) state, skyrmion crystal with $n_{\mathrm{sk}}=1$ (SkX-1), triple-Q II (3Q II) state, skyrmion crystal with $n_{\mathrm{sk}}=2$ (SkX-2), sextuple-Q I (6Q I) state, and sextuple-Q II (6Q II) state. The boundaries are determined from anomalies in the magnetization $M^z$, the scalar spin chirality ${\chi }^{\mathrm{sc}}$, and the Fourier amplitudes $m_{{\mathit{Q}}_{\nu }}$. Below, we discuss each phase in detail by examining the real-space spin textures in Figure 3, local scalar spin chirality textures in Figure 4, and reciprocal-space spin structure factor in Figure 5 and Figure 6.

• Single-Q (1Q) state. At $K=0$, the bilinear exchange interaction alone stabilizes a single-Q spiral configuration. The spin structure factor $S_s\left(\mathit{q}\right)$ exhibits a pair of sharp peaks at one of the symmetry-related ordering wave vectors, reflecting a spiral modulation in a single direction. The corresponding real-space spin texture forms a coplanar spiral without amplitude modulation at zero magnetic field, as shown in Figure 3(a), and thus both local and uniform scalar spin chiralities vanish, ${\chi }^{\mathrm{sc}}=0$. When an external magnetic field is applied, the spiral plane is locked within the $xy$ plane to maximize the Zeeman energy gain. The spins are uniformly canted toward the field direction, acquiring a finite out-of-plane component. This canting introduces a locally nonzero scalar spin chirality owing to the slight noncoplanarity of neighboring spins. However, because the scalar spin chirality alternates for upward and downward triangle plaquettes, its spatial average cancels out, leaving the phase topologically trivial with ${\chi }^{\mathrm{sc}}=0$. The single-Q state forms the basic reference from which multiple-Q states develop with increasing K.
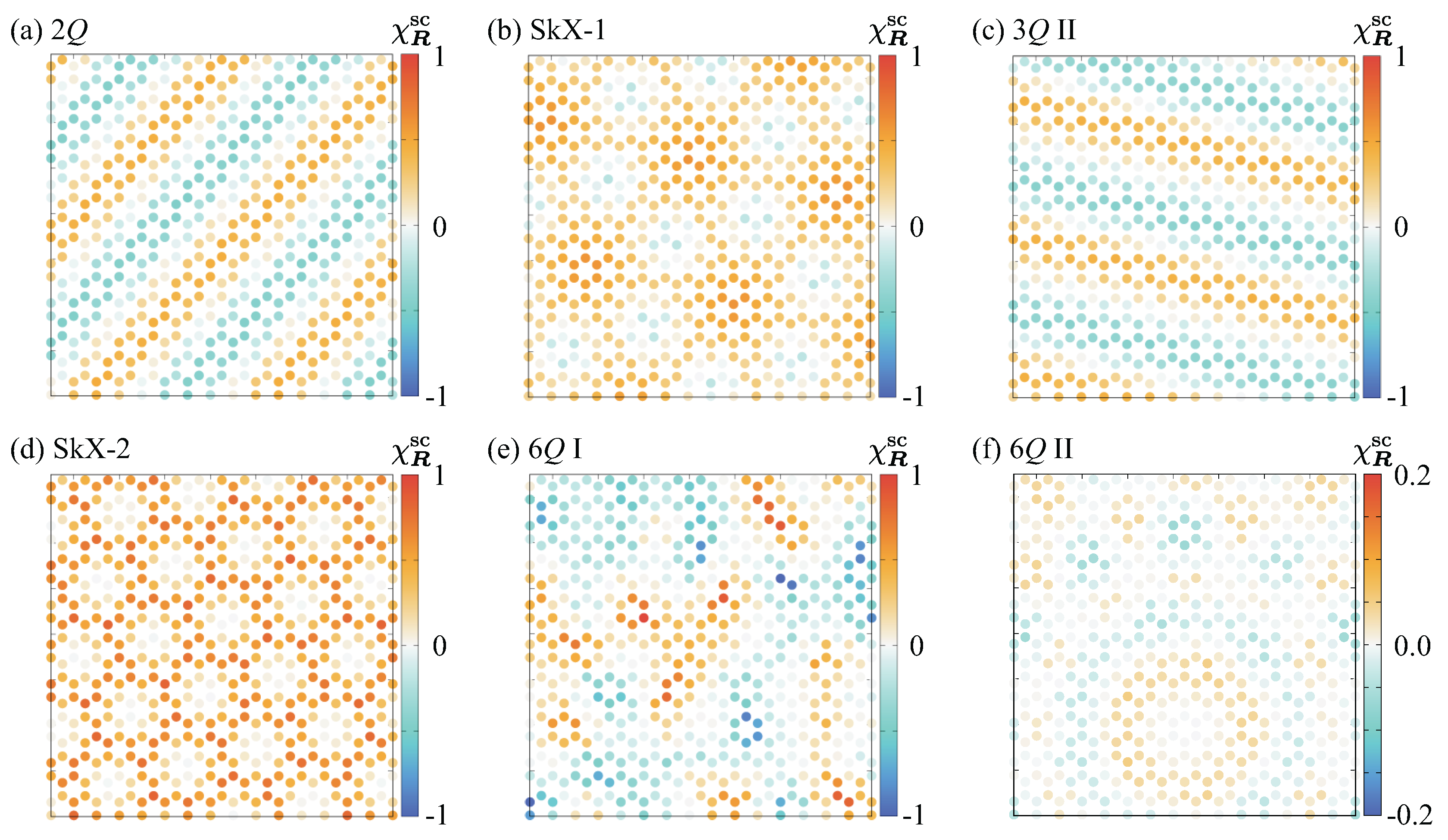
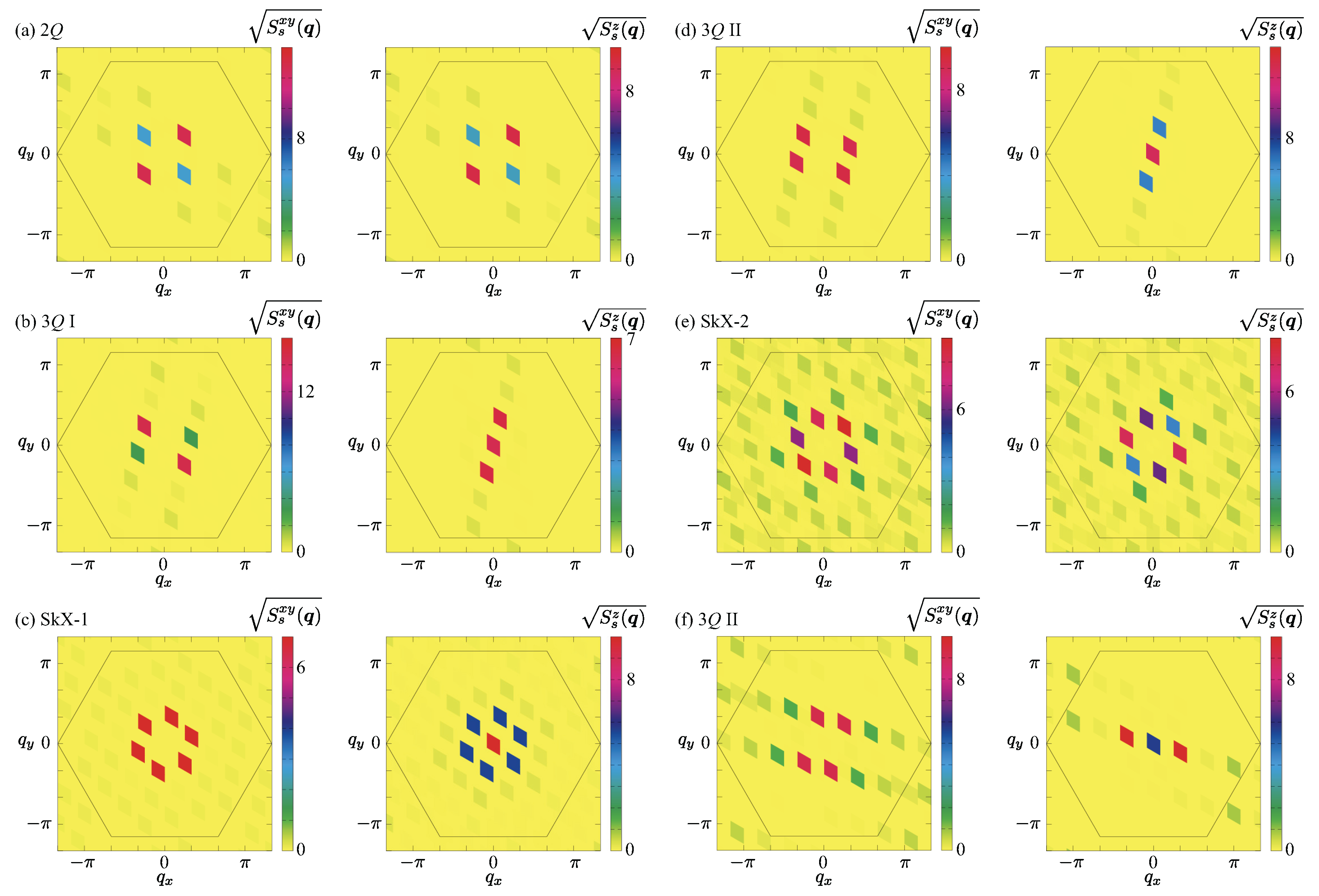
• Double-Q (2Q) state. With the introduction of K at zero magnetic field, interference between two symmetry-related ordering wave vectors becomes energetically favorable, stabilizing a double-Q state [111]. The real-space spin texture in Figure 3(b) exhibits a noncoplanar configuration arising from the superposition of a spiral wave at the primary ordering wave vector and a sinusoidal modulation at the secondary one. This superposition induces a finite local scalar spin chirality whose sign alternates spatially, resulting in no net uniform component (${\chi }^{\mathrm{sc}}=0$), as visualized in the local scalar spin chirality distribution in Figure 4(a). In reciprocal space, the spin structure factor shows four dominant peaks corresponding to two of the six ordering wave vectors, with unequal intensities in both in-plane and out-of-plane components, signaling the emergence of an anisotropic double-Q state, as shown in Figure 5(a). The spin configuration of this state continuously evolves into the single-Q spiral state by suppressing the modulation at the secondary wave vector, i.e., by decreasing K. Thus, the double-Q phase represents a noncoplanar, topologically trivial extension of the single-Q spiral state, serving as an intermediate state preceding the formation of the triple-Q spin configuration at larger K.
• Triple-Q I (3Q I) state. Upon further increasing K in the single-Q state at $H>0$, or increasing H in the double-Q state at $K>0$, the interference among the three symmetry-related ordering wave vectors, ${\mathit{Q}}_1$, ${\mathit{Q}}_2$, and ${\mathit{Q}}_3$ (or ${\mathit{Q}}_4$, ${\mathit{Q}}_5$, and ${\mathit{Q}}_6$), becomes nearly balanced, leading to the stabilization of the triple-Q I phase. In real space, the spin configuration retains a resemblance to that of the double-Q state, exhibiting a noncoplanar texture as shown in Figure 3(c). This noncoplanarity locally induces scalar spin chirality, similar to the double-Q state; however, the alternating sign of the local scalar spin chirality results in a vanishing uniform component (${\chi }^{\mathrm{sc}}=0$), indicating that the state remains topologically trivial. In reciprocal space, the spin structure factor exhibits six dominant peaks corresponding to $\pm {\mathit{Q}}_1$, $\pm {\mathit{Q}}_2$, and $\pm {\mathit{Q}}_3$, as shown in Figure 5(b). The in-plane component shows double-Q-type peaks, whereas the out-of-plane component retains a single-Q feature, reflecting an anisotropic triple-Q superposition. The corresponding Fourier amplitudes satisfy $S_s\left({\mathit{Q}}_1\right)\ne S_s\left({\mathit{Q}}_2\right)\ne S_s\left({\mathit{Q}}_3\right)$, confirming the unequal contributions from the three ordering wave vectors.
• SkX with the skyrmion number of one (SkX-1). Upon further increasing H in the triple-Q I state, the system undergoes a phase transition into the SkX phase with a skyrmion number of one (SkX-1). In real space, the spin texture in Figure 3(d) reveals a well-ordered triangular lattice of skyrmions, each containing a single topological winding within the magnetic unit cell. The in-plane spin components form a vortex-like swirling pattern around the skyrmion cores, while the out-of-plane components alternate between pointing downward at the cores and upward in the interstitial regions. This continuous twisting of spins ensures that all local spin triads acquire finite scalar spin chirality with almost the same sign, resulting in a uniform positive ${\chi }^{\mathrm{sc}}>0$. The local scalar spin chirality distribution shown in Figure 4(b) confirms this feature, exhibiting strongly positive values at the skyrmion cores and only weak residual modulation between them. It is noted that the SkX with the negative scalar spin chirality (skyrmion number) is energetically degenerate with the SkX with the positive one owing to the absence of magnetic anisotropy [112]. The helicity of the skyrmion is also undetermined owing to the spin rotational symmetry of the model [113]. In reciprocal space, the spin structure factor displays a sixfold-symmetric pattern originating from the coherent superposition of the fundamental components at $\pm {\mathit{Q}}_{\nu }$ ($\nu =1$–3), as shown in Figure 5(c). The equal intensities of the six primary peaks reflect the full restoration of threefold rotational symmetry, in contrast to the anisotropic triple-Q I phase.
• Triple-Q II (3Q II) state. The triple-Q II phase emerges upon increasing H from the SkX-1 phase. This state is characterized by triple-Q peaks located at ${\mathit{Q}}_1$, ${\mathit{Q}}_2$, and ${\mathit{Q}}_3$ (or ${\mathit{Q}}_4$, ${\mathit{Q}}_5$, and ${\mathit{Q}}_6$), whose relative amplitudes differ from those in the triple-Q I state. In the triple-Q II phase, the in-plane component of the spin structure factor exhibits equal intensities at the double-Q ordering wave vectors, as shown in Figure 5(d), whereas these intensities are unequal in the triple-Q I state [Figure 5(b)]. Such a subtle rearrangement of the amplitude balance and phase relation results in a real-space spin configuration similar to that of the triple-Q I phase, as illustrated in Figure 3(e), which exhibits a noncoplanar texture. The local scalar spin chirality distribution shown in Figure 4(c) confirms this behavior: the scalar spin chirality alternates in sign across real space, yielding no net uniform component (${\chi }^{\mathrm{sc}}=0$). A similar triple-Q II configuration also appears between the SkX-1 and SkX-2 phases, whose real-space spin arrangement and corresponding spin structure factor are presented in Figure 3(g) and Figure 5(f), respectively.
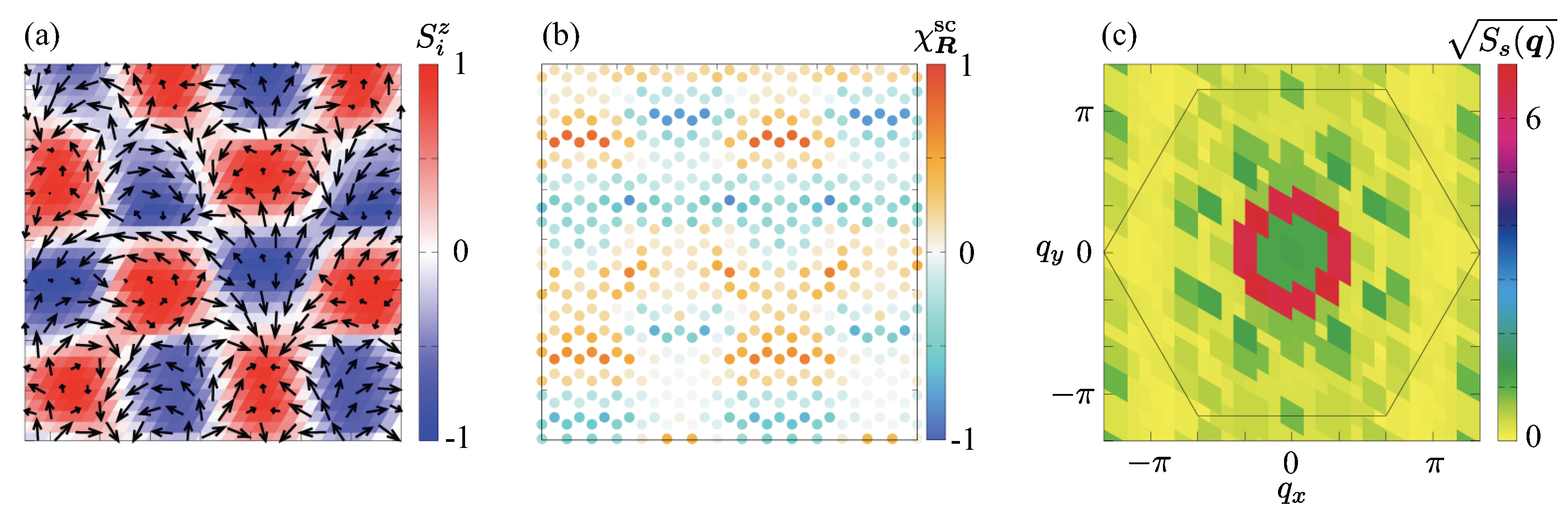
• SkX with the skyrmion number of two (SkX-2). For larger K at zero magnetic field, the system stabilizes another SkX phase with a skyrmion number of two per magnetic unit cell, referred to as SkX-2. This phase arises from the coherent superposition of triple-Q sinusoidal waves at ${\mathit{Q}}_1$, ${\mathit{Q}}_2$, and ${\mathit{Q}}_3$ (or ${\mathit{Q}}_4$, ${\mathit{Q}}_5$, and ${\mathit{Q}}_6$), whose amplitudes are equivalent but whose relative phases are arranged so as to produce a double-winding topological structure within each skyrmion core. The resulting spin configuration in Figure 3(f) exhibits a well-ordered triangular lattice of doubly wound skyrmions. Each skyrmion core undergoes two full rotations of the spin direction, forming a tightly twisted configuration with out-of-plane spin polarization at the core center and nearly in-plane spin alignment in the surrounding region. The in-plane spin components form vortex-like patterns that rotate twice around each core compared with SkX-1, giving rise to a more intricate twisting of the spin texture. The local scalar spin chirality distribution in Figure 4(d) highlights intense positive scalar spin chirality concentrated at the skyrmion cores, consistent with the double-winding nature. Consequently, the uniform scalar spin chirality ${\chi }^{\mathrm{sc}}$ becomes larger than that in SkX-1, reflecting the increased topological charge density. In reciprocal space, the total spin structure factor maintains a sixfold-symmetric pattern at $\pm {\mathit{Q}}_4$, $\pm {\mathit{Q}}_5$, and $\pm {\mathit{Q}}_6$, as shown in Figure 5(e), similar to that of SkX-1. The intensities of the spin structure factors for the in-plane ($xy$) and out-of-plane (z) components appear to differ, but their sums are equivalent owing to the spin rotational symmetry in the absence of the magnetic field. A similar $n_{\mathrm{sk}}=2$ SkX has been reported in both the Kondo lattice model [114,115,116] and the square-lattice spin model [117,118].
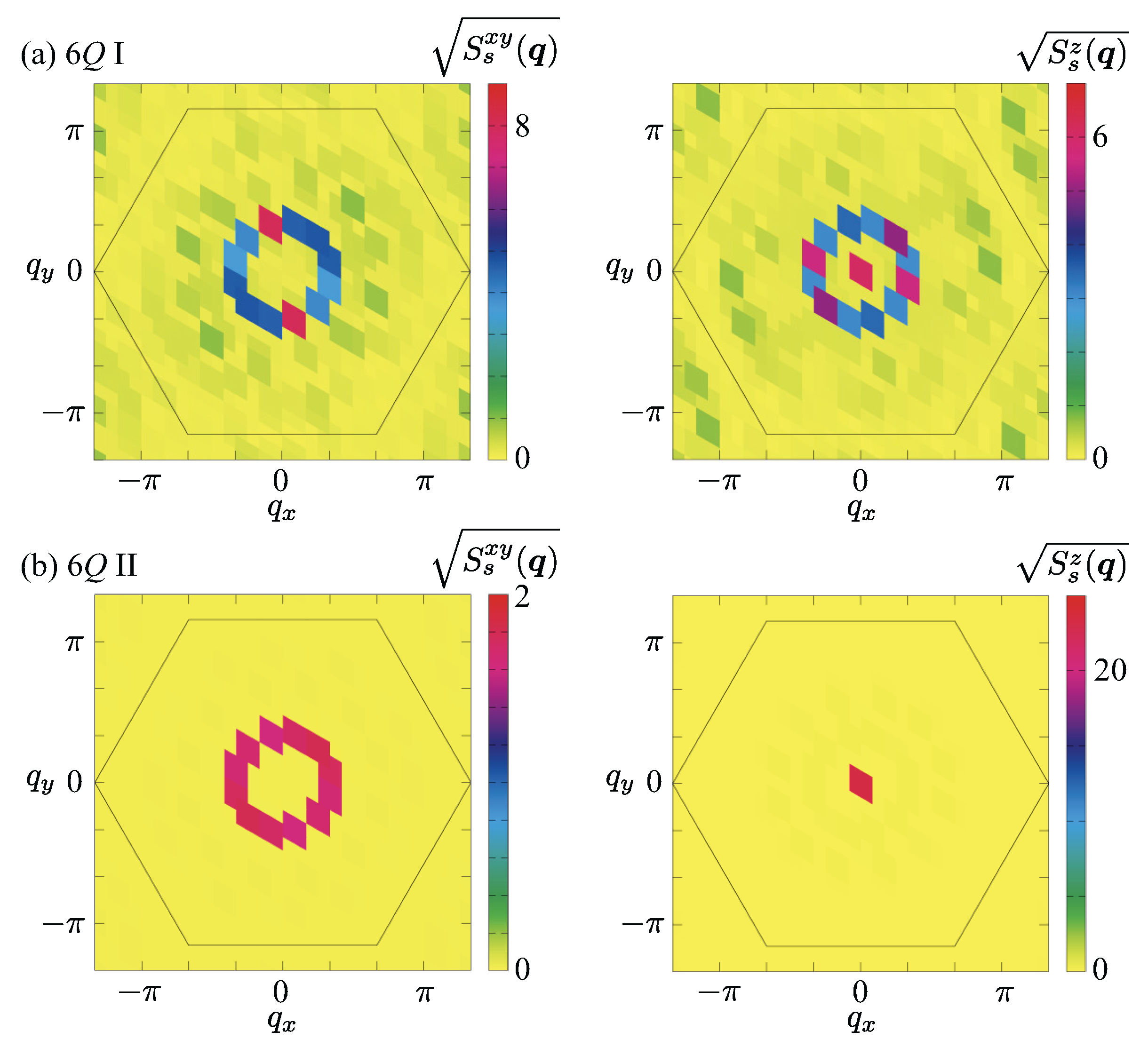
• Sextuple-Q I (6Q I) phase. For sufficiently large K at intermediate magnetic fields, the system undergoes a remarkable transition into a sextuple-Q state, referred to as the 6Q I phase, in which all six symmetry-related ordering wave vectors $\pm {\mathit{Q}}_{\nu }$ ($\nu =1$–6) participate coherently. This phase constitutes one of the main findings of the present study, representing a novel type of multiple-Q magnetic order that originates from the interference among symmetry equivalent ordering wave vectors located at low-symmetry positions inherent to the hexagonal lattice. In real space, the spin configuration shown in Figure 3(h) exhibits a densely modulated spin texture that can be well described as a coherent superposition of six spin density waves. Both the in-plane and out-of-plane spin components contribute to an intricate interference pattern; in contrast to the SkX phases, the spin texture contains skyrmion and anti-skyrmion cores, forming a globally noncoplanar but topologically neutral structure. As illustrated in Figure 4(e), the local scalar spin chirality alternates in sign across the lattice, forming a multiple-Q chirality density wave. Consequently, the uniform component of the scalar spin chirality vanishes (${\chi }^{\mathrm{sc}}=0$), consistent with the topologically trivial nature of this state. The spin structure factor in reciprocal space displays six inequivalent Bragg peaks forming a slightly distorted hexagonal pattern, as shown in Figure 6(a), indicating coherent but anisotropic interference among all six ${\mathit{Q}}_{\nu }$ components.

The emergence of the sextuple-Q I phase highlights the essential role of the biquadratic interaction K in stabilizing complex multiple-Q interference involving all symmetry-equivalent ordering wave vectors at low-symmetry positions in the Brillouin zone. Unlike the SkX phases, which carry a quantized topological charge, the sextuple-Q I phase corresponds to a topologically trivial multiple-Q spin density wave. This finding demonstrates that increasing K continuously drives the hierarchy of noncoplanar phases, from the single-Q state to the double-Q state, the triple-Q SkX, culminating in the fully developed sextuple-Q state. It thus establishes a framework for understanding how competing bilinear and biquadratic interactions generate emergent real-space textures and complex spin superpositions in itinerant magnets.

• Sextuple-Q II (6Q II) phase. At higher magnetic fields and deeper in the large-K regime, the system further evolves into another sextuple-Q state, denoted as the 6Q II phase. In real space, the spin configuration shown in Figure 3(i) exhibits a noncoplanar texture in which the in-plane spin components form vortex-like patterns, while the out-of-plane component becomes nearly uniform. Compared with the sextuple-Q I phase, the modulation amplitude of the spin texture is reduced, leading to a smoother spatial variation. As shown in Figure 4(f), this state also hosts a complex scalar spin chirality density wave without a uniform component, indicating that it remains topologically trivial despite the multiple-Q interference. In reciprocal space, the in-plane spin structure factor in Figure 6(b) displays six nearly equivalent peaks forming a regular hexagon, in contrast to the slightly distorted pattern found in the sextuple-Q I phase. This suggests a reorganization of the phase relations among the six ordering wave-vector components, which results in the partial suppression of the scalar spin chirality modulation in real space.

The appearance of the sextuple-Q II phase highlights the remarkable flexibility of the multiple-Q manifold stabilized by the biquadratic interaction K. It demonstrates that the cooperative interference among all six symmetry-related ordering wave vectors ${\mathit{Q}}_{\nu }$ can sustain multiple symmetry-distinct yet topologically trivial configurations, especially near the magnetic saturation field. Interestingly, when the ordering wave vectors lie along a high-symmetry line such as $\mathit{q}\Vert (1,0)$, an analogous state characterized by a triple-Q superposition has been reported near the saturation field [119,120]. The present sextuple-Q II phase thus generalizes this concept to a higher-order multiple-Q interference near the saturation field, demonstrating the robustness and diversity of field-induced noncoplanar states in frustrated itinerant magnets.

Figure 7. H dependence of (a,d,g) the magnetization $M^z$, (b,e,h) the scalar spin chirality ${\chi }^{\mathrm{sc}}$, and (c,f,i) the squared magnetic moments ${\left(m_{{\mathit{Q}}_{\nu }}\right)}^2$ for $\nu =1$–6. The values of K are taken at $K=0.05$ for (a,b,c), $K=0.3$ for (d,e,f), and $K=0.6$ for (g,h,i). The vertical dashed lines denote the phase boundaries between different magnetic phases. In all the cases, the states at $H=0$ and $H=2$ are the double-Q and fully polarized states, respectively.

Figure 7. H dependence of (a,d,g) the magnetization $M^z$, (b,e,h) the scalar spin chirality ${\chi }^{\mathrm{sc}}$, and (c,f,i) the squared magnetic moments ${\left(m_{{\mathit{Q}}_{\nu }}\right)}^2$ for $\nu =1$–6. The values of K are taken at $K=0.05$ for (a,b,c), $K=0.3$ for (d,e,f), and $K=0.6$ for (g,h,i). The vertical dashed lines denote the phase boundaries between different magnetic phases. In all the cases, the states at $H=0$ and $H=2$ are the double-Q and fully polarized states, respectively.

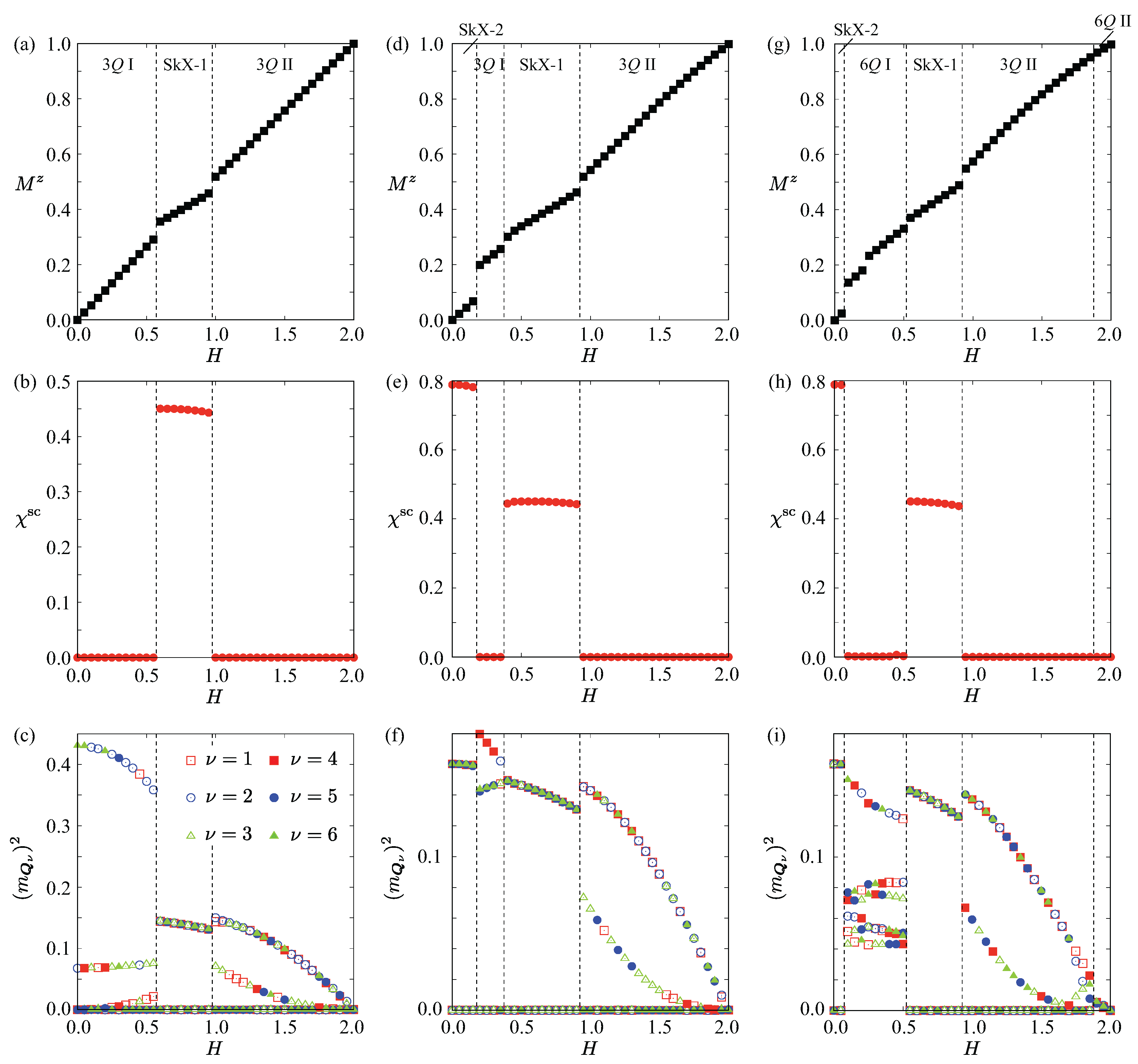
• Nature of phase transitions. The sequence of magnetic phases with increasing magnetic field H and biquadratic coupling K reveals a hierarchical buildup of multiple-Q order and distinct types of phase transitions between them, as summarized in Figure 7. The successive activation of symmetry-related ordering-wave-vector components from one in the single-Q state to two in the double-Q state, three in the triple-Q state and the SkX, and six in the sextuple-Q state is quantitatively reflected in the evolution of the Fourier amplitudes $m_{{\mathit{Q}}_{\nu }}$, as shown in Figure 7(c), Figure 7(f), and Figure 7(i). These changes correlate closely with discontinuities or crossovers in the magnetization $M^z$ as a function of H or K.

At small K with $K=0.05$, the system exhibits a clear sequence as triple-Q I— SkX-1—triple-Q II, as shown in Figure 7(a)–Figure 7(c). The transition from the triple-Q I state to the SkX-1 is characterized by a step-like increase in $M^z$ and a sudden emergence of a positive plateau in ${\chi }^{\mathrm{sc}}$, evidencing a first-order transition driven by the abrupt onset of uniform scalar spin chirality. Within the SkX-1, three ordering wave-vector components attain nearly equal Fourier amplitudes, forming a coherent triple-Q superposition with a quantized skyrmion number of one. Upon further increasing H, the transition to the triple-Q II state leads to the inequivalence among the ${\mathit{Q}}_{\nu }$ components and simultaneously suppresses ${\chi }^{\mathrm{sc}}$ to zero, marking another first-order transition into a topologically trivial state.

At intermediate coupling with $K=0.3$, the system stabilizes a richer sequence of noncoplanar states, including the SkX-2 phase at lower fields, as shown in Figure 7(d)–Figure 7(f). The transition from the SkX-2 to the triple-Q I state shows a pronounced jump in both $M^z$ and ${\chi }^{\mathrm{sc}}$, characteristic of a first-order phase transition with the change of the skyrmion number. The evolution of the spin configuration and scalar spin chirality through the transitions between the triple-Q I state, the SkX-1, and the triple-Q II state closely resembles that found at $K=0.05$.

For larger $K=0.6$, the system accommodates all six ordering wave vectors $\pm {\mathit{Q}}_{\nu }$, giving rise to sextuple-Q I and II phases, as shown in Figure 7(g)–Figure 7(i). All the transitions among the SkX-2, the sextuple-Q I state, the SkX I, the triple-Q II state, and the sextuple-Q II state seem to be discontinuous. This is evidenced by the abrupt changes in both the magnetization $M^z$ and the uniform scalar spin chirality ${\chi }^{\mathrm{sc}}$, as well as by the sudden reconstruction of the Fourier amplitudes $m_{{\mathit{Q}}_{\nu }}$ across the phase boundaries. In particular, each transition involves a distinct rearrangement of the relative phases among the six ${\mathit{Q}}_{\nu }$ components, leading to discontinuous changes in the real-space spin texture and the associated scalar spin chirality pattern. For instance, the transition from the SkX-2 to the sextuple-Q I phase is accompanied by a collapse of the uniform ${\chi }^{\mathrm{sc}}$ and the emergence of alternating-sign scalar spin chirality domains, whereas the subsequent transition to the SkX-1 phase restores a uniform finite ${\chi }^{\mathrm{sc}}$. The later transitions, from the SkX-1 to the triple-Q II and then to the sextuple-Q II phases, are also first-order in nature, characterized by discrete jumps in $M^z$ and abrupt redistributions of $m_{{\mathit{Q}}_{\nu }}$ intensities. These features indicate that the high-K regime hosts a complex energy landscape with multiple competing multiple-Q minima stabilized by different phase-locking conditions among the six ordering wave vectors. Consistently, the averaged scalar spin chirality maps in Figure 7(b), Figure 7(e), and Figure 7(h) reveal the topological nature of each phase: the SkX-1 and SkX-2 exhibit uniform positive ${\chi }^{\mathrm{sc}}$, whereas the other single-Q and multiple-Q states display alternating-sign scalar spin chirality distributions with vanishing net components.

Figure 8. K dependence of (a) the scalar spin chirality ${\chi }^{\mathrm{sc}}$ and (b) the squared magnetic moments ${\left(m_{{\mathit{Q}}_{\nu }}\right)}^2$ for $\nu =1$–6 at $H=0$. The vertical dashed lines denote the phase boundaries between different magnetic phases. The state at $K=0$ corresponds to the single-Q state.

Figure 8. K dependence of (a) the scalar spin chirality ${\chi }^{\mathrm{sc}}$ and (b) the squared magnetic moments ${\left(m_{{\mathit{Q}}_{\nu }}\right)}^2$ for $\nu =1$–6 at $H=0$. The vertical dashed lines denote the phase boundaries between different magnetic phases. The state at $K=0$ corresponds to the single-Q state.

Figure 9. (a) Real-space spin configuration, (b) scalar spin chirality, and (c) square root of the spin structure factor of the sextuple-Q III state at $K=0.7$ and $H=0$. In (a), spin orientations are indicated by arrows, with color denoting the z-component of the spin.

Figure 9. (a) Real-space spin configuration, (b) scalar spin chirality, and (c) square root of the spin structure factor of the sextuple-Q III state at $K=0.7$ and $H=0$. In (a), spin orientations are indicated by arrows, with color denoting the z-component of the spin.

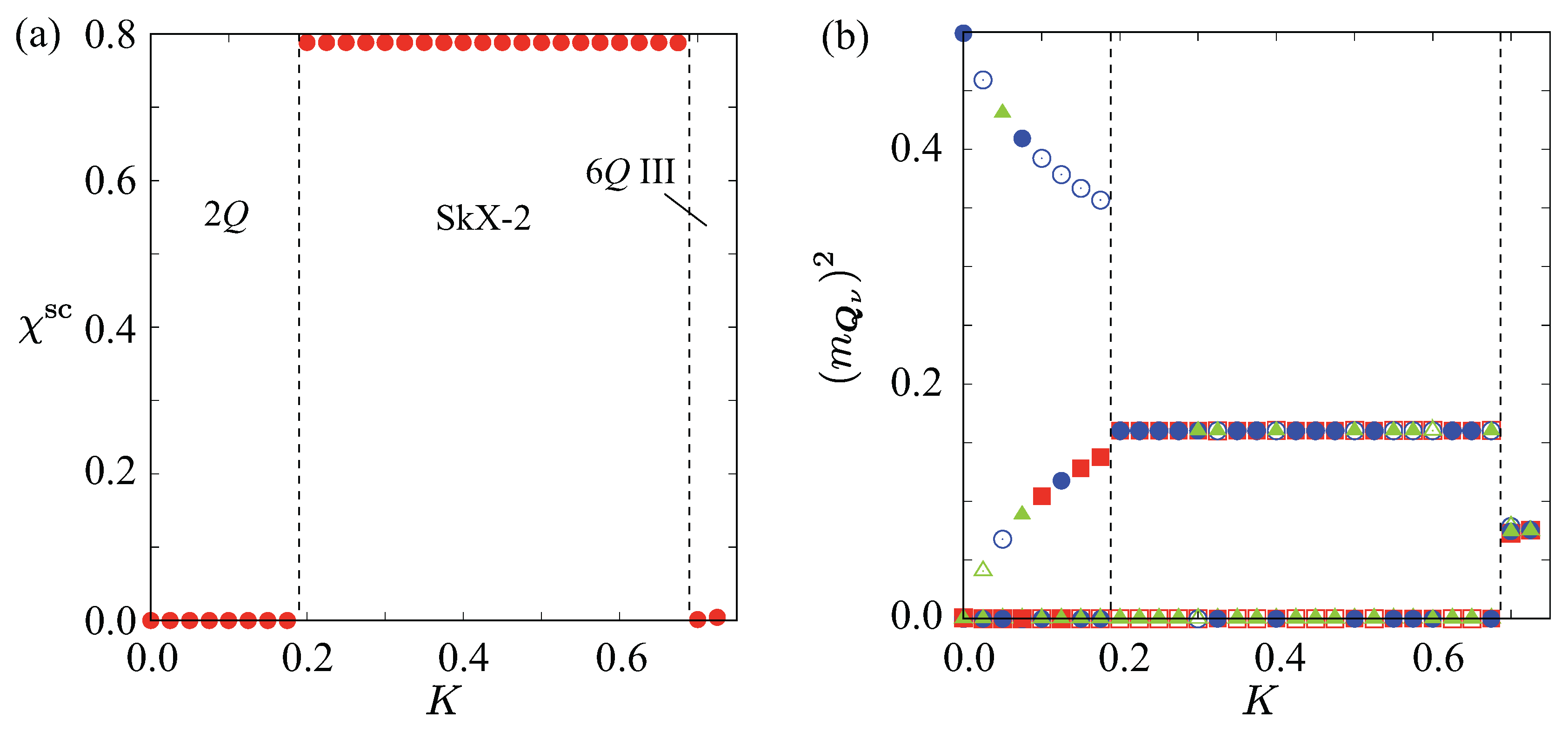
• Zero-field sextuple-Q state. To further clarify the role of the biquadratic interaction K in the absence of a magnetic field, we examine the zero-field ($H=0$) spin configurations for various values of K, as summarized in Figure 8(a) and Figure 8(b). For $K=0$, the ground state is a single-Q state characterized by a single dominant peak in the spin structure factor, as shown in Figure 8(b). As K increases, interference among symmetry-related ordering wave vectors becomes energetically favorable, leading successively to the double-Q and triple-Q SkX-2 states. When K is further enhanced, all six ordering wave-vector components $\pm {\mathit{Q}}_{\nu }$ ($\nu =1$–6) coherently participate, resulting in the stabilization of a new zero-field phase, the sextuple-Q III state. This spontaneous formation of the sextuple-Q III phase at $H=0$ demonstrates that a fully developed sextuple-Q superposition can be stabilized purely by the biquadratic interaction without the aid of an external magnetic field.

The real-space spin texture of the sextuple-Q III state, shown in Figure 9(a), exhibits a highly modulated and noncoplanar pattern originating from the coherent superposition of six spin density waves. Both the in-plane and out-of-plane spin components contribute to the interference, forming a periodic array of skyrmion- and antiskyrmion-like cores arranged on a hexagonal lattice. As illustrated in Figure 9(b), the corresponding local scalar spin chirality ${\chi }_{\mathbf{R}}^{\mathrm{sc}}$ alternates in sign throughout the lattice, producing a scalar spin chirality density wave with zero spatial average. Consequently, the sextuple-Q III state is topologically trivial but magnetically noncoplanar, characterized by strong local scalar spin chirality and the absence of a uniform ${\chi }^{\mathrm{sc}}$ component.

In reciprocal space, the spin structure factor in Figure 9(c) displays sixfold-symmetric Bragg peaks located at $\pm {\mathit{Q}}_{\nu }$, confirming the coherent participation of all symmetry-related ordering wave vectors. The total intensities of the spin structure factor are identical, indicating the isotropic sixfold rotational symmetry in reciprocal space, distinguishing the sextuple-Q III state from the anisotropic sextuple-Q I state. The emergence of the sextuple-Q III phase at zero magnetic field highlights the crucial role of the biquadratic interaction K as a microscopic origin of multiple-Q coherence.

4. Conclusions

We have theoretically investigated sextuple-Q magnetic instabilities in centrosymmetric hexagonal magnets by employing a minimal spin model that incorporates bilinear and biquadratic interactions under an external magnetic field. Systematic simulated-annealing calculations have revealed a rich sequence of noncoplanar spin textures that emerge as the biquadratic interaction K and magnetic field H are varied. The resulting low-temperature phase diagram hosts single-Q, double-Q, triple-Q, and sextuple-Q phases, as well as two types of SkXs (SkX-1 and SkX-2) carrying distinct spatial distributions of topological charges.

With increasing magnetic field or the biquadratic coupling, the system exhibits a hierarchical buildup of multiple-Q order through successive phase transitions: from single-Q and double-Q phases to triple-Q and SkX phases, and finally to sextuple-Q phases at large K. The transitions between these states are mostly discontinuous, as evidenced by abrupt changes in the magnetization, scalar spin chirality, and Fourier amplitudes of the ordering wave vectors. In the high-K regime, all six symmetry-related ordering wave vectors coherently participate, giving rise to three distinct sextuple-Q phases. All the sextuple-Q states are topologically trivial yet exhibit intricate modulations of the scalar spin chirality with alternating signs in real space. In particular, we have shown that the sextuple-Q state is realized by increasing the biquadratic interaction even at zero magnetic field.

The present results establish a unified framework for understanding hierarchical multiple-Q ordering in hexagonal itinerant magnets. The interplay between bilinear and biquadratic couplings governed by the lattice symmetry provides a route toward realizing sextuple-Q states and topologically nontrivial spin textures in centrosymmetric systems. The present study thus expands the landscape of multiple-Q magnetism and offers microscopic insight into the emergence of noncoplanar spin superstructures in frustrated itinerant magnets.