1. Introduction
In a crystal lattice, randomly oriented spins can spontaneously self-organize into collectively ordered states as the temperature decreases, such as ferromagnetic order with uniform magnetization or antiferromagnetic order with sublattice magnetization. These ordered states are characterized by local order parameters exhibiting translational symmetry. In contrast, quantum spin liquids lack any form of local order despite strong spinCspin interactions. Unlike the direct product state of disordered spins in a paramagnetic phase, the collective wavefunction of a quantum spin liquid is a highly entangled quantum state that hosts exotic quasiparticles obeying fractional statistics. The quantum spin liquid state was first proposed by Anderson in 1987 as the underlying mechanism for superconductivity of
by Anderson in 1987 [
1]. Later, an exact realization of a quantum spin liquid was theoretically established in the Kitaev honeycomb model, which supports non-abelian anyons in its gapless phase [
2]..
Unlike the long-range order found in conventional magnetic phases, the spin-spin correlations in the gapless phase of the Kitaev spin liquid are strictly short-ranged [
3,
4,
5,
6]. This indicates that its intrinsic order is not captured by traditional magnetic correlations but is instead characterized by a topological invariant, namely the Chern number [
2,
3,
7]. The application of an external magnetic field opens a gap in this gapless phase, thereby exciting pairs of anyons [
8,
9,
10,
11]. These anyonic excitations are of significant interest due to their potential application in topological quantum computation [
12,
13,
14].
The iridium-based honeycomb oxides
have been experimentally studied as candidate systems for realizing the Kitaev spin liquid, stimulating extensive research into both two-dimensional [
15,
16] and three-dimensional [
17] material platforms for Kitaev-type models [
18]. It was not until 2022 that a quantum spin liquid state was experimentally verified, with the observation of a U(1) quantum spin liquid in the triangular lattice magnet
[
19]. Moreover, Abelian anyons associated with spin liquids have been detected in fractional quantum Hall fluids via quantum interference experiments [
20,
21]. Nevertheless, the non-Abelian anyon expected in the Kitaev spin liquid remains experimentally elusive to date.
The gapped and gapless phases of the Kitaev spin liquid are characterized by zero and non-zero Chern numbers, respectively [
2,
3]. However, revealing the underlying topological order in the highly degenerate Kitaev spin liquid states remains a theoretical challenge. The collective pattern decomposition method for quantum spin Hamiltonians has proven effective in identifying quantum phase transitions in various many-body systems, including the quantum Rabi model [
22], the quantum transverse Ising model [
23,
24], and the Heisenberg model [
25]. In this approach, the total Hamiltonian is decomposed into a sum of sub-Hamiltonians, each contributing the energy of an individual pattern [
24,
25]. In this work, we employ the collective pattern decomposition method to uncover the fine structure of the Kitaev spin liquid state and use the density matrix renormalization group to locate the critical point of the phase transition associated with the sub-Hamiltonians.
2. The Pattern of Kitaev Model on Honeycomb Lattice
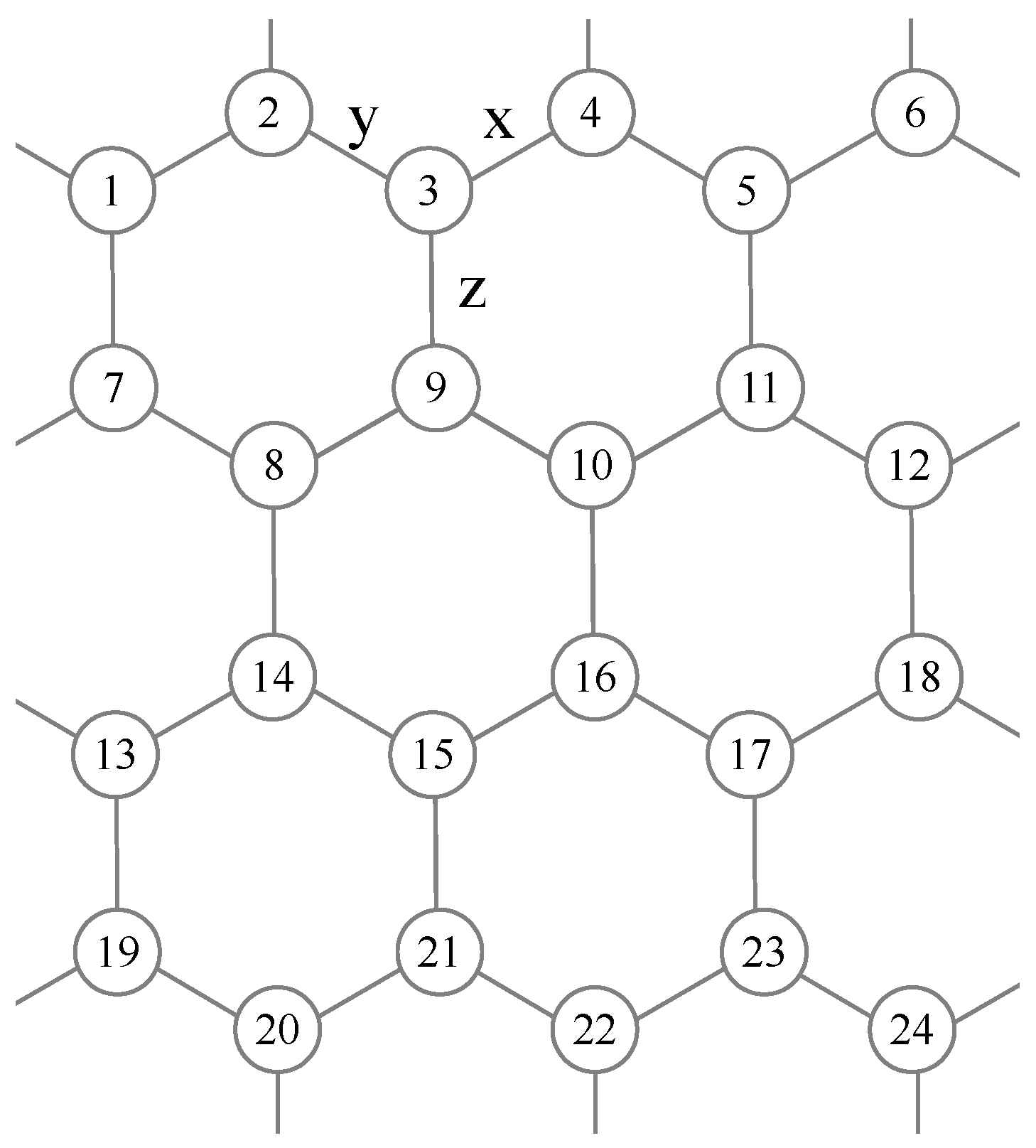
The Kitaev model on a finite honeycomb lattice consisting of 24 lattice sites is demonstrated in
Figure 1. Both the horizontal and vertical bonding directions of the honeycomb lattice obey periodic boundary conditions, mapping the Kitaev model into intersecting spin chain loops on torus. The exact Hamiltonian of Kitaev model is consists of direction dependent spin-spin couplings,
The exact ground state energy is derived by mapping spins into Majorana fermions[
2] or Jordan-Wigner transformation [
3,
4].
where
is the momentum vector of electron on honeycomb lattice. The ground states are divided into the gapped phase and gapless phase. The spin-spin coupling parameters in the gapless phase satisfy the following inequalities,
Without losing generality for the following discussions, the parameters for the gapped phase is chosen as (
), while the gapless phase is derived by the parameter setting, (
,
,
).
In
Figure 1, there are 24 electrons in total locating at 24 lattices sites. Each electron carries three spin components to interact with its nearest neighbors. The quadratic Hamiltonian Equation (
1) of the 24 electrons is the sum of Kitaev-type interacting bonds, which is reexpressed into a 72 by 72 matrix form,
Exact digonalization of the Hamiltonian matrix Equation (
4) yields 6 independent eigenvalues,
(
), i.e.,
. Each of the six eigenvalue has 12 fold degeneracy. The
th degenerated eigenvectors at the
ith site with respect to the
nth eigenvalue
is denoted as
, i.e.,
. For example, the first degenerate eigenvector
with respect to the eigenvalue
has only non-zero
at
.
Each electron at one site contributes its three spin components as three nearest neighboring elements to the 72 dimensional column vector in Equation (
4). Since the interacting 24 particles are no longer free particles, a collective composite operator
with respect to the
nth eigenvalue
is introduced to represent one collective pattern, which is expressed as the linear combinations of the spin components of 24 electrons,
(
; i = 1,2,...,24),
The coefficient
in front of the spin operator
measures its weight in the Hamiltonian. The total Hamiltonian Equation (
1) is divided into 6 sub-Hamiltonian of the collective composite operator according to the six eigenvalues,
For example, the sub-Hamiltonian
with respect to the first eigenvalue
reads
The sub-Hamiltonian
with respect to the second eigenvalue
shares similar chain operator with
, but carries different coefficients,
The total Hamiltonian describes six collective patterns, living in six subspaces expanded by 12 degenerated eigenvectors. Each composite operator
generates a collective pattern with eigen-energy
,
where
is the collective wave function of ground state. The eigenvectors with respect to
expands 12 dimensional subspace. The coefficients of adjacent
within the operator chain of composite operator (
,
,
) have the same sign (as shown in Equation (
7)), representing a collective pattern in phase, which is named after the symmetric pattern. While the coefficients of adjacent
within the composite operator (
,
,
) have opposite signs (as shown in Equation (
8)), representing a collective pattern out of phase, which is called the antisymmetric pattern. The 12 dimensional degenerated subspace with respect to an eigenvalue
is further divided into two more 6 dimensional subspaces, the symmetric subspace and the antisymmetric subspace.
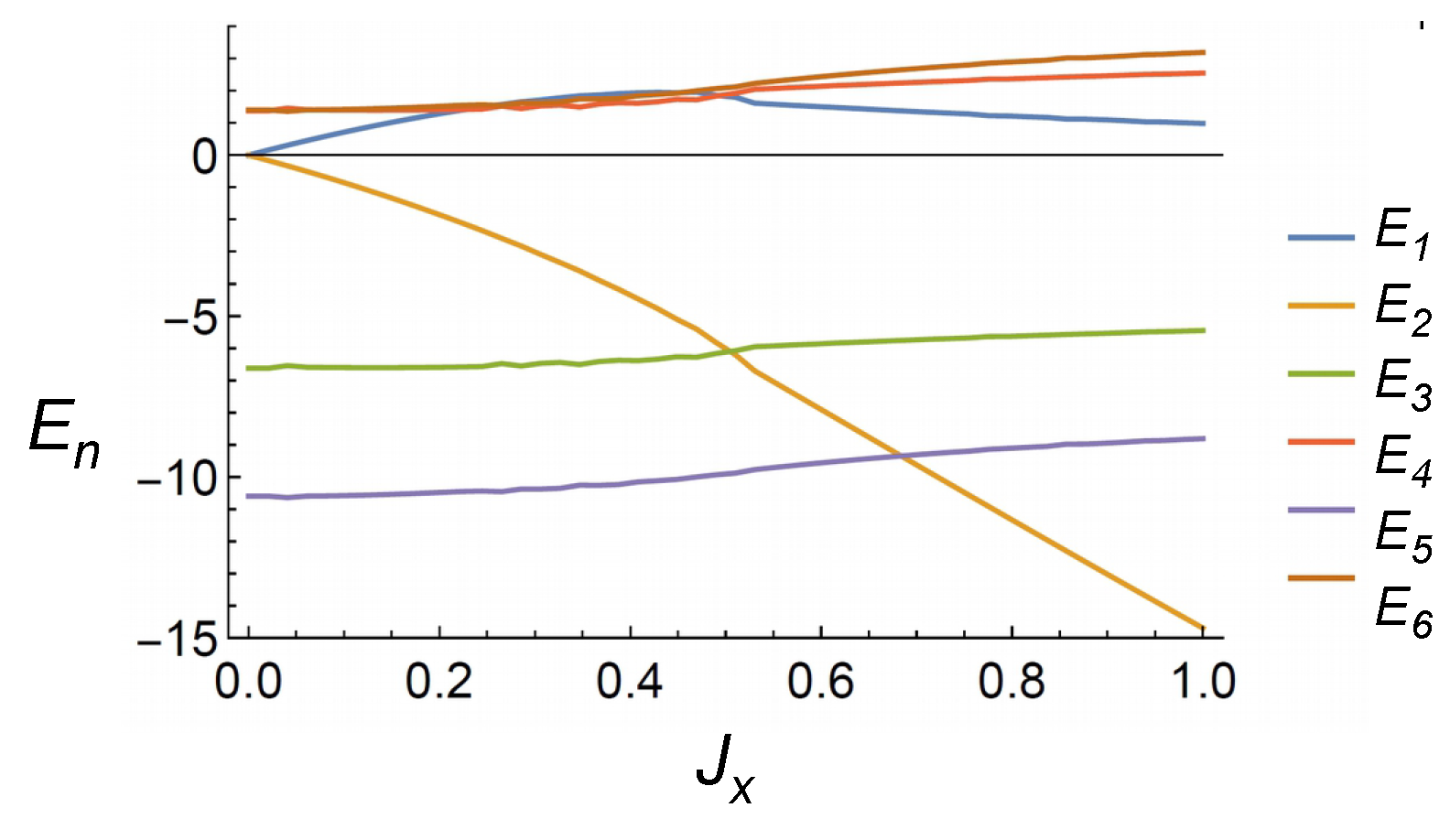
The ground state energy of the six sub-Hamiltonian evolves into different branches with coupling strength. In the gapped phase as showed in
Figure 2 (a), the three energy branches, (
,
,
), grows with
above zero, while the other two branches, (
,
), show a monotonic growth below zero. The second energy branch
decreases with
, bringing the total energy to the minimal value. Therefore,
subbranch dominates the evolution of Kitaev spin liquid. The same evolution behavior shows in the gapless phase in
Figure 2 (b), the
subbranch drops quickly to ground state with
. But the energy gap between and
and
is highly suppressed. Therefore, the collective pattern of
dominates the evolution of Kitaev spin liquid.
The eigenenergy with respect to the six sub-Hamiltonian are computed by numerical diagonalization with density matrix renormalization group. The six energy branches are obtained from energy Equation (
9).
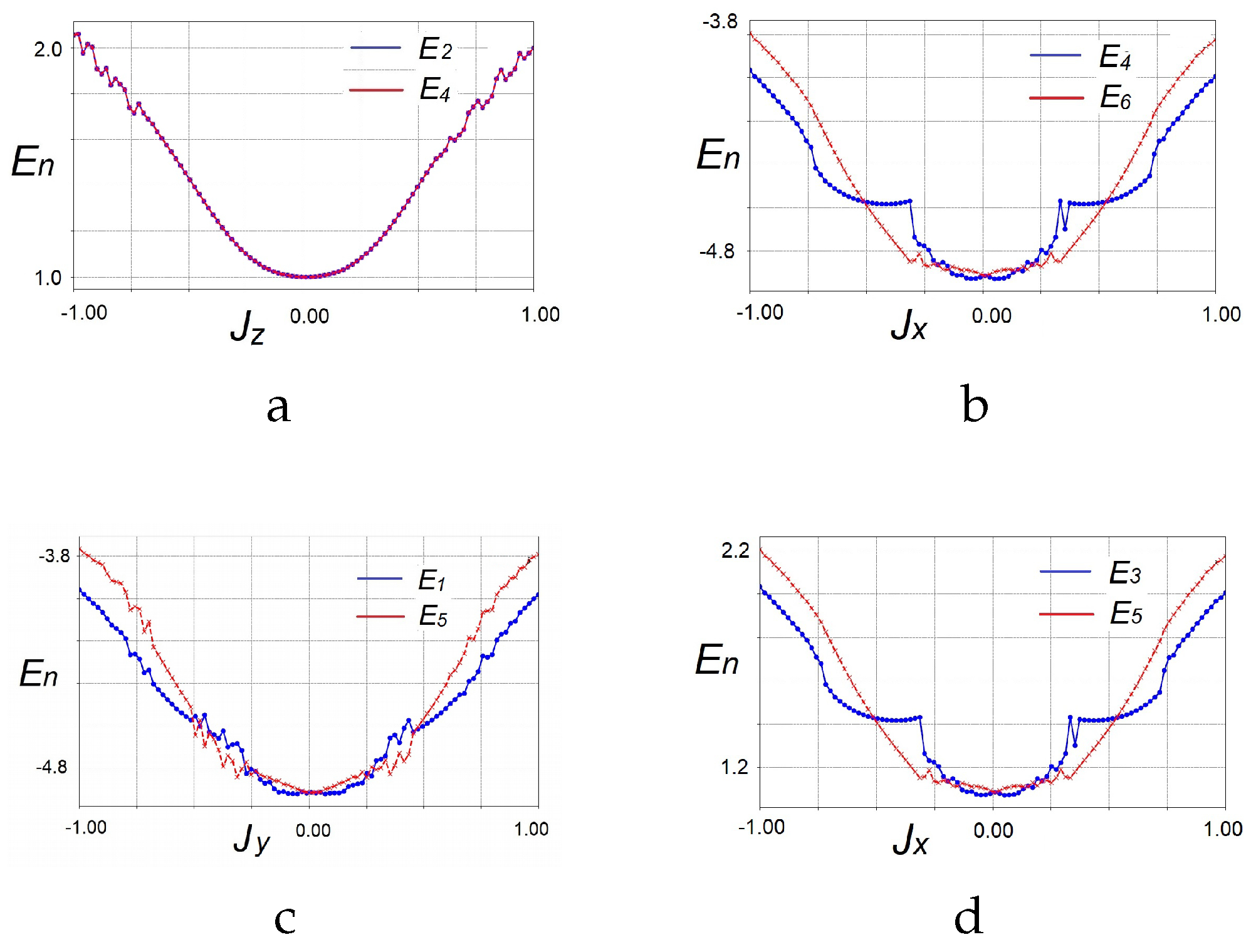
Figure 3 (a) shows the overlapped energy branches,
and
evolves with coupling parameter
, which agree with the cross section of the exact solution of energy spectrum in
Figure 4. The
branches shows a parabola curve with coupling parameter
in
Figure 3 (b). But the
branch evolves against coupling strength
shows two sudden dropping points around
, indicating the phase transition point from gapped phase to gapless phase. The energy branches,
and
against coupling strength
, also exist similar oscillating behavior around
. According to the exact energy Equation (
2), exchanging the
with
yields the same energy spectrum, resulting in the similar evolution behavior in
Figure 3 (b),
Figure 3 (c) and
Figure 3 (d).
3. The Hexagon-Rhombus Visualization of Collective Pattern on Honeycomb Lattice
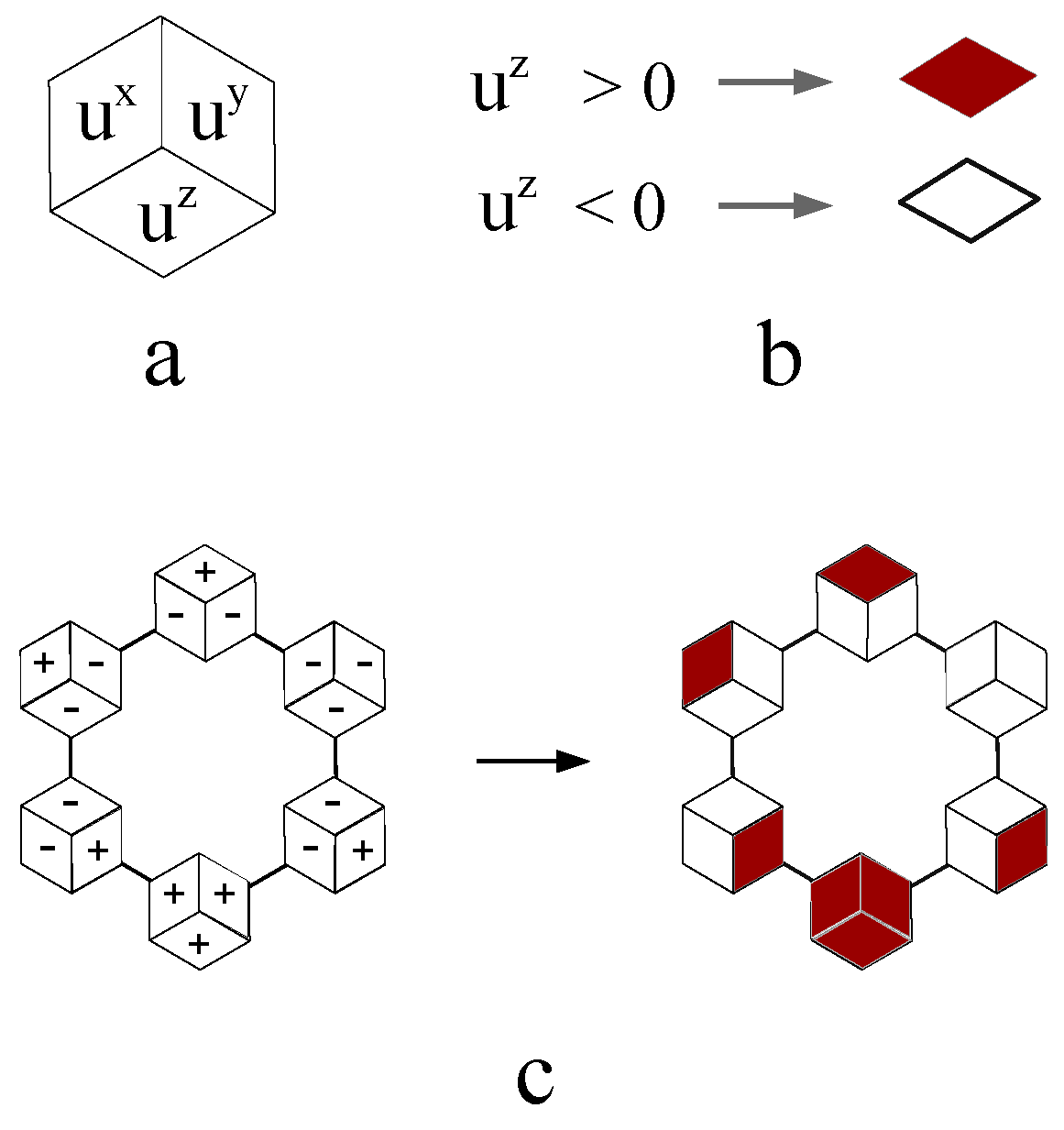
A more intuitive way of visualizing the collective patterns is to locate the three weight coefficients of three spin components at the lattice sites in real space. The weight coefficients at every lattice site is denoted as a vector,
As the exemplar Equation (
7) and Equation (
8) shows, only the sign of the weight coefficient changes in different pattern Hamiltonian. Therefore a filled or unfilled rhombus is chosen to label a positive
or a negative
, as showed in
Figure 5 (b). Every weight coefficient vector at the
ith site,
, is represented by a hexagon composed of three rhombuses, as shown in
Figure 5 (a). For the exemplar weight distribution of collective pattern in the left panel of
Figure 5 (c), the dying internal rhombus of six hexagons at six lattice sites are explicitly visualized in the right panel of
Figure 5 (c).
For the original Kitaev Hamiltonian Equation (
4), most weight coefficients
in front of spin operators are zero, due to the high degeneracy of eigenvectors induced by Kitaev coupling rules between nearest neighboring spins. In order to lift the degeneracy of the matrix eigenvalues of Kitaev Hamiltonian Equation (
4), a small external field is applied along the three spin-spin coupling bonds,
The external field strengths along the three bonds are
. These small external field does not change the exact ground state energy Equation (
2) due to
. In the numerical calculations, the small external field is set to
. The highly degenerated ground state energy level is loosen into closely stacked energy bundles, which are far separated from the first excited state. The hidden collective patterns become more apparent after eliminating the degenerated zeros. However, the eigenvalues is no longer real number, but carries an imaginary part, which is still much smaller than the real part, indicating stable fine energy levels. The eigenvalues
share the same absolute values with that without the external field. The sign of the real part of
is labeled to the hexagon of three rhombuses to visualize the collective patterns. These stable collective patterns are independent of the specific values of external field.
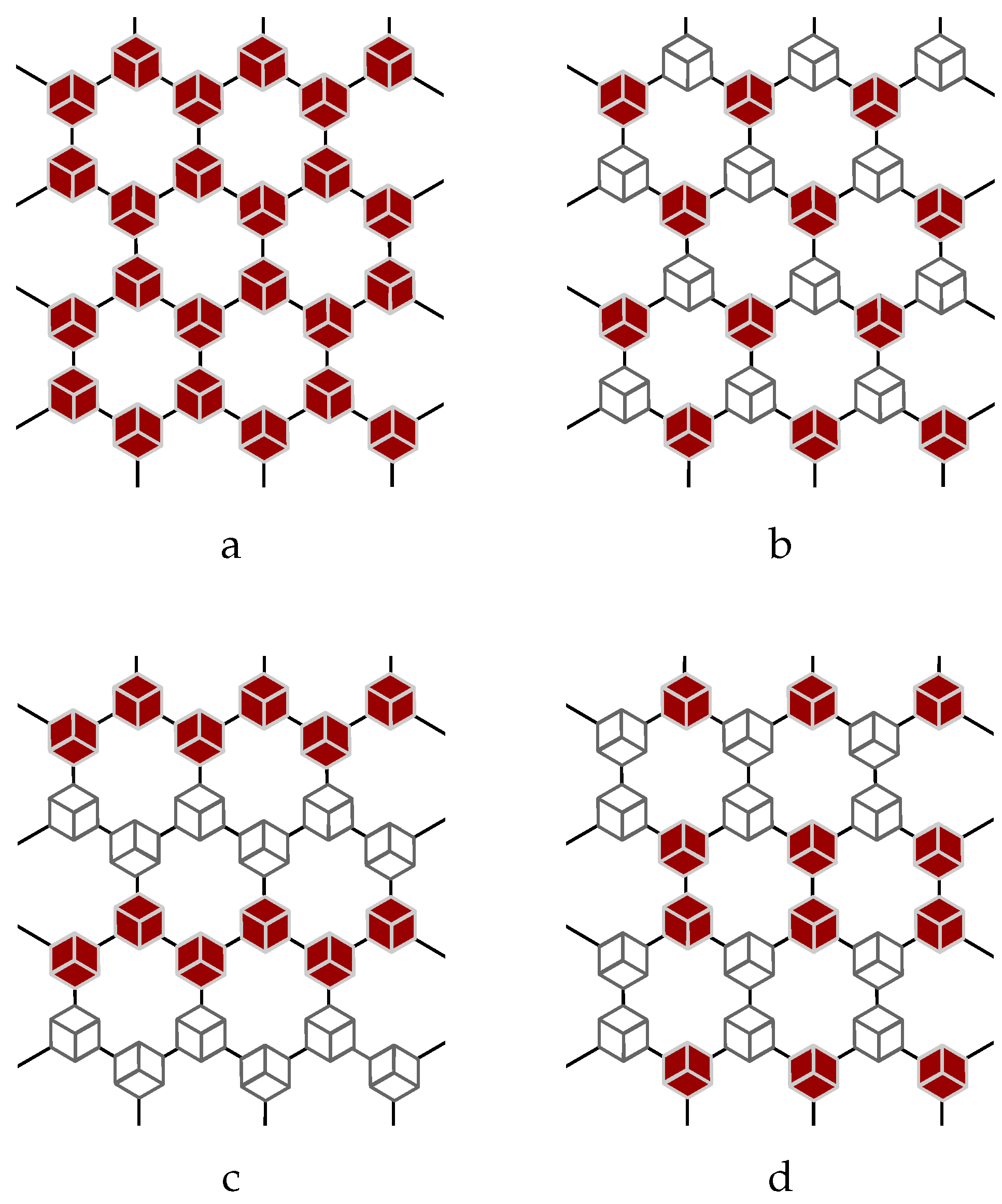
The
vectors with uniform signs translate to form collective pattern lattice in the gapped phase of Kitaev spin liquid. In the ferromagnetic phase in
Figure 6 (a), all weight coefficients with respect to eigenvalue
are positive, which are represented by uniformly dyed rhombus in red. In the antiferromagnetic pattern in
Figure 6 (b), the rhombus triple within a hexagon are dyed in the same way. The nearest neighboring hexagons have opposite signs, demonstrating a similar antiferromagnetic order as classical Ising spins. Unlike the Ising model, the eigenvalues
of the ferromagnetic and antiferromagnetic pattern are not the largest absolute values among all
.
Figure 6 (c) shows a striped phase, in which each row of fully dyed hexagon are all dyed in the same way, while the nearest neighboring rows are dyed in opposite ways. The nearest neighboring electrons may combine into a vertical dimer composed of two hexagons uniformly dyed in red, as shown in
Figure 6 (d).
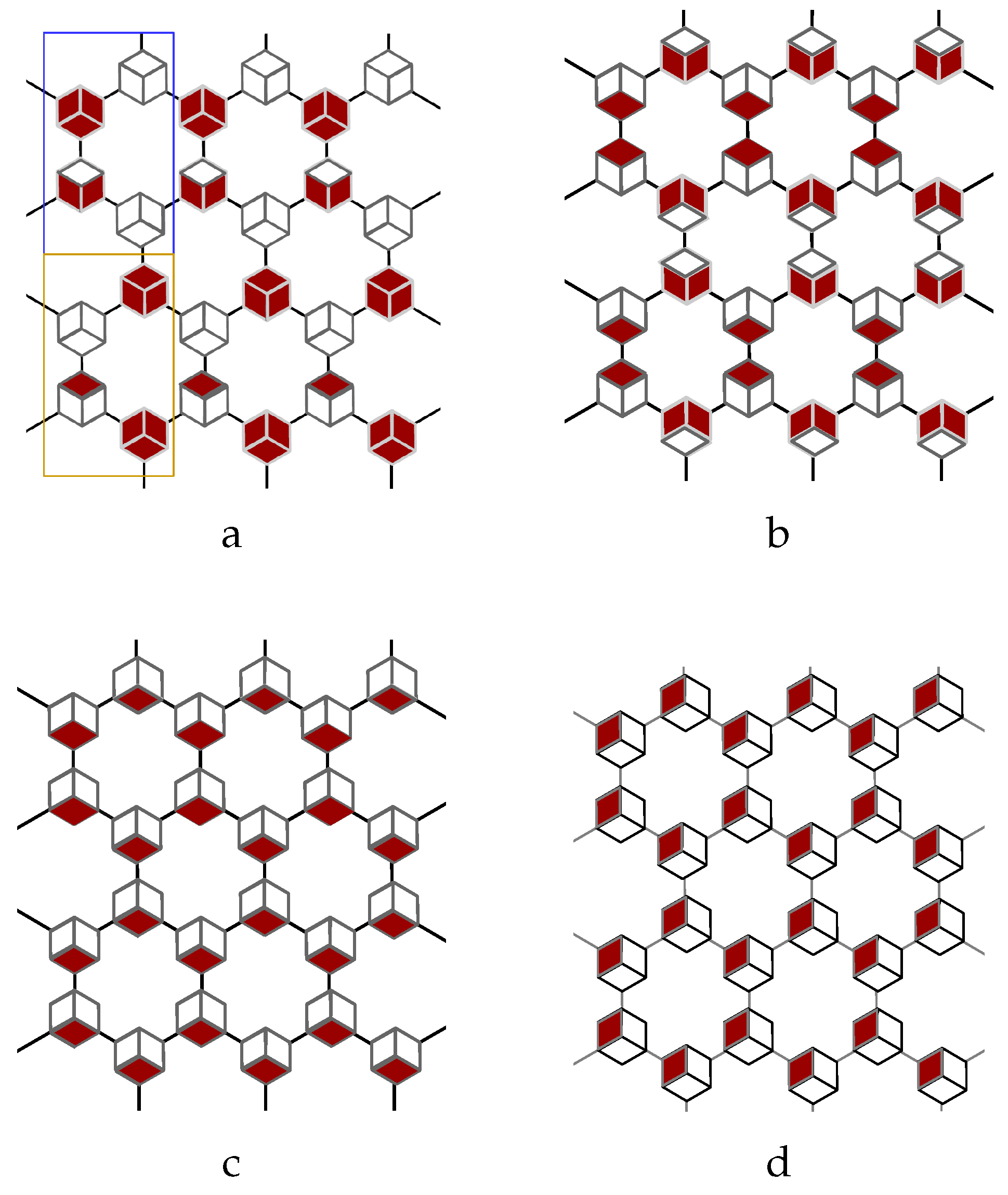
The collective pattern lattice composed of inhomogeneous
vectors also exist as eigenvector of the sub-Hamiltonian. The vector cluster composed of two unfilled hexagons, one fully filled hexagon and one partly filled hexagon represents an unit cell with four electrons, which are enveloped by the red rectangle on the left-up corner in
Figure 7 (a). The four
vectors on the left-bottom corner is exactly dyed in an opposite way to that on the upper corner in
Figure 7 (a). The two oppositely dyed vector clusters, as labeled by the red rectangle and the yellow rectangle in
Figure 7 (a), form the unit cell of an antiferromagnetic lattice of collective pattern with respect to eigenvalue
.
Figure 7 (b) is a ferromagnetic pattern lattice of unit cluster with four partly filled hexagons, as showed by the four lattice sites on the left-up corner in
Figure 7 (b), the eigenvalue of this ferromagnetic pattern is
. The ferromagnetic pattern lattice of
Figure 7 (c) with
shares the same eigenvalue with
Figure 7 (b), belonging to the same degenerated subspace. The ferromagnetic pattern lattice of
Figure 7 (d) is generated by translation of unit cell of hexagon partly filled by
, with respect to
.
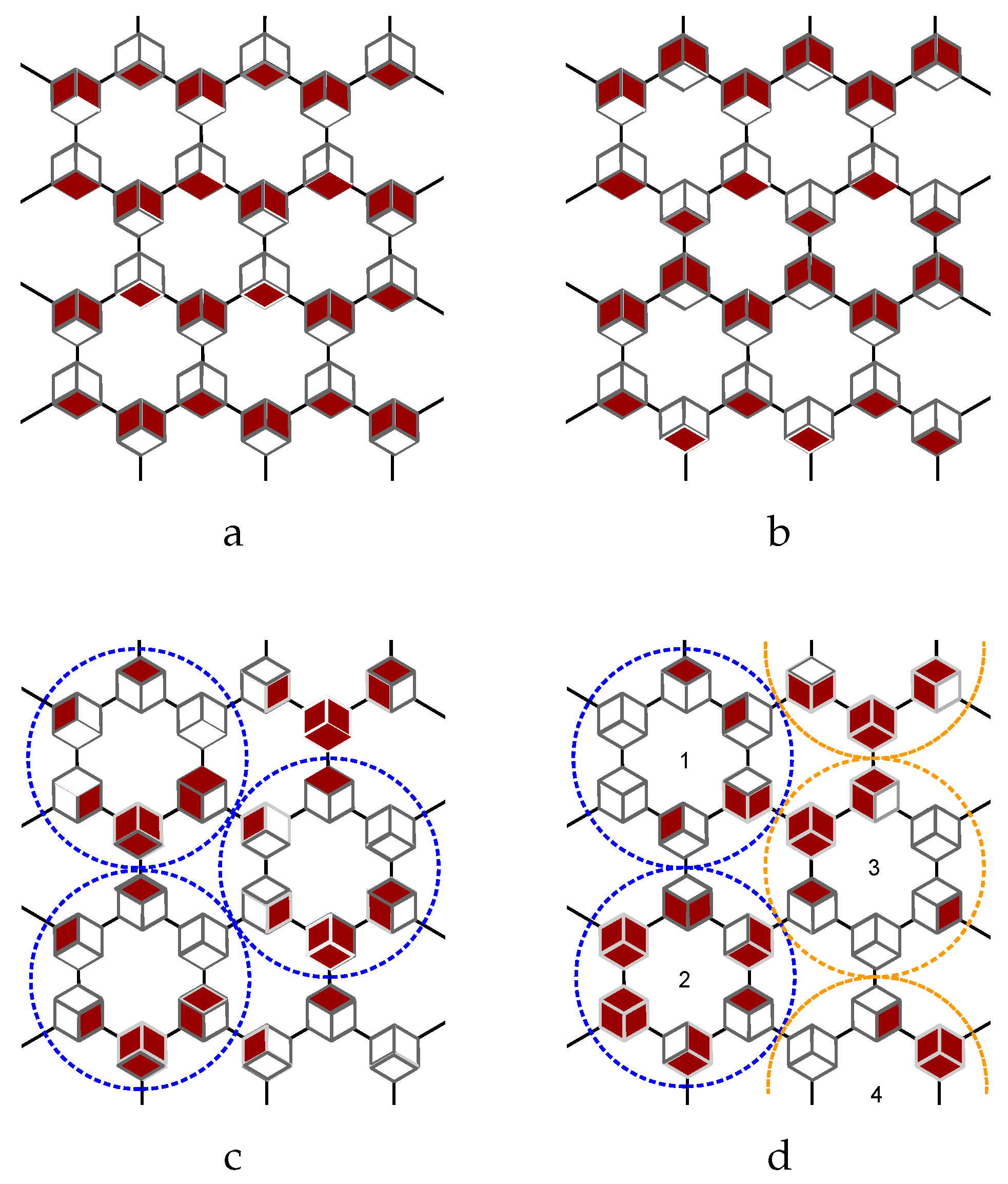
The kitaev spin liquid encodes more complex collective pattern lattice, that is generated by translating unit cell composed of six or twelve lattice sites. The unit cell of the pattern lattice in
Figure 7 (a) is composed two sites with (
,
) and two sites with (
,
), the four hexagons on the left-up corner in
Figure 8 (a).
Figure 8 (b) represents an antiferromagnetic strip pattern lattice, in which the nearest neighboring horizontal strips carry opposite signs.
Figure 8 (a)-(b) belong to the same eigenspace with respect to eigenvalue
. The unit cell of pattern lattice with eigenvalue
in
Figure 8 (c) is the hexagon plaquette that covers six lattice sites, which is enveloped by the blue dashed circle in
Figure 8 (c). The collective pattern with eigenvalue
in
Figure 8 (d) is not formed by the translation operation of small unit cell. The vertical dimer of two hexagon plaquette on the left hand side, as enclosed by the two blue circles (No. 1 and No. 2 in
Figure 8 (d)), carry exactly the opposite sign to that vertical dimer on the right hand side, which are enveloped by the two red dashed circles (No. 3 and No. 4 in
Figure 8 (d)). The collective pattern in
Figure 8 (d) covering the whole 24 lattice sites is an unit cell for pattern lattice of honeycomb lattice with more lattice sites.
A complete check of all of the 72 patterns in the gapped phase or gapless phase confirms that the pattern lattices are generated by translating unit cell of different sizes. The collective patterns are independent of the specific values of . This collective pattern revealed the hidden translation symmetry of Kitaev Hamiltonian.
4. Summary
The topological phase transition in Kitaev spin liquid states is typically characterized by the Chern number. In this work, we employ the pattern decomposition method to investigate the phase transition between gapped and gapless phases. The total Hamiltonian is expressed as the sum of six sub-Hamiltonians, each corresponding to a degenerate subspace. Each subspace is spanned by 12 collective patterns. Among the six sub-Hamiltonians, two exhibit a sharp drop in the ground state energy at the phase transition point, whereas the other four result in smooth energy variations.
By introducing a small external field, the collective patterns are visualized as colored hexagons on a honeycomb lattice. Periodic structures are generated by translating unit cells of varying sizes. These pattern lattices reveal the intrinsic translational symmetry of the Kitaev model Hamiltonian, regardless of the underlying lattice structures.
This Hamiltonian decomposition approach has been successfully applied to the transverse Ising model and the Heisenberg model with spin-spin couplings. In these cases, the collective patterns are found to be independent of the coupling strength and are entirely determined by the definitions of the electron couplings.
Figure 1.
The lattice sites of finite honeycomb lattice for Kitaev model are labeled in order.
Figure 1.
The lattice sites of finite honeycomb lattice for Kitaev model are labeled in order.
Figure 2.
The exact ground state energy of six sub-Hamiltonian demonstrate different behavior with coupling parameters.
Figure 2.
The exact ground state energy of six sub-Hamiltonian demonstrate different behavior with coupling parameters.
Figure 3.
(a) The pattern energy and with , (b) The pattern energy and with , (c) The pattern energy and with , (d) The pattern energy and with .
Figure 3.
(a) The pattern energy and with , (b) The pattern energy and with , (c) The pattern energy and with , (d) The pattern energy and with .
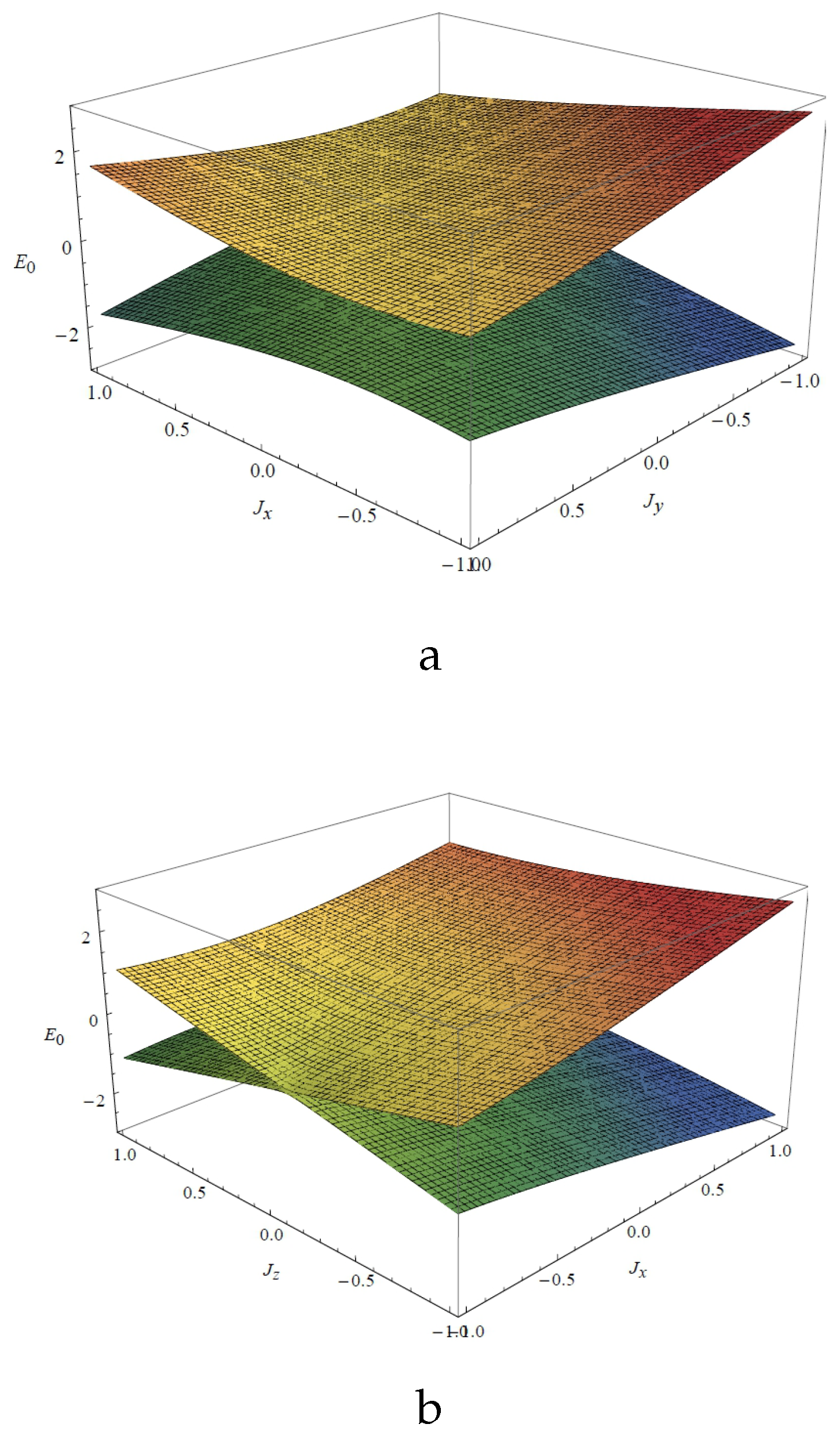
Figure 4.
The ground state energy varies with coupling parameters, for fixed momentum vectors, . (a) The gapped phase, ; (b) The gapless phase, .
Figure 4.
The ground state energy varies with coupling parameters, for fixed momentum vectors, . (a) The gapped phase, ; (b) The gapless phase, .
Figure 5.
(a) The coefficient vector at the ith site is illustrated by dyed rhombuses within one hexagon. (b) The red rhombus represents positive , and the unfilled rhombus represents negative . (c) The coefficient vector distribution around one hexagonal plaquette is represented by six dyed hexagons around the plaquette.
Figure 5.
(a) The coefficient vector at the ith site is illustrated by dyed rhombuses within one hexagon. (b) The red rhombus represents positive , and the unfilled rhombus represents negative . (c) The coefficient vector distribution around one hexagonal plaquette is represented by six dyed hexagons around the plaquette.
Figure 6.
The collective pattern with following parameters: . (a) ferromagnetic pattern, ; (b) anti-ferromagnetic pattern, ; (c) strip pattern, ; (d) dimer lattice pattern, .
Figure 6.
The collective pattern with following parameters: . (a) ferromagnetic pattern, ; (b) anti-ferromagnetic pattern, ; (c) strip pattern, ; (d) dimer lattice pattern, .
Figure 7.
The collective pattern of inhomogeneous vectors with following parameters: . (a) ferromagnetic pattern, ; (b) anti-ferromagnetic pattern, ; (c) strip pattern, ; (d) dimer lattice pattern, .
Figure 7.
The collective pattern of inhomogeneous vectors with following parameters: . (a) ferromagnetic pattern, ; (b) anti-ferromagnetic pattern, ; (c) strip pattern, ; (d) dimer lattice pattern, .
Figure 8.
The collective pattern of inhomogeneous vectors , . (a) ferromagnetic pattern lattice of four sites, ; (b) anti-ferromagnetic strip pattern, ; (c) plaquette pattern lattice, ; (d) plaquette dimer lattice, .
Figure 8.
The collective pattern of inhomogeneous vectors , . (a) ferromagnetic pattern lattice of four sites, ; (b) anti-ferromagnetic strip pattern, ; (c) plaquette pattern lattice, ; (d) plaquette dimer lattice, .