Submitted:
02 November 2024
Posted:
05 November 2024
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The Partition Function in the Case of PBC’s and ABC’s
2.1. The Case of the PBC’s
2.2. The Case of the ABC’s
3. Finite-Size Magnetization in the Case of PBC’s and ABC’s
3.1. Finite-Size Magnetization (PBC)
3.2. Finite-Size Magnetization (ABC)
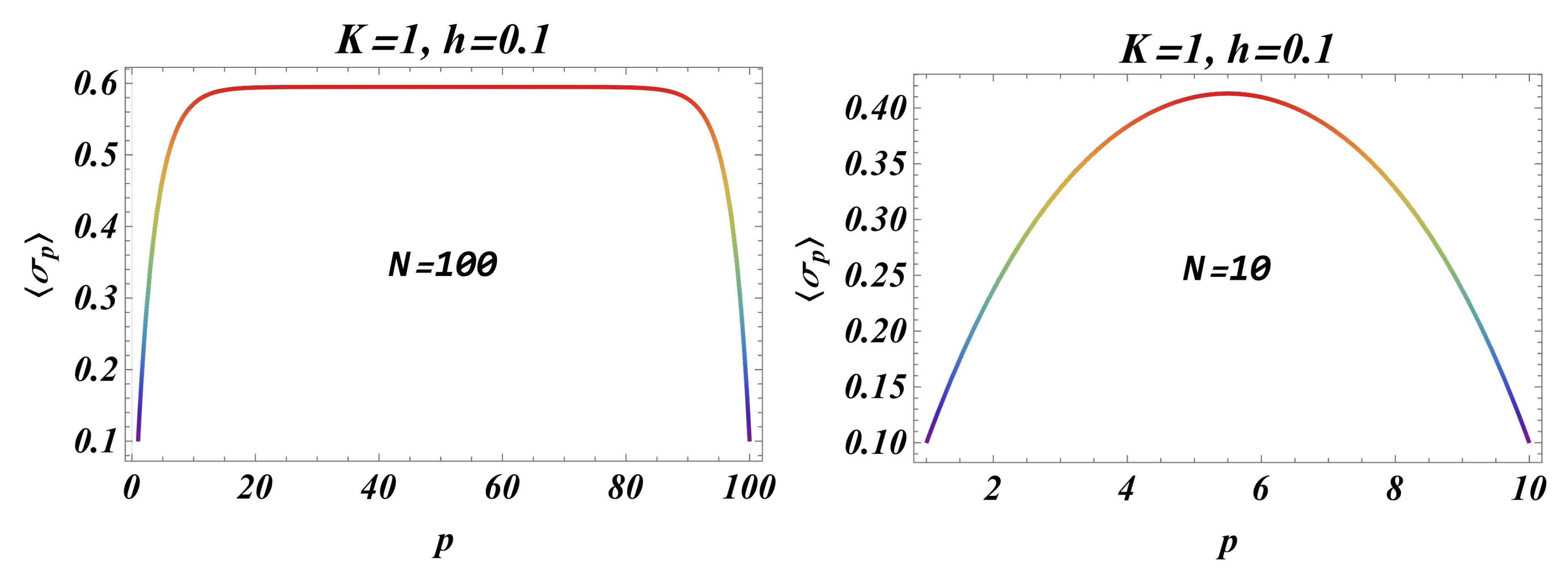
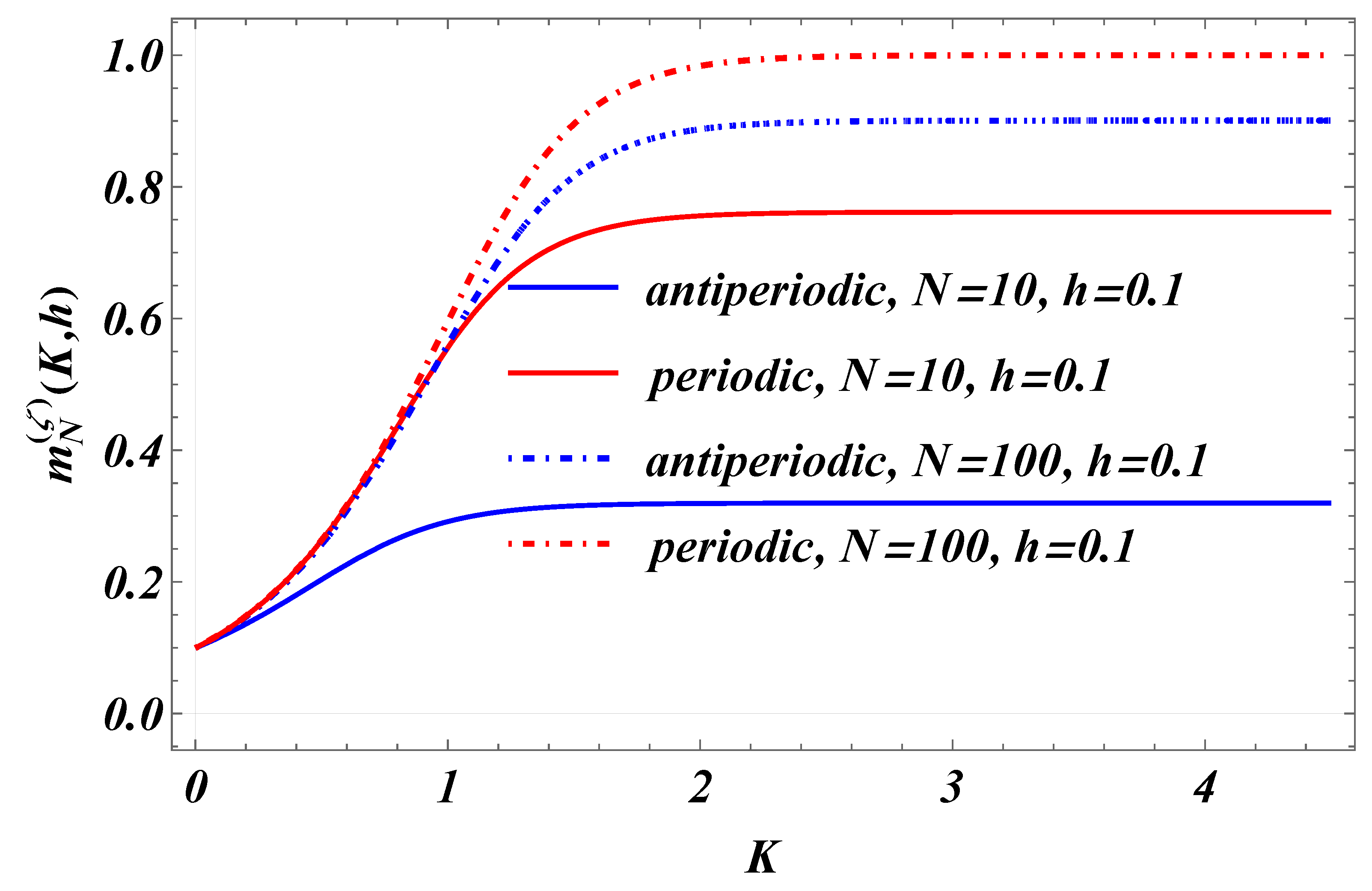
3.3. The Behavior of the Average Finite-Size Magnetization per Site for PBC’s and ABC’s
4. Yang-Lee Zeros
4.1. The Case of PBC
4.2. The Case of ABC
5. Chebyshev Recursion Relations and Exact RG Transformation
5.1. Periodic Boundary Conditions
5.2. Antiperiodic boundary conditions
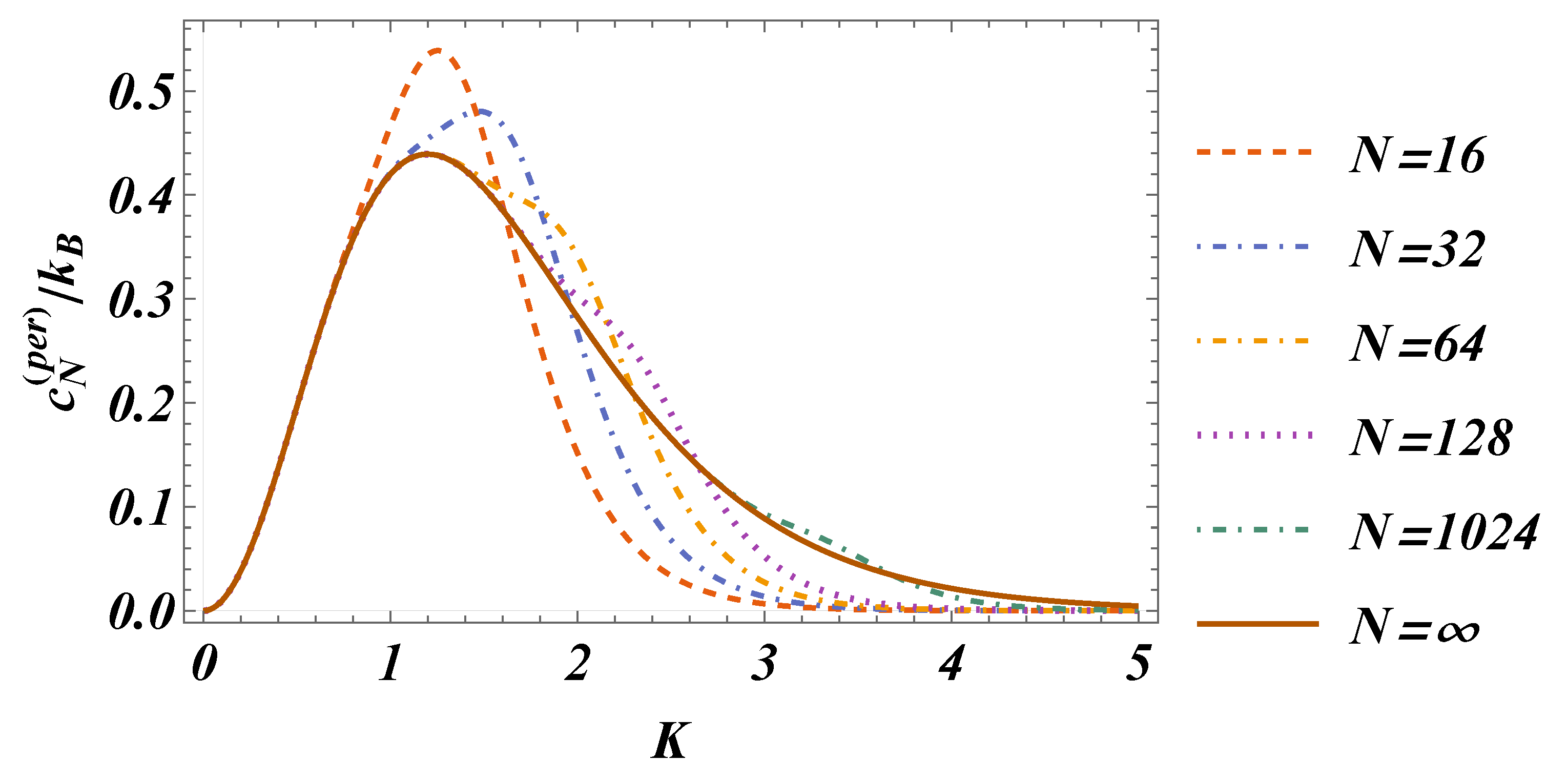
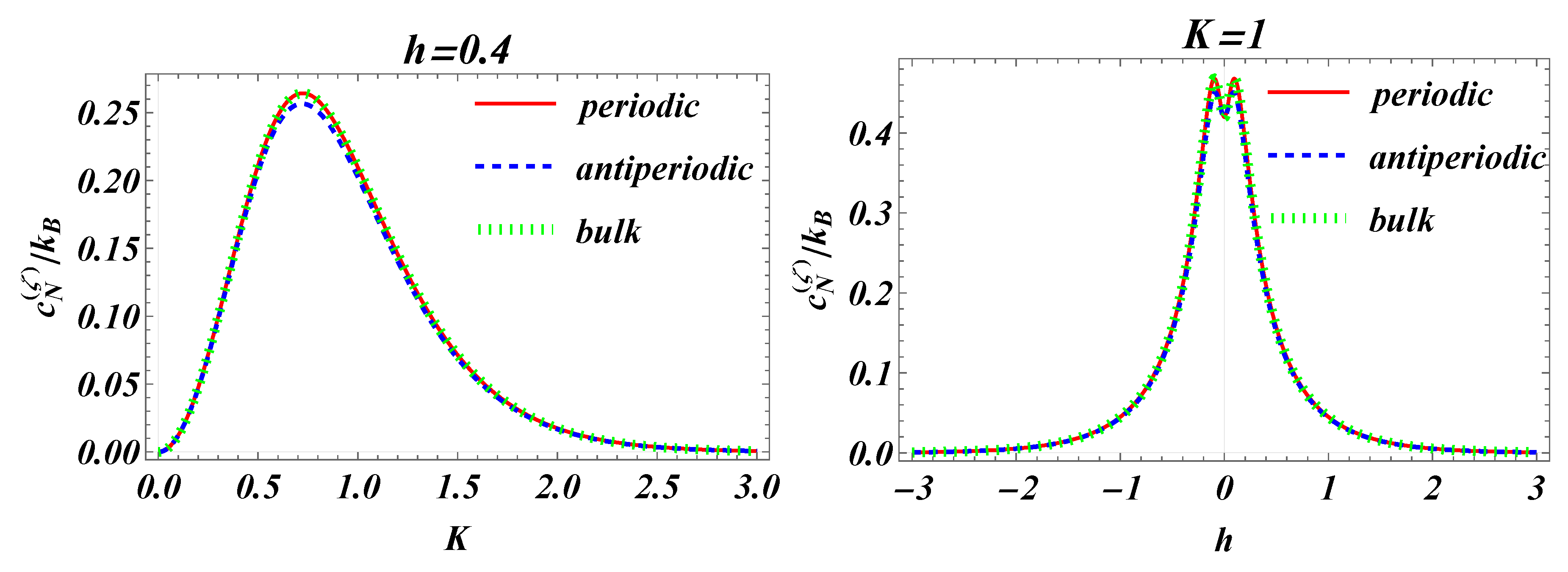
6. Schottky Anomaly
7. Discussion and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PBC | Periodic Boundary Conditions |
| ABC | Antiperiodic Boundary Conditions |
| RG | Renormalization Group |
Appendix A. Chebyshev Polynomials
Appendix B
References
- Sitarachu, K.; Zia, R.K.P.; Bachmann, M. Exact microcanonical statistical analysis of transition behavior in Ising chains and strips. J. Stat. Mech: Theory Exp. 2020, 2020, 073204.
- Magare, S.; Roy, A.K.; Srivastava, V. 1D Ising model using the Kronecker sum and Kronecker product. Eur. J. Phys. 2022, 43, 035102.
- Stepanyan, V.; Tzortzakakis, A.F.; Petrosyan, D.; Allahverdyan, A.E. Thermal transitions in a one-dimensional, finite-size Ising model. J. Stat. Mech: Theory Exp. 2024, 2024, 033202. [CrossRef]
- Balcerzak, T. Application of the integral operator method for multispin correlation function calculations in the one-dimensional Ising model. Phys. Rev. E 2024, 109, 024133. [CrossRef]
- Yessen, W.N. Properties of 1D Classical and Quantum Ising Models: Rigorous Results. Annales Henri Poincaré 2013, 15, 793–828. [CrossRef]
- Fierro, A.; Coniglio, A.; Zannetti, M. Condensation of fluctuations in the Ising model: A transition without spontaneous symmetry breaking. Phys. Rev. E 2019, 99, 042122. [CrossRef]
- Bena, I.; Droz, M.; Lipowski, A. Statistical mechanics of equilibrium and nonequilibrium phase transitions: the Yang–lee formalism. Int. J. Mod. Phys. B 2005, 19, 4269–4329. [CrossRef]
- Lee, J. Low-temperature behavior of the finite-size one-dimensional Ising model and the partition function zeros 2014. 65, 676683.
- Barata, J.C.A.; Goldbaum, P.S. On the Distribution and Gap Structure of Lee–Yang Zeros for the Ising Model: Periodic and Aperiodic Couplings. 103, 857–891. [CrossRef]
- Fronczak, A. Cluster properties of the one-dimensional lattice gas: The microscopic meaning of grand potential. Phys. Rev. E 2013, 87, 022131. [CrossRef]
- Dantchev, D.; Rudnick, J. Exact expressions for the partition function of the one-dimensional Ising model in the fixed-M ensemble. Phys. Rev. E 2022, 106, L042103. [CrossRef]
- Dantchev, D.M.; Tonchev, N.S.; Rudnick, J. Casimir versus Helmholtz forces: Exact results. Annals of Physics 2023, 459, 169533. [CrossRef]
- Dantchev, D.M.; Tonchev, N.S.; Rudnick, J. Casimir and Helmholtz forces in one-dimensional Ising model with Dirichlet (free) boundary conditions. Ann. Phys., 464, 169647. [CrossRef]
- Dantchev, D. On Casimir and Helmholtz Fluctuation-Induced Forces in Micro- and Nano-Systems: Survey of Some Basic Results. Entropy 2024, 26, 499. [CrossRef]
- Dantchev, D.; Tonchev, N. A Brief Survey of Fluctuation-induced Interactions in Micro- and Nano-systems and One Exactly Solvable Model as Example 2024. [2403.17109]. [CrossRef]
- Baake, M.; Grimm, U.; Joseph, D. Trace Maps, Invariants, and Some of Their Applications. Int. J. Mod. Phys. B 1993, 07, 1527–1550. [CrossRef]
- da Conceição, C.M.S.; Maia, R.N.P. Recurrence relations in one-dimensional Ising models. Phys. Rev. E 2017, 96, 032121. [CrossRef]
- Seth, S. Combinatorial approach to exactly solve the 1D Ising model. Eur. J. Phys. 2016, 38, 015104. [CrossRef]
- Maniwa, Y.; Kataura, H.; Matsuda, K.; Okabe, Y. A one-dimensional Ising model for C70molecular ordering in C70-peapods. New J. Phys. 2003-10, 5, 127–127. [CrossRef]
- Taherkhani, F.; Daryaei, E.; Parsafar, G.; Fortunelli, A. Investigation of size effects on the physical properties of one-dimensional Ising models in nanosystems. Mol. Phys. 2011, 109, 385–395. [CrossRef]
- Abelès, F. Sur l’itération des matrices carrées a quatre éléments. Ann. de Physique 1950, 5, 777–782.
- Born, M.; Wolf, E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light; Pergamon Press, New York, 1980.
- Gradshteyn, I.S.; Ryzhik, I.H. Table of Integrals, Series, and Products; Academic, New York, 2007.
- Griffiths, D.J.; Steinke, C.A. Waves in locally periodic media. American Journal of Physics 2001, 69, 137–154.
- Nandhini, G.; Sangaranarayanan, M.V. Partition function of nearest neighbour Ising models: Some new insights. J. Chem. Sci. 2009, 121, 595–599. [CrossRef]
- Baxter, R.J. Exactly Solved Models in Statistical Mechanics; Academic, London, 1982.
- Yang, C.N.; Lee, T.D. Statistical theory of equations of state and phase transitions. I. Theory of condensation. Physical Review 1952, 87, 404.
- Lee, T.D.; Yang, C.N. Statistical theory of equations of state and phase transitions. II. Lattice gas and Ising model. Physical Review 1952, 87, 410.
- Dolan, B.P. Chaotic behavior of renormalization flow in a complex magnetic field. Physical Review E 1995, 52, 4512.
- Kardar, M. Statistical Physics of Fields; Cambridge University Press, Cambridge, 2007.
- Elaydi, S.N. Discrete chaos: with applications in science and engineering; CRC press, 2007.
- Hao, B.; Zheng, W. Applied symbolic dynamics and chaos, second ed.; World Scientific, 2018.
- Strogatz, S.H. Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering; CRC press, 2018.
- Dolan, B.P.; Johnston, D. One-dimensional Potts model, Lee-Yang edges, and chaos. Physical Review E 2002, 65, 057103.
- Geisel, T.; Fairen, V. Statistical properties of chaos in Chebyshev maps. Phys. Lett. A 1984, 105, 263–266. [CrossRef]
- Pathria, R.K.; Beale, P.D. Statistical Mechanics, third ed.; Elsevier, Amsterdam, 2011.
- Goldenfeld, N. Frontiers in Physics. In Lecture on phase transitions and the renormalization group; Pines, D., Ed.; Frontiers in Physics, Addison-Wesley, New York, 1992.
- Ferreira, L.S.; Plascak, J.A. Finite-Size Effects of the One-Dimensional Ising Model. Braz. J. Phys. 2023, 53, 77. [CrossRef]
- Snyder, M.A. Chebyshov Methods in Numerical Approximations; Prentice-Hall Inc., Englewood Cliffs N.J., 1966; chapter 2.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



