The Exceptional Simple Lie Group E8 and the Human Neocortex

1. Introduction

The quest to uncover the principles underlying consciousness, cognition, and neural computation has long been at the forefront of both neuroscience and theoretical physics. As research deepens across domains, a new class of interdisciplinary models seeks to unify abstract mathematical structures with the empirical complexities of the brain. Among these, the exceptional Lie group E₈ has emerged as a compelling candidate for modeling the intricate organization and functional dynamics of the human neocortex.

E₈ is a 248-dimensional, highly symmetric, and algebraically rich structure that plays a prominent role in string theory, grand unified theories, and algebraic geometry. Its elaborate network of root systems, weight lattices, and transformation invariants lends itself to the modeling of complex, high-dimensional systems. In parallel, the human neocortex embodies a densely interconnected, hierarchically modular architecture that exhibits nonlinear dynamics, feedback control, and topological diversity.

The central hypothesis of this paper is that E₈ symmetry provides a functional and structural analog to cortical computation. We propose that the manifold of neural states explored by the neocortex during cognition may be modeled as trajectories within the symmetry space of E₈. In this view, feedback loops, attractor states, and inter-regional connectivity can be interpreted as operations on or transformations within this high-dimensional Lie algebra.

In the sections that follow, we develop a mathematical and conceptual foundation for mapping E₈ to the neocortex. We begin with a historical overview of the theoretical roots of this hypothesis and its relation to prior work in neuroscience and mathematical physics. We then introduce a topological description of cortical manifolds, followed by the construction of a computational model architecture based on E₈ generators.

To assess the validity and scope of the proposed framework, we outline neuroscientific validation strategies involving imaging, modeling, and theoretical constraints. We also address limitations and criticisms, including concerns about reductionism, testability, and philosophical overreach. Finally, we explore the implications of E₈-inspired models for artificial intelligence and epistemology, proposing that such approaches could unify symbolic, statistical, and geometric perspectives in cognition.

2. Mathematical Background on E8

E8 is a complex, simply connected, compact exceptional Lie group of dimension 248. It is notable for being the largest of the five exceptional simple Lie groups and has a root system composed of 240 roots in 8-dimensional Euclidean space. The Lie algebra ${\mathfrak{e}}_8$ is particularly difficult to visualize but can be partially represented using projection techniques.

The group E8 is built over a Dynkin diagram consisting of 8 nodes with a particular connectivity. Let us denote $\mathfrak{g}$ as the Lie algebra associated with E8. Then we define:

$$\mathfrak{g}={\mathfrak{e}}_8=\underset{\alpha \in \Delta }{⨁}{\mathfrak{g}}_{\alpha }\oplus \mathfrak{h},$$

(1)

where $\mathfrak{h}$ is a Cartan subalgebra and ${\mathfrak{g}}_{\alpha }$ are root spaces indexed by roots $\alpha$ in the root system $\Delta$. The number of positive roots is 120, and they are balanced by 120 negative roots, along with 8 simple roots.

Furthermore, E8 exhibits properties of triality, a rare symmetry in which three representations are interchangeable. The adjoint representation of E8, being 248-dimensional, can be decomposed under specific subgroups like $\mathfrak{so}\left(16\right)$ or $E_7\times SU\left(2\right)$.

One critical object is the Killing form, defined as:

$$K(X,Y)=\mathrm{Tr}\left(\mathrm{ad}\right(X)\circ \mathrm{ad}(Y\left)\right),$$

(2)

which is invariant under the Lie algebra automorphisms and plays a role in determining group metric properties. This intrinsic metric may inspire the geometric analogy with cortical metric spaces defined over neural activity manifolds.

3. Structural Mapping with the Neocortex

The neocortex contains six distinct laminar layers, typically labeled I through VI, each characterized by unique cellular compositions, connectivity profiles, and functional contributions. Layer IV, for example, is the primary recipient of thalamic input, while Layers II/III are involved in cortico-cortical communications, and Layers V/VI primarily manage output to subcortical regions.

In our theoretical model, we propose to view the six cortical layers as projections of a subgroup structure within E8. While E8 contains no direct six-dimensional subgroup, we consider decompositions into lower-dimensional algebras where different sets of generators correspond metaphorically to layer-specific functionality.

If we define an isomorphic mapping $\varphi$ from a subset of E8 generators $\left\{e_i\right\}$ to cortical functional operators $\left\{C_j\right\}$, then the mapping may be expressed as:

$$\varphi :e_i\mapsto C_j,\mathrm{such}\mathrm{that}[e_i,e_k]\mapsto [C_j,C_l],$$

(3)

where the bracket denotes either the Lie bracket in algebra or the commutator in operator theory. The neurobiological equivalent is to assume cortical modules operate under transformation-like rules, possibly simplified through mathematical analogs.

This analogy gains strength when considering connectome data, which reveals small-world and modular properties of brain networks, comparable to how root structures in Lie algebras group under symmetries. Neural manifolds, derived from dimensionality reduction of neural firing data, often reside in high-dimensional vector spaces, akin to the algebraic space of E8.

4. Consciousness and Symmetry Operations

Consciousness as an emergent phenomenon remains an open problem. Integrated Information Theory (IIT) and Global Workspace Theory (GWT) attempt to formalize aspects of consciousness using mathematical and computational models. Here, we hypothesize that transitions between conscious states may correspond to discrete symmetry-breaking events within an E8-like structure.

In mathematical terms, consider a state vector $\Psi$ in the space V under E8 group action G:

$${\Psi }^{\prime }=g·\Psi ,\forall g\in G.$$

(4)

A conscious event may correspond to a transition between invariant subspaces of V under certain group elements. We can define a consciousness operator $\mathcal{C}$ that measures this transition:

$$\mathcal{C}(\Psi )={\int }_{G^{\prime }}\langle \Psi ,g·\Psi \rangle dg,$$

(5)

where $G^{\prime }\subset G$ represents a symmetry-reduced subgroup relevant for functional states of awareness. The higher this integral, the more symmetric (and possibly less conscious) the state, and conversely, localized symmetry-breaking may mark moments of conscious individuation.

Such notions mirror spontaneous symmetry breaking in physics, where lower-energy configurations emerge with reduced symmetry. In the cortical context, focused cognitive attention may be interpreted as a collapse from a higher-symmetry, unconscious background.

5. Historical Context and Related Work

The pursuit of understanding consciousness and brain function through mathematical formalisms dates back to early cybernetics in the mid-twentieth century. During the 1940s and 1950s, researchers such as Norbert Wiener and Warren McCulloch attempted to use systems theory and logical calculus to describe the neural activity that gives rise to cognition. Although these models were largely Boolean and linear, they laid the groundwork for more sophisticated representations in modern computational neuroscience.

The emergence of group theory in physics, particularly in quantum field theory, brought attention to the powerful explanatory role of symmetry. Lie groups, first introduced by Sophus Lie in the 19th century, became instrumental in formulating gauge theories. The Standard Model of particle physics relies heavily on symmetry groups such as SU(3), SU(2), and U(1). Exceptional Lie groups, including G₂, F₄, E₆, E₇, and most notably E₈, were initially mathematical curiosities due to their complexity.

The E₈ Lie group is an exceptional, simply connected, complex Lie group of dimension 248, possessing a highly symmetric structure that resists decomposition into simpler classical groups. It became a candidate for a grand unified theory when, in 1985, Green and Schwarz proposed E₈ × E₈ heterotic string theory as a framework that could unify all fundamental forces, including gravity . This placed E₈ at the intersection of mathematics, cosmology, and fundamental physics.

In parallel, neuroscience continued to explore the structural and functional organization of the human neocortex. Vernon Mountcastle’s work in the 1950s and 1970s demonstrated that the neocortex is composed of vertically organized units known as cortical columns . These columns exhibit repetitive architecture across cortical areas, despite substantial functional diversity. This insight led to models in which the neocortex acts as a hierarchical, modular processing system.

The search for a rigorous mathematical language that captures the integrative and recursive nature of neocortical function has included tensor algebra, information theory, and topological data analysis. Integrated Information Theory (IIT), developed by Tononi and colleagues, provides one such framework by measuring the extent to which a system generates information as a whole, beyond its parts . Despite its utility, IIT does not directly employ high-dimensional symmetry groups like E₈.

Recent interdisciplinary work has begun to explore whether mathematical symmetries such as those in E₈ can represent not just physical forces but also cognitive structures or mental states. Meijer and Geesink proposed that E₈ quasicrystal geometry might underlie a universal information matrix in the brain . Their model suggests that the nested and recursive structure of E₈ may provide a scaffolding for non-local information processing, a concept that aligns with certain quantum theories.

Further developments by Pitkänen incorporated E₈ into a topological model of EEG phenomena, suggesting that consciousness emerges from symmetry-breaking in a multidimensional configuration space . While speculative, such approaches signal a growing willingness in the theoretical neuroscience community to adopt advanced mathematical structures from theoretical physics.

The common thread uniting these disparate efforts is the recognition that cognition, consciousness, and cortical architecture are deeply complex and may require mathematical frameworks with sufficient expressive power. E₈, with its intricate web of internal relationships and multi-layered substructures, offers one such possibility. Although experimental validation is presently lacking, conceptual models that employ E₈ symmetry provide fertile ground for theoretical exploration and hypothesis generation.

As neuroscience continues to integrate insights from artificial intelligence, theoretical physics, and complex systems, it is plausible that exceptional symmetry groups will find more concrete applications in modeling mental phenomena. The historical trajectory of E₈ from mathematical abstraction to a candidate for modeling consciousness mirrors broader trends in science where unifying formalisms migrate across disciplines.

6. Topology of Cortical Manifolds

The topology of cortical manifolds refers to the abstract, multidimensional structure underlying patterns of neural activity across the neocortex. While the cortex is a physical sheet of neural tissue with laminar and columnar organization, the activity of neurons in response to stimuli or during cognitive states often spans a space that is better understood as a nonlinear, high-dimensional manifold. This section explores how mathematical topology, particularly the use of manifolds and differential geometrycan be used.

In theoretical neuroscience, a manifold is defined as a topological space that locally resembles Euclidean space but may exhibit complex global properties. Cortical manifolds arise when neural population activity is embedded into a high-dimensional space using techniques such as principal component analysis (PCA), independent component analysis (ICA), or more recently, manifold learning algorithms like Isomap and t-SNE.

To understand this space’s topology, we consider the embedding function $f:\mathcal{N}\to {\mathbb{R}}^n$, where $\mathcal{N}$ denotes the neural state space and ${\mathbb{R}}^n$ is the ambient Euclidean space. If the neural data lie close to a lower-dimensional manifold $\mathcal{M}\subset {\mathbb{R}}^n$, then local neighborhoods in $\mathcal{N}$ are homeomorphic to open subsets in ${\mathbb{R}}^k$, where $k\ll n$.

The structure of such manifolds can be studied using persistent homology, a method from topological data analysis (TDA) that tracks features such as connected components, holes, and voids across multiple scales. Let $X\subset {\mathbb{R}}^n$ represent a finite point cloud of neural activity vectors. Constructing a family of simplicial complexes $\left\{K_{ϵ}\right\}$ parameterized by scale $ϵ$, one obtains a persistence diagram encoding the birth and death of topological features.

More concretely, suppose we observe a recurrent neural population whose firing trajectories during task performance follow a toroidal topology. If the neural activity $\mathbf{x}\left(t\right)$ traces a loop in ${\mathbb{R}}^3$, then its projection may obscure underlying dimensions, but persistent homology can recover Betti numbers ${\beta }_0,{\beta }_1,{\beta }_2$ indicating the presence of a circle (hole) or voids. The Betti numbers are algebraic invariants defined as

$${\beta }_k=\mathrm{rank}\left(H_k\left(X\right)\right),$$

(6)

where $H_k\left(X\right)$ denotes the k-th homology group of the topological space X. For a 2-torus, the Betti numbers satisfy ${\beta }_0=1$, ${\beta }_1=2$, and ${\beta }_2=1$. These topological signatures suggest the presence of nonlinear integration mechanisms and cyclic dynamics, which may play a role in memory, attention, or sensory encoding.

From a geometrical standpoint, the neocortex may also be viewed as a Riemannian manifold endowed with a metric tensor g. If $\mathcal{M}$ is a differentiable manifold, then each tangent space $T_p\mathcal{M}$ at point p allows for inner products defined by $g_p(u,v)$, where $u,v\in T_p\mathcal{M}$. The curvature of this manifold, measured via the Riemann curvature tensor R, provides insight into how trajectories evolve under geodesic flow.

$$R(X,Y)Z={\nabla }_X{\nabla }_{Y}Z-{\nabla }_Y{\nabla }_{X}Z-{\nabla }_{[X,Y]}Z,$$

(7)

where ∇ is the covariant derivative and $X,Y,Z$ are vector fields on the manifold. This formalism allows us to model signal propagation, neural dynamics, and even phase transitions in cortical states as geometric flows on manifolds.

The notion of cortical manifolds is not purely theoretical. Empirical studies have demonstrated that motor cortex activity during reach tasks lies on a low-dimensional manifold with conserved geometry across time and trials . Similarly, visual and prefrontal cortices exhibit representational manifolds whose topology evolves with learning and attention . These findings support the hypothesis that the brain performs dimensionality reduction to achieve efficient encoding.

There is increasing interest in relating these observed manifolds to mathematical structures from group theory and algebraic topology. Some researchers have proposed that the symmetry properties of these manifolds may correspond to group actions, with the E₈ Lie group as a candidate for describing transitions between stable neural states. The intuition is that high-dimensional symmetries can constrain or organize the allowed configurations of cortical activity patterns.

In summary, the topology of cortical manifolds offers a powerful lens through which to understand the emergent properties of neural computation. By framing neural activity within the language of differential topology and geometric flows, it becomes possible to unify seemingly disparate aspects of brain function under a coherent mathematical framework. Continued research in this direction may ultimately bridge the gap between abstract mathematical symmetry and biological neural dynamics.

7. Computational Model Architecture

A computational model that attempts to reflect the organizational and functional features of the neocortex inspired by E₈ symmetry must integrate hierarchical representation, modularity, and non-linear transformations. In this section, we propose a theoretical architecture grounded in symmetry-preserving transformations that mimic key attributes of the E₈ Lie algebra. This architecture is designed to explore how exceptional algebraic structures might serve as scaffolds for simulating conscious processes.

The model is structured in hierarchical layers that parallel the neocortex’s laminar organization, with six functional layers indexed as $L_1,L_2,\dots ,L_6$. Each layer is composed of computational nodes or modules that encode transformation operations drawn from the decomposition of E₈ into subalgebras such as $\mathfrak{so}\left(16\right)$, $E_7$, and $SU\left(2\right)$. The interconnections between these modules follow commutation rules inspired by Lie algebra relations.

$$h^{\left(l\right)}=\sigma \left(W^{\left(l\right)}{h}^{(l-1)}+b^{\left(l\right)}\right),$$

(8)

where $h^{\left(l\right)}\in {\mathbb{R}}^n$ is the activation vector in layer l, $W^{\left(l\right)}\in {\mathbb{R}}^{n\times n}$ is the transformation matrix reflecting E₈ symmetries, $b^{\left(l\right)}$ is a bias vector, and $\sigma$ is a non-linear activation function. These matrices are constructed to respect algebraic properties such as anti-symmetry and closure under bracket operations. The overall transformation across layers becomes:

$$H=\mathcal{F}\left(x\right)=\sigma \left(W^{\left(6\right)}\sigma \left(W^{\left(5\right)}\dots \sigma \left(W^{\left(1\right)}x+b^{\left(1\right)}\right)\dots +b^{\left(5\right)}\right)+b^{\left(6\right)}\right),$$

(9)

where x is the input stimulus and H the final output state vector, potentially corresponding to a conscious percept or decision.

The matrices $W^{\left(l\right)}$ are initialized using structured sparsity based on E₈’s root lattice. Given that E₈ has 248 generators and 240 roots, the model selects a 248-dimensional space to represent full symmetry. To make the model tractable, subspaces of lower dimensionality are projected using orthogonal transformation matrices $P_k$, leading to:

$$W^{\left(l\right)}=P_k^{\top }\Lambda P_k,$$

(10)

where $\Lambda$ is a diagonal matrix encoding the eigenvalues associated with selected symmetry generators, and $P_k\in {\mathbb{R}}^{n\times 248}$ projects E₈ space into the neural subspace ${\mathbb{R}}^n$. These projections preserve group-theoretic relationships while reducing computational cost.

Modularity is enforced via cluster decomposition, where node groups operate on distinct root subsystems such as $E_6\subset E_7\subset E_8$. Each cluster is governed by a set of commuting matrices satisfying:

$$[W^{\left(i\right)},W^{\left(j\right)}]=0\mathrm{if}i,j\in C_k,$$

(11)

where $C_k$ denotes the k-th cluster. This design mimics cortical modularity, allowing information to be processed in a partially segregated yet integrative manner. Non-commuting operations between clusters simulate long-range cortical interactions.

One important dynamical feature of the model is state collapse, analogous to decision-making or conscious report. This is modeled using a symmetry-breaking potential function V, defined over output activations:

$$V\left(H\right)=\sum _{i=1}^n\left({\displaystyle \frac{1}{4}}{H}_i^4-{\displaystyle \frac{1}{2}}{\mu }^2{H}_i^2\right),$$

(12)

where $\mu$ is a control parameter. This double-well potential introduces bistability, simulating how symmetrical input states may collapse into distinct output attractors, analogous to perceptual bifurcation.

Training the model involves minimizing a loss function $\mathcal{L}$ defined as:

$$\mathcal{L}={\displaystyle \frac{1}{N}}\sum _{i=1}^N{∥H_i-y_i∥}^2+\lambda \sum _{l=1}^6{∥[W^{\left(l\right)},W^{\left(l\right)\top }]∥}_F^2,$$

(13)

where $y_i$ is the target output, $\lambda$ is a regularization coefficient, and the second term penalizes deviation from symmetry-preserving transformations by minimizing Frobenius norm of the commutators. This term encourages the matrices to maintain their algebraic constraints.

This computational architecture is currently theoretical but could be instantiated in simulation frameworks such as TensorFlow or PyTorch. Its design draws from the interplay between algebraic structure and neural function and offers a testbed to explore whether E₈-inspired dynamics yield cognitive phenomena observed in biological systems. In addition to mathematical elegance, the architecture potentially opens pathways for explainable AI systems rooted in neurobiological plausibility.

8. Mathematical Analogues for Cortical Feedback Loops

Cortical feedback loops are fundamental to cognitive processes such as attention, working memory, and predictive coding. These loops facilitate top-down modulation of sensory information and maintain internal representations across time. To better understand these feedback mechanisms, it is useful to construct mathematical analogues that formalize the dynamic interactions between cortical areas. The E₈ Lie algebra offers a rich structural foundation for this modeling due to its dense connectivity.

Let us consider a simplified model where cortical regions are represented by nodes $R_i$ in a directed graph $G=(V,E)$, with edges corresponding to directional synaptic influence. The dynamics of each node are given by a system of coupled differential equations:

$${\displaystyle \frac{d{\mathbf{u}}_i}{dt}}=-\alpha {\mathbf{u}}_i+\sum _{j\in \mathcal{N}\left(i\right)}{W}_{ij}·\varphi \left({\mathbf{u}}_j\right),$$

(14)

where ${\mathbf{u}}_i\in {\mathbb{R}}^n$ is the state vector of region $R_i$, $\alpha$ is a decay constant, $W_{ij}$ is a connection weight matrix encoding symmetry properties, and $\varphi$ is a non-linear activation function. This formulation captures both excitation and inhibition via feedback interactions.

To incorporate algebraic structure from E₈, we define each weight matrix $W_{ij}$ as a projection from an element in the Lie algebra ${\mathfrak{e}}_8$. Let $T^a\in {\mathfrak{e}}_8$ be the generator basis, with commutation relations:

$$[T^a,T^b]=f^{abc}{T}^c,$$

(15)

where $f^{abc}$ are the structure constants of E₈. The feedback loop is modeled by recursive applications of these generators to the state vectors, yielding transformation chains such as:

$${\mathbf{u}}_i(t+\Delta t)=exp\left(\Delta t\sum _a{\lambda }^a{T}^a\right)·{\mathbf{u}}_i\left(t\right),$$

(16)

where ${\lambda }^a\in \mathbb{R}$ are dynamically adjusted coefficients representing modulation strength. These exponentials form elements of the Lie group $E_8$, simulating rotational and symmetry-preserving transformations of neural states.

Feedback pathways often form closed circuits across multiple cortical areas. These loops can be abstracted as algebraic cycles within the symmetry group. Consider a feedback circuit $R_1\to R_2\to \dots \to R_k\to R_1$, whose net effect is represented by the product of group elements $g_1,g_2,\dots ,g_k\in E_8$. If the resulting product $g_{\mathrm{loop}}=g_k\dots g_2{g}_1$ is the identity element, the loop is symmetry-preserving.

To analyze stability, one can define a Lyapunov function $V\left(\mathbf{u}\right)$ associated with the state dynamics. If V is minimized over time, then the feedback system is stable. For instance, a potential of the form

$$V\left(\mathbf{u}\right)={\displaystyle \frac{1}{2}}\sum _{i=1}^N{\parallel {\mathbf{u}}_i-\overline{\mathbf{u}}\parallel }^2,$$

(17)

quantifies the deviation from a target state $\overline{\mathbf{u}}$. Feedback weights that respect E₈ commutation relations tend to maintain or restore symmetry, guiding the system toward low-energy configurations.

Importantly, feedback systems also implement predictive coding. Let ${\widehat{\mathbf{u}}}_i$ be the predicted state of a lower-level region and ${\mathbf{u}}_i$ its observed state. The prediction error ${\epsilon }_i={\mathbf{u}}_i-{\widehat{\mathbf{u}}}_i$ can be minimized through gradient descent in the weight space:

$${\displaystyle \frac{d{W}_{ij}}{dt}}=-\eta {\displaystyle \frac{\partial {\epsilon }_i^2}{\partial W_{ij}}},$$

(18)

where $\eta$ is the learning rate. When $W_{ij}$ are constrained to lie in subalgebras of E₈, the optimization is confined to symmetry-respecting directions. This constraint may facilitate efficient learning and robust generalization.

Incorporating mathematical structures like fiber bundles further refines the model. Each cortical area corresponds to a base space, with fiber spaces encoding local activity patterns. The transition functions between fibers are group-valued maps $g_{ij}:U_i\cap U_j\to E_8$, ensuring consistent transformation across overlapping domains. This formalism naturally leads to gauge-theoretic interpretations of cortical feedback.

Ultimately, these mathematical analogues provide a systematic approach to represent cortical feedback loops not just as signal pathways but as symmetry-governed transformations in high-dimensional state spaces. By employing E₈ as a constraint space, the model proposes a novel way to formalize and possibly unify dynamical feedback mechanisms observed across the neocortex.

9. Information-Theoretic Perspectives

Information theory offers a powerful framework for quantifying the dynamics and structure of neural computations in the brain. Originally developed by Claude Shannon, information theory has evolved into a foundational tool in neuroscience for characterizing the entropy, mutual information, and redundancy of neural codes. Within the context of E₈ symmetry, information-theoretic measures can be embedded in the algebraic and topological structure of neural state spaces.

Let us denote the state of a neural population as a random variable X with probability distribution $P\left(x\right)$, where $x\in {\mathbb{R}}^n$. The Shannon entropy of this distribution is given by:

$$H\left(X\right)=-\sum _{x}P\left(x\right)logP\left(x\right),$$

(19)

which quantifies the average uncertainty or information content in the state of the system. If the activity vectors lie on a manifold structured by E₈ symmetries, the entropy can be analyzed across invariant subspaces. The symmetry constraints reduce the effective dimensionality, potentially compressing information representation while preserving expressive power.

Consider now two interacting neural populations X and Y, corresponding to different cortical regions. The mutual information between them is:

$$I(X;Y)=\sum _{x,y}P(x,y)log{\displaystyle \frac{P(x,y)}{P\left(x\right)P\left(y\right)}},$$

(20)

which measures how much knowing one variable reduces uncertainty about the other. Within an E₈-inspired architecture, the mutual information can be constrained by the group’s representation theory. Specifically, if X and Y evolve under commuting group actions $g_X$ and $g_Y\in E_8$, the invariance properties imply that mutual information is preserved under these transformations.

Another important quantity is the multi-information or total correlation for a set of n regions $X_1,X_2,\dots ,X_n$, defined as:

$$TC(X_1,\dots ,X_n)=\left(\sum _{i=1}^{n}H\left(X_i\right)\right)-H(X_1,\dots ,X_n),$$

(21)

which measures the deviation from statistical independence. High total correlation may indicate integrative processing or synchronized activity, potentially aligned with invariant submanifolds of the E₈ configuration space.

Integrated Information Theory (IIT) introduces another useful quantity $\Phi$, which quantifies how much information is lost when a system is partitioned. Although IIT does not explicitly rely on Lie group symmetries, the mathematical formalism could be extended. Suppose a system’s state is represented by a vector $\mathbf{x}\in {\mathbb{R}}^{248}$, with dynamics governed by a Lie algebra ${\mathfrak{e}}_8$. Partitioning the system corresponds to breaking ${\mathfrak{e}}_8$ into independent submanifolds.

To compute integrated information, let $P\left(\mathbf{x}\right)$ be the probability distribution over full states and $P_A\left({\mathbf{x}}_A\right)P_B\left({\mathbf{x}}_B\right)$ be the distribution over partitioned states. Then $\Phi$ is defined as:

$$\Phi =D_{KL}\left(P\left(\mathbf{x}\right)\parallel P_A\left({\mathbf{x}}_A\right)P_B\left({\mathbf{x}}_B\right)\right),$$

(22)

where $D_{KL}$ is the Kullback–Leibler divergence. High values of $\Phi$ indicate strong interdependence across the system, which in this framework corresponds to inseparability within the E₈ symmetry network.

Entropy production in non-equilibrium systems is another concept relevant to neural dynamics. Let $P(x,t)$ be the time-dependent distribution over neural states. The entropy production rate is:

$$\dot{S}=\sum _x{\displaystyle \frac{dP(x,t)}{dt}}log{\displaystyle \frac{P(x,t)}{P_{\mathrm{eq}}\left(x\right)}},$$

(23)

where $P_{\mathrm{eq}}$ is the equilibrium distribution. Feedback and feedforward pathways organized by group transformations from E₈ may stabilize or accelerate convergence to equilibrium. These symmetries could minimize entropy production, aligning with the free energy principle proposed by Friston .

E₈ symmetry may also help define new types of entropy constraints. For example, entropy conditioned on subgroup structures $G\subset E_8$, such as $E_7$ or $SU\left(3\right)$, can be used to localize information dynamics within modules. Suppose G acts on a subspace ${\mathcal{M}}_G\subset {\mathbb{R}}^{248}$, and we define the conditional entropy as:

$$H\left(X\right|{\mathcal{M}}_G)=-\sum _{x\in {\mathcal{M}}_G}P\left(x\right)logP\left(x\right).$$

(24)

Such a formalism provides a multi-scale, symmetry-informed framework for representing functional specialization within cortical networks.

In summary, information-theoretic tools can be systematically embedded within E₈-based models of cortical computation. These tools allow quantification of uncertainty, integration, and predictive capacity while preserving the algebraic invariants that define the system’s structure. The integration of entropy, mutual information, and integrated information into the framework of E₈ offers a rich, mathematically grounded pathway for modeling cognitive phenomena in the brain.

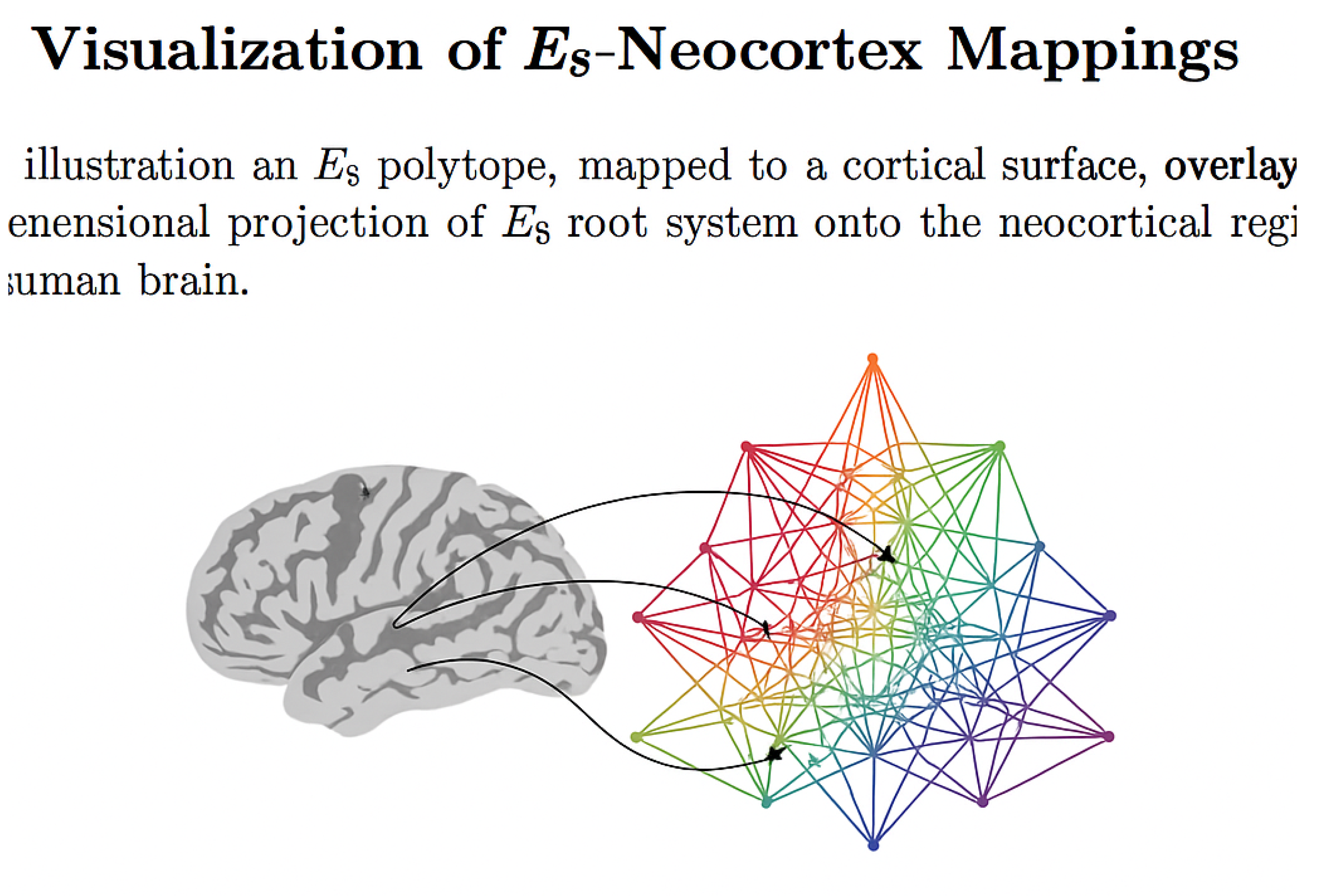
10. Visualization of E₈–Neocortex Mappings

Visualizing the connection between E₈ symmetry and the neocortex requires a projection from a highly abstract, 248-dimensional mathematical object to the biological three-dimensional structure of the brain. A fundamental strategy involves the projection of E₈’s root system into two or three dimensions and then mapping these geometrical embeddings onto flattened cortical surfaces.

A promising approach is to align the E₈ root lattice projection with topological representations of cortical columns or regional networks in the brain. These projections can be generated using root diagram reduction techniques and visualized using force-directed layout algorithms. The connections between E₈ root vectors are interpreted as relational symmetries or signal pathways among cortical modules. This technique emphasizes the structural correspondence rather than spatial congruence.

To facilitate conceptual integration, we provide a figure illustrating a 2D projection of the E₈ polytope overlaid on a schematic of the neocortex. In this mapping, colored vertices in the E₈ graph represent neural clusters or processing modules, and the edges correspond to functional or anatomical connections. These connections mirror the commutators or symmetry-preserving transformations in the E₈ Lie algebra. The image exemplifies how specific parts of the polytope may relate to functional cortical areas.

Figure 1. Conceptual mapping of the E₈ root system onto a neocortical surface. The diagram illustrates functional analogies between cortical areas and E₈ symmetry vectors.

Figure 1. Conceptual mapping of the E₈ root system onto a neocortical surface. The diagram illustrates functional analogies between cortical areas and E₈ symmetry vectors.

Such visual models provide heuristic tools to explore hypothetical alignments between brain structure and high-dimensional symmetry. While purely theoretical at this stage, they offer frameworks for constructing testable models and simulations in computational neuroscience, further illuminating the potential informational role of exceptional symmetry in biological systems.

11. Neuroscientific Validation Strategies

The theoretical alignment between E₈ symmetry and neocortical function offers a fertile ground for hypothesis generation, but its legitimacy must ultimately rest upon empirical validation. This section outlines strategies for testing the plausibility of E₈-inspired models through neuroscientific experimentation and computational simulation. The core challenge lies in operationalizing abstract algebraic structures within the context of biological data.

One possible approach is to investigate whether neural dynamics observed in the brain exhibit symmetry properties analogous to those in E₈. Functional connectivity matrices, derived from functional magnetic resonance imaging (fMRI), electroencephalography (EEG), or magnetoencephalography (MEG), can be subjected to eigenvalue decomposition to extract dominant modes of interaction. The resulting spectra can show degeneracies or invariant subspaces corresponding to representations of Lie algebras.

Let $C\left(t\right)\in {\mathbb{R}}^{n\times n}$ be the time-varying functional connectivity matrix between n cortical regions. The spectral decomposition is given by:

$$C\left(t\right)=Q\left(t\right)\Lambda \left(t\right)Q{\left(t\right)}^{\top },$$

(25)

where $Q\left(t\right)$ is an orthogonal matrix of eigenvectors and $\Lambda \left(t\right)$ is the diagonal matrix of eigenvalues. A stationary symmetry would be evidenced by conservation of eigenspace topology over time. Furthermore, symmetries across subgroups such as E₆ or E₇ nested within E₈ may appear as structured degeneracies in subsets of the spectrum.

High-resolution diffusion-weighted imaging (DWI) can provide structural connectivity maps, allowing researchers to compare anatomical modules with projections of E₈’s root lattice. Suppose the cortical areas are indexed by a set $\left\{R_i\right\}$, and the edge strength between nodes is given by a matrix A. A mapping $\varphi :R_i\to e_j$, where $e_j\in {\mathfrak{e}}_8$, could be constructed to test whether cortical adjacency correlates with proximity in E₈ root space.

$$\rho ={\displaystyle \frac{\mathrm{Cov}(d_A,d_E)}{{\sigma }_{d_A}{\sigma }_{d_E}}},$$

(26)

where $d_A$ is the cortical distance matrix and $d_E$ is the pairwise Euclidean distance between mapped E₈ roots, quantifies this alignment. A statistically significant positive correlation would suggest that E₈ captures some latent organization in neocortical structure.

Another strategy is to employ topological data analysis (TDA) to investigate the geometry of neural manifolds. Persistent homology can be applied to neural activity vectors collected from multi-electrode recordings or neural simulations. Suppose $\mathcal{X}\subset {\mathbb{R}}^n$ is a point cloud representing neural states. The persistent homology barcodes can be compared with expected Betti numbers from E₈-derived topological spaces.

Time-series data from EEG or MEG can also be modeled using state-space models whose dynamics are constrained by symmetry. Suppose the neural state vector $x\left(t\right)\in {\mathbb{R}}^n$ evolves according to:

$${\displaystyle \frac{dx}{dt}}=f\left(x\right)+\sum _{a=1}^{248}{\lambda }^a{T}^{a}x,$$

(27)

where $T^a\in {\mathfrak{e}}_8$ are Lie algebra generators and ${\lambda }^a$ are time-dependent modulation coefficients. Fitting such models to empirical data and evaluating prediction accuracy compared to unconstrained alternatives offers a direct validation pathway.

In addition to brain imaging, behavioral experiments involving perceptual bistability, working memory, or decision making can be used to test predictions of symmetry-induced attractor dynamics. For instance, if certain cognitive transitions correspond to symmetry breaking in an E₈ configuration space, reaction time distributions and error rates may align with simulated trajectories in this abstract space. Measuring such correspondences would require careful experimental design and computational models.

Finally, artificial neural networks structured with E₈-based architectures can be trained on cognitive tasks. Their internal representations, connectivity matrices, and activation dynamics can be compared with brain data. If these models not only match human performance but also exhibit structural similarity to cortical data, it would suggest that E₈ provides a functionally relevant inductive bias.

In conclusion, neuroscientific validation of the E₈–neocortex hypothesis must proceed through a combination of empirical brain data analysis, computational modeling, and simulation of E₈-constrained systems. While the hypothesis is currently speculative, these methodologies offer a concrete path toward assessing its viability and uncovering whether high-dimensional symmetries may indeed underpin cognitive computation.

12. Implications for Artificial Intelligence

The exploration of E₈ symmetry within the context of the neocortex opens new directions for artificial intelligence (AI), particularly in the development of architectures that emulate high-dimensional, symmetry-governed computation. Traditional AI models, especially deep learning systems, rely on layer-wise transformations of data using matrices learned from task-specific data distributions. While effective, these systems lack the structural regularity and mathematical elegance seen in biological systems.

One promising implication is the use of E₈ as a constraint space for network design. In typical neural networks, transformation matrices $W^{\left(l\right)}$ between layers are initialized randomly or using heuristics like Xavier initialization. By contrast, an E₈-inspired architecture constrains the weight space to lie within or project from the Lie algebra ${\mathfrak{e}}_8$. Let $T^a$ be the 248 generators of E₈, and define a layer-wise transformation as:

$$h^{\left(l\right)}=\sigma \left(\sum _{a=1}^{248}{\lambda }_a^{\left(l\right)}{T}^a{h}^{(l-1)}+b^{\left(l\right)}\right),$$

(28)

where ${\lambda }_a^{\left(l\right)}$ are trainable coefficients, $b^{\left(l\right)}$ is the bias term, and $\sigma$ is a non-linear activation function. This approach embeds structured transformations into the learning process, potentially improving generalization and interpretability.

Moreover, E₈’s nested symmetry allows for multi-resolution representations. For instance, subnetworks can be structured to reflect the subalgebra nesting $E_6\subset E_7\subset E_8$, enabling hierarchical feature learning across scales. The model naturally decomposes into modules that preserve intra-module symmetry and inter-module transformation paths. Let ${\mathcal{N}}_i$ be the set of nodes in module i, and let transformations within modules satisfy:

$$[T^a,T^b]=f^{abc}{T}^c,\mathrm{for}{T}^a,T^b\in {\mathfrak{g}}_i,$$

(29)

where ${\mathfrak{g}}_i\subset {\mathfrak{e}}_8$ is the subalgebra associated with module i. Interactions between modules are mediated by non-commuting transformations, producing rich representational dynamics analogous to feedback in the cortex.

The generative capacity of such a network can be evaluated using an entropy-based loss function. Suppose the output distribution of the network is $P\left(y\right|x)$, and the target distribution is $Q\left(y\right)$. A combined loss that includes Kullback–Leibler divergence and a symmetry regularization term can be expressed as:

$$\mathcal{L}=D_{KL}(Q\parallel P)+\lambda \sum _{l=1}^L{∥[W^{\left(l\right)},W^{\left(l\right)\top }]∥}_F^2,$$

(30)

where the second term penalizes deviations from symmetry-preserving structure, and $\lambda$ is a regularization parameter. Networks trained under such constraints may not only learn faster but also resist overfitting by operating within a reduced, meaningful subspace.

Another implication involves few-shot learning. The high symmetry of E₈ may enable better generalization from sparse data. A model with E₈ symmetry encodes a large number of relational invariants, which effectively serve as inductive priors. This could be especially useful in meta-learning, where the goal is to learn new tasks quickly using prior knowledge embedded in the architecture. In this view, the symmetry group encodes meta-knowledge about transformation invariance and relational structure.

Furthermore, such models may lend themselves to more interpretable AI. Since the transformations are not arbitrary but derived from known algebraic generators, the path of feature evolution through the network can be decomposed and attributed to specific components of ${\mathfrak{e}}_8$. This transparency aligns with current research trends in explainable AI, providing an avenue to trace how and why decisions are made.

The implications extend to reinforcement learning as well. If agent policies are parametrized using E₈-constrained networks, then action selection can occur within a structured manifold of possibilities. This may improve exploration strategies and convergence in high-dimensional action spaces, especially in continuous control problems. Let $\pi \left(a\right|s)$ be the policy distribution. Embedding this in an E₈-structured latent space allows for latent policy updates driven by symmetry-preserving vector.

Finally, E₈-inspired architectures may have hardware implications. Emerging fields like neuromorphic computing can exploit the sparsity and symmetry of E₈ to design energy-efficient circuits that encode complex transformations with minimal resource expenditure. Specialized hardware that implements Lie group operations could enhance speed and robustness in real-time AI applications.

In conclusion, importing the structure of E₈ into artificial intelligence offers a rich landscape of innovation. From enhanced generalization and robustness to interpretability and efficiency, the implications span multiple subfields. While still speculative, these directions provide testable hypotheses and engineering opportunities for next-generation AI systems.

13. Limitations and Criticisms

While the theoretical linkage between the exceptional Lie group E₈ and the structure of the human neocortex is conceptually appealing, this hypothesis faces several substantial limitations and criticisms. These challenges span mathematical, neuroscientific, computational, and philosophical domains. This section offers a critical examination of these limitations, providing a balanced perspective on the feasibility and scope of this interdisciplinary proposal.

One of the principal limitations is the sheer abstraction of the E₈ group. E₈ is a highly complex mathematical object defined in 248-dimensional space, and while its algebraic properties are well-understood in theoretical physics, particularly in string theory and grand unified theories, the mapping to a biological system such as the neocortex remains speculative. The brain is not known to operate explicitly using Lie algebras.

Moreover, the dimensional mismatch between the biological neocortex and the algebraic structure of E₈ is nontrivial. While the neocortex comprises billions of neurons distributed over a convoluted 3D sheet, E₈ lies in a 248-dimensional abstract space with no natural embedding into Euclidean three-space. Attempts to project E₈’s symmetry structure onto cortical manifolds may oversimplify or misrepresent both systems. There exists no established mechanism by which biological evolution would have favoured this.

There are also criticisms regarding the risk of overfitting and pattern-seeking. The human brain is particularly adept at identifying patterns, even where none exist. Imposing the structure of E₈ onto cortical connectivity may be an example of mathematical pareidolia—the tendency to impose a theoretical framework that appears elegant or complete without sufficient empirical basis. This problem is exacerbated when visualizations and root projections are interpreted too literally.

On the computational side, constraining AI or brain-inspired models to obey E₈ symmetries introduces significant overhead. Training networks within Lie algebraic constraints is computationally intensive and may offer only marginal benefits unless the symmetry aligns very closely with the structure of the task or data distribution. The learning landscape under such constraints may become more rugged or degenerate, hampering convergence.

Formally, any such symmetry-constrained learning model must obey:

$$W=\sum _{a=1}^{248}{\lambda }_a{T}^a,{\lambda }_a\in \mathbb{R},$$

(31)

where $T^a\in {\mathfrak{e}}_8$ are the generators of the Lie algebra. Ensuring closure under such representations during training demands projection operations and algebraic regularization, which may introduce instability in optimization dynamics. Empirical AI models have succeeded not because of symmetry per se but because of their flexibility and scalability on real-world data.

From the neuroscientific perspective, most evidence of brain symmetry is found at macrostructural or mesoscopic scales, such as bilateral symmetry or laminar organization. These do not suggest high-order algebraic structures like E₈, which is characterized by exceptional triality and reflection symmetries absent from known cortical topology. Cortical dynamics tend to be nonlinear, non-equilibrium, and highly stochastic, all properties that are difficult to reconcile with the algebraic determinism.

Furthermore, the model may be criticized for epistemological overreach. E₈ is often invoked in attempts to build “theories of everything,” and using it to explain consciousness or neural computation may be perceived as an extension of that tradition without sufficient methodological rigor. Such associations may undermine the credibility of the framework unless clear, falsifiable predictions and testable consequences are derived and validated.

The notion of mathematical beauty as a guide to truth is itself contested. While symmetry has proven powerful in physics, biology often favors functionality, robustness, and adaptivity over elegance. As such, models grounded in symmetry must be shown not merely to fit data but to outperform asymmetric alternatives in predictive, generative, or explanatory power.

In conclusion, while the E₈–neocortex hypothesis is intellectually stimulating and potentially unifying, it is currently speculative and must be approached with caution. Its limitations include lack of empirical evidence, potential for conceptual overreach, biological implausibility, and computational inefficiency. Nevertheless, these criticisms serve a valuable role by guiding the development of more grounded, testable, and interdisciplinary frameworks.

14. Philosophical and Epistemological Reflections

The intersection of high-dimensional algebraic symmetry and neural computation invites deep philosophical and epistemological inquiry. The proposition that the E₈ Lie group—an object of extraordinary mathematical structure—could be meaningfully mapped onto the architecture of the human neocortex challenges traditional views of both cognition and mathematics. It provokes foundational questions about the nature of scientific models, the criteria for explanatory adequacy, and the metaphysical status.

One of the most significant philosophical issues pertains to the **nature of mathematical realism**. If E₈ accurately models aspects of neocortical processing, this may support the Platonist position that mathematical entities have objective existence independent of human cognition. The human brain, in this view, would not merely use mathematics as a descriptive tool but would itself be a system that enacts or instantiates deep mathematical truths.

Furthermore, the proposal engages the **epistemology of symmetry**. In physics, symmetry principles are often considered more fundamental than the equations they constrain. The Standard Model, general relativity, and string theory all rely on symmetry as an organizing principle. If similar principles underlie cognition, then symmetry may be epistemologically prior to function, and understanding the brain may require an algebraic rather than algorithmic perspective.

The notion of symmetry guiding scientific explanation also connects to ideas of **aesthetic rationality**. Many scientists and philosophers have argued that simplicity, elegance, and beauty are not merely subjective aesthetic preferences but indicators of deep truth. The E₈ structure is often cited as a pinnacle of mathematical elegance. Its invocation in modeling the neocortex may reflect a desire to unify cognitive science under the same principles that structure the physical universe.

In epistemology, another tension arises between **explanatory depth and empirical testability**. Deep theories often entail concepts far removed from observable phenomena. Theories involving E₈, while deep and unifying, face difficulties in making falsifiable predictions. In Popperian terms, a scientific hypothesis must be refutable. If E₈–neocortex models cannot be tested, they risk becoming metaphysical rather than scientific. This limitation forces a reevaluation of what constitutes explanation.

The **problem of reductionism** is also central. The application of E₈ to the brain implies a reduction of neurobiological complexity to algebraic form. Yet complex systems theory has long cautioned against such reductions, arguing that higher-level phenomena possess emergent properties not explicable by their lower-level constituents alone. Philosophers like Anderson have emphasized that "more is different" .

Moreover, the model invites reflection on **epistemic humility**. The history of science is replete with elegant theories that failed to correspond to reality. From phlogiston to epicycles, many conceptually beautiful systems were eventually discarded due to lack of empirical support. The use of E₈ must therefore be accompanied by caution and openness to revision, even as it seeks to chart novel explanatory terrain.

Lastly, the project challenges conventional **boundaries between disciplines**. Mathematics, physics, neuroscience, and philosophy converge in this effort. Such interdisciplinarity can be epistemically fruitful but also epistemologically hazardous. Concepts from one domain, when transferred to another, risk distortion or misuse. The philosophical task is to ensure conceptual coherence across domains and to guard against category errors—such as treating metaphorical correspondences as literal identities

In summary, the hypothesis connecting E₈ symmetry to neocortical structure is not merely a scientific proposition but a philosophical one. It touches on the foundations of mathematics, the role of symmetry in explanation, the tension between beauty and truth, and the limits of reductionism. As such, it demands a reflective stance that is both rigorous and speculative, disciplined and open, grounded in formalism yet alert to the contingencies of empirical science.

15. Discussion and Implications

The hypothesis connecting the E₈ Lie group with the architecture and function of the neocortex presents a speculative but potentially transformative avenue in cognitive neuroscience and mathematical modeling. The discussion of this hypothesis invites reflection across several dimensions, including computational, neuroscientific, epistemological, and philosophical domains. The central premise is that the neocortex may instantiate or approximate high-dimensional symmetry operations.

From a computational standpoint, one implication is the proposal of a radically different inductive bias for artificial neural networks. By replacing traditional unconstrained weight matrices with transformations derived from the algebraic structure of E₈, it may be possible to create AI systems with more robust generalization, efficient representation, and interpretable internal dynamics. The high dimensionality and structured redundancy of E₈ permit a greater diversity of transformational trajectories.

In neuroscience, the use of E₈ as a generative scaffold offers novel hypotheses about the topological organization of cortical manifolds. For example, feedback loops and cross-regional signaling could correspond to transformations within specific subalgebras, while persistent neural states may resemble attractors embedded in the root lattice. This approach offers a rigorous framework within which known biological features—such as recurrent connectivity, dimensional reduction in perception, fit in.

Moreover, the approach invites new tools for analysis and validation. Algebraic decomposition of connectivity matrices, persistent homology of neural data, and dynamic models constrained by Lie group generators all provide avenues for empirical evaluation. These methods create the possibility of testing whether the high-order symmetries postulated by E₈ are in any sense present in real neural dynamics or are useful abstractions for approximating them.

Philosophically, the hypothesis forces a reconsideration of the relationship between mathematics and mind. If the human brain exploits structures resembling those of E₈, it may suggest that cognition is not just modeled by mathematics but is itself a mathematical phenomenon. Such a claim moves beyond metaphor toward a metaphysical assertion that the very fabric of cognitive dynamics could be algebraic in nature. This view aligns with recent work in mathematical Platonism and information-theoretic approaches.

Additionally, implications extend to epistemology and the philosophy of science. E₈–based modeling demands a rethinking of how theories are judged: not only by empirical adequacy but also by structural coherence, mathematical elegance, and generative power. These criteria may guide the development of hybrid theories that integrate biological realism with abstract formalism.

Finally, in the domain of artificial intelligence, adopting E₈-constrained architectures could redefine what is considered an optimal inductive bias. Traditional AI has been grounded in statistical learning and hierarchical representation. The E₈ hypothesis suggests that future models may benefit from a symmetry-centric approach that encodes functional relations within an algebraically structured latent space.

16. Conclusions

The investigation into the correspondence between the E₈ Lie group and the structural and functional architecture of the human neocortex presents a bold interdisciplinary hypothesis. Throughout this paper, we have proposed that the profound symmetry and high-dimensional geometry of E₈ offer a mathematically rigorous lens through which the dynamics of cortical computation may be understood. This hypothesis, while speculative, serves as a framework for unifying algebraic formalism with neural architecture.

Our exploration began with a historical and theoretical context, tracing the mathematical properties of E₈ and its emergence in high-energy physics and algebraic geometry. We then examined the relevance of topological and geometric methods in describing cortical manifolds, drawing parallels between persistent neural dynamics and invariant structures within E₈. From this foundation, we introduced a computational model architecture grounded in E₈ algebra, designed to represent cortical feedback loops.

In seeking validation, we considered a range of neuroscientific strategies, including imaging techniques, topological data analysis, and Lie algebraic modeling of neural time series. These methods not only provide pathways for empirical grounding but also highlight the technical challenges inherent in operationalizing such a high-dimensional and abstract mathematical construct within the domain of biological cognition.

The paper further elaborated on the implications of this framework for artificial intelligence, suggesting that E₈-inspired architectures may lead to more generalizable, interpretable, and structured forms of machine learning. Philosophical reflections emphasized the relevance of this inquiry for debates on mathematical realism, the epistemology of symmetry, and the nature of explanatory adequacy in complex systems.

Nonetheless, the proposal is not without limitations. The abstraction level of E₈, the absence of direct biological evidence, and the computational demands of symmetry-constrained modeling all pose significant hurdles. These limitations, however, do not undermine the value of the hypothesis as a conceptual scaffold. Rather, they encourage the formulation of testable predictions, rigorous modeling strategies, and interdisciplinary collaborations.

In summary, the proposed E₈–neocortex correspondence is an ambitious theoretical construct that aims to bridge mathematics and mind. While much work remains to be done to validate or falsify the framework, its potential to stimulate new research directions in neuroscience, mathematics, and artificial intelligence justifies its continued exploration. By embedding cognition within a space of algebraic elegance and geometric coherence, the E₈ hypothesis invites us to reimagine the foundations of intelligence.