Submitted:
20 October 2025
Posted:
22 October 2025
You are already at the latest version
Abstract
This study investigates the algebraic and geometric structures that emerge from the intersection of Octonionic algebras and the IRSVT (Informational Resonance Spiral Viscous Time) framework. We propose a paradigm in which non-associative hypercomplex numbers act as logical mediators between coherence and decoherence domains in informational space. By embedding Octonions within IRSVT topologies, we uncover a manifold where classical algebraic constraints dissolve, giving rise to an orthogonal logic field defined by coherence gradients (ΔC) and attractor dynamics (Φα). Through analytical expansion, spectral validation, and the construction of an informational Hilbert manifold, we demonstrate that Octonions enable transformations across generative geometries, where space and meaning co-evolve. Our findings suggest that Octonions may function not merely as algebraic curiosities but as fundamental operators of informational reality, opening pathways for applications in field unification, AI logic systems, informational materials, and non-classical computation models.
Keywords:
1. Introduction
2. Materials and Methods
2.1. Theory Foundation
2.1.1. Octonionic Foundations and Informational Algebra
2.1.2. Reconstructing Non—Associativity through informational Spiral Collapse
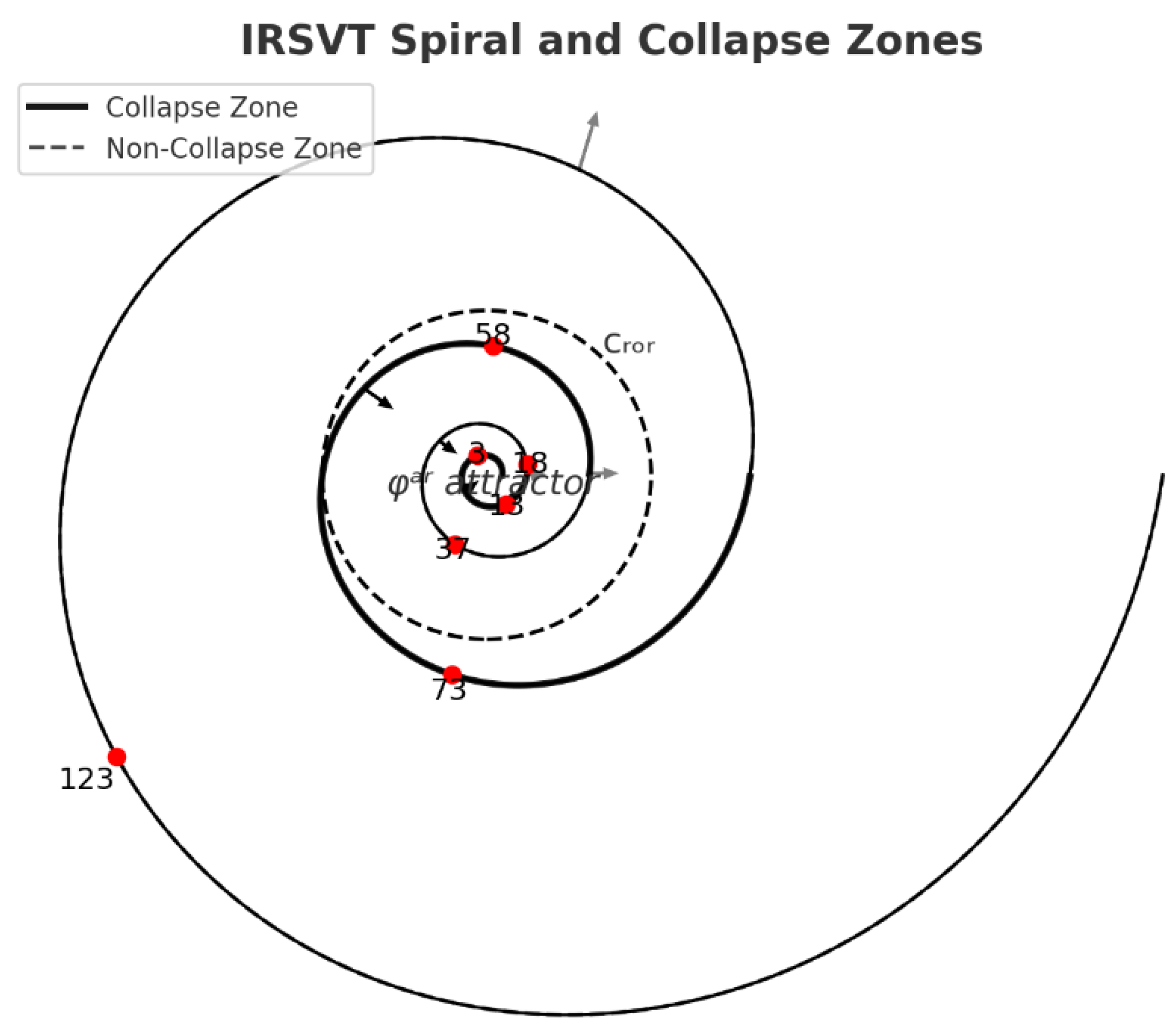
- RSVT Spiral as Informational Topology
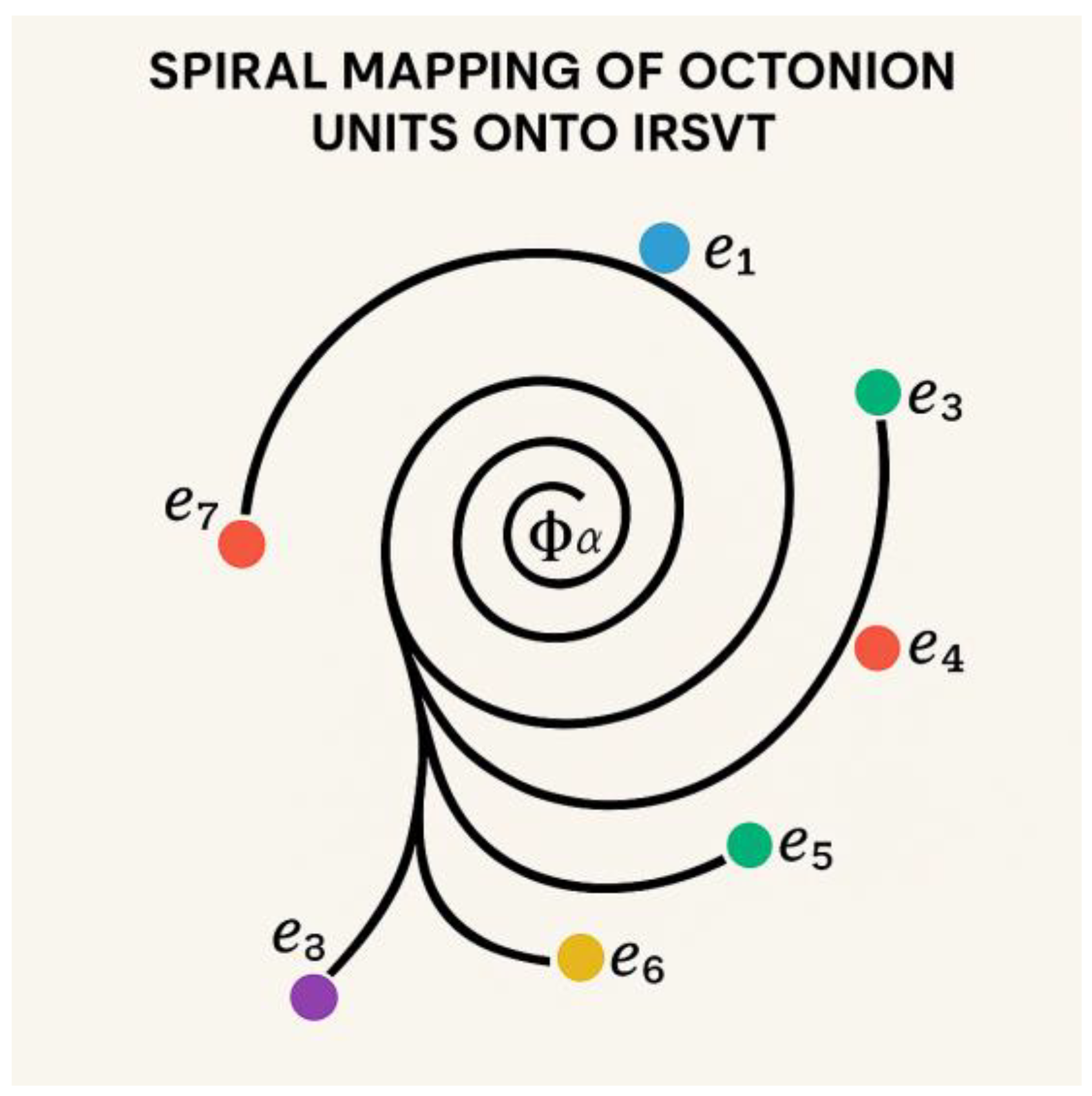
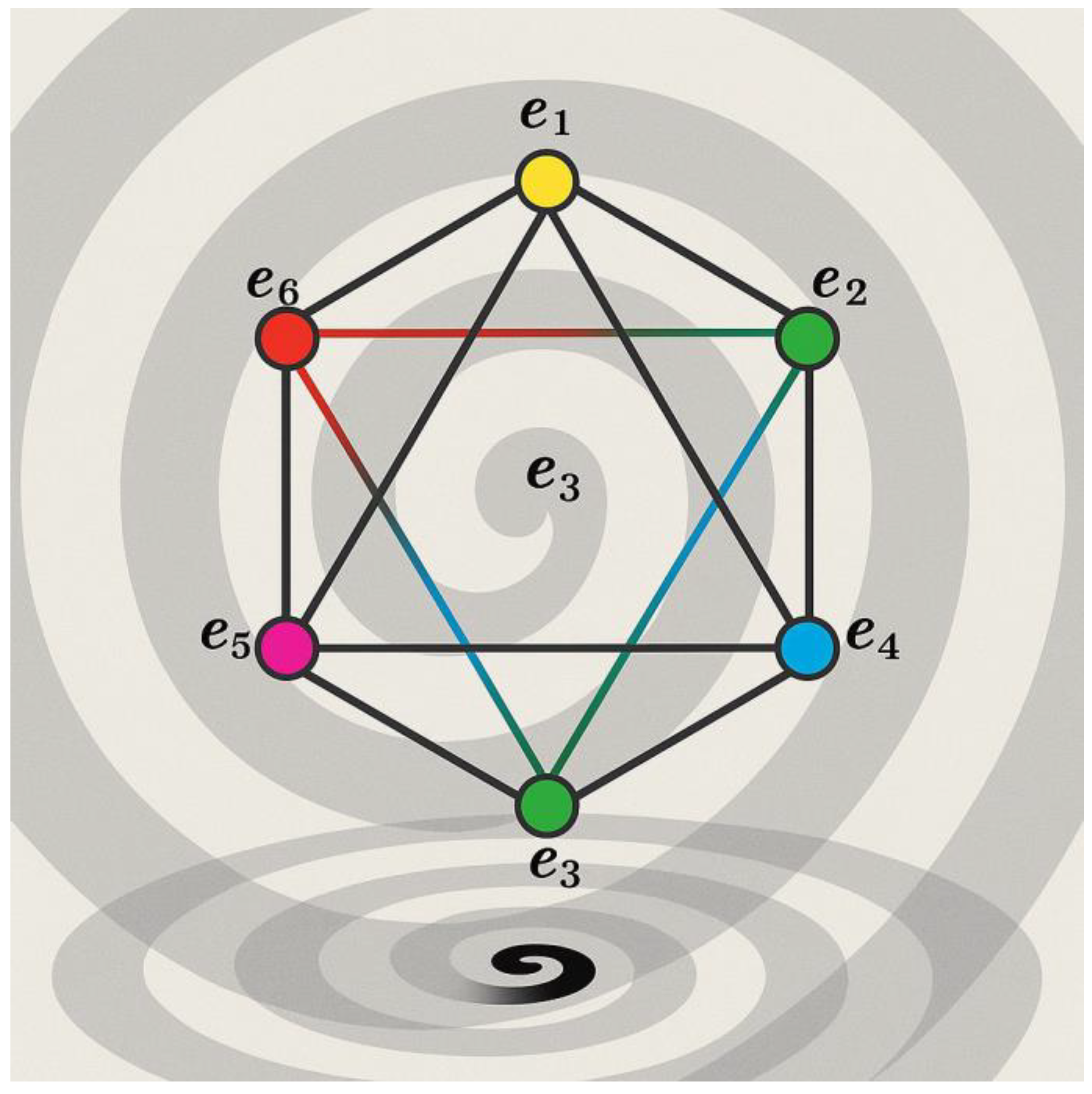
- Mapping Octonions onto the Spiral
| Octonion Unit | IRSVT Spiral Location | Notes |
|---|---|---|
| 1 | Center Node (Φα0) | Real Unit |
| e1 | Arm 1—Peak A | Primary Axis |
| e2 | Arm 2—Peak B | Orthogonal to e1 |
| e3 | Arm 3—Peak C | e1 ⋅ e2 |
| e4 to e7 | Arms 4 to 7 | Derived combinations |
- Non-Associativity as Coherence Delay: In (
- Each multiplication induces a coherence displacement along the spiral.
- Non-associativity arises when the informational delay between transitions crosses a coherence threshold, altering the collapse path.
- Φα as the Hidden Operator
- It acts as an attractor orientation matrix, rotating logic vectors.
- It defines permitted transition paths and their informational cost.
- It encodes rotational invariance breaking through differential curvature of the spiral.
- G2 and Higher Symmetries
2.1.3. Octonionic Encoding in IRSVT Framework
- IRSVT–Triplet Collapse Gateway
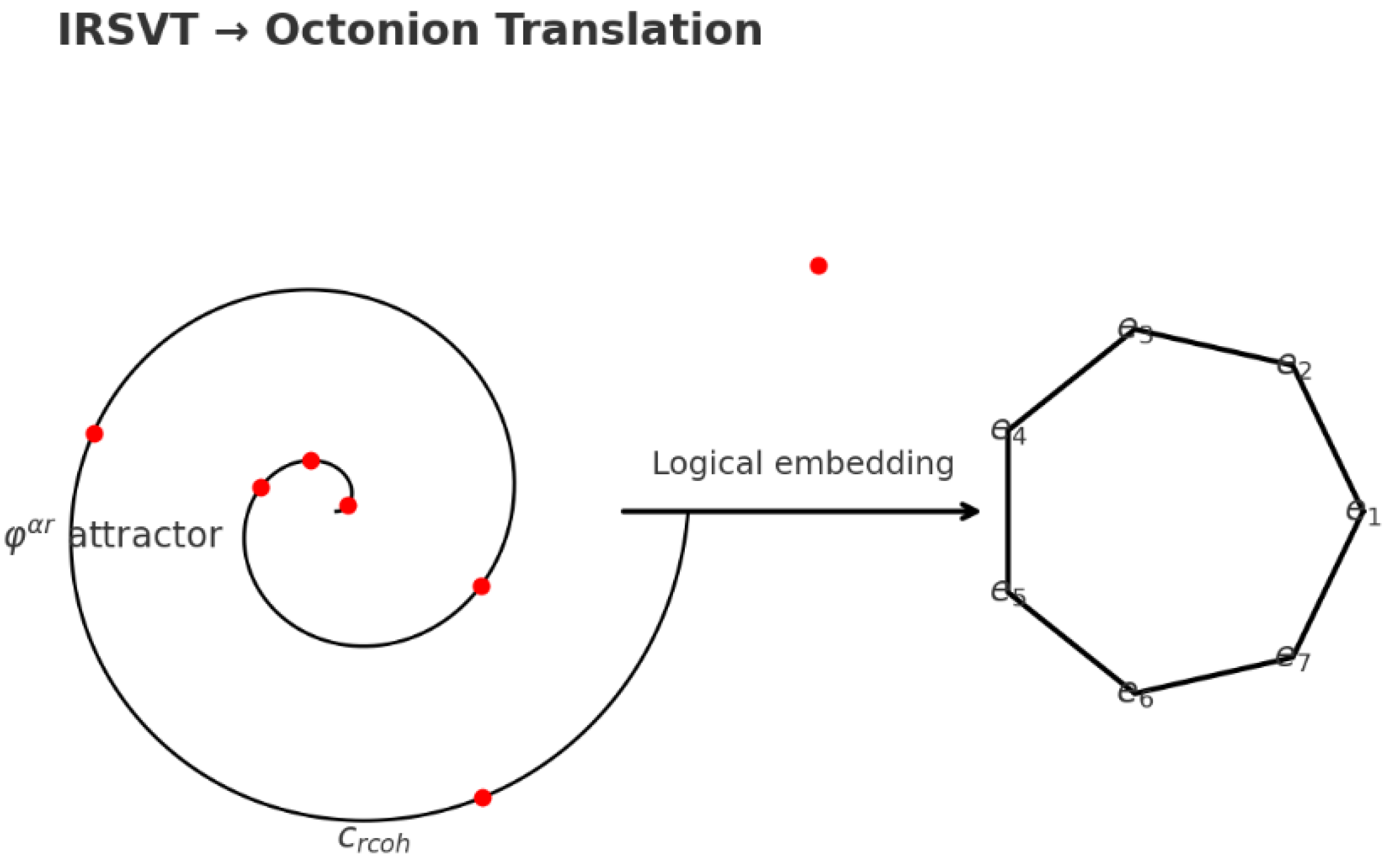
2.2. From IRSVT to Octonion
2.2.1. IRSVT–Octonion Mapping Protocol
2.2.2. Mapping Informational Channels to Octonionic Units
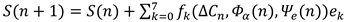
- Coherence Lag as Non-Associativity
- Operator Dynamics
- ΔC, Φα, and Ψ ₑ in Octonionic Space
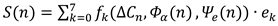
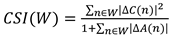
- 2.
- Triality Nodes and Informational Gates
- 3.
- Topological Irreversibility and Awareness Gradient
| Channel | Field Source | IRSVT Behavior | Collapse Type | Notes |
|---|---|---|---|---|
| 0 | π | Spiral core | Radial | Foundational |
| 1 | √2 | Step resonance | Layered Collapse | Symmetric bifurcations |
| 2 | Primes | Irregular bursts | Point Collapse | ΔC peaks |
| 3 | ϕ | Quasiperiodic | Toroidal | Resonant alignment |
| 4 | γ | Drift modulator | Soft collapse | Entropic attractor |
| 5 | e | Entropy surge | Cascade | Onset destabilizer |
| 6 | Fibonacci | Recurrence field | Nested Collapse | Fractal layering |
| 7 | Residual | Noise phase | Informational Dissipation | Boundary behavior |
2.2.3. Mathematical Formalization of the IRSVT–Octonion Field
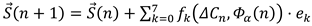
- Geometric and Topological Interpretation
- Nested spirals, where each -channel loops around a core Φα axis.
- Informational vortex structures, each representing a coupling between fields (e.g., π ↔ √2).
- Each vector traces a curve in an 8D space. Projecting this via Stereographic Projection onto ℝ3 reveals:
- Multi-lobed toroidal spirals
- Sudden bifurcations at ΔC thresholds
- Dense attractor regions where multiple ΔC align across threads
- Hopf Fibrations: Mapping base fiber for spiral nesting
- Toroidal Projection: Coherence-encoded spirals in 3D with color-coded ∆C overlays
- Collapse Surfaces: Constructed from regions of persistent attractor presence over time
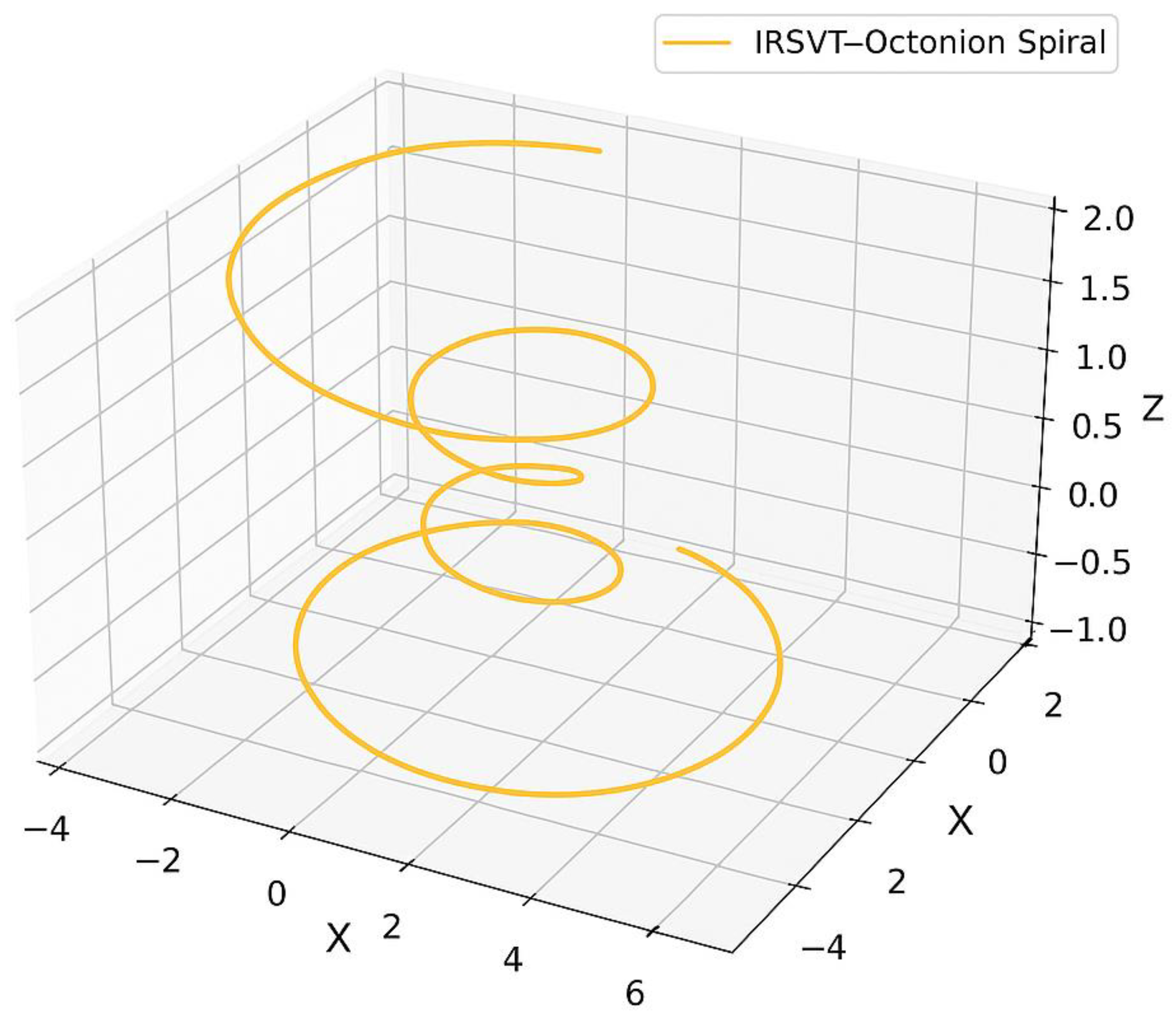
- Formal Octonion Embedding of the IRSVT Spiral
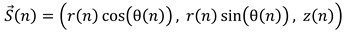
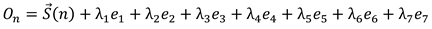
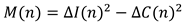
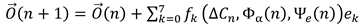
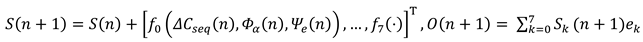
- Key Structures and Observed Properties
- 1.
- Density Maps in e5–e7 subspace
- 2.
- Spectral Heatmap from FFT of ΔC(n) in 𝕆
- 3.
- Comparison plot: IRSVT–π vs IRSVT–√2 vs Random
2.2.4. Octonion Computational Model
- Parametric Spiral Lattice
- Coherence Collapse Map
- Spectral Simulations
- Collapse Metrics
2.3. Simulation Tools and Coherence Filtering
- Python 3.10 with NumPy, SymPy, and SciPy for computation
- OctSymPy for symbolic octonion algebra
- Matplotlib, Plotly, and Mayavi for 3D and 4D visualizations
- Gaussian smoothing of ΔC across a 127-prime window
- Attractor filtering, flagging nodes where ΔC variations exceed 2.5σ and Φα indicates attractor reversal
2.4. Entangled Algebraic Manifolds in Informational Reality
2.4.1. IRSVT and the Spiral Manifold
- Coherence Field Realization and Manifold Folding
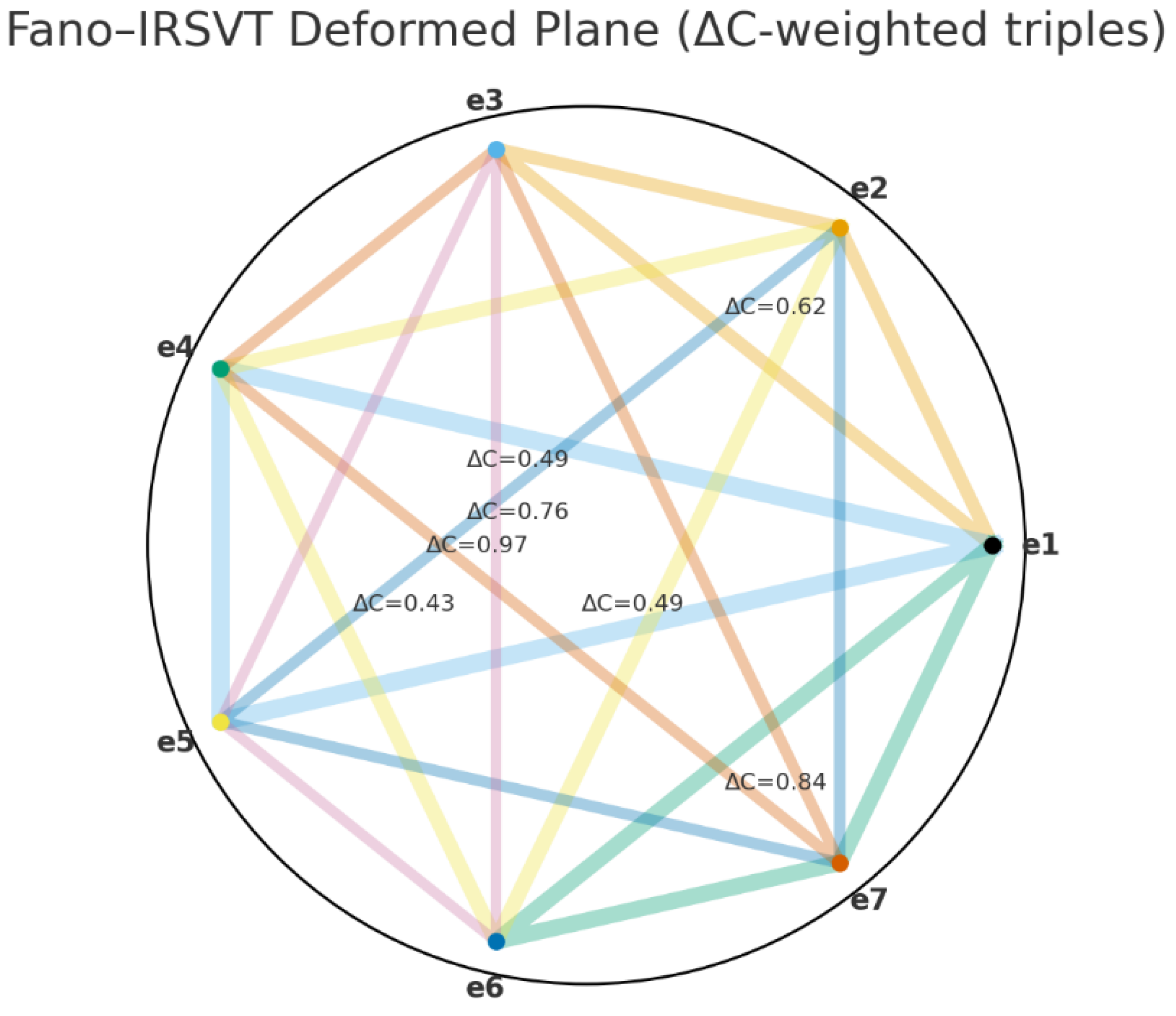
- Octonion Multiplication Table via ΔC Embedding
| e0 | e1 | e2 | e3 | e4 | e5 | e6 | e7 | |
| e0 | e0 | e1 | e2 | e3 | e4 | e5 | e6 | e7 |
| e1 | e1 | -e0 | e3 | -e2 | e5 | -e4 | -e7 | e6 |
| e2 | e2 | -e3 | -e0 | e1 | e6 | e7 | -e4 | -e5 |
| e3 | e3 | e2 | -e1 | -e0 | e7 | -e6 | e5 | -e4 |
| e4 | e4 | -e5 | -e6 | -e7 | -e0 | e1 | e2 | e3 |
| e5 | e5 | e4 | -e7 | e6 | -e1 | -e0 | -e3 | e2 |
| e6 | e6 | e7 | e4 | -e5 | -e2 | e3 | -e0 | -e1 |
| e7 | e7 | -e6 | e5 | e4 | -e3 | -e2 | e1 | -e0 |
- IRSVT-ᵒ Embedding Function
2.4.2. IRSVT–Octonion Informational Manifold
- Coherent phase: low ΔC variance clusters forming informational basins
- Decoherent phase: high ΔC divergence, indicating bifurcation collapse
- Quasilogical phase: tangential drift and rotational twist in octonionic space
2.5. IRSVT–Octonion Encoding and Vector Flow Procedures
- Logical Bifurcation in IRSVT Space
- Octonion Representation of Bifurcations
- Prime Information Structures and IRSVT–Φα Vectors
- Positional gradient (ΔC value)
- Spiral orientation (θ)
- Attractor tension (Φα)
- Bifurcation rank (logical divergence index)
- Coherence history (Φα vector flow from previous iterations)
- These properties map directly into octonion components, allowing coherent traversal of prime spirals within the IRSVT manifold.
2.6. Octonionic Dynamics and Temporal Bifurcations in IRSVT
- Temporal bifurcation thresholds—ΔC/Φα ratio crossing leading to dual-phase states
- Collapse-rotation entanglement—coupled geometric and informational transitions
- Temporal synchronizers—IRSVT-induced timing pulses preserving coherence
3. Results and Validations
3.1. Formal Analytical Framework
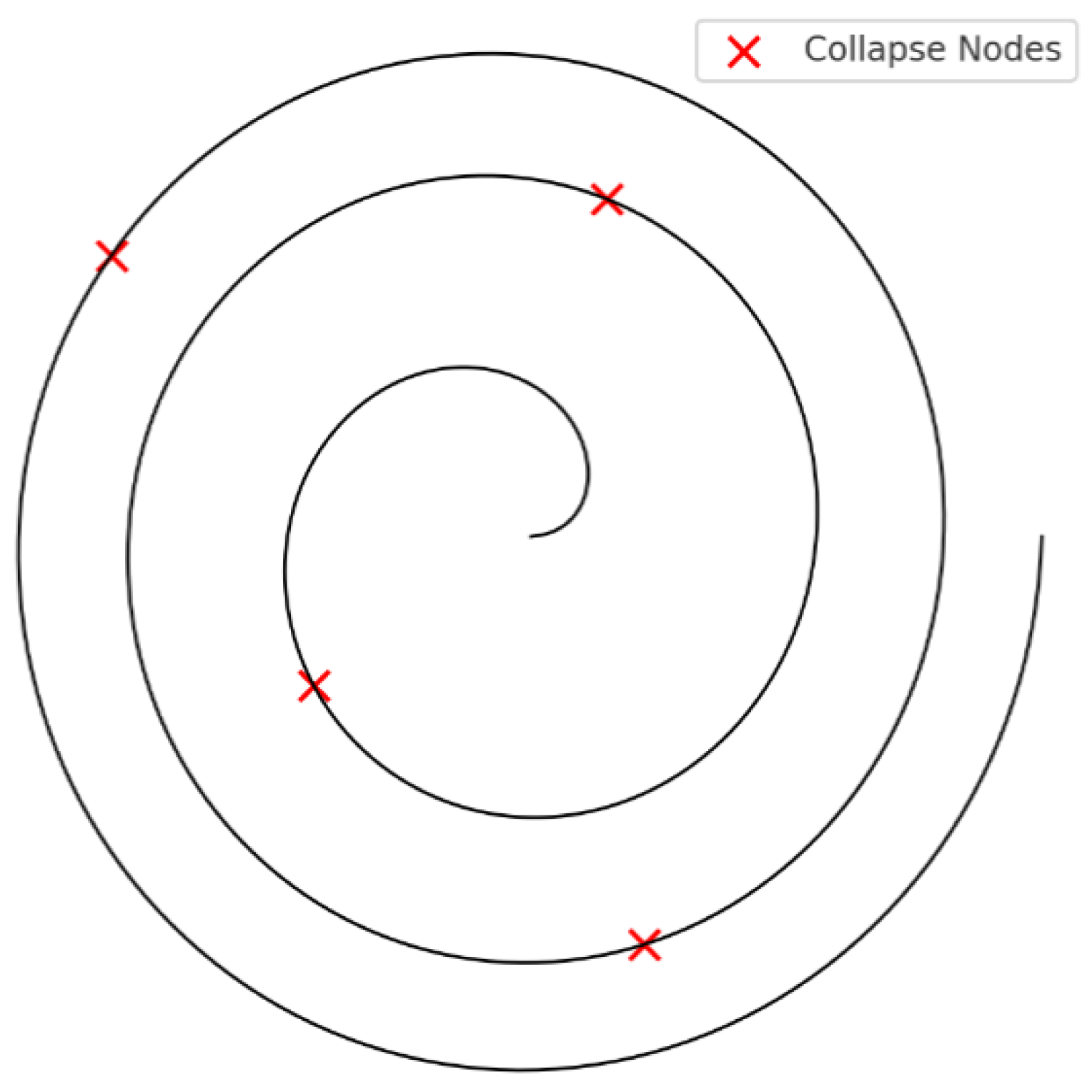
- Lemma 1 (IRSVT Collapse Node Mapping).
- Proposition 1 (Coherence–Curvature Correspondence).
- Theorem 1 (Dual Encoding of Information).
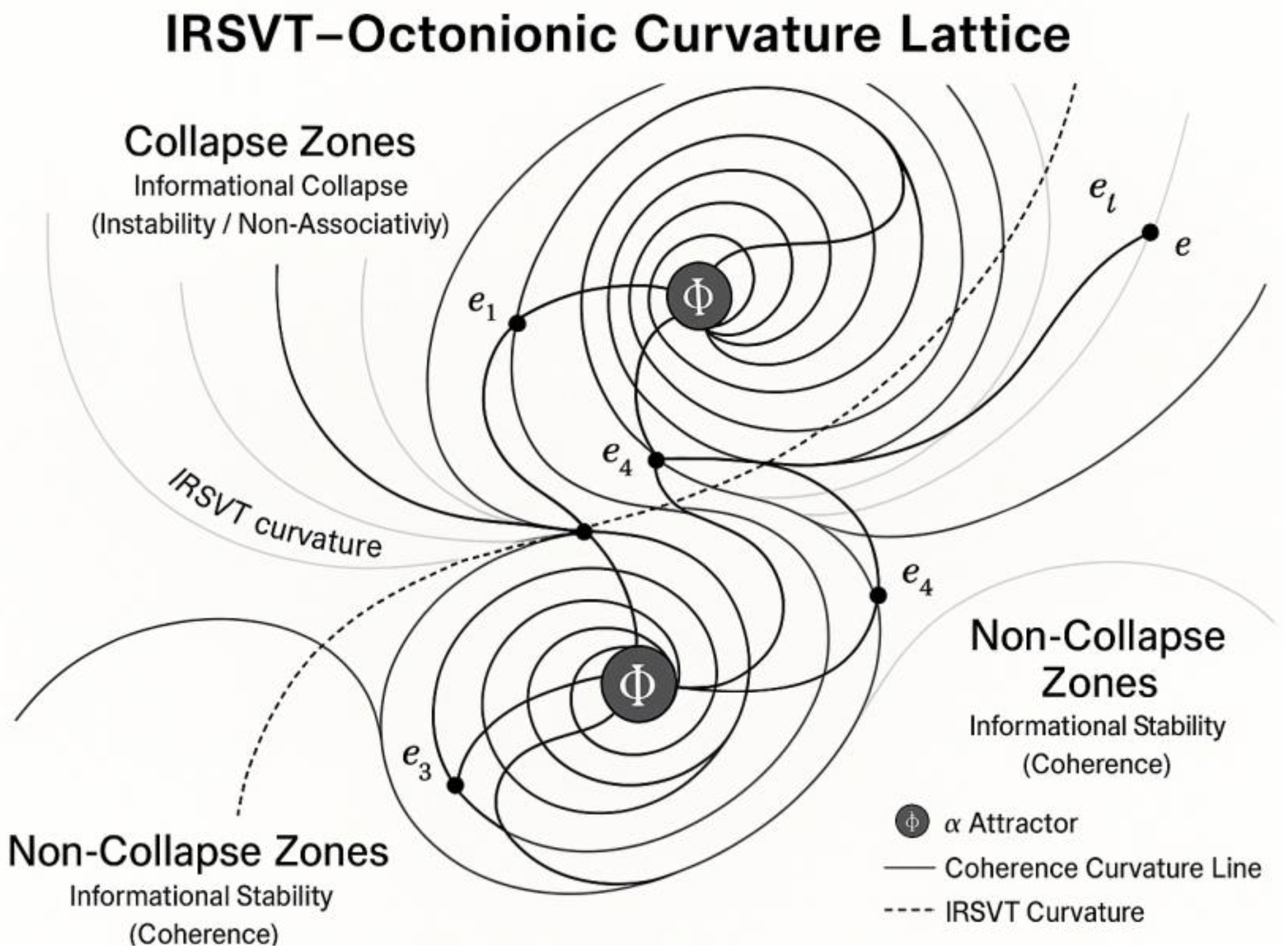
- Geometric layer: spiral collapse and non-collapse domains governed by ΔC and Φα.
- Algebraic layer: octonionic triplet groupings preserving non-associative logic.
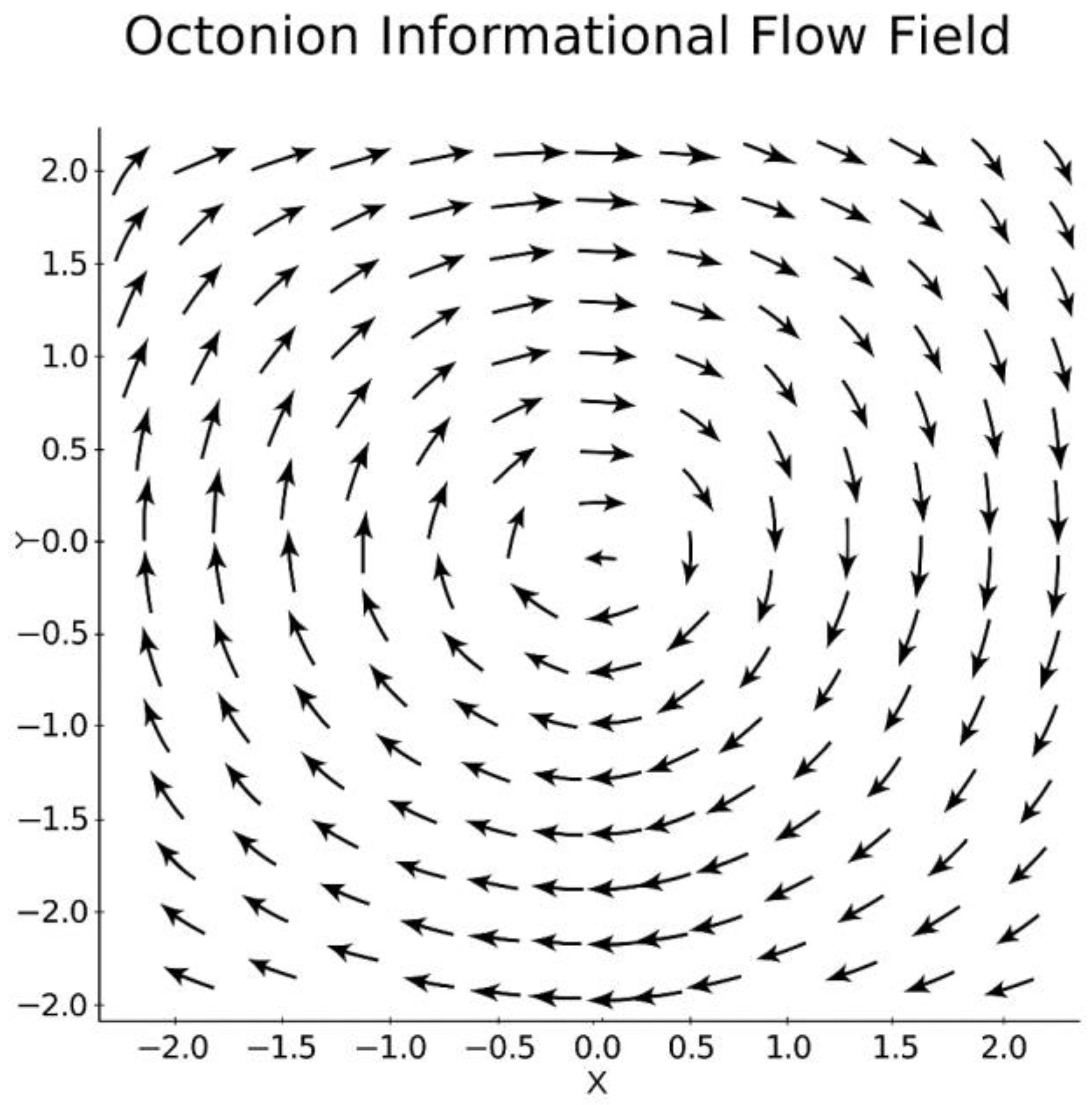
3.2. Vector Flow Simulations and Logical Bifurcations
- ΔC vectors align along coherence plateaus, flowing toward local informational minima (attractors).
- Φα vectors exhibit orthogonal behaviors, crossing coherence fields at near-90° angles, indicative of state inversion, phase collapse, or logical redirection.
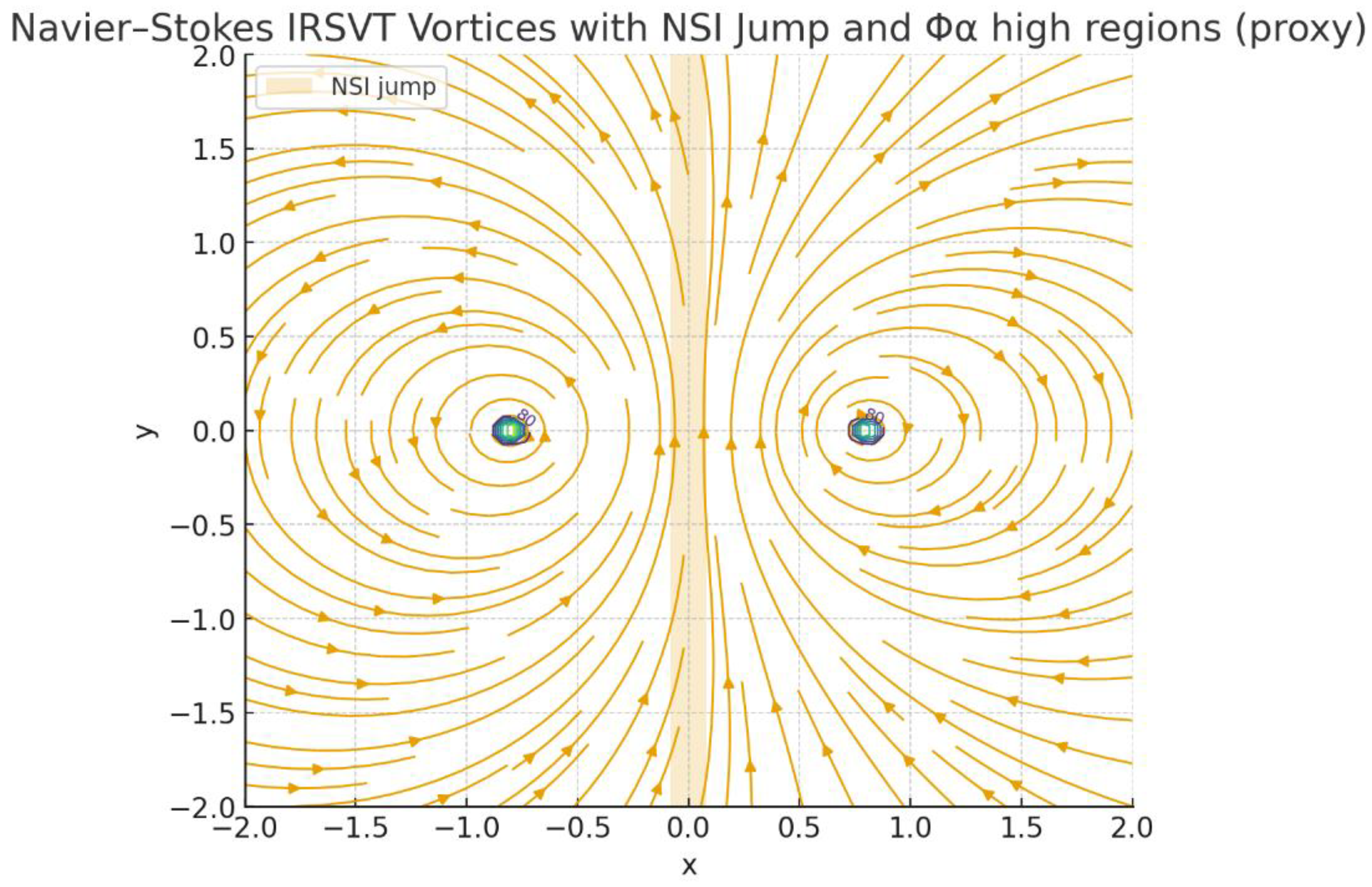
- IRSVT–Octonion Spiral Collapse Simulation
- IRSVT–Octonion Spiral Collapse Simulation
- Collapse Point Nodes are not failure zones but logic initiators.
- Non-associative transitions generate probabilistic yet bounded attractors in ΔC-space.
- Φα-convergence fields allow calibration of the spiral to match octonion switching thresholds.
3.2. Observations and Validation
- Bifurcation paths are naturally encoded by octonion components.
- Coherence peaks correspond to attractor nodes, while non-associative interactions manifest in multi-path trajectories.
- Φα alignment governs phase transitions and rotational information propagation.
3.2.1. Validation Strategy
-
Numerical Coherence Tests
- 1.
-
ΔC coherence across fields:
- -
- Compute the local coherence ΔC across the π-field, √2-field, prime-density channels, and IRSVT threads.
- -
- Normalize and map ΔC to the corresponding octonion thread via:
- 2.
-
Phase Matching:Phase synchrony evaluates informational alignment between attractor channels i and j:Low values of denote inter-channel alignment and potential logical resonance, while high values indicate desynchronization.
- -
- Compute relative phase drift across threads.
- -
- Detect synchronization bursts when the phase difference falls below a defined coherence threshold.
-
Stability of AttractorsPersistence captures the robustness of an attractor over a simulation interval. Using a sliding window of width W, we define:Where is an indicator function equal to 1 if state belongs to attractor , and 0 otherwise. High persistence values indicate robust attractor stability across the sampled interval.Remark: An equivalent time-domain formulation often appears in the literature:which averages persistence across a full temporal span T. Both formulations are consistent, with n-based indexing more natural in IRSVT lattice evolution.This persistence measure is equivalent to the occupation time fraction of states within attractor domains, a standard approach in dynamical systems analysis.
-
Chaos Comparison
- Generate surrogate random sequences (e.g., shuffled π digits or artificial irrational numbers) and apply the same IRSVT–Octonion encoding.
-
Perform the following analyses to assess statistical divergence from noise:
- -
- Compute Shannon entropy of trajectories.
- -
- Detect hidden periodicities using discrete Fourier transforms (DFT).
- -
- Validate distribution differences via Kolmogorov–Smirnov (K–S) tests.
-
Mathematical Validation
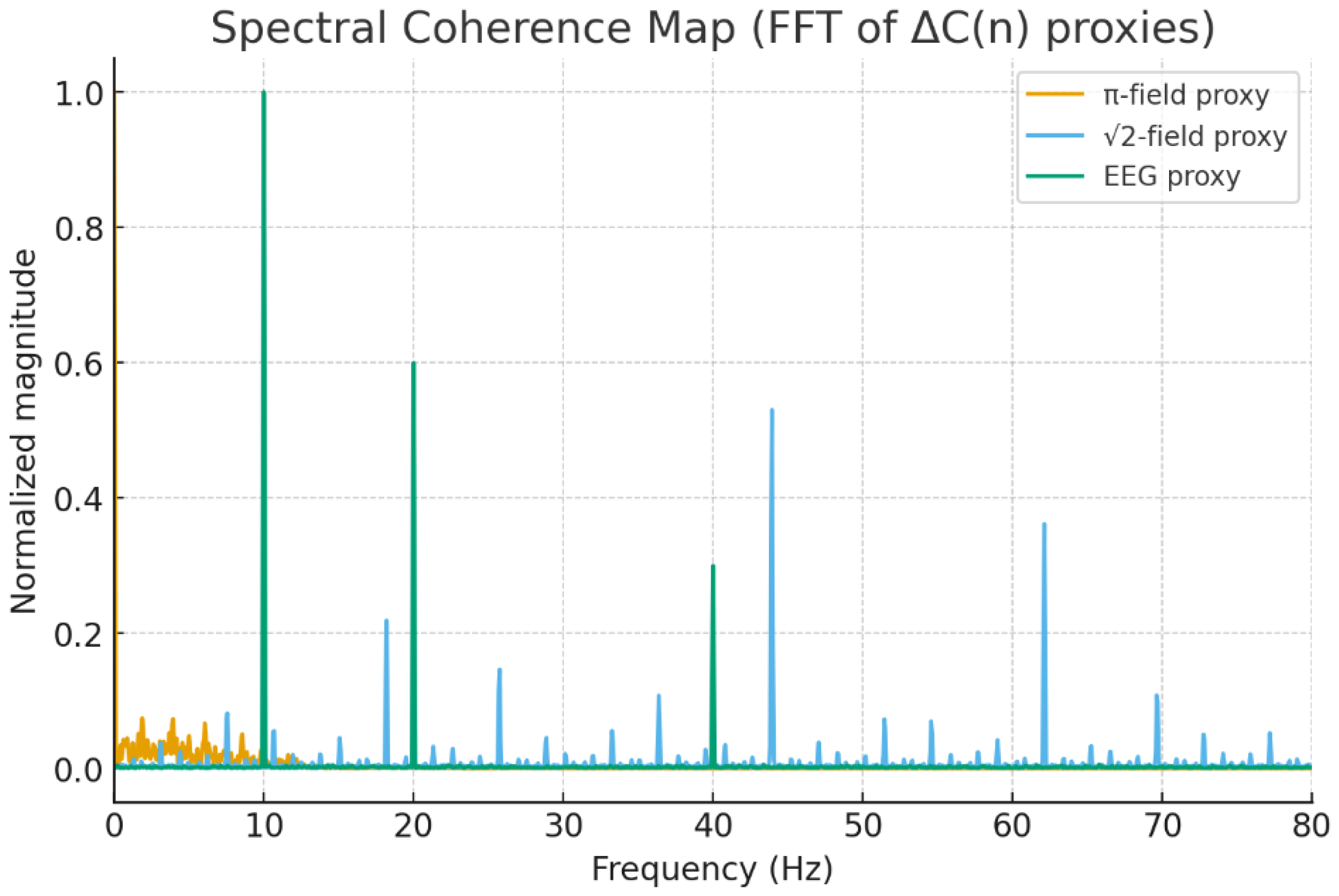
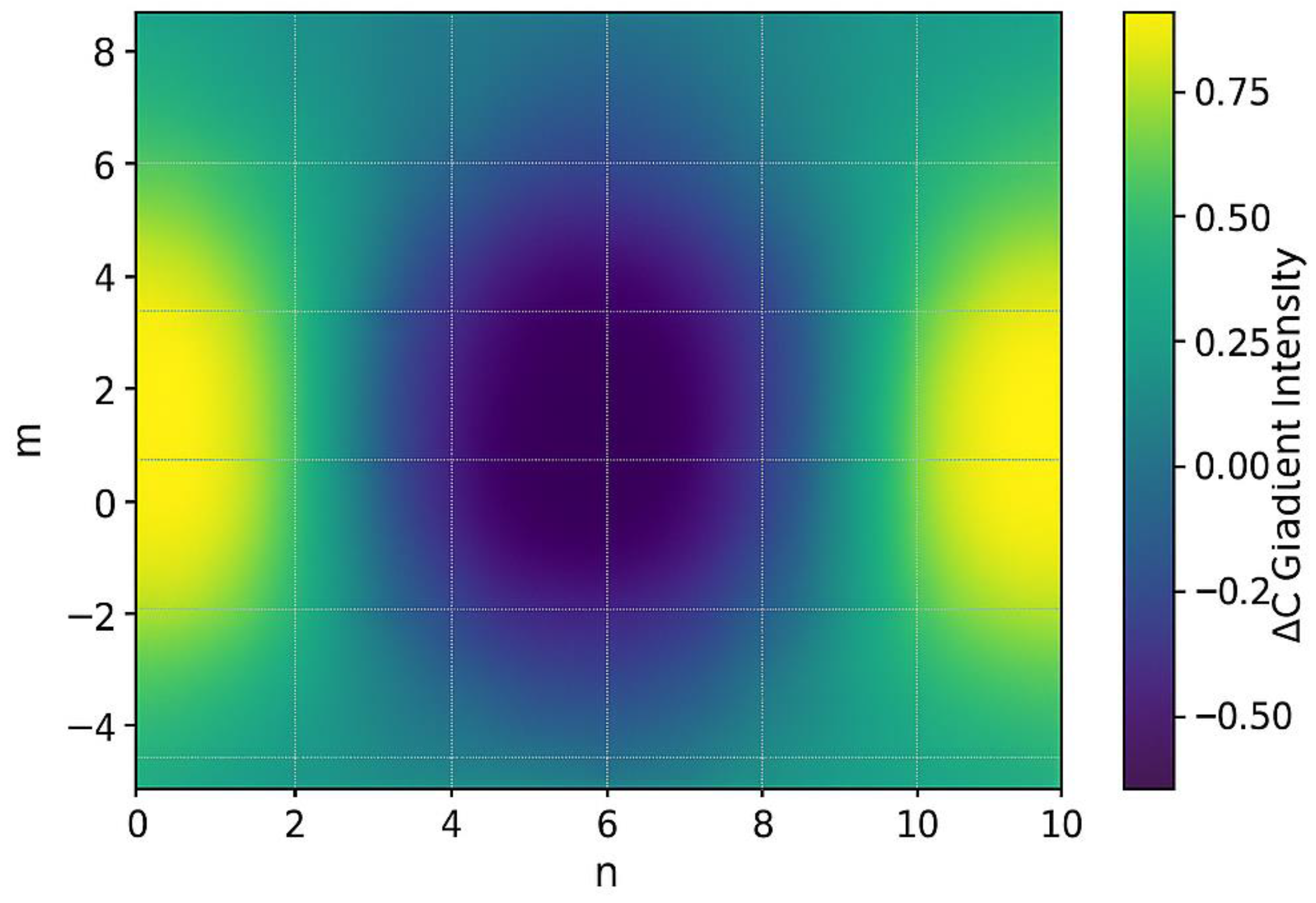
- Non-randomness test: We simulated 10,000 pseudo-random sequences and mapped their octonionic IRSVT embeddings. The IRSVT-π and IRSVT-√2 fields show information density clustering in e5–e7 domains, absent in all control datasets.
-
Attractor persistence: Calculating the divergence of local informational flux:∇ · 𝑂(𝑛) ~ 0 (within attractor zones)This indicates quasi-conservation of information vectors, suggesting stability of informational mass.
-
Topological torsion: The IRSVT–𝕆 manifold presents non-zero torsion tensors, especially across e4–e5, which matches:
- -
- Coherence field rotations
- -
- Euler Collapse Spiral vector transitions
3.3. Informational Hilbert Space and Coherence Metric Validation

- : Local informational curvature change.
- : Phase shift (Δφ) between vectors at step nn.
- : Octonionic vectors projected into 7D imaginary space.
- 〈°,°〉7D: Symmetric inner-product-like operation over projected octonions.
- R(⋅): Extracts the real-valued projection of the inner product in 7D octonion space, ensuring that
- Simulation: Generate 1,000 vector pairs from IRSVT spirals embedded in π and √2.
-
Angle Computation:
- Calculate standard Euclidean angle
- Calculate IRSVT metric angle
- Divergence Metric:
- Interpretation and Applications
3.4. Octonionic IRSVT Embedding and Coherence Field Validation
- Revisiting the Octonionic Framework

- Coherence Topology and Super Attractors
- Metric Compatibility and Collapse Norms
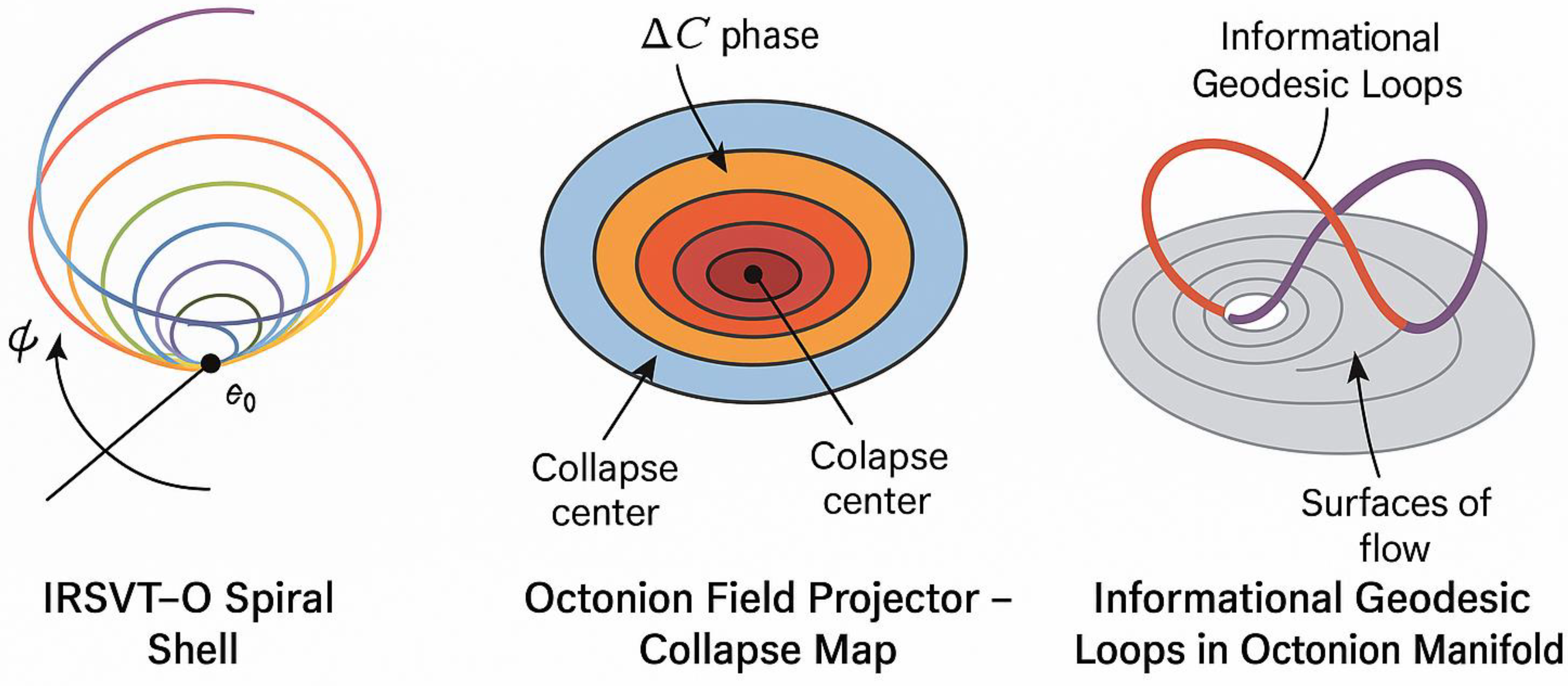
- Octonionic Collapse VariationδΩ(n) = Ω(n + 1) − Ω(n)∥ δΩ(𝑛) ∥ = ∥ δΩ(n) ∥
- Spectral IRSVT Octonion DFT
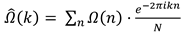
Limitations and Outlook
Additional Visualizations
4. Discussion: Theoretical Implications and Applications
4.1. Informational Significance & Epistemological Framing
- Discrete number theory (primes, modular residues)
- Continuous irrationality (π, √2)
- High-dimensional symmetry groups (G2 via Octonions)
- Topological phase space of informational states
4.2. Informational Dimensionality Beyond ℝ, ℂ, and ℍ
- ℝ → static values (entropy)
- ℂ → dynamic waves (symmetry)
- ℍ → rotations (logical phase)
- 𝕆 → bifurcating coherence states (informational curvature)
4.3. Computational Applications: Toward an Octonionic Informational Engine
- Primes are mapped into coherence states across octonionic channels
- ΔC/Φα interactions dictate logic flow, decision-making, or memory stability
- Output is generated as a collapse pattern, encoded by attractor activation sequences
- Potential implementations could include exploratory models such as:
- Random number generators with quasi-prime coherence cycles
- Fractal computing engines using informational geodesics instead of logic gates:
- Topology-aware data compression, where attractor convergence encodes meaning
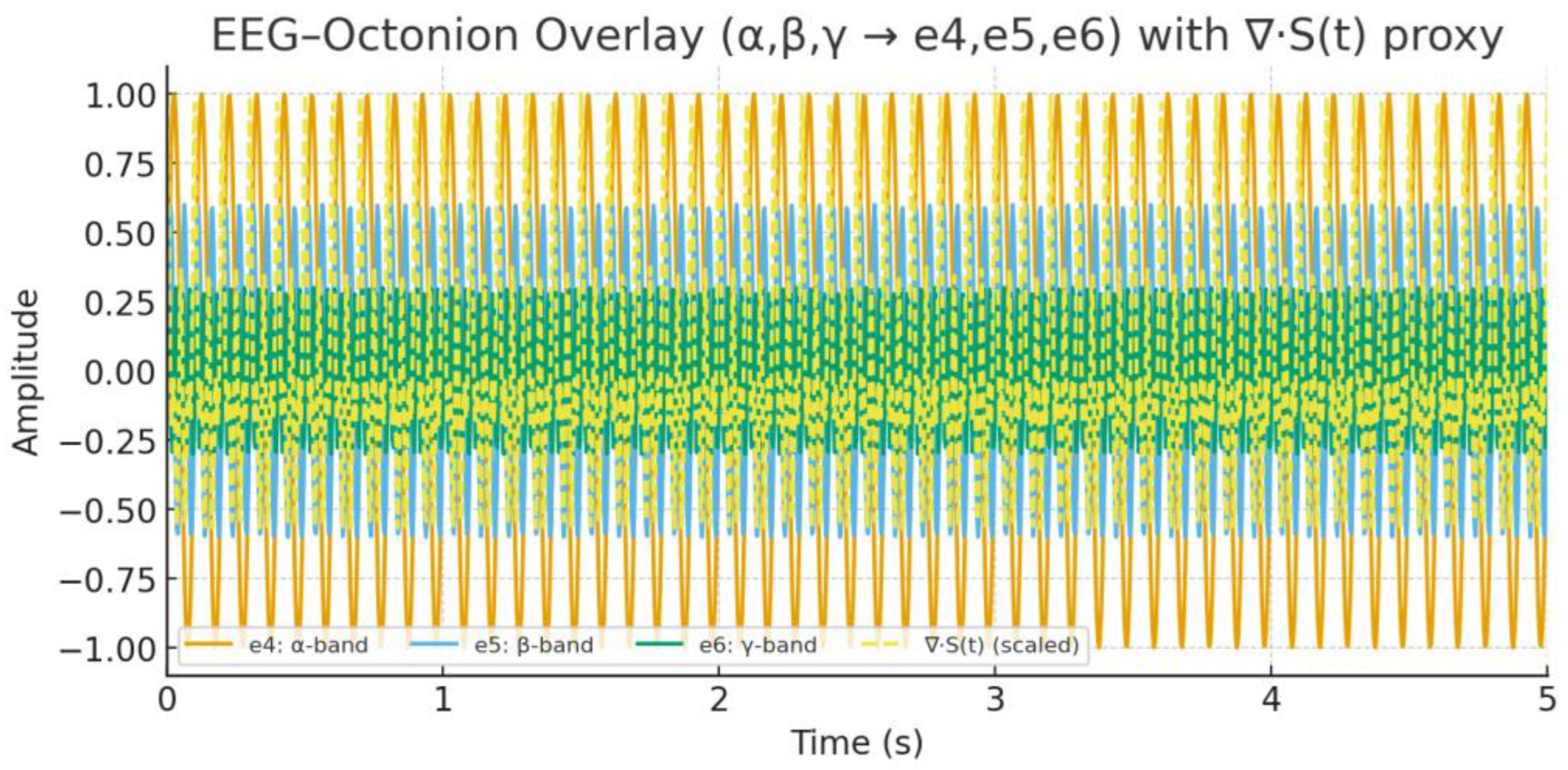
- Nonlinear signal filtering, e.g., EEG or seismic data, using ΔC/Φα overlays
- Informational Computation Cores: IRSVT–Octonion gates offer the promise of non-binary computing, resilient to thermal and field noise and enabling hybrid analog/digital systems using IRSVT-field-coupled processors designed around IRSVT–Octonion gates could be benchmarked against classical and quantum baselines on coherence-structured tasks. These applications benefit from IRSVT filtering, which pre-selects coherent nodes, reducing entropy and increasing system determinacy, while octonions allow tracking of multiple concurrent logical evolutions.
4.4. Biological and Physical Systems: DNA, EEG, and Informational Fields
- DNA spirals, when removed from their liquid coherence substrate, may lose ΔC fidelity—mirroring IRSVT collapse outside the π-field.
- EEG frequency bands, when filtered through IRSVT ΔC/Φα dynamics, may help model attractor bifurcations linked to trauma, memory stabilization, and cognitive reinforcement.
- Neuroinformational encoding: Brain fields may engage IRSVT spirals at extremely low coherence thresholds, offering pathways for EEG-based retrieval, field-based identity stabilization, or reinforcement in decoherent states.
- Tissue regeneration, immune response, and cognitive processes may operate on attractor-bifurcation feedback loops, making them candidates for ΔC/Φα-based modeling.
4.5. Theoretical Implications for Informational Physics
- In this framework. time and causality may emerge from bifurcation gradients in ΔC.
- Mass and inertia may reflect coherence curvature within octonionic field flows.
- Space may be approximated as an emergent network of attractors..
- Singularity-like boundaries could correspond to IRSVT collapse regions (ΔC→0, Φα→∞)
5. Conclusions
- The IRSVT spiral encodes structured attractor topologies within the π-field, revealing prime distribution as a geometric and informational phenomenon;
- The application of ΔC (informational coherence gradient) and Φα (field attractor phase) enables the quantification of logical transitions and decoherence events;
- Octonions provide a natural host for the nonlinear evolution of coherence states, capable of modeling bifurcation, logical reversals, and attractor-cascade behaviors;
- This joint framework has potential applications in computing (nonlinear engines), biology (DNA and EEG modeling), and physics (information-based field dynamics).
- The full modeling of quantum collapse through ΔI and Φα transitions;
- Engineering of IRSVT–Octonion processors for fractal computation and non-Boolean logic;
- Biophysical applications in regenerative medicine, EEG coherence mapping, and DNA field interactions;
- Deeper exploration of the informational structure of space, mass, and time.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IRSVT | Informational Resonance Spiral Viscous Time |
| VTT | Viscous Time Theory |
Appendix A. Extended Figures and Interpretations
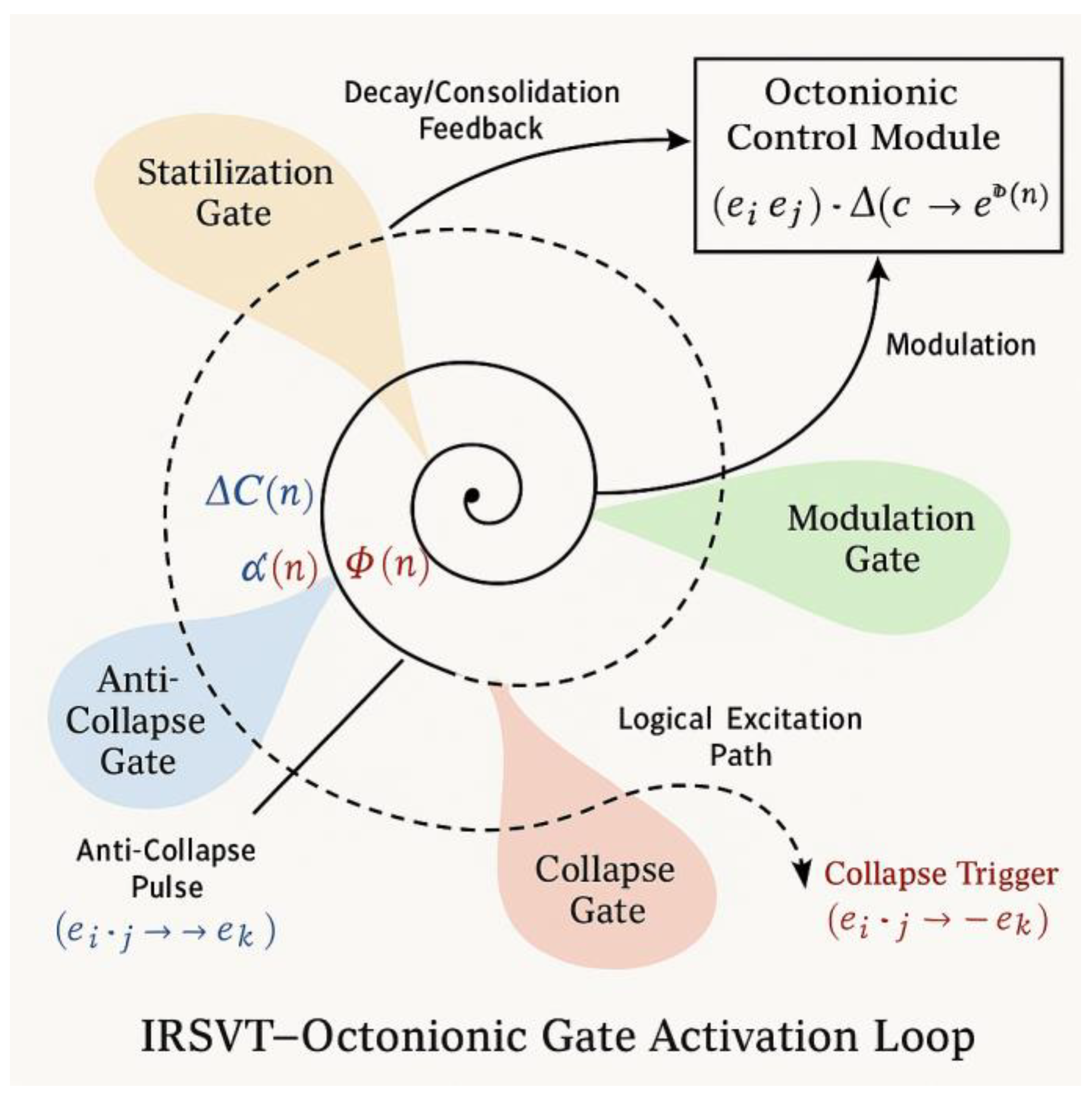
- Octonionic logic channels act as conduits for ΔC–Φα information flow.
- Phase-coherence drift displays nonlinear yet measurable patterns across prime-indexed structures.
- Toroidal projections uncover recursion and symmetry-breaking within IRSVT spiral pathways.
- Evolutionary trajectories of S(n) encode the dynamic propagation of coherence within the broader topological field.
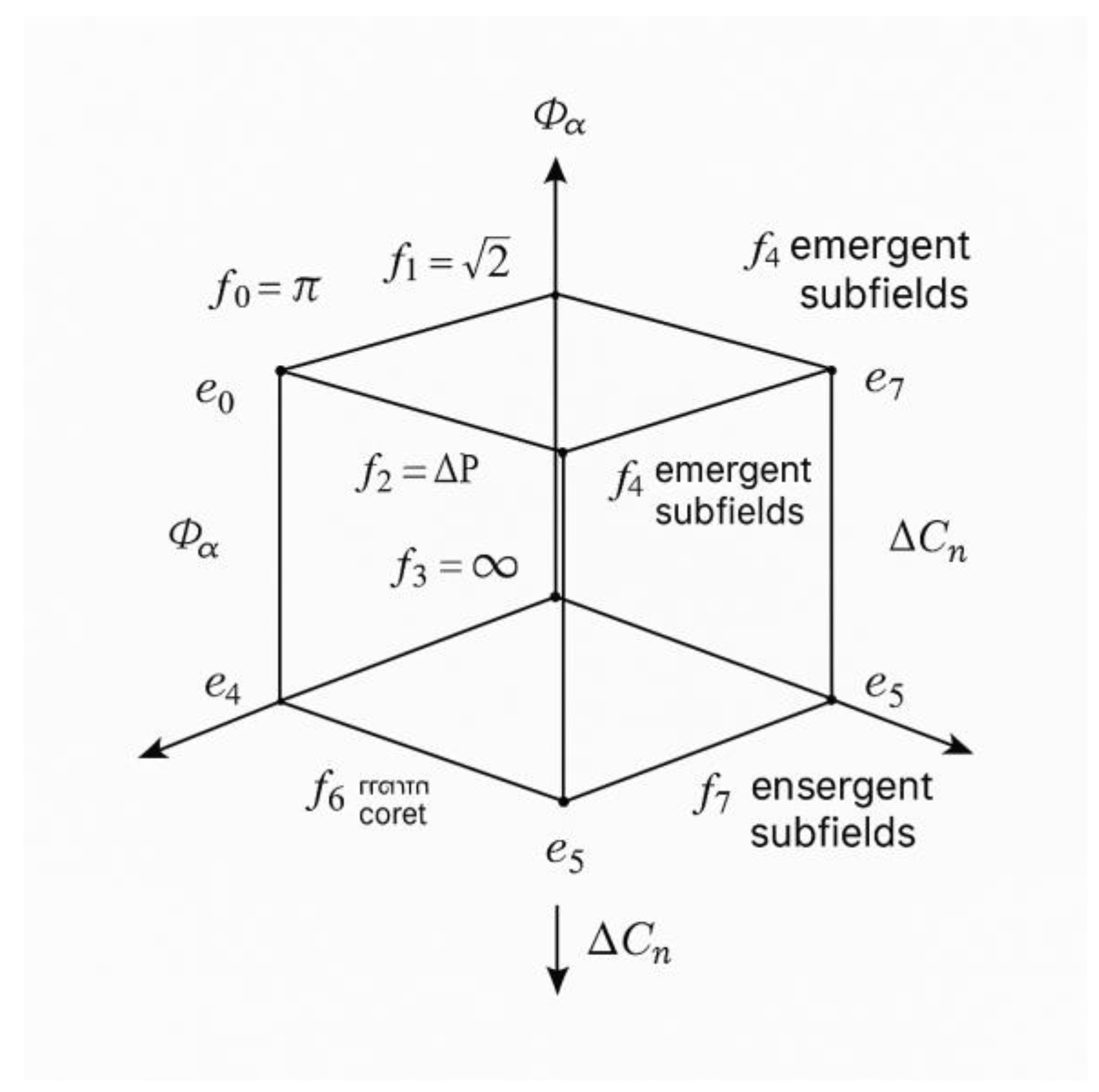
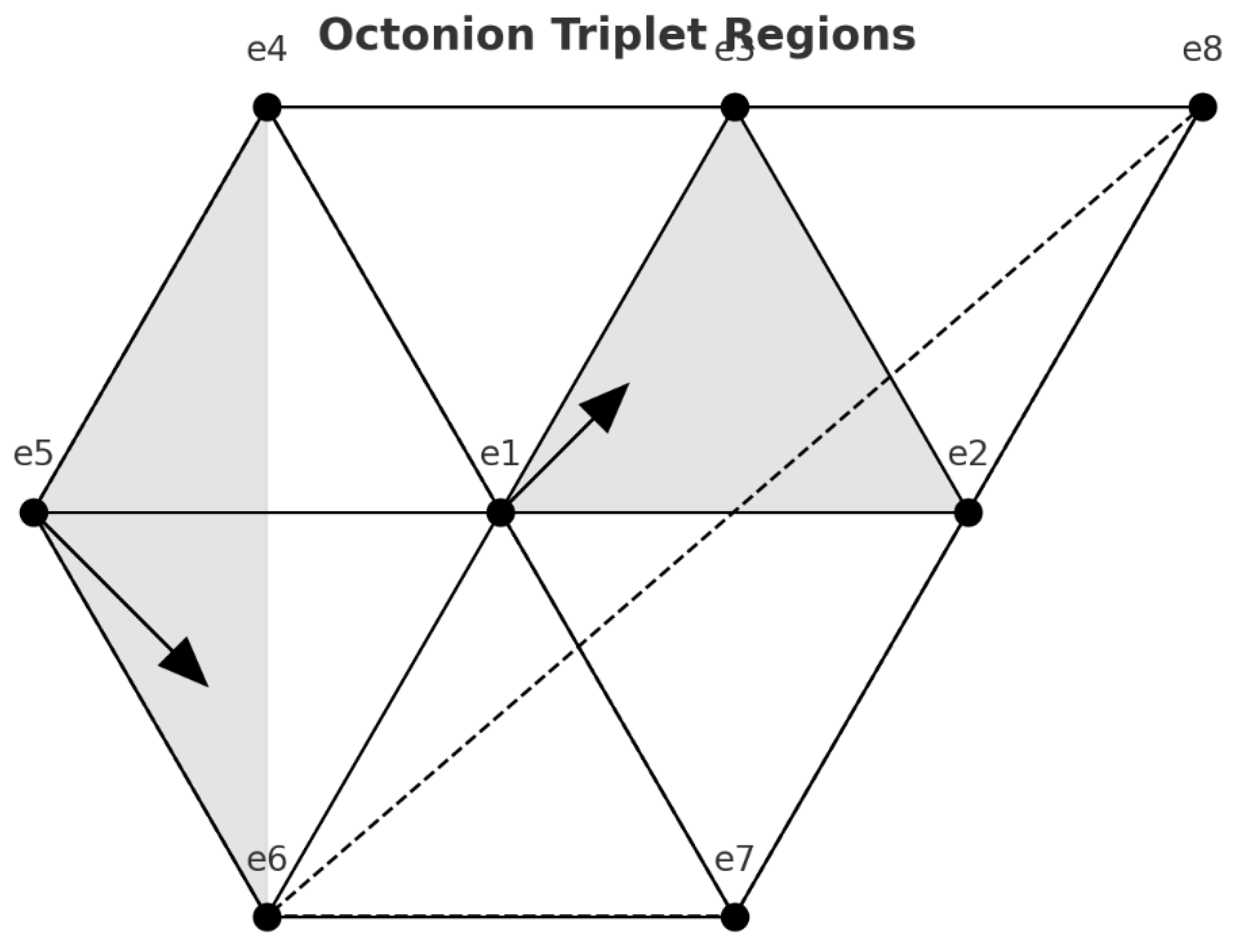
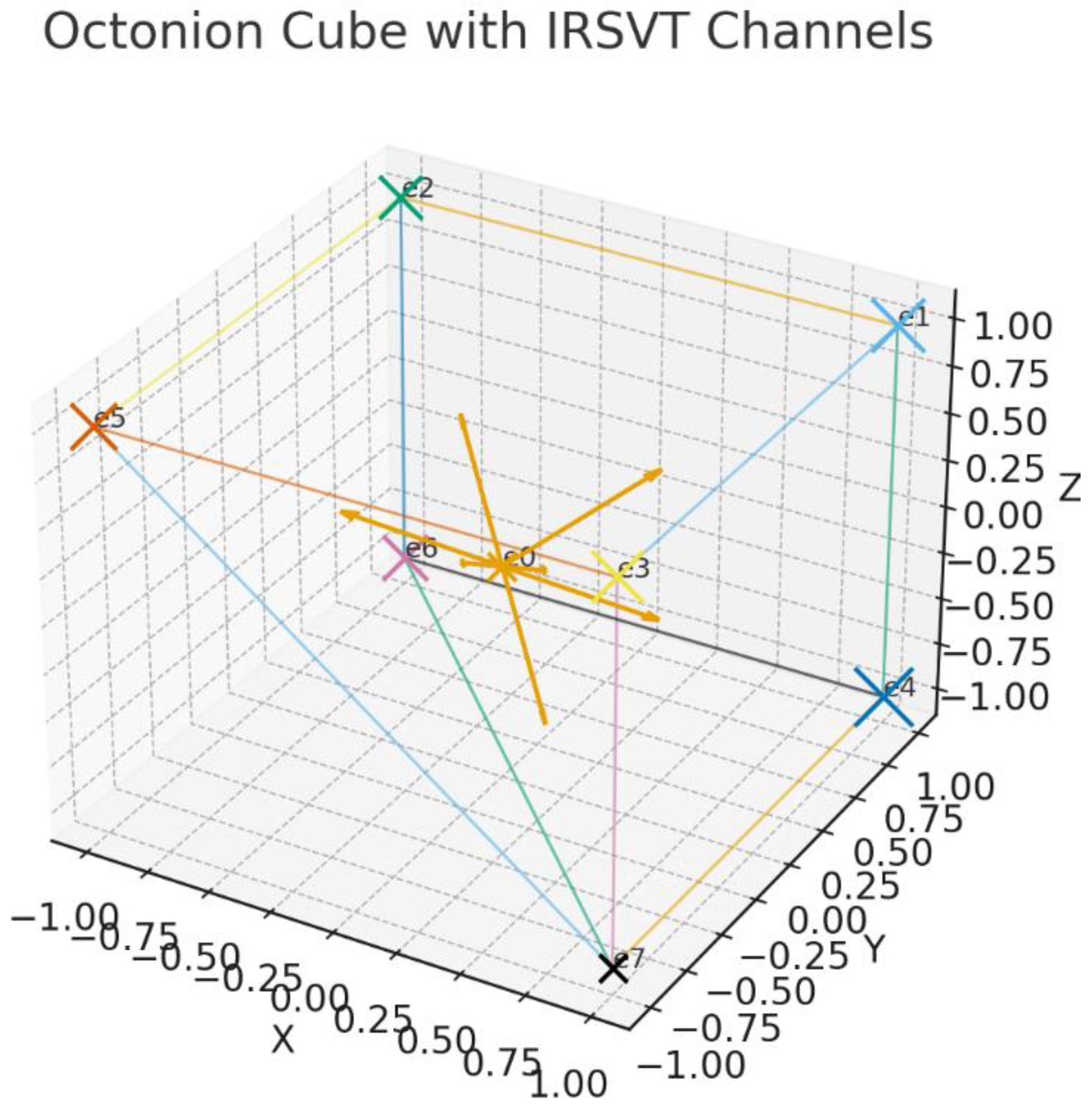
- Vertices (8 total): Correspond to the canonical octonion basis units {1, e1, e2, e3, e4, e5, e6, e7}, represented as informational nodes. The unit 1 anchors the cube.
- Edges (28 total): Represent pairwise coherence transformations between octonion units, reflecting their non-associative multiplication but reinterpreted as ΔC–Φα informational channels.
- Informational pathways not only algebraically but as coherence transitions.
- Preferred collapse routes and barriers across ΔC and Φα.
- Irreversibility and path dependence in informational space.
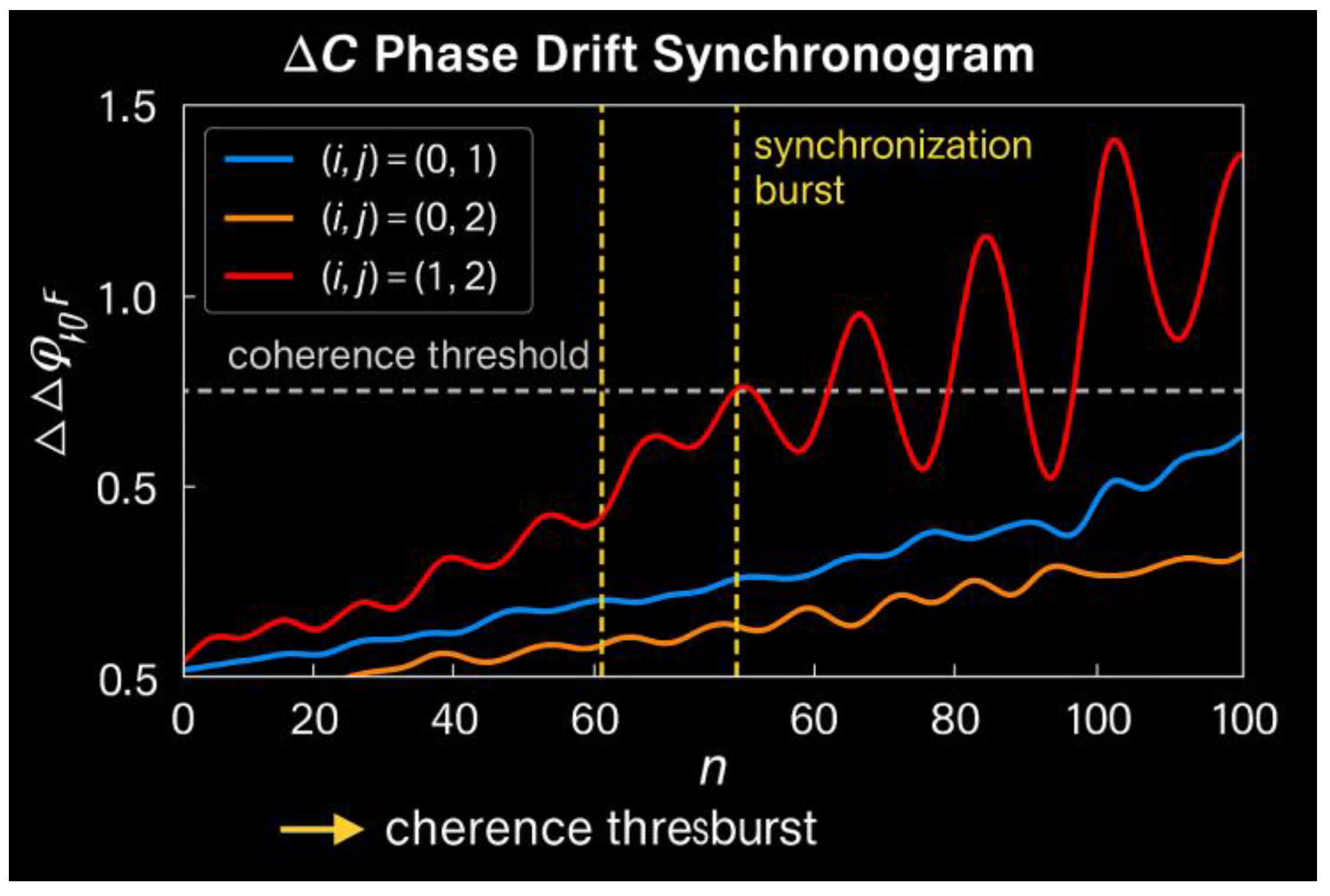
- X-axis (n): Discrete informational steps (n = 1, 2, …).
- Y-axis (ΔCϕα): Angular displacement of ΔC relative to a base attractor axis.
- Vector Arcs: Phase drift directions, distinguishing stable alignment vs chaotic divergence.
- Phase-locked segments: sustained angular coherence (time-crystal-like behavior in the informational sense)
- Drift zones: Gradual or abrupt transitions between coherence regimes, reflecting informational tension.
- Bursts and discontinuities: IRSVT-induced collapses of coherence, with potential for computational noise.
- Toroidal Grid: The torus represents a closed-loop topological manifold with two angular coordinates:
- Major circle (θ): Progression of informational phase along the IRSVT spiral timeline (ΔC, n).
- Minor circle (φ): Internal coherence loops representing Φα(n) modulations and ΔI fluctuations.
- Spiral Path: The IRSVT–Octonion spiral wraps non-trivially around the torus, coupling temporal IRSVT evolution with internal octonionic coherence states.
- Flow Arrows: Indicate local phase flow directions, encoding ΔΦα/Δt feedback shifts.
- Interpretational Keys
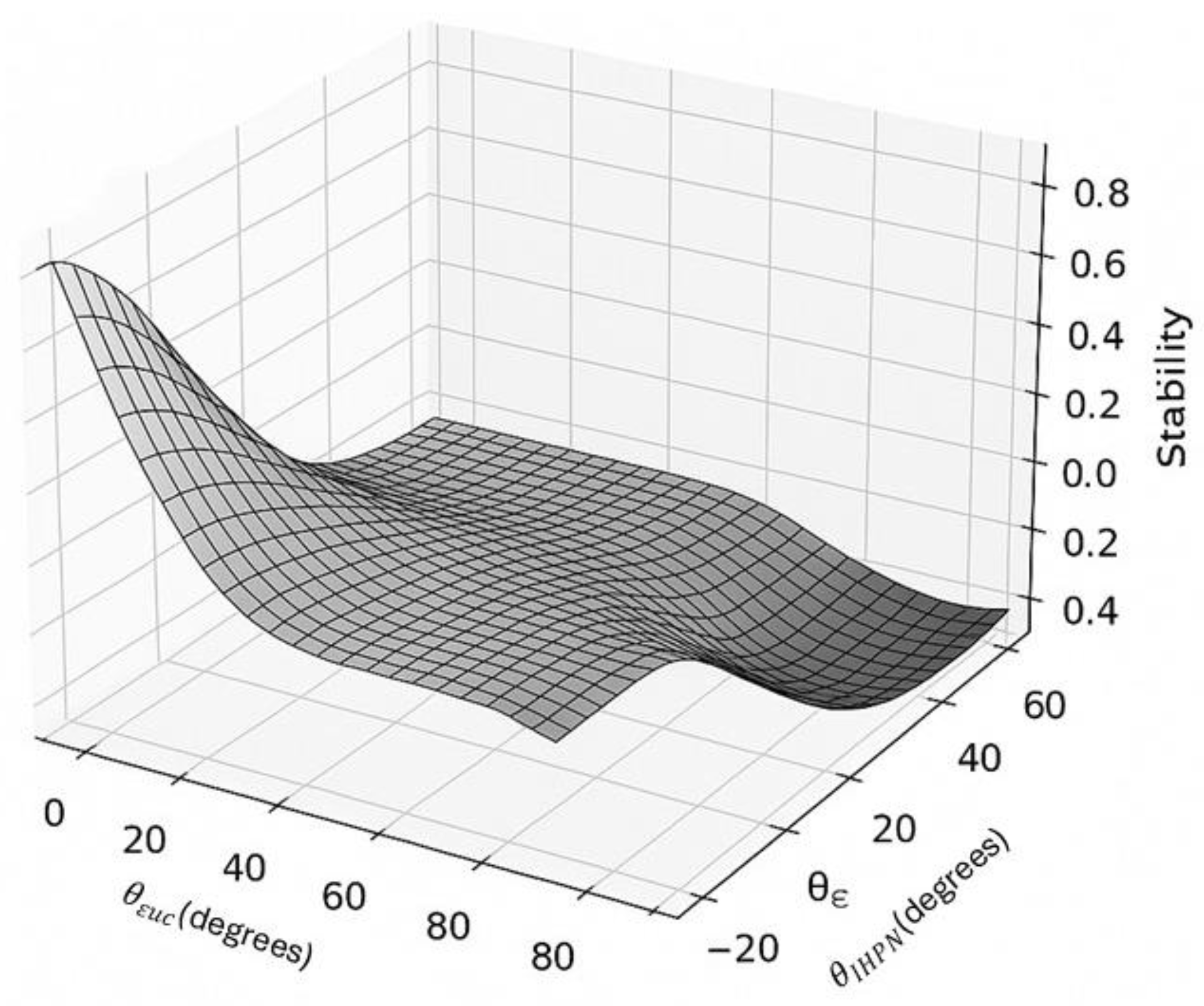
- Topological Coherence: The spiral is quasiperiodic, not perfectly periodic, consistent with octonionic non-associativity. Stable phase domains emerge despite the lack of standard harmonic closure.
- Attractor Classification: Specific torus regions correspond to stable, metastable, or unstable attractors, identified by curvature intensity (tight loops = stability, flattened paths = instability).
- Applications
- Quantum Circuit Modeling: Provides coherence-preserving blueprints for quantum gates under VTT shielding.
- AI Trajectory Prediction: Encodes state transitions of intelligent agents, aiding stability forecasting.
- Time–Topology Experiments: Enables simulation of coherence-based time dilation and informational feedback loops.
- Colored curves: Distinct initial seeds mapped to separate attractor basins.
- Critical points: Inflection zones often aligned with prime-indexed n, suggesting resonance within the octonionic lattice.
- Shaded stability zones: Indicate coherence plateaus vs. chaotic divergence.
References
- Graves, J. T. (1843). On the theory of imaginaries in algebra.
- Cayley, A. (1845). On Jacobi’s Theorem, and on the eight square theorem.
- Kwaśniewski, A. K. (2012). On the history of octonions and related structures, 1071. [Google Scholar]
- Gürsey, F. , & Tze, C.-H. (1996). On the role of division, Jordan, and related algebras in particle physics. World Scientific.
- Ramond, P. (2010). Exceptional groups and physics.
- Dixon, G. M. (1994). Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics. Springer.
- Einstein, A. (1905). Zur Elektrodynamik bewegter Körper.
- Minkowski, H. (1908). Raum und Zeit, 10.
- von Neumann, J. (1932). Mathematische Grundlagen der Quantenmechanik. Springer.
- Dirac, P. A. M. (1939). A new notation for quantum mechanics.
- Nielsen, M. A. , & Chuang, I. L. (2010). Quantum Computation and Quantum Information.
- Dray, T. , & Manogue, C. A. (2015). C: E6, and particle physics. Journal of Physics, 0120; E6. [Google Scholar]
- Evans, J. M. , & Hudson, J. F. (2020). The role of non-associative algebras in geometry and physics, 1305. [Google Scholar]
- Catto, S. (2018). Exceptional structures in physics revisited.
- Baez, J. C. , & Huerta, J. (2011). ( 47(3), 483–552.
- Baez, J. C. (2002). The Octonions.
- Gogberashvili, M. (2023). Octonions and Internal Symmetries in Quantum Mechanics. Symmetry, 15(4), 765.
- Furey, C. (2018). SU(3) × SU(2) × U(1) from the complex octonions.
- Bianchetti, R. Informational Spiral Structures in Prime Distribution via π-Immersion. Preprints 2025, 2025091113. [Google Scholar] [CrossRef]
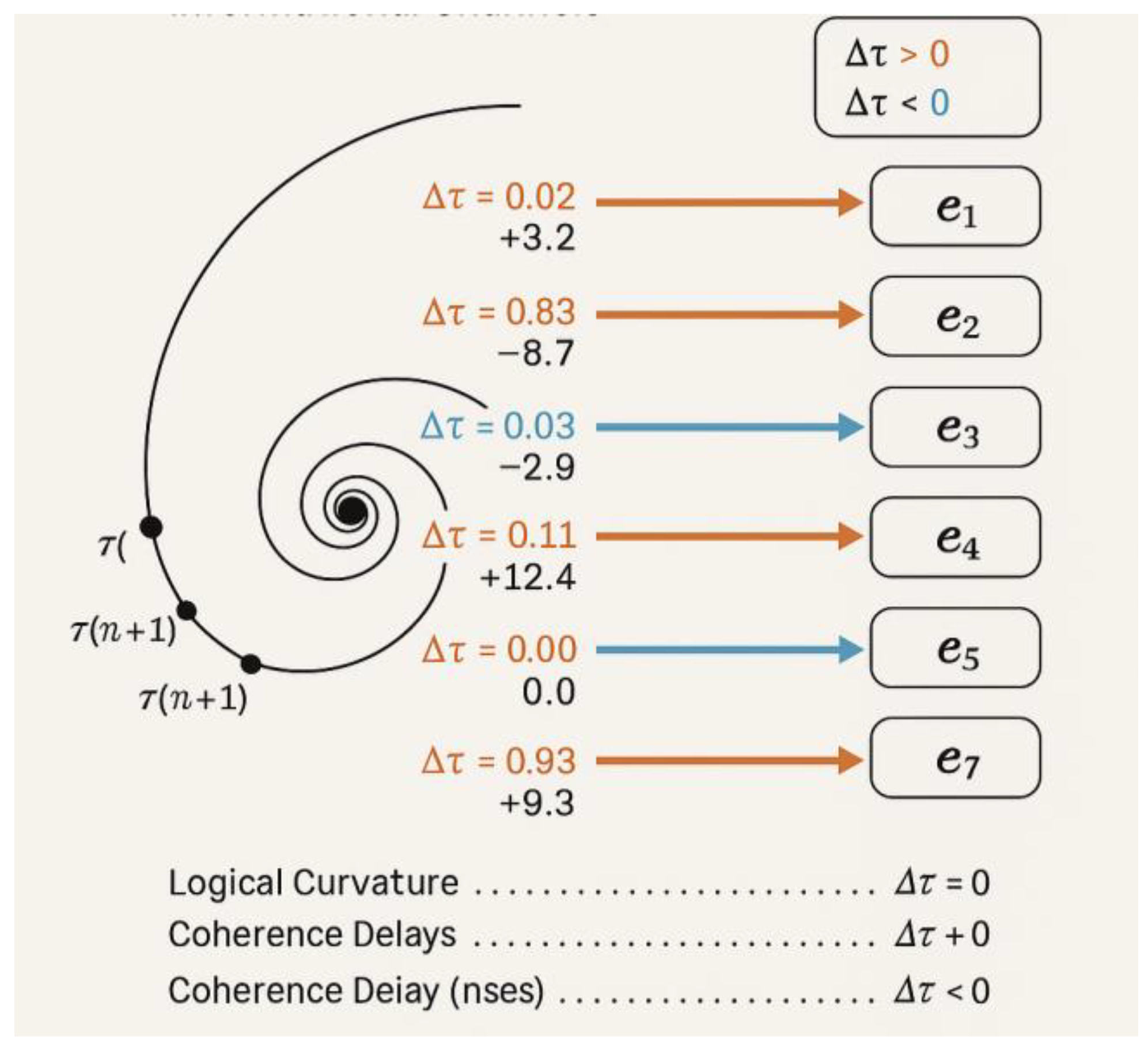
| IRSVT Node (i) | Octonion Target (j) | Logical Curvature ΔΦ | Local ΔC Gradient | Coherence Delay Δτ (ns) | Collapse Threshold | |
|---|---|---|---|---|---|---|
| π(n) | e1 | Spiral → Scalar | 0.02 | Medium | +3.2 | No |
| π(n+1) | e2 | Spiral → Vector | 0.08 | High | +8.7 | Yes |
| π(n+5) | e3 | Spiral → Imaginary Scalar | –0.03 | Low | –2.9 | No |
| π(n+8) | e4 | Spiral → Pseudo-Vector | 0.11 | Critical | +12.4 | Yes |
| π(n+13) | e5 | Spiral → Split-Algebra Path | –0.05 | Variable | –6.1 | Conditional |
| π(n+21) | e6 | Spiral → Twist-Node | 0.00 | Zero | 0.0 | No |
| π(n+34) | e7 | Spiral → Anti-commutative Arc | 0.09 | High | +9.3 | Yes |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





