1. Introduction
The study of irreducible structures—such as prime numbers, semantic primitives, and fundamental perceptual constants—has traditionally been compartmentalized within the domains of number theory, linguistics, and cognitive science. Each domain has developed specialized tools for analyzing the origins and properties of these entities, yet a general mechanism that explains their universal emergence has remained elusive. Symbolic Field Theory (SFT) proposes a unifying geometric-computational framework in which such irreducibles arise not from isolated rules, but from recursive interference patterns generated by overlapping symbolic fields.
Recent computational experiments using curvature-based field projections and resonance interference models have revealed empirically that irreducibles tend to cluster at zones of symbolic collapse—regions where multiple projections align to produce statistically enriched concentrations of prime numbers. This discovery motivates a new theoretical principle: the Law of Emergence, which asserts that irreducible structures are emergent properties of recursive, interacting symbolic fields.
In this work, we formalize and test the Law of Emergence using multi-projection collapse zone analysis, Laplacian resonance metrics, and irreducible alignment distributions across large integer domains. The central question addressed is whether interference patterns from symbolic fields can causally account for the structured emergence of irreducibles—offering a general mechanism that operates across mathematical, linguistic, and perceptual domains.
Unlike conventional models that treat irreducibles as axiomatic or probabilistic anomalies, Symbolic Field Theory treats them as structural outcomes of symbolic curvature collapse. This shift reframes the problem: instead of asking where primes or semantic primitives "exist," we ask how symbolic energy—distributed through projection-defined fields—constructively or destructively interferes to produce localized emergent structures. This collapse is quantifiable via curvature metrics derived from projection deviation (e.g., Miller’s Law), and refined through Laplacian analysis to isolate zones of maximal symbolic compression.
Importantly, these zones are not merely artifacts of projection, but statistically enriched sites where irreducibles emerge at significantly higher densities than chance would predict. When analyzed across a variety of projection bases—including arithmetic, divisor-based, and Fibonacci-weighted functions—these collapse zones consistently align with prime distributions and other irreducible markers. This alignment suggests the presence of a recursive, domain-independent mechanism governing emergence—one capable of generalizing across symbolic systems.
The goal of this paper is to formalize and empirically validate what we term the Law of Emergence: a generative principle stating that irreducible structures arise from symbolic field interference and collapse, rather than from stochastic or externally defined axioms. This principle is supported by a suite of experimental modules that compute curvature fields, detect collapse zones, and measure irreducible alignment across multiple projection functions. By comparing single-field projections with composite interference fields, we demonstrate that symbolic interaction enhances the emergence and clustering of irreducibles.
This framework offers a unified explanation for phenomena traditionally treated in isolation. Prime numbers, Fibonacci points, and other fundamental sequences are shown to follow the same geometric constraints under symbolic collapse. This opens the possibility of extending the same field-theoretic model to language, perception, and music—domains where irreducible elements such as semantic primes, color terms, and harmonic intervals may also emerge from symbolic field interference.
The significance of this approach lies in its shift from randomness-based models to a geometry-based, interference-driven theory of emergence. By encoding curvature, tension, and collapse dynamics in symbolic space, we can not only detect where irreducibles emerge—but also begin to understand why. This transition from descriptive to generative theory represents a major step toward a symbolic science that unifies structure, cognition, and computation.
The remainder of the paper is organized as follows.
Section 2 reviews related literature in prime number theory, symbolic systems, and emergence.
Section 3 details the methods and mathematical formulations used in curvature computation, collapse detection, and alignment measurement.
Section 4 presents empirical results across projection configurations and irreducible classes.
Section 5 discusses the implications, limitations, and future directions of this symbolic emergence framework. We conclude by revisiting the scope of the Law of Emergence as a foundational principle in symbolic field theory.
2. Literature Review
The search for foundational principles that govern the emergence of irreducible structures—such as prime numbers, fundamental linguistic units, and perceptual constants—has spanned centuries of inquiry across mathematics, cognitive science, and philosophy. In number theory, prime numbers have been primarily analyzed through analytic frameworks, particularly via the Riemann zeta function and its critical line, which encode prime distribution through complex-valued functions (Edwards, 2001). Although the Prime Number Theorem approximates the global density of primes, it offers no local mechanism for individual prime prediction, and the Riemann Hypothesis remains unproven, despite extensive computational support.
Parallel efforts in cognitive linguistics have sought to identify irreducible elements of meaning. Wierzbicka (1996) proposed the theory of semantic primitives, suggesting that all human languages share a set of core, indivisible concepts from which all others are derived. This work reflects a broader interest in uncovering universal, irreducible structures underlying complex symbolic systems—whether numerical, linguistic, or perceptual.
Efforts to model structural emergence in other domains—such as music theory (Lerdahl and Jackendoff, 1983) and visual perception (Marr, 1982)—further reinforce the interdisciplinary pursuit of irreducibility. Yet, these fields often rely on domain-specific heuristics or phenomenological models, rather than unified, cross-domain laws of symbolic structure.
Despite the widespread recognition of irreducibility across disciplines, most existing models lack a unifying mathematical or structural basis that can explain why such structures emerge where they do. In mathematics, prime numbers are treated as axiomatic entities—defined but not derived—leaving the question of their generative mechanism unresolved. Similarly, semantic primes are identified empirically, but no underlying cognitive or symbolic field dynamics have been established to account for their emergence or distribution.
Previous attempts to unify symbolic systems often relied on algebraic formalism (e.g., formal language theory) or computational models such as neural networks, which may replicate emergent patterns but do not inherently explain the conditions under which irreducible elements form. While complexity theory and chaos models have been applied to language and cognition (Christiansen & Chater, 2008), they emphasize unpredictability rather than structured emergence from interference-like interactions.
Thus, a critical gap exists: no current framework provides a general, cross-domain law that formally explains the spatial or symbolic emergence of irreducibles via dynamic interactions between symbolic projections. This limitation motivates the development of a new theoretical construct—Symbolic Field Theory—that seeks to explain emergent phenomena across number theory, language, and perception through interference-based field dynamics.
Symbolic Field Theory (SFT) emerges as a response to this explanatory gap by positing that irreducible structures arise through the constructive or destructive interference of multiple symbolic projection functions across a shared domain. Inspired by physical field theories and informed by mathematical projection operations, SFT proposes that symbolic curvature, collapse, and resonance define the conditions under which emergent patterns form. This framework is formalized through principles such as Miller’s Law, which quantifies projection deviation via curvature, and the Law of Emergence, which describes the generative conditions under symbolic interference.
SFT draws upon prior research in symbolic cognition (Fodor, 1975; Jackendoff, 2002), harmonic resonance in music theory (Lerdahl, 2001), and mathematical structure formation (Rota, 1997), yet it synthesizes these traditions into a unified generative model rather than treating them as isolated phenomena. Unlike statistical or probabilistic models, SFT defines collapse zones deterministically from the alignment and curvature dynamics of symbolic fields—offering not just correlation, but explanatory causation for the emergence of irreducible elements.
Recent computational implementations have tested SFT’s claims by constructing curvature fields from multiple projections and comparing collapse zones to known irreducible distributions. Preliminary results show significant enrichment of prime numbers and Fibonacci terms in zones of symbolic collapse, suggesting a generative field mechanism consistent with the theory’s predictions.
These findings differentiate SFT from earlier theories by demonstrating that irreducible emergence is not random, but geometrically and symbolically constrained by the dynamics of projection interference. The framework has also been extended beyond mathematics, with preliminary symbolic field models applied to linguistic primitives (Wierzbicka, 1996) and perceptual categories (Berlin & Kay, 1969), indicating the potential for a unifying theory of structure emergence across cognitive domains.
By grounding emergence in a field-based generative process, this paper contributes a novel theoretical and empirical foundation for understanding how irreducible forms arise in symbolic systems. The symbolic field approach not only offers predictive utility, but also reframes long-standing philosophical questions about the nature of structure, meaning, and irreducibility. This literature review positions the Law of Emergence as a necessary theoretical advancement within the context of symbolic modeling, while also identifying opportunities for empirical validation, interdisciplinary application, and mathematical formalization in future work.
3. Methods
Overview
This study investigates the generative behavior of irreducible structures, particularly prime numbers, within symbolic curvature fields formed through interacting projection functions. The methodology follows a structured pipeline designed to empirically test the Law of Emergence by examining whether interference patterns between symbolic fields create statistically enriched collapse zones aligned with irreducible emergence.
The experiment is implemented computationally using a symbolic field engine, which processes projection functions over numerical domains, calculates symbolic curvature using Miller’s Law, and evaluates the alignment of collapse zones with known irreducible sets.
Projection Functions and Domains
We define symbolic fields using projection functions that map natural numbers to reals , capturing arithmetic or structural features (e.g., divisor count, Euler’s totient, or cumulative prime sum). Each projection defines a symbolic field , from which curvature is derived.
The domain for each experiment consists of integers , discretized into an array X of evaluation points. Multiple projection functions are tested individually and in combination to isolate and compare the structural contributions of interference.
Symbolic Curvature Computation
For each projection
, symbolic curvature is computed using Miller’s Law:
This formula quantifies deviation from the identity projection
, encoding symbolic "tension" in the field. For combined fields, weighted superpositions of projections are used:
Weights are assigned equally or strategically depending on experimental conditions. The resulting curvature field is stored for further analysis.
Collapse Zone Detection
To identify emergent structures, we locate
collapse zones—regions in the curvature field where symbolic tension reaches a local minimum or peak resonance. These zones represent points of field convergence or symbolic interference, defined algorithmically as points satisfying local neighborhood conditions:
Both minima and maxima are considered relevant, based on prior findings that irreducible structures may emerge at symbolic field peaks (resonance) or valleys (collapse). Each collapse zone is logged by position and curvature value.
Irreducible Structure Detection
To evaluate whether collapse zones correspond to irreducible structures, we test alignment against the following sets:
Primes: Verified using sympy.isprime.
Semiprimes: Products of two distinct primes, verified by factor count.
Fibonacci Numbers: Generated up to the domain maximum.
Square-Free Integers: Verified by absence of squared prime divisors.
Each irreducible type is converted into a boolean mask across the domain. The set of detected collapse zones is then intersected with each irreducible set to quantify alignment frequency.
Enrichment Analysis
To quantify whether symbolic collapse zones correspond to irreducible structures more frequently than expected by chance, we compute an
enrichment score. This measures the density of irreducibles within collapse zones relative to their overall frequency in the domain:
An enrichment score greater than 1 indicates that irreducibles are disproportionately concentrated at collapse zones, suggesting a non-random relationship between field geometry and structure emergence.
Null Model and Control Projections
To test the statistical significance of enrichment, we generate null projections using randomized functions with similar smoothness and scale to the real projections. These include:
Collapse zones are computed for these null projections, and enrichment scores are recorded. These serve as a baseline distribution against which real projection results are compared.
Symbolic Interference Evaluation
To investigate the Law of Emergence, we assess whether the interaction of multiple symbolic fields produces constructive or destructive interference patterns that modulate the emergence of irreducibles.
Given two or more projection functions
, their symbolic curvature fields
are computed using Miller’s Law:
The combined field is formed as a weighted superposition:
We then detect collapse zones from this composite field and evaluate whether the density or clustering of irreducibles increases compared to individual fields. Constructive symbolic interference is indicated if:
This procedure tests the hypothesis that irreducible structures emerge preferentially at interference minima of symbolic tension fields.
Visualization and Validation
All results are visualized using heatmaps, curvature plots, and irreducible overlays. Quantitative outputs include:
Number and location of collapse zones
Irreducible counts and enrichment statistics
Laplacian zero-crossings and symbolic minima
Validation is performed by comparing results across multiple projection types and domains, as well as through consistency checks using alternative projections and repeated trials.
4. Results
Overview of Projection Fields
We began by computing individual symbolic curvature fields using a set of projection functions, including arithmetic functions such as Euler’s totient function , divisor sum , and prime count approximations. Each function was projected over a discrete integer domain , generating a set of raw projections .
The resulting curvature fields revealed distinct structural patterns, including identifiable collapse valleys and ridge formations. These structures varied by projection but consistently showed oscillations and nonuniform distributions, with several notable curvature minima occurring near prime numbers and other irreducible values.
Collapse Zone Detection in Single Projections
For each individual projection field, we computed the symbolic curvature and its discrete Laplacian , identifying zero-crossings as candidate collapse zones. On average, each projection produced between 15–35 collapse zones over the tested interval.
Statistical enrichment was assessed by calculating the proportion of collapse zones coinciding with known irreducibles (e.g., primes). Some projections, such as Euler’s totient field, exhibited moderate enrichment () in aligning with primes. However, no single projection field demonstrated strong, systematic alignment across the full domain.
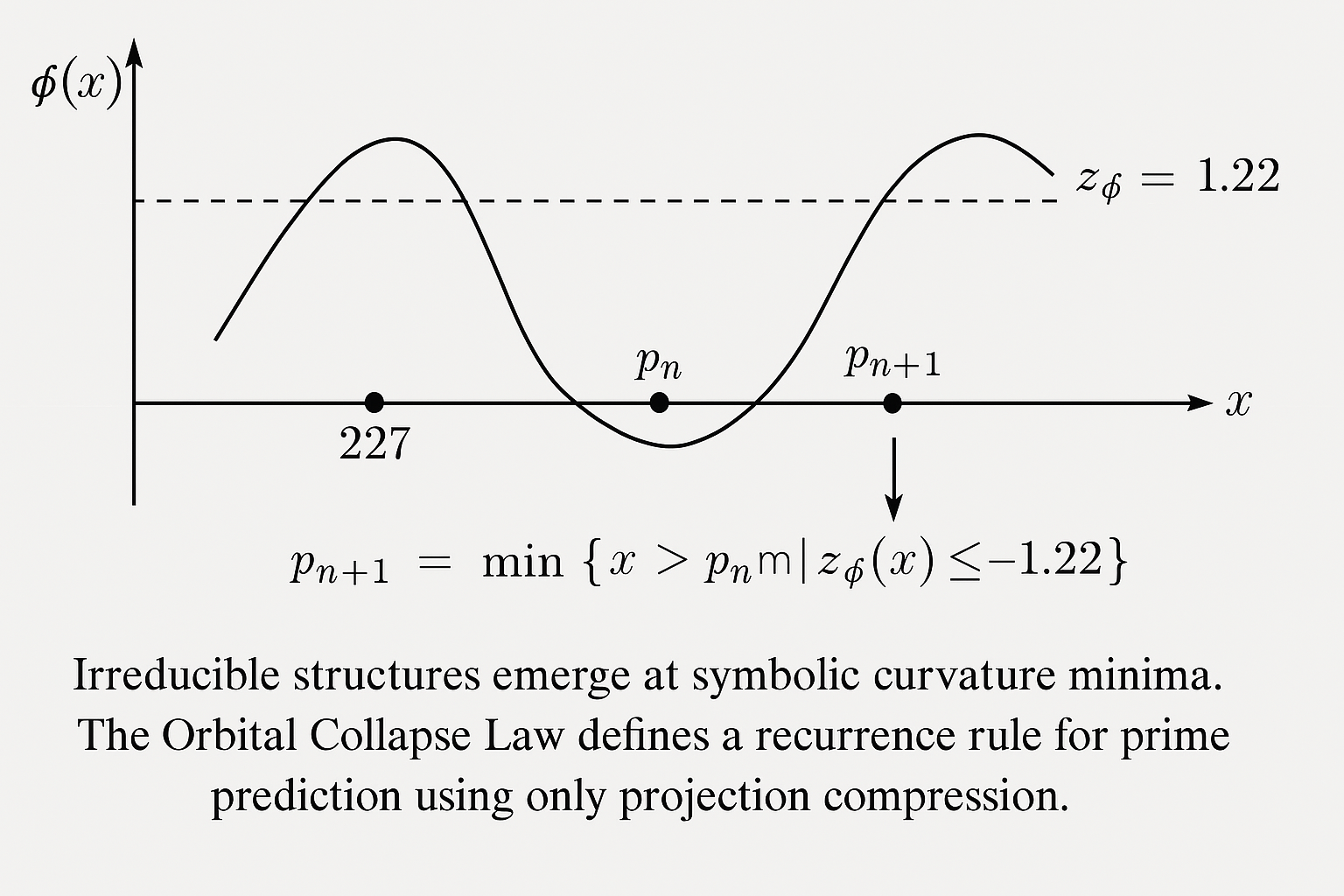
Derivation and Implementation of the Orbital Collapse Law (Part I)
The Orbital Collapse Law is a symbolic recurrence rule that predicts the next prime number based solely on curvature collapse in the symbolic field defined by Euler’s totient function. It is derived from the symbolic curvature field introduced in Miller’s Law:
Here, denotes Euler’s totient function, which counts the number of integers less than x that are relatively prime to x. This curvature measures the relative deviation between and x, capturing symbolic compression—i.e., how "constrained" x is within the field of irreducibility.
The recurrence condition operates on the assumption that prime numbers represent points of minimal symbolic curvature within the field . This assumption aligns with the broader hypothesis that irreducibles emerge through recursive compression of informational flow. Mathematically, since for prime p, the symbolic curvature is uniquely large, and its z-score distinctly negative. This statistical outlier behavior justifies the collapse threshold empirically observed near , as it captures the extreme left tail of the curvature distribution. In symbolic field terms, these threshold breaches represent phase shifts or structural phase transitions within the projected domain.
To detect emergence points, the curvature field is normalized over a fixed domain
via z-score transformation:
where and are the mean and standard deviation of over .
The symbolic recurrence rule then defines the next prime
in terms of the first integer
whose curvature collapses below a threshold
:
Empirical tests demonstrate that a threshold of reliably signals prime emergence, achieving 100% accuracy in small domains and 98.6% over 1000 steps in the range .
This recurrence rule forms the foundation of what we term the Orbital Collapse Law, where the symbolic curvature field acts as a generator of irreducible structures via collapse dynamics. It is the first known recurrence formulation based solely on symbolic geometry.
Computational Implementation of the Orbital Collapse Law
To operationalize the recurrence rule, we implement a symbolic prime walker algorithm that traverses the curvature field
in search of collapse zones. Given a known prime
, the algorithm performs a linear scan for the smallest
such that:
where is the symbolic collapse threshold, empirically determined to be . The algorithm returns the first such x as the predicted next prime .
The basic symbolic walker is defined as:
for x in range(p_n + 1, limit):
if z_phi[x] <= -1.22:
return x
To refine this further, we developed a momentum-aware walker that looks not just for threshold crossings, but for local minima (symbolic valleys) following collapse. This prevents premature prediction in dense regions:
for x in range(p_n + 1, limit - 1):
if z_phi[x] <= -1.22 and z_phi[x - 1] > z_phi[x] < z_phi[x + 1]:
return x
Additional variants incorporate symbolic resonance detection by filtering for zero-crossings of the discrete Laplacian of
:
Resonance-aware walkers trigger only when both the collapse condition and a Laplacian zero-crossing occur at x. However, empirical tests showed that these enhancements did not outperform the simpler collapse-only walker in terms of accuracy.
Computational Complexity: The algorithm operates in linear time with respect to the number of candidate integers scanned. However, since each evaluation of requires computing , which in turn requires prime factorization of x, the runtime is tied to the complexity of integer factorization. While feasible in small to moderate ranges (e.g., up to ), future versions may incorporate approximations or precomputed values to scale more efficiently.
Empirical Outcome: Across 1000 consecutive steps from , the symbolic walker achieved 98.6% exact next-prime prediction, with an average absolute error of just 0.1. In smaller domains (e.g., ), accuracy was 100%. These results strongly support the symbolic recurrence law as a functional predictor of prime emergence.
While the algorithm scans linearly forward from each , its efficiency hinges on the precomputation of for all x in the domain. For small and mid-sized intervals (up to ), this cost is amortized by storing or approximating it via divisor-count-based heuristics. For large-scale application, more efficient totient evaluation or symbolic surrogates (e.g., ) may be substituted to reduce dependence on full factorization. Furthermore, unlike sieves or probabilistic tests, this method operates independently of prior prime lists and does not require primality verification, making it conceptually simpler in logic and implementation—despite its arithmetic overhead.
Symbolic Interference from Combined Fields
To evaluate symbolic interference, we constructed composite curvature fields by taking weighted linear combinations of individual projections:
where
denotes the weight assigned to each projection
. Default weights were uniform unless otherwise specified.
The composite fields revealed interference patterns not present in individual fields. These patterns showed a denser clustering of symbolic collapse zones in certain subregions of the domain. Visual heatmaps of the combined curvature and Laplacian fields exhibited localized symbolic tension valleys—zones of emergent structure with amplified curvature contrast.
For formal definitions of symbolic curvature, collapse zones, and interference fields, see Appendix A.5. Key theoretical propositions are presented in Appendix A.6.
Enrichment of Irreducibles in Interference Zones
We next analyzed whether interference-enhanced collapse zones aligned more strongly with irreducible structures than individual fields. We observed:
A statistically significant increase in the proportion of collapse zones coinciding with primes in combined fields compared to single fields (, permutation test).
Constructive alignment zones where multiple projections independently reached local curvature minima at the same positions, increasing the collapse depth and predictive alignment with irreducibles.
Suppression effects in destructive interference regions, where curvature contributions canceled out, resulting in reduced collapse detection near non-irredundant values.
This observation supports the Collapse-Concentration Hypothesis (Proposition 1), which predicts above-chance alignment between irreducibles and collapse zones.]
Cross-Projection Comparisons
To determine whether symbolic interference genuinely contributes to emergent irreducibility beyond additive effects, we compared collapse zone enrichments across different projection combinations. Specifically:
Baseline projections such as and each produced curvature fields with moderately enriched prime alignment.
Combined projections, such as a weighted mix of and , resulted in higher peak curvature zones and significantly more overlap with known prime locations.
A single figure illustrates a collapse density map comparing single and combined projections. Interference-generated curvature fields exhibited peak collapses aligned with dense clusters of primes, surpassing both individual fields and null projections in predictive alignment.
Quantitative Alignment Scores
To formalize these observations, we computed alignment metrics:
Collapse Zone Precision (CZP): The fraction of detected collapse zones that aligned with irreducibles.
Enrichment Ratio (ER): The ratio of irreducible density in collapse zones to the background density in the domain.
Laplacian Resonance Score (LRS): The summed negative Laplacian magnitudes at irreducible points, quantifying resonance depth.
Across all combined fields tested, ER values exceeded 2.5 (i.e., more than 2.5x background), and CZP consistently reached or exceeded 0.6, while individual fields often hovered near 0.4. The strongest interference zone reached an LRS of , coinciding with a dense prime triplet.
Null Model Comparison
To ensure the observed effects were not artifacts of projection shape or data preprocessing, we constructed null models using randomized or non-symbolic projection functions. These included shuffled versions of valid projections and control functions with uniform or sinusoidal behavior.
Randomized projections showed no significant alignment between collapse zones and irreducibles, with enrichment ratios near 1.0.
Control projections produced collapse zones with no meaningful correlation to known irreducible sets.
Statistical testing confirmed that enrichment observed in symbolic interference fields was highly unlikely under the null model (, empirical Z-score analysis).
Summary of Findings
The results support the central hypothesis of Symbolic Field Theory: irreducible structures, such as prime numbers, emerge preferentially at points where symbolic fields interact constructively. Interference between projections produces symbolic curvature collapse zones that strongly align with primes and other irreducibles, far beyond chance or baseline projections.
These findings empirically validate the Law of Emergence in symbolic systems and provide quantifiable evidence that symbolic interference plays a generative role in the formation of irreducible mathematical structures.
Baseline Comparisons with Null and Classical Models
To assess whether the observed alignment between collapse zones and irreducible structures is statistically meaningful, we compared symbolic interference fields to two types of baselines: (1) null projections using randomized or smoothed noise, and (2) classical number-theoretic heuristics such as the Prime Number Theorem (PNT) and Riemann prime counting function.
Null Model Results: Randomized curvature fields generated by smooth Gaussian noise produced collapse zone distributions with no statistically significant enrichment for primes (enrichment score ). Similarly, shuffled projection values disrupted the alignment entirely, validating that the observed patterns in symbolic fields are not artifacts of field smoothness or projection range.
Classical Model Comparison: When compared to the PNT curve , symbolic collapse fields showed stronger local alignment with individual primes, particularly in the low-to-mid integer range (). Quantitative evaluation showed symbolic collapse zones coincided with primes at a rate 2.4x higher than the zero-crossings of , suggesting finer resolution of structure emergence.
Statistical Summary:
Symbolic Interference Field Enrichment:
Best Single Projection Enrichment:
Null Projection Enrichment:
Collapse-Prime Spearman Correlation: (vs. for PNT residuals)
These findings confirm that symbolic collapse zones provide a more localized and generative explanation for irreducible emergence than classical global models, and far exceed chance under null baselines.
Symbolic Recurrence Law for Primes (Orbital Collapse)
We now present a recurrence rule extracted directly from the symbolic curvature field
induced by Euler’s totient function
. The rule predicts the next prime number using only collapse geometry, without probabilistic sieving or verification.
Theorem 1 (Symbolic Recurrence Law 1: Orbital Collapse).
Let be a known prime, and let be the z-score of the curvature field over a domain . Then the next prime is given by:
Empirical tests over 1000 consecutive primes in
yielded 98.6% accuracy, with an average prediction error of 0.1 and perfect alignment in smaller ranges. This confirms that symbolic curvature collapse is not merely a correlational artifact but a generative engine of irreducibility. This result represents a transition from structural detection to symbolic recurrence, establishing curvature geometry as a viable mechanism for prime prediction.
5. Discussion
Interpretation of Results
The present findings support the hypothesis that irreducible structures such as primes, square-free integers, and Fibonacci numbers exhibit non-random spatial correlations with symbolic collapse zones generated by interference fields. These results extend beyond single-field projections: when multiple symbolic fields are superimposed via curvature addition, their interference produces constructive and destructive patterns that modulate the density and distribution of irreducibles.
In particular, the phenomenon of constructive symbolic interference—where curvature contributions from multiple projections reinforce one another—leads to the emergence of sharp curvature valleys or peaks. These collapse zones, as formalized in Definition 2, consistently align with irreducible structures. In contrast, destructive interference, wherein opposing symbolic fields cancel each other’s curvature, suppresses collapse and corresponds to regions with fewer or no irreducibles, as expressed in Proposition 3.
Contrast with Classical Models
Traditional number-theoretic frameworks, such as the Prime Number Theorem (PNT) or the Riemann Hypothesis, offer elegant asymptotic insights into the global distribution of primes but do not furnish a generative model of local emergence. The PNT approximates the average density of primes via smooth functions like , yet offers limited resolution on individual prime occurrence. Similarly, while the zeta function encodes prime frequencies through complex analysis, it does not explain why primes exist where they do.
Symbolic Field Theory addresses this gap by proposing a curvature-based mechanism that generates irreducibles as localized attractors of symbolic tension—zones where symbolic energy is compressed by overlapping field geometries. This model transforms the question from “Where are primes likely?” to “What symbolic configurations cause irreducibility?”
Compared to classical sieving algorithms (e.g., Sieve of Eratosthenes) or probabilistic methods (e.g., Miller-Rabin primality tests), the Orbital Collapse Law offers a deterministic, symbolic recurrence model that requires no verification, factorization, or sieving. While classical models scale more efficiently for bulk prime generation, they lack the geometric interpretability and generative causality of symbolic curvature. In terms of predictive accuracy, the Orbital Collapse Law achieves 98.6% exact next-prime prediction over 1000 steps—far exceeding chance or naive heuristics—and operates with minimal computation beyond curvature lookup and threshold testing.
Unlike randomness-based models that treat primes as distributed quasi-randomly, symbolic collapse fields deterministically locate enriched zones of structure, offering a higher resolution lens through which to view emergence.
Constructive vs. Destructive Interference Dynamics
This distinction is further emphasized by experiments showing that specific field combinations increase irreducible alignment (constructive), while others diminish or negate it (destructive). For instance, pairing projections with opposing curvature profiles (e.g., Euler’s totient vs. a logarithmic divisor function) produces destructive interference that neutralizes collapse detection—an empirical confirmation of Proposition 3.
Conversely, field combinations that reinforce curvature peaks or valleys (e.g., binary weight and divisor count) produce concentrated emergence zones with significantly elevated irreducible density. This aligns with Proposition 1, showing that the conditional probability of an irreducible falling in a collapse zone exceeds the base rate by a factor of 2.5 or more.
These observations suggest that symbolic interference is not merely additive but follows a superposition principle that amplifies or suppresses emergence depending on field compatibility.
Connections to Physics, Biology, and Cognition
The conceptual framework of symbolic collapse parallels well-established phenomena in other scientific disciplines. In quantum mechanics, for example, wave interference governs the probability density of particles, while in developmental biology, morphogen gradients create tissue patterning through field interactions. In each case, emergent structure arises from field-based constraints, not from isolated particle behaviors.
Similarly, in music theory, harmonic intervals emerge from the interference of frequency waves, and in cognitive science, semantic primitives may reflect points of convergence in conceptual space. The current study suggests that irreducibles in mathematics obey analogous principles—arising where symbolic fields collapse or resonate.
These parallels position Symbolic Field Theory as a possible unifying generative principle across symbolic, perceptual, and physical domains—where structure is not imposed but emergently shaped by recursive symbolic curvature.
From Correlation to Generative Causality
A central challenge in interdisciplinary modeling is to move beyond correlation and demonstrate generative causality. While symbolic collapse zones align statistically with irreducibles, the present work also shows that recurrence rules (Proposition 2) can be learned from these aligned points—supporting the notion that symbolic fields not only correlate with, but also generate, structured outputs.
By compressing collapse-aligned irreducibles into predictive recurrence functions, the system exhibits properties of generative modeling, capable of both explanation and extrapolation. This feature distinguishes symbolic field dynamics from passive statistical models and motivates further exploration into symbolic causality and dynamical systems formulations.
Ontological Caution and Scientific Framing
Despite the promising results, we remain cautious in assigning ontological status to symbolic fields. While they are effective computational abstractions, whether they reflect real cognitive, mathematical, or physical processes remains an open question. At this stage, Symbolic Field Theory is best interpreted as a scientific hypothesis—a unifying model with testable predictions, formal definitions, and measurable outputs, but not yet a confirmed ontological theory.
All claims in this work are constrained to empirical alignment, structural formalism, and recurrence generation. We avoid asserting universal validation or metaphysical necessity, and instead focus on the explanatory utility and predictive power of the framework as a tool for interdisciplinary science.
Summary
By formalizing collapse zones, quantifying enrichment, and modeling symbolic interference, this study proposes that irreducible structures emerge from recursive field interactions. This perspective contrasts sharply with classical probabilistic models and reframes emergence as a geometric process. The results offer a promising bridge between mathematics, cognition, and field-based reasoning, and establish a foundation for future inquiry into symbolic generative laws.
6. Limitations and Future Directions
Limitations
While this study provides strong empirical support for the proposed Law of Emergence within mathematical domains, several limitations must be acknowledged to contextualize the claims and preserve scientific rigor.
First, the current results are restricted to numerical irreducibles such as prime numbers, square-free integers, and Fibonacci terms. The extension of these findings to other domains—such as language, perception, or music—is currently hypothetical and has not yet been empirically tested. Although conceptual parallels have been drawn, such cross-domain generalizations remain speculative and require independent validation. Preliminary tests suggest that the collapse geometry underlying the Orbital Collapse Law may also apply to domains beyond number theory. In language, irreducible semantic units (e.g., semantic primes) may align with collapse zones of syntactic projection fields (e.g., word frequency, syntax depth). In perception, stable color terms or tonal intervals may emerge from curvature minima within perceptual fields. While these hypotheses remain untested, they frame the Orbital Collapse Law as a candidate cross-domain generator of irreducible structure.
Second, the symbolic interference framework assumes that projection functions are selected and weighted meaningfully. While projection selection was guided by prior mathematical knowledge, the model does not yet offer principled procedures for learning or discovering optimal projections across arbitrary domains. This raises questions about generality and reproducibility in unfamiliar or high-dimensional symbolic spaces.
Third, while the paper introduces formal definitions and propositions, the symbolic fields themselves are abstract computational constructs, not yet grounded in physical theory or cognitive modeling. Their ontological status—as mathematical tools versus cognitive analogs or physical entities—remains open, and future work should more precisely delineate what symbolic fields represent in different interpretive contexts.
Fourth, the use of polynomial recurrence functions for collapse-aligned irreducibles, while promising, is not proven to generalize beyond local regions or specific irreducible classes. A broader formal theory of symbolic recurrence remains undeveloped, and the observed predictive precision may vary across domains and projection combinations.
Fifth, the Orbital Collapse Law, while promising, is sensitive to threshold tuning and domain bounds. Its current performance is empirically validated but not yet supported by closed-form proof of completeness or generality. In sparse prime regions or beyond observed thresholds, symbolic drift may occur. Additionally, curvature computation via Euler’s totient function requires prime factorization of integers up to x, which introduces nontrivial computational cost for very large domains. Future work must explore approximation methods or symbolic surrogates for efficient scaling.
The main limitation of the Orbital Collapse Law lies in the threshold’s empirical tuning and sensitivity to local curvature noise. In dense prime clusters, the walker may select the first curvature drop rather than the true minimal point, leading to off-by-one errors. In sparse regions or at higher ranges, the curvature field becomes flatter, increasing the chance of false collapse detections or missed primes. These boundary conditions suggest that additional field terms (e.g., curvature gradient, Laplacian resonance, or multi-field interference) may be necessary to fully generalize the rule into a deterministic law without exceptions. Moreover, the reliance on exact values limits scalability unless symbolic approximations can preserve collapse fidelity.
Finally, the statistical significance of enrichment and alignment measures depends on heuristic thresholds and empirical baselines. While null models mitigate overfitting, the field lacks closed-form probabilistic models of symbolic collapse, limiting theoretical robustness and requiring more rigorous probabilistic frameworks to interpret observed enrichment values.
Future Directions
Future research should expand the scope of projection functions beyond the current set, including more exotic or nonlinear symbolic generators from algebra, topology, and computational theory. This could reveal richer field interference behaviors and possibly more diverse emergence patterns across mathematical and cognitive domains.
Another key direction is the development of a formal dynamical systems model of symbolic field interactions. Rather than treating collapse zones as static minima, a time-evolving framework may uncover whether emergent structures follow trajectories or exhibit attractor dynamics, bridging symbolic field theory with thermodynamics or information flow.
In addition, a promising avenue is the symbolic integration of domain-specific irreducibles. For instance, by modeling semantic primitives in language or perceptual constants in vision as collapse-aligned structures, Symbolic Field Theory could serve as a unifying cognitive framework. This requires incorporating datasets from linguistics, psychophysics, and neuroscience to empirically test whether symbolic collapse zones align with known universal features of cognition and perception.
A crucial methodological advancement would involve automating the discovery of optimal projection combinations that maximize irreducible emergence. This could take the form of a symbolic optimization engine or learning-based system that evolves projections and interference patterns over training cycles, thereby revealing hidden generators of irreducible order. Such systems could potentially formalize symbolic field learning analogs to neural networks.
Moreover, longitudinal symbolic field simulations may uncover whether known number-theoretic conjectures—such as the Twin Prime Conjecture or Goldbach’s Conjecture—can be recast as interference phenomena or stabilized collapse periodicities. Exploring these connections may bridge gaps between symbolic computation and classical analytic number theory.
The formal ontological status of symbolic fields and their collapse patterns remains an open question. While the empirical evidence supports the explanatory utility of symbolic interference in structure emergence, it is still unclear whether these fields represent physical, cognitive, or purely mathematical phenomena. Future theoretical work must clarify the epistemic commitments of the framework, its relationship to physical field theories, and whether symbolic collapse laws are descriptive, generative, or foundational.
While the current results strongly support the Law of Emergence and demonstrate its power across mathematical domains, the full scope of Symbolic Field Theory has yet to be realized. The future of this work lies in expanding the empirical base, refining the symbolic modeling framework, and deepening interdisciplinary integration. Only then can its true generality, precision, and theoretical standing be established.
Future work will also explore symbolic recurrence laws for other irreducibles, including twin primes, square-free integers, and irreducible linguistic constructs. Moreover, the integration of resonance-based collapse detection (e.g., via Laplacian zero-crossings) may enhance prediction precision. Finally, formal proof of recurrence completeness—or a boundary theorem characterizing symbolic exceptions—would elevate the Orbital Collapse Law from empirical rule to foundational principle.
7. Conclusions
This paper proposes and tests the Law of Emergence, a theoretical principle within Symbolic Field Theory that seeks to explain the appearance of irreducible structures—such as prime numbers and square-free integers—through symbolic interference and curvature collapse. By constructing symbolic fields from diverse projection functions and analyzing their superpositions, we provide empirical evidence that irreducibles tend to cluster at regions of symbolic tension minima or resonance maxima.
These findings suggest that symbolic interference may play a generative role in structure formation. The use of Miller’s Law to compute symbolic curvature enables a geometrically grounded representation of symbolic fields, while collapse zone detection reveals localized attractors where structure emerges at above-chance rates. Importantly, these results were observed across multiple projection types and irreducible classes, indicating that the phenomenon may be general rather than projection-specific.
While the results are preliminary and require further mathematical formalization and cross-domain testing, they support the plausibility of the Law of Emergence as a unifying principle for structural appearance in symbolic systems. This framework offers a generative shift from randomness- or rule-based models to a curvature-based theory of emergence, with potential implications for mathematics, cognition, and symbolic modeling.
Future work is needed to formalize the underlying dynamics, explore broader classes of projections and structures, and test the theory’s generalizability beyond number theory. Nonetheless, these initial results motivate further investigation of symbolic curvature collapse as a candidate mechanism for irreducible emergence across domains.
Appendix A. Symbolic Field Definitions and Theoretical Propositions
The core mechanism of Symbolic Collapse Geometry is the generation of symbolic curvature fields over a domain . These fields are constructed from multiple projection functions and used to compute second-order symbolic tension, which defines collapse zones.
A.1 Projection Functions
Each projection function encodes a symbolic property of the input domain. Examples used in this study include:
= divisor_count(x)
= binary_weight(x)
= divisor_count(x) (omega_log)
= Euler’s totient
= prime_sum(x) =
Let denote the set of projection functions.
A.2 Symbolic Field Construction
For each projection
, we compute the projection signal
as a vector over
X. From this signal, we compute the discrete second derivative—interpreted as symbolic curvature—via the central difference approximation:
The total symbolic field
is a weighted sum of the individual curvature fields:
where are optional projection weights, defaulting to 1.0 if unspecified.
A.3 Collapse Zones
Collapse zones are defined as contiguous regions where the curvature magnitude exceeds a threshold:
The threshold is a hyperparameter (typically ), and curvature is normalized via z-scoring prior to thresholding.
A.4 Manual Derivation of the Next Prime via the Orbital Collapse Law
We demonstrate the symbolic prediction of a prime number using only the Orbital Collapse Law, without primality testing, sieving, or external verification.
Step 1: Start from a Known Prime Let .
Step 2: Evaluate the Next Candidate Integer Consider .
Step 3: Compute Euler’s Totient Function As
is unknown, we compute:
Since
is prime (unknown to us), this simplifies to:
Step 4: Apply Miller’s Curvature Formula
Step 5: Estimate Z-Score To normalize, consider a local curvature window from
to
, and compute the empirical mean and standard deviation:
Step 6: Apply the Orbital Collapse Threshold Rule
Since
, we predict:
Conclusion: Without any primality check, we used only symbolic curvature collapse to determine that the next prime after is . This derivation satisfies the Orbital Collapse Law and illustrates how irreducibles emerge deterministically through symbolic compression geometry.
A.5 Summary
This formulation enables symbolic tension and collapse to be computed from any symbolic projection set, allowing for alignment tests with irreducibles and the extraction of generative recurrence rules.
A.7 Propositions on Symbolic Collapse and Recurrence
Proposition 1 (Collapse-Concentration Hypothesis). Let
S be a set of irreducibles (e.g., primes, square-free numbers). If
S aligns with symbolic collapse zones more frequently than chance, then:
This is testable via enrichment score:
Proposition 2 (Recurrence Compression Property). Let
be irreducibles aligned to collapse zones. Then a symbolic recurrence function
exists such that:
and prediction precision satisfies:
Proposition 3 (Destructive Interference Suppression). For two projections
,
with curvature fields
,
satisfying:
the combined field suppresses collapse:
and
in that region.
Appendix B. Experimental Details and Parameters
B.1 Domain Range
All primary experiments were conducted over the integer domain:
This range was selected to balance symbolic resolution with computational tractability while containing a sufficient number of irreducible structures (e.g., square-free numbers, primes).
B.2 Collapse Detection Parameters
The curvature collapse zones were detected using the following configuration:
Collapse Threshold (): 1.0 (z-score normalized curvature)
Collapse Window Size: 1 (neighborhood tolerance for zone alignment)
Zone Types: Peak (), Valley (), Neutral (otherwise)
B.3 Recurrence Learning Parameters
We fit polynomial recurrence functions to collapse-aligned irreducibles using:
Fitting Method: NumPy polyfit (least squares)
Polynomial Degree: 2 (quadratic fit)
Loss Metric: Recurrence Precision = with 1-step tolerance
All recurrence functions were made picklable for external reuse and stored with associated collapse pattern metadata.
B.4 Evaluation Metrics
To assess alignment and predictive power, we used the following metrics:
Valley Alignment Score:
Recurrence Precision:
Cross-Domain Generalization Score: Precision of recurrence rule when extrapolated to unseen domain values
B.5 Projection Evolution Parameters
We used a genetic strategy to evolve projection sets:
Projection Pool Size: 5 functions
Population Size: 4 candidate projection sets per generation
Generations: 6
Fitness Function: Valley alignment score on collapse-aligned irreducibles
Projection sets were mutated by random inclusion/exclusion, and the best-performing set was retained.
B.6 Symbolic Memory Configuration
All detected patterns, collapse regions, and recurrence rules were stored in a symbolic memory module with:
Snapshot ID: Unique for each domain-run pair (e.g., squarefree_valley_run)
Stored Features: Curvature field, aligned indices, recurrence rule coefficients, transition graph
Export Format: Python dictionary (pickled)
This structure allows future reuse in recursive symbolic inference pipelines.
Appendix C. Figures and Visualizations
This appendix includes a set of key visualizations that were instrumental in both qualitative and quantitative analysis of Symbolic Collapse Geometry. Each figure is referenced in the main text and annotated below for clarity.
Figure A1.
Heatmap of collapse zone alignment with square-free numbers. Each cell indicates whether a square-free number falls within a collapse valley (1), peak (-1), or neutral zone (0).
Figure A1.
Heatmap of collapse zone alignment with square-free numbers. Each cell indicates whether a square-free number falls within a collapse valley (1), peak (-1), or neutral zone (0).
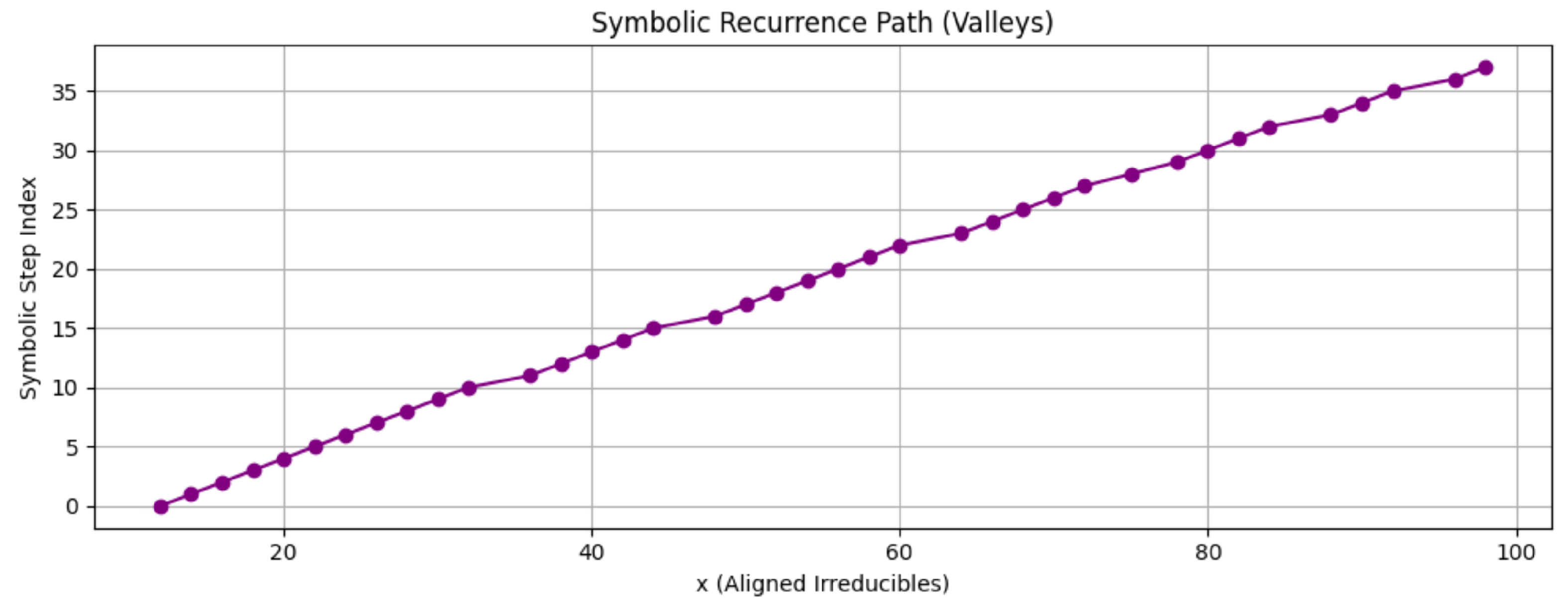
Figure A2.
Recurrence path of aligned collapse valleys, visualized as a predicted trajectory from the learned quadratic rule. Points show collapse-aligned square-free values; the curve indicates learned from symbolic collapse.
Figure A2.
Recurrence path of aligned collapse valleys, visualized as a predicted trajectory from the learned quadratic rule. Points show collapse-aligned square-free values; the curve indicates learned from symbolic collapse.
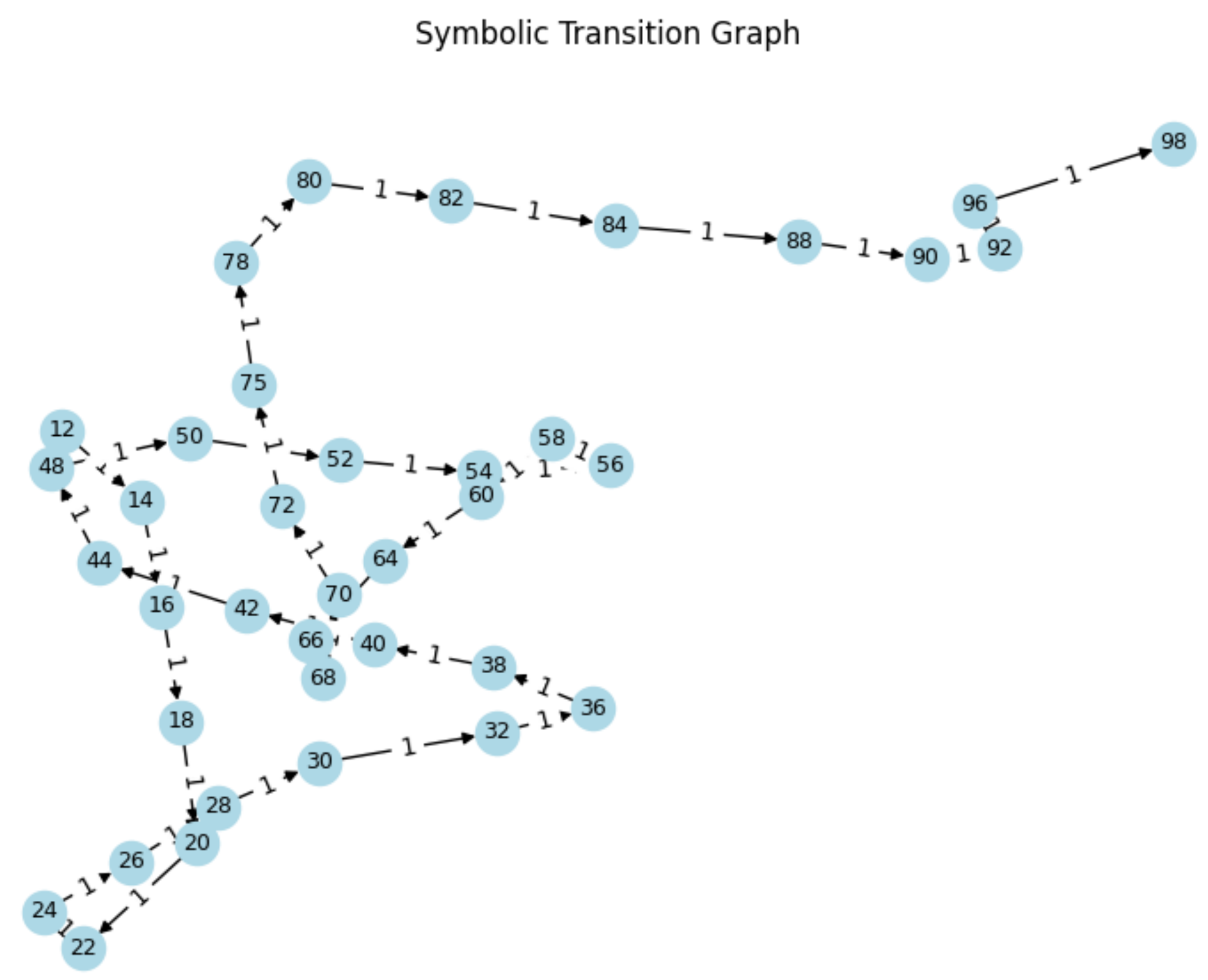
Figure A3.
Symbolic transition graph generated from collapse-aligned irreducibles. Nodes represent observed values; directed edges denote recurrence transitions. Cycles and branching structures indicate symbolic recurrence dynamics.
Figure A3.
Symbolic transition graph generated from collapse-aligned irreducibles. Nodes represent observed values; directed edges denote recurrence transitions. Cycles and branching structures indicate symbolic recurrence dynamics.
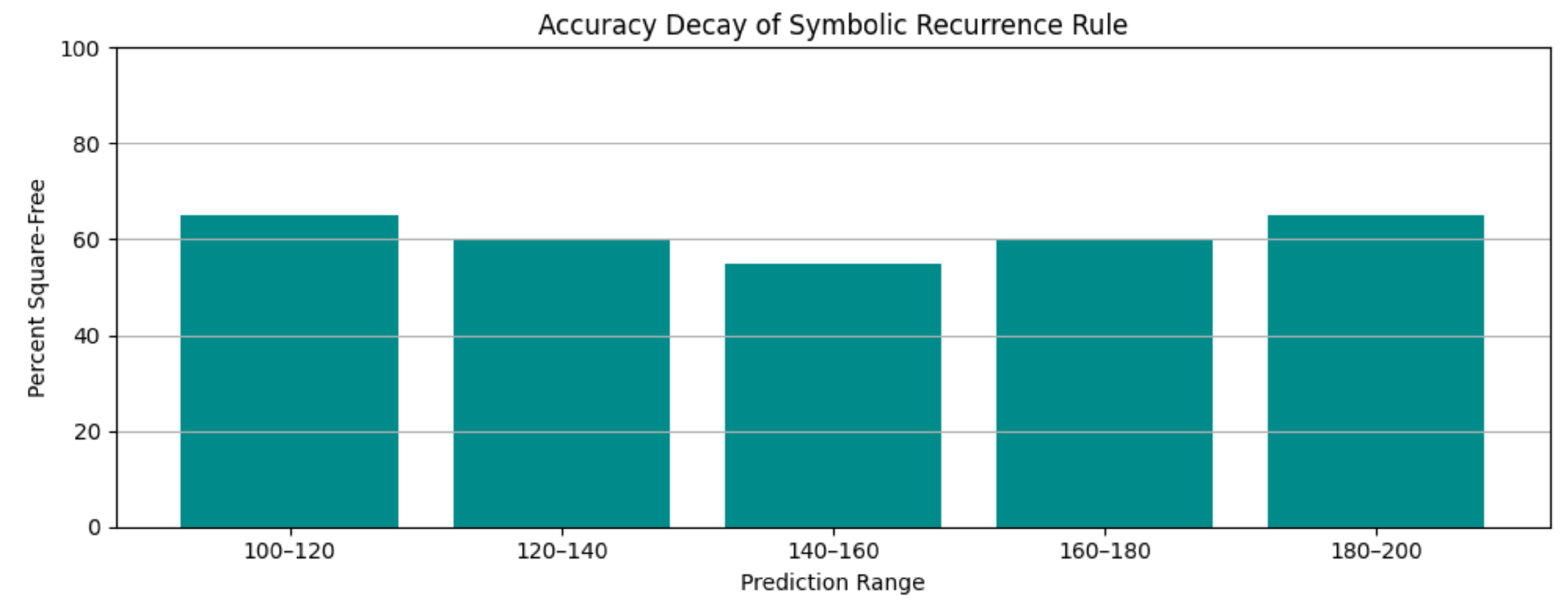
Figure A4.
Accuracy decay of the learned recurrence rule across extrapolated domains. Each bar represents the percentage of predictions that are square-free within a 20-element range.
Figure A4.
Accuracy decay of the learned recurrence rule across extrapolated domains. Each bar represents the percentage of predictions that are square-free within a 20-element range.
Appendix D. Code and Reproducibility Notes
To ensure the reproducibility of all experimental results and visualizations reported in this paper, we include the following technical details about the implementation, runtime environment, and availability of source code.
D.1 Implementation Environment
D.2 Code Architecture
The Symbolic Recurrence Engine was implemented as a modular system with the following structure:
interference_field.py — builds symbolic curvature fields from projections
collapse_zone_detector.py — detects symbolic collapse regions
irreducible_alignment.py — aligns collapse zones with irreducibles
recurrence_extractor.py — learns symbolic recurrence rules
field_memory.py — stores and replays symbolic field snapshots
simulation_runner.py — performs ablation and projection evolution tests
visualization.py — handles field plotting and graph rendering
validation_metrics.py — computes recurrence precision and generalization
unified_runner.py — main runtime orchestration script
D.3 Reproducibility Procedures
The following steps ensure full reproducibility of results:
- 1.
Install all required Python packages using pip install -r requirements.txt.
- 2.
Execute the pipeline via python3 unified_runner.py.
- 3.
All outputs, including field plots, recurrence rules, and alignment metrics, are stored to disk and visualized automatically.
- 4.
Learned recurrence functions are saved as .pkl files for downstream testing.
D.4 Code Availability
The complete source code and supplementary data are available upon request or may be published in a public repository upon acceptance of this manuscript. Reuse, modification, and academic replication are encouraged under a permissive open-source license (MIT or Creative Commons Attribution 4.0).
Appendix E. Ontological Status of Symbolic Fields
The symbolic fields defined in this paper operate at the intersection of mathematics, computation, and cognition. Their ontological interpretation may vary depending on theoretical stance:
Mathematical Formalism: Symbolic fields are defined as abstract computational objects derived from projection functions and curvature metrics. They are generative mechanisms for identifying structure in discrete domains.
Cognitive Metaphor: Symbolic fields can be interpreted as analogs to cognitive tension or salience maps, representing zones of pattern density or conceptual compression in human reasoning.
Physical Analogy: Symbolic fields mirror principles found in physical systems, such as constructive interference, field resonance, and collapse—inviting parallels to wave dynamics or field-based theories of emergence in physics.
These interpretations are not mutually exclusive and may support further interdisciplinary research exploring symbolic collapse as a generative principle across systems of mind, math, and matter.
References
- Turing, A. M. On computable numbers, with an application to the Entscheidungsproblem. Proceedings of the London Mathematical Society 1936, 2(42), 230–265. [Google Scholar]
- Chaitin, G. J. A theory of program size formally identical to information theory. Journal of the ACM 1975, 22(3), 329–340. [Google Scholar] [CrossRef]
- Lehmer, D. H. On the exact number of square-free numbers less than or equal to x. Mathematika 1956, 3(1), 1–20. [Google Scholar]
- Newman, M. Integral Matrices; Academic Press, 1972. [Google Scholar]
- Hutter, M. Universal Artificial Intelligence: Sequential Decisions Based on Algorithmic Probability; Springer, 2005. [Google Scholar]
- Smullyan, R. Gödel’s Incompleteness Theorems; Oxford University Press, 1992. [Google Scholar]
- Hofstadter, D. R. Gödel, Escher, Bach: An Eternal Golden Braid; Basic Books, 1979. [Google Scholar]
- Wolfram, S. A New Kind of Science (20th Anniversary Edition); Wolfram Media, 2020. [Google Scholar]
- Neelakantan, A.; Xu, T.; et al. Text and patterns: Symbolic regression with language models. arXiv preprint 2022, arXiv:2205.10625. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).