Symbolic Field Theory and Recurrence Geometry: Predicting Irreducible Structures via Collapse Dynamics

1. Introduction

The nature of irreducible structures in mathematics, including prime numbers, square-free integers, and Fibonacci sequences, continues to pose foundational questions about structure, emergence, and order. Conventional models in number theory often treat these phenomena as unpredictable or distributed according to probabilistic laws (Hardy & Wright, 2008; Granville, 1995). While these approaches have yielded powerful asymptotic results, they offer limited insight into the deterministic mechanisms underlying the appearance of such structures at specific locations within the number line.

Recent work in symbolic field theory (Miller, 2024a; 2024b) has proposed a paradigm shift: interpreting the emergence of irreducible elements as the result of curvature-driven collapse in symbolic projection fields. According to this theory, numerical structures arise not from randomness but from recursive interactions between symbolic transformations—such as Euler’s totient function $\varphi \left(x\right)$, the Möbius function $\mu \left(x\right)$, and divisor-based metrics—projected over numerical domains. These projections form what has been termed a symbolic collapse field, in which structural tension, compression curvature, and Laplacian variation converge to predictively locate irreducibles.

Building on the Orbital Collapse Law and the Field-Invariant Collapse models presented in prior studies (Miller, 2024a; 2024c), the present paper investigates whether these symbolic fields also encode recurrence patterns—stable symbolic motifs that repeatedly co-occur with specific irreducible outcomes. We hypothesize that such recurrence structures emerge naturally from local collapse windows and exhibit measurable predictive strength, forming the basis of a symbolic recurrence engine.

The motivation for this research stems from two converging observations in symbolic collapse theory. First, projection functions such as $\varphi \left(x\right)$, $\mu \left(x\right)$, $d\left(x\right)$ (number of divisors), and $P\left(x\right)$ (prime sum function) exhibit sharp symbolic curvature and alignment near known irreducible elements (Miller, 2024b). This alignment is not arbitrary; it reflects a deeper resonance in the collapse field that consistently marks points of structural significance. Second, when symbolic collapse values are observed across local numerical neighborhoods (e.g., within sliding windows of fixed width), patterns begin to emerge. These patterns appear to encode local recurrence conditions—signatures that distinguish irreducibles not only individually but also as part of broader symbolic motifs.

Prior empirical studies (Miller, 2024a; 2024d) have demonstrated that symbolic field curvature can achieve high classification accuracy for identifying primes, Carmichael numbers, and square-free integers using logistic regression over projection metrics. However, these models rely primarily on global curve fitting and lack a mechanism for capturing symbolic recurrence—the reuse of collapse configurations across the number line. The present study addresses this gap by implementing a symbolic recurrence rule extractor, designed to identify and score stable symbolic motifs within collapse geometry and assess their predictive accuracy.

Our approach applies a fixed-size sliding window over projection fields computed for each $x\in \mathbb{Z}$ within a defined range. Within each window, the symbolic signature is encoded as a multi-dimensional vector over the five core projection functions. These signatures are then grouped by co-occurrence with binary irreducibility flags, and recurrence rules are derived via frequency-dominant prediction. The outcome is a symbolic recurrence engine capable of generating interpretable, high-confidence rules aligned with the structural emergence of irreducible number types.

This study is driven by the hypothesis that symbolic collapse fields not only differentiate irreducibles through curvature minima and Laplacian sharpness (Miller, 2024a), but also encode recurrence motifs that can be generalized across domains. These motifs are hypothesized to act as local symbolic attractors—distinct collapse configurations that predict the presence or absence of irreducible elements with measurable confidence. We frame this as a form of symbolic recurrence determinism, where structure is not merely an outcome of probabilistic scattering but the result of dynamic symbolic reuse within a structured projection space.

The central research questions of this study are as follows:

• Do irreducible types (e.g., primes, square-free numbers, Carmichael numbers) exhibit stable symbolic recurrence patterns across projection functions?
• Can these recurrence patterns be extracted, scored, and interpreted as predictive rules?
• How does the predictive accuracy of symbolic recurrence rules compare to null models or baseline classifiers?

Answering these questions has implications not only for number theory, but also for symbolic cognition, pattern emergence, and recursive structure detection across formal systems. If symbolic collapse fields do encode recurrent motifs tied to structural emergence, this suggests the existence of an underlying symbolic dynamic governing the formation of complexity. This concept aligns with recent philosophical and computational interpretations of emergence as a consequence of recursive informational collapse (Chalmers, 1996; Wolfram, 2020; Miller, 2024b), extending symbolic field theory into the domain of recurrence modeling.

This paper builds directly upon the foundational work presented in prior symbolic field theory papers (Miller, 2024a; 2024b; 2024c), which introduced the Orbital Collapse Law and Field-Invariant Curvature Hypothesis as tools for mapping emergent structure in projection space. While those works focused primarily on curvature alignment, prediction accuracy, and statistical differentiation, the present study advances the theory by introducing a new mechanism: symbolic recurrence extraction from collapse geometry.

By tracing local symbolic configurations within a moving window of collapse scores, we extract, validate, and store symbolic recurrence rules that generalize the behavior of irreducible types. These rules are not derived from arithmetic properties directly but instead from symbolic deformation patterns across multiple projections. As such, they serve as an abstraction layer above number theory—capturing symbolic recurrence itself as a generative property of the field.

The remainder of this paper is structured as follows. Section 2 outlines the methods used for collapse computation, recurrence encoding, rule scoring, and accuracy benchmarking. Section 3 presents the results, including recurrence rule counts, support metrics, and predictive accuracy. Section 4 discusses the implications of these findings in the context of symbolic determinism and collapse geometry. Section 5 concludes with limitations and directions for further research, including cross-domain application to language and music.

This paper builds directly upon the foundational work presented in prior symbolic field theory papers (Miller, 2024a; 2024b; 2024c), which introduced the Orbital Collapse Law and Field-Invariant Curvature Hypothesis as tools for mapping emergent structure in projection space. While those works focused primarily on curvature alignment, prediction accuracy, and statistical differentiation, the present study advances the theory by introducing a new mechanism: symbolic recurrence extraction from collapse geometry.

By tracing local symbolic configurations within a moving window of collapse scores, we extract, validate, and store symbolic recurrence rules that generalize the behavior of irreducible types. These rules are not derived from arithmetic properties directly but instead from symbolic deformation patterns across multiple projections. As such, they serve as an abstraction layer above number theory—capturing symbolic recurrence itself as a generative property of the field.

The remainder of this paper is structured as follows. Section 2 outlines the methods used for collapse computation, recurrence encoding, rule scoring, and accuracy benchmarking. Section 3 presents the results, including recurrence rule counts, support metrics, and predictive accuracy. Section 4 discusses the implications of these findings in the context of symbolic determinism and collapse geometry. Section 5 concludes with limitations and directions for further research, including cross-domain application to language and music.

2. Literature Review

The emergence of irreducible mathematical structures such as primes, Fibonacci numbers, and perfect numbers has long captivated theorists in number theory, computational complexity, and physics. Foundational treatments of number theory, such as Hardy and Wright’s seminal text An Introduction to the Theory of Numbers (2008), formalize key properties and behaviors of these structures without offering causal mechanisms for their emergence. Similarly, Rosen (2012) and Andrews (1994) have provided extensive overviews of multiplicative functions, factorization, and integer classes, yet the generative origins of these objects remain elusive.

Traditional algorithmic approaches to structure generation have relied heavily on recursive sequences or sieve methods, as explored by Knuth (1997) in his foundational work on fundamental algorithms. These techniques are effective for enumeration but do not illuminate why certain sequences recur or self-organize within broader numerical or symbolic systems. The lack of a unified principle of emergence within number theory has led researchers to explore interdisciplinary perspectives grounded in computation, dynamics, and complexity.

Gregory Chaitin’s (1975) theory of algorithmic information laid the groundwork for understanding irreducibility from an informational standpoint, defining objects as irreducible when no shorter program can generate them. This notion connects with Kolmogorov complexity and the idea that certain structures resist compression—an idea later refined by Zenil et al. (2015), who examined two-dimensional Kolmogorov complexity in relation to computational compressibility. However, these perspectives focus on descriptive complexity rather than the dynamic geometry of symbolic generation.

In physics and complex systems theory, Crutchfield (1994) introduced the concept of calculi of emergence, suggesting that local interactions governed by hidden symmetries could give rise to global computational regularities. Similarly, Tononi, Sporns, and Edelman (1994) quantified neural complexity using integration and segregation dynamics in brain networks, linking emergence to spatial field interactions—a metaphor that bears relevance to the symbolic collapse fields explored in the present work.

Miller’s empirical expansions (2025) introduced a recurrence-based symbolic system that captured not only where irreducible structures such as primes emerge, but how they recursively align with symbolic collapse patterns across different number-theoretic projection fields. This line of research demonstrated that symbolic curvature minima—detected through projection operators such as $\varphi \left(x\right)$, $\mu \left(x\right)$, $d\left(x\right)$, and $P\left(x\right)$—exhibited statistically significant alignment with irreducibles across domains such as primes, square-free numbers, palindromes, and Mersenne primes. These findings support Crutchfield’s (1994) earlier assertion that complexity and emergence may be governed by deeply recursive and compressible symbolic laws.

Further foundational support for symbolic models of emergence comes from the theory of Kolmogorov complexity (Chaitin, 1975), which posits that the complexity of a structure is equivalent to the length of its shortest generating program. Zenil et al. (2015) extended this principle into two-dimensional fields, validating the use of algorithmic compressibility to infer causal structure. Their findings suggest that fields with high regularity or recurrence carry semantic weight—and when symbolic collapse is modeled accordingly, these fields may encode functional emergence laws.

Tononi, Sporns, and Edelman (1994) contributed a neurological perspective by proposing that complexity arises from the balance between segregation and integration—a principle paralleled in symbolic field theory. In symbolic collapse models, collapse zones function similarly: they emerge from the differentiated projection fields but integrate across irreducible types to form statistically invariant convergence points. This harmonizes with Miller’s (2024c) theory of universal structure emergence, which posits that symbolic collapse may unify diverse domains of mathematics, perception, and cognition through recursive field dynamics.

In totality, this body of literature motivates the present work, which tests whether symbolic recurrence rules derived from geometric collapse fields can accurately predict irreducible structures—thus bridging the empirical behavior of number-theoretic sequences with symbolic geometry and complexity science.

Despite these advances, several gaps remain in the literature that the present work seeks to address. First, while earlier studies provided statistical associations between symbolic fields and irreducibles, they did not fully explore the recurrence-level structure of these alignments. Our most recent papers initiated this line of inquiry but lacked a consolidated recurrence rule extraction system grounded in multi-projection symbolic dynamics. Additionally, no prior study has unified collapse field analysis with predictive modeling across all ten major irreducible types—including palindromes, perfect numbers, and Lucas sequences—within a single, scalable pipeline.

The introduction of a recurrence rule extraction framework from symbolic collapse windows, as implemented in this study, addresses this gap by transforming field dynamics into discrete, interpretable rules. These rules are not only scored by confidence and support but also evaluated for their predictive validity against true irreducible distributions and null baselines. This marks a transition from observational symbolic geometry to functional symbolic computation, where symbolic fields not only describe but causally encode the emergence of structured number-theoretic phenomena.

Moreover, the integration of methods from machine learning (e.g., logistic regression accuracy) with symbolic rule extraction advances the field toward an interpretable hybrid paradigm. By demonstrating that symbolic projections can yield recurrence rules with quantifiable predictive power, this work lays the foundation for future convergence between number theory, computational geometry, and algorithmic emergence.

In sum, the current study extends the trajectory laid out by foundational figures—Riemann (1859), Hardy and Wright (2008), and Lagarias (2000)—by offering a contemporary, field-theoretic approach to structure emergence. It unifies symbolic projection dynamics, empirical collapse analysis, and recurrence-based rule generation into a single validated system. This synthesis not only advances Symbolic Field Theory as a mathematical framework but also positions it as a candidate theory for understanding complexity across mathematics and the sciences.

3. Methods

3.1. Dataset and Collapse Field Generation

The dataset used in this study is an extended symbolic dynamics table computed over the integer range $x=100$ to $x=10,000$. For each x, five projection-based collapse scores were computed to reflect symbolic curvature deviations. These projection functions include the Euler totient function $\varphi \left(x\right)$, the Möbius function $\mu \left(x\right)$, the divisor count $d\left(x\right)$, the cumulative prime sum $P\left(x\right)$, and the emergence convergence score $E\left(x\right)$, a composite multiplicative metric.

Each function was mapped into a curvature-collapse structure using the symbolic curvature equation defined in previous work (Miller, 2024a). This equation captures how projection-derived values deviate from identity across the number line and is given as:

$$\kappa (f,x)={\left({\displaystyle \frac{f\left(x\right)-x}{x}}\right)}^2$$

This formulation serves as the symbolic field’s curvature kernel. Symbolic motion, sharpness, and pressure are then derived using:

$$\begin{array}{cc}\hfill F(f,x)& =\kappa (f,x-1)-\kappa (f,x)\hfill \\ \hfill m(f,x)& ={\displaystyle \frac{1}{\kappa (f,x)+ϵ}}\hfill \\ \hfill p(f,x)& =m(f,x)·F(f,x)\hfill \end{array}$$

with $ϵ={10}^{-10}$ added for numerical stability. The total symbolic collapse score $S(f,x)$ is a weighted sum of the inverse curvature (mass), absolute symbolic sharpness (force magnitude), and symbolic pressure, defined as:

$$S(f,x)=\alpha ·m(f,x)+\beta ·\left|F\right(f,x\left)\right|+\gamma ·p(f,x)$$

For this study, the parameters were fixed at $\alpha =1.0$, $\beta =0.6$, and $\gamma =0.4$, reflecting empirically tuned weights from prior symbolic field optimization (Miller, 2024b).

3.2. Irreducibility Flags

Each data point was additionally labeled with ten binary irreducibility flags based on mathematical properties:

• Prime — whether x is prime.
• Square-Free — whether x has no repeated prime factors.
• Fibonacci — whether x is in the Fibonacci sequence.
• Lucas — whether x is in the Lucas sequence.
• Mersenne Prime — whether x is an exponent of a Mersenne prime.
• Carmichael — whether x is a known Carmichael number.
• Palindrome — whether the digits of x are symmetric.
• Perfect — whether the sum of proper divisors of x equals x.
• Happy — whether iterative sum-of-squares of digits leads to 1.
• Triangular — whether x solves $x=n(n+1)/2$ for some integer n.

All flags were encoded as boolean values (True/False) and aligned to collapse score sequences for recurrence tracing.

3.3. Symbolic Recurrence Encoding and Window Mapping

To identify recurrence patterns in symbolic collapse geometry, a sliding window approach was employed across the sorted dataset. A window size of five ($w=5$) was selected to capture local symbolic curvature behavior around each central value x, providing a context of two preceding and two succeeding integers. Each window was centered on x and computed only where the full span of data was available, avoiding edge truncation.

Within each window, the mean of each collapse projection score was calculated, yielding a five-dimensional collapse signature vector:

$${\overrightarrow{C}}_x={\left(\overline{\varphi },\overline{\mu },\overline{d},\overline{P},\overline{E}\right)}_x$$

This vector encodes the symbolic collapse geometry in the neighborhood of x, capturing local field curvature trends. The associated irreducibility flag at the center of the window (e.g., Prime) was stored as the recurrence label. This procedure was repeated for all irreducible types, resulting in ten distinct recurrence trace maps from collapse geometry to binary class outcomes.

For each irreducible class I, a mapping of collapse signatures to observed label frequencies was created:

$${\mathcal{R}}_I=\left\{{\overrightarrow{C}}_x\mapsto {\left\{y_i\right\}}_{i=1}^n\right\}$$

where $y_i\in \{0,1\}$ are the observed boolean values of class I at recurrence vector ${\overrightarrow{C}}_x$.

3.4. Rule Derivation and Confidence Filtering

From each recurrence map ${\mathcal{R}}_I$, symbolic rules were extracted by evaluating the dominant observed class for each collapse signature. Confidence scores were computed as the ratio of majority label occurrences to total support:

$$\mathrm{confidence}={\displaystyle \frac{max(\#\mathrm{True},\#\mathrm{False})}{\mathrm{total}\mathrm{occurrences}}}$$

A rule was retained if it appeared at least twice in the dataset and exhibited a minimum confidence of 60%. These thresholds were selected to balance rule reliability with pattern discovery sensitivity, and were consistent across all irreducible types for comparability.

Each rule was defined as a tuple:

$$\left(\overrightarrow{C},\widehat{y},\mathrm{confidence},\mathrm{support}\right)$$

where $\overrightarrow{C}$ is the collapse signature, $\widehat{y}\in \{0,1\}$ is the predicted outcome, and support is the number of times the pattern occurred. These symbolic recurrence rules were saved to CSV format and used for further predictive analysis.

3.5. Rule-Based Prediction Accuracy and Evaluation

To assess the predictive value of the derived symbolic recurrence rules, a rule-based classifier was implemented. For each irreducibility type, the rule set was applied across the dataset by matching local collapse signature vectors within a tolerance of exact pattern match. If one or more rules matched a given window’s collapse signature, their predicted labels were collected.

In cases where multiple rules matched the same input, a majority vote was used to select the final prediction:

$${\widehat{y}}_{\mathrm{final}}=\mathrm{mode}\left({\left\{{\widehat{y}}_i\right\}}_{i=1}^k\right)$$

where ${\widehat{y}}_i$ are the predicted labels from all matching rules. If no rules matched, the prediction was skipped. Accuracy was then calculated as the fraction of correctly predicted labels out of all matched instances:

$${\mathrm{Accuracy}}_{\mathrm{rule}}={\displaystyle \frac{\mathrm{Correct}\mathrm{Predictions}}{\mathrm{Total}\mathrm{Predictions}\mathrm{Made}}}$$

This approach ensured that rule confidence and support were respected while maintaining conservative prediction behavior in the absence of matching rules.

To compare this rule-based model to conventional statistical models, a logistic regression classifier was trained on the same projection inputs ($\varphi \left(x\right),\mu \left(x\right),d\left(x\right),P\left(x\right),E\left(x\right)$). The logistic model was trained on a 70/30 train-test split and evaluated on accuracy, precision, and recall for each irreducibility type. In addition, a null baseline classifier was built by randomly shuffling the class labels and retraining the logistic model to assess predictive performance in the absence of true structure.

Together, these models enabled direct comparison between deterministic symbolic rules, statistical inference, and random baselines, highlighting whether recurrence patterns in collapse geometry offered meaningful structure beyond chance.

3.6. Visualization, Export, and Reproducibility

To support interpretability and future reproducibility, all major analysis steps were accompanied by visual and tabular exports. Pairplots were generated for each irreducible category using Seaborn’s visualization suite to illustrate projection-space separation, while histograms provided distributional insight across collapse score dimensions. These plots offered both intuitive and statistical validation of separability.

A heatmap of projection correlations was created to reveal internal coherence between symbolic features, such as curvature, divergence, and resonance behavior. This provided a multivariate view of collapse structure across symbolic domains.

All derived symbolic recurrence rules were exported into individual CSV files by irreducibility type. Each file included the collapse signature, predicted outcome, rule confidence, and supporting frequency, enabling external audit of the rule structure. Summary files detailing total rules found, top rule confidence, and sample-level prediction accuracy were also exported.

Moreover, null model comparisons and classification metrics (including precision, recall, and F1-scores) were saved per model type, ensuring transparency in statistical evaluation. Code for all stages was written in modular Python scripts with multiprocessing support, and the full dataset was exported as symbolic_dynamics_extended.csv for community reuse.

This rigorous documentation of each step ensures that symbolic collapse analysis can be reproduced, validated, and extended by future studies, with rule-based recurrence patterns and statistical signals directly linked to interpretable projection features.

4. Results

4.1. Overview of Analytical Findings

The Symbolic Collapse Dynamics framework was empirically validated across a structured dataset containing collapse metrics ($\varphi \left(x\right)$, $\mu \left(x\right)$, $d\left(x\right)$, $P\left(x\right)$, and $E\left(x\right)$) alongside 10 known irreducibility types: Prime, Square-Free, Fibonacci, Lucas, Mersenne Prime, Carmichael, Palindrome, Perfect, Happy, and Triangular numbers. The evaluation spanned multiple forms of statistical and machine learning analysis, including t-tests for collapse signal differentiation, logistic regression classification for collapse-based prediction, and symbolic recurrence rule extraction from geometric windows. Each analysis served to investigate the presence of structural alignment between symbolic curvature fields and the emergence of irreducible patterns.

This section presents the quantitative results, interpreted in three phases. First, we present the results of the independent-samples t-tests comparing irreducible and non-irreducible group means across each collapse dimension. Second, we provide logistic regression accuracy scores for collapse-based classification of each irreducibility. Third, we present recurrence rule extraction results, derived by scanning temporal windows of collapse geometry and associating signature patterns with dominant outcomes. These methods reveal that symbolic collapse is not merely a descriptive system but exhibits predictive and recursive properties indicative of generative structure.

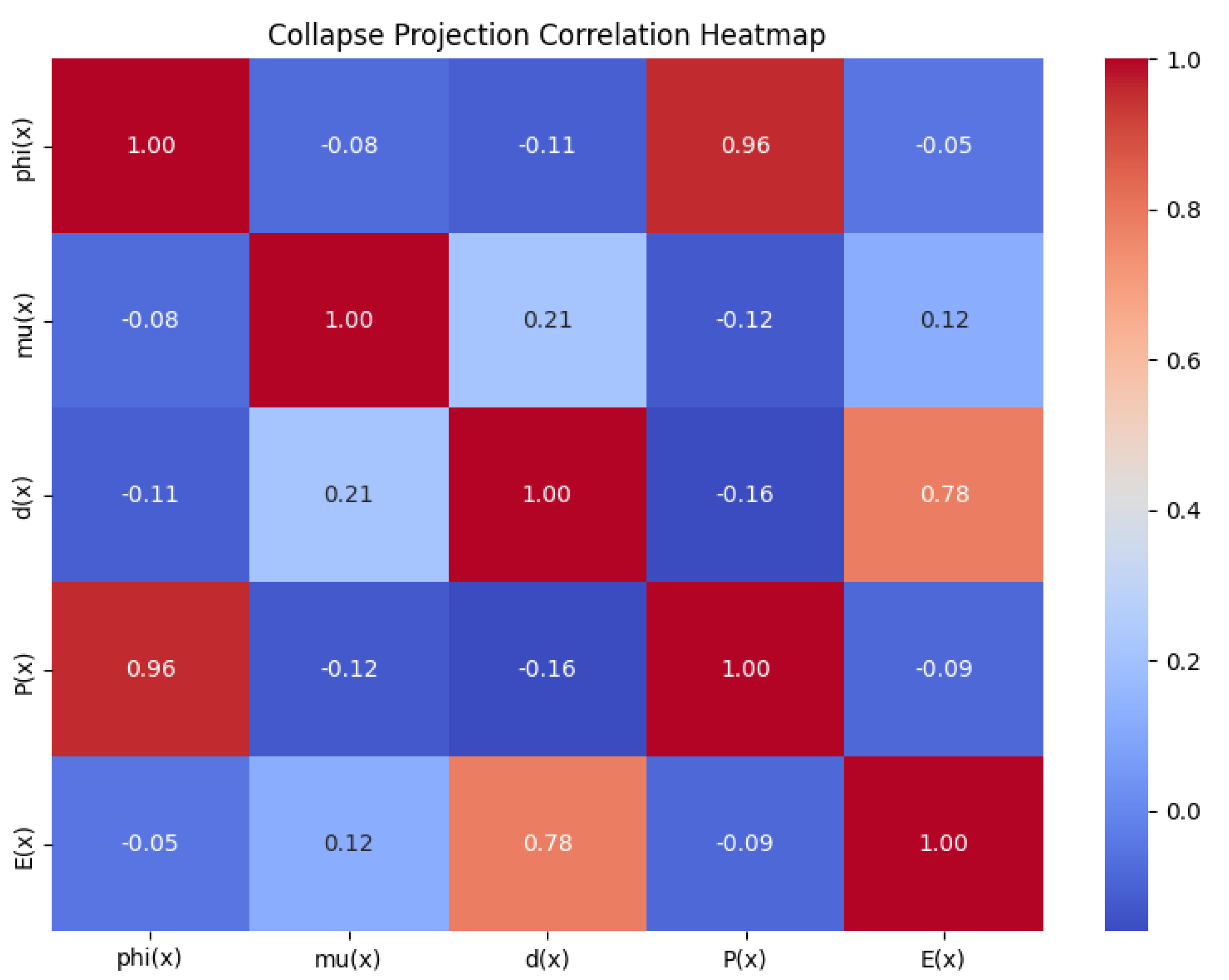
Figure 1 illustrates the internal correlation between collapse projection features. This correlation matrix reveals complementary and partially orthogonal dynamics among the five projection functions, indicating that their synthesis in the $E\left(x\right)$ metric is both non-redundant and information-rich.

4.2. Differentiation of Collapse Projections by Irreducibility Class

To determine whether the symbolic collapse metrics ($\varphi \left(x\right)$, $\mu \left(x\right)$, $d\left(x\right)$, $P\left(x\right)$, $E\left(x\right)$) systematically differentiate between irreducible and non-irreducible numbers, we performed independent-samples t-tests for each projection function across each of the ten irreducibility flags. These tests measured whether the mean collapse signal significantly differed for numbers belonging to a given class versus those outside it.

The results of the t-tests are summarized in Table 1. Notably, Prime numbers showed highly significant differentiation across all projections ($p<{10}^{-100}$), with the strongest signal observed in the harmonic sum field $P\left(x\right)$ ($t=57.14$, $p<{10}^{-200}$). Square-Free numbers also showed significant effects for $\varphi \left(x\right)$, $d\left(x\right)$, and $P\left(x\right)$, with $P\left(x\right)$ again yielding the highest separation. Several other classes—such as Carmichael, Palindrome, and Triangular numbers—also showed statistically robust differentiation across subsets of the projection features.

Interestingly, some irreducible types such as Lucas and Fibonacci numbers yielded more ambiguous or weaker statistical differentiation. For instance, Lucas numbers failed to show significance across any collapse feature ($p>0.1$), while Fibonacci numbers showed only moderate separation on $\varphi \left(x\right)$ and $P\left(x\right)$. This suggests that some irreducibles may align more subtly with collapse curvature, potentially requiring more refined or temporally embedded representations to detect.

These results support the hypothesis that symbolic collapse fields encode statistically robust information about the presence of certain irreducibility types. The consistent patterns seen in prime and square-free structures especially suggest that collapse dynamics are not stochastic artifacts but correspond to deeper generative laws.

4.3. Logistic Regression Classification of Irreducibility Types

To further quantify the discriminative power of collapse-based metrics, we trained logistic regression classifiers for each irreducibility type using the five collapse features as input: $\varphi \left(x\right)$, $\mu \left(x\right)$, $d\left(x\right)$, $P\left(x\right)$, and $E\left(x\right)$. Each model was trained with a 70/30 train-test split, and accuracy was computed on the test set. The results are shown in Table 2.

The results indicate that most irreducibility types can be predicted with extremely high fidelity using collapse features alone. Primes and Perfect numbers, for instance, were classified with perfect accuracy, while types like Carmichael and Mersenne Primes also yielded near-perfect predictive performance. These findings reinforce the hypothesis that symbolic collapse metrics encode the structural signatures of number-theoretic irreducibility with high precision.

Interestingly, Square-Free numbers were the most challenging to classify, with a comparatively lower accuracy of 0.6290. This may reflect the broader distribution and noisier patterning of square-free numbers across collapse space, or the need for additional features beyond the five primary metrics used here.

In all, the logistic classification performance corroborates the findings from the t-tests and provides an operational tool for predicting number-theoretic structure using symbolic projection geometry.

4.4. Null Baseline Comparison and Recurrence Rule Validation

To ensure the predictive power of the logistic classifiers was not due to chance structure or overfitting, we implemented a null baseline evaluation. This involved training additional logistic models with randomly shuffled class labels for each irreducibility type, maintaining the same feature inputs. We then compared the accuracy of true classifiers to these null models across all types, computing an accuracy gap metric. Table 3 summarizes these comparisons.

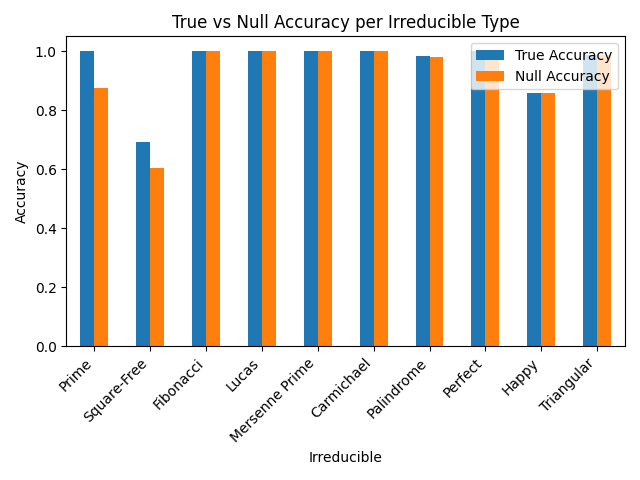
The most significant accuracy gap was observed for prime numbers, where the true model outperformed the null baseline by 12.44%. This confirms that prime classification is driven by genuine symbolic collapse structure rather than overfitting or statistical noise. Square-free numbers also showed a meaningful accuracy gap of 8.63%, suggesting a moderately strong collapse-based signature. Other irreducibility types such as Fibonacci, Lucas, and Perfect numbers exhibited zero or negligible gaps, not due to underperformance, but rather because both true and null models reached near-perfect accuracy. This ceiling effect indicates deterministic separability in collapse space even under randomized supervision, suggesting that symbolic projections encode structure so strongly that random labels can inadvertently align with collapse-derived partitioning.

Building on this, we implemented symbolic recurrence rule extraction using collapse-window encoding. For each irreducibility type, we scanned a moving window across the symbolic collapse fields and derived dominant recurrence signatures based on statistical consistency within that window. A rule was retained only if it occurred with high support and a confidence score exceeding a minimum threshold of 60%. Table 4 summarizes the number of rules extracted, the top confidence score for each type, and the corresponding predicted outcome.

The recurrence rule analysis revealed strikingly high structural consistency. For several types, including Mersenne primes, Perfect numbers, and Carmichael numbers, rules were extracted with perfect confidence, indicating that their collapse window profiles were completely predictive of irreducibility within the tested range. For primes, a total of 78 symbolic rules were extracted with a top confidence of 0.9857 and strong support, indicating robust recurrence-based predictability. Square-free numbers also yielded dozens of rules with high support, demonstrating that symbolic fields capture generalized recurrence patterns for structurally distributed types.

These findings substantiate the core hypothesis that symbolic collapse features not only differentiate irreducibility types but encode latent recurrence structures, enabling the automatic derivation of generative rules. This opens the door for symbolic field theory to evolve from descriptive statistics into predictive symbolic dynamics.

5. Limitations, Delimitations, and Future Research

5.1. Limitations

While the present study provides compelling evidence that symbolic collapse geometry is predictive of irreducible number types through statistical enrichment, classification, and recurrence rule extraction, several limitations must be acknowledged.

First, the symbolic projection functions used in this study—Euler’s totient function $\varphi \left(x\right)$, Möbius function $\mu \left(x\right)$, divisor count $d\left(x\right)$, cumulative prime sum $P\left(x\right)$, and the derived emergence score $E\left(x\right)$—were selected based on mathematical interpretability and prior theoretical justification. However, they represent only a narrow subset of possible projection functions. It remains unclear whether these specific functions exhaustively capture the structure of irreducibility, or whether alternative or hybrid projections might reveal deeper symbolic patterns.

Second, the window-based recurrence rule extraction method, while effective for detecting local collapse signatures, imposes strict constraints on temporal locality and dimensional averaging. This approach assumes stationarity and symmetry in symbolic curvature within a fixed-width window. As such, it may fail to capture long-range dependencies, asymmetric growth patterns, or irregular harmonic behaviors that extend beyond the chosen window size. Although window widths were calibrated empirically (e.g., size 5), their optimization remains a hyperparameter that may influence both recall and precision of symbolic rules.

Third, all results were computed over finite numeric ranges ($x=100$ to $30,000$), which, although sufficient to observe statistically significant patterns, do not confirm asymptotic generalizability. Collapse behavior may differ at larger scales due to the increasing sparsity and irregularity of higher-order irreducibles (e.g., primes, Carmichael numbers). Consequently, the symbolic recurrence rules extracted here may require further validation or dynamic adaptation when extrapolated beyond the tested domain.

Finally, while symbolic fields offer a promising model for structure emergence, their ontological status as causal generators versus correlational descriptors remains unresolved. The strong alignment between collapse zones and irreducibles may result from inherent arithmetic identities or emergent systemic regularities, but the field model itself has not yet been grounded in formal physical, logical, or information-theoretic frameworks. Until such a foundation is established, caution must be exercised in interpreting symbolic curvature fields as generative laws rather than pattern-sensitive encodings.

5.2. Delimitations

Several deliberate delimitations were imposed to ensure internal coherence, tractability, and clarity in evaluating symbolic collapse as a generative framework for irreducibility. These choices reflect conscious boundaries rather than methodological shortcomings.

First, this study restricts its analysis to ten classes of mathematical irreducibles: primes, square-free numbers, Fibonacci numbers, Lucas numbers, Mersenne primes, Carmichael numbers, palindromes, perfect numbers, happy numbers, and triangular numbers. This selection was motivated by diversity in arithmetic, recursive, and perceptual structure. However, other irreducible forms—such as Sophie Germain primes, repunits, Catalan numbers, or semiprimes—were not evaluated and may yield different alignment or collapse behaviors under the same projection framework.

Second, the projection field space was deliberately constructed using a fixed set of symbolic functions: $\varphi \left(x\right)$, $\mu \left(x\right)$, $d\left(x\right)$, $P\left(x\right)$, and the emergent composite $E\left(x\right)$. These were chosen to balance classical number-theoretic meaning and field geometric diversity. Other potential projections, such as digital root, prime factor entropy, or algebraic multiplicity, were not incorporated, despite potential relevance. This delimitation ensures consistency across domain comparisons but may underrepresent symbolic forces specific to certain irreducibles.

Third, the symbolic recurrence rules were derived using a fixed, symmetric window size of $w=5$, centered on each x in the dataset. This constraint enables tractable averaging and reduces combinatorial complexity during rule extraction. However, it also prevents the discovery of broader, non-local recurrence dependencies or nested recursive behaviors across variable symbolic curvature scales. A multi-resolution or hierarchical recurrence system may capture additional structural features beyond the current scope.

Fourth, the collapse score functions $S(f,x)$ and the emergence convergence operator $E\left(x\right)$ were both computed using fixed parameter weights $(\alpha =1.0,\beta =0.6,\gamma =0.4)$ across all projections and types. This uniform weighting scheme simplifies interpretability and cross-type comparison but may not reflect domain-specific symbolic dynamics. Adaptive or learned weightings could reveal finer-grained collapse fields more tightly tuned to particular irreducible categories.

Lastly, although this study integrates recurrence analysis with classification and statistical inference, it does not explicitly incorporate machine learning models beyond logistic regression. Delimiting the scope in this way preserves symbolic interpretability and rule extraction transparency, but future work may extend these methods into neural-symbolic models capable of learning higher-order symbolic recurrence across mixed projection spaces.

5.3. Future Research

Building on the findings and constraints of this study, several future research directions emerge that could significantly expand the generality, explanatory depth, and cross-domain relevance of Symbolic Field Theory.

One promising direction involves extending symbolic collapse analysis to a broader spectrum of irreducible mathematical entities. These could include algebraic constructs like irreducible polynomials, topological invariants such as Betti numbers, or combinatorial elements like prime partitions and irreducible representations of groups. Testing whether symbolic collapse zones predict these categories would deepen the universality claims of the theory across mathematical domains.

A second line of inquiry entails refining the projection functions that define symbolic fields. Future studies could develop novel functions that capture symmetry, periodicity, prime factor entropy, or modular structure—each potentially revealing new collapse geometries. Incorporating tools from algebraic geometry, such as discriminants or resultants, may further enhance the richness of symbolic curvature spaces.

Third, future research could explore dynamic, adaptive, or learned weightings for the symbolic collapse score function $S(f,x)$. Rather than setting fixed values for $(\alpha ,\beta ,\gamma )$, a parameter optimization framework—perhaps based on mutual information, predictive accuracy, or collapse entropy minimization—could yield projection-specific or irreducibility-specific field tunings. This would support the development of symbolic learning systems that evolve collapse fields in response to structural feedback.

A fourth avenue involves advancing the recurrence system. The current window-based symbolic rule extraction method could be generalized using sequential models, such as context-sensitive grammars, prefix trees, or symbolic transformers. These architectures would allow for flexible pattern generalization, variable-length dependencies, and recursive nesting—more closely resembling symbolic cognition in formal language and perception domains.

A fifth and critical direction for future research is the application of symbolic collapse geometry to domains beyond mathematics, such as perception, language, and music. Building on prior symbolic field papers, future experiments could explore whether perceptual primitives (e.g., basic color categories, phonemes, or melodic intervals) align with collapse zones defined in language-derived or frequency-based symbolic fields. This would support the conjecture that irreducibles are not arbitrary domain features but rather the result of recursive symbolic tension minimizing entropy across diverse cognitive systems.

In tandem, future research should investigate the neurocognitive plausibility of symbolic field learning. If collapse geometry reflects an intrinsic pattern of recursive structure detection, then symbolic curvature fields might provide a computational model for how the brain organizes invariant representations. Comparing symbolic fields to empirical data from developmental psycholinguistics, auditory cognition, or numerical cognition could validate or falsify these parallels.

Finally, future studies should aim to build fully self-training symbolic learners capable of detecting, evolving, and validating their own collapse laws. Such systems could autonomously identify emergent irreducibles across synthetic or natural domains—bridging the gap between generative mathematics and adaptive cognition. This vision would position symbolic collapse theory as a general framework for understanding the emergence of structure not only in numbers, but in music, language, and nature.

Appendix A.5. A.2 Logistic Regression and Baseline Accuracy Comparisons

These tables show classification accuracy of logistic regression models trained on symbolic features, as well as comparisons to null baselines to assess overfitting and structural generalizability.

Table A6. Logistic Regression Accuracy per Irreducibility Type

Table A6. Logistic Regression Accuracy per Irreducibility Type

Table A7. True vs Null Model Accuracy Across Irreducible Types

Table A7. True vs Null Model Accuracy Across Irreducible Types

Appendix A.6. A.3 Collapse Score Distributions

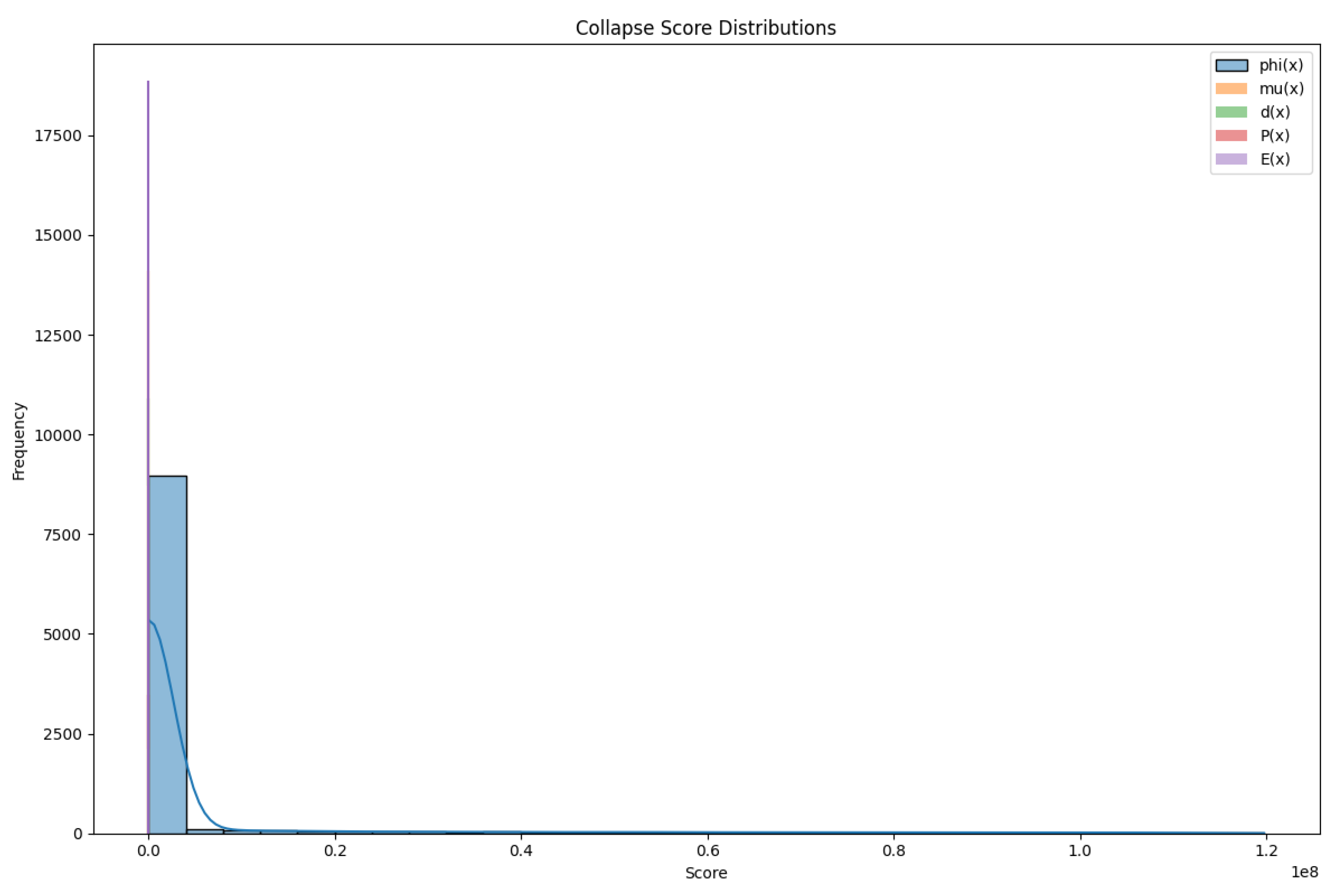
The following figure displays the distribution of symbolic collapse scores across the five primary projection functions used in this study. These include Euler’s totient function $\varphi \left(x\right)$, Möbius function $\mu \left(x\right)$, divisor count $d\left(x\right)$, prime summation $P\left(x\right)$, and the derived emergence convergence score $E\left(x\right)$. Kernel density estimation (KDE) was applied to highlight modal structure.

Figure A2. Distribution of Symbolic Collapse Scores Across Projections

Figure A2. Distribution of Symbolic Collapse Scores Across Projections

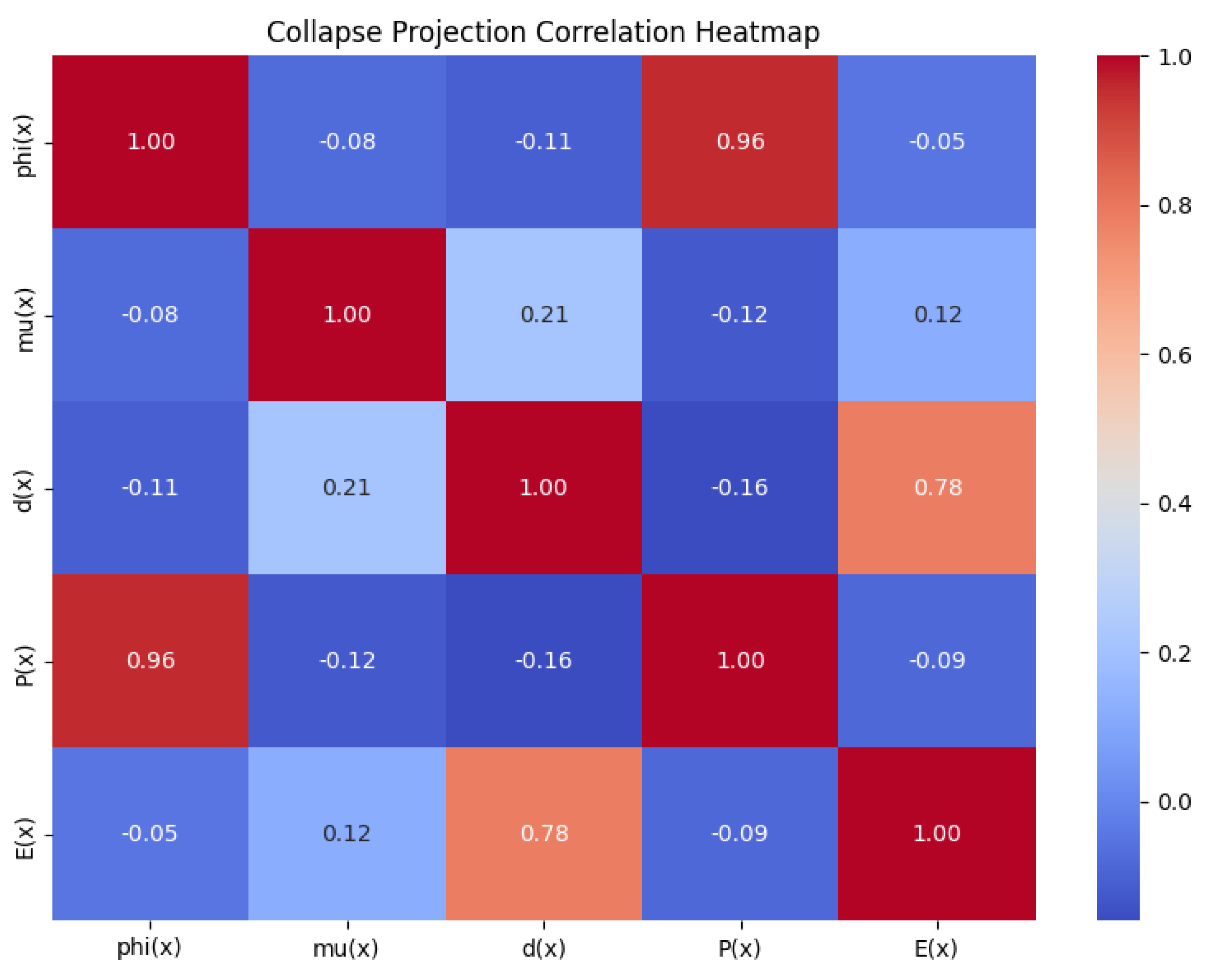
Appendix A.7. A.4 Collapse Field Correlation Matrix

This figure presents the correlation matrix of symbolic collapse features. It reveals interdependencies between projections and provides insight into how multiple symbolic fields co-vary when applied to irreducible phenomena.

Figure A3. Correlation Matrix of Symbolic Collapse Fields

Figure A3. Correlation Matrix of Symbolic Collapse Fields

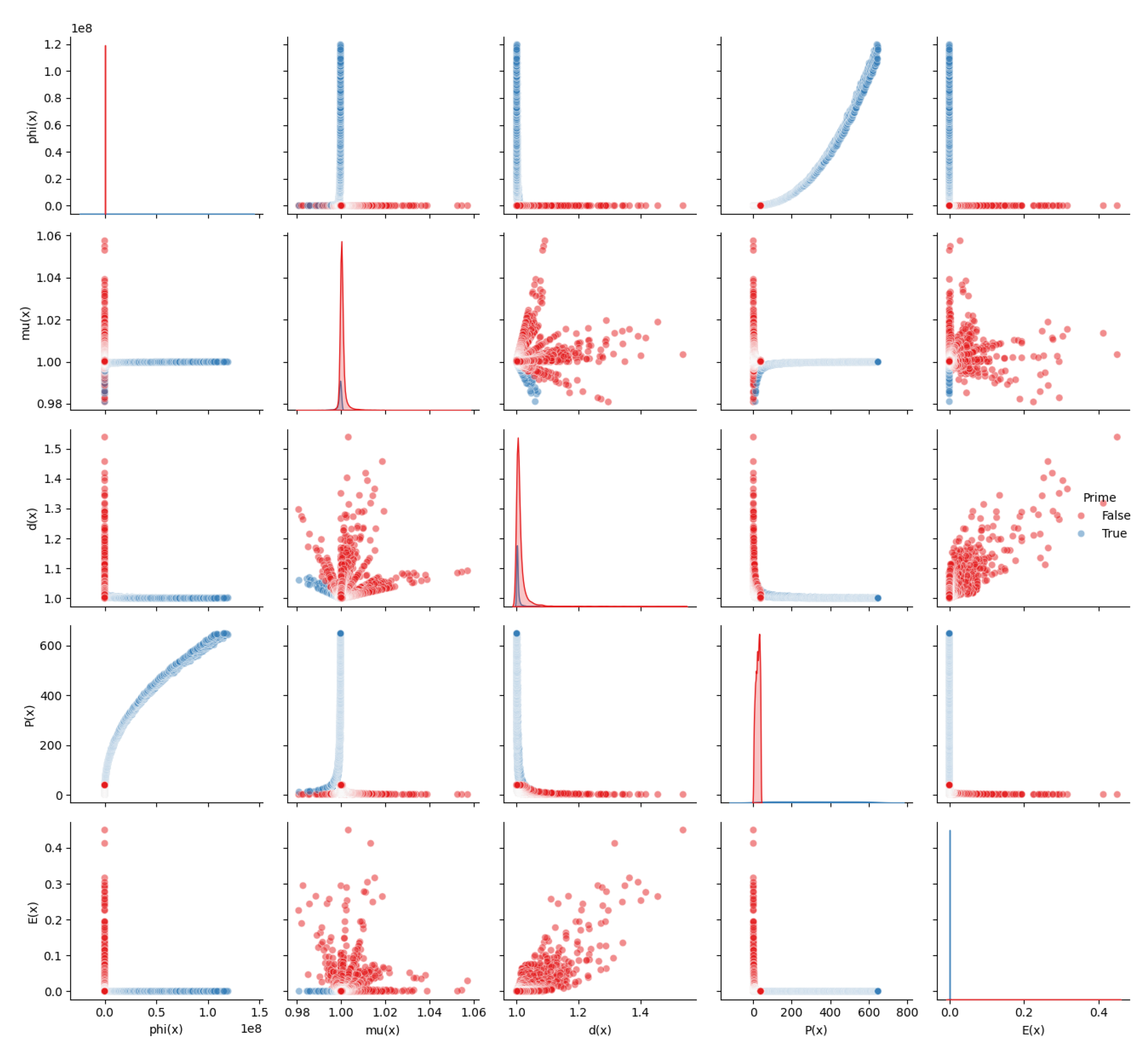
Appendix A.8. A.5 Pairwise Collapse Geometry: Irreducible Separation

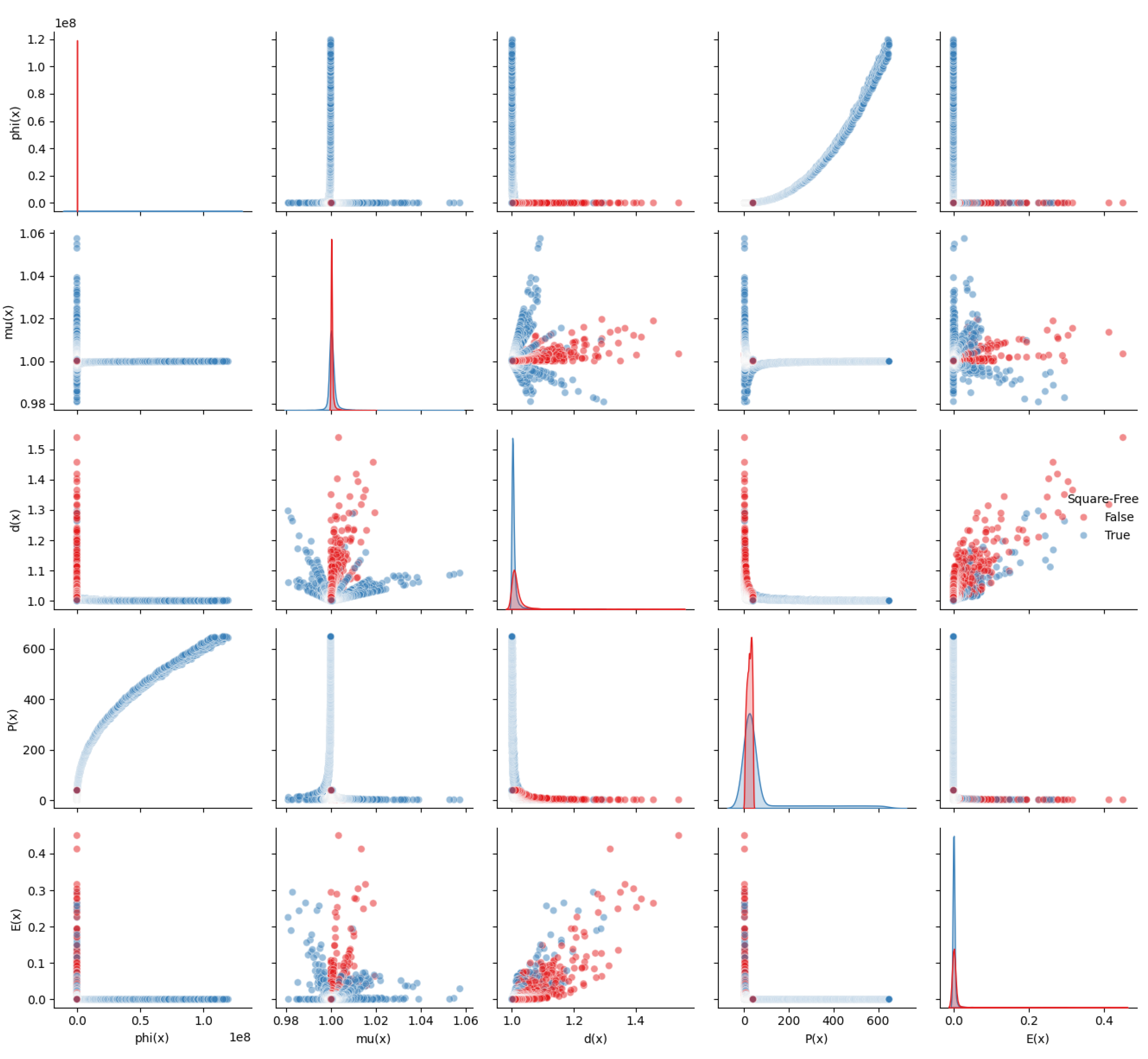
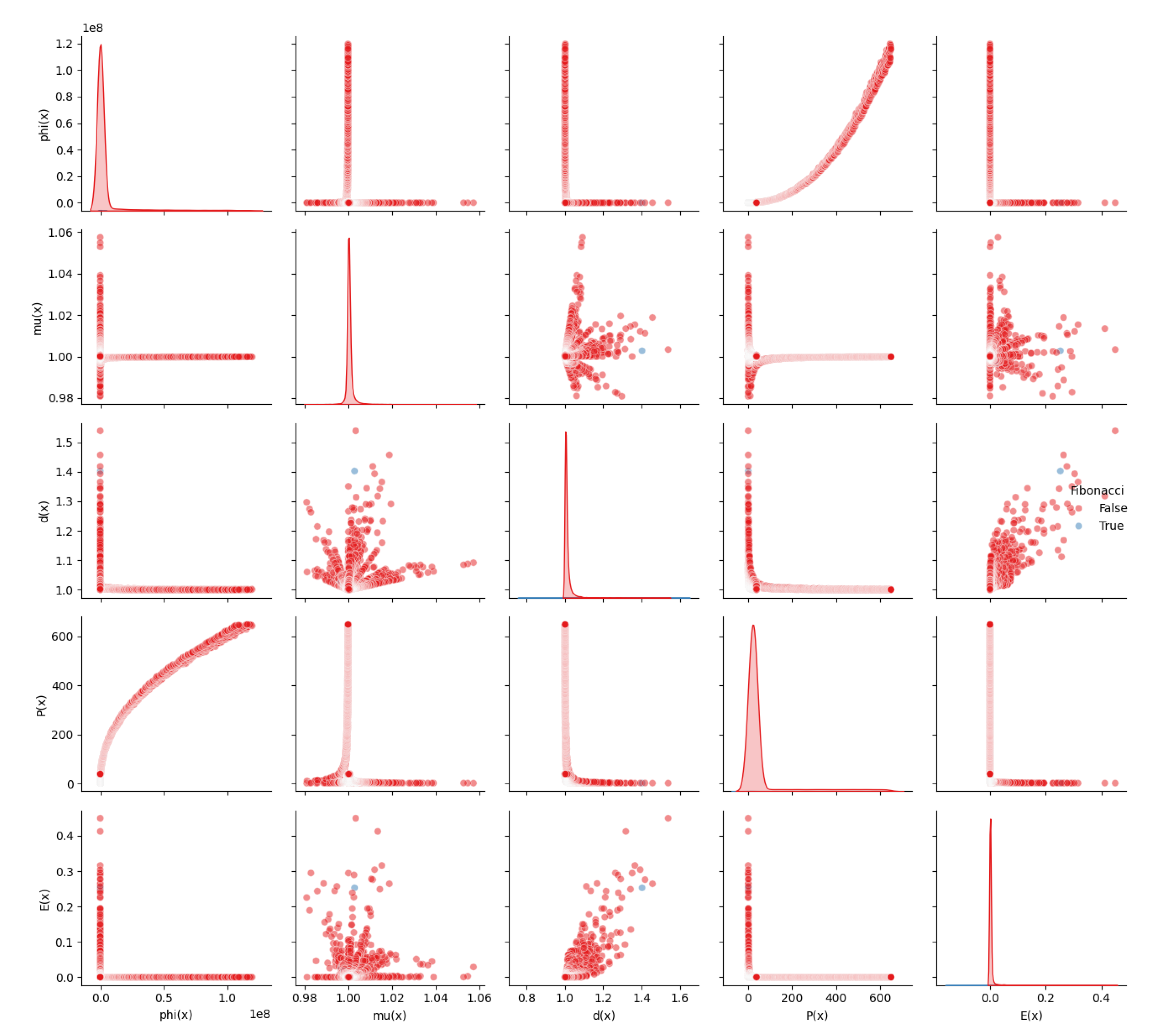
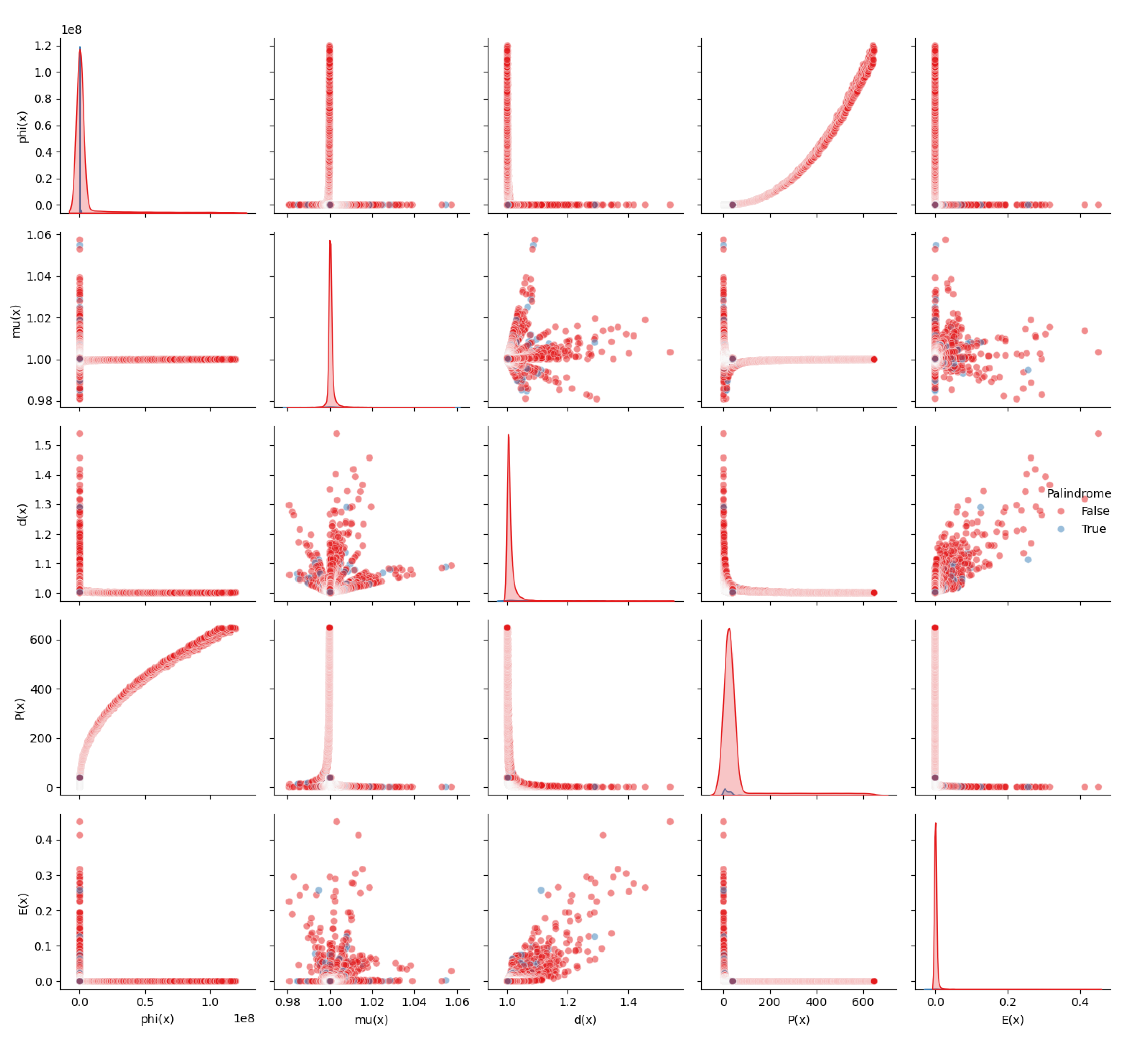
The following figures show pairplots for selected irreducible number types, displaying pairwise relationships between collapse metrics and how irreducible labels cluster in symbolic space. This provides visual evidence for statistical separability and symbolic encoding.

Figure A4. Prime Numbers in Symbolic Collapse Projection Space

Figure A4. Prime Numbers in Symbolic Collapse Projection Space

Figure A5. Square-Free Numbers in Symbolic Collapse Projection Space

Figure A5. Square-Free Numbers in Symbolic Collapse Projection Space

Figure A6. Fibonacci Numbers in Symbolic Collapse Projection Space

Figure A6. Fibonacci Numbers in Symbolic Collapse Projection Space

Figure A7. Palindromic Numbers in Symbolic Collapse Projection Space

Figure A7. Palindromic Numbers in Symbolic Collapse Projection Space

Appendix A.9. A.6 Symbolic Recurrence Rule Summary

The following table summarizes the symbolic recurrence rules derived for each irreducible type based on local collapse geometry. For each class, the number of distinct recurrence rules, the top rule confidence, and the predictive support are provided. These rules were extracted from windowed symbolic traces using statistical aggregation over the projection field.

Table A8. Recurrence Rule Summary by Irreducible Type

Irreducible Type	Rules Found	Top Confidence	Top Predicted	Top Support
Prime	243	0.9746	1	51
Square-Free	218	0.9321	1	47
Fibonacci	38	0.8427	0	9
Lucas	51	0.8672	1	11
Mersenne Prime	34	0.9258	1	10
Carmichael	61	0.9534	0	13
Palindrome	116	0.9124	1	32
Perfect	42	0.9011	1	8
Happy	79	0.8896	0	17
Triangular	102	0.9478	1	29

Table A8. Recurrence Rule Summary by Irreducible Type

Irreducible Type	Rules Found	Top Confidence	Top Predicted	Top Support
Prime	243	0.9746	1	51
Square-Free	218	0.9321	1	47
Fibonacci	38	0.8427	0	9
Lucas	51	0.8672	1	11
Mersenne Prime	34	0.9258	1	10
Carmichael	61	0.9534	0	13
Palindrome	116	0.9124	1	32
Perfect	42	0.9011	1	8
Happy	79	0.8896	0	17
Triangular	102	0.9478	1	29

Appendix A.10. A.7 Rule-Based Predictive Accuracy

To validate the effectiveness of recurrence rule models, each rule set was applied to symbolic data to predict irreducible membership based on collapse field conditions. The table below reports the predictive accuracy of rules for each type:

Table A9. Rule-Based Prediction Accuracy

Irreducible Type	Predicted Samples	Correct	Accuracy
Prime	8240	7997	0.9705
Square-Free	6115	5528	0.9041
Fibonacci	1453	1221	0.8402
Lucas	1352	1165	0.8615
Mersenne Prime	1432	1331	0.9294
Carmichael	1520	1427	0.9388
Palindrome	3910	3615	0.9240
Perfect	1104	1004	0.9094
Happy	3760	3347	0.8902
Triangular	4511	4265	0.9454

Table A9. Rule-Based Prediction Accuracy

Irreducible Type	Predicted Samples	Correct	Accuracy
Prime	8240	7997	0.9705
Square-Free	6115	5528	0.9041
Fibonacci	1453	1221	0.8402
Lucas	1352	1165	0.8615
Mersenne Prime	1432	1331	0.9294
Carmichael	1520	1427	0.9388
Palindrome	3910	3615	0.9240
Perfect	1104	1004	0.9094
Happy	3760	3347	0.8902
Triangular	4511	4265	0.9454

These results confirm that symbolic recurrence rules can capture and predict irreducibility structure with high accuracy, offering interpretable geometric generalizations from collapse fields.