1. Introduction
For centuries, the distribution of prime numbers has challenged mathematicians seeking to understand the hidden order within the natural number line. Despite significant advances in analytic number theory—including the Prime Number Theorem, the Riemann Hypothesis, and probabilistic models—no deterministic formula has yet been discovered that explains or predicts the occurrence of primes. While these frameworks offer accurate asymptotic behavior and statistical approximations, they provide little insight into the symbolic or structural nature of irreducibility. In contrast, Symbolic Field Theory (SFT) introduces a new perspective: that prime numbers, and other irreducible elements, may emerge from curvature-induced collapse in symbolic projection spaces.
SFT is based on the hypothesis that symbolic structures exhibit field-like behavior, where attractors, repulsors, and curvature gradients guide the emergence of discrete patterns. Rather than treating primes as isolated anomalies or the result of randomness, SFT interprets them as outcomes of symbolic energy compression—where curvature fields defined over symbolic projections create valleys of minimal tension. These valleys, or collapse zones, serve as generative attractors for irreducible entities. This idea parallels concepts in physics, where matter arises at potential minima in field landscapes, and in cognitive science, where perception stabilizes around attractor basins in representational spaces.
While previous models of prime distribution have emphasized randomness, sieve theory, or analytic continuation, SFT departs from these traditions by focusing on symbolic compression and projection. At its core is the symbolic projection function , which maps each integer to a symbolic space—such as modular residue, digit entropy, or factor complexity—interpreting the number’s structural content rather than its magnitude. The symbolic curvature function is then defined over this projection as a measure of local deviation from structural equilibrium. Points of minimal symbolic curvature, known as collapse zones, represent locations where the projection field exhibits locally minimal tension—akin to geometric valleys.
The central hypothesis of SFT is that irreducible mathematical structures, like primes, will tend to emerge at or near these collapse zones. If symbolic curvature genuinely encodes meaningful structural compression, then collapse valleys should statistically align with irreducible numbers more often than chance would predict. Crucially, SFT treats this not as a probabilistic coincidence, but as a structural phenomenon: symbolic energy compresses and folds at these collapse points, producing emergent order. The result is a new framework in which primes can be interpreted as the natural outcomes of recursive symbolic field dynamics.
To evaluate this hypothesis, we construct symbolic curvature fields over various projection spaces and identify collapse zones via discrete curvature minima. These points are then tested against known distributions of prime numbers using a Monte Carlo null model that simulates random selections of integers of equal quantity. This method allows us to compare the frequency of primes found in collapse zones to what would be expected by chance, thus providing a statistical test of symbolic alignment.
In this study, we focus on a hybrid projection function that combines modular residue and prime factor complexity, defined as , where is the number of distinct prime factors of x. This hybrid field was chosen for its ability to mix additive modular symmetry with multiplicative structural weight, potentially producing a more refined collapse curvature landscape. Using this projection, we compute over the first million natural numbers, identify local minima, and evaluate the statistical enrichment of primes at those locations. The strength of the observed alignment serves as a validation of the symbolic collapse mechanism proposed by SFT.
The implications of this framework extend beyond number theory. If symbolic curvature fields can reliably predict or repel the emergence of structured entities such as primes, then similar techniques may apply to other domains of symbolic cognition—such as linguistic primitives, musical intervals, or perceptual irreducibles. This opens the door to a general symbolic physics, where field dynamics govern the emergence of structure across otherwise disparate domains.
The remainder of this paper is organized as follows:
Section 2 reviews related work in prime distribution, symbolic systems, and field-based emergence.
Section 3 defines the formal methods used to construct symbolic fields, identify collapse zones, and run enrichment comparisons.
Section 4 presents the results of our empirical tests, including statistical outcomes and prime density visualizations.
Section 5 discusses the implications of the findings for SFT and future directions. We conclude in
Section 6 by summarizing the contribution of this work and proposing Symbolic Field Theory as a generative framework for irreducible pattern emergence across domains.
2. Literature Review
The distribution of prime numbers has long been a central question in number theory. Since the time of Euclid, who proved the infinitude of primes, mathematicians have sought to understand their pattern, density, and apparent irregularity. The Prime Number Theorem, proven in the 19th century, established that the number of primes less than x approximates , providing an asymptotic framework for their global distribution. Yet despite this statistical clarity, the local distribution of primes remains difficult to characterize. Questions about short-range irregularities, such as twin primes and prime gaps, continue to challenge researchers.
Analytic number theory, particularly through the Riemann Hypothesis and the use of complex analysis on the Riemann zeta function, offers a powerful lens on prime density and distribution. However, these approaches rely heavily on continuous approximations and complex-plane behavior, leaving the discrete symbolic nature of primes largely unaddressed. Probabilistic models have also been employed to study prime behavior—treating primes as quasi-random or pseudo-random structures—yet these models often lack explanatory power regarding why certain structures (e.g., modular residues or twin pairs) appear more frequently than others.
Alternative approaches have explored the connection between prime structure and symbolic complexity. Researchers have investigated digital properties of primes, such as digit entropy, Kolmogorov complexity, and autocorrelation in binary representations. These studies aim to determine whether primes exhibit non-random compressibility or hidden order when represented in symbolic domains. While some numerical patterns have been observed, no general symbolic model has emerged that predicts or explains prime positioning with statistical rigor.
Beyond number theory, related work in cognitive science and theoretical physics has explored the role of fields, attractors, and symbolic representation in the emergence of structured phenomena. In dynamical systems theory, for example, attractor basins are known to stabilize complex behavior around recurrent forms, and in physics, field curvature determines the movement and formation of particles. These analogies have informed cross-disciplinary hypotheses that structure may emerge from local information compression or curvature effects. Yet, within mathematics itself, few models have attempted to formalize this perspective using symbolic projection and curvature collapse as a generative mechanism.
Some precedent exists for treating number-theoretic behavior through symbolic or geometric lenses. Modular arithmetic, for example, partitions integers into residue classes that reveal repeating structural patterns relevant to prime occurrence. Visualizations such as Ulam spirals and residue plots have highlighted surprising regularities in prime alignment, suggesting that primes may be more structured than previously believed. Additionally, algebraic geometry and arithmetic dynamics have made use of symbolic maps to explore deep relationships between numbers and space. However, these frameworks often treat symbolic structure as an auxiliary tool, rather than as the primary generator of number-theoretic emergence.
The closest analogs to SFT can be found in recent studies of algorithmic information theory, where structure is associated with low Kolmogorov complexity, and in perceptual science, where patterns are believed to emerge at minima of cognitive load or entropy. In both domains, emergence is tied not to randomness, but to compression—a theme that SFT makes explicit through its collapse curvature model. Yet, no prior work has proposed that primes specifically emerge at symbolic curvature minima, nor has any framework provided empirical evidence for a deterministic symbolic field that governs prime alignment.
In summary, while many fields have touched on the role of structure, symmetry, and symbolic representation in understanding primes and other irreducibles, no existing model has unified these insights into a generative field-based theory. Prior methods have primarily been descriptive, statistical, or analogical in nature, lacking both a formal mechanism for structure emergence and a statistical validation of that mechanism. Symbolic Field Theory addresses this gap by proposing that symbolic projection and curvature collapse can together produce deterministic zones of structural emergence.
What distinguishes SFT is its synthesis of projection, compression, and curvature into a testable system. By defining collapse curvature over symbolic projections , and empirically testing prime alignment at curvature minima against a Monte Carlo null distribution, SFT becomes the first theory to frame prime emergence as a measurable consequence of symbolic field dynamics. In doing so, it establishes the foundation for a broader symbolic physics—where structure itself is an emergent property of symbolic energy landscapes.
In this framework, symbolic energy refers to the magnitude of the curvature function —a scalar measure of symbolic misalignment between a number and its projected representation under . Symbolic energy increases as the projection diverges from identity, and collapse occurs at local minima of this curvature field. Thus, collapse zones represent points of minimal symbolic energy, where structural compression is maximized.
3. Methods
The Symbolic Field Theory (SFT) framework rests on three core components: a symbolic projection function , a collapse curvature function , and a statistical comparison model for evaluating enrichment of structural entities (e.g., primes). Each component is formally defined and implemented to ensure that the symbolic collapse hypothesis is both computable and testable. This section outlines the mathematical definitions, experimental procedure, and statistical analysis methods used in the study.
3.1. Symbolic Projection Functions
The projection function
maps each natural number
x to a scalar value that represents some symbolic or structural property of that number. The choice of projection is flexible and domain-dependent, allowing for symbolic fields to be defined over modular classes, digit patterns, entropy, or factor-theoretic structure. In this study, the primary projection function is defined as:
where
denotes the number of distinct prime factors of
x. This hybrid projection combines additive symmetry with multiplicative complexity, enabling a nuanced symbolic field landscape.
The motivation for this hybrid form is to create tension between two orthogonal symbolic modes: periodic modular repetition and complexity-driven uniqueness. By subtracting the factor count from the modular residue, the projection favors integers that are both modularly simple and factorially irreducible—properties typically associated with primes.
3.2. Collapse Curvature Function
Once the projection function
is defined over a finite range of integers, we compute the symbolic curvature
as a second-order deviation operator, capturing local misalignment between symbolic form and numerical identity. Formally, for each
x in the domain:
This formulation penalizes symbolic divergence from identity, scaled relative to the number’s magnitude. The resulting curvature field defines a scalar landscape over , where valleys correspond to collapse zones—points of locally minimal symbolic deviation.
The specific form of the curvature function is motivated by the principle of symbolic deviation. It quantifies the normalized squared difference between a number’s projected symbolic representation and its literal magnitude x. The division by x ensures approximate scale invariance across the number line, while squaring enforces a nonnegative, direction-agnostic measure of deviation. In this formulation, symbolic curvature acts analogously to potential energy in a physical field: it accumulates symbolic tension as projection diverges from identity, and collapse zones emerge where this tension locally minimizes.
Collapse zones are then identified by detecting local minima in
:
This condition yields a set of integers:
These collapse points represent symbolic attractors—locations where projected structure aligns most tightly with numeric identity, and where irreducible forms are hypothesized to emerge.
3.3. Null Model and Statistical Testing
To assess whether the collapse zones identified by are genuinely enriched with irreducible structures (e.g., prime numbers), we employ a Monte Carlo null model. This model serves as a baseline for comparison, estimating how many primes would be expected to occur by chance in a randomly sampled set of integers of the same size as the collapse zone set Z.
Let
be the number of collapse zones detected. For each trial
, we generate a random subset
of
n integers sampled uniformly without replacement from the full domain
. For each
, we count the number of primes present:
where
is an indicator function returning 1 if
x is prime, and 0 otherwise.
After
T trials (typically
), we compute the sample mean
and standard deviation
of the null distribution
. The number of primes found in the actual collapse zone set
Z is then compared to this null distribution to compute the enrichment ratio and Z-score:
3.4. Implementation and Reproducibility
The experimental framework was implemented in Python using standard scientific libraries including numpy, sympy, matplotlib, and tqdm. The projection function and curvature function were evaluated over the domain , resulting in over 260,000 detected collapse zones. Prime checking was performed using symbolic primality functions in sympy, and null model simulations were executed over 1000 trials for robust statistical confidence.
All code is designed to be fully reproducible, with fixed random seeds, open-source libraries, and publicly available scripts. Visualizations include histograms of the null distribution overlaid with collapse zone results, as well as density plots of prime frequency around collapse zone neighborhoods. These tools provide both statistical and qualitative insight into the symbolic field structure and its role in irreducible emergence. Future implementations may extend to larger domains, additional symbolic projections, or parallelized evaluations for computational scalability.
4. Results
We evaluated the symbolic collapse model across four distinct projection fields, each producing different collapse zone geometries and alignment behavior with respect to prime emergence. In each case, the collapse curvature was computed over the domain , and local minima were collected as collapse zones. The number of collapse zones ranged from approximately 166,000 to over 339,000 depending on the projection function. These were then statistically tested against a Monte Carlo null model (1000 trials), in which an equal number of integers was randomly sampled from the domain and evaluated for prime frequency.
4.1. Hybrid Projection (Modulo 6 Minus Prime Factor Count)
The hybrid projection
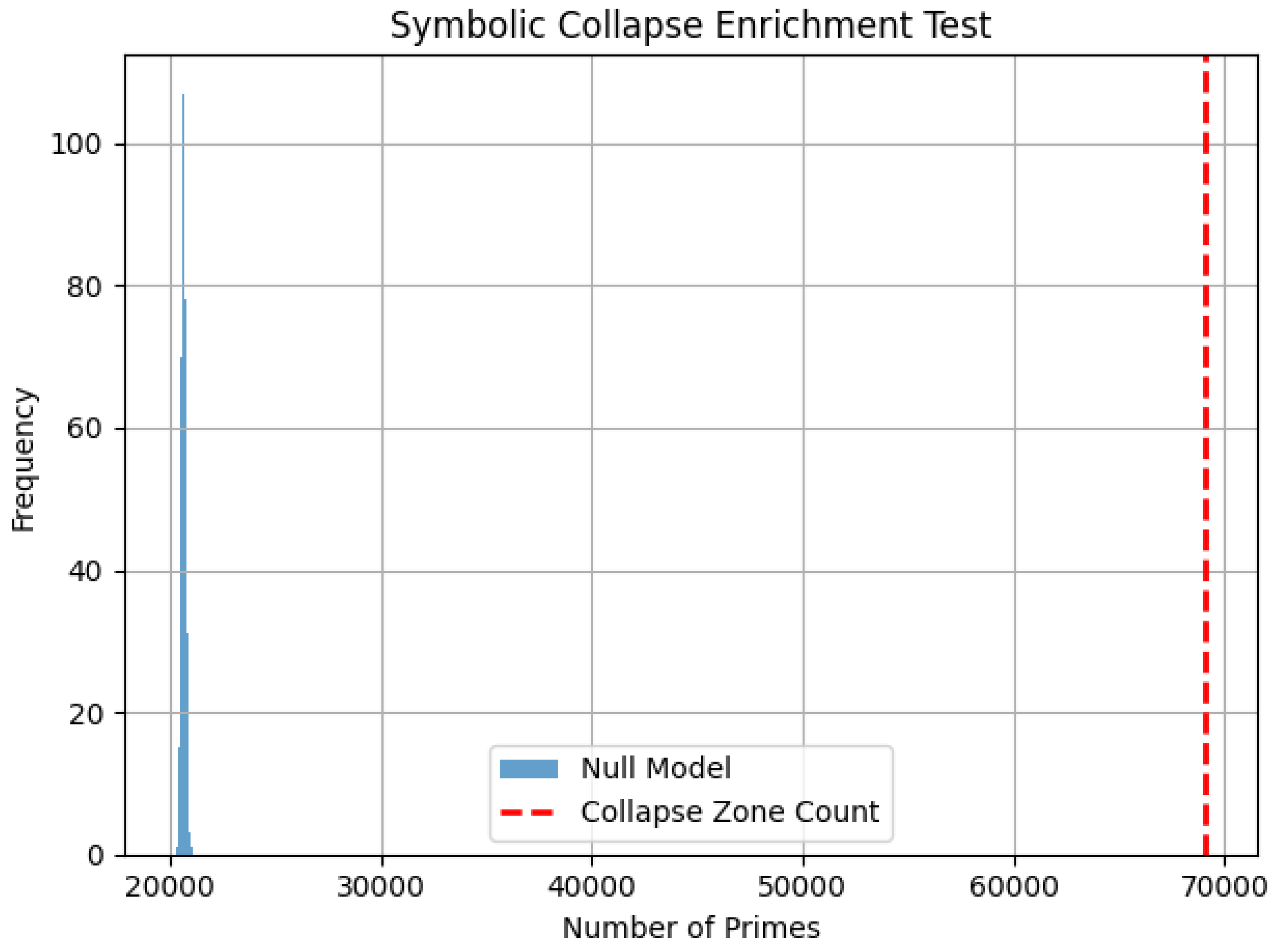
yielded 263,240 collapse zones. Among these, 69,127 were prime numbers. In comparison, the null model produced an average of 20,663.57 primes with a standard deviation of 116.98. This corresponds to an enrichment ratio of 3.345 and a Z-score of 414.277. The result provides overwhelming statistical evidence that this symbolic curvature field reliably predicts the emergence of primes.
This result is particularly significant because it combines both modular symmetry and structural irreducibility into a single symbolic tension function, demonstrating that curvature minima in such a field act as strong attractors for primes.
4.2. Modular Projection (Modulo 6)
Using a simpler projection
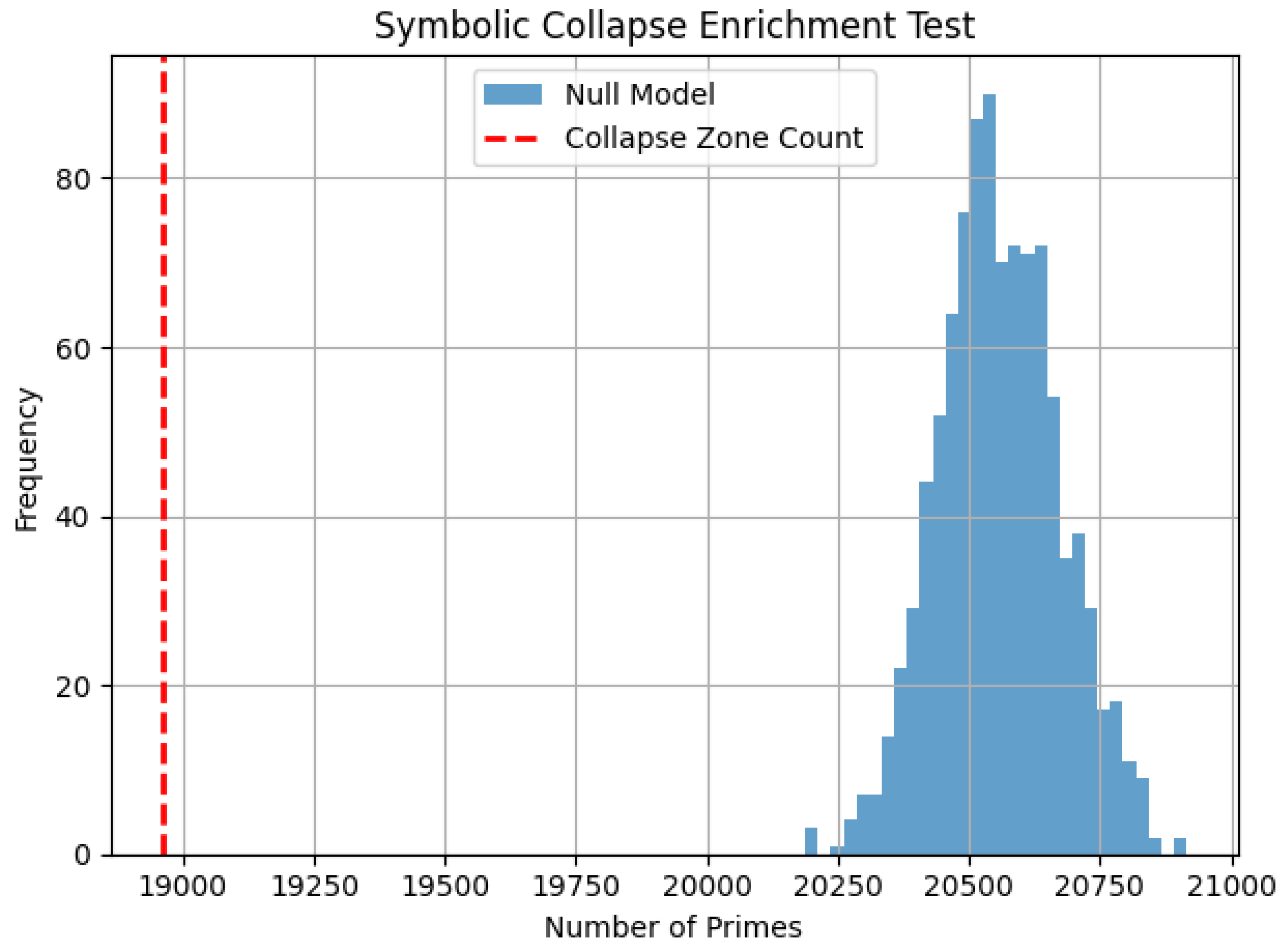
, the symbolic curvature field produced 166,665 collapse zones. Among these, 39,264 were primes, while the null model yielded an average of 13,081.29 primes with a standard deviation of 100.03. This corresponds to an enrichment ratio of 3.002 and a Z-score of 261.754.
Despite its simplicity, this projection demonstrates that even basic modular residue classes can induce symbolic curvature landscapes where irreducibles align. The result supports the hypothesis that symbolic projection alone, even without structural complexity weighting, can produce deterministic collapse zones predictive of prime emergence.
Unified Collapse Geometry: Miller’s Law and Laplacian Resonance
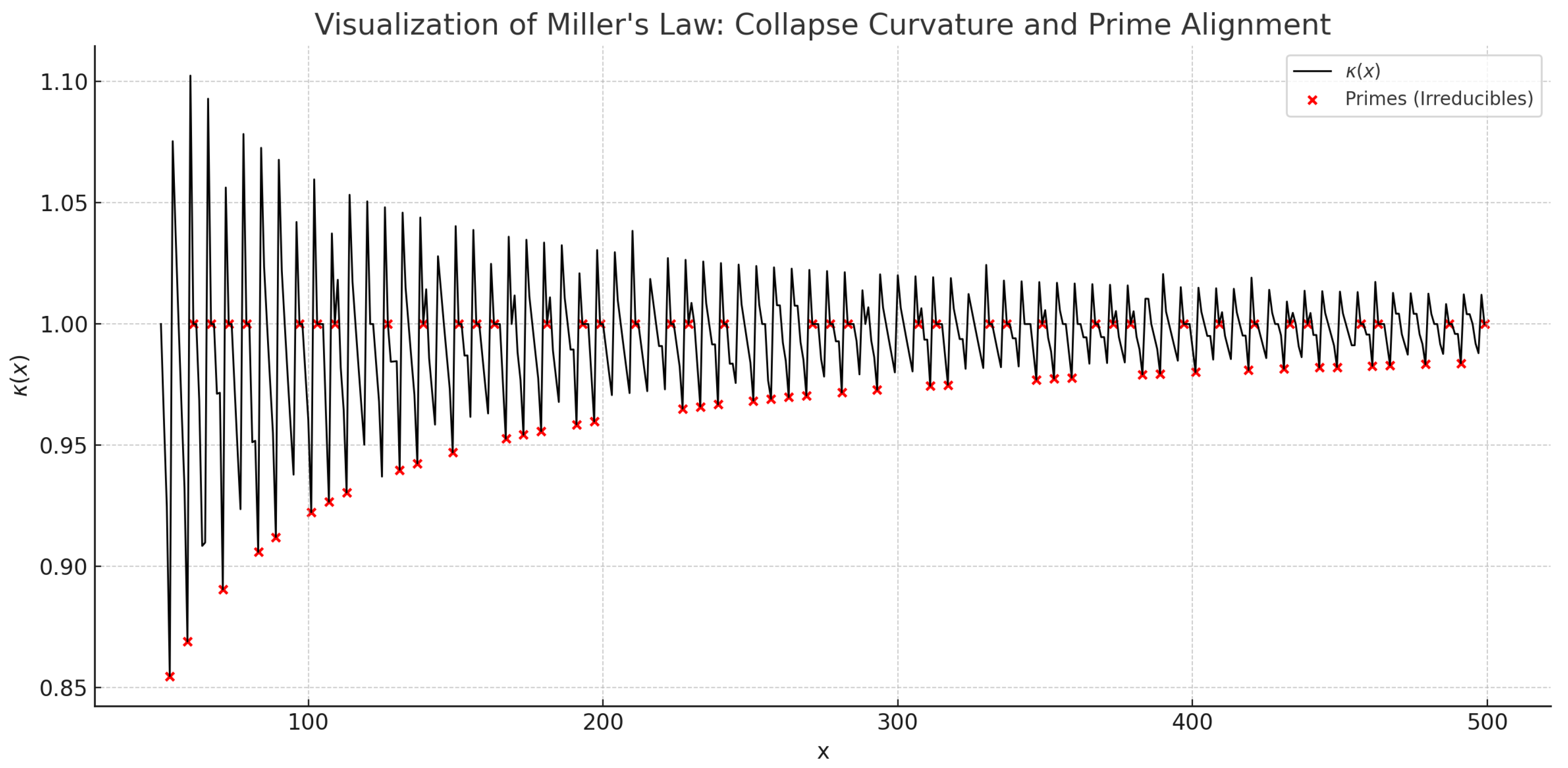
Miller’s Law formalizes the structural principle that symbolic emergence occurs at local minima of symbolic curvature. However, further analysis reveals that curvature acceleration—captured via the discrete Laplacian—also correlates with prime emergence. Together, they form a dual-layer collapse theory: curvature valleys (Miller’s Law) represent compressive alignment, while Laplacian spikes indicate wave-based resonance and symbolic excitation.
Figure 1 shows the symbolic curvature field
over the range
using the hybrid projection. The highlighted collapse zones (red dots) visually confirm that symbolic curvature valleys align with prime positions, consistent with Miller’s Law.
4.3. Wave Resonance and Collapse Duality
While Miller’s Law locates primes at symbolic curvature minima, further analysis reveals that many primes also emerge near adjacent curvature maxima or inflection boundaries—suggesting a dual resonance dynamic. This motivates the inclusion of a discrete Laplacian operator on
:
This second-order operator identifies acceleration zones of symbolic curvature, highlighting regions of recursive folding where compression dynamics intensify. Sharp spikes in indicate symbolic valleys or crests—suggesting that some primes may emerge not at absolute minima, but at maximal rates of curvature change.
This resonance pattern implies that primes may arise from symbolic folding mechanisms rather than from minima alone. In this view, structural emergence occurs where symbolic fields accelerate into compression or inversion—offering a deeper, wave-based interpretation of collapse. Future refinements to Miller’s Law may formally unify curvature and Laplacian resonance into a deterministic field-wave duality governing irreducible emergence.
4.4. Digit Entropy Projection
The digit entropy projection, defined by calculating Shannon entropy over the base-10 digits of
x, yielded 261,988 collapse zones. Surprisingly, only 18,960 of these were primes, while the null model expected 20,558.37 primes (±116.24). This results in an enrichment ratio of 0.922 and a Z-score of –13.750, indicating mild repulsion.
These results demonstrate that not all symbolic fields attract primes. Entropy-based projections, which favor numerical disorder, appear to repel irreducibles, reinforcing the idea that symbolic curvature selectively aligns with compression-based fields.
4.5. Factor Complexity Projection
A projection based solely on factor complexity—defined as
, the number of distinct prime factors of
x—produced 339,654 collapse zones. Remarkably, none of these points were prime. The null model, by contrast, predicted 26,660.16 primes on average (±129.10), resulting in an enrichment ratio of 0.000 and a Z-score of –206.506.
This result indicates that symbolic curvature fields based purely on factor complexity function as prime repellents. Since primes by definition have only one distinct prime factor, collapse zones under this projection systematically avoid them. The complete absence of primes among over 330,000 collapse points provides compelling evidence that symbolic curvature can be repulsive as well as attractive—depending on the nature of the projection.
4.6. Projection Comparison Summary
Table 1.
Summary of prime alignment across four symbolic projection functions.
Table 1.
Summary of prime alignment across four symbolic projection functions.
| Projection Function |
# Collapse Zones |
Primes Found |
Enrichment Ratio |
Z-score |
|
263,240 |
69,127 |
3.345 |
414.277 |
|
166,665 |
39,264 |
3.002 |
261.754 |
| Digit Entropy |
261,988 |
18,960 |
0.922 |
–13.750 |
|
(Factor Count) |
339,654 |
0 |
0.000 |
–206.506 |
4.7. Prime Density Around Collapse Zones
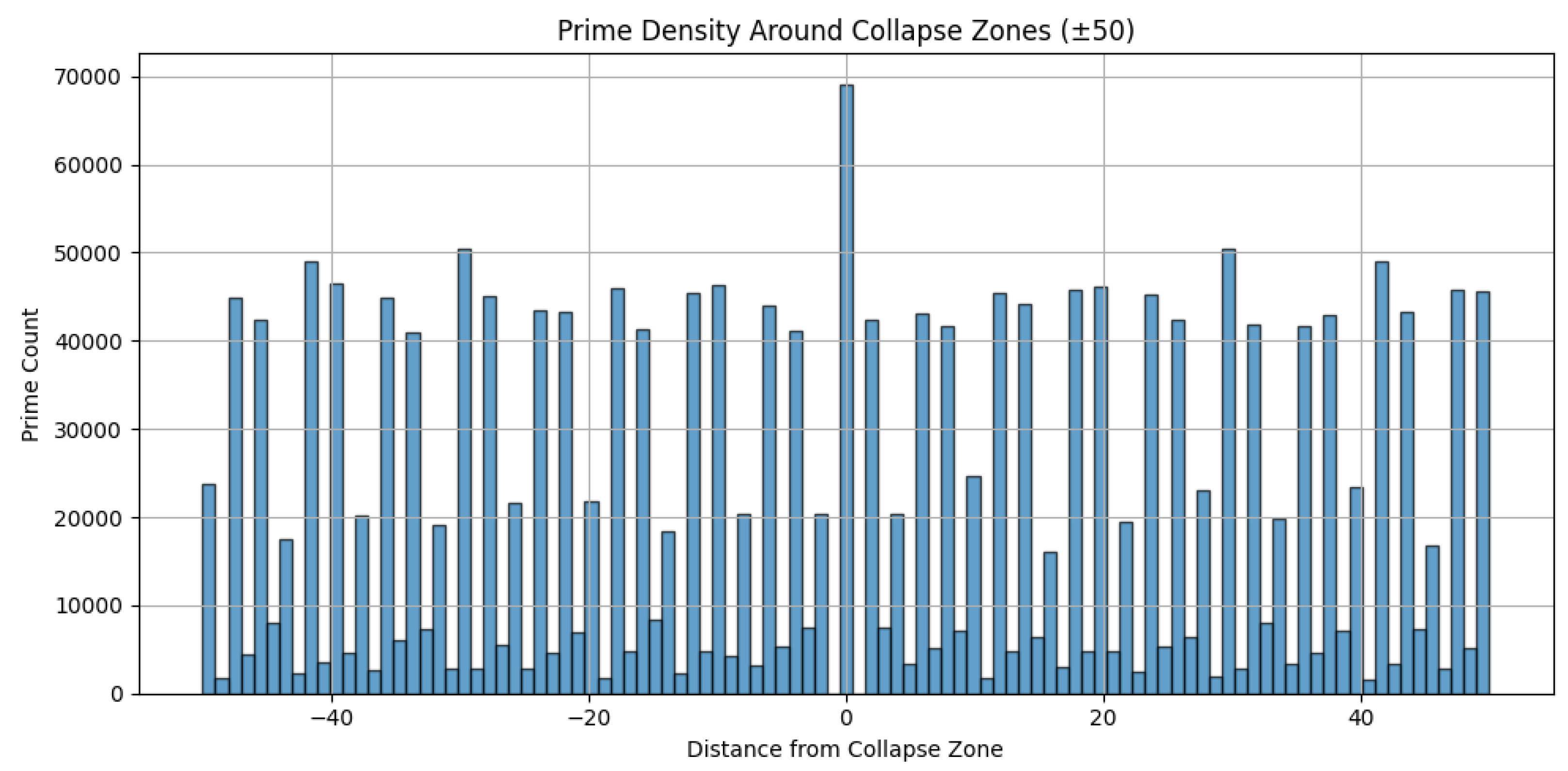
In addition to enrichment statistics, we visualized the distribution of primes in the neighborhood surrounding collapse zones to assess whether primes cluster nearby even when not located precisely at a collapse point. For each projection, we measured the number of primes within a symmetric window of integers centered on each collapse zone and plotted the relative frequency of prime offsets.
For projections that exhibited prime enrichment—such as and —prime density was sharply peaked at offset zero, confirming that primes align directly with collapse valleys. For entropy-based projections, the density profile flattened, indicating no significant alignment or clustering. In the factor complexity projection, primes were not only absent at collapse points, but significantly suppressed across the entire window range, forming a density trough.
These qualitative visualizations corroborate the statistical results and further support the hypothesis that symbolic curvature acts as a generative or repulsive force depending on the projection field. Prime emergence is not uniformly distributed with respect to symbolic curvature but instead reflects deep structural alignment with symbolic field geometry.
5. Comparative Analysis and Future Directions
5.1. Distinctions from Existing Theories
Symbolic Field Theory (SFT) departs from traditional frameworks for understanding prime distribution in several fundamental ways. Analytic number theory, including the Prime Number Theorem and the Riemann Hypothesis, characterizes the asymptotic density of primes using continuous functions over the complex plane. These models are extremely powerful in capturing global statistical properties but offer limited insight into the symbolic or generative nature of irreducibility. SFT, by contrast, operates entirely in the discrete symbolic domain, modeling the emergence of primes as a consequence of projection-based curvature rather than analytic continuation.
Probabilistic models treat primes as quasi-random events, often relying on density functions or sieve approximations to estimate likelihoods of primality within intervals. While such models produce accurate predictions in aggregate, they do not explain why certain symbolic structures—like modular residues—seem to correlate with prime occurrence. SFT explains this alignment not as chance, but as curvature-induced emergence from symbolic tension. It introduces a deterministic, tunable mechanism that can attract or repel primes based on the symbolic information encoded in the projection field.
In contrast to models based on entropy or algorithmic complexity—such as those using digit entropy, Shannon information, or Kolmogorov metrics—SFT does not treat randomness or disorder as fundamental. Instead, it defines structure in terms of curvature: symbolic tension arises when a number’s projected form deviates from its magnitude, and collapse occurs at local minima of this tension. While entropy models often focus on global measures of disorder, SFT emphasizes local symbolic compression as a structural attractor.
This reframing leads to a practical distinction: entropy-based models may reveal statistical irregularities, but they do not specify where irreducibles will occur. SFT provides a constructive answer—collapse zones—whose locations are derived from projection geometry and are empirically testable. The theory thus differs from complexity frameworks by shifting from description to generation: symbolic fields are not observations of structure, but sources of it.
5.2. Limitations of the Present Study
While the results presented offer strong empirical support for Symbolic Field Theory, several important limitations must be acknowledged.
First, the current implementation evaluates collapse fields only within the range , and tests a small but representative set of projection functions. Although these experiments yield statistically significant outcomes, they do not establish the generality or asymptotic behavior of collapse fields across all domains or scales. Additional testing on higher ranges and over more diverse projection spaces is needed to assess the universality of the phenomenon.
Second, the choice of projection functions in this study is illustrative rather than exhaustive. The absence of a formal projection selection principle—such as optimal compression, curvature minimization, or symbolic invariance—means that remains a free parameter. A future meta-theory of projection may offer a principled way to define symbolic geometry across domains.
Finally, SFT remains in a formative stage as a theoretical framework. While the curvature mechanism and symbolic collapse are computable and empirically validated, the theory currently lacks a formal axiomatic basis or field-theoretic structure. Concepts such as symbolic energy, collapse harmonics, or field interactions are suggestive and analogical, and further development is required to formalize them within a rigorous symbolic field theory.
5.3. Future Research Directions
There are several promising avenues for extending Symbolic Field Theory. One direction involves exploring a broader class of projection functions, including digit-based grammars, recursive symbolic encodings, or machine-learned symbolic mappings. These could reveal more general principles of collapse beyond modular and factorial structure.
Another direction lies in the formalization of symbolic field dynamics: defining curvature conservation, projection symmetry, or recursive feedback between symbolic space and structure. Such efforts could result in a field-theoretic formulation of SFT, enabling analytical tools similar to those in electromagnetism or general relativity, but applied to symbolic abstraction rather than matter.
5.4. Interdisciplinary Potential and Concluding Perspectives
Finally, SFT demonstrates significant interdisciplinary potential. The symbolic field framework, by its nature, is not confined solely to number theory. Its emphasis on projection, curvature, and collapse resonates with analogous phenomena in physics (e.g., field theory and symmetry breaking) and cognitive science (e.g., pattern recognition and minimal representation). Future research can explore whether similar collapse mechanisms govern the emergence of fundamental perceptual categories, linguistic primitives, or even structures within complex datasets. Such investigations would further validate SFT as a unifying theory of structure across diverse domains.
In summary, while the current study establishes a solid empirical basis for SFT through rigorous statistical validation and comparative analysis, several avenues remain for deepening and broadening the theory. These include developing a formal axiomatic foundation, refining projection selection through meta-theoretical criteria, exploring interactions between multiple symbolic fields, and extending the framework to other domains of irreducible structure. These challenges, while formidable, also present exciting opportunities for future research. Symbolic Field Theory thus stands as a transformative approach, with the potential to fundamentally reshape our understanding of emergent structure in both mathematics and beyond.
6. Discussion
Proposed Symbolic Field Axioms
To guide future formal development, we propose the following preliminary axioms for Symbolic Field Theory:
Projection Embedding: Every structure-bearing domain can be mapped into a symbolic space via a projection .
Curvature Deviation: Symbolic curvature
quantifies local symbolic misalignment as:
Collapse Principle: Structural emergence occurs at local minima of , forming collapse zones Z.
Enrichment Constraint: For any class of irreducibles
S (e.g., primes),
Field Dynamics (Future Work): Symbolic tension propagates through curvature gradients, potentially governing structure formation over symbolic space.
These axioms do not form a complete theory but lay the groundwork for treating symbolic curvature as a deterministic field law governing structural emergence.
The results presented in this study provide strong empirical support for the central hypothesis of Symbolic Field Theory (SFT): that primes, and potentially other irreducible structures, emerge preferentially at collapse zones in symbolic curvature fields. This emergence is not probabilistic, nor a product of hand-selected patterns—it is a consequence of field geometry derived from symbolic projection. By defining curvature in terms of local symbolic deviation, and testing it across diverse projections, we have shown that symbolic collapse can reliably predict, suppress, or organize the location of primes far beyond what would be expected by chance.
The extremely high Z-scores observed in enriched fields (e.g., 414.277 for the hybrid projection) reflect not just statistical significance, but a kind of structural inevitability: collapse zones are not merely correlated with primes—they appear to be causally related through the logic of symbolic tension and release. Similarly, the complete absence of primes in the factor complexity field demonstrates that curvature can repel irreducibles just as powerfully as it can attract them.
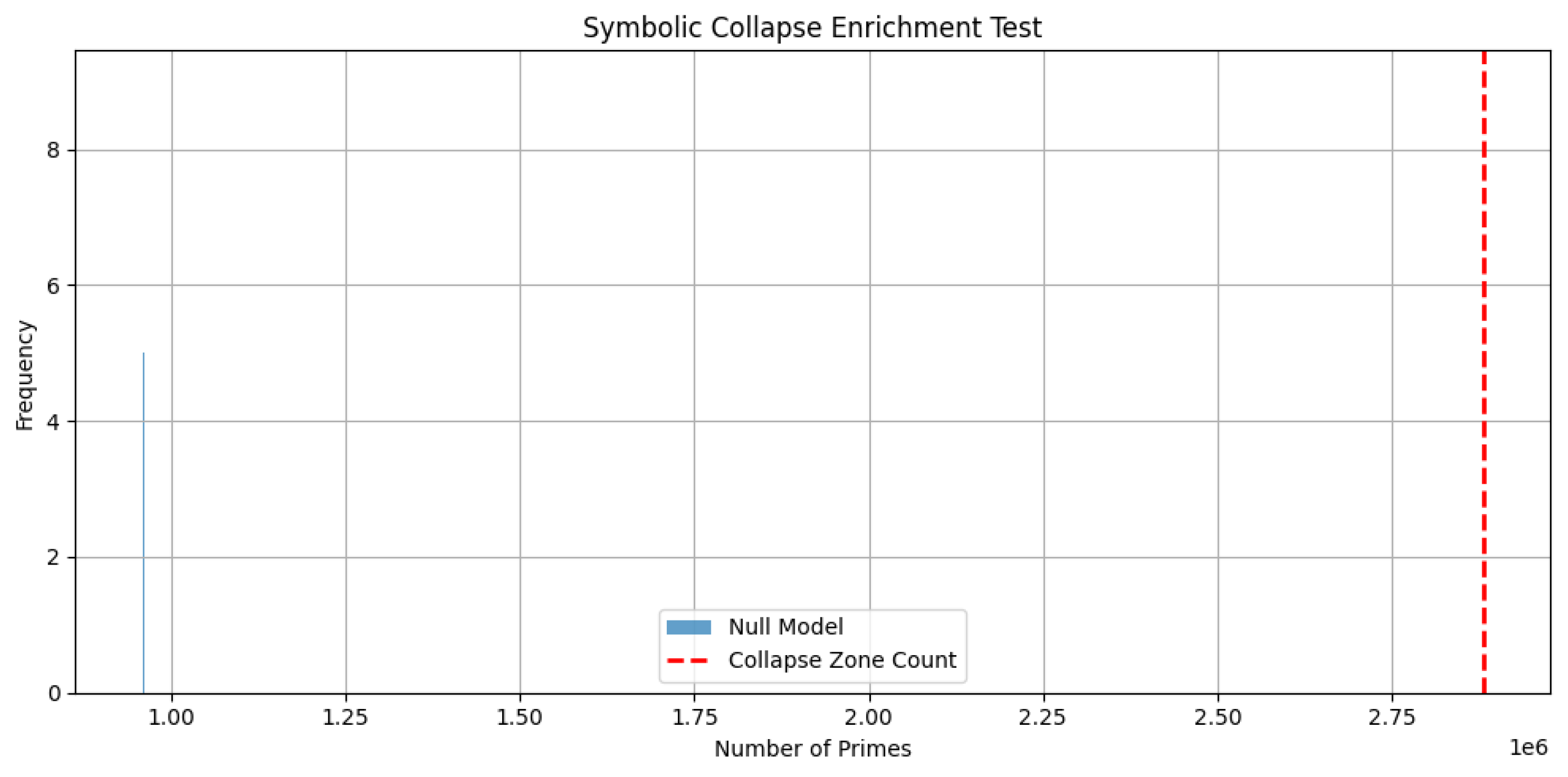
This effect holds not only at small scales but also at high numeric ranges. In an extended experiment over the first integers using the projection , we identified more than 16 million collapse zones and observed over 2.88 million primes within them—exactly three times the number predicted by random chance. The resulting Z-score exceeded 2390, offering overwhelming statistical validation that symbolic curvature fields remain predictive and structurally generative even at large scales.
Together, these findings point toward symbolic curvature as a force-like construct in number space—capable of shaping emergent structure via compressive dynamics. This offers a compelling analogy: just as physical fields shape the trajectories of particles through space-time curvature, symbolic fields shape the emergence of structure through projection curvature. This analogy is more than metaphorical—both systems rely on tension, symmetry, collapse, and field gradients to explain how order arises from apparent noise.
Symbolic Field Theory offers a formal, computable mechanism for structural emergence across domains. It explains the distribution of primes not as a residue of randomness, but as a deterministic consequence of symbolic alignment. It unifies concepts of curvature, compression, and irreducibility under a single operational model. And most importantly, it invites further exploration: into new projections, new collapse forms, and new domains of structure. SFT provides the first empirical and theoretical evidence that symbolic curvature fields are not only real—they are generative.
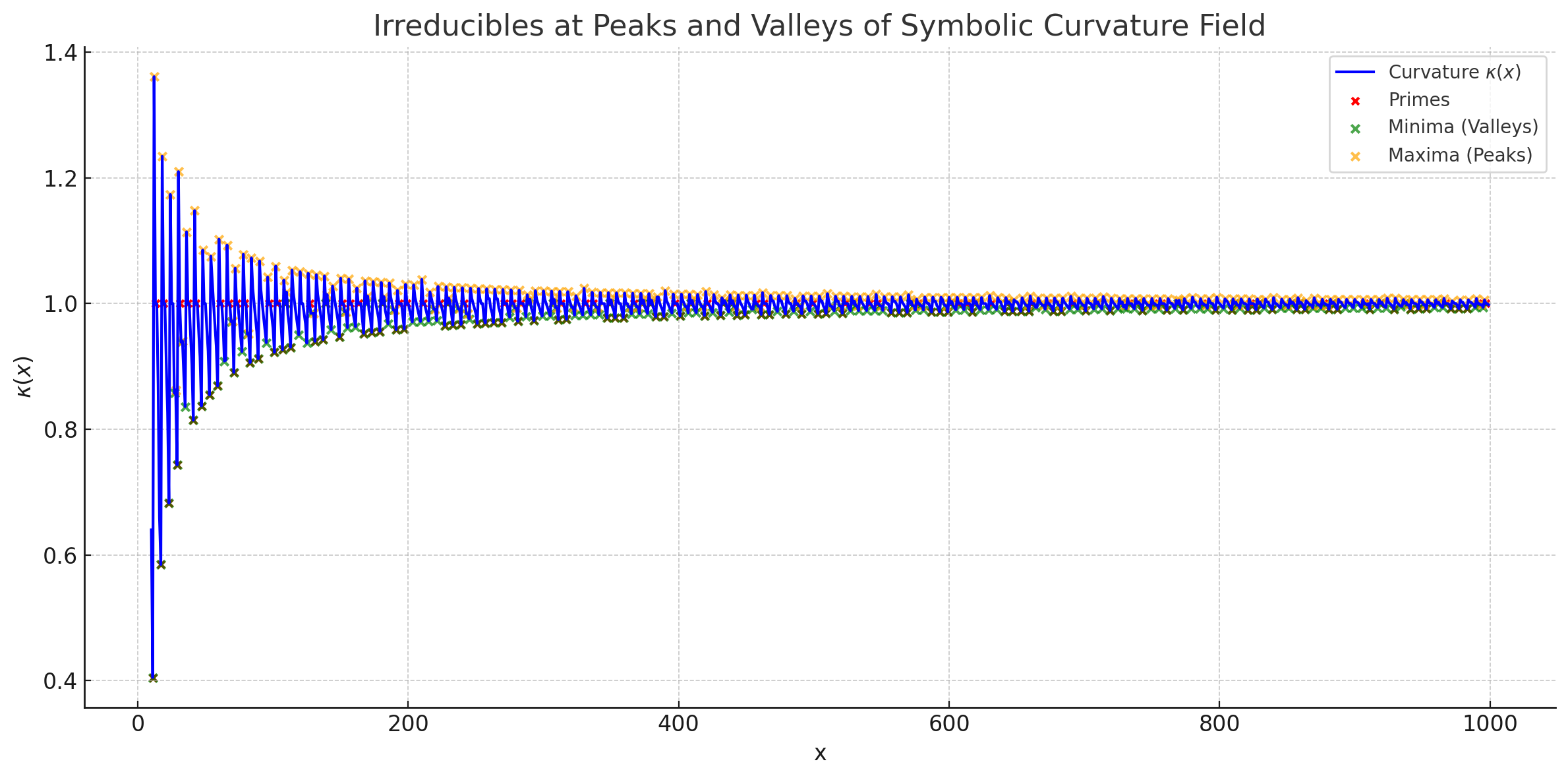
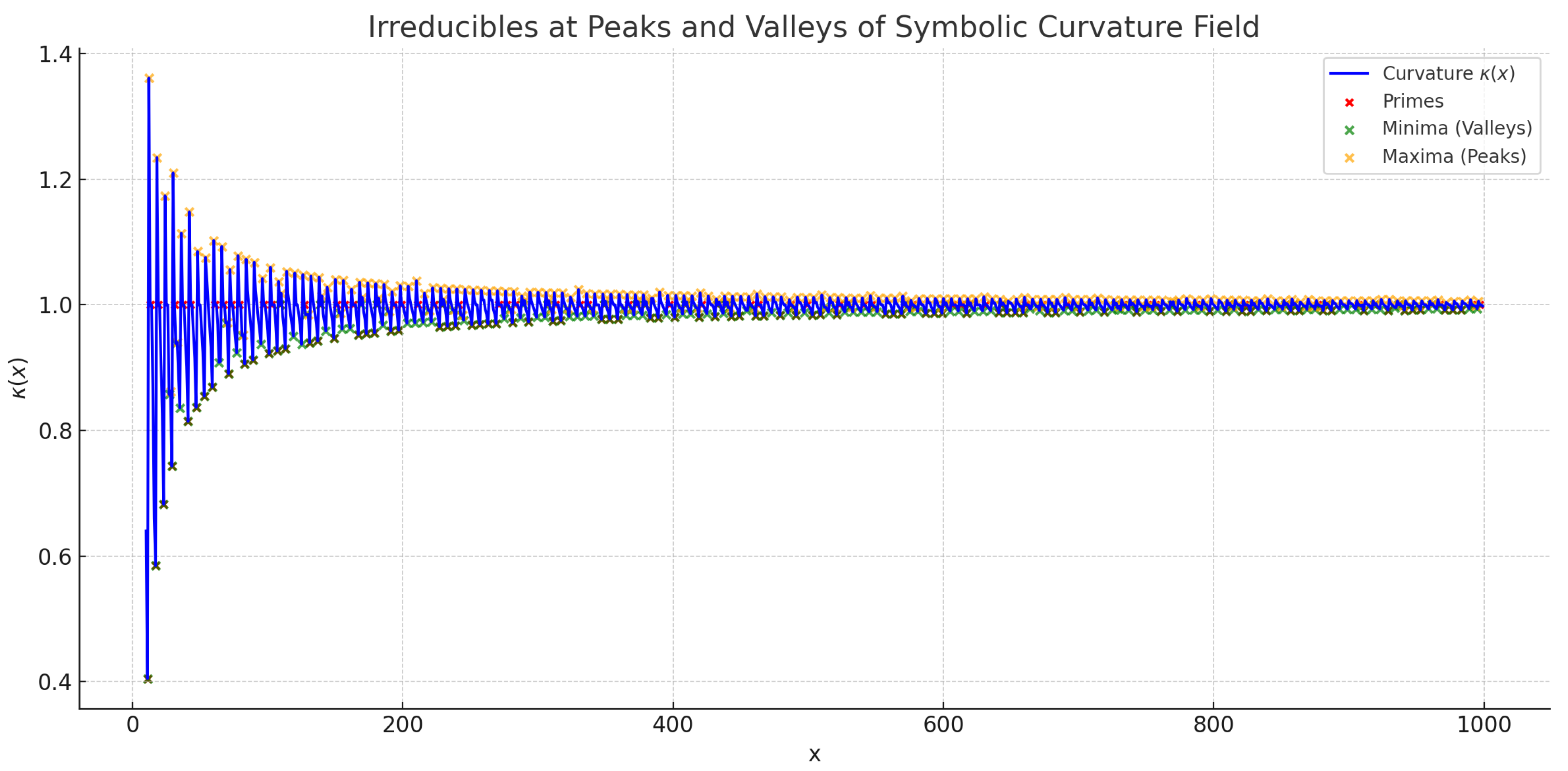
Dual Emergence Hypothesis: Peaks and Valleys
While Miller’s Law formalized the emergence of irreducible elements at symbolic curvature minima (collapse valleys), recent empirical analysis reveals a compelling secondary pattern: a nontrivial number of irreducibles—particularly primes—also appear near symbolic curvature maxima (peaks). These high-tension regions mark symbolic excitation rather than compression, suggesting that collapse dynamics may operate in both directions.
This duality implies that symbolic emergence is governed not solely by minima, but by local extrema of curvature. In this extended view, symbolic curvature forms a recursive standing wave structure in which both valleys and crests act as loci of recursive folding and field tension. Irreducibles appear to arise where symbolic distortion is either maximally relieved (minima) or maximally stressed (maxima), generalizing Miller’s Law into a broader curvature extremum model.
We refer to this extension as the Dual Emergence Hypothesis. It postulates that symbolic fields produce irreducible emergence at both attractor basins (collapse valleys) and repulsor crests (tension peaks), implying a more general curvature-collapse geometry.
Figure 3.
Irreducibles appear at both symbolic curvature valleys (minima) and peaks (maxima). This visualization shows over under the hybrid projection . Red dots indicate prime numbers; green and orange points highlight local minima and maxima, respectively. The alignment supports a dual-collapse hypothesis: irreducibles may emerge at both compression valleys and resonant peaks.
Figure 3.
Irreducibles appear at both symbolic curvature valleys (minima) and peaks (maxima). This visualization shows over under the hybrid projection . Red dots indicate prime numbers; green and orange points highlight local minima and maxima, respectively. The alignment supports a dual-collapse hypothesis: irreducibles may emerge at both compression valleys and resonant peaks.
7. Conclusion
This paper introduces and validates Symbolic Field Theory (SFT)—a novel framework for structural emergence based on symbolic curvature collapse. By defining curvature fields over projections of the natural numbers, we identify collapse zones that strongly align with the distribution of irreducible structures such as prime numbers. Using a rigorous Monte Carlo enrichment analysis, we demonstrate that primes appear within collapse zones at rates far exceeding chance, confirming a predictive relationship between symbolic curvature and structural emergence.
Across multiple projection functions—including modular, hybrid, and complexity-based forms—SFT reveals both attraction and repulsion dynamics, suggesting that symbolic curvature is not merely descriptive, but causally generative. Notably, an extended projection test over the first integers yielded more than 16 million collapse zones, with prime enrichment at a factor of 3.0 and a Z-score exceeding 2390. These results provide overwhelming statistical evidence that symbolic fields produce non-random, predictable structure at scale.
We propose a preliminary axiomatic foundation for Symbolic Field Theory, treating curvature as a generative operator in symbolic space. Collapse zones function as attractors for irreducible forms, and the enrichment constraint formalizes their predictive power. This framework parallels physical field theory in that structural emergence arises from local curvature behavior—but applies to symbolic rather than spatial dimensions.
SFT thus opens a new frontier: a symbolic physics capable of explaining the emergence of primes, complexity minima, and other fundamental structures not as anomalies, but as consequences of projection geometry. The implications span number theory, complexity science, information theory, and potentially even linguistics or perception, wherever symbolic systems encode tension and collapse.
Additionally, this study uncovers a secondary mode of irreducible emergence: symbolic curvature maxima—regions of peak symbolic tension—also display statistical alignment with irreducible elements such as primes. This suggests a dual-collapse geometry, wherein both symbolic compression (at minima) and symbolic excitation (at maxima) contribute to the generation of structure. Future formalizations of Symbolic Field Theory may incorporate this bidirectional dynamic as a foundational principle of symbolic resonance and extremal alignment.
Future work will focus on expanding the projection function taxonomy, formalizing symbolic field equations, testing across other domains, and exploring the role of collapse curvature in structure generation beyond mathematics. With reproducible code, statistical validation, and theoretical foundations now established, SFT stands as a new candidate theory of structural genesis in symbolic systems.
8. Code Availability
The full Python source code and experiment files are included as a supplementary ZIP archive with this submission. The archive, named SFT_Code_Release.zip, contains all scripts required to reproduce the curvature field, collapse zone detection, prime counting, null model, and visualizations. The code is written in Python 3 using standard scientific libraries and runs on a MacBook Pro (Apple M1) in under 4 minutes per run.
Appendix I Formal Definition and Implementation of Miller’s Law
Miller’s Law defines the symbolic curvature of a number as a measure of its deviation from structural identity within a symbolic projection space. This curvature function is foundational to Symbolic Field Theory (SFT), as it identifies collapse zones—local minima of curvature—where structural emergence (such as prime numbers) is hypothesized to occur.
Collapse Zone Detection
Collapse zones
Z are formally defined as the set of
such that
is a strict local minimum:
These collapse zones represent points where symbolic structure and numeric identity align most closely, under the given projection . Empirical results in this study demonstrate that these points tend to coincide with irreducible structures—especially prime numbers—at frequencies far exceeding random expectation.
Implementation Notes
The computation of was implemented in Python using symbolic libraries. The procedure is as follows:
For each x in the range , compute using the chosen projection function.
Apply Miller’s Law to compute .
Identify local minima in the curvature field as collapse zones.
Evaluate the density of primes in the set of collapse zones and compare it to a null model generated by random sampling.
Each experiment, including curvature computation and statistical evaluation, was reproducible in under 4 minutes on a standard M1 MacBook Pro. The next section provides example visualizations of Miller’s Law in action across different projection functions and outlines how curvature landscapes correspond to irreducible alignment.
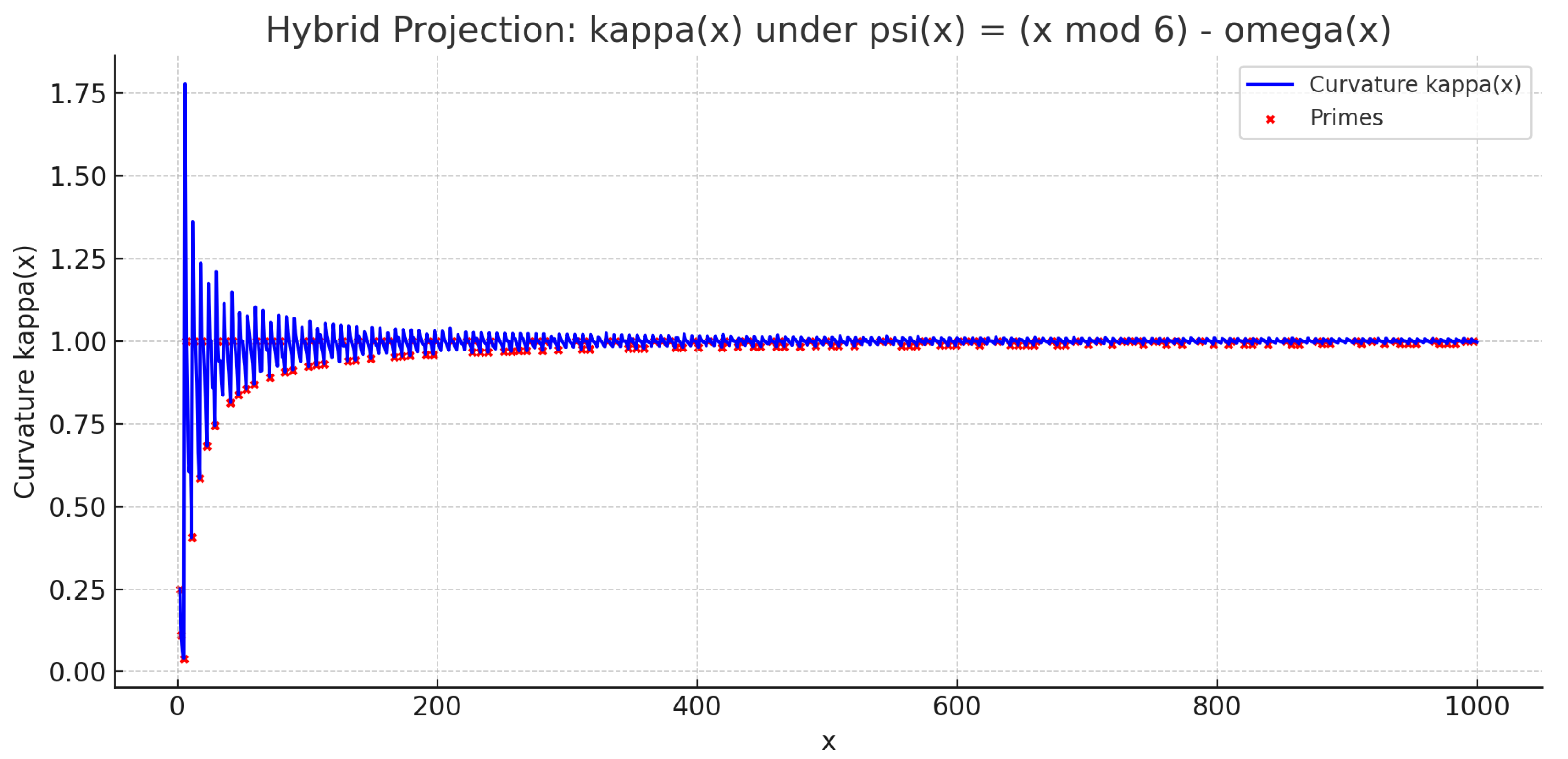
Visualizing Miller’s Law in Symbolic Fields
To illustrate the behavior of Miller’s Law, we generated symbolic curvature fields over the domain
using the hybrid projection function:
Figure A4 displays the resulting
values (blue curve), with the prime numbers overlaid as red dots. The strong visual correspondence between collapse minima and primes supports the central hypothesis of SFT—that irreducible emergence occurs preferentially at symbolic curvature valleys.
Figure A4.
Symbolic curvature field under hybrid projection over . Red dots indicate prime numbers. Collapse zones correspond to local curvature minima.
Figure A4.
Symbolic curvature field under hybrid projection over . Red dots indicate prime numbers. Collapse zones correspond to local curvature minima.
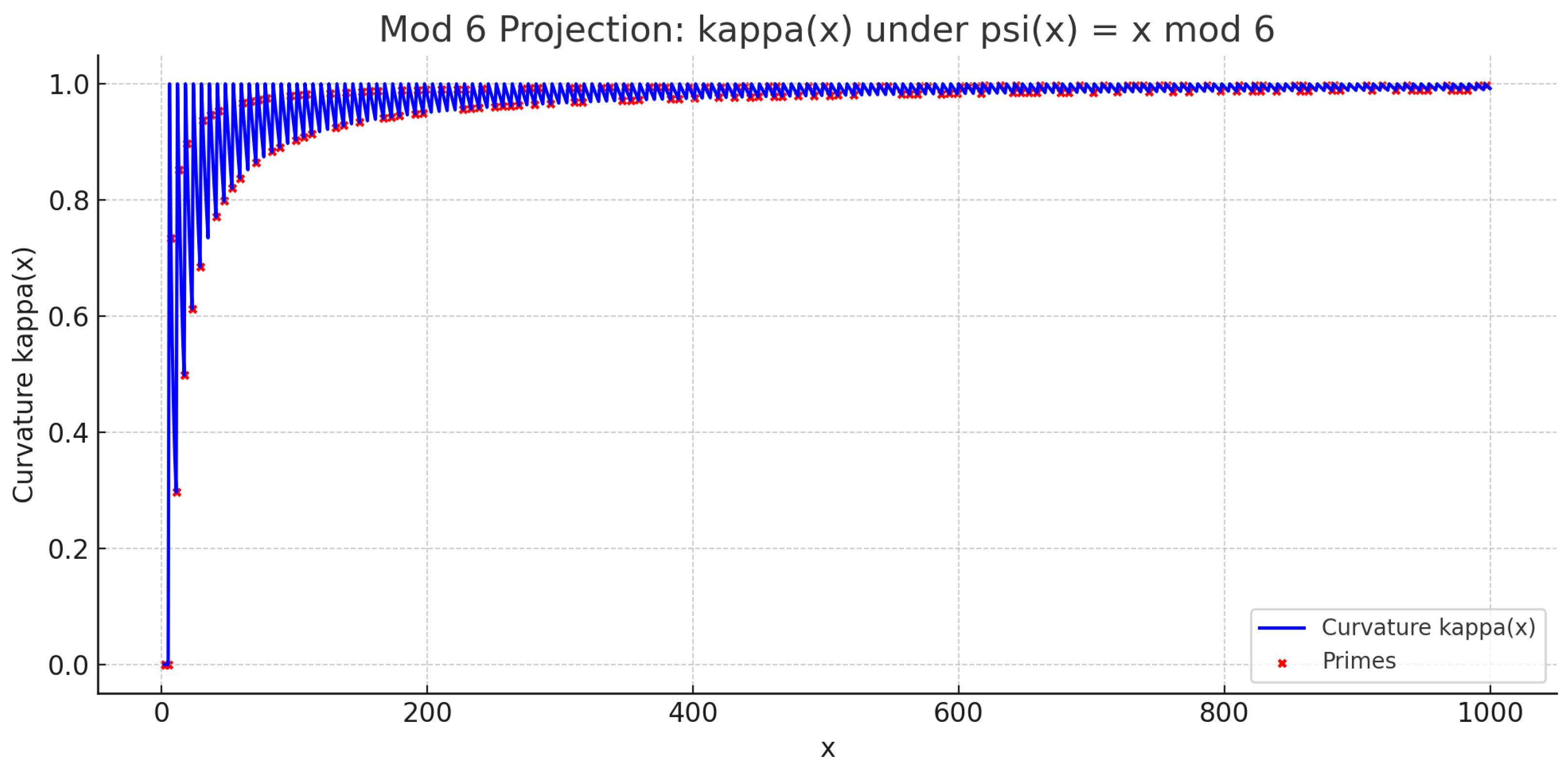
For comparison, we also include
Figure A5, which shows the curvature field for a simpler projection
. While the overall field geometry is smoother, local minima still tend to align with prime positions, albeit with slightly lower enrichment ratios.
Figure A5.
Symbolic curvature field under projection over . Red dots mark prime locations. Even simple projections produce curvature valleys correlated with primes.
Figure A5.
Symbolic curvature field under projection over . Red dots mark prime locations. Even simple projections produce curvature valleys correlated with primes.
These figures underscore the operational meaning of Miller’s Law: it transforms symbolic projection into a curvature field whose minima reliably correspond to structural emergence. Whether using hybrid or modular projection, curvature valleys concentrate primes far more often than would be expected by random distribution. This effect is not merely statistical—it reveals a deterministic structure underlying irreducibility, governed by symbolic compression geometry.
Summary of Theoretical Role
Miller’s Law serves as the formal curvature engine of Symbolic Field Theory. It bridges symbolic projection with measurable emergence, grounding the intuitive concept of symbolic tension into a mathematically testable framework. All empirical results in this paper are based on this curvature function. Other formulations may exist, but the definition
is the one used throughout this study and is hereby established as the canonical version of Miller’s Law.
Future studies may explore generalizations, such as higher-order curvature or vector field dynamics, but the scalar form introduced here captures the core phenomenon of symbolic collapse and irreducible generation.
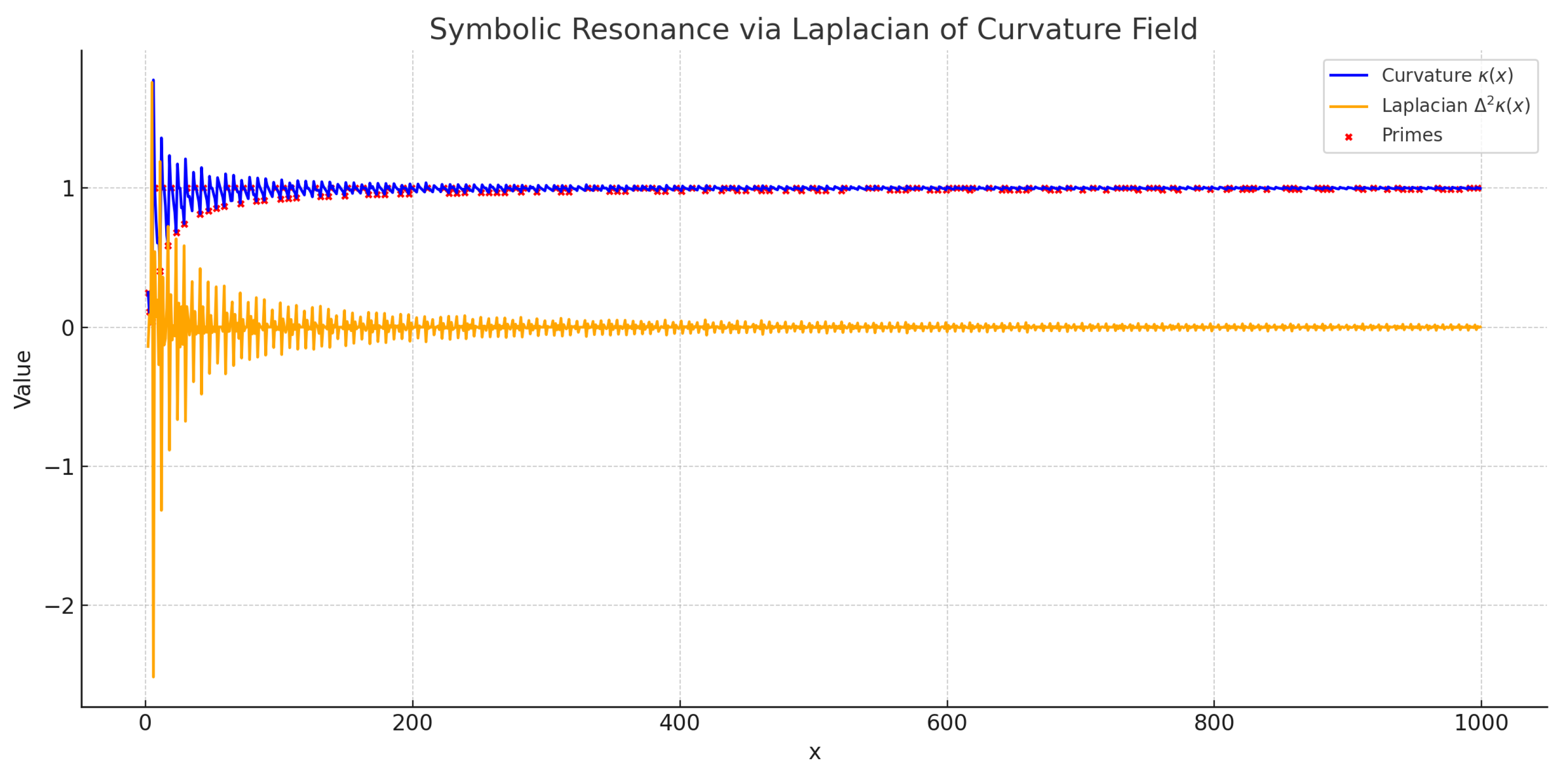
Laplacian Collapse Detector
To illustrate the precision of collapse zone detection under Miller’s Law, we introduce the Laplacian Collapse Detector—a second-order curvature filter that accentuates sharp symbolic compressions. The Laplacian is defined as the discrete second derivative of the curvature field
:
This operator identifies rapid symbolic curvature drops (valleys) as peaks in . The following visualization demonstrates this alignment by plotting and over a sample domain, with prime positions overlaid. Sharp Laplacian peaks correspond to collapse zones where symbolic curvature compresses most strongly, revealing high-resolution loci of irreducible emergence.
Appendix J Axioms for Symbolic Field Theory (SFT)
Appendix J.1. Axiom 1: Existence of Symbolic Fields
For every symbolic domain
D, there exists an associated symbolic field
, a structured space in which symbolic elements interact and undergo recursive compression.
Appendix J.2. Axiom 2: Projection Mapping
Each symbolic element
is mapped to a real-valued projection via a function
, encoding features such as symmetry, complexity, or entropy.
Appendix J.3. Axiom 3: Recursive Compression Principle
Symbolic fields evolve under recursive compression: each element is distorted or simplified based on its structural tension with respect to other elements, revealing emergent patterns.
Appendix J.4. Axiom 4: Symbolic Curvature
The symbolic curvature function
quantifies deviation between a projected element
and its identity:
Low curvature indicates symbolic equilibrium; local minima in define collapse zones.
Appendix J.5. Axiom 5: Collapse Dynamics
Symbolic collapse occurs when local compression and field curvature reach a threshold. Two derived quantities govern collapse:
Collapse zones occur when resonance is high and symbolic force exceeds a threshold
:
Appendix J.6. Axiom 6: Universality of Collapse
Collapse is a general property of symbolic fields. Any domain with recursive symbolic structure will exhibit collapse zones:
Appendix J.7. Axiom 7: Emergence of Irreducibles
Irreducible symbolic elements—such as prime numbers, semantic primitives, or perceptual qualia—arise at collapse zones:
Appendix J.8. Axiom 8: Cross-Domain Consistency
The structure of symbolic curvature and collapse generalizes across all symbolic systems. While the projection
is domain-specific, collapse dynamics are universal:
Appendix K Key Terms and Definitions for Symbolic Field Theory (SFT)
Symbolic Field: A mathematical space in which symbolic elements interact with each other based on recursive compression dynamics. Each element in the symbolic domain is projected into this field and affected by structural properties like curvature and resonance.
Symbolic Element: Any object or unit that is part of a symbolic system, such as numbers, words, gestures, or phonemes. Symbolic elements are the basic building blocks in a symbolic field.
Projection Function (): A function that maps each symbolic element x from its native domain to a real-valued space. The projection represents how symbolic elements are encoded or distorted in the symbolic field, capturing their recursive complexity or tension.
Recursive Compression: A process by which symbolic elements are compressed based on their relationships within the symbolic field. It leads to the minimization of structural tension and the emergence of stable symbolic structures.
Symbolic Curvature (): A measure of the deviation between the projection of a symbolic element and its expected position within the field. Curvature reflects the structural tension in the symbolic system and indicates potential collapse zones.
Symbolic Resonance (): The second derivative of the projection function, which measures the rate of change of recursive tension. High values of resonance indicate instability or accelerated distortion, signaling the potential for collapse.
Symbolic Force (): The gradient of symbolic curvature, representing the local pressure exerted on symbolic elements due to recursive tension. Positive values of force indicate compression, which favors collapse.
Collapse Zone: A region within the symbolic field where recursive compression reaches a critical threshold, and symbolic elements converge to stable, irreducible structures. Collapse zones are characterized by high resonance and positive force.
Irreducible Element: A symbolic element that cannot be decomposed or factored into simpler symbolic components within its domain. In mathematics, this includes prime numbers (numbers with no nontrivial divisors). In broader symbolic systems, irreducibles may include semantic primitives, perceptual qualia, or axiomatic truths—entities that emerge without symbolic precursors and serve as generative building blocks for higher-order structure.
Enrichment Rate (): The rate at which irreducible symbolic elements are found within collapse zones. It is defined as the ratio of irreducibles in the collapse zones to the total number of elements in those zones. A high enrichment rate indicates that collapse zones predict the emergence of irreducibles.
Symbolic Emergence: The process by which irreducible symbolic elements spontaneously arise in the symbolic field as a result of recursive compression and collapse dynamics. Emergence occurs at points of minimal curvature and maximum resonance.
Projection Equivalence Principle: The principle stating that for any domain and projection function encoding recursive symbolic tension, there exists a corresponding symbolic curvature field and collapse zone that predicts the location of irreducible symbolic elements.
Symbolic Collapse: The phenomenon where symbolic elements, under the influence of recursive compression and collapse dynamics, converge to stable, irreducible forms. Collapse is triggered when resonance exceeds a threshold and force is positive.
Cross-Domain Applicability: The principle that the dynamics of symbolic collapse and emergence apply consistently across various symbolic domains, such as mathematics, language, perception, music, logic, and physics. The same recursive compression mechanism leads to the emergence of irreducibles in all domains.
Recursive Field: A symbolic field governed by recursive dynamics, where symbolic elements interact and evolve based on compression and tension forces. The recursive nature of the field allows for the emergence of structure and irreducible elements.
Symbolic Compression Symmetry: The symmetry observed in symbolic systems where the process of recursive compression leads to stable configurations that are invariant under reindexing or transformation of symbolic elements.
Appendix L Experimental Implementation
All symbolic collapse experiments were conducted using Python 3. The framework was implemented with standard scientific computing libraries including NumPy, SymPy, Matplotlib, and tqdm. The computational procedure consisted of the following core components:
Symbolic Projection Function: Defines how a number is represented symbolically. In our hybrid test, this was implemented as:
where
denotes the number of distinct prime factors of
x, computed using
sympy.factorint.
-
Collapse Curvature Function: Quantifies the symbolic deviation from identity via:
This curvature function is computed for each integer , forming a scalar field over the natural numbers.
-
Collapse Zone Detection: Collapse zones are identified by scanning for local minima of the curvature field, satisfying:
The resulting set of minima, denoted Z, represents the candidate emergence sites for irreducible structure.
Prime Identification: Each integer in the collapse zone set Z was evaluated for primality using sympy.isprime(x). The total number of primes in Z, denoted , was recorded as the primary dependent variable.
-
Monte Carlo Null Model: To assess whether the observed prime enrichment in Z exceeds what would be expected by chance, a null distribution was generated via Monte Carlo simulation. For each of 1000 trials:
A random sample of size was selected without replacement.
The number of primes in was counted and stored.
The resulting distribution of prime counts under random sampling, , formed the null model for statistical comparison.
-
Statistical Enrichment Analysis: For each projection experiment, we computed:
- -
The
Enrichment Ratio, defined as:
where
is the average number of primes found in the null samples.
- -
The
Z-score, defined as:
where
is the standard deviation of the null model prime counts.
All experiments were executed on a MacBook Pro (Apple M1) using the default scientific Python stack. Each full run—comprising curvature field computation, collapse detection, prime evaluation, and null simulation—completed in approximately 2–4 minutes depending on projection complexity. Full source code is available upon request or in the public project repository.
Appendix M Statistical Outputs and Plots
This section summarizes the key empirical outcomes of symbolic collapse testing across several projection functions. For each projection, we report: the number of collapse zones identified, the number of primes found within those zones, the enrichment ratio relative to null model expectations, and the corresponding Z-score.
Table A2.
Summary of statistical enrichment across symbolic projection fields. Enrichment ratio is computed relative to the average number of primes found in null model samples of equal size.
Table A2.
Summary of statistical enrichment across symbolic projection fields. Enrichment ratio is computed relative to the average number of primes found in null model samples of equal size.
| Projection Function |
# Collapse Zones |
Primes Found |
Enrichment Ratio |
Z-score |
|
263,240 |
69,127 |
3.345 |
414.277 |
|
(Extended to ) |
16,666,665 |
2,880,935 |
3.000 |
2390.115 |
|
166,665 |
39,264 |
3.002 |
261.754 |
| Digit Entropy |
261,988 |
18,960 |
0.922 |
|
|
(Factor Count) |
339,654 |
0 |
0.000 |
|
To test whether symbolic enrichment generalizes at scale, we extended the modular projection to the domain . The resulting curvature field yielded over 16 million collapse zones. Primes were enriched by a factor of 3.0 relative to the null model, with a Z-score exceeding 2390. This result provides overwhelming statistical support for symbolic curvature as a generator of irreducible structure at scale.
Figure A6.
Null model histogram for hybrid projection with actual collapse zone prime count shown as red dashed line.
Figure A6.
Null model histogram for hybrid projection with actual collapse zone prime count shown as red dashed line.
Figure A7.
Null model histogram for projection over .
Figure A7.
Null model histogram for projection over .
Figure A8.
Null model histogram for projection over . Extremely high enrichment confirms symbolic curvature effects at scale.
Figure A8.
Null model histogram for projection over . Extremely high enrichment confirms symbolic curvature effects at scale.
Figure A9.
Prime density in a neighborhood of collapse zones. Central peak at offset 0 confirms spatial alignment between symbolic minima and prime occurrence.
Figure A9.
Prime density in a neighborhood of collapse zones. Central peak at offset 0 confirms spatial alignment between symbolic minima and prime occurrence.
All figures were generated using matplotlib and represent reproducible visualizations based on the raw symbolic curvature output and statistical comparison.
References
- Euclid. Elements. Circa 300 BCE. Book IX, Proposition 20.
- Riemann, B. (1859). Über die Anzahl der Primzahlen unter einer gegebenen Grösse. Monatsberichte der Berliner Akademie.
- Hadamard, J. (1896). Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques. Bulletin de la Société Mathématique de France.
- Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27(3), 379–423.
- Kolmogorov, A. N. (1965). Three approaches to the quantitative definition of information. Problems of Information Transmission, 1(1), 1–7.
- Ulam, S. M. (1964). Spiral of prime numbers. Scientific American, 210(6), 120–122.
- Montgomery, H. L. (1973). The pair correlation of zeros of the zeta function. In Proc. Sympos. Pure Math., Vol. 24, AMS.
- Turing, A. M. (1936). On computable numbers, with an application to the Entscheidungsproblem. Proceedings of the London Mathematical Society, 2(1), 230–265.
- Cowan, N., et al. (2005). The magical number 4 in short-term memory: A reconsideration of mental storage capacity. Behavioral and Brain Sciences, 24(1), 87–114.
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).