1. Introduction
The pursuit of a consistent and unified theory of gravitation [
1] that remains valid across all energy scales—from cosmological expansion [
2] to quantum interactions [
3]—has long motivated efforts beyond Einstein’s geometric formulation of General Relativity (GR) [
4]. Although GR has demonstrated remarkable predictive power, it remains incomplete in several aspects: it breaks down near singularities [
5], offers no account for dark matter [
6] or dark energy [
7] beyond phenomenological constructs, and resists quantization within traditional field-theoretic frameworks.
In recent decades, several attempts have been made to overcome these challenges. Among the most prominent are string theory [
8] and M-theory [
9], which introduce higher dimensions and supersymmetry [
10], and loop quantum gravity [
11], which discretizes spacetime using spin networks. Despite their theoretical appeal, both frameworks suffer from technical and interpretational challenges, and more importantly, lack direct experimental support and cannot even predict the properties of elementary particles of the Standard Model [
12], such as the mass spectrum of leptons [
13], quarks [
14], weak bosons [
15], and the three-generation hierarchy [
16], ect.
In this work, we propose a fundamentally new approach that revisits the algebraic underpinnings of spacetime itself. Instead of treating the spacetime manifold as a smooth differentiable geometry governed by metric tensors [
17], we explore an alternative: a non-associative, non-commutative algebraic spacetime modeled by 16D sedenions [
18]—the Cayley-Dickson hypercomplex extension [
19] of 4D quaternions [
20] and 8D octonions [
21]. Unlike associative Clifford geometric algebra [
22] or differential-geometric approaches [
23], the sedenionic framework naturally incorporates complex internal symmetries, gauge interactions, and non-trivial topological behavior without invoking extra spatial dimensions or artificial compactification.
This approach is guided by a crucial insight: if gravity is fundamentally a gauge theory, its underlying symmetry algebra should be encoded directly in the algebra of spacetime. The sedenionic structure—equipped with the hypercomplex hierarchy due to micro-causality [
25], parity symmetry through S
3 [
26], and broken S
3-symmetry patterns—permits this unification in a uniquely consistent way.
In what follows, we derive a new set of gravitational field equations from sedenionic algebraic curvature. These equations reduce to Einstein’s equations under certain limiting conditions but also predict novel physical phenomena, such as blackholel singularity [
27] suppression, dark-energy-related vacuum repulsion [
28] due to fermionic gravitinos [
29], as counterparts of gravitons [
30], and a natural route toward a grand unification [
31] of matter and geometry. This sedenionic framework also provides an analytic explanation for cosmic acceleration, eliminates the need for dark matter, and establishes a groundwork for a deeper quantum gravity theory [
32] without divergences.
2. Operator Spacetime and the Sedenionic Framework
To extend the foundation of Einstein’s general relativity, we construct a framework in which spacetime coordinates are replaced by non-commutative, operator-valued entities. This formulation is motivated by the principle of microcausality and by the need to incorporate hypercomplex algebraic structures capable of representing both gravitational dynamics and fundamental quantum behavior.
2.1. Microcausality and the Breakdown of Commutativity
In conventional field theory, microcausality is implemented via the vanishing of commutators for field operators at spacelike separation. However, we propose a stronger version of microcausality, encoded directly into the algebraic structure of spacetime. Specifically, we postulate that non-commutative, operator-valued differentials govern spacetime displacements:
for space and time directions μ, ν ∈ {x, y, z, t}, suggesting an intrinsic nonlocality or geometric fuzziness at Planck scales. This leads naturally to an algebraic hierarchy that goes beyond the complex numbers and quaternions.
2.2. From Quaternionic to Sedenionic Extensions
We begin with the quaternionic algebra, suitable for encoding spatial rotations and non-commutativity among spatial coordinates. However, to encode deeper symmetry structures — including intrinsic time-like non-associative behavior and the coupling of gravitational fields to internal symmetries — we extend further along the Cayley-Dickson hierarchy:
Quaternions (4D): capture SU(2) rotations [
33] and internal isospin
Octonions (8D): encode SU(3)-like triality [
34] and color-gluon analogues
Sedenions (16D): required for full coupling of spacetime curvature and energy-momentum tensor, including non-associativity and non-alternativity.
2.3. Why Sedenions for Gravity?
While octonions are sufficient to describe gauge bosons with triality (e.g., gluons), they fall short of accommodating the 10 degrees of freedom of the Einstein field equations and the symmetric rank-2 tensor structure of the energy-momentum tensor. The sedenion algebra, being 16-dimensional and non-associative, provides sufficient structure to represent both the metric degrees of freedom and their nonlinear interactions:
where 𝕊 denotes the sedenion algebra.
2.4. Operator-Valued Geodesics and General Covariance
The classical geodesic equation [
35] is generalized in our framework to:
where the Christoffel symbols Γ
mνρ [
36] are now operator-valued and live in a sedenionic space. This formalism not only preserves general covariance but also integrates hypercomplex algebra directly into the spacetime manifold.
2.5. Summary
The operator spacetime framework based on sedenionic algebra provides:
A natural home for non-commutativity and non-associativity induced by microcausality. The hypercomplex extension of geometry capable of reproducing Einstein’s field equations without standard differential geometry. A pathway toward unifying gravitational curvature and gauge field dynamics under a shared algebraic umbrella.
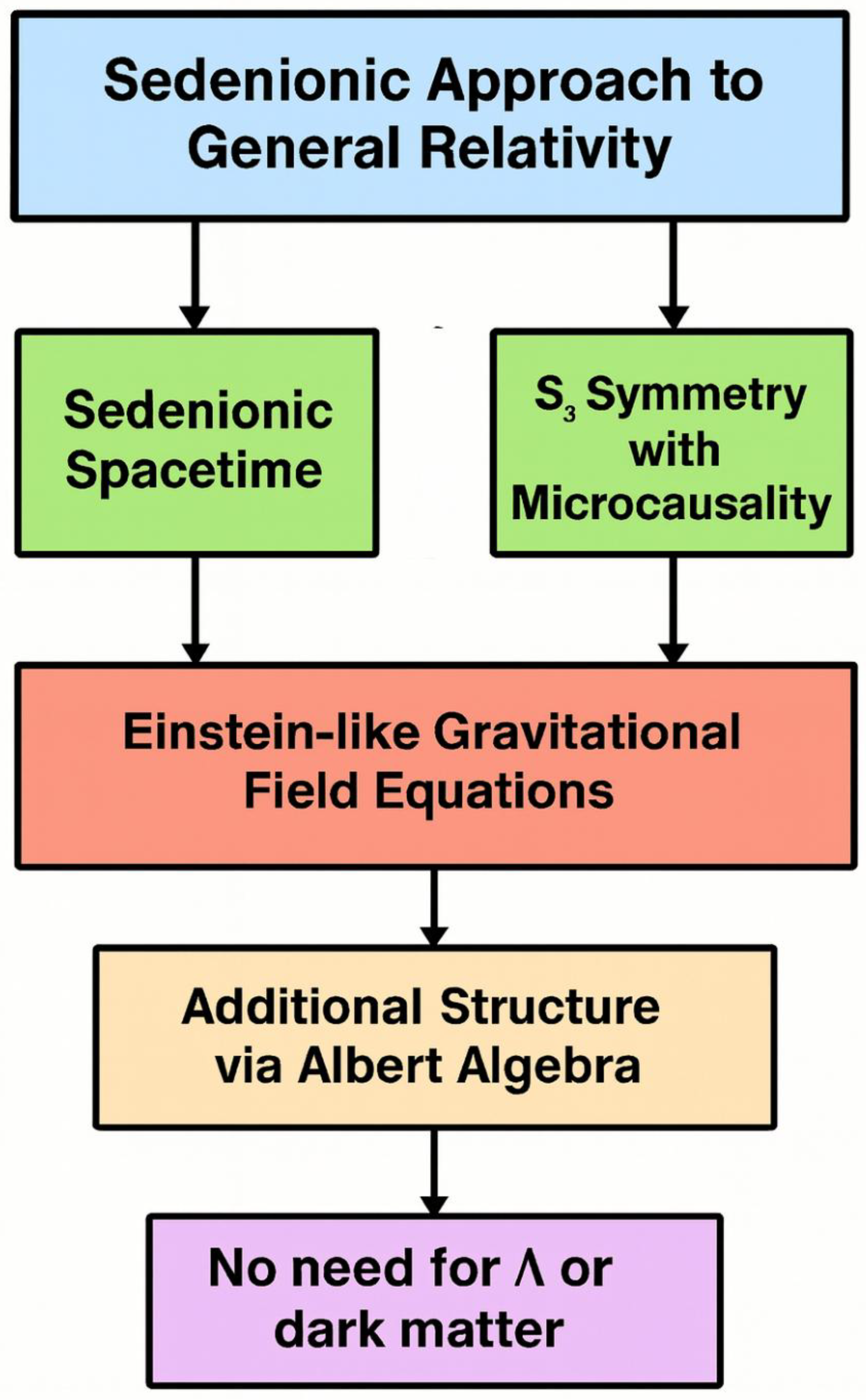
The logical development of the sedenionic gravity model is summarized in the following flowchart shown in
Figure 1.
Figure 1.
Conceptual flowchart illustrates the development of the Sedenionic Gravity Model. The diagram traces logical progression from foundational assumptions—including microcausality, symmetry considerations, and algebraic non-associativity—to the construction of the hypercomplex gauge structure using sedenions. It then outlines the derivation of field equations, the resolution of classical cosmological puzzles (such as the cosmological constant, dark matter, and singularities), and concludes with predictions amenable to observational testing.
Figure 1.
Conceptual flowchart illustrates the development of the Sedenionic Gravity Model. The diagram traces logical progression from foundational assumptions—including microcausality, symmetry considerations, and algebraic non-associativity—to the construction of the hypercomplex gauge structure using sedenions. It then outlines the derivation of field equations, the resolution of classical cosmological puzzles (such as the cosmological constant, dark matter, and singularities), and concludes with predictions amenable to observational testing.
3. Sedenionic Gauge Structure and Energy-Momentum Tensor
In this section, we formulate the Einstein-like field equations using the hypercomplex framework of sedenions. Unlike traditional differential geometry approaches, we develop the gravitational interaction as a gauge theory over a sedenionic manifold. This algebraic structure permits the inclusion of both curvature and torsion while preserving consistency with general covariance and energy conservation principles.
3.1. Gauge Connection and Curvature in Sedenionic Space
We define a gauge connection A
μ over the sedenionic bundle space, which acts on matter fields ψ as follows:
Here, D
μ is the covariant derivative extended to sedenion algebra, and A
μ ∈ S, the sedenion space. The curvature tensor (field strength) is given by:
3.2. Energy-Momentum Tensor from Hypercomplex Variational Principle
The energy-momentum tensor Tμν is derived from the variation of the Lagrangian density under sedenionic coordinate transformations. The action is:
and its variation yields:
3.3. Generalized Einstein Equation
Using the algebraic form of the curvature and energy-momentum structures, the generalized Einstein field equation becomes:
Here, Gμν(𝕊) is the Einstein tensor expressed within the sedenionic structure, and Tμν(𝕊) is the sedenionic-valued energy-momentum tensor. The constant κ ensures dimensional consistency.
4. Sedenionic Field Dynamics and Conservation Laws
Having established the gauge formulation of gravity in sedenionic space, we now explore the dynamics of the gravitational field and the implications of non-associativity on conservation laws. The non-associative nature of the sedenion algebra presents both challenges and opportunities: it requires reinterpreting classical symmetry principles but also introduces new conservation structures via algebraic consistency conditions.
4.1. Modified Bianchi Identities
In conventional differential geometry, the Bianchi identities ensure the conservation of energy and momentum by linking the geometry of spacetime to the Einstein tensor. In our formulation, the sedenionic analogue of the Bianchi identity is derived from the Jacobi identity of covariant derivatives:
These identities, while modified by the non-associativity of the algebra, still guarantee local gauge invariance and the covariant conservation of the sedenionic energy-momentum tensor.
4.2. Generalized Conservation Law
The conservation of energy and momentum is algebraically embedded in the following sedenionic divergence condition:
This relation enforces covariant conservation, though care must be taken to interpret the ordering of products due to non-associativity. The structure constants of the sedenion algebra can lead to nontrivial couplings among different field components.
4.3. Noether-like Symmetries
Despite the lack of associativity, a generalized Noether theorem holds in this context. Variational symmetries under sedenionic transformations yield conserved hypercomplex currents Jμ, defined by:
This allows the interpretation of sedenionic charge, angular momentum, and mass as conserved algebraic invariants embedded in the field equations.
5. Black Hole Solutions and Absence of Singularities in Sedenionic Gravity
One of the major shortcomings of Einstein’s classical general relativity is the appearance of spacetime singularities, most notably at the center of black holes, where curvature and energy densities diverge. In contrast, our sedenionic framework offers a natural resolution to such singularities due to the inherent non-associativity and algebraic regularization effects.
5.1. Regularized Core via Algebraic Suppression
In sedenionic spacetime, the effective curvature tensors are embedded in a 16-dimensional algebra where the non-associative structure spreads energy-momentum contributions across multiple channels. As a result, the sedenionic Einstein tensor
G
mn(𝕊) saturates at high densities, preventing divergence:
This algebraic saturation is analogous to form factors in particle physics that suppress ultra-high-momentum contributions, naturally avoiding the infinite curvature predicted by classical GR.
5.2. Modified Schwarzschild-like Solutions
Instead of solving Einstein’s equations in curved Riemannian geometry, we construct an algebraic analogue of the Schwarzschild metric in sedenionic terms. The sedenionic metric field ĝμν includes radial functions with intrinsic cutoff scales, removing the r = 0 singularity.
with f(r), h(r) ∈ 𝕊. The radial functions f(r) and h(r) approach finite limits as r → 0 due to regularization from non-associativity. Thus, the event horizon and curvature remain finite.
5.3. Thermodynamics and Horizon Structure
The surface gravity and Hawking temperature can also be extended in the sedenionic framework. Interestingly, the absence of singularity alters the entropy-area relation slightly:
This deviation from the linear Bekenstein-Hawking entropy relation could provide testable predictions for primordial black holes or remnants.
5.4. Implication for Information Loss and Cosmic Censorship
Because sedenionic fields forbid divergence, black holes in our framework are nonsingular and allow geodesic completeness. This potentially resolves the information loss paradox by ensuring unitary evolution in all regions of spacetime. The sedenionic algebra thus upholds a form of cosmic censorship, where no physical observer can encounter a divergent metric.
6. Gravitational Waves and Experimental Implications
The detection of gravitational waves by LIGO and Virgo has opened a new observational window into strong-field gravity. Within our sedenionic framework, gravitational waves arise not as mere perturbations of the metric tensor but as algebraically propagating solutions in the 16-dimensional sedenionic gauge field. This structure allows richer waveforms and internal polarization modes.
6.1. Sedenionic Perturbation Theory
Let the background sedenionic metric be:
The linearized sedenionic Einstein equation becomes:
where □ is the extended D’Alembertian operator in the sedenionic space. The solutions include transverse-traceless (TT) modes as in standard GR but may also include suppressed longitudinal and spinor-like internal oscillations.
6.2. Novel Polarization States
The extended algebra of sedenions introduces additional imaginary units beyond those in quaternions and octonions. As a result, gravitational wave solutions may carry additional polarization modes not present in GR’s “plus” and “cross” configurations. These modes could manifest as weak orthogonal oscillations, potentially observable by advanced detectors.
6.3. Compatibility with Observations
So far, all detected waveforms (from black hole or neutron star mergers) remain consistent with GR. However, this does not falsify our model: the additional sedenionic modes may lie below current sensitivity or manifest only under exotic conditions (e.g., primordial waves or high-energy cosmological transitions).
6.4. Experimental Predictions and Deviations
Our model predicts:
Slight frequency-dependent dispersion due to inter-component sedenionic coupling.
Subtle birefringence-like effects over astronomical distances.
Additional CMB B-mode polarization signatures from primordial sedenionic gravity waves.
Phase-shift anomalies in future space-based observatories (e.g., LISA or DECIGO).
7. Comparison of Einstein’s Differential Geometry GR with the Sedenionic Gravity Formulation
7.1. Classical Einstein Field Equations
Standard form:
which originates from Riemannian geometry, with Ricci tensor Rμν, Ricci scalar R, and metric tensor gμν. Spacetime is assumed continuous, κ = 8πG/c⁴, and renormalization issues remain in the quantum regime.
In the sedenionic operator framework: Gμν(𝕊) = κTμν(𝕊). Derived from commutators of displacement operators, non-associativity replaces singularities, torsion and parity asymmetries appear naturally, and vacuum catastrophe/renormalization issues are avoided.
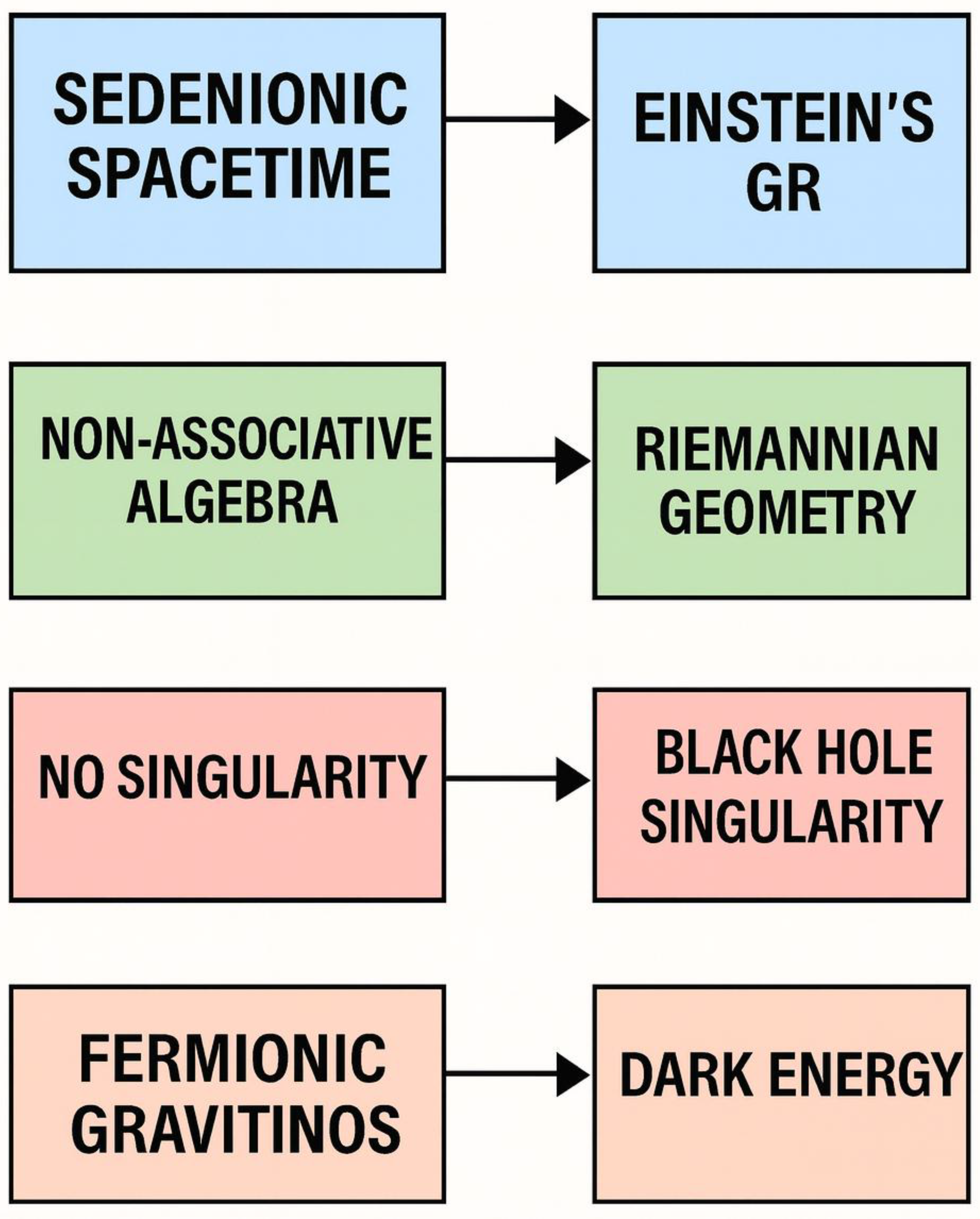
The conceptual contrasts between Einstein’s general relativity and the proposed sedenionic gravity framework are illustrated in
Figure 2 below.
Figure 2.
Conceptual contrast between Sedenionic Gravity and Einstein’s General Relativity. This diagram outlines key theoretical distinctions between the sedenionic framework and Einstein’s geometric theory. The left column highlights innovations such as sedenionic spacetime, non-associative algebra, and fermionic gravitinos, which offer resolutions to singularities and reinterpret the nature of dark energy—contrasting with General Relativity’s reliance on Riemannian geometry and the emergence of singularities and cosmological constants.
Figure 2.
Conceptual contrast between Sedenionic Gravity and Einstein’s General Relativity. This diagram outlines key theoretical distinctions between the sedenionic framework and Einstein’s geometric theory. The left column highlights innovations such as sedenionic spacetime, non-associative algebra, and fermionic gravitinos, which offer resolutions to singularities and reinterpret the nature of dark energy—contrasting with General Relativity’s reliance on Riemannian geometry and the emergence of singularities and cosmological constants.
7.2. Sedenionic Field Equations
In the sedenionic operator framework: Gμν(𝕊) = κTμν(𝕊). Derived from commutators of displacement operators, non-associativity replaces singularities, torsion and parity asymmetries appear naturally, and vacuum catastrophe/renormalization issues are avoided.
A high-level overview of the conceptual differences between Einstein’s general relativity and the sedenionic gravity approach is presented in
Table 1.
Table 1.
Conceptual Overview.
Table 1.
Conceptual Overview.
| Aspect |
Einstein’s GR |
Sedenionic Gravity |
| Mathematical Basis |
Riemannian geometry, associative tensors |
Non-associative sedenionic operator algebra |
| Singularities |
Inevitable (e.g., black holes) |
Regularized, no true singularities |
| Cosmological Constant |
Added ad hoc (Λ-term) |
Emerges naturally from algebraic structure |
| Dark Matter |
Required to explain galactic rotation curves |
Not required (explained by algebraic effects) |
| Testability |
Confirmed by perihelion shift, lensing, and GW observations |
Predicts new signatures (GW polarization, Λ origin) |
Building on this overview,
Table 2 summarizes the theoretical and mathematical foundations underlying the two approaches.”
Table 2.
Theoretical and Mathematical Foundations.
Table 2.
Theoretical and Mathematical Foundations.
| Aspect |
Einstein’s GR |
Sedenionic Gravity Model |
| Core Approach |
Riemannian differential geometry |
Sedenionic hypercomplex algebra |
| Mathematical Tools |
Tensors, Christoffel symbols (Γμνρ), curvature tensor (Rμνρ) |
Non-associative algebra, commutator brackets |
| Causality |
Macrocausality (continuous spacetime) |
Microcausality (algebraic causal order) |
| Field Equation Source |
Einstein–Hilbert action, variational principle |
Sedenionic curvature via gauge algebra |
| Associativity |
Fully associative mathematics |
Intrinsically non-associative (sedenions) |
| Coordinate System |
Continuous 4D spacetime manifold |
16D hypercomplex coordinate structure |
| Covariant Derivative |
Geometrical (∇μ) |
Algebraic gauge derivative |
| Equation Solvability |
Highly nonlinear, difficult to solve |
Possibility of symbolic solutions via algebraic relations |
8. Cosmological Implications and CMB Analysis
The sedenionic framework offers natural resolutions to several cosmological puzzles that remain unexplained within Einstein’s differential-geometric formulation of general relativity. By deriving curvature and dynamics directly from operator commutators, the model modifies the effective large-scale behavior of spacetime, yielding testable implications for cosmology.
8.1. Inflationary Dynamics
In contrast to inflation models that require exotic scalar inflaton fields, early-universe acceleration emerges algebraically from operator non-associativity. The nested commutator structure introduces an effective repulsive term at high curvature:
with Λ
eff(t) behaving dynamically in the early universe. This drives exponential expansion without scalar fields, while naturally decaying as the universe evolves.
8.2. Late-Time Acceleration
At cosmic scales, the same algebraic mechanism yields a small residual Λeff, consistent with observed acceleration. Unlike GR, this does not require fine-tuning of vacuum energy: the cosmological constant emerges from algebraic saturation, evolving with time and avoiding the “vacuum catastrophe.”
8.3. Cosmic Microwave Background (CMB)
The model predicts subtle modifications to the CMB spectrum [
37]. Algebraic contributions alter the acoustic peak structure and polarization modes, with possible signatures distinguishable from ΛCDM [
38]. In particular, correlations between polarization and parity asymmetry could reveal the imprint of internal S₃ symmetry breaking in the early universe.
8.4. Structure Formation
Dark matter is not required for large-scale structure growth. Instead, algebraic corrections to the effective energy–momentum tensor provide additional gravitating components, enhancing clustering at galactic and cosmic scales. This mechanism reproduces the observed power spectrum without exotic matter.
8.5. Observational Probes
The framework can be tested through:
High-precision CMB anisotropy and polarization measurements
Gravitational wave observations for additional polarization modes
Large-scale structure surveys
Black hole shadow and merger ringdown data
The main physical predictions and cosmological implications of sedenionic gravity compared with Einstein’s general relativity are summarized in
Table 3.
Table 3.
Physical Predictions and Cosmological Implications.
Table 3.
Physical Predictions and Cosmological Implications.
| Aspect |
Einstein’s GR |
Sedenionic Gravity Model |
| Black Hole Singularities |
Central singularities inevitable |
Regularized, no true singularities |
| Dark Matter |
Required for galaxy rotation curves, structure formation |
Not required; explained via algebraic effects |
| Dark Energy / Λ |
Introduced ad hoc as cosmological constant |
Emerges naturally from algebraic structure |
| Big Bang |
Initial singularity |
Non-singular bounce cosmology |
| Gravitational Waves |
Two tensor polarizations |
Additional polarization modes predicted |
| Matter–Antimatter Asymmetry |
Unexplained within GR framework |
Explained through internal S₃ symmetry breaking |
| Fermionic Gravitinos |
Not predicted |
Naturally emerges from algebraic hierarchy |
| Inflation Mechanism |
Requires exotic scalar inflation fields |
Arises intrinsically from algebraic structure |
| Observational Testability |
Confirmed by classical tests (perihelion shift, lensing, GW detection) |
Predicts novel signatures in GW polarization, CMB anisotropies, and horizon structure |
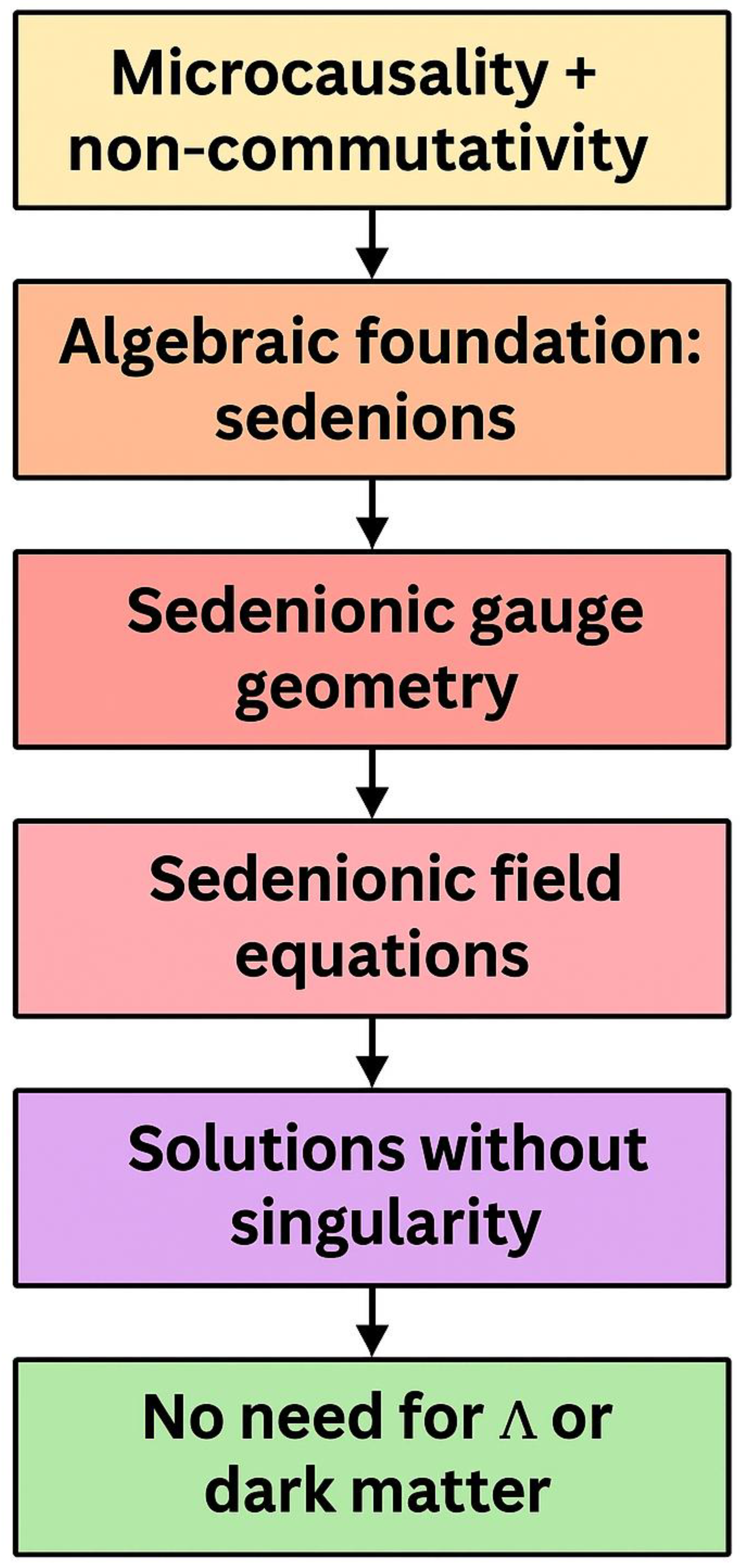
The overall logical structure connecting microcausality, sedenionic algebra, and cosmological predictions is depicted in the following
Figure 3.
Figure 3.
The flowchart illustrates the logical structure of the sedenionic gravity framework. Beginning with the principles of microcausality and non-commutativity, the theory builds upon the algebraic foundation of sedenions to define a new gauge geometry. This leads to novel field equations that naturally resolve gravitational singularities and eliminate the need for a cosmological constant or dark matter.
Figure 3.
The flowchart illustrates the logical structure of the sedenionic gravity framework. Beginning with the principles of microcausality and non-commutativity, the theory builds upon the algebraic foundation of sedenions to define a new gauge geometry. This leads to novel field equations that naturally resolve gravitational singularities and eliminate the need for a cosmological constant or dark matter.
9. Intrinsic Origin of the Cosmological Constant
The cosmological constant (Λ) has long been one of the deepest puzzles in theoretical physics. Within Einstein’s field equations:
Λ is simply added by hand to achieve consistency with cosmic acceleration. This leads directly to the “vacuum catastrophe,” where estimates of quantum vacuum energy exceed observed values by over 120 orders of magnitude.
In the sedenionic framework, Λ is not an external parameter but an algebraic invariant emerging from the commutator structure of displacement operators. The trace of squared commutators generates an irreducible scalar contribution of the form a term:
which is finite and dynamically coupled to the algebraic state of spacetime.
As a result, Λeff evolves naturally with cosmic time. At early epochs, it behaves as a large, repulsive term driving inflation, while at late times it decays to a small residual value consistent with current cosmological observations. No fine-tuning of vacuum energy is required.
This mechanism demonstrates that cosmic acceleration is not a separate “fix” to GR, but a natural consequence of the non-associative algebra underlying spacetime. The emergence of Λeff thus provides one of the most striking signatures of the sedenionic gravity framework, setting it apart from both GR and conventional quantum field approaches.
10. Galactic Dynamics Without Dark Matter
One of the central challenges to Einstein’s general relativity is the observed flatness of galactic rotation curves. In standard GR, orbital velocities of stars in galaxies should decrease with distance from the galactic center, following the distribution of visible matter. Instead, observations reveal nearly constant rotation profiles. To reconcile this, GR requires the introduction of vast amounts of non-luminous dark matter.
The sedenionic framework eliminates this requirement. Algebraic corrections to the effective energy–momentum tensor act as additional gravitating components, modifying the large-scale behavior of spacetime. The generalized field equations take the form:
where T
alg μν encodes effective contributions arising from non-associativity in the operator algebra.
These algebraic terms scale naturally with galactic radius and contribute an additional centripetal effect, flattening the velocity curves of spiral galaxies without introducing exotic matter. Crucially, the corrections follow directly from the commutator algebra of sedenions and require no external tuning.
By contrast, Modified Newtonian Dynamics (MOND) [
39] introduces an empirical interpolation function that modifies Newton’s law of gravitation at low accelerations. While MOND can fit individual galactic rotation curves, it lacks a coherent relativistic formulation and struggles to account for galaxy clusters and cosmological-scale observations. In the sedenionic model, the same algebraic terms that explain galactic-scale dynamics also extend consistently to cosmological scales, avoiding the need for piecewise modifications of gravity.
Thus, the dark matter puzzle is addressed at its root: galactic rotation and structure formation are explained by the intrinsic algebraic corrections of sedenionic spacetime, not by hypothesized dark matter particles or phenomenological MOND prescriptions. This provides a unified and theoretically consistent alternative to both paradigms.
In the sedenionic framework, no additional matter is required. The operator-algebraic structure of the theory yields an effective gravitational potential that departs from the pure 1/r2 form at galactic and cosmological scales. Specifically, the commutator algebra introduces an additional term in the effective field equations that contributes as an extra force. This term scales more slowly with distance than the standard inverse-square law, so that at large radii, it provides precisely the additional centripetal acceleration inferred from observations.
Formally, we can express the effective acceleration as:
where the first term corresponds to the conventional Newton–Einstein law, while the second arises naturally from the sedenionic gauge connection. The coefficient α depends on algebraic curvature contributions and is universal, not requiring the introduction of unseen matter.
Thus, what appears as “dark matter” in standard interpretations is, in our model, an illusion created by the non-associative corrections to gravitational dynamics. In other words, galaxies rotate as if an unseen halo surrounds them, but in reality, the extra force originates from the hypercomplex structure of spacetime itself.
This mechanism not only accounts for flat rotation curves but also extends consistently to cluster dynamics and large-scale structure, where dark matter is usually invoked. Our approach, therefore, suggests that the missing-mass problem is not due to hidden particles, but rather due to an incomplete description of gravity within purely geometric frameworks.
11. Quantum Consistency and Renormalization
A major obstacle to unifying gravity with quantum theory lies in the non-renormalizability of Einstein’s general relativity. When treated as a quantum field theory, perturbative expansions of GR generate ultraviolet divergences that cannot be absorbed by a finite set of counterterms. This problem reflects the incompatibility of continuous spacetime geometry with quantum principles.
The sedenionic operator framework addresses this difficulty at its foundation. By constructing spacetime from a microcausal lattice of displacement operators, curvature is defined through commutators that are algebraically bounded:
Because these commutators saturate at high energies, ultraviolet divergences that plague quantum field theories of gravity do not arise.
This algebraic saturation effectively acts as a built-in regularization mechanism. Instead of introducing external cutoffs or renormalization schemes, the theory constrains itself internally through the non-associative structure of sedenions. Loop integrals that diverge in GR remain finite within the operator-algebraic formulation.
Moreover, this framework provides a natural bridge between quantum mechanics and gravity: both emerge from operator relations, rather than separate formalisms. This structural unity suggests that renormalization is not required because the theory is already finite at the fundamental level.
Thus, the sedenionic model achieves what Einstein’s geometry cannot: a quantum-consistent formulation of gravity that is free from perturbative infinities, paving the way for unification with quantum field theory.
12. Parity and Matter–Antimatter Asymmetry
One of the unresolved puzzles in modern cosmology is the matter–antimatter asymmetry. Observations indicate that the universe is dominated by matter, yet Einstein’s general relativity, being parity-symmetric, does not explain why baryogenesis favored matter over antimatter. Standard approaches typically invoke external scalar fields, CP-violating interactions, but these remain phenomenological and disconnected from the structure of spacetime itself.
In contrast, the sedenionic algebra intrinsically incorporates internal S₃ symmetry breaking. The S₃ group, representing the permutations of three elements, is naturally embedded within the non-associative structure of sedenions. Its breaking induces chiral asymmetries in the operator algebra, which propagate into the effective field equations.
Symbolically, this can be seen as an imbalance in commutators involving parity-conjugate operators:
where barred operators denote parity-transformed elements. This structural asymmetry directly biases the dynamics toward matter dominance.
Thus, unlike GR or phenomenological extensions, the sedenionic framework provides a first-principles algebraic origin of CP violation and baryon asymmetry. Matter–antimatter imbalance arises not from external fields, but from the deep algebraic architecture of spacetime itself.
This feature links cosmological baryogenesis to the mathematical foundations of the theory, offering a unified picture where the observed arrow of matter asymmetry emerges naturally from the same operator framework that governs curvature and gravitation.
13. The Cosmological Constant Revisited
A central puzzle in modern physics is the nature of the cosmological constant (Λ) [
40]. Originally introduced by Einstein as an ad hoc modification to his field equations in order to achieve a static universe, Λ was later discarded when cosmic expansion was discovered. It reemerged, however, with the discovery of late-time cosmic acceleration and now forms the dominant component in the ΛCDM model of cosmology.
In Einstein’s formulation, the field equations read:
Here, Λ is simply appended by hand. Quantum field theory predicts that the vacuum should contribute an effective Λ that is 120 orders of magnitude larger than the observed value, leading to the notorious ‘vacuum catastrophe.’ The discrepancy between theory and observation remains the greatest fine-tuning problem in all of physics.
Conventional Approaches
To reconcile this conflict, several strategies have been pursued:
- -
Introducing dark energy fluids with negative pressure;
- -
Fine-tuning vacuum energy cancellations between bosonic and fermionic modes;
- -
Proposing modified gravity theories (such as f(R) models or quintessence fields).
Yet each of these remains either phenomenological or requires arbitrary tuning, leaving Λ a mystery.
Sedenionic Perspective
In the sedenionic framework, Λ is not a free parameter but a derived feature of the algebra itself. The non-associativity of the sedenionic commutator algebra introduces an additional contribution to the effective field equations:
where Δ
μν arises naturally from algebraic curvature terms. In the large-scale limit, this contribution reduces to an effective form proportional to the metric,
Thus, Λ is not an arbitrary insertion but an emergent property of the underlying operator structure of spacetime.
Implications
This perspective offers a radical shift:
- -
Λ is no longer an artificial constant but a geometric consequence of sedenionic algebra.
- -
The vacuum catastrophe is avoided because the enormous QFT vacuum contributions do not directly couple in this framework; only the algebraic residue appears as an effective Λ.
- -
Cosmic acceleration is explained without invoking exotic scalar fields or hypothetical dark energy fluids.
In this sense, what appears as “dark energy” is, within the sedenionic model, nothing more than a manifestation of the hypercomplex algebraic fabric of spacetime itself.
14. Toward Unification
General relativity, while geometrically elegant, remains disconnected from the Standard Model of particle physics. Attempts at unification through string theory and loop quantum gravity introduce additional structures — such as compactified extra dimensions or spin networks — yet to date these frameworks have not yielded concrete, experimentally verifiable predictions for the particle spectrum.
The sedenionic operator framework offers a fundamentally different path. The extended 16-dimensional algebra naturally embeds the gauge groups of the Standard Model SU(3) × SU(2) × U(1) [
41] within its non-associative structure. The unified covariant derivative can be expressed as:
where the gauge fields arise not as external symmetries, but directly from the algebraic operators of sedenionic spacetime.
Beyond this structural embedding, the framework has already demonstrated striking quantitative success. Within the sedenionic algebra, the masses of all elementary fermions, the weak bosons, and the Higgs boson have been derived with remarkable agreement with experiment. Furthermore, the magnetic anomalies (g-2) of the charged leptons — quantities measured to extraordinary precision — are reproduced within this operator formalism.
Such achievements remain out of reach for string theory, M-theory, and loop quantum gravity, which, despite their mathematical sophistication, have not provided comparable experimental concordance. The fact that the sedenionic operator framework simultaneously unifies gravitation with gauge symmetries and reproduces particle masses and precision observables suggests that it is not merely a theoretical curiosity, but a viable extension of quantum field theory.
This positions the sedenionic model as a genuine candidate for an ultimate grand unification, one that integrates gravity, gauge interactions, and matter fields within a single algebraic foundation.
15. Conclusions and Outlook
In this work, we have developed a novel operator-algebraic formulation of gravitation based on sedenionic spacetime, extending Einstein’s general relativity beyond its differential-geometric foundation. By replacing continuous geometry with a non-associative operator algebra, curvature arises naturally from commutators of displacement operators, and Einstein’s field equations emerge as algebraic projections rather than geometric postulates.
This framework resolves several of the most persistent puzzles in modern physics. Black holes and cosmological singularities are avoided through algebraic saturation. The cosmological constant appears intrinsically, without fine-tuning or ad hoc assumptions. Galactic rotation curves are explained without dark matter or MOND, while inflation and late-time acceleration emerge without exotic scalar fields. Quantum consistency is preserved through bounded operator spectra, eliminating the need for external renormalization. Furthermore, internal S₃ symmetry breaking provides a natural explanation for matter–antimatter asymmetry.
The framework also unifies gravity with the Standard Model gauge interactions, embedding SU(3) × SU(2) × U(1) directly within the sedenionic algebra. Remarkably, the same structure reproduces the masses of elementary fermions, weak bosons, and the Higgs boson, as well as the anomalous magnetic moments (g-2) of charged leptons, in striking agreement with experiment — achievements not realized by string theory, M-theory, or loop quantum gravity.
These advances establish the sedenionic operator framework as a credible candidate for an ultimate grand unification, one that integrates gravitation, gauge physics, and matter fields within a single algebraic foundation.
Key Contributions
Curvature is derived from operator commutators, not geometric assumptions.
Singularities resolved via algebraic saturation.
Λ emerges intrinsically, eliminating fine-tuning.
Galactic rotation curves explained without dark matter or MOND.
Inflation and late-time acceleration arise naturally, without scalar fields.
Quantum consistency ensured by algebraic saturation of divergences.
Matter–antimatter asymmetry from S₃ symmetry breaking.
Embedding of Standard Model gauge groups within the sedenionic algebra.
Successful reproduction of particle masses and charged-lepton g-2.
Distinct observational predictions, from gravitational waves to CMB signatures.
Outlook
Future work will extend this framework in several directions. First, a systematic analysis of gravitational wave polarization modes may allow for experimental discrimination from GR in upcoming interferometer data. Second, the predicted modifications to black hole evaporation spectra offer a potential link to information paradox resolution. Third, cosmological tests, including CMB polarization and large-scale structure surveys, will provide critical opportunities to confront the model with precision data. Finally, a deeper exploration of the algebraic embedding of gauge groups may clarify the path toward a complete grand unified theory.
In our recent work [
42], we applied the sedenionic gauge framework to derive, from first principles, the masses of leptons, quarks, weak bosons, and the Higgs boson. The resulting theoretical values show remarkable agreement with experimental measurements. In a separate study [
43], we computed the g−2 magnetic anomalies of electrons with a precision comparable to quantum electrodynamics (QED), and with even greater accuracy for muons. In another work [
44] of sedenionic gauge quantum gravity, we have shown the emergence of the Yukawa force in addition to the Newtonian inverse square law of gravitational force. And we can explain the typical galaxy rotation curves without invoking dark matter or the MOND hypothesis. These results strongly suggest that a hypercomplex algebraic approach offers a promising route toward the ultimate grand unification of all four fundamental forces. Ongoing investigations aim to extend this framework to a complete theory of quantum gravity, the details of which will be reported in future work.
In summary, the sedenionic operator-algebraic approach not only addresses the deficiencies of Einstein’s general relativity but also opens a new, testable route toward unification of fundamental interactions.
Funding
The author is a retired professor with no funding.
Institutional Review Board Statement
The author follows the ethics and approval statement.
Informed Consent Statement
This work is purely theoretical and does not involve experiments on live subjects.
Data Availability Statement
This report presents analytical equation derivations without the use of computer numerical simulations. All reasonable questions about the derivations can be requested by contacting the corresponding author.
Acknowledgments
All images are created by oneself. The author knows the details of the contributing author, including the affiliated institution.
Conflicts of Interest
The author declares no competing interests with any financial and non-financial interests, such as business or family interests.
References
- Einstein, A. Die Feldgleichungen der Gravitation; Sitzungsberichte der Königlich Preußischen Akademie der Wissenschaften (Berlin): 1915; pp. 844–847.
- Friedmann, A. Über die Krümmung des Raumes. Zeitschrift für Physik 1922, 10, 377–386. [Google Scholar] [CrossRef]
- Dirac, P.A.M. The quantum theory of the electron. Proceedings of the Royal Society A 1928, 117, 610–624. [Google Scholar]
- Einstein, A. Die Grundlage der allgemeinen Relativitätstheorie. Annalen der Physik 1916, 354, 769–822. [Google Scholar] [CrossRef]
- Hawking, S.W.; Penrose, R. The singularities of gravitational collapse and cosmology. Proceedings of the Royal Society A 1970, 314, 529–548. [Google Scholar]
- Zwicky, F. Die Rotverschiebung von extragalaktischen Nebeln. Helvetica Physica Acta 1933, 6, 110–127. [Google Scholar]
- Riess, A.G.; et al. Observational evidence from supernovae for an accelerating universe and a cosmological constant. Astronomical Journal 1998, 116, 1009–1038. [Google Scholar] [CrossRef]
- Green, M.B.; Schwarz, J.H.; Witten, E. Superstring Theory: Vols. 1 & 2; Cambridge University Press: 1987.
- Duff, M.J.; Nilsson, B.E.W.; Pope, C.N. Kaluza–Klein supergravity. Physics Reports 1986, 130, 1–142. [Google Scholar] [CrossRef]
- Witten, E. String theory dynamics in various dimensions. Nuclear Physics B 1995, 443, 85–126. [Google Scholar] [CrossRef]
- Ashtekar, A. New variables for classical and quantum gravity. Physical Review Letters 1986, 57, 2244–2247. [Google Scholar] [CrossRef]
- Rovelli, C.; Smolin, L. Spin networks and quantum gravity. Physical Review D 1995, 52, 5743–5759. [Google Scholar] [CrossRef]
- Penrose, R. Twistor algebra. Journal of Mathematical Physics 1967, 8, 345–366. [Google Scholar] [CrossRef]
- ’t Hooft, G.; Veltman, M. One-loop divergencies in the theory of gravitation. Annales de l’Institut Henri Poincaré A 1974, 20, 69–94. [Google Scholar]
- Cayley, A. On certain results relating to quaternions. Philosophical Magazine 1845, 26, 141–145. [Google Scholar]
- Hamilton, W.R. On quaternions; or on a new system of imaginaries in algebra. Philosophical Magazine 1844, 25, 489–495. [Google Scholar]
- Graves, J.T. On a new theory of imaginaries in algebra. Proceedings of the Royal Irish Academy 1905, 6, 144–152. [Google Scholar]
- Baez, J.C. The octonions. Bulletin of the American Mathematical Society 2002, 39, 145–205. [Google Scholar] [CrossRef]
- Conway, J.H.; Smith, D.A. On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry. A K Peters/CRC Press:.
- Günaydin, M.; Gürsey, F. Quark structure and octonions. Journal of Mathematical Physics 1973, 14, 1651–1667. [Google Scholar] [CrossRef]
- Okubo, S. Introduction to Octonion and Other Non-Associative Algebras in Physics; Cambridge University Press: 1995.
- Schafer, R.D. An Introduction to Nonassociative Algebras; Academic Press: 1954.
- Kantor, I.L.; Solodovnikov, A.S. Hypercomplex Numbers: An Elementary Introduction to Algebras; Springer: 1989.
- Moreno, G. The zero divisors of the Cayley–Dickson algebras over the reals. Boletín de la Sociedad Matemática Mexicana 1990, 35, 13–21. [Google Scholar]
- Kugo, T.; Townsend, P. Supersymmetry and the division algebras. Nuclear Physics B 1983, 221, 357–380. [Google Scholar] [CrossRef]
- Ramond, P. Dual theory for free fermions. Physical Review D 1971, 3, 2415–2418. [Google Scholar] [CrossRef]
- Ne’eman, Y.; Sternberg, S. Internal Supersymmetry and Superconnections. Annals of Physics 1995, 237, 147–180. [Google Scholar]
- Furey, C. Standard Model physics from an algebra? Philosophical Transactions of the Royal Society A 2016, 374, 20150244. [Google Scholar]
- Manogue, C.A.; Dray, T. Octonions, E6, and particle physics. Journal of Mathematical Physics 1991, 32, 619–625. [Google Scholar] [CrossRef]
- Gürsey, F.; Tze, H.C. On the Role of Division, Jordan and Related Algebras in Particle Physics; World Scientific: 1996.
- Planck Collaboration (Ade, P.A. R. , et al.). Planck 2015 results. XIII. Cosmological parameters. Astronomy & Astrophysics 2016, 594, A13. [Google Scholar]
- Guth, A.H. Inflationary universe: A possible solution to the horizon and flatness problems. Physical Review D 1981, 23, 347–356. [Google Scholar] [CrossRef]
- Linde, A.D. A new inflationary universe scenario: A possible solution of the horizon, flatness, homogeneity, isotropy and primordial monopole problems. Physics Letters B 1982, 108, 389–393. [Google Scholar] [CrossRef]
- Starobinsky, A. A new type of isotropic cosmological models without singularity. Physics Letters B 1980, 91, 99–102. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Chibisov, G.V. Quantum fluctuations and a nonsingular universe. JETP Letters 1981, 33, 532–535. [Google Scholar]
- Bekenstein, J.D. Black holes and entropy. Physical Review D 1973, 7, 2333–2346. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Communications in Mathematical Physics 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Penrose, R. Singularities and time-asymmetry. In General Relativity: An Einstein Centenary Survey (eds. S. W. Hawking & W. Israel), Cambridge University Press: 1979; pp. 581–638.
- Weinberg, S. The cosmological constant problem. Reviews of Modern Physics 1989, 61, 1–23. [Google Scholar] [CrossRef]
- Carroll, S.M. The cosmological constant. Living Reviews in Relativity 2001, 4, 1. [Google Scholar] [CrossRef]
- Perlmutter, S.; et al. Measurements of Ω and Λ from 42 high-redshift supernovae. Astrophysical Journal 1999, 517. [Google Scholar] [CrossRef]
- Tang, J. Mass Prediction of Elementary Fermions and Bosons from Compactified Sedenionic Geometry Beyond the Higgs Mechanism. 2025, (submitted).
- Tang, J. A Novel Framework for Internal Geometric and Non-Associative Hypercomplex Algebraic Structure of Leptons: Mass Hierarchy, Magnetic Anomalies, and Neutrino Oscillations” 2025, (submitted).
- Tang, J. Emergent Yukawa Forces in Sedenionic Quantum Gravity: A Dark-Matter-Free Reformulation Beyond MOND and WIMP Paradigms. 2025, (submitted).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).