Submitted:
10 November 2025
Posted:
12 November 2025
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Case Study: Eindhoven Water Resource Recovery Facility
2.1.1. Eindhoven WRRF: Layout and Model Structure
2.1.2. Calibration Dataset and Parameter Specification
2.2. Novel Calibration Methodology: ES-NEAT
2.2.1. NEAT: Neuro-Evolution of Augmenting Topologies
2.2.2. ES: Expert Systems
2.2.3. Transfer Learning for Recalibration
2.3. Benchmark Comparison Cases Against the Proposed Method
2.3.1. Baseline Manual Calibration
2.3.2. Particle Swarm Optimization (PSO) Benchmark
2.3.3. Objective Function and Performance Metrics
- KGE improvement threshold: The algorithm terminated when the final fitness score (i.e., average KGE) reached or exceeded 0.75, indicating satisfactory model performance.
- Maximum iterations: A maximum iteration limit of 100 was imposed to prevent excessive computational time, with the algorithm terminating after reaching this threshold regardless of KGE performance.
- Final number of iterations: The total number of optimization iterations required to reach convergence (either by satisfying the KGE threshold or reaching maximum iterations).
- Final accuracy: The best fitness score (average KGE across all effluent parameters) achieved at termination.
2.4. Experimental Design Framework for Model Recalibration
2.4.1. Main Calibration Scenarios
2.4.2. Recalibration Frequency Analysis
2.4.3. Statistical Validation
2.5. Implementation Computational Setup
3. Results and Discussion
3.1. Performance Comparison of Calibration Methods
3.2. Transfer Learning Effectiveness
3.3. Parameter Stability and Recalibration Needs
3.4. Impact of Recalibration Frequency
3.5. Model Performance Across Variables
4. General Discussion
4.1. Advancing Operational Digital Twins Through Knowledge Preservation
4.2. Limitations, Structural Boundaries, and Diagnostic Insights
5. Conclusions
- Automated calibration achieved robust performance improvements through knowledge preservation. Across six months, 33 parameters, and two model structures, ES-NEAT delivered 72.1% (TIS) and 49.0% (CM) KGE improvements over manual calibration. These gains occurred despite the manual baseline already operating near the structural performance ceiling imposed by known model limitations in solids stratification and nitrate dynamics, establishing a stringent validation benchmark where enhancement potential is inherently constrained.
- Transfer learning transformed recalibration from episodic events into cumulative learning processes. Sequential recalibrations achieved 50-70% computational time reductions: September scenarios completed in 3-4 hours versus 10-12 hours when starting from scratch, while maintaining accuracy. Unlike conventional approaches that discard accumulated understanding, ES-NEAT’s evolved neural network topologies encode parameter interaction patterns, enabling subsequent optimizations to refine rather than rediscover optimal regions.
- Performance degradation analysis revealed 2-month intervals as optimal for accuracy-efficiency tradeoffs under Eindhoven conditions. Variable-specific decay patterns with 5-6 week half-lives enable adaptive recalibration strategies: monitoring validation metrics or detecting influent regime shifts can trigger updates based on actual performance deterioration rather than fixed schedules, supporting practical digital twin implementation through automated, knowledge-preserving workflows.
Repository
Declaration of Competing Interest
Acknowledgments
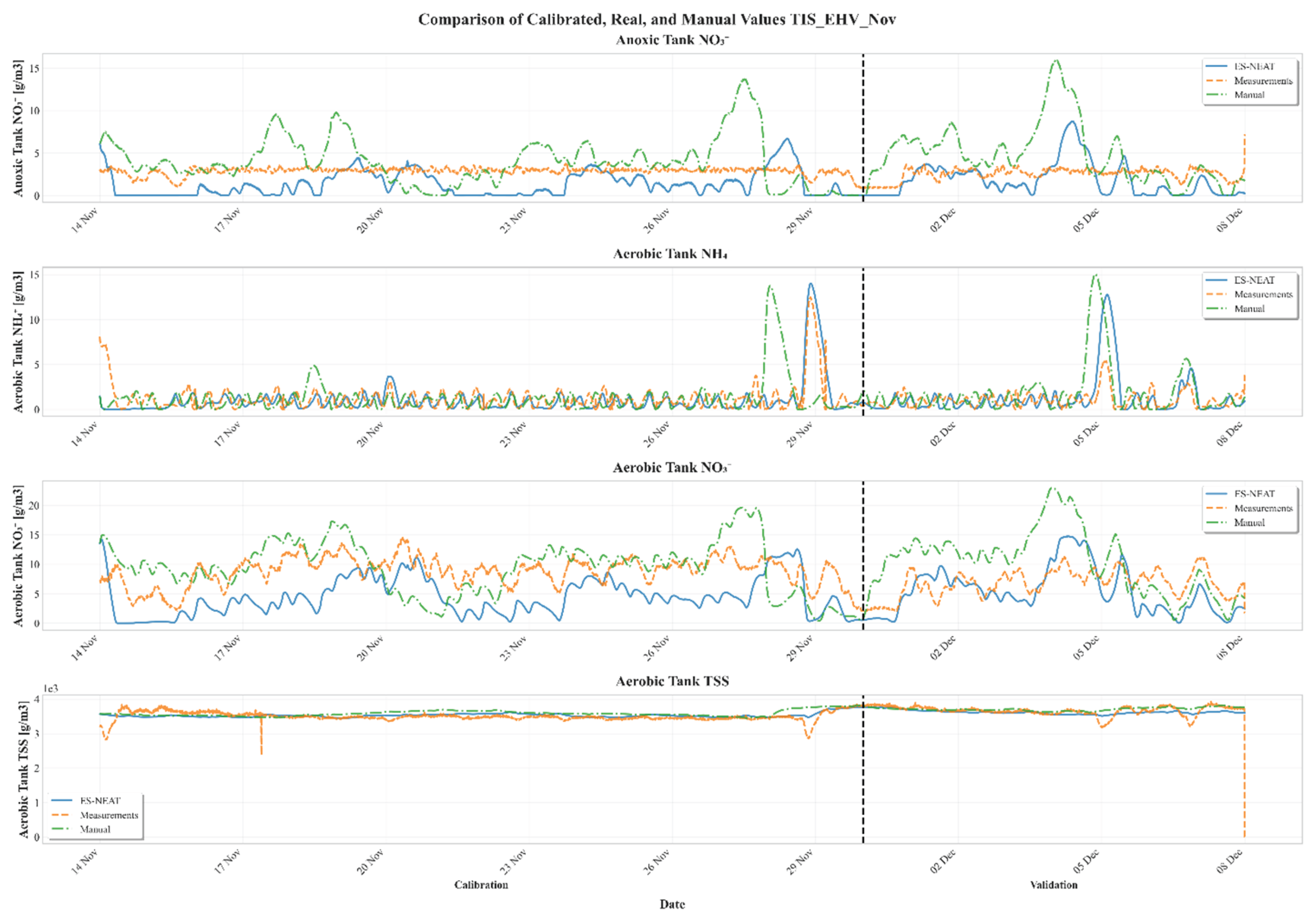
Appendix A. Time-Series Comparisons Across Calibration Periods and Models
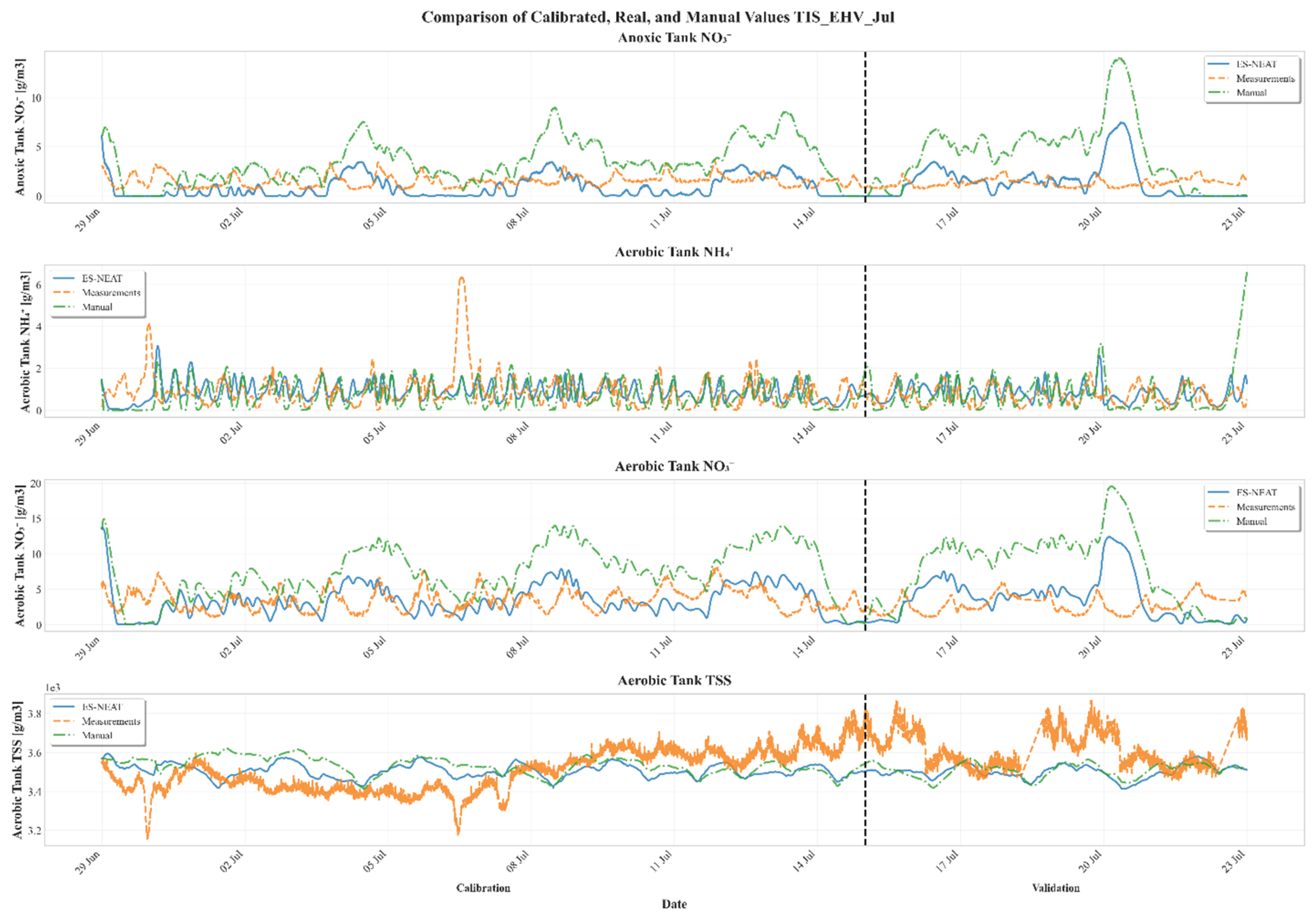
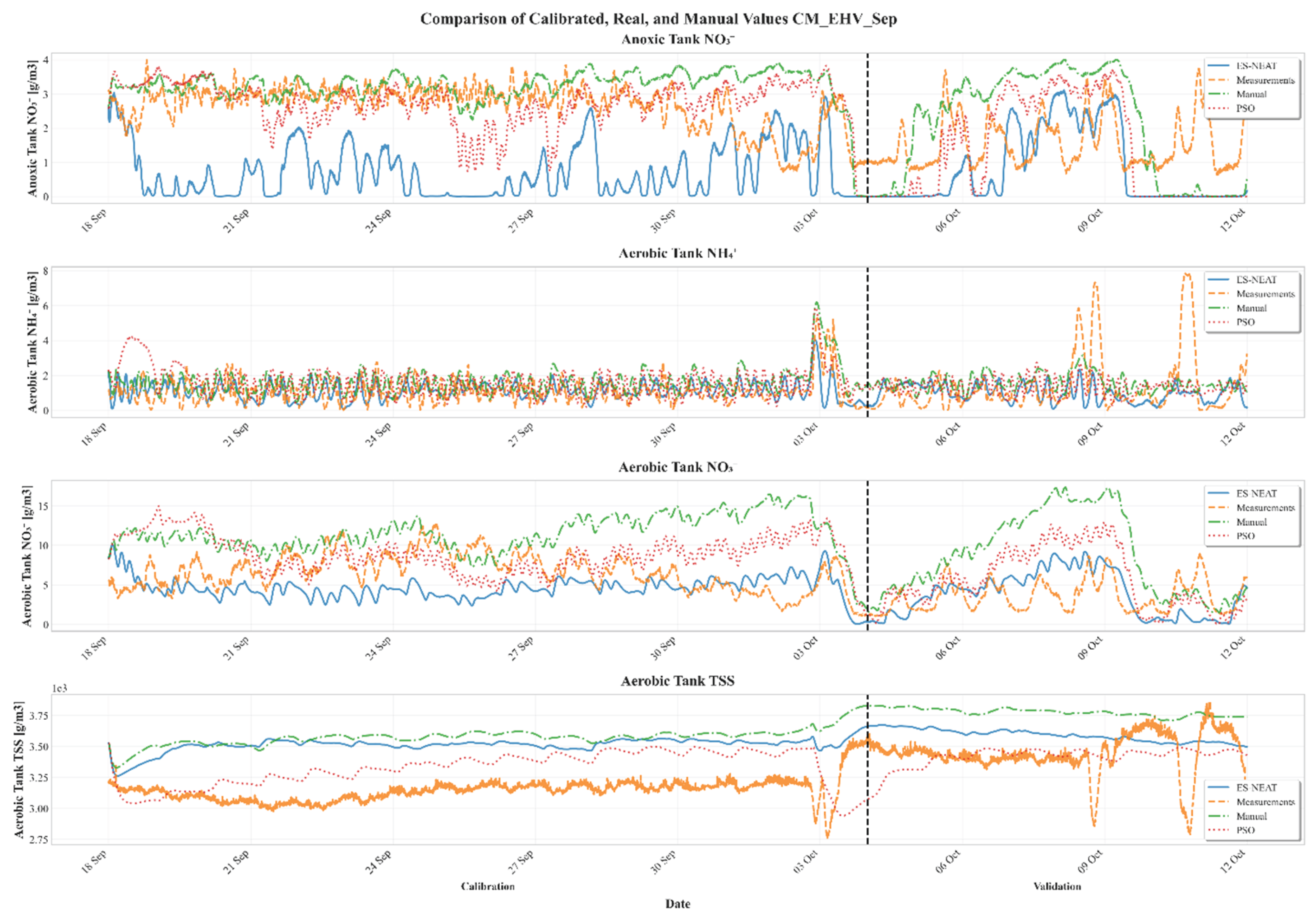
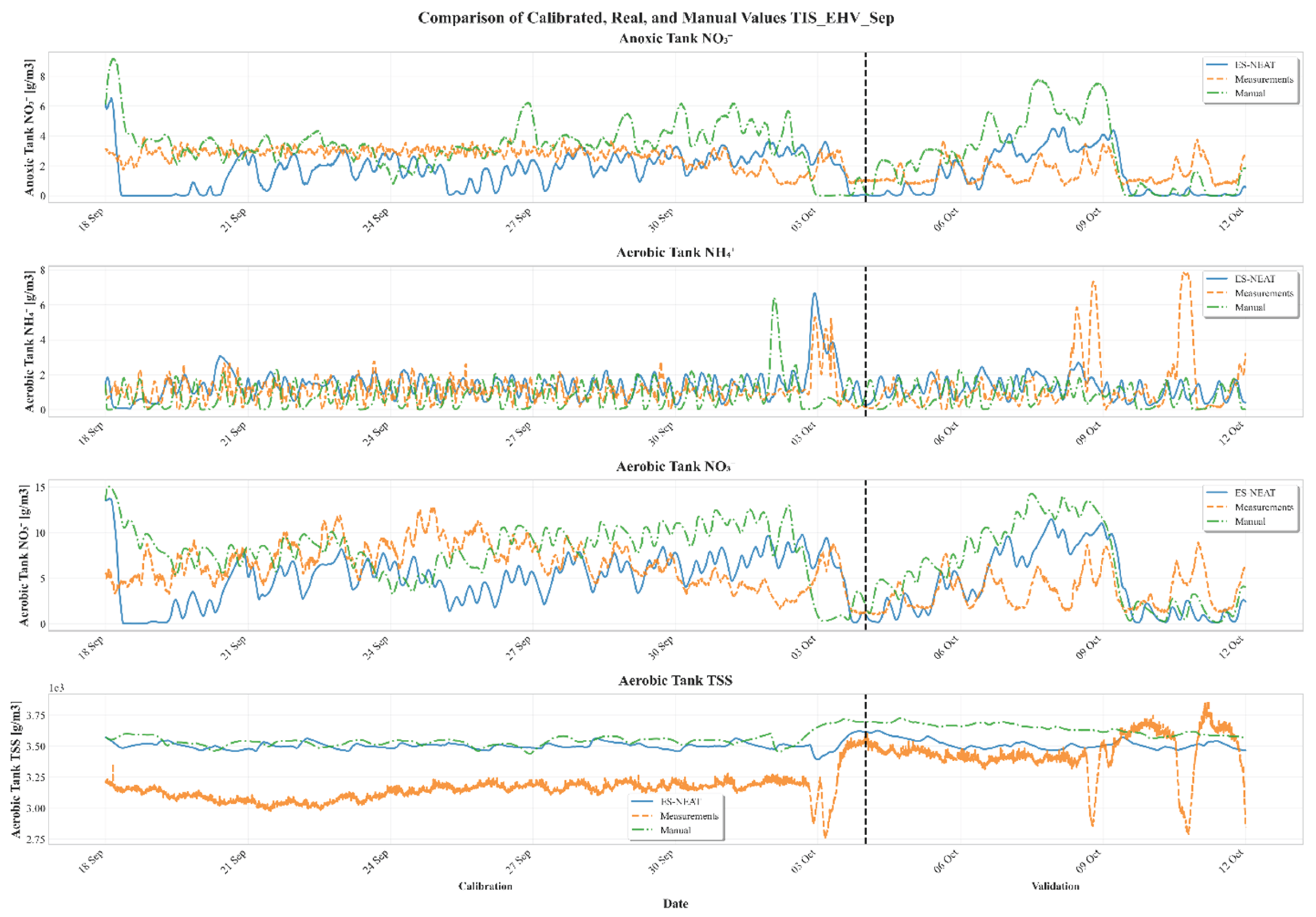
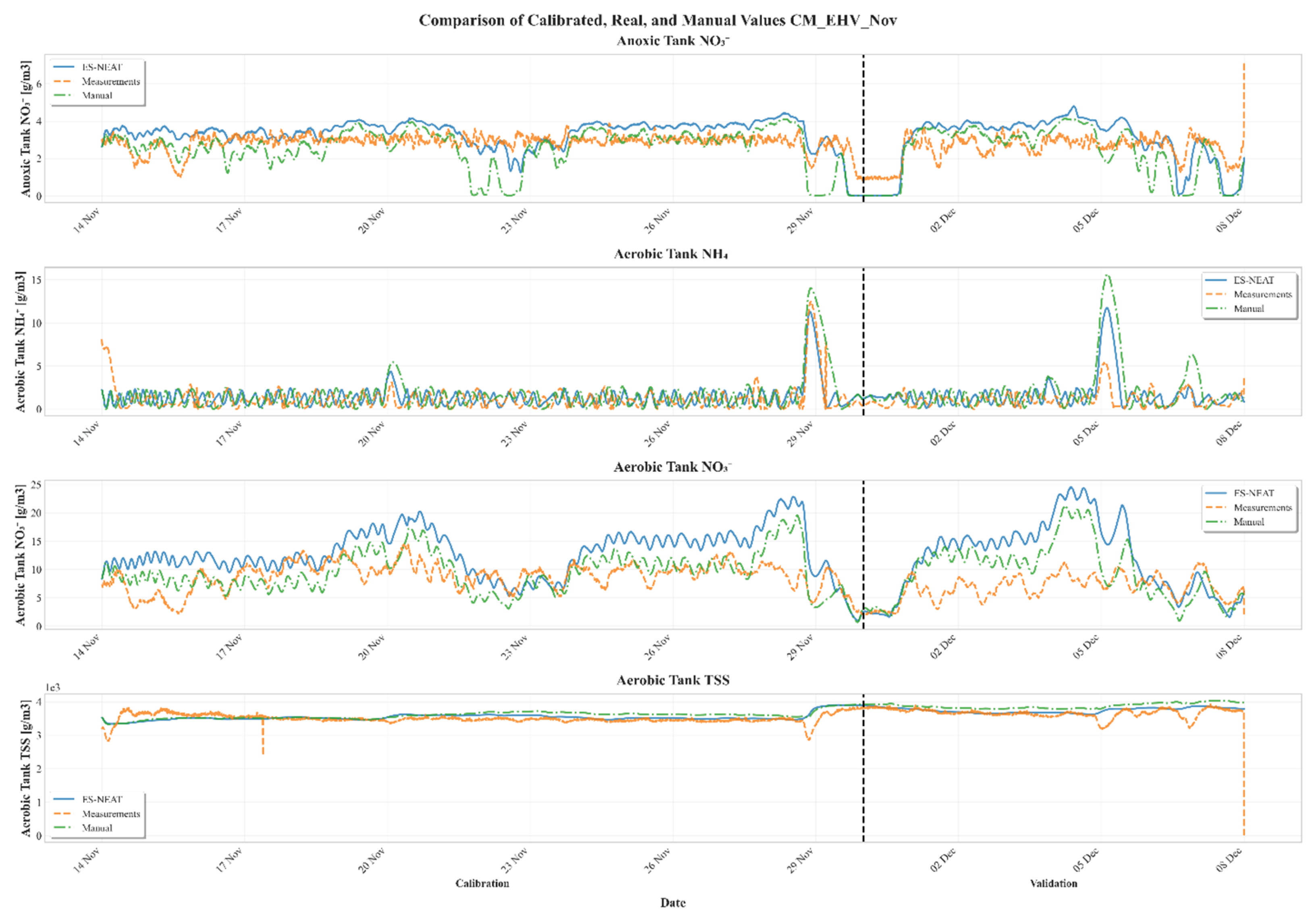
Appendix B. Variable-Level Performance Metrics
| Scenario | Variable | Period | Method | Metric | Mean | SD | CI_Lower | CI_Upper |
| Jul | ANOXIC_NO3 | Calibration | Manual | KGE | -0.47 | 0.136 | -0.687 | -0.254 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.368 | 0.219 | -0.717 | -0.019 |
| Jul | ANOXIC_NO3 | Calibration | PSO | KGE | -0.341 | 0.269 | -0.768 | 0.087 |
| Jul | ANOXIC_NO3 | Validation | Manual | KGE | -0.998 | 0.036 | -1.321 | -0.675 |
| Jul | ANOXIC_NO3 | Validation | NEAT | KGE | -1.436 | 0.014 | -1.562 | -1.311 |
| Jul | ANOXIC_NO3 | Validation | PSO | KGE | -1.547 | 0.019 | -1.72 | -1.374 |
| Jul | LAST_NH4 | Calibration | Manual | KGE | -0.013 | 0.084 | -0.147 | 0.12 |
| Jul | LAST_NH4 | Calibration | NEAT | KGE | -0.26 | 0.135 | -0.474 | -0.046 |
| Jul | LAST_NH4 | Calibration | PSO | KGE | -0.046 | 0.111 | -0.223 | 0.13 |
| Jul | LAST_NH4 | Validation | Manual | KGE | -0.187 | 0.103 | -1.108 | 0.735 |
| Jul | LAST_NH4 | Validation | NEAT | KGE | -0.119 | 0.083 | -0.864 | 0.625 |
| Jul | LAST_NH4 | Validation | PSO | KGE | 0.039 | 0.098 | -0.839 | 0.917 |
| Jul | LAST_NO3 | Calibration | Manual | KGE | -0.982 | 0.365 | -1.563 | -0.401 |
| Jul | LAST_NO3 | Calibration | NEAT | KGE | 0.016 | 0.119 | -0.174 | 0.206 |
| Jul | LAST_NO3 | Calibration | PSO | KGE | 0.008 | 0.169 | -0.261 | 0.276 |
| Jul | LAST_NO3 | Validation | Manual | KGE | -2.655 | 0.247 | -4.872 | -0.438 |
| Jul | LAST_NO3 | Validation | NEAT | KGE | -0.779 | 0.009 | -0.864 | -0.693 |
| Jul | LAST_NO3 | Validation | PSO | KGE | -0.905 | 0.058 | -1.424 | -0.386 |
| Jul | LAST_TSS | Calibration | Manual | KGE | 0.202 | 0.14 | -0.021 | 0.424 |
| Jul | LAST_TSS | Calibration | NEAT | KGE | 0.088 | 0.392 | -0.537 | 0.712 |
| Jul | LAST_TSS | Calibration | PSO | KGE | 0.079 | 0.261 | -0.336 | 0.495 |
| Jul | LAST_TSS | Validation | Manual | KGE | -0.097 | 0.238 | -2.24 | 2.046 |
| Jul | LAST_TSS | Validation | NEAT | KGE | 0.107 | 0.004 | 0.073 | 0.142 |
| Jul | LAST_TSS | Validation | PSO | KGE | -0.28 | 0.444 | -4.27 | 3.71 |
| Nov | ANOXIC_NO3 | Calibration | Manual | KGE | -1.563 | 1.458 | -3.883 | 0.758 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.52 | 0.536 | -1.374 | 0.333 |
| Nov | ANOXIC_NO3 | Validation | Manual | KGE | -0.208 | 0.795 | -7.347 | 6.932 |
| Nov | ANOXIC_NO3 | Validation | NEAT | KGE | -0.264 | 0.587 | -5.535 | 5.006 |
| Nov | LAST_NH4 | Calibration | Manual | KGE | -0.006 | 0.237 | -0.384 | 0.372 |
| Nov | LAST_NH4 | Calibration | NEAT | KGE | 0.24 | 0.41 | -0.412 | 0.892 |
| Nov | LAST_NH4 | Validation | Manual | KGE | -1.051 | 1.298 | -12.712 | 10.61 |
| Nov | LAST_NH4 | Validation | NEAT | KGE | -0.328 | 0.257 | -2.636 | 1.98 |
| Nov | LAST_NO3 | Calibration | Manual | KGE | -0.038 | 0.06 | -0.133 | 0.057 |
| Nov | LAST_NO3 | Calibration | NEAT | KGE | -0.338 | 0.203 | -0.662 | -0.015 |
| Nov | LAST_NO3 | Validation | Manual | KGE | -0.617 | 0.809 | -7.881 | 6.648 |
| Nov | LAST_NO3 | Validation | NEAT | KGE | -1.332 | 0.832 | -8.803 | 6.139 |
| Nov | LAST_TSS | Calibration | Manual | KGE | 0.282 | 0.283 | -0.168 | 0.732 |
| Nov | LAST_TSS | Calibration | NEAT | KGE | 0.253 | 0.279 | -0.191 | 0.698 |
| Nov | LAST_TSS | Validation | Manual | KGE | 0.331 | 0.348 | -2.791 | 3.454 |
| Nov | LAST_TSS | Validation | NEAT | KGE | 0.382 | 0.642 | -5.39 | 6.154 |
| Sep | ANOXIC_NO3 | Calibration | Manual | KGE | -0.08 | 0.036 | -0.137 | -0.022 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.672 | 0.454 | -1.395 | 0.05 |
| Sep | ANOXIC_NO3 | Calibration | PSO | KGE | -0.31 | 0.416 | -0.973 | 0.352 |
| Sep | ANOXIC_NO3 | Validation | Manual | KGE | -0.391 | 0.073 | -1.046 | 0.265 |
| Sep | ANOXIC_NO3 | Validation | NEAT | KGE | -0.022 | 0.052 | -0.491 | 0.447 |
| Sep | ANOXIC_NO3 | Validation | PSO | KGE | -0.169 | 0.077 | -0.857 | 0.519 |
| Sep | LAST_NH4 | Calibration | Manual | KGE | 0.053 | 0.183 | -0.239 | 0.344 |
| Sep | LAST_NH4 | Calibration | NEAT | KGE | 0.183 | 0.174 | -0.095 | 0.461 |
| Sep | LAST_NH4 | Calibration | PSO | KGE | -0.011 | 0.447 | -0.723 | 0.7 |
| Sep | LAST_NH4 | Validation | Manual | KGE | -0.121 | 0.201 | -1.923 | 1.68 |
| Sep | LAST_NH4 | Validation | NEAT | KGE | -0.022 | 0.218 | -1.984 | 1.941 |
| Sep | LAST_NH4 | Validation | PSO | KGE | -0.13 | 0.009 | -0.21 | -0.051 |
| Sep | LAST_NO3 | Calibration | Manual | KGE | -0.602 | 0.657 | -1.649 | 0.444 |
| Sep | LAST_NO3 | Calibration | NEAT | KGE | -0.066 | 0.327 | -0.587 | 0.455 |
| Sep | LAST_NO3 | Calibration | PSO | KGE | -0.261 | 0.29 | -0.723 | 0.2 |
| Sep | LAST_NO3 | Validation | Manual | KGE | -1.316 | 0.103 | -2.242 | -0.39 |
| Sep | LAST_NO3 | Validation | NEAT | KGE | 0.236 | 0.126 | -0.9 | 1.371 |
| Sep | LAST_NO3 | Validation | PSO | KGE | -0.268 | 0.013 | -0.383 | -0.153 |
| Sep | LAST_TSS | Calibration | Manual | KGE | -0.014 | 0.418 | -0.679 | 0.651 |
| Sep | LAST_TSS | Calibration | NEAT | KGE | -0.316 | 0.514 | -1.133 | 0.502 |
| Sep | LAST_TSS | Calibration | PSO | KGE | -0.202 | 0.524 | -1.037 | 0.632 |
| Sep | LAST_TSS | Validation | Manual | KGE | -0.12 | 0.643 | -5.899 | 5.66 |
| Sep | LAST_TSS | Validation | NEAT | KGE | 0.012 | 0.669 | -6.003 | 6.027 |
| Sep | LAST_TSS | Validation | PSO | KGE | -0.851 | 0.581 | -6.072 | 4.371 |
| Jul | ANOXIC_NO3 | Calibration | Manual | R2 | 0.043 | 0.028 | -0.001 | 0.088 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.013 | 0.014 | -0.009 | 0.035 |
| Jul | ANOXIC_NO3 | Calibration | PSO | R2 | 0.023 | 0.019 | -0.007 | 0.054 |
| Jul | ANOXIC_NO3 | Validation | Manual | R2 | 0.027 | 0.037 | -0.305 | 0.358 |
| Jul | ANOXIC_NO3 | Validation | NEAT | R2 | 0.083 | 0.059 | -0.443 | 0.608 |
| Jul | ANOXIC_NO3 | Validation | PSO | R2 | 0.08 | 0.113 | -0.932 | 1.092 |
| Jul | LAST_NH4 | Calibration | Manual | R2 | 0.017 | 0.018 | -0.011 | 0.045 |
| Jul | LAST_NH4 | Calibration | NEAT | R2 | 0.022 | 0.018 | -0.007 | 0.05 |
| Jul | LAST_NH4 | Calibration | PSO | R2 | 0.035 | 0.036 | -0.022 | 0.093 |
| Jul | LAST_NH4 | Validation | Manual | R2 | 0.035 | 0.026 | -0.197 | 0.267 |
| Jul | LAST_NH4 | Validation | NEAT | R2 | 0.032 | 0.032 | -0.255 | 0.32 |
| Jul | LAST_NH4 | Validation | PSO | R2 | 0.072 | 0.049 | -0.365 | 0.509 |
| Jul | LAST_NO3 | Calibration | Manual | R2 | 0.088 | 0.07 | -0.024 | 0.2 |
| Jul | LAST_NO3 | Calibration | NEAT | R2 | 0.036 | 0.033 | -0.017 | 0.088 |
| Jul | LAST_NO3 | Calibration | PSO | R2 | 0.061 | 0.068 | -0.048 | 0.169 |
| Jul | LAST_NO3 | Validation | Manual | R2 | 0.058 | 0.081 | -0.669 | 0.785 |
| Jul | LAST_NO3 | Validation | NEAT | R2 | 0.111 | 0.073 | -0.548 | 0.77 |
| Jul | LAST_NO3 | Validation | PSO | R2 | 0.119 | 0.119 | -0.952 | 1.189 |
| Jul | LAST_TSS | Calibration | Manual | R2 | 0.142 | 0.095 | -0.009 | 0.293 |
| Jul | LAST_TSS | Calibration | NEAT | R2 | 0.289 | 0.284 | -0.164 | 0.741 |
| Jul | LAST_TSS | Calibration | PSO | R2 | 0.155 | 0.131 | -0.053 | 0.363 |
| Jul | LAST_TSS | Validation | Manual | R2 | 0.05 | 0.055 | -0.446 | 0.545 |
| Jul | LAST_TSS | Validation | NEAT | R2 | 0.175 | 0.071 | -0.463 | 0.813 |
| Jul | LAST_TSS | Validation | PSO | R2 | 0.131 | 0.101 | -0.78 | 1.043 |
| Nov | ANOXIC_NO3 | Calibration | Manual | R2 | 0.115 | 0.215 | -0.228 | 0.457 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.142 | 0.259 | -0.27 | 0.553 |
| Nov | ANOXIC_NO3 | Validation | Manual | R2 | 0.517 | 0.316 | -2.319 | 3.353 |
| Nov | ANOXIC_NO3 | Validation | NEAT | R2 | 0.583 | 0.225 | -1.435 | 2.601 |
| Nov | LAST_NH4 | Calibration | Manual | R2 | 0.184 | 0.33 | -0.342 | 0.709 |
| Nov | LAST_NH4 | Calibration | NEAT | R2 | 0.216 | 0.376 | -0.382 | 0.815 |
| Nov | LAST_NH4 | Validation | Manual | R2 | 0.172 | 0.234 | -1.929 | 2.274 |
| Nov | LAST_NH4 | Validation | NEAT | R2 | 0.211 | 0.296 | -2.444 | 2.867 |
| Nov | LAST_NO3 | Calibration | Manual | R2 | 0.172 | 0.146 | -0.061 | 0.405 |
| Nov | LAST_NO3 | Calibration | NEAT | R2 | 0.176 | 0.184 | -0.116 | 0.469 |
| Nov | LAST_NO3 | Validation | Manual | R2 | 0.38 | 0.12 | -0.702 | 1.461 |
| Nov | LAST_NO3 | Validation | NEAT | R2 | 0.399 | 0.138 | -0.839 | 1.637 |
| Nov | LAST_TSS | Calibration | Manual | R2 | 0.225 | 0.246 | -0.167 | 0.617 |
| Nov | LAST_TSS | Calibration | NEAT | R2 | 0.163 | 0.148 | -0.072 | 0.398 |
| Nov | LAST_TSS | Validation | Manual | R2 | 0.414 | 0.429 | -3.44 | 4.269 |
| Nov | LAST_TSS | Validation | NEAT | R2 | 0.385 | 0.507 | -4.173 | 4.942 |
| Sep | ANOXIC_NO3 | Calibration | Manual | R2 | 0.021 | 0.042 | -0.045 | 0.088 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.022 | 0.032 | -0.029 | 0.073 |
| Sep | ANOXIC_NO3 | Calibration | PSO | R2 | 0.034 | 0.055 | -0.053 | 0.121 |
| Sep | ANOXIC_NO3 | Validation | Manual | R2 | 0.054 | 0.054 | -0.433 | 0.541 |
| Sep | ANOXIC_NO3 | Validation | NEAT | R2 | 0.053 | 0.031 | -0.228 | 0.333 |
| Sep | ANOXIC_NO3 | Validation | PSO | R2 | 0.127 | 0.107 | -0.831 | 1.084 |
| Sep | LAST_NH4 | Calibration | Manual | R2 | 0.175 | 0.333 | -0.355 | 0.705 |
| Sep | LAST_NH4 | Calibration | NEAT | R2 | 0.082 | 0.131 | -0.127 | 0.292 |
| Sep | LAST_NH4 | Calibration | PSO | R2 | 0.131 | 0.256 | -0.276 | 0.538 |
| Sep | LAST_NH4 | Validation | Manual | R2 | 0.097 | 0.104 | -0.833 | 1.027 |
| Sep | LAST_NH4 | Validation | NEAT | R2 | 0.071 | 0.031 | -0.208 | 0.351 |
| Sep | LAST_NH4 | Validation | PSO | R2 | 0.043 | 0.04 | -0.316 | 0.402 |
| Sep | LAST_NO3 | Calibration | Manual | R2 | 0.027 | 0.026 | -0.016 | 0.069 |
| Sep | LAST_NO3 | Calibration | NEAT | R2 | 0.071 | 0.108 | -0.1 | 0.243 |
| Sep | LAST_NO3 | Calibration | PSO | R2 | 0.073 | 0.106 | -0.096 | 0.242 |
| Sep | LAST_NO3 | Validation | Manual | R2 | 0.118 | 0.096 | -0.747 | 0.983 |
| Sep | LAST_NO3 | Validation | NEAT | R2 | 0.166 | 0.106 | -0.786 | 1.119 |
| Sep | LAST_NO3 | Validation | PSO | R2 | 0.192 | 0.061 | -0.353 | 0.738 |
| Sep | LAST_TSS | Calibration | Manual | R2 | 0.225 | 0.174 | -0.053 | 0.502 |
| Sep | LAST_TSS | Calibration | NEAT | R2 | 0.33 | 0.301 | -0.148 | 0.809 |
| Sep | LAST_TSS | Calibration | PSO | R2 | 0.213 | 0.113 | 0.033 | 0.392 |
| Sep | LAST_TSS | Validation | Manual | R2 | 0.238 | 0.226 | -1.793 | 2.269 |
| Sep | LAST_TSS | Validation | NEAT | R2 | 0.266 | 0.34 | -2.788 | 3.32 |
| Sep | LAST_TSS | Validation | PSO | R2 | 0.33 | 0.441 | -3.631 | 4.292 |
| Jul | ANOXIC_NO3 | Calibration | Manual | RMSE | 1.586 | 0.132 | 1.376 | 1.796 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | RMSE | 1.455 | 0.08 | 1.328 | 1.581 |
| Jul | ANOXIC_NO3 | Calibration | PSO | RMSE | 1.407 | 0.096 | 1.255 | 1.559 |
| Jul | ANOXIC_NO3 | Validation | Manual | RMSE | 2.272 | 0.088 | 1.485 | 3.058 |
| Jul | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.453 | 0.038 | 1.114 | 1.793 |
| Jul | ANOXIC_NO3 | Validation | PSO | RMSE | 1.471 | 0.034 | 1.169 | 1.772 |
| Jul | LAST_NH4 | Calibration | Manual | RMSE | 1.022 | 0.222 | 0.668 | 1.376 |
| Jul | LAST_NH4 | Calibration | NEAT | RMSE | 1.075 | 0.303 | 0.592 | 1.557 |
| Jul | LAST_NH4 | Calibration | PSO | RMSE | 0.966 | 0.272 | 0.533 | 1.398 |
| Jul | LAST_NH4 | Validation | Manual | RMSE | 0.825 | 0.069 | 0.21 | 1.441 |
| Jul | LAST_NH4 | Validation | NEAT | RMSE | 0.745 | 0.04 | 0.389 | 1.101 |
| Jul | LAST_NH4 | Validation | PSO | RMSE | 0.683 | 0.06 | 0.146 | 1.22 |
| Jul | LAST_NO3 | Calibration | Manual | RMSE | 5.883 | 1.389 | 3.672 | 8.093 |
| Jul | LAST_NO3 | Calibration | NEAT | RMSE | 2.183 | 0.396 | 1.553 | 2.813 |
| Jul | LAST_NO3 | Calibration | PSO | RMSE | 2.177 | 0.297 | 1.704 | 2.65 |
| Jul | LAST_NO3 | Validation | Manual | RMSE | 9.875 | 0.891 | 1.87 | 17.881 |
| Jul | LAST_NO3 | Validation | NEAT | RMSE | 3.716 | 0.253 | 1.441 | 5.991 |
| Jul | LAST_NO3 | Validation | PSO | RMSE | 4.12 | 0.52 | -0.551 | 8.79 |
| Jul | LAST_TSS | Calibration | Manual | RMSE | 120.484 | 43.606 | 51.097 | 189.872 |
| Jul | LAST_TSS | Calibration | NEAT | RMSE | 177.559 | 111.135 | 0.719 | 354.399 |
| Jul | LAST_TSS | Calibration | PSO | RMSE | 107.442 | 28.792 | 61.628 | 153.256 |
| Jul | LAST_TSS | Validation | Manual | RMSE | 133.965 | 14.904 | 0.056 | 267.874 |
| Jul | LAST_TSS | Validation | NEAT | RMSE | 155.082 | 3.123 | 127.026 | 183.137 |
| Jul | LAST_TSS | Validation | PSO | RMSE | 145.49 | 20.36 | -37.435 | 328.414 |
| Nov | ANOXIC_NO3 | Calibration | Manual | RMSE | 1.028 | 0.244 | 0.639 | 1.416 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | RMSE | 0.828 | 0.128 | 0.625 | 1.032 |
| Nov | ANOXIC_NO3 | Validation | Manual | RMSE | 1.084 | 0.435 | -2.824 | 4.993 |
| Nov | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.091 | 0.067 | 0.486 | 1.696 |
| Nov | LAST_NH4 | Calibration | Manual | RMSE | 1.566 | 0.482 | 0.799 | 2.333 |
| Nov | LAST_NH4 | Calibration | NEAT | RMSE | 1.167 | 0.338 | 0.628 | 1.705 |
| Nov | LAST_NH4 | Validation | Manual | RMSE | 2.457 | 2.013 | -15.631 | 20.544 |
| Nov | LAST_NH4 | Validation | NEAT | RMSE | 1.584 | 0.874 | -6.269 | 9.437 |
| Nov | LAST_NO3 | Calibration | Manual | RMSE | 3.239 | 0.694 | 2.134 | 4.344 |
| Nov | LAST_NO3 | Calibration | NEAT | RMSE | 5.354 | 1.122 | 3.569 | 7.139 |
| Nov | LAST_NO3 | Validation | Manual | RMSE | 5.234 | 0.449 | 1.197 | 9.271 |
| Nov | LAST_NO3 | Validation | NEAT | RMSE | 7.617 | 0.464 | 3.448 | 11.786 |
| Nov | LAST_TSS | Calibration | Manual | RMSE | 177.937 | 51.278 | 96.343 | 259.532 |
| Nov | LAST_TSS | Calibration | NEAT | RMSE | 144.327 | 56.155 | 54.972 | 233.681 |
| Nov | LAST_TSS | Validation | Manual | RMSE | 256.23 | 140.957 | -1010.22 | 1522.677 |
| Nov | LAST_TSS | Validation | NEAT | RMSE | 156.471 | 149.071 | -1182.88 | 1495.816 |
| Sep | ANOXIC_NO3 | Calibration | Manual | RMSE | 0.823 | 0.604 | -0.138 | 1.784 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | RMSE | 2.171 | 0.561 | 1.278 | 3.064 |
| Sep | ANOXIC_NO3 | Calibration | PSO | RMSE | 0.907 | 0.302 | 0.426 | 1.387 |
| Sep | ANOXIC_NO3 | Validation | Manual | RMSE | 1.703 | 0.173 | 0.145 | 3.262 |
| Sep | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.381 | 0.077 | 0.685 | 2.077 |
| Sep | ANOXIC_NO3 | Validation | PSO | RMSE | 1.401 | 0.307 | -1.354 | 4.156 |
| Sep | LAST_NH4 | Calibration | Manual | RMSE | 0.87 | 0.122 | 0.675 | 1.065 |
| Sep | LAST_NH4 | Calibration | NEAT | RMSE | 0.713 | 0.146 | 0.48 | 0.945 |
| Sep | LAST_NH4 | Calibration | PSO | RMSE | 0.997 | 0.324 | 0.482 | 1.512 |
| Sep | LAST_NH4 | Validation | Manual | RMSE | 1.51 | 0.758 | -5.302 | 8.322 |
| Sep | LAST_NH4 | Validation | NEAT | RMSE | 1.508 | 1.16 | -8.913 | 11.929 |
| Sep | LAST_NH4 | Validation | PSO | RMSE | 1.525 | 0.926 | -6.797 | 9.848 |
| Sep | LAST_NO3 | Calibration | Manual | RMSE | 5.633 | 2.759 | 1.243 | 10.023 |
| Sep | LAST_NO3 | Calibration | NEAT | RMSE | 3.251 | 1.461 | 0.926 | 5.576 |
| Sep | LAST_NO3 | Calibration | PSO | RMSE | 4.005 | 1.955 | 0.894 | 7.116 |
| Sep | LAST_NO3 | Validation | Manual | RMSE | 7.178 | 0.473 | 2.929 | 11.427 |
| Sep | LAST_NO3 | Validation | NEAT | RMSE | 2.785 | 0.839 | -4.757 | 10.327 |
| Sep | LAST_NO3 | Validation | PSO | RMSE | 4.102 | 0.515 | -0.523 | 8.726 |
| Sep | LAST_TSS | Calibration | Manual | RMSE | 436.808 | 29.651 | 389.627 | 483.989 |
| Sep | LAST_TSS | Calibration | NEAT | RMSE | 378.341 | 31.405 | 328.369 | 428.313 |
| Sep | LAST_TSS | Calibration | PSO | RMSE | 233.916 | 74.026 | 116.125 | 351.707 |
| Sep | LAST_TSS | Validation | Manual | RMSE | 371.807 | 2.454 | 349.76 | 393.854 |
| Sep | LAST_TSS | Validation | NEAT | RMSE | 228.335 | 30.557 | -46.211 | 502.881 |
| Sep | LAST_TSS | Validation | PSO | RMSE | 191.352 | 65.815 | -399.968 | 782.673 |
| Scenario | Variable | Period | Method | Metric | Mean | SD | CI_Lower | CI_Upper |
| Jul | ANOXIC_NO3 | Calibration | Manual | KGE | -1.923 | 1.146 | -3.748 | -0.099 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.403 | 0.249 | -0.798 | -0.007 |
| Jul | ANOXIC_NO3 | Validation | Manual | KGE | -6.37 | 3.778 | -40.312 | 27.573 |
| Jul | ANOXIC_NO3 | Validation | NEAT | KGE | -2.266 | 2.179 | -21.846 | 17.313 |
| Jul | LAST_NH4 | Calibration | Manual | KGE | 0.042 | 0.254 | -0.362 | 0.445 |
| Jul | LAST_NH4 | Calibration | NEAT | KGE | -0.056 | 0.095 | -0.206 | 0.095 |
| Jul | LAST_NH4 | Validation | Manual | KGE | -0.443 | 0.939 | -8.88 | 7.994 |
| Jul | LAST_NH4 | Validation | NEAT | KGE | 0.243 | 0.092 | -0.583 | 1.07 |
| Jul | LAST_NO3 | Calibration | Manual | KGE | -0.968 | 0.252 | -1.369 | -0.567 |
| Jul | LAST_NO3 | Calibration | NEAT | KGE | -0.072 | 0.141 | -0.296 | 0.152 |
| Jul | LAST_NO3 | Validation | Manual | KGE | -2.885 | 1.348 | -14.997 | 9.227 |
| Jul | LAST_NO3 | Validation | NEAT | KGE | -0.965 | 1.121 | -11.039 | 9.109 |
| Jul | LAST_TSS | Calibration | Manual | KGE | 0.111 | 0.165 | -0.151 | 0.372 |
| Jul | LAST_TSS | Calibration | NEAT | KGE | 0.035 | 0.118 | -0.153 | 0.223 |
| Jul | LAST_TSS | Validation | Manual | KGE | -0.179 | 0.147 | -1.495 | 1.137 |
| Jul | LAST_TSS | Validation | NEAT | KGE | -0.114 | 0.058 | -0.634 | 0.406 |
| Nov | ANOXIC_NO3 | Calibration | Manual | KGE | -5.624 | 4.183 | -12.28 | 1.031 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | KGE | -2.402 | 1.776 | -5.228 | 0.424 |
| Nov | ANOXIC_NO3 | Validation | Manual | KGE | -3.709 | 2.894 | -29.714 | 22.296 |
| Nov | ANOXIC_NO3 | Validation | NEAT | KGE | -1.272 | 2.264 | -21.615 | 19.071 |
| Nov | LAST_NH4 | Calibration | Manual | KGE | -0.062 | 0.25 | -0.46 | 0.336 |
| Nov | LAST_NH4 | Calibration | NEAT | KGE | 0.332 | 0.465 | -0.408 | 1.071 |
| Nov | LAST_NH4 | Validation | Manual | KGE | -0.887 | 1.199 | -11.658 | 9.885 |
| Nov | LAST_NH4 | Validation | NEAT | KGE | -0.351 | 0.681 | -6.474 | 5.771 |
| Nov | LAST_NO3 | Calibration | Manual | KGE | -0.261 | 0.514 | -1.079 | 0.558 |
| Nov | LAST_NO3 | Calibration | NEAT | KGE | 0.168 | 0.005 | 0.16 | 0.176 |
| Nov | LAST_NO3 | Validation | Manual | KGE | -0.783 | 0.579 | -5.984 | 4.417 |
| Nov | LAST_NO3 | Validation | NEAT | KGE | -0.025 | 0.72 | -6.495 | 6.444 |
| Nov | LAST_TSS | Calibration | Manual | KGE | 0.1 | 0.364 | -0.479 | 0.679 |
| Nov | LAST_TSS | Calibration | NEAT | KGE | 0.079 | 0.528 | -0.76 | 0.919 |
| Nov | LAST_TSS | Validation | Manual | KGE | 0.202 | 0.247 | -2.022 | 2.425 |
| Nov | LAST_TSS | Validation | NEAT | KGE | 0.375 | 0.49 | -4.031 | 4.781 |
| Sep | ANOXIC_NO3 | Calibration | Manual | KGE | -1.548 | 0.636 | -2.56 | -0.535 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | KGE | -1.091 | 1.081 | -2.81 | 0.628 |
| Sep | ANOXIC_NO3 | Validation | Manual | KGE | -1.361 | 0.027 | -1.602 | -1.121 |
| Sep | ANOXIC_NO3 | Validation | NEAT | KGE | -0.231 | 0.077 | -0.921 | 0.459 |
| Sep | LAST_NH4 | Calibration | Manual | KGE | -0.179 | 0.108 | -0.35 | -0.008 |
| Sep | LAST_NH4 | Calibration | NEAT | KGE | 0.239 | 0.152 | -0.003 | 0.481 |
| Sep | LAST_NH4 | Validation | Manual | KGE | -0.3 | 0.064 | -0.874 | 0.274 |
| Sep | LAST_NH4 | Validation | NEAT | KGE | -0.005 | 0.057 | -0.515 | 0.505 |
| Sep | LAST_NO3 | Calibration | Manual | KGE | -0.508 | 0.481 | -1.275 | 0.258 |
| Sep | LAST_NO3 | Calibration | NEAT | KGE | -0.024 | 0.254 | -0.428 | 0.38 |
| Sep | LAST_NO3 | Validation | Manual | KGE | -0.655 | 0.321 | -3.538 | 2.229 |
| Sep | LAST_NO3 | Validation | NEAT | KGE | -0.095 | 0.076 | -0.773 | 0.584 |
| Sep | LAST_TSS | Calibration | Manual | KGE | 0.051 | 0.331 | -0.475 | 0.577 |
| Sep | LAST_TSS | Calibration | NEAT | KGE | -0.073 | 0.368 | -0.659 | 0.512 |
| Sep | LAST_TSS | Validation | Manual | KGE | -0.244 | 0.604 | -5.674 | 5.185 |
| Sep | LAST_TSS | Validation | NEAT | KGE | 0.324 | 0.606 | -5.125 | 5.772 |
| Jul | ANOXIC_NO3 | Calibration | Manual | R2 | 0.01 | 0.008 | -0.003 | 0.023 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.009 | 0.01 | -0.007 | 0.025 |
| Jul | ANOXIC_NO3 | Validation | Manual | R2 | 0.187 | 0.211 | -1.713 | 2.087 |
| Jul | ANOXIC_NO3 | Validation | NEAT | R2 | 0.117 | 0.158 | -1.304 | 1.539 |
| Jul | LAST_NH4 | Calibration | Manual | R2 | 0.067 | 0.05 | -0.012 | 0.147 |
| Jul | LAST_NH4 | Calibration | NEAT | R2 | 0.029 | 0.033 | -0.023 | 0.081 |
| Jul | LAST_NH4 | Validation | Manual | R2 | 0.059 | 0.073 | -0.594 | 0.713 |
| Jul | LAST_NH4 | Validation | NEAT | R2 | 0.089 | 0.077 | -0.604 | 0.782 |
| Jul | LAST_NO3 | Calibration | Manual | R2 | 0.024 | 0.03 | -0.024 | 0.071 |
| Jul | LAST_NO3 | Calibration | NEAT | R2 | 0.012 | 0.021 | -0.021 | 0.046 |
| Jul | LAST_NO3 | Validation | Manual | R2 | 0.259 | 0.238 | -1.88 | 2.398 |
| Jul | LAST_NO3 | Validation | NEAT | R2 | 0.161 | 0.214 | -1.762 | 2.084 |
| Jul | LAST_TSS | Calibration | Manual | R2 | 0.089 | 0.138 | -0.131 | 0.309 |
| Jul | LAST_TSS | Calibration | NEAT | R2 | 0.035 | 0.035 | -0.02 | 0.09 |
| Jul | LAST_TSS | Validation | Manual | R2 | 0.023 | 0.002 | 0.008 | 0.039 |
| Jul | LAST_TSS | Validation | NEAT | R2 | 0.008 | 0.004 | -0.028 | 0.044 |
| Nov | ANOXIC_NO3 | Calibration | Manual | R2 | 0.069 | 0.078 | -0.056 | 0.194 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.058 | 0.066 | -0.046 | 0.163 |
| Nov | ANOXIC_NO3 | Validation | Manual | R2 | 0.131 | 0.001 | 0.118 | 0.143 |
| Nov | ANOXIC_NO3 | Validation | NEAT | R2 | 0.247 | 0.19 | -1.461 | 1.954 |
| Nov | LAST_NH4 | Calibration | Manual | R2 | 0.033 | 0.011 | 0.015 | 0.05 |
| Nov | LAST_NH4 | Calibration | NEAT | R2 | 0.365 | 0.331 | -0.161 | 0.891 |
| Nov | LAST_NH4 | Validation | Manual | R2 | 0.128 | 0.17 | -1.4 | 1.656 |
| Nov | LAST_NH4 | Validation | NEAT | R2 | 0.263 | 0.333 | -2.725 | 3.252 |
| Nov | LAST_NO3 | Calibration | Manual | R2 | 0.186 | 0.163 | -0.073 | 0.445 |
| Nov | LAST_NO3 | Calibration | NEAT | R2 | 0.236 | 0.037 | 0.177 | 0.294 |
| Nov | LAST_NO3 | Validation | Manual | R2 | 0.287 | 0.088 | -0.504 | 1.077 |
| Nov | LAST_NO3 | Validation | NEAT | R2 | 0.337 | 0.027 | 0.09 | 0.583 |
| Nov | LAST_TSS | Calibration | Manual | R2 | 0.09 | 0.07 | -0.022 | 0.201 |
| Nov | LAST_TSS | Calibration | NEAT | R2 | 0.233 | 0.252 | -0.169 | 0.634 |
| Nov | LAST_TSS | Validation | Manual | R2 | 0.369 | 0.323 | -2.531 | 3.27 |
| Nov | LAST_TSS | Validation | NEAT | R2 | 0.519 | 0.389 | -2.974 | 4.012 |
| Sep | ANOXIC_NO3 | Calibration | Manual | R2 | 0.031 | 0.043 | -0.038 | 0.099 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.04 | 0.039 | -0.022 | 0.101 |
| Sep | ANOXIC_NO3 | Validation | Manual | R2 | 0.133 | 0.03 | -0.137 | 0.402 |
| Sep | ANOXIC_NO3 | Validation | NEAT | R2 | 0.141 | 0.087 | -0.643 | 0.925 |
| Sep | LAST_NH4 | Calibration | Manual | R2 | 0.025 | 0.015 | 0.001 | 0.049 |
| Sep | LAST_NH4 | Calibration | NEAT | R2 | 0.205 | 0.305 | -0.279 | 0.69 |
| Sep | LAST_NH4 | Validation | Manual | R2 | 0.067 | 0.053 | -0.408 | 0.541 |
| Sep | LAST_NH4 | Validation | NEAT | R2 | 0.115 | 0.044 | -0.282 | 0.511 |
| Sep | LAST_NO3 | Calibration | Manual | R2 | 0.056 | 0.042 | -0.011 | 0.123 |
| Sep | LAST_NO3 | Calibration | NEAT | R2 | 0.077 | 0.073 | -0.04 | 0.194 |
| Sep | LAST_NO3 | Validation | Manual | R2 | 0.113 | 0.038 | -0.23 | 0.455 |
| Sep | LAST_NO3 | Validation | NEAT | R2 | 0.182 | 0.085 | -0.584 | 0.949 |
| Sep | LAST_TSS | Calibration | Manual | R2 | 0.14 | 0.18 | -0.146 | 0.426 |
| Sep | LAST_TSS | Calibration | NEAT | R2 | 0.245 | 0.254 | -0.16 | 0.65 |
| Sep | LAST_TSS | Validation | Manual | R2 | 0.167 | 0.002 | 0.146 | 0.188 |
| Sep | LAST_TSS | Validation | NEAT | R2 | 0.35 | 0.32 | -2.527 | 3.226 |
| Jul | ANOXIC_NO3 | Calibration | Manual | RMSE | 2.821 | 0.759 | 1.614 | 4.029 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | RMSE | 1.348 | 0.083 | 1.216 | 1.48 |
| Jul | ANOXIC_NO3 | Validation | Manual | RMSE | 4.492 | 1.441 | -8.452 | 17.436 |
| Jul | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.786 | 1.021 | -7.385 | 10.957 |
| Jul | LAST_NH4 | Calibration | Manual | RMSE | 0.932 | 0.316 | 0.429 | 1.436 |
| Jul | LAST_NH4 | Calibration | NEAT | RMSE | 0.873 | 0.291 | 0.41 | 1.336 |
| Jul | LAST_NH4 | Validation | Manual | RMSE | 0.923 | 0.467 | -3.269 | 5.114 |
| Jul | LAST_NH4 | Validation | NEAT | RMSE | 0.517 | 0.056 | 0.018 | 1.016 |
| Jul | LAST_NO3 | Calibration | Manual | RMSE | 5.392 | 1.125 | 3.602 | 7.183 |
| Jul | LAST_NO3 | Calibration | NEAT | RMSE | 2.516 | 0.269 | 2.088 | 2.943 |
| Jul | LAST_NO3 | Validation | Manual | RMSE | 7.471 | 1.37 | -4.834 | 19.776 |
| Jul | LAST_NO3 | Validation | NEAT | RMSE | 3.532 | 1.615 | -10.979 | 18.043 |
| Jul | LAST_TSS | Calibration | Manual | RMSE | 122.193 | 37.477 | 62.559 | 181.827 |
| Jul | LAST_TSS | Calibration | NEAT | RMSE | 107.589 | 19.198 | 77.041 | 138.137 |
| Jul | LAST_TSS | Validation | Manual | RMSE | 143.35 | 14.828 | 10.127 | 276.572 |
| Jul | LAST_TSS | Validation | NEAT | RMSE | 146.485 | 1.829 | 130.054 | 162.916 |
| Nov | ANOXIC_NO3 | Calibration | Manual | RMSE | 2.829 | 1.075 | 1.118 | 4.54 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | RMSE | 2.073 | 0.244 | 1.685 | 2.462 |
| Nov | ANOXIC_NO3 | Validation | Manual | RMSE | 4.126 | 0.013 | 4.008 | 4.244 |
| Nov | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.861 | 0.98 | -6.94 | 10.662 |
| Nov | LAST_NH4 | Calibration | Manual | RMSE | 2.049 | 1.652 | -0.58 | 4.679 |
| Nov | LAST_NH4 | Calibration | NEAT | RMSE | 1.158 | 0.564 | 0.261 | 2.055 |
| Nov | LAST_NH4 | Validation | Manual | RMSE | 2.325 | 1.952 | -15.217 | 19.867 |
| Nov | LAST_NH4 | Validation | NEAT | RMSE | 1.607 | 1.259 | -9.706 | 12.919 |
| Nov | LAST_NO3 | Calibration | Manual | RMSE | 4.292 | 1.113 | 2.52 | 6.064 |
| Nov | LAST_NO3 | Calibration | NEAT | RMSE | 5.129 | 0.213 | 4.79 | 5.468 |
| Nov | LAST_NO3 | Validation | Manual | RMSE | 6.247 | 1.346 | -5.85 | 18.343 |
| Nov | LAST_NO3 | Validation | NEAT | RMSE | 3.439 | 1.385 | -9.001 | 15.88 |
| Nov | LAST_TSS | Calibration | Manual | RMSE | 172.79 | 37.397 | 113.283 | 232.297 |
| Nov | LAST_TSS | Calibration | NEAT | RMSE | 119.319 | 55.946 | 30.297 | 208.34 |
| Nov | LAST_TSS | Validation | Manual | RMSE | 141.745 | 119.131 | -928.6 | 1212.091 |
| Nov | LAST_TSS | Validation | NEAT | RMSE | 132.24 | 107.92 | -837.386 | 1101.865 |
| Sep | ANOXIC_NO3 | Calibration | Manual | RMSE | 1.633 | 0.73 | 0.471 | 2.794 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | RMSE | 1.541 | 0.556 | 0.656 | 2.426 |
| Sep | ANOXIC_NO3 | Validation | Manual | RMSE | 2.587 | 0.152 | 1.224 | 3.95 |
| Sep | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.437 | 0.301 | -1.266 | 4.139 |
| Sep | LAST_NH4 | Calibration | Manual | RMSE | 1.111 | 0.409 | 0.46 | 1.762 |
| Sep | LAST_NH4 | Calibration | NEAT | RMSE | 0.769 | 0.139 | 0.548 | 0.99 |
| Sep | LAST_NH4 | Validation | Manual | RMSE | 1.667 | 1.059 | -7.849 | 11.182 |
| Sep | LAST_NH4 | Validation | NEAT | RMSE | 1.5 | 0.963 | -7.15 | 10.149 |
| Sep | LAST_NO3 | Calibration | Manual | RMSE | 4.096 | 1.497 | 1.714 | 6.477 |
| Sep | LAST_NO3 | Calibration | NEAT | RMSE | 3.601 | 0.898 | 2.172 | 5.029 |
| Sep | LAST_NO3 | Validation | Manual | RMSE | 5.198 | 0.619 | -0.36 | 10.755 |
| Sep | LAST_NO3 | Validation | NEAT | RMSE | 3.476 | 0.528 | -1.271 | 8.222 |
| Sep | LAST_TSS | Calibration | Manual | RMSE | 407.389 | 35.31 | 351.203 | 463.575 |
| Sep | LAST_TSS | Calibration | NEAT | RMSE | 364.218 | 47.415 | 288.77 | 439.665 |
| Sep | LAST_TSS | Validation | Manual | RMSE | 265.179 | 17.207 | 110.583 | 419.776 |
| Sep | LAST_TSS | Validation | NEAT | RMSE | 166.267 | 85.339 | -600.47 | 933.003 |
Appendix C. Transfer Learning Effectiveness Analysis
| Scenario | Variable | Period | Method | Metric | Mean | SD | CI_Lower | CI_Upper |
| Jul | ANOXIC_NO3 | Calibration | Manual | KGE | -0.470 | 0.136 | -0.687 | -0.254 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.368 | 0.219 | -0.717 | -0.019 |
| Jul | ANOXIC_NO3 | Calibration | PSO | KGE | -0.341 | 0.269 | -0.768 | 0.087 |
| Jul | ANOXIC_NO3 | Validation | Manual | KGE | -0.998 | 0.036 | -1.321 | -0.675 |
| Jul | ANOXIC_NO3 | Validation | NEAT | KGE | -1.436 | 0.014 | -1.562 | -1.311 |
| Jul | ANOXIC_NO3 | Validation | PSO | KGE | -1.547 | 0.019 | -1.720 | -1.374 |
| Jul | LAST_NH4 | Calibration | Manual | KGE | -0.013 | 0.084 | -0.147 | 0.120 |
| Jul | LAST_NH4 | Calibration | NEAT | KGE | -0.260 | 0.135 | -0.474 | -0.046 |
| Jul | LAST_NH4 | Calibration | PSO | KGE | -0.046 | 0.111 | -0.223 | 0.130 |
| Jul | LAST_NH4 | Validation | Manual | KGE | -0.187 | 0.103 | -1.108 | 0.735 |
| Jul | LAST_NH4 | Validation | NEAT | KGE | -0.119 | 0.083 | -0.864 | 0.625 |
| Jul | LAST_NH4 | Validation | PSO | KGE | 0.039 | 0.098 | -0.839 | 0.917 |
| Jul | LAST_NO3 | Calibration | Manual | KGE | -0.982 | 0.365 | -1.563 | -0.401 |
| Jul | LAST_NO3 | Calibration | NEAT | KGE | 0.016 | 0.119 | -0.174 | 0.206 |
| Jul | LAST_NO3 | Calibration | PSO | KGE | 0.008 | 0.169 | -0.261 | 0.276 |
| Jul | LAST_NO3 | Validation | Manual | KGE | -2.655 | 0.247 | -4.872 | -0.438 |
| Jul | LAST_NO3 | Validation | NEAT | KGE | -0.779 | 0.009 | -0.864 | -0.693 |
| Jul | LAST_NO3 | Validation | PSO | KGE | -0.905 | 0.058 | -1.424 | -0.386 |
| Jul | LAST_TSS | Calibration | Manual | KGE | 0.202 | 0.140 | -0.021 | 0.424 |
| Jul | LAST_TSS | Calibration | NEAT | KGE | 0.088 | 0.392 | -0.537 | 0.712 |
| Jul | LAST_TSS | Calibration | PSO | KGE | 0.079 | 0.261 | -0.336 | 0.495 |
| Jul | LAST_TSS | Validation | Manual | KGE | -0.097 | 0.238 | -2.240 | 2.046 |
| Jul | LAST_TSS | Validation | NEAT | KGE | 0.107 | 0.004 | 0.073 | 0.142 |
| Jul | LAST_TSS | Validation | PSO | KGE | -0.280 | 0.444 | -4.270 | 3.710 |
| Nov | ANOXIC_NO3 | Calibration | Manual | KGE | -1.563 | 1.458 | -3.883 | 0.758 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.520 | 0.536 | -1.374 | 0.333 |
| Nov | ANOXIC_NO3 | Validation | Manual | KGE | -0.208 | 0.795 | -7.347 | 6.932 |
| Nov | ANOXIC_NO3 | Validation | NEAT | KGE | -0.264 | 0.587 | -5.535 | 5.006 |
| Nov | LAST_NH4 | Calibration | Manual | KGE | -0.006 | 0.237 | -0.384 | 0.372 |
| Nov | LAST_NH4 | Calibration | NEAT | KGE | 0.240 | 0.410 | -0.412 | 0.892 |
| Nov | LAST_NH4 | Validation | Manual | KGE | -1.051 | 1.298 | -12.712 | 10.610 |
| Nov | LAST_NH4 | Validation | NEAT | KGE | -0.328 | 0.257 | -2.636 | 1.980 |
| Nov | LAST_NO3 | Calibration | Manual | KGE | -0.038 | 0.060 | -0.133 | 0.057 |
| Nov | LAST_NO3 | Calibration | NEAT | KGE | -0.338 | 0.203 | -0.662 | -0.015 |
| Nov | LAST_NO3 | Validation | Manual | KGE | -0.617 | 0.809 | -7.881 | 6.648 |
| Nov | LAST_NO3 | Validation | NEAT | KGE | -1.332 | 0.832 | -8.803 | 6.139 |
| Nov | LAST_TSS | Calibration | Manual | KGE | 0.282 | 0.283 | -0.168 | 0.732 |
| Nov | LAST_TSS | Calibration | NEAT | KGE | 0.253 | 0.279 | -0.191 | 0.698 |
| Nov | LAST_TSS | Validation | Manual | KGE | 0.331 | 0.348 | -2.791 | 3.454 |
| Nov | LAST_TSS | Validation | NEAT | KGE | 0.382 | 0.642 | -5.390 | 6.154 |
| Sep | ANOXIC_NO3 | Calibration | Manual | KGE | -0.080 | 0.036 | -0.137 | -0.022 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.672 | 0.454 | -1.395 | 0.050 |
| Sep | ANOXIC_NO3 | Calibration | PSO | KGE | -0.310 | 0.416 | -0.973 | 0.352 |
| Sep | ANOXIC_NO3 | Validation | Manual | KGE | -0.391 | 0.073 | -1.046 | 0.265 |
| Sep | ANOXIC_NO3 | Validation | NEAT | KGE | -0.022 | 0.052 | -0.491 | 0.447 |
| Sep | ANOXIC_NO3 | Validation | PSO | KGE | -0.169 | 0.077 | -0.857 | 0.519 |
| Sep | LAST_NH4 | Calibration | Manual | KGE | 0.053 | 0.183 | -0.239 | 0.344 |
| Sep | LAST_NH4 | Calibration | NEAT | KGE | 0.183 | 0.174 | -0.095 | 0.461 |
| Sep | LAST_NH4 | Calibration | PSO | KGE | -0.011 | 0.447 | -0.723 | 0.700 |
| Sep | LAST_NH4 | Validation | Manual | KGE | -0.121 | 0.201 | -1.923 | 1.680 |
| Sep | LAST_NH4 | Validation | NEAT | KGE | -0.022 | 0.218 | -1.984 | 1.941 |
| Sep | LAST_NH4 | Validation | PSO | KGE | -0.130 | 0.009 | -0.210 | -0.051 |
| Sep | LAST_NO3 | Calibration | Manual | KGE | -0.602 | 0.657 | -1.649 | 0.444 |
| Sep | LAST_NO3 | Calibration | NEAT | KGE | -0.066 | 0.327 | -0.587 | 0.455 |
| Sep | LAST_NO3 | Calibration | PSO | KGE | -0.261 | 0.290 | -0.723 | 0.200 |
| Sep | LAST_NO3 | Validation | Manual | KGE | -1.316 | 0.103 | -2.242 | -0.390 |
| Sep | LAST_NO3 | Validation | NEAT | KGE | 0.236 | 0.126 | -0.900 | 1.371 |
| Sep | LAST_NO3 | Validation | PSO | KGE | -0.268 | 0.013 | -0.383 | -0.153 |
| Sep | LAST_TSS | Calibration | Manual | KGE | -0.014 | 0.418 | -0.679 | 0.651 |
| Sep | LAST_TSS | Calibration | NEAT | KGE | -0.316 | 0.514 | -1.133 | 0.502 |
| Sep | LAST_TSS | Calibration | PSO | KGE | -0.202 | 0.524 | -1.037 | 0.632 |
| Sep | LAST_TSS | Validation | Manual | KGE | -0.120 | 0.643 | -5.899 | 5.660 |
| Sep | LAST_TSS | Validation | NEAT | KGE | 0.012 | 0.669 | -6.003 | 6.027 |
| Sep | LAST_TSS | Validation | PSO | KGE | -0.851 | 0.581 | -6.072 | 4.371 |
| Jul | ANOXIC_NO3 | Calibration | Manual | R2 | 0.043 | 0.028 | -0.001 | 0.088 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.013 | 0.014 | -0.009 | 0.035 |
| Jul | ANOXIC_NO3 | Calibration | PSO | R2 | 0.023 | 0.019 | -0.007 | 0.054 |
| Jul | ANOXIC_NO3 | Validation | Manual | R2 | 0.027 | 0.037 | -0.305 | 0.358 |
| Jul | ANOXIC_NO3 | Validation | NEAT | R2 | 0.083 | 0.059 | -0.443 | 0.608 |
| Jul | ANOXIC_NO3 | Validation | PSO | R2 | 0.080 | 0.113 | -0.932 | 1.092 |
| Jul | LAST_NH4 | Calibration | Manual | R2 | 0.017 | 0.018 | -0.011 | 0.045 |
| Jul | LAST_NH4 | Calibration | NEAT | R2 | 0.022 | 0.018 | -0.007 | 0.050 |
| Jul | LAST_NH4 | Calibration | PSO | R2 | 0.035 | 0.036 | -0.022 | 0.093 |
| Jul | LAST_NH4 | Validation | Manual | R2 | 0.035 | 0.026 | -0.197 | 0.267 |
| Jul | LAST_NH4 | Validation | NEAT | R2 | 0.032 | 0.032 | -0.255 | 0.320 |
| Jul | LAST_NH4 | Validation | PSO | R2 | 0.072 | 0.049 | -0.365 | 0.509 |
| Jul | LAST_NO3 | Calibration | Manual | R2 | 0.088 | 0.070 | -0.024 | 0.200 |
| Jul | LAST_NO3 | Calibration | NEAT | R2 | 0.036 | 0.033 | -0.017 | 0.088 |
| Jul | LAST_NO3 | Calibration | PSO | R2 | 0.061 | 0.068 | -0.048 | 0.169 |
| Jul | LAST_NO3 | Validation | Manual | R2 | 0.058 | 0.081 | -0.669 | 0.785 |
| Jul | LAST_NO3 | Validation | NEAT | R2 | 0.111 | 0.073 | -0.548 | 0.770 |
| Jul | LAST_NO3 | Validation | PSO | R2 | 0.119 | 0.119 | -0.952 | 1.189 |
| Jul | LAST_TSS | Calibration | Manual | R2 | 0.142 | 0.095 | -0.009 | 0.293 |
| Jul | LAST_TSS | Calibration | NEAT | R2 | 0.289 | 0.284 | -0.164 | 0.741 |
| Jul | LAST_TSS | Calibration | PSO | R2 | 0.155 | 0.131 | -0.053 | 0.363 |
| Jul | LAST_TSS | Validation | Manual | R2 | 0.050 | 0.055 | -0.446 | 0.545 |
| Jul | LAST_TSS | Validation | NEAT | R2 | 0.175 | 0.071 | -0.463 | 0.813 |
| Jul | LAST_TSS | Validation | PSO | R2 | 0.131 | 0.101 | -0.780 | 1.043 |
| Nov | ANOXIC_NO3 | Calibration | Manual | R2 | 0.115 | 0.215 | -0.228 | 0.457 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.142 | 0.259 | -0.270 | 0.553 |
| Nov | ANOXIC_NO3 | Validation | Manual | R2 | 0.517 | 0.316 | -2.319 | 3.353 |
| Nov | ANOXIC_NO3 | Validation | NEAT | R2 | 0.583 | 0.225 | -1.435 | 2.601 |
| Nov | LAST_NH4 | Calibration | Manual | R2 | 0.184 | 0.330 | -0.342 | 0.709 |
| Nov | LAST_NH4 | Calibration | NEAT | R2 | 0.216 | 0.376 | -0.382 | 0.815 |
| Nov | LAST_NH4 | Validation | Manual | R2 | 0.172 | 0.234 | -1.929 | 2.274 |
| Nov | LAST_NH4 | Validation | NEAT | R2 | 0.211 | 0.296 | -2.444 | 2.867 |
| Nov | LAST_NO3 | Calibration | Manual | R2 | 0.172 | 0.146 | -0.061 | 0.405 |
| Nov | LAST_NO3 | Calibration | NEAT | R2 | 0.176 | 0.184 | -0.116 | 0.469 |
| Nov | LAST_NO3 | Validation | Manual | R2 | 0.380 | 0.120 | -0.702 | 1.461 |
| Nov | LAST_NO3 | Validation | NEAT | R2 | 0.399 | 0.138 | -0.839 | 1.637 |
| Nov | LAST_TSS | Calibration | Manual | R2 | 0.225 | 0.246 | -0.167 | 0.617 |
| Nov | LAST_TSS | Calibration | NEAT | R2 | 0.163 | 0.148 | -0.072 | 0.398 |
| Nov | LAST_TSS | Validation | Manual | R2 | 0.414 | 0.429 | -3.440 | 4.269 |
| Nov | LAST_TSS | Validation | NEAT | R2 | 0.385 | 0.507 | -4.173 | 4.942 |
| Sep | ANOXIC_NO3 | Calibration | Manual | R2 | 0.021 | 0.042 | -0.045 | 0.088 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.022 | 0.032 | -0.029 | 0.073 |
| Sep | ANOXIC_NO3 | Calibration | PSO | R2 | 0.034 | 0.055 | -0.053 | 0.121 |
| Sep | ANOXIC_NO3 | Validation | Manual | R2 | 0.054 | 0.054 | -0.433 | 0.541 |
| Sep | ANOXIC_NO3 | Validation | NEAT | R2 | 0.053 | 0.031 | -0.228 | 0.333 |
| Sep | ANOXIC_NO3 | Validation | PSO | R2 | 0.127 | 0.107 | -0.831 | 1.084 |
| Sep | LAST_NH4 | Calibration | Manual | R2 | 0.175 | 0.333 | -0.355 | 0.705 |
| Sep | LAST_NH4 | Calibration | NEAT | R2 | 0.082 | 0.131 | -0.127 | 0.292 |
| Sep | LAST_NH4 | Calibration | PSO | R2 | 0.131 | 0.256 | -0.276 | 0.538 |
| Sep | LAST_NH4 | Validation | Manual | R2 | 0.097 | 0.104 | -0.833 | 1.027 |
| Sep | LAST_NH4 | Validation | NEAT | R2 | 0.071 | 0.031 | -0.208 | 0.351 |
| Sep | LAST_NH4 | Validation | PSO | R2 | 0.043 | 0.040 | -0.316 | 0.402 |
| Sep | LAST_NO3 | Calibration | Manual | R2 | 0.027 | 0.026 | -0.016 | 0.069 |
| Sep | LAST_NO3 | Calibration | NEAT | R2 | 0.071 | 0.108 | -0.100 | 0.243 |
| Sep | LAST_NO3 | Calibration | PSO | R2 | 0.073 | 0.106 | -0.096 | 0.242 |
| Sep | LAST_NO3 | Validation | Manual | R2 | 0.118 | 0.096 | -0.747 | 0.983 |
| Sep | LAST_NO3 | Validation | NEAT | R2 | 0.166 | 0.106 | -0.786 | 1.119 |
| Sep | LAST_NO3 | Validation | PSO | R2 | 0.192 | 0.061 | -0.353 | 0.738 |
| Sep | LAST_TSS | Calibration | Manual | R2 | 0.225 | 0.174 | -0.053 | 0.502 |
| Sep | LAST_TSS | Calibration | NEAT | R2 | 0.330 | 0.301 | -0.148 | 0.809 |
| Sep | LAST_TSS | Calibration | PSO | R2 | 0.213 | 0.113 | 0.033 | 0.392 |
| Sep | LAST_TSS | Validation | Manual | R2 | 0.238 | 0.226 | -1.793 | 2.269 |
| Sep | LAST_TSS | Validation | NEAT | R2 | 0.266 | 0.340 | -2.788 | 3.320 |
| Sep | LAST_TSS | Validation | PSO | R2 | 0.330 | 0.441 | -3.631 | 4.292 |
| Jul | ANOXIC_NO3 | Calibration | Manual | RMSE | 1.586 | 0.132 | 1.376 | 1.796 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | RMSE | 1.455 | 0.080 | 1.328 | 1.581 |
| Jul | ANOXIC_NO3 | Calibration | PSO | RMSE | 1.407 | 0.096 | 1.255 | 1.559 |
| Jul | ANOXIC_NO3 | Validation | Manual | RMSE | 2.272 | 0.088 | 1.485 | 3.058 |
| Jul | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.453 | 0.038 | 1.114 | 1.793 |
| Jul | ANOXIC_NO3 | Validation | PSO | RMSE | 1.471 | 0.034 | 1.169 | 1.772 |
| Jul | LAST_NH4 | Calibration | Manual | RMSE | 1.022 | 0.222 | 0.668 | 1.376 |
| Jul | LAST_NH4 | Calibration | NEAT | RMSE | 1.075 | 0.303 | 0.592 | 1.557 |
| Jul | LAST_NH4 | Calibration | PSO | RMSE | 0.966 | 0.272 | 0.533 | 1.398 |
| Jul | LAST_NH4 | Validation | Manual | RMSE | 0.825 | 0.069 | 0.210 | 1.441 |
| Jul | LAST_NH4 | Validation | NEAT | RMSE | 0.745 | 0.040 | 0.389 | 1.101 |
| Jul | LAST_NH4 | Validation | PSO | RMSE | 0.683 | 0.060 | 0.146 | 1.220 |
| Jul | LAST_NO3 | Calibration | Manual | RMSE | 5.883 | 1.389 | 3.672 | 8.093 |
| Jul | LAST_NO3 | Calibration | NEAT | RMSE | 2.183 | 0.396 | 1.553 | 2.813 |
| Jul | LAST_NO3 | Calibration | PSO | RMSE | 2.177 | 0.297 | 1.704 | 2.650 |
| Jul | LAST_NO3 | Validation | Manual | RMSE | 9.875 | 0.891 | 1.870 | 17.881 |
| Jul | LAST_NO3 | Validation | NEAT | RMSE | 3.716 | 0.253 | 1.441 | 5.991 |
| Jul | LAST_NO3 | Validation | PSO | RMSE | 4.120 | 0.520 | -0.551 | 8.790 |
| Jul | LAST_TSS | Calibration | Manual | RMSE | 120.484 | 43.606 | 51.097 | 189.872 |
| Jul | LAST_TSS | Calibration | NEAT | RMSE | 177.559 | 111.135 | 0.719 | 354.399 |
| Jul | LAST_TSS | Calibration | PSO | RMSE | 107.442 | 28.792 | 61.628 | 153.256 |
| Jul | LAST_TSS | Validation | Manual | RMSE | 133.965 | 14.904 | 0.056 | 267.874 |
| Jul | LAST_TSS | Validation | NEAT | RMSE | 155.082 | 3.123 | 127.026 | 183.137 |
| Jul | LAST_TSS | Validation | PSO | RMSE | 145.490 | 20.360 | -37.435 | 328.414 |
| Nov | ANOXIC_NO3 | Calibration | Manual | RMSE | 1.028 | 0.244 | 0.639 | 1.416 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | RMSE | 0.828 | 0.128 | 0.625 | 1.032 |
| Nov | ANOXIC_NO3 | Validation | Manual | RMSE | 1.084 | 0.435 | -2.824 | 4.993 |
| Nov | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.091 | 0.067 | 0.486 | 1.696 |
| Nov | LAST_NH4 | Calibration | Manual | RMSE | 1.566 | 0.482 | 0.799 | 2.333 |
| Nov | LAST_NH4 | Calibration | NEAT | RMSE | 1.167 | 0.338 | 0.628 | 1.705 |
| Nov | LAST_NH4 | Validation | Manual | RMSE | 2.457 | 2.013 | -15.631 | 20.544 |
| Nov | LAST_NH4 | Validation | NEAT | RMSE | 1.584 | 0.874 | -6.269 | 9.437 |
| Nov | LAST_NO3 | Calibration | Manual | RMSE | 3.239 | 0.694 | 2.134 | 4.344 |
| Nov | LAST_NO3 | Calibration | NEAT | RMSE | 5.354 | 1.122 | 3.569 | 7.139 |
| Nov | LAST_NO3 | Validation | Manual | RMSE | 5.234 | 0.449 | 1.197 | 9.271 |
| Nov | LAST_NO3 | Validation | NEAT | RMSE | 7.617 | 0.464 | 3.448 | 11.786 |
| Nov | LAST_TSS | Calibration | Manual | RMSE | 177.937 | 51.278 | 96.343 | 259.532 |
| Nov | LAST_TSS | Calibration | NEAT | RMSE | 144.327 | 56.155 | 54.972 | 233.681 |
| Nov | LAST_TSS | Validation | Manual | RMSE | 256.230 | 140.957 | -1010.218 | 1522.677 |
| Nov | LAST_TSS | Validation | NEAT | RMSE | 156.471 | 149.071 | -1182.875 | 1495.816 |
| Sep | ANOXIC_NO3 | Calibration | Manual | RMSE | 0.823 | 0.604 | -0.138 | 1.784 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | RMSE | 2.171 | 0.561 | 1.278 | 3.064 |
| Sep | ANOXIC_NO3 | Calibration | PSO | RMSE | 0.907 | 0.302 | 0.426 | 1.387 |
| Sep | ANOXIC_NO3 | Validation | Manual | RMSE | 1.703 | 0.173 | 0.145 | 3.262 |
| Sep | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.381 | 0.077 | 0.685 | 2.077 |
| Sep | ANOXIC_NO3 | Validation | PSO | RMSE | 1.401 | 0.307 | -1.354 | 4.156 |
| Sep | LAST_NH4 | Calibration | Manual | RMSE | 0.870 | 0.122 | 0.675 | 1.065 |
| Sep | LAST_NH4 | Calibration | NEAT | RMSE | 0.713 | 0.146 | 0.480 | 0.945 |
| Sep | LAST_NH4 | Calibration | PSO | RMSE | 0.997 | 0.324 | 0.482 | 1.512 |
| Sep | LAST_NH4 | Validation | Manual | RMSE | 1.510 | 0.758 | -5.302 | 8.322 |
| Sep | LAST_NH4 | Validation | NEAT | RMSE | 1.508 | 1.160 | -8.913 | 11.929 |
| Sep | LAST_NH4 | Validation | PSO | RMSE | 1.525 | 0.926 | -6.797 | 9.848 |
| Sep | LAST_NO3 | Calibration | Manual | RMSE | 5.633 | 2.759 | 1.243 | 10.023 |
| Sep | LAST_NO3 | Calibration | NEAT | RMSE | 3.251 | 1.461 | 0.926 | 5.576 |
| Sep | LAST_NO3 | Calibration | PSO | RMSE | 4.005 | 1.955 | 0.894 | 7.116 |
| Sep | LAST_NO3 | Validation | Manual | RMSE | 7.178 | 0.473 | 2.929 | 11.427 |
| Sep | LAST_NO3 | Validation | NEAT | RMSE | 2.785 | 0.839 | -4.757 | 10.327 |
| Sep | LAST_NO3 | Validation | PSO | RMSE | 4.102 | 0.515 | -0.523 | 8.726 |
| Sep | LAST_TSS | Calibration | Manual | RMSE | 436.808 | 29.651 | 389.627 | 483.989 |
| Sep | LAST_TSS | Calibration | NEAT | RMSE | 378.341 | 31.405 | 328.369 | 428.313 |
| Sep | LAST_TSS | Calibration | PSO | RMSE | 233.916 | 74.026 | 116.125 | 351.707 |
| Sep | LAST_TSS | Validation | Manual | RMSE | 371.807 | 2.454 | 349.760 | 393.854 |
| Sep | LAST_TSS | Validation | NEAT | RMSE | 228.335 | 30.557 | -46.211 | 502.881 |
| Sep | LAST_TSS | Validation | PSO | RMSE | 191.352 | 65.815 | -399.968 | 782.673 |
| Scenario | Variable | Period | Method | Metric | Mean | SD | CI_Lower | CI_Upper |
| Jul | ANOXIC_NO3 | Calibration | Manual | KGE | -1.923 | 1.146 | -3.748 | -0.099 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | KGE | -0.403 | 0.249 | -0.798 | -0.007 |
| Jul | ANOXIC_NO3 | Validation | Manual | KGE | -6.370 | 3.778 | -40.312 | 27.573 |
| Jul | ANOXIC_NO3 | Validation | NEAT | KGE | -2.266 | 2.179 | -21.846 | 17.313 |
| Jul | LAST_NH4 | Calibration | Manual | KGE | 0.042 | 0.254 | -0.362 | 0.445 |
| Jul | LAST_NH4 | Calibration | NEAT | KGE | -0.056 | 0.095 | -0.206 | 0.095 |
| Jul | LAST_NH4 | Validation | Manual | KGE | -0.443 | 0.939 | -8.880 | 7.994 |
| Jul | LAST_NH4 | Validation | NEAT | KGE | 0.243 | 0.092 | -0.583 | 1.070 |
| Jul | LAST_NO3 | Calibration | Manual | KGE | -0.968 | 0.252 | -1.369 | -0.567 |
| Jul | LAST_NO3 | Calibration | NEAT | KGE | -0.072 | 0.141 | -0.296 | 0.152 |
| Jul | LAST_NO3 | Validation | Manual | KGE | -2.885 | 1.348 | -14.997 | 9.227 |
| Jul | LAST_NO3 | Validation | NEAT | KGE | -0.965 | 1.121 | -11.039 | 9.109 |
| Jul | LAST_TSS | Calibration | Manual | KGE | 0.111 | 0.165 | -0.151 | 0.372 |
| Jul | LAST_TSS | Calibration | NEAT | KGE | 0.035 | 0.118 | -0.153 | 0.223 |
| Jul | LAST_TSS | Validation | Manual | KGE | -0.179 | 0.147 | -1.495 | 1.137 |
| Jul | LAST_TSS | Validation | NEAT | KGE | -0.114 | 0.058 | -0.634 | 0.406 |
| Nov | ANOXIC_NO3 | Calibration | Manual | KGE | -5.624 | 4.183 | -12.280 | 1.031 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | KGE | -2.402 | 1.776 | -5.228 | 0.424 |
| Nov | ANOXIC_NO3 | Validation | Manual | KGE | -3.709 | 2.894 | -29.714 | 22.296 |
| Nov | ANOXIC_NO3 | Validation | NEAT | KGE | -1.272 | 2.264 | -21.615 | 19.071 |
| Nov | LAST_NH4 | Calibration | Manual | KGE | -0.062 | 0.250 | -0.460 | 0.336 |
| Nov | LAST_NH4 | Calibration | NEAT | KGE | 0.332 | 0.465 | -0.408 | 1.071 |
| Nov | LAST_NH4 | Validation | Manual | KGE | -0.887 | 1.199 | -11.658 | 9.885 |
| Nov | LAST_NH4 | Validation | NEAT | KGE | -0.351 | 0.681 | -6.474 | 5.771 |
| Nov | LAST_NO3 | Calibration | Manual | KGE | -0.261 | 0.514 | -1.079 | 0.558 |
| Nov | LAST_NO3 | Calibration | NEAT | KGE | 0.168 | 0.005 | 0.160 | 0.176 |
| Nov | LAST_NO3 | Validation | Manual | KGE | -0.783 | 0.579 | -5.984 | 4.417 |
| Nov | LAST_NO3 | Validation | NEAT | KGE | -0.025 | 0.720 | -6.495 | 6.444 |
| Nov | LAST_TSS | Calibration | Manual | KGE | 0.100 | 0.364 | -0.479 | 0.679 |
| Nov | LAST_TSS | Calibration | NEAT | KGE | 0.079 | 0.528 | -0.760 | 0.919 |
| Nov | LAST_TSS | Validation | Manual | KGE | 0.202 | 0.247 | -2.022 | 2.425 |
| Nov | LAST_TSS | Validation | NEAT | KGE | 0.375 | 0.490 | -4.031 | 4.781 |
| Sep | ANOXIC_NO3 | Calibration | Manual | KGE | -1.548 | 0.636 | -2.560 | -0.535 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | KGE | -1.091 | 1.081 | -2.810 | 0.628 |
| Sep | ANOXIC_NO3 | Validation | Manual | KGE | -1.361 | 0.027 | -1.602 | -1.121 |
| Sep | ANOXIC_NO3 | Validation | NEAT | KGE | -0.231 | 0.077 | -0.921 | 0.459 |
| Sep | LAST_NH4 | Calibration | Manual | KGE | -0.179 | 0.108 | -0.350 | -0.008 |
| Sep | LAST_NH4 | Calibration | NEAT | KGE | 0.239 | 0.152 | -0.003 | 0.481 |
| Sep | LAST_NH4 | Validation | Manual | KGE | -0.300 | 0.064 | -0.874 | 0.274 |
| Sep | LAST_NH4 | Validation | NEAT | KGE | -0.005 | 0.057 | -0.515 | 0.505 |
| Sep | LAST_NO3 | Calibration | Manual | KGE | -0.508 | 0.481 | -1.275 | 0.258 |
| Sep | LAST_NO3 | Calibration | NEAT | KGE | -0.024 | 0.254 | -0.428 | 0.380 |
| Sep | LAST_NO3 | Validation | Manual | KGE | -0.655 | 0.321 | -3.538 | 2.229 |
| Sep | LAST_NO3 | Validation | NEAT | KGE | -0.095 | 0.076 | -0.773 | 0.584 |
| Sep | LAST_TSS | Calibration | Manual | KGE | 0.051 | 0.331 | -0.475 | 0.577 |
| Sep | LAST_TSS | Calibration | NEAT | KGE | -0.073 | 0.368 | -0.659 | 0.512 |
| Sep | LAST_TSS | Validation | Manual | KGE | -0.244 | 0.604 | -5.674 | 5.185 |
| Sep | LAST_TSS | Validation | NEAT | KGE | 0.324 | 0.606 | -5.125 | 5.772 |
| Jul | ANOXIC_NO3 | Calibration | Manual | R2 | 0.010 | 0.008 | -0.003 | 0.023 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.009 | 0.010 | -0.007 | 0.025 |
| Jul | ANOXIC_NO3 | Validation | Manual | R2 | 0.187 | 0.211 | -1.713 | 2.087 |
| Jul | ANOXIC_NO3 | Validation | NEAT | R2 | 0.117 | 0.158 | -1.304 | 1.539 |
| Jul | LAST_NH4 | Calibration | Manual | R2 | 0.067 | 0.050 | -0.012 | 0.147 |
| Jul | LAST_NH4 | Calibration | NEAT | R2 | 0.029 | 0.033 | -0.023 | 0.081 |
| Jul | LAST_NH4 | Validation | Manual | R2 | 0.059 | 0.073 | -0.594 | 0.713 |
| Jul | LAST_NH4 | Validation | NEAT | R2 | 0.089 | 0.077 | -0.604 | 0.782 |
| Jul | LAST_NO3 | Calibration | Manual | R2 | 0.024 | 0.030 | -0.024 | 0.071 |
| Jul | LAST_NO3 | Calibration | NEAT | R2 | 0.012 | 0.021 | -0.021 | 0.046 |
| Jul | LAST_NO3 | Validation | Manual | R2 | 0.259 | 0.238 | -1.880 | 2.398 |
| Jul | LAST_NO3 | Validation | NEAT | R2 | 0.161 | 0.214 | -1.762 | 2.084 |
| Jul | LAST_TSS | Calibration | Manual | R2 | 0.089 | 0.138 | -0.131 | 0.309 |
| Jul | LAST_TSS | Calibration | NEAT | R2 | 0.035 | 0.035 | -0.020 | 0.090 |
| Jul | LAST_TSS | Validation | Manual | R2 | 0.023 | 0.002 | 0.008 | 0.039 |
| Jul | LAST_TSS | Validation | NEAT | R2 | 0.008 | 0.004 | -0.028 | 0.044 |
| Nov | ANOXIC_NO3 | Calibration | Manual | R2 | 0.069 | 0.078 | -0.056 | 0.194 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.058 | 0.066 | -0.046 | 0.163 |
| Nov | ANOXIC_NO3 | Validation | Manual | R2 | 0.131 | 0.001 | 0.118 | 0.143 |
| Nov | ANOXIC_NO3 | Validation | NEAT | R2 | 0.247 | 0.190 | -1.461 | 1.954 |
| Nov | LAST_NH4 | Calibration | Manual | R2 | 0.033 | 0.011 | 0.015 | 0.050 |
| Nov | LAST_NH4 | Calibration | NEAT | R2 | 0.365 | 0.331 | -0.161 | 0.891 |
| Nov | LAST_NH4 | Validation | Manual | R2 | 0.128 | 0.170 | -1.400 | 1.656 |
| Nov | LAST_NH4 | Validation | NEAT | R2 | 0.263 | 0.333 | -2.725 | 3.252 |
| Nov | LAST_NO3 | Calibration | Manual | R2 | 0.186 | 0.163 | -0.073 | 0.445 |
| Nov | LAST_NO3 | Calibration | NEAT | R2 | 0.236 | 0.037 | 0.177 | 0.294 |
| Nov | LAST_NO3 | Validation | Manual | R2 | 0.287 | 0.088 | -0.504 | 1.077 |
| Nov | LAST_NO3 | Validation | NEAT | R2 | 0.337 | 0.027 | 0.090 | 0.583 |
| Nov | LAST_TSS | Calibration | Manual | R2 | 0.090 | 0.070 | -0.022 | 0.201 |
| Nov | LAST_TSS | Calibration | NEAT | R2 | 0.233 | 0.252 | -0.169 | 0.634 |
| Nov | LAST_TSS | Validation | Manual | R2 | 0.369 | 0.323 | -2.531 | 3.270 |
| Nov | LAST_TSS | Validation | NEAT | R2 | 0.519 | 0.389 | -2.974 | 4.012 |
| Sep | ANOXIC_NO3 | Calibration | Manual | R2 | 0.031 | 0.043 | -0.038 | 0.099 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | R2 | 0.040 | 0.039 | -0.022 | 0.101 |
| Sep | ANOXIC_NO3 | Validation | Manual | R2 | 0.133 | 0.030 | -0.137 | 0.402 |
| Sep | ANOXIC_NO3 | Validation | NEAT | R2 | 0.141 | 0.087 | -0.643 | 0.925 |
| Sep | LAST_NH4 | Calibration | Manual | R2 | 0.025 | 0.015 | 0.001 | 0.049 |
| Sep | LAST_NH4 | Calibration | NEAT | R2 | 0.205 | 0.305 | -0.279 | 0.690 |
| Sep | LAST_NH4 | Validation | Manual | R2 | 0.067 | 0.053 | -0.408 | 0.541 |
| Sep | LAST_NH4 | Validation | NEAT | R2 | 0.115 | 0.044 | -0.282 | 0.511 |
| Sep | LAST_NO3 | Calibration | Manual | R2 | 0.056 | 0.042 | -0.011 | 0.123 |
| Sep | LAST_NO3 | Calibration | NEAT | R2 | 0.077 | 0.073 | -0.040 | 0.194 |
| Sep | LAST_NO3 | Validation | Manual | R2 | 0.113 | 0.038 | -0.230 | 0.455 |
| Sep | LAST_NO3 | Validation | NEAT | R2 | 0.182 | 0.085 | -0.584 | 0.949 |
| Sep | LAST_TSS | Calibration | Manual | R2 | 0.140 | 0.180 | -0.146 | 0.426 |
| Sep | LAST_TSS | Calibration | NEAT | R2 | 0.245 | 0.254 | -0.160 | 0.650 |
| Sep | LAST_TSS | Validation | Manual | R2 | 0.167 | 0.002 | 0.146 | 0.188 |
| Sep | LAST_TSS | Validation | NEAT | R2 | 0.350 | 0.320 | -2.527 | 3.226 |
| Jul | ANOXIC_NO3 | Calibration | Manual | RMSE | 2.821 | 0.759 | 1.614 | 4.029 |
| Jul | ANOXIC_NO3 | Calibration | NEAT | RMSE | 1.348 | 0.083 | 1.216 | 1.480 |
| Jul | ANOXIC_NO3 | Validation | Manual | RMSE | 4.492 | 1.441 | -8.452 | 17.436 |
| Jul | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.786 | 1.021 | -7.385 | 10.957 |
| Jul | LAST_NH4 | Calibration | Manual | RMSE | 0.932 | 0.316 | 0.429 | 1.436 |
| Jul | LAST_NH4 | Calibration | NEAT | RMSE | 0.873 | 0.291 | 0.410 | 1.336 |
| Jul | LAST_NH4 | Validation | Manual | RMSE | 0.923 | 0.467 | -3.269 | 5.114 |
| Jul | LAST_NH4 | Validation | NEAT | RMSE | 0.517 | 0.056 | 0.018 | 1.016 |
| Jul | LAST_NO3 | Calibration | Manual | RMSE | 5.392 | 1.125 | 3.602 | 7.183 |
| Jul | LAST_NO3 | Calibration | NEAT | RMSE | 2.516 | 0.269 | 2.088 | 2.943 |
| Jul | LAST_NO3 | Validation | Manual | RMSE | 7.471 | 1.370 | -4.834 | 19.776 |
| Jul | LAST_NO3 | Validation | NEAT | RMSE | 3.532 | 1.615 | -10.979 | 18.043 |
| Jul | LAST_TSS | Calibration | Manual | RMSE | 122.193 | 37.477 | 62.559 | 181.827 |
| Jul | LAST_TSS | Calibration | NEAT | RMSE | 107.589 | 19.198 | 77.041 | 138.137 |
| Jul | LAST_TSS | Validation | Manual | RMSE | 143.350 | 14.828 | 10.127 | 276.572 |
| Jul | LAST_TSS | Validation | NEAT | RMSE | 146.485 | 1.829 | 130.054 | 162.916 |
| Nov | ANOXIC_NO3 | Calibration | Manual | RMSE | 2.829 | 1.075 | 1.118 | 4.540 |
| Nov | ANOXIC_NO3 | Calibration | NEAT | RMSE | 2.073 | 0.244 | 1.685 | 2.462 |
| Nov | ANOXIC_NO3 | Validation | Manual | RMSE | 4.126 | 0.013 | 4.008 | 4.244 |
| Nov | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.861 | 0.980 | -6.940 | 10.662 |
| Nov | LAST_NH4 | Calibration | Manual | RMSE | 2.049 | 1.652 | -0.580 | 4.679 |
| Nov | LAST_NH4 | Calibration | NEAT | RMSE | 1.158 | 0.564 | 0.261 | 2.055 |
| Nov | LAST_NH4 | Validation | Manual | RMSE | 2.325 | 1.952 | -15.217 | 19.867 |
| Nov | LAST_NH4 | Validation | NEAT | RMSE | 1.607 | 1.259 | -9.706 | 12.919 |
| Nov | LAST_NO3 | Calibration | Manual | RMSE | 4.292 | 1.113 | 2.520 | 6.064 |
| Nov | LAST_NO3 | Calibration | NEAT | RMSE | 5.129 | 0.213 | 4.790 | 5.468 |
| Nov | LAST_NO3 | Validation | Manual | RMSE | 6.247 | 1.346 | -5.850 | 18.343 |
| Nov | LAST_NO3 | Validation | NEAT | RMSE | 3.439 | 1.385 | -9.001 | 15.880 |
| Nov | LAST_TSS | Calibration | Manual | RMSE | 172.790 | 37.397 | 113.283 | 232.297 |
| Nov | LAST_TSS | Calibration | NEAT | RMSE | 119.319 | 55.946 | 30.297 | 208.340 |
| Nov | LAST_TSS | Validation | Manual | RMSE | 141.745 | 119.131 | -928.600 | 1212.091 |
| Nov | LAST_TSS | Validation | NEAT | RMSE | 132.240 | 107.920 | -837.386 | 1101.865 |
| Sep | ANOXIC_NO3 | Calibration | Manual | RMSE | 1.633 | 0.730 | 0.471 | 2.794 |
| Sep | ANOXIC_NO3 | Calibration | NEAT | RMSE | 1.541 | 0.556 | 0.656 | 2.426 |
| Sep | ANOXIC_NO3 | Validation | Manual | RMSE | 2.587 | 0.152 | 1.224 | 3.950 |
| Sep | ANOXIC_NO3 | Validation | NEAT | RMSE | 1.437 | 0.301 | -1.266 | 4.139 |
| Sep | LAST_NH4 | Calibration | Manual | RMSE | 1.111 | 0.409 | 0.460 | 1.762 |
| Sep | LAST_NH4 | Calibration | NEAT | RMSE | 0.769 | 0.139 | 0.548 | 0.990 |
| Sep | LAST_NH4 | Validation | Manual | RMSE | 1.667 | 1.059 | -7.849 | 11.182 |
| Sep | LAST_NH4 | Validation | NEAT | RMSE | 1.500 | 0.963 | -7.150 | 10.149 |
| Sep | LAST_NO3 | Calibration | Manual | RMSE | 4.096 | 1.497 | 1.714 | 6.477 |
| Sep | LAST_NO3 | Calibration | NEAT | RMSE | 3.601 | 0.898 | 2.172 | 5.029 |
| Sep | LAST_NO3 | Validation | Manual | RMSE | 5.198 | 0.619 | -0.360 | 10.755 |
| Sep | LAST_NO3 | Validation | NEAT | RMSE | 3.476 | 0.528 | -1.271 | 8.222 |
| Sep | LAST_TSS | Calibration | Manual | RMSE | 407.389 | 35.310 | 351.203 | 463.575 |
| Sep | LAST_TSS | Calibration | NEAT | RMSE | 364.218 | 47.415 | 288.770 | 439.665 |
| Sep | LAST_TSS | Validation | Manual | RMSE | 265.179 | 17.207 | 110.583 | 419.776 |
| Sep | LAST_TSS | Validation | NEAT | RMSE | 166.267 | 85.339 | -600.470 | 933.003 |
Appendix D. Paired T-Test Statistical Comparison
| Scenario | Jul | Sep | Nov | Jul | Sep | Nov | Jul | Sep | Nov |
| Comparison | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual |
| Metric | KGE | KGE | KGE | R2 | R2 | R2 | RMSE | RMSE | RMSE |
| Mean_Difference | 0.266 | 0.141 | 0.160 | 0.031 | 0.014 | 0.008 | 10.054 | -22.292 | -13.536 |
| SD | 0.692 | 0.713 | 0.698 | 0.109 | 0.122 | 0.073 | 48.724 | 44.960 | 35.794 |
| Cohens_d | 0.384 | 0.198 | 0.229 | 0.282 | 0.113 | 0.113 | 0.206 | -0.496 | -0.378 |
| T_Statistic | 1.880 | 0.972 | 1.123 | 1.379 | 0.555 | 0.552 | 1.011 | -2.429 | -1.853 |
| P_Value | 0.073 | 0.341 | 0.273 | 0.181 | 0.584 | 0.586 | 0.323 | 0.023 | 0.077 |
| CI_Lower | -0.027 | -0.160 | -0.135 | -0.015 | -0.038 | -0.022 | -10.520 | -41.277 | -28.651 |
| CI_Upper | 0.558 | 0.442 | 0.455 | 0.077 | 0.065 | 0.039 | 30.629 | -3.307 | 1.579 |
| N_Pairs | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
| P_Value_Raw | 0.073 | 0.341 | 0.273 | 0.181 | 0.584 | 0.586 | 0.323 | 0.023 | 0.077 |
| P_Value_FDR | 0.218 | 0.341 | 0.341 | 0.543 | 0.586 | 0.586 | 0.323 | 0.070 | 0.115 |
| Significant_Raw | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE | TRUE | FALSE |
| Significant_FDR | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE | FALSE |
| Scenario | Jul | Sep | Nov | Jul | Sep | Nov | Jul | Sep | Nov |
| Comparison | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual | NEAT vs Manual |
| Metric | KGE | KGE | KGE | R2 | R2 | R2 | RMSE | RMSE | RMSE |
| Mean_Difference | 0.939 | 0.419 | 0.996 | -0.030 | 0.078 | 0.123 | -3.495 | -15.846 | -10.322 |
| SD | 1.314 | 0.477 | 1.643 | 0.059 | 0.198 | 0.205 | 11.460 | 34.764 | 25.960 |
| Cohens_d | 0.714 | 0.877 | 0.606 | -0.511 | 0.396 | 0.603 | -0.305 | -0.456 | -0.398 |
| T_Statistic | 3.500 | 4.295 | 2.970 | -2.502 | 1.938 | 2.952 | -1.494 | -2.233 | -1.948 |
| P_Value | 0.002 | 0.000 | 0.007 | 0.020 | 0.065 | 0.007 | 0.149 | 0.036 | 0.064 |
| CI_Lower | 0.384 | 0.217 | 0.302 | -0.055 | -0.005 | 0.037 | -8.335 | -30.526 | -21.284 |
| CI_Upper | 1.493 | 0.620 | 1.690 | -0.005 | 0.162 | 0.210 | 1.344 | -1.166 | 0.640 |
| N_Pairs | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 | 24 |
| P_Value_Raw | 0.002 | 0.000 | 0.007 | 0.020 | 0.065 | 0.007 | 0.149 | 0.036 | 0.064 |
| P_Value_FDR | 0.003 | 0.001 | 0.007 | 0.030 | 0.065 | 0.021 | 0.149 | 0.096 | 0.096 |
| Significant_Raw | TRUE | TRUE | TRUE | TRUE | FALSE | TRUE | FALSE | TRUE | FALSE |
| Significant_FDR | TRUE | TRUE | TRUE | TRUE | FALSE | TRUE | FALSE | FALSE | FALSE |
Appendix E. Mixed-Effects Model Interaction Analysis
| Effect | Estimate | P_Value | CI_Lower | CI_Upper | P_Value_FDR | Significant_FDR | Metric |
| Intercept | -0.62 | 0.00 | -0.92 | -0.32 | 0.00 | TRUE | KGE |
| Method[T.NEAT] | 0.11 | 0.51 | -0.22 | 0.43 | 0.75 | FALSE | KGE |
| Method[T.PSO] | 0.15 | 0.42 | -0.22 | 0.53 | 0.72 | FALSE | KGE |
| Variable[T.LAST_NH4] | 0.50 | 0.00 | 0.18 | 0.83 | 0.02 | TRUE | KGE |
| Variable[T.LAST_NO3] | -0.22 | 0.18 | -0.55 | 0.10 | 0.42 | FALSE | KGE |
| Variable[T.LAST_TSS] | 0.76 | 0.00 | 0.44 | 1.09 | 0.00 | TRUE | KGE |
| Scenario[T.Nov] | 0.09 | 0.57 | -0.21 | 0.39 | 0.78 | FALSE | KGE |
| Scenario[T.Sep] | 0.11 | 0.40 | -0.15 | 0.38 | 0.72 | FALSE | KGE |
| Period[T.Validation] | -0.28 | 0.01 | -0.50 | -0.06 | 0.06 | FALSE | KGE |
| Method[T.NEAT]:Variable[T.LAST_NH4] | 0.02 | 0.94 | -0.44 | 0.48 | 0.99 | FALSE | KGE |
| Method[T.PSO]:Variable[T.LAST_NH4] | -0.03 | 0.89 | -0.55 | 0.48 | 0.99 | FALSE | KGE |
| Method[T.NEAT]:Variable[T.LAST_NO3] | 0.47 | 0.05 | 0.01 | 0.93 | 0.18 | FALSE | KGE |
| Method[T.PSO]:Variable[T.LAST_NO3] | 0.45 | 0.09 | -0.07 | 0.96 | 0.24 | FALSE | KGE |
| Method[T.NEAT]:Variable[T.LAST_TSS] | -0.16 | 0.48 | -0.62 | 0.30 | 0.75 | FALSE | KGE |
| Method[T.PSO]:Variable[T.LAST_TSS] | -0.49 | 0.06 | -1.00 | 0.02 | 0.19 | FALSE | KGE |
| Group Var | 0.21 | 0.27 | -0.16 | 0.58 | 0.57 | FALSE | KGE |
| Group x Method[T.NEAT] Cov | -0.03 | 0.88 | -0.38 | 0.33 | 0.99 | FALSE | KGE |
| Method[T.NEAT] Var | 0.00 | 0.99 | -0.51 | 0.51 | 0.99 | FALSE | KGE |
| Group x Method[T.PSO] Cov | -0.09 | FALSE | KGE | ||||
| Method[T.NEAT] x Method[T.PSO] Cov | 0.01 | 0.95 | -0.40 | 0.42 | 0.99 | FALSE | KGE |
| Method[T.PSO] Var | 0.04 | FALSE | KGE | ||||
| Intercept | 0.00 | 0.95 | -0.12 | 0.13 | 1.00 | FALSE | R2 |
| Method[T.NEAT] | 0.01 | 0.77 | -0.07 | 0.10 | 1.00 | FALSE | R2 |
| Method[T.PSO] | -0.01 | 0.92 | -0.10 | 0.09 | 1.00 | FALSE | R2 |
| Variable[T.LAST_NH4] | 0.01 | 0.80 | -0.07 | 0.10 | 1.00 | FALSE | R2 |
| Variable[T.LAST_NO3] | 0.02 | 0.66 | -0.07 | 0.10 | 1.00 | FALSE | R2 |
| Variable[T.LAST_TSS] | 0.10 | 0.02 | 0.02 | 0.19 | 0.30 | FALSE | R2 |
| Scenario[T.Nov] | 0.17 | 0.04 | 0.01 | 0.33 | 0.31 | FALSE | R2 |
| Scenario[T.Sep] | 0.05 | 0.45 | -0.09 | 0.19 | 1.00 | FALSE | R2 |
| Period[T.Validation] | 0.08 | 0.20 | -0.04 | 0.21 | 0.84 | FALSE | R2 |
| Method[T.NEAT]:Variable[T.LAST_NH4] | -0.02 | 0.70 | -0.14 | 0.10 | 1.00 | FALSE | R2 |
| Method[T.PSO]:Variable[T.LAST_NH4] | 0.01 | 0.88 | -0.12 | 0.15 | 1.00 | FALSE | R2 |
| Method[T.NEAT]:Variable[T.LAST_NO3] | 0.00 | 1.00 | -0.12 | 0.12 | 1.00 | FALSE | R2 |
| Method[T.PSO]:Variable[T.LAST_NO3] | 0.02 | 0.73 | -0.11 | 0.16 | 1.00 | FALSE | R2 |
| Method[T.NEAT]:Variable[T.LAST_TSS] | 0.04 | 0.48 | -0.08 | 0.16 | 1.00 | FALSE | R2 |
| Method[T.PSO]:Variable[T.LAST_TSS] | 0.04 | 0.54 | -0.09 | 0.18 | 1.00 | FALSE | R2 |
| Group Var | 0.99 | 0.16 | -0.38 | 2.36 | 0.84 | FALSE | R2 |
| Group x Method[T.NEAT] Cov | 0.03 | 0.95 | -0.95 | 1.01 | 1.00 | FALSE | R2 |
| Method[T.NEAT] Var | 0.00 | FALSE | R2 | ||||
| Group x Method[T.PSO] Cov | -0.20 | FALSE | R2 | ||||
| Method[T.NEAT] x Method[T.PSO] Cov | -0.01 | FALSE | R2 | ||||
| Method[T.PSO] Var | 0.04 | FALSE | R2 | ||||
| Intercept | -13.33 | 0.27 | -37.02 | 10.36 | 1.00 | FALSE | RMSE |
| Method[T.NEAT] | 0.10 | 1.00 | -34.90 | 35.10 | 1.00 | FALSE | RMSE |
| Method[T.PSO] | -7.01 | 0.73 | -46.71 | 32.69 | 1.00 | FALSE | RMSE |
| Variable[T.LAST_NH4] | -0.02 | 1.00 | -35.03 | 34.98 | 1.00 | FALSE | RMSE |
| Variable[T.LAST_NO3] | 4.43 | 0.80 | -30.57 | 39.43 | 1.00 | FALSE | RMSE |
| Variable[T.LAST_TSS] | 246.73 | 0.00 | 211.72 | 281.73 | 0.00 | TRUE | RMSE |
| Scenario[T.Nov] | 2.05 | 0.81 | -14.64 | 18.73 | 1.00 | FALSE | RMSE |
| Scenario[T.Sep] | 45.70 | FALSE | RMSE | ||||
| Period[T.Validation] | -3.78 | 0.65 | -20.05 | 12.49 | 1.00 | FALSE | RMSE |
| Method[T.NEAT]:Variable[T.LAST_NH4] | -0.32 | 0.99 | -49.82 | 49.18 | 1.00 | FALSE | RMSE |
| Method[T.PSO]:Variable[T.LAST_NH4] | -0.20 | 0.99 | -55.55 | 55.14 | 1.00 | FALSE | RMSE |
| Method[T.NEAT]:Variable[T.LAST_NO3] | -1.89 | 0.94 | -51.39 | 47.61 | 1.00 | FALSE | RMSE |
| Method[T.PSO]:Variable[T.LAST_NO3] | -2.25 | 0.94 | -57.59 | 53.10 | 1.00 | FALSE | RMSE |
| Method[T.NEAT]:Variable[T.LAST_TSS] | -32.56 | 0.20 | -82.06 | 16.94 | 1.00 | FALSE | RMSE |
| Method[T.PSO]:Variable[T.LAST_TSS] | -78.05 | 0.01 | -133.39 | -22.71 | 0.05 | FALSE | RMSE |
| Group Var | 0.00 | 1.00 | -0.38 | 0.38 | 1.00 | FALSE | RMSE |
| Group x Method[T.NEAT] Cov | 0.00 | 1.00 | -0.18 | 0.18 | 1.00 | FALSE | RMSE |
| Method[T.NEAT] Var | 0.00 | FALSE | RMSE | ||||
| Group x Method[T.PSO] Cov | 0.00 | 1.00 | -0.65 | 0.65 | 1.00 | FALSE | RMSE |
| Method[T.NEAT] x Method[T.PSO] Cov | 0.00 | FALSE | RMSE | ||||
| Method[T.PSO] Var | 0.00 | 1.00 | -1.18 | 1.18 | 1.00 | FALSE | RMSE |
| Effect | Estimate | P_Value | CI_Lower | CI_Upper | P_Value_FDR | Significant_FDR | Metric |
| Intercept | -3.30 | 0.00 | -4.05 | -2.54 | 0.00 | TRUE | KGE |
| Method[T.NEAT] | 2.01 | 0.00 | 1.26 | 2.76 | 0.00 | TRUE | KGE |
| Variable[T.LAST_NH4] | 3.07 | 0.00 | 2.34 | 3.80 | 0.00 | TRUE | KGE |
| Variable[T.LAST_NO3] | 2.43 | 0.00 | 1.70 | 3.16 | 0.00 | TRUE | KGE |
| Variable[T.LAST_TSS] | 3.33 | 0.00 | 2.60 | 4.06 | 0.00 | TRUE | KGE |
| Scenario[T.Nov] | -0.08 | 0.81 | -0.78 | 0.61 | 0.81 | FALSE | KGE |
| Scenario[T.Sep] | 0.31 | 0.37 | -0.37 | 1.00 | 0.52 | FALSE | KGE |
| Period[T.Validation] | -0.21 | 0.48 | -0.80 | 0.38 | 0.52 | FALSE | KGE |
| Method[T.NEAT]:Variable[T.LAST_NH4] | -1.68 | 0.00 | -2.71 | -0.65 | 0.00 | TRUE | KGE |
| Method[T.NEAT]:Variable[T.LAST_NO3] | -1.25 | 0.02 | -2.28 | -0.21 | 0.03 | TRUE | KGE |
| Method[T.NEAT]:Variable[T.LAST_TSS] | -1.97 | 0.00 | -3.00 | -0.93 | 0.00 | TRUE | KGE |
| Group Var | 0.39 | 0.15 | -0.15 | 0.93 | 0.24 | FALSE | KGE |
| Group x Method[T.NEAT] Cov | -0.21 | 0.48 | -0.78 | 0.37 | 0.52 | FALSE | KGE |
| Method[T.NEAT] Var | 0.11 | 0.45 | -0.17 | 0.39 | 0.52 | FALSE | KGE |
| Intercept | 0.00 | 1.00 | -0.09 | 0.09 | 1.00 | FALSE | R2 |
| Method[T.NEAT] | 0.01 | 0.91 | -0.09 | 0.10 | 1.00 | FALSE | R2 |
| Variable[T.LAST_NH4] | -0.02 | 0.67 | -0.10 | 0.07 | 1.00 | FALSE | R2 |
| Variable[T.LAST_NO3] | 0.06 | 0.18 | -0.03 | 0.14 | 0.50 | FALSE | R2 |
| Variable[T.LAST_TSS] | 0.06 | 0.17 | -0.03 | 0.14 | 0.50 | FALSE | R2 |
| Scenario[T.Nov] | 0.10 | 0.08 | -0.01 | 0.21 | 0.35 | FALSE | R2 |
| Scenario[T.Sep] | 0.03 | 0.48 | -0.06 | 0.12 | 0.95 | FALSE | R2 |
| Period[T.Validation] | 0.09 | 0.00 | 0.03 | 0.15 | 0.02 | TRUE | R2 |
| Method[T.NEAT]:Variable[T.LAST_NH4] | 0.12 | 0.04 | 0.00 | 0.24 | 0.30 | FALSE | R2 |
| Method[T.NEAT]:Variable[T.LAST_NO3] | 0.01 | 0.87 | -0.11 | 0.13 | 1.00 | FALSE | R2 |
| Method[T.NEAT]:Variable[T.LAST_TSS] | 0.07 | 0.23 | -0.05 | 0.19 | 0.54 | FALSE | R2 |
| Group Var | 0.00 | 1.00 | -0.59 | 0.59 | 1.00 | FALSE | R2 |
| Group x Method[T.NEAT] Cov | 0.00 | 1.00 | -0.97 | 0.97 | 1.00 | FALSE | R2 |
| Method[T.NEAT] Var | 0.52 | 0.54 | -1.16 | 2.21 | 0.95 | FALSE | R2 |
| Intercept | -11.70 | 0.41 | -39.65 | 16.24 | 0.91 | FALSE | RMSE |
| Method[T.NEAT] | -1.20 | 0.95 | -35.99 | 33.60 | 0.99 | FALSE | RMSE |
| Variable[T.LAST_NH4] | -1.41 | 0.94 | -36.20 | 33.38 | 0.99 | FALSE | RMSE |
| Variable[T.LAST_NO3] | 2.30 | 0.90 | -32.49 | 37.09 | 0.99 | FALSE | RMSE |
| Variable[T.LAST_TSS] | 214.36 | 0.00 | 179.57 | 249.15 | 0.00 | TRUE | RMSE |
| Scenario[T.Nov] | 4.87 | 0.65 | -16.08 | 25.83 | 0.99 | FALSE | RMSE |
| Scenario[T.Sep] | 50.84 | 0.00 | 30.70 | 70.97 | 0.00 | TRUE | RMSE |
| Period[T.Validation] | -12.01 | 0.20 | -30.46 | 6.44 | 0.56 | FALSE | RMSE |
| Method[T.NEAT]:Variable[T.LAST_NH4] | 0.77 | 0.98 | -48.44 | 49.97 | 0.99 | FALSE | RMSE |
| Method[T.NEAT]:Variable[T.LAST_NO3] | -0.31 | 0.99 | -49.51 | 48.90 | 0.99 | FALSE | RMSE |
| Method[T.NEAT]:Variable[T.LAST_TSS] | -35.22 | 0.16 | -84.43 | 13.98 | 0.56 | FALSE | RMSE |
| Group Var | 0.00 | FALSE | RMSE | ||||
| Group x Method[T.NEAT] Cov | 0.00 | FALSE | RMSE | ||||
| Method[T.NEAT] Var | 0.00 | FALSE | RMSE |
Appendix F. Parameter Stability Classification
| Parameter | Group | CV_% | Range width | Classification | Mean_Dev_from_Default_% | Mean_Dev_from_Manual_% |
| i_N_BM | Nitrogen Content | 0.00 | 0 | Stable | 7.14 | 7.14 |
| K_NH_AUT | Half-Saturation | 0.00 | 0 | Stable | 66.00 | 580.00 |
| K_fe | Half-Saturation | 0.00 | 0 | Stable | 12.50 | 12.50 |
| i_TSS_BM | TSS Fractions | 2.80 | 0.04 | Stable | 8.52 | 8.52 |
| in.f_S_F | Influent Fractions | 4.45 | 0.03 | Stable | 11.97 | 11.97 |
| in.F_VSS_TSS | Influent Fractions | 4.95 | 0.06 | Stable | 5.41 | 5.41 |
| PST.E_R_XCOD_DW | Settler (PST) | 6.67 | 0.1 | Stable | 11.76 | 11.76 |
| i_N_X_S | Nitrogen Content | 7.53 | 0.005 | Stable | 4.17 | 4.17 |
| i_TSS_X_I | TSS Fractions | 8.07 | 0.13 | Stable | 8.44 | 8.44 |
| K_NH | Half-Saturation | 8.66 | 0.01 | Stable | 33.33 | 33.33 |
| i_N_X_I | Nitrogen Content | 8.77 | 0.004 | Stable | 31.67 | 31.67 |
| i_TSS_X_S | TSS Fractions | 8.92 | 0.13 | Stable | 6.22 | 6.22 |
| Y_AUT | Growth & Yield | 12.37 | 0.05 | Moderate | 8.33 | 8.33 |
| K_NO | Half-Saturation | 13.32 | 0.1 | Moderate | 13.33 | 13.33 |
| SST.v0 | Settler (SST) | 13.50 | 113 | Moderate | 11.81 | 11.81 |
| Y_H | Growth & Yield | 14.07 | 0.13 | Moderate | 14.67 | 14.67 |
| in.f_S_A | Influent Fractions | 17.27 | 0.13 | Moderate | 11.40 | 11.40 |
| mu_H | Growth & Yield | 21.98 | 2.3 | Variable | 17.22 | 17.22 |
| i_N_S_I | Nitrogen Content | 23.41 | 0.005 | Variable | 30.00 | 62.63 |
| mu_AUT | Growth & Yield | 24.05 | 0.5 | Variable | 23.33 | 23.33 |
| in.f_X_S | Influent Fractions | 25.80 | 0.27 | Variable | 27.91 | 27.91 |
| i_N_S_F | Nitrogen Content | 26.49 | 0.013 | Variable | 21.11 | 21.11 |
| PST.E_R_XII_DW | Settler (PST) | 26.96 | 0.25 | Variable | 20.26 | 20.26 |
| K_O | Half-Saturation | 33.86 | 0.13 | Variable | 25.00 | 25.00 |
| b_H | Decay Rates | 37.78 | 0.34 | Variable | 32.50 | 32.50 |
| k_h | Growth & Yield | 39.61 | 2.6 | Variable | 35.56 | 35.56 |
| SST.r_H | Settler (SST) | 42.86 | 0.0006 | Variable | 41.90 | 41.90 |
| SST.r_P | Settler (SST) | 44.95 | 0.0041 | Variable | 84.15 | 84.15 |
| SST.f_ns | Settler (SST) | 45.83 | 0.0009 | Variable | 338.60 | 338.60 |
| b_AUT | Decay Rates | 51.63 | 0.11 | Variable | 33.33 | 33.33 |
| K_F | Half-Saturation | 53.99 | 2.6 | Variable | 38.33 | 38.33 |
| K_O_AUT | Half-Saturation | 57.74 | 0.3 | Variable | 40.00 | 40.00 |
| K_X | Half-Saturation | 61.49 | 0.09 | Variable | 40.00 | 40.00 |
| Parameter | Group | CV_% | Range | Classification | Mean_Dev_from_Default_% | Mean_Dev_from_Manual_% |
| in.f_S_A | Influent Fractions | 0.00 | 0 | Stable | 15.79 | 15.79 |
| K_X | Half-Saturation | 0.00 | 0 | Stable | 10.00 | 10.00 |
| in.F_VSS_TSS | Influent Fractions | 2.44 | 0.03 | Stable | 4.05 | 4.05 |
| PST.E_R_XCOD_DW | Settler (PST) | 4.03 | 0.05 | Stable | 15.69 | 15.69 |
| i_TSS_X_I | TSS Fractions | 4.81 | 0.06 | Stable | 4.00 | 4.00 |
| i_TSS_X_S | TSS Fractions | 6.55 | 0.09 | Stable | 6.67 | 6.67 |
| SST.v0 | Settler (SST) | 7.09 | 56 | Stable | 4.01 | 4.01 |
| i_TSS_BM | TSS Fractions | 7.23 | 0.11 | Stable | 12.59 | 12.59 |
| i_N_X_I | Nitrogen Content | 9.12 | 0.003 | Stable | 8.33 | 8.33 |
| i_N_X_S | Nitrogen Content | 9.12 | 0.005 | Stable | 20.83 | 20.83 |
| in.f_S_F | Influent Fractions | 11.45 | 0.07 | Moderate | 21.37 | 21.37 |
| K_NO | Half-Saturation | 13.32 | 0.1 | Moderate | 13.33 | 13.33 |
| K_fe | Half-Saturation | 14.29 | 1 | Moderate | 12.50 | 12.50 |
| Y_H | Growth & Yield | 14.58 | 0.13 | Moderate | 26.93 | 26.93 |
| b_H | Decay Rates | 15.85 | 0.17 | Moderate | 34.17 | 34.17 |
| i_N_S_F | Nitrogen Content | 15.91 | 0.009 | Moderate | 12.22 | 12.22 |
| in.f_X_S | Influent Fractions | 16.25 | 0.17 | Moderate | 21.71 | 21.71 |
| PST.E_R_XII_DW | Settler (PST) | 16.37 | 0.15 | Moderate | 13.73 | 13.73 |
| SST.r_P | Settler (SST) | 17.86 | 0.001 | Moderate | 13.05 | 13.05 |
| i_N_BM | Nitrogen Content | 18.90 | 0.025 | Moderate | 14.29 | 14.29 |
| mu_AUT | Growth & Yield | 20.15 | 0.4 | Variable | 16.67 | 16.67 |
| Y_AUT | Growth & Yield | 22.91 | 0.12 | Variable | 22.22 | 22.22 |
| K_F | Half-Saturation | 24.74 | 1.8 | Variable | 18.33 | 18.33 |
| K_O | Half-Saturation | 26.28 | 0.13 | Variable | 33.33 | 33.33 |
| SST.f_ns | Settler (SST) | 27.27 | 0.0006 | Variable | 382.46 | 382.46 |
| i_N_S_I | Nitrogen Content | 27.32 | 0.013 | Variable | 140.00 | 27.27 |
| K_O_AUT | Half-Saturation | 33.33 | 0.2 | Variable | 40.00 | 40.00 |
| SST.r_H | Settler (SST) | 34.64 | 0.0003 | Variable | 18.75 | 18.75 |
| mu_H | Growth & Yield | 35.34 | 4.5 | Variable | 27.22 | 27.22 |
| K_NH | Half-Saturation | 39.03 | 0.04 | Variable | 33.33 | 33.33 |
| k_h | Growth & Yield | 46.21 | 3.5 | Variable | 55.56 | 55.56 |
| K_NH_AUT | Half-Saturation | 69.47 | 0.58 | Variable | 56.67 | 766.67 |
| b_AUT | Decay Rates | 81.34 | 0.23 | Variable | 60.00 | 60.00 |
| Scenario | All | All | Jul | Sep | Nov | Jul | Sep | Nov | Jul | Sep |
| Model | Both | Both | CM | CM | CM | TIS | TIS | TIS | CM | CM |
| Method | Default | Manual | NEAT | NEAT | NEAT | NEAT | NEAT | NEAT | PSO | PSO |
| .i_N_BM | 0.07 | 0.07 | 0.075 | 0.075 | 0.075 | 0.065 | 0.085 | 0.06 | 0.06 | 0.055 |
| .i_N_S_F | 0.03 | 0.03 | 0.037 | 0.024 | 0.024 | 0.033 | 0.028 | 0.024 | 0.033 | 0.019 |
| .i_N_S_I | 0.01 | 0.033 | 0.014 | 0.009 | 0.014 | 0.018 | 0.023 | 0.031 | 0.005 | 0.031 |
| .i_N_X_I | 0.02 | 0.02 | 0.025 | 0.029 | 0.025 | 0.018 | 0.021 | 0.018 | 0.025 | 0.029 |
| .i_N_X_S | 0.04 | 0.04 | 0.035 | 0.04 | 0.04 | 0.03 | 0.035 | 0.03 | 0.045 | 0.025 |
| .i_TSS_BM | 0.9 | 0.9 | 0.85 | 0.81 | 0.81 | 0.77 | 0.74 | 0.85 | 0.81 | 0.85 |
| .i_TSS_X_I | 0.75 | 0.75 | 0.81 | 0.74 | 0.87 | 0.74 | 0.74 | 0.68 | 0.68 | 0.65 |
| .i_TSS_X_S | 0.75 | 0.75 | 0.74 | 0.84 | 0.71 | 0.71 | 0.65 | 0.74 | 0.74 | 0.68 |
| .K_F | 4 | 4 | 1 | 3.6 | 2.8 | 3.6 | 5.4 | 3.6 | 3.6 | 2.8 |
| .K_NH | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.06 | 0.07 | 0.03 | 0.03 | 0.08 |
| .K_NH_AUT | 1 | 0.05 | 0.34 | 0.34 | 0.34 | 0.77 | 0.34 | 0.19 | 0.19 | 0.19 |
| .K_NO | 0.5 | 0.5 | 0.4 | 0.4 | 0.5 | 0.4 | 0.5 | 0.4 | 0.4 | 0.3 |
| .K_O | 0.2 | 0.2 | 0.27 | 0.14 | 0.18 | 0.18 | 0.27 | 0.31 | 0.27 | 0.27 |
| .K_O_AUT | 0.5 | 0.5 | 0.2 | 0.2 | 0.5 | 0.4 | 0.2 | 0.3 | 0.3 | 0.8 |
| .K_X | 0.1 | 0.1 | 0.03 | 0.07 | 0.12 | 0.09 | 0.09 | 0.09 | 0.07 | 0.09 |
| .K_fe | 4 | 4 | 3.5 | 3.5 | 3.5 | 3 | 3.5 | 4 | 4.5 | 2.5 |
| .b_AUT | 0.15 | 0.15 | 0.16 | 0.05 | 0.11 | 0.05 | 0.28 | 0.11 | 0.11 | 0.05 |
| .b_H | 0.4 | 0.4 | 0.62 | 0.28 | 0.45 | 0.54 | 0.62 | 0.45 | 0.45 | 0.62 |
| .k_h | 3 | 3 | 4.5 | 3.6 | 1.9 | 5.4 | 1.9 | 4.5 | 2.8 | 1 |
| .mu_AUT | 1 | 1 | 0.8 | 1.3 | 1.2 | 1.1 | 0.8 | 1.2 | 1.1 | 0.8 |
| .mu_H | 6 | 6 | 5.2 | 6.4 | 4.1 | 6.4 | 4.1 | 8.6 | 8.6 | 9.8 |
| .Y_AUT | 0.24 | 0.24 | 0.25 | 0.2 | 0.25 | 0.2 | 0.32 | 0.28 | 0.23 | 0.3 |
| .Y_H | 0.625 | 0.625 | 0.49 | 0.49 | 0.62 | 0.44 | 0.4 | 0.53 | 0.44 | 0.53 |
| .PST.E_R_XCOD_DW | 0.85 | 0.85 | 0.8 | 0.7 | 0.75 | 0.75 | 0.7 | 0.7 | 0.7 | 0.75 |
| .PST.E_R_XII_DW | 0.51 | 0.51 | 0.6 | 0.35 | 0.45 | 0.45 | 0.55 | 0.4 | 0.45 | 0.35 |
| .in.f_S_A | 0.38 | 0.38 | 0.44 | 0.31 | 0.38 | 0.44 | 0.44 | 0.44 | 0.44 | 0.44 |
| .in.f_S_F | 0.39 | 0.39 | 0.36 | 0.34 | 0.33 | 0.34 | 0.27 | 0.31 | 0.29 | 0.29 |
| .in.f_X_S | 0.43 | 0.43 | 0.66 | 0.52 | 0.39 | 0.52 | 0.61 | 0.44 | 0.48 | 0.66 |
| .in.F_VSS_TSS | 0.74 | 0.74 | 0.72 | 0.66 | 0.72 | 0.69 | 0.72 | 0.72 | 0.63 | 0.72 |
| .SST.f_ns | 0.000228 | 0.000228 | 0.0005 | 0.0014 | 0.0011 | 0.0014 | 0.0011 | 0.0008 | 0.0005 | 0.0008 |
| .SST.r_H | 0.000576 | 0.000576 | 0.001 | 0.0007 | 0.0004 | 0.0003 | 0.0006 | 0.0006 | 0.0007 | 0.001 |
| .SST.r_P | 0.00286 | 0.00286 | 0.0039 | 0.008 | 0.0039 | 0.0029 | 0.0039 | 0.0029 | 0.0018 | 0.0039 |
| .SST.v0 | 474 | 474 | 475 | 419 | 362 | 475 | 419 | 475 | 362 | 419 |
Appendix G. Recalibration Frequency Performance Analysis
| Frequency | 4-month | 4-month | 2-month | 2-month | 3-week | 3-week |
| Last_Calibration | Jul | Jul | Sep | Sep | Nov | Nov |
| Method | NEAT | Manual | NEAT | Manual | NEAT | Manual |
| KGE_Before | -0.65 | -0.68 | -0.60 | -0.68 | -0.25 | -0.68 |
| KGE_After | -0.15 | -0.13 | -0.09 | -0.13 | -0.03 | -0.13 |
| KGE_Improvement_% | -2.33 | -108.90 | 74.88 | -108.90 | -614.63 | -108.90 |
| R2_Before | 0.02 | 0.00 | 0.01 | 0.00 | 0.03 | 0.00 |
| R2_After | 0.06 | 0.08 | 0.10 | 0.08 | 0.09 | 0.08 |
| R2_Improvement_% | 460.09 | 2740.69 | 2107.70 | 2740.69 | 6714.07 | 2740.69 |
| RMSE_Before | 113.24 | 60.16 | 80.19 | 60.16 | 62.33 | 60.16 |
| RMSE_After | 36.03 | 45.82 | 42.51 | 45.82 | 33.46 | 45.82 |
| RMSE_Improvement_% | -33.21 | -47.64 | -45.01 | -47.64 | -31.56 | -47.64 |
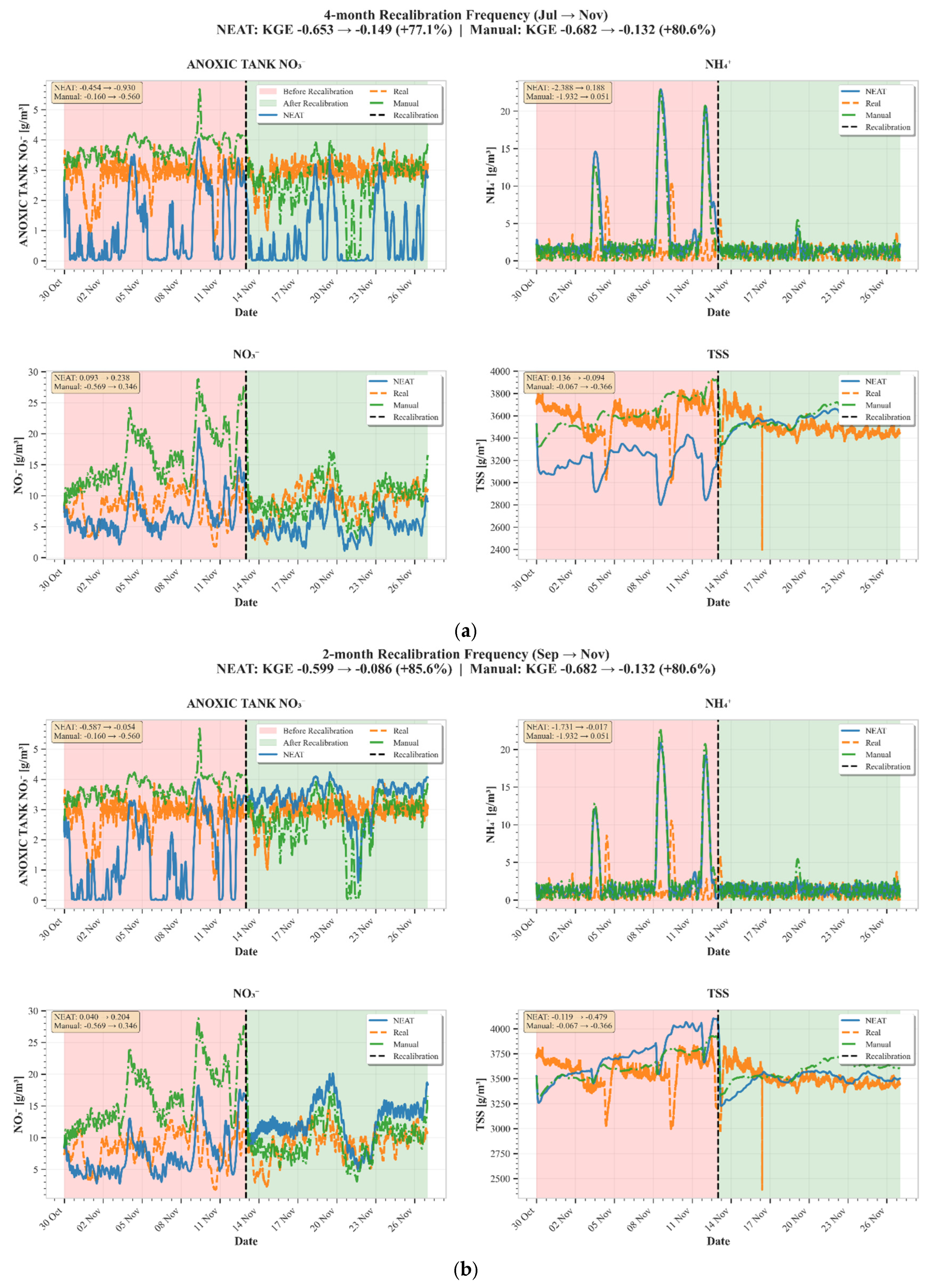
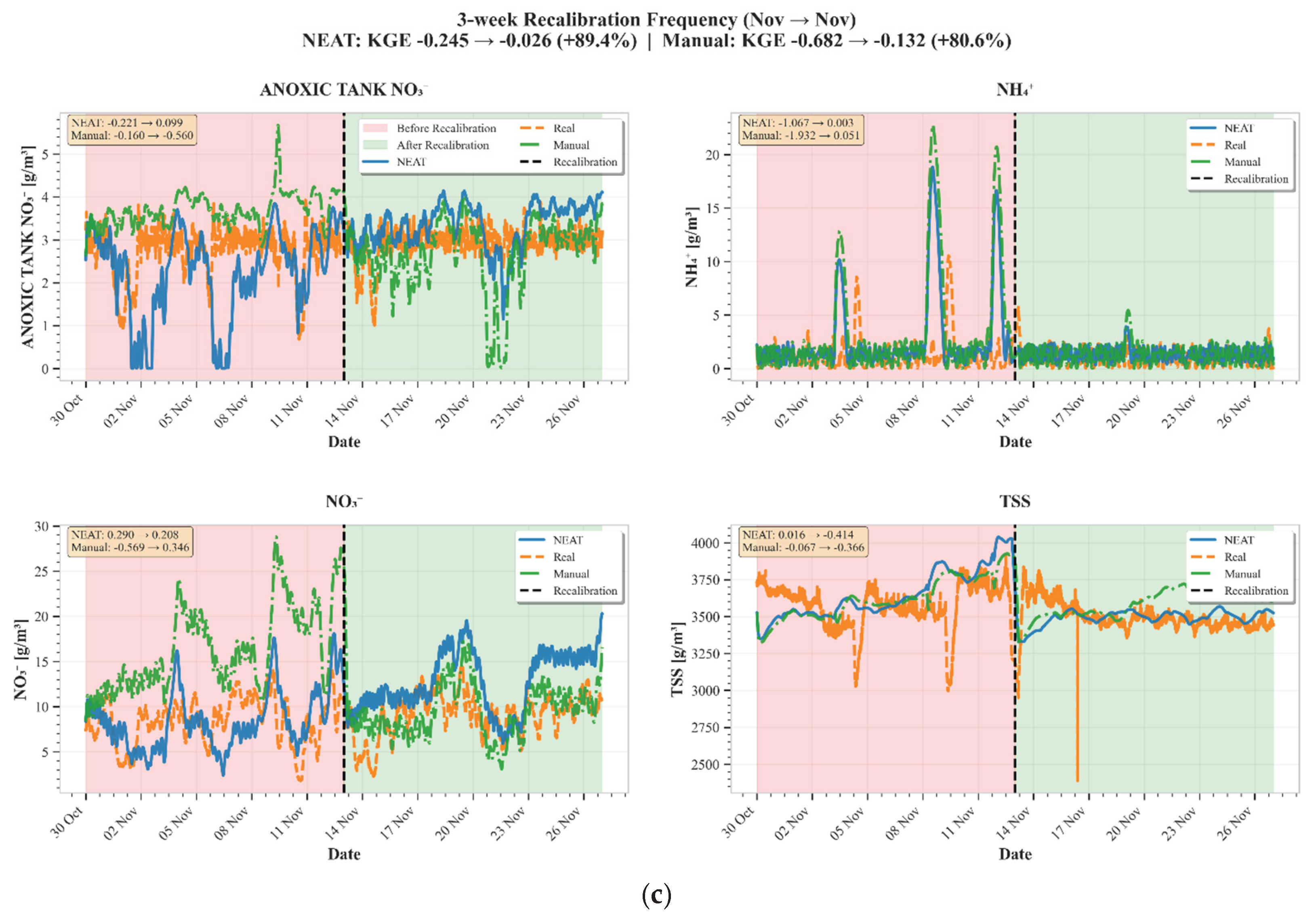
Appendix H. Secondary Metrics
References
- Amerlinck, Y. (2015). Model refinements in view of wastewater treatment plant optimization: Improving the balance in sub-model detail. http://hdl.handle.net/1854/LU-6952234.
- Benedetti, L.; Batstone, D.J.; De Baets, B.; Nopens, I.; Vanrolleghem, P.A. Global sensitivity analysis of biochemical, design and operational parameters of the Benchmark Simulation Model no. 2. In Proceedings of the iEMSs2008: International Congress on Environmental Modelling and Software, Barcelona, Spain, 7–10 July 2008. [Google Scholar]
- Borzooei, S.; Daneshgar, S.; Torfs, E.; Rehman, U.; Duchi, S.; Peeters, R.; Weijers, S.; Nopens, I. Next-Generation Compartmental Models for Applications in Digital Twinning of WRRFs. In Proceedings of the 8th IWA Water Resource Recovery Modelling Seminar, Stellenbosch, South Africa, 18–22 January 2023. [Google Scholar] [CrossRef]
- Bürger, R.; Diehl, S.; Nopens, I. A consistent modelling methodology for secondary settling tanks in wastewater treatment. Water Res. 2011, 45, 2247–2260. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; N’Doye, I.; Myshkevych, Y.; Alouini, M.-S.; Hong, P.-Y.; Laleg-Kirati, T.-M. Viral particle prediction in wastewater treatment plants using nonlinear lifelong learning models. npj Clean Water 2025, 8, 28. [Google Scholar] [CrossRef]
- Cierkens, K.; Nopens, I.; De Keyser, W.; Van Hulle, S.; Plano, S.; Torfs, E.; Amerlinck, Y.; Benedetti, L.; van Nieuwenhuijzen, A.; Weijers, S.; et al. Integrated model-based zoptimization at the WWTP of Eindhoven. Water Pract. Technol. 2012, 7, wpt2012035. [Google Scholar] [CrossRef]
- Corominas, L.; Garrido-Baserba, M.; Villez, K.; Olsson, G.; Cortés, U.; Poch, M. Transforming data into knowledge for improved wastewater treatment operation: A critical review of techniques. Environ. Model. Softw. 2018, 106, 89–103. [Google Scholar] [CrossRef]
- Daneshgar, S.; Polesel, F.; Borzooei, S.; Sørensen, H.R.; Peeters, R.; Weijers, S.; Nopens, I.; Torfs, E. A full--scale operational digital twin for a water resource recovery facility—A case study of Eindhoven Water Resource Recovery Facility. Water Environ. Res. 2024, 96, 11016. [Google Scholar] [CrossRef]
- De Mulder, C. Tying up Loose Ends: Optimization of Data Treatment and Hydrodynamic Model Structure of the Eindhoven Wastewater Treatment Plant Model. Ph.D. Dissertation, Faculty of Bioscience Engineering, Ghent University, Ghent, Belgium, 2019. [Google Scholar]
- De Mulder, C.; Flameling, T.; Weijers, S.; Amerlinck, Y.; Nopens, I. An open software package for data reconciliation and gap filling in preparation of water and resource recovery facility modeling. Environ. Model. Softw. 2018, 107, 186–198. [Google Scholar] [CrossRef]
- DHI. WEST: Modelling Biological Wastewater Treatment; DHI Group: Des Moines, IA, USA, 2022. [Google Scholar]
- Duarte, M.S.; Martins, G.; Oliveira, P.; Fernandes, B.; Ferreira, E.C.; Alves, M.M.; Lopes, F.; Pereira, M.A.; Novais, P. A review of computational modeling in Wastewater Treatment Processes. ACS EST Water 2023, 4, 784–804. [Google Scholar] [CrossRef]
- EnviroSim Associates Ltd. User Manual for BioWin 3.0; EnviroSim Associates Ltd.: Hamilton, ON, Canada, 2008. [Google Scholar]
- Esmaeili, H.; Afshar Kazemi, M.A.; Radfar, R.; Pilevari, N. From chaotic errors to natural curves: Real-coded genetic calibration of Wastewater Treatment Systems. Int. J. Environ. Sci. Technol. 2025, 22, 13557–13570. [Google Scholar] [CrossRef]
- Gomez, C.; Solon, K.; Haest, P.-J.; Morley, M.; Nopens, I.; Torfs, E. Enhancing accuracy and efficiency in calibration of drinking water distribution networks through evolutionary artificial neural networks and expert systems. J. Hydroinformatics 2025, 27, 1554–1578. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of Hydrology 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Hansen, B.D.; Hansen, T.B.; Moeslund, T.B.; Jensen, D.G. Data-driven drift detection in real process tanks: Bridging the gap between academia and Practice. Water 2022, 14, 926. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; van Loosedrecht, M. Activated sludge models ASM1, ASM2, ASM2d and ASM3. Water Intell. Online 2006, 5, 9781780402369. [Google Scholar] [CrossRef]
- Hulsbeek, J.J.W.; Kruit, J.; Roeleveld, P.J.; van Loosdrecht, M.C.M. A practical protocol for dynamic modelling of Activated Sludge Systems. Water Sci. Technol. 2002, 45, 127–136. [Google Scholar] [CrossRef]
- Hydromantis Environmental Software Solutions Inc. GPS-X Technical Reference; Hydromantis Environmental Software Solutions Inc.: Hamilton, ON, Canada, 2017. [Google Scholar]
- Kaisler, S. Expert systems: An overview. IEEE J. Ocean. Eng. 1986, 11, 442–448. [Google Scholar] [CrossRef]
- Koksal, E.S.; Aydin, E. A hybrid approach of transfer learning and physics-informed modelling: Improving dissolved oxygen concentration prediction in an industrial wastewater treatment plant. Chem. Eng. Sci. 2025, 304, 121088. [Google Scholar] [CrossRef]
- Lumley, D.J.; Polesel, F.; Refstrup Sørensen, H.; Gustafsson, L.-G. Connecting Digital Twins to control collections systems and water resource recovery facilities: From Siloed to integrated urban (waste)water management. Water Pract. Amp; Technol. 2024, 19, 2267–2278. [Google Scholar] [CrossRef]
- Martins, A.C.; Silva, M.C.; Benetti, A.D. Evaluation and optimization of ASM1 parameters using large-scale WWTP monitoring data from a subtropical climate region in Brazil. Water Pract. Technol. 2021, 17, 268–284. [Google Scholar] [CrossRef]
- Melcer, H.; Dold, P.L.; Jones, R.M.; Bye, C.M.; Takács, I.; Stensel, H.D.; Wilson, A.W.; Sun, P.; Bury, S. Methods for Wastewater Characterization in Activated Sludge Modeling (WERF Project 99-WWF-3); Water Environment Research Foundation: Alexandria, VA, USA, 2003. [Google Scholar]
- Miranda, L.J.V. PySwarms: A research toolkit for Particle Swarm Optimization in Python. J. Open Source Softw. 2018, 3, 433. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Graves, A.; Antonoglou, I.; Wierstra, D.; Riedmiller, M. Playing Atari with deep reinforcement learning. arXiv 2013, arXiv:1312.5602. [Google Scholar] [CrossRef]
- Mustajab, A.H.; Lyu, H.; Rizvi, Z.; Wuttke, F. Physics-informed neural networks for high-frequency and multi-scale problems using transfer learning. Appl. Sci. 2024, 14, 3204. [Google Scholar] [CrossRef]
- Peirovi Minaee, R.; Afsharnia, M.; Moghaddam, A.; Ebrahimi, A.A.; Askarishahi, M.; Mokhtari, M. Calibration of water quality model for distribution networks using genetic algorithm, particle swarm optimization, and hybrid methods. MethodsX 2019, 6, 540–548. [Google Scholar] [CrossRef]
- Petersen, B.; Gernaey, K.; Devisscher, M.; Dochain, D.; Vanrolleghem, P.A. A simplified method to assess structurally identifiable parameters in monod-based activated sludge models. Water Res. 2003, 37, 2893–2904. [Google Scholar] [CrossRef] [PubMed]
- Pisa, I.; Morell, A.; Vilanova, R.; Vicario, J.L. Transfer learning in Wastewater Treatment Plant Control Design: From conventional to long short-term memory-based controllers. Sensors 2021, 21, 6315. [Google Scholar] [CrossRef]
- Prantikos, K.; Chatzidakis, S.; Tsoukalas, L.H.; Heifetz, A. Physics-informed neural network with transfer learning (TL-PINN) based on domain similarity measure for prediction of nuclear reactor transients. Sci. Rep. 2023, 13, 16840. [Google Scholar] [CrossRef]
- Protoulis, T.; Kalogeropoulos, I.; Kordatos, I.; Sarimveis, H.; Alexandridis, A. A machine learning dynamic modelling scheme for wastewater treatment plants using cooperative particle swarm optimization and neural networks. Comput. Aid. Chem. Eng. 2023, 52, 1789–1794. [Google Scholar] [CrossRef]
- Rashid, M.M.; Mhaskar, P.; Swartz, C.L.E. Optimizing wastewater treatment through artificial intelligence: Recent advances and future prospects. Water Sci. Technol. 2024, 90, 1067–1091. [Google Scholar] [CrossRef]
- Rehman, U. (2016). Next generation bioreactor models for wastewater treatment systems by means of detailed combined modelling of mixing and biokinetics. http://hdl.handle.net/1854/LU-8109100.
- Rieger, L.; Gillot, S.; Langergraber, G.; Ohtsuki, T.; Shaw, A.; Takacs, I.; Winkler, S. Guidelines for Using Activated Sludge Models; IWA Publishing: London, UK. [CrossRef]
- Rodríguez-Alonso, C.; Pena-Regueiro, I.; García, Ó. Digital Twin Platform for water treatment plants using microservices architecture. Sensors 2024, 24, 1568. [Google Scholar] [CrossRef] [PubMed]
- Ruela, I.C.S.; Carvalho, T.M.N.; Alves, R.; Rocha, G.H.O.; Rocher, V.; Poch, M.; Sin, G. A review of computational modeling in wastewater treatment processes. ACS EST Water 2023, 3, 908–931. [Google Scholar] [CrossRef]
- Samuelsson, O.; Lindblom, E.U.; Björk, A.; Carlsson, B. To calibrate or not to calibrate, that is the question. Water Res. 2023, 229, 119338. [Google Scholar] [CrossRef]
- Sin, G.; Al, R. Activated sludge models at the crossroad of Artificial Intelligence—A perspective on advancing process modeling. npj Clean Water 2021, 4, 16. [Google Scholar] [CrossRef]
- Sin, G.; Gernaey, K.V.; Lantz, A.E. Good modeling practice for pat applications: Propagation of input uncertainty and sensitivity analysis. Biotechnol. Prog. 2009, 25, 1043–1053. [Google Scholar] [CrossRef]
- Sin, G.; De Pauw, D.J.W.; Weijers, S.; Vanrolleghem, P.A. An efficient approach to automate the manual trial and error calibration of activated sludge models. Biotechnol. Bioeng. 2007, 100, 516–528. [Google Scholar] [CrossRef]
- Sin, G.; Vanhulle, S.; Depauw, D.; Vangriensven, A.; Vanrolleghem, P. A critical comparison of systematic calibration protocols for Activated Sludge Models: A SWOT analysis. Water Res. 2005, 39, 2459–2474. [Google Scholar] [CrossRef] [PubMed]
- Stanley, K.O.; Miikkulainen, R. Evolving neural networks through augmenting topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
- Stentoft, P.A.; Munk-Nielsen, T.; Møller, J.K.; Madsen, H.; Valverde-Pérez, B.; Mikkelsen, P.S.; Vezzaro, L. Prioritize effluent quality, operational costs or global warming?—Using predictive control of wastewater aeration for flexible management of objectives in WRRFs. Water Res. 2021, 196, 116960. [Google Scholar] [CrossRef] [PubMed]
- Tay, J.-H. Development of a settling model for primary settling tanks. Water Res. 1982, 16, 1413–1417. [Google Scholar] [CrossRef]
- Torfs, E.; Nicolaï, N.; Daneshgar, S.; Copp, J.B.; Haimi, H.; Ikumi, D.; Johnson, B.; Plosz, B.B.; Snowling, S.; Townley, L.R.; et al. The transition of WRRF models to Digital Twin Applications. Water Sci. Technol. 2022, 85, 2840–2853. [Google Scholar] [CrossRef]
- Vanrolleghem, P.A.; Insel, G.; Petersen, B.; Sin, G.; De Pauw, D.; Nopens, I.; Dovermann, H.; Weijers, S.; Gernaey, K. A Comprehensive Model Calibration Procedure for Activated Sludge Models. In Proceedings of the 76th Annual Conference of the Water Environment Federation, Los Angeles, CA, USA, 11–15 October 2003. [Google Scholar]
- Xie, F.; Tian, C.; Ma, X.; Ji, L.; Zhao, B.; Danish, M.E.; Gao, F.; Yang, Z. Seasonal temperature effects on EPS composition and sludge settling performance in full-scale wastewater treatment plant: Mechanisms and mitigation strategies. Fermentation 2025, 11, 532. [Google Scholar] [CrossRef]
- Ye, G.; Wan, J.; Deng, Z.; Wang, Y.; Chen, J.; Zhu, B.; Ji, S. Prediction of effluent total nitrogen and energy consumption in wastewater treatment plants: Bayesian Optimization Machine Learning Methods. Bioresour. Technol. 2024, 395, 130361. [Google Scholar] [CrossRef] [PubMed]
- Yu, H.; Wang, Y.; Li, T.; Gan, Q.; Qu, D.; Qu, F. Calibrating activated sludge models through hyperparameter optimization: A new framework for Wastewater Treatment Plant Simulation. npj Clean Water 2025, 8, 80. [Google Scholar] [CrossRef]
- Zheng, Y.; Zhang, X.; Zhou, Y.; Zhang, Y.; Zhang, T.; Farmani, R. Deep representation learning enables cross-basin water quality prediction under data-scarce conditions. npj Clean Water 2025, 8, 33. [Google Scholar] [CrossRef]
- Zhou, M.; Mei, G. Transfer learning-based coupling of smoothed finite element method and physics-informed neural network for solving elastoplastic inverse problems. Mathematics 2023, 11, 2529. [Google Scholar] [CrossRef]
- Zhu, A.; Guo, J.; Ni, B.-J.; Wang, S.; Yang, Q.; Peng, Y. A novel protocol for model calibration in biological wastewater treatment. Sci. Rep. 2015, 5, 8493. [Google Scholar] [CrossRef] [PubMed]
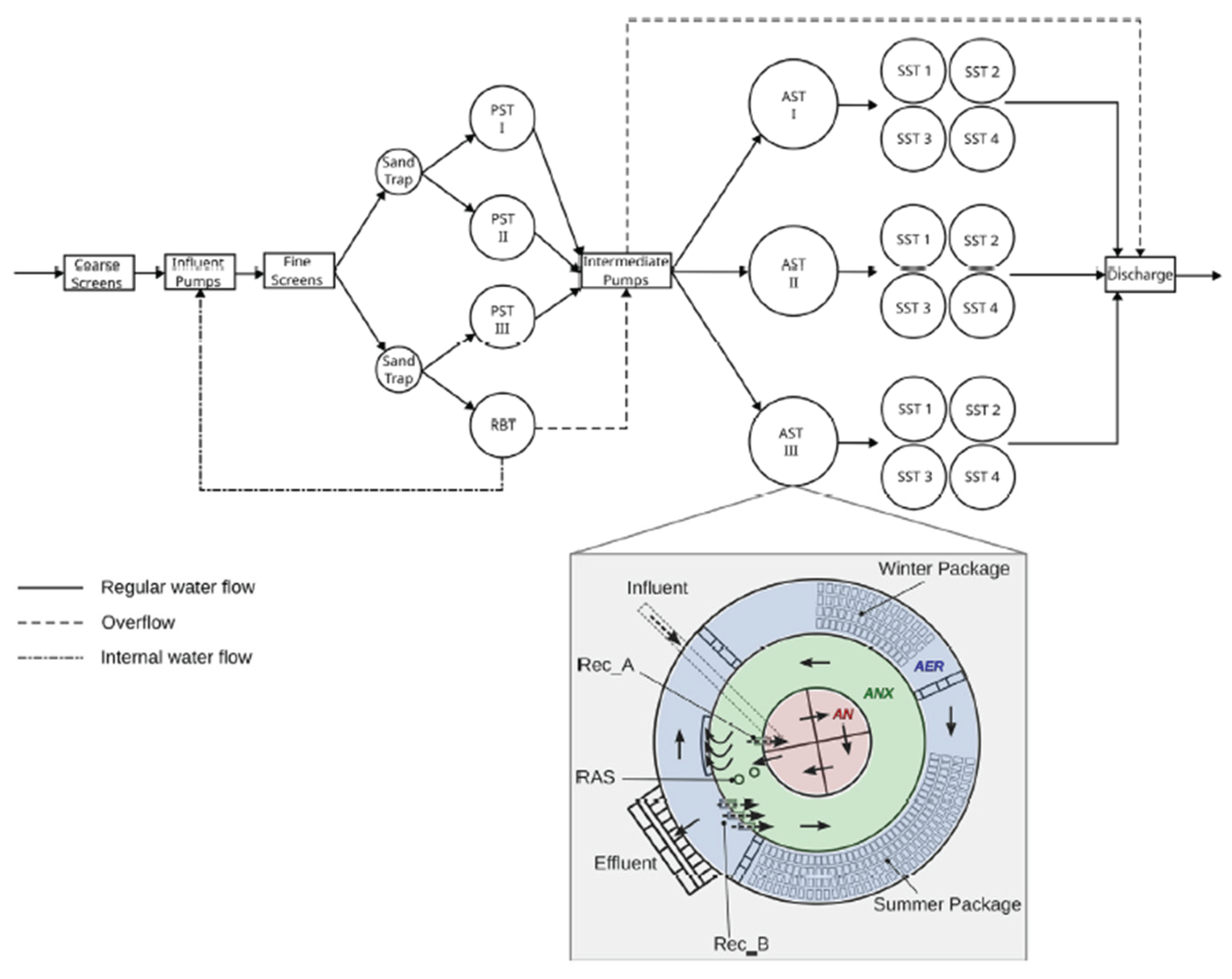
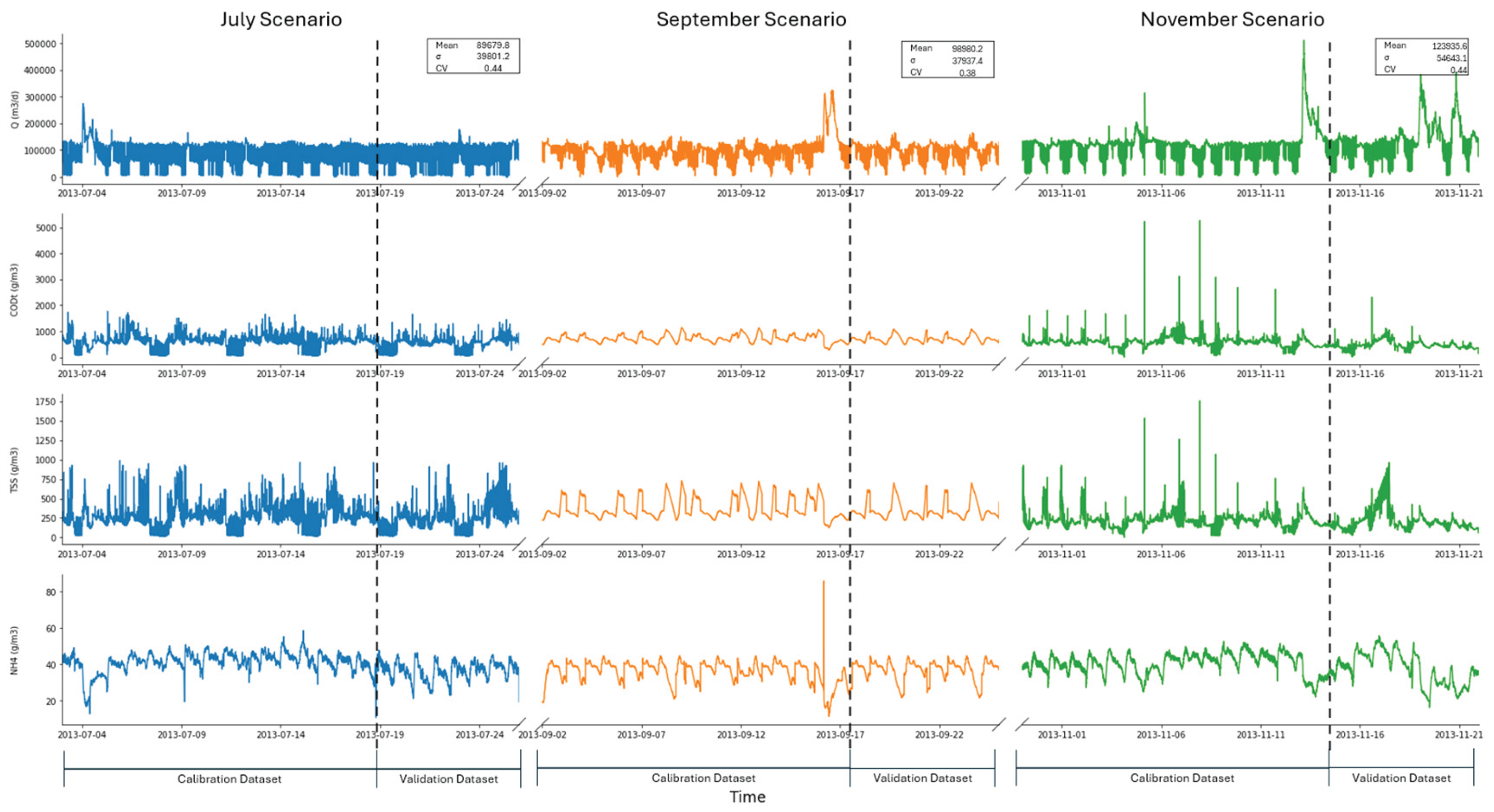
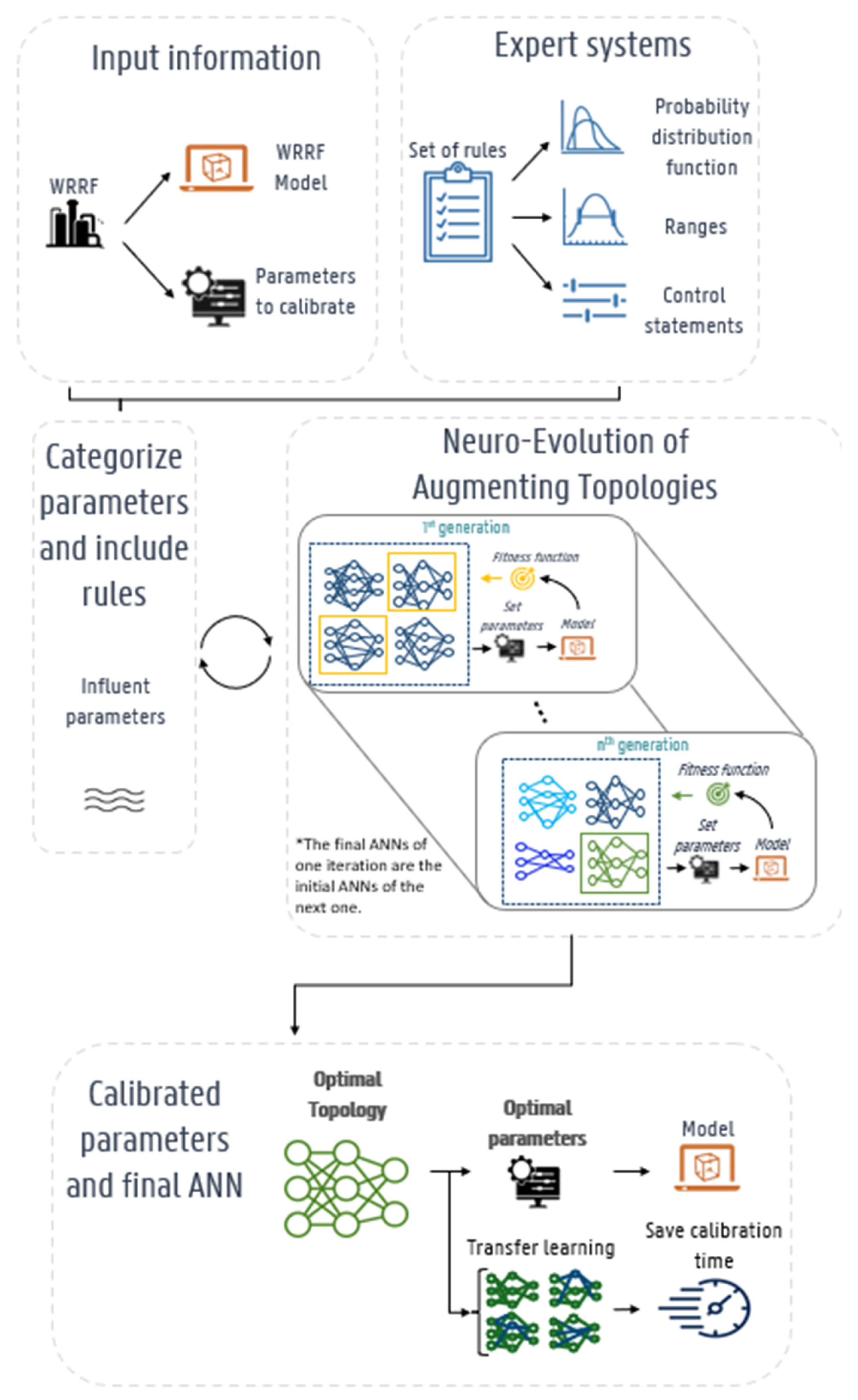
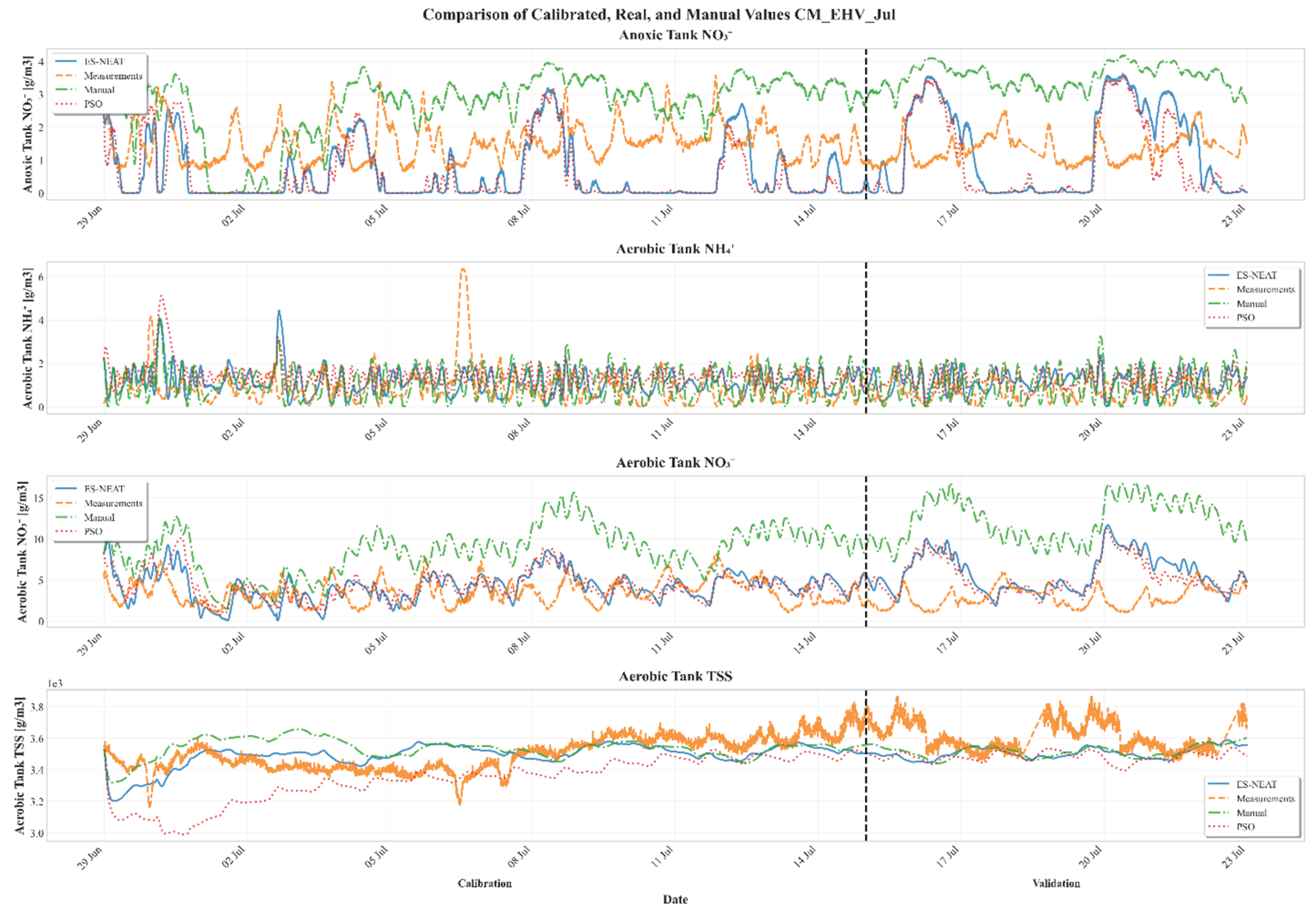
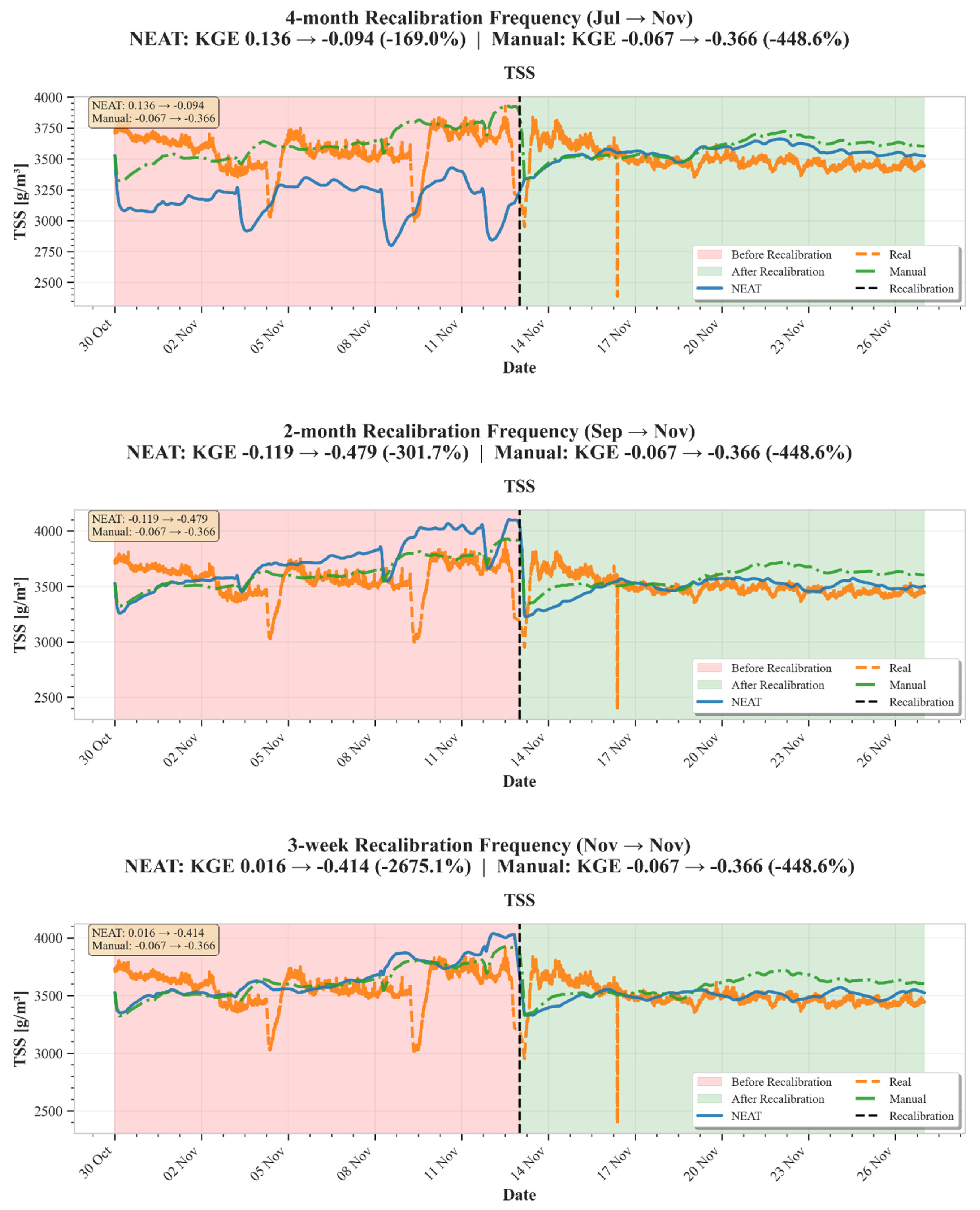
| Parameter | Symbol | Group | Default value | Bottom Limit | Upper Limit |
| Nitrogen content of biomass X_H, X_PAO, X_AUT | i_N_BM | Composition parameters | 0.07 | 0.05 | 0.09 |
| Nitrogen content of soluble substrate S_F | i_N_S_F | Composition parameters | 0.03 | 0.015 | 0.05 |
| Nitrogen content of inert soluble COD S_I | i_N_S_I | Composition parameters | 0.01 | 0.005 | 0.04 |
| Nitrogen content of inert particulate COD X_I | i_N_X_I | Composition parameters | 0.02 | 0.01 | 0.04 |
| Nitrogen content of particulate substrate X_S | i_N_X_S | Composition parameters | 0.04 | 0.02 | 0.06 |
| TSS to biomass ratio for X_H, X_PAO, X_AUT | i_TSS_BM | Composition parameters | 0.9 | 0.7 | 1 |
| TSS to X_I ratio | i_TSS_X_I | Composition parameters | 0.75 | 0.65 | 0.9 |
| TSS to X_S ratio | i_TSS_X_S | Composition parameters | 0.75 | 0.65 | 0.9 |
| Saturation/inhibition coefficient for growth on S_F | K_F | Kinetic | 4 | 1 | 8 |
| Saturation coefficient for ammonium (nutrient) | K_NH | Kinetic | 0.05 | 0.01 | 0.1 |
| Saturation coefficient of autotrophs for ammonium | K_NH_AUT | Kinetic | 1 | 0.05 | 1.2 |
| Saturation/inhibition coefficient for nitrate | K_NO | Kinetic | 0.5 | 0.1 | 0.8 |
| Saturation/inhibition coefficient for oxygen | K_O | Kinetic | 0.2 | 0.05 | 0.4 |
| Saturation/inhibition coefficient of autotrophs for oxygen | K_O_AUT | Kinetic | 0.5 | 0.2 | 1 |
| Saturation coefficient for particulate COD | K_X | Kinetic | 0.1 | 0.03 | 0.2 |
| Saturation coefficient for fermentation on S_F | K_fe | Kinetic | 4 | 2 | 6 |
| Decay rate for autotrophic biomass | b_AUT | Kinetic | 0.15 | 0.05 | 0.5 |
| Decay rate for heterotrophic biomass | b_H | Kinetic | 0.4 | 0.1 | 0.8 |
| Maximum hydrolysis rate | k_h | Kinetic | 3 | 1 | 8 |
| Maximum growth rate | mu_AUT | Kinetic | 1 | 0.5 | 1.4 |
| Maximum growth rate on substrate | mu_H | Kinetic | 6 | 3 | 12 |
| Yield For Autotrophic Biomass | Y_AUT | Stoichiometry | 0.24 | 0.15 | 0.35 |
| Yield For Heterotrophic Biomass | Y_H | Stoichiometry | 0.625 | 0.4 | 0.75 |
| Removal efficiency for particulate COD at dry weather flows | PST.E_R_XCOD_DW | Primary settler | 0.51 | 0.6 | 1 |
| Removal efficiency for inert inorganic particulates at dry weather flows | PST.E_R_XII_DW | Primary settler | 0.85 | 0.3 | 0.7 |
| Fraction of fermentation products (S_A) in the soluble COD | in.f_S_A | Influent fractionation | 0.38 | 0.25 | 0.5 |
| Fraction of fermentable readily biodegradable products (S_F) in the soluble COD | in.f_S_F | Influent fractionation | 0.39 | 0.25 | 0.4 |
| Fraction slowly biodegradable substrate (X_S) in the particulate COD | in.f_X_S | Influent fractionation | 0.43 | 0.35 | 0.7 |
| VSS to TSS ratio | in.F_VSS_TSS | Influent fractionation | 0.74 | 0.6 | 0.85 |
| Non-settleable fraction of suspended solids | SST.f_ns | Secondary settler | 0.00023 | 0.0005 | 0.003 |
| Settling parameter (hindered settling) | SST.r_H | Secondary settler | 0.00058 | 0.0002 | 0.0012 |
| Settling parameter (low concentration) | SST.r_P | Secondary settler | 0.00286 | 0.0008 | 0.009 |
| Maximum theoretical settling velocity | SST.v0 | Secondary settler | 474 | 250 | 700 |
| Variable | # Components | Description |
| Model Structure | 2 | Tank-in-Series (TIS) and Compartmental Model (CM) |
| Temporal Scenario | 3 | July 2013, September 2013, November 2013 |
| Calibration Method | Varies by scenario | July: ES-NEAT, PSO, Original calibration; September & November: ES-NEAT, Original calibration |
| Target Variable | 4 | Anoxic zone NO3−, End of aeration zone NH4+, End of aeration zone NO3−, End of aeration zone TSS |
| Temporal Period | 3 per scenario | Days 1-8, Days 9-16, Days 17-24 of each 24-day calibration scenario |
| Performance Metric | 3 | KGE, R2, RMSE |
| Manual calibration | Calculated | Jul TIS | Jul CM | Sep TIS | Sep CM | Nov TIS | Nov CM | |
| KGE | Calibration | -0.836 | -0.333 | -0.204 | 0.110 | -1.162 | 0.099 | |
| Validation | -2.627 | -0.981 | -0.706 | -0.545 | -1.295 | -0.492 | ||
| Total | -1.732 | -0.657 | -0.455 | -0.217 | -1.229 | -0.196 | ||
| R2 | Calibration | 0.014 | 0.003 | 0.043 | 0.142 | 0.042 | 0.188 | |
| Validation | 0.052 | 0.019 | 0.064 | 0.059 | 0.124 | 0.252 | ||
| Total | 0.033 | 0.011 | 0.054 | 0.100 | 0.083 | 0.220 | ||
| RMSE | Calibration | 33.945 | 33.725 | 103.937 | 111.383 | 46.419 | 47.340 | |
| Validation | 39.213 | 36.843 | 68.773 | 95.577 | 44.509 | 71.036 | ||
| Total | 36.579 | 35.284 | 86.355 | 103.480 | 45.464 | 59.188 | ||
| PSO calibration | Calculated | Jul TIS | Jul CM | Sep TIS | Sep CM | Nov TIS | Nov CM | |
| KGE | Calibration | -0.125 | 0.017 | 0.065 | -0.069 | -0.109 | 0.240 | |
| Validation | -0.877 | -0.562 | -0.107 | -0.069 | -0.312 | -0.356 | ||
| Total | -0.501 | -0.272 | -0.021 | -0.069 | -0.210 | -0.058 | ||
| R2 | Calibration | 0.004 | 0.085 | 0.148 | 0.050 | 0.260 | 0.225 | |
| Validation | 0.073 | 0.091 | 0.092 | 0.052 | 0.280 | 0.305 | ||
| Total | 0.039 | 0.088 | 0.120 | 0.051 | 0.270 | 0.265 | ||
| RMSE | Calibration | 28.413 | 51.685 | 93.150 | 96.439 | 34.313 | 39.945 | |
| Validation | 38.162 | 40.254 | 45.868 | 58.825 | 40.019 | 49.770 | ||
| Total | 33.287 | 45.969 | 69.509 | 77.632 | 37.166 | 44.858 | ||
| Computational Time (hours) | 10 | 12 | 3 | 4 | 5 | 6 | ||
| Number of generations | 100 | 100 | 11 | 14 | 19 | 24 | ||
| PSO calibration | Calculated | Jul CM | Sep CM | |||||
| KGE | Calibration | 0.037 | -0.040 | |||||
| Validation | -0.671 | -0.197 | ||||||
| Total | -0.317 | -0.118 | ||||||
| R2 | Calibration | 0.033 | 0.040 | |||||
| Validation | 0.049 | 0.074 | ||||||
| Total | 0.041 | 0.057 | ||||||
| RMSE | Calibration | 28.723 | 62.217 | |||||
| Validation | 38.123 | 51.031 | ||||||
| Total | 33.423 | 56.624 | ||||||
| Computational Time (hours) | 12 | 12 | ||||||
| Number of generations | 100 | 100 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





