On Reproducing Quantum Core-Shell Systems

1. Introduction

John von Neumann’s concept of the universal constructor introduced a foundational vision: that machines could not only construct other machines, but also reproduce and evolve — much like biological organisms do [1]. This led to the development of cellular automata [2], where discrete units evolve according to local update rules. Conway’s Game of Life is a well-known example, demonstrating emergent complexity including self-replication and even universal computation [3,4]. Cellular automata have since been applied to modeling a range of natural phenomena, including crystallization and biological pattern formation [5,6].

While powerful, classical automata are inherently deterministic: each cell is either “on” or “off,” and the system evolves in a fully predictable manner. Quantum systems, by contrast, are governed by probabilistic dynamics and superposition. In quantum mechanics, state evolution is unitary, but measurement outcomes are inherently uncertain. Only recently have experimental advances begun to realize self-replicating behaviors in quantum systems [7], and the theoretical exploration of quantum self-replication remains in its infancy.

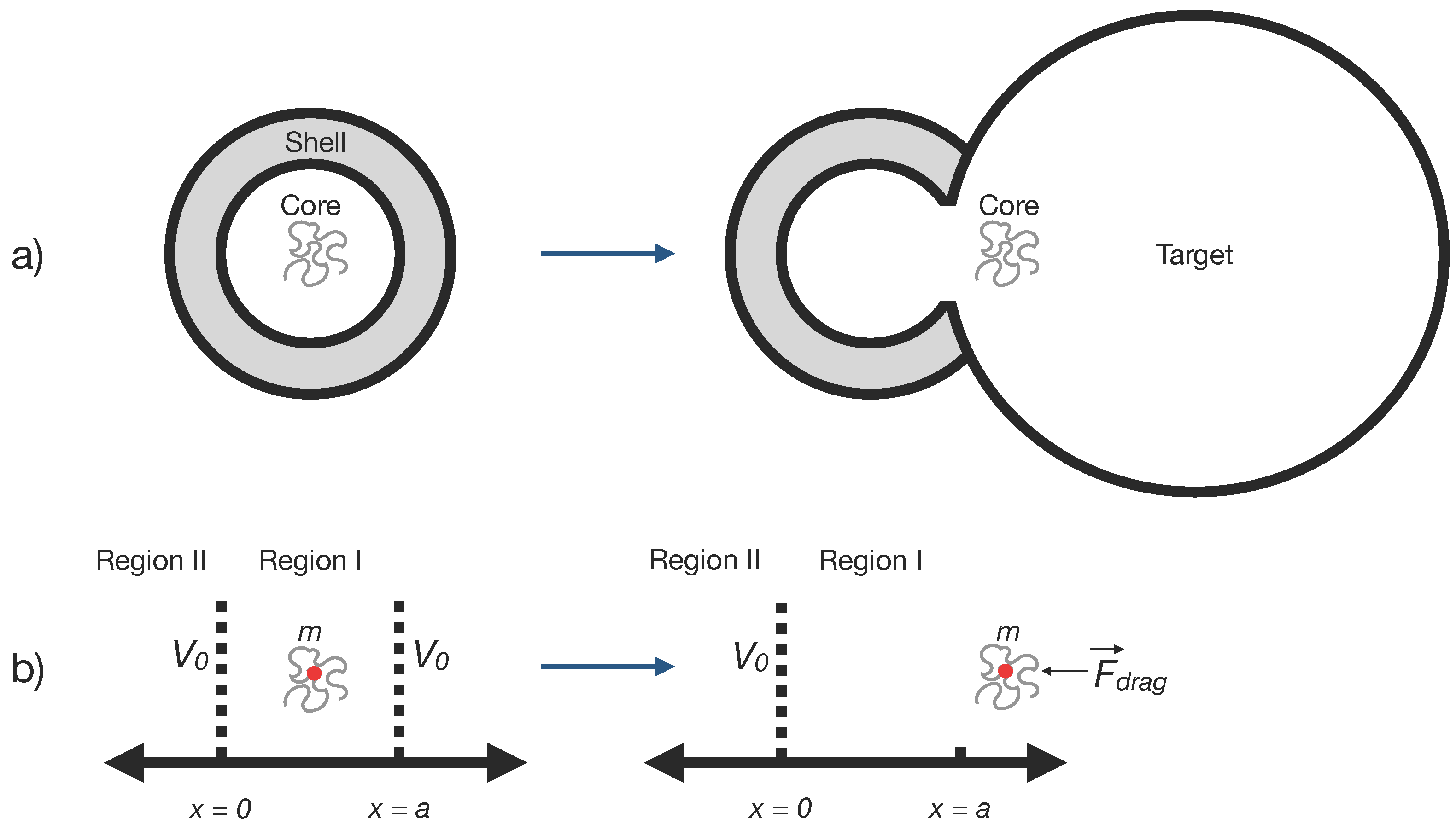
In this work, we develop a simplified quantum mechanical model of a reproducing system inspired by biological structures, particularly viruses. Our primary goal is not to provide a detailed mechanistic description of viral ejection, but to use this process as a natural example of confinement–release dynamics. We consider a core-shell particle confined in a finite potential well; at $t=0$, the shell potential vanishes, allowing the ‘core’ wavepacket to propagate under the influence of an external force field representing environmental resistance. Using a split-operator method, we track the evolution of the wavepacket and compute replication intensity through a localized nonlinear interaction functional. The model exhibits clear scaling behavior: the propagation depth is set by the ratio of initial energy to resisting force, $x_{max}=E/F$, with sharp suppression beyond this classical turning point. When the core reaches a designated target region, a field-theoretic interaction term $H_I\propto {\varphi }^3\left(x\right)$ triggers a replication event, modeled as the annihilation of the core and target followed by the creation of new core-shell systems. We model the process by numerically solving the time-dependent Schrödinger equation to quantify how propagation and overlap govern the replication probability.

Our model is biologically inspired: viruses inject their genomes (the core) from a capsid (the shell) into a host. The genome then travels within the host environment, potentially triggering replication. We adopt this terminology to convey intuition, but the model is broadly applicable to synthetic quantum systems capable of confinement, propagation, and interaction-triggered replication. Analogous processes of field-driven particle creation and amplification occur in several established areas of quantum physics. In high-energy theory, the Schwinger effect describes spontaneous electron–positron pair production from the quantum vacuum under a strong external field [8,9]. Likewise, the dynamical Casimir effect converts vacuum fluctuations into real photons when boundary conditions are rapidly modulated, as demonstrated experimentally in superconducting circuits [10]. In engineered quantum simulators, coherent mode-splitting and population branching have been realized in optical lattices and superconducting platforms, such as the wave-packet branching through engineered conical intersections reported by Wang et al. [11]. Related excitation-generation mechanisms also appear in analog gravity experiments, where effective spacetime curvature leads to Hawking-like emission in Bose–Einstein condensates [12]. Across these diverse contexts, coherent particle creation arises through well-understood quantum field interactions that remain fully unitary.

Our model is solved numerically using a standard split-operator method for the time-dependent Schrödinger equation. A Gaussian wavepacket is released from the origin and evolves under the linear potential. The wavefunction exhibits characteristic Airy behavior, with the propagation depth determined by the classical turning point $x_{max}=E/F$. We verify this behavior numerically and then introduce a nonlinear functional to represent a localized replication process. Finally, we reformulate the problem in the language of quantum field theory, where replication corresponds to a cubic interaction Hamiltonian. While the individual components of our analysis—Airy propagation under a linear potential and cubic interactions producing branching—are well-established, the novelty of this work lies in their synthesis into a unified, minimal model linking confinement, release, and replication-like branching. This provides a conceptual bridge between classical self-replication analogies and quantum field dynamics, rather than introducing new analytic results.

The paper is structured as follows: In Section I, we describe the free propagation of the quantum core following shell disintegration. Section II introduces the interaction Hamiltonian responsible for replication and presents the numerical simulation of this process. We conclude with discussion on physical interpretations, parameter scaling, and possible extensions of this minimal model toward more complex quantum replication frameworks.

2. Probability of Core Particle Propagation

The basic constituent of the quantum reproducing system is a core-shell particle, consisting of an internal core surrounded by a shell that acts as a spherically symmetric potential barrier (see Fig. 1).

In general, such a system with N interacting constituents in the core confined by the shell barrier has a Hamiltonian of the form

$$\begin{array}{c}\hfill H=\sum _{i=1}^N{\displaystyle \frac{p_i^2}{2m_i}}+\sum _{i\ne j}{V}_{ij}+\sum _i{V}_i^{shell}\end{array}$$

(1)

where $V_{ij}$ is the interaction potential between the constituents, and $V_i^{shell}$ is the confining spherically symmetric potential provided by the shell.

When triggered by an external interaction, the shell breaks (the spherical barrier potential goes to zero), and the core particles then propagate toward a target and reproduce. The advantage of the model we propose here is that it can lead to the design of a general quantum mechanical reproducing system. In particular, for 3D confining potentials, it captures the fascinating characteristics of the reproduction of already existing systems in nature, such as small viruses and chain reactions in fission, and their potential treatment as quantum self-reproducing systems.

2.1. Simplified Model

Due to the difficulty in solving the quantum many-body problem shown in Equation 1, we simplify the general 3D model to a 1D propagation of the center of mass of the core. The core, at position x, is originally confined by the shell with radius a (that is, $0<x<a$ in Fig. Figure 1). The shell breaks at $x=a$ and the core propagates forward. There is a potential barrier $V_0$ behind the core (left side in Fig. 1b) and a drag force, F, in front of the diffusing core (right side in Fig. 1b) that retards its motion toward the target. The simplified Hamiltonian for this model is

$$\begin{array}{c}\hfill H={\displaystyle \frac{p^2}{2m}}+\Theta \left(x\right)Fx+\Theta (-x)V_0,\end{array}$$

(2)

where $\Theta$ is the Heaviside step function, F is a drag force ($F>0$), $V_0$ is a constant potential and m is the mass of the core particle (shown in Fig. 1b). We define regions $x>0$ as Region I and $x<0$ as Region II. That is,

$$\psi (x,t)=\left\{\begin{array}{cc}{\psi }_{II}(x,t),\hfill & \mathrm{if}x<0\hfill \\ {\psi }_I(x,t),\hfill & \mathrm{if}x>0.\hfill \end{array}\right.$$

(3)

The stationary Schrödinger equation is

$$-{\displaystyle \frac{{\hslash }^2}{2m}}{\psi }^{″}\left(x\right)+[\Theta \left(x\right)Fx+\Theta (-x)V_0]\psi \left(x\right)=E\psi \left(x\right).$$

(4)

For Region I ($x>0$), the stationary Schrödinger equation

$$-{\displaystyle \frac{{\hslash }^2}{2m}}{\psi }^{″}\left(x\right)+Fx\psi \left(x\right)=E\psi \left(x\right),$$

(5)

and leads to the Airy equation solutions

$$\psi \left(x\right)=AAi\left({\alpha }^{1/3}(x-x_t)\right)+BBi\left({\alpha }^{1/3}(x-x_t)\right),$$

where $\alpha =2Fm/{\hslash }^2$, $x_t=E/F$, and A and B are constants. We set $B=0$ since the Bi function diverges as $x\to \infty$ and would violate the physical boundary condition of a vanishing probability at infinity. Thus

$$\psi \left(x\right)={\psi }_I\left(x\right)=AAi\left({\alpha }^{1/3}(x-x_t)\right),$$

(6)

For Region II ($x<0$), the solutions are plane waves (for $E>V_0$) or exponentials (for $E<V_0$). For $E<V_0$,

$$\psi \left(x\right)={\psi }_{II}\left(x\right)=C{e}^{kx},$$

(7)

where $k={\displaystyle \frac{\sqrt{2m(V_0-E)}}{\hslash }}$ and C is a constant. Because $V\left(x\right)$ is finite at $x=0$, both $\psi \left(x\right)$ and ${\psi }^{\prime }\left(x\right)$ are continuous there, fixing the coefficients

$$C=AAi(-{\alpha }^{1/3}{\displaystyle \frac{E}{F}}),Ck=A{\alpha }^{1/3}A{i}^{\prime }(-{\alpha }^{1/3}{\displaystyle \frac{E}{F}}).$$

(8)

This leads to

$$A{i}^{\prime }(-{\displaystyle \frac{{\alpha }^{1/3}E}{F}})=\sqrt{{\displaystyle \frac{{\alpha }^{1/3}{V}_0}{F}}-{\displaystyle \frac{{\alpha }^{1/3}E}{F}}}Ai(-{\displaystyle \frac{{\alpha }^{1/3}E}{F}}).$$

(9)

The spectrum is continuous in E; we use Dirac normalization

$${\int }_{-\infty }^{+\infty }dx{\psi }_E\left(x\right){\psi }_{E^{\prime }}^{*}\left(x\right)=\delta (E-E^{\prime }).$$

(10)

Completeness is $\int dE{\psi }_E\left(x\right){\psi }_E^{*}\left(x^{\prime }\right)=\delta (x-x^{\prime })$.

We perform simulations of the simplified 1D model described above. To simplify the numerical implementation, we used a scaled time unit, $\tau$, and a scaled position unit of a, the shell’s diameter, such that $\chi =x/a$. These parameters ($\tau$ and $\chi$) are used as needed to label the x-axis in Fig. 2. The simulation was performed in the ranges $0.0\le \tau \le 100.0$ and $-2\le \chi \le 10$.

The red graph in Fig. 2 shows the probability density ${|\Psi (\chi ,\tau )|}^2$ of the particle as a function of position $\chi$ at a fixed time $\tau =20$, arbitrarily chosen. The initial energy distribution corresponds to a particle released from a confining potential (representing the core emerging from its shell), and the probability density shows the resulting spatial profile. The sharp cutoff near $\chi =0$ reflects the initial confinement boundary. For $\chi <0$, the small probability density represents the tunneling through the potential barrier. The probability density decay is determined by the potential height $V_0$. The dominant peak near $\chi =1.5$ indicates the most probable location of the particle at this time. For $\chi >0$ the probability of finding the core is significantly dependent on the ratio $E/F$, where the drag force F defines the slope of the potential. The external force acts as another barrier to the left, such that the probability of finding the core assumes an oscillatory behavior observed in the blue graph Fig. 2.

The blue graph illustrates the time-dependent probability of finding the particle at a fixed position $\chi =1.5$, plotted as a function of time $\tau$. The oscillatory behavior results from the quantum time evolution of the superposed energy components, each evolving with its own phase factor. These phase differences create interference patterns over time, causing the probability to rise and fall periodically. This behavior reflects how a quantum wavepacket approaches, overlaps with, and then moves past a specific spatial point — in this case, modeling how the core dynamically propagates forward.

The dependence of the propagation depth on the external force F follows the analytical scaling $x_{max}=E/F$, as detailed in Appendix B. This confirms that the model reproduces the expected sensitivity of the turning point to the driving potential.

3. Probability of Core Particle Reproduction

The single-particle Schrödinger equation provides a useful starting point for describing the propagation of the core after the shell breaks. However, once replication is allowed—that is, the creation of additional cores from an initial one—the single-particle formalism becomes insufficient because it assumes a fixed particle number. We note that in this work, the term replication refers strictly to the branching process; which corresponds to the annihilation of one excitation and creation of two others, analogous to parametric down-conversion or boson branching in standard field theory. It does not represent replication in an algorithmic or biological sense, nor does it imply information copying or self-replication of a quantum state. The purpose of this term is to introduce a minimal nonlinear channel that transforms single-particle amplitude into multi-particle probability density, serving as an analog of a “reproduction event” in a simplified physical system. To describe creation and annihilation events consistently, we adopt the framework of second quantization, or quantum field theory (QFT). In this approach, the wavefunction $\psi (x,t)$ is replaced by a field operator $\varphi \left(x\right)$, which can both create and destroy excitations of the core at position x. The states of the system are then represented in Fock space, where the number of cores is not fixed but determined dynamically by the Hamiltonian. This transition allows replication to be modeled as an interaction term that converts one excitation into two, analogous to particle creation processes in nonlinear bosonic systems [13,14,15,16].

We describe the creation and destruction of the core particle using many-body quantum mechanics with creation and annihilation operators. When the core encounters a target (“cell”), both are annihilated to form two (or more) new particles identical to the core. This process is analogous to a virus infecting a cell: the virus and cell are transformed to yield multiple new viruses. Fig. 3 shows a schematic of this step. For simplicity, we set length units of $a=1$ and $\hslash =1$.

Let $V_E^{†}$ be the creation operator for a core-shell particle (or simply ’core’) with energy E; that is, the state $|1\rangle =V_E^{†}|0\rangle$, where the vacuum (no genome) state is defined by $V_E|0\rangle =0$ (the vacuum is denoted by $|0\rangle$), and $V_E$ is the annihilation operator, the adjoint of the creation operator. These operators satisfy the commutation relation $[V_E,V_{E^{\prime }}^{†}]=\delta (E-E^{\prime })$, and mode normalization $\int dx{\Psi }_E\left(x\right){\Psi }_{E^{\prime }}^{*}\left(x\right)=\delta (E-E^{\prime })$.

Given this background we want to construct the Hamiltonian for a free core that is drifting to the right under a retarding force F due to the medium the core finds itself in. That is to say, at time $t=0$ the shell collapses, revealing a core of size a and mass m, described by a wave function ${\psi }_{t=0}$, which then drifts to the right a distance D at which point it encounters a cell. The Hamiltonian for this part of the process is given by

$$\begin{array}{ccc}\hfill H_v& =& \int dEE{V}_E^{†}{V}_E,\hfill \end{array}$$

(11)

so that a one-particle wave packet $|\Psi \left(t\right)\rangle =\int dEa\left(E\right)e^{-iEt/\hslash }{V}_E^{†}|0\rangle$ evolves consistently with the Schrödinger equation.

We introduce the bosonic field operator

$$\begin{array}{ccc}\hfill \varphi \left(x\right)& =& \int dE[V_E{\Psi }_E\left(x\right)+V_E^{†}{\Psi }_E^{*}\left(x\right)],\hfill \end{array}$$

(12)

This field and its conjugate obey the commutation relations

$$\begin{array}{ccc}\hfill [\varphi \left(x\right),{\varphi }^{†}\left(x^{\prime }\right)]& =& \int dE{\Psi }_E\left(x\right){\Psi }_E\left(x^{\prime }\right)=\delta (x-x^{\prime }).\hfill \end{array}$$

(13)

For the interacting Hamiltonian we take the cell to be located a distance $x=D\ge a$ from where the shell broke and assume that the cell supplies energy $E_c$ to the core to create two new cores, each of mass m. Then the interacting Hamiltonian that annihilates the core to create two new cores with the help of the energy supplied by the cell is

$$\begin{array}{ccc}\hfill H_I& =& \lambda \int dx{g}_{\sigma }(x-D){\varphi }^3\left(x\right),\hfill \end{array}$$

(14)

where $\lambda$ is a coupling strength and $g_{\sigma }\left(x\right)$ is a normalized finite-range kernel centered at zero, e.g.

$$g_{\sigma }\left(x\right)={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}exp(-{\displaystyle \frac{x^2}{2{\sigma }^2}}),$$

(15)

$$\int dx{g}_{\sigma }\left(x\right)=1.$$

(16)

The kernel $g_{\sigma }(x-D)$ ensures that replication occurs only when the core overlaps the localized interaction region.

This cubic term is the lowest-order local bosonic interaction capable of annihilating one excitation and creating two, thus representing the minimal form of a $1\to 2$ replication event.

Energy conservation is enforced through oscillatory time factors in the interaction-picture operator $H_I\left(t\right)$; after coarse-graining, these contribute an effective constant $C_f$ that encodes daughter overlaps and energy-matching conditions. To obtain probabilities, one must also compute a matrix element such as $|\langle 2|H_I{|0\rangle |}^2$, where $|2\rangle$ is the two core-shell state and $|0\rangle$ the original core-shell state propagated near the cell.

For $t<0$, we assume the core inside the shell can be represented by a Gaussian of "size" a. After the shell breaks the core wave function evolves according to Equation 11 until it drifts close to a cell at position $x=D$. In the interaction picture, the leading-order amplitude to generate two daughter cores from an initial one-particle packet is

$$A\left(t\right)={\displaystyle \frac{-i}{\hslash }}{\int }_0^{t}d{t}^{\prime }\langle 2|H_I\left(t^{\prime }\right)|\Psi \left(0\right)\rangle ,$$

(17)

Which reduces to

$$A\left(t\right)\approx {\displaystyle \frac{-i\lambda }{\hslash }}{C}_f{\int }_0^{t}d{t}^{\prime }\int dx{g}_{\sigma }(x-D)\Psi {(x,t^{\prime })}^3,$$

(18)

where $\Psi (x,t)=\langle 0|\varphi \left(x\right)|\Psi \left(t\right)\rangle$ is the amplitude of a single particle and $C_f$ collects daughter-mode overlaps and energy-matching factors.

A practical expression is obtained by coarse-graining over long times and internal daughter states. Under a Markov approximation one finds a replication rate density

$$\Gamma \left(D\right)=C_f^2{\lambda }^2\int dt{|\int dx{g}_{\sigma }(x-D)\Psi {(x,t)}^3|}^2.$$

(19)

The probability that replication occurs during a single passage is obtained by integrating the rate over the passage time window,

$$P_{rep}\left(D\right)\approx {\int }_{t_i}^{t_f}\Gamma (D,t)dt\approx C_f^2{\lambda }^2{\int }_{t_i}^{t_f}dt{|\int dx{g}_{\sigma }(x-D)\Psi {(x,t)}^3|}^2.$$

(20)

The derivation leading to Eq. (20) assumes that variations of the interaction kernel occur on time scales much slower than the intrinsic oscillations of the wavefunction. Dimensional consistency is preserved by requiring $\left[\lambda \right]=E·L$, ensuring that the interaction term contributes an energy density to the Hamiltonian. The prefactors $C_f$ and $\lambda$ were chosen for qualitative illustration rather than quantitative calibration. A full treatment would require solving the coupled field equations self-consistently, which lies beyond the present heuristic scope.

In principle, replication could be modeled as an interaction between two distinct fields — one representing the core and another representing a target structure or “environmental receptor.” However, in the minimal model considered here, the target is not treated as a dynamic degree of freedom but rather as a static background potential or localized interaction region. This approximation is justified when the target is much heavier, slower, or otherwise unaffected by the replication event, so that its quantum state can be effectively integrated out. Similar effective-field descriptions are widely used in reaction–diffusion and birth–death models, where the medium or catalyst is treated implicitly rather than as a separate dynamical entity [15,16].

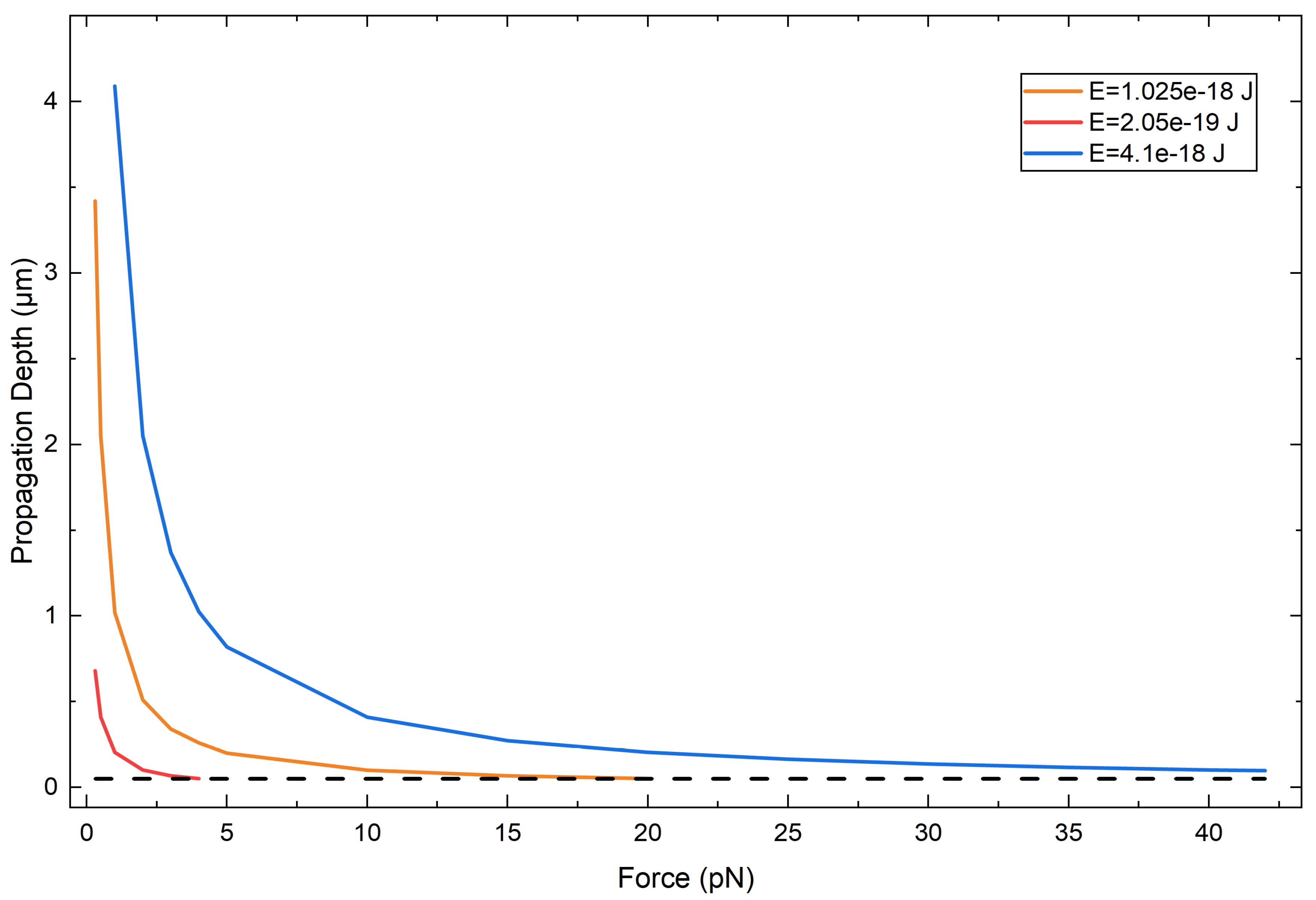
Nondimensionalization: To make the dynamics more transparent, we rescale lengths and times using the natural Airy scales of a particle in a constant force. The characteristic length is

$$l={\left({\displaystyle \frac{{\hslash }^2}{2mF}}\right)}^{1/3},$$

(21)

and the corresponding time scale is

$$t_0={\displaystyle \frac{m{l}^2}{\hslash }}$$

(22)

We define dimensionless variables

$$\begin{array}{c}\hfill \chi ={\displaystyle \frac{x}{l}},\tau ={\displaystyle \frac{t}{t_0}},\delta ={\displaystyle \frac{D}{l}},s={\displaystyle \frac{\sigma }{l}}.\end{array}$$

(23)

The dimensionless Schrödinger equation for the free propagation becomes

$$i{\partial }_{\tau }\psi (\chi ,\tau )=(-{\displaystyle \frac{1}{2}}{\partial }_{\chi }^2+\chi )\psi (\chi ,\tau ),$$

(24)

with the turning point at ${\chi }_{max}={\displaystyle \frac{E}{Fl}}$.

In these units, the replication rate density simplifies to

$$\Gamma \left(\delta \right)={\displaystyle \frac{{\lambda }^2}{\hslash l}}\tilde{k}\int d\tau {|\int d\chi g_s(\chi -\delta )\psi {(\chi ,\tau )}^3|}^2,$$

(25)

where $g_s$ is the dimensionless kernel and $\tilde{k}$ is a dimensionless overlap constant. Thus, the problem is governed primarily by the ratios $ϵ={\displaystyle \frac{E}{Fl}}$ (energy-to-force scale), $\nu ={\displaystyle \frac{V_0}{Fl}}$ (potential offset), and $s=\sigma /l$ (interaction range). This reduction shows that replication probability depends only on a small set of dimensionless parameters, rather than the absolute values of m, F, and E.

Validity and Limitations: Our formulation is deliberately minimal and therefore subject to several important limitations:

• Perturbative validity. All results are derived at leading (Born) order in the coupling $\lambda$. This approximation is valid as long as the replication probability per passage satisfies $P_{rep}\ll 1$. In this regime back-reaction and higher-order multiparticle processes can be neglected. For larger $\lambda$ or repeated passages, one would require a full kinetic or master-equation treatment.
• Finite interaction range. The replacement of a pointlike $\delta (x-D)$ by a finite kernel $g_{\sigma }(x-D)$ regularizes the interaction and introduces the physically meaningful length scale $\sigma$. Predictions depend weakly on $\sigma$ over a broad range, but a full microscopic model would be needed to determine it quantitatively.
• Energy supply. Replication requires an external energy input, modeled here phenomenologically by the coupling constant and overlap factor ($\lambda$, k). The “cell” or reservoir that supplies this energy is not explicitly included in the Hamiltonian. In a more complete description, one would couple the core particle to an explicit bath or ancilla system.
• No-cloning consistency. The daughters are created in a fixed, prepared internal state determined by the vertex. The process does not clone an arbitrary unknown quantum state and is therefore consistent with the quantum no-cloning theorem.
• Dimensional reduction. The model treats only the one-dimensional center-of-mass motion of the core. Internal degrees of freedom, orientation, and environmental decoherence are neglected. Inclusion of these effects would modify quantitative outcomes but not the qualitative dependence on the control ratios $E/F$, $V_0/E$ and $\sigma /l$.
• Closed-system assumption. The present treatment assumes coherent Schrödinger evolution up to the replication event. In realistic biological or experimental systems, coupling to an environment would introduce decoherence and dissipation. A Lindblad or master-equation extension would be required to capture these effects.

Simulation Setup: The time-dependent Schrödinger equation was solved using the standard split-operator Fourier method with absorbing boundary conditions [17]. The algorithm is unitary and well-suited for smooth potentials; details of the implementation are provided in Appendix A. The spatial domain was taken as $x\in [-L,L]$ with $L=200$ (dimensionless units), discretized on a uniform grid of $N=2048$ points. The time step was chosen as $\Delta t=5\times {10}^{-3}$, and wavefunction snapshots were stored every 20 time steps for subsequent post-processing. This ensures adequate resolution both in configuration and momentum space while keeping numerical dispersion and Trotter splitting errors negligible on the simulated time scales.

The initial state was a normalized Gaussian wavepacket,

$$\psi (x,t=0)={\left({\displaystyle \frac{1}{\pi {\sigma }_0^2}}\right)}^{1/4}exp[-{\displaystyle \frac{{(x-x_0)}^2}{2{\sigma }_0^2}}]exp\left(i{k}_{0}x\right),$$

(26)

with initial position $x_0=0$, width ${\sigma }_0=3$, and central wavenumber $k_0=5$. These parameters correspond to an initial kinetic energy $E_0={\displaystyle \frac{{\hslash }^2{k}_0^2}{2m}}$ and a classical turning point at $x_{t}urn=E_0/F$, where F is the constant force associated with the linear potential. Unless stated otherwise, we used $\hslash =1$, $m=1$, and $F=1$ to work in fully nondimensionalized units.

The potential was taken as

$$V\left(x\right)=Fx,$$

(27)

so that the wavepacket initially propagates in the positive x-direction and decelerates until reaching the turning point, reproducing the Airy-like behavior characteristic of a particle in a uniform field.

A Gaussian kernel

$$g_{\sigma }(x-\delta )={\displaystyle \frac{1}{\sqrt{2\pi }\sigma }}exp[-{\displaystyle \frac{{(x-\delta )}^2}{2{\sigma }^2}}]$$

(28)

with $\sigma =0.5$ was used to model the localized interaction with a target placed at position $\delta$. For each stored time step, the integral

$$I(\delta ,t)=\int g_{\sigma }(x-\delta ){\psi }^3(x,t)dx$$

(29)

The intensity $I(\delta ,t)$ was calculated for a range of $\delta$ values and the intensity ${\left|I(\delta ,t)\right|}^2$ was plotted as a function of $\delta$ and the time to obtain heatmaps of replication intensity.

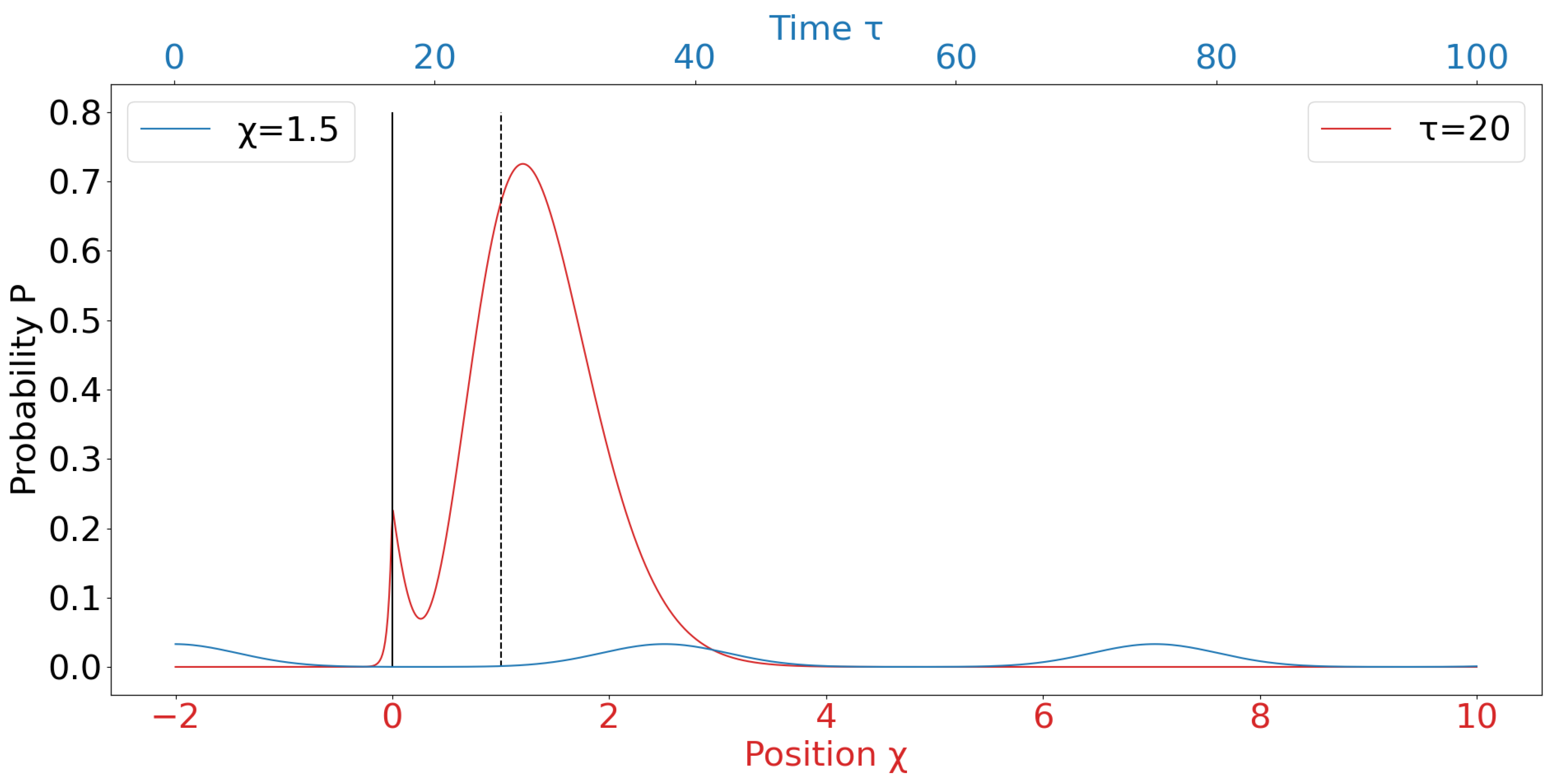
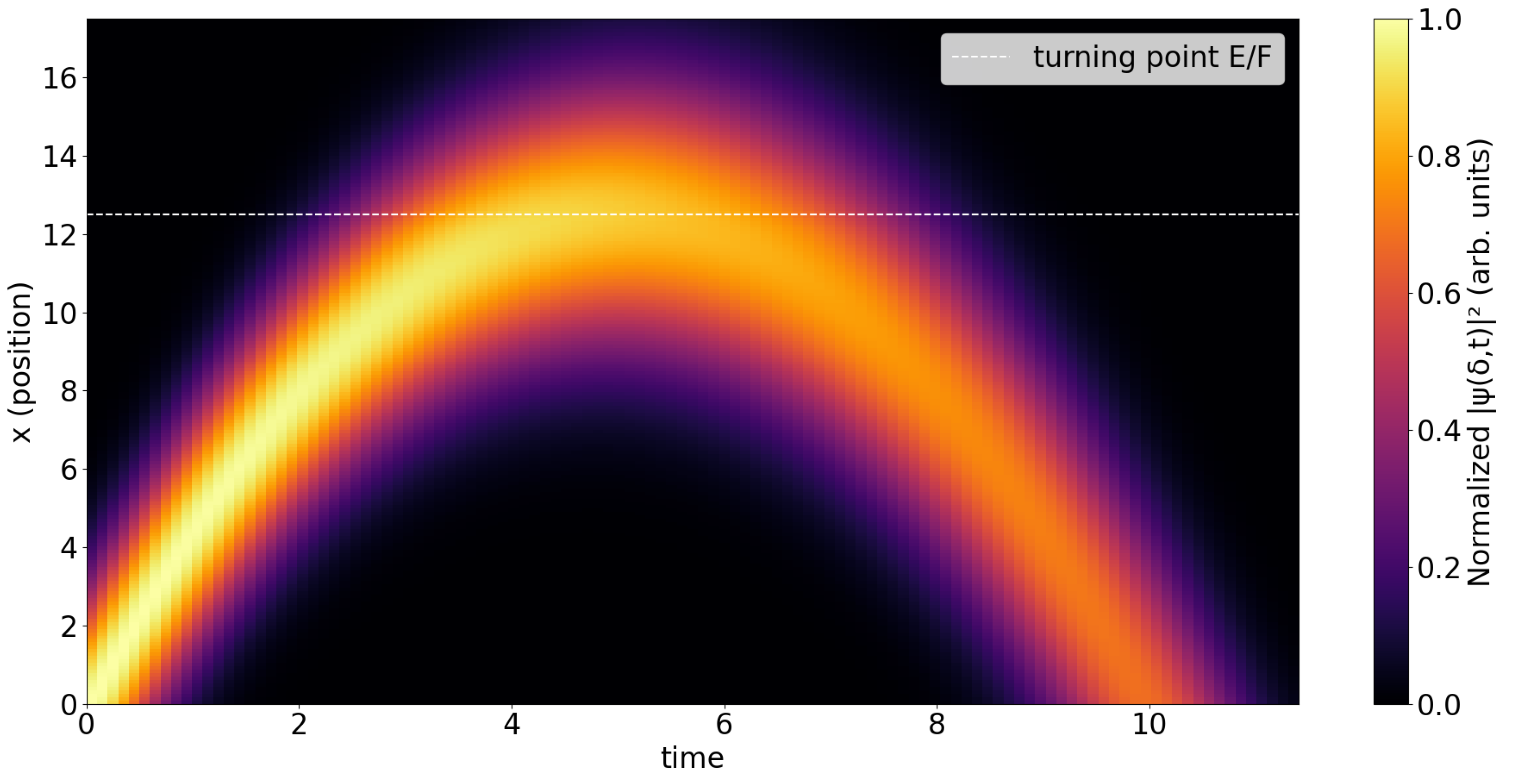
Fig. 4 shows the probability density heatmap,

$$P(x,t)=\int g_{\sigma }(x^{\prime }-x){\left|\psi (x^{\prime },t)\right|}^{2}d{x}^{\prime },$$

(30)

which reveals the parabolic trajectory of the wavepacket’s center of mass under the linear potential. The diagonal structure (from initial position toward the turning point) corresponds to the classical propagation of the wavepacket, while the gradual spreading reflects dispersion. The bright parabolic structure corresponds to the classical propagation of the wavepacket under a linear potential. The arrival time at each x increases monotonically, as expected for ballistic motion with constant acceleration. The signal diminishes after the turning point, where the wavepacket is reflected.

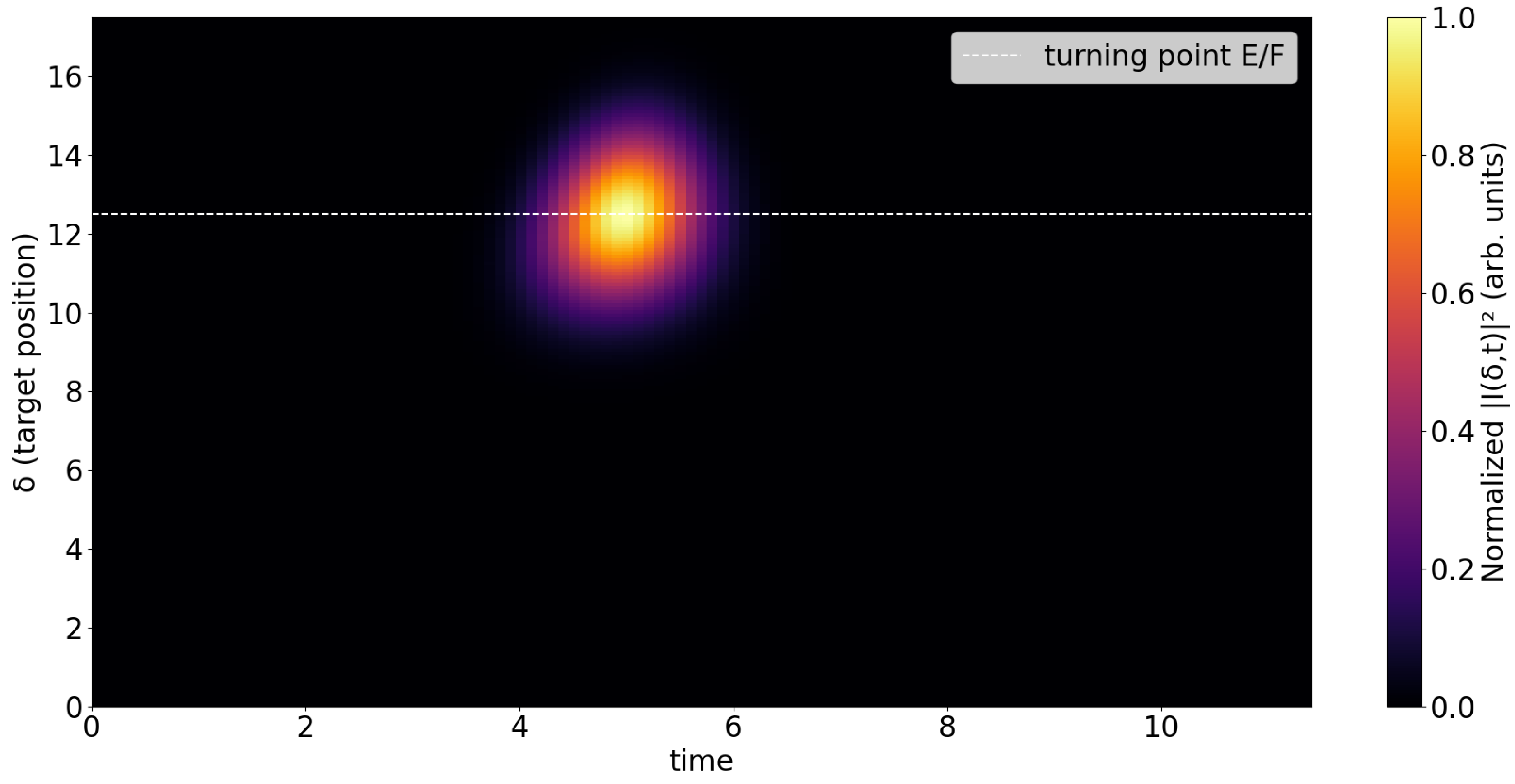
Fig. 5 shows the heatmap of ${\left|I(\delta ,t)\right|}^2$ as a function of target position $\delta$ and time t. Unlike the probability density, this quantity reflects nonlinear phase-sensitive interactions. The signal is localized around specific $\delta$ and t values, typically near the classical turning point, where the wavepacket overlaps maximally with the kernel and the cubic phase contributions interfere constructively. This figure highlights the regions where replication is most likely to occur, rather than the wavepacket’s full trajectory.

In both figures, the horizontal dashed line marks the expected turning point position $x_{turn}=E_0/F$. The probability density heatmap clearly tracks the propagation, while the replication intensity is concentrated near the turning region, consistent with the cubic dependence of $I(\delta ,t)$ on the local wavefunction amplitude.A systematic scan over the coupling $\lambda$ and kernel width $\sigma$ can be performed within the same framework and will be explored in future work. Preliminary checks show that the qualitative dynamics are robust to moderate variations of these parameters.

4. Discussion and Conclusions

We have presented a quantum-mechanical framework for modeling self-replicating core–shell systems. The model begins with a core confined by a potential barrier representing the shell. When the barrier dissipates, the core propagates under a linear potential toward a localized interaction region, where an effective cubic coupling leads to its annihilation and the creation of replicas.

The system was first analyzed in the single-particle Schrödinger picture to describe confinement and propagation, and then extended to a quantum-field formalism using creation and annihilation operators to represent replication as a $1\to 2$ branching process. The model’s contribution is primarily conceptual: it demonstrates how standard quantum processes (linear propagation and cubic interaction) can be interpreted as analogs of reproduction and branching within a consistent Hamiltonian framework.

Numerical simulations based on the split-operator method show that the replication intensity ${\left|I(\delta ,t)\right|}^2$ is concentrated near the classical turning point of the wavepacket, where the overlap between the core and the target kernel is maximal. The probability-density heatmap follows the expected parabolic trajectory under the uniform force, confirming the model’s internal consistency.

Together, these results demonstrate how unitary quantum dynamics can, in principle, describe replication-like processes without invoking non-quantum mechanisms. The framework may provide a starting point for exploring quantum analogs of reaction–diffusion and birth–death dynamics, as well as potential applications in synthetic quantum systems and open-quantum-system modeling.