Understanding how biological systems maintain their extraordinary complexity remains a major challenge in science. This paper presents a highly speculative theoretical framework: a hypothetical informational field—analogous in spirit to dark matter—that may influence biological and possible future artificial systems through hidden attractors operating at the quantum level. These attractors are hypothesized to modulate probability distributions beyond the standard Born rule, potentially guiding processes such as protein folding, DNA repair, or neural coherence. The framework connects concepts from quantum biology, complexity theory, and dynamical systems, and offers testable predictions using current spectroscopic and quantum sensing techniques. It also outlines implications for artificial intelligence, suggesting that future self-organizing architectures may require integration of non-classical informational dynamics.
1. Introduction
The probability paradox of life's emergence and continued existence has been extensively documented in recent literature [
1,
2]. Statistical analyses of spontaneous RNA formation demonstrate extraordinarily low probabilities (approximately 1:10
78 for 40-100 monomer autocatalytic RNA) that challenge conventional explanations based purely on random processes and natural selection [
3]. While various hypotheses have been proposed to address this paradox, including extended statistical ensembles through cosmic inflation scenarios [
1], these approaches remain fundamentally probabilistic and fail to address the broader question of biological complexity maintenance across multiple organizational levels.
Contemporary complexity theory, pioneered by Prigogine and colleagues [
4,
5], has made significant advances in understanding
self-organization and emergent phenomena. However, as noted by recent work in systems biology and artificial intelligence [
6,
7], current models of emergence and autopoiesis [
8] remain incomplete in explaining the remarkable stability and convergent evolution observed in biological systems. The limitations of purely reductionist approaches have been increasingly recognized in both biological systems research and artificial intelligence development [
9,
10].
Recent advances in quantum biology have revealed quantum coherence effects in biological processes such as photosynthesis [
11], avian navigation [
12], and potentially in neural microtubules [
13]. These discoveries suggest that quantum mechanical effects may play a more significant role in biological organization than previously recognized, opening new avenues for theoretical exploration. Simultaneously, developments in artificial intelligence, particularly in deep learning architectures and emergent behaviors in large language models [
14,
15], have highlighted the gap between artificial and biological information processing systems.
This paper proposes a novel theoretical framework that extends complexity theory through the introduction of "dark information" - an informational field that manifests through "hidden attractors" to influence biological organization and potentially artificial systems. This framework draws inspiration from the successful application of hypothetical entities (dark matter and dark energy) in cosmology [
16] while addressing fundamental questions about the nature of information processing in both biological and artificial systems. We emphasize that this framework remains highly speculative and requires extensive experimental validation.
2. Theoretical Framework: Dark Information and Hidden Attractors
2.1. Conceptual Foundation
The concept of
dark information emerges from the recognition that biological systems exhibit organizational principles that cannot be fully explained by current physical and chemical theories alone. Similar to how dark matter and dark energy were proposed to explain astronomical observations that could not be accounted for by visible matter and known forces [
17], dark information represents a hypothetical informational substrate that influences biological organization through mechanisms not yet fully characterized by contemporary science.
Hidden attractors, in the context of this framework, represent stable organizational states that direct molecular and cellular interactions toward specific configurations. Unlike traditional attractors in dynamical systems theory [
18], hidden attractors operate through quantum-level modulations of probability distributions, particularly through subtle deviations from Born's statistical rule [
19]. This approach is consistent with recent developments in quantum information theory and its applications to biological systems [
20].
2.2. Mathematical Formulation
The influence of dark information on biological processes can be mathematically expressed through modifications to standard quantum mechanical probability calculations. The probability of a given biological process (such as correct protein folding or DNA repair) can be formulated as:
where:
Pstatistical represents the conventional quantum mechanical probability (Born rule)
f(HA, N, Q, E) represents the contribution of hidden attractors
N is the number of interacting particles
Q represents the degree of quantum coherence/entanglement
E represents environmental factors (temperature, pH, electromagnetic fields)
The function f can be further specified based on system characteristics:
where k is a fundamental constant characterizing the strength of dark information coupling,α and β are scaling exponents that may vary with system type, and g(E) represents environmental modulation factors.
Note: This mathematical formulation represents a conceptual framework rather than a precisely defined equation. The specific forms of the scaling exponents α, β and the environmental function g(E) remain to be determined through empirical investigation.
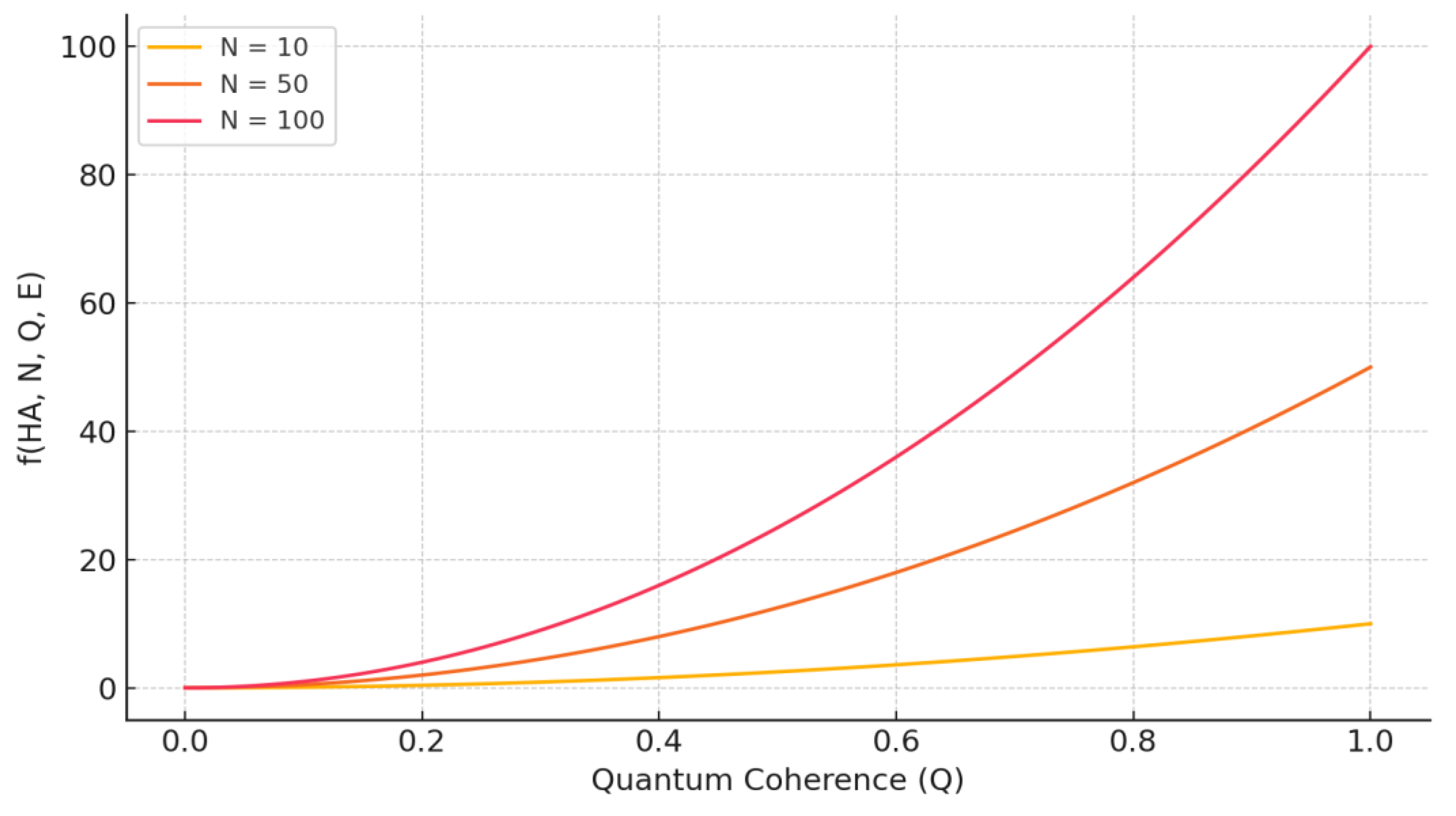
Figure 1.
The graph shows how the function f increases with quantum coherence Q for different particle counts N. The function reaches higher values for systems with more particles. The parameter values were chosen for illustrative purposes: α = 1, β = 2, g(E) = 1. In real biological systems, the particle count N can reach into the billions (N ~ 10⁹ or higher), and the actual values of α, β, and g(E) may vary significantly depending on the specific biological context.
Figure 1.
The graph shows how the function f increases with quantum coherence Q for different particle counts N. The function reaches higher values for systems with more particles. The parameter values were chosen for illustrative purposes: α = 1, β = 2, g(E) = 1. In real biological systems, the particle count N can reach into the billions (N ~ 10⁹ or higher), and the actual values of α, β, and g(E) may vary significantly depending on the specific biological context.
This formulation allows for testable predictions while remaining consistent with established quantum mechanical principles in limiting cases where dark information effects become negligible. Figure 2 illustrates the hypothetical relationship between biological and artificial organization.
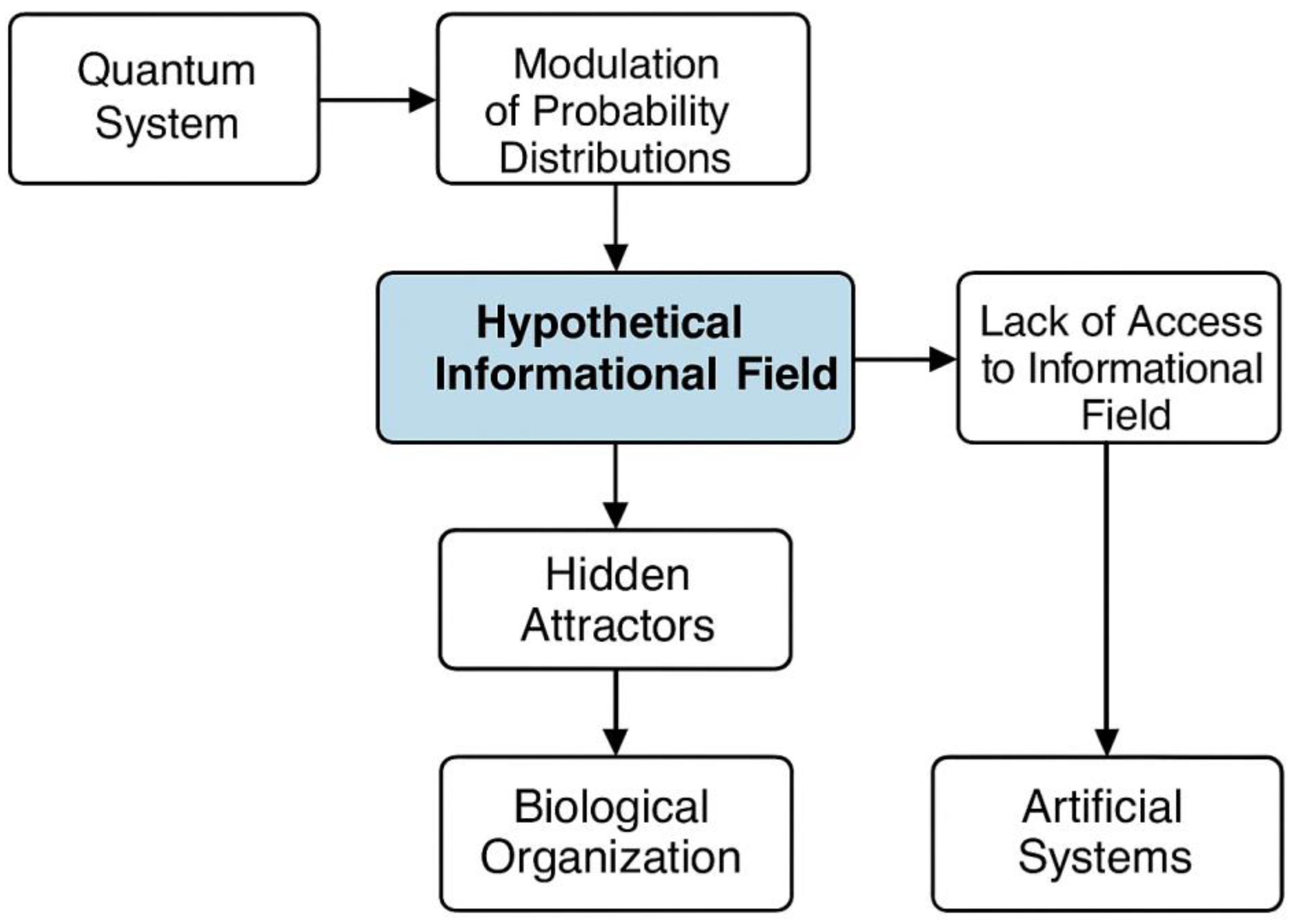
Figure 2.
Conceptual comparison between biological and artificial systems. On the left, a biological system is shown as being hypothetically influenced by an underlying informational field via hidden attractors. This influence is represented in the model by an additional term in the probability expression: Pbiological=Pstatistical + f(HA,N,Q,E). On the right, an artificial system lacks access to such hidden informational dynamics and relies solely on classical computation, modeled by: Partificial=Pstatistical.
Figure 2.
Conceptual comparison between biological and artificial systems. On the left, a biological system is shown as being hypothetically influenced by an underlying informational field via hidden attractors. This influence is represented in the model by an additional term in the probability expression: Pbiological=Pstatistical + f(HA,N,Q,E). On the right, an artificial system lacks access to such hidden informational dynamics and relies solely on classical computation, modeled by: Partificial=Pstatistical.
2.3. Relationship to Artificial Intelligence Systems
The dark information framework provides insights into
fundamental differences between biological and artificial information processing systems. Current AI architectures, including advanced deep learning networks and large language models [
21,
22], rely primarily on computational algorithms operating within classical information theory frameworks. In contrast, biological systems may utilize dark information through quantum coherence mechanisms that are not replicated in current artificial systems.
This distinction suggests potential pathways for developing more robust and self-organizing AI systems that incorporate quantum coherence effects and hidden attractor dynamics. Recent work in quantum machine learning [
23] and neuromorphic computing [
24] provides preliminary evidence for the viability of such approaches.
3. Experimental Predictions and Validation Protocols
3.1. Protein Folding Studies
The dark information hypothesis predicts specific deviations in protein folding kinetics and thermodynamics that should be detectable through advanced spectroscopic techniques. Nuclear magnetic resonance (NMR) spectroscopy should reveal energy state anomalies on the order of 10
-6 eV, representing subtle but measurable deviations from classical folding models [
25].
Experimental protocols should compare folding kinetics in systems with varying degrees of quantum coherence, potentially through controlled electromagnetic field exposure or isotopic substitution experiments. Temperature-dependent studies could reveal non-classical temperature scaling that indicates hidden attractor influence.
3.2. DNA Repair Mechanisms
Hidden attractors should manifest in DNA repair systems through enhanced repair accuracy and novel kinetic profiles. Comparative studies of repair efficiency in vivo versus in vitro systems could reveal systematic differences attributable to dark information effects [
26]. Topoisomerase activity studies, particularly regarding chromatin conformation changes, offer specific targets for experimental investigation [
27].
3.3. Quantum Coherence in Biological Systems
Recent developments in quantum biology provide experimental frameworks for testing dark information effects. Studies of quantum coherence in photosynthetic complexes [
11], magnetoreception mechanisms [
12], and potentially in neural systems [
28] could reveal signatures of hidden attractor influence.
Advanced quantum sensing techniques, including nitrogen-vacancy center magnetometry and superconducting quantum interference devices (SQUIDs), offer sufficient sensitivity to detect the subtle quantum coherence modulations predicted by the dark information framework [
29].
3.4. Artificial Intelligence Applications
The framework suggests specific modifications to AI architectures that could enhance performance and robustness. Quantum-inspired neural networks incorporating coherence mechanisms could potentially access hidden attractor dynamics [
30]. Comparative studies between classical and quantum-enhanced AI systems could provide indirect evidence for dark information effects in biological systems.
Table 1 presents theoretical predictions of the dark information framework across various domains.
Table 1.
Summary of predicted phenomena associated with the hypothetical informational field across different domains. The table outlines specific biological and artificial contexts in which the influence of hidden attractors may manifest, along with suggested experimental or observational methods for detecting such effects. While speculative, these predictions offer potential entry points for empirical testing of the proposed framework.
Table 1.
Summary of predicted phenomena associated with the hypothetical informational field across different domains. The table outlines specific biological and artificial contexts in which the influence of hidden attractors may manifest, along with suggested experimental or observational methods for detecting such effects. While speculative, these predictions offer potential entry points for empirical testing of the proposed framework.
| Field |
Hypothesis Prediction |
Possible Measurable Deviation / Method |
| Protein folding |
Non-standard folding kinetics under high coherent conditions |
NMR spectra, isotope effects |
| DNA repair |
Higher accuracy than predicted by classical models |
In vivo vs in vitro comparison |
| Quantum biology |
Coherence lasting longer than decoherence limit |
NV center magnetometry, SQUID detection |
| Artificial intelligence |
Lack of self-organization without access to informational field |
Comparison of classical and quantum-inspired systems |
4. Implications for Complex Systems Theory
4.1. Extensions to Complexity Theory
The dark information framework
extends contemporary complexity theory by providing a mechanism for information-driven self-organization that operates independently of environmental pressures. This addresses long-standing questions about the apparent directionality of evolutionary processes and the emergence of complex biological structures [
31].
The
framework is compatible with established complexity theory concepts such as emergence, autopoiesis, and self-organization while providing additional mechanisms for understanding these phenomena. It particularly addresses the "hard problem" of biological complexity - how organized structures can emerge and persist in apparent violation of thermodynamic principles [
32].
4.2. Relationship to Chaos Theory and Dynamical Systems
Hidden attractors, as defined in this framework, represent a novel class of attractors in dynamical systems theory. Unlike classical attractors that emerge from deterministic dynamics, hidden attractors operate through quantum-level probability modulations that create organizing influences not captured by classical phase space analysis [
33].
This extension of attractor theory has implications for understanding complex biological rhythms, developmental processes, and ecosystem dynamics. It also suggests new approaches to controlling and predicting complex system behavior in both biological and artificial contexts.
5. Philosophical and Theoretical Implications
5.1. Information-Theoretic Foundations
The dark information hypothesis raises fundamental questions about the nature of information in physical systems. It suggests that information may have a more fundamental role in physical processes than currently recognized, potentially requiring extensions to information theory analogous to those required in cosmology with dark matter and dark energy [
34].
This perspective aligns with recent developments in digital physics and information-theoretic approaches to quantum mechanics [
35], while extending these concepts to biological and potentially artificial systems.
5.2. Implications for Artificial Intelligence Development
The framework suggests that current AI systems may be fundamentally limited by their reliance on classical information processing architectures. True artificial general intelligence may require incorporation of quantum coherence mechanisms and hidden attractor dynamics that are naturally present in biological systems but absent from current artificial architectures [
36].
This has practical implications for AI safety, robustness, and capability development, suggesting research directions that could lead to more stable and self-maintaining artificial systems.
6. Future Research Directions
6.1. Experimental Validation
Priority should be given to developing experimental protocols capable of detecting the subtle quantum coherence modulations predicted by the dark information framework. This includes:
Advanced spectroscopic studies of protein folding with quantum coherence monitoring
Comparative studies of biological process efficiency under controlled quantum decoherence conditions
Development of artificial systems incorporating quantum coherence mechanisms
Long-term stability studies of biological versus artificial complex systems
6.2. Theoretical Development
Further theoretical work should focus on:
Detailed mathematical formulations of hidden attractor dynamics
Integration with established quantum field theory and statistical mechanics frameworks
Development of computational models incorporating dark information effects
Exploration of connections to fundamental physics theories including string theory and extra-dimensional models
6.3. Applications to Artificial Intelligence
Research should explore:
Quantum-enhanced machine learning architectures
Self-organizing AI systems incorporating hidden attractor dynamics
Biomimetic approaches to artificial intelligence based on dark information principles
Hybrid biological-artificial systems for testing theoretical predictions
7. Conclusion
The dark information framework presents a novel approach to understanding biological complexity that extends contemporary complexity theory while offering testable predictions for experimental validation. By proposing that biological systems access organizational information through quantum coherence mechanisms not present in current artificial systems, the framework addresses fundamental questions about the nature of life and intelligence.
The theoretical implications extend beyond biology to artificial intelligence development, suggesting new approaches to creating more robust and self-organizing artificial systems. While the framework remains hypothetical, it provides specific experimental predictions that could validate or refute the existence of dark information effects.
Future research based on this framework could lead to revolutionary advances in synthetic biology, quantum computing, and artificial intelligence, while providing deeper insights into the fundamental nature of information processing in complex systems. The framework ultimately suggests that the distinction between biological and artificial systems may lie not merely in their physical substrate, but in their access to fundamental organizational information that shapes the emergence and maintenance of complexity.
Acknowledgments
The author thanks colleagues for discussions that shaped this work. This research was conducted independently without institutional funding. Some passages of this manuscript were prepared or refined with the assistance of a large language model (LLM). The author takes full responsibility for the content and conclusions presented herein.
References
- Totani, T. Emergence of life in an inflationary universe. Sci Rep10, 1671 (2020). [CrossRef]
- Kauffman, S. A. The Origins of Order: Self-Organization and Selection in Evolution. (Oxford University Press, 1993).
- Joyce, G. F. The antiquity of RNA-based evolution. Nature418, 214-221 (2002). [CrossRef]
- Prigogine, I. & Stengers, I. Order out of Chaos: Man's New Dialogue with Nature. (Bantam Books, 1984).
- Nicolis, G. & Prigogine, I. Self-Organization in Nonequilibrium Systems. (Wiley, 1977).
- Mitchell, M. Complexity: A Guided Tour. (Oxford University Press, 2009).
- Bar-Yam, Y. Dynamics of Complex Systems. (Addison-Wesley, 1997).
- Maturana, H. R. & Varela, F. J. Autopoiesis and Cognition: The Realization of the Living. (D. Reidel Publishing Company, 1980).
- Anderson, P. W. More is different. Science177, 393-396 (1972). [CrossRef]
- Laughlin, R. B. & Pines, D. The theory of everything. Proc. Natl. Acad. Sci. USA97, 28-31 (2000). [CrossRef]
- Engel, G. S. et al. Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature446, 782-786 (2007). [CrossRef]
- Ritz, T., Adem, S. & Schulten, K. A model for photoreceptor-based magnetoreception in birds. Biophys. J.78, 707-718 (2000). [CrossRef]
- Penrose, R. & Hameroff, S. Consciousness in the universe: A review of the 'Orch OR' theory. Phys. Life Rev.11, 39-78 (2014). [CrossRef]
- Brown, T. et al. Language models are few-shot learners. Adv. Neural Inf. Process. Syst.33, 1877-1901 (2020).
- Wei, J. et al. Emergent abilities of large language models. Trans. Mach. Learn. Res.2022 (2022).
- Weinberg, S. The cosmological constant problem. Rev. Mod. Phys.61, 1-23 (1989). [CrossRef]
- Peebles, P. J. E. & Ratra, B. The cosmological constant and dark energy. Rev. Mod. Phys.75, 559-606 (2003). [CrossRef]
- Strogatz, S. H. Nonlinear Dynamics and Chaos. (Westview Press, 2014).
- Born, M. Zur Quantenmechanik der Stoßvorgänge. Z. Phys.37, 863-867 (1926). [CrossRef]
- Lloyd, S. Quantum coherence in biological systems. J. Phys.: Conf. Ser.302, 012037 (2011). [CrossRef]
- Vaswani, A. et al. Attention is all you need. Adv. Neural Inf. Process. Syst.30, 5998-6008 (2017).
- Bommasani, R. et al. On the opportunities and risks of foundation models. arXiv preprint arXiv:2108.07258 (2021). arXiv:2108.07258 (2021).
- Biamonte, J. et al. Quantum machine learning. Nature549, 195-202 (2017). [CrossRef]
- Schuman, C. D. et al. Opportunities for neuromorphic computing algorithms and applications. Nat. Comput. Sci.2, 10-19 (2022). [CrossRef]
- Clore, G. M. & Iwahara, J. Theory, practice, and applications of paramagnetic relaxation enhancement for the characterization of transient low-population states of biological macromolecules. Chem. Rev.109, 4109-4139 (2009). [CrossRef]
- Hoeijmakers, J. H. DNA damage, aging, and cancer. N. Engl. J. Med.361, 1475-1485 (2009). [CrossRef]
- Pommier, Y., Sun, Y., Huang, S. N. & Nitiss, J. L. Roles of eukaryotic topoisomerases in transcription, replication and genomic stability. Nat. Rev. Mol. Cell Biol.17, 703-721 (2016). [CrossRef]
- Lambert, N. et al. Quantum biology. Nat. Phys.9, 10-18 (2013). [CrossRef]
- Degen, C. L., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys.89, 035002 (2017). [CrossRef]
- Schuld, M. & Petruccione, F. Supervised Learning with Quantum Computers. (Springer, 2018).
- Gould, S. J. Wonderful Life: The Burgess Shale and the Nature of History. (W. W. Norton, 1989).
- Schrödinger, E. What is Life? The Physical Aspect of the Living Cell. (Cambridge University Press, 1944).
- Leonov, G. A. & Kuznetsov, N. V. Hidden attractors in dynamical systems. From hidden oscillations in Hilbert-Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurcation Chaos23, 1330002 (2013). [CrossRef]
- Wheeler, J. A. Information, physics, quantum: The search for links. Proc. 3rd Int. Symp. Foundations of Quantum Mechanics354, 309-336 (1989).
- Lloyd, S. Programming the Universe: A Quantum Computer Scientist Takes on the Cosmos. (Knopf, 2006).
- Russell, S. & Norvig, P. Artificial Intelligence: A Modern Approach. 4th edn. (Pearson, 2020).
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).