The Geometry of Reality: Modeling Complex Systems with Cone and Funnel Structures

1. Introduction

Complex systems—ranging from galaxy formation to cellular behavior—are often described using disparate models across disciplines. This paper introduces a unified geometric framework built on the notion that cones and funnels represent essential resolution shapes for gradients, information compression, and field behavior. Inspired by classical geometry and modern observations, this approach does not replace existing models but offers a supplemental lens that identifies recurring structures across scale a.

2. Core Framework

The Faulkner Conical Method posits that three principles underlie the utility of cones in natural systems:

• Directional Collapse: Systems moving from high complexity toward constraint resolve directionally into cones.
• Resolution Geometry: Funnels and cones act as natural intermediaries between fields of high entropy and localized identity.
• Conical Invariance: Across scale, conical forms appear in black holes, tornadoes, vision cones, quantum collapse, and cellular morphogenesis—not as coincidence, but as underlying structural invariants.

3. Cross-Disciplinary Evidence

3.1. Cosmology

Accretion disks and black holes form natural funnels of matter collapse. Space-time itself curves in a conical gradient around gravitational wells. These are not merely artistic representations—they reflect real topological structures.

3.2. Biology

Morphogenesis in plants and cellular budding frequently occur in spiral-cone patterns. Neural attention in humans is modeled by visual cones, and auditory localization often follows a narrowing field of detection.

3.3. Thermodynamics and Entropy

Entropy gradients often express through radial expansion or inward collapse—each following an implied conical path as matter or heat disperses from or resolves toward equilibrium.

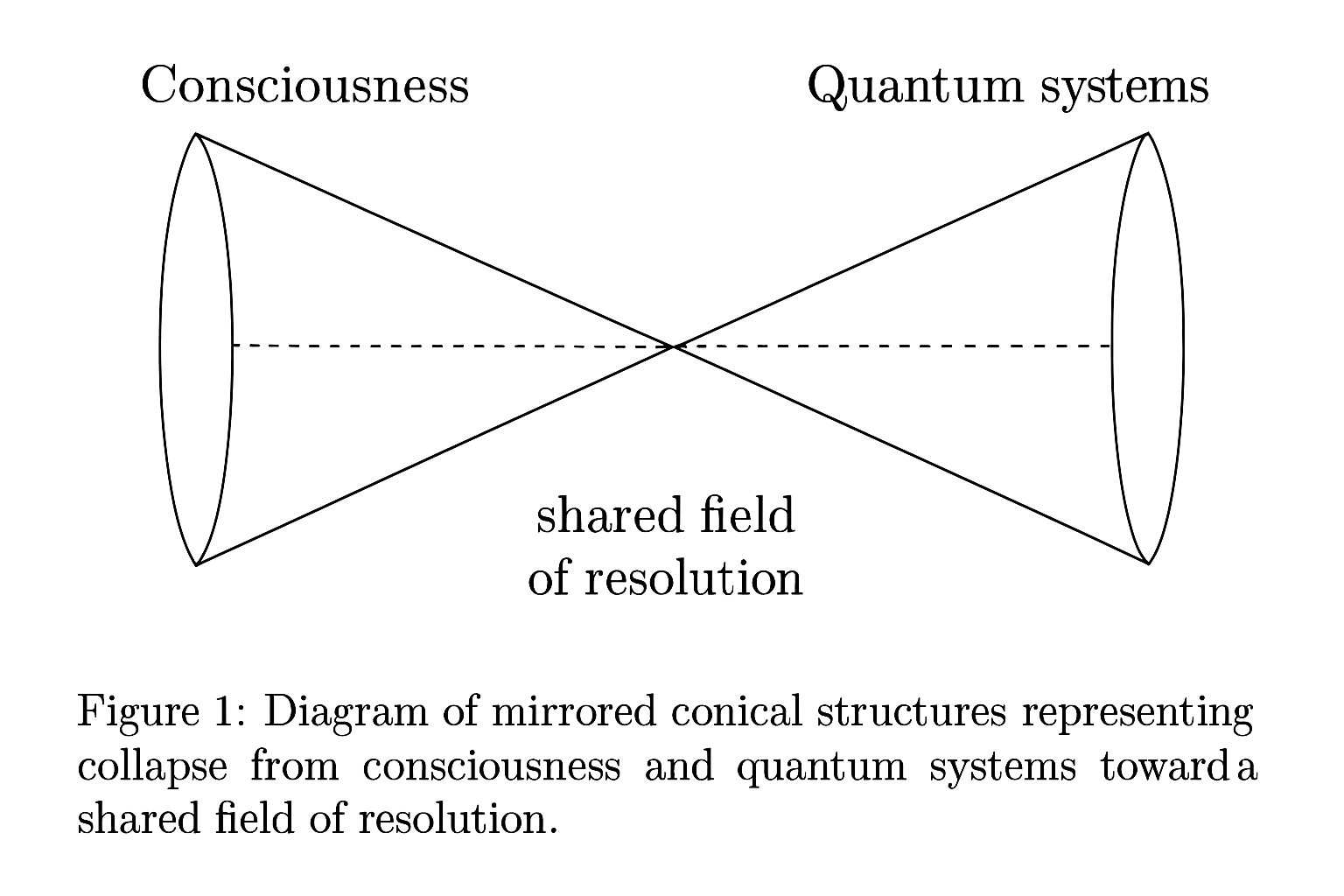
3.4. Quantum Mechanics

The measurement problem in quantum theory may be interpreted as a collapse into a conical funnel of resolution. Rather than wave function collapse being a drop-off, it may be geometrically directional—forming structured selection paths among entangled states.

4. Discussion

This framework provides not a single equation but a topological mapping tool—cones and funnels become reference shapes across diverse disciplines. The structure invites exploration into:

• Why complexity resolves into conical symmetry
• Whether collapse in quantum, physical, and cognitive systems shares a directional geometric identity
• If the mind’s perception structures emerge from conical filtering of environmental information

5. Conclusions

The Faulkner Conical Method is offered as a new geometric approach to understanding natural complexity. It does not claim to replace existing science but asks whether the commonality of conical forms across scale might reveal a missing universal structure behind collapse, motion, and identity formation. This proposal is intended to inspire further mathematical development and empirical testing.